Practical approach to subject-specific estimation of knee joint contact force

Abstract

Compressive forces experienced at the knee can significantly contribute to cartilage degeneration. Musculoskeletal models enable predictions of the internal forces experienced at the knee, but validation is often not possible, as experimental data detailing loading at the knee joint is limited. Recently available data reporting compressive knee force through direct measurement using instrumented total knee replacements offer a unique opportunity to evaluate the accuracy of models. Previous studies have highlighted the importance of subject-specificity in increasing the accuracy of model predictions; however, these techniques may be unrealistic outside of a research setting. Therefore, the goal of our work was to identify a practical approach for accurate prediction of tibiofemoral knee contact force (KCF). Four methods for prediction of knee contact force were compared: (1) standard static optimization, (2) uniform muscle coordination weighting, (3) subject-specific muscle coordination weighting and (4) subject-specific strength adjustments. Walking trials for three subjects with instrumented knee replacements were used to evaluate the accuracy of model predictions. Predictions utilizing subject-specific muscle coordination weighting yielded the best agreement with experimental data, however this method required in vivo data for weighting factor calibration. Including subject-specific strength adjustments improved models’ predictions compared to standard static optimization, with errors in peak KCF less than 0.5 body weight for all subjects. Overall, combining clinical assessments of muscle strength with standard tools available in the OpenSim software package, such as inverse kinematics and static optimization, appears to be a practical method for predicting joint contact force that can be implemented for many applications.

INTRODUCTION

Compressive forces experienced at the knee can have significant impact on cartilage degeneration and contribute to the initiation and progression of osteoarthritis (Blagojevic et al. 2010; Felson et al. 1988). As knee osteoarthritis progresses, causing pain and reduced function, the only effective treatment is knee arthroplasty, a costly and intensive procedure. Compressive forces continue to be relevant and arguably more important following knee arthroplasty, as these forces influence the wear, and therefore lifetime, of the implant. Subject-specific factors such as age, sex, body mass index and strength influence disease progression and are likely related to the magnitude of the knee loads which may be useful in the design of a treatment plan.

Traditionally, external knee loads have been used to estimate internal tibiofemoral knee contact forces (KCF) (Komistek et al. 2005), however it has been suggested more recently that external loads and electromyography are not good indicators of changes in knee contact forces (Meyer et al. 2013). The use of musculoskeletal models enables predictions of the internal forces experienced at the knee, namely the muscle, ligament and articular contact forces. Given the advantage of modeling for assessing knee loading, the accurate prediction of compressive force at the knee through musculoskeletal modeling can be a useful tool for understanding the mechanisms behind joint loading. Validating model results, however, is often not possible, as experimental data detailing loading at the knee joint is limited. Recently available data which directly measures compressive knee force using instrumented total knee replacements offer a unique opportunity to evaluate the accuracy of models.

Several groups have reported good agreement of model predicted knee compressive force with experimentally measured data, using a variety of methods (Kinney et al. 2013). Steele et al. (2012) used a weighted static optimization technique to find the optimal match between experimental (as measured by an instrumented knee implant) and simulated knee joint contact force (Steele et al. 2012). Using this technique, weighting constants for the quadriceps, hamstrings, and plantar flexor muscle groups were included to alter the distribution of muscle activations during the simulation, resulting in a 20% body weight difference between the peak experimental and model-predicted knee compressive force. However, the validation performed in this study focused on only one subject and it is unclear whether this method would result in similar accuracy when applied across multiple individuals. Other methods utilized subject-specific measurements included alongside the experimental knee contact force data to enhance the accuracy of model predictions. These subject-specific measurements include subject – specific geometry data obtained from CT scans (Gerus et al. 2013), or electromyography (EMG) measured during experimental collections (Manal & Buchanan 2013; Hast & Piazza 2013).

These previous studies have highlighted the importance of subject-specificity in increasing the accuracy of model predictions. These techniques, however, involve time-intensive data collection and processing, as well as access to expensive equipment and resources for imaging that may be unrealistic outside of a research setting. In addition, these techniques often employ complex models or algorithms that are not readily available outside of research settings (Manal & Buchanan 2013; Lundberg et al. 2013; Hast & Piazza 2013). In contrast to the prohibitive nature of some subject-specific measurements and techniques involving EMG or imaging, measurements involving maximum muscle strength are readily attainable in a clinical or research setting. Strength data has been shown to be related to multiple variables than can be influential when considering a subject’s gait such as walking speed, gender and age (Berger et al. 2012; Aagaard et al. 1997), and pain and function in knee osteoarthritis (O’Reilly et al. 1998). While it is unclear whether strength and joint contact force are directly correlated, it is possible that muscle strength influences knee joint contact force through its relationship with many gait related factors. Furthermore, the likelihood of a muscle to be recruited should be related to its strength, and should directly affect model predictions. Indeed, previous work has shown that simulated atrophy and activation failure in muscle groups can alter model predictions of muscle activations (Thompson et al. 2013; Knarr et al. 2013) and the use of experimentally measured, subject-specific muscle force data has shown increased accuracy of muscle activation predictions in other populations such as stroke (Knarr et al. 2014).

The importance of including subject-specific parameters into model predictions of knee joint contact force has been demonstrated in many recent studies, however previously reported methods have been either limited in scope or prohibitively complex to implement in common clinical settings. Therefore, the goal of our work was to identify a practical approach which enables accurate predictions of knee joint contact force without prohibitively increasing the complexity of the methodology. In this study we identified and evaluated four approaches for improving predictions of knee joint compressive force: (1) standard static optimization, (2) uniform muscle coordination weighting, (3) subject-specific muscle coordination weighting, and (4) subject-specific strength adjustments.

METHODS

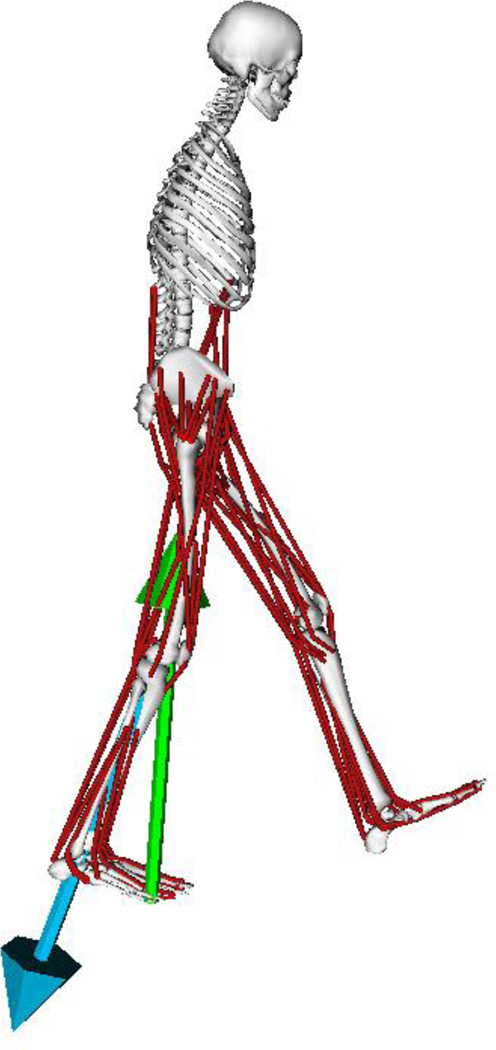
Three dimensional simulations were created from the stance phase of gait for 3 subjects with an instrumented knee implant using OpenSim 3.0.1 (Delp et al. 2007) (Table 1). Subject data were collected and distributed as part of the first three years of the Grand Challenge Competition to predict in vivo knee loads (Fregly et al. 2012) (Table 1). The implant was instrumented with either four uniaxial force transducers, one each in the four quadrants of the tibial tray, or a six-axis load cell in the stem of the tibial tray, with load cell measurements telemetered using a micro-transmitter and antenna. A previously developed musculoskeletal model of the lower body and torso was used, which included 92 actuators, with three degrees of freedom at the pelvis-torso and hip joints, and one degree of freedom at the knee, ankle and toe joints (Demers et al. 2014) (Figure 1). In addition, the model includes a frictionless patella which articulates with the femur as prescribed by knee angle and directs the quadriceps forces along the patellar ligament (Demers et al. 2014). Two to four walking trials were used for each subject, resulting in ten total walking trials. All analysis was focused on the limb with the instrumented knee.

Table 1.

Subject demographics, uniform and subject-specific weighting coefficients, and error between experimental and simulated joint contact forces. Errors expressed in terms of root mean squared error (RMSE), as well as first and second peak errors relative to body weight (BW) for four methods: standard optimization (SO), uniform weighting (UW), subject-specific weighting (SSW) and subject-specific strength (SSS). See text for details.

		Subject 1	Subject 2	Subject 3
Gender		M	M	F
Height (m)		1.66	1.72	1.67
Weight (kg)		64.6	67	78.4
Knee		R	R	L
Uniform Weights	PF	7	7	7
	H	3	3	3
	Q	1	1	1
Subject- Specific Weights	PF	2	2	1
	H	6	10	1
	Q	3	6	3
RMSE (BW)	SO	0.67	0.59	0.37
	UW	0.43	0.48	0.48
	SSW	0.34	0.41	0.33
	SSS	0.40	-	0.37
Peak 1 Error (BW)	SO	0.56	0.95	0.14
	UW	0.31	0.62	0.39
	SSW	0.11	0.22	0.24
	SSS	0.10	-	0.24
Peak 2 Error (BW)	SO	1.37	0.83	0.40
	UW	0.59	0.46	0.74
	SSW	0.01	0.15	0.09
	SSS	0.42	-	0.33

Figure 1.

Musculoskeletal model of the human legs and torso used for prediction of tibiofemoral knee contact force. Ground reaction force and predicted tibiofemoral knee contact force can be seen in green and blue, respectively.

Inverse kinematics was used to determine the model joint kinematics which creates a model position that best matches experimental data. Kinematics and kinetic data were filtered at 6 Hz. Simulations were created from heel strike to toe off of the instrumented limb and all data was reported for the instrumented limb. Four methods for prediction of knee joint contact force were compared.

Static Optimization

The muscle forces required to reproduce the measured kinematics and kinetics were calculated using static optimization in OpenSim with the default cost function minimizing the sum of the activations squared (Delp et al. 2007). Knee joint contact force was calculated using the muscle force results from static optimization using the joint reaction force tool in OpenSim and expressed in the tibial reference frame. Resultant knee contact forces were filtered at 10 Hz to minimize influence of high frequency changes in force during weight acceptance (prior to the first peak in KCF), arising from the discrete static optimization solution. Filtering was performed because high frequency changes were not present in the experimentally measured data, which may be dampened by soft tissue or filtered during processing.

Muscle coordination weighting: uniform and subject-specific

A weighted static optimization technique similar to Steele et al. (2012) was used to find the optimal match between experimental (as measured by the instrumented knee) and simulated knee joint contact force (Steele et al. 2012). Using this technique, weighting constants for the quadriceps, hamstrings, and plantar flexor muscle groups were included to alter the distribution of muscle activations during the simulation.

To investigate the generalizability of applying uniform muscle coordination weight across subjects to produce accurate predictions of knee contact forces during stance, two simulations were created per subject. The first simulation used the reported values for weighting constants for a single subject from previous literature (Steele et al. 2012). This method allows for us to investigate the generalizability of weighting constants across additional subjects and trials. For the second simulation, subject-specific weighting constants were determined using an optimization technique. While performing a subject-specific optimization using in vivo data is unlikely to be a practical and widely applicable methodology, it provides us with a “best case” scenario with which to compare the other, more generalizable methods. For this method, a pattern search optimization was performed to find an optimal set of weighting constants which minimize the difference between the experimental and simulated knee contact force across all trials for a subject simultaneously. The pattern search optimization was performed using MATLAB (Mathworks, Inc., Natick, MA) with an initial seed of one for all muscle groups using the GPS Positive basis 2N polling method, with a mesh tolerance of 0.99 and 40 maximum iterations. Initial seeds and other relevant optimization parameters were tested to ensure that the global minimum was found. This process was repeated for each of the three subjects.

Applying this set of weighting constants yields the subject-specific muscle coordination that best reproduces the knee contact force measured during the gait trials. A cost function of the sum of the root mean squared error (RMSE) across the stance phase of gait and the absolute errors in the first and fsecond peaks of KCF was used to optimize the values of the weight constants (Eq. 1):

$$J=RMSE+\left|E_{pk1}\right|+\left|E_{pk2}\right|$$ (1)

Subject-specific strength adjustments

Isometric knee extension and flexion strength data was collected for subjects 1 and 3 as part of the grand challenge to predict in vivo knee loads. Using the maximum torque generated during testing, the maximum isometric force parameter of the model was scaled for the quadriceps (rectus femoris, vastus medialis, vastus intermedius, and vastus lateralis.) and hamstrings (semimembranosus, semitendinousus, biceps femoris long head, and biceps femoris short head) muscle groups such that the model torque capacity was equal to the experimental data when in the same posture. Static optimization was run for all subject trials using the model with subject-specific strength. With this method, the forces predicted through static optimization for the quadriceps and hamstrings muscle groups are constrained to values that more closely reflect the subject’s capacity to produce force.

Statistical Analysis

The primary outcome for comparison across methods was the peak error between experimental and model predicted KCF at each of the two peaks in KCF which occur during the stance phase of gait. Peak KCF error was averaged across trials for each subject. In addition, the average RMSE between experimental and model predicted KCF over the entire stance phase was compared for each subject and method relative to body weight (BW). Average RMSE over the stance phase provides an assessment of overall shape and timing agreement between the experimental and simulated results. Optimized muscle coordination weights was compared to the uniform weight for each subject. Due to the low sample size of this dataset, traditional statistical analysis is not applicable. Instead, a qualitative analysis of the results was performed.

RESULTS

A total of 40 predictions of KCF were generated, with ten simulations for each of the 4 methods: Standard, uniform and subject-specific muscle coordination, and subject-specific strength adjustment.

Standard static optimization

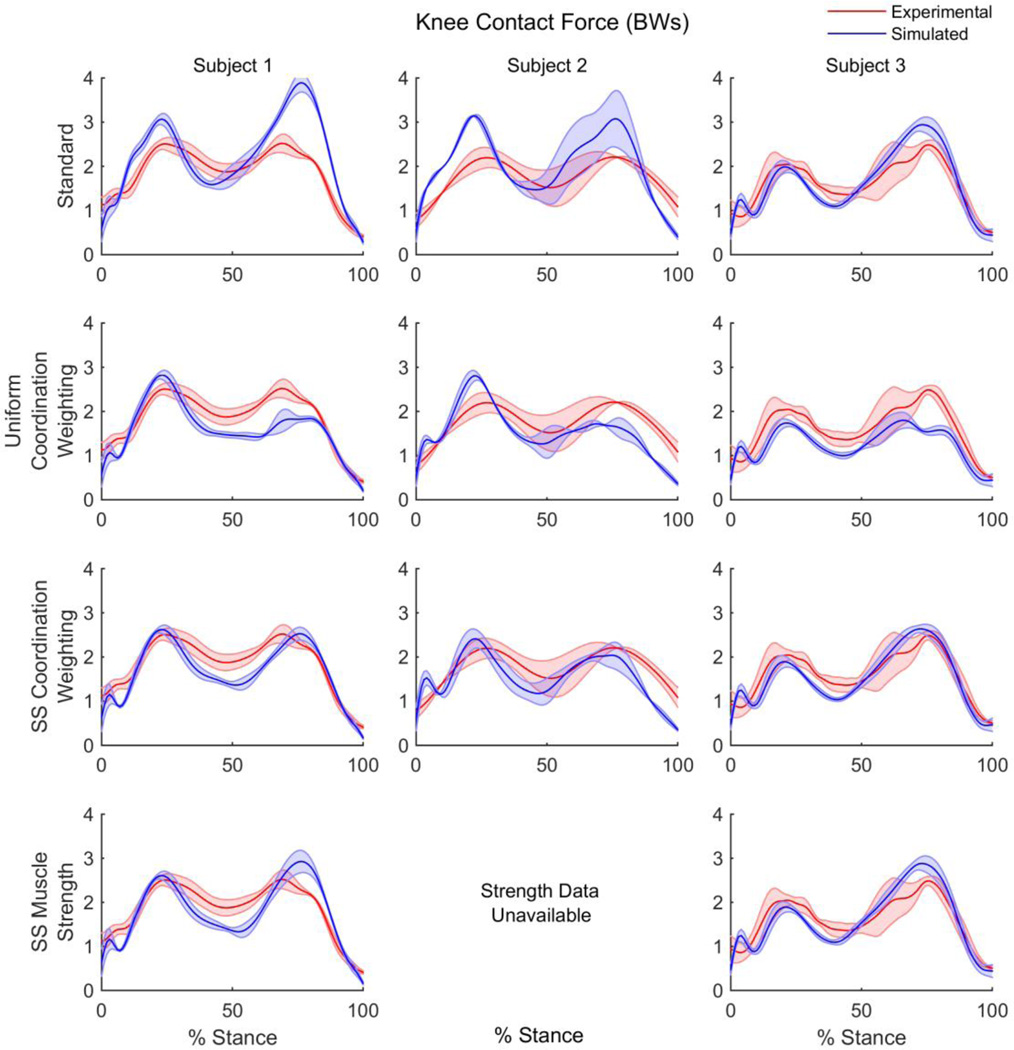
Using static optimization with all muscles weighted equally and the generic muscle strength included in the model, average error in the model predicted KCF for each subject ranged from 0.14–0.95 BW for the first peak and 0.4–1.37 BW for the second peak during stance (Figure 2, Table 1). Average RMSE ranged from 0.37–0.67 BW across the subjects.

Figure 2.

Experimental and simulated knee contact force during stance phase resulting from standard optimization, uniform muscle coordination weighting, subject-specific muscle coordination weighting and subject-specific muscle strength adjustments for three subjects.

Muscle coordination weighting: uniform and subject-specific

Using the same muscle coordination weights for all three subjects as reported by previous studies (Steele et al. 2012), predicted knee contact force decreased compared to the standard static optimization method, yielding errors of 0.31–0.62 BW for the first peak and 0.46–0.74 BW for the second peak. Average RMSE was consistent across the subjects, ranging from 0.43–0.48 BW.

After optimization of the muscle coordination weights on a subject-specific basis, errors were reduced to 0.11–0.24 BW for the first peak and 0.01–0.15 BW for the second peak. Optimization weights varied between subjects, with subjects 1 and 2 requiring significant hamstrings weighting, while subject 2 required the highest quadriceps weighting compared to a standard weight of 1. Average RMSE of the subject-specific muscle coordination weighting simulations were the lowest of all simulation methods ranging from 0.33–0.41 BW.

Subject-specific strength adjustments

Finally, after adjusting the model to include subject-specific strength from the quadriceps and hamstrings, and using the standard static optimization method, errors ranged from 0.1–0.24 BW in the first peak and 0.33–0.42 BW in the second peak. Average RMSE ranged from 0.37–0.4 BW.

DISCUSSION

This study assessed the accuracy of four methods of predicting knee joint contact force using musculoskeletal modeling by comparing the simulated forces to experimentally measured forces from instrumented tibial implants. Additionally, this study included data from 3 different individuals, which allowed us to test the generalizability of previously used methods across a population. Overall, the methods which included subject-specific information in the model (Subject-specific muscle coordination weighting and subject-specific strength) yielded predictions which were closer to the experimental data, suggesting that subject-specificity is important when modeling knee contact force. Although using subject-specific weight factors produced the most accurate predictions of joint contact force, this method relies on known loads to optimize the weight factors and is impractical for general use in individuals without instrumented knee implants. Furthermore, while the method of incorporating muscle strength into the model was less accurate than optimizing for muscle coordination, the combination of improved accuracy (< 0.5 BW error) and accessibility of the data may make this method ideal for clinical and research environments with limited resources.

The standard static optimization method produced generally poor agreement between the simulated and experimental knee contact force. One exception is subject 3, where the errors in the peak contact forces were less than 0.5 BW. There are several possible explanations for the poor agreement between knee contact force predictions using the standard static optimization algorithm and the experimental data. One possibility is that the default cost function for static optimization, minimization of the squared activation, is not appropriate for individuals with knee replacements, as they may employ unique coordination patterns. Secondly, the default OpenSim model, while subject-specific in skeletal anthropometrics and mass, may lack subject-specificity in properties that are unique to these individuals/population, such as muscle weakness.

The lowest errors between simulated and experimental knee contact force were produced from the subject-specific muscle coordination weighting method. This method was exceptionally accurate, producing errors as low as 0.01 BW at the second peak and within 0.41 BW across all subjects, however this method is not practical for most situations as it required in vivo experimental data to calibrate the coordination weights.

While using uniform muscle coordination resulted in lower absolute error compared to the standard static optimization method, errors remained greater than 0.5 BW for both the first and second peaks in knee contact force. This suggests that the muscle coordination weights obtained for one subject are not generalizable to other individuals. In addition, when solving for subject-specific muscle coordination weights in our study, the coordination weights were sensitive to the selected cost function (e.g. minimization of RMSE vs. RMSE + peak errors) as well as the data used (e.g. gait trials, stance vs. full gait cycle). Ultimately, we chose the cost function used in this study as it placed emphasis on accurately predicting the two peaks in knee contact force. This likely accounts for differences seen between the previously reported coordination weights (Steele et al. 2012) and the subject-specific weights calculated in this study.

The default OpenSim static optimization cost function minimizing the sum of the activations squared used in this study is often used for healthy gait (Crowninshield & Brand 1981), however it is unknown how applicable it is for individuals post total knee arthroplasty. Using the default OpenSim implementation avoided introducing further complexity to the methods, however future work to identify the most appropriate static optimization cost function is warranted. It is conceivable that the selection of static optimization cost function also contributes to the underestimation of tibial contact force in mid-stance seen in this and previous Grand Challenge winners (Kinney et al. 2013). For our simulations, the assumptions of static optimization lead to a minimization of co-activation. It is possible that co-activation during mid-stance may be present to help stabilize the knee, especially in a TKA population. Further investigation into the recorded EMG during these trials may help explain the mid-stance predictions.

Including subject-specific muscle strength in the model yielded similar, although slightly less accurate results compared to the subject-specific muscle coordination weighting method. This method, however, maintained errors less than 0.5 BW for both subjects with available data, and is significantly less intensive than other subject-specific methods that have been employed previously (Gerus et al. 2013; Steele et al. 2012). It is interesting to note that subject 3, who demonstrated the best agreement for the standard static optimization technique, had experimentally measured muscle strength values similar to the default model, and maintained a good prediction when incorporating this data. This is in contrast to subject 1, whose predicted knee contact force was markedly improved when accounting for the approximately 50% reduction in strength from the default values when incorporating subject-specific data.

Based on existing instrumented knee data sets, we postulate that using subject-specific strength measurements to inform a scaled musculoskeletal model yields predictions of peak knee contact force within 0.5 BW of measured values, with RMSE comparable to previously reported values for models using subjects from this dataset (Kinney et al. 2013). In contrast to previous studies, this study evaluated multiple trials across multiple subjects to help determine the generalizability of the methods across individuals. However, it is unknown whether the accuracy (i.e. 0.5 BW) reported in this and previous studies is sufficient to provide meaningful clinical application, especially with the low sample size available to develop and validate models. Despite this, it is important to note that the methodology used to generate these predictions is generally feasible for most clinical and research settings with motion capture capabilities. Without an accessible method to obtain knee contact force predictions, it would be difficult to implement on the large scale necessary to assess the effectiveness of predictions in a clinical environment. Strength assessment of the quadriceps and hamstrings is routinely performed in a clinical setting for individuals with knee pain or pathology and is simple to integrate into musculoskeletal models. Additionally, the use of OpenSim, an open-source software designed to make musculoskeletal modeling accessible, allows for models to be built without personnel with an extensive computational background. Combining clinical assessments of muscle strength with standard tools available in the OpenSim software package, such as inverse kinematics and static optimization, appears to be a practical method for predicting joint contact force which may provide useful insight for development of a treatment plan.