Development of an Algorithm to Classify Colonoscopy Indication from Coded Health Care Data

Abstract

Introduction:

Electronic health data are potentially valuable resources for evaluating colonoscopy screening utilization and effectiveness. The ability to distinguish screening colonoscopies from exams performed for other purposes is critical for research that examines factors related to screening uptake and adherence, and the impact of screening on patient outcomes, but distinguishing between these indications in secondary health data proves challenging. The objective of this study is to develop a new and more accurate algorithm for identification of screening colonoscopies using electronic health data.

Methods:

Data from a case-control study of colorectal cancer with adjudicated colonoscopy indication was used to develop logistic regression-based algorithms. The proposed algorithms predict the probability that a colonoscopy was indicated for screening, with variables selected for inclusion in the models using the Least Absolute Shrinkage and Selection Operator (LASSO).

Results:

The algorithms had excellent classification accuracy in internal validation. The primary, restricted model had AUC= 0.94, sensitivity=0.91, and specificity=0.82. The secondary, extended model had AUC=0.96, sensitivity=0.88, and specificity=0.90.

Discussion:

The LASSO approach enabled estimation of parsimonious algorithms that identified screening colonoscopies with high accuracy in our study population. External validation is needed to replicate these results and to explore the performance of these algorithms in other settings.

Introduction

Colorectal cancer (CRC) is the third leading cause of cancer mortality in the United States in both men and women.1 Colonoscopy is widely used for CRC screening, surveillance, and diagnosis.2 It is currently the predominant method of CRC screening in the United States,3 the single recommended test for surveillance of patients at elevated risk of CRC due to a personal history of adenomas, and the test used to follow up gastrointestinal (GI) signs and symptoms and abnormal outcomes detected by other CRC screening tests.2

Health care data sets are potentially valuable research resources for evaluating screening colonoscopy utilization, safety, and effectiveness. The data represent the routine clinical care received by large segments of the population. For purposes of this article we define “health care data” as being electronically formatted, secondary data originally generated in the course of routine health care, and minimally including standardized diagnosis and procedure codes—International Classification of Disease (ICD), Current Procedural Terminology (CPT), and Healthcare Common Procedure Coding System (HCPCS)—together with dates of service. Electronic health record databases may include additional, richer clinical data, such as laboratory results, physician orders, and narrative clinical progress notes.4

The standardized colonoscopy procedure codes included in health care databases have been shown to be accurate in identifying patients who have undergone colonoscopy,5,6 which is prerequisite for using the data in research. However a major limitation in using these data is that the procedure codes do not reliably distinguish between screening colonoscopies and those procedures conducted for diagnosis or surveillance purposes.7,8 Some CRC screening researchers have chosen to use health care data ignoring colonoscopy indication. This is equivalent to treating all colonoscopies as if they were intended for screening, which can bias study results.7,9–11

Other health services researchers have applied algorithms to distinguish between screening and nonscreening colonoscopies in their data.9,12–16 The algorithms take the form of decision rules, using GI-related ICD-9 diagnosis codes assigned prior to or at the time of the index colonoscopy, and CPT and HCPCS gastrointestinal (GI) procedure codes assigned prior to the colonoscopy. A typical algorithm classifies a colonoscopy as nonscreening if codes for GI signs, symptoms, conditions or procedures are present within the look-back period, and as screening otherwise (e.g., 9,13). But unfortunately none of the algorithms reported to date have demonstrated simultaneously high sensitivity and specificity in discriminating between screening and nonscreening colonoscopies.8,13,17–19

Earlier algorithms were based primarily on the researcher’s judgment. Recently two research groups developed new algorithms based on a hybrid approach. These groups used expert judgment to create initial lists of candidate variables, and then applied statistical methods to select smaller sets of classification variables to include in their final algorithms.8,19

Developers of algorithms have used various combinations of codes to represent GI-related health conditions and look-back intervals. Fisher et al. reported that test performance of colonoscopy indication algorithms differed substantially according to the specific codes included, and reported whether or not codes assigned the day of the procedure were counted.18 A challenge in developing a more accurate algorithm is the selection of the strongest classification variables from among the large number of plausible GI-related codes and combinations of codes available.

The purpose of this study was to develop new algorithms to identify screening colonoscopy in average-risk subjects using electronic health data. We used regression with Least Absolute Shrinkage and Selection Operator (LASSO) and tenfold cross-validation to identify the strongest classification variables while avoiding overfitting. This study was approved by the human subjects research review boards of all participating institutions.

Methods

We developed and tested two new algorithms to classify screening colonoscopies in electronic health data. The algorithms were developed using logistic regression models applied to an expert-adjudicated reference data set. The reference indication classifications were derived from the narrative text portions of electronic health records (EHRs)—clinical progress notes, referral notes, and procedure reports—of the patients of four health plans, whereas the procedure and diagnosis codes were taken from utilization records contained in the EHRs of these patients. We tested the performance of the algorithms using tenfold cross-validation, and we created receiver operating characteristic (ROC) curves to characterize test performance over a range of sensitivities and specificities.

Reference Data Set and Study Population

The reference data set contained adjudicated colonoscopy indication and GI-related diagnosis and procedure codes for 596 colonoscopies contributed by 493 distinct subjects. These data were originally collected for a case-control study evaluating the association between CRC screening and risk of late-stage CRC among average-risk patients of four health plans within the Cancer Research Network.20,21 The study population and methods for medical record data abstraction, classification of colonoscopy indication, and adjudication have been previously described.21,22

Eligible subjects for the case-control study from which the reference data were obtained were from 55 to 85 years old on their reference date between January 1, 2006, and December 31, 2008, and were enrolled for five or more years prior. Subjects were excluded from the case-control study if they had a strong family history of CRC (defined as a history of CRC in one or more first-degree relatives before age 50, in two or more second-degree relatives at any age, or a history of other familial syndromes), history of CRC or inflammatory bowel disease, or a total resection of the colon.

The reference colonoscopy classifications were based on clinical information extracted from patient clinical progress notes, referral reports, and colonoscopy reports available from EHRs. The initial classifications were assigned based on a set of decision rules; final classification was adjudicated by a panel of experts. For the current analysis, observations in the reference data set deemed to represent high risk screening or for which no indication could be determined were removed. Because it is common for individuals to be screened or tested periodically, we allowed multiple colonoscopies per subject. Among the 493 distinct subjects, 75 (12 percent) had two or more colonoscopies included in the reference data set (56 had two exams, 15 had three exams, 3 had four exams, and one had nine exams included, respectively).

We defined screening colonoscopy as an exam performed as a primary screening modality for CRC and colorectal adenomas; that is, the exam was not conducted to follow up another screening test (e.g., fecal-based tests, flexible sigmoidoscopy), to evaluate symptoms or GI conditions, or for surveillance of previously diagnosed CRC or colorectal adenomas. This definition corresponded to the “definitely screening” category in the reference data set.21,22 Sixty reference standard colonoscopies met these criteria. Colonoscopies classified as “probably diagnostic,” “definitely diagnostic,” surveillance, or “probably screening (with symptoms)” in the reference data set were dichotomized as nonscreening.

Candidate Classification Variables

We created a list of candidate variables using ICD-9, CPT, and HCPCS code group definitions published by other researchers,9,13,17,23 additional clinically relevant variables that we created using slightly different diagnosis code groupings, age, and sex. Some GI conditions were represented by multiple code groupings (e.g., anemia, diarrhea). We initially applied two look-back intervals to each of the code groupings to create two candidate variables for each; one version included codes assigned the day of the colonoscopy procedure (day 0–365), and a second excluded codes from the day of the colonoscopy procedure (day 1–365).18

We created a cancer screening code grouping using the ICD-9 “special screening for malignant neoplasm” V-codes (V76.41, V76.50, and V76.51) and the HCPCS procedure code for a preventative physical examination (G0344) using multiple look-back periods of 31, 180, and 365 days. Because subjects with a family history of CRC or inflammatory bowel disease were excluded from the case-control study, we did not include variables representing these conditions.

We then reduced the initial list of candidate variables based on frequency of occurrence in our data set. Our rationale was that codes occurring at low frequency are unlikely to be selected, and if selected are unlikely to have stable out-of-sample performance. We removed candidate variables that occurred fewer than 10 times in our reference data set. Similarly, when there were fewer than 5 occurrences of a symptom, sign, or condition noted on the same day as the colonoscopy, we used only the 0–365 day look back, excluding the same variable with a 1–365 day look-back. After applying these restrictions, 65 candidate predictors remained (Table 1).

Table 1.

Candidate Predictors: Variables Included in Selection Algorithms Used for Algorithm Development

CODE OR CODE GROUP DESCRIPTION	ICD-9, CPT, OR HCPCS CODE OR CODE GROUP	LOOK-BACK (DAYS)f	SOURCE
DEMOGRAPHICS
Age on procedure date, age squared		0
Gender		0
GI SIGNS, SYMPTOMS, CONDITIONSa
Iron deficiency anemia	280.0, 280.9	0–365, 1–365	g
Anemia (1)b	285.1, 285.9	0–365, 1–365	9, 13
Anemia (2)	281.9, 285.1, 285.9	0–365, 1–365	g
Colitis (1)	558.9	0–365, 1–365	17
Colitis (2)	558.x	0–365, 1–365	g
Diarrhea (1)	558.9, 564.5	0–365, 1–365	9, 13
Diarrhea (2)	9.2, 9.3, 564.5, 787.91	0–365, 1–365	23
Diarrhea (3)	9.2, 9.3, 558.9, 564.5, 787.91	0–365, 1–365	g
Diarrhea (4)	9, 9.0, 9.1, 9.2, 9.3, 558.9, 564.5, 787.91	1–365	g
Intestinal obstruction	560, 560.0, 560.89, 560.9	0–365	23
Diverticula	562.1x	0–365, 1–365	g
Constipation	564.00, 564.09	1–365	g
Irritable colon (Irritable bowel syndrome)	564.1	0–365	9, 13
Functional digestive disorder	564.0, 564.00, 564.09, 564.1, 564.7, 564.81, 564.89, 564.9	0–365, 1–365	g
Rectal bleeding, Hemorrhage, BRBPR	569.3	0–365, 1–365	13, 17
GI bleed, stool (1), Melena	578.1	0–365, 1–365	17
GI bleed, stool (2), Hematochezia	578.9	0–365, 1–365	17
GI bleed, stool (3), Melena or hematochezia	578.1, 578.9	0–365, 1–365	9, 13, 17, 23
Heme-positive stool	792.1	0–365, 1–365	9, 13
GI bleed, stool (4)	578, 578.1, 578.9, 792.1	0–365, 1–365	23
Abdominal pain	789.0, 789.00, 789.01, 789.02, 789.03, 789.04, 789.05, 789.06, 789.07, 789.09	0–365, 1–365	9, 13
Abdominal swelling	789.3, 789.30, 789.31, 789.32, 789.33, 789.34, 789.35, 789.36, 789.37, 789.39	0–365, 1–365	9, 13
Other digestive system symptoms	787.99	0–365, 1–365	23
Weight loss	783.2X, 799.4	0–365, 1–365
Nausea/vomiting	787.0, 787.01, 787.02, 787.03, 787.04	0–365, 1–365	9, 13
Abdominal distension	787.3	0–365	9, 13
Abnormal GI findings	793.4	0–365	23
Rectal polyp	569.0	0–365, 1–365	g
SCREENING STATUSc
Cancer screeningd	G0344, v76.41, v76.50, v76.51	0–31, 0–180, 1–180, 0–365, 1–365	g
Family history of CRC	V16.0	0–365, 1–365	23
Personal history of colon polyps	V12.72	0–365, 1–365	9, 13, 17, 23
PREVIOUS COLORECTAL PROCEDURESe
FOBT	82270, 82271, 82272, 82273, 82274, G0107, G0328, G0394	1–365
Flexible sigmoidoscopy	45300, 45303, 45305, 45307, 45308, 45309, 45315, 45317, 45320, 45321, 45327, 45330, 45331, 45332, 45333, 45334, 45335, 45336, 45337, 45338, 45339, 45340, 45341, 45342, 45345, G0104; 45.24, 48.21, 48.22, 48.23, 48.24, 48.36	1–365
Previous colonoscopy	44388, 44389, 44390, 44391, 44392–44394, 44397, 45355, 45378, 45379, 45380, 45381, G0105, G0121, 45382, 45383, 45384, 45385, 45386, 45387, 45388, 45391, 45392; 45.23, 45.21, 45.25, 45.43, 98.04	1–365

Notes: Abbreviations: BRBPR, Bright red blood per rectum; Gl, Gastrointestinal; FOBT, fecal occult blood test; ICD, International Classification of Disease; CPT, Current Procedural Terminology; HCPCS, Health Care Procedure Coding System

^aThese variables are constructed from ICD-9 diagnosis codes and code groups.

^bWe included multiple candidate variables for anemia, colitis, diarrhea, and Gl bleed; each coded slightly differently based on the source. For example, we created “anemia (1)” using diagnosis codes based on our own judgment and adapted “anemia (2)” from the Cooper et al. and El-Serag et al. algorithm.9,13

^cThese variables are constructed from ICD-9 V-codes and HCSPCS procedure codes.

^dIncluded as candidate predictors for the primary algorithm only.

^eThese variables are constructed from CPT, HCPCS, and ICD-9 procedure codes.

^fMost variables had two versions: one that included codes assigned to the day of the procedure, the other didn’t. The 0–365 day look-back interval included symptoms, signs, and conditions assigned on the day of the procedure (day 0) and up to 365 days prior to the procedure. The 1–365 day look-back excluded codes assigned on the day of the procedure.

Statistical Approach

We developed two algorithms. The primary, restricted model is intended for use in health care data that either do not include cancer screening codes or for which these codes are believed to be underrepresented, whereas the secondary, extended model is intended for health care data in which these screening codes are available.

We used multivariable logistic regression with LASSO to select variables for inclusion in the algorithms and to estimate their coefficients. The LASSO provides a simple method for variable selection and protects against overfitting by constraining the sum of the absolute value of the coefficients.24,25 Analyses were carried out using the glmnet package in R 26,27 with tenfold cross-validation to estimate classification error.

Because the reference data were collected for a case-control study of late-stage CRC, the data set included a disproportionately high proportion of colonoscopies from individuals who were later diagnosed with CRC. To account for this and to estimate performance in a general population, we weighted observations to adjust for the case-control study design with a higher probability of case selection from the population. These adjustments reduced the influence of cases’ colonoscopies on estimates and increased the influence of controls’ colonoscopies. Colonoscopies from cases averaged a probability weight of 0.034, whereas those from controls averaged 1.74.

We classified colonoscopies as “screening” or “nonscreening” by dichotomizing estimated probabilities and categorizing exams with predicted probabilities above a selected threshold as “screening” and exams with predicted probabilities below this threshold as “not screening.” For any threshold, we described the accuracy of an algorithm in terms of its ability to discriminate between a screening and a not-screening colonoscopy using sensitivity (the probability of correctly identifying a true screening colonoscopy) and specificity (the probability of correctly identifying a truly not-screening colonoscopy). We described the accuracy of the new algorithm using ROC curves that plot sensitivity against (1-specificity) across the range of thresholds, and summarized the overall performance using the area under the ROC curve (AUC).28 We used the Youden Index (the maximum value of the sum of sensitivity and specificity at each potential cut-point) to select cut-points that optimize the operating characteristics of the algorithm giving equal weight to false positive and false negative errors.29

We based logistic regression models on all available data (i.e., allowing multiple colonoscopies per subject) and we ignored correlation resulting from inclusion of multiple colonoscopies for some subjects. We used sensitivity analysis to assess the impact of correlation on estimates. We created 100 data sets that included a single colonoscopy per person by randomly selecting one exam from individuals with multiple exams. For each data set we repeated the estimation process by selecting variables using the LASSO and then estimating the logistic regression model and the associated AUC.

Results

Most (63.7 percent) colonoscopies in our data set were performed between 2006 and 2008. Similar numbers of procedures were available for men and women, with the majority (68 percent) performed on subjects who were from 50 to 75 years old at the time of the exam (Table 2).

Table 2.

Characteristics of Colonoscopies in the Reference Data Set

CHARACTERISTIC	N	%	WEIGHTEDb %
Male	314	52.7	52.8
Female	282	47.3	47.2
AGE AT EXAM (YEARS)
50–59	83	13.9	25.9
60–75	323	54.2	59.7
76–85	190	31.9	14.5
CASE-CONTROL STATUS
Case	404	67.8	4.0
Control	192	32.2	96.0
REFERENCE STANDARD INDICATION
Nonscreening	536	90.0	75.4
Screening	60	10.1	24.6
CALENDAR YEAR COLONOSCOPY WAS PERFORMED
1996–2000	53	8.9	11.1
2001–2005	167	28.0	45.2
2006–2008	376	63.1	43.7

Notes:

^aOnly colonoscopies classified as “definitely screening” in the reference data set were considered average-risk screening in the present analyses. Reference colonoscopies classified as “definite diagnostic,” “probable diagnostic,” surveillance, and “probably screening (with symptoms)” were dichotomized as nonscreening.

^bWeighted by the inverse sampling fraction based on age, calendar year, and CRC case status.

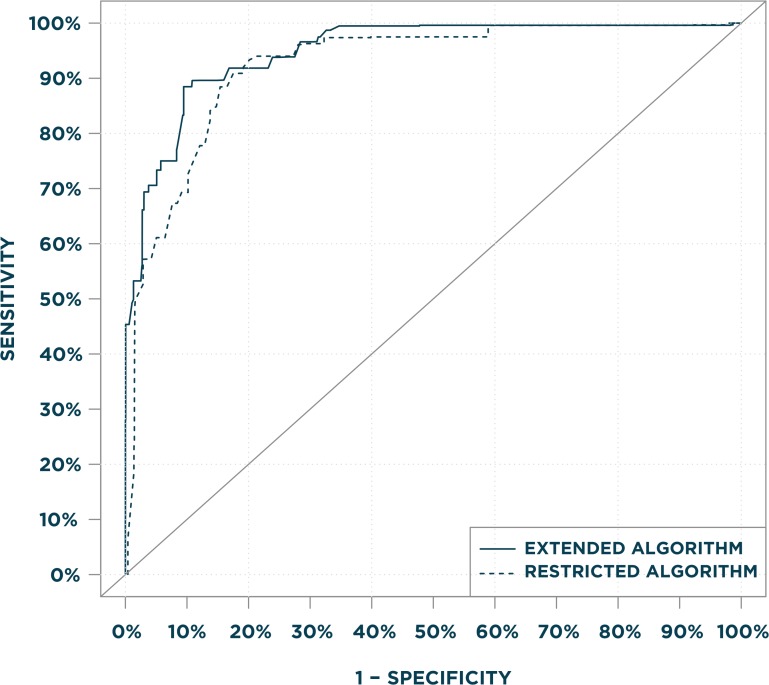
Table 3 shows estimated logistic regression coefficients (log-odds ratios) selected for inclusion in the two algorithms. The primary, restricted algorithm used information from 10 variables including age; GI signs, symptoms, and conditions; and history of polyps in the previous year. The secondary, extended algorithm included the same predictors as the primary algorithm, but with different coefficient values and in some instances different look-back periods, and three of the five candidate cancer-screening variables. Both algorithms had similar discriminative accuracy based on visual comparisons of ROC curves (Figure 1) and similar AUC statistics: 0.94 for the primary, restricted algorithm and 0.96 for the secondary, extended algorithm. The restricted algorithm had sensitivity=0.91 and specificity=0.82, with the estimated probability dichotomized at 0.305. The secondary, extended algorithm had sensitivity=0.88 and specificity=0.90 at the optimal operating point, with the estimated probability dichotomized at 0.261. Sensitivities, specificities, positive predictive values, and negative predictive values for a range of thresholds in our data are provided in Table 4.

Table 3.

Logistic Regression Coefficients for Colonoscopy Indication Algorithms^a

		LOGISTIC REGRESSION COEFFICIENTS, ß
PREDICTOR VARIABLE	LOOK-BACK PERIOD (DAYS)b	PRIMARY, RESTRICTED ALGORITHMc	SECONDARY, EXTENDED ALGORITHM
(Intercept)		1.64852	1.74247
Age	0	0	−0.04521
Age squared	0	−0.00046	−0.00033
Iron deficiency anemia	0–365	−0.91922	−0.59150
Anemia (1)	0–365	0	−0.05479
Functional digestive disorder	0–365	−0.86536	−0.25237
Rectal bleeding, hemorrhage, BRBPR	1–365	0	−0.07013
Rectal bleeding, Hemorrhage, BRBPR	0–365	−1.34397	−1.45248
GI bleed, stool (4)	0–365	−1.16778	−0.83575
Abdominal distension	0–365	−0.73345	−0.73452
Abdominal pain	0–365	−0.18429	−0.27980
Nausea/vomiting	1–365	−0.05580	0
Nausea/vomiting	0–365	−0.64995	−0.02046
Rectal polyp	1–365	−1.81902	−2.05020
Cancer screening	0–31	–	0.63791
Cancer screening	1–180	–	−0.28645
Cancer screening	0–180	–	1.56963

Notes: Abbreviations: BRBPR, Bright red blood per rectum; Gl, gastrointestinal

^aThe algorithms use the logistic regression coefficients to predict the probability that a colonoscopy is a screening exam is estimated using the equation p̂=l/(l+exp(1*Xß), where Xß is the linear combination of the covariates and coefficient values.

^bThe 0–365 day look-back interval included code groupings assigned on the day of the procedure (day 0) and up to 365 days prior. The 1–365 day look-back excluded codes assigned on day 0.

^cThe secondary, extended algorithm was developed using a model that included screening V-codes (V76.41, V75.50, V76.51) and the HCPCS average risk procedure code (G0344) as candidate variables, whereas the primary, restricted model excludes codes as candidates.

Figure 1.

Legend: Area under the Receiver Operating Characteristics (ROC) Curves for the Restricted and Extended Algorithms.

The primary, restricted algorithm did not include ICD-9 screening V-codes (V76.41, V76.50, V76.51) and the HCPCS preventative examination code (G0344) as candidate variables, whereas the secondary, extended algorithm included these variables.

Table 4:

Predictive Model Test Characteristics for the Restricted and Extended Algorithms across a Range of Values^a,b

	SENSITIVITY	SPECIFICITY	POSITIVE PREDICTIVE VALUE	NEGATIVE PREDICTIVE VALUE	CUT-POINT
PRIMARY, RESTRICTED ALGORITHM
	0.487	0.985	0.912	0.855	0.509
	0.611	0.95	0.798	0.882	0.438
	0.693	0.909	0.712	0.901	0.379
	0.778	0.879	0.677	0.924	0.364
	0.824	0.862	0.661	0.938	0.349
OPTIMAL OPERATING POINT	0.909	0.825	0.628	0.965	0.305
	0.933	0.799	0.602	0.973	0.291
	0.961	0.719	0.527	0.983	0.236
	0.974	0.677	0.496	0.988	0.214
SECONDARY, EXTENDED ALGORITHM
	0.492	0.989	0.938	0.857	0.651
	0.694	0.962	0.857	0.906	0.536
	0.706	0.949	0.819	0.908	0.476
	0.750	0.921	0.756	0.919	0.356
	0.833	0.907	0.744	0.943	0.311
OPTIMAL OPERATING POINT	0.885	0.905	0.753	0.960	0.261
	0.918	0.832	0.640	0.969	0.216
	0.938	0.761	0.561	0.974	0.184
	0.975	0.687	0.503	0.988	0.156

Notes:

^aThe primary, restricted algorithm included the predictor variables selected by the primary regression model (see Table 3) from the candidate predictors shown in Table 1 and a model intercept. The secondary, extended algorithm included the same predictors as selected by the restricted regression model but with different coefficient values, and a model intercept. The secondary algorithm additionally included cancer screening variables representing 3 look-back intervals.

^bSelected combinations of sensitivity, specificity, positive predictive value, and negative predictive value. At each combination of test characteristics, the predicted probability threshold is the level at or above which colonoscopies are classified as screening. The optimal point on the ROC curve is defined by the Youden Index, the point at which the sum of sensitivity and specificity is maximized.

Sensitivity analysis exploring the impact of multiple exams on our results demonstrated some variability in the particular codes included in the data sets with a single colonoscopy per person, especially with respect to timing. There was little variability in the estimated accuracy of algorithms across repeated samples, and all had accuracy estimates exceeding the accuracy of the algorithms using all available data.

Use of the algorithm to classify colonoscopies in new subjects is a three-step process (see also Appendix). The user first selects a threshold cut-point for classifying colonoscopies as screening (vs. nonscreening), based on the desired trade-off of test characteristics. Test characteristics and their corresponding cut-points are provided in Table 4. The second step is to estimate the predicted probability that each colonoscopy was indicated for screening, using the linear combination of algorithm coefficients provided in Table 3 and subject covariate values from the user’s data. The third step is to compare the predicted probability for each colonoscopy with the threshold cut-point selected in the first step. Predicted probabilities equal to or greater than the cut-point are classified as screening; those less than the cut-point are classified as nonscreening.

Discussion

We developed two new regression-based algorithms for classification of screening colonoscopies in health care data. The algorithms distinguish between screening and nonscreening colonoscopies with high accuracy based on internal validation. These algorithms were developed using an adjudicated reference standard data set. We used LASSO variable selection and tenfold cross validation as measures to protect against overfitting.25,30 Our primary, restricted algorithm uses the ICD-9 and CPT procedure codes widely used in health care data. It is intended for use in situations in which ICD-9 screening V-codes are unavailable or underutilized. Screening V-codes were strong predictors of screening colonoscopy in our extended model, and in settings where these variables are available the algorithm that includes V-codes may provide better accuracy.

The ROC curves (Figure 1) coupled with the test characteristics table (Table 4) demonstrate the algorithms’ discriminative accuracy over a wide range of sensitivity and specificity values.28 This information allows users to select alternative probability cut-points based on the relative importance of sensitivity and specificity in their applications.31 Alternatively, users can apply the estimated probabilities directly in analyses examining screening colonoscopy.32

Although these new algorithms have not yet been tested in external populations, our internal validation results appear stronger than the internal validation results reported for other new algorithms. The Haque et al. algorithm was 84 percent sensitive and 24 percent specific17 (our recalculation of specificity from their Table 1). More recently, Ko et al. reported 56 percent sensitivity and 97 percent specificity for their two-level model.19 Our extended model appeared to have somewhat higher sensitivity at this high level of specificity. Sewitch et al. reported 85 percent sensitivity and 63 percent specificity.8 Other results reported in the literature are not comparable with the internal validation results presented here, because they represent either external validation results, or validation of algorithms that were modified from previous models.18 (We consider the validation results reported by El-Serag to represent external validation of the previously reported Cooper algorithm.)9,13

We attribute the strong test performance of the new algorithms to our use of modern variable selection methods. Similar to recent algorithm development efforts, we built our models using a hybrid approach using statistical methods rather than relying primarily on content knowledge.8,19 We began with a set of clinically relevant potential candidate predictors and then eliminated those that occurred infrequently. We employed regression with LASSO automated selection to select the subset of variables that most strongly classified colonoscopy indication in the reference data set. Automated selection has the advantage of testing large numbers of covariate combinations simultaneously. It is an attractive option where a large number of potential candidate predictors exist, and with no strong a priori basis for choosing among them.

Automated selection models have been criticized as prone to overfitting; which occurs when a statistical model is fit to noise in the sample and leads to a model that does not generalize to new subjects.25,33 The LASSO is designed to protect against overfitting and thereby to improve prediction in new subjects. The LASSO applies a penalty function that drives the selection algorithm to choose a parsimonious model and, thereby, to improve prediction in new subjects. The LASSO was designed to select the strongest predictors in sparse data, that is, in situations where the number of potential predictors is large relative to the number of observations, as was the case in our data.34

Although other recently developed algorithms were also developed using statistical methods,8,19 ours differ in that they estimate a predicted probability of screening for each colonoscopy while preserving the probabilistic structure of the multiple regression model from which they were derived. This provides several advantages. The predicted probability is based on the subject’s overall covariate pattern, that is, the algorithm considers the combined attributes of the subject at the time of colonoscopy and weighs each factor according to its predictive strength. To prevent loss of information, the continuous-scale predicted probability is dichotomized only in the final step when it is compared with a threshold value. Building the algorithm around the linear combination of predictors allowed us to weigh the combined influence of multiple variables, including age. In contrast, previous algorithms were structured as relatively simple, deterministic decision trees; in other words, the presence of any of the included variables in the subject’s data is sufficient to determine the indication.

Potential users of these algorithms should first verify their applicability and accuracy within their own health care systems. Patterns of collection, coding, and preservation of procedure and diagnosis data differ across health care systems and over time, and this may impact the accuracy of the algorithms. For example, three of the four health care systems from which these data were drawn are health maintenance organizations; their providers typically assign codes to document patients’ health conditions and services provided, but not to bill for these services. Primary source assignment of codes may differ in settings where the codes are used directly for reimbursement.

Although we used methods designed to reduce model overfitting, the accuracy estimates may be optimistic because test performance was estimated with the same data used for algorithm development. Predictions typically are not as accurate in new settings as they are with the data from which they were developed. Validation of our new algorithms in other populations will be an important test of their generalizability.

If these algorithms are found to be generalizable in other study settings they offer several potential advantageous features to users. The reference data set was based on a geographically diverse patient population that included similar numbers of men and women. Most of the colonoscopies were performed in recent years, which should be an advantage to researchers working with newer data. Moreover, we developed the algorithms using standard diagnosis and procedure codes widely available in health care data. The algorithms do not require extraction and interpretation of narrative text or laboratory results.

Our decision to allow multiple colonoscopies per individual had both benefits and costs. In the real world, patients often undergo multiple colonoscopies over time; researchers using longitudinal data will need to classify these procedures when they are encountered. However LASSO techniques are not available to account for correlated error due to multiple observations per individual in weighted data. Ignoring the clustering of multiple exams per patient could potentially affect variable selection. Our sensitivity analyses suggest that inclusion of multiple colonoscopies per person reduced estimated accuracy. This may occur because patients have colonoscopies with different indications, weakening the predictive ability of stable person-level characteristics.

This study demonstrates that a logistic regression model can be used to identify screening colonoscopies in coded health care data with a high degree of accuracy based on internal validation. External validation is needed to replicate these results and explore their performance in other settings.

Appendix: Classification of Screening Colonoscopy Using Dichotomized Predicted Probabilities

Application of the algorithm is a three step process. The user first chooses the model (restricted or unrestricted) and desired test characteristics. Each set of desired test characteristics has a corresponding predicted probability threshold. For a user choosing the restricted algorithm at its optimal operating point, the corresponding probability threshold for classifying a colonoscopy as screening would be 0.305 (Table 4). Alternatively the user can choose other desired test characteristics from the ROC curve, and apply the corresponding probability threshold. For example, a user could prioritize specificity over sensitivity, choosing desired specificity of 0.91 with sensitivity of 0.69. The resulting cut-point would be 0.379.

The second step is estimation of a predicted probability (that the colonoscopy was intended for screening) for each colonoscopy in the user’s dataset. The predicted probability of screening indication is estimated using the linear combination of the regression model coefficients and the subject’s covariate values (covariates provided in Table 3). The estimated probability that a colonoscopy is screening, p̂, is calculated using a log odds transformation of the linear predictor, Xß.

$$\widehat{\text{p}}=1/(1+\text{exp}(-1*\text{X}ß)),\text{where}\hspace{0.17em}\text{X}ß={ß}_0+{ß}_1*\text{predictor}1+{ß}_2*\text{predictor}2+\dots {ß}_{\text{n}}*\text{predictor}\hspace{0.17em}\text{n}$$

Finally the predicted probability for each colonoscopy in the user’s dataset is compared with the probability threshold. If the predicted probability is equal to or greater than the threshold, the colonoscopy is classified as screening. Otherwise the colonoscopy is classified as non-screening.