Widespread Transient Hoogsteen Base-Pairs in Canonical Duplex DNA with Variable Energetics

Abstract

Hoogsteen base-pairing involves a 180 degree rotation of the purine base relative to Watson-Crick base-pairing within DNA duplexes, creating alternative DNA conformations that can play roles in recognition, damage induction, and replication. Here, using Nuclear Magnetic Resonance R_1ρ relaxation dispersion, we show that transient Hoogsteen base-pairs occur across more diverse sequence and positional contexts than previously anticipated. We observe sequence-specific variations in Hoogsteen base-pair energetic stabilities that are comparable to variations in Watson-Crick base-pair stability, with Hoogsteen base-pairs being more abundant for energetically less favorable Watson-Crick base-pairs. Our results suggest that the variations in Hoogsteen stabilities and rates of formation are dominated by variations in Watson-Crick base pair stability, suggesting a late transition state for the Watson-Crick to Hoogsteen conformational switch. The occurrence of sequence and position-dependent Hoogsteen base-pairs provide a new potential mechanism for achieving sequence-dependent DNA transactions.

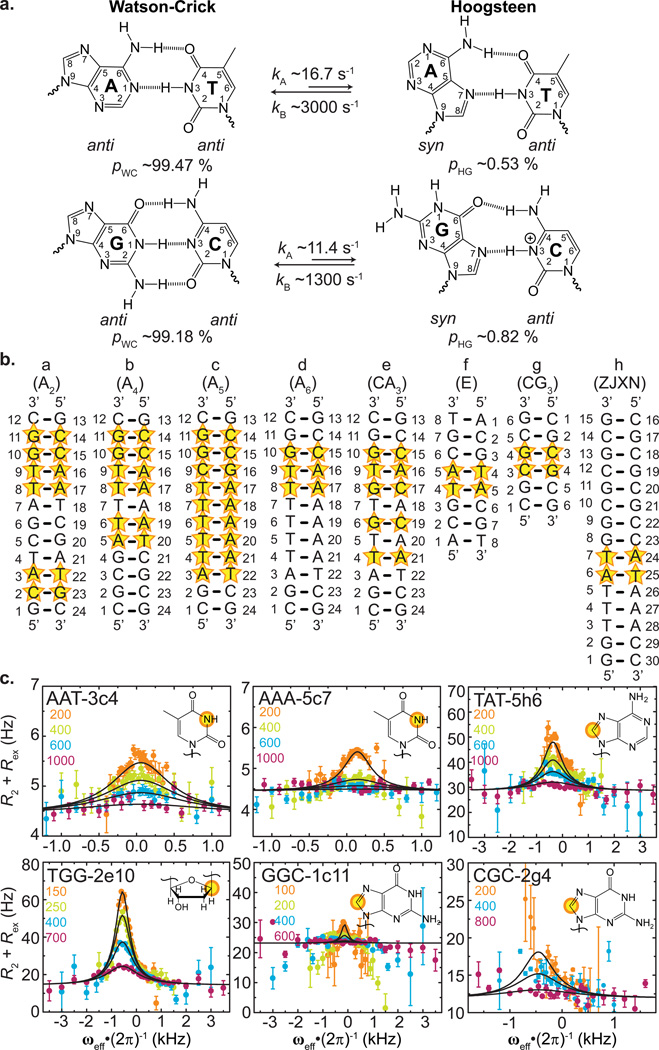
We recently showed^1–3 using Nuclear Magnetic Resonance (NMR) R_1ρ relaxation dispersion (RD)^4–6 that A•T and G•C Watson-Crick (WC) base-pairs (bps) in CA/TG and TA/TA steps of duplex DNA transiently form Hoogsteen (HG) bps⁷ with populations ranging between 0.14% and 0.49% and lifetimes between 0.3 and 2.5 ms at pH ~6 (Fig. 1a). HG bps form through 180-degree rotation of the purine base around the glycosidic bond from an anti to syn conformation (Fig. 1a). HG bps modify the structural and chemical presentation of DNA and thereby can play unique roles (reviewed in ref⁸) in DNA-protein recognition^9–12, damage induction¹³ and repair^14,15 as well as replication^16,17. For example, by narrowing the minor groove, HG bps have been shown to alter the DNA electrostatic potential “seen” by DNA-binding proteins at the bp edges in the DNA grooves in the context of p53-DNA complexes^12,18,19. HG bps can also transiently expose DNA sites that are otherwise inaccessible in WC bps, and thereby provide new mechanisms for damage induction. For example, using computational mapping, Bohnuud et al.¹³ recently showed that transient G•C⁺ HG bps could explain the susceptibility and accessibility of cytosines to hydroxymethylation by formaldehyde, thus explaining a long-standing mystery that has persisted for over 25 years. There is also structural and biochemical evidence that some members of the low fidelity Y-family polymerases replicate DNA using HG pairing as the dominant mechanism, thus providing a mode for bypassing a variety of lesions on the WC face during replication^16,17,20. Naked duplexes consisting entirely of HG bps have been reported in A–T rich sequences that form parallel²¹ and anti-parallel stranded^22,23 DNA. Computational studies on duplexes also suggest that the HG bpis a reasonable conformation, only slightly less stable than the canonical WC bp^24,25.

Figure 1. Widespread occurrence of transient A•T and G•C⁺ Hoogsteen base-pairs in canonical duplex DNA.

(a) The equilibrium between Watson-Crick and Hoogsteen base-pairs. Shown are the average forward (k_A) and reverse (k_B) rate constants and populations of Watson-Crick (p_A) and Hoogsteen (p_B) base-pairs obtained in this study. (b) DNA duplexes used in this study. Base-pairs targeted for relaxation dispersion measurements are highlighted with a star. (c) Representative off-resonance ¹³C and ¹⁵N R_1ρ relaxation dispersion profiles showing chemical exchange outside TA and CA steps of canonical duplex DNA. Spin lock powers (Hz) are shown in the inset. Data are fit to Equation 2. Error bars represent experimental uncertainty (one standard deviation) estimated from monoexponential fitting of duplicate R_1ρ data and analysis of signal-to-noise. See Methods for buffer conditions.

Considering that HG bps are an energetically favorable alternative to WC bps that can provide new mechanisms in a wide variety of DNA biochemical processes, it is of great interest to explore whether the transient HG bps observed by NMR are confined to flexible CA and TA steps, or occur more broadly across distinct sequence and position contexts in duplex DNA. Likewise, it is of interest to examine the sequence-specificity of transient HG bp formation as this could provide new mechanisms for achieving sequence-specific DNA transactions that are based on shape¹⁹.

By carrying out ¹³C and ¹⁵N R_1ρ NMR RD measurements on 33 bps in eight distinct canonical DNA duplexes, we show that transient HG bps are not limited to CA and TA steps, but rather occur broadly across diverse sequence and positional contexts. We find that both the energetic stability and rates of HG bp formation exhibit a dependence on sequence and position, with HG bps forming faster and being more abundant in energetically less favorable WC bps.

Results

Widespread Transient Hoogsteen Base-Pairs in Duplex DNA

To more broadly examine the occurrence and sequence-specificity of transient HG bps in canonical duplex DNA, we carried out ¹³C and ¹⁵N R_1ρ NMR RD measurements targeting sugar C1′ and base C6/8 or N1/3 resonances in 20 A•T and 13 G•C bps in eight DNA duplexes that encompass a variety of sequence motifs, including (A•T)_n repeats of varying length (n=2, 4, 5 and 6), a (CA)₃ repeat, a duplex sequence that forms HG bps upon binding to the antibiotic echinomycin,^1,26,27 a (CG)₃ repeat capable of forming Z-DNA,²⁸ and a B/Z junction forming sequence^29,30 (Fig. 1b). The targeted bps (Fig. 1b, highlighted in stars) encompass 6/10 dinucleotide steps that are positioned 1 to 6 bps away from the closest terminal end. R_1ρ RD experiments were performed at pH 5.2–7.5 and 5.2–5.4 for A•T and G•C bps, respectively. We use low pH conditions for transient (and protonated) G•C bps in order to increase the WC-to-HG chemical exchange signature detected by NMR R_1ρ RD³. We recently reported a detailed analysis of the pH dependence of chemical exchange corresponding to transient HG bp formation and how measurements at such lower pH conditions can be qualitatively interpolated to assess exchange at higher pH³.

The R_1ρ NMR RD experiment measures the line broadening contribution to resonances of interest due to chemical exchange with a transient, lowly populated species^4,5. In all cases, we measured significant ¹³C and/or ¹⁵N R_1ρ RD(Supplementary Table 1) consistent with chemical exchange (Fig. 1c and Supplementary Fig. 1). A two-state analysis $(\mathrm{A}\underset{k_B}{\overset{k_A}{\rightleftarrows }}\mathrm{B})$ of the R_1ρ data^4–6 (see Methods) yielded populations (p_B = ~0.08–2.73 %) and lifetimes (τ_B = ~0.12–2.57 ms) for the transient state (Supplementary Fig. 2 and Supplementary Table 2) that are similar to those reported previously for transient HG bps (p_B = ~0.14–0.49 % and τ_B = ~0.3–2.5 ms)^1,2. The chemical shifts (ω_B) of the transient state obtained using this analysis (Supplementary Fig. 3 and Supplementary Table 2) are also consistent with HG bps, including significantly downfield shifted purine C8 (Δω≈ 2.72 ppm), purineC1′ (Δω≈ 3.41 ppm), cytosine C6 (Δω≈ 2.40 ppm) and upfield shifted imino N1/3 (Δω≈ −1.84 ppm)^1,2. Consistent with HG bps, we did not observe significant chemical exchange at adenine C2 and thymine C6, which do not experience large chemical shift changes upon HG bp formation^1,2(Supplementary Fig. 1 and Supplementary Table 2).These results show that transient HG bps are not confined to CA/TG and TA/TA steps but rather occur broadly across a wide variety of sequence and positional contexts, including GA/TC, AA/TT, TA/TA, GG/CC, CG/CG and TG/CA dinucleotide steps (where the HG bp is underlined).

Position- and Sequence-Dependent Energetic Variability

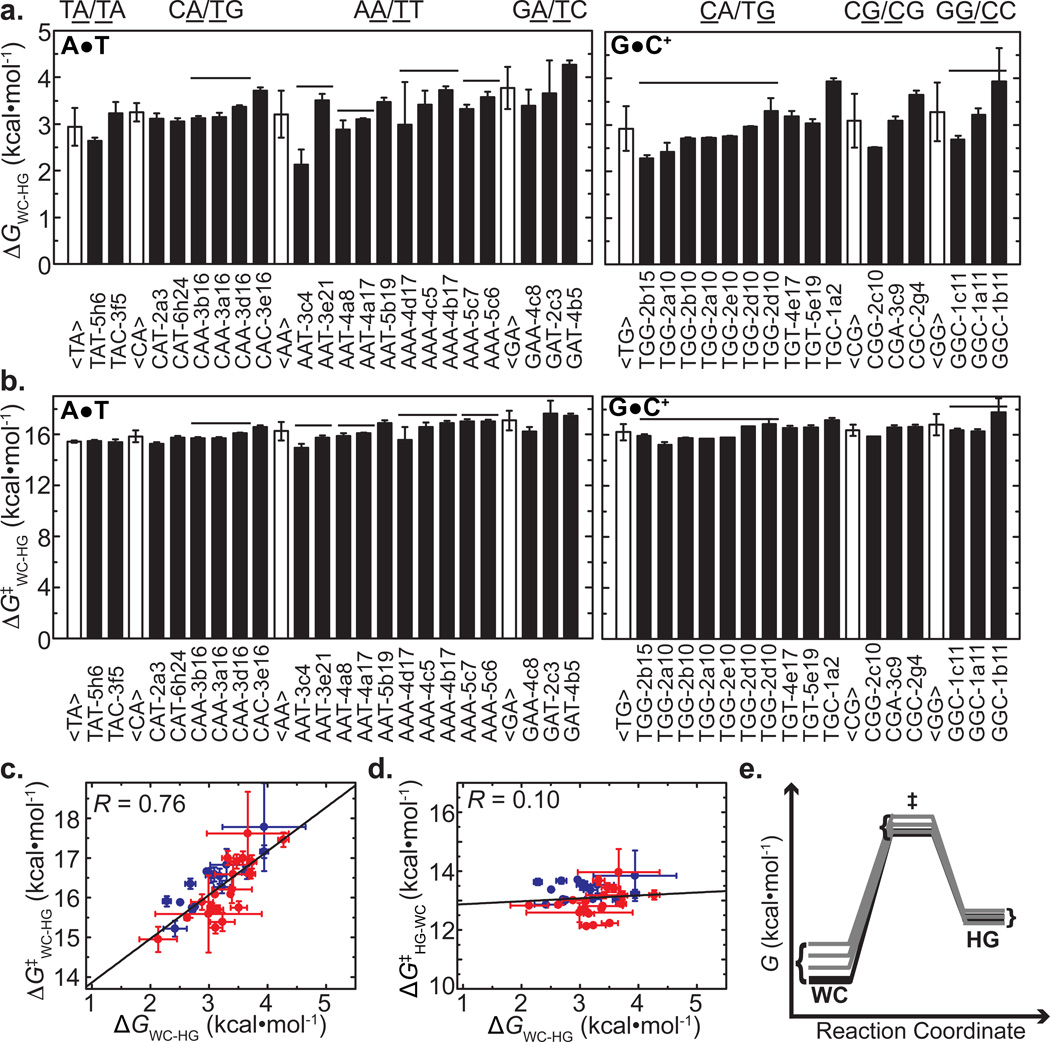
We observe ~30-fold variations in the transient HG population (0.08–2.73% and 0.13–2.11% for A•T and G•C⁺ bps, respectively) and ~20-fold variations in lifetimes (0.12–2.57 ms and 0.40–2.08 ms for A•T and G•C⁺ bps, respectively) (Supplementary Fig. 2 and Supplementary Table 2). This corresponds to ~2.1 kcal•mol⁻¹ and ~2.8 kcal•mol⁻¹ variations in the relative thermodynamic stability (ΔΔG_WC-HGwith ΔG_WC-HG = G_HG−G_WC) (Fig. 2a) and forward free energy barriers (ΔΔG^‡_WC-HG with ΔG^‡_WC-HG = G_TS−G_WC, where TS is the transition state), respectively (Fig. 2b). These variations could reflect real sequence or position dependencies for transient HG bp formation. Alternatively, they could arise due to small differences in buffer conditions used for some of the duplexes (see Methods), particularly pH, which can affect the energetics of transient G•C⁺ HG bp formation^1–3. However, systematic deviations in ΔG_WC-HG and ΔG^‡_WC-HG are not observed across DNA duplexes (Supplementary Fig. 4a). Furthermore, no correlations are observed between duplex melting temperatures measured by Circular Dichroism (CD) (Supplementary Fig. 4b,c and Supplementary Table 3) and either ΔG_WC-HG or ΔG^‡_WC-HG (Supplementary Fig. 4a). Consistent with sequence and/or position dependent contributions, the variations in ΔG_WC-HG and ΔG^‡_WC-HG are smaller (~1 kcal•mol⁻¹) when comparing bps across different duplexes that share identical 5′ and 3′ neighbors and positions relative to duplex ends (indicated using horizontal lines in Fig. 2a,b; Supplementary Fig. 2 and Supplementary Table 2).

Figure 2. Sequence and position dependent thermodynamic and kinetic parameters describing the Watson-Crick to Hoogsteen transition.

(a) Free energy difference (ΔG_WC-HG) and (b) forward free energy barrier (ΔG^‡_WC-HG) for the Watson-Crick to Hoogsteen transition as derived from a two-state analysis of the R_1ρ data. Error bars represent experimental uncertainty (one standard deviation) estimated from propagation of errors from monoexponential fitting of duplicate R_1ρ data and analysis of signal-to-noise. Average and standard deviations for dinucleotide steps are shown using white bars. Horizontal lines denote bps with same triplet sequence and positions relative to nearest terminal end. X-axis labels denote the triple sequence context (“XYZ”) with Hoogsteen base-pair in the middle; the position relative to the closest terminal end (“−n”), and name of duplex as denoted in Figure 1b. Correlation between (c) ΔG^‡_WC-HG and ΔG_WC-HG as well as (d) ΔG^‡_HG-WC and ΔG_WC-HG. A•T and G•C⁺ base-pairs are shown in red and blue, respectively. The best line of fit and corresponding Pearson coefficient (R) are shown. (e) Free energy diagram of the Watson-Crick to Hoogsteen transition depicting relative variations in free energy of Watson-Crick, transition and Hoogsteen states.

We observe significant variations in ΔG_WC-HG and ΔG^‡_WC-HG for the same dinucleotide step, which may arise due to differences in position and/or differences in the broader sequence context. Notwithstanding these variations, the average stabilities of HG bps relative to WC bps (ΔG_WC-HG) calculated for individual dinucleotide steps(Fig. 2a) follow an order (TA/TA>AA/TT>CA/TG>GA/TC for A•T and TG/CA≥CG/CG≥GG/CC for G•C⁺) that is nearly inverted relative to the well-documented WC dinucleotide stabilities (GA/TC≥CA/TG>AA/TT>TA/TA for A•T and CG/CG>GG/CC>TG/CA for G•C), which measure the stability of WC bps relative to the melted state³¹. Thus, transient HG bps seem to be more abundant in less stable WC dinucleotide steps such as CA/TG and TA/TA steps. The energetic preference for HG bps at TA/TA steps observed here is consistent with a large body of data showing that HG bps are favored in A-T rich sequences, particularly TA/TA steps (reviewed in⁸).

Origin of Variable Transient Hoogsteen Base-Pair Energetics

Strikingly, we observe a clear correlation (R = 0.76) between ΔG_WC-HG and ΔG^‡_WC-HG (Fig. 2c) and a relatively uniform backward free energy barrier (ΔG^‡_HG-WC= G_TS−G_HG) of ~13 kcal•mol⁻¹ (Fig. 2d). Thus, changing the sequence context has little effect on the relative energetic stability of the TS and HG bp. This could either be because the stabilities of the TS and HG bp are not significantly affected by changes in sequence, or because their stabilities vary in a correlated manner. In contrast, a change in sequence context does change the relative stability of both the TS and HG bp relative to the WC bp (Fig. 2e).

One possibility is that sequence-specific variations are dominated by changes in variations in the WC bp without significantly affecting the stabilities of the TS and HG bp (Fig. 2e). Indeed, the observed variations in HG bp stability (~2.1 kcal•mol⁻¹) are comparable in size to variations in WC bp stability (~2 kcal•mol⁻¹) measured across dinucleotide steps using melting experiments³³. This would also explain why transient HG bps are specifically more abundant at dinucleotide steps that have weakened WC stabilities (Fig. 2a,b). If the observed variations are indeed dominated by variations in WC stability, one might expecta similar correlation between the ΔG_cl-op and ΔG^‡_cl-op values describing transitions between WC bps and the bp open state, especially since stability of the open state is not expected to vary significantly with sequence. Indeed, a previous analysis of ΔG_cl-op and ΔG^‡_cl-op correlation reported by Russu and co-workers³² based on imino proton exchange measurements³³ reveals a comparably strong correlation (R = 0.8)³⁴. Our results suggest that the free energy of the TS varies less relative to the HG bp with sequence/position as compared to the WC bp. If one were to assume that a similar sequence/position dependent free energy implies a similar structure, even if the sequence/position dependence is very small, then these results would suggest that the TS is structurally more similar to the HG bp – consistent with a “late” TS.

Φ-Value Analysis Suggests a “Late” Transition State

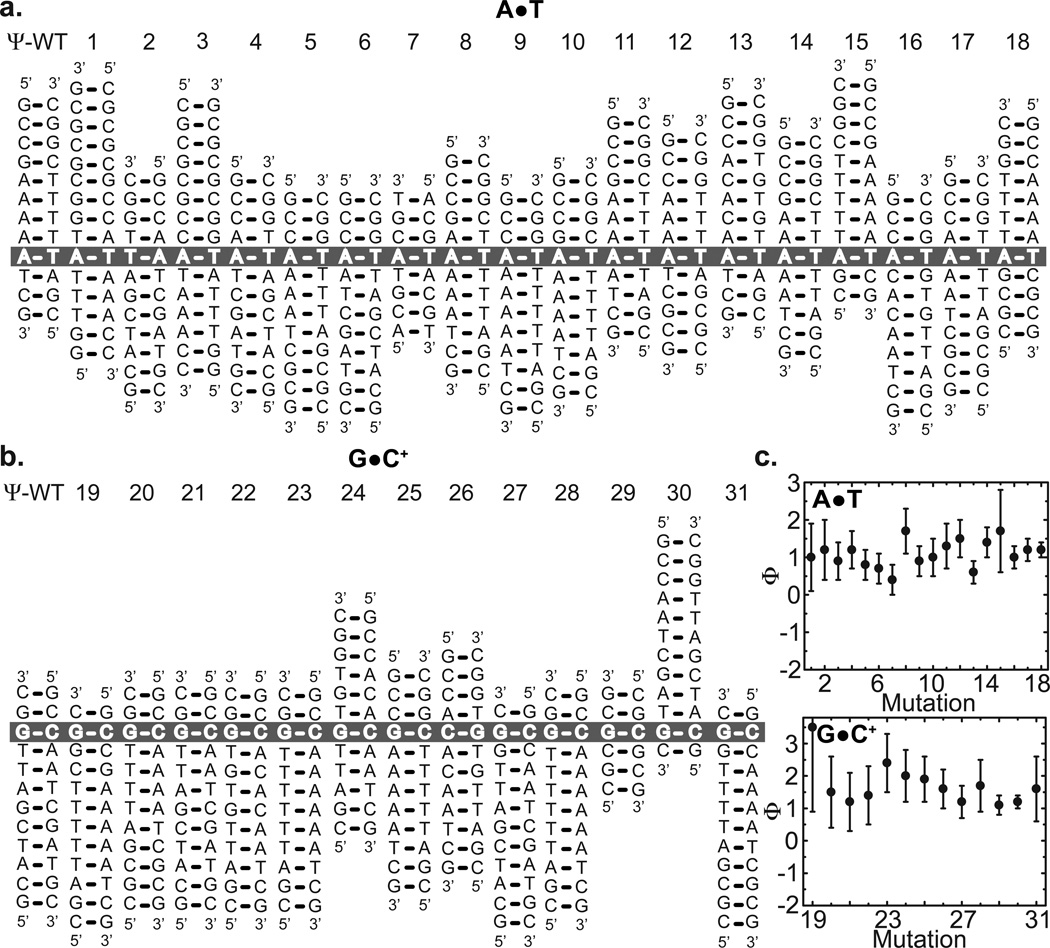
To quantify the extent to which the sequence-specific TS energetic are more similar to HG bps versus WC bps, we subjected the measured ΔG_WC-HG and ΔG^‡_WC-HG values to Φ-value analysis^34,35 (Methods and Fig. 3). In this approach one computes a Φ-value, which quantifies the relative magnitude of the sequence/position dependent free energy differences between the TS and WC bps and those between WC bps and HG bps,

$$\mathrm{\Phi }=\mathrm{\Delta }\mathrm{\Delta }{G}_{TS–WC}/\mathrm{\Delta }\mathrm{\Delta }{G}_{WC–HG}$$ (1)

where ΔΔG_TS-WC= (G_TS − G_WC)_mut − (G_TS − G_WC)_Ψ-WT and ΔΔG_WC-HG= (G_HG − G_WC)_mut − (G_HG −G_WC)_Ψ-WT are the changes in the forward free energy barrier and free energy difference between WC and HG bps, respectively, upon mutating (mut) the sequence/position of a reference (Ψ-WT) bp. It is instructive to consider two limiting cases to help understand how this analysis can be used to quantify the extent to which the sequence-specific TS energetics are more similar to HG bps versus WC bps and whether a TS is “early” or “late”. In the case that the TS and HG share identical sequence specific energetics as might be expected for a late TS, a given sequence-specific perturbation equally affects G_TS and G_HG (i.e. G_HG − G_TS = constant for all mutants) and ΔΔG_TS-WC = ΔΔG_WC-HG and Φ=1. On the other hand, if TS and WC share identical sequence specific energetics as might be expected for an early TS, then G_TS − G_WC = constant for all mutants and ΔΔG_TS-WC = 0 and Φ = 0.In practice, the Φ value can range between 0 and 1, with intermediate Φ values being more difficult to interpret in the context of a structural mechanism¹⁴.

Figure 3. Φ-value analysis.

Perturbing the Watson-Crick to Hoogsteen equilibrium in (a) A•T and (b) G•C⁺ base-pairs by varying the sequence and/or positional context of individual base-pairs. All duplexes are re-drawn after aligning each A•T or G•C⁺ base-pair with a reference sequence variant (Ψ-WT). (c) Φ values for A•T and G•C⁺ base-pairs. The sequence variant number is shown above each secondary structure.

We arbitrarily assign reference A•T and G•C bps to be those having the smallest ΔG_WC-HG values, and which therefore form the most stable HG bps among those studied herein (Ψ-WT, Fig. 3a,b). Next, we computed Φ for each A•T and G•C⁺ bp. This analysis was preformed separately for A•T and G•C⁺ bps and repeated multiple times assuming a different bp as the designated wild-type reference (data not shown). In the vast majority of the cases, we measure Φ values near 1, consistent with a “late” TS (Fig. 3c and Supplementary Table 4). It should be noted that similar sequence/position dependent energetics for the TS and HG bp does not have to imply similarity in structure, and that we cannot rule out the possibility of an early TS that has structural features similar to WC but sequence/position dependent energetics that are more similar to HG.

Discussion

Our results suggest that HG bps can occur ubiquitously in canonical duplex DNA across different sequence and positional contexts. This can help explain how polymerases such as the human DNA polymerase iota can use HG pairing as a general mechanism to replicate DNA and thereby bypass lesions that diminish the ability to form WC bps^8,16. Our findings also raise the possibility that HG bps may be widespread in genomic DNA, especially given that the energetic differences between WC and HG bps are small compared to forces in living cells, including those arising due to supercoiling, torsional stress, and protein binding. It is worth noting that difficulties in distinguishing between WC and HG bps based on X-ray crystallography data have been reported.^8,36 Our finding that transient HG bps can occur ubiquitously in duplex DNA calls for the re-examination of current X-ray structures of DNA to more critically assess for the occurrence of HG bps.

Our studies suggest that the occurrence of HG base-pairs depends in a complex manner on both sequence context and position. This is consistent with the hypothesis by Honig and Rohs that the observation of Hoogsteen base-pairing makes it is unlikely that protein-DNA binding is driven by a simple linear code³⁷. Nevertheless, our results together with prior studies⁸ suggest that HG bps are likely to exist in greater abundance within unstable and structurally stressed environments, such as kinks and turns, which can destabilize WC bps, including stacking interactions. Indeed, while only a few X-ray structures have documented the existence of HG bps in DNA, in many cases HG bps occur near structurally stressed environments. For example, HG bps are observed near kinks or nicks in X-ray structures of DNA bound to TATA box binding protein¹¹ and integration host factor⁹, and near a hairpin loop in structures of DNA bound to TnpA transposase³⁸. HG bps have also been observed for DNA in complex with antibiotics that contribute unique stacking interactions^27,39. Previous studies³ have shown that changes in counterion concentration have a measurable effect on the population and lifetime of HG bps. Future studies should therefore also examine how the sequence- and position-dependent HG energetics vary with increasing counterion concentration (Na⁺ and Mg²⁺). Studies so far suggest that Na⁺ and Mg²⁺ stabilize A•T HG but destabilize G•C⁺ HG bps in the case of CA/TG steps³. Although further studies are needed to more quantitatively understand the sequence- and position-dependence of transient HG bp formation, these energetic preferences may provide a new mechanism for shape-based DNA recognition^12,19 via indirect read out mechanisms⁴⁰. Our study has focused on the occurrence of single transient HG bps surrounded by WC bps. Additional studies are needed to examine sequence-specific propensities for forming longer stretches of HG bps, and HG tracts interspersed by WC bps. Such mixtures of WC and HG bps can endow genomic DNA with a new level of structural complexity similar to Z-DNA.

Our results suggest that the sequence and position specific variations in HG bp stabilities and lifetimes are dominated by variations in the WC bp stability and to a lesser extent by variations in the stabilities of the TS and HG bp. Interestingly, a similar trend has been reported for base opening³². Future studies should further explore the WC-to-HG transition pathways and examine whether they share a similar TS with base opening and whether there can be pathways toward HG that proceed via the base opened state. Conjugate peak refinement simulations suggest a pathway in which the purine base rotates toward the major groove inside the double helix¹, however further experimental characterization is required. The observation that the sequence and/or position variations in the TS free energies are more similar to the HG bp versus the WC bp suggests the TS is structurally more similar to HG versus WC, consistent with a“late” TS for the WC-to-HG transition. However, we cannot rule out an early TS that is structurally more similar to WC but has sequence/position dependent energetics that are more similar to the HG bp. Although the structure of the TS remains unclear, an equally important question is why the energetic stabilities of HG bps appear to be only weakly dependent on sequence. Further studies are required to understand the structure and specific interactions that may help stabilize the TS and HG bp.

Methods

NMR Samples and Resonance Assignments

Unlabeled DNA samples were purchased as single stranded oligos from Integrated DNA Technologies, Inc. (IDT, Inc.) with standard desalting purification. The DNA oligos were resuspended to ~ 200 µM in 15 mM Phosphate buffer with corresponding pH (see below), 25 mM NaCl, 0.1 mM EDTA. Duplexes were annealed by mixing an eqimolar ratio of the complementary DNA strands, heating at 95°C for 2 min followed by gradual cooling at room temperature for ~ 30 min. Unlabeled DNA duplexes were washed 3× in resuspension buffer by micro-centrifugation using an Amicon Ultra-4 centrifugal filter with a 3 kDa cutoff, concentrated to ~2 – 3 mM and ~ 250 µL, then supplied with 10 % D₂O. Natural abundance CG₃ was resuspended in ~ 4 mL of milliQ H₂O and dialyzed against 2 L of milliQ H₂O with two exchanges for a total of 6 L of milliQ H₂O, using a dialysis tube from G-Biosciences with a 1 kDa cutoff. Dialyzed CG₃ was lyophilized and resuspended in NMR buffer to ~ 4 mM and supplied with 10 % D₂O. Hemi- ¹³C/¹⁵N labeled A₅ duplex was prepared by annealing a uniformly ¹³C/¹⁵N labeled thymine-rich strand to a natural abundance adenosine-rich strand. Fully ¹³C/¹⁵N labeled DNA duplexes were prepared by annealing two labeled strands together. All labeled single strands were synthesized in vitro by the method of Zimmer and coworkers⁴¹ using a DNA hairpin template with a 5′ overhang corresponding to the complement of the target labeled strand and a 3′ ribose (IDT, Inc.). In this study we used the same hairpin sequence as Zimmer and coworkers⁴¹, Klenow fragment DNA polymerase (NEB, Inc.) NEB2 buffer (NEB, Inc.), and uniformly ¹³C/¹⁵N-labeled dNTPs (Isotec, Sigma-Aldrich and Silantes). Base- and heat-catalyzed cleavage separated the hairpin template from the ¹³C/¹⁵N-labeled synthesized product. The single-stranded DNA product was purified by 20 % denaturing polyacrylamide gel electrophoresis, isolated by passive elution from crushed gel pieces and desalted on a C18 reverse-phase column (Sep-Pak, Waters). The oligo was lyophilized and suspended in NMR buffer. The semi-labeled DNA samples were prepared by titrating the unlabeled strand directly into an NMR tube containing the ¹³C/¹⁵N-labeled strand and monitoring the disappearance of single-stranded DNA peaks using HSQC experiments. The fully labeled samples were annealed in a similar fashion. 2D ¹H-¹H NOESY experiments at 26 °C (A₂, A₄, A₅, A₆, CA₃, E) or 25 °C (CG₃ and ZJXN) and pH 5.2 (A₅), 5.4 (A₂, A₄, A₆, CA₃, CG₃), 6.8 (E) or 7.5 (ZJXN) were used to assign resonances as described previously¹. See NMR R_1ρ Relaxation Dispersion for R_1ρ RD pH values.

NMR R_1ρ Relaxation Dispersion

All NMR experiments were performed on a Bruker Avance 600 MHz NMR spectrometer equipped with a 5 mm triple-resonance cryogenic probe. R_1ρ RD experiments were performed at pH 5.2–7.5 and 5.2–5.4 for A•T and G•C⁺ bps, respectively. Buffer conditions for R_1ρ RD measurements are 15 mM Sodium phosphate, 25 mM NaCl, 0.1 mM EDTA, 10 % D₂O pH = 5.2 (A₅, A₄: C15 C6, A16 C1′, G10 C1′), pH = 5.4 (A₂, A₄, A₆, CA₃, CG₃), pH = 6.8 (E) and pH = 7.5 (ZJXN) at 26 °C (A₂, A₄, A₅, A₆, CA₃, E) or 25 °C (A₂ A3 C1′, CG₃, ZJXN). CG₃ and E are unlabeled DNA samples, the T-rich strand of A₅ is ¹³C/¹⁵N labeled while A₆, A₄, A₂ CA₃ and ZJXN are fully ¹³C/¹⁵N-labeled. We use low pH conditions for transient (and protonated) G•C⁺ bps in order to increase the WC-to-HG chemical exchange signature detected by R_1ρ RD³. We recently reported a detailed analysis of the pH dependence of chemical exchange corresponding to transient HG bp formation and how measurements at such lower pH conditions can be qualitatively interpolated to assess exchange at higher pH³. Carbon and nitrogen R_1ρ RD profiles for guanine/adenine C8, guanine/adenine C1′, cytosine C6, guanine N1 and thymine N3 were measured using a 1D acquisition scheme which uses selective Hartmann-Hahn polarization transfer⁴² to selectively excite one C-H or N-H spin system at a time⁶. The spin lock power and offset frequencies are summarized in Supplementary Table 4. The following delays were used: A₂: A3 C1′, G10 C1′, A17 C1′; A₄: A5 C1′, G10 C1′, A16 C1′, A19 C1′; CA₃: G10 C1′; A₅: A3 C1′, C5 C1′ [0, 4, 8, 12, 18, 26, 34, 42, 12, 42]; A₅ G11 C8 [0, 12, 32, 26, 32]; A₄ A17 C8, A₆ A17 C8 [0, 4, 12, 32, 26, 32]; A₂: C2 C6, T9 C6, G11 C8, A16 C8, A17 C2; CA₃: A16 C8, C17 C6, C19 C6, A21 C1′; A₄: C15 C6, G11 C8; A₅: C9 C6, G10 C8; A₆: G10 C8, A16 C8 [0, 4, 8, 12, 16, 20, 26, 32, 12, 32]; A₂: T8 N3, G10 N1, G23 N1; A₅: T4 N3, T5 N3, T6 N3, T7 N3, T8 N3; A₆ G10 N1 [0, 8, 16, 24, 36, 48, 60, 80, 100, 16, 70, 100]; CG₃ G4 C8 [0, 60, 60]; ZJXN: A6 C8, A24 C8 [0, 4, 8, 12, 16, 20, 24, 30, 12, 30]; E A5 C8: [0, 48, 48]. Data points meeting C-C Hartmann-Hahn matching conditions were omitted as described previously⁶. Data were processed using NMRPipe⁴³ and R_1ρ values were determined from monoexponential decay fits of the resonance intensities using a script⁴⁴ in Mathematica 9 (Wolfram Research, Inc.). On- and off-resonance R_1ρ data were fit to the Laguerre equation⁴⁵ (Equation 2) using Origin 8.6 (OriginLab),

$$R_{1\rho }=R_1{\text{cos}}^2\theta +R_2{\text{sin}}^2\theta +\frac{{\text{sin}}^2\theta p_A{p}_B\mathrm{\Delta }{\omega }^2{k}_{\mathit{\text{ex}}}}{{\omega }_A^2{\omega }_B^2/{\omega }_{\mathit{\text{eff}}}^2+k_{\mathit{\text{ex}}}^2-{\text{sin}}^2\theta p_A{p}_B\mathrm{\Delta }{\omega }^2(1+\frac{2k_{\mathit{\text{ex}}}^2(p_A{\omega }_A^2+p_B{\omega }_B^2}{{\omega }_A^2{\omega }_B^2+{\omega }_{\mathit{\text{eff}}}^2{k}_{\mathit{\text{ex}}}^2})}$$ (2)

where ${\omega }_{\mathit{\text{eff}}}^2={\mathrm{\Omega }}^2+{\omega }_1^2,{\omega }_A^2={({\mathrm{\Omega }}_A-{\omega }_{rf})}^2+{\omega }_1^2$ and ${\omega }_B^2={({\mathrm{\Omega }}_B-{\omega }_{rf})}^2+{\omega }_1^2․\mathrm{\Delta }{\omega }_{\mathrm{A}\mathrm{B}}={\mathrm{\Omega }}_{\mathrm{B}}-{\mathrm{\Omega }}_{\mathrm{A}}$, where Ω_A and Ω_B are the chemical shifts of the ground (A) and transient (B) states in Hz. R₁ and R₂ are the intrinsic longitudinal and transverse relaxation rate constants, respectively, and are assumed to be identical for the ground (A) and transient (B) states. θ = arctan(ω₁ / Ω) where ω₁ is the spin lock power strength. Ω = Ω_obs − ω_rf where Ω is the offset of the spin lock carrier frequency (ω_rf) from the observed resonance frequency (Ω_obs). Ω_obs = p_AΩ_A + p_BΩ_B where p_A and p_B are the ground and transient state populations, respectively and p_A + p_B = 1. k_ex is the chemical exchange rate constant for a two-state exchange process where k_ex = k_A + k_B, k_A = k_exp_B and k_B = k_exp_A. k_A and k_B are the forward and reverse rate constants, respectively.

Plots of R_1ρ data are presented as R_2eff (R_2eff = R₂ + R_ex) in Figure 1c and Supplementary Figure 1 where,

$$R_{2,\mathit{\text{eff}}}=\frac{R_{1\rho }}{{\text{sin}}^2\theta }-\frac{R_1}{{\text{tan}}^2\theta }$$ (3)

In cases where large errors were accompanied by small R_ex, model selection comparing presence and absence of exchange was carried out using the F- and Akaike’s Information Criterion (AIC)⁴⁶ tests to discriminate between exchange and no detectable exchange (data not shown). The F-Test compares two nested models fit to the same data under the null hypothesis that the residual sum of squares of the less complex, restricted model is not significantly larger than that of the more complex, full model. The AIC Test assesses the likelihood of a model given the data and seeks to minimize loss of information embedded within the data. For A₂ G23 N1 no exchange is the selected model under the conditions used. Because of lower sensitivity to exchange, we did not interpret absence of ¹⁵N dispersion as evidence for absence of transient HG bps.

The free energy difference between the WC GS and HG transient state (ΔG_WC-HG) was computed using,

$$\mathrm{\Delta }{G}_{WC–HG}=-RT\left(\text{ln}\right(\frac{k_{1}h}{k_{B}T})-\text{ln}(\frac{k_{2}h}{k_{B}T}\left)\right)$$ (4)

where k₁ and k₂ are the forward and reverse rate constants, respectively, h is Planck’s constant, k_B is Boltzmann’s constant, R is the gas constant and T is temperature. The forward barrier of the transition (ΔG^‡_WC-HG) was computed using,

$$\mathrm{\Delta }{G}_{WC–HG}^{\pm }=-RT\text{ln}\left(\frac{k_{1}h}{\kappa k_{B}T}\right)$$ (5)

where κ is the transmission coefficient which is assumed to be unity.

CD Melting

DNA duplexes (IDT, Inc.) were prepared using ultracentrifugation as described in NMR Samples and Resonance Assignments in 15 mM Phosphate buffer, 0.1 mM EDTA, 25 mM NaCl pH 5.4 and supplied with 10 % D₂O. Duplexes were prepared by diluting complementary single stranded stocks to 50 µM in the same tube with a final volume of 200 µL. Samples were denatured at 95 °C for 5 min followed by annealing of at least 10 min on the bench top. Samples were transferred to a 1 mm cuvette (Starna Cells), mineral oil was added to the top of the solution and the cuvette was capped. Melting experiments were performed on a Jasco Spectropolarimeter equipped with a recirculating water bath and Peltier temperature control unit. Temperature ramps were performed from 5 °C to 80 °C with a bandwidth of 5 nm (1 nm for ZJXN), ramp rate of 1 °C/min, equilibration time of 20 sec and sensitivity of 100 mdeg. Wavelength scans used the same sensitivity and bandwidth as melting runs. Spectral measurements were performed between 220 nm to 330 nm with a scan rate of 100 nm/min. Temperature ramp profiles were fit to the Boltzmann model⁴⁷, which has previously been used to determine nucleic acid melting temperatures⁴⁸,

$$\theta =LL+\frac{UL-LL}{1+e^{\frac{T_m-T}{a}}}$$ (6)

where θ is the elipticity at 254 nm normalized to the signal change magnitude, LL and UL are the lower and upper limits of the transition, respectively, a is the Hill slope, Tm is the melting temperature defined as the point of inflection of the melting curve and T is the independent variable temperature.

Phi (Φ)-value analysis

Φ-value analysis³⁴ was carried out by computing Φ using Equation 1 (Φ = Δ ΔG_TS–WC / ΔΔG_WC–HG) where ΔΔG_TS-WC= ΔG^‡_WC-HG,mut−ΔG^‡_WC-HG,Ψ-WT and ΔΔG_WC-HG= ΔG_WC-HG,mut−ΔG_WC-HG,Ψ-WT are the change in the forward free energy barrier (ΔG^‡_WC-HG) and free energy difference between WC and HG bps (ΔG_WC-HG), respectively, upon introduction of one or multiple mutations (mut) as compared to “wild-type” (Ψ-WT). We defined Ψ-WT to be A₅ T4 N3 and A₂ G10 N1 for A•T and G•C⁺ bps, respectively, given that they have the lowest ΔG_WC-HG values. To control for systematic errors in Φ arising due to use of a ¹⁵N Ψ-WT reference resonance, we also performed Φ-value analysis assigning a ¹³C resonance as Ψ-WT for A•T and G•C⁺ bps, respectively. In all cases we observe Φ-values concentrated around ~1 consistent with a “late” TS. Note that Φ≈ 0 when ΔΔG_TS-WC≈ 0 relative to ΔΔG_WC-HG implying an early WC-like TS, whereas Φ≈ 1 when ΔΔG_TS-WC≈ ΔΔG_WC-HG and implies a late HG-like TS. Errors for calculated Φ-values for A₆ A17 C8, A₂ A3 C1′, A₄ C15 C6 and A₅ G10 C8 were larger than the corresponding values and thus could not be determined accurately.