The Representation of Orientation in Macaque V2: Four Stripes Not Three

Daniel J Felleman; Heejin Lim; Youping Xiao; Yi Wang; Anastasia Eriksson; Arun Parajuli

doi:10.1093/cercor/bhu033

. 2014 Mar 9;25(9):2354–2369. doi: 10.1093/cercor/bhu033

The Representation of Orientation in Macaque V2: Four Stripes Not Three

Daniel J Felleman ¹, Heejin Lim ^1,², Youping Xiao ^1,³, Yi Wang ^1,⁴, Anastasia Eriksson ¹, Arun Parajuli ¹

PMCID: PMC4537415 PMID: 24614951

Abstract

Area V2 of macaque monkeys is traditionally thought to consist of 3 distinct functional compartments with characteristic cortical connections and functional properties. Orientation selectivity is one property that has frequently been used to distinguish V2 stripes, however, this receptive field property has been found in a high percentage of neurons across V2 compartments. Using quantitative intrinsic cortical imaging, we derived maps of preferred orientation, orientation selectivity, and orientation gradient in thin stripes, thick stripes, and interstripes in area V2. Orientation-selective responses were found in each V2 stripe, but the magnitude and organization of orientation selectivity differed significantly from stripe to stripe. Remarkably, the 2 pale stripes flanking each cytochrome oxidase dense stripe differed significantly in their representation of orientation resulting in their distinction as type-I and type-II interstripes. V2 orientation maps are characterized by clockwise and anticlockwise “orientation pinwheels”, but unlike V1, they are not homogeneously distributed across V2. Furthermore, V2 stripes contain large-scale sequences of preferred orientation. These analyses demonstrate that V2 consists of 4 distinct functional compartments; thick stripes and type-II interstripes, which are strongly orientation selective and thin stripes and type-I interstripes, which are significantly less selective for orientation and exhibit larger orientation gradient magnitudes.

Keywords: cortical modules, cortical streams, cytochrome oxidase, intrinsic imaging, visual cortex

Introduction

Area V2 in monkeys receives the majority of cortical input from V1 and projects to a number of higher cortical areas including V3, V4, and MT (Zeki 1971; DeYoe and Van Essen 1985; Shipp and Zeki 1985, 1989; Zeki and Shipp 1989; DeYoe et al. 1994; Felleman, Burkhalter et al. 1997; Gattass et al. 1997). Histologically, V2 is characterized by repeating cycles of cytochrome oxidase (CO) dense thick and thin stripes separated by CO-pale interstripes (e.g., Livingstone and Hubel 1983; Tootell et al. 1983). Although there are twice as many pale stripes as dense stripes in each cycle, the 2 interstripes have generally been grouped together resulting in a tripartite modular organization. Early single-unit studies supported this tripartite model with reports of high degrees of functional specialization across stripes. Color-selective cells were preferentially found in thin stripes, orientation-selective cells in thick and interstripes, end-stopped cells mostly in interstripes, and disparity-selective cells were preferentially found in thick stripes (DeYoe and Van Essen 1985; Hubel and Livingstone 1987). However, subsequent studies reported only moderate segregation of neuronal properties in different V2 stripes, thus challenging the notion of a strict tripartite functional specialization in V2 (Peterhans and Heydt 1993; Levitt et al. 1994; Gegenfurthner et al. 1996; Shipp and Zeki 2002; Friedman et al. 2003). Specifically relevant to this study, these investigators found a high preponderance of orientation-selective neurons in each stripe compartment as well as numerous examples of cells with joint selectivity for 2 features such as color-direction or color-orientation.

The tripartite model of V2 is generally supported by functional imaging studies where color-preferring or brightness/luminance-change loci and maps of hue are localized to thin stripes (Ts'o et al. 1990, 2001; Xiao et al. 2003; Wang et al. 2007; Lu and Roe 2008; Lim et al. 2009b), orthogonal orientation-preferring loci are localized to thick stripes and interstripes (e.g., Ts'o et al. 1990, 2001; Xiao et al. 2003), and differential responses to binocular disparity or motion stimuli are localized to thick stripes (Chen et al. 2008; Ts'o et al. 2009; Lu et al. 2010).

Although spatially organized maps of orientation are a key feature of the functional architecture of area V1 (e.g., Hubel and Wiesel 1977; Landisman and Ts'o 2002), surprisingly little is known about how orientation is represented in macaque V2. While several investigations have derived V2 orientation maps (e.g., Lim et al. 2009b; Ts'o et al. 2009; Lu et al. 2010), the spatial organization of and selectivity for orientation across macaque V2 stripes has not been studied quantitatively. Furthermore, since the degree of orientation selectivity is asymmetrically represented in the CO-pale stripes in owl monkey V2 (Xu et al. 2004), it is important to determine whether a similar functional asymmetry exists in macaque V2. Our analyses of orientation preferred angle, selectivity, and gradient demonstrate that its representation varies systematically across V2 and indicates that macaque V2 consists of 4 distinct sets of functional compartments. Portions of these results have been presented previously (Lim et al. 2009a).

Materials and Methods

General

The general animal preparation and experimental procedures were carried out using methods described previously (Xiao et al. 2003; Wang et al. 2007; Lim et al. 2009b). All procedures were consistent with the guidelines of the Society for Neuroscience for the use of laboratory animals and approved by the Animal Welfare Committee of University of Texas-Houston Health Science Center. Briefly, 7 long tailed macaque monkeys (Macaca fascicularis) were prepared for semichronic optical recording by sterile implantation of custom recording chambers over V2 of both hemispheres. After postoperative recovery, animals began a series of biweekly recording sessions. Animals were anesthetized with Sufentanil citrate (6–12 µg/kg/h.) and paralyzed with pancuronium bromide (0.05 mg/kg/h) delivered by intravenous infusion (10 mL/kg/h.; lactated Ringer's 5% dextrose). Electro-cardiogram, spO₂, end-tidal CO₂ and temperature were monitored continuously. A craniotomy and durectomy were performed to reveal portions of areas V1 and V2 adjacent to the lunate sulcus. Eyes were brought into convergence on the screen of a Trinitron monitor by custom fit contact lenses and a prism. The whole screen (19 × 14°) covered the visual field of the recorded portions of V2 (2–7° along the vertical meridian).

Optical Recording

During recording sessions, the chamber was filled with sterile silicone oil and sealed with an antireflection coated glass lid. The cortical surface was illuminated with 605 or 630 nm light that was generated by a tungsten source (100 W halogen, Zeiss), driven by an ultrastable power supply (Kepco), and delivered by fiber optics. The cortex was imaged using one of 2 cooled, slow-scan CCD cameras (Photometrics CH 250 EEV0206 or Photometrics Quantix EEV0206) using a dual lens macroscope (Nikon 50 mm, f 1.2). The data from the CH250 camera (Cases 1, 4–5) consisted of a series of 8 images (focused 0–300 µm below the surface), beginning before stimulus presentation and continuing for 3 s through the stimulation period. Image frames were 105 ms in duration and were acquired at a frame rate of 2/s. An interstimulus interval of 10 s allowed cortical activity to return to baseline conditions before the presentation of the next randomized stimulus. The data from the newer Quantix camera (Cases 3–4) consisted of a series of 40–50 images of 40 ms duration that were acquired at a frame rate of 10 frames/s. In all experiments, stimuli were repeated 50 times in a pseudorandom sequence and the respiration-synchronized frames were averaged to reduce noise. During the recording sessions, differential single-condition images were calculated to visualize cortical responses and to optimize data acquisition parameters.

Visual Stimuli and Data Analysis

Visual stimuli were generated using custom software implemented on one of 2 visual stimulation systems. In Cases 1, 4–5, visual stimuli were presented using a Silicon Graphics Indigo XZ workstation and CRT monitor. In Cases 2–3, stimuli were generated using the Visage visual stimulation hardware/software environment (Cambridge Research Systems) and were presented on a Hitachi CRT monitor. In both systems, custom programs enabled the presentation of grating stimuli of variable spatial and temporal frequencies, luminance contrasts, average luminance (10–35 cd/m², and isoluminant chromatic content. The luminance and chromaticity of the stimulus were calibrated using a Tektronix J17 LumaColor meter with a J1803 luminance head and a J1820 chromaticity head, and different chromatic gratings were adjusted for equal luminance (within 3%).

Single-condition Responses

Single-condition responses were calculated by comparing pixel values before stimulus presentation to those occurring during the stimulus presentation. In Cases 1, 4, and 5, the single-condition response at each pixel in each frame (105 ms) was calculated as the average deviation from the no-stimulus first frame divided by the first-frame intensity (ΔR/R). The resultant single-condition responses were filtered by Gaussian filters of 105 and 1050 µm to remove high and low frequency noise, respectively. The mean single-condition response to each stimulus condition was calculated as the pixel-by-pixel average of the single-condition responses observed during the last 4 image frames (1.3–2.9 s). In Cases 2–3, which used a higher frame rate camera system, single-condition responses were calculated using the pixel averages from 10 prestimulus frames (1 s) and stimulus-driven responses occurring during the last 3 s of the 4-s long stimulus. As in the other cases, single-condition images were filtered and the mean response was calculated during the period 1.3–2.9 s after stimulus onset.

The statistical significance of single-condition responses was calculated by Student's t-test (one-way) based on the pixel means and variances observed during the prestimulus and stimulus-driven responses. The statistical analysis of single-condition responses in Cases 1, 4, and 5 were based on the mean and variance of the first-frame pixel values across all stimulus conditions in a given data run (typically 4–6 stimuli) compared against mean and variance of pixel values during the 4 stimulus-driven frames beginning 1 s after stimulus onset (7–9 degrees of freedom. The statistical analysis of single-condition responses in Cases 2 and 3 were based on the mean and variance of the 10 prestimulus frames compared with the last 15 stimulus-driven frames beginning 2.5 s after stimulus onset (24 degrees of freedom).

Ocular Dominance and Chromatic-responses

The pattern of ocular dominance in V1 was revealed in the differential imaging of left eye versus right eye responses to high contrast gratings (100% contrast; 1–2 cycles/degree, 1–2 cycles/s) averaged across 4 orientations. Color-preferring thin stripes were identified in the differential images of responses to isoluminant chromatic gratings as compared with luminance-contrast gratings (Xiao et al. 2003). In several experiments, thin stripes were first identified in differential images and the spatial organization of hue maps thin stripes were later characterized from the statistically significant, peak single-condition responses to 4–8 isoluminant hue stimuli (see Xiao et al. 2003).

Orientation Maps

The organization and selectivity for stimulus orientation were analyzed using the vector summation method (e.g., Blasdel 1992). In these experiments, orientation maps were generated in response to high contrast luminance sine wave gratings (1–2 cycles/degree), presented at 2–8 equally spaced orientations with the responses average across both directions of movement. The calculated single-condition response to 50 repetitions of each stimulus was expressed as a vector orientation (θ) and all vectors were summed and divided by sum of the absolute values of the vectors to define a bias vector whose magnitude varied from 0 (equal responses to all θ) to 1 (response to only 1θ). The angle of the resultant bias vector corresponds to the cells preferred orientation. The resultant vector angles were illustrated by color-coded preferred angle maps. The degree of orientation selectivity was illustrated separately in gray-scale maps of orientation vector magnitude in which bright pixels indicated large vector magnitude. The distribution of orientation selectivity and preferred orientations was then illustrated through the logical AND of the RGB preferred angle and vector magnitude maps (ImageJ) such that the degree of orientation selectivity was encoded by the brightness of each pixel color; bright colors indicate strong orientation selectivity while dark colors indicate poor orientation selectivity.

Support Vector Machine Analysis of Orientation Preferred Angle and Selectivity

In Cases 2 and 3, calculation of V2 orientation preferred angle and selectivity maps were also calculated using the multivariate, Support Vector Machine (SVM) method (Xiao et al. 2008). In contrast to traditional univariate methods that rely solely on the distribution of response magnitudes for each stimulus, the SVM method utilizes the correlated variability of responses across the cortical surface to maximize the information about each stimulus encoded by the spatial distribution of responses to each stimulus. A major advantage of the SVM method is that the usually noisy “responses” generated by blood vessels are systematically removed due to their inherent variability. Unfortunately, the SVM method could not be applied to the data from Cases 1, 4, and 5, so comparisons across cases utilize the traditional method and the SVM maps are only introduced for comparison.

Orientation Pinwheels

Similar to V1, orientation maps in V2 were characterized by iso-orientation domains where the calculated preferred angle was relatively constant across the cortical surface. Furthermore, like V1, these iso-orientation domains often converged at orientation pinwheel centers. The locations of orientation pinwheel centers were identified quantitatively using a Matlab routine that identified pixel locations within the preferred angle map in which preferred angle values progressed in a complete sequence within a 5 or 7 pixel radius. These orientation pinwheels were further distinguished as clockwise or anticlockwise on the basis of the direction of change in preferred orientation observed around their centers. These pinwheel types are indicated by black and white circles centered on the quantitatively identified pinwheel centers in the preferred angle maps.

Orientation Gradient

The rate of change of preferred angle was expressed in gray-scale encoded orientation gradient maps in which regions of constant or low rate of preferred angle change were encoded by dark gray pixels while regions characterized by rapid changes in preferred angle were encoded by the brightest pixels. Orientation gradient was calculated on a pixel-by-pixel fashion as the average change in preferred angle over a 1–3 pixel radius. Orientation gradient was thus defined as average preferred angle change over an ∼21–66 µm radius (21 µm/pixel). These orientation gradient maps facilitated the identification of stripe compartments with high orientation gradients (e.g., type-I interstripes) and also identified regions of rapid orientation change that often occurred in association with orientation pinwheels and orientation fractures within thick or type-II interstripes stripes or along their borders with other stripes.

Statistical Analysis of Orientation Map Features

Orientation selectivity within each stripe was quantified by the average orientation vector magnitude resulting from the vector summation of single-condition responses at each pixel. In each case, orientation vector magnitudes were calculated separately for each stripe (e.g., thin1, thin2, thick1, thick2, etc.) and the pixel number-weighted average values were calculated when multiple instances of a stripe-type were observed in any given hemisphere (e.g., multiple thin stripes). Similar analyses were performed using the calculate orientation gradient magnitudes. The nonparametric Wilcoxon's test of rank order was then applied to test for the significance of the observed differences in selectivity between individual stripes and between average differences between stripe-types.

Since traditional statistical methods depend on the independence of samples within a population, yet nearby pixels are likely to correlated, 2 statistical approaches were employed to assess the significance of stripe differences. Since individual pixels represent ∼21 µm of cortical space, adjacent pixels are expected to be highly correlated due to hemodynamic and light scattering functions that extend ∼50 µm.) In the first method, pixel values within each stripe compartment were randomly subsampled to minimize the probability of locally correlated samples. Pixel values within individual stripes were subsampled at 30, 10, 3, and 1% and the resultant pixel distributions between stripe pairs were then evaluated using the Wilcoxon's test of rank order. Although each randomly subsampling procedure produced very similar results, the 10% method was finally chosen in order to both minimize the possible correlations between adjacent pixels and to minimize the number of pixels within each sample. Furthermore, very similar results were observed using a bootstrap statistical method in which the ratio of average orientation selectivity magnitude was first calculated from the full sample of pixel values from a given pair of V2 stripe compartments which was then followed by random assignments of individual pixels to either of the 2 stripes under investigation. This randomization procedure was then repeated 10 000 times to form a ranked distribution of selectivity ratios to which the “real” ration was compared.

The overall significance of the differences in average vector magnitude observed in the individual stripe compartments in each case was evaluated by comparing the vector magnitudes in each stripe compartment across all 4 cases using the nonparametric Kruskal–Wallis test. The significance of the difference in vector magnitude between specific stripe-type pairs was evaluated using the nonparametric Wilcoxon's rank order test. Similar methods were used for the analysis of orientation gradient.

Anatomical Methods

In all cases, multiple neuroanatomical tracers were injected into functionally characterized loci. Their positions relative to the orientation maps were made with reference to the detailed patterns of cortical surface vasculature. At the termination of the anatomical transport period, the monkey was deeply anesthetized with Nembutal (75–100 mg/kg, i.v.) and briefly perfused intracardially with saline followed by 4% paraformaldehyde in 0.1 M phosphate buffer (pH 7.4). The brain was removed from the skull and the occipital operculum was dissected, unfolded slightly, gently pressed between glass slides, briefly postfixed in the final cryoprotective solution, and later sectioned in the tangential plane.

Frozen sections were cut at 31 µm in thickness. The pattern of CO activity in V1 and V2 was demonstrated according to Wong-Riley and Carroll (1984). Briefly, free-floating sections were incubated in a large volume of oxygenated reaction mixture for 5–24 h at 37°C. Sections were then washed, mounted on subbed slides, and air dried before dehydration and cover-slipping. The locations of CO dense and pale regions in V1 and V2 were determined using a computer-interfaced microscope scoring system or were digitized using a high resolution flatbed scanner (1200 dpi). The CO-stained sections were used to compare the optical activation to the CO structure of V2, and to confirm the injection sites relative to CO stripes. Histological sections were aligned to cortical functional maps using the pattern of surface vasculature and the locations of tracer injection sites. In 2 cases, the first histological sections contained detailed patterns of the surface vasculature that were readily aligned to images of the surface vasculature in vivo. Radially aligned blood vessels, injection sites, and other fine edge landmarks were used to align multiple histological sections.

Results

Overview

The representation of orientation in different CO-defined V2 stripes was determined in 8 regions from 6 hemispheres of 4 macaque monkeys. In the first case (2 hemispheres; 4 fields of view), the spatial distributions of the responses to 2 orthogonal orientations were compared with the distributions of chromatic-preferring responses to evaluate the relationship of orientation selectivity to the CO stripe location. In the remaining 4 cases, quantitative maps of orientation angle preference and orientation selectivity were computed from 4–12 single-condition images acquired from parafoveal V2 along the dorsal V1–V2 border. In these cases, orientation pinwheels were identified in the preferred angle maps by determining the pattern of preferred orientations surrounding each pixel at different radii. Furthermore, maps of the orientation gradient were determined by calculating the rate of change in preferred orientation within a 100 µm radius of each pixel. In all cases, robust orientation selectivity was observed in V2 thick stripes and a strong asymmetry in the orientation selectivity was observed in the interstripes flanking each CO-dense stripe. While robust orientation selectivity was observed in each interstripe located medial to each thick stripe, only weak orientation selectivity was observed in the interstripes located lateral to the thick stripes. Following the terminology of Xu et al. (2004) we call these 2 types of interstripes the type-II and type-I interstripes, respectively. These results demonstrate that orientation selectivity varies systematically across 4 functionally distinguishable V2 stripes. Robust orientation selectivity was observed in thick stripes and type-II interstripes, whereas weak selectivity was observed in thin stripes and type-I interstripes.

Distribution of Statistically Significant Responses Across CO Compartments

The distribution of statistically significant responses to moving oriented gratings was determined by aligning intrinsic optical responses, referenced to the cortical surface vasculature, to histological sections stained for the demonstration of CO. This alignment was achieved by recovering the locations of 2–6 neuroanatomical tracer injections in stacks of histological sections themselves aligned using the pattern of radial blood vessels that extended across the flattened, tangential sections. In 2 of these cases, the alignment was further facilitated by directly recovering the pattern of the cortical surface vasculature in the most superficial histological sections.

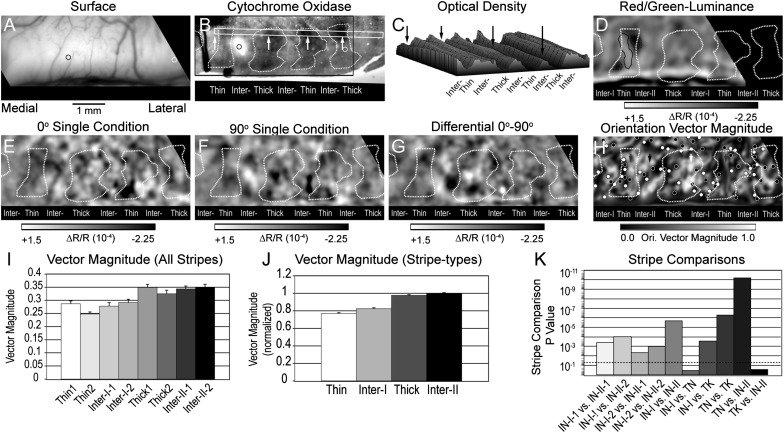
The distribution of significant single-condition responses and differential orientation responses across CO compartments for one exemplary case are illustrated in Figure 1. In this case (Case 1; w04l02b), 4 neuroanatomical tracer injections were placed relative to the surface vasculature (Fig. 1A) and were recovered in the CO sections (Fig. 1B–C). A low magnification view of a CO-stained section in Figure 1B illustrates 5 CO-dense stripes in this region. The central region containing 3 CO-dense stripes and 2 CO-pale interstripes corresponds to the field of view of the remaining functional images (Fig. 1C). The central CO-dense stripe was identified as a thin stripe on the basis of 2 different observations. First, this CO-dense stripe is coincident with the spatially segregated isoluminant hue responses (see insets in Fig. 1A) that are characteristic of thin stripes (Xiao et al. 2003). Second, these hue-specific responses were located within the dark region correspond to the color-preferring region indicated in the differential image comparing red/green isoluminant responses to luminance-contrast responses (Fig. 1D). In both the 45° (Fig. 1C) and 135° (Fig. 1D) single orientation condition images, robust responses were observed within the flanking CO-dense thick stripes and within the CO-pale region immediately medial to the more lateral thick stripe. Although statistically significant (P < 0.05) responses to individual oriented gratings were observed in each stripe compartment (Fig. 1H), clearly segregated single-condition responses, characteristic of robust orientation selectivity was only observed within the 2 thick stripes and in the interstripe medial to the lateral thick stripe (Fig. 1G).

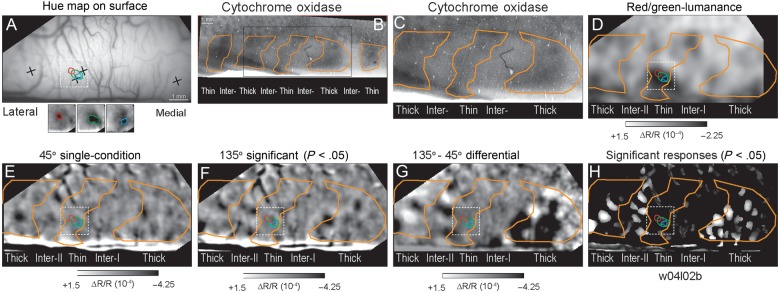
Figure 1. — Statistically significant responses aligned to CO stripes. (A) Cortical surface vasculature used to align functional images to histological tissue. Crosses indicate the positions of neuroanatomical tracer injections subsequently recovered in tissue sections. Red, green, and blue contours within the black square indicate the cortical positions of significant isoluminant single hue responses indicated in the functional image inserts below and superimposed on panels D–H. (B) Low magnification view of CO pattern in this hemisphere. The black rectangle indicates the region corresponding to the imaged portion of this case. (C) CO section corresponding to the imaged portion of the hemisphere. Orange contours indicate borders of CO-dense stripes. (D) Differential image comparing responses to isoluminant red/green grating and luminance-contrast grating. The single-condition hue responses align with the color-preferring (dark pixels) of the thin stripe. (E) Single-condition (ΔR/R) image resulting from stimulation with a moving 45° luminance-contrast grating moved in both directions. (F) Single-condition (ΔR/R) image resulting from stimulation with a moving 135° luminance-contrast grating moved in both directions. (G) Differential image indicating the activation pattern in response to 135–45° gratings. (H) Sum of the statistically significant single-condition activations in response to 45 and 135° gratings. (Case 1; w04l02b).

Quantitative Analysis of Orientation Selectivity in Different CO Compartments

The relationships among CO architecture, chromatic-preferring and orientation-selective domains are illustrated for Case 2 (s06) in Figure 2. In this hemisphere, 2 distinguishable neuroanatomical tracers were injected into V2 and their positions were recorded with reference to the cortical surface vasculature (Fig. 2A). These injection site locations were subsequently recovered in the stack of histological tissue including the CO section illustrated in Figure 2B. The alternating pattern of CO-staining density across the CO-dense and CO-pale stripes within the rectangular ROI (white box) in this section is illustrated as an optical density surface plot in Figure 2C. The cyclical variation in relative optical density within this ROI demonstrates the positions of the CO-dense and CO-pale stripes in this case.

Four CO-dense stripes were distinguished as thin or thick on the basis of (1) the color-preferring responses observed in the differential image of red/green isoluminant minus luminance-contrast grating responses (Fig. 2D) and (2) the robust orientation responses in the differential image comparing responses to 0 and 90° gratings (Fig. 2G). The dark pixels in the red/green-luminance differential image (dashed black contours; Fig. 2D) are coincident with the CO-dense stripe on the left of this figure, whereas the area devoid of the color-preferring activations coincides with the CO-dense stripe to the right of the central thick stripe. Conversely, the central CO-dense stripe demonstrated robust activations in the 0–90° orientation differential image (Fig. 2G) that was lacking in the CO-dense (thin) stripe at the left of this figure. Unfortunately, the red/green-luminance and the 0–90° orientation differential images only partially overlap, so it was not possible to determine whether color-preferring activations were also coincident with the CO-dense stripe to the right of the central thick stripe in Figure 2G. On the basis of these response distributions, the central CO-dense stripe was identified as a thick stripe and the 2 flanking stripes were identified as thin stripes. Finally, the orientation-specific responses associated with the most laterally positioned CO-dense stripe and immediately medial interstripe are consistent with the view that this most lateral stripe is also a CO-dense thick stripe.

Orientation selectivity was quantified by the orientation vector magnitude resulting from the normalized vector summation of the 4 single-orientation responses (vectors) calculated on a pixel by pixel basis. The resulting distribution of orientation selectivity and its relationship to the pattern of CO architecture is illustrated in gray-scale in Figure 2H. In this and all other cases, the average and distribution of orientation selectivity in each CO compartment was quantified from all pixels demonstrating statistically significant (P < 0.05) response to at least one stimulus orientation. In the resulting vector magnitude maps, pixels exhibiting robust orientation selectivity are bright, while pixels with low orientation selectivity are dark.

In this case, the most highly orientation-selective responses were observed in the centrally located CO-dense thick stripe (white arrow) and in the CO-pale stripe (black arrow) immediately medial to it. High orientation selectivity was also seen in the lateral CO-dense thick stripe and in the immediately medial interstripe. In contrast, lower pixel values of vector magnitude were observed in each thin stripe and in the CO interstripe lateral to the thick stripe (gray arrow). Statistically significant orientation-selective responses are also observed within the 2 thin stripes and in the interstripe lateral to the thick stripe. The asymmetrical distribution in the magnitude of orientation selectivity in sequential V2 interstripes is consistent with that originally reported for V2 of owl monkey (Xu et al. 2004). Accordingly, the interstripe exhibiting low orientation selectivity and located lateral to a thick stripe is designated as a type-I interstripe, whereas the high selectivity interstripe located medial to a thick stripe is designated as a type-II interstripe.

The average orientation selectivity for statistically significant responses in each cytochrome oxidase stripe compartment is illustrated by the histogram in Figure 2I. As indicated in the Materials and Methods, 10% random sampling of pixels within each stripe compartment was used to summarize stripe tuning properties and to facilitate the statistical evaluation of the differences in average vector magnitude between stripes. It should be noted that the mean and variance of pixel values was largely independent of sampling strategy (100, 30, 10, or 1%), but the 10% statistics are reported here because they facilitate statistical comparisons between ROIs in different CO compartments (see Materials and Methods) while maintaining adequate sampling without excess degrees of freedom. In this case, orientation selectivity was assessed separately for the 5 CO-defined compartments (Fig. 2I). The highest orientation selectivity was observed in the 2 type-II interstripes (0.344 and 0.350) and in the 2 thick stripes (0.349 and 0.325). In contrast, the lowest orientation selectivity was exhibited by the 2 type-I interstripes (0.278 and 0.291) and in the 2 thin stripes (0.287 and 0.248).

The normalized average orientation selectivity for each stripe-type, based on the pixel number-weighted average of the orientation vector magnitude exhibited by the 2 thin, thick, interstripe type-I, and interstripe type-II, is illustrated in the histogram in Figure 2J. As with the individual stripe orientation vector magnitudes, the highest normalized orientation selectivity was observed in the type-II interstripes (1.00) and thick stripes (0.976), while lower selectivity was observed in the thin stripes (0.770) and type-I interstripes (0.824). Overall, orientation vector magnitude varied significantly across stripe compartments (P < 0.0038, Kruskal–Wallis, nonparametric). A priori, nonparametric tests (Wilcoxon's rank sum) were then used to determine the significance of the observed differences in average orientation vector magnitude between pairs of individual stripes and stripe-types (Fig. 2K; see Table 1). Overall, the type-II interstripes exhibited greater orientation selectivity than the type-I interstripes (P < 2.00 × 10⁻⁶) and thin stripes (P < 6.32 × 10⁻¹¹). The overall difference between type-I and type-II interstripes was also born out in the comparisons between individual stripes. Thus, interstripe-I-1 was less selective than interstripe-II-1 (P < 3.72 × 10⁻⁴) and interstripe-II-2 (P < 9.96 × 10⁻⁵), and interstripe-I-2 was less selective than interstripe-II-1 (P < 4.34 × 10⁻³) and interstripe-II-2 (P < 1.05 × 10⁻³). Similarly, thick stripes were significantly more selective than both the type-I interstripes (P < 2.73 × 10⁻⁴) and thin stripes (P < 5.35 × 10⁻⁷). Finally, the average orientation selectivity in thin stripes was indistinguishable from the type-I interstripes (P > 0.339) and thick stripes were indistinguishable from type-II interstripes (P > 0.283).

Table 1.

Statistical significance of each stripe-type and stripe comparison of orientation vector magnitude for each case and across all 4 cases (right column)

Case	2	3	4	5	All cases
Comparison	s06g	s07f	m32e	m31g
Thin versus Inter-I	0.339	2.15E−03	0.927	0.063	0.4848
Thin versus thick	5.35E−07	3.16E−11	3.07E−13	0.004	0.018
Thin versus Inter-II	6.32E−11	8.73E−05	5.76E−37	0.008	6.66E−04
Inter-I versus Thick	2.73E−04	2.62E−33	2.73E−06	1.40E−07	0.0076
Inter-I versus Inter-II	2.00E−06	1.38E−14	3.84E−19	1.07E−06	6.66E−04
Thick versus Inter-II	0.283	0.022	2.26E−11	0.917	0.3543
				K/W	0.0038
Inter-I-1 versus Inter-II-1	3.72E−04	1.90E−07		1.64E−06
Inter-I-1 versus Inter-II-2	9.96E−05			0.001
Inter-I-2 versus Inter-II-1	4.34E−03	1.27E−14	3.11E−13
Inter-I-2 versus Inter-II-2	1.05E−03		4.93E−15
Inter-I-2 versus Inter-II-3			4.20E−10

Open in a new tab

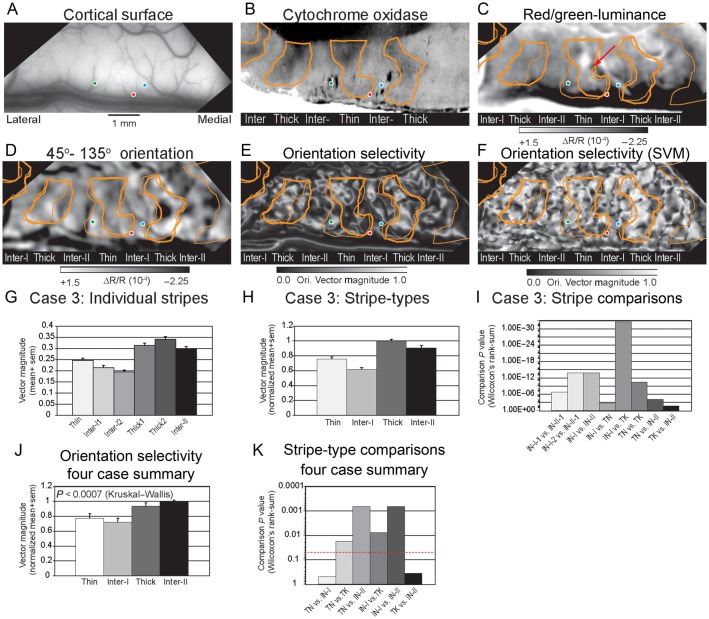
The systematic differences in orientation selectivity between different CO-dense stripes and CO-pale interstripes are illustrated for a second case (Case 3; s07) in Figure 3. In this case, the positions of 3 neuroanatomical tracer injections, encoded relative to the cortical surface vasculature were later recovered in the histological sections (Fig. 3A,B) which facilitated the alignment if the functional images to the pattern of CO architecture. Unfortunately, the CO histology in this case was suboptimal due to a poor postmortem perfusion. The centrally located CO-dense stripe was determined to be a thin stripe due to the robust hue and luminance activations in the red/green-luminance different image (Fig. 3C). This stripe assignment is also consistent with the distribution of orientation-specific responses observed in the CO-dense stripes flanking the central thin stripe in the 45–135° orientation differential image (Fig. 3D).

Consistent with Case 2, high orientation selectivity, indicated by bright pixels in the orientation vector magnitude map (Fig. 3E), was observed in the 2 thick stripes and the type-II interstripe located medial to the thick stripe. The average orientation vector magnitudes exhibited by the individual CO-stripe compartments are illustrated in Figure 3G and the statistical significance of these differences is illustrated in Figure 3I. The orientation selectivity of the type-II interstripe (0.297) was significantly greater than both type-I interstripe-1 (0.214; P < 1.90 × 10⁻⁷) and type-I interstripe-2 (0.195; P < 1.27 × 10⁻¹⁴). Similarly, the vector magnitude of thick stripe1 (0.313) was significantly greater than type-I interstripe-1 (P < 1.17 × 10⁻¹⁵) and type-I interstripe-2 (P < 3.91 × 10⁻²⁰). Thick stripe2 (0.341) was similarly more selective than both type-I interstripe-1 (P < 2.53 × 10⁻¹⁵) and type-I interstripe-2 (P < 1.96 × 10⁻²⁰). Finally, the orientation selectivity of the thin stripe (0.247) was indistinguishable from type-I interstripe-1 (P > 0.472) and type-I interstripe-2 (P > 0.096).

The normalized average orientation selectivity for each CO stripe-type in this case is illustrated in Figure 3H. The statistical significance of the observed differences in orientation vector magnitude is illustrated in Figure 3I and in Table 1. Similar to the pattern of orientation selectivity observed in Case 2, the average orientation vector magnitude in the type-II interstripe was significantly greater than in the type-I interstripe (P < 1.38 × 10⁻¹⁴) and the thin stripes (P < 8.73 × 10⁻⁵). In addition, the thick stripes were significantly more selective than the type-I interstripes (P < 2.62 × 10⁻³³) and thin stripes (P < 3.16 × 10⁻¹¹). Finally, unlike Case 2, the orientation selectivity observed in this thin stripe was significantly greater than the average selectivity of type-I interstripe (P < 2.15 × 10⁻³).

Across 4 cases, a total of 31 stripe compartments were analyzed quantitatively for their orientation selectivity; 6 thin stripes, 6 type-I interstripes, 10 thick stripes, and 9 type-II interstripes. The average orientation vector magnitude for each stripe in each case is summarized in Table 2. In 3 cases, the largest orientation vector magnitude was observed in a type-II interstripe (Case 2, 4, and 5), whereas in Case 3, the greatest orientation selectivity was observed in a thick stripe. The smallest orientation vector magnitude was observed in a type-I interstripe in 2 cases (Cases 3 and 5), in a thin stripe in Cases 2 and 4. The average normalized orientation selectivity for each stripe-type in each case is summarized in Table 3. In 3 cases the highest orientation selectivity was observed in type-II interstripes, whereas in Case 3, the highest selectivity was observed in thick stripes. In 2 cases, the lowest orientation selectivity was observed in thin stripes (Cases 2 and 4), whereas the lowest selectivity was observed in the type-I interstripe in Cases 3 and 5.

Table 2.

Average orientation vector magnitude (orientation selectivity) for each stripe in each quantitatively analyzed case

Case	2	3	4	5
Stripe	s06g	s07f	m32e	m31g
Thin-1	0.287	0.247	0.281	0.556
Thin-2	0.248			0.549
Interstripe-I-1	0.278	0.214	0.323	0.491
Interstripe-I-2	0.291	0.195
Thick-1	0.349	0.313	0.465	0.642
Thick-2	0.325	0.341	0.321	0.623
Thick-3			0.494
Interstripe-II-1	0.344	0.297	0.529	0.668
Interstripe-II-2	0.350		0.545	0.615
Interstripe-II-3			0.557

Open in a new tab

Table 3.

Normalized average orientation vector magnitude in the 4 V2 stripe-type compartments in each quantitatively analyzed case

Case	2	3	4	5	Average
Stripe	s06g	s07f	m32e	m31g
Thin	0.770	0.756	0.519	0.896	0.773
Interstripe-I	0.824	0.620	0.599	0.603	0.721
Thick	0.976	1.000	0.792	0.957	0.932
Interstripe-II	1.00	0.909	1.000	1.000	1.00

Open in a new tab

Although a complete analysis of orientation selectivity across stripe compartments was performed in Cases 4 and 5 (summarized in Tables 1–3, this section focuses primarily on the observed differences in selectivity between the 2 types of interstripes in these cases. Although the functional imaging In Case 4 (m32) spanned more than 2 stripe cycles, the CO staining was ambiguous in the vicinity of thin stripe1 and type-I interstripe1 and thus their selectivity has been excluded from this analysis. The other type-I interstripe was significantly less orientation selective than type-II interstripe 1 (P < 3.11 × 10⁻¹³), type-II interstripe 2 (P < 4.93 × 10⁻¹⁵), and type-II interstripe 3 (P < 4.20 × 10⁻¹⁰). In Case 5 (m31) the type-I interstripe was significantly less orientation selectivity than the type-II interstripe 1 (P < 1.64 × 10⁻⁶) and type-II interstripe 2 (P < 0.001).

The normalized average orientation selectivity exhibited by the 4 types of CO compartments across all 4 cases is summarized in the histogram in Figure 3J. Overall, high normalized orientation selectivity was observed in type-II interstripes (1.00) and thick stripes (0.932) and lower selectivity was observed in type-I interstripes (0.721) and thin stripes (0.773). The statistical significance of each a priori stripe-type comparison across these 4 cases is summarized in Figure 3K and in the right-most column in Table 1. Orientation selectivity (vector) magnitude varied significantly across stripe-type (P < 0.0007; Kruskal–Wallis). A priori comparisons (Wilcoxon's rank sum test) were then used to determine the sources of this overall difference. Type-II interstripes were found to be significantly more orientation selective than type-I interstripes (P < 6.66 × 10⁻⁴), thin stripes (P < 6.66 × 10⁻⁴), but their selectivity was indistinguishable from thick stripes (P > 0.3543). Furthermore, type-I interstripes were significantly less orientation selective than thick stripes (P < 0.0076), but were indistinguishable from thin stripes (P > 0.4848). When considered on a case-by-case basis, orientation selectivity in type-I interstripes was indistinguishable from thin stripes in 3 of 4 cases. Similarly, orientation selectivity in thick stripes was indistinguishable from type-II interstripes in 2 of 4 cases.

Organization of Orientation Preferred Angle and Selectivity

The organization of orientation preferred angle and selectivity was analyzed quantitatively using the previously described single-condition vector summation method. The preferred orientation of each pixel was defined as the angle resulting from the summation of the individual single-condition response vectors, whereas the degree of orientation selectivity was defined as the magnitude of this normalized vector summation. In the following preferred angle and orientation selectivity maps, the preferred angle is illustrated using a 6 or 8 orientation color code. In this section, the organization of orientation preferred angle and its relationship to CO stripe compartments is described in 2 cases to illustrate some of the basic principles underlying the representation of orientation in V2.

The organization of orientation preferred angle and orientation selectivity in Case 2 (s06) are illustrated in Figure 4A–D The global preferred angle (Fig. 4A) and higher magnification insert of the central full stripe cycle (Fig. 4B) maps illustrate several important aspects of the representation of orientation across V2 CO stripe compartments. First, preferred angle varies smoothly both within each V2 CO stripe compartment. Second, like V1, preferred angle maps in V2 are characterized by both clockwise and anticlockwise orientation pinwheel centers that indicate loci in which a full set of sequentially ordered iso-orientation domains converge. Third, in addition to orientation pinwheels, larger sequences of preferred angles are observed within individual CO compartments and many of these sequences span across stripe borders. These features of the representation of preferred angle are discussed below.

In general, each V2 stripe compartment contains a systematic representation of preferred orientation, but stripe-types differ in the size of iso-orientation domains and in their degree of orientation selectivity. For example, the centrally located type-II interstripe and thick stripe in Figure 4A,B, contain relatively large iso-orientation domains. The relatively bright pixels in the corresponding orientation selectivity maps in Figure 4C and d indicate that these stripes are also highly selective for their preferred orientation. In contrast, the color-coded clusters of preferred angle within the type-I interstripe and thin stripe are smaller than those observed in thick stripes and type-II interstripes (Fig. 4A,B). In addition, the relatively dim pixels in the corresponding orientation selectivity map indicate they are also less orientation selective (Fig. C,D).

Similar to area V1, V2 orientation maps are characterized by orientation pinwheels that tend to be organized in pairs; in one set of pinwheels (white circles) orientation changes from 0 to 180° in a clockwise progression, while in the other set (black circles), orientation changes in an a counterclockwise order. However, in contrast to V1 where pinwheel center separation and iso-orientation domain size are largely homogeneous, the distribution of orientation pinwheels in V2 is highly variable within and between stripes. As described in the next section, the average rate of change of preferred angle is an important factor that governs pinwheel density and is largest within thin stripes and type-I interstripes. Although orientation pinwheels are a critical organizing feature of the local representation within each CO compartment, their overall distribution also plays a critical role in determining more global aspects of orientation sequences within and across V2 stripes.

In addition to local preferred angle sequences dictated by the largely alternating pattern of clockwise and counterclockwise pinwheel centers, V2 stripes also contain larger scale sequences of preferred orientation. Multiple examples of these large-scale sequences are indicated by the white arrows superimposed on the preferred angle (Fig. 4A) and orientation selectivity maps (Fig. 4C) as well as on the corresponding enlargements of the central stripe cycle illustrated in Figure 4B,D, respectively. In general, each stripe compartment contains multiple examples of these large-scale orientation sequences. Furthermore, these sequences generally “flow” in an orderly, continuous fashion across adjacent stripes. However, in some instances, these large-scale orientation sequences reverse order at the stripe border.

The organization of these large-scale orientation sequences in this case is best discussed with respect to the enlargement of the central stripe set illustrated in Figure 4B,D. For example, the central thick stripe contains multiple orientation sequences (white arrows) whose preferred angles progress smoothly in a clockwise order from medial to lateral. One complete orientation sequence is demonstrated by the white arrow at the bottom of this thick stripe. Specifically, this portion of the thick stripe contains a sequence that begins at 90° (aqua) and shifts through 120° (green), 150° (yellow), through vertical (180°/0°; red), 30° (purple), and ending at 60° (blue). A similar, more extensive orientation sequence is depicted by the white arrow located in the central portion of this thick stripe.

Large-scale orientation sequences are also readily observed within the medially adjacent type-II interstripe. Similar to the thick stripe, clockwise progression of preferred angle are displayed along the medial to lateral paths. In general, the large-scale orientation sequences observed within this type-II interstripe appear to “flow” continuously across the border with the thick stripe.

The organization of large-scale orientation sequences in type-I interstripes and thin stripes was generally more complex, primarily due to the smaller size of iso-orientation domains and somewhat higher pinwheel center density. Nevertheless, clear examples of large-scale orientation sequences were observed in this case. For example, a long sequence that progressed from ∼30° (purple), 90° (aqua), 180°/0° (red), and repeated the sequence through 135° (yellow) is illustrated by the white arrow in the lower portion of the type-I interstripe. In contrast to the type-II interstripe/thick stripe border, the order of this orientation sequence appears to reverse at the thick stripe border. However, sequence reversal is only seen in this lower portion of the stripe, whereas largely continuous orientation progression is seen in the upper portion of the type-I interstripe/thick stripe border. Finally, multiple large-scale orientation sequences are observed in the thin stripe with more simple progression located anteriorly and more complex, mirror-symmetrical sequences located posteriorly.

Similar patterns of orientation preferred angles, orientation selectivity, orientation pinwheels, and large-scale orientation sequences were observed in Case 4 (m32; Fig. 4E–J). The orientation preferred angle and orientation selectivity maps, extending across nearly 2 full stripe cycles, are illustrated in Figures 4G,H, respectively. The preferred angle and selectivity maps from the lateral thick and type-II interstripes are illustrated in Figure 4F,I, respectively. In addition, a close-up view of the preferred angle and selectivity of the more medially situated thick, thin and intervening type-II interstripe are illustrated in Figure 4G,J, respectively. As in Case 2, large iso-orientation domains and distinct large-scale orientation sequences were observed within the type-II interstripes and thick stripes. This case further demonstrates how stripe borders impact orientation preferred angle sequences. For example, the preferred angle sequence is largely continuous across the type-II interstripe/thick stripe border in Figure 4F, whereas the sequence of preferred angles appears to reverse along this type of border in the more medially situated stripe pair (Fig. 4G). Finally, this figure also demonstrates that the preferred angle can also progress in parallel, as indicated by the white arrows along the anterior portions of this type-II interstripe/thick stripe border.

Orientation Gradient and its Relationship to Vector Magnitude

The magnitude of the orientation gradient quantifies, for each pixel, the average rate of change of preferred angle calculated over a ∼21–63 µm radius and averaged over 4 directions. Orientation gradient magnitude varies from a minimum of ∼0⁰/100 µm within the center of large iso-orientation domains to a maximum of 90° when a pixel is surrounded by pixels with maximal preferred angle differences. The relationship between orientation gradient and CO-compartment was visualized in gray-scale maps in which dark pixels represent low rate of change in preferred angle while bright pixels indicate a high rate of preferred angle change. High rates of preferred angle change were associated with orientation pinwheel centers, orientation fractures associated with rapid changes of preferred angle within and/or between CO-stripe compartments, and relatively rapid changes in preferred angle associated with small iso-orientation domains within thin stripes and type-I interstripes. In this section, the relationships between orientation gradient and orientation selectivity as a function of CO compartment are illustrated for 2 cases. The section concludes with a summary of the relative magnitude of orientation gradient across CO stripe-types in all 4 cases and the statistical analysis of CO-stripe differences in orientation gradient magnitude.

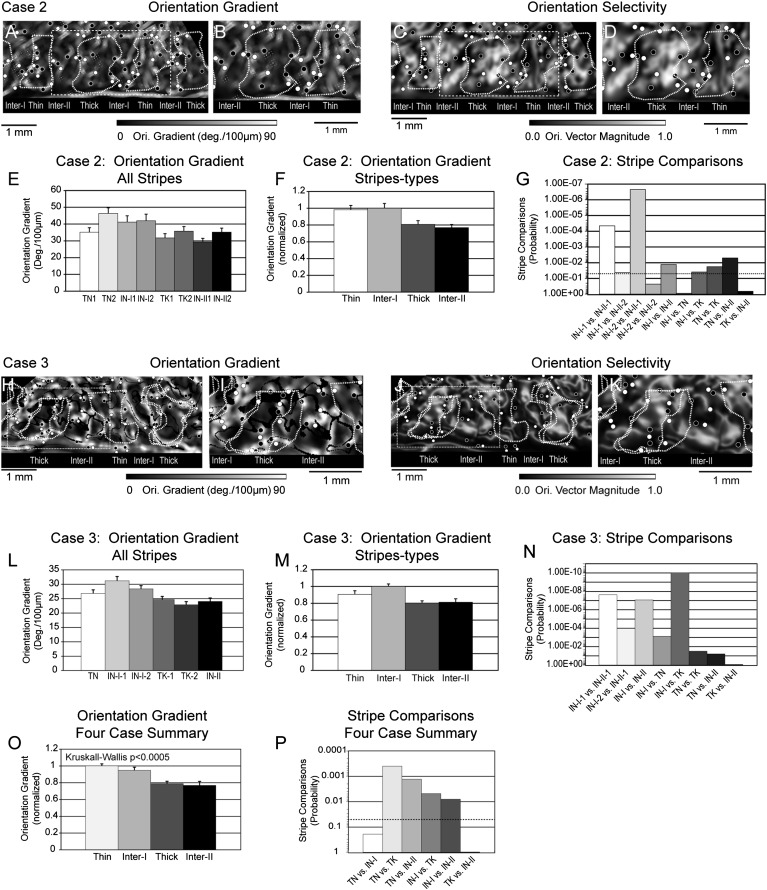
The relationships among orientation gradient magnitude, orientation vector magnitude, and CO-compartment from Case 2 is illustrated in Figure 5A–G. The orientation gradient map (Fig. 5A) and the higher magnification insert covering the central 4 stripe compartments (Fig. 5B) demonstrate that relatively low average gradient magnitudes are found within the thick stripe and type-II interstripe (dark pixels) and somewhat higher average gradient magnitudes are found within the thin stripe and type-I interstripe (bright pixels). These panels also illustrate that the clockwise (white circles) and anticlockwise (dark circles) orientation pinwheel centers are almost exclusively located within bands of high orientation gradient. However, not all regions of high orientation gradient contain orientation pinwheel centers.

The orientation vector magnitude maps (Fig. 5C–D) are illustrated here to highlight the near complementary relationship between orientation gradient magnitude and orientation selectivity. In general, regions of low gradient magnitude are associated with high orientation vector magnitude. This relationship is most obvious in the central thick stripe (compare Fig. 5C–D) where the region of high orientation selectivity and bright, smoothly varying preferred angle (see orientation sequences in Fig. 4C–D) exhibit very low gradient magnitude. Conversely, the portions of the type-I interstripe and thin stripe that exhibit high orientation gradient magnitudes are associated with low vector magnitude.

The average orientation gradient magnitude observed within each of the 7 CO stripe compartments in this case is illustrated in Figure 5E. The largest average orientation gradients were observed in thin stripe 2 (46.35°/100 µm) and type-I interstripe-2 (41.98°/100 µm). The type-I interstripe exhibited the third largest gradient magnitude (32.59°/100 µm), whereas the lowest gradient magnitudes were observed in type-II interstripe-1 (29.36°/100 µm) and thick stripe 1 (31.77°/100 µm).

The normalized orientation gradient magnitude observed within the 4 CO stripe-types indicates that the type-I interstripe (1.00) and thin stripe (0.983) had the largest normalized gradient magnitudes, whereas the type-II interstripes (0.770) and thick stripe (0.808) had the smallest relative orientation gradient (Fig. 5F; see Table 4). A priori, nonparametric tests (Wilcoxon's rank sum) were then used to determine the significance of the observed stripe differences. The gradient within type-I interstripes was significantly greater than in type-II interstripes (P < 0.013) and thick stripes (P < 0.039), but was indistinguishable from the gradient observed in the thin stripe (P > 0.879). Furthermore, the overall difference in orientation gradient observed for type-I and type-II interstripe types was observed in 3 of 4 possible stripe comparisons; type-I interstripe-1 had a larger gradient than both type-II interstripe-1 (P < 4.49 × 10⁻⁰⁵) and type-II interstripe-2 (P < 0.043), whereas type-I interstripe-2 was significantly different from type-II interstripe-1 (P < 2.26 × 10⁻⁰⁷), but was indistinguishable from type-II interstripe-2 (P > 0.229). Finally, the orientation gradient of thick stripes was significantly lower than thin stripes (P < 0.018), but was indistinguishable from that of type-II interstripes (P > 0.660).

Table 4.

Normalized average orientation gradient magnitude in the 4 stripe-types in each of 4 quantitatively analyzed cases

Case	2	3	4	5	Average
Stripe	s06	s07	m32	m31
Thin	0.983	0.907	1.00	1.00	1.00
Interstripe-I	1.00	1.00	0.79	0.97	0.948
Thick	0.808	0.803	0.81	0.75	0.790
Interstripe-II	0.770	0.813	0.68	0.80	0.768

Open in a new tab

Case 3 illustrates a similar pattern of orientation gradient magnitude and orientation selectivity as a function of CO compartment. In this case (s07), the low magnification (Fig. 5H) and higher magnification (Fig. 5I) orientation gradient maps illustrate relatively low average gradients within the thick stripes and type-II interstripe (dark pixels) and higher average gradients within the thin stripe and type-I interstripes (bright pixels). Similar to Case 2, orientation gradient magnitude was generally complementary to the magnitude of orientation selectivity. For example, the CO stripes exhibiting high orientation selectivities, indicated by bright pixels in the orientation selectivity maps (Fig. 5J,K), exhibit low orientation gradients, indicated by dark pixels in the gradient maps (Fig. 5H,I).

The average orientation gradient exhibited within the 6 CO stripes in this case is illustrated in the histogram Figure 5L. The highest orientation gradients were observed in type-I interstripe-1 (31.23°/100 µm) and type-I interstripe-2 (28.42°/100 µm). Conversely, the lowest gradients were observed in thick stripe-2 (22.86°/100 µm), thick stripe-2 (24.6°/100 µm), and interstripe-II (24.03°/100 µm). The normalized orientation gradient, calculated for the 4 CO stripe-types is illustrated in Figure 5M. As expected from the single-stripe data, the largest normalized gradients were observed in the type-I interstripe (1.00) and thin stripe (0.907) and the smallest gradients were observed in the thick stripe (0.803) and type-II interstripe (0.813). The statistical significance of these stripe differences is illustrated in Figure 5N. Similar to Case 2, the type-I interstripe orientation gradient magnitude was significantly greater than the gradient of type-II interstripes (P < 8.32 × 10⁻⁰⁸) and of thick stripes (P < 9.40 × 10⁻¹¹). Unlike Case 2, the orientation gradient magnitude in the Case 3 thin stripes was significantly smaller than type-I interstripes (P < 7.35 × 10^–04), but was indistinguishable from that observed in the type-II interstripes (P > 0.061).

The average orientation gradient for each stripe-type in the 4 cases is summarized in Table 5. Furthermore, the average normalized orientation gradient for each stripe-type in these 4 cases is illustrated in the histogram in Figure 5O and is summarized in Table 4. In 2 of the 4 cases, the largest orientation gradient was observed in thin stripes whereas in the 2 other cases the largest average gradient was observed in the type-I interstripe. Furthermore, in 2 of the 4 cases the smallest average gradient magnitude was observed in type-II interstripes, whereas in the other 2 cases the smallest gradient was observed in the thick stripe.

Table 5.

Average orientation gradient magnitude for each stripe in each quantitatively analyzed case

Case	2	3	4	5
Stripe	s06	s07	m32	m31
Thin-1	35.10	26.80		27.37
Thin-2	46.35		25.71	27.50
Interstripe-I-1	41.19	31.23		26.72
Interstripe-I-2	41.98	28.42	20.41
Thick-1	31.77	24.66	21.64	21.97
Thick-2	35.79	22.86	20.09	16.27
Thick-3			21.04
Interstripe-II-1	29.36	24.03	12.63	22.84
Interstripe-II-2	35.24		21.86	19.19
Interstripe-II-3			17.14

Open in a new tab

The statistical significance of the comparisons of gradient magnitude between stripe-types in the 4 cases is illustrated in Figure 5P and summarized for each case in Table 6. Overall, orientation gradient magnitude was found to vary significantly across V2 stripe type (P < 6.28 × 10⁻⁴; Kruskal–Wallis). A priori nonparametric comparisons (Wilcoxon's rank sum test) were then used to determine the sources of this overall difference in orientation gradient magnitude and to determine the significance of stripe-type differences within each case. A total of eleven interstripe-type pairs were evaluated for the significance of the differences in average orientation gradient magnitude. Only in 2 of these comparisons did the magnitude difference fail to meet statistical significance (Case 2 Interstripe-I-2 vs. Interstripe-II-2; P > 0.229 and Case 4 Interstripe-I-2 vs. Interstripe-II-2; P > 0.665).

Table 6.

Statistical significance of each stripe-type comparisons of orientation gradient magnitude for each case and across all 4 cases (right column)

Case	2	3	4	5	All cases
Comparison	s06	s07	m32	m31
Thin versus Interstripe-I	0.879	7.35E−04	0.043	0.340	0.017
Thin versus Thick	0.018	0.031	6.63E−04	2.29E−08	0.001
Thin versus Interstripe-II	0.005	0.061	1.00E−12	1.31E−08	1.20E−03
Interstripe-I versus Thick	0.039	9.40E−11	0.670	0.001	0.030
Interstripe-I versus Interstripe-II	0.013	8.32E−08	3.94E−04	5.10E−04	0.018
Thick versus Interstripe-II	0.660	0.865	5.15E−07	0.771	0.397
				K/W	6.28E−04
Inter-I-1 versus Inter-II-1	4.49E−05	2.38E−08		0.009
Inter-I-1 versus Inter-II-2	0.043			1.8E−05
Inter-I-2 versus Inter-II-1	2.26E−07	1.03E−04	9.24E−10
Inter-I-2 versus Inter-II-2	0.229		0.665
Inter-I-2 versus Inter-II-3			0.033

Open in a new tab

When examined across all 4 cases, the orientation gradient magnitude of thin stripes was significantly greater than type-I interstripes (P < 0.017), thick stripes (P < 0.001), and type-II interstripes (P < 1.20 × 10⁻³). Furthermore, the type-I interstripe gradient was significantly greater than thick stripes (P < 0.030) and type-II interstripes (P < 0.018). Finally, the average gradient magnitude of thick stripes was indistinguishable from that of type-II interstripes (P > 0.387).

V2 Stripe-types Differ in Their Orientation Selectivity and Gradient Magnitude

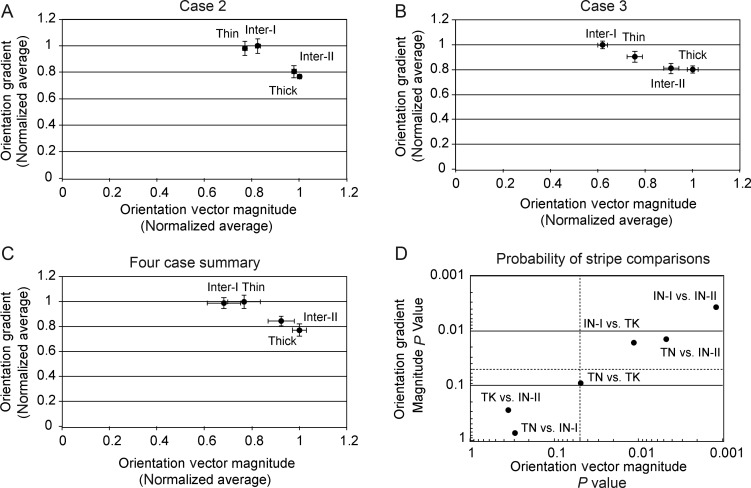
In the previous sections, the 4 CO stripe compartments were distinguished separately on the basis of their orientation selectivity and orientation gradient magnitude. In this section, these 2 properties are plotted together in order to determine whether and how these stripe-types can be distinguished in this multidimensional space. Two individual cases are illustrated in Figure 6 along with the average result from the 4 cases in which orientation gradient was computed using 4 stimulus orientations. In Case 2 (Fig. 6A), the 4 stripe-types were largely segregated into 2 clusters; one consisting of the thin and type-I interstripe that exhibited lower orientation magnitude and higher orientation gradient magnitude, and a second cluster consisting of the thick stripe and type-II interstripes that exhibited higher orientation selectivity and lower orientation gradient magnitude. The overall cluster pattern observed in Case 3 (Fig. 6B) was similar to case 2 except that the type-I interstripe was the least orientation selective, the thin stripe had a slightly smaller orientation gradient, and the thick stripe was the most orientation selective.

Figure 6. — V2 stripe-types distinguished by vector magnitude and orientation gradient. (A) Normalized average orientation vector magnitude versus normalized orientation gradient for 4 stripe-types in Case 2. The 4 stripe types form 2 clusters. The thin and type-I interstripe cluster is characterized by low orientation selectivity and high orientation gradient. The thick and type-II interstripe cluster is characterized by higher orientation selectivity and lower orientation gradient. (B) Normalized average orientation vector magnitude versus normalized orientation gradient for 4 stripe-types in Case 3. Compared with Case 2, the type-I interstripe in Case 3 had lower orientation selectivity, giving the appearance of a weaker clustering with the thin stripe. See text for details. (C) Normalized average orientation vector magnitude versus normalized orientation gradient for 4 stripe-types across all 4 cases. (D) Plot of the probability values associated with a priori pair-wise comparisons (Wilcoxon's rank sum test) of orientation vector magnitude and orientation gradient magnitude between stripe-types across 4 cases. Dashed lines indicate P < 0.05 value for each metric. Three of the 6 stripe-type comparisons were statistically significant for both orientation selectivity and gradient magnitude and thick stripes and thin stripes were only distinguishable by orientation selectivity. The comparisons of thick stripes versus type-II interstripes and thin stripes versus type-I interstripes were not significant for either orientation selectivity or gradient.

The normalized, average orientation selectivity and orientation gradient magnitude of these 4 stripe-types across all 4 cases is illustrated in Figure 6C. Overall, type-II interstripes exhibited the highest orientation vector magnitude and the lowest orientation gradient magnitude, whereas the type-I interstripes were the least orientation selective and thin stripes had the largest orientation gradient magnitude. In 3 of the 4 cases, the thick stripes were slightly but significantly less orientation selective than the type-II interstripes and in 3 of the 4 cases also had significantly higher orientation gradient magnitude. The overall statistical significance of the pair-wise stripe-type comparisons of orientation selectivity and gradient magnitude is summarized in Figure 6D. This figure demonstrates that 3 of the 6 stripe-types comparisons were statistically significant for both orientation selectivity and gradient magnitude. However, thick stripes and thin stripes were only distinguishable by their orientation selectivity. Finally, the comparisons of thick stripes to type-II interstripes and thin stripes to type-I interstripes were not statistically significant for either orientation vector magnitude or orientation gradient.

Discussion

Representation of Orientation in V2: 4 Stripe Compartments not 3

Quantitative analysis of the representation of orientation in V2 revealed several organizational features that are common to several cortical areas and some features that may be unique to area V2, perhaps due to its characteristic CO stripe architecture. As in V1, the representation of orientation in V2 is characterized by iso-orientation domains which tend to converge at orientation singularities (pinwheel centers) that are generally organized into complementary pairs characterized by clockwise and anticlockwise sequences of orientation change (e.g., Bartfeld and Grinvald 1992). However, unlike V1 where orientation is homogeneously mapped across the cortical surface, the representation of orientation in V2 is more heterogeneous. This heterogeneity is manifested in systematic differences in orientation selectivity, iso-orientation domain size, distributions of orientation pinwheels, and large-scale orientation sequences that differ across the CO stripes.

Orientation Selectivity

In contrast to prevailing views of the organization of V2, the current results indicate that macaque V2 consists of 4 distinct functional compartments. Specifically, these results indicate that the interstripes that flank each CO dense stripe are not functionally equivalent to each other since they differ profoundly both in the selectivity for oriented contours and in the fine structure of their orientation maps. The most robust orientation selective responses were observed in thick stripes and in a subset of interstripes. In agreement with the pioneering investigation of orientation selectivity in owl monkey V2 (Xu et al. 2004), only one set of macaque interstripes exhibited robust orientation selectivity. Consistent with the terminology introduced by Xu et al. (2004) type-II interstripes, located medial to thick stripes, exhibited robust orientation selectivity, whereas type-I interstripes, located lateral to thick stripes, exhibit weak orientation selectivity.

Orientation Gradient

The rate of change of orientation (orientation angle gradient) also differentiates the 2 types of interstripes from each other and thus further distinguishes the 4 functional compartments in V2. In both thick stripes and type-II interstripes, preferred orientation bands tend to be large and to vary smoothly along the stripe axis except for regions of rapid angle change (orientation fractures). In contrast, iso-orientation domains in thin stripes and type-I interstripes are smaller and thus preferred orientation angle changes more rapidly across the cortical surface.

The joint distribution of orientation selectivity (orientation vector magnitude) and rate of orientation angle change (orientation gradient magnitude) provides a powerful method to distinguish different V2 stripe compartments in vivo. As summarized in Figure 6, these 2 parameters can readily distinguish thin stripe/type-I interstripes from thick stripe/type-II interstripes. Additional response features are generally necessary to distinguish the stripe types within each of these 2 clusters. It is generally accepted that color-preferring domains and spatially organized hue maps are only found in V2 thin stripes (Xiao et al. 2003; Wang et al. 2007; Lu and Roe 2008). Therefore, the localization of these color/hue features in V2 functional maps can lead to the clear distinction of thin stripes from type-I interstripes.

Additional Stripe-specific Selectivities

The in vivo distinction of thick stripes from type-II interstripes is somewhat more difficult when considering only color/hue and orientation responses. These 2 stripe types tend to differ in the locations and density of orientation pinwheels. Orientation pinwheels are rarely observed within the body of type-II interstripes, while multiple pinwheel centers are often observed in thick stripes. V2 thick stripes can also be readily distinguished from type-II interstripes by the systematic representation of binocular disparity that has been observed only in thick stripes (Ts'o et al. 2001; Chen et al. 2008). Finally, the consistency in the order of stripe types observed in these and other experiments indicates that if the location of a thin stripe can be ascertained, then a type-II interstripe will be located immediately lateral to it.

Additional Evidence for 2 Types of V2 Interstripes

Several lines of evidence have previously indicated that the 2 interstripes within each CO stripe cycle are not equivalent, thus raising the possibility that V2 consists of 4, not 3, functional compartments. In their combined optical imaging and single-unit mapping study, Roe and Ts'o (1995) reported that each V2 stripe contained a well ordered topographic map that was discontinuous at sits borders, resulting in the remapping of visual space for each stripe within a given stripe cycle. Unexpectedly they found that neurons in the interstripes medial to color (thin) stripes (type-I) generally had smaller RF scatter and smaller receptive fields than neurons located in the interstripes lateral to the color (thin) stripe (type-II). Subsequently, Shipp and Zeki (2002) found that multiunit activity in the core of the interstripe and marginal (border) zone lateral to thin stripes had slightly lower levels of orientation selectivity, higher levels of color selectivity, and more frequent length antagonism compared with the marginal zone and interstripe medial to the thin stripe (type-I interstripe).

It is difficult to reconcile the current evidence of robust orientation selectivity and high orientation gradient magnitude with the results of Shipp and Zeki (2002). The intrinsic optical recording method employed in this study provides an estimate of orientation selectivity that is largely the product of individual neuron tuning for orientation and a spatial averaging function that is limited by the hemodynamic properties of the cortical tissue. In contrast, estimates of orientation selectivity based on single- and multi-unit recording are largely due only to the tuning properties of individual neurons. Therefore, the optical recording method provides a population estimate of neuronal tuning that is biased by the local organization/clustering of neuronal properties. Thus, while microelectrode recording estimates of percentage selectivity may demonstrate subtle differences between stripe compartments, the optical recording method will either amplify or minimize these differences in neuronal tuning according to the local clustering of those features.

Evidence for asymmetrical projections from V1 to interstripes flanking CO-dense stripes was first reported by Federer et al. (2009) in their study of V1 projections to V2 in marmoset monkeys. The results demonstrated both tangential and laminar differences in the V1 projections to pale_med (our type-II) and pale_lat (our type-I) interstripes. Following injections into both interstripe types, the majority of labeled cells were located in layer 2/3 of V1 but cells labeled after pale_med injections were located closer to V1 interblob centers and in all cases (4 of 4) avoided V1 blob centers. In addition, pale_lat, but not pale_med, injections resulted in small numbers of labeled cells in layers 4B and 5/6 of V1. (4B projections accounted for 4.3% following thin stripe, 9% following pale_lat, and 24% following thick stripe injections).

Recently, Federer et al. (2013) reexamined the V1 projections to V2 interstripes using both “blind” and intrinsic optical imaging-guided minute injections of multiple neuroanatomical tracers. In contrast to the findings of Sincich et al. (2010), the 2 interstripes flanking each CO-dense stripe were found to differ in both the relative contribution of projections from layer 4B and in the relative density of the inputs from layer 2/3. Specifically, they reported that the interstripe (type-I) located lateral to each thick stripe (pale_lat) received ∼16 ± 4.5% of its V1 input from layer 4B, whereas the interstripe (type-II) medial to the thick stripe (pale_med) only received ∼1.7 ± 0.9% of its V1 input from layer 4B (P < 0.0014; Mann–Whitney U test). Additionally, the pale_lat interstripe was found to receive a more robust input from layer 2/3 than the pale_lmed stripe. The differences in the layer 4B V1 projection to V2 interstripes are largely consistent with the previous report from marmosets (Federer et al. 2009), differing primarily in that marmoset medial interstripes received essentially no input from layer 4B.

These results differ from those of Sincich et al. (2010) who did not observe different V1 projection patterns following retrograde tracer injections into interstripes medial (n = 4) and lateral (n = 4) to thick stripes in macaque V2. The differences in V1 projection patterns reported by these 2 groups of investigators may be due to the significantly smaller tracer injections used by Federer et al. (2013) (50 vs. 140 nl) which resulted in much smaller injection site diameters (0.3 vs. 1.0 mm). Perhaps these smaller injections were more restricted to the narrow CO-pale regions and thus avoided any erroneous contributions from the adjacent thick stripes which are known to receive robust projections from layer 4B (Livingstone and Hubel 1983; Hubel and Livingstone, 1987; Sincich and Horton 2002a,b; Sincich et al. 2010). Finally, the V1 projections to the different V2 interstripes appears to be another example of parallel cortical streams since only 1–2% of double labeled cells following paired injections into sequential interstripes representing the same portion of the visual field (Federer et al. 2013).

Functional Significance of 4 V2 Stripe Compartments

Feedforward Projections

The present results complement and extend previous findings indicating that the 2 interstripes that flank each CO dense stripe are functionally distinct and should no longer be considered a single functional compartment of V2. If this assertion is correct, further insight into their functional significance may be revealed through a more thorough investigation of the feedforward connections of interstripes. Previous studies which injected retrograde tracers into areas V3 (Felleman, Burkhalter et al. 1997) and V4 (DeYoe et al. 1985; Felleman, Xiao et al. 1997; or posterior inferotemporal cortex (TEO; Nakamura et al. 1993) resulted in the labeling of cells that flank each CO-dense stripe. Thus it appears that both types of V2 interstripes project to areas V3, V4, and TEO. Since these studies employed relatively large tracer injections, small spatial segregations of type-I and type-II axonal projection fields, consistent with the preservation of the modular segregation of 2 distinct cortical streams, would be very difficult or impossible to detect. However, V3 of owl monkeys is characterized by a modular architecture consisting of CO-dense and CO-pale domains that exhibit high and low orientation selectivity, respectively (Xu et al. 2004). While it remains unknown whether owl monkey type-II and type-I interstripes have differential projections to these V3 domains, this is highly likely. Whether macaque V3 also contains a modular organization of orientation selectivity which may be associated with differential projections from V2 type-I and type-II interstripes must await future investigation.

In our previous study of the feedforward connections of V2 to V4, multiple distinguishable anterograde tracers were injected into functionally characterized V2 color-preferring loci (thin stripes) and into interstripe regions exhibiting high degrees of orientation selectivity, most certainly type-II interstripes (Xiao et al. 1999). The resultant axonal projection fields in V4 were highly divergent and were largely segregated from each other. The individual stripe projection fields in V4 were generally dense but often included characteristic gaps that were often “filled-in” by axon terminals derived from the other stripe-type. In addition, these V2 thin stripe and interstripe (type-II) projection fields generally failed to completely cover the topographically corresponding portion of V4, raising the possibility that another afferent “stream” fills in these large gaps. Since the projection patterns of functionally identified type-I interstripes have not been systematically examined, it remains to be determined whether axons from type-I interstripes terminate in these V4 gaps resulting in the modular segregation, at least in layer 4, of 3 V2 afferent streams in area V4.

Functional Properties of V2

It is interesting to speculate that the observed differences in the proportion of input from layer 4B is reflected in a yet undetected feature of V2 interstripes that may be conveyed to segregated fields in V4. For example, the substantial input from layer 4B to the pale stripes lateral to the thick stripes (pale_lat or type-I interstripes) may be an important conduit for information about binocular disparity to reach V4 and other areas in the ventral-temporal cortical pathway.

Low levels of orientation selectivity and the lack of spatially organized, hue-specific responses suggests that type-I interstripes are involved in an aspect of vision that is more complicated than simple orientation or color processing. Although functional imaging studies or guided single-unit investigations have yet to reveal this “hidden” function, it is reasonable to speculate that they participate in some aspect of higher-order shape processing. Van Essen and colleagues (e.g., Hegde and Van Essen 2000; Anzai et al. 2007) have demonstrated a population of V2 neurons that are highly selective for the precise spatial configuration of 2 or more oriented elements such that different parts of the receptive field display different orientation preferences. Since these provocative experiments were conducted in alert, behaving monkeys the correlation of these neuron's positions to the CO pattern in V2 remains unknown. However, since similar receptive field properties have been observed in area V4 (e.g., Hegde and Van Essen 2007) it is reasonable to speculate that these cells were located in V2 interstripes. Nevertheless, it will be important for future studies to determine whether neurons that are selective for higher-order shapes or texture borders are preferentially located in specific V2 compartments.

Funding

The project was supported by US National Institute of Health grants R01 EY 08372 (D.J.F.), R01 EY018897 (D.J.F.), R01 EY021575 (Y.X.) National Eye Institute Core Grant EY-01876 (UTHSC), and the Whitehall Foundation (D.J.F.).

Notes

We thank Qian Huang and Sandip Biswas for technical assistance. We also thank Valentin Dragoi for helpful comments on an earlier draft of this manuscript. Conflict of Interest: None declared.

References

Anzai A, Peng X, Van Essen DC. 2007. Neurons in monkey visual area V2 encode combinations of orientations. Nat. Neurosci. 10:1313–1321. [DOI] [PubMed] [Google Scholar]
Bartfeld E, Grinvald A. 1992. Relationship between orientation-preference pinwheels, cytochrome oxidase blobs, and ocular dominance columns in primate striate cortex. Proc Natl Acad Sci USA. 89:11905–11909. [DOI] [PMC free article] [PubMed] [Google Scholar]
Blasdel GG. 1992. Orientation selectivity, preference, and continuity in monkey striate cortex. J Neurosci. 12:3139–3161. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen G, Lu HD, Roe AW. 2008. A map for horizontal disparity in monkey V2. Neuron. 58:442–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
DeYoe EA, Felleman DJ, Van Essen DC, McClendon E. 1994. Multiple processing streams in occipitotemporal visual cortex. Nature. 371:151–154. [DOI] [PubMed] [Google Scholar]
DeYoe EA, Van Essen DC. 1985. Segregation of efferent connections and receptive field properties in visual area V2 of the macaque. Nature. 317:58–61. [DOI] [PubMed] [Google Scholar]
Federer F, Ichida J, Jeff J, Schiessl I, McLoughlin N, Angelucci A. 2009. Four projection streams from primate V1 to the cytochrome oxidase stripes of V2. J Neurosci. 29:15455–15471. [DOI] [PMC free article] [PubMed] [Google Scholar]
Federer F, Williams D, Ichida JM, Merlin S, Angelucci A. 2013. Two projection streams from macaque V1 to the pale cytochrome oxidase stripes of V2. J Neurosci. 33:11530–11539. [DOI] [PMC free article] [PubMed] [Google Scholar]
Felleman DJ, Burkhalter A, Van Essen DC. 1997. Cortical connections of areas V3 and VP of macaque monkey extrastriate visual cortex. J Comp Neurol. 379:21–47. [DOI] [PubMed] [Google Scholar]
Felleman DJ, Xiao Y, McClendon E. 1997. Modular organization of occipito-temporal pathways: cortical connections between visual area 4 and visual area 2 and posterior inferotemporal ventral area in macaque monkeys. J Neurosci. 17:3185–3200. [DOI] [PMC free article] [PubMed] [Google Scholar]
Friedman HS, Zhou H, von der Heydt R. 2003. The coding of uniform colour figures in monkey visual cortex. J Physiol. 548:593–613. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gattass R, Sousa APB, Mishkin M, Ungerleider LG. 1997. Cortical projections of area V2 in the macaque. Cereb Cortex. 7:110–129. [DOI] [PubMed] [Google Scholar]
Gegenfurthner KR, Kiper DC, Fenstemaker SB. 1996. Processing of color, form, and motion in macaque area V2. Vis Neurosci. 13:161–172. [DOI] [PubMed] [Google Scholar]
Hegde J, Van Essen DC. 2000. Selectivity for complex shapes in primate visual area V2. J Neurosci. 20:(RC61):1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hegde J, Van Essen DC. 2007. A comparative study of shape representation in macaque visual areas V2 and V4. Cereb Cortex. 17:1100–1116. [DOI] [PubMed] [Google Scholar]
Hubel DH, Livingstone MS. 1987. Segregation of form, color, and stereopsis in primate area 18. J Neurosci. 7:3378–3415. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hubel DH, Wiesel TN. 1977. Ferrier lecture. Functional architecture of macaque monkey visual cortex. Proc R Soc Lond B Biol Sci. 198:1–59. [DOI] [PubMed] [Google Scholar]
Landisman CE, Ts'o DY. 2002. Color processing in macaque striate cortex: relationships to ocular dominance, cytochrome oxidase, and orientation. J Neurophysiol. 87:3126–3137. [DOI] [PubMed] [Google Scholar]
Levitt JB, Kiper DC, Movshon JA. 1994. Receptive fields and functional architecture of macaque V2. J Neurophysiol. 71:2517–2542. [DOI] [PubMed] [Google Scholar]
Lim H, Felleman DJ, Xiao J, Wang Y. 2009a. Organization of orientation selectivity across macaque V2 stripes: 4 stripes not 3. Soc Neurosci Abstr. 38:850–858. [Google Scholar]
Lim H, Xiao Y, Wang Y, Hu M, Felleman DJ. 2009b. Organization of Hue selectivity in macaque V2 thin stripes. J Neurophysiol. 102:2603–2615. [DOI] [PMC free article] [PubMed] [Google Scholar]
Livingstone MS, Hubel DH. 1983. Specificity of cortico-cortical connections in monkey visual system. Nature. 304:531–534. [DOI] [PubMed] [Google Scholar]
Lu HD, Chen G, Tanigawa H, Roe AW. 2010. A motion direction map in macaque V2. Neuron. 68:1002–1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lu HD, Roe AW. 2008. Functional organization of color domains in V1 and V2 of macaque monkey revealed by optical imaging. Cereb Cortex. 18:516–533. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nakamura M, Gattass R, Desimone R, Ungerleider LG. 1993. The modular organization of projections from areas V1 and V2 to areas V4 and TEO in macaques. J Neurosci. 13:3681–3691. [DOI] [PMC free article] [PubMed] [Google Scholar]
Peterhans E, Heydt RVD. 1993. Functional organization of area V2 in the alert macaque. Eur J Neurosci. 5:509–524. [DOI] [PubMed] [Google Scholar]
Roe AW, Ts'o DY. 1995. Visual topography in primate V2: Multiple representations across functional stripes. J Neurosci. 15:3689–3715. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shipp S, Zeki SM. 1985. Segregation of pathways leading from area V2 to areas V4 and V5 of macaque monkey visual cortex. Nature. 315:322–325. [DOI] [PubMed] [Google Scholar]
Shipp S, Zeki SM. 1989. The organization of connections between areas V5 and V2 in macaque monkey visual cortex. Eur J Neurosci. 1:333–354. [DOI] [PubMed] [Google Scholar]
Shipp S, Zeki SM. 2002. The functional organization of area V2 I: specialization across stripes and layers. Vis Neurosci. 19:187–210. [DOI] [PubMed] [Google Scholar]
Sincich LC, Horton JC. 2002a. Divided by cytochrome oxidase: a map of the projections from V1 to V2 in macaques. Science. 295:1734–1737. [DOI] [PubMed] [Google Scholar]
Sincich LC, Horton JC. 2002b. Pale cytochrome oxidase stripes in V2 receive the richest projections from macaque striate cortex. J Comp Neurol. 447:18–33. [DOI] [PubMed] [Google Scholar]
Sincich LC, Jocswon CM, Horton JC. 2010. V1 interpatch projections to V2 thick stripes and pale stripes. J Neurosci. 30:6963–6974. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tootell RBH, Silverman MS, DeValois RL, Jacobs GH. 1983. Functional organization of the second cortical visual area in primates. Science. 220:737–739. [DOI] [PubMed] [Google Scholar]
Ts'o DY, Frostig RD, Lieke EE, Grinvald A. 1990. Functional organization of primate visual cortex revealed by high resolution optical imaging. Science. 249:417–420. [DOI] [PubMed] [Google Scholar]
Ts'o DY, Roe AW, Gilbert CD. 2001. A hierarchy of the functional organization for color, form and disparity in primate visual area V2. Vis Res. 41:1333–1349. [DOI] [PubMed] [Google Scholar]
Ts'o DY, Zarella M, Burkitt G. 2009. Whither the hypercolumn? J Physiol. 587:2791–2805. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang Y, Xiao Y, Felleman DJ. 2007. V2 thin stripes contain spatially organized representations of achromatic luminance change. Cereb Cortex. 17:116–129. [DOI] [PubMed] [Google Scholar]
Wong-Riley MT, Carroll EW. 1984. Quantitative light and electron microscopic analysis of cytochrome oxidase-rich zones in V-II prestriate cortex of the squirrel monkey. J Comp Neurol. 222:18–37. [DOI] [PubMed] [Google Scholar]
Xiao Y, Rao R, Cecchi G, Kaplan E. 2008. Improved mapping of information distribution across the cortical surface with the support vector machine. Neural Network. 21:341–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
Xiao Y, Wang Y, Felleman DJ. 2003. A spatially organized representation of hue in macaque area V2. Nature. 421:535–538. [DOI] [PubMed] [Google Scholar]
Xiao Y, Zych A, Felleman DJ. 1999. Segregation and convergence of functionally defined V2 thin stripe and interstripe compartment projections to area V4 of macaques. Cereb Cortex. 9:792–804. [DOI] [PubMed] [Google Scholar]
Xu X, Bosking W, Sary G, Stefansic J, Shima D, Casagrande V. 2004. Functional organization of visual cortex in the owl monkey. J Neurosci. 24:6237–6247. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zeki SM. 1971. Cortical projections from two prestriate areas in the monkey. Brain Res. 34:19–35. [DOI] [PubMed] [Google Scholar]
Zeki SM, Shipp S. 1989. Modular connections between areas V2 and V4 of macaque monkey visual cortex. Eur J Neurosci. 1:494–506. [DOI] [PubMed] [Google Scholar]

[BHU033C1] Anzai A, Peng X, Van Essen DC. 2007. Neurons in monkey visual area V2 encode combinations of orientations. Nat. Neurosci. 10:1313–1321. [DOI] [PubMed] [Google Scholar]

[BHU033C2] Bartfeld E, Grinvald A. 1992. Relationship between orientation-preference pinwheels, cytochrome oxidase blobs, and ocular dominance columns in primate striate cortex. Proc Natl Acad Sci USA. 89:11905–11909. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C3] Blasdel GG. 1992. Orientation selectivity, preference, and continuity in monkey striate cortex. J Neurosci. 12:3139–3161. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C4] Chen G, Lu HD, Roe AW. 2008. A map for horizontal disparity in monkey V2. Neuron. 58:442–450. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C5] DeYoe EA, Felleman DJ, Van Essen DC, McClendon E. 1994. Multiple processing streams in occipitotemporal visual cortex. Nature. 371:151–154. [DOI] [PubMed] [Google Scholar]

[BHU033C6] DeYoe EA, Van Essen DC. 1985. Segregation of efferent connections and receptive field properties in visual area V2 of the macaque. Nature. 317:58–61. [DOI] [PubMed] [Google Scholar]

[BHU033C7] Federer F, Ichida J, Jeff J, Schiessl I, McLoughlin N, Angelucci A. 2009. Four projection streams from primate V1 to the cytochrome oxidase stripes of V2. J Neurosci. 29:15455–15471. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C8] Federer F, Williams D, Ichida JM, Merlin S, Angelucci A. 2013. Two projection streams from macaque V1 to the pale cytochrome oxidase stripes of V2. J Neurosci. 33:11530–11539. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C9] Felleman DJ, Burkhalter A, Van Essen DC. 1997. Cortical connections of areas V3 and VP of macaque monkey extrastriate visual cortex. J Comp Neurol. 379:21–47. [DOI] [PubMed] [Google Scholar]

[BHU033C10] Felleman DJ, Xiao Y, McClendon E. 1997. Modular organization of occipito-temporal pathways: cortical connections between visual area 4 and visual area 2 and posterior inferotemporal ventral area in macaque monkeys. J Neurosci. 17:3185–3200. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C11] Friedman HS, Zhou H, von der Heydt R. 2003. The coding of uniform colour figures in monkey visual cortex. J Physiol. 548:593–613. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C12] Gattass R, Sousa APB, Mishkin M, Ungerleider LG. 1997. Cortical projections of area V2 in the macaque. Cereb Cortex. 7:110–129. [DOI] [PubMed] [Google Scholar]

[BHU033C13] Gegenfurthner KR, Kiper DC, Fenstemaker SB. 1996. Processing of color, form, and motion in macaque area V2. Vis Neurosci. 13:161–172. [DOI] [PubMed] [Google Scholar]

[BHU033C14] Hegde J, Van Essen DC. 2000. Selectivity for complex shapes in primate visual area V2. J Neurosci. 20:(RC61):1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C15] Hegde J, Van Essen DC. 2007. A comparative study of shape representation in macaque visual areas V2 and V4. Cereb Cortex. 17:1100–1116. [DOI] [PubMed] [Google Scholar]

[BHU033C16] Hubel DH, Livingstone MS. 1987. Segregation of form, color, and stereopsis in primate area 18. J Neurosci. 7:3378–3415. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C17] Hubel DH, Wiesel TN. 1977. Ferrier lecture. Functional architecture of macaque monkey visual cortex. Proc R Soc Lond B Biol Sci. 198:1–59. [DOI] [PubMed] [Google Scholar]

[BHU033C18] Landisman CE, Ts'o DY. 2002. Color processing in macaque striate cortex: relationships to ocular dominance, cytochrome oxidase, and orientation. J Neurophysiol. 87:3126–3137. [DOI] [PubMed] [Google Scholar]

[BHU033C19] Levitt JB, Kiper DC, Movshon JA. 1994. Receptive fields and functional architecture of macaque V2. J Neurophysiol. 71:2517–2542. [DOI] [PubMed] [Google Scholar]

[BHU033C20] Lim H, Felleman DJ, Xiao J, Wang Y. 2009a. Organization of orientation selectivity across macaque V2 stripes: 4 stripes not 3. Soc Neurosci Abstr. 38:850–858. [Google Scholar]

[BHU033C21] Lim H, Xiao Y, Wang Y, Hu M, Felleman DJ. 2009b. Organization of Hue selectivity in macaque V2 thin stripes. J Neurophysiol. 102:2603–2615. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C22] Livingstone MS, Hubel DH. 1983. Specificity of cortico-cortical connections in monkey visual system. Nature. 304:531–534. [DOI] [PubMed] [Google Scholar]

[BHU033C23] Lu HD, Chen G, Tanigawa H, Roe AW. 2010. A motion direction map in macaque V2. Neuron. 68:1002–1013. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C24] Lu HD, Roe AW. 2008. Functional organization of color domains in V1 and V2 of macaque monkey revealed by optical imaging. Cereb Cortex. 18:516–533. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C25] Nakamura M, Gattass R, Desimone R, Ungerleider LG. 1993. The modular organization of projections from areas V1 and V2 to areas V4 and TEO in macaques. J Neurosci. 13:3681–3691. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C26] Peterhans E, Heydt RVD. 1993. Functional organization of area V2 in the alert macaque. Eur J Neurosci. 5:509–524. [DOI] [PubMed] [Google Scholar]

[BHU033C27] Roe AW, Ts'o DY. 1995. Visual topography in primate V2: Multiple representations across functional stripes. J Neurosci. 15:3689–3715. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C28] Shipp S, Zeki SM. 1985. Segregation of pathways leading from area V2 to areas V4 and V5 of macaque monkey visual cortex. Nature. 315:322–325. [DOI] [PubMed] [Google Scholar]

[BHU033C29] Shipp S, Zeki SM. 1989. The organization of connections between areas V5 and V2 in macaque monkey visual cortex. Eur J Neurosci. 1:333–354. [DOI] [PubMed] [Google Scholar]

[BHU033C30] Shipp S, Zeki SM. 2002. The functional organization of area V2 I: specialization across stripes and layers. Vis Neurosci. 19:187–210. [DOI] [PubMed] [Google Scholar]

[BHU033C31] Sincich LC, Horton JC. 2002a. Divided by cytochrome oxidase: a map of the projections from V1 to V2 in macaques. Science. 295:1734–1737. [DOI] [PubMed] [Google Scholar]

[BHU033C32] Sincich LC, Horton JC. 2002b. Pale cytochrome oxidase stripes in V2 receive the richest projections from macaque striate cortex. J Comp Neurol. 447:18–33. [DOI] [PubMed] [Google Scholar]

[BHU033C33] Sincich LC, Jocswon CM, Horton JC. 2010. V1 interpatch projections to V2 thick stripes and pale stripes. J Neurosci. 30:6963–6974. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C34] Tootell RBH, Silverman MS, DeValois RL, Jacobs GH. 1983. Functional organization of the second cortical visual area in primates. Science. 220:737–739. [DOI] [PubMed] [Google Scholar]

[BHU033C35] Ts'o DY, Frostig RD, Lieke EE, Grinvald A. 1990. Functional organization of primate visual cortex revealed by high resolution optical imaging. Science. 249:417–420. [DOI] [PubMed] [Google Scholar]

[BHU033C36] Ts'o DY, Roe AW, Gilbert CD. 2001. A hierarchy of the functional organization for color, form and disparity in primate visual area V2. Vis Res. 41:1333–1349. [DOI] [PubMed] [Google Scholar]

[BHU033C37] Ts'o DY, Zarella M, Burkitt G. 2009. Whither the hypercolumn? J Physiol. 587:2791–2805. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C38] Wang Y, Xiao Y, Felleman DJ. 2007. V2 thin stripes contain spatially organized representations of achromatic luminance change. Cereb Cortex. 17:116–129. [DOI] [PubMed] [Google Scholar]

[BHU033C39] Wong-Riley MT, Carroll EW. 1984. Quantitative light and electron microscopic analysis of cytochrome oxidase-rich zones in V-II prestriate cortex of the squirrel monkey. J Comp Neurol. 222:18–37. [DOI] [PubMed] [Google Scholar]

[BHU033C40] Xiao Y, Rao R, Cecchi G, Kaplan E. 2008. Improved mapping of information distribution across the cortical surface with the support vector machine. Neural Network. 21:341–348. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C41] Xiao Y, Wang Y, Felleman DJ. 2003. A spatially organized representation of hue in macaque area V2. Nature. 421:535–538. [DOI] [PubMed] [Google Scholar]

[BHU033C42] Xiao Y, Zych A, Felleman DJ. 1999. Segregation and convergence of functionally defined V2 thin stripe and interstripe compartment projections to area V4 of macaques. Cereb Cortex. 9:792–804. [DOI] [PubMed] [Google Scholar]

[BHU033C43] Xu X, Bosking W, Sary G, Stefansic J, Shima D, Casagrande V. 2004. Functional organization of visual cortex in the owl monkey. J Neurosci. 24:6237–6247. [DOI] [PMC free article] [PubMed] [Google Scholar]

[BHU033C44] Zeki SM. 1971. Cortical projections from two prestriate areas in the monkey. Brain Res. 34:19–35. [DOI] [PubMed] [Google Scholar]

[BHU033C45] Zeki SM, Shipp S. 1989. Modular connections between areas V2 and V4 of macaque monkey visual cortex. Eur J Neurosci. 1:494–506. [DOI] [PubMed] [Google Scholar]

PERMALINK

The Representation of Orientation in Macaque V2: Four Stripes Not Three

Daniel J Felleman

Heejin Lim

Youping Xiao

Yi Wang

Anastasia Eriksson

Arun Parajuli

Abstract

Introduction

Materials and Methods

General

Optical Recording

Visual Stimuli and Data Analysis

Single-condition Responses

Ocular Dominance and Chromatic-responses

Orientation Maps

Support Vector Machine Analysis of Orientation Preferred Angle and Selectivity

Orientation Pinwheels

Orientation Gradient

Statistical Analysis of Orientation Map Features

Anatomical Methods

Results

Overview

Distribution of Statistically Significant Responses Across CO Compartments

Figure 1.

Quantitative Analysis of Orientation Selectivity in Different CO Compartments

Figure 2.

Table 1.

Figure 3.

Table 2.

Table 3.

Organization of Orientation Preferred Angle and Selectivity

Figure 4.

Orientation Gradient and its Relationship to Vector Magnitude

Figure 5.

Table 4.

Table 5.

Table 6.

V2 Stripe-types Differ in Their Orientation Selectivity and Gradient Magnitude

Figure 6.

Discussion

Representation of Orientation in V2: 4 Stripe Compartments not 3

Orientation Selectivity

Orientation Gradient

Additional Stripe-specific Selectivities

Additional Evidence for 2 Types of V2 Interstripes

Functional Significance of 4 V2 Stripe Compartments

Feedforward Projections

Functional Properties of V2

Funding

Notes

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases