Influence of human behavior on cholera dynamics

Abstract

This paper is devoted to studying the impact of human behavior on cholera infection. We start with a cholera ordinary differential equation (ODE) model that incorporates human behavior via modeling disease prevalence dependent contact rates for direct and indirect transmissions and infectious host shedding. Local and global dynamics of the model are analyzed with respect to the basic reproduction number. We then extend the ODE model to a reaction-convection-diffusion partial differential equation (PDE) model that accounts for the movement of both human hosts and bacteria. Particularly, we investigate the cholera spreading speed by analyzing the traveling wave solutions of the PDE model, and disease threshold dynamics by numerically evaluating the basic reproduction number of the PDE model. Our results show that human behavior can reduce (a) the endemic and epidemic levels, (b) cholera spreading speeds and (c) the risk of infection (characterized by the basic reproduction number).

1 Introduction

Mathematical modeling, analysis and simulation for infectious diseases have long provided useful insight into disease dynamics that could guide public health administration for designing effective prevention and control measures against epidemics. Over the past few decades, compartmental models such as SIR (susceptible-infected-recovered) and SEIR (susceptible-exposed-infected-recovered) and their threshold dynamics have been established as the standard framework in mathematical epidemiology (see review [33] and references therein). Meanwhile, numerous extensions of these basic mathematical models have been proposed that incorporate more detailed biological, ecological, demographic, and geographical information, such as spatial heterogeneities, age-structures, seasonal variations, and others, with significant advances in almost all of these directions.

The mechanisms of disease transmission and spread are usually complex and possibly involve social, economic and psychological factors in addition to the intrinsic disease biology and ecology. In particular, human behavior could have significant influence on disease transmission and vice versa. For example, individuals avoid close contact with obviously sick persons to protect themselves and therefore the frequency and strength of contacts between uninfected and infected people generally are reduced. In case of severe disease outbreaks, people will attempt to change their routine schedules (including, but not limited to, work, recreation, and travel), wash hands often with soap and clean water, receive vaccines or preventive treatment if available, so as to minimize their risk of infection. Nowadays, the fast growth of information technology allows prompt and up-to-date reports on the details of disease outbreaks from internet (especially those popular social networking sites), newspaper, television and radio stations, and government announcements. Consequently, these media coverage and health education will, to a large extent, affect human behavior which can lead to a significant reduction in outbreak morbidity and mortality.

It is clear that human behavior could play an important role in shaping the complex epidemic and endemic pattern of a disease [3, 26]. There are an increasing number of studies on the mathematical epidemiological modeling of human behavior [13]. Funk et al. [14] classified epidemic models under the impact of behavioral changes into belief-based and prevalence-based. Cui et al. [11] proposed a simple SIS model that incorporated the effects of media coverage. Gao and Ruan [16] extended the work in [11] to a patch model with nonconstant transmission coefficients. Liu et al. [25] investigated psychological impact on disease dynamics that involve multiple outbreaks and sustained infections. Collinson and Heffernan [10] found that the outcome of an epidemic model with the effects of mass media is strongly affected by the choice of media function. Recently, Chowell et al. [9] fitted logistic growth models to the cumulative reported number of Ebola cases to reflect changes in population behavior and interventions. In addition, Mummert and Weiss [27] modeled and analyzed the social distancing strategies in limiting disease transmission and spread, particularly for short-term outbreaks.

A goal of this paper is to improve our quantitative understanding of the impact of human behavior on disease dynamics. Particularly, we will incorporate human behavior into mathematical modeling of cholera, a severe water-borne disease caused by the bacterium Vibrio cholerae. There have been many studies published in recent years on cholera modeling and analysis (see, e.g., [5, 6, 7, 17, 28, 29, 34, 37, 38, 41, 42, 43, 44]), yet, to our knowledge, few of these have specifically taken human behavior into consideration (see Capasso [6, 5], Al-Arydah et al. [1], and Carpenter [7]). In the present paper, we will modify the cholera model proposed by Mukandavire et al. [28] to explicitly include disease prevalence dependent contact rates (for both the direct and indirect transmissions) and host shedding rate, and analyze the resulting dynamics. Particularly, we will show that the reduction of contact rates due to human behavior leads to reduced epidemic and endemic sizes. We will then extend the ODE system to a reaction-convection-diffusion PDE system to investigate the interaction among human behavior, host and pathogen movement, and the disease intrinsic transmission dynamics. We will pay special attention to the traveling wave solutions and threshold dynamics of the PDE model. Our study regarding cholera spatial dynamics is different from the work of Bertuzzo et al. [4, 31]. Our PDE model formulation is more general in terms of inclusion of multiple transmission pathways. Specifically, our model incorporates both direct (or, human-to-human) and indirect (or, environment-to-human) transmission pathways whereas their model has considered only indirect transmission route. The scope of our work is also different from that in [4, 31] as our focus is on the impact of human behavior on cholera transmission.

We organize the remainder of the paper as follows. In Section 2 we introduce the ODE cholera model that incorporates human behavior, with relevant notations and assumptions. We then conduct a thorough epidemic and endemic analysis of the model in Section 3, for both local and global dynamics. In Section 4 we present the PDE model and investigate its traveling wave solutions under the impact of human behavior, followed by a threshold dynamics analysis in Section 5. We conclude the paper in Section 6 with discussion.

2 Model formulation

The cholera model proposed in [28] incorporates both the environment-to-human (or, indirect) and human-to-human (or, direct) infection routes, and all the model parameters take constant values. The model has standard SIR (susceptible-infected-recovered) compartments, with an additional compartment B that denotes the concentration of the bacteria Vibrio cholerae in the contaminated water. We now extend this model by assuming that the direct and indirect transmission rates and the bacterial shedding rate are all dependent on the number of infectives, representing the influence of human behavior change due to health education, hygiene and sanitation practices. In addition, we assume that recovered individuals become susceptible to cholera again after a certain period of time, taking into account the immunity loss in the real life. The new model takes the form

$$\frac{dS}{dt}=\mu N-{\beta }_1(I)SI-{\beta }_2(I)\frac{SB}{B+K}-\mu S+\sigma R,$$

$$\frac{dI}{dt}={\beta }_1(I)SI+{\beta }_2(I)\frac{SB}{B+K}-(\gamma +\mu )I,$$ (2.1)

$$\frac{dR}{dt}=\gamma I-(\mu +\sigma )R,$$

$$\frac{dB}{dt}={\beta }_3(I)I-\delta B.$$

The total population, N = S + I + R, is fixed. The definition and base values of the model parameters are provided in Appendix A, Table 1.

The most important feature of our model is the incorporation of disease prevalence dependent contact rates and host shedding rate. For i = 1, 2, 3, we formulate that

$${\beta }_i(I)=a_i-b_i{m}_i(I),$$

where a_i is the usual contact rate (or shedding rate) without considering the influence of human behavior, b_i is the maximum reduced contact rate due to behavior change, and m_i(I) is a saturation function. These functions satisfy

$$a_i>b_i\ge 0,m_i(I)\in C^1([0,I_u])\text{with}{m}_i^{\prime }(I)\ge 0,m_i(0)=0,0<m_i(I_u)\le 1,$$

where I_u ∈ (0, N] is an upper bound of the solution {I(t) : t ≥ 0}. Some typical examples of m(I) with such properties are 1 − k/(k + Iⁿ) with k > 0 and n > 0, 1 − e^−kI with k > 0, and I/I_u [16].

One can easily verify that the disease-free equilibrium is given by (N, 0, 0, 0). Let F denote the matrix characterizing the generation of secondary infection, and V denote the matrix depicting transition rates between compartments. Based on the standard next-generation matrix technique [40, 12] and our assumptions, matrices F and V can be written as:

$$F=\left[\begin{array}{cc}\hfill a_{1}N\hfill & \hfill a_{2}N/K\hfill \\ \hfill a_3\hfill & \hfill 0\hfill \end{array}\right]\text{and}V=\left[\begin{array}{cc}\hfill \mu +\gamma \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \delta \hfill \end{array}\right].$$

The next generation matrix is

$$\mathit{M}=F{V}^{-1}=\left[\begin{array}{cc}\hfill \frac{a_{1}N}{\mu +\gamma }\hfill & \hfill \frac{a_{2}N}{\delta K}\hfill \\ \hfill \frac{a_3}{\mu +\gamma }\hfill & \hfill 0\hfill \end{array}\right].$$

Hence, the basic reproduction number ℛ₀ of model (2.1) is given by

$${ℛ}_0={ℛ}_0^{ODE}=\rho (\mathit{M})=\frac{1}{2}[\frac{a_{1}N}{\mu +\gamma }+\sqrt{{\left(\frac{a_{1}N}{\mu +\gamma }\right)}^2+4\frac{a_2{a}_{3}N}{\delta (\mu +\gamma )K}}].$$

Here ρ denotes the spectral radius. Note that the basic reproduction number ℛ₀ is independent of b_i for i = 1, 2, 3. This is due to our model assumption that behavior change only starts when the disease has already started and ℛ₀ is calculated at the disease-free state. An implication is that behavior change alone is usually not sufficient to terminate an outbreak. Nevertheless, previous studies have shown that it can significantly reduce the burden of an endemic disease [16]. We will demonstrate this for our cholera model in the next section.

Meanwhile, if disease control is targeted at a particular host type, a useful threshold is known as the type reproduction number, T. The type reproduction number defines the expected number of secondary infective cases of a particular population type caused by a typical primary case in a completely susceptible population [32, 18]. It is an extension of the basic reproduction number ℛ₀. Particularly, the type reproduction number T₁ for control of infection among humans is defined in references [32, 18] as

$$T_1={\mathit{e}}_1^T\mathit{M}{(\mathit{I}-(\mathit{I}-{\mathit{P}}_1)\mathit{M})}^{-1}{\mathit{e}}_1,$$

provided the spectral radius of matrix (I − P₁)M is less than one, i.e., ρ((I − P₁)M) < 1. Here I is the 2 × 2 identity matrix, vectors e₁ = (1, 0)^T, M is the next generation matrix, and P₁ is the 2 × 2 projection matrix with all zero entries except that the (1,1) entry is 1. Write M = (m_ij). The type reproduction T₁ can be easily defined in terms of the elements m_ij :

$$T_1=m_{11}+\frac{m_{12}{m}_{21}}{1-m_{22}},$$ (2.2)

T₁ exists provided m₂₂ < 1. In view of m₂₂ = 0, by (2.2), the type reproduction number associated with the infectious humans is given by

$$T_1=\frac{a_{1}N}{\mu +\gamma }+\frac{a_2{a}_{3}N}{\delta K(\mu +\gamma )}.$$

Moreover, it has been shown in [32] that

$${ℛ}_0<1(=1,>1)\iff T_1<1(=1,>1).$$

When β_i(I) = a_i (i = 1, 2, 3), it has been shown that the disease dynamics of (2.1) are completely determined by its basic reproduction number ℛ₀ [44].

In what follows, we will use both ℛ₀ and T₁ in our analysis, with the understanding that the two are equivalent in characterizing disease threshold dynamics.

3 Equilibrium Analysis

By direct calculation, we find that (2.1) always has a disease-free equilibrium (DFE), and its endemic equilibrium (EE) satisfies

$$N=S+I+R,$$ (3.1)

$$R=\frac{\gamma }{\mu +\sigma }I,$$ (3.2)

$$B=\frac{{\beta }_3(I)I}{\delta },$$ (3.3)

$$S=\frac{(\mu +\gamma )I}{{\beta }_1(I)I+{\beta }_2(I)B/(B+K)}.$$ (3.4)

Substituting (3.2) into (3.1) yields

$$S=\varphi (I)≔N-\alpha I,\text{with}\alpha =1+\gamma /(\mu +\sigma ).$$

Likewise, by plugging (3.3) into (3.4), we find

$$S=\psi (I)≔\frac{\mu +\gamma }{g(I)},$$

where

$$g(I)={\beta }_1(I)+\frac{{\beta }_2(I){\beta }_3(I)}{I{\beta }_3(I)+\delta K}.$$

Thus, the intersections of the curves S = ϕ(I) and S = ψ(I) in [0, N]² determine the nontrivial equilibria. Notice that

$$g\prime (I)={\beta }_1^{\prime }(I)+{\beta }_2^{\prime }(I)\frac{{\beta }_3(I)}{I{\beta }_3(I)+\delta K}+{\beta }_2(I)\frac{\delta K{\beta }_3^{\prime }(I)-{({\beta }_3(I))}^2}{{(I{\beta }_3(I)+\delta K)}^2}.$$

It then follows directly from assumptions on β_i(I) (for i = 1, 2, 3) that g′(I) < 0. This implies that ψ(I) is a strictly increasing function. Meanwhile, it is clear that ϕ(I) is a strictly decreasing function. Together with ϕ(0) = N, ψ(0) = N/T₁, ϕ(N) < 0, and ψ(N) > 0, we see that: (1) if T₁ > 1, then ϕ(0) > ψ(0), which implies that there is a unique intersection in ${ℝ}_{+}^2$ between ϕ(I) and ψ(I); (2) if T₁ ≤ 1, then ϕ(0) ≤ ψ(0), which indicates that there is no intersection between these curves in the interior of ${ℝ}_{+}^2$. Moreover, we have the following existence, uniqueness and local stability theorem on DFE and EE of (2.1). The proof is postponed to Appendix B.

Theorem 3.1

1. If T₁ ≤ 1, then system (2.1) has a unique equilibrium, and it is the DFE. Furthermore, the DFE is locally asymptotically stable when T₁ < 1, and it is Lyapunov stable when T₁ = 1.

2. If T₁ > 1, then system (2.1) has two equilibria: the DFE and the EE. Moreover, the DFE is unstable, whereas the EE is locally asymptotically stable.

In view of the equivalent relationship between ℛ₀ and T₁ (2), we obtain the following result for the local disease threshold dynamics of model (2.1).

Corollary 3.2

1. If ℛ₀ ≤ 1, the system (2.1) has a unique equilibrium, and it is the DFE. Furthermore, the DFE is locally asymptotically stable when ℛ₀ < 1, and it is Lyapunov stable when ℛ₀ = 1.

2. If ℛ₀ > 1, the system (2.1) has two equilibria: the DFE and the EE. Moreover, the DFE is unstable, whereas the EE is locally asymptotically stable.

In the remainder of this section, we focus on the global stability of the equilibrium solutions of (2.1). By a simple comparison theorem, we find that 0 ≤ B(t) ≤ B_u provided that 0 ≤ B(0) ≤ B_u := a₃N/δ. Consider the domain

$$\mathrm{\Omega }=\{(S,I,R,B)\in {ℝ}_{+}^4:S+I+R\le N,B\le B_u\}.$$

It is clear that if any solution of system (2.1) starting in Ω will remain in Ω; that is, the domain Ω is positively invariant for (2.1). The following results (i.e., Theorems 3.3–3.4) establish the global disease threshold dynamics of model (2.1).

Theorem 3.3

If ℛ₀ ≤ 1, the system (2.1) has a unique disease-free equilibrium that is globally asymptotically stable in the region Ω.

Proof

Let

$$F_1=\left[\begin{array}{cc}\hfill a_{1}N\hfill & \hfill a_{2}N/K\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\text{and}{V}_1=\left[\begin{array}{cc}\hfill \mu +\gamma \hfill & \hfill 0\hfill \\ \hfill -a_3\hfill & \hfill \delta \hfill \end{array}\right].$$

Write 𝒴 = (I, B)^T. By assumptions β_i(I) ≤ a_i for i = 1, 2, 3, the system (2.1) satisfies

$$\frac{d𝒴}{dt}\le (F_1-V_1)𝒴.$$

Let w = (a₁N, a₂N/K). In view of $T_1=\rho (F_1{V}_1^{-1})=\rho (V_1^{-1}{F}_1)$, one can verify that $w{V}_1^{-1}{F}_1=T_{1}w$ Motivated by [35], we define a Lyapunov function as follows:

$$ℒ=w{V}_1^{-1}𝒴.$$

Differentiating ℒ along solutions of (2.1), we have

$$ℒ\prime =w{V}_1^{-1}\frac{d𝒴}{dt}\le w{V}_1^{-1}(F_1-V_1)𝒴=(T_1-1)w𝒴.$$

If T₁ < 1, ℒ′ ≤ 0. Then ℒ′ = 0 implies that w𝒴 = 0 and hence I = B = 0. It follows from the first and third equations of (2.1) that S = N and R = 0. Hence, the only invariant set where ℒ′ = 0 is the singleton {(N, 0, 0, 0)}.

In the case T₁ = 1, ℒ′ = 0 implies that β₁(I)SI = a₁NI and β₂(I)SB/(B + K) = a₂NB/K. By the assumption on β_i (i = 1, 2), this can only happen when S = N or I = B = 0. Then, by a similar argument as that in the case where T₁ < 1, we find that the largest invariant set where ℒ′ = 0 is the singleton {(N, 0, 0, 0)}.

Since ℛ₀ < 1 iff T₁ < 1, by LaSalle’s Invariant Principle [22], the DFE is globally asymptotically stable in Ω if ℛ₀ ≤ 1.

Theorem 3.4

If ℛ₀ > 1, the EE is globally asymptotically stable in Ω⁰, the interior of Ω, provided that sup {S(β₁(I)I)′: S ≥ 0, I ≥ 0, S + I ≤ N} ≤ (γ − σ)/2.

The detailed proof for Theorems 3.4 is provided in Appendix C.

A mathematically simple but biologically important conclusion can be made from the above analysis on the endemic equilibrium. Namely, when β_i (1 ≤ i ≤ 3) is decreased as a result of incorporating human behavior, the endemic level is reduced as well.

Proposition 3.5

If ℛ₀ > 1, then the I-coordinate of the unique endemic equilibrium of model (2.1), I_e, is strictly decreasing in the maximum reduced transmission coefficient (or shedding rate) due to behavior change, b_i, for i = 1, 2, 3.

Proof

Since ℛ₀ > 1 iff T₁ > 1, there exists a unique endemic equilibrium (S_e, I_e, R_e, B_e) of the system (2.1), when ℛ₀ > 1. By equations (3.5) and (3.6), we have

$$\varphi (I_e)=\psi (I_e)\iff N-\alpha I_e=\frac{\mu +\gamma }{g(I_e)},$$ (3.5)

where $g(I_e)={\beta }_1(I_e)+\frac{{\beta }_2(I_e){\beta }_3(I_e)}{I_e{\beta }_3(I_e)+\delta K}$ and β₁(I_e) = a₁ − b₁m₁(I_e). Differentiating both sides of equation (3.5) with respect to b₁ yields

$$-\alpha \frac{\partial I_e}{\partial b_1}=-\frac{\mu +\gamma }{{(g(I_e))}^2}·(-m_1(I_e)-b_1{m}_1^{\prime }(I_e)\frac{\partial I_e}{\partial b_1}+\frac{p(I_e)}{{(I_e{\beta }_3(I_e)+\delta K)}^2}\frac{\partial I_e}{\partial b_1})\iff -\frac{\mu +\gamma }{{(g(I_e))}^2}{m}_1(I_e)=\frac{\partial I_e}{\partial b_1}(\alpha +\frac{\mu +\gamma }{{(g(I_e))}^2}{b}_1{m}_1^{\prime }(I_e)-\frac{\mu +\gamma }{{(g(I_e))}^2}·\frac{p(I_e)}{{(I_e{\beta }_3(I_e)+\delta K)}^2}),$$

where

$$p(I_e)=({\beta }_2^{\prime }(I_e){\beta }_3(I_e)+{\beta }_2(I_e){\beta }_3^{\prime }(I_e))(I_e{\beta }_3(I_e)+\delta K)-{\beta }_2(I_e){\beta }_3(I_e)({\beta }_3(I_e)+I_e{\beta }_3^{\prime }(I_e))={\beta }_2^{\prime }(I_e){\beta }_3(I_e)(I_e{\beta }_3(I_e)+\delta K)+{\beta }_2(I_e){\beta }_3^{\prime }(I_e)\delta K-{\beta }_2(I_e){({\beta }_3(I_e))}^2<0.$$

Thus $\frac{\partial I_e}{\partial b_1}<0$. We can similarly show that $\frac{\partial I_e}{\partial b_2}<0$ and $\frac{\partial I_e}{\partial b_3}<0$.

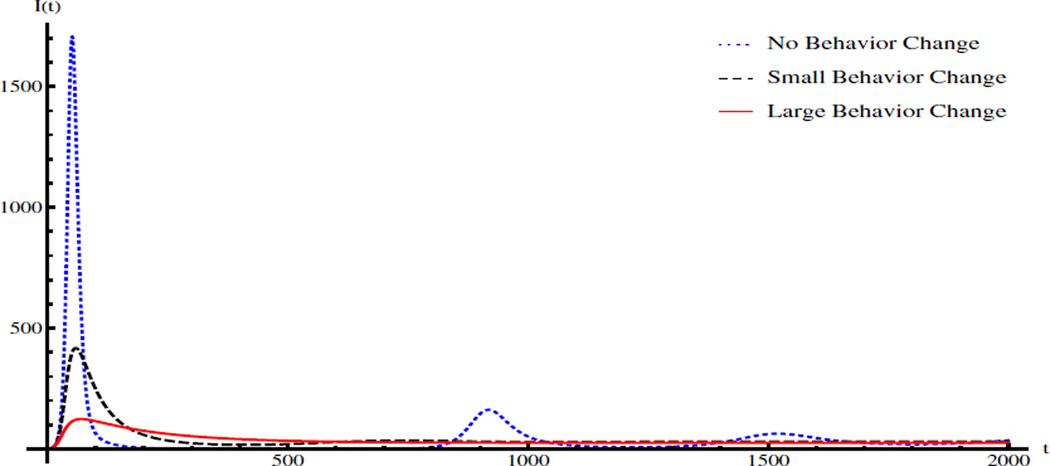
We numerically verify Proposition 3.5 as follows. The values of parameters and initial condition are: K = 2 × 10⁶, γ = 1/5, δ = 1/30, μ = 1/(43.5 × 365), a₁ = 3 × 10⁻⁵, a₂ = 0.02, a₃ = 15, σ = 1/(3 × 365), and (S(0), I(0), R(0), B(0)) = (12346, 1, 0, 0). The corresponding basic reproduction number is ℛ₀ = 1.99. Consider the saturation functions $m_i(I_i)=\frac{I}{I+K_i}$ for i = 1, 2, 3. The blue dotted line, black dashed line, and red solid line in Figure 1 show the number of infectious individuals for the model (2.1) with no behavior change (b_i = 0 for i = 1, 2, 3), small behavior change (b_i = 0.8a_i and K_i = 500 for i = 1, 2, 3), and large behavior change (b_i = 0.8a_i and K_i = 100 for i = 1, 2, 3), respectively. Clearly, behavior change alone cannot eliminate the disease, but can significantly reduce the epidemic/endemic level and larger behavior change leads to less infections. In addition, the infection curve of the cholera model with large behavior change does not experience damped oscillations over time.

Figure 1.

Infection curves of the ODE model without behavior change, with small behavior change, and with large behavior change. The values of parameters and initial condition are: K = 2 × 10⁶, γ = 1/5, δ = 1/30, μ = 1/(43.5 × 365), a₁ = 3 × 10⁻⁵, a₂ = 0.02, a₃ = 15, σ = 1/(3 × 365), and (S(0), I(0), R(0), B(0)) = (12346, 1, 0, 0).

4 Cholera Traveling Waves

In order to further understand the effects of human behavior on cholera transmission dynamics, we extend the ODE model (2.1) to a PDE system taking into account the diffusion of human hosts and bacteria and the convection of vibrios. Consequently, we will investigate the propagation of epidemic waves and related threshold dynamics, under the impact of human behavior.

Consider cholera dynamics along a one-dimensional theoretical river. Incorporating into (2.1) the bacterial and human diffusion, and bacterial convection due to river flow, we obtain the following cholera epidemic PDE model

$$\frac{\partial S}{\partial t}=\mu N-S{\beta }_1(I)I-S{\beta }_2(I)B/(B+K)-\mu S+\sigma R+D_1\frac{{\partial }^{2}S}{\partial x^2},$$

$$\frac{\partial I}{\partial t}=S{\beta }_1(I)I+S{\beta }_2(I)B/(B+K)-(\mu +\gamma )I+D_2\frac{{\partial }^{2}I}{\partial x^2},$$ (4.1)

$$\frac{\partial R}{\partial t}=\gamma I-(\mu +\sigma )R+D_3\frac{{\partial }^{2}R}{\partial x^2},$$

$$\frac{\partial B}{\partial t}={\beta }_3(I)I-\delta B-\upsilon \frac{\partial B}{\partial x}+D_4\frac{{\partial }^{2}B}{\partial x^2},$$

where x ∈ [0, 1] and t ≥ 0 are the location and time variable, respectively. S(x, t), I(x, t), and R(x, t) measure the number of susceptible, infectious, and recovered human hosts at location x and time t, respectively. B = B(x, t) denotes the cholera concentration in the water environment. D_i > 0 (1 ≤ i ≤ 4) is the diffusion coefficient of S, I, R and B, respectively, and υ ≥ 0 represents the convection coefficient that describes the effect of the river flow on the bacterial movement. The definition of model parameters can be found in Table 1.

A useful approach to study the spatial spread of cholera is to investigate the travel wave solution of model (4.1) and to determine the critical speeds of the traveling fronts. Introduce a variable u = x − ct where c is the speed of the disease traveling front. Assume that N = S + I + R is a constant. Then (4.1) can be rewritten as

$$I\prime =X,$$

$$R\prime =Y,$$

$$B\prime =Z,$$

$$X\prime =\frac{1}{D_2}[(-cX)-(N-I-R)({\beta }_1(I)I+{\beta }_2(I)B/(B+K))+(\mu +\gamma )I],$$ (4.2)

$$Y\prime =\frac{1}{D_3}[(-cY)-\gamma I+(\mu +\sigma )R],$$

$$Z\prime =\frac{1}{D_4}[(\upsilon -c)Z-{\beta }_3(I)I+\delta B].$$

where $\prime =\frac{d}{du}$.

We will now focus on the case where ${ℛ}_0^{ODE}>1$ since our interest is the spatial spread of the disease. Notice that model (4.2) has two spatially homogeneous stationary solutions, 𝒱₀ = (0, 0, 0, 0, 0, 0) and 𝒱₁ = (I_e, R_e, B_e, 0, 0, 0); these equilibria correspond to the disease-free and endemic equilibrium points of the ODE model, respectively. Thus, any traveling wave solution of (4.2) can be regarded as a heteroclinic orbit connecting 𝒱₀ and 𝒱₁. More specifically, (1) in the case of a progressive wave front, 𝒱₀ is a saddle and the heteroclinic orbit goes from 𝒱₁ to 𝒱₀. This depicts downstream propagation of the disease, for instance, from inland areas to coasts; (2) in the case of a regressive wave front, 𝒱₀ is an unstable node and the heteroclinic orbit connects 𝒱₀ to 𝒱₁. It captures the upstream propagation of the disease, for example, from coasts to inland regions. Meanwhile, we notice that an orbit with oscillatory dynamics around V₀ will destroy the non-negative property of the state variables I, R and B. Therefore, in either case, all the eigenvalues of the Jacobian matrix 𝒥 associated with the linearized system of (4.2) evaluated at 𝒱₀ must be real for a wave font to exist. Direct computation yields

$$𝒥=\left[\begin{array}{cc}\hfill 0_3\hfill & \hfill I_3\hfill \\ \hfill {𝒥}_{21}\hfill & \hfill {𝒥}_{22}\hfill \end{array}\right],$$

where 0₃ is the 3 × 3 zero matrix, I₃ denotes the 3 × 3 identity matrix,

$${𝒥}_{21}=\left[\begin{array}{ccc}\hfill \frac{1}{D_2}(-a_{1}N+(\mu +\gamma ))\hfill & \hfill 0\hfill & \hfill \frac{-a_{2}N}{D_{2}K}\hfill \\ \hfill -\frac{\gamma }{D_3}\hfill & \hfill \frac{\mu +\sigma }{D_3}\hfill & \hfill 0\hfill \\ \hfill -\frac{a_3}{D_4}\hfill & \hfill 0\hfill & \hfill \frac{\delta }{D_4}\hfill \end{array}\right],$$

and

$${𝒥}_{22}=\text{diag}[-c/D_2,-c/D_3,(\upsilon -c)/D_4].$$

The characteristic equation of matrix 𝒥 is

$$({\lambda }^2+c/D_3\lambda -(\mu +\sigma )/D_3)({\lambda }^4+b_1{\lambda }^3+b_2{\lambda }^2+b_3\lambda +b_4)=0,$$ (4.3)

where

$$b_1=c/D_2+(c-\upsilon )/D_4,$$

$$b_2=-(\mu +\gamma -a_{1}N)/D_2-\delta /D_4+c(c-\upsilon )/(D_2{D}_4),$$

$$b_3=[-c\delta +(\mu +\gamma -a_{1}N)(\upsilon -c)]/(D_2{D}_4),$$

$$b_4=[(\mu +\gamma -a_{1}N)\delta -a_2{a}_{3}N/K]/(D_2{D}_4).$$

The critical value of c occurs only if the characteristic equation (4.3) has repeated real roots. We only need to focus on its second term p(λ) = λ⁴ + b₁λ³ + b₂λ² + b₃λ + b₄, since the first term of this equation has two distinct real roots, and none of these roots satisfies p(λ) = 0. It follows from ${ℛ}_0^{ODE}>1$ that b₄ < 0 and hence p(λ) has at least one positive and one negative zeros. We now proceed to find the condition for the existence of repeated roots. The work of Jury and Mansour [21] shows that double zeros of this quartic polynomial p(λ) occurs if

$$\mathrm{\Delta }=4M^3-W^2=0,$$ (4.4)

where $M=b_2^2+12b_4-3b_1{b}_3$ and $W=72b_2{b}_4+9b_1{b}_2{b}_3-2b_2^3-27b_3^2-27b_4{b}_1^2$. If υ = 0, equation (4.4) becomes

$$e_1{(c^2)}^4+e_2{(c^2)}^3+e_3{(c^2)}^2+e_4(c^2)+e_5=0,$$ (4.5)

whose coefficients depend on the model parameters. Particularly,

$$e_1={(D_2-D_4)}^2[{(\mu +\gamma -a_{1}N-\delta )}^2+4a_2{a}_{3}N/K]\ge 0,$$

and e₁ > 0 when D₂ ≠ D₄. Meanwhile, if ${ℛ}_0^{PDE}$, then

$$e_5=16D_2{D}_4[\delta (\mu +\gamma -a_{1}N)-a_2{a}_{3}N/K]\times {[{(D_4(\mu +\gamma -a_{1}N)-D_2\delta )}^2+4D_2{D}_4{a}_2{a}_{3}N/K]}^2<0.$$

Thus, equation (4.5) has at least one positive zero with respect to c²; namely, this equation has at least a pair of real roots in terms of c which have the same magnitude but opposite signs.

There are typically two critical speeds, denoted c₊ and c₋, such that the wave front with speed c ∈ (c₋, c₊) cannot exist. Furthermore, it has been established [2, 24] that for large t, the progressive disease spreading velocity is exactly c = c₊ and the regressive spreading velocity is exactly c = c₋, among the infinitely many waves propagating at c ≥ c₊ (progressive waves) or c ≤ c₋ (regressive waves).

We have numerically calculated the critical wave speeds c₊ and c₋ under a variety of settings. Our particular emphasis here is the impact of human behavior on the spatial spread of cholera. We note that the variation of β_i(I) can, alternatively, be reflected by the change of values of a_i, i = 1, 2, 3. Thus, it is convenient to treat c₊ and c₋ as functions of a_i (1 ≤ i ≤ 3), and study the variation of wave speeds in terms of a_i.

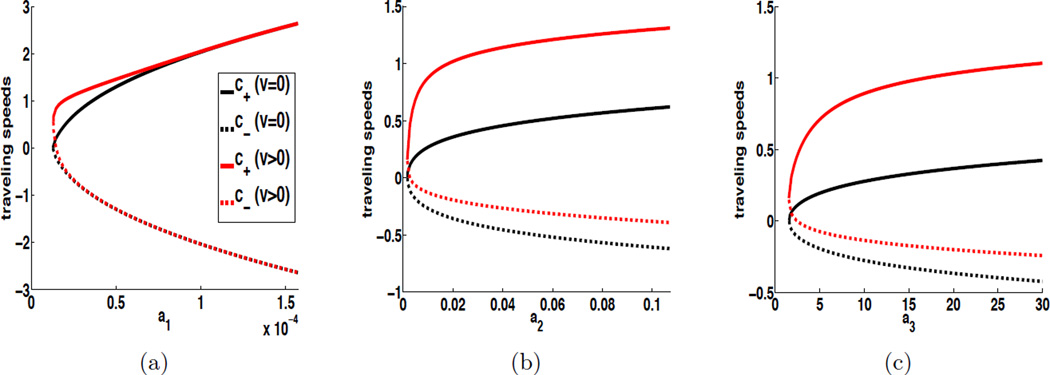
In Figure 2, we plot c_± vs. a_i with two choices of convection coefficients: υ = 0 and υ = 1, while the diffusion coefficients are fixed at D₂ = D₄ = 1. We pick the base values of a_i (i = 1, 2, 3) from [28]. In Figure 2-a, we plot c_± vs. a₁, with fixed a₂ and a₃ at their base values; in Figure 2-b, we plot c_± vs. a₂ while fixing a₁ and a₃; and so on. For each plot, we clearly observe that when υ = 0, the progressive speed c₊ and regressive speed c₋ are symmetric with respect to the horizontal axis, as predicted by equation (4.5). When υ = 1, however, the curves lose symmetry and show that incorporation of a downstream convection process for bacteria tends to strengthen the wave propagation in the positive (or, downstream) direction, while weakening the wave propagation in the negative (or, upstream) direction.

Figure 2.

Cholera traveling wave speeds vs a_i (i = 1, 2, 3) when D₂ = D₄ = 1. The base values of a₁, a₂ and a₃ are set as a₁ = 1.57 × 10⁻⁵ (day⁻¹), a₂ = 0.011 (person⁻¹·day⁻¹), and a₃ = 10 (cells · ml⁻¹·day⁻¹). In each figure, one parameter is varied while the other two are fixed at their base values. For each plot, the upper solid curve refers to the progressive velocity c₊ and the lower dashed curve refers to the regressive velocity c₋. The curves in black (resp. red) show the critical cholera spreading speeds when υ = 0 (resp. υ = 1).

The most important pattern in these figures, however, is that the wave speeds in both directions are increasing when a_i (i = 1, 2, 3) increases. It indicates that a reduction for the value of a_i (say, due to human behavior) would weaken the epidemic wave propagation and reduce the spread of the disease. For the case υ = 1, a more careful examination of the regressive wave speeds reveals that c₋ becomes positive, and close to 0, when a_i (i = 1, 2, 3) is much smaller than its base value, implying that there is no upstream wave propagation. An explanation is that the random diffusion process, particularly from the coast to the inland regions, contributes to the upstream propagation of the disease (represented by the regressive waves with negative speeds). When one of those contact rates is sufficiently low, the diffusion of infected human hosts and/or bacteria cannot compete with the effects of the downstream convection of bacteria, resulting in no upstream propagation of the disease. This result indicates that reduction of a_i can not only reduce the wave speeds, but also impact the direction of wave propagation. Further, as can be clearly seen from each figure, if each a_i can be made sufficiently close to 0, then no traveling wave will be generated.

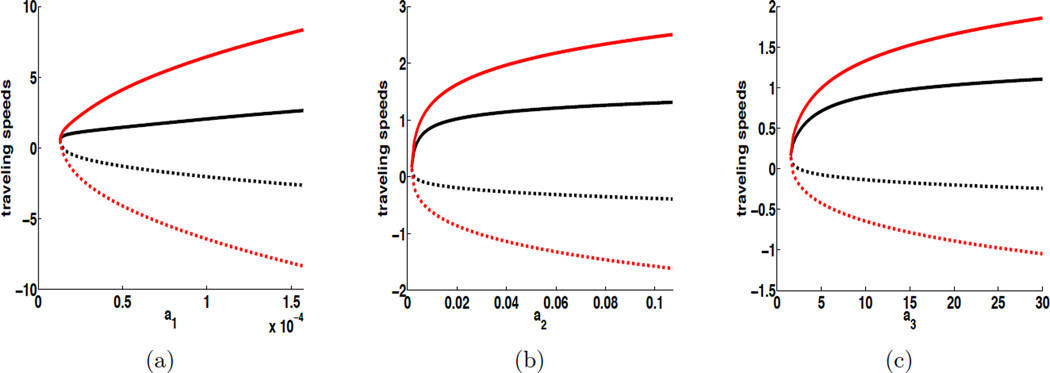
In Figure 3, under similar settings for a_i (i = 1, 2, 3), we plot c_± vs. a_i with two different choices of diffusion coefficients, while fixing the convection speed at υ = 1. We again observe that, in each case, the increase of a_i leads to faster wave propagation in both directions. Meanwhile, as the diffusion becomes stronger, the traveling wave speeds also increase for both upstream and downstream propagation.

Figure 3.

Influence of D₂ and D₄ on cholera traveling wave speeds when υ = 1, which is illustrated by plotting cholera traveling wave speeds as a function of a_i (i = 1, 2, 3). The base values of a₁, a₂ and a₃ are a₁ = 1.57 × 10⁻⁵ (day⁻¹), a₂ = 0.011 (person⁻¹·day⁻¹), and a₃ = 10 (cells · ml⁻¹·day⁻¹). For each plot, the upper solid curve refers to the progressive velocity c₊ and the lower dashed curve refers to the regressive velocity c₋. The curves in black (resp. red) show the critical cholera spreading speeds when D₂ = D₄ = 1 (resp. D₂ = D₄ = 10).

5 PDE Model Threshold Dynamics

We now study the spatial threshold dynamics of cholera by analyzing the basic reproduction number associated with the PDE model (4.1). Though originally proposed for ODE epidemic models, the concept of the basic reproduction number has been extended to reaction-diffusion and reaction-convection-diffusion epidemic systems with homogeneous Neumann boundary conditions in recent years (e.g., Thieme [39], Wang and Zhao [45], and Hsu et al. [20]). Based on these studies, the basic reproduction number ℛ₀ for a PDE epidemic system is defined as the spectral radius of the operator

$$L[\varphi (x)]={\int }_0^{\infty }F(x)T(t)\varphi dt=F(x){\int }_0^{\infty }T(t)\varphi dt,$$

where F is the matrix characterizing the generation of new infection, in the corresponding ODE system (i.e., without diffusion terms); T(t) denotes the solution semigroup associated with the linearized reaction-convection-diffusion system for disease compartments; ϕ describes the distribution of the initial infection. In [45], it is shown that

$${\int }_0^{\infty }T(t)\varphi dt={-ℬ}^{-1}\varphi ,$$

and

$$L=-F{ℬ}^{-1}$$

for which ℬ ≔ ∇· (d_I∇) − υ_I∇ − V where the matrix V denotes the transition between compartments. Here d_I and υ_I are the diffusion and convection coefficient vectors, respectively.

In the case of our cholera epidemic model (4.1), we have:

$$d_I=\text{diag}[D_2,D_4],{\upsilon }_I=\text{diag}[0,\upsilon ],$$

$$F=\left[\begin{array}{cc}\hfill a_{1}N\hfill & \hfill a_{2}N/K\hfill \\ \hfill a_3\hfill & \hfill 0\hfill \end{array}\right]\text{and}V=\left[\begin{array}{cc}\hfill \mu +\gamma \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \delta \hfill \end{array}\right],$$

and

$$ℬ=\left[\begin{array}{cc}\hfill D_2\frac{{\partial }^2}{\partial x^2}-(\mu +\gamma )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill D_4\frac{{\partial }^2}{\partial x^2}-\upsilon \frac{\partial }{\partial x}-\delta \hfill \end{array}\right].$$

To analyze the basic reproduction number of the PDE system (4.1),

$${ℛ}_0^{\mathrm{P}\mathrm{D}\mathrm{E}}=\rho (L),$$

we consider the eigenvalue problem L[ϕ] = λϕ ; that is,

$$-F{ℬ}^{-1}\varphi =\lambda \varphi ,$$ (5.1)

where ϕ = (ϕ₁, ϕ₂)^T ∈ C([0, 1], ℝ²). With some algebraic manipulation (see details in Appendix E), the eigenvalue problem (5.1) can be put into the form

$$k_{i1}{\int }_0^x\text{sin}\mathrm{h}[\sqrt{\frac{\mu +\gamma }{D_2}}(x-\tau )]{\varphi }_1(\tau )d\tau +k_{i2}\text{cos}\mathrm{h}\left(\sqrt{\frac{\mu +\gamma }{D_2}}x\right){\int }_0^1\text{cos}\mathrm{h}[\sqrt{\frac{\mu +\gamma }{D_2}}(1-\tau )]{\varphi }_1(\tau )d\tau +k_{i3}{\int }_0^x{e}^{\frac{\upsilon }{2D_4}(x-\tau )}\text{sin}\mathrm{h}[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\delta }{D_4}}(x-\tau )]{\varphi }_2(\tau )d\tau +k_{i4}{e}^{-\frac{\upsilon }{2D_4}(1-x)}\left\{\text{cos}\mathrm{h}\right[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\delta }{D_4}}x]-\frac{\upsilon }{\sqrt{{\upsilon }^2+4\delta D_4}}\text{sin}\mathrm{h}[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\delta }{D_4}}x\left]\right\}{\int }_0^1{e}^{\frac{\upsilon }{2D_4}(1-\tau )}\left\{\frac{\upsilon }{2D_4}\text{sin}\mathrm{h}\right[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\delta }{D_4}}(1-\tau )]+\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\delta }{D_4}}\text{cos}\mathrm{h}[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\delta }{D_4}}(1-\tau )\left]\right\}{\varphi }_2(\tau )d\tau =\lambda {\varphi }_i(x),(i=1,2).$$ (5.2)

where

$$k_{11}=\frac{-a_{1}N}{\sqrt{D_2(\mu +\gamma )}},k_{12}=\frac{a_{1}N}{\sqrt{D_2(\mu +\gamma )}\text{sin}\mathrm{h}\left(\sqrt{\frac{d+\gamma }{D_2}}\right)}$$

$$k_{13}=\frac{-2a_{2}N/K}{\sqrt{{\upsilon }^2+4D_4\delta }},k_{14}=\frac{a_{2}N/K}{\delta \text{sin}\mathrm{h}\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\delta }{D_4}}},$$

$$k_{21}=\frac{-a_3}{\sqrt{D_2(\mu +\gamma )}},k_{22}=\frac{a_3}{\sqrt{D_2(\mu +\gamma )}\text{sin}\mathrm{h}(\sqrt{\frac{\mu +\gamma }{D_2}})},$$

and k₂₃ = k₂₄ = 0.

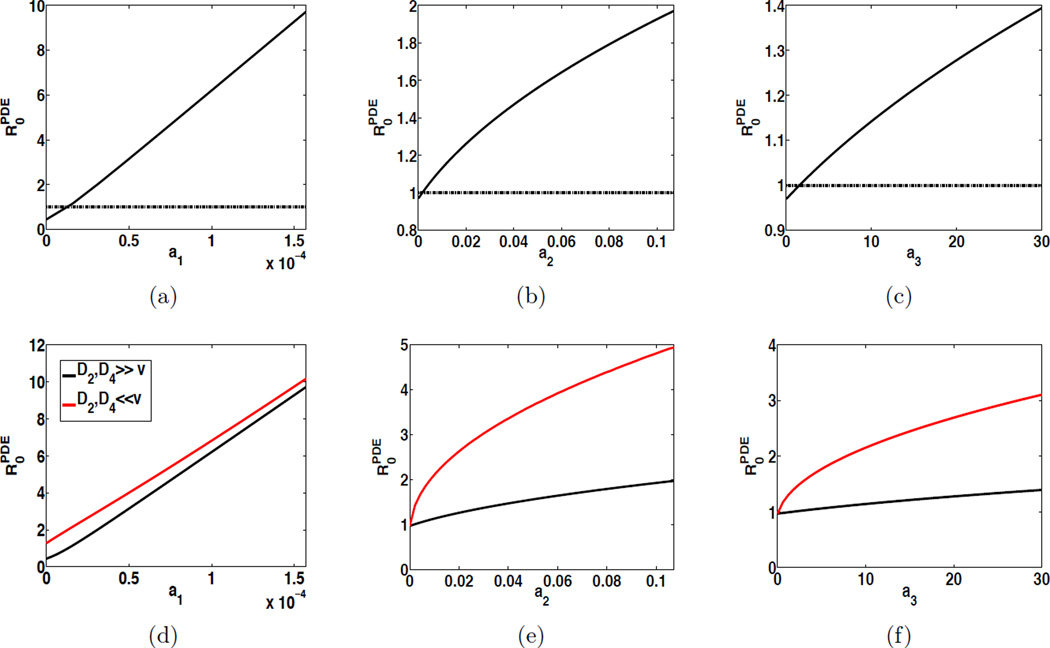
The disease threshold ${ℛ}_0^{PDE}$ can then be numerically evaluated by reducing the operator eigenvalue problem (5.2) into a matrix eigenvalue problem, an approach originated from the work in [44]. We have investigated the impact of human behavior on the disease threshold in three scenarios: (1) human and bacterial diffusions and bacterial convection equally important; i.e., D₂, D₄ = O(υ); (2) diffusions dominant; i.e., D₂, D₄ ≫ υ; and (3) convection dominant; i.e., D₂, D₄ ≪ υ. The results are displayed in Figure 4. It shows that in each scenario ${ℛ}_0^{PDE}$ is decreasing as a_i (i = 1, 2, 3) decays, indicating that as human surveillance tends to decrease direct and indirect transmission rates and bacterial shedding rate, this will lead to a lower infection risk. One can see from Figure 4 (a)–(c) that, in scenario (1), if the surveillance (through human behavior) is strong enough, ${ℛ}_0^{PDE}$ can be reduced below the critical threshold value 1, which indicates that human behavior can significantly reduce the infection risk and control the disease. Moreover, in our PDE cholera model, we have numerically found that the difference between ${ℛ}_0^{PDE}$ and ${ℛ}_0^{ODE}$ is small when D₂ = D₄ = υ, and almost invisible when D₂, D₄ ≫ υ. For instance, if D₂ = D₄ = υ = 1, the difference is about 10⁻⁴; if D₂ = D₄ = 10⁶ and υ = 1, the difference is about 10⁻⁹. Moreover, when bacterial convection is dominant, ${ℛ}_0^{PDE}$ tends to be elevated; that is, the associated infection risk is prone to be higher as shown in Figure 4 (d)–(f). In such cases, although the human behavior can still reduce ${ℛ}_0^{PDE}$, it may not bring down ${ℛ}_0^{PDE}$ back to 1. In other words, when bacterial convection is dominant, human surveillance focused on reducing transmission rates and bacterial shedding rate may not be sufficient in controlling cholera epidemics.

Figure 4.

Influence of human behavior on the cholera infection risk on a spatial domain, illustrated by displaying ${ℛ}_0^{PDE}$ as a function a_i (i = 1, 2, 3). (a)–(c): the solid curve refers to the case where D₂, D₄ = O(υ), and the dashed line indicates where y = 1; (d)–(f): for each plot, the black curve refers to the case where D₂, D₄ ≫ υ, and the red curve refers to the case where D₂, D₄ ≪ υ.

6 Discussion

We have presented a modeling framework for the impact of human behavior on cholera dynamics. Fundamental in our assumption is that people are well informed of the development and severity of the disease outbreak, made possible by the media coverage and reports from various resources, thus will take action to reduce contact with other individuals and/or the contaminated environment, to eat well-cooked food, and to introduce safe disposal of excreta. Our models involve transmission rates and host shedding rates represented as decreasing functions of the infection size, applicable to a variety of effects resulting from changes in human behavior. Our analysis is centered on the impact of human behavior on cholera dynamics, for both a homogeneous environment (represented by an ODE model) and a more heterogeneous environment where spatial movement of the hosts and bacteria becomes important (represented by a reaction-convection-diffusion PDE model). For the ODE model, we have rigorously proved that the basic reproduction number ℛ₀ (or, equivalently, the type reproduction number T₁) remains a sharp threshold for disease dynamics despite the incorporation of human behavior. In particular, when ℛ₀ > 1 the disease will persist and the endemic equilibrium will be globally asymptotically stable. For the PDE model, a sharp threshold reproduction number is also defined and analyzed, and we have numerically computed the value of the PDE ℛ₀ with various contact rates and compared the results with the ODE ℛ₀. Their values reflect the (possibly different) predictions of disease risks based on the homogeneous and heterogeneous settings. These results could provide useful insight to help public heath administrations for disease prevention and intervention.

Cholera transmission occurs through direct (i.e., human-to-human) or indirect (i.e., environment-to-human) routes. The multiple transmission pathways and related bacterial dynamics in the aquatic environments, together with human behavior, and spatial heterogeneity characterized by movements (diffusion and/or convection) of hosts and pathogen, complicate the pattern of disease dynamics. Our models aim to investigate the interplay of these different biological, ecological, environmental, and sociological factors. Our results quantify the natural expectation of human behavior in reducing the severity of an epidemic, particularly for a cholera outbreak. Specifically, the results in this paper provide mathematical justification of several consequences of human behavior: (1) reducing the epidemic and endemic levels; (2) reducing the spread speeds (i.e., traveling wave speeds) of the disease; (3) reducing the infection risks (characterized by the basic reproduction numbers) in both homogeneous and heterogeneous environments.

We have assumed that human behavior is “rational" in responding to an epidemic. Practically, however, media coverage and news broadcasting could contain false information on the outbreak details which may lead to inappropriate behavioral response. In such cases, the contact rates β_i(I) in our models will not be monotonic functions of the infection size. During the outbreak of a fatal or novel pathogen, human behavior is more likely to be affected by the cumulative total numbers of cases and deaths than by the real-time number of infectious individuals [19, 9]. In practice, the movement of humans is not random but strongly affected by socioeconomic factors. The current paper did not include such factors, though these might be as well worthwhile to model and analyze mathematically. Meanwhile, there are several other limitations in our work. For instance, the contact rates and the dynamics of Vibrio cholerae in the environment may change subject to seasonality [8]. It would be more practical to study a non-autonomous system to better reflect seasonality [30]. The work is true under the assumption: bacteria population is decreasing in the absence of human contribution (e.g. shedding from infected individuals). Furthermore, rather than using a simplistic 1D space dimension, constructing the system on a 2D spatial domain would be more realistic for cholera modeling. The diffusion and convection coefficients as well as several parameters of disease transmission rates can be taken as space dependent, instead of constants, to adequately capture the details of spatial heterogeneity. Collection of data on disease epidemiology, behavior change in response to an epidemic, hosts, pathogen, and their diffusion is challenging, but vital to test the validity and reliability of our models [15].

Highlights.

• Both ODE and PDE cholera models with the influence of human behavior are proposed.

• Contact rates and shedding rate are decreasing functions of the number of infectives.

• Threshold dynamics of the ODE model are established with respect to its R0.

• The traveling wave speed and threshold dynamics of the PDE model are analyzed.

• Health education campaign can help to improve cholera control programs.

A Model Parameters and Functions

The definition and base values of parameters in our ODE and PDE cholera models are provided in Table 1. Here p (resp. y and d) represents a person (resp. year and day)

Table 1.

Definition of cholera model parameters

Parameter	Definition	Value	References
N	Total population size of humans	12, 347 p	[28]
μ	Natural death rate of humans	(43.5 y)−1	[46]
a1	Direct transmission rate	1.57 × 10−5 d−1	[28]
a2	Indirect transmission rate	0.011 p−1d−1	[28]
K	Half saturation rate	106 cells · ml−1	[17]
γ	Recovery rate	(5 d)−1	[17]
σ	Rate of host immunity loss	(3 y)−1	[29]
δ	Bacterial net death rate	(30 d)−1	[17]
a3	Shedding rate	10 [cells · ml−1d−1]	[17]
D1	Diffusion coefficient of susceptible hosts	Varied [km2 d−1]
D2	Diffusion coefficient of infectious hosts	Varied [km2 d−1]
D3	Diffusion coefficient of recovered hosts	Varied [km2 d−1]
D4	Diffusion coefficient of bacteria in the water environment	Varied [km2 d−1]
υ	Convection coefficient of bacteria	Varied [km · d−1]

B Proof of Theorem 3.1

Proof

1. Since S = N − I − R, we consider an equivalent system of (2.1)

   $$\frac{dI}{dt}=(N-I-R)({\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K})-(\mu +\gamma )I,$$

   $$\frac{dR}{dt}=\gamma I-(\mu +\sigma )R,$$ (B.1)

   $$\frac{dB}{dt}={\beta }_3(I)I-\delta B.$$
   The Jacobian matrix of the vector field described by (B.1) is

   $$J=[J_{ij}]=\left[\begin{array}{ccc}\hfill J_{11}\hfill & \hfill -{\beta }_1(I)I-{\beta }_2(I)\frac{B}{B+K}\hfill & \hfill {\beta }_2(I)S\frac{K}{{(B+K)}^2}\hfill \\ \hfill \gamma \hfill & \hfill -(\mu +\sigma )\hfill & \hfill 0\hfill \\ \hfill {\beta }_3^{\prime }(I)I+{\beta }_3(I)\hfill & \hfill 0\hfill & \hfill -\delta \hfill \end{array}\right],$$ (B.2)

   where

   $$J_{11}={\beta }_1^{\prime }(I)SI-{\beta }_1(I)I+{\beta }_1(I)S+{\beta }_2^{\prime }(I)S\frac{B}{B+K}-{\beta }_2(I)\frac{B}{B+K}-(\mu +\gamma )$$

   and S = N − I − R. Evaluating the Jacobian matrix (B.2) at the DFE, (N, 0, 0, 0), gives

   $$J{|}_{DFE}=\left[\begin{array}{ccc}\hfill a_{1}N-(\mu +\gamma )\hfill & \hfill 0\hfill & \hfill a_{2}N/K\hfill \\ \hfill \gamma \hfill & \hfill -(\mu +\sigma )\hfill & \hfill 0\hfill \\ \hfill a_3\hfill & \hfill 0\hfill & \hfill -\delta \hfill \end{array}\right]$$

   Let λ₁, λ₂ and λ₃ denote the eigenvalues of J|_DFE. Without loss of generality, we write λ₃ = −(μ + σ), which is clearly negative. It is easy to verify that τ₂ ≔ λ₁ + λ₂ = a₁N − (μ + γ) − δ and 𝒟₂ ≔ λ₁λ₂ = (a₁N − (μ + γ))(−δ) − a₂a₃N/K. Hence the local stability of the DFE is determined by the sign of τ₂ and 𝒟₂. Notice that one can rewrite τ₂ and 𝒟₂ in terms of the type reproduction number T₁ as follows: ${𝒟}_2=-\frac{1}{\delta (\mu +\gamma )}(T_1-1)$ and ${\tau }_2=(\mu +\gamma )(T_1-1-\frac{a_2{a}_{3}N}{(\mu +\gamma )K\delta })$. It then follows from T₁ ≤ 1 that we have 𝒟₂ ≥ 0 and τ₂ < 0; meanwhile 𝒟₂ = 0 holds only if T₁ = 1. This implies that both λ₁ and λ₂ are non-positive and at least one of them is strictly negative. Therefore, we show that the DFE is locally asymptotically stable (resp. Lyapunov stable) when T₁ < 1 (resp. T₁ = 1).
2. By a similar approach as that in the first case, we can show that the DFE is unstable when T₁ > 1. Our focus now is the local stability of the EE. We want to prove that the EE is locally asymptotically stable. Evaluating the Jacobian matrix (B.2) at the EE, we find that the characteristic equation of J|_EE is given by

   $${\lambda }^3+c_1{\lambda }^2+c_2\lambda +c_3=0,$$

   where

   $$c_1=-(J_{11}+J_{22}+J_{33}){|}_{EE},$$

   $$c_2=(-J_{12}{J}_{21}+J_{11}{J}_{22}+J_{22}{J}_{33}+(J_{11}{J}_{33}-J_{13}{J}_{31})){|}_{EE},$$

   $$c_3=(-J_{22}(J_{11}{J}_{33}-J_{13}{J}_{31})+J_{12}{J}_{21}{J}_{33}){|}_{EE}.$$

   According to the Routh-Hurwitz criterion, it remains to show that

   $$c_1>0,c_2>0,c_3>0,c_1{c}_2-c_3>0,$$ (B.3)

   In the following, we assume that $(S,I,R,B)\in {ℝ}_4^{+}$ is the EE of (2.1) and the rest of arguments is all restricted to the EE. By the equilibrium equation (3.4), we can rewrite J₁₁ as follows:

   $$J_{11}=-({\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K})+S({\beta }_1^{\prime }(I)I+{\beta }_2^{\prime }(I)\frac{B}{B+K})-{\beta }_2(I)\frac{SB}{I(B+K)}.$$

   It follows from β_i(I) > 0 and ${\beta }_i^{\prime }(I)\le 0$ for i = 1, 2 that J₁₁ < 0. Moreover, it is clear that J₁₂ < 0, J₁₃ > 0, J₂₁ > 0, J₂₂ < 0, and J₃₃ < 0. Meanwhile, we notice that

   $$c_1{c}_2-c_3=-J_{11}{c}_2-x{J}_{22}[-J_{12}{J}_{21}+J_{22}(J_{11}+J_{33})]-J_{33}[J_{22}(J_{11}+J_{33})+(J_{11}{J}_{33}-J_{13}{J}_{31})].$$

   Thus, (B.3) is valid by the fact that

   $$J_{11}{J}_{33}-J_{13}{J}_{31}\ge -({\beta }_1(I)S-(\mu +\gamma ))\delta -{\beta }_3(I){\beta }_2(I)SK/{(B+K)}^2={\beta }_2(I)\frac{SB}{B+K}\frac{\delta }{I}-{\beta }_2(I){\beta }_3(I)\frac{SK}{{(B+K)}^2}={\beta }_2(I)\frac{S}{B+K}(\frac{B\delta }{I}-{\beta }_3(I)\frac{K}{B+K})={\beta }_2(I)\frac{S}{B+K}({\beta }_3(I)-{\beta }_3(I)\frac{K}{B+K})={\beta }_2(I){\beta }_3(I)\frac{SB}{{(B+K)}^2}>0.$$

   The proof is complete.

C Proof of Theorem 3.4

Proof

Suppose that ℛ₀ > 1. Hence, by Theorem 3.1, the system (2.1) has two equilibria: the DFE and the EE. We now proceed to prove the global stability of the endemic equilibrium of (2.1) by using the geometric approach based on the second additive compound matrix [23]. The details on the geometric approach can be found in Appendix D. By Theorem 3.1, the DFE is unstable, and it is on the boundary of the domain Ω. This implies that the disease is uniformly persistent in Ω⁰, namely,

$$\underset{t\to \infty }{\text{lim inf}}(I(t),B(t))>(c,c)$$

for some c > 0. It then follows from the compactness of Ω and the uniform persistence of system (2.1) that there exists a compact absorbing set in Ω. Meanwhile, the EE is the unique equilibrium in Ω⁰. By the geometric method [23], it remains to prove that the generalized Bendixson criterion q̄₂ < 0 (see an outline of the geometric method and definition of q̄₂ in the Appendix D). The idea of the proof is to choose a norm in ℝ³ and to construct a matrix-valued function P(S, I, B) such that q̄₂ < 0.

First, dropping the equation for R in system (2.1) and using the constant host population, i.e., R = N − S − I, we obtain

$$\frac{dS}{dt}=\mu N-S({\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K})-\mu S+\sigma (N-S-I),$$

$$\frac{dI}{dt}=S({\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K})-(\mu +\gamma )I,$$ (C.1)

$$\frac{dB}{dt}={\beta }_3(I)I-\delta B.$$

For simplicity,

$$\begin{array}{cc}{\theta }_1={\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K},\hfill & {\theta }_2=S[{\beta }_1^{\prime }(I)I+{\beta }_1(I)+{\beta }_2^{\prime }(I)\frac{B}{B+K}],\hfill \\ {\theta }_3=S{\beta }_2(I)\frac{K}{{(B+K)}^2},\hfill & {\theta }_4={\beta }_3^{\prime }(I)I+{\beta }_3(I).\hfill \end{array}$$

The Jacobian matrix associated with the linearized system of (C.1) is

$$\tilde{J}=\left[\begin{array}{ccc}\hfill -{\theta }_1-(\mu +\sigma )\hfill & \hfill -{\theta }_2-\sigma \hfill & \hfill -{\theta }_3\hfill \\ \hfill {\theta }_1\hfill & \hfill {\theta }_2-(\mu +\gamma )\hfill & \hfill {\theta }_3\hfill \\ \hfill 0\hfill & \hfill {\theta }_4\hfill & \hfill -\delta \hfill \end{array}\right]$$

and its second additive compound matrix is

$${\tilde{J}}^{[2]}=\left[\begin{array}{ccc}\hfill -{\theta }_1+{\theta }_2-(2\mu +\sigma +\gamma )\hfill & \hfill {\theta }_3\hfill & \hfill {\theta }_3\hfill \\ \hfill {\theta }_4\hfill & \hfill -{\theta }_1-(\mu +\sigma +\delta )\hfill & \hfill -{\theta }_2-\sigma \hfill \\ \hfill 0\hfill & \hfill {\theta }_1\hfill & \hfill {\theta }_2-(\mu +\gamma +\delta )\hfill \end{array}\right].$$

We now take

$$P=\text{diag}[1,\frac{I}{B},\frac{I}{B}].$$

Then P is nonsingular and C¹ in Ω⁰. Let f denote the vector field of (2.1). Thus,

$$P_f{P}^{-1}=\text{diag}[0,\frac{I\prime }{I}-\frac{B\prime }{B},\frac{I\prime }{I}-\frac{B\prime }{B}]$$

and

$$P{\tilde{J}}^{[2]}{P}^{-1}=\left[\begin{array}{ccc}\hfill -{\theta }_1+{\theta }_2-(2\mu +\sigma +\gamma )\hfill & \hfill {\theta }_3\frac{B}{I}\hfill & \hfill {\theta }_3\frac{B}{I}\hfill \\ \hfill {\theta }_4\frac{I}{B}\hfill & \hfill -{\theta }_1-(\mu +\sigma +\delta )\hfill & \hfill -{\theta }_2-\sigma \hfill \\ \hfill 0\hfill & \hfill {\theta }_1\hfill & \hfill {\theta }_2-(\mu +\gamma +\delta )\hfill \end{array}\right].$$

Thus, the matrix Q = P_fP⁻¹ + PJ̃^[2]P⁻¹ can be written in the following block form:

$$Q=\left[\begin{array}{cc}\hfill Q_{11}\hfill & \hfill Q_{12}\hfill \\ \hfill Q_{21}\hfill & \hfill Q_{22}\hfill \end{array}\right],$$

where

$$Q_{11}=-({\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K})+S[{\beta }_1^{\prime }(I)I+{\beta }_1(I)+{\beta }_2^{\prime }(I)\frac{B}{B+K}]-(2\mu +\sigma +\gamma ),$$

$$Q_{12}=S{\beta }_2(I)\frac{K}{{(B+K)}^2}\frac{B}{I}[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \end{array}],$$

$$Q_{21}=\left[\begin{array}{c}\hfill ({\beta }_3^{\prime }(I)I+{\beta }_3(I))\frac{I}{B}\hfill \\ \hfill 0\hfill \end{array}\right],$$

$$Q_{22}=\left[\begin{array}{cc}\hfill q_{11}\hfill & \hfill q_{12}\hfill \\ \hfill q_{21}\hfill & \hfill q_{22}\hfill \end{array}\right]$$

with

$$q_{11}=-({\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K})-(\mu +\sigma +\delta )+I\prime /I-B\prime /B,$$

$$q_{12}=-S[{\beta }_1^{\prime }(I)I+{\beta }_1(I)+{\beta }_2^{\prime }(I)\frac{B}{B+K}]-\sigma ,$$

$$q_{21}={\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K},$$

$$q_{22}=S[{\beta }_1^{\prime }(I)I+{\beta }_1(I)+{\beta }_2^{\prime }(I)\frac{B}{B+K}]-(\mu +\gamma +\delta )+I\prime /I-B\prime /B.$$

The vector norm |·| in ℝ³ is chosen as

$$|(x_1,x_2,x_3)|=\text{max}\{|x_1|,|x_2|+|x_3|\}.$$

One can verify that the Lozinskiĭ measure ℳ(Q) with respect to this norm can be estimated as

$$ℳ(Q)\le \text{sup}\{g_1,g_2\},$$

where

$$g_1={ℳ}_1(Q_{11})+|Q_{12}|,$$

$$g_2=|Q_{21}|+{ℳ}_1(Q_{22}).$$

Here |Q₁₂| and |Q₂₁| are matrix norms induced by the l₁ vector norm, ℳ₁ denotes the Lozinskiĭ measure with respect to the l₁ norm. More specifically,

$$g_1=Q_{11}+|Q_{12}|=-({\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K})+S[{\beta }_1^{\prime }(I)I+{\beta }_1(I)+{\beta }_2^{\prime }(I)\frac{B}{B+K}]-(2\mu +\sigma +\gamma )+\frac{S{\beta }_2(I)K}{{(B+K)}^2}\frac{B}{I},$$

$$g_2=|Q_{21}|+\text{max}\{q_{11}+|q_{21}|,|q_{12}|+q_{22}\}=({\beta }_3^{\prime }(I)I+{\beta }_3(I))\frac{I}{B}-(\mu +\sigma +\delta )+\frac{I\prime }{I}-\frac{B\prime }{B}+\text{sup}\{0,2(S[{\beta }_1^{\prime }(I)I+{\beta }_1(I)+{\beta }_2^{\prime }(I)\frac{B}{B+K}]+\sigma )-\gamma \}.$$

Since $I\prime =S({\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K})-(\mu +\gamma )I$, we have

$$-(\mu +\gamma )=\frac{I\prime }{I}-S{\beta }_1(I)-\frac{S}{I}{\beta }_2(I)\frac{B}{B+K}.$$

This leads to

$$g_1=-({\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K})+S[{\beta }_1^{\prime }(I)I+{\beta }_1(I)+{\beta }_2^{\prime }(I)\frac{B}{B+K}]-(\mu +\sigma )+\frac{S{\beta }_2(I)K}{{(B+K)}^2}\frac{B}{I}+\frac{I\prime }{I}-S{\beta }_1(I)-\frac{S}{I}{\beta }_2(I)\frac{B}{B+K}=-({\beta }_1(I)I+{\beta }_2(I)\frac{B}{B+K})+S[{\beta }_1^{\prime }(I)I+{\beta }_2^{\prime }(I)\frac{B}{B+K}]-\frac{S{\beta }_2(I)B}{(B+K)I}(1-\frac{K}{B+K})+\frac{I\prime }{I}-(\mu +\sigma )\le \frac{I\prime }{I}-(\mu +\sigma ).$$ (C.2)

The last inequality follows from the assumptions on β_i(I), i.e., β_i(I) ≥ 0 and ${\beta }_i^{\prime }(I)\le 0$ for i = 1, 2. Applying the similar argument together with assumption on β₂(I), β₃(I) and B′/B = β₃(I)I/B − δ, we have

$$g_2=({\beta }_3^{\prime }(I)I)\frac{I}{B}+{\beta }_3(I)\frac{I}{B}-\delta -(\mu +\sigma )+I\prime /I-B\prime /B+\text{sup}\{0,2(S[{\beta }_1^{\prime }(I)I+{\beta }_1(I)+{\beta }_2^{\prime }(I)\frac{B}{B+K}]+\sigma )-\gamma \}\le \frac{I\prime }{I}-(\mu +\sigma )+\text{sup}\{0,2(S[{\beta }_1^{\prime }(I)I+{\beta }_1(I)+{\beta }_2^{\prime }(I)\frac{B}{B+K}]+\sigma )-\gamma \}\le \frac{I\prime }{I}-\mu +\text{sup}\{0,2S({\beta }_1(I)I)\prime +\sigma -\gamma \}\le \frac{I\prime }{I}-\mu ,\text{if}S({\beta }_1(I)I)\prime \le (\gamma -\sigma )/2.$$ (C.3)

Thus, (C.2) and (C.3) yield

$$ℳ(Q)\le \frac{I\prime }{I}-\mu .$$

It follows from 0 ≤ I(t) ≤ N that

$$\frac{\text{ln}(I(t))-\text{ln}(I(0))}{t}\le \frac{\mu }{2},$$

for t sufficiently large. We then obtain

$$\frac{1}{t}{\int }_0^tℳ(Q)ds\le \frac{1}{t}{\int }_0^t(\frac{I\prime (s)}{I(s)}-\mu )ds=\frac{\text{ln}(I(t)))-\text{ln}(I(0))}{t}-\mu \le -\frac{\mu }{2},$$

if t is large enough. This in turn implies that q̄₂ ≤ −μ/2 < 0 and it completes the proof.

D The Geometric Approach

Here we present the main result of the geometric approach for global stability, originally developed by Li and and Muldowney [23].

We consider a dynamical system

$$\frac{dX}{dt}=f(X)$$ (D.1)

where f : D ↦ ℝⁿ is a C¹ function and D ⊂ ℝⁿ is a simply connected open set. Let P(X) be a $\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)\times \left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)$ matrix-valued C¹ function in D, and set

$$Q=P_f{P}^{-1}+P{J}^{[2]}{P}^{-1},$$

where P_f is the derivative of P (entry-wise) along the direction of f, and J^[2] is the second additive compound matrix of the Jacobian J(X) = Df(X). Let m(Q) be the Lozinskiĭ measure of Q with respect to a matrix norm; i.e.,

$$ℳ(Q)=\underset{h\to 0^{+}}{\text{lim}}\frac{|𝕀+hQ|-1}{h},$$

where 𝕀 represent the identity matrix. Define a quantity $\overline{q_2}$ as

$$\overline{q_2}=\underset{t\to \infty }{\text{lim sup}}\underset{X_0\in K}{\text{sup}}\frac{1}{t}{\int }_0^tℳ(Q(X(s,X_0)))ds,$$

where K is a compact absorbing subset of D. Then the condition $\overline{q_2}<0$ provides a Bendixson criterion in D. As a result, the following theorem holds:

Theorem D.1

Assume that there exists a compact absorbing set K ⊂ D and the system (D.1) has a unique equilibrium point X* in D. Then X* is globally asymptotically stable in D if $\overline{q_2}<0$.

E Derivation of Eigenvalue Problem (5.2)

To analyze the basic reproduction number of the PDE system (4.1), ${ℛ}_0^{\mathrm{P}\mathrm{D}\mathrm{E}}=\rho (L)$, we proceed to calculate ℬ⁻¹ by solving ℬ(ϕ₁, ϕ₂)^T = (y₁, y₂)^T. First, let us consider the boundary value problem

$${ℬ}_1[{\varphi }_1]≔D_2\frac{{\partial }^2{\varphi }_1}{\partial x^2}-(\mu +\gamma ){\varphi }_1=y_1,0<x<1;$$

$${\varphi }_1^{\prime }(0)=0,{\varphi }_1^{\prime }(1)=0.$$ (E.1)

The explicit representation of the solution to (E.1) can be found (e.g., using Laplace transform) as

$${\varphi }_1(x)={ℬ}_1^{-1}[y_1]=\frac{1}{\sqrt{D_2(\mu +\gamma )}}{\int }_0^x\text{sin}\mathrm{h}[\sqrt{\frac{\mu +\gamma }{D_2}}(x-\tau )]y_1(\tau )d\tau -\frac{\text{cos}\mathrm{h}(\sqrt{\frac{\mu +\gamma }{D_2}}x)}{\sqrt{D_2(\mu +\gamma )}\text{sin}\mathrm{h}(\sqrt{\frac{\mu +\gamma }{D_2}})}{\int }_0^1\text{cos}\mathrm{h}[\sqrt{\frac{\mu +\gamma }{D_2}}(1-\tau )]y_1(\tau )d\tau .$$ (E.2)

Similarly, solving the equation

$${ℬ}_2[{\varphi }_2]≔D_4\frac{{\partial }^2{\varphi }_2}{\partial x^2}-\upsilon \frac{\partial {\varphi }_2}{\partial x}-\partial {\varphi }_2=y_2,0<x<1;$$

$${\varphi }_2^{\prime }(0)=0,{\varphi }_2^{\prime }(1)=0,$$

we find that

$${\varphi }_2(x)={ℬ}_2^{-1}[y_2]=\frac{2}{\sqrt{{\upsilon }^2+4D_4\delta }}{\int }_0^x{e}^{\frac{\upsilon }{2D_4}(x-\tau )}\text{sin}\mathrm{h}[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\partial }{D_4}}(x-\tau )]y_2(\tau )d\tau -\frac{e^{-\frac{\upsilon }{2D_4}(1-x)}}{\partial \text{sin}\mathrm{h}\left[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\partial }{D_4}}\right]}\left(\text{cos}\mathrm{h}\right[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\partial }{D_4}x}]-\frac{\upsilon }{\sqrt{{\upsilon }^2+4\delta D_4}}\text{sin}\mathrm{h}[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\partial }{D_4}}x\left]\right)$$

$${\int }_0^1{e}^{\frac{\upsilon }{2D_4}(1-\tau )}\left\{\frac{\upsilon }{2D_4}\text{sin}\mathrm{h}\right[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\delta }{D_4}}(1-\tau )]+\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\delta }{D_4}}\text{cos}\mathrm{h}[\sqrt{\frac{{\upsilon }^2}{4D_4^2}+\frac{\delta }{D_4}}(1-\tau )\left]\right\}{y}_2(\tau )d\tau .$$ (E.3)

Since

$$L[\varphi ]=-F{ℬ}^{-1}\varphi =\lambda \varphi ,$$ (E.4)

substituting (E.2) and (E.3) into (E.4) leads to the eigenvalue problem (5.2).