New algorithm of mortality risk prediction for cardiovascular patients admitted in intensive care unit

Abstract

Objective: Recognizing and managing of admitted patients in intensive care unit (ICU) with high risk of mortality is important for maximizing the patient’s outcomes and minimizing the costs. This study is based on linear and nonlinear analysis of heart rate variability (HRV) to design a classifier for mortality prediction of cardio vascular patients admitted to ICU. Methods: In this study we evaluated 90 cardiovascular ICU patients (45 males and 45 females). Linear and nonlinear features of HRV include SDNN, NN50, low frequency (LF), high frequency (HF), correlation dimension, approximate entropy; detrended fluctuation analysis (DFA) and Poincaré plot were analyzed. Paired sample t-test was used for statistical comparison. Finally, we fed these features to the Multi-Layer Perceptron (MLP) and Support Vector Machines (SVMs) to find a robust classification method to classify the patients with low risk and high risk of death. Results: Almost all HRV features measuring heart rate complexity were significantly decreased in the episode of half-hour before death. The results generated based on SVM and MLP classifiers show that SVM classifier is enable to distinguish high and low risk episodes with the total classification sensitivity, specificity, positive productivity and accuracy rate of 97.3%, 98.1%, 92.5% and 99.3%, respectively. Conclusions: The results of the current study suggest that nonlinear features of the HRV signals could be show nonlinear dynamics.

Introduction

The intensive care unit is a speculated area where medical devices, doctors and nurses are focused for treating severely ill patients in a hospital. The main goal of ICU is to recover the life of patients with reversible medical conditions or offer comfortable death for non-salvageable patients with adverse condition.

Presently health care groups are focused to research on techniques for improving effectiveness of the treatment for the critically ill patients in ICU. The concept of providing cost-effective intensive care has now generalized to all developed countries, becoming a major interest of clinicians, hospital administrations, health care managers, medical economists and governmental policy makers [1].

The acute physiology and chronic health evaluation (APACHE) [2], mortality probability model (MPM) [3], and simplified acute physiology score (SAPS) [4] are among the most commonly used models for predicting risk of mortality in ICU patients [5]. Though widely used and having multiple revisions to accommodate changes in patient populations and advances in hospital care, these scoring systems still have some limitations. The most comprehensive and accurate of these scoring systems, APACHE, is a proprietary tool that requires licensing and is heavily dependent on selecting the correct admission diagnosis [6]. MPM and SAPS examine only a few variables, resulting ease of use, but overly simplistic models that might overlook important physiological measurements.

While using only a few key data elements to develop predictive models made sense historically, the availability of detailed electronic medical records and modern machine learning methods has made this rationale obsolete. Most importantly, these models are unable to deal with missing data and assume that unobserved parameters are normal, which can result in under predicted risk [6].

More recently, the techniques based on neural networks have been proved to be useful in the ICU mortality prediction. They are widely used because of their capabilities like nonlinear learning, multi-dimensional mapping and noise tolerance. Previous studies reported that the neural network models were better than or at least similar to the linear regression models [7-9].

Outcome prediction in intensive care is a challenging process. It requires accurate synthesis of quality data and application of prior experience to the analysis. Evaluation of HRV can be helpful in clinical assessment and intervention strategies. It has been proved that nonlinear analysis of HRV might provide more valuable information for the physiological interpretation of heart rate fluctuations [10]. The nonlinear analysis of HRV is a valuable tool in both clinical practice and physiological research reflecting the ability of the cardiovascular system [11].

In this study, we propose an algorithm to estimate the risk of mortality based on linear and non-linear analysis of HRV during 48-hours admission in ICU. We investigated how the most common nonlinear HRV measures vary in admitted patients in ICU during death episode. Finally, we proposed a classifier for automatic detection of patients close to death.

This paper is organized as follows: Section 2 presents the database, feature extraction methods and details of the proposed algorithm. Section 3 demonstrates the results and briefly discusses the rationale for the proposed algorithm. Section 4 and 5 represent the discussion and conclusions, respectively.

Methods

Database

In this paper we used the data belong to MIMIC-II database, include the physiological data streams obtained from the patients admitted in ICU. The MIMIC II database includes continuous physiologic waveforms such as electrocardiogram (ECG), blood pressure and discrete physiologic variables such as pH and Glucose. MIMICII database focused on patient-specific mortality prediction using the information collected during the first two days of admission in ICU, to predict which patient survive his/her hospitalizations and which do not [12].

The proposed algorithm

The block diagram of the proposed algorithm is demonstrated in Figure 1. As it can be seen, the algorithm comprises of five steps include preprocessing, feature extraction, PCA-based feature reduction, death and non-death episodes classification based on MLP and SVM and classification performance. In the following, each block is described with more details.

Figure 1.

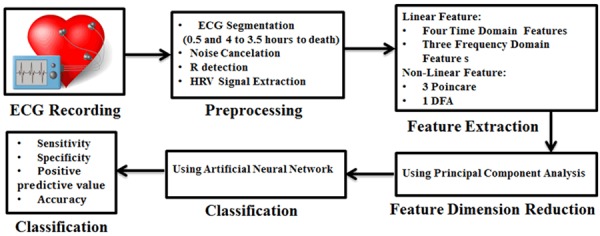
The block diagram of the proposed classification algorithm.

Preprocessing

In this paper, we apply an improved least mean square (LMS) adaptive filtering algorithm [13] to remove the 50 Hz power line interference from ECG signal. As current study is based on HRV analysis, the HRV should be extracted from the ECG signals. Therefore, the first stage of this study is R wave detection. We used the proposed algorithm by Pan-Tompkins [14] for R wave detection. After determining the exact position of R peaks the HRV signal is made by calculaing the time interval between each two successive R wave. Then, the HRV signal of each patient is divided into segments include 2000 samples to extract the linear and nonlinear features of each segment.

Feature extraction

The second step in the block diagram is the feature extraction. In general, the cardiovascular system, hence the HRV signal, demonstrates both linear and nonlinear behavior of autonomic nervous system. In this study, a combination of linear and nonlinear features is considered for HRV analysis. Time and frequency domain features are among the standard linear measures of the HRV signals.

Linear features extraction

Usually linear feature extraction of the HRV signal is done in both time and frequency domain. In this paper, we used of linear features extracted from time and frequency domain for classification between two time periods [15-17].

Time domain features

Features that are extracted from the time domain consists of a set of statistical features. Linear HRV indicators determined are listed in Table 1.

Table 1.

Linear time domain indicators of HRV

Features	Description
SDNN	Standard deviation of NN intervals (beat-to-beat intervals) calculated over a 24-hour period.
RMSSD	Root mean square of successive difference (RMSSD) is the square root of the mean of the sum of the squares of the successive differences between adjacent NNs.
NN50	The number of pairs of successive NNs that differ by more than 50 millisecond.
pNN50	The ratio obtained of NN50 divided by the total number of NNs.

Ferequency domain features

In frequency-domain methods, frequency components of the HRV signal are identified. In HRV spectrum obtained from ECG recordings, some components are detected such as VLF (very low frequency), LF (low frequency) and HF (high frequency). The LF is a measure of sympathetic activity (frequency range: 0.05-0.15 Hz) and HF is a marker of parasympathetic activity (frequency range: 0.15-0.5 Hz). The LF/HF ratio is an important feature in the frequency domain, which determines the equilibrium rate of sympathovagal. In addition to LF, HF and LF/HF features, we used another feature in the frequency domain called total power (TP).

Non-linear features extraction

In general, a supposition is accepted for electrocardiogram time series. It is assumed that the HRV is not both linear and deterministic [18]. However, this assumption is commonly valid because some hearts may show linear and deterministic behavior; usually those that have very low heart rate variability. Finally, to specify if the heart shows deterministic or stochastic non-linear behavior, a method utilizing attractor reconstruction dimension d, and correlation dimension D_c is utilized [18,19]. If in some d dimensional description of the system, the attractor correlation dimension of D_c reaches to saturation state, the system can be specified deterministic. If the ECG signal has too much noise, it will be a stochastic system because the attractor is masked and its correlation dimension never saturates [18].

Chaos theory applied to feature extraction

The one dimensional deterministic nonlinear system can be determined using the following Formula 1:

Where function f is a non-linear function based on the present value of the system state variable (x_n) and controls the parameter (α) which is a constant value. x_{n +1} is the subsequent value of this variable.

The special characteristic of a chaotic system is aperiodicity, determinism, confinement and sensitive dependence on initial conditions. When the values of a state variable show no obvious periodic schema, the system is aperiodicity, and the values of the state variable never repeat [18]. Meaning of determinism is that the values of system state variables can be computed in every moment if their previous value is specified [20].

Confinement denotes that the values of system variables are always constrained between some boundary values. Every chaotic system has sensitive dependence on initial conditions. It means that a very small difference may lead to a very large trajectory divergence of the variable after a number of cycles.

The basic problem of nonlinear time series analysis is to determine whether a given time series is a deterministic signal of a dynamic system with low dimension or not. If this is true, what is the phase space dimension related to this data, and are the time series chaotic. The answers of these questions are in the phase space reconstruction that has been agreed by Saur and Taken [21].

Phase space is a space in which every point represents two or more states of a system variable. The number of states that can be used in phase space is called phase space dimension or reconstruction dimension. Phase space reconstruction is a standard method when analyzing chaotic systems. It shows the trajectory of the system in time.

Phase space in m dimensions will display a number of points X(i) of the system, where each point is given by Formula 2:

Where, i is a moment in time of a system variable, τ is a period between two consecutive measurements of the variable or called delay time and m is embedding dimension. Choosing different τ and m values create a different reconstructed trajectory. The trajectory in m dimensional space is a set of k consecutive points, where i = t0,t0 + τ,...,t0 + (k - 1)τ is the starting time of observation [18,22].

Taken embedding theory claims that if a time series is part of an attractor (with the dimension of d), topological properties of the attractor with topological properties of the embedded attractor, which formed with the m-dimensional phase space vectors, are equal to conditional. m > 2d + 1 Therefore, the first step in the non-linear dynamic analysis is the attractor reconstruction in the phase space. The main technique for the phase space reconstruction is using the time delay method. In time delay method, the vectors in the new space and the embedding space are constructed using the delay values. Thus, in order to reconstruct a dynamic system attractor, two problems must be solved. The first challenge relates to the choice of the optimal delay for trajectory reconstruction in phase space, and the second one is to determine the embedding dimension. Different methods for selecting optimum time delay and embedding dimension are usable. In this paper, mutual information (MI) method for choosing the time delay and the false nearest neighbor method is used for selecting the embedding dimension.

Mutual information method

The mutual information method is examined on dynamic systems and chaotic data. This method used a powerful approach to find the relationships between data sets [23]. The advantage of this method in comparison with the autocorrelation function, which was used previously, is that unlike the autocorrelation function this method considered the linear correlations in the time series.

The most common method for computing time delay is based on the value of mutual information between the pair of observed values x_i and x_i+1 The main idea in this method is to look for the minimum τ for which the mutual information between observations is lowest [22]. The average mutual information function for different τ values can be computed using Formula 3:

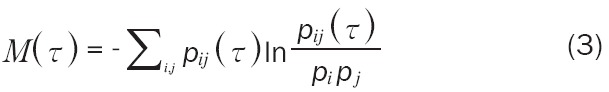Where p_i is the probability to find a time series value in the i^th interval of the interval, p_ij(τ) is the joint probability to find a time series value in the i^th interval and a time series value in the j^th interval after a time τ, i.e. the probability of transition in τ time from the i^th to the j^th interval [24].

False nearest neighbor method

False nearest neighbor method is a method to determine the minimal sufficient embedding dimension m which was proposed by Kennel et al. [q25]. The idea is quite intuitive. Suppose m ₀ is the minimal embedding dimension for a specific time series x{i}. It means that the reconstructed attractor in a m ₀- dimensional delay space is in one-to-one correspondence with the attractor in the original phase space. In fact, the topological characteristics are preserved. Therefore, the neighbors of a specific point are mapped onto neighbors in the delay space. Under the assumption of dynamics smoothness, neighborhoods of the points are mapped onto neighborhoods again. Based on the basics of Lyapunov exponents, the shape and the diameter of the neighborhoods are changed. Suppose we embed in a m dimensional space (the attractor embedding dimension is less than original dimension: m < m ₀). Because of this projection, the topological structure is not well preserved. Points are projected into neighborhoods of other points to which they wouldn’t belong in higher dimensions. These points are called false neighbors. The main idea of the false nearest method is the following.

For each point in the time series look for its nearest neighbor in a m dimensional space. Calculate the distance [25,26]. Iterate both points and compute R_i using the Formula 4:

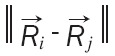If R_i exceeds a given heuristic threshold of R_i, that point is labeled as having a false nearest neighbor [q25]. The criterion that the embedding dimension is high enough is that the fraction of points for which R_i > R_j is zero or at least close to zero. In other words, the plot of R_i/R_j achieve to the saturation state. To explain more clearly associated with the false nearest neighbor method, a simple example will be explained using Figure 2. When the red, yellow and blue samples are projected in one dimension, it seems that the samples are in the neighborhood. When the samples projected in two dimensions, the yellow samples are no longer near the red and blue samples. When the samples projected in three dimensions, there is no further change in the relative distances between the samples.

Figure 2.

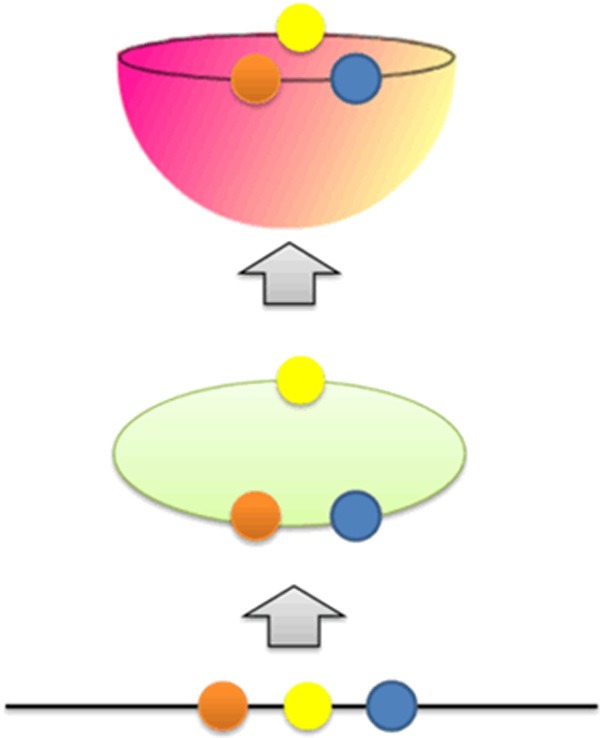
A simplified explanation of false nearest neighbors.

Correlation dimension

Correlation dimension is the degree of complexity of the system and gives the number of independent variables needed to describe the behavior of the system. The linear determinism system has integer correlation dimension, while chaotic systems have the fractional correlation dimension. This method estimates the embedding dimension based on the phase space pattern.

Correlation dimension can be calculated using the distances between each pair of points in the set of N number of points (s(i,j) = |X_i - X_j|). Where X_i, X_j are points of the trajectory in the phase space [27,28]. A correlation function, C(r), can be calculated using Formula 5, where N is the number of data points in phase space and r is the radial distance around each reference point X_i.

C(r) has been found to follow a power law similar to the one seen in the capacity dimension (C(r) = kr^D). Therefore, we can find D_corr with estimation techniques derived from the Formula 6:

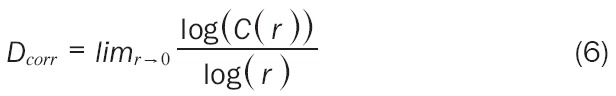Where C(r) can be written in a more mathematical form as the Formula 7:

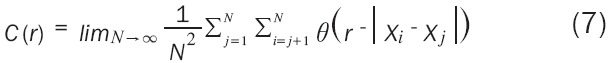Where θ is the Heaviside step function described as Formula 8 [27]:

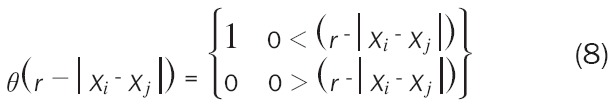Detrended fluctuation analysis (DFA)

Detrended fluctuation analysis (DFA) is used in analysis of biological data and computes the root-mean-square fluctuation of integrated and detrended time series, permits the detection of intrinsic self-similarity embedded in a non-stationary time series, and also avoids the spurious detection of apparent self-similarity. The algorithm is used in a large range of physiological and simulated time series in recent years [28]. To represent the DFA algorithm, we calculate the total length of the heart rate signal (N) as shown in Formula 9:

Where HR(i) is the i^th heart rate signal and HR_αvg is the average heart rate of N samples. Next, the integrated time series is divided into segments of equal length n, a least-squares line is fit to the data (representing the trend in that segment). They coordinate of the straight line segments is denoted by y(k). Then, we detrend the heart rate data y(k), by subtracting the local trend, y(k), in each segment. The root mean square fluctuation of this integrated and detrended heart rate data is calculated by Formula 10:

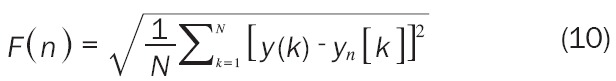This calculations is repeated over all the segment sizes to provide a relationship between F(n), the average fluctuation as a function of the segment size n. In this paper, the segment size is ranged from 4-300 beats. A box size larger than 300 beats would give a less accurate fluctuation value because of finite length effects of data. Typically, F(n) will increases with the segment size. A linear relationship on a double-log graph indicates the presence of scaling, i.e. F(n)≈n ^α. Under such conditions, the fluctuations can be characterized by a scaling exponent a, the slope of the line relating logF(n) to log(n). A good linear fit of the logF(n) to log(n) plot (DFA plot) indicates that F(n) is proportional to n ^α, where α is the single exponent describing the correlation properties of the entire range of heart rate data.

However in some cases, the DFA plot was not strictly linear but rather consisted of two distinct regions of different slopes separated at a break point n_bp [27]. This observation suggests there is a short range scaling exponent, α_s, over periods of 4-l3 [n_bp] beats, and a long-range exponent, α_i, over long periods [27].

Poincaré plot analysis

Poincaré plot technique is derived from nonlinear dynamics. In Poincaré plot, each RR interval is plotted against next RR interval (a type of delay map). Thus, the time series of RR interval is plotted in phase space. The Poincaré plot is analyzed quantitatively by calculating the standard deviation of RR intervals with the lines y = x and y = -x + 2 × RR_m which RR_m is RR_i the average of . Poincaré plot provides useful information from short-term and long-term fluctuations and demonstrate patterns of heart rate dynamics resulting from nonlinear processes. It is quantified by measuring SD ₁ and SD ₂, which are standard deviation of the instantaneous RR variability and standard deviation of the long term variability of the heart rate, respectively. The SD1/SD2 ratio shows the relation between short and long variations of RR intervals [29]. Figure 3 shows a geometrical representation of Poincaré plot for a healthy subject.

Figure 3.

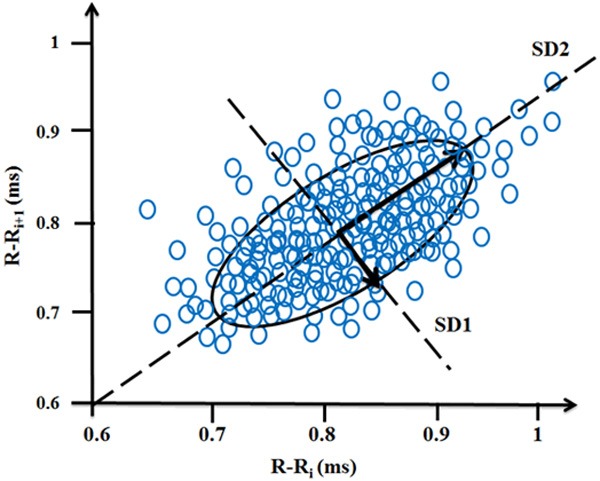
A standard Poincaré plot (τ=1) of RR intervals of a healthy subject.

Feature dimension reduction

We tried to combine the best features to the maximum difference between two groups. First, the classification was applied to each feature, separately and the best features are selected according to the highest classification accuracy. Then, this feature is combined with each feature individually. Finally, the best combination is selected. Similarly, this process continues until the resulting combination that makes the most difference is achieved. This combination is comprised of eleven features (four features of time, there features of frequency and four non-linear features).

Principal component analysis (PCA) is used in order to continue improving the performance of clustering and reduce the learning time. PCA is a supervised method for dimension reduction. The purpose of PCA is to find a transformation matrix on the data vectors, which are belong to different classes in order to image to a space with lower dimension so that the ratio of scattering between the classes to the scattering into classes to be maximized.

Statistical analysis

In this paper, we computed mean, standard deviation of extracted indicators of HRV to illustrate the distribution of HRV features during two episodes (death episode and non-death episode). We used the paired sample t-test to investigate the statistical significance of indicators within each subject. The statistical analysis was performed using related software developed in MATLAB version R2014b.

Classification and performance measurement

The finalized optimal features obtained based on the combination of linear and nonlinear features were given to a classifier to predict the mortality risk. In this paper, MLP and SVM were selected as classifier.

Multi-layer perceptron

Artificial Neural Network (ANN) is versatile tool widely used to tackle issues. Feed-Forward Neural Networks (FNN) is popular among ANNs. These networks solve complex problems through modeling complex input-output relationships. The back-propagation algorithm is the workhorse for design of special class of layered feed-forward networks known as MLP [30].

MLP is a generalization of single layer perceptron that consists of an input layer, one or more hidden layer and an output layer [31]. The visualization of MLP is depicted in Figure 4. The MLP uses the back-propagation learning algorithm. In current paper, the number of neurons in the hidden layer is equal to the sum of the input neurons and output neurons divided by 2.

Figure 4.

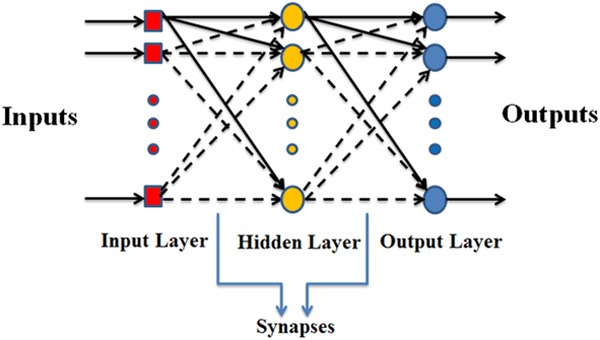
Multi-layer perceptron neural network structure.

Support vector machine

SVM is proven to be very robust and reduces the need for extensive parameter tuning for better classification performances compared to other machine learning methods [32]. It is based on the structural risk minimization principle from computational learning theory. SVM tries to find hyper planes that best separate the classes with maximum distance between hyper planes based on the input features. The issue of low dimensionality feature vector always results in poor class separation. However, in SVM, this low dimensionality data is projected into higher dimensionality vector using different kernel functions for improving the class separation rate of input.

In order to design an efficient SVM classifier, the type of kernel and the hyper-plane separating method should be specified. Kernel functions used to project low dimension data into higher dimension [33]. There are three hyper-plane separating methods considered repeatedly in the literature in SVM based pattern recognition such as Quadratic Programming (QP), Sequential Minimal Optimization (SMO) and Least Squares (LS). Choosing the best kernel function is done through trial and error. In this work, Radial Basis Function (RBF) kernel with scaling factor (σ) of one [34] was chosen, and QP was used for mortality prediction. The given parameters to SVM are summarized in Table 2 [35].

Table 2.

Given parameters to SVM

Parameters	Description
Input vector	60×7
Target vector	60×1
Kernel function	Radial basis function with σ=1
Hyper plane searching method	Quadratic programming

In order to analyze the output data obtained from the classifier, the number of true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN) are used. Using the formulae mentioned in Table 3, we calculated the common measures for binary classification performance measurement [36] to evaluate the classifier. Considering positive to the test those records classified as death episode. Total classification accuracy represents the ability of the classifier to discriminate between the two groups (death and non-death episode), sensitivity refers to the ability to identify records in the death episode and specificity refers to the ability to identify records in the non-death episode [37].

Table 3.

Binary Classification Performance Measures

Measure	Abbreviation	Formulae
Sensitivity	SEN	TP/TP + FN
Specificity	SPE	TN/TN + FP
Positive predictive value	PPV	TP/TP + FP
Accuracy	ACC	TP + TN/TP + FN + FP + TN

TP, the number of records performed during university examination correctly detected; TN, the number of records performed on holidays correctly detected; FP, the number of records performed on holidays incorrectly labeled as during university examination; FN, the number of records performed during university examination incorrectly labeled as on holidays.

Total classification accuracy represents the ability of the classifier to discriminate between the two groups (death and non-death episode), sensitivity refers to the ability to identify records in the death episode and specificity refers to the ability to identify records in the non-death episode [37].

Results

Table 4 represents a comparison between the non-linear characteristics of two time periods include: half-hours before death (group 1) and 4 to 3.5 hours before death (group 2). The delay time required for phase space reconstruction from 4 to 3.5 hours before death is lower than 30 min before death.Therfore, more data should be used to reconstruct the phase space of HRV time series belongs to group 2. In other words, the correlation between the data of group 2 are lower than group 1.

Table 4.

Non-linear features extracted from the two groups

Adequate embedding dimension to reconstruct the phase space of HRV time series for the data of group 2 is higher than group 1. This shows that, the data of group 2 are more random than group 1 or in the other words, the complexity and the correlation existing in the data of group 1 are higher.

The correlation dimension extracted from the data of group 2 is higher than group 1. Since this feature shows the number of variables needed to model the system, it can be concluded that modeling of the HRV time series of group 2 needs more variables.This result is similar to the results obtained by the delay time and the embedding dimension, which stated that the correlation between the data of group 2 is lower in comparison with group 1.

The ApEn of group 2 is higher than group 1, which emphasize more complexity of HRV time series of group 2 in comparisin with group 1. SD ₁ of group 2 is higher than group 1, while SD ₂ of group 1 is higher than group 2. Therefore, short and long-term fluctuations of group 1 are high. Lower SD ₁ and higher SD ₂ of group 2 leads to significantly higher SD ₂/SD ₁ compared to group 1.

Fractal characteristics (α_long, α_short) extracted from group 1 and group 2 indicate that group 1 has α_long < α_short. However, it is contrariwise in group 2. Table 4 shows non-linear features extracted from the two groups and the differences between them.

Table 5 shows the sensitivity, specificity, positive predictive value and accuracy obtained by different classifiers based on the combination of linear and non-linear features. As can be seen, the SVM neural network classifiers showed better performance. MLP classifier can’t separate feature vectors of two groups as well as SVM.

Table 5.

The classification results of MLP and SVM classifiers

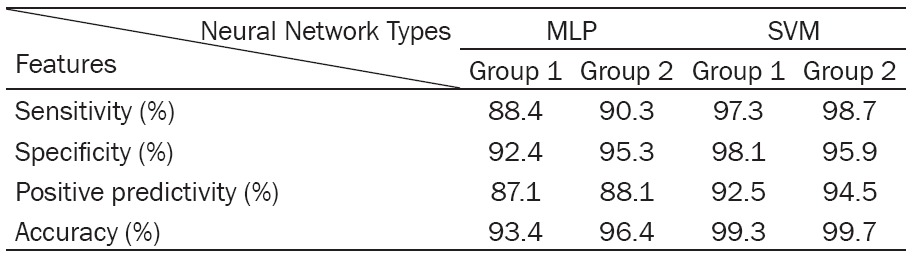
Discussion

The purpose of this present study was to examine the potential of HRV as a predictor of mortality risk in patients admitted in ICU. Therefore, the linear and nonlinear analysis of HRV has been carried out.

The results of this study cannot be compared directly with previous studies worked on mortality prediction of ICU patients. Although APACHE and SAPS have almost been accompanied by good results in mortality prediction [2,4], to the best of our knowledge there is not any study focus on HRV to predict the mortality risk of ICU patients instead of physiopathologic variables. As there are significant changes in dynamic of HRV in episodes near death, it seems that non-linear features are better predictor of mortality than pathologic parameters were used in previous studies [38].

However, our algorithm for mortality prediction appears to be a more sensible way with less parameters and computation to predict mortality risk compared to other methods. Previous studies required more physiologic parameters to predict mortality risk. This time is not enough for a medical person to prepare the necessary preventive actions. This work managed to improve the prediction accuracy compared to previous studies.

The main advantage of the proposed approach is using HRV, which keep the method simple and fully interpretable from a clinical point of view. The crucial reason for this improvement is utilization of fewer features, which are more effective and proven to be statistically significant. Further reason for accuracy of prediction in this algorithm is due to implementation of the SVM. SVM is superior to MLP and when combined with good feature vectors improved prediction accuracy.

This experimental result indicates that, this proposed algorithm can predict mortality risk using small set of features. Furthermore, this proposed method required less computation and time in contrast with earlier works. Due to availability of limited number of samples from the databases and focusing on one type of admitted patients in ICU this algorithm could not be generalized for larger population of samples. Future work depends on availability of reliable database in other types of ICU patients.

The current study has several limitations, which have to be improved. First, our data are representative of a single ICU and a limited population sample. Therefore, future work should lead towards a prospective study, to validate the generalizability of the method. Second, the data were not serially collected over the 2-years interval, and we cannot exclude the possible changes in outcomes related to differences in quality of care.

Conclusion

In this work, we had presented an algorithm with the goal of predicting mortality risk of the cardiovascular patients admitted in ICU. The good performance of our algorithm demonstrates that the combination of linear and non-linear analysis of HRV, combined with robust machine learning techniques, is a successful strategy to yield accurate predictions in terms of probability estimates of the subject’s death. The features were fed into SVM and MLP for mortality prediction. In our analyses, the SVM classifier showed better performance in discriminating the patients with low and high risk than MLP classifier.

This paradigm provides a solid base for developing a computational tool, which could be used in clinical settings to offer patient-specific critical information to medical staff and guide their supervision activities, therapeutic actions, and life-support interventions. Further research on a large sample size and different ICU types of patients will help to further elucidate the findings of this study and effectiveness of HRV analysis for differentiation between low and high risk condition. Our future work would focus on getting large datasets with other types of ICU patients and novel features for mortality prediction.

Disclosure of conflict of interest

None.

Abbreviations

APACHE

Acute physiology and chronic health evaluation

ApEn

approximate entropy

ANN

artificial neural network

DFA

detrended fluctuation analysis

FNN

feed-forward neural networks

HF

high frequency

HR

heart rate

HRV

heart rate variability

ICU

intensive care unit

HF

high frequency

LF

low frequency

LMS

least mean square

LS

least squares

MI

mutual information

MLP

multi-layer perceptron

MPM

mortality probability model

NN50

total number of adjacent RR intervals with a difference of duration greater than 50 ms

PCA

Principal component analysis

PHP

Poincare HRV plot

QP

quadratic programming

RBF

radial basis function

RMSSD

root-mean square of differences between adjacent normal RR intervals in a time interval

SAPS

simplified acute Physiology Score

SMO

sequential minimal optimization

SNDD

standard deviation of normal-to-normal RR intervals

SVM

support vector machine

TP

total power

VLF

very low frequency