Controlled Living Nanowire Growth: Precise Control over the Morphology and Optical Properties of AgAuAg Bimetallic Nanowires

Abstract

Inspired by the concept of living polymerization reaction, we are able to produce silver–gold–silver nanowires with a precise control over their total length and plasmonic properties by establishing a constant silver deposition rate on the tips of penta-twinned gold nanorods used as seed cores. Consequently, the length of the wires increases linearly in time. Starting with ∼210 nm × 32 nm gold cores, we produce nanowire lengths up to several microns in a highly controlled manner, with a small self-limited increase in thickness of ∼4 nm, corresponding to aspect ratios above 100, whereas the low polydispersity of the product allows us to detect up to nine distinguishable plasmonic resonances in a single colloidal solution. We analyze the spatial distribution and the nature of the plasmons by electron energy loss spectroscopy and obtain excellent agreement between measurements and electromagnetic simulations, clearly demonstrating that the presence of the gold core plays a marginal role, except for relatively short wires or high-energy modes.

Plasmons, the collective excitations of conduction electrons supported by metallic nanostructures, enable the confinement of electromagnetic radiation on a subwavelength nanometer scale. This phenomenon holds great potential for a vast range of applications in optics, including metamaterials design,¹⁻³ biosensing,^4,5 therapeutics,^6,7 solar energy harvesting,⁸ and photocatalysis.⁹ Alongside the continued progress in the synthesis of noble metal nanoparticles with new exotic shapes and increased monodispersity, the manufacture of bimetallic nanostructures represents an alternative strategy to enrich the library of plasmonic structures at our disposal.¹⁰ Epitaxial seeded growth is one of the most widely used approaches for the preparation of such structures, where one or more metal precursors are reduced or coreduced on the surface of a previously prepared core of a different metal.¹¹ The geometry of the obtained bimetallic system mainly depends on the lattice matching of the metal species involved,^12,13 on the seed morphology,¹⁴ and on the growth mode on different crystallographic facets, which can be influenced by facet-specific capping agents.¹⁵ The particular case of Au@Ag bimetallic nanoparticles has attracted much attention from the scientific community because of their complementary properties: though gold nanoparticles can be easily modulated in shape and size,¹⁶⁻¹⁹ the lower optical losses of silver render a better plasmonic performance, for instance, in the amplification of weak optical processes such as Raman scattering,²⁰ fluorescence,²¹ and IR spectroscopy.²² Among many other examples, Seo et al. reported the preparation of silver–gold–silver pentatwinned nanorods through epitaxial growth of silver on a pentatwinned gold nanorod core in an ethylene glycol solution of polyvinylpyrrolidone.²³ Recently, Li et al. performed the same reaction in water,²⁴ which was further studied by Gómez-Graña et al. to elucidate the growth mechanism behind the formation of the silver shell using high-resolution electron microscopy in combination with density functional theory (DFT) calculations.¹⁹ It is important to underline that the production of high aspect ratio nanowires relies on the selective deposition of Ag on {111} tip facets, whereas a similar overgrowth reaction with gold would lead to a decrease in aspect ratio, as previously reported.²⁵ Such elongated structures can be regarded as the plasmonic analogues of radiofrequency antennas, but with the resonance shifted into the visible-near IR (Vis-NIR) range of the electromagnetic spectrum.²⁶ Like their radiofrequency counterparts, optical antennas are characterized by several multipolar plasmon oscillations, which can be separated into bright and dark modes, depending on their ability to couple efficiently (bright) or not (dark) to incident/scattered far-field radiation.^27,28 Although the former can be exploited in the development of signal processing devices²⁹ and Raman/IR/fluorescence-based sensors, the latter is useful for enhanced absorption spectroscopy and photothermia.³⁰

In order to efficiently engineer the near-field electromagnetic confinement and implement the application of optical antennas, it is useful to have a detailed understanding of the relationship between the antenna structure and the spatial/spectral distributions of the different plasmon modes.^31,32 In this respect, the near-field properties of pure gold and silver nanorods have been investigated by various research groups, both theoretically^28,33 and experimentally, using different imaging techniques that exploit either resonant optical illumination (e.g., dark-field spectroscopy,^34,35 apertureless scanning near-field optical microscopy³⁶⁻³⁸ (aSNOM), and photoemission electron microscopy^39,40) or fast electrons (cathodoluminescence⁴¹ and electron energy-loss spectroscopy^27,42−44 (EELS)). In contrast, detailed studies of the plasmon near-field behavior of Au@Ag bimetallic nanostructures have not been reported. Rodríguez-González et al. studied the effect of a silver shell on the plasmonic behavior of gold nanodumbbell cores, describing a complex plasmonic scenario where the transversal mode of the core–shell system cannot be directly related to an equivalent silver nanorod.⁴⁵ To the best of our knowledge, the only available study of the plasmonic properties of silver–gold–silver nanorods is the work by Ahn et al. using dark-field spectroscopy, which indicated no influence of the gold core.³⁵

The most important prerequisites for a precise engineering of the plasmonic properties of noble metal nanoparticles are monodispersity and size tunability. As maintaining a narrow size distribution becomes more difficult when anisotropy is increased, we developed, as we report here, the concept of controlled living nanowire growth for the production of monodisperse silver–gold–silver nanowires (AgAuAg NWs), by analogy with controlled living polymerization reactions.⁴⁶ Controlling the addition of silver precursors by means of a syringe pump device, we managed to achieve a linear growth rate of silver on the gold cores. This procedure allowed us to prevent the nucleation of silver nanoparticles during nanowire growth, to significantly improve the monodispersity of the product, and to accurately predict the final dimensions of the bimetallic system. As a result, AgAuAg NW colloids were obtained which display up to nine well-defined plasmon resonance peaks spreading over the entire Vis-NIR wavelength range, with a tight control on the total NW length up to several microns, corresponding to aspect ratios above 100. Direct electron-microscopy-based visualization of the plasmon near-field spatial distributions provided essential information toward eventual optimization and rational application of this bimetallic system. We thus present here a complete optical-extinction and EELS analysis of plasmon modes supported by AgAuAg NWs, which are compared to boundary-element method (BEM) electromagnetic simulations,^47,48 allowing us to assess the influence of the central gold nanorod. We show that the presence of the gold core influences the high-energy spectral range, whereas it becomes progressively irrelevant in the Vis-NIR region, where the spectroscopic behavior resembles that of a monometallic silver nanowire.

To push the quality of Ag NW synthesis beyond the existing limits, any side reactions and secondary nucleation should be suppressed completely. Thus, the aims in NW synthesis are similar to those in polymer synthesis, where a small polydispersity index is desired. Consequently, we can apply the well-known concept of controlled living polymerization reactions (CLPR) to the one-dimensional NW growth reaction. The criteria for CLPR as defined by IUPAC standards involve the complete suppression of termination and side reactions and a constant number of actively growing chains throughout the polymerization.⁴⁶ Furthermore, the initiation reaction should be much faster than the propagation reaction. As a consequence, the degree of polymerization—and thus the resulting chain length—is determined only by the ratio of monomer to initiator concentrations P_n = [M₀]/[I₀]. In the following, we introduce the concept of controlled living nanowire growth, which allows us to synthesize bimetallic AgAuAg NWs with remarkably narrow size distributions and nanometer precision in length. As previously described by various groups, epitaxial silver overgrowth of pentatwinned gold nanorods (PT Au NRs) in the presence of surfactants with chloride counterions leads to one-dimensional growth of bimetallic AgAuAg rods/wires.^19,24,35 This can be explained by the adsorption of chloride onto the lateral {100} facets resulting in less favored silver reduction. Consequently, silver is only reduced and deposited epitaxially on the {111} facets at the NR tips, so the PT Au NR seeds can act as bifunctional initiators bearing two initiation sites. After deposition of the very first silver monolayer the initiator becomes an active species that is subsequently overgrown in one-dimensional fashion by continuous reduction of silver ions at the metal surface during NW growth. We identify the following requirements to obtain a living controlled nanocrystal growth mechanism: (i) the initiation of crystal growth takes place simultaneously and much faster than the continuous reduction of Ag⁺ ions at the metal surface of the active species; (ii) all particles have to persist as active growing species for selective deposition of Ag atoms throughout the complete experiment; and (iii) the reduction and deposition of Ag⁺ must be quantitative, so that the growth of the particles is proportional to the amount of added silver precursor and a precise control over the final NW dimensions can be achieved.

• (i)The first condition is met by using PT Au NRs with a narrow size distribution as seeds, uncoupling completely nucleation and elongation. Furthermore, the ex-situ synthesis of the PT initiator guarantees a homogeneous and simultaneous initiation at both ends upon addition of silver precursor. Consequently, the preparation of high quality PT Au NR seeds is of primary importance toward a precise growth of monodisperse AgAuAg NWs. PT Au NRs with average length of 210 ± 10 nm and width of 34 ± 1 nm were prepared as previously described by Pérez-Juste et al., with minor modifications (see Experimental Section).⁴⁹ The purified PT Au NRs show a shape yield around 99%, (Figure S1A–C, Supporting Information) and can be used as seeds after redispersion in 10 mM benzyldimethylhexadecylammonium chloride (BDAC). As evidenced by UV–vis-NIR spectroscopy (Figure S1F, Supporting Information), the characteristic transversal and longitudinal dipolar, as well as longitudinal quadrupolar plasmon modes can be identified for the pure PT Au NR dispersion. Further inspection of the high-energy region reveals the presence of an octupolar mode as a shoulder below 600 nm (inset Figure S1F, Supporting Information). The narrow dipolar plasmon band, with a quality factor of 6.45 (Figure S2, Supporting Information), and the high intensity ratio between the dipolar and the transversal modes confirm the narrow size distribution of the PT Au NR seeds.
• (ii)The second requirement can be fulfilled through careful adjustment of a low silver reduction rate to facilitate anisotropic growth.^10,50 Therefore, the silver overgrowth reaction conditions were set according to the following three conditions: (1) slow silver reduction at slightly acidic conditions and elevated temperature;¹⁹ (2) BDAC as surfactant, which drastically reduces the reduction rate as compared to nonaromatic surfactants;⁵¹ and most importantly, (3) continuous addition of silver nitrate and ascorbic acid by means of a microfluidic pump setup from separated reservoirs. The continuous and slow addition prevents the accumulation of unreacted Ag⁺ within the growth solution, which might lead to secondary nucleation and nonspecific silver deposition.

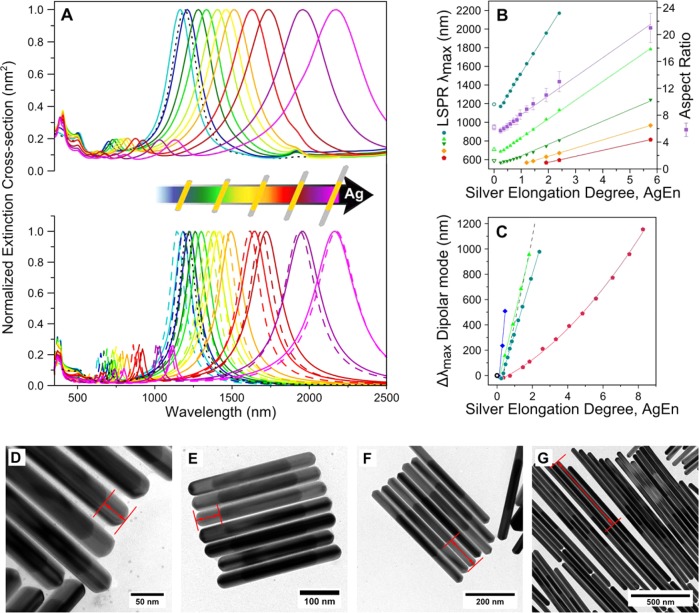
  UV–vis-NIR extinction spectra after various reaction times during NW growth were correlated with TEM images. All spectra were collected after transferring the NWs into heavy water so as to expand the detection wavelength window up to 2500 nm, avoiding the strong absorbance of water around 1350 nm (see experimental section). We observed an initial blue shift of about 20 nm, along with a slight reduction of the overall aspect ratio when a thin silver layer (approximately 2 nm) grows on all facets (sides and tips). However, after coverage of the PT Au NR cores with this initial thin layer, silver deposits on the nanowire tips only. This results in a significant and gradual redshift of all plasmon modes, whereas multipolar, higher energy plasmon modes emerge as silver deposition continues. Optical extinction spectra of the resulting length-controlled AgAuAg NWs are shown in Figure 1A, top, along with representative TEM images for selected sizes (Figure 1D–G), illustrating the striking monodispersity typically achieved by the growth method described above (see Table S1 and Figure S3, Supporting Information). In particular, the plasmon spectral features are narrow and mainly limited by intrinsic absorption and radiative losses, rather than by particle size dispersion (see below). The corresponding BEM calculated extinction spectra (Figure 1A, bottom solid lines, see Methods) show an excellent agreement with the experimental spectra, as well as a gradually increasing similarity with spectra calculated for pure Ag NWs with the same overall dimensions (Figure 1A, bottom dashed lines).

  The quality factor (Q-factor) is the characteristic figure of merit of any resonator, as it indicates how many oscillations are undergone by a particular oscillator (see Supporting Information for the calculation details). During silver elongation, the Q-factor of the dipolar mode decays exponentially (Figure S2, Supporting Information), which can be explained considering that radiative coupling to the far-field increases with the length of the antenna, together with the relative dissipation, causing the peaks to broaden.⁵² When comparing the experimental Q-factors with the ones obtained from the BEM simulated spectra of Figure 1A, the calculated ones are found to be only 25% higher compared to the experimental ones. This clearly emphasizes the low polydispersity of the samples. Interestingly, the decay slope is similar in both experiment and theory, suggesting again that there is no significant increase in the polydispersity of AgAuAg NWs during silver growth. Overall, the resulting polydispersity of the product is remarkably narrow and clearly emphasized by the narrowness of the plasmon bands in Figure 1A. In order to achieve a more meaningful comparison between the widths of experimental and calculated spectra, we used TEM analysis to predict the contribution of the polydispersity to the FWHM, which is missing in the calculation. In fact, the FWHM of the experimental peaks is constituted by a Lorentzian component, intrinsically related to the nanoparticle properties, and a Gaussian component, related to the size distribution in the colloidal solution. The latter is what we normally evaluate using different techniques like transmission electron microscopy (TEM), dynamic light scattering (DLS), or small-angle X-ray scattering (SAXS). The finite size distribution within each sample accounts for a moderate increase in FWHM of the observed plasmon features (see Figure S4, Supporting Information). A more precise assessment is provided by comparing the wavelength width of the measured (Δλ_exp) and theoretical (Δλ_th) spectra, assuming that the excess in the former one originates from the finite size distribution of NW sizes for each given sample (ΔL). We then have Δλ_exp ∼ Δλ_th+m·ΔL, where m is the slope of the plot of plasmon wavelength peak vs NW length, extracted from Figure 1B. In Table 1 the values of ΔL extracted from this analysis of the optical spectra (ΔL_OPT) are compared with the size distributions obtained from TEM analysis (ΔL_TEM). The results show an acceptable agreement, considering that the number of NWs measured by TEM for each sample is much smaller than those contributing to UV–vis-NIR spectra.

• (iii)The last requirement to achieve a living polymerization reaction (linear growth) can be met by selecting an addition rate that is slower than the reaction rate. In this way, a linear zero-order kinetic path is enforced and the resonance wavelengths of the longitudinal modes, as well as the corresponding aspect ratios evaluated from TEM measurements (see Table S1, Supporting Information), turn out to scale linearly with time. Furthermore, as the conversion rate for silver is close to 100%, the linear shifts are directly proportional to the amount of added Ag⁺. This proportionality is referred to in what follows as the degree of silver elongation, AgEn, defined as the molar ratio of added silver salt to gold seeds (i.e., [Ag⁺]/[Au⁰]), in analogy to the concept of degree of polymerization. We plotted in Figure 1B the resonance wavelengths for all the longitudinal plasmons that were recorded within our measurement spectral window (ranging from the dipolar mode up to the fifth order mode) vs AgEn. Note that we disregarded some high-energy spectral features that cannot be clearly resolved apart from the transverse mode. This plot clearly reveals a linear slope for all modes, up to aspect ratios above 20 and AgEn value of almost 6. In other words, this plot indicates that the reaction proceeds according to zero order kinetics and that no termination or passivation occurs. The corresponding regression fits (solid lines) yield a Pearson R² above 0.999 for all the modes and for the aspect ratio. As a control experiment, we increased the rate of Ag⁺ addition by a factor of 1.25. The resulting plasmon shifts were plotted in Figure 1C (red dots), showing that the faster addition rate leads to nonlinear shifts. Because the reaction does not comply in the case of a higher addition rate, the apparent AgEn increases significantly faster than the plasmon band shift, which represents the actual growth rate. Furthermore, under these conditions, excess silver nitrate accumulates in solution, leading to secondary nucleation, formation of AgCl nuclei, nonspecific deposition of silver on the growing particle surface, and uncontrolled increase of the reaction rate. All these effects reduce the amount of available silver ions for deposition on the NW tips and consequently compromise the linear growth and impair an accurate prediction of the final length of the produced AgAuAg NWs. Interestingly, spherical particles with diameters around 500 nm were observed upon TEM inspection of the resulting colloid, which are likely due to crystallization of AgCl present in solution upon drying of the dispersion on the TEM grid (Figure S5, Supporting Information). We also found that the thickness of the NWs was significantly larger than expected, in contrast to living reaction conditions (see Table S2, Supporting Information). An increase of the reaction temperature also leads to faster reaction rates and uncontrolled growth, so we conclude that the living reaction conditions are highly sensitive to changes in reaction kinetics, either induced by increased temperature or faster precursor addition. The generality of this method was confirmed by carrying out different experiments under controlled living nanowire growth conditions but starting with different PT Au NR core dimensions, which also led to linear growth and reproducible evolution of the plasmonic features (Figure 1C). We used the silver to gold volume ratio of a single bimetallic nanowire as the AgEn parameter for BEM simulations (Figure 1A, bottom), so as to estimate the theoretical linear behavior (dashed line in Figure 1C). The observed deviation can be explained taking into account the presence of a small amount of Au byproducts (different particle shapes), on which silver is also reduced, as well as some uncertainty in the initial Au nanorod concentration, due to the purification step ([Au⁰] was estimated using the absorbance at 400 nm, as detailed in the experimental section). The obtained agreement is a strong confirmation that all added silver ions were reduced and selectively deposited on the AgAuAg NW tips. It is worth noting that we have not found any limitation in the final length of the NWs, our longest experiment resulting in 3.4 μm NWs (corresponding to a AgEn of 40.32) (Figure S6, Supporting Information).

Figure 1.

(A) Upper panel: Vis-NIR spectra recorded during silver growth; the PT Au NR core is displayed as a black dotted curve; Lower panel: calculated (BEM) extinction spectra of AgAuAg (solid curves) and pure Ag (dashed curves) NWs with dimensions corresponding to the experimental ones (same color code). (B) Resonance wavelengths for the dipolar (cyan) and second through fifth order multipolar modes (green, dark green, orange, and red, respectively) vs AgEn. The aspect ratio (purple) is also plotted for reference. Solid lines are linear fits to the data. The position of the corresponding modes for the PT Au NR cores are plotted as open symbols. (C) Wavelength shift of the dipolar plasmon mode for growth with a faster addition rate (red), and for the standard rate on PT Au NRs with different dimensions (180 × 34 nm, blue; 180 × 32 nm, green; 210 × 32 nm, cyan). The dashed gray line represents a theoretical estimate, using the silver-to-gold volume ratio in one nanowire as AgEn. The open black circle is the common origin. D-G: Representative TEM images at four different values of AgEn = 0.72, 1.2, 2.4, 11.52, corresponding to silver elongations per tip of 33 ± 6 nm, 61 ± 9 nm, 130 ± 20 nm, and 660 ± 90 nm, and longitudinal dipolar plasmon resonances at 1405, 1630, and 2170 nm, respectively. The dipolar plasmon for G lies beyond our measurement spectral window.

Table 1. Total Length Distribution for AgAuAg NWs with Increasing Elongation Degrees AgEn, Evaluated by TEM Analysis, ΔL_TEM, and Comparing Experimental and Calculated Optical Spectra, ΔL_OPT.

AgEn	ΔLTEM (nm)	ΔLOPT (nm)
0.24	20.3	17.6
0.36	19.5	18.7
0.48	19.8	24.3
0.72	21.9	27.5
0.84	29.2	29.7
1.20	36.3	29.7
1.92	39.8	34.2
2.40	42.9	39.1

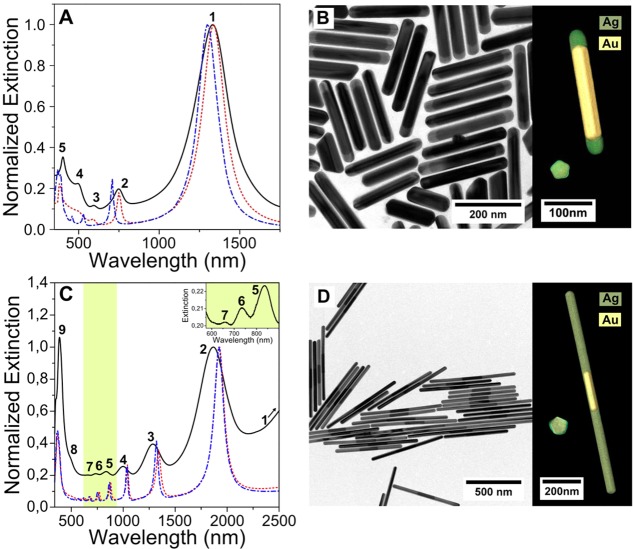
We selected two samples with significantly different NW lengths to discuss the influence of the PT Au NR core on the optical properties of the bimetallic particles. We analyzed the optical extinction spectra from NWs in heavy water solution (Figure 2) and carried out a detailed EELS analysis (Figures 3,4). Both experimental methods were supported by BEM calculations. The first sample had AgEn = 0.5, corresponding to a total aspect ratio of 6.7, and 25 nm Ag extending beyond each tip of the PT Au NR core. We compare in Figure 2A the Vis-NIR spectrum (black solid curve) with the calculated extinction spectrum of a NW with the average dimensions, either containing the PT Au NR core (red-dotted curve) or being made of pure Ag (blue dash-dotted curve). The simulations reveal in this case a clear influence of the PT Au NR core on all the plasmon modes, particularly in the short wavelength (high energy) region. The second sample corresponds to AgEn = 5.3, aspect ratio 25, and 360 nm of Ag from each tip. The 3D reconstructed volume of the two samples obtained by the Total Variation Minimization (TVM)⁵³ technique, applied to a tilt series of HAADF-STEM images (Figure 2B and 2D) clearly shows that the PT Au NR core is located in the center, with 2 nm of silver on the lateral facets (also considered for the simulations). The pentagonal cross section of the particle–characteristic for PT NRs–is preserved, as evidenced by the cross section in Figure 2B and 2D. Remarkably, the low polydispersity of the synthesized AgAuAg NWs allowed us to detect nine LSPR bands in solution (Figure 2C), and we find again a good agreement with the BEM simulated extinction spectrum. In this case, however, the differences between simulations with and without the gold core are significantly smaller, and mainly observed in the high-energy region. It should be noted that the permittivities of silver and gold are well described through a common Drude expression ε(ω) = ε_b – ω_p²/ω(ω + iγ) in the IR region, where the so-called classical plasma energy is given by ℏω_p ∼ 9 eV,⁵⁴ as determined by the density of s conduction electrons (i.e., the same in both metals, because each atom contributes with one s electron and their atomic densities are nearly identical). The difference between these two metals lies in the level of losses (ℏγ = 25 meV for silver and 71 meV for gold) and in the background screening produced by d-band polarization (ε_b = 4 in silver and 9.5 in gold). Consequently, in the infrared spectral region (i.e., λ > ∼1000 nm), the second term dominates in the Drude expression, the precise value of ε_b becomes irrelevant, and both silver and gold behave in a similar fashion, except that the latter produces more inelastic optical losses (through a larger damping rate γ). Besides these intrinsic material properties, which lead to similar optical behavior in the NIR, there is a geometrical effect associated with the NW: for a given mode order (e.g., the lowest-order dipolar mode), the wavelength shifts deeper into the IR with increasing NW length, and eventually the mode size becomes comparable to λ/2, giving rise to a relatively larger contribution of radiative damping, which again makes the two metals look more similar. These considerations explain why the AgAuAg bimetallic NWs have similar properties to those of pure Ag wires with the same outer geometry, particularly for infrared modes and long NWs (Figure 1A).

Figure 2.

(A) Vis-NIR spectrum of a colloid of short (AgEn = 0.5) AgAuAg NWs (black line) compared to simulated spectra in the presence (red) and absence (blue) of the PT Au NR core. (B) Representative TEM image showing the high monodispersity of the sample. (C), (D) Same as (A) and (B) for a sample of longer NWs (AgEn = 5.3). Inset of (C) Zoom of the highlighted area discerning high order modes 5, 6, and 7. At the right subpanels of (B) and (D), 3D TEM visualizations of the reconstructed nanowires are presented (green and yellow correspond to silver and gold, respectively), both from one tip (left) and along their length (right).

Figure 3.

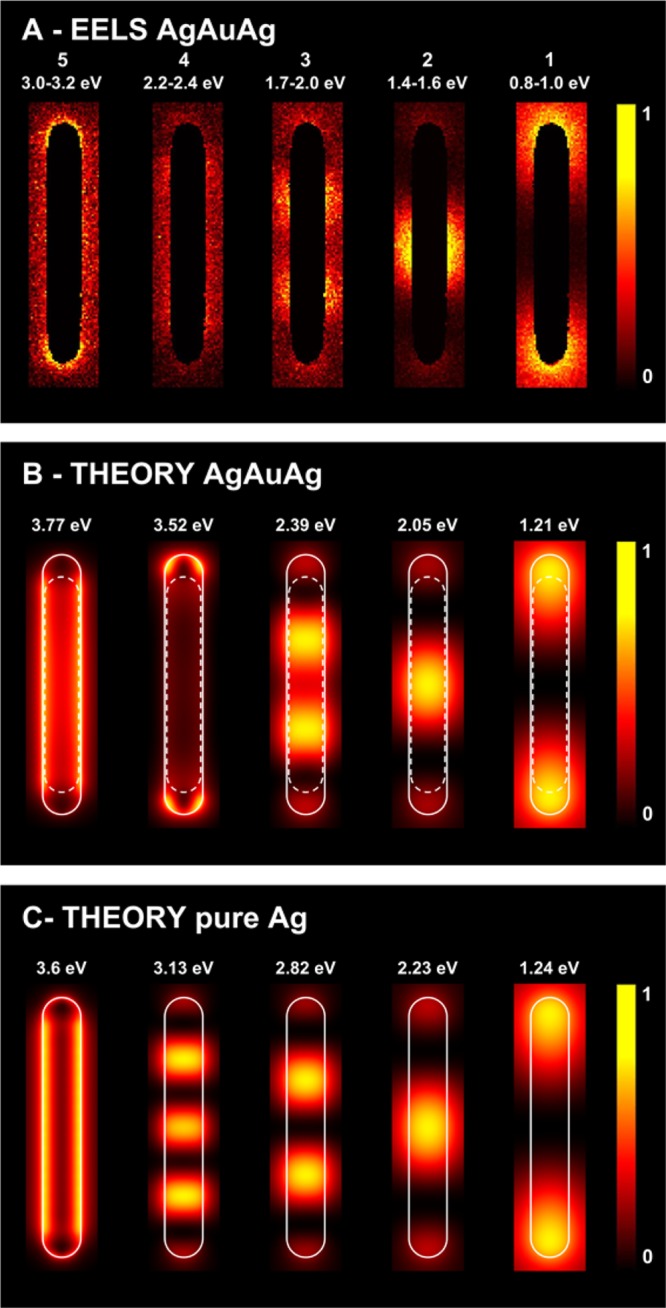
(A) Spatial distribution of plasmon modes for a short AgAuAg NW (AgEn = 0.5) as measured by EELS; the numbers refer to the same modes as in the Vis-NIR spectrum of Figure 2A. (B) BEM simulations of EELS maps associated with the plasmon modes shown in A, for a NW containing the PT Au NR core. (C) Simulations for a pure Ag NW with the same dimensions. The simulated maps are normalized to the maximum intensity in each case. The silver (gold) surface is indicated with solid (broken) white lines in the calculated maps.

Figure 4.

(A) Spatial distribution of plasmon modes for a long AgAuAg NW (AgEn = 5.3) as measured by EELS; the numbers refer to the same modes as in the vis-NIR spectrum of Figure 2A. (B) BEM simulations of EELS maps associated with the plasmon modes shown in (A), for a NW containing the PT Au NR core. (C) Simulations for an Ag NW with the same dimensions. The simulated maps are normalized to the maximum intensity in each case. The silver (gold) surface is indicated with solid (broken) white lines in the calculated maps.

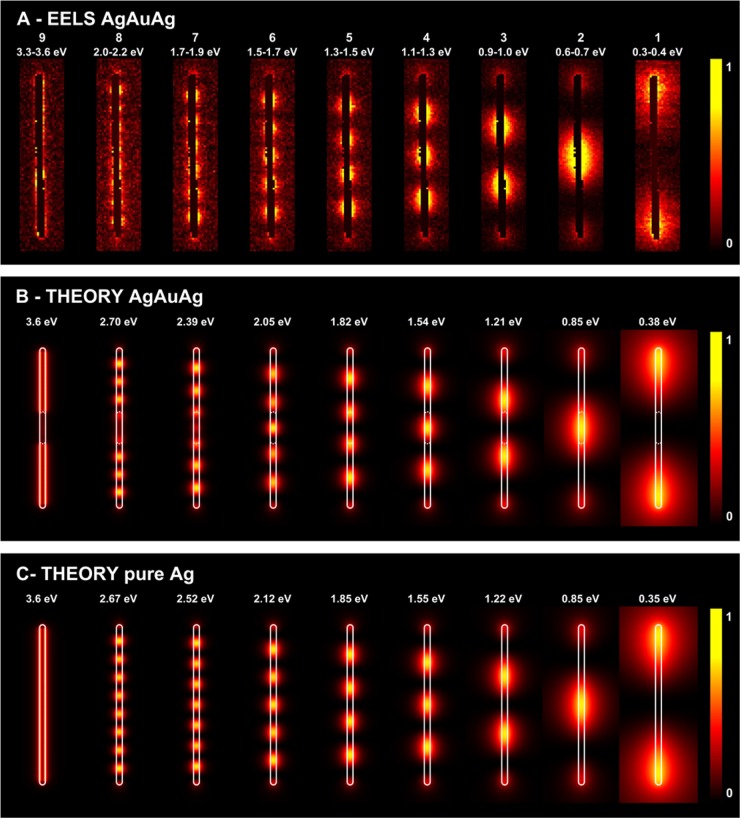
To confirm these observations, we carried out a detailed near-field study by EELS, also supported by BEM calculations. Plasmon mapping confirmed the symmetry and standing-wave nature of the modes under study. We summarize in Figures 3 and S8 (Supporting Information) the results for the short NWs (AgEn = 0.5): all of the extinction bands observed in the far-field Vis-NIR spectrum are also found in EELS (Figure 3A). The spatial distribution of the plasmons clearly indicates the even or odd nature of each mode: modes (1–3) are the dipolar, quadrupolar, and octupolar longitudinal modes, respectively, whereas modes (4–5) are the accumulation of several modes (see below). Incidentally, only odd modes can be excited using light incident with its electric field parallel to the NW, in contrast to EELS in which even modes are also excited due to the multipolar character of the electron exciting field. This conclusion can be actually extended to NWs of arbitrary orientation relative to the externally applied field when they are sufficiently small as to neglect retardation effects (e.g., an exp(i2πr/λ) dependence on position r and light wavelength λ). However, we are dealing here with long NWs, with lengths that are comparable to λ, so there is strong retardation and this is the reason why our optical spectra reveal modes with both odd and even symmetry.^30,37,41,55 The EELS experimental maps were compared to numerically computed maps using BEM. Simulations were carried out both in the presence (middle panel) and in the absence (bottom panel) of the PT Au NR core. Although the agreement between theoretical and experimental plasmon energies in the optical measurements is excellent (see above), the EELS modes are noticeably red-shifted with respect to theory, presumably because of the effect of the substrate, which is not accounted for in our simulations. However, the features in the measured and calculated EELS spectra are in good mutual agreement (see Figure S7, Supporting Information), and we argue that the spatial distribution of the plasmon excitation should not be too sensitive to the observed shift. This intuition is corroborated when comparing modes of the same symmetry, which yield very similar spatial distributions in theory and experiment. It is important to keep in mind that the highest-order modes observed in EELS (modes 4 and 5 in Figure 3) are in fact the accumulation of several modes, which are integrated over the finite energy range covered within the energy-filtered images. Note that we are instead showing monochromatic maps in the calculations, so that these high-order maps are understandably different from those experimentally acquired. Additionally, the number of plasmon modes (an infinite, discrete set) has an accumulation point toward the electrostatic planar surface plasmon (signaled by ε₁ = −1 in vacuum), as they undergo fast oscillations, so that the surface is locally seen as flat. This explains the rather uniform distribution of the observed map at that energy (3.7 eV for the silver-vacuum interface). The theoretical calculations also allow us to explore the role of the PT Au NR core in the plasmonic response, which essentially produces a redshift of the plasmon energies, along with additional broadening in the EELS spectra (see Figure S7, Supporting Information). It is thus not surprising that the silver NW has better-defined higher-order modes (second maps from the left in Figure 3B,C).

For a long NW (Figure 4 and S9, Supporting Information, AgEn = 5.3), EELS characterization did allow us to identify the dipolar longitudinal mode (1), as well as six additional multipolar modes (2—7 corresponding to increasing order, that is, number of sign changes in the associated induced charge along the wire), whereas the last two peaks (8–9) correspond to an accumulation of several modes, as discussed above for short NWs. In this case, the effect of the PT Au NR core is qualitatively similar, but nearly marginal for low energy modes. In particular, the lowest-order dipolar plasmon involves high plasmon strength (larger enhancement of the near field) near the NW tips, and consequently the near field plot looks nearly identical for the calculated AgAuAg (Figure 4B) and the pure-Ag NW (Figure 4C), also in excellent agreement with the experimental EELS maps (Figure 4A). Because the NIR response of gold and silver is similar, as they both behave as Drude metals, and interband transitions contribute marginally in this spectral region, the position of the low-energy, low-order plasmons should not change significantly between pure Au and pure Ag NWs; nonetheless we expect to observe additional broadening in the case of gold, because it shows higher intrinsic damping losses compared to silver (71 vs 21 meV). In Figure S10 (Supporting Information), we show calculated spectra for the corresponding pure Au NWs. In conjunction with a higher broadening, we observed a reduction in the plasmon extinction cross section. Therefore, the PT Au NR core can only be identified in the higher-order modes, which involve a large intensity in the central NW region, whereas their high energies involve very different and relatively moderate values of the dielectric functions of the two metals. Interestingly, the second-order mode, which also has a large weight in the center of the NW, appears at a sufficiently low energy as to feel a similar response from both gold and silver, as we argued above, and consequently, the calculated energies of this mode in the long NWs are similar to those obtained without the PT Au NR core. For such low order modes, the NW acts as a whole plasmonic entity. In contrast, the vacuum/silver interface plasmon is both experimentally and theoretically found to be localized on the silver parts only. For this mode, corresponding to high wave vectors (short wavelengths), the plasmons feel differently each metal, and consequently the gold and silver parts act as two separated plasmonic entities in this regime.

In conclusion, the synthesis of AgAuAg bimetallic nanowires has been largely improved by enforcing living growth conditions to the deposition of silver on the tips of pentatwinned Au nanorods, which allowed us to achieve high quality colloidal dispersions with remarkably low polydispersity. As a result, the plasmon bands observed in colloidal NW dispersions are much narrower than those reported for other types of both lithographic and colloidal nanoparticles within the same IR spectral range (see Figure 5). The measured quality factor (i.e., the ratio of plasmon energy to spectral energy FWHM, which is equal to 1/(2π) times the number of plasmon oscillations before the near-field intensity is attenuated by a factor 1/e) is in fact reasonably close to the calculated one for NWs of well defined size, and as we discuss above, the difference between these two is well explained in terms of the experimental finite size distribution, thus emphasizing our understanding of the optical response of the NWs in terms of the local permittivities of gold and silver. The new protocol provides the opportunity to fine-tune the NWs length up to the micrometer scale (AR > 100), so that the obtained optical antennas displayed a large number of plasmonic modes that spread over the entire UV–vis-IR region (up to nine detectable modes directly in the colloidal suspension). The role of the gold cores on the optical response was carefully investigated by EELS, and we demonstrated that it does not have a large effect on plasmon propagation along the NW surface, whereas its influence is limited to higher energy modes. The procedure opens up new possibilities for the exploitation of plasmon resonances in the near and mid IR regions.

Figure 5.

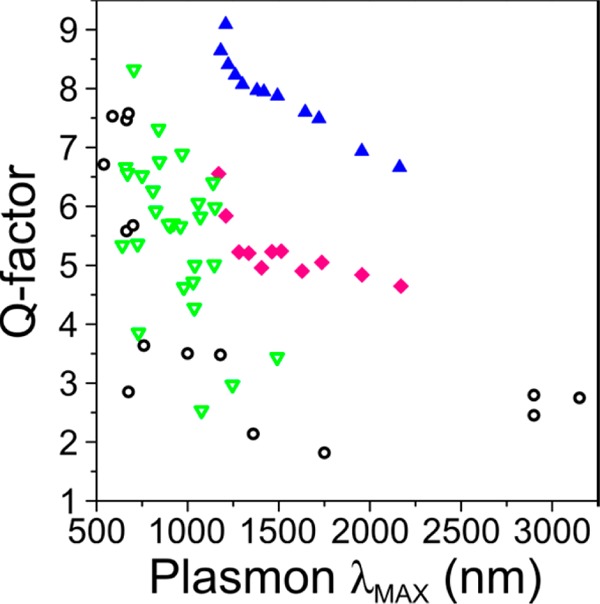
Comparison of the quality factor of vis-NIR plasmons reported in the literature for different nanoparticles preparation: lithography (black opened circles) and wet-chemistry (green opened triangles). These are compared with our results from AgAuAg NWs experiments (pink diamonds) and calculations (blue triangles).⁶³⁻⁷⁵

Materials

Benzyldimethylhexadecylammonium chloride, hexadecyltrimethylammonium bromide (CTAB, ≥96.0%), hexadecyltrimethylammonium chloride (CTAC, 25 wt % in water), hydrogen tetrachloroaurate trihydrate (HAuCl₄·3H₂O, ≥99.9%), silver nitrate (AgNO₃, ≥99.9%), l-ascorbic acid (AA, ≥99%), deuterium oxide (D₂O, 99.9 atom % D), sodium borohydride (NaBH₄, 99%), and trisodium citrate (≥98%) were purchased from Aldrich. All chemicals were used as received. Milli-Q water (resistivity 18.2 MΩ·cm at 25 °C) was used in all experiments. All glassware was washed with aqua regia, rinsed with water, sonicated three times for 3 min with Milli-Q water, and dried before use.

PT Au NR Synthesis

The pentatwinned gold nanorod synthesis was adopted from the protocol of Pérez-Juste et al. with some minor modifications.⁴⁹ These changes mainly refer to an increase of NaBH₄ concentration during citrate-capped seed growth to improve reproducibility and increase of AA concentration during AuNR growth to improve the final yield.

3.5 nm Citrate-Capped Au Seeds

Briefly, 20 mL of a 0.125 mM HAuCl₄, 0.25 mM trisodium citrate aqueous solution was prepared and stirred for 10 min at room temperature. Next, 600 μL of a freshly prepared 0.1 M NaBH₄ solution was added quickly under vigorous stirring. After 2 min, the stirring rate was reduced and the seeds were aged 40 min under slow stirring at room temperature. To ensure for complete removal of excessive NaBH₄, the solution was stirred at 40—45 °C for another 15 min.

5.5 nm CTAB-Capped Au Seeds

A 5 mL growth solution was prepared consisting of 40 mM CTAB and 0.125 mM HAuCl₄. The Au(III) was reduced to Au(I) with 12.5 μL of a 0.1 M AA solution (f.c. 0.25 mM), indicated by a fast color change from yellow-orange to transparent. Then, 835 μL of the citrate-capped Au seeds was added quickly and the solution was mixed by hand-shaking thoroughly. The 5.5 nm CTAB-capped Au seeds were aged for 3 h at 23 °C prior final overgrowth.

PT Au NR Synthesis

A 500 mL growth solution was prepared containing 8 mM CTAB and 0.125 mM HAuCl₄. The solution was thermostated at 20 °C. Next 1560 μL of a 0.1 M AA (f.c. 0.313 mM) was added and gently stirred leading to a clearance of the solution. Finally, 750 μL of 5.5 nm CTAB-capped Au seeds was added quickly and mixed thoroughly. The solution was thermostated at 20 °C overnight.

PT Au NR Purification

Purification was carried out as described by Scarabelli et al.⁵⁶ For PT Au NRs of length and width ca. 200 and 30 nm, respectively, the final surfactant concentration was set to 0.1 M through the addition of 67.5 mL of a 25 wt % CTAC solution, leading to flocculation and sedimentation overnight (see Supporting Information for more details about the calculation). The supernatant was discarded and the sediment containing the NRs was redispersed in a 10 mM BDAC solution to obtain a final Au(0) concentration of 0.25 mM (measured using the absorbance at 400 nm).^57,58

AgAuAg NWs Synthesis

A total of 20 mL of the purified PT Au NR solution containing 10 mM BDAC and 0.25 mM Au(0) was heated to 60 °C. AgNO₃ (0.004 M in water) and AA (0.016 M in 20 mM BDAC, in order to keep the BDAC concentration constant) were added continuously in separate syringes by a syringe pump with a rate of 0.24 mol of Ag(I) per mol of Au(0) per hour (effective rate starting at 300 μL/h) under slow stirring at 60 °C. Samples of 1 mL were taken after defined time frames and the effective rate adjusted to maintain the rate of 0.24 mol of Ag(I) per mol of Au(0) per hour during the whole experiment (see Table S3, Supporting Information for the effective rates). For UV–vis-NIR measurements beyond the water limit at around 1350 nm, the path length was reduced using a 1 mm cuvette and water was exchanged by deuterated water to reduce vibrational modes and consequently reduce overall extinction. The samples were washed three times by centrifugation (1000—3000 rpm) and redispersing in deuterated water (concentrating the sample down to 400 μL) to allow UV–vis-NIR measurements in the range of 300—2500 nm in a 1 mm pathway cuvette to be performed.

Spectroscopic and TEM Characterization

Transmission electron microscopy (TEM) images were collected with a JEOL JEM1400PLUS instrument operating at 120 kV with carbon-coated 400 square mesh copper grids. All samples were centrifuged twice before blotting on the grid to reduce surfactant concentration. Optical extinction spectra were recorded using an Agilent Cary 5000 UV–vis-NIR spectrophotometer in deuterated water. All the presented UV–vis-NIR spectra were multiplied by the respective dilution factors to facilitate comparison of the data. HAADF-STEM images and electron tomography series were acquired using an aberration corrected cubed FEI Titan 60—300 electron microscope operated at 200 kV. For the reconstruction of the series, the total variation minimization technique (TVM) was used. EELS plasmon maps, were acquired using a monochromated double aberration corrected cubed FEI Titan 50—80 electron microscope operated at 300 kV and yielding an energy resolution of 0.12 eV. For the analysis of the two EELS data sets, first a Richardson–Lucy deconvolution of the ZLP from the data was performed and then the ZLP was fitted and subtracted from the result, by using Hyperspy.⁵⁹ Because the points of the map passing over the rod still present a large background due to multiple phonon scattering and are also noisier due to the lower counts, reducing the signal quality from those areas, a mask was used in the place of the NW.⁶⁰

Electromagnetic and EELS Simulations

Optical extinction spectra, electric near-field intensity maps, and EELS intensities are calculated by solving the Maxwell equations in the presence of either an external light plane wave or an electron point charge moving with constant velocity (v = 0.78c, corresponding to an acceleration voltage of 300 kV), respectively. The extinction calculations are averaged over NW orientations and light polarizations. For EELS, the electron is incident along a direction normal to the long wire axis. For simplicity, the wires are simulated as axially symmetric rods of the same volume as the actual PT NWs, using the boundary-element method and exploiting the axial symmetry of the particles, as described elsewhere.⁴⁸ More precisely, the outer gold and silver NW interfaces are modeled as circular cylinders with hemispherical caps. The radius of the silver wire is considered to be 2 nm larger than that of the gold core. The latter has a length (diameter) of 210 nm (34 nm) in the simulations of Figure 1 and 180 nm (32 nm) in Figures 2–4. Gold and silver are represented by their tabulated frequency-dependent complex dielectric functions.⁶¹ The NWs are considered to be in vacuum (ε = 1) for EELS and in deuterated water (ε = 1 – 0.30637 λ²/(λ² + 47.26686) + 0.74659λ²/(λ² – 0.00893), where λ is the free-space light wavelength in microns under optical illumination⁶²) for optical extinction.

Supporting Information Available

Further experimental details, optical data, theoretical derivations and detailed interpretations are provided in Supporting Information. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.5b01833.

Author Contributions

^○ Martin Mayer and Leonardo Scarabelli contributed equally.

The authors declare no competing financial interest.