Population Pharmacokinetic Modeling of Itraconazole and Hydroxyitraconazole for Oral SUBA-Itraconazole and Sporanox Capsule Formulations in Healthy Subjects in Fed and Fasted States

Abstract

Itraconazole is an orally active antifungal agent that has complex and highly variable absorption kinetics that is highly affected by food. This study aimed to develop a population pharmacokinetic model for itraconazole and the active metabolite hydroxyitraconazole, in particular, quantifying the effects of food and formulation on oral absorption. Plasma pharmacokinetic data were collected from seven phase I crossover trials comparing the SUBA-itraconazole and Sporanox formulations of itraconazole. First, a model of single-dose itraconazole data was developed, which was then extended to the multidose data. Covariate effects on itraconazole were then examined before extending the model to describe hydroxyitraconazole. The final itraconazole model was a 2-compartment model with oral absorption described by 4-transit compartments. Multidose kinetics was described by total effective daily dose- and time-dependent changes in clearance and bioavailability. Hydroxyitraconazole was best described by a 1-compartment model with mixed first-order and Michaelis-Menten elimination for the single-dose data and a time-dependent clearance for the multidose data. The relative bioavailability of SUBA-itraconazole compared to that of Sporanox was 173% and was 21% less variable between subjects. Food resulted in a 27% reduction in bioavailability and 58% reduction in the transit absorption rate constant compared to that with the fasted state, irrespective of the formulation. This analysis presents the most extensive population pharmacokinetic model of itraconazole and hydroxyitraconazole in the literature performed in healthy subjects. The presented model can be used for simulating food effects on itraconazole exposure and for performing prestudy power analysis and sample size estimation, which are important aspects of clinical trial design of bioequivalence studies.

INTRODUCTION

Itraconazole is a broad-spectrum orally active triazole antifungal used for both prophylaxis and treatment of systemic fungal infections (1, 2). Itraconazole exerts antifungal activity through the inhibition of fungal cytochrome P450 (CYP) 3A isoenzymes, which mediate the synthesis of ergosterol, a vital component of the fungal cell membrane (3). Itraconazole undergoes extensive hepatic metabolism by human CYP3A4 isoenzymes. Both itraconazole and its major active metabolite, hydroxyitraconazole, inhibit mammalian CYP3A4, although to a lesser extent than that with the fungal CYP3A isoenzymes (4).

Itraconazole is currently available as oral capsules in two marketed formulations: Sporanox, the brand product (Janssen Pharmaceuticals, Inc. [5]), and SUBA-itraconazole, the alternative product. SUBA-itraconazole is a novel formulation containing a solid dispersion of itraconazole in a pH-dependent polymeric matrix to enhance its dissolution and intestinal absorption; therefore, it exhibits greater bioavailability than the innovator product. As of 30 June 2015, SUBA-itraconazole has marketing approval in Australia, Spain, Germany, Sweden, and United Kingdom; currently, it is available in Australia under the trade name Lozanoc (Mayne Pharma International Pty Ltd. [6]), and in Spain under the trade name Itragerm.

Itraconazole is a weakly basic Biopharmaceutics Classification System (BCS) class II (low solubility/high permeability) drug that has a pH-dependent dissolution (pK_a value, 3.7) and thus typically requires an acidic gastric environment for sufficient drug dissolution and adequate absorption. The coadministration of itraconazole with agents that inhibit gastric acidity, such as antacids and proton pump inhibitors, reduce the extent of itraconazole absorption (7, 8).

The pharmacokinetics of itraconazole is complex and highly variable, especially after oral administration. Both itraconazole and hydroxyitraconazole have nonlinear kinetics in a comparison of single- versus multiple-dose administration (9, 10). Various literature studies of the effect of food on itraconazole absorption showed that the absorption is highly varied between subjects, with considerable interstudy variability in the observed area under the concentration-time curve (AUC) values in the fed and fasted states (e.g., see references 11–14).

The primary aim of the present analysis was to develop a population pharmacokinetic model for itraconazole and hydroxyitraconazole that could effectively describe pharmacokinetic data from single-dose and multidose studies for SUBA-itraconazole and Sporanox, with particular emphasis on quantifying the effects of food and formulation on oral absorption and their implications on itraconazole exposure metrics.

MATERIALS AND METHODS

Pharmacokinetic data.

The pharmacokinetic data used in the analysis were collated data from seven different trials comparing SUBA-itraconazole with Sporanox in healthy subjects conducted by Mayne Pharma International. The designs and dosing schedules are summarized in Table 1. Two of the studies were conducted in the United Kingdom, and five studies were conducted in the United States. Overall, there were 238 subjects providing a total of 24,965 plasma concentrations, with an average of 105 observations per subject over 2 to 4 treatment periods. The studies differed by the country of origin of the reference Sporanox (sourced from the United States or the United Kingdom).

TABLE 1.

Studies comparing SUBA-itraconazole with Sporanox in the fed and fasted states^a

Study	No. of subjects	Single/multiple dose	No. of treatment periods per subject	Daily dosing (mg) per subject for:		Sporanox source	Fed (yes/no)	Fasted (yes/no)	Replicate design (yes/no)
				SUBA-itraconazole	Sporanox
MPG009	52	Single	4	1 × 65/2 periods	1 × 100/2 periods	USA	Y	Y	N
HGN007b	36	Single	4	1 × 50/2 periods	1 × 100/2 periods	UK	Y	Y	N
HGN008b	48	Single	4	1 × 50/2 periods	1 × 100/2 periods	UK	Y	N	Y
10850702	24	Single	4	1 × 50/1 period	1 × 100/1 period	USA	N	Y	Y
				2 × 50c/1 period	1 × 200/1 period
10850703	36	Single	4	1 × 50/2 periods	1 × 100/2 periods	USA	Y	Y	N
10850705	24	Multiple	2	2 caps × 50d q.d. × 15 days/1 period	2 caps × 100d q.d. × 15 days/1 period	USA	Y	N	N
10850706	24	Multiple	2	2 caps × 50e b.i.d. × 15 days/1 period	2 caps × 100e b.i.d. × 15 days/1 period	USA	Y	N	N

^aAll studies were randomized crossover design studies with 2 or 4 treatment periods per subject.

^bStudies performed in the United Kingdom.

^cTwo capsules were given at once as a single dose (total daily dose, 100 mg).

^dTwo capsules were given at once as a single dose every day up to 15 days (total daily dose, 100 mg for SUBA-itraconazole and 200 mg for Sporanox). q.d., once daily.

^eTwo capsules were given at once as a single dose twice daily (total daily dose, 200 mg for SUBA-itraconazole and 400 mg for Sporanox). b.i.d., twice daily.

All studies were randomized crossover design studies with either four or two treatment periods per subject for the single-dose and multidose studies, respectively. Plasma concentrations were available for a range of doses for single-dose administration, in both fed and fasted states, and multidose administration in the fed state only.

The single-dose studies (HGN007, HGN008, MPG009, 10850702, and 10850703) compared either 50, 65, or 100 mg of SUBA-itraconazole with 100 or 200 mg of Sporanox administered once daily in the fed and fasted states. Itraconazole formulations were administered to subjects following an overnight fast of ≥10 h for the fasted periods and following a standardized high-fat high-calorie breakfast for the fed periods. All itraconazole doses were administered with 240 ml of water. Each subject received four treatments within a study according to a 4-sequence randomization schedule. There was a 7-day interval between each treatment period.

For studies HGN007, HGN008, 10850702, and 10850703, blood samples (∼7 ml) for the determination of itraconazole and hydroxyitraconazole concentrations were taken at 0, 0.5, 1, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 24, 36, 48, and 72 h after the dose. Study HGN008 had additional samples collected at 96 and 120 h. A similar but more extensive pharmacokinetic (PK) sampling schedule for the determination of itraconazole was performed for study MPG009, with additional samples collected at 3.5, 4.5, 5.5, 6.5, 7, 9, 16, 96, and 120 h.

For multidose studies (10850705 and 10850706), 100 mg of SUBA-itraconazole was administered either once or twice daily and compared to 200 mg of Sporanox administered in a similar dosing schedule for 15 days under fed conditions. Blood samples for a determination of itraconazole and hydroxyitraconazole concentrations were taken at −48, −24, 0, 0.5, 1, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 24, 36, 48, and 72 h, all relative to the time after dose on day 15.

All subjects who participated in the studies were non-tobacco-using males and nonpregnant nonlactating females who were ≥18 years of age. All subjects were healthy, as determined by the lack of abnormalities in the health assessments performed prior to study participation. Subjects with histories of gastrointestinal disease, malabsorption, and those who received any known CYP3A inhibitors or inducers in the 30 days prior to the study were excluded. All studies were conducted according to the International Conference of Harmonisation (ICH) guidelines for good clinical practice (15), the Declaration of Helsinki on the ethical conduct of medical research (16), and applicable regulatory requirements. Each subject signed and dated a written informed consent before study participation.

Scheduled blood samples were collected in sodium heparin collection tubes and centrifuged within 60 min of collection. The resulting plasma samples were stored frozen at −20°C or below and shipped overnight on dry ice to the analytical facility. For the United Kingdom studies, the analyses of itraconazole and hydroxyitraconazole concentrations were conducted by Covance Laboratory, Inc. (Harrogate, United Kingdom) using a fully validated liquid chromatography-tandem mass spectrometry (LC-MS/MS) method after solid-phase extraction of the plasma samples. For the U.S. studies, the analysis was conducted by PPD Laboratory Services (Middleton, WI) using a fully validated high-performance liquid chromatography (HPLC) method with fluorescence detection. The lower limits of quantification of the assays were 0.2 ng/ml and 0.5 ng/ml for the studies performed in the United States and the United Kingdom, respectively.

Population pharmacokinetic analysis. (i) Software.

Modeling was performed using a Dell PowerEdge R910 server with 4 by 10 core Xeon 2.26-Ghz processors running Windows Server 2008 R2 Enterprise 64-bit software. Log-transformed plasma itraconazole and hydroxyitraconazole concentrations were used for pharmacokinetic modeling. Model development employed nonlinear mixed-effects modeling using NONMEM (version 7.3; ICON Development Solutions, Ellicott City, MD) (17), ADVAN5 (for modeling itraconazole data only), and ADVAN6 subroutine (for concurrent modeling of itraconazole and hydroxyitraconazole) with the Wings for NONMEM (version 7.3) interface (http://wfn.sourceforge.net) and IFort compiler. First-order conditional estimation method with interaction (FOCE-I) was used to fit models. Processing of the NONMEM output and generation of plots were conducted with the R software version 3.1.1 (18) using the ggplot2, doBy, plyr, reshape2, and scales packages (19–23).

(ii) General modeling strategy.

Model development was conducted in a stepwise manner. First, a base model of itraconazole single-dose data was developed, which allowed a focused investigation of food effects on itraconazole absorption, as only the single-dose studies had fed and fasted periods. The base model of single-dose data was then extended to describe the multidose data (and the single-dose studies). Different mechanisms were investigated to describe the accumulation kinetics of itraconazole in the multidose studies. Covariate effects (other than those needed for an accurate structural model) were investigated on the base model of combined single-dose and multidose data. The final covariate model was then extended to describe the concurrent kinetics of itraconazole and hydroxyitraconazole. A simultaneous estimation of the pharmacokinetic parameters of the parent drug and metabolite was also assessed.

Population parameter variability was modeled on pharmacokinetic parameters using a log-normal distribution:

$$P_{\mathrm{i}}=P_{\text{pop}}\times \exp ({\text{η}}_{\text{i}}),{\text{η}}_{\text{i}}\sim N(0,{\omega }^2)$$ (1)

where P_i represents the parameter estimate of i^th individual, P_pop represents the typical population parameter estimate, and η_i (ETA) is the deviation of P_i from P_pop.

Residual variability was modeled using a combined proportional and additive model of itraconazole and hydroxyitraconazole:

$$C_{\text{ij}}=C_{\text{pred},\text{ij}}(1+{\text{ε}}_{\text{ij}1})+{\text{ε}}_{\text{ij}2},{\text{ε}}_{\text{ij}1}\sim N(0,{\sigma }_1^2),{\text{ε}}_{\text{ij}2}\sim N(0,{\sigma }_2^2)$$ (2)

where C_ij represents the j^th observation of the i^th individual, C_pred,ij represents the model-predicted C_ij, and ε_ij1 and ε_ij2 represent the residual additive and proportional error, respectively, of the j^th observation of the i^th individual. The combined residual model was adapted for use using the log-transform both sides (LTBS) approach (24); see Appendix S1 in the supplemental material for the code used.

(iii) Base model development of single-dose data.

Base model development for single-dose data was conducted following sequential stages in which the best model was selected and carried forward to the next stage. Stage 1 models examined the basic form of the structural model (1, 2, or 3 compartment) and the benefit of a “common variability on bioavailability” approach (FVAR).

Base models included a parameter for SUBA-itraconazole relative bioavailability compared to that of Sporanox (reference value 1), given the known bioavailability differences. First-order oral absorption was assumed for the stage 1 models. The effect of fed status on the absorption parameters was examined in case the effect of fed status on the observed data influenced model selection.

Transit chain absorption models (1- to 6-transit compartments) (25) were examined at stage 2 using the best structural model from stage 1. Stage 3 models examined the effect of fed status on the fixed-effects model parameters of the best model carried from stage 2.

Different methods for representing between-occasion variability (BOV) on PK model parameters were investigated at stage 4. For this purpose, two levels of random effects corresponding to two subject identification codes were defined in the data. The first level was unique by subject (ID) and therefore had common random-effects values for each dose period within a subject. The second level was unique by the dose period (ID2) within a subject and therefore allowed different random-effects values for each treatment period within a subject (i.e., assuming the BOV is equal to between-stage variability [BSV]).

The best model from stage 4 was carried forward to stage 5, which examined: (i) the effects of adding between-study variability on random-effects parameters to further improve the fit of dosing periods and (ii) the hypothesis that the kinetics of itraconazole differed in variability for Sporanox compared to that of SUBA-itraconazole. A scaling factor (ETASCALE) was introduced to allow population parameter variability to differ between the two formulations and was examined systemically on all population PK parameters.

(iv) Base model development of single-dose and multidose data.

The best base model of single-dose data was carried forward to develop a model of the combined single-dose and multidose data. Previous studies using noncompartmental approaches revealed nonlinear kinetic behavior for itraconazole and hydroxyitraconazole in a comparison of single-dose versus multidose kinetics or in comparisons of single-dose kinetics of itraconazole across a range of doses (9, 10). A number of mechanisms representing the nonlinearity were examined during the model-building process. The mechanisms investigated included (i) saturable elimination models, (ii) competitive inhibition models, in which an inhibition rate constant was introduced to the saturable elimination model (26) and inhibition was assumed to be a function of either itraconazole or hydroxyitraconazole concentrations, (iii) models invoking time-dependent changes in clearance and/or bioavailability, and (iv) models invoking time- and dose-dependent changes in clearance and/or bioavailability.

(v) Covariate model building.

The available covariates in the data were body weight (BW), lean body weight (LBW), total daily dose, formulation (SUBA-itraconazole versus Sporanox), Sporanox origin (United Kingdom versus U.S. origin), study population (United Kingdom versus U.S. population), ethnic group, race, and sex. Potential significant covariates were identified by visualizing plots of the covariates versus the BSV of the parameter estimates. Physiologically plausible covariates were evaluated for statistical significance using a stepwise covariate modeling of forward addition and backward elimination (27). Additionally, it was considered that there may have been an interaction between formulation and dose occasions such that, for example, the first dose occasion of Sporanox differed from all other Sporanox dose occasions. Such interactions were also examined in the model. The statistical criteria for retaining a covariate in the model were a P value of <0.005 during forward addition and a P value of <0.001 for backward elimination.

Continuous covariates were modeled using a power function referenced to the median value of the covariate in the data set (COV_median) using the equation:

$$P_{\text{ij}}=P_{\text{pop}}\times {\left(\frac{CO{V}_{\text{j}}}{CO{V}_{\text{median}}}\right)}^{\theta }$$ (3)

where the individual parameter estimate of the j^th individual (P_ij) with the covariate value COV_j was modified from the population value (P_pop) by the value of θ.

Categorical covariates were modeled using a proportional function:

$$P_{\text{ij}}=P_{\text{pop}}\times \left(1+\theta \times COV\right)$$ (4)

where P_pop was the population parameter estimate when the covariate was absent (COV = 0), and θ represented the change in the parameter associated when the categorical covariate was present (COV = 1).

(vi) Metabolite model.

Metabolite modeling was performed using a sequential 2-stage approach (28). The final parent drug model was coded with differential equations using the ADVAN6 subroutine in NONMEM.

As the fraction of itraconazole metabolized to hydroxyitraconazole is not known, the metabolic conversion ratio was assumed to be 1 (i.e., all itraconazole cleared from the parent model entered the metabolite model). The clearance and volume parameters for the metabolite model were therefore the apparent values scaled by the unknown metabolic conversion ratio.

The model-building process was analogous to the method used for modeling the parent drug. The most appropriate structural model for hydroxyitraconazole was identified, and then a number of mechanisms were investigated to describe the nonlinearity in the hydroxyitraconazole data. The mechanisms investigated included: (i) similar models used to examine the nonlinearity for the parent drug, (ii) models with enterohepatic recycling for the metabolite, (iii) models with transit compartments for metabolite formation, (iv) mixture models of metabolite clearance, and (v) mixed linear and nonlinear elimination models. Separate residual variability terms were used for itraconazole and hydroxyitraconazole concentrations for the single-dose and multidose data.

The model was fitted to all available itraconazole and hydroxyitraconazole data from the single-dose and multidose studies, with the parameters for itraconazole fixed at the values determined from the final model of the itraconazole data only. Importance sampling was used to assess the precision of the estimated metabolite parameters.

(vii) Model selection and predictive performance.

Model selection was guided by the following criteria: (i) plausibility and precision of parameter estimates, (ii) the Akaike information criterion (AIC), (iii) the minimum objective function value (MOFV), and (iv) the inspection of various standard diagnostic plots. The AIC was used to compare nonnested models, in which models with lower AIC were preferred for base model selection. Candidate base models were considered for further analysis if the standard errors of θs and ηs were <30% and 50%, respectively. The likelihood ratio test (LRT) was used to compare nested models with a significance level of a P value of 0.005. Covariates with standard errors (SE) of <51.2% were considered for further analysis.

Visual predictive checks (VPC) (29) were performed to evaluate the predictive performance and adequacy of the models for describing itraconazole and hydroxyitraconazole single-dose and multidose data. For itraconazole and hydroxyitraconazole, the final model was used to simulate 200 versions of the original data set based on the final estimated parameter values of the parent and the metabolite. The observed concentrations and the median and 90% confidence interval of the observed and simulated concentrations were plotted. The VPCs of hydroxyitraconazole were constructed for up to 72 h due to the relatively low number of samples beyond 72 h that resulted in large confidence intervals of the predicted concentrations. VPCs of itraconazole were also constructed for key noncompartmental analysis (NCA) exposure metrics (area under the concentration-time curve from time zero to the last measurable concentration [AUC_0–t], maximum concentration in serum [C_max], and time to C_max [T_max]) and were presented as boxplots for comparison. NCA metrics of simulated data below the 2.5th and 97.5th percentiles were not used for summary statistics, as they presented as outliers, and their inclusion was considered to produce summary statistics that were not representative of the model predictions.

Simulations. (i) Food effects.

The final model of itraconazole was used to simulate the effect of food on the time course of predicted itraconazole concentrations in fed and fasted states. A crossover design study was simulated 1,000 times using single oral doses of SUBA-itraconazole (58 mg) and Sporanox (100 mg), which would provide equal exposure given the final model estimate of the relative bioavailability. A sample size of 52 subjects was chosen, as this represented the largest number of subjects in the clinical trials included in the present analysis. The median and 90% confidence interval of the predicted itraconazole concentrations were plotted. Itraconazole exposure was assessed by the area under the concentration-time curve from time zero to infinity (AUC_0–∞), C_max, and T_max. C_max and T_max were collated directly from the simulated data. The area under the concentration-time curve from time zero to the last measurable concentration (AUC_0–t) was calculated using linear trapezoidal integration of model-predicted concentrations. The area under the concentration-time curve from time zero to infinity (AUC_0–∞) was calculated as follows: AUC_0–∞ = AUC_0–t + C_t/k_el, where C_t is the last measurable drug concentration and k_el is the elimination rate constant. Calculations were performed in R using an R script.

(ii) Power analysis.

The final model of itraconazole was used to perform a power analysis of bioequivalence between the two marketed itraconazole formulations: 50 mg of SUBA-itraconazole compared to a reference 100 mg of Sporanox in fed and fasted states. A crossover design study of 24 and 52 subjects was simulated 1,000 times. Pharmacokinetic exposure parameters (AUC_0–∞, AUC_0–t, and C_max) were calculated, as described in “Food effects” above, for the reference (Sporanox) and tested (SUBA-itraconazole) formulations in the fed and fasted states. For each simulated study, the 90% confidence interval (CI) of the geometric mean ratios (obtained from the log-transformed data) of the pharmacokinetic exposure parameters were calculated. Bioequivalence was demonstrated if the 90% confidence interval (CI) of the test/reference ratio for AUC_0–∞, AUC_0–t, and C_max for itraconazole fell within the range of 0.8 to 1.25. The percentage of bioequivalence studies was computed for different fed/fasted comparisons of the test versus the reference formulation. The percentage of bioequivalence studies was interpreted as the chance of establishing bioequivalence between the two formulations given the trial design and dose selection used in the trial.

(iii) shiny application.

The final model of itraconazole was implemented as a Web application that allows users not familiar with the details of population modeling to perform simulations using the model (30). The application utilizes the shiny package in R programming language (31) and uses validated ADVAN-style analytical solutions (32) of the final itraconazole model.

RESULTS

Study populations and pharmacokinetic data.

The U.S. and United Kingdom plasma concentration data used for pharmacokinetic modeling included 15,097 itraconazole plasma samples from 238 subjects and 9,868 hydroxyitraconazole plasma samples from 186 of the subjects. A summary of the subject demographics for the U.S. and United Kingdom studies is presented in Table 2. The observed itraconazole concentrations were 0.2 to 2,850 ng/ml, and the hydroxyitraconazole concentrations were 0.5 to 4,070 ng/ml. Overall, 12.5% and 17.5% of the itraconazole and hydroxyitraconazole data were missing, respectively. The missing data were primarily below the lower limit of quantitation (LLOQ) and occurred primarily at the beginning or the end of the observation period. Models accounting for LLOQ-censored data using the YLO and M3 methods (33) were investigated and were found to be characterized by unreliable minimization and covariance step status. Samples below the limit of quantitation (BLQ) were thus excluded a priori from the data set (M1 method). No impact on parameter estimates was demonstrated, as there were sufficient data points in the elimination phase of itraconazole, and the hydroxyitraconazole data were unaffected by censoring (figures not shown). This was subsequently confirmed by the final model.

TABLE 2.

Demographic characteristics of study population^a

Demographic	U.S. studies	UK studies
Age (yr)	37.7 (38, 18–60)	32.1 (28, 19–56)
Wt (kg)	82.3 (83.7, 49–108)	74.2 (37.5, 49.3–98.3)
Ht (cm)	178 (178, 157–198)	174 (174, 151–194)
Lean body mass (kg)b	51.6 (52.2, 33.8–62.6)	54.4 (57.4, 34.3–72.6)
Sex (no. of males/no. of females)	36, 118	57, 27
Race (no.)	103 White, 23 Black, 28 other	79 White, 1 Asian, 2 Black, 2 other
Ethnicity (no.)	50 Hispanic, 104 not Hispanic or Latino	84 not Hispanic or Latino

^aAll values calculated as mean (median, range), unless stated otherwise.

^bCalculated as per reference 56.

Base model of single-dose studies.

The best structural model identified at stage 1 was a two-compartment first-order absorption model including common variability on bioavailability coding and the effect of fed status on absorption parameters (bioavailability and absorption rate constant). The model allowed the magnitude of the residual error to differ with fed status. The transit compartment models at stage 2 performed substantially better than the first-order absorption models. The 4-transit compartment model was the best model to describe oral absorption and was associated with an AIC reduction of 1,295 units compared to the use of first-order absorption with a lag time.

The stage 3 models examined the effect of fed status on fixed-effects parameters of the 4-transit absorption model selected at stage 2. The best model that passed the selection criteria incorporated the effect of fed status on the transit-compartment rate constant (KTR) and bioavailability (F). The bioavailability model lowered the AIC by 4,381 units compared to the reference model (the best model at stage 2) and was carried forward to the next stage.

The models at stage 4 differed in the level of random effects by subject identification (ID) (ID-class models) or by dose period (ID2-class models). Initially, the best model at stage 3 was extended by the addition of BOV on random-effects parameters using subject ID as the level of random effects. Incorporating BOV into the ID-class models resulted in a large drop in the AIC (e.g., adding BOV on F and KTR dropped the AIC >10,800 units), which suggests that the BOV was substantially larger than the BSV. However, most of ID-class models terminated unsuccessfully, and all failed to pass a covariance step (either aborted or none), taken as an indication of overparameterization. In addition, all models were characterized by low eta P values of random effects, which indicated a biased distribution of the empirical base estimate etas (EBE-etas). To allow more freedom in finding a description of the dose periods within a subject, it was assumed that an ID-class model with BOV on all parameters was equivalent to an ID2-class model when BOV is substantially larger than BSV. Therefore, the best ID2-class model was carried forward to stage 5, this being the best model from stage 3.

Adding between-study variability on random-effects parameters did not improve the fit of the model any further (ΔOFV, 0). Incorporating an ETASCALE parameter of the formulation on the population variability in bioavailability lowered the AIC by 15 units, and all model parameters were estimated precisely (percent standard error [%SE], <30%). Adding a scale parameter on the other population variability parameters resulted either in imprecise parameter estimates or terminated runs. Therefore, the best model at stage 5 incorporated an ETASCALE parameter of the formulation on the population variability in F and was declared as the final base model of single-dose data.

The base model supported BSV on the apparent central clearance (CL/F), apparent central volume of distribution (V₁/F), and KTR. All base model parameters were estimated precisely (%SE, <30%), and diagnostic plots were able to describe the data very well, with no systematic bias. The estimated population pharmacokinetic parameters of the best base model of single-dose data and representative diagnostic plots of the model are provided in Table S1 and Fig. S1 in the supplemental material.

Base model of single-dose and multidose data.

Initial fitting of the combined single- and multidose data using the best single-dose model showed that the multidose concentrations were substantially underestimated (data not shown). Nonlinear elimination kinetics can cause changes in both clearance (lower clearance with higher doses due to systemic saturation of clearance) and bioavailability (higher bioavailability for higher doses due to reduced first-pass effect). Among the different methods examined to investigate the nonlinearity of the multidose data, itraconazole nonlinear kinetics was best described by the total effective daily dose- and time-dependent changes in clearance and bioavailability for multidose studies compared to those of the single-dose studies.

The total effective daily dose- and time-dependent changes in clearance allowed the clearance of the multidose studies to decrease exponentially compared to that of the single-dose studies, depending on the total effective daily dose of itraconazole (equation 5). The effective daily dose (EDD) was the total daily dose of itraconazole corrected for the relative bioavailability difference between the two formulations. As per Lehr et al. (34), itraconazole approaches steady state after ∼7 days of continuous administration. The rise to steady-state concentration with time (i.e., the decrease in clearance with time) was described exponentially by equation 6. The rate constant (k_ss) for the exponential decrease in clearance with time was fixed to 0.5 day⁻¹, as no data were available during the approach to steady state.

$${DDCL}_{\text{ss}}=(1-{DD}_{\max \hspace{0.17em}})\times \exp (-1\times DDK\times EDD)+{DD}_{\max \hspace{0.17em}}$$ (5)

where DDCL_ss represents the effect of effective daily dose on clearance, DD_max represents the maximum effect of EDD on clearance, and DDK was a rate constant for EDD on clearance.

$$\begin{array}{c}DDCL=\left([1-DDC{L}_{\text{ss}}]\times \exp \hspace{0.17em}[-1\times K_{\text{ss}}\times \{DAY-1\}]\right)+DDC{L}_{\text{ss}}\end{array}$$

$$\begin{array}{c}CL=C{L}_{\text{pop}}\times DDCL\end{array}$$ (6)

where DDCL represents the change in clearance with time, k_ss represents the rate constant for the rise to steady-state concentration, and DAY is the time in days since the first dose.

Similarly, the time course of the change in bioavailability for the multidose studies during the accumulation phase was described by equation 7.

$$\begin{array}{c}DDF=\left([1-DD{F}_{\text{SS}}]\times \exp [-1\times K_{\text{ss}}\times \{DAY-1\}]\right)+DD{F}_{\text{ss}}\end{array}$$

$$\begin{array}{c}F=1\times DDF\end{array}$$ (7)

where DDF represents the change in bioavailability with time (days) and DDF_ss represents the effect of effective daily dose on bioavailability at steady state.

Introducing dose- and time-dependent changes on clearance and bioavailability for the multidose studies resulted in drops in the AIC of 661 units and 280 units, respectively, compared to the reference model without introducing these effects.

The parameters for the best base model of single-dose and multidose data were estimated precisely (%SE, <30%), and diagnostic plots were compatible with a well-formed population model (data not shown). This model was declared the base model for testing the addition of covariates.

Covariate models.

The following potential significant covariate relationships (in addition to those used in building of structural model) were assessed during covariate model building: weight (WT) on CL/F and central volume of distribution of itraconazole (V₂)/F, LBW on CL/F and V₂/F, total daily dose on CL/F and KTR, weight on V₂/F and KTR, formulation and ethnic group on KTR, an interaction between dose occasions for Sporanox on KTR, and Sporanox origin and study population on all pharmacokinetic model parameters.

Significant univariate models identified in the first forward addition step had an effect of study population on KTR (ΔOFV, −5,597.7), CL/F (ΔOFV, −45.7), and an effect of WT on CL/F (ΔOFV, −9.8) compared to the base model. The inclusion of other covariates failed to meet the selection criteria. The best univariate model with an effect of study population on KTR was investigated in combination with the other significant covariates. Adding the weight covariate in the second forward addition step resulted in an imprecise parameter estimate (%SE, 80.5%) and therefore, was not considered further. The best model in the second forward addition step had an effect of study population on the KTR and CL/F of itraconazole and was retained significant in the backward deletion step.

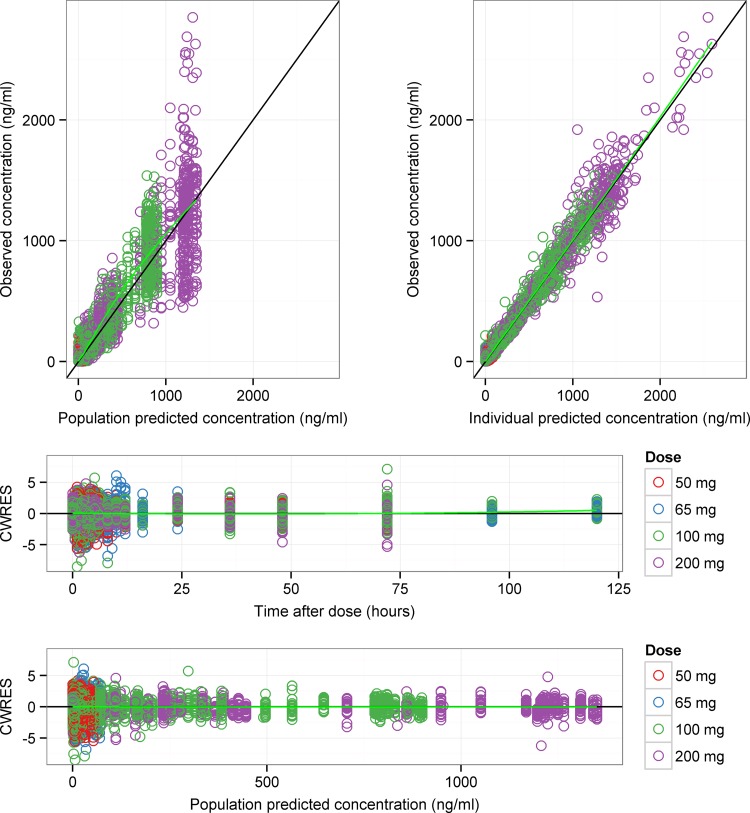
The final estimated population pharmacokinetic parameters for all fixed and random effects in the final itraconazole model are presented in Table 3, and diagnostic plots are given in Fig. 1. The NONMEM control stream for the final itraconazole model is provided in Appendix S1 in the supplemental material. As shown in Table 3, all model parameters were estimated precisely and had acceptable standard errors (%SE, <30%). The standard goodness-of-fits plots in Fig. 1 show that the data were symmetrically distributed around the unit slope lines of with no major systematic bias. The observed versus individual predicted concentrations were tightly clustered around the identity line across the range of measured values, indicating that these data were adequately described by the model. Similar diagnostic plots were obtained when the data were conditioned by formulation and fed status (see Fig. S2 and S3 in the supplemental material).

TABLE 3.

Population parameter estimates of itraconazole from the final model of single-dose and multidose itraconazole data

Parametera	Population estimate	%SE
CL/F (liters/h)	129	4.0
V2/F (liters)	861	3.9
Q/F (liters/h)	153	4.2
V3/F (liters)	2,340	4.0
KTR (h−1)	2.05	2.2
ETASCALE	−0.213	31.0
FORMF	0.729	8.6
FEDKTR	−0.583	2.1
FEDF	−0.269	12.2
DDFss	3.26	4.9
STUDYPOP-CL/F	−0.166	11.6
STUDYPOP-KTR	0.338	14.4
DDKSPOR	0.0065	6.2
DDKSUBA	0.00596	6.2
DDmax	0 FIX
BSV (%CV [% shrinkage])
BSV-CL/F	22.1 (27.4)	5.4
BSV-V2/F	30.8 (44.4)	9.4
BSV-KTR	44.8 (4.5)	3.0
FVAR	56.4 (5.0)	4.3
RV
Single-dose studies
Proportional error-fasted (%CV)	29.3	3.2
Additive error-fasted (ng/ml)	0.168	7.6
Proportional error-fed (%CV)	39.9	3.1
Additive error-fed (ng/ml)	0.14	5.0
Multidose studies
Proportional error (%CV)	14.1	4.3
Additive error (ng/ml)	0.267	10.5

^aCL/F, apparent clearance; V₂/F, apparent central volume of distribution; Q/F, apparent intercompartmental clearance; V₃/F, apparent peripheral volume of distribution; KTR, transit compartment rate constant; RV, residual variability; ETASCALE, effect of formulation on bioavailability variability; FORMF, effect of formulation on bioavailability; FEDKTR, effect of fed status on transit compartment rate constant; FEDF, effect of fed status on bioavailability; DDF_ss, effect of daily dose on bioavailability for multidose studies; STUDYPOP, effect of study population (United Kingdom versus United States) on CL/F or KTR; DDKSPOR and DDKSUBA, rate constants for effective daily dose on CL/F for Sporanox and SUBA-itraconazole, respectively; DD_max, maximum effect of effective daily dose on CL/F; BSV, between-subject variability; CV, coefficient of variation; FVAR, common random effect for bioavailability.

FIG 1.

Goodness-of-fits plots of the final itraconazole model of single- and multidose data. In each plot, the symbols are data points, the solid black line is a line of identity with slope 1 (top two panels) or 0 (bottom two panels), and the solid green line is a Loess smooth of the data. Itraconazole data points for the different itraconazole doses used in the pharmacokinetic studies are colored in red (50 mg), blue (65 mg), green (100 mg), and purple (200 mg). CWRES, conditional weighted residuals.

SUBA-itraconazole had a relative bioavailability of 173% compared to that of Sporanox, and the bioavailability was 21.3% less variable (Table 3). The fed status influenced the kinetics of itraconazole via two mechanisms: (i) a decrease in the relative bioavailability to 73.1% of the fasted state, and (ii) a decrease in transit absorption rate constant (KTR) to 41.7% of the fasted state, which corresponds to an increase in the mean transit time (MTT) of the drug from a population value of 1.95 h in the fasted state to 4.68 h in the fed state. The apparent central clearance (CL/F) and KTR for subjects from the United Kingdom studies were 83.4% and 133.8%, respectively, compared to those for subjects from the U.S. studies (Table 3).

Metabolite model.

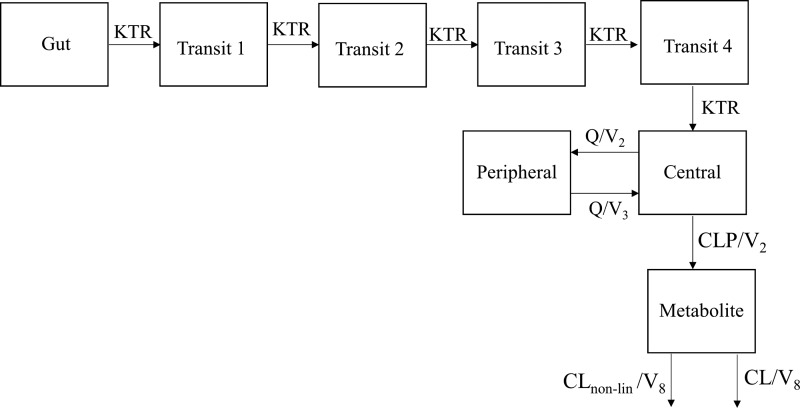
Hydroxyitraconazole data were best described by a one-compartment model with mixed linear (first-order) and nonlinear (Michaelis-Menten) elimination for the single-dose hydroxyitraconazole data and a time-dependent linear clearance for hydroxyitraconazole multidose data. The final parent-metabolite model is presented in Fig. 2.

FIG 2.

Two-compartment itraconazole model with 4-transit absorption compartments connected to a one-compartment hydroxyitraconazole model with mixed linear (first-order) and nonlinear (Michaelis-Menten) hydroxyitraconazole elimination. KTR, transit absorption rate constant; Q, intercompartmental clearance; V₂ and V₃, central and peripheral volume of distribution of itraconazole, respectively; CLP, clearance of the parent drug; CL_non-lin, nonlinear hydroxyitraconazole clearance; V₈, volume of distribution for the metabolite.

The time-dependent clearance allowed the metabolite clearance of multidose studies to differ with passage of time from the single-dose studies (reference value = 1) by a factor that might represent changes of clearance due to enzyme inhibition (or induction). Equation 8 shows the change in clearance for the multidose hydroxyitraconazole data:

$${\text{CL}}_{\text{m}}=\text{C}{\text{L}}_{\text{pop}}*TIMECL*\exp (\text{η})$$ (8)

where TIMECL represents the change in clearance for multidose studies from the single-dose studies. CL_m, CL_pop, and η represent individual metabolite clearance, typical metabolite clearance, and between-subject variability, respectively.

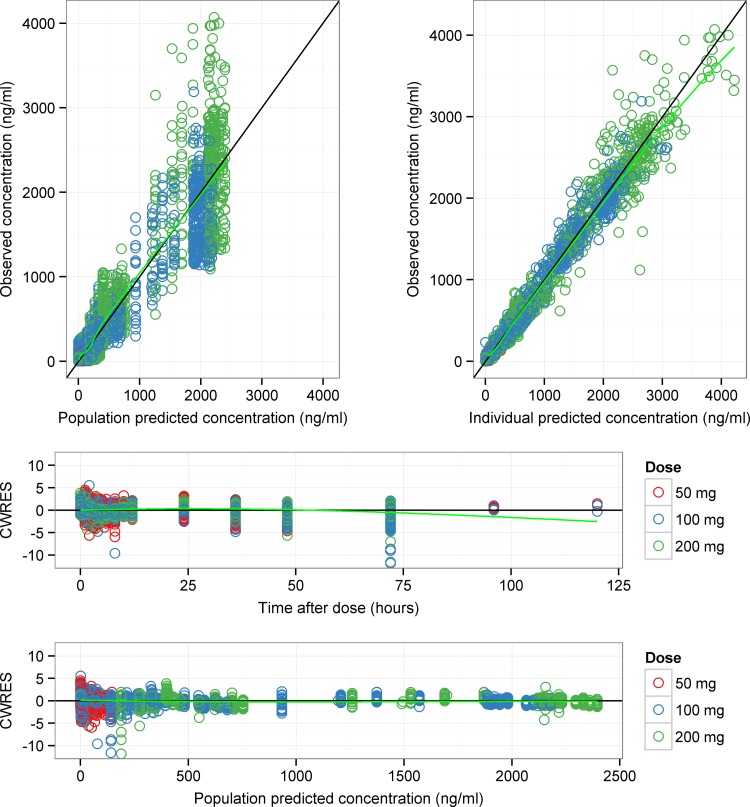
The addition of time-dependent clearance with linear elimination for the multidose studies adequately described hydroxyitraconazole concentrations and was associated with an AIC reduction of 2,150 units compared to a reference one-compartment model. Despite providing a good description of the multiple-dose data, the model was associated with biased predictions for the single-dose data. The addition of mixed linear (first-order) and nonlinear (Michaelis-Menten) elimination for the single-dose data resulted in a further reduction in the AIC by 2,353 units and was the best model to adequately describe hydroxyitraconazole concentrations in the single-dose studies. The final parameter estimates for the metabolite component of the model are presented in Table 4, and key diagnostic plots are given in Fig. 3. The NONMEM control stream of the final metabolite model is provided in Appendix S2 in the supplemental material. All parameters were precisely estimated (%SE, <38%). The conditional weighted residuals-versus-time plot showed that most of the data points were symmetrically distributed within −6 and +6 units, as appears in Fig. 3. The few data points outside this range were examined and were from 4 different subjects (3 subjects from the multidose studies and one subject from a single-dose study). However, there was no bias observed, and none of these points were justifiably deleted from the data set. Only study 8 had metabolite data after 72 h, and most of them (∼86%) were missing.

TABLE 4.

Parameter estimates of hydroxyitraconazole for the final metabolite model of combined single-dose and multidose data

Parametera	Population estimate	%SE
CLm/Fm (liters/h)	45.6	1.5
Vmax (liters/h)	403	5.2
Km (ng/ml)	1.64	34.8
CLM5	−0.208	24.4
CLM6	−0.643	5.7
V1m/Fm (liters)	5.28	14.2
BSV (%CV [% shrinkage])
BSV (CLm/Fm)	27.9 (35.2)
RV
Single-dose studies
Proportional error (%CV)	38.7	6.1
Additive error (ng/ml)	0.329	38
Multidose studies
Proportional error (%CV)	19.6	10.4
Additive error (ng/ml)	0.257	8

^aCL_m/F_m, apparent metabolite clearance; V_max, maximum elimination rate of the metabolite for the single-dose studies; K_m, Michaelis-Menten constant; CL_M5 and CL_M6, magnitude of reduction in metabolite apparent clearance for studies 10850705 and 10850706, respectively; V_1m/F_m, apparent central volume of distribution; BSV, between-subject variability; RV, residual variability.

FIG 3.

Goodness-of-fits plots of hydroxyitraconazole model of single-dose and multidose data. In each plot, symbols are data points, the solid black line is a line of identity with slope 1 (top two panels) or 0 (bottom two panels), and the green line is a Loess smooth of the data. Hydroxyitraconazole data points for the different itraconazole doses used in the pharmacokinetic studies are colored in red (50 mg), blue (100 mg), and green (200 mg). The 65-mg dose study has no hydroxyitraconazole data. CWRES, conditional weighted residuals.

Visual predictive checks.

The visual predictive check (VPC) plots for itraconazole and hydroxyitraconazole are presented in Fig. 4, 5, and 6. Itraconazole VPCs for key noncompartmental analysis (NCA) exposure metrics (AUC_0–t, C_max, and T_max) are provided in Fig. S4 to S6 in the supplemental material.

FIG 4.

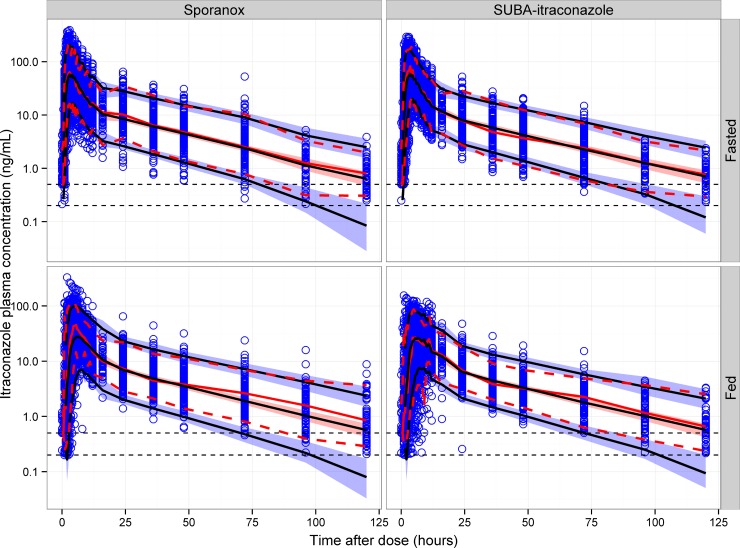
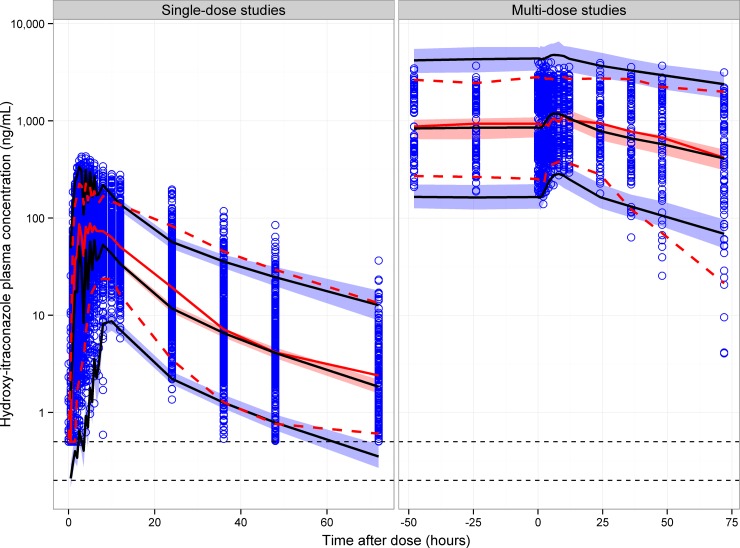
Visual predictive checks of itraconazole for single-dose and multidose studies. Open circles represent observed itraconazole concentrations. The solid black lines represent the 5th, 50th, and 95th percentiles of the simulated concentrations. The shaded area represents the 90% confidence interval of the 5th, 50th, and 95th percentiles of the simulated concentrations. The solid red line represents the median of the observed concentrations. The dashed red lines represent the 5th and 95th percentiles of the observed concentrations. The horizontal dotted lines represent the lower limit of quantitation (LLOQ) of itraconazole for the U.S. (upper line) and United Kingdom (lower line) studies.

FIG 5.

Visual predictive checks of itraconazole for single-dose studies stratified by fed status and formulation. In each plot, open circles represent observed itraconazole concentrations. The solid black lines represent the 5th, 50th, and 95th percentiles of the simulated concentrations. The shaded area represents the 90% confidence interval of the 5th, 50th, and 95th percentiles of the simulated concentrations. The solid red line represents the median of the observed concentrations. The dashed red lines represent the 5th and 95th percentiles of the observed concentrations. The horizontal dotted lines represent the lower limit of quantitation (LLOQ) of itraconazole for the U.S. (upper line) and United Kingdom (lower line) studies.

FIG 6.

Visual predictive checks of hydroxyitraconazole for single-dose and multidose studies. Open circles represent observed hydroxyitraconazole concentrations. The solid black lines represent the 5th, 50th, and 95th percentiles of the simulated concentrations. The shaded area represents the 90% confidence interval of the 5th, 50th, and 95th percentiles of the simulated concentrations. The solid red line represents the median of the observed concentrations. The dashed red lines represent the 5th and 95th percentiles of the observed concentrations. The horizontal dotted lines represent the lower limit of quantitation (LLOQ) of hydroxyitraconazole for the U.S. (upper line) and United Kingdom (lower line) studies.

The VPC of itraconazole showed that the final model has good predictive performance for single-dose and multidose data (Fig. 4) and for single-dose data conditioned on formulation and fed status (Fig. 5). The time course of the median and 5th and 95th percentiles were similar for the observed and simulated concentrations. The model also showed good predictive performance for itraconazole when the plots were conditioned on study, dose, formulation, and fed status (figures not shown). The itraconazole exposure metrics VPCs showed an acceptable agreement between the model predictions and observed data for AUC, C_max, and T_max.

The VPCs of hydroxyitraconazole in Fig. 6 demonstrated an acceptable agreement between the observed and simulated concentrations for multidose data; however, there was a deficiency in the model in predicting the early time course of hydroxyitraconazole concentrations in single-dose studies.

Simulations. (i) Food effects.

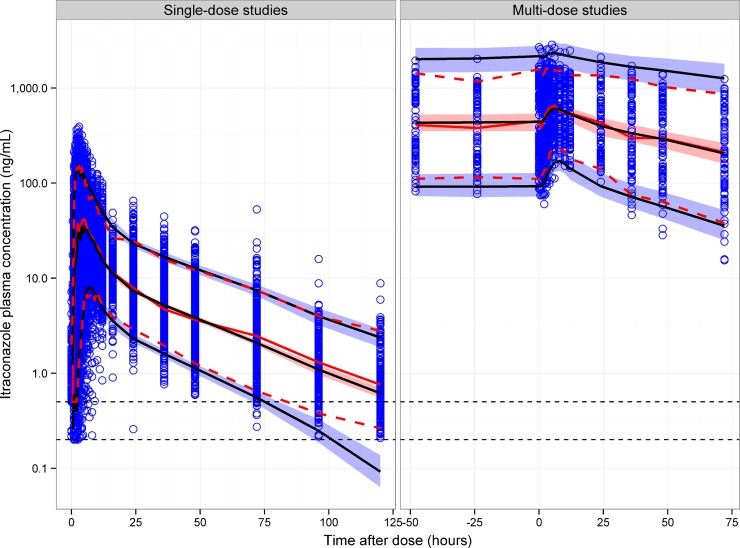
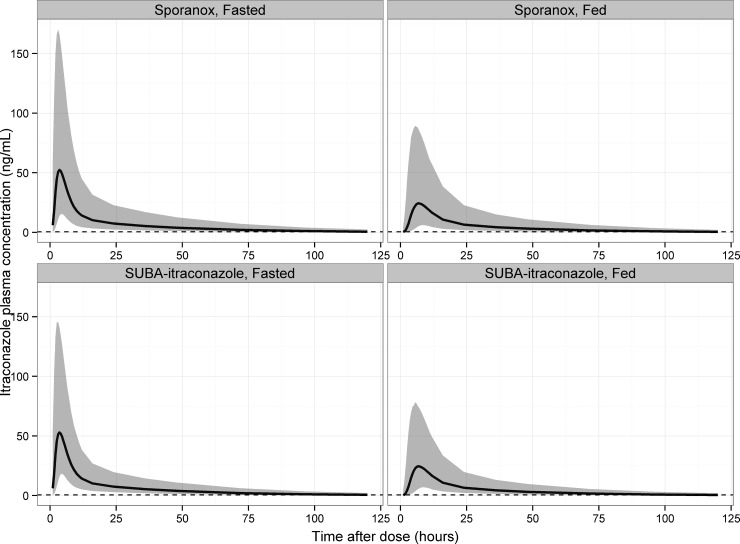
The effect of fed status on model-predicted itraconazole concentrations using single-dose studies as an example is shown in Fig. 7, and the effect on model-predicted NCA metrics is summarized in Table 5. The population effect of food was to decrease the AUC_0–∞ of itraconazole to 78 to 81% of that in the fasted state, to decrease the C_max to 62 to 65% of that in the fasted state, and to increase T_max to 177 to 184% of that in the fasted state. The effect of fed status on itraconazole exposure was independent of formulation, other than the lower variability in exposure for SUBA-itraconazole due to the less variable relative bioavailability.

FIG 7.

Predicted food effects on itraconazole concentrations for Sporanox and SUBA-itraconazole in the fed and fasted states. The black line and gray ribbon represent the median and 90% confidence interval of model-predicted concentrations for 1,000 simulations using bioequivalent Sporanox and SUBA-itraconazole doses (100 mg of Sporanox and 58 mg SUBA-itraconazole). Simulations are based on data from study MPG009.

TABLE 5.

Model-predicted food effects on itraconazole noncompartmental analysis metrics using bioequivalent dose for Sporanox (100 mg) and SUBA-itraconazole (58 mg)

Drug	Fed/fasted state	Geometric means (90% CI) for:
		AUC0–∞ (ng/ml · h)	Cmax (ng/ml)	Tmax (h)
Sporanox	Fed	675.39 (653.22–701.53)	51.37 (50.01–53.12)	6.83 (6.72–6.92)
	Fasted	831.52 (805.94–860.94)	78.31 (75.72–80.84)	3.86 (3.76–3.94)
	Fed/fasted (%)	81.22 (77.82–84.96)	65.60 (63.08–68.76)	176.94 (172.57–182.10)
SUBA-itraconazole	Fed	653.60 (634.83–671.21)	50.23 (48.59–51.74)	6.83 (6.72–6.94)
	Fasted	833.52 (806.99–862.55)	81.18 (78.83–83.27)	3.87 (3.80–3.93)
	Fed/fasted (%)	78.41 (74.99–81.71)	61.88 (59.10–64.15)	184.33 (176.66–180.41)

(ii) Power analysis.

While the final model suggested that a 58-mg (95% CI, 52.6 to 64.0 mg) SUBA-itraconazole dose was expected to have the same exposure by AUC as 100 mg of Sporanox, the predicted performance of the marketed 50-mg tablet in bioequivalence studies is of interest, as it provides some insight into the difficulties of establishing bioequivalence for a drug with varied kinetics and a pronounced food effect. The percentages of bioequivalence studies for 50 mg of SUBA-itraconazole (test) compared to a reference 100 mg of Sporanox (reference) in the fed and fasted states are shown in Tables 6 and 7 for studies with 24 and 52 subjects, respectively. The comparison with the highest overall power was test/fasted versus reference/fasted, with a study size of 52 subjects (average power, 84.8% across all 3 exposure metrics), with the next highest power being test/fed versus reference/fed with a study size of 52 subjects (average power, 74.5% across all 3 exposure metrics). The reduction in study power when using 24 subjects rather than 52 was relatively small (e.g., from 84.8% to 74.1% average for test/fasted versus reference/fasted); however, as the power to find bioequivalence for all three exposure metrics concurrently is likely to be lower than the individual values (i.e., the product of the three probabilities if they are independent), the relatively small increase in power between a study with 52 rather than 24 subjects may be important in cases in which the criterion is to test bioequivalence for all three exposure metrics. Comparisons of test/fed versus reference/fasted or vice versa were characterized by low power for finding bioequivalence by C_max. However, comparisons of both fed and fasted 50-mg SUBA-itraconazole doses with a fed 100-mg Sporanox dose were adequately powered for finding bioequivalence by AUC, in keeping with the labels for SUBA-itraconazole and Sporanox. It is notable that comparisons of the fed and fasted states for the same formulation (for both AUC and C_max) generally had lower power than the comparisons of formulation, with much lower power for finding bioequivalence by C_max (<10.6%). This reinforces the important role that fed status (and presumably gastric pH) has in dictating itraconazole exposure for these formulations.

TABLE 6.

Percentage of bioequivalent studies of 50 mg of SUBA-itraconazole versus 100 mg of Sporanox in fed and fasted states

Treatmenta	% of bioequivalent studies (Gmean: 90% CI)b
	AUC0–∞	AUC0–120	Cmax
T fed/R fed	60.8 (0.88: 0.61–1.27)	71.0 (0.88: 0.69–1.13)	65.6 (0.88: 0.66–1.184)
T fasted/R fed	67.8 (1.08: 0.76–1.49)	74.6 (1.11: 0.86–1.43)	22.7 (1.41: 1.09–1.85)
T fed/R fasted	28.5 (0.72: 0.52–1.03)	22.3 (0.72: 0.56–0.92)	1.7 (0.57: 0.44–0.74)
T fasted/R fasted	68.3 (0.90: 0.67–1.23)	78.2 (0.91: 0.71–1.16)	75.9 (0.91: 0.70–1.16)
T fasted/T fed	48.4 (1.24: 0.91–1.67)	42.7 (1.27: 1.00–1.59)	5.3 (1.61: 1.24–2.09)
R fasted/R fed	51.2 (1.21: 0.83–1.75)	51.6 (1.23: 0.94–1.62)	10.6 (1.55:1.16–2.09)

^aT, test formulation (SUBA-itraconazole); R, reference formulation (Sporanox). A study of 24 subjects was simulated 1,000 times.

^bGmean, geometric mean of the ratios for the 1,000 studies.

TABLE 7.

Percentage of bioequivalent studies of 50 mg of SUBA-itraconazole versus 100 mg of Sporanox in fed and fasted states

Treatmenta	% of bioequivalent studies (Gmean: 90% CI)b
	AUC0–∞	AUC0–120	Cmax
T fed/R fed	67.8 (0.87: 0.67–1.10)	79.7 (0.87: 0.74–1.03)	75.9 (0.87: 0.71–1.05)
T fasted/R fed	84.1 (1.08: 0.87–1.34)	87.3 (1.11: 0.95–1.31)	13.4 (1.4: 1.18–1.67)
T fed/R fasted	22.8 (0.72: 0.567–0.91)	13.2 (0.72: 0.60–0.85)	0.0 (0.57: 0.47–0.69)
T fasted/R fasted	77.7 (0.89: 0.72–1.09)	88.6 (0.91: 0.77–1.07)	88.0 (0.92: 0.77–1.11)
T fasted/T fed	52.2 (1.24: 1.01–1.53)	40.2 (1.27: 1.10–1.48)	0.8 (1.60: 1.35–1.92)
R fasted/R fed	58.4 (1.24: 0.95–1.53)	55.1 (1.22: 1.03–1.46)	4.2 (1.53: 1.25–1.85)

^aT, test formulation (SUBA-itraconazole); R, reference formulation (Sporanox). A study of 52 subjects was simulated 1,000 times.

^bGmean, geometric mean of the ratios for the 1,000 studies.

Shiny application.

The shiny application for the final itraconazole model can be accessed at https://acp-unisa.shinyapps.io/Itraconazole_PopPK_Model/. The application allows one to simulate once- or twice-daily dosing of Sporanox or of SUBA-itraconazole in the fed or fasted state and for various doses and treatment durations. Users are required to click the “start simulation” button every time they change the slider input(s) or widget value(s). Simulated data using the selected dosing regimen can be downloaded as a *.csv file. The ADVAN-style analytical solution of the final model and the R codes for the shiny apps are provided in Appendix S3 in the supplemental material.

DISCUSSION

A population pharmacokinetic model was developed for itraconazole and hydroxyitraconazole using extensive single-dose and multidose oral data collated from seven clinical trials to compare SUBA-itraconazole with the innovator product Sporanox. The analysis was performed with a particular emphasis on capturing the differences between the two formulations and quantifying the effects of food on itraconazole absorption kinetics. To our knowledge, this paper presents the most extensive population pharmacokinetic model of itraconazole and hydroxyitraconazole in the literature and is the first paper to investigate the effects of food on the absorption of itraconazole in healthy subjects using the population approach.

The final model of itraconazole consists of a 2-compartment model with oral absorption described by 4-transit compartments. The final model used a common variability parameter on bioavailability, which allowed parameters affected by bioavailability to share a source of variability. This approach was considered to stabilize the model by accounting for an important source of correlation between affected parameters and reducing unexplained between-subject variability in the parameters (24).

Population pharmacokinetic models of itraconazole kinetics in the literature to date have used linear elimination kinetics (35–40). Linear itraconazole kinetics was also found for the model of single-dose data developed in this analysis, but this model underpredicted multidose concentrations, suggesting a deviation from the assumption of linearity outside the single-dose setting. Nonlinear kinetics of itraconazole and hydroxyitraconazole have been reported when NCA methods were used to compare single- versus multiple-dose administration or single-dose administration across a range of doses (9, 10).

Various models for an apparent decrease in clearance, an increase in bioavailability, or both were investigated to describe the accumulation kinetics of itraconazole for the multidose data. Models invoking saturable elimination or time-dependent changes in clearance and/or bioavailability were not adequate in describing itraconazole accumulation and were characterized by goodness-of-fits plots with population-predicted values substantially below the observed values for the multidose data. Lehr et al. (34) also found that saturable elimination alone was not sufficient to describe the accumulation kinetics of itraconazole when it was used as an inhibitor in a drug-drug interaction study. However, Lehr et al. (34) was able to identify a competitive inhibition model based on assumed hydroxyitraconazole concentrations and sparse itraconazole concentrations collected over approximately 1 week. For the data used in the current analysis, there were limited data to inform the time course of itraconazole/hydroxyitraconazole accumulation. All competitive inhibition models invoking an inhibitory effect of the parent drug or the metabolite on the clearance of the parent drug were characterized by unreliable minimization and were not able to adequately describe itraconazole accumulation. However, a semiempirical description of itraconazole nonlinear kinetics was achieved in the final model by allowing the clearance and bioavailability of the multidose studies to change with time based on the evidence that the rise to steady state was as described by Lehr et al. (34), in which itraconazole approaches steady state after ∼7 days of continuous administration. The equations describing the change in clearance and bioavailability (equations 6 and 7) allowed predictions of itraconazole concentrations on days other than day 15. Both equations assumed that the reference values for clearance and bioavailability were as for the single-dose studies.

The kinetics of oral itraconazole was characterized by high variability (% coefficient of variation [CV]) between dose occasions in clearance (22.1%), central volume of distribution (30.7%), transit absorption rate constant (44.8%), and bioavailability (56.4%). The high variability in itraconazole kinetics resulted in a high variability in exposure for a given dose. The effect of study population on KTR and CL/F was the only covariate (other than the effect of fed status and formulation) that was statistically significant in the final covariate analysis. Other subject-related covariates available in the data, including body size (weight), body shape (LBW), and race, were not able to explain the high variability in itraconazole kinetics. Therefore, it is most likely that this variability is related to local conditions in the gastrointestinal tract (GI), such as pH and transit time, which may affect dissolution and absorption of the drug for which subject-specific and occasion-specific data were not available. Also, there is considerable variability in CYP3A4 activity between subjects (41), which may be another major source of intersubject variability in itraconazole pharmacokinetics via its impact on clearance and first-pass metabolism.

The main difference between the SUBA-itraconazole and Sporanox formulations of itraconazole was the relative bioavailability. SUBA-itraconazole had a relative bioavailability of 173% (95% CI, 156 to 190%) compared to that of Sporanox. Thus, a 58-mg (95% CI, 52.6 to 64 mg) dose of SUBA-itraconazole would provide equivalent exposure to the marketed 100-mg Sporanox formulation. The model also supported the hypothesis that SUBA-itraconazole provides more consistent itraconazole exposure than Sporanox, as the variability in the relative bioavailability of SUBA-itraconazole was 78.7% of that of Sporanox. The solid dispersion of itraconazole in the pH-dependent polymeric matrix of SUBA-itraconazole enhances drug dissolution and targets drug release in the proximal small intestine, which is the primary site of itraconazole absorption. On the other hand, itraconazole dissolution in the Sporanox formulation is limited to the gastric environment, resulting in a supersaturated solution of the drug in the stomach. Various studies have demonstrated improved oral bioavailability of poorly water-soluble drugs via targeting of drug supersaturation to the intestinal lumen, rather than the stomach, by the use of pH-dependent carrier polymers (42–44). In one study, Kohri et al. (42) evaluated the use of a solid dispersion system with a pH-dependent polymeric carrier (hypromellose/hypromellose phthalate) to improve oral bioavailability of albendazole, a poorly water-soluble weakly basic drug with a pH solubility profile similar to that of itraconazole. In vitro dissolution tests, using a pH shift method, confirmed that the polymer maintained albendazole supersaturation following a pH shift from pH 1.2 to 6.5. In vivo studies conducted on rabbits with elevated gastric pH showed 3.2-fold improvement in the bioavailability of albendazole compared to that with a crystalline drug. The improvement in the bioavailability was attributed to the targeted supersaturation of the drug to the small intestine, which is a result of the pH-dependent release of the drug from the solid dispersion formulation. In another in vivo study conducted in rats, Miller et al. (44) demonstrated that the addition of Carbopol974P into the Eudragit L-based solid dispersion system of itraconazole exhibited a 5-fold improvement in the oral absorption compared to that of the reference formulation (44). The increase in the bioavailability was suggested to be attributed to the targeted intestinal delivery and prolonged supersaturation of itraconazole in the small intestine.

In the present analysis, food decreased the rate and extent of drug absorption, mediated by a decrease in bioavailability and a lower absorption rate compared to those of the fasted state. The observed food effects on itraconazole kinetics were irrespective of the formulation. Simulated food effects for Sporanox in this analysis are in contrast to the product label for Sporanox, which states that Sporanox should be given with food to enhance absorption (5).

The observed food effects on itraconazole are in contrast to the general trend of BCS class II drugs, which are more likely to show a positive food effect on absorption, mainly due to micellar solubilization. However, it is recognized that BCS class II drugs should not be grouped together but rather subdivided into weak acids and weak bases, with low or high pK_a, and lipophilic compounds (45). Each of these may respond differently to food effects. In fact, the majority of BCS class II drugs are weak acids/bases with high pK_a and generally show a positive food effect on absorption (45). However, BCS class II drugs with low pK_a (e.g., itraconazole and ketoconazole) may precipitate in the stomach or upper small intestine, partially due to the net increase of the gastrointestinal pH after the ingestion of meals; therefore, they may show a negative food effect. Significant luminal intestinal precipitation was observed previously for ketoconazole (a poorly water-soluble weakly dibasic drug, pK_a 2.95 and 6.51) administered as an oral solution (pH 2.7) to 12 healthy subjects at both low- and high-dose levels (46). Precipitation of the dissolved drug was also suggested by Carver et al. (47), further to the reduced dissolution, as a potential mechanism for the reduced bioavailability of indinavir (a poorly water-soluble weakly basic BCS class II drug; pK_a, 3.7 and 5.9) when administered to HIV-infected patients after a high-protein meal (47).

Prandial status has different effects on the absorption and bioavailability of marketed triazole antifungals. Voriconazole (pK_a, 1.7) administered with a high-fat breakfast resulted in a significant decrease in both the AUC_0–t and C_max by 35% and 22%, respectively (48). On the other hand, a high-fat meal significantly enhanced the rate and extent of posaconazole absorption (pK_a, 3.6 and 4.6) administered as an oral suspension in healthy subjects (49, 50). However, unlike itraconazole, posaconazole is mainly excreted unchanged in the feces, so the effect of food on intestinal and/or hepatic metabolism is expected to be minimal (51).

Reports in the literature of food effects on itraconazole absorption for Sporanox, using noncompartmental analysis, show substantial interstudy variability in the reported AUC values in the fed and fasted states (e.g., see references 11–14). Yun et al. (11) suggest that the variability in fasting AUC across studies might be related to the volume of fluid administered with the dose. In addition, the dissolution of itraconazole is a function of GI pH, which is highly varied between and within subjects, even under fasted conditions (52, 53). The variability in fed AUC also appears to be a function of the acid content and fat content of the meal (11, 14). The standardized high-fat high-calorie breakfast in the present analysis behaved like the rice meal of Yun et al. (11), with lower overall simulated AUC values in the fed state than those in the fasted state (Fig. 7 and Table 5).

Various models have been investigated for modeling hydroxyitraconazole single-dose and multidose data sets, including similar models investigated for modeling the parent drug. Neither linear nor saturable elimination kinetics alone with/without time-dependent nonlinear clearance were adequate in describing the elimination kinetics of hydroxyitraconazole. Enterohepatic recycling, transit compartment models for metabolite formation, and competitive inhibition models, invoking an inhibitory effect of the parent drug and/or the metabolite (which included simultaneous fitting of parent and metabolite), on the clearance of the metabolite were characterized by unreliable minimization and were not considered further. Similarly, using mixture models of metabolite clearance in an attempt to account for the heterogeneity in CYP3A4 enzyme activity, assuming that hydroxyitraconazole underwent further metabolism by CYP3A4 enzymes, was not successful. The best hydroxyitraconazole model used mixed linear and nonlinear elimination for single-dose data and allowed a separate change in clearance for multidose studies with the passage of time by a factor that might represent changes in clearance due to enzyme inhibition (or induction). However, only the final magnitude of this change at day 15 (as opposed to its magnitude and time course) could be estimated from the available data. The final hydroxyitraconazole model gave an adequate description for multidose data; however, it underpredicted the early time course of hydroxyitraconazole in the single-dose data (Fig. 6). Nevertheless, this was the best model that can be attained from the available data, and it may indicate that the formation of the metabolite may be more complicated than can be represented using simple compartmental models.

One application of the presented model is to perform a prestudy power analysis, which is an important aspect of clinical trial design of bioequivalence studies. The presented model can be used, through simulations, to assist in sample size and dose selection to be used in the trial. However, one insight from the present analysis is that the conclusions drawn from single-dose bioequivalence studies may not fully reflect the behavior of itraconazole in clinical use due to the combined effects of low study power/high variability in kinetics, nonlinearity in accumulation kinetics, and the inherent between-subject and between-study variability in itraconazole absorption, presumably due to variability in the effects of food and gastric pH.

One limitation of the present analysis is that trials were conducted on healthy subjects, with the majority having a body mass index (BMI) in the normal range, but not on actual patients with invasive fungal diseases who may have different absorption kinetics for the drug. Therefore, it is unproven at this time whether the presented model can be used for a clinical evaluation of therapeutic efficacy of the drug in patients with fungal diseases.

The model presented here is acceptable for the intended purposes of quantitating relative bioavailability, food effects, and power analysis in healthy subjects. However, we postulate that a more detailed mechanistic understanding of the influence of pH, food, and first-pass processes on the oral absorption of itraconazole will require using semiphysiological models of first-pass metabolite production (54) and the linking of in vitro dissolution profiles with in vivo kinetics (55). We are currently investigating such models.