Flexible brain network reconfiguration supporting inhibitory control

Significance

The ability to inhibit distracting stimuli from interfering with goal-directed behavior is crucial for success in most spheres of life and is disrupted across a variety of disorders. Here we show via network analysis that global brain connectivity patterns change when inhibitory demands increase, including greater communication efficiency and robustness against disruption. In addition, the connectivity pattern of regions previously identified as crucial for inhibitory control (right inferior frontal gyrus and anterior insula) become more central network hubs, whereas dorsal anterior cingulate becomes more interconnected within its local network. Findings provide a framework to elucidate and differentiate difficulties in inhibitory control in clinical groups by examining connectivity of specific global network metrics and/or critical hubs known to influence inhibitory control.

Abstract

The ability to inhibit distracting stimuli from interfering with goal-directed behavior is crucial for success in most spheres of life. Despite an abundance of studies examining regional brain activation, knowledge of the brain networks involved in inhibitory control remains quite limited. To address this critical gap, we applied graph theory tools to functional magnetic resonance imaging data collected while a large sample of adults (n = 101) performed a color-word Stroop task. Higher demand for inhibitory control was associated with restructuring of the global network into a configuration that was more optimized for specialized processing (functional segregation), more efficient at communicating the output of such processing across the network (functional integration), and more resilient to potential interruption (resilience). In addition, there were regional changes with right inferior frontal sulcus and right anterior insula occupying more central positions as network hubs, and dorsal anterior cingulate cortex becoming more tightly coupled with its regional subnetwork. Given the crucial role of inhibitory control in goal-directed behavior, present findings identifying functional network organization supporting inhibitory control have the potential to provide additional insights into how inhibitory control may break down in a wide variety of individuals with neurological or psychiatric difficulties.

The ability to exert cognitive control to inhibit distracting stimuli from interfering with goal-directed behavior is crucial for success in most spheres of life, including academic, occupational, health, and general well-being (1). However, such control is impaired under certain conditions in both psychologically/neurologically typical individuals [e.g., overeating during stressful periods (2)] and those with pathological conditions [e.g., addiction (3)]. Consequently, understanding the neural circuitry supporting inhibitory aspects of cognitive control has the potential to provide key insights into a wide array of difficulties, ranging from common activities of daily life to psychiatric disorders.

Substantial uncertainty remains regarding the neurobiology supporting inhibitory aspects of cognitive control (4), with the majority of recent research focusing on which particular regions of prefrontal cortex (PFC) are important for which specific aspects of inhibitory control. A large body of research has identified a set of brain regions that appear generally crucial for inhibitory control. For example, consistent activation was identified in several critical regions in a recent meta-analysis of studies using the color-word Stroop (5), which is a classic cognitive control probe (6) and which we use in the present study. This task indexes inhibitory control, because an individual must maintain a task set in the face of irrelevant, but prepotent, information that must be inhibited. The meta-analysis revealed a number of regions, including dorsal anterior cingulate cortex (dACC), lateral PFC (e.g., BA 9/44/45/46), insula, and lateral parietal cortex (e.g., BA 39/40). A similar set of regions has been identified in a meta-analysis of studies using the Go/NoGo task (7) and a meta-analysis across a range of inhibitory control tasks (8).

Furthermore, recent evidence suggests that PFC connectivity [e.g., assessed by integrity of white matter connections to PFC (9)] is crucial for successful inhibitory control. Indeed, most models of the brain networks supporting inhibitory control assume that regions of PFC exert control by modulating activity in more distant and often posterior regions (e.g., refs. 10–12). Furthermore, some (e.g., refs. 13–15) have argued that modulatory processes between key PFC regions (e.g., dorsolateral PFC, dACC) are critical for inhibitory control. Despite this large body of theoretical and empirical work, there remains a dearth of research as to how such modulatory processes are instantiated in functional brain networks. Although a small set of studies has examined connectivity patterns associated with inhibitory control, no study to date has elucidated the manner in which brain networks may functionally reconfigure to support such control. To adapt to new control demands, it is necessary to up-regulate brain networks needed to meet the demands of the current environment and down-regulate networks that may hinder meeting these demands. Hence, dynamic shifts should occur in overall functional network organization in response to contextual change, but the nature of these shifts remains unknown. For example, brain networks might shift into a configuration with more efficient intercommunication between functionally diverse regions, or particular regions might take on a more prominent role. Given that networks are a fundamental unit of brain organization (16, 17), an in-depth characterization of network reconfiguration is a crucial step in building a comprehensive understanding of the neural circuitry supporting inhibitory control.

Extant studies of connectivity in inhibitory control can be grouped into two sets with regard to the methodology used. In all cases, there is a comparison between conditions that differ with respect to the level of inhibitory control required (e.g., when conflicting information is presented vs. when all information is consistent). The first set of studies used independent components analysis (ICA) or similar techniques (18–20). In these studies, sets of voxels with similar time courses were identified, reducing the multivariate dataset into “components.” Next, the mean time course of each component was correlated with task condition or the difference between conditions to determine how strongly that component tracked the task. This technique is useful, because the identification of the network of regions engaged in the task is relatively unconstrained. However, because this approach identifies “networks” as a whole, it cannot shed light on whether a particular connection between two nodes (i.e., brain regions) varies with inhibitory control demand. Rather, inferences can be made only about the mean time course of all regions in a given component. Furthermore, the studies discussed above did not test whether connection strength differed by condition, which is necessary to infer that the connection itself is recruited to meet inhibitory control demand. Even had they done so, the validity of such approaches has been questioned (21). In summary, the methods used in these studies could indicate only that a particular component is (de)activating concurrently with the task.

The second set of studies used psychophysiological interaction (PPI) analysis (22–28). In these studies, one to three “seed” regions were chosen a priori, and clusters of voxels elsewhere were identified in which the correlation between the time courses of the seed and cluster differed significantly by condition. This approach has advantages over ICA-related methods, because (i) it directly tests whether connection strength itself depends on task condition; and (ii) each connection is tested separately. However, PPI is strictly constrained by the choice of a priori seed regions (i.e., only connectivity with seed clusters is examined). Thus, important connections can be missed, and this oversight is particularly likely to occur when only a small number of seed clusters are examined, as is the case in the existing studies of inhibitory control networks.

Of greatest importance is that neither approach provides insight into whether engaging inhibitory control is associated with dynamic restructuring in the functional organization of the network. Thus, a comprehensive understanding of the particular network connections crucial for inhibitory control, and the manner in which networks reorganize to support such control, remains unknown. Addressing this issue is the focus of the present study.

Recent methodological advances—in particular, graph theory (29)—allow for analysis of brain networks at a level of complexity not possible in previous work, including characterization of network functional organization. Graph theory can identify clusters of network connections in which the strength of each connection varies with the demand for inhibitory control, and this identification is accomplished without selecting a specific subset of seed regions a priori. In addition, graph theory can test whether inhibitory control demands lead to shifts in key topological properties (indices of network organization) of the global network, subnetworks, and the function of nodes within local and global networks (29). Categories of topological properties include: functional segregation, how optimized the network is for specialized processing; functional integration, how well the network can combine specialized information across distributed regions; centrality, how well a particular node facilitates network intercommunication; and resilience, the vulnerability of the network to disruption (29). Thus, examining graph theory properties under varying levels of inhibitory control can help to delineate the manner in which brain networks reorganize to exert inhibitory control.

To address these critical gaps, we applied graph theory to functional magnetic resonance imaging (fMRI) data collected while a large sample of adults (n = 101) performed the color-word Stroop. We first identified clusters of interregional coupling in which connection strength differed with inhibitory control demand (e.g., incongruent vs. congruent task condition). Next, we computed graph-theory properties for both the global network and key network hubs. We then tested whether graph properties differed with inhibitory control demand. To elucidate the behavioral impact of network shifts, significant network measures were correlated with performance [reaction time (RT) and errors].

Based on evidence that PFC is critical for top-down control, we hypothesized that PFC regions would emerge as prominent within both global and local networks. In particular, we predicted that lateral PFC regions (e.g., BA 9/46) would show increased connectivity with dACC and lateral parietal cortex when demand for inhibitory control was greater, based on prior work by our group suggesting such relationships (30). In addition, computational models suggest that a critical component of inhibitory control is up-regulating the strength of the desired response [vs. solely inhibiting processing related to inappropriate responses (31)]. This up-regulation may occur when global network communication becomes more efficient, increasing the influence of PFC control regions over more distal motor regions. Thus, we also predicted that inhibitory control would be associated with restructuring in the global network into a configuration characterized by more efficient communication (functional integration).

Results

Inhibitory Control-Related Network Connections.

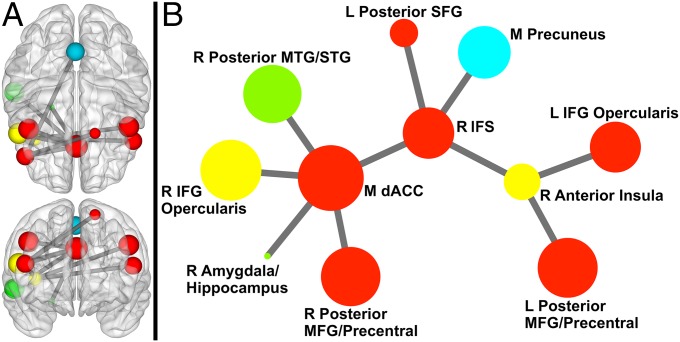
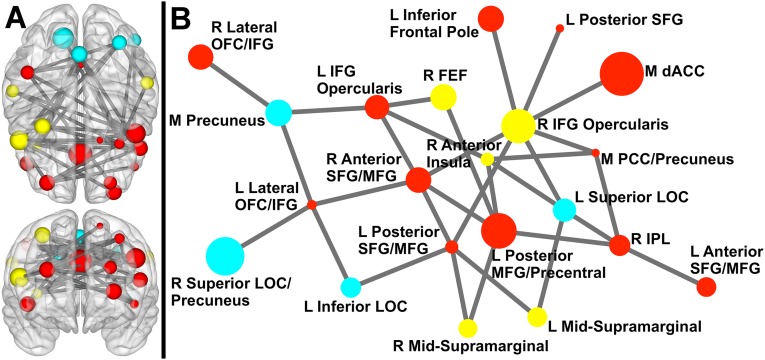
The Network Based Statistic (NBS) toolbox (32) was used to identify specific network connections that varied with demand for inhibitory control. Higher demand for inhibitory control (incongruent > congruent) was associated with stronger coupling in a network (11 nodes, 10 links; corrected P < 0.001) centered on medial dACC, right inferior frontal sulcus (IFS; BA46), and right anterior insula (AI). As shown in Fig. 1, more than half of the nodes in the network were prefrontal. Fig. 2 shows connection strengths for the relevant links by condition. See SI Results for analyses of incongruent vs. neutral.

Fig. 1.

Network exhibiting greater coupling when demand for inhibitory control is high compared with low. (A) Sphere color represents module membership; sphere size reflects node strength (across incongruent and congruent). Upper is a 3D axial view from above the brain; Lower is a 3D coronal view from anterior to the brain (to maintain the right side of the brain on the right side of the image for both views, posterior is positioned on top for the axial view). Sphere placement reflects the center of mass node location. (B) Circle color represents module membership; circle size reflects node strength. This representation was created via Kamada– Kawai spring embedder algorithm. Only links (and corresponding nodes) identified in NBS analyses are shown above. IFG, inferior frontal gyrus; L, left; M, medial; MFG, middle frontal gyrus; MTG, middle temporal gyrus; R, right; SFG, superior frontal gyrus; STG, superior temporal gyrus.

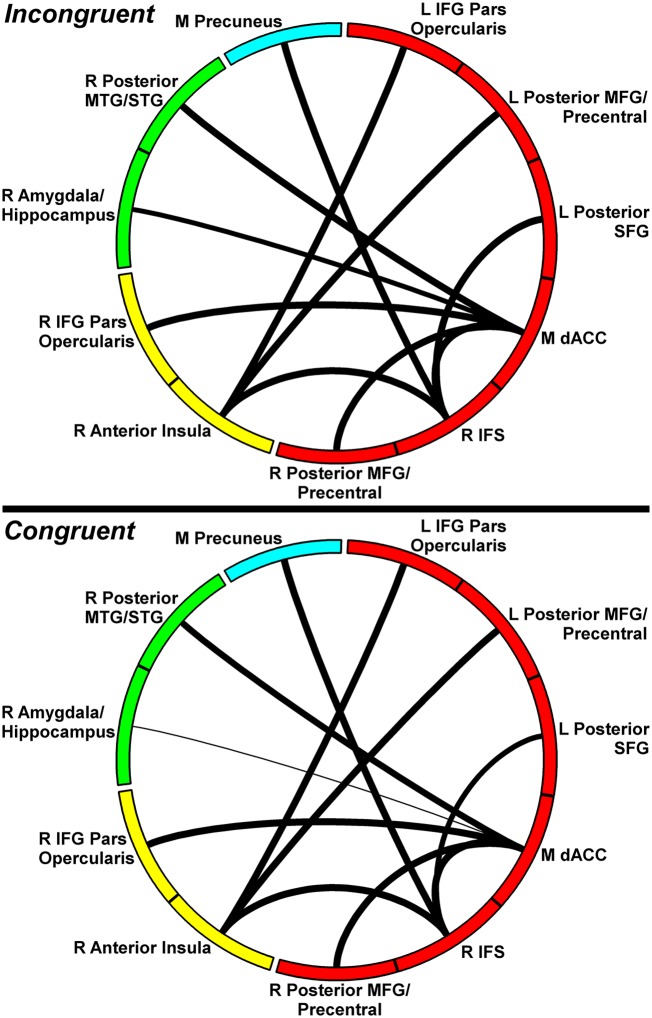
Fig. 2.

Connection strength of the inhibition-related network by condition. Circle segment color reflects module, and connection width reflects connection strength. Upper corresponds to incongruent condition; Lower corresponds to congruent. Only links (and corresponding nodes) identified in NBS analyses are shown above. IFG, inferior frontal gyrus; L, left; M, medial; MFG, middle frontal gyrus; MTG, middle temporal gyrus; R, right; SFG, superior frontal gyrus; STG, superior temporal gyrus.

Inhibitory Control-Related Graph Theory Properties.

The Graph Theoretic GLM (GTG) toolbox (33) was used to identify properties that varied with inhibitory control demands. Local efficiency and transitivity indexed functional segregation; global efficiency indexed functional integration; node strength, participation coefficient, and within-module degree Z-score indexed distinct aspects of centrality; and assortativity and local assortativity indexed resilience. Three measures reflect a property of the global network (i.e., including all nodes in the brain): assortativity, the extent to which highly connected nodes are linked to other highly connected nodes; global efficiency, the efficiency of global network communication (i.e., the extent to which nodes are connected to each other through the fewest possible number of nodes); and transitivity, the amount of clustering present in the network (i.e., the extent to which neighbors of a node also connect to each other). Condition-related differences in global properties reflect overall network restructuring. Five measures reflect a property of an individual node: local efficiency, the efficiency of communication in the local subnetwork (nodes connected to that specific node); node strength, the overall influence of a node on the network; local assortativity, the extent to which a node is connected to nodes with a similar influence on the network (i.e., whether a node is highly connected to nodes with similar vs. stronger or weaker node strength); participation coefficient, the extent to which a node is connected to nodes in different modules; and within-module degree Z-score, the extent to which a node is connected to other nodes within its own module. Modules are sets of nodes having more within- than between-module coupling. Node-specific properties were examined only for dACC, right IFS, and right AI, because these nodes exhibited greater than or equal to three connections that differed significantly across task condition in the NBS analysis. Multiple-comparison-corrected P values are in brackets.

Higher demand for inhibitory control was associated with increases in all network-wide properties: transitivity (P = 0.002 [0.015]), global efficiency (P = 0.003 [0.024]), and assortativity (P < 0.001 [0.002]). Higher transitivity is often associated with greater functional specialization, whereas greater global efficiency indicates more efficient overall network communication, and higher assortativity suggests that the network is more resilient to disruption (34, 35).

For all regions of interest (ROIs) examined, higher demand for inhibitory control was related to increases in node strength (dACC, P < 0.001 [<0.001]; right IFS, P < 0.001 [0.004]; right AI, P < 0.001 [<0.001]) and local efficiency (dACC, P < 0.001 [<0.001]; right IFS, P < 0.001 [0.011]; right AI, P < 0.001 [<0.001]). Thus, each node had a greater overall impact on network processing when the environment required stronger inhibitory control (node strength), and, at the same time, the network of connections surrounding each node also became more tightly clustered together (local efficiency).

Higher demand for inhibitory control was also linked to higher participation coefficient for right IFS (P = 0.004 [0.034]) and right AI (P = 0.003 [0.008]) (dACC, P > 0.9). This finding suggests that engagement of inhibitory control leads these nodes to connect with a greater diversity of functional modules, which may reflect a stronger influence on more diverse types of processes. Higher demand for inhibitory control was associated with stronger within-module degree Z-score for only medial dACC (P < 0.001 [<0.001]) (IFS and AI, P > 0.9). This finding indicates that dACC became more tightly interconnected with nodes in the same module when stronger inhibitory control was needed, suggesting that dACC had a greater influence on the specific processes occurring within this module. Finally, higher demand for inhibitory control was associated with stronger local assortativity for only right AI (P = 0.002 [0.009]) (IFS and AI, P > 0.8). Given the concurrent increase in node strength, this result suggests that greater demand for inhibitory control led right AI to become more tightly coupled with other high-influence nodes and relatively less coupled with low-influence regions. See SI Results for similar analyses for incongruent vs. neutral.

Relationship with Individual Differences in Behavior.

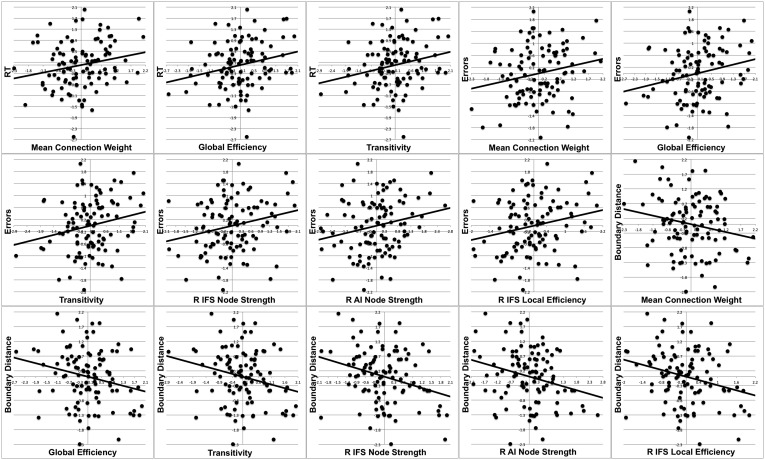
Several network parameters correlated positively with (incongruent vs. congruent) RT: mean NBS network connection strength (r = 0.214, P = 0.039), global efficiency (r = 0.243, P = 0.019), and transitivity (r = 0.235, P = 0.023). Similarly, several network parameters correlated with incongruent vs. congruent error rate: mean NBS network connection strength (r = 0.212, P = 0.041), global efficiency (r = 0.223, P = 0.032), transitivity (r = 0.216, P = 0.037), right IFS node strength (r = 0.234, P = 0.024), right AI node strength (r = 0.221, P = 0.033), and right IFS local efficiency (r = 0.228, P = 0.028). See SI Results for analyses using drift diffusion model parameters.

Regional Task Activation.

To provide a context for network analyses, we also ran a typical general linear model (GLM) analysis to determine which regions showed greater regional task activation (Supporting Information). Details regarding overlap and relationships with behavior are in SI Results. Briefly, increased activation was found for incongruent > congruent in regions that also emerged in network analyses (e.g., dACC) and regions that did not (e.g., thalamus).

Discussion

The goal of the present study was to identify and better understand the manner in which functional brain networks adapt to support the ability to inhibit distracting stimuli from interfering with goal-directed behavior. Using graph theory to analyze data from a color-word Stroop task, we provide a novel characterization of the manner in which brain networks functionally restructure to support inhibitory control. First, we identified a network of nodes that exhibited greater interconnectivity during periods of higher demand for inhibitory control (Figs. 1 and 2). Prefrontal regions dominated this network, with medial dACC, right IFS, and right AI occupying central positions as network hubs (regions essential for network interconnectivity). In addition, we identified several ways in which global network organization shifted to meet demand for inhibitory control (i.e., increased transitivity, global efficiency, and assortativity). Observed network shifts significantly predicted behavior (RT/accuracy), underscoring the functional importance of network restructuring.

Reorganization in the Global Network.

A number of network metrics indicated that the global network (i.e., including all 114 nodes, not limited to nodes found in NBS analyses) exhibited significant restructuring when demand for inhibitory control was higher (i.e., network connectivity shifted into a configuration with different topological features). First, increased assortativity was observed, which indicates that nodes with high levels of connectivity (i.e., influence) tend to be coupled with other highly connected nodes, and nodes with little influence tend to be coupled with similarly low-influence nodes. This pattern is commonly observed in networks that are resilient to disruption (e.g., removal of nodes), because the core of highly influential nodes provides redundancy (35). Second, increases in global efficiency were observed, which indicates that the overall efficiency of communication (i.e., functional integration) was greater during periods of higher demand for inhibitory control. Thus, increased inhibitory control was linked to a pattern often observed in networks able to optimally integrate their processing. At the same time, we observed increased transitivity. Transitivity reflects the extent to which nodes form tightly clustered groupings (i.e., functional segregation), and higher transitivity is often associated with greater functional specialization (34). Together, increased global efficiency and transitivity indicate that increased inhibitory control is associated with a global network that allows the products of different types of specialized processing to be integrated (29). The combination of both high segregation and integration is found in diverse types of networks (e.g., social, power grids) and has been termed a “small world” organization (36). A small world is thought to be an optimal configuration, because networks of this type tend to show greater computational power, low wiring cost, efficient parallel processing, and rapid adaptive reconfiguration (36).

Examination of individual differences in behavior revealed that inhibition-related increases in both transitivity and global efficiency were related to longer RT and more errors. One potential interpretation of these findings is that, counterintuitively, greater transitivity and global efficiency are in fact detrimental to performance. Alternatively, it is also possible that greater clustering and more efficient communication in the global network are critical for inhibitory control, and those individuals for whom the task is more difficult must engage these network shifts to a greater extent.

Although far from definitive, two pieces of evidence are in favor of the second interpretation. First, transitivity and global efficiency were higher in the incongruent condition across all participants, indicating that these forms of network restructuring occur generally in response to greater demand for inhibitory control. It would be counterproductive for this reorganization to occur if higher transitivity and global efficiency were in fact detrimental. Second, individuals who had greater activation (observed in the regional task analyses) in bilateral dorsolateral PFC (dlPFC) also produced more errors under the high-demand condition. Although this finding could be similarly interpreted as dlPFC activation being detrimental to inhibitory control, we know from past lesion work (37) that dlPFC is crucial for such control.

In summary, measures of global network organization suggest that greater demand for inhibitory control is associated with network restructuring into a more efficient and resilient configuration. These findings provide novel insights into the neural circuitry supporting inhibitory control, because, to our knowledge, this work is the first study to (i) show that shifts in the global network are crucial for such control; and (ii) characterize the particular patterns of global network restructuring that occur.

Putative Inhibitory Control Network Hubs.

Medial dACC, right IFS, and right AI appear to serve as key network hubs, as evidenced by the large number of differential links associated with each node and the observed increases in node strength and local efficiency when inhibitory demand was greater. Higher node strength indicates that these nodes had a greater influence on general network processing (i.e., not limited to the specific subnetwork observed in the NBS analyses). Greater local efficiency indicates that the nodes connected to these putative hubs also became more tightly clustered together (i.e., interconnected with each other). Thus, higher demand for inhibitory control appears to lead to increased efficiency in the subnetworks surrounding these hubs, which may reflect greater specialized processing within these subnetworks. Although past research and theory would predict greater node strength (i.e., that these regions become more influential on the network), the concurrent increase in local efficiency is a novel finding. Specifically, this finding indicates that reorganization of connectivity patterns around these key hubs is crucial for inhibitory control, beyond connectivity with the hubs themselves.

Unlike node strength and local efficiency, only dACC evidenced greater within-module degree Z-score when stronger inhibitory control was required. This finding indicates that dACC became more tightly interconnected with nodes in the same module, which is consistent with evidence suggesting that dACC plays a prominent role in determining whether an error has been made and subsequent engagement of lateral PFC regions (part of the same module) to exert stronger top-down control (13, 30, 38). Present findings are also in line with the cascade of control model, in which dACC plays a role in late-stage aspects of control (control not previously imposed by lateral PFC) (13, 30).

The role of right IFS [encompassing parts of nearby inferior frontal gyrus (IFG)/middle frontal gyrus (MFG)] as a hub in the identified network is consistent with proposals that right IFG serves as a context-general “brake” (39). For example, lesions to right IFG impair inhibitory control, as does transcranial magnetic stimulation (40). This proposal is also supported by our finding of increased right IFS participation coefficient, which indicates that engaging inhibitory control leads right IFS to connect with a greater diversity of functional modules. Thus, the influence of right IFS on functionally different processes appears to be broader in contexts requiring inhibitory control. Behavioral findings further support the central role of right IFS in inhibitory control, given significant associations between accuracy and right IFS node strength and local efficiency.

Similar to right IFS, right AI also evidenced increased participation coefficient, which may reflect a stronger influence of AI on more diverse types of processes. This finding is consistent with evidence suggesting that right AI influences brain network reorganization to support attention to—and further processing of—salient events by bringing cognitive control networks online and disengaging the default mode network (41). Interestingly, the particular right AI ROI identified in the present work corresponds to what has been labeled dorsal AI (42), which tends to coactivate with fronto-parietal association cortex, as opposed to ventral AI, which is thought to be more relevant for affective processes (43). Evidence also suggests that AI influences dynamic switching between networks involved in internally (e.g., posterior cingulate) and externally (e.g., dorsolateral PFC) directed action, based on current needs (43). Thus, our finding of increased right AI participation coefficient provides support for the role of this region in adjusting network balance in accordance with which information is currently salient.

Finally, only right AI was associated with greater local assortativity, further underscoring the crucial and potentially unique role for this region in inhibitory control. Combined with the observed increase in right AI node strength, this finding indicates that inhibitory control is associated with preferential connectivity between right AI and other highly influential nodes. Thus, right AI may orchestrate switches between different functional networks by signaling highly connected hubs to bring their module online or to down-regulate, depending on current needs.

Comparison with Neutral Baseline.

Several differences emerged when using the neutral condition as a baseline. As evident in Supporting Information, the network is larger and more bilateral; medial dACC is no longer central (although it is present); and a different region of IFG is central [pars opercularis vs. IFS (anterior to pars opercularis)]. These differences must be interpreted in the context of the different processes occurring during each condition (13, 44). For example, there are two streams of color information (word meaning and ink color) that must be disambiguated in both congruent and incongruent (but not neutral). In addition, there is direct conflict between the two streams of color information (only) in incongruent, which requires top-down inhibitory control. Thus, contrasting incongruent to congruent isolates top-down inhibitory control, whereas the network observed when contrasting against neutral also reflects disambiguation of color information, and this result is reflected in the fact that a wider set of circuitry is engaged.

The fact that using congruent as a baseline isolates inhibitory control to a greater degree than when using neutral provides insight into why medial dACC is no longer prominent, given the key role of this region in regulating response conflict and late-stage selection (13). One possible reason for why right IFG pars opercularis (IFGpo) emerges as central when using neutral as a baseline is that this contrast also includes disambiguation of the two streams of color-related information. Thus, this network also reflects processing related to regulating color-related word meaning in general (aside from conflict per se), hence the more central role of right IFGpo, which has been implicated as a context-general “brake” (39). In summary, the incongruent vs. neutral contrast revealed a broader network, likely reflecting the additional processing isolated in this contrast.

Relation to Task-Activated Regions.

The set of network nodes found in the network analyses substantially overlapped the set of regions found in regional task activation analyses (Supporting Information). However, the sets of regions emerging from the two analyses were not identical, with nodes such as amygdala/hippocampus emerging in network, but not regional task, analyses, underscoring the need for both techniques. More importantly, even had there been complete overlap in the two sets, network analyses provided a wealth of information not available otherwise. For example, network analyses offer insight into which nodes functionally interact to support inhibition, as opposed to simply activating during approximately the same period. Furthermore, network analyses identified medial dACC, right IFS, and right AI as critical network hubs, and this importance is not necessarily reflected in indices of regional task analysis (e.g., cluster size). Finally, network findings provide insights into the manner in which the organizational properties of both the global network and identified hubs shifted to support inhibitory control. Analysis of regional task activation alone cannot provide any insight into these processes, supporting the necessity to assay brain networks, particularly via sophisticated analysis techniques such as graph theory. Thus, the network analyses conducted in the present study provide unique insights into the functional organization of brain circuitry supporting inhibitory control.

Strengths and Limitations.

The present study benefited from a number of strengths, including a large sample size (n = 101) and a methodology that allowed brain networks to be explored with a high level of sophistication. As with any study, several limitations must be considered when making inferences about present findings. For example, although the color-word Stroop powerfully recruits inhibitory control, the version used in the present study cannot differentiate among the component subprocesses (e.g., imposing a task set, differentiating between two potentially relevant streams of information, response selection, and evaluation). Future research using more sophisticated paradigms is needed to parse the network components specific to these subprocesses. In addition, the temporal resolution of fMRI is relatively slow, both in terms of sampling rate and the hemodynamic response (HDR). Recent advances in fMRI acquisition (e.g., multiband) can dramatically increase sampling rate (e.g., from 2 down to 0.4 s), and the use of such acquisitions to probe inhibitory control networks would likely be of great utility. However, these acquisitions are still limited by HDR. Thus, obtaining the most accurate representation of these networks will likely require the combination of fMRI with methods such as EEG/magnetoencephalography that possess exquisite temporal resolution. Finally, two of the graph properties examined (participation coefficient and within-module degree Z-score) relied on a division of nodes into several modules. Thus, bias may have been introduced into findings related to these properties by any error in the assignment of nodes into modules.

Summary and Conclusions

Despite these limitations, present findings provide critical insights into the network connections that are particularly crucial for inhibitory control and the manner in which brain networks reorganize to support such control. To meet demand for inhibitory control, the global brain network appears to reorganize to become more optimized for specialized processing, more efficient at communicating the output of such processing across the network, and more resilient to potential interruption. In addition, dACC, right IFS, and right AI appear to be particularly important hubs in the network instantiating inhibitory control. In addition, findings provide preliminary evidence for specific roles for each hub in inhibitory control. In particular, in response to higher demand for inhibitory control, dACC preferentially increased connectivity with other regions involved in top-down control, which may indicate that dACC martials control resources when necessary. In contrast, increased control demand led right IFS to increase connectivity with regions involved in functionally diverse processes, suggesting that this region more directly influences response-related processes. Finally, right AI preferentially linked to other highly influential nodes in response to higher demand for inhibitory control, suggesting that right AI orchestrates the up-/down-regulation of different functional networks by signaling communication hubs in these networks.

Although present findings do not have direct clinical implications, they do provide a framework for deeper insight into the particular network dysfunction occurring in populations with known inhibitory difficulties [e.g., attention-deficit/hyperactivity disorder (ADHD)]. For example, present findings indicate that the global network reorganizes into a pattern with greater global efficiency, transitivity, and assortativity to support inhibitory control, and future research could examine these properties in individuals with ADHD. If only a subset of properties is disrupted, this finding would provide insight into the particular mechanisms that are failing. For example, global efficiency and transitivity might increase with higher demand for inhibitory control, but assortativity is unaltered. Such a pattern would suggest that overall communication and specialized processing are intact, but that there is a failure to create processing redundancy, leaving the system less resistant to potential disruption (e.g., by distracting stimuli). In summary, given the crucial role of inhibitory control in goal-directed behavior, present findings have the potential to provide key insights into a wide array of difficulties.

Materials and Methods

First-Level Processing.

Final sample size was 101 (63% female, mean age = 34.2 y, range 19–51 y). See SI Materials and Methods for details regarding the sample, task design, MRI acquisition and preprocessing, and creation of connectivity matrices.

Identification of Inhibitory Control-Related Network Connections.

To identify network connections that varied with the demand for inhibitory control, connectivity matrices were entered as repeated-measures dependent variables into the NBS toolbox, with task condition (e.g., incongruent vs. congruent) as the repeated measure. An individual-connection-level threshold of t = 3.4 was used with extent-based correction for multiple comparisons, 5,000 permutations, and an overall corrected α < 0.05.

Identification of Inhibitory Control-Related Graph Theory Properties.

To identify topological properties that varied with inhibitory control demands, connectivity matrices were entered into the GTG toolbox (www.nitrc.org/projects/metalab_gtg), which computed properties for each condition/participant by using the Brain Connectivity Toolbox (29). Seven graph-theory properties were computed separately for each task condition by using matrices thresholded to include only positive connections (see SI Materials and Methods for follow-up analyses to rule out bias due to this threshold and detail on modularity assignment).

Node-specific properties were examined only for nodes with greater than or equal to three differential connections. Each graph property was entered as a repeated-measure dependent variable into the GTG toolbox, with task condition (e.g., incongruent vs. congruent) as the repeated measure. Significance was determined via permutation tests (5,000 permutations). In addition, permutation-based correction (10,000 permutations) was used to correct for multiple comparisons across all graph property analyses, which provided a very high (but valid) bar for significance. Only significant analyses are reported. One participant’s assortativity value was an outlier (>4 SD) and winsorized to the 2.5 SD value.

Relationships with Behavior.

To elucidate the behavioral impact of network shifts, significant network measures were correlated with behavioral measures (mean RT and error rate). Condition difference scores were created, and partial correlations were computed between network and behavioral measures, removing the variance associated with age and block counterbalancing order (see SI Materials and Methods for details).

Regional Task-Activation.

To provide context for network analyses, we ran a typical GLM analysis to determine which regions showed greater regional task activation in incongruent than congruent (SI Materials and Methods). Partial correlations were computed with behavior.

SI Materials and Methods

Participants.

A total of 120 participants were recruited from the community. Exclusion criteria were as follows: claustrophobia, left-handedness, prior serious brain injury, abnormal hearing/vision, metal in body, pregnancy, and nonnative English. Data from 19 participants were not used because of movement ≥3.3 mm relative to the middle volume or ≥2 mm relative to the previous volume, ≥15% task errors, significant signal loss due to susceptibility artifact, and/or serious motion-related activation patterns. The final sample size was 101 (63% female, mean age = 34.2 y, range 19–51 y).

Color-Word Stroop Task.

A total of 256 trials were presented in 16 blocks (4 congruent, 4 incongruent, and 8 neutral), with a variable intertrial interval (2,000 ± 225 ms). Additional neutral trials were intermixed 50:50 in congruent and incongruent blocks to prevent the development of word-reading strategies. Each trial consisted of one word presented in one of four ink colors, with each color occurring equally often with each word type. Word meaning was the same as ink color in congruent trials (e.g., “RED” in red ink), whereas word meaning differed from ink color in incongruent trials (e.g., “GREEN” in red ink), and the two were unrelated in neutral trials (e.g., “LOT” in red ink). Task condition alternated by block, and order was counterbalanced.

Acquisition.

fMRI data were 370 EPI images (duration = 12.33 min, repetition time = 2,000 ms, echo time = 25 ms, flip angle = 80°, field of view = 220 cm), each consisting of 38 axial slices (slice thickness = 3 mm, 0.3 mm gap, resolution = 3.4375 × 3.4375 mm), acquired on a Siemens 3T Trio scanner, along with a 1-mm³ anatomical acquisition.

Preprocessing.

Data were preprocessed primarily via the GTG toolbox. Data were motion-corrected, field map-corrected (via FSL’s Fugue), despiked (via AFNI’s 3dDespike), and second-order detrended, and each participant’s mean global, ventricular, and white-matter signals were partialled out, along with estimated motion parameters. To ensure that task effects were not artificially inflating connectivity estimates, analyses were recomputed after first partialling condition-related responses from the full time series (after preprocessing, but before deconvolution). The resultant connectivity estimates were virtually identical, and all findings remained significant.

Creation of Connectivity Matrices.

A 130 ROI atlas was used [created by Craddock et al. (45) via two-level spatially constrained spectral clustering]. ROIs in cerebellum (n = 16) were removed, due to inconsistent spatial coverage of cerebellum during acquisition. Time series for each ROI were extracted by calculating the mean (across voxels) signal per time point. Each time series was deconvolved for the HDR via SPM’s method. Time series were divided by block; blocks were concatenated by condition; and a 114 × 114 Pearson correlation matrix was created for each participant separately for each condition.

Follow-Up Analyses to Rule Out Bias due to Atlas Choice.

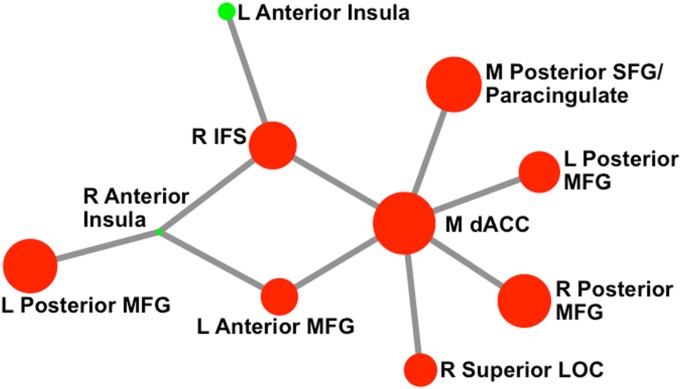
To ensure that our choice of atlas did not bias findings, analyses were recomputed by using a Craddock et al. atlas with 50% more ROIs (total number of ROIs = 171 after cerebellum removal). A similar network was observed in the NBS analyses (Fig. S1). In addition, all graph property findings were significant using this new atlas.

Fig. S1.

Network that emerged for the 171 node atlas. Circle color represents module membership, and circle size reflects node strength (across conditions). This network representation was created by using the Kamada–Kawai spring embedder algorithm. Only links (and the corresponding nodes) that were identified in the NBS analyses as differing significantly by condition are shown above. M, medial; R, right; L, left; LOC, lateral occipital cortex.

Follow-Up Analyses to Rule Out Bias due to Thresholding to Include Only Positive Weights.

To ensure that the use of only a single threshold (to include only positive weights) did not bias findings, graph properties were recomputed across a series of density thresholds by using the GTG toolbox. A minimum density of 0.23 was chosen, because this value was the lowest threshold at which all nodes remained (at least indirectly) connected in a set of mean matrices (mean across participants within each condition and mean across conditions). A maximum density of 0.60 was used along with a step size between densities of 0.01, resulting in 38 density thresholds examined. Graph properties were calculated for each threshold, and the area under the curve was computed to create one value per property. This procedure (using series of densities) was used to ensure that findings were not biased by the choice of a single, arbitrary threshold. Importantly, all analyses remained significant when using this alternate set of graph properties.

Modularity Assignment.

Modularity was computed on the mean network by using the Louvain algorithm followed by the Kernighan–Lin fine-tuning algorithm (10,000 repetitions, modularization with the highest modularity chosen; see Table S1 for module structure). Given that a condition with higher overall connectivity (e.g., incongruent) could bias module assignment, we computed modularity using data from the neutral condition.

Table S1.

Module membership

Module	Constituent nodes
1	R IFGpo; L & R frontal eye field; L posterior insula/putamen; M mid-cingulate; L & R precentral; R postcentral/precentral; L precentral/superior temporal gyrus; L & R postcentral/superior parietal lobule (×2); R superior temporal gyrus/posterior insula L & R mid-supramarginal; M precuneus; M posterior SFG/MFG; L & R AI; R putamen/globus pallidum; M paracentral (×2); L & R precentral/postcentral; L postcentral; R postcentral/precentral/superior temporal gyrus; L postcentral/inferior parietal lobule; L & R superior temporal gyrus; L & R parietal operculum
2	M anterior paracingulate/medial orbitofrontal cortex; L posterior middle orbitofrontal cortex; L superior temporal gyrus/posterior insula; L & R uncus/temporal pole; R mid-superior temporal gyrus; L mid-middle temporal gyrus; L & R posterior temporal fusiform; L & R hippocampus/amygdala; M subgenual anterior cingulate cortex/medial orbitofrontal cortex; R posterior orbitofrontal cortex/AI; L & R temporal pole/superior temporal gyrus; L & R posterior middle temporal gyrus/superior temporal gyrus; L posterior middle temporal gyrus/superior temporal gyrus; L middle temporal gyrus/superior; temporal gyrus; L lingual
3	L anterior middle orbitofrontal cortex; L & R lateral orbitofrontal cortex/IFG; L & R inferior frontal pole; M anterior SFG; L & R anterior MFG; L & R IFS; L & R mid-SFG/MFG; L posterior SFG/MFG; M pregenual anterior cingulate cortex; M mid-cingulate/posterior cingulate cortex; R superior temporal gyrus/angular; R inferior parietal lobule; L & R superior lateral occipital cortex; R middle orbitofrontal cortex; M frontal pole; R inferior frontal pole; L & R anterior SFG/MFG; M anterior paracingulate gyrus/SFG; L IFGpo; L & R posterior SFG; L & R posterior MFG/precentral; M dACC/paracingulate; M posterior cingulate cortex/precuneus; L angular/superior temporal gyrus/middle temporal gyrus; L inferior parietal lobule/superior parietal lobule; L & R caudate
4	R posterior cingulate cortex/precuneus; M precuneus; R posterior middle temporal gyrus/inferior temporal gyrus; L & R superior lateral occipital cortex (×2); L & R inferior lateral occipital cortex (×2); M cuneus/occipital pole; L occipital pole; L precuneus; R superior lateral occipital cortex/precuneus; L temporal-occipital inferior temporal gyrus; L superior lateral occipital cortex; R lingual; L & R occipital pole/lingual
5	M thalamus/brainstem; M thalamus; L & R ventral striatum; L & R thalamus

L, left; M, medial; R, right; x2, there are two ROIs within the same anatomical area.

Relationships with Behavior.

For RT and error rate, difference scores were divided by the sum of incongruent and congruent to remove individual differences in mean RT/errors. To ensure that outliers did not drive findings, data were winsorized to 2.5 SDs from the mean.

Exploratory analyses were also conducted by using drift rate and boundary distance derived from a variant of the EZ-Diffusion model (46). Drift rate is thought to reflect the ability of the participant to exhibit inhibitory control, whereas boundary distance is thought to reflect the conservativeness of the response criterion (the amount of information/confidence needed before responding). For this model, mean starting point, z, was assumed to be 0.25 instead of 0.5 to account for the fact that four response options were possible, only one of which (i.e., 0.25) was correct on a given trial. Findings revealed negative correlations between several network parameters and (incongruent vs. congruent) boundary distance: mean NBS network connection strength (r = −0.205, P = 0.048), global efficiency (r = −0.227, P = 0.029), transitivity (r = −0.227, P = 0.028), right IFS node strength (r = −0.290, P = 0.005), right AI node strength (r = −0.257, P = 0.013), right IFS local efficiency (r = −0.265, P = 0.010), and right IFS participation coefficient (r = −0.236, P = 0.023). No network parameters correlated with drift rate. See Fig. S2 for scatterplots of all relationships.

Fig. S2.

Scatterplots of brain–behavior relationships. All variables are difference scores (incongruent – congruent) and have been residualized with respect to counterbalancing order and age. R, right.

Incongruent vs. Neutral.

To ascertain whether a similar pattern of findings emerged when the neutral condition was used as a baseline instead of congruent, NBS and GTG analyses were recomputed, substituting in the neutral condition.

SI Results

Higher demand for inhibitory control (i.e., incongruent > neutral) was associated with stronger coupling in a network (order 21, size 31; Fig. S3) that overlapped the network found when congruent was used as a baseline. Node-specific topological properties were tested for the three regions examined for incongruent vs. congruent, along with right IFGpo, given that this region exhibited the largest number of differential connections when using neutral as a baseline. Similar to the analyses using congruent as a baseline, higher demand for inhibitory control (i.e., incongruent > neutral) was associated with increases in transitivity (P < 0.001 [< 0.001]) and global efficiency (P < 0.001 [< 0.001]); greater node strength for medial dACC (P < 0.001 [< 0.001]), right IFS (P < 0.001 [<. 001]), and right AI (P < 0.001 [< 0.001]); greater local efficiency for medial dACC (P < 0.001 [< 0.001]), right IFS (P < 0.001 [< 0.001]), and right AI (P < 0.001 [< 0.001]); stronger within-module degree Z-score for medial dACC (P = 0.002 [0.024]); and increased participation coefficient for right AI (P = 0.034 [0.347]), although this last effect did not survive correction for multiple comparisons. The only effects not present when using neutral as a baseline were higher assortativity and participation coefficient for right IFS.

Fig. S3.

Network exhibiting greater coupling for incongruent than neutral. (A) Sphere color represents module membership, and sphere size reflects node strength (across task conditions). Upper is a 3D axial view from above the brain; Lower is a 3D coronal view from anterior to the brain (to maintain the right side of the brain on the right side of the image for both views, posterior is positioned on top for the axial view). Sphere placement in the brain reflects the center of mass location of that node. (B) Circle color represents module membership and circle size reflects node strength. This network representation was created using the Kamada–Kawai spring embedder algorithm. Only links (and the corresponding nodes) that were identified in the NBS analyses as differing significantly by condition are shown above. FEF, frontal eye field; L, left; LOC, lateral occipital cortex; M, medial; OFC, orbitofrontal cortex; PCC, posterior cingulate cortex; R, right.

An additional effect emerged that was not present when using congruent as a baseline. Specifically, higher demand for inhibitory control was associated with stronger within-module degree Z-score for right IFS (P = 0.002 [0.016]). Several effects also emerged for the additional node examined, right IFGpo: greater node strength (P < 0.001 [< 0.001]) and local efficiency (P < 0.001 [< 0.001]) and weaker within-module degree Z-score (P = 0.003 [0.024]).

Regional Task Activation Methods.

Preprocessing.

Image processing and statistical analysis was implemented primarily via FSL’s FEAT. Functional data for each participant were motion-corrected, intensity-normalized, temporally high-pass filtered, and spatially smoothed (FWHM = 5 mm). Temporal low-pass filtering was carried out by using AFNI's 3dDespike.

First-Level Data Processing.

Regression analyses were performed voxel-wise on the processed functional time series. Four HDR-convolved predictors, one for each word type block (congruent, incongruent, and neutral) and one modeling the rest condition, were included. The comparison of interest was the contrast of the incongruent with the congruent condition. Functional data were nonlinearly warped into the MNI152 nonlinear template via FNIRT.

Group-Level Processing.

Group inferential statistical analyses were carried out by using FLAME. The mean incongruent > congruent response across the sample was calculated via voxel-wise one-sample t tests. Gaussian-random-field correction for multiple comparisons was computed via FSL’s Cluster, with voxel-level threshold of z = 4.

Regional Task Activation Results.

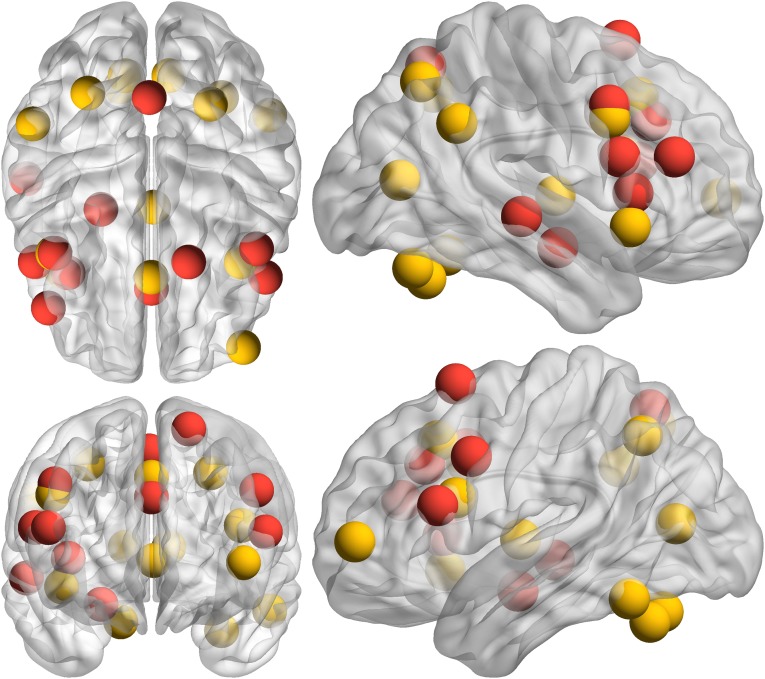
Findings from the incongruent > congruent regional task activation analyses are provided in Table S2 and Fig. S4. Nodes present in both network and regional task activation analyses were medial dACC/paracingulate, right AI, bilateral IFGpo, left posterior MFG, right precentral, and medial precuneous. Nodes present in network, but not regional task activation, analyses were right IFS (although a nearby region of MFG is present, and activation extends into IFS at lower thresholds), left precentral, right posterior superior/middle temporal gyrus, left posterior superior frontal gyrus (SFG), right posterior MFG/precentral gyrus, and right amygdala/hippocampus. Nodes present in regional task activation, but not in network, analyses were left inferior frontal pole, bilateral angular gyrus, left posterior supramarginal gyrus, left AI, bilateral posterior orbitofrontal cortex, medial thalamus, bilateral superior parietal lobule, left inferior temporal gyrus temporooccipital part, bilateral superior lateral occipital cortex, and bilateral intracalcarine gyrus. See Fig. S5 for a depiction of overlap.

Table S2.

Incongruent > congruent within-region task activation

Region	Volume, mm3	Max z	x	y	z
Medial thalamus	23,640	6.61	−2	−12	4
Left angular gyrus/superior lateral occipital cortex/posterior supramarginal gyrus/superior parietal lobule/*medial precuneus	20,344	6.89	−29	−60	44
Left AI/posterior orbitofrontal cortex/*IFGpo/*posterior MFG	18,878	7.21	−42	13	20
Medial *dorsal anterior cingulate/*paracingulate	12,760	6.65	−1	20	42
Right *AI/posterior orbitofrontal cortex	5,320	6.40	40	17	−8
Right *IFGpo/*precentral gyrus	1,465	5.11	44	9	34
Left inferior temporal gyrus, temporooccipital part	1,296	5.38	−55	−54	−19
Right superior parietal lobule/superior lateral occipital cortex	973	5.24	28	−54	48
Right intracalcarine cortex	826	5.62	11	−72	10
Left intracalcarine cortex	507	4.61	−9	−72	10
Right angular gyrus	362	4.67	53	−50	32
Left inferior frontal pole	359	4.92	−43	52	3

Region names correspond to the ROIs used in the network analyses.

^*Regions that were also present in the network analyses. x, y, z = coordinates for center of mass.

Fig. S4.

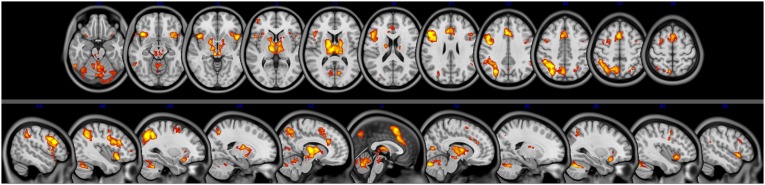
Incongruent > congruent within-region task activation. Axial (Upper; z = −21 to 59, slices every 8 mm) and sagittal (Lower, x = −50 to 50, slices every 10 mm) views of the within-region findings for the incongruent > congruent contrast.

Fig. S5.

Overlap of nodes in incongruent > congruent network and within-region task activation. Red spheres are those identified in the network analysis, and yellow spheres are those identified in the within-region task activation analysis. Sphere placement in the brain reflects the center of mass location of that ROI. Upper Left is a 3D axial view from above the brain. Lower Left is a 3D coronal view from anterior to the brain (to maintain the right side of the brain on the right side of the image for both views, posterior is positioned on top for the axial view). Upper Right is a 3D sagittal view from right of the brain. Lower Right is a 3D sagittal view from left of the brain.

Activation in no regions correlated with incongruent vs. congruent RT. Activation in several regions correlated with incongruent vs. congruent error rate: left frontal pole (r = 0.214, P = 0.039), right angular gyrus (r = 0.303, P = 0.003), left intracalcarine cortex (r = 0.299, P = 0.004), IFGpo/precentral gyrus (r = 0.226, P = 0.029), right AI/posterior orbitofrontal cortex (r = 0.313, P = 0.002), medial dACC/posterior paracingulate (r = 0.257, P = 0.013), left AI/posterior orbitofrontal cortex/IFGpo/posterior MFG (r = 0.259, P = 0.012), left lateral occipital cortex/angular gyrus (r = 0.223, P = 0.032), and medial thalamus (r = 0.239, P = 0.021).

Several regions correlated with drift rate: left intracalcarine cortex (r = −0.213, P = 0.040), right AI/posterior orbitofrontal cortex (r = −0.305, P = 0.003), medial dACC/posterior paracingulate (r = −0.292, P = 0.005), and left AI/posterior orbitofrontal cortex/IFGpo/posterior MFG (r = −0.261, P = 0.011). Two regions correlated with boundary distance: right angular gyrus (r = −0.249, P = 0.016) and right insula/posterior orbitofrontal cortex (r = −0.207, P = 0.047).

Age Analyses.

Supplementary analyses investigated whether age moderated task effects in behavior, brain networks (i.e., via the NBS toolbox), or graph properties (i.e., via the GTG toolbox). Specifically, the correlation between age and the incongruent vs. congruent difference score for mean RT/errors was computed. In addition, NBS and GTG analyses were recomputed, with the addition of age as a between-subject predictor. As well, the correlation between age and mean connection weight in the task-related network identified previously via NBS was computed. No significant effects were observed.