Mechanics of torque generation in the bacterial flagellar motor

Significance

Locomotion in many bacterial species is driven by the rotation of one or more long flagellar filaments, each powered by a bacterial flagellar motor (BFM) at its base. The BFM, then, plays a central role in processes such as chemotaxis, bacterial pathogenicity, and biofilm formation. Using information from structural and biophysical experiments on the BFM, we construct a testable model for the mechanism of torque generation. Our model is, to our knowledge, the first to propose and test a specific physical mechanism for this process, and it provides a mechanical explanation for several fundamental properties of the BFM. In addition to fitting current experimental results, model predictions suggest further experiments to shed light on various aspects of motor function.

Abstract

The bacterial flagellar motor (BFM) is responsible for driving bacterial locomotion and chemotaxis, fundamental processes in pathogenesis and biofilm formation. In the BFM, torque is generated at the interface between transmembrane proteins (stators) and a rotor. It is well established that the passage of ions down a transmembrane gradient through the stator complex provides the energy for torque generation. However, the physics involved in this energy conversion remain poorly understood. Here we propose a mechanically specific model for torque generation in the BFM. In particular, we identify roles for two fundamental forces involved in torque generation: electrostatic and steric. We propose that electrostatic forces serve to position the stator, whereas steric forces comprise the actual “power stroke.” Specifically, we propose that ion-induced conformational changes about a proline “hinge” residue in a stator α-helix are directly responsible for generating the power stroke. Our model predictions fit well with recent experiments on a single-stator motor. The proposed model provides a mechanical explanation for several fundamental properties of the flagellar motor, including torque–speed and speed–ion motive force relationships, backstepping, variation in step sizes, and the effects of key mutations in the stator.

The bacterial flagellar motor (BFM) is one of only two known protein motors that uses the potential energy stored in the transmembrane ion gradient (the ion motive force, or IMF) instead of ATP, the near-universal cellular energy currency. The other such motor is the F_O motor of ATP synthase, responsible for the synthesis of ATP. Understanding how these ion-driven machines generate useful mechanical work is a fundamental issue in cellular biology.

One of the principle diagnostics for a rotary motor is the relationship between torque and rotational speed. Theoretical models attempt to reproduce these empirically measured relationships. The torque–speed curve of the BFM appears to display two distinct regimes: a constant-torque plateau at low speeds that sharply transitions into a near-linear decrease in torque at high speeds (1). Importantly, recent experiments show that the number of torque-generating units (or stators) is likely not constant across this curve (2). This is akin to a car in which the number of active cylinders changes as the car goes uphill and downhill.

In an attempt to reproduce experimentally measured torque-speed curves, most of the currently published models assume that the number of working stators is constant. However, recent measurements of single-stator torque–speed curves provides insight into the physics of the rotor–stator interaction (3). Here, we focus on the mechanism of torque generation in single-stator motors. Understanding the physics of the torque–speed curve of multiple-stator motors requires consideration of load-dependent stator recruitment, which is beyond the scope of this work.

The recently reported single-stator torque–speed curves (3) make a theoretical reexamination of the BFM’s torque generation mechanism especially timely. Currently published models describe torque generation phenomenologically as an energy surface without committing to a specific physical mechanism. Here we combine the currently available structural information with published biophysical and biochemical studies on the dynamical behavior of the motor to propose a mechanically specific and experimentally testable model of torque generation in the BFM.

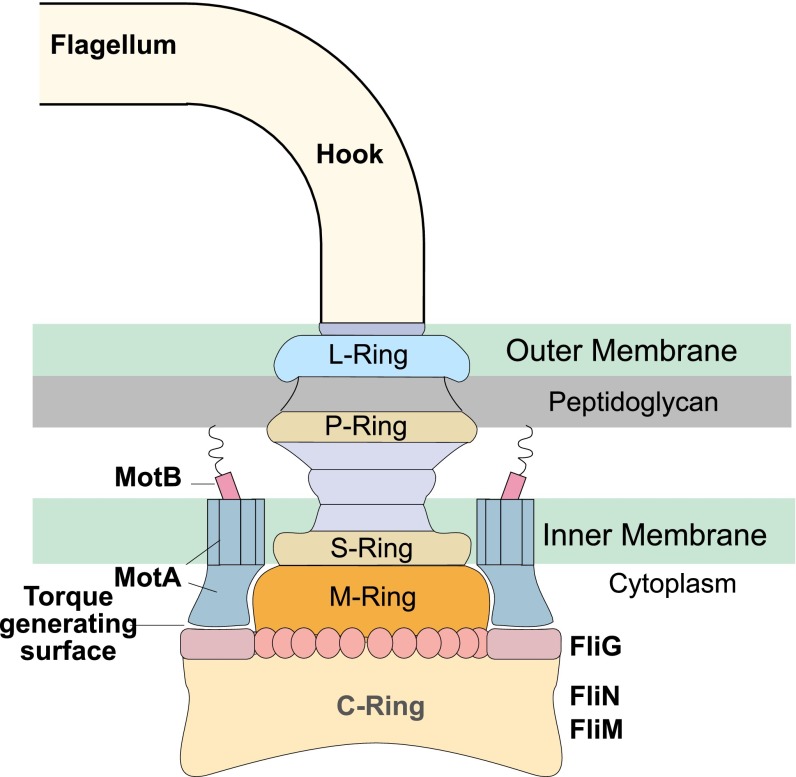
The BFM consists of a series of concentric rings embedded in the cell envelope connected to an extracellular helical propeller by a flexible hook (Fig. 1). The cytoplasmic C-ring acts as the rotor and the membrane-embedded Mot (Motility protein) complexes act as the stators. A working motor can have between 1 and 11 such stator units. Each stator unit is composed of 4 MotA and 2 MotB helix bundles (4, 5). A MotA bundle consists of four membrane-embedded α-helices linked by two large cytoplasmic loops. Interaction between the cytoplasmic loops and FliG proteins located on the periphery of the rotor is implicated in torque generation. We note that although there is some controversy on the exact number of FliGs, this detail does not affect the main points of our model. For ease of exposition, in the following, we assume that there are 26 FliG “spokes” on the rotor.

Fig. 1.

Schematic showing the basic parts of the BFM. A bacterium has, on average, four flagellae, each attached to the basal body of a motor via a flexible hook. The M, S, and C rings of the basal body are together called the rotor. FliG proteins (26 copies of which are assumed here) are placed around the periphery of the C ring. These interact with the MotA loops of the stator to generate torque and rotate the flagella. Stators are composed of MotA and MotB subunits, the latter of which attaches the stators to the peptidoglycan layer, allowing for torque generation via the MotA–FliG interaction. A motor can have between 1 and 11 engaged stators, depending on the load (2, 31, 32).

The feat of coupling an ion gradient to the generation of mechanical work is attributed to the MotB complexes. These complexes each contain an ion-conducting channel with a negatively charged aspartate residue (Asp32) that binds cations. This residue is one of the most strongly conserved residues across bacterial species (1, 5). The interaction between Asp32 and a cation passing through the inner bacterial membrane (between the periplasm and the cytoplasm) was previously suggested to induce conformational changes in the stator complex, resulting in the torque-generating power stroke (5).

A crystal structure of the stator complex will be necessary for a complete understanding of the power stroke. However, the available structural knowledge, combined with information about the motor’s dynamical performance, is sufficient to propose a plausible model that is experimentally testable. Using this information, we present a mechanical model for torque generation involving proline-induced conformational changes in MotA cytoplasmic loops (5, 6). To the best of our knowledge, our model is the first to incorporate known structural information about the BFM stator and rotor complexes into a quantitative physical mechanism for the generation of the power stroke. As part of this study, we aim to address the following fundamental questions: (i) What are the kinematics and dynamics of the BFM power stroke? (ii) What role do charged residues on the stator and rotor play in torque generation, and how does this role explain mutational experiments which show only a partial reduction in motor efficiency? (iii) What is the physics behind the shape of the torque-speed curve for single-stator motors? (iv) Why does the motor exhibit backsteps even in the absence of an external ‘reversal’ signal (usually the small protein CheY-P)?

In addressing these issues, we primarily discuss the proton (H⁺) powered motor of Escherichia coli. However, our model is sufficiently general so as to apply to the sodium (Na⁺) powered motors found in alkalophiles and marine Vibrio species.

Mechanochemical Model

An Electrosteric Power Stroke.

Due to the modest magnitude of the forces involved relative to thermal fluctuations, it has long been assumed that nearly any form of interaction between rotor and stator is sufficient to explain the rotation of the BFM (1). For this reason, previous models have avoided committing to a particular physical origin for these forces, instead treating the interaction between the stators and the rotor phenomenologically as a free-energy surface and the stator as an ad hoc stochastic stepper (7–9).

However, knowledge gained from recent structural (4, 10, 11) and biophysical (3) studies has led us to conclude that the power stroke of the BFM is electrosteric—that is, it is driven by both electrostatic and steric forces. Hence, we propose a mechanochemical model consisting of two phases. (i) Before the power stroke, electrostatic forces position the stator. (ii) Once positioned, the stator delivers a steric push (i.e., a contact force) on a FliG protein located along the periphery of the rotor. A more detailed description of the nature of contact forces is found in SI Text and in ref. 12.

In the following, we lay out the assumptions involved in the construction of our model, followed by a detailed description of the mechanism. Details of the mathematical formulation are provided in Materials and Methods and SI Text.

Electrostatic Forces Steer the Stator into Place.

The first step in constructing our model is the steering and positioning of the stator by electrostatic forces. This hypothesis originates from the results of the mutagenesis experiments performed by Zhou et al. (13). These studies were aimed at elucidating the structure of the MotA loops. They found that mutations of certain charged residues on the cytoplasmic portions of the loops degraded—but did not eliminate—motor function. Notably, the deleterious effects of mutations on the stator were often countered by corresponding mutations (in particular, compensating charge reversals on the FliGs). Certain mutations were also found to have very small effects, or even to cause slight improvements, on bacterial motility.

These results correspond to the idea that mutations of charged residues may result in imperfect steering and consequently in a less efficient—but still functioning—power stroke. Similarly, certain mutations may position the cytoplasmic loops closer to the adjacent FliG, resulting in a larger power stroke and corresponding improved motility.

Because detailed structural information on the stator is not yet available, we performed a simple example calculation to demonstrate how electrostatic interactions can position the stator ready for a power stroke. Explicit calculations, as well as a full explanation of model assumptions, can be found in SI Text. For computational convenience, we approximate the important charged residues on the FliG (Flagellar motor switch protein G) proteins (10) and stator loops (14) implicated in torque generation. The assumption that FliG proteins can be modeled as dipoles is based on previous studies (10, 15). Modeling the electrostatic forces between the stator and rotor by point charge interactions produces results comparable to those obtained from a dipole approximation.

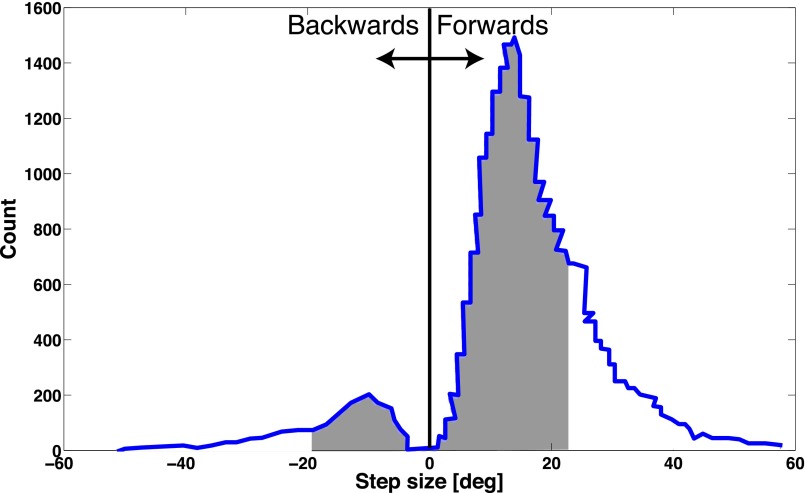
The distribution of observed rotor step-sizes has been shown experimentally to be centered around 2π/26 radians (∼13.8°), the average spacing between consecutive FliGs (16, 17). The positioned charges result in a weak electrostatic force that is sufficient to position the MotA loop without significantly wasting energy to free the stator at the end of the power stroke. Furthermore, the width of the well leads to somewhat imprecise positioning. Although this result is hardly unexpected, the wide spread of this distribution—in particular, the tendency toward smaller step sizes—has been somewhat puzzling.

Because a wide energy well may result in stators being positioned at nonoptimal locations, electrostatic positioning may contribute to this variance. Because we propose that the stator’s power stroke is imparted via a contact force on the rotor, imperfect electrostatic positioning will result in the stator being in contact for only a portion of its trajectory. This results in the stator delivering a stroke that is smaller than average. Of course, imperfect steering is not likely to be the only factor determining the variance in the observed step size distribution: The uneven spacing of FliGs along the periphery of the rotor (18, 19), as well as experimental errors, is also likely to contribute.

Note that, in the case of a reciprocal motion of the stator, attractive electrostatic forces strong enough to comprise the entire power stroke would require a nonnegligible energy to separate the stator and the rotor at the end of the power stroke. This penalty for letting go would likely obviate the rotor torque, resulting in a motor with a far lower Stokes efficiency (20) than has been calculated for the BFM ($\sim$95%) (1). In contrast, the mechanism we propose here efficiently generates mechanical work from the ion motive force.

We note that the above calculation is speculative: Changes in parameter choices will vary the resulting energy landscape. However, our mechanism presupposes that the energy well produced by the electrostatic interactions will be shallow and wide (Fig. 2). We have performed an example calculation to show that such a mechanism is feasible given our limited structural information. A more precise calculation can be performed only when more detailed structures are available.

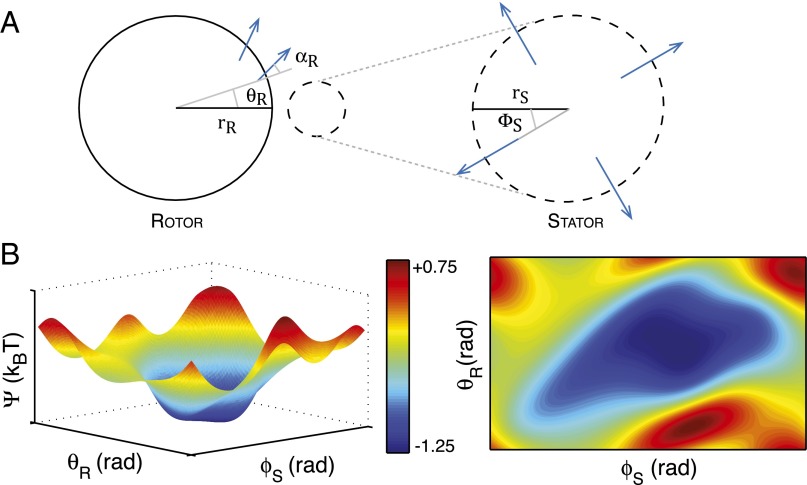
Fig. 2.

The predicted energy landscape during electrostatic steering. (A) Schematic of rotor and stator configurations; ${\varphi }_S$ and ${\theta }_R$ are the angular coordinates of the stator and the rotor with respect to the horizontal; ${\alpha }_R$ is the positive angle of the individual FliGs with respect to the radius. Blue arrows denote the direction of the dipole (10, 15). (B) Predicted surface and contour plots of the electrostatic energy vs. the stator and rotor angles. The predicted surface shows the existence of a wide and gently sloping energy well. Note that ${\varphi }_S$ and ${\theta }_R$ are periodic variables with periods $\pi /2$ and $\pi /13$, respectively; the above plots show one period of each. Our calculations consider a single stator centered at (21,−2,1) with the rotor centered at the origin (all distances in nanometers). Computations using this dipole approximation suggest a well of depth $\sim$1 k_BT for this configuration (see SI Text for details).

Motion About a Proline Hinge Provides a Steric Push.

As proposed previously (5), we assume that the steric portion of the power stroke is the result of a conformational change in the cytoplasmic MotA loop. Evidence of such conformational changes has also been shown experimentally (21). In our model, this motion consists of hinged movements of the MotA helices that result in a “kink and swivel” motion, as shown in Fig. 3 (6). The steric mechanism proposed below remains valid regardless of which residue, or group of residues, on the MotA/MotB helices acts as the inducer. However, we have chosen to focus on MotA’s Pro173 residue because (i) along with Asp32 on MotB, this amino acid is strongly conserved across bacterial species (22) and (ii) previous molecular dynamics simulations have found that proline residues induce hinges in transmembrane helices (6), resulting in a movement analogous to the one proposed in the model. The specific mechanism we propose is as follows.

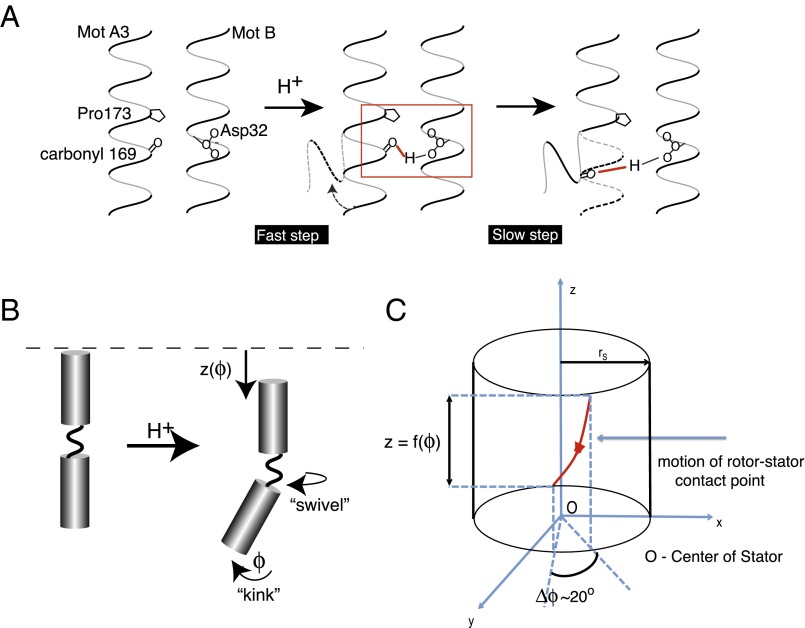
Fig. 3.

Ion binding onto Asp32 induces a kink and swivel conformational change (6). (A) Binding of a proton to Asp32 of MotB drives a rapid local reorganization of hydrogen bonds (including those of water). In particular, we focus on the creation of a hydrogen bond between the side chain of MotB’s Asp32 and the carbonyl group of MotA’s residue 169. Ion binding thus creates a local elastic strain in the MotA helix. The release of this strain leads to the proposed conformational change in MotA about the Pro173 residue. Adapted from Kim et al. (5). (B) Upon ion binding, MotA undergoes a rapid conformational change consisting of three motions: (i) a bending about Pro173 ϕ, (ii) a downward motion, $z\left(\varphi \right)$, and (iii) a rotation about its central axis. Inspired by the work of Cordes et al. (6), we propose that this kink and swivel motion generates the power stroke. Importantly, we note that this figure is a 2D depiction of a 3D process, with the motion of the loop extending out of the plane of the page. (C) Our envisioned motion of the contact point between a FliG and a stator loop during the power stroke. The kink and swivel motion induces the contact point to follow a helical path on a cylinder of radius approximately equal to the radius of the stator. For simplicity, we assume that the vertical motion is a function of the angle ϕ subtended by the stator loop. Therefore, we explicitly model only the rotational motion ϕ of the stator loop.

When a cation binds to the negatively charged Asp32 residue on MotB, the hydrogen bonds (including those of water) in the vicinity of Asp32 and Pro173 on the A3 helix of MotA collectively rearrange. This rearrangement induces an elastic strain in the MotA–MotB complex centered around the proline residue in the A3 loop of MotA. Fig. 3A shows a candidate scenario, where the carbonyl group of residue 169 on MotA forms a hydrogen bond with Asp32 on MotB after proton binding, as proposed in ref. 5. This elastic strain induces the kink and swivel movement around the proline residue and drives the proposed motion of the lower part of the A3 helix, constituting the power stroke (see Fig. 3B). The binding of the ion and the rearrangement of the hydrogen bonds (10⁻¹² s to 10⁻⁹ s) are near-instantaneous processes compared with the much slower motion of the kink and swivel conformational change (10⁻⁵ s to 10⁻³ s). Thus, the chemical steps can be treated as transitions between states in a Markov chain.

The above proposal is supported by a few simple calculations. The maximum torque of the BFM in E. coli is $\sim$2,000 pN⋅nm (23). Given that up to 11 torque-generating units may be acting, this corresponds to a maximum motor torque of $\sim$200 pN⋅nm per stator (24). As the radius of the motor is $\sim$20 nm, the force generated by a single stator during a power stroke is $\sim$10 pN. Direct observation of stepping behavior has shown that the motor takes 26 elementary steps per revolution, corresponding to a displacement of $\sim$5 nm per step. As explained below, our model supposes that each elementary step is actually composed of two half-steps, each imparted by the power stroke of a MotA helix. This results in a displacement of $\sim$2.5 nm per power stroke. Molecular dynamics studies show the angles subtended by proline hinge motifs from various transmembrane helices to be between 18° and 25° (6). From this, we can estimate the length of the cytoplasmic loop measured from the proline hinge to its tip to be $\sim$ 7 nm, a reasonable estimate as the majority of the stator residues have been shown to extend into the cytoplasm (13). Such a lever arm would result in $\sim$25 pN⋅nm ($\sim$ 6–8 k_BT) of work per half-step, corresponding to the rearrangement of one to two hydrogen bonds (and the free energy released by the passage of one proton). This energy barrier is sufficient to ensure an efficient directional process, as suggested in ref. 25.

An In-Phase Two-Cylinder Engine.

There are four MotA subunits in each stator complex; see Fig. 4 for a schematic of the stator structure. Our model supposes that two of these subunits are inactive during torque generation while the motor is moving predominantly in a single direction. We base this presumption on the idea that switches between counterclockwise (CCW) and clockwise (CW) rotation result from changes in FliG orientation (15). Given this, we propose that two MotA loops are responsible for the power stroke in one direction, whereas the other two interact with the alternately oriented FliG to drive rotation in the other direction. We suppose that loops 1 and 3 are responsible for CCW motion and loops 2 and 4 are responsible for CW motion, but note that this designation is arbitrary. This mechanism predicts that the intrinsic mechanics for power strokes in both directions are equivalent; this has been observed experimentally (17).

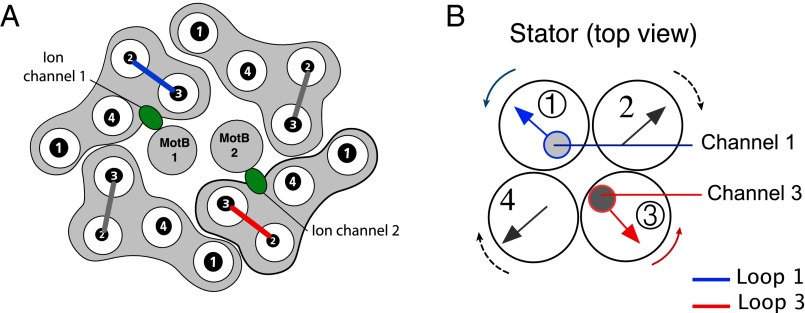
Fig. 4.

Stator structure and coordinated motion between stator subunits. (A) Proposed arrangement of stator components as viewed from the periplasm. A stator has four MotA helix bundles, each consisting of four α-helices. The four MotA subunits surround a pair of MotB helices. The ion channels associated with the MotBs (shown in green) contain the Asp32 residues essential for proton binding. The stator is attached to the peptidoglycan via a linker region on MotB. The power stroke is delivered to the rotor FliGs by the cytoplasmic loops between helices A2 and A3 in each MotA bundle (shown as solid bars). Loops 1 and 3 (highlighted in blue and red, respectively) are associated with the ion channels. Adapted from Braun et al. and Kim et al. (4, 5). (B) Due to the helical structure of the MotA loops, we can make an analogy between their motion and that of a bundle of four gears. Our model proposes that loops 1 and 3 (shown in blue and red, respectively) drive CCW rotation via contact with FliG, whereas loops 2 and 4 drive CW rotation.

We propose that an elementary step is composed of a pair of power strokes, analogous to the mechanism of a two-cylinder engine. Experiments on motors driven at extremely low speeds may allow the direct observation of these substeps, in support of our model. This can be done using chimeric sodium-driven flagellar motors. As extremes in sodium concentration are tolerated far more easily than extremes in pH, these chimeric motors can be driven at very low sodium motive forces (SMFs). Thus far, speeds as low as 10 Hz have been obtained (16).

A two-ion mechanism can either be in phase, in which the energetic profiles of the two stator loops are identical, or out-of-phase, in which their dynamics are offset by a half-cycle. In an experiment using a slowly driven chimeric motor, measuring the rate-limiting step between mechanical substeps can differentiate between these two scenarios. For example, if slower ion binding (e.g., by lowering IMF) extends the dwell time between half-steps, the out-of-phase engine model is supported.

The mechanics of these two scenarios are equivalent within the framework of our model. For this reason, we discuss only one of these mechanisms in detail: the one in which the two stator loops act in phase with each other (as shown in Fig. 5B). We choose this alternative because the passage of two protons across a membrane provides more energy, which contributes (along with the work done by the MotA loops) to a more reliably directional process in the presence of thermal noise. Interestingly, a single proton passage under standard conditions generates $\sim$ 6 k_BT, slightly less than the calculated length of “time’s arrow” (the energy barrier required for a such a reliably directional process) (25).

Fig. 5.

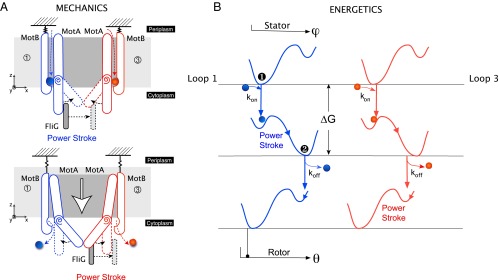
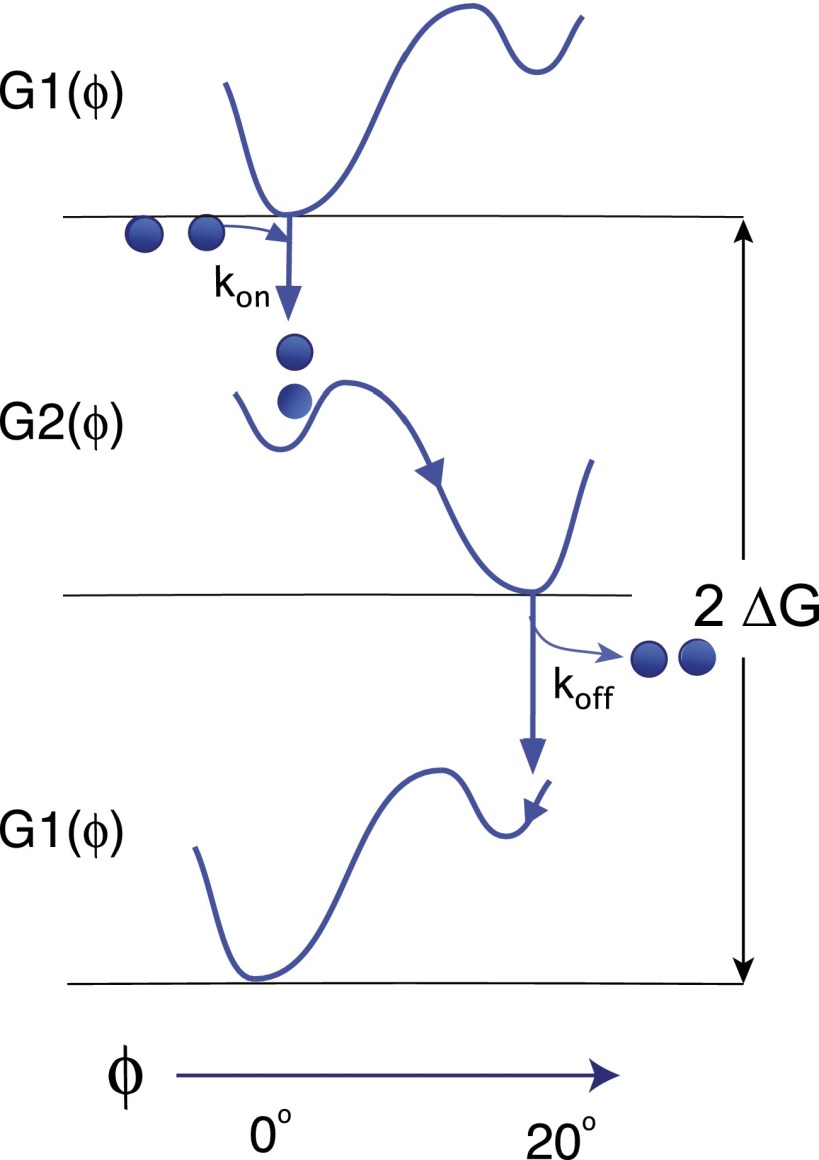
Dynamics of the rotor–stator interaction. (A) Mechanics of the power stroke. (Top) After the initial electrostatic steering, two protons bind to the charged Asp32 residues on the MotBs. The consequent rearrangement of hydrogen bonds induces an elastic strain in the straight MotA loops. Release of this strain results in synchronous kink and swivel motions about the proline hinge in both MotAs. As a result, a steric push is imposed on FliG, and the first half of the power stroke is performed by loop 1. Importantly, this motion also has a vertical component—the loops lower themselves out of the membrane. (Bottom) The lowering of the MotA loops exposes the protons in MotB to the cytoplasm, whereupon they are released. This results in a reset of the MotA loops, during which loop 3 carries out the second half of the power stroke. We note that this image depicts a 2D projection of a 3D motion: The motion of the stators is not constrained to the plane of the page. An observer sitting on the rotor axis sees the stator inchworm walking along the rotor using the FliGs as steppingstones. (B) Energetics of the power stroke. Because the two loops move in phase with each other, their energetic pictures are identical. We describe the free-energy landscapes using double-well Landau potentials. These landscapes are shown in blue for loop 1 and red for loop 3 with respect to the angles of the stator ϕ and rotor θ. We model the stator and rotor interaction using a steric force. This ensures that their motion and the values of the corresponding angles are very tightly tied to one another. The initial entrance of the proton into the ion channel ($k_{\text{on}}$) places the system within ${\mathrm{k}}_{\mathrm{B}}\mathrm{T}$ of the energy barrier. Thermal motions then result in the first half of the power stroke (Top and Middle). Exit of the protons into the cytoplasm ($k_{\text{off}}$) drives the reset, and the second half of the power stroke (Middle and Bottom).

Full Revolution Requires the Passing of at Least 52 Protons

Our model for torque generation assumes that the rotation of the BFM is tightly coupled to the transmembrane ion gradient. This means that each elementary power stroke is tied directly to the passage of protons across the membrane. Given our prior assumption of 26 elementary steps per revolution, our model thus requires 52 protons for a full revolution. Previously, a lower bound for the number of ions per full revolution was determined by calculating the work done as $\langle \tau \rangle \times 2\pi$ and equating it to the free-energy $n\times$ IMF, where n is the number of ions per revolution and IMF is the ion motive force, as before (3). The above calculation resulted in an estimate of $n=37$, lower than the 52 ions per revolution supposed by our model.

This discrepancy can be explained as follows. Although the above is indeed a lower bound, a tighter bound can be computed. The calculation of work as stated above suggests that the power output per revolution is $\tilde{P}=\langle \tau \rangle \langle \omega \rangle$. However, power is formally calculated as $P=\langle \tau \cdot \omega \rangle$, which differs from $\tilde{P}$ by a covariance term, $\text{cov}\left(\tau ,\omega \right)$. This follows from the fact that, for any two stochastic processes X and Y, $\langle XY\rangle =\langle X\rangle \langle Y\rangle +\text{cov}\left(X,Y\right)$.

Note that the number of protons per revolution assumed by our model is also a lower bound; that is, we have assumed that 52 working ions are required per revolution. Many factors can result in the passing of more ions than predicted, including leakiness of the ion channels, loose coupling between the rotational and vertical movements of the stator, irregular arrangement of FliGs around the rotor, or imperfect placement of stators by electrostatic steering forces. This can be quite easily extended within our mathematical framework by replacing the step function associated with ion binding with a sigmoidal function.

The Mechanical Escapement.

Fig. 5A depicts the mechanics associated with the power stroke. We choose the angle subtended by a stator loop ${\varphi }_S^i$ with respect to the bilayer normal (where i corresponds to the loop number) as the order parameter. That is, we consider the energy landscape along the arc length of the mechanical trajectory of the stator loop. A stator loop has two stable configurations: straight (${\varphi }_S^i=0°$) and bent (${\varphi }_S^i\sim 20°$). Both of these configurations correspond to energy minima in different chemical environments: When the negative Asp32 is not neutralized by a proton, the loops prefer to maintain a straight posture (${\varphi }_S^i=0°$). The presence of bound protons induces a free-energy change sufficient such that a thermal fluctuation can induce the conformational change to the bent state (${\varphi }_S^i\sim 20°$).

During a power stroke, the entire stator complex undergoes a collective gear-like motion as shown in Fig. 4B. The conformational change due to the hopping on of the ion produces the first half of the power stroke: Here, loop 1 pushes the FliG, while loop 3 is put in place to carry out the second half of the power stroke during the reset (Fig. 5A). This reset corresponds to the hopping off of the proton, resulting once again in the stator loops surmounting the energy barrier between configurations and reverting to the straight position (${\varphi }_S^i=0°$). Note that the numbering of the loops is arbitrary; the mechanism proposed here is equivalent to one in which loop 1 performs the first half of the power stroke and loop 3 performs the second.

In summary, a torque generation cycle by a single stator of the BFM proceeds as follows:

• i)Electrostatic interactions between charged residues on MotA and FliG steer a stator tip close to a rotor FliG.
• ii)In the presence of a membrane potential, the two MotB aqueous ion channels open and two protons bind to the negatively charged Asp32 residues on the MotBs. This triggers a reorganization of the hydrogen bonds in the vicinity of the Pro173 on MotA (see Fig. 3A).
• iii)The hydrogen bond rearrangements induce elastic strain in the straight MotA loops. This strain drives a kink and swivel motion of the MotA loop, increasing the bend angle (from ${\varphi }_S^i=0°$ to $20°$, as shown in Fig. 3B).
• iv)One MotA loop (loop 1, shown in blue in Fig. 5A) applies a steric push to the nearest FliG, resulting in one half of a power stroke.
• v)At the same time, the movement of the stator ion-binding pocket moves downward so that the pocket is exposed to the cytoplasm. The ion channel is now closed to the periplasm. The protons hop off MotB into the cytoplasm, now inverting the strain in the bent MotA loops.
• vi)The inverse strain drives the movement of the loops in the reverse direction, straightening the bent MotAs (i.e., from ${\varphi }_S^i\sim 20°$ to $0°$).
• vii)The other MotA loop (loop 3, shown in red in Fig. 5A) now applies a steric push to the same FliG, completing the second half of the power stroke.

Consequently, to the rotor, the stator appears to be an “inchworm” stepper with FliGs as the stepping stones.

Results and Predictions

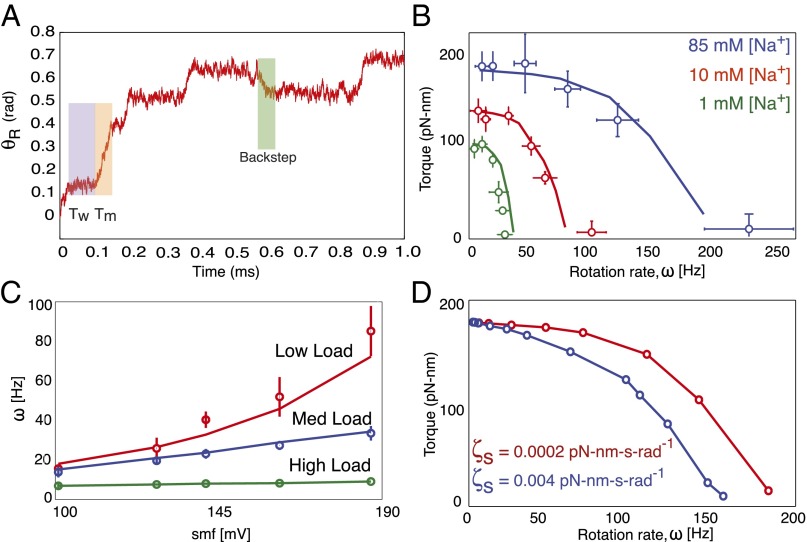
Using the mathematical model described in Materials and Methods, we performed both analytic calculations and numeric stochastic simulations. Statistics from simulated trajectories—an example of which is shown in Fig. 6A—were used to calculate various experimental quantities including average motor torque and angular speed.

Fig. 6.

Summary of recent experiments and comparisons with model simulations. Results are derived from numerical simulations. In all plots, model calculations are shown by solid lines, and experimental data are shown as open colored circles. (A) Sample trajectory generated by the model. Moving ($T_M$) and waiting ($T_W$) times are shown with orange and purple backgrounds, respectively. Two half-steps separated by a very short pause can be seen in the highlighted forward step (orange). Occasionally, reversals (shown with green background) appear when MotA loops 2 and 4 are engaged due to conformational changes in FliG. (B) Single-stator torque–speed curves measured in a chimeric sodium motor for various sodium concentrations at pH 7.0. Curves show a concave-down shape, with the length of their plateaus being SMF dependent [data from Lo et al. (3)]. (C) Motor speed vs. SMF in a chimeric sodium motor shows a nearly linear relationship across various loads [data from Lo et al. (3)]. (D) Effect of stator viscosity on the shape of BFM torque–speed curves. The reduction in the plateau region is mainly due to the nature of the steric forces during the power stroke.

In the sample trajectory for the rotor motion, the duration of a power stroke ($T_m$) and the waiting time between consecutive power strokes ($T_w$) are highlighted in orange and purple, respectively. The highlighted power stroke shows two half-steps, corresponding to the two sequential steric pushes by the two MotA loops involved. As in experimental trajectories, occasional reverse steps are also observed in our simulations, one of which is shown in the sample path in Fig. 6A. An explanation for backsteps that is compatible with our model is provided below.

The results shown in Fig. 6 were obtained via simulation. Analytic calculations on an approximate deterministic model (explicitly provided in SI Text) were also performed for illustrating different aspects of the model. These calculations were also used to obtain suitable ranges for the parameters (e.g., stator and rotor drags) used in Langevin simulations.

Single-Stator Motors Exhibit Concave-Down Torque–Speed Curves.

Until recently, BFM experiments were performed on motors with multiple stators, with no direct accounting for the number of engaged stators at a given load. Therefore, the existence of the torque–speed plateau and “knee” have been assumed to be innate characteristics of the rotor–stator interaction, largely because there was no evidence to the contrary. However, Lo et al. (3) performed experiments using a chimeric single-stator motor showing smoother torque-speed curves without a dramatic plateau as observed for wild-type motors. Although these curves are still concave-down in shape, the extents of the plateau regions are quite variable and depend on the IMF.

The physics behind the two regimes of the torque–speed curve have been interpreted by previous models as a competition between waiting and moving timescales (7, 8). Thus, the general concave-down shape is largely independent of the exact structural and mechanistic details of the model. It requires only that the model is tightly coupled and the moving time exceeds the waiting time at high loads. Our model for single-stator motors fulfills both of these properties.

Our simulations show torque-speed relationships consistent with these single-stator experiments (Fig. 6B). The behavior of the torque–speed curves results from a competition between the time taken for a mechanical half-step ($T_M$) and the waiting time between ion-binding events ($T_W$). For example, our simulations show that the average time in moving a half-step $\langle T_M\rangle$ can be $\sim$20 ms at high loads and $\sim$0.01 ms at low loads. The average waiting time under standard conditions $\langle T_W\rangle$ is $\sim$0.2 ms (8). Therefore, at low loads, the motor is in a kinetically limited regime, where the waiting time between steps is generally higher than the time required to complete a step. Conversely, the motor is mechanically limited at high loads when $\langle T_M\rangle >\langle T_W\rangle$, resulting in the observed plateau. Consequently, as shown in Fig. 6B, this plateau region grows smaller as the IMF decreases (i.e., as $\langle T_W\rangle$ increases).

This competition is also manifested in the relationship between speed and IMF: Speed depends linearly on IMF at high loads, but in a slightly nonlinear fashion at low loads (Fig. 6C). Given that the rotor moves $2\pi /26$ radians per step, the speed of the rotor (${\omega }_R$) can be approximated as

$${\omega }_R\approx \frac{2\pi }{26}\times \frac{1}{\langle T_M\rangle +\langle T_W\rangle }.$$

At high loads, $\langle T_M\rangle \gg \langle T_W\rangle$. Because the time to complete a power stroke is inversely proportional to the ion motive force, $\langle {\omega }_R\rangle \propto$ IMF at high loads. In contrast, the waiting time eclipses the time for a mechanical step at low loads, and therefore ${\omega }_R\propto 1/\langle T_W\rangle \propto \exp \left(q\times \text{IMF}/{\mathrm{k}}_{\mathrm{B}}\mathrm{T}\right)$. Further details to this end are provided in SI Text.

Backstepping in the Absence of CheY-P Is Due to Thermal Flipping of FliG.

The BFM plays a central role in bacterial chemotaxis: The direction of rotation of the motor determines whether a bacterium will move in a straight line (CCW) or “tumble” (CW) to move in a random new direction. This switching is typically initiated via a signal transduction pathway, in which a response regulator protein, CheY, is phosphorylated into an activated form, CheY-P, to induce tumbling. For more information on this pathway and bacterial chemotaxis, we refer the reader to several excellent reviews (26, 27).

However, occasional backsteps (e.g., CW motion during primarily CCW rotation) are observed even in the absence of CheY-P. This has been attributed to microscopic reversibility, of which three possible models are discussed in SI Text. For example, Mora et al. ascribed switching in the BFM to the diffusive motion of the rotor through a “bumpy” 26-fold periodic potential (28). However, recent structural studies have found that there exist two main configurations for the FliGs (15, 17), lending support to the idea that a flipping between these states is the molecular basis for backstepping. We note that despite a general agreement on the existence of two distinct FliG configurations, the exact nature of the conformational change to the CCW direction remains controversial.

In our model, the probability of observing a backward step is equivalent to the probability of finding a FliG oriented in the CW state (assuming a primarily CCW-rotating motor). Within the framework of our model, whenever a FliG changes its state and is close to a stator, then the stator uses loops 2 and 4 to apply a contact force and pushes the FliG in the CW direction. To model the flipping between CW and CCW states for the FliGs, we use a nearest-neighbor periodic Ising model with the 26 FliGs arranged on a one-dimensional ring. Such models have been used successfully to explain rotational switching (see, e.g., refs. 29 and 30).

In our model, when the FliGs are oriented at an angle of roughly 10–20° with respect to the radial direction, as shown in Fig. 2A, the motor moves in the CW direction by virtue of contact forces from loops 2 and 4. Conversely, when the FliGs are pointed either orthogonal or at an angle of 180° with respect to the CW orientation, the motor steps in the CCW direction using loops 1 and 3. The numerical values for the above parameters will likely change with the resolution of a structure. However, the above calculation is meant to demonstrate the general framework of our predicted mechanism, which is independent of these choices. Using an Ising model for the flipping of FliGs, we calculate the probability of a backstep to be $\sim$8%. This probability was calculated to be $\sim$7.3% from stepping statistics collected by Sowa et al. (16), demonstrating that a backstep might indeed be simply due to fluctuations in FliG orientation. Further details on these calculations are provided in SI Text.

High Stator Drag Reduces the Torque–Speed Plateau Region.

Because our mechanism crucially depends on steric forces, we expect the drag coefficient of the stator to have a significant effect on motor behavior. Because we explicitly model the motion of the stator, we are able to study directly the effect of this parameter on the BFM’s torque–speed curve. Our model predicts that increasing the stator drag truncates the torque–speed plateau, thus reducing the concave-down shape of the BFM torque–speed curve (Fig. 6D).

This is a direct consequence of the steric forces: Some portion of the stator-generated force must go toward moving the stator itself. As the drag of the stator increases, so does the amount of its generated force allocated to this task. Then, for a given load, the torque transferred to the rotor is relatively low for large stator drag coefficients. This reduces the constant-torque plateau, as well as the overall concave-down shape of the torque–speed curve. This simple prediction may be experimentally tested by increasing the viscosity of the stator’s membrane environment. We note that this prediction is not compatible with a linear potential for the rotor–stator interaction (for a detailed discussion, we refer the reader to SI Text).

Discussion

The ability to convert a transmembrane ion gradient into rotary torque is rare, observed so far in only two protein motors: the F_O motor of ATP synthase and the BFM. The mechanism behind the torque generation in the latter has been a longstanding mystery, driven by the fundamental role of this machine in bacterial locomotion and chemotaxis.

Here we have combined known structural information on the BFM (5, 15), as well as the experimental measurements on single-stator motors by Lo et al. (3), to construct and test, to our knowledge, the first mechanically specific model of torque generation. Using this information, we are able to present an explicit model of the dynamics of the stator during a torque generation cycle. Our model implicates a steric interaction between the cytoplasmic MotA stator loops and the FliG proteins of the rotor. We have tested the feasibility that this interaction is driven by conformational changes in the MotA loops due to the binding of cations to essential aspartate residues on the two MotBs, as was proposed by Blair and coworkers (5). Results from our model simulations reproduce recently measured torque–speed and speed–IMF curves from single-stator motors. A directly testable prediction of our mechanism is that increasing the stator drag coefficient (e.g., via increasing the membrane viscosity) will reduce the constant-torque plateau, as well as the overall concave-down shape of the torque speed curve.

The mechanism we have proposed is akin to a two-cylinder engine, where two of the four MotA loops act when the motor is moving in the CCW direction and the other two loops act in the CW direction. We have proposed that the two loops act in phase with each other, moving in synchrony as two protons bind to the MotBs and are subsequently released into the cytoplasm. In this manner, the first loop executes its half of the power stroke when the protons bind to the MotBs, and the second loop drives the second half of the power stroke once the protons have hopped off into the cytoplasm.

Experiments performed at low IMF can be used to differentiate between a stator acting as an engine that is in phase or out of phase. Because ion binding is rate limiting under these conditions, trajectories would show clear half-steps only if the BFM acts as an out-of-phase engine. However, given that the mechanics of the power stroke for both scenarios are equivalent, the corresponding out-of-phase mechanism would lead to a calculation analogous to the one presented in this work.

Recently measured torque–speed curves revealed that the number of torque-generating units in the flagellar motor increases with load (2). This opens several fundamental questions regarding the physics of this molecular machine. A fuller treatment of motors with multiple stators requires a model of stator recruitment—a compelling topic for future work.

Finally, viewing our model in a larger context, if it turns out that the proline hinge motif is not the stator structure driving rotation, but another structural motif, then essentially the same equations would have to be solved, albeit using a different set of collective coordinates.

Materials and Methods

The mechanochemistry of the torque generation cycle of a flagellar motor with a single stator unit can be modeled by the following Langevin equations. The dynamics of the angular positions of the stator loops ${\varphi }_S^i\left(t\right),$ $i\in \left\{\mathrm{1,3}\right\}$ are given as

$${\zeta }_S\frac{d{\varphi }_S^i}{dt}=\underset{\begin{array}{c}\text{Torque}\hspace{0.17em}\text{from}\\ \text{Proline}\hspace{0.17em}\text{hinge}\end{array}}{\underbrace{-\frac{\partial G}{\partial {\varphi }_S^i}{\ell }_p}}-\underset{\begin{array}{c}\text{Reaction}\\ \text{from}\hspace{0.17em}\text{rotor}\end{array}}{\underbrace{\frac{\partial V_{RS}}{\partial {\varphi }_S^i}}}-\underset{\begin{array}{c}\text{Electrostatic}\\ \text{attraction}\end{array}}{\underbrace{\frac{\partial \psi }{\partial {\varphi }_S^i}{\ell }_p}}+\underset{\text{Thermal}\hspace{0.17em}\text{fluctuations}}{\underbrace{\sqrt{2{\mathrm{k}}_{\mathrm{B}}\mathrm{T}{\zeta }_S}{f}_n\left(t\right).}}$$ [1]

Here, as in the following equations, the last term is the stochastic Brownian force, where $N\left(t\right)$ is uncorrelated white noise; ${\zeta }_S$ is the effective drag coefficient of the stator. $G=G\left({\varphi }_S^i,j\right)$ denotes the free energy of stator loop i, modeled in Fig. 5B as a Landau potential. However, because of thermal fluctuations, the exact shape of the potentials is immaterial. Accordingly, we approximate this potential by piecewise quadric functions for ease of computation. The parameter $j\in \left\{\mathrm{0,2}\right\}$ corresponds to the chemical state of the system: $j=2$ if two protons are bound to the MotB helices and $j=0$ if not. The switching between the two chemical states corresponds to a jump between potential curves, as shown in Fig. 5B.

As the stator moves between the two configurations, it induces a contact force, and subsequent torque, on the rotor. Unlike previous models, we do not assume that this torque is constant across loads but rather depends on the ${\zeta }_L$ (see SI Text for more information). To this end, we do not allow a linear interaction potential between the stator and the FliG; this would result in a constant applied force, which is not true for contact forces. We model the steric interaction potential $V_{RS}$ as

$$V_{RS}\left({\varphi }_S^i,{\theta }_R\right)=\{\begin{array}{ll}-F_{RS}\frac{{\left(R{\theta }_R-{\ell }_P{\varphi }_S^i\right)}^2}{X_{RS}}\hfill & \text{if}\hspace{0.17em}0\le x\le X_{RS}\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$

where $x=X_{RS}+R{\theta }_R-{\ell }_p{\varphi }_S^i$ denotes the distance between the position of the stator loop and the nearest FliG. For a graphical depiction, see SI Text. From this, the torque imposed on the rotor is calculated as ${\tau }_{\text{contact}}=-\partial V_{RS}/\partial {\theta }_R$, whereas the corresponding reaction torque on a stator loop is given by ${\tau }_{\text{reaction}}=-\partial V_{RS}/\partial {\varphi }_S^i$.

The charges on the FliG and the stator loop exert weak attractive forces on each other. These forces prevent the drifting of the rotor with respect to the stator during the chemical transition events. We refer the reader to SI Text for more on the effects of attractive electrostatic forces on the torque–speed curves. With the contact torque and the weak electrostatic forces, the total instantaneous torque on the rotor is given by $\tau ={\tau }_{\text{contact}}-R\left(\partial \psi /\partial {\theta }_R\right)$. The average torque on the rotor is a time (or ensemble) average of the instantaneous torque. Finally, the rotor and load are connected by a linear spring with elastic constant κ; the elastic coupling terms in the equations for the rotor and the load thus appear with opposite signs.

Given this, the rotor dynamics are described by a corresponding Langevin equation,

$${\zeta }_R\frac{d{\theta }_R}{dt}=\underset{\begin{array}{c}\text{Torque}\\ \text{from}\hspace{0.17em}\text{stator}\end{array}}{\underbrace{-\frac{\partial V_{RS}}{\partial {\theta }_R}}}-\underset{\begin{array}{c}\text{Electrostatic}\\ \text{attraction}\end{array}}{\underbrace{\frac{\partial \psi }{\partial {\theta }_R}R}}-\underset{\begin{array}{c}\text{Connection}\\ \text{to}\hspace{0.17em}\text{load}\end{array}}{\underbrace{\kappa \left({\theta }_R-{\theta }_L\right)}}+\underset{\text{Thermal}\hspace{0.17em}\text{fluctuations}}{\underbrace{\sqrt{2{\mathrm{k}}_{\mathrm{B}}\mathrm{T}{\zeta }_R}{f}_n\left(t\right),}}$$ [2]

where ${\zeta }_R$ is the effective rotor drag coefficient. Finally, the dynamics of the load are then driven by the motion of the rotor,

$${\zeta }_L\frac{d{\theta }_L}{dt}=\underset{\begin{array}{c}\text{Spring}\hspace{0.17em}\text{connection}\\ \text{to}\hspace{0.17em}\text{rotor}\end{array}}{\underbrace{\kappa \left({\theta }_R-{\theta }_L\right)}}+\underset{\text{Thermal}\hspace{0.17em}\text{fluctuations}}{\underbrace{\sqrt{2{\mathrm{k}}_{\mathrm{B}}\mathrm{T}{\zeta }_L}{f}_n\left(t\right).}}$$ [3]

As above, ${\zeta }_L$ is the effective drag coefficient of the load. All parameter values are provided in Table 1.

Table 1.

List of parameters with units, values, and reference

Parameter	Definition	Units	Values	Reference
R	radius of the rotor	nm	20	(1)
$r_S$	radius of the stator	nm	2	—
${\ell }_P$	length of the proline hinge arm	nm	7	(13)
${\zeta }_S$	drag coefficient of the stator	pN⋅nm⋅s⋅rad−1	0.0002	—
${\zeta }_R$	drag coefficient of the rotor	pN⋅nm⋅s⋅rad−1	0.017	—
${\zeta }_L$	drag coefficient of the load	pN⋅nm⋅s⋅rad−1	0.0–10	(33)
${\varphi }_S$	angular position of the stator	rad	—	—
${\theta }_R$	angular position of the rotor	rad	—	—
${\theta }_L$	angular position of the load	rad	—	—
κ	hook spring constant	pN⋅nm⋅rad−1	1,000	(34)
N	number of stators	—	1–11	(33)
τ	rotor torque from stator	pN⋅nm	—	—
$f_n$	white noise	—	—	—
$\Psi$	electrostatic potential	—	1.5–2 kBT	—

The above model can be collapsed to explicitly include only the dynamics of a stator with a single loop that generates torque both during its bending (${\varphi }_S^i$ increasing) and unbending (${\varphi }_S^i$ decreasing). This description is isomorphic to the mechanism described previously (see Fig. 5) because the mechanics of the two halves of the power stroke are equivalent as described above. The equations corresponding to this reduced model are provided in SI Text.

As previously (7), we ensure that chemical transitions are localized near potential minima. We choose rate constants for these transitions such that detail balance is maintained. Further details on our modeling of the chemical kinetics, including explicit forms of the rate constants, is provided in SI Text.

Model Equations

In Materials and Methods, we presented Langevin equations describing the dynamics of the two stator loops, the rotor, and the load. As described previously, the mechanics of the two stator loops are equivalent. Here, we provide a reduced model describing the dynamics of a stator with a single loop that generates torque both during bending (${\varphi }_S$ increasing) and unbending (${\varphi }_S$ decreasing). This model is isomorphic to the one described in the main text.

As described in Mechanochemical Model (and in ref. 5), the motion of the stator has two components: vertical and rotational. The vertical motion is necessary to describe partial power strokes and loose chemical coupling. The stator’s ion-binding residue (Asp32) is very close to the cytoplasmic side of the membrane, and so the reaction coordinate for ion binding and release likely depends on both the stator’s vertical z and rotational position ${\varphi }_S$.

Moreover, thermal fluctuations allow rapid movements of the Asp32 residue into the membrane and the cytoplasm, leading to an increased probability for the unbinding of ions before the power stroke is completed. This coupled reaction coordinate may also account for a reduction in the overall efficiency of the stator due to ion leakage. Furthermore, inclusion of the vertical motion of the stator allows consideration of the stator springs that connect MotB residues to the peptidoglycan layer of the bacterial cell wall (35, 36).

$$\mathbf{Stator}\left(\mathbf{rotation}\right)\mathbf{:}{\zeta }_S\frac{d{\varphi }_S}{dt}=\underset{\begin{array}{c}\text{Internal}\hspace{0.17em}\text{flexibility}\\ \text{of}\hspace{0.17em}\text{stator}\end{array}}{\underbrace{K\left(z-f\left({\varphi }_S\right)\right)}}-\underset{\begin{array}{c}\text{Torque}\hspace{0.17em}\text{from}\\ \text{Proline}\hspace{0.17em}\text{hinge}\end{array}}{\underbrace{\frac{\partial G\left({\varphi }_S,j\right)}{\partial {\varphi }_S}{\ell }_p}}-\underset{\begin{array}{c}\text{Reaction}\\ \text{from}\hspace{0.17em}\text{rotor}\end{array}}{\underbrace{\frac{\partial V_{RS}}{\partial {\varphi }_S}}}-\underset{\begin{array}{c}\text{Electrostatic}\\ \text{attraction}\end{array}}{\underbrace{\frac{\partial \psi }{\partial {\varphi }_S}{\ell }_p}}+\underset{\text{Thermal}\hspace{0.17em}\text{fluctuations}}{\underbrace{\sqrt{2{\mathrm{k}}_{\mathrm{B}}\mathrm{T}{\zeta }_S}{f}_n\left(t\right)}}$$ [S1]

$$\mathbf{Stator}\left(\mathbf{vertical}\right)\mathbf{:}{\tilde{\zeta }}_S\frac{d{z}_S}{dt}=-\underset{\begin{array}{c}\text{Internal}\hspace{0.17em}\text{flexibility}\\ \text{of}\hspace{0.17em}\text{stator}\end{array}}{\underbrace{K\left(z-f\left({\varphi }_S\right)\right)}}-\underset{\begin{array}{c}\text{Reaction}\\ \text{from}\hspace{0.17em}\text{rotor}\end{array}}{\underbrace{k_s\left(z-z^0\right)}}+\underset{\text{Thermal}\hspace{0.17em}\text{fluctuations}}{\underbrace{\sqrt{2{\mathrm{k}}_{\mathrm{B}}\mathrm{T}{\tilde{\zeta }}_S}{f}_n\left(t\right)}}$$ [S2]

$$\mathbf{Rotor}\mathbf{:}{\zeta }_R\frac{d{\theta }_R}{dt}=-\underset{\begin{array}{c}\text{Spring}\hspace{0.17em}\text{connection}\\ \text{to}\hspace{0.17em}\text{load}\end{array}}{\underbrace{\kappa \left({\theta }_R-{\theta }_L\right)}}-\underset{\begin{array}{c}\text{Torque}\\ \text{from}\hspace{0.17em}\text{stator}\end{array}}{\underbrace{\frac{\partial V_{RS}}{\partial {\theta }_R}}}-\underset{\begin{array}{c}\text{Electrostatic}\\ \text{attraction}\end{array}}{\underbrace{\frac{\partial \psi }{\partial {\theta }_R}R}}+\underset{\text{Thermal}\hspace{0.17em}\text{fluctuations}}{\underbrace{\sqrt{2{\mathrm{k}}_{\mathrm{B}}\mathrm{T}{\zeta }_R}{f}_n\left(t\right)}}$$ [S3]

$$\mathbf{Load}\mathbf{:}{\zeta }_L\frac{d{\theta }_L}{dt}=\underset{\begin{array}{c}\text{Spring}\hspace{0.17em}\text{connection}\\ \text{to}\hspace{0.17em}\text{rotor}\end{array}}{\underbrace{\kappa \left({\theta }_R-{\theta }_L\right)}}+\underset{\text{Thermal}\hspace{0.17em}\text{fluctuations}}{\underbrace{\sqrt{2{\mathrm{k}}_{\mathrm{B}}\mathrm{T}{\zeta }_L}{f}_n\left(t\right).}}$$ [S4]

Here, as before, ${\zeta }_S$, ${\zeta }_R$, and ${\zeta }_L$ are the effective rotational drag coefficients of the stator, rotor, and load; $\widetilde{{\zeta }_S}$ is the linear drag coefficient of the stator. The last term in each equation is the stochastic Brownian force, where $f_n\left(t\right)$ is uncorrelated white noise. All other symbols are as described in Table 1. In writing the equations of motion, we assume that the stator rotates about the proline hinge. Similarly, the rotor rotates about the axis normal to the plane of the rotor and passing through its center.

In Eq. S1, the internal force driving the stator due to the rearrangement of hydrogen bonds caused by a proton-binding event is denoted by $F_p=-\frac{\partial G}{\partial {\varphi }_S}$. Here, $G\left({\varphi }_S,j\right)$ denotes the free energy of the stator. Due to the fact that thermal fluctuations are of a comparable magnitude to the free energies considered, the exact shape of the potentials is relatively unimportant. For ease of computation, we approximate the potential using a piecewise linear function. The exact mathematical formulation of these potentials is given in Interaction Potentials. In this setup, for a given proton motive force, the force applied on the rotor by the stator loop is constant and positive during each mechanical power stroke. At other times, there is little elastic strain on the MotA loops, and accordingly, the applied force is near zero.

Eq. S2 governs the vertical motion of the MotB helix. The proposed kink-and-swivel motion of the MotA α-helices (see Fig. 3) may also shift the vertical position of the associated MotB helix. This collective motion would bring Asp32 residue into the cytoplasm during a power stroke. Here, K denotes the internal flexibility of the rotor and couples the motion of the proline-induced kink and swivel motion of MotA and the vertical motion of MotB helices. This coefficient is dependent on the hydrogen bonds between the MotA and MotB helices. For a perfect stator, the motion of the MotA and MotB helices are tightly coupled. The vertical motion of the stator complex is also determined by the stiffness coefficient $k_S$ of the springs connecting the MotB helix to the peptidoglycan layer.

The torque generated by the stator is dependent on the applied load ${\zeta }_L$ as a natural consequence of steric forces. A general discussion on contact forces and the explicit formulation of the repulsive interaction potential $V_{RS}$, are provided in Overview of Steric Forces and Rotor–stator interaction potential, respectively. The contact torque applied to the rotor (in Eq. S3), and consequent reaction torque applied to the stator (in Eq. S1), are given by ${\tau }_{\text{contact}}=-\frac{\partial V_{RS}}{\partial {\theta }_R}$ and ${\tau }_{\text{reaction}}=-\frac{\partial V_{RS}}{\partial {\varphi }_S}$.

Additionally, the charges on the FliG and the stator loop also exert weak attractive forces on each other. These forces prevent the drifting of the rotor with respect to the stator during the chemical transition events. Further discussion of these forces is included later in Electrostatic Steering. In the above equations, we denote this term via the term $-\frac{\partial \psi }{\partial {\theta }_R}R$; it detracts from the repulsive torque imposed by the steric force of the stator.

The rotor and load are connected by a linear spring with constant κ; the elastic coupling terms in the equations for the rotor and the load thus appear with opposite signs (in Eqs. S3 and S4, respectively). The elastic constant in the experiments can vary depending on the length of the hook when attaching the bead. In some cases, the hook is very short or is stiffened by an antibody linker. This corresponds to a large spring coefficient (34). An analysis of this model in the corresponding limit $\kappa \to \infty$ is provided in Approximation: Model Without Spring.

For the computations in this manuscript, we have assumed that the stator is internally rigid—that is, the internal spring coefficient K is very large. This leads to a tightly coupled motion between the rotation and the vertical motion of the stator (i.e., $z=f\left({\varphi }_S\right)$), and allows us to ignore the thermal fluctuations and the effect of the peptidoglycan springs. A soft connection between the stator and the peptidoglycan layer was originally assumed to explain resurrection experiments showing that the zero-torque speed was independent of stator number (36). However, recent reports that these low-load experiments were likely performed on motors with a single stator (2) remove the need for the assumption of soft stator springs. Given this, we obtain the following reduced set of equations for the motion of the stator, rotor, and load:

$$\mathbf{Stator}\mathbf{:}{\zeta }_S\frac{d{\varphi }_S}{dt}=-\underset{\begin{array}{c}\text{Torque}\hspace{0.17em}\text{from}\\ \text{Proline}\hspace{0.17em}\text{hinge}\end{array}}{\underbrace{\frac{\partial G\left({\varphi }_S,j\right)}{\partial {\varphi }_S}{\ell }_p}}-\underset{\begin{array}{c}\text{Reaction}\\ \text{from}\hspace{0.17em}\text{rotor}\end{array}}{\underbrace{\frac{\partial V_{RS}}{\partial {\varphi }_S}}}-\underset{\begin{array}{c}\text{Electrostatic}\\ \text{attraction}\end{array}}{\underbrace{\frac{\partial \psi }{\partial {\varphi }_S}{\ell }_p}}+\underset{\text{Thermal}\hspace{0.17em}\text{fluctuations}}{\underbrace{\sqrt{2{\mathrm{k}}_{\mathrm{B}}\mathrm{T}{\zeta }_S}{f}_n\left(t\right)}}$$ [S5]

$$\mathbf{Rotor}\mathbf{:}{\zeta }_R\frac{d{\theta }_R}{dt}=-\underset{\begin{array}{c}\text{Torque}\\ \text{from}\hspace{0.17em}\text{stator}\end{array}}{\underbrace{\frac{\partial V_{RS}}{\partial {\theta }_R}}}-\underset{\begin{array}{c}\text{Electrostatic}\\ \text{attraction}\end{array}}{\underbrace{\frac{\partial \psi }{\partial {\theta }_R}R}}-\underset{\begin{array}{c}\text{Spring}\hspace{0.17em}\text{connection}\\ \text{to}\hspace{0.17em}\text{load}\end{array}}{\underbrace{\kappa \left({\theta }_R-{\theta }_L\right)}}+\underset{\text{Thermal}\hspace{0.17em}\text{fluctuations}}{\underbrace{\sqrt{2{\mathrm{k}}_{\mathrm{B}}\mathrm{T}{\zeta }_R}{f}_n\left(t\right)}}$$ [S6]

$$\mathbf{Load}\mathbf{:}{\zeta }_L\frac{d{\theta }_L}{dt}=\underset{\begin{array}{c}\text{Spring}\hspace{0.17em}\text{connection}\\ \text{to}\hspace{0.17em}\text{rotor}\end{array}}{\underbrace{\kappa \left({\theta }_R-{\theta }_L\right)}}+\underset{\text{Thermal}\hspace{0.17em}\text{fluctuations}}{\underbrace{\sqrt{2{\mathrm{k}}_{\mathrm{B}}\mathrm{T}{\zeta }_L}{f}_n\left(t\right).}}$$ [S7]

We use Eqs. S5–S7 to obtain the majority of the results presented in the main text.

Simplified Deterministic Model

By taking an average over many trajectories, it is possible to generate a deterministic analog of the model presented above. Although numerical simulations on the full stochastic model were used for the results in this manuscript, the below formulation is convenient primarily for expository purposes. In particular, it admits explicit analytic solutions for many experimental situations. Before we provide the numerical implementation of the full Langevin equations (Eqs. S5–S7), we use the following model to introduce several important concepts.

The deterministic equations of motion can be obtained by time averaging Eqs. S5–S7 as

$${\zeta }_S\frac{d{\varphi }_S}{dt}=F_p{\ell }_p-\frac{\langle \tau \rangle }{R}{\ell }_p$$ [S8]

$${\zeta }_R\frac{d{\theta }_R}{dt}=\langle \tau \rangle -\kappa \left({\theta }_R-{\theta }_L\right)$$ [S9]

$${\zeta }_L\frac{d{\theta }_L}{dt}=\kappa \left({\theta }_R-{\theta }_L\right).$$ [S10]

Note that in addition to time averaging, we have neglected the electrostatic term for computational convenience, as it tends to be quite small in value. Here, the average torque on the rotor $\langle \tau \rangle$ results from averaging the torque on the rotor as ${\tau }_{\text{contact}}=-\partial V_{RS}/\partial {\theta }_R$ over many trajectories. The return force then can be calculated by $\langle \tau \rangle /R$, which is then multiplied by ${\ell }_p$ to calculate the return torque. The internal torque of the proline hinge for a given IMF is $F_p{\ell }_p=-\frac{\partial G}{\partial {\varphi }_S}\propto \text{IMF}$. The averaged equations do not contain a noise term because the terms $f_n\left(t\right)$ are Gaussian with mean zero. In the following, we compute expressions for the average torque and speed during a single power stroke of the motor from the above deterministic model.

Under the assumption that all active stators act in synchrony, Eq. S8 can be generalized to a motor with N stators as follows. An analog of Eq. S8 now corresponds to the motion of the ith stator ($i\in \mathrm{1,2},\dots N$),

$${\zeta }_S\frac{d{\varphi }_S^i}{dt}=F_p{\ell }_p-\frac{\langle {\tau }_i\rangle }{R}{\ell }_p,\hspace{1em}i\in \mathrm{1,2},\dots ,N.$$ [S11]

We then can sum the equations of all stators, which results in

$$N{\zeta }_S\frac{d{\varphi }_S^i}{dt}=N{F}_p{\ell }_p-\frac{\langle \tau \rangle }{R}{\ell }_p.$$ [S12]

Note that we have used the fact that $N\langle {\tau }_i\rangle =\langle \tau \rangle$. Similarly, an equation for the rotor in a motor with multiple stators can be written as

$${\zeta }_R\frac{d{\theta }_R}{dt}={\displaystyle \sum _{i=1}^N\langle {\tau }^i\rangle -\kappa \left({\theta }_R-{\theta }_L\right)}=\langle \tau \rangle -\kappa \left({\theta }_R-{\theta }_L\right),$$ [S13]

which is the same form as Eq. S9. Note that only the terms corresponding to the stators are summed (i.e., the connection term between the rotor and the load is not multiplied by N). Eq. S10 also remains as for the single-stator case because the spring connection term is unaffected by the addition of torque-generating units.

The three equations of motion, Eqs. S8–S10, for a single stator contain four unknowns $\left\{{\theta }_R,{\theta }_L,{\varphi }_S,\langle \tau \rangle \right\}$. This results in an indeterminate system, and requires the addition of an equation to generate a unique solution. This additional equation can be obtained from a fundamental property of contact forces. Because the stator loop is in contact with the rotor during the power stroke, the velocities of the stator loop and the rotor must be equal. This leads to a contact condition for the tangential velocities of the stator loop and the rotor,

$$\begin{array}{|c|}\hline {\ell }_p\frac{d{\varphi }_S}{dt}=R\frac{d{\theta }_R}{dt}.\\ \hline\end{array}$$ [S14]

Analysis.

Multiplying Eq. S12 by $R/{\ell }_p$ and summing with Eq. S9 gives

$$\frac{NR{\zeta }_S}{{\ell }_p}\frac{d{\varphi }_S}{dt}+{\zeta }_R\frac{d{\theta }_R}{dt}=N{F}_{p}R-\kappa \left({\theta }_R-{\theta }_L\right).$$ [S15]

Rearranging Eq. S14, we get

$$\frac{d{\varphi }_S}{dt}=\frac{R}{{\ell }_p}\frac{d{\theta }_R}{dt}.$$ [S16]

Substituting into Eq. S15,

$$\begin{array}{c}\frac{N{R}^2{\zeta }_S}{{\ell }_p^2}\frac{d{\theta }_R}{dt}+{\zeta }_R\frac{d{\theta }_R}{dt}=N{F}_{p}R-\kappa \left({\theta }_R-{\theta }_L\right)\\ {\zeta }_R\frac{d{\theta }_R}{dt}\left(\frac{N{R}^2{\zeta }_S}{{\ell }_p^2{\zeta }_R}+1\right)=N{F}_{p}R-\kappa \left({\theta }_R-{\theta }_L\right)\\ {\zeta }_R\frac{d{\theta }_R}{dt}\left(NM+1\right)=N{F}_{p}R-\kappa \left({\theta }_R-{\theta }_L\right),\end{array}$$ [S17]

where $M=\left(R^2{\zeta }_S\right)/\left({\ell }_p^2{\zeta }_R\right)$. Rewriting Eq. S17 gives us

$$\frac{d{\theta }_R}{dt}=\frac{N{F}_{p}R}{{\zeta }_R\left(NM+1\right)}-\frac{\kappa }{{\zeta }_R\left(NM+1\right)}\left({\theta }_R-{\theta }_L\right).$$ [S18]

Dividing Eq. S10 by ${\zeta }_L$ and subtracting Eq. S18 leads to

$$\frac{d\left({\theta }_R-{\theta }_L\right)}{dt}=\frac{F_{p}R}{{\zeta }_R\left(NM+1\right)}-\kappa \left(\frac{1}{{\zeta }_R\left(NM+1\right)}+\frac{1}{{\zeta }_L}\right)\left({\theta }_R-{\theta }_L\right).$$ [S19]

This differential equation has the solution

$$\begin{array}{|c|}\hline \left({\theta }_R-{\theta }_L\right)\left(t\right)=\frac{A^{*}\left(1-e^{-{\alpha }^{*}t}\right)}{{\alpha }^{*}},\\ \hline\end{array}$$ [S20]

where $A^{*}≔F_{p}R/\left[{\zeta }_R\left(NM+1\right)\right]$ and ${\alpha }^{*}≔\kappa \left(\left[1/{\zeta }_R\left(NM+1\right)\right]+\left(1/{\zeta }_L\right)\right)$.

Substituting expressions for $d{\varphi }_S/dt$ and $d{\theta }_R/dt$ from Eqs. S12 and S9, respectively, into the equation for contact condition (Eq. S14) leads to

$$\frac{{\ell }_p^2}{N{\zeta }_S}\left(N{F}_{p}R-\tau \right)=\frac{R^2}{{\zeta }_R}\left[\tau -\kappa \left({\theta }_R-{\theta }_L\right)\right].$$ [S21]

Note that, because we are interested in the full time course, we consider $\tau =\tau \left(t\right)$ rather than the average torque $\langle \tau \rangle$. Rearranging and solving for τ,

$$\tau =\frac{N{\zeta }_{R}R\left[F_p{\ell }_p^2-{\zeta }_{S}R\kappa \left({\theta }_R-{\theta }_L\right)\right]}{{\zeta }_R{\ell }_p^2+N{\zeta }_S{R}^2}.$$ [S22]

Plugging in the derived expression for $\left({\theta }_R-{\theta }_L\right)$ from Eq. S20,

$$\tau =\frac{F_p{\ell }_p^{2}NR{\zeta }_R{\zeta }_S\left[\frac{1}{{\zeta }_S}+\frac{\left(1-\text{exp}\left[\kappa t\left(\frac{1}{{\zeta }_L}+\frac{1}{{\zeta }_R+N{R}^2{\zeta }_S/{\ell }_p^2}\right)\right]\right)N{R}^2{\zeta }_S}{{\zeta }_R\left({\ell }_p^2\left({\zeta }_L+{\zeta }_R\right)+N{R}^2{\zeta }_S\right)}\right]}{{\ell }_p^2{\zeta }_R+N{R}^2{\zeta }_S}.$$ [S23]

From this value, we can calculate the average torque in a single step $\langle \tau \rangle$ by

$$\begin{array}{|c|}\hline \langle \tau \rangle =\frac{1}{T_m}{\displaystyle \underset{0}{\overset{T_m}{\int }}\tau \left(t\right)dt}\\ =\frac{F_p{\ell }_p^{2}NR\left(\left(-1+\exp \left[\kappa T_m\left(-\frac{1}{{\zeta }_L}-\frac{1}{{\zeta }_R+N{R}^2{\zeta }_S/{\ell }_p^2}\right)\right]\right)N{R}^2{\zeta }_L^2{\zeta }_S+\kappa T_m\left({\zeta }_L+{\zeta }_R\right)\left({\ell }_p^2\left({\zeta }_L+{\zeta }_R\right)+N{R}^2{\zeta }_S\right)\right)}{\kappa T_m{\left({\ell }_p^2\left({\zeta }_L+{\zeta }_R\right)+N{R}^2{\zeta }_S\right)}^2}\\ \hline\end{array}$$ [S24]

where $T_m$ is the time spent moving during a step. Likewise, we can also calculate the speed of the load $d{\theta }_L/dt$ from Eqs. S10 and S20,

$$\frac{d{\theta }_L}{dt}=\frac{1}{{\zeta }_L}\kappa \left({\theta }_R-{\theta }_L\right)=\frac{\left(1-\exp \left[-\kappa t\left(\frac{1}{{\zeta }_L}+\frac{1}{{\zeta }_R+N{R}^2{\zeta }_S/{\ell }_p^2}\right)\right]\right)F_p{\ell }_p^{2}NR}{{\ell }_p^2\left({\zeta }_L+{\zeta }_R\right)+N{R}^2{\zeta }_S}.$$ [S25]

As with torque, we integrate over a time step to find the average speed $\langle d{\theta }_L/dt\rangle$,

$$\begin{array}{|c|}\hline \langle \frac{d{\theta }_L}{dt}\rangle =\frac{F_p{\ell }_p^{2}NR\left[\left(-1+\exp \left[\kappa T_m\left(-\frac{1}{{\zeta }_L}-\frac{1}{{\zeta }_R+N{R}^2{\zeta }_S/{\ell }_p^2}\right)\right]\right){\zeta }_L\left({\ell }_p^2{\zeta }_R+N{R}^2{\zeta }_S\right)+\kappa T_m\left(L^2\left({\zeta }_L+{\zeta }_R\right)+N{R}^2{\zeta }_S\right)\right]}{\kappa T_m{\left({\ell }_p^2\left({\zeta }_L+{\zeta }_R\right)+N{R}^2{\zeta }_S\right)}^2}.\\ \hline\end{array}$$ [S26]

Using Eqs. S24 and S26, we can calculate a family of parametric torque−speed curves (parametrized by the load ${\zeta }_L$), where each curve corresponds to a motor with a constant number of synchronously stepping stators. Computed curves for motors with $\mathrm{1,2},\dots ,7$ stators are shown in Fig. S4.

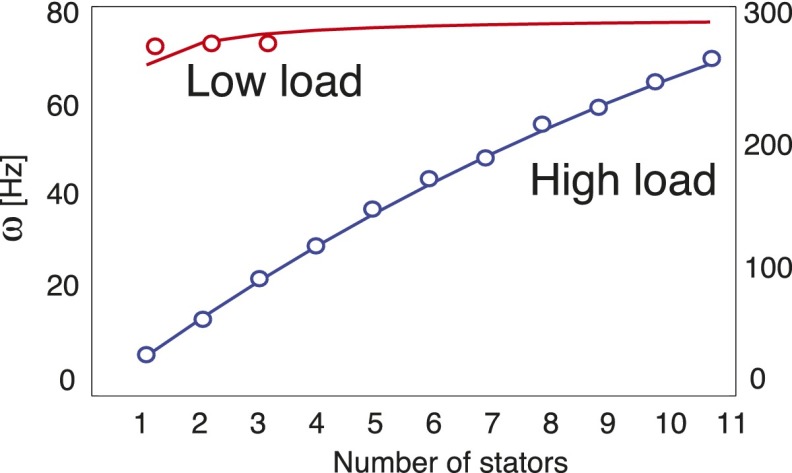
Fig. S4.

Resurrection experiments at high and low load both show a nonlinear relationship between motor speed and stator number. Our model suggests that nonlinearities at high load may result from the nature of steric forces. Markers denote data from ref. 35; lines are model fits assuming synchronously stepping stators.

Fig. S1.

(A) Rotor speed and (B) torque as a function of the load drag. ${\zeta }_L$. Plotted from Eqs. S26 and S24, respectively.

Fig. S2.

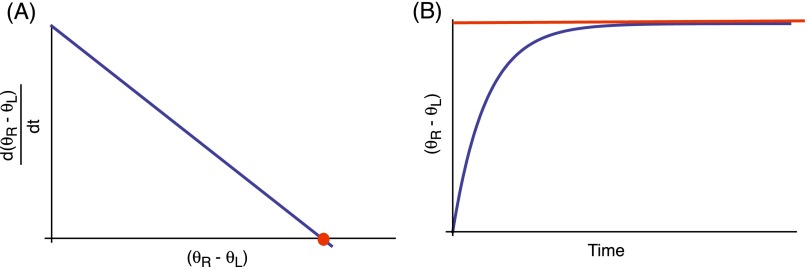
Angular difference between rotor and load. (A) The change in $\left({\theta }_R-{\theta }_L\right)$ with time decreases steadily until a fixed point is reached (marked in red). (B) Accordingly, $\left({\theta }_R-{\theta }_L\right)$ increases and asymptotically reaches a steady state. The steady state is denoted by a red line, corresponding to the zero of $\left[d\left({\theta }_R-{\theta }_L\right)\right]/dt$, shown as the red dot in A.

Approximation: Model Without Spring.

In most experimental setups, the filament is removed and a bead is attached to a shortened hook connection. Additionally, the hook is sometimes stiffened with an antibody linker. These setups have a rigid connection between the rotor and the load, corresponding to a large spring constant. In this section, we perform a similar analysis to that in Analysis for the limit $\kappa \to \infty$. The calculations performed in this section provide analytic formulas for a clear physical understanding of several important properties of the model.

The rotation rates of the rotor and load become equal after an initial wind-up period. That is, the rotor and load move at the same angular speed (i.e., $d{\theta }_R/dt=d{\theta }_L/dt$) after the system reaches a steady state. Note, however, that the angular positions ${\theta }_R$ and ${\theta }_L$ still maintain a (constant) offset. This can be seen explicitly by subtracting Eqs. S9 and S10,

$$\begin{array}{l}\frac{d{\theta }_R}{dt}-\frac{d{\theta }_L}{dt}=\frac{\langle \tau \rangle }{{\zeta }_R}-\kappa \left(\frac{1}{{\zeta }_R}+\frac{1}{{\zeta }_L}\right)\left({\theta }_R-{\theta }_L\right)\\ \frac{d\left({\theta }_R-{\theta }_L\right)}{dt}=\frac{\langle \tau \rangle }{{\zeta }_R}-\kappa \left(\frac{1}{{\zeta }_R}+\frac{1}{{\zeta }_L}\right)\left({\theta }_R-{\theta }_L\right).\end{array}$$ [S27]

To simplify some notation, we define $x≔\left({\theta }_R-{\theta }_L\right)$, $\alpha ≔\kappa \left[\left(1/{\zeta }_R\right)+\left(1/{\zeta }_L\right)\right]$ and $A≔\langle \tau \rangle /{\zeta }_R$, and rewrite Eq. S27,

$$\frac{dx}{dt}=A-\alpha x.$$ [S28]

As in Analysis, we can solve for the time course $x\left(t\right)=\left({\theta }_R-{\theta }_L\right)\left(t\right)$,

$$\begin{array}{|c|}\hline x\left(t\right)=\left({\theta }_R-{\theta }_L\right)\left(t\right)=\frac{A\left(1-e^{-\alpha t}\right)}{\alpha }.\\ \hline\end{array}$$ [S29]

By definition, $\alpha >0$, and so it is clear that $x\left(t\right)$ will reach a constant value after an initial startup. As $\kappa \to \infty$, the wind-up time goes to zero and $d{\theta }_R/dt=d{\theta }_L/dt$ in this limit.

Summing Eqs. S9 and S10 gives us

$${\zeta }_R\frac{d{\theta }_R}{dt}+{\zeta }_L\frac{d{\theta }_L}{dt}=\langle \tau \rangle .$$ [S30]

We approximate $\frac{d{\theta }_R}{dt}=\frac{d{\theta }_L}{dt}$ when κ is large, and Eq. S30 reduces to

$$\left({\zeta }_R+{\zeta }_L\right)\frac{d{\theta }_R}{dt}=\langle \tau \rangle .$$ [S31]

We multiply Eqs. S12 and S31 by ${\ell }_p$ and R, respectively. After some algebra,

$${\ell }_p\frac{d{\varphi }_S}{dt}=\frac{{\ell }_p^2}{N{\zeta }_S}\left(N{F}_p-\frac{\langle \tau \rangle }{R}\right)$$ [S32]

$$R\frac{d{\theta }_R}{dt}=\frac{R\langle \tau \rangle }{\left({\zeta }_L+{\zeta }_R\right)}.$$ [S33]

Given the relationship S14, we equate the two right-hand sides of Eqs. S32 and S33,

$$\begin{array}{c}\frac{{\ell }_p^2}{N{\zeta }_S}\left(N{F}_p-\frac{\langle \tau \rangle }{R}\right)=\frac{R\langle \tau \rangle }{\left({\zeta }_L+{\zeta }_R\right)}\\ \frac{{\ell }_p^{2}R}{{\zeta }_S}\left(N{F}_{p}R-\langle \tau \rangle \right)=\frac{N{R}^2\langle \tau \rangle }{\left({\zeta }_L+{\zeta }_R\right)}.\end{array}$$ [S34]

Here, the second line is obtained simply by multiplying through by N and R. Solving for $\langle \tau \rangle$,

$$\begin{array}{|c|}\hline \langle \tau \rangle =\frac{N{F}_{p}R}{\left(1+\frac{N{R}^2{\zeta }_S}{\left({\zeta }_L+{\zeta }_R\right){\ell }_p^2}\right)}.\\ \hline\end{array}$$ [S35]

We can use this expression to attempt some intuition for the result of Sowa et al. (16) regarding torque and stator number at high and low loads. Consider the following two limits of Eq. S35: (i) high load, when ${\zeta }_L\gg {\zeta }_R$, and (ii) low load, where ${\zeta }_L\ll {\zeta }_R$.

In the first case, we have

$${\langle \tau \rangle }_{\text{high}}=\frac{N{F}_{p}R}{\left(1+\frac{N{R}^2{\zeta }_S}{\left({\zeta }_L+{\zeta }_R\right){\ell }_p^2}\right)}\approx \frac{N{F}_{p}R}{\left(1+\frac{N{R}^2{\zeta }_S}{{\zeta }_L{\ell }_p^2}\right)}\approx N{F}_{p}R.$$ [S36]

The third line follows from the fact that ${\zeta }_S<{\zeta }_R\ll {\zeta }_L$. For very high loads, the observed torque is 180 pN⋅nm, and therefore the force $F_p\approx 9.5$ pN. Eq. S36 suggests that the torque increases linearly with stator number under extremely large loads as observed in the experiments. However, for a given ${\zeta }_L$, it can be seen that nonlinearities can arise in the torque versus number of stators even in the high load limit. This property is primarily due to the nature of contact forces, and is not applicable to previous models that assume constant torque between stator and rotor.

Conversely, at low loads (${\zeta }_L/{\zeta }_R\ll 1$),

$${\langle \tau \rangle }_{\text{low}}=\frac{N{F}_{p}R}{\left(1+\frac{N{R}^2{\zeta }_S}{\left({\zeta }_L+{\zeta }_R\right){\ell }_p^2}\right)}\approx \frac{N{F}_{p}R}{\left(1+\frac{N{R}^2{\zeta }_S}{{\zeta }_R{\ell }_p^2}\right)}.$$ [S37]

The torque measured at high speeds is ∼20 pN⋅nm (3). Then, from Eq. S37, the nondimensional number $N{R}^2{\zeta }_S/{\zeta }_R{\ell }_p^2\approx 10$. Also, Eq. S37 shows that the torque and speed are not linearly dependent on the number of stators at low loads. This is consistent with previous experimental observations (35).

The above approximations to the full model are primarily laid out for expository purposes, to introduce general properties of the model. As such, there are several limitations due to the assumptions made, which we outline below.

Firstly, the observations from Sowa et al. are under question given that motors with more than one (or a few) stator may not have been considered in low-load measurements. To determine whether the stators do indeed act independently or in synchrony, experiments that directly account for the number of active stators must be performed. The extension of our model to N stators is dependent on the assumption that all stators step in synchrony, and the above results will not hold if stators are independent stochastic steppers. Because of the recent measurements made on single-stator motors, we have chosen to largely focus on the explicit modeling of the intrinsic mechanism of torque generation in the BFM rather than on the potential interaction between stators. Although a thorough exploration of the dynamics of multiple-stator motors is extremely worthwhile, it is out of the scope of the current paper.

There are also some inconsistencies in the approximation of an infinitely stiff spring at intermediate and low loads when the motor is not in the mechanically limited regime. We have that ${\ell }_p\approx$ 7 nm, $R\approx$ 20 nm, and the nondimensional number $N{R}^2{\zeta }_S/{\zeta }_R{\ell }_p^2\approx 10$ at low loads. Then, from Eq. S37, the ratio of the stator and rotor drags ${\zeta }_S/{\zeta }_R\approx 1$. Using this, we can estimate the viscosities of the stator and rotor. The drag of the rotor is given by

$${\zeta }_R=\frac{32}{3}{\eta }_R{R}^3,$$ [S38]

where ${\eta }_R$ is the viscosity of the rotor. An estimate for the drag coefficient of the stator can be obtained by using Eq. S31 and the maximum observed speed of the wild-type motor (200 Hz), yielding ${\zeta }_S=0.017$ pN⋅nm⋅s⋅rad⁻¹. Because the drag ratio of the stator and rotor is approximately unity, ${\zeta }_R\approx 0.017$ pN⋅nm⋅s⋅rad⁻¹. Using Eq. S38, the viscosity of the rotor is ∼2 poise. This is consistent with the fact that the cytoplasm is a mixture of water and proteins (1).

Likewise, the drag coefficient of the stator loop with a lever arm of length ${\ell }_p$ is given by

$${\zeta }_S=\frac{\pi }{3}\frac{{\eta }_S{\ell }_p^3}{\log \left(\frac{{\ell }_p}{R_p}\right)-0.66},$$ [S39]

where ${\eta }_S$ is the viscosity of the stator and $R_p$ is the radius of the stator loop. Then, using Eq. S39 and a length to width ratio ${\ell }_p/R_p\approx 10$, we estimate the viscosity of the stator to be 800 poise. This value is three orders of magnitude higher than the viscosity of a regular lipid membrane and two orders of magnitude higher than the viscosity of a biological membrane. As this calculation of stator drag arises from estimates of limiting speed, it ignores the contribution of the kinetics of ion movement, particularly the diffusion-limited arrival at the channel ($T_W$). The discrepancy between this estimated drag coefficient and biologically reasonable values highlights the importance of the inclusion of chemical kinetics in the model, which are detailed in Addition of Chemical Kinetics.

Moreover, the torque−speed curves produced by the stiff-spring approximation are linear, in contrast to the concave-down torque speed curves observed in single-stator motors (3). Because the IMF enters only through the dependence of the torque, the speed−IMF curves are also linear at all loads, again in contrast to the recent 100-nm bead experiments on a single stator (3).

Addition of Chemical Kinetics.

The linear torque−speed curves of a mechanically rate-limiting model elucidate the importance of the inclusion of ion-binding kinetics. In this case, these are events related to the binding of a cation from the periplasm to Asp32 and the unbinding of the cation from Asp32 into the cytoplasm. In this section, we recompute model torque−speed curves explicitly including the dwell times corresponding to the ion-binding and unbinding events between the power strokes.

As done by Meacci and Tu (8), a torque generation cycle is divided into two parts: (i) moving time $T_m$ and (ii) waiting time $T_w$. Assuming that the ions bind only when the stators are around the minimum of the respective free-energy potentials, we may use the above model during $T_m$ and sample $T_w$ from an exponential distribution at the end of each moving step.

In a motor with a single stator ($N=1$), the instantaneous torque is obtained from Eq. S35 as

$$\tau =\frac{F_{p}R}{\left(1+\frac{R^2{\zeta }_S}{\left({\zeta }_L+{\zeta }_R\right){\ell }_p^2}\right)}.$$ [S40]

The force applied by the proline hinge is given as $F_p=-\left(\mathrm{\Delta }G/\mathrm{\Delta }\varphi \right)=-\left(2q\hspace{0.17em}\text{IMF}/\mathrm{\Delta }\varphi \right)$, where q is the charge of the ion. The time required to move an angular distance of 2π/26 in step i can be calculated from Eq. S40 through the relationship $\omega =\tau /\left({\zeta }_R+{\zeta }_L\right)$.

$$T_m^i=T_m=\frac{2\pi }{26}\left({\zeta }_R+{\zeta }_L\right)\left(1+\frac{R^2{\zeta }_S}{\left({\zeta }_L+{\zeta }_R\right){\ell }_p^2}\right)\frac{1}{F_{p}R}.$$ [S41]

Let $T_w^i$ be the waiting time that follows step i. During the waiting time, the instantaneous torque is zero. When the system reaches the steady state, the average torque $\langle \tau \rangle$ can be obtained via a time average

$$\langle \tau \rangle =\underset{T\to \infty }{\text{lim}}\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{\int }}\tau \left(t^{\prime }\right)t^{\prime }},$$ [S42]

where T is large. If there are N steps in time T, then there are N waiting times. Therefore, Eq. S42 can be approximated as

$$\langle \tau \rangle =\underset{T\to \infty }{\text{lim}}\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{\int }}\tau \left(t^{\prime }\right)t^{\prime }}\approx \frac{{\displaystyle {\sum }_{i=1}^N\tau T_m}}{T}=\frac{{\displaystyle {\sum }_{i=1}^N\tau T_m}}{{\displaystyle {\sum }_{i=1}^N{T}_m^i}+{\displaystyle {\sum }_{i=1}^N{T}_w^i}}=\frac{\tau T_m}{T_m+\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{T}_w^i}}.$$ [S43]

The average dwell time $\left(1/N\right){\displaystyle {\sum }_{i=1}^N{T}_w^i}$ can be approximated as $\langle T_w\rangle ={\left[k_0\text{exp}\left(\text{IMF}/{\mathrm{k}}_{\mathrm{B}}\mathrm{T}\right)\right]}^{-1}$, where $k_0$ is a proportionality constant related to the rate of hopping of the ions. Using this, Eq. S43 reduces to

$$\langle \tau \rangle =\frac{\tau T_m}{T_m+\langle T_w\rangle }.$$ [S44]

Likewise, the speed of the rotor (or the bead in the large spring constant limit) can be written as a time average

$$\langle \frac{d{\theta }_R}{dt}\rangle \approx \underset{T\to \infty }{\text{lim}}\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{\int }}\frac{{\theta }_R\left(t^{\prime }\right)}{t^{\prime }}{t}^{\prime }}=\frac{\frac{2\pi }{26T_m}{T}_m}{T_m+\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{T}_w^i}}=\frac{\frac{2\pi }{26T_m}{T}_m}{T_m+\langle T_w\rangle }$$ [S45]

where the instantaneous speed is $\left(2\pi /26\right)\times \left(1/T_m\right)$ during the power stroke and zero during the dwell time.

The torque during a power stroke τ, the time taken by a single step $T_m$, and the dwell time $T_w$ all depend on the IMF. Thus, Eqs. S43 and S45 point to the existence of nonlinearity in the torque−speed and speed−proton motive force (PMF) curves. These curves are presented and explained in Results and Predictions.

Overview of Steric Forces

In this section, we describe our modeling of the steric forces between the stator and the rotor, as well as a general discussion on the nature of contact/steric forces in a low Reynolds number environment. The behavior of objects moving at low Reynolds number is counterintuitive. When the Reynolds number is small, viscous forces dominate over inertial forces and inertia can be ignored (32). In the following, we illustrate some of these properties using a simple linear momentum balance. We can then extend this analysis to angular momentum balances, which are directly relevant to the BFM.

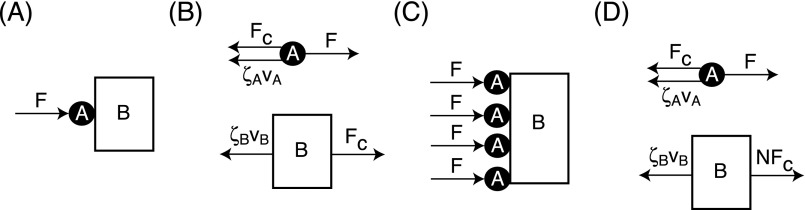
Consider a force F pushing an object A that is in contact with a larger object, B, as shown in Fig. S3. We denote the drag coefficients on objects A and B as ${\zeta }_A$ and ${\zeta }_B$, respectively. Let us consider the following two situations.

Fig. S3.

Contact forces. (A) Case 1. A force F is applied to object A, which is in contact with object B. (B) Free-body diagrams for objects A and B arranged as in case 1. (C) Case 2. N objects of type A are in contact with object B, each with a force F applied to it. (D) Free-body diagrams for each object of type A as well as type B for case 2.

Case 1.

For Case 1, if F is applied to A, how much force is transferred to B when they are in contact, as shown in Fig. S3A? The corresponding free-body diagrams for A and B are shown in Fig. S3B; in the steady state, the force balances can be written as

$$\begin{array}{c}F-F_c-{\zeta }_A{v}_A=0\\ F_c-{\zeta }_A{v}_A=0.\end{array}$$ [S46]

In Eq. S46, $v_A$ and $v_B$ are the velocities of objects A and B, respectively, and $F_c$ is the contact force between objects A and B. When the two objects are in contact and are moving together, the following contact condition ensures that the velocity of the objects are equal:

$$v_A=v_B.$$ [S47]

In this case, the force transferred by A to B (the contact force, $F_c$) is obtained by solving Eq. S46,

$$F_c=\frac{F}{1+{\zeta }_A/{\zeta }_B}.$$ [S48]

When the drag on B is large, i.e., ${\zeta }_A/{\zeta }_B\ll 1$, almost all of force F is transferred to object B. Conversely, when ${\zeta }_A/{\zeta }_B\gg 1$, then most of the force is consumed to drag object A with little force transferred to object B.

Case 2.

Case 2 is when there are N objects of type A in contact with B, each with a force F applied to them. This case is shown in Fig. S3C. As in the first case, we are concerned with how much of F is transferred to B. Again, using free-body diagrams (shown in Fig. S3D), we can write the equations of motion for the objects as

$$\begin{array}{c}F-F_c^i-{\zeta }_A{v}_A^i=0\hspace{1em}i\in \left\{1,\dots ,N\right\},\\ {\displaystyle \sum _{i=1}^N{F}_c^i}-{\zeta }_B{v}_B=0,\end{array}$$ [S49]

where $F_c^i$ is the contact force between the ith object of type A and object B. As before, when the objects are in contact, the contact condition ensures that $v_A^i=v_B$ for all i. Therefore, the force transferred to B by N objects of type A can be derived from Eq. S49 as

$$F_c={\displaystyle \sum _{i=1}^B{F}_c^i}=\frac{NF}{1+N{\zeta }_A/{\zeta }_B}.$$ [S50]

When ${\zeta }_A/{\zeta }_B\ll 1$, $F_c\approx NF$. Therefore, the force transferred is multiplied by the number of objects pushing B. However, when ${\zeta }_A/{\zeta }_B\gg 1$, then the force transferred is $F_c\approx F/\left({\zeta }_A/{\zeta }_B\right)\approx 0.$ Finally, when ${\zeta }_A/{\zeta }_B\approx 1$, then the force transferred is $F_c\approx F$ (i.e., the force transferred in this system is approximately the same as a single object A pushing B).

The above properties of contact forces can be applied to the BFM by identifying object A as the stator and B as the rotor–load system (i.e., the rotor and the bead), and F as the internal force generated by the proline hinge pushing the stator from its straight to bent state.

For large loads (e.g., large beads), almost all of the force generated by the stator is transferred to the rotor; i.e., the torque is close to stall. Moreover, as more stators are recruited, the force transferred increases linearly with the number of active stators, in accordance with the observed linear speed dependence on the number of stators near stall torque. By contrast, at zero load, if there exists a situation where the stator and rotor drags are comparable, then the above analysis suggests that the force transferred during a single step is equivalent to a single stator pushing the rotor. This suggests that, if the assumption that stators step in synchrony holds, torque and speed at low loads may be independent of the number of active stators.

In addition to the above, contact forces also have the following important implications for the BFM: (i) Because it operates at low Reynolds number, the rotor moves only as long as it is pushed by the stator. This assures that the rotor never moves faster than the stator. (ii) Experiments based on torque−speed curves alone may never be able to detect the number of operating stators at different loads (e.g., if both torque and speed are independent of the number of stators at low load). Rather, one likely needs chemical markers such as GFP tags as used in ref. 31 to identify the number of docked and engaged stators for a given load. (iii) The torque generated by the BFM depends on the bead size and is not constant across applied loads, as it was considered to be by previous models (7–9).

Interestingly, the speed of the BFM has been shown to be slightly nonlinearly dependent on the number of stators at high loads (Fig. S4). A linear relationship between speed and stator number would imply (i) that the applied force of the stator is independent of the load and (ii) that all stators act independently. Our results suggest that this nonlinearity may arise as a natural consequence of the steric force in (at least partially) coupled stators. Further experiments will be needed to further explore this hypothesis.

Numerical Implementation

In Model Equations, Simplified Deterministic Model, Approximation: Model without Spring, and Addition of Chemical Kinetics, we have provided the equations of our model, as well as analytic solutions for reduced deterministic approximations. In this section, we provide details on numerical implementation of the full stochastic model, using several arguments from our discussion on steric forces.

Interaction Potentials.

In this section, we provide explicit forms of the free-energy potentials in terms of the order parameters we choose to describe the motion of the stator and the rotor.

Stator potentials.

The order parameter describing the motion of the stator is the angle subtended by the stator loops ${\varphi }_S^{\mathrm{1,3}}$ with respect to the vertical MotB ion channels. When two ions bind to the Asp32 residues, the two loops undergo a conformational change from their straight (${\varphi }_S^{\mathrm{1,3}}=0°$) to bent state (${\varphi }_S^{\mathrm{1,3}}=20°$). In this work, we have assumed that the stator loops move in phase. Therefore, as previously, we model the two-stator loop configurations using a single collective parameter ${\varphi }_S$.

Before the ions bind to the Asp32 residues, the motion of the stators is governed by the potential $G_1\left({\varphi }_S\right)$, where the minimum is around ${\varphi }_S=0°$, as shown in Fig. S5. When two ions bind to two Asp32s, the stator potential switches from $G_1$ to $G_2$. This compels the stator angle to move from ${\varphi }_S=0°$ to ${\varphi }_S=20°$.

Fig. S5.

A schematic of the stator potentials.

During this transformation, the loop pushes the rotor via a steric force. At the end of the conformational change, when the loops are at the minimum of the potential $G_2$, the two ions bound to two Asp32s exit into the cytoplasm. The potential then switches back from to $G_1$, and the loops traverse back to ${\varphi }_S=0°$. During this time, the loops apply a contact force on the same FliG as in the previous substep.

As noted previously, thermal fluctuations are of the same order of magnitude as the free energies considered, and the precise form of the potentials is not important. In our simulations, we choose

$$G_1\left(\varphi \right)=\{\begin{array}{ll}\beta {\varphi }^2\hfill & \text{if}\hspace{0.17em}\varphi \le 0\hfill \\ F_p\varphi \hfill & \text{if}\hspace{0.17em}0\le \varphi \le {\varphi }_{max}\hfill \\ F_p{\varphi }_{max}+\beta {\left(\varphi -{\varphi }_{max}\right)}^2\hfill & \text{if}\hspace{0.17em}\varphi \ge {\varphi }_{max}\hfill \end{array}$$

and

$$G_2\left(\varphi \right)=\{\begin{array}{ll}\beta {\varphi }^2\hfill & \text{if}\hspace{0.17em}\varphi \le 0\hfill \\ -F_p\left(\varphi \right)\hfill & \text{if}\hspace{0.17em}0\le \varphi \le {\varphi }_{max}\hfill \\ -F_p{\varphi }_{max}+\beta {\left(\varphi -{\varphi }_{max}\right)}^2\hfill & \text{if}\hspace{0.17em}\varphi \ge {\varphi }_{max}.\hfill \end{array}$$

Rotor–stator interaction potential.

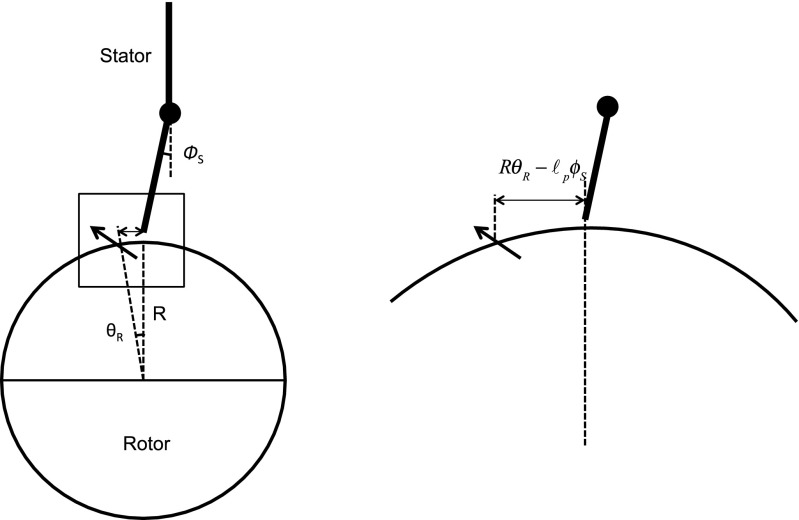
The steric force between the stator and the rotor can be simulated using a soft linear repulsive force with a cutoff distance $X_{RS}$.

$$V_{RS}\left({\varphi }_S^i,{\theta }_R\right)=\{\begin{array}{ll}-F_{RS}\frac{{\left(R{\theta }_R-{\ell }_P{\varphi }_S\right)}^2}{X_{RS}}\hfill & \text{if}\hspace{0.17em}0\le x\le X_{RS}\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

The torque on the rotor can be obtained as ${\tau }_{\text{contact}}=-\partial V_{RS}/\partial {\theta }_R$,

$${\tau }_{\text{contact}}\left(x\right)=\{\begin{array}{ll}-F_{RS}R\frac{R{\theta }_R-{\ell }_P{\varphi }_S}{X_{RS}}=F_{RS}R\left(1-\frac{x_{RS}}{X_{RS}}\right)\hfill & \text{if}\hspace{0.17em}0\le x_{RS}\le X_{RS}\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

Likewise, the reaction torque on the stator is $-\left(\partial V_{RS}/\partial {\varphi }_S\right)$. $F_{RS}$ is the maximum force that can be applied by the proline hinge, and $x_{RS}=X_{RS}+R{\theta }_R-{\ell }_p{\varphi }_S$ denotes the distance between the position of the stator loop and the nearest FliG (see Fig. S6). All other parameters are defined as described previously.

Fig. S6.

A schematic of the geometry of rotor−stator contact during a half-step. The distance between the nearest FliG and the stator is then given by $x_{RS}=X_{RS}+R{\theta }_R-{\ell }_p{\varphi }_S$. The contact force is zero whenever $x_{RS}\ge X_{RS}$. Moreover, the stator never is ahead of the rotor. This is ensured by choosing a time step such that the fluctuations from the random noise terms are small.

Note that we assume that weak electrostatic forces place the stator at most 0.5 nm from the nearest FliG on the rotor ($X_{RS}\approx$ 0.5 nm) before the start of the power stroke, as shown in Fig. S6. During the half-step, the stator moves from ${\varphi }_S=0°$ to ${\varphi }_S=20°$. In this process, a contact force is applied on the rotor when $0\le x_{RS}\le X_{RS}$. The contact force is zero when $x_{RS}\ge X_{RS}$.

All previous theoretical studies of the BFM have chosen to model the interactions between the stator and the rotor as a load-independent force. In Simplified Deterministic Model, we have shown that the dependence of steric forces on the load reproduces many of the mechanical characteristic features of the motor found in experiments (e.g., the nonlinearities in the relationship between speed and stator number at high loads).

Although the exact form of the potential used to model the rotor−stator interaction is not very important, we note that linear potentials cannot be used. Such potentials result in a constant torque, independent of ${\zeta }_L$, and thus do not reproduce several properties of steric forces.

Kinetics of Ion Binding.

In this section, we will describe how to model ion-binding events as part of the Langevin equation framework. In many problems related to motors, the ion-binding events may occur only in a certain window of a continuous coordinate describing the mechanical motion of the system. In the BFM, there are two main ion-binding events involved in the torque generation cycle.

• i)
  Two cations (here, protons) from the periplasm bind to the Asp32 residue on two MotBs or unbind into the cytoplasm when the cytoplasmic loops are straight.

  $$\text{Asp}{32}^{-}+{\text{H}}_{\mathrm{periplasm}}^{+}\underset{k_{21}}{\overset{k_{12}}{\rightleftarrows }}\text{Asp}32-\text{H}.$$ [S51]
• ii)
  Once the protons are bound, the cytoplasmic loops undergo conformational change from the straight state into the bent state. At the end of the conformational process, the two channels close with respect to the periplasm and instead open toward the cytoplasm. Once this occurs, the two protons unbind from Asp32 residues into the cytoplasm (or, in the reverse reaction, bind from cytoplasm to Asp32).

  $$\text{Asp}32-\text{H}\underset{{\tilde{k}}_{21}}{\overset{{\tilde{k}}_{12}}{\rightleftarrows }}\text{Asp}{32}^{-}+{\text{H}}_{\text{cytoplasm}}^{+}.$$ [S52]

First, we will describe the case for the kinetics at equilibrium (i.e., at zero IMF), followed by the procedure to model the kinetics under a nonzero IMF.

Equilibrium kinetics under zero IMF.

In the following, we consider the proton-driven motor of E. coli, and so the IMF concerned is the PMF. When there is no PMF, the forward and backward reaction rates for the reaction in Eq. S51 must satisfy

$$\frac{k_{12}}{k_{21}}=\frac{\left[\text{Asp}32-\text{H}\right]}{\left[\text{Asp}32\right]}.$$ [S53]

Let the equilibrium dissociation constant of reaction S51 be defined as

$${\mathrm{K}}_{\text{a}}^p=\frac{\left[\text{Asp}32\right]\left[{\text{H}}_{\text{periplasm}}^{+}\right]}{\left[\text{Asp}32-\text{H}\right]}.$$ [S54]

If ${\text{pK}}_{\text{a}}^p=-{\log }_{10}{\mathrm{K}}_{\text{a}}^p$, then the forward and backward rates should satisfy

$$\frac{k_{12}}{k_{21}}={10}^{\left({\text{pK}}_{\text{a}}^p-{\text{pH}}_{\text{periplasm}}\right)}.$$ [S55]

Note that the acid dissociation constant value of ${\text{pK}}_{\text{a}}^p$ should be determined from experiments. A similar relation to the above can be derived for the reaction in Eq. S52 .

Kinetics under nonzero IMF.

To satisfy detailed balance when the PMF is nonzero, the kinetic coefficients for the reaction should satisfy

$$\frac{k_{12}}{k_{21}}={10}^{\left({\text{pK}}_{\text{a}}^p-{\text{pH}}_{\text{periplasm}}\right)}\text{exp}\left(\frac{e{\psi }_p+G_1-G_2}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}\right).$$ [S56]

There exist multiple choices for the expressions $k_{12}$ and $k_{21}$. For convenience and symmetry, we choose the following for the rate constants:

$$k_{12}={10}^{-{\text{pH}}_{\text{periplasm}}}\text{exp}\left(\alpha \left(\frac{e{\psi }_p+G_1-G_2}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}\right)\right),$$ [S57]

$$k_{21}={10}^{-{\text{pK}}_{\text{a}}^p}\text{exp}\left(-\left(1-\alpha \right)\left(\frac{e{\psi }_p+G_1-G_2}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}\right)\right).$$ [S58]

For symmetry, we have chosen $\alpha =0.5$.

Electrostatic Steering

In this section, we provide more detailed calculations for our electrostatic steering hypothesis, as shown in the main text. We also provide support for the dipole approximation via comparison with an analogous calculation with point charges.

We note that, because no structure of the stator is yet available, the purpose of these calculations is quite qualitative. Our goal is to simply to predict what the electrostatic energy landscape should look like to support our steering hypothesis.

Dipole Approximation.

As a first-order approximation, we consider the relevant charges on the FliG helix and the stator loops to be dipoles. We denote the rotor dipole moment as ${\overrightarrow{p}}_R^k$, where $k\in \left\{1\dots 26\right\}$ enumerates the number of FliGs on the rotor periphery. Likewise, the stator dipole moment is denoted as ${\overrightarrow{p}}_S^{i,N}$, where N enumerates the number of stator units, and i is the number of loops on a single stator. Here, for ease of exposition, we show electrostatic calculations for a single stator with a single loop ($i=1$ and $N=1$), but note that this calculation can be easily extended to the full stator model.

We calculate the electric field felt by the stator loop as

$$E={\displaystyle \sum _{k=1}^{26}{E}_k},$$ [S59]

where

$$E_k=\frac{1}{4\pi \mathit{ϵ}{\left|r_k\right|}^3}\left[3\left({\overrightarrow{p}}_R^k\cdot {\widehat{r}}_k\right){\widehat{r}}_k-{\overrightarrow{p}}_R^k\right].$$ [S60]

Here ϵ is relative permittivity of cytoplasm and ${\overrightarrow{r}}_k$ is a vector quantity that denotes the distance between the stator loop and the kth FliG.

From $E_k$, we calculate the interaction energy between the dipole on the stator loop ${\overrightarrow{p}}_S$ and the kth FliG ${\overrightarrow{p}}_R^k$ as

$$U_k=-{\overrightarrow{p}}_S\cdot E_k=\frac{1}{4\pi \mathit{ϵ}{\left|r_k\right|}^3}\left[\left({\overrightarrow{p}}_R^k\cdot {\overrightarrow{p}}_S\right)-3\left({\overrightarrow{p}}_R^k\cdot {\widehat{r}}_k\right)\left({\overrightarrow{p}}_S\cdot {\widehat{r}}_k\right)\right].$$ [S61]

Similar to the calculation for total electric field, we have

$$U_{\text{stator}}={\displaystyle \sum _{k=1}^{26}{U}_k}.$$ [S62]

Note that, as the distance from the stator loop increases, the terms in the total electric field sum drop off as $1/\left|r^3\right|$, and so the contribution by FliGs located far from the stator loop is not appreciable.

To calculate the total energy in the system, we also add in the interaction energies between pairs of FliG molecules. However, we note that their relative positions do not change as the stator rotates, and so this consideration results simply in a translation of the entire landscape and has no effect on the topology.

$$U_{\text{total}}=U_{\text{stator}}+{\displaystyle \sum _{i=1}^{26}{\displaystyle \sum _{j=1,j\ne i}^{26}\frac{1}{4\pi \mathit{ϵ}{\left|r_{i,j}\right|}^3}\left[\left({\overrightarrow{p}}_R^i\cdot {\overrightarrow{p}}_R^j\right)-3\left({\overrightarrow{p}}_R^i\cdot {\widehat{r}}_{i,j}\right)\left({\overrightarrow{p}}_R^j\cdot {\widehat{r}}_{i,j}\right)\right]}},$$ [S63]

where $r_{i,j}$ is the displacement vector between the ith and jth FliG.

Comparison with Calculation Using Point Charges.

We also performed the above calculations using point charges for the relevant residues on FliG and MotA loops. Because of the uncertainty in the position of the charges, we are interested primarily in a qualitative affirmation of our approximation—that is, the existence of a gently sloping, relatively wide energy well.

As in our dipole calculations, we consider the charged residues on the FliG to be positioned at π/4 to the horizontal (i.e., the charges are positioned along the dipole as shown in Fig. 2). Similarly, we position the charges on the stator loop along the dipole, positioned radially outward from the stator center. Given this configuration, we calculate the electrostatic energy as

$$U_{\text{pc}}=\underset{\text{Interaction}\hspace{0.17em}\text{between}\hspace{0.17em}\text{stator}\hspace{0.17em}\text{charges}}{\underbrace{{\displaystyle \sum _{i=1}^8{\displaystyle \sum _{j=1,j\ne i}^8\frac{q_i{q}_j}{4\pi \mathit{ϵ}\left|r_{i,j}\right|}{e}^{-\left|r_{i,j}\right|/{\lambda }_D}}}}}+\underset{\text{Interaction}\hspace{0.17em}\text{between}\hspace{0.17em}\text{stator}\hspace{0.17em}\text{charges}}{\underbrace{{\displaystyle \sum _{i=1}^{52}{\displaystyle \sum _{j=1,j\ne i}^{52}\frac{q_i{q}_j}{4\pi \mathit{ϵ}\left|r_{i,j}\right|}{e}^{-\left|r_{i,j}\right|/{\lambda }_D}}}}}+\underset{\text{Interaction}\hspace{0.17em}\text{between}\hspace{0.17em}\text{charges}\hspace{0.17em}\text{on}\hspace{0.17em}\text{stator}\hspace{0.17em}\text{and}\hspace{0.17em}\text{FliGs}}{\underbrace{\stackrel{8}{{\displaystyle \sum }_{i=1}}\stackrel{8}{{\displaystyle \sum }_{j=1}}\frac{q_i{q}_j}{4\pi \mathit{ϵ}\left|r_{i,j}\right|}{e}^{-\left|r_{i,j}\right|/{\lambda }_D}}}.$$ [S64]

We screen charges using a Debye length of ${\lambda }_D=0.5$ nm. As before, $r_{i,j}$ denotes the displacement vector between charge i and charge j. Note that, similar to our dipole calculations, the first two terms of the energy are invariant to rotation of the stator. Therefore, they only serve to translate the entire energy landscape and do not affect the topology.

As shown in Fig. S7, the topology generated is indeed similar to that using the dipole approximation in the main text. The removal of certain charges may modify the energy landscape via a flattening or widening of the energy well. In conjugation with our electrostatic steering hypothesis, this may point to a possible explanation for experimental studies that show that mutation of charged residues reduces, but does not eliminate, motor function. Our methods can easily be extended using positional information from solved structures to more quantitatively analyze the effects of these charges. Although such an investigation is certainly warranted, it is out of the scope of the current paper.

Fig. S7.

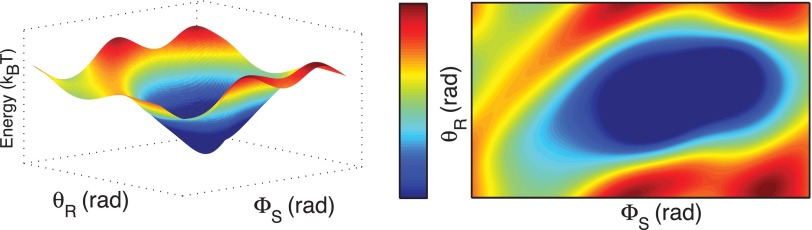
Energy landscape during electrostatic steering calculated using point charges rather than dipoles. All parameters are defined as in the main text; the stator is centered at (21,-2,1), and the rotor is centered at the origin (all distances in nanometers).

Centering the Stator.

There is little structural information for the stator of the BFM. Therefore, in our calculations, we choose a possible position of the stator that is consistent with our model and experimental results. Firstly, we center the stator so that all four stator loops are able to access the FliG molecules. The occasionally observed backsteps imply that both pairs of loops must be able to execute a power stroke during motor function.

Preliminary calculations strongly suggest that the loop charges cannot be in plane with the charges on the FliG. The close proximity of the charges results in an electrostatic interaction far too strong to be feasible given the known efficiency of the BFM (i.e., far too much energy would be wasted in letting go). In-plane configurations that do not present both extremely steep and deep wells must place the stator out of reach of the FliGs.

Given these considerations, and noting that the stator and rotor have radii of respective lengths $\sim$ 20 nm and $\sim$ 2 nm, we center the stator at $\left(x_S,y_S,z_S\right)=\left(21,-\mathrm{2,1}\right)$ using a coordinate system with the rotor centered at the origin.

Ising Model to Describe Conformational Changes in FliG

The existence of motor backsteps in the absence of CheY-P has been largely attributed to microscopic reversibility. Given this constraint, there are three possibilities in explaining the backstep: (i) a backward transit of an ion from the cytoplasm to the periplasm; (ii) a sufficiently strained hook relaxes by moving the rotor backward; and (iii) a fluctuation that changes the orientation of FliG from its CCW to CW orientation.

The first two possibilities contradict our proposed model. For example, if the first case were correct, then a backstep would correspond to a reversal of the entire conformational change process. In this case, an ion bound to the Asp32 from the cytoplasm should restore the MotA helix from its bent state to the straight state in the presence of the ion. This is in direct contradiction to one of our model assumptions that MotA relaxes to the bent state due to the rearrangement in the hydrogen bonds caused by the binding of the ion to the Asp32 residue.

The second possibility (that the relaxation of an elastically strained hook due to several sequential forward steps leads to an occasional backstep) is also not feasible within the context of our model: A contact force guarantees that the rotor always follows the stator.

In this work, we attribute the molecular basis for the backstep to the third possible scenario: a conformational change in one (or more) individual FliGs on the periphery of the rotor. A FliG can exist in two states; in our model, these states correspond to two orientations of the FliG dipole vector. Our electrosteric model, in conjunction with an Ising model corresponding to the states of FliG, explains the existence of occasional backsteps in a self-consistent manner.

Briefly, a backstep results from a fluctuation of FliG from the CCW to the CW position. In this case, when the motor is predominantly moving in the CCW direction and whenever a FliG changes its state from CCW state to CW state and is close to a stator, then the stator—using MotA loops 2 and 4—applies the contact force and pushes the FliG in the backward direction.

Although the configuration of the FliGs in the CW orientation is fairly well agreed upon, the exact CCW configuration is still under debate. At least three possible orientations have been suggested, including directions orthogonal or $180°$ with respect to the CW orientation. Despite this uncertainty, it is generally believed that there are two significantly different orientations for each FliG.

As in other models, we describe the transitions between the two FliG orientations by a one-dimensional periodic Ising model consisting of 26 spins (corresponding to 26 FliGs). Each individual spin $s_i$ can exist in two possible states corresponding to the two orientations of FliGs: $s_i=+1$ (CCW) and $s_i=-1$ (CW). The Hamiltonian is

$$H=-J{\displaystyle \sum _{i,j=1}^N{s}_i{s}_j}-h{\displaystyle \sum _{i=1}^N{s}_i}$$ [S65]

where J denotes the nearest-neighbor pairwise interaction energy and h denotes the field biasing the FliGs to preferentially orient in a certain direction. Let $\left\{s_i\right\}=\left(s_1,s_2,s_3,\dots ,s_{26}\right)$ denote a possible state of the rotor. The probability of such a state is given by the Boltzmann distribution $e^{-\beta H\left(\left\{s_i\right\}\right)}/Z\left(J,H,\beta \right)$, where $Z\left(J,H,\beta \right)$ is the partition function. The partition function for a one-dimensional Ising model (Eq. S65 ) is obtained exactly using the transfer matrix approach and is given by

$$Z\left(J,h,\beta \right)={\lambda }_{+}^N+{\lambda }_{-}^N$$ [S66]

where

$${\lambda }_{\pm }=e^{\beta J}\cosh \left(\beta h\right)\pm \sqrt{e^{2\beta J}{\sinh }^2\left(\beta h\right)+e^{-2\beta J}}.$$ [S67]

To understand the backsteps while the motor is running predominantly in CCW direction, we calculate the probability that any FliG (or any spin) points in the CW direction. This is given by

$$p\left(s_i=-1\right)={\displaystyle \sum _{\left(s_1,\dots ,s_{i-1},-1,s_{i+1},\dots ,s_{26}\right)}\frac{e^{-\beta H\left(\left(s_1,\dots ,s_{i-1},-1,s_{i+1},\dots ,s_{26}\right)\right)}}{Z}}$$ [S68]

where the summation is over all possible states fixing $s_i=-1$. In the following, we derive an analytical expression for the probability $p\left(s_i=-1\right)$.

Let us denote the probability for the spin $s_i=+1$ as $p\left(s_i=+1\right)$. Given the probabilities $p\left(s_i=+1\right)$ and $p\left(s_i=-1\right)$, the average value $\langle s_i\rangle$ of the spin $s_i$ can be calculated as

$$\langle s_i\rangle =\left(1\right)p\left(s_i=+1\right)+\left(-1\right)p\left(s_i=-1\right)=1-2p\left(s_i=-1\right).$$ [S69]

Moreover, the derivative of the partition function Z with respect to the field h yields

$$\frac{1}{N\beta Z}\frac{\partial Z}{\partial h}=\frac{1}{N}{\displaystyle \sum _{\left\{s_i\right\}}{\displaystyle \sum _i{s}_i\frac{e^{-\beta H\left(\left\{s_i\right\}\right)}}{Z}=\langle s_i\rangle }}.$$ [S70]

Therefore, using Eqs. S69 and S70 , the probability that spin $s_i=-1$ can be obtained as

$$p\left(s_i=-1\right)=\frac{1-\frac{1}{N\beta Z}\frac{\partial Z}{\partial h}}{2}.$$ [S71]

The derivative of the partition function with respect to the field h can be evaluated using the derivatives of the ${\lambda }_{\pm }$ functions, which are given by

$$\frac{\partial {\lambda }_{\pm }}{\partial h}=\beta \sinh \left(\beta h\right)\left(e^{\beta J}\pm \frac{e^{2\beta J}\cosh \left(\beta h\right)}{\sqrt{e^{2\beta J}{\sinh }^2\left(\beta h\right)+e^{-2\beta J}}}\right).$$ [S72]

Within the context of our model, the likelihood of a flip in FliG conformation corresponds directly to the likelihood of a backstep. That is, the probability that a FliG is in the CW state is given by Eq. S71 . This is because the fundamental mechanics of a backstep is the same as that of a forward step; the difference between these two scenarios is wholly described by the difference in FliG configuration.

Suppose that the motor is moving primarily in the CCW direction. This means that the FliGs in close proximity to the stator loops are oriented to favor CCW rotation (that is, to favor interaction with MotA loops 1 and 3). However, if a FliG close to the stator is oriented to favor CW rotation, then the FliG interacts with MotA loops 2 and 4, resulting in a step in the CW direction (a backstep when the motor is moving primarily CCW). This probability is given by Eq. S71 .

For the choice of the energy scale $\beta J=2$ at room temperature and a biasing field of $\beta h=0.05$, the probability that any FliG is in the CW state is $p\left(s_i=-1\right)=0.08$. That is, on average, 8 out of every 100 torque-generating cycles will result in a backstep. Areas under the curve corresponding to forward and backward steps from data collected by Sowa et al. (16) indicate that $p\left(s_i=-1\right)\approx$ 0.073 (Fig. S8).

Fig. S8.

Probabilities of backward steps relative to forward steps can be estimated using statistics from stepping experiments (data shown from ref. 16). The area under the curve for steps below and above 0° corresponds to forward and backward step probabilities, respectively. The areas on either side are calculated as highlighted in gray. Curves are truncated where each shows a second peak, corresponding to two steps being blurred together due to limitations in experimental resolution. The relative areas calculated for the data above suggest that the probability of a backward step is 7.3%.

The above analysis provides an explanation for how backsteps in the absence of CheY-P can arise from fluctuations in FliG configurations. However, it does not take into account how the above probabilities are affected by load or PMF. For example, the timescale of a single step depends on the load. If one assumes that this step is a backstep, then this particular FliG is pinned in the backwards orientation for the duration of that step. This CW defect in the FliG ring can affect the switching probabilities of the neighboring FliGs, resulting in further defects along the ring. Therefore, at higher loads, the probability of two (or more) subsequent backsteps may not be negligible. However, a complete understanding of the above requires a far more detailed analysis of an Ising model in conjunction with the proposed electrosteric model than is within the scope of this work.