Numerical models based on a minimal set of sarcolemmal electrogenic proteins and an intracellular Ca²⁺ clock generate robust, flexible, and energy-efficient cardiac pacemaking

Abstract

Recent evidence supports the idea that robust and, importantly, FLEXIBLE automaticity of cardiac pacemaker cells is conferred by a coupled system of membrane ion currents (an “M-clock”) and a sarcoplasmic reticulum (SR)-based Ca²⁺ oscillator (“Ca²⁺clock”) that generates spontaneous diastolic Ca²⁺ releases. This study identified numerical models of a human biological pacemaker that features robust and flexible automaticity generated by a minimal set of electrogenic proteins and a Ca²⁺clock. Following the Occam’s razor principle (principle of parsimony), M-clock components of unknown molecular origin were excluded from Maltsev-Lakatta pacemaker cell model and thirteen different model types of only 4 or 5 components were derived and explored by a parametric sensitivity analysis. The extended ranges of SR Ca²⁺ pumping (i.e. Ca²⁺clock performance) and conductance of ion currents were sampled, yielding a large variety of parameter combination, i.e. specific model sets. We tested each set’s ability to simulate autonomic modulation of human heart rate (minimum rate of 50 to 70 bpm; maximum rate of 140 to 210 bpm) in response to stimulation of cholinergic and β-adrenergic receptors. We found that only those models that include a Ca²⁺clock (including the minimal 4-parameter model “I_CaL+I_Kr+I_NCX+Ca²⁺clock”) were able to reproduce the full range of autonomic modulation. Inclusion of I_f or I_CaT decreased the flexibility, but increased the robustness of the models (a relatively larger number of sets did not fail during testing). The new models comprised of components with clear molecular identity (i.e. lacking I_bNa & I_st) portray a more realistic pacemaking: A smaller Na⁺ influx is expected to demand less energy for Na⁺ extrusion. The new large database of the reduced coupled-clock numerical models may serve as a useful tool for the design of biological pacemakers. It will also provide a conceptual basis for a general theory of robust, flexible, and energy-efficient pacemaking based on realistic components.

Introduction

Efforts to date to create biological pacemakers for patients with pacemaker insufficiency have focused on manipulating membrane currents (e.g. increasing I_f and decreasing I_K1) [1,2]. This approach was inspired by classical pacemaker theory (based on Hodgkin-Huxley formalism) that postulates that an ensemble of voltage-gated ion currents (membrane voltage clock or M-clock) is not only necessary, but is also sufficient as a mechanism that generates and regulates automaticity of cardiac pacemaker cells. While the first numerical model of the M-clock (developed by Noble in 1960 [3]) was rather simple, with just a couple hypothetical voltage-gated currents, it closely predicted the shape of pacemaker action potential (AP). Further extensive voltage clamp studies of pacemaker cells under many experimental conditions in various species, identified numerous ion currents that differ in selectivity and kinetics. Presently, the most advanced formulations of pacemaker function of sinoatrial node cell (SANC) include about a dozen ion currents.

More recent evidence, however, supports the idea that robust and, importantly, flexible automaticity of pacemaker cells is conferred by a coupled system of M-clock and a sarcoplasmic reticulum (SR)-based Ca²⁺ oscillator (“Ca²⁺clock”) that generates rhythmic spontaneous diastolic Ca²⁺ releases. These spontaneous local Ca²⁺ releases (LCRs) are driven by cAMP- and calmodulin-dependent phosphorylation of Ca²⁺ cycling proteins in the basal state [4]. The M- and Ca²⁺clocks are strongly dynamically coupled by several Ca²⁺- and voltage- dependent molecular mechanisms [e.g. Na⁺/Ca²⁺ exchanger (NCX) and L-type Ca²⁺ channel] [4]. Recent approaches in developing biological pacemakers target the integrated function of M-clock and Ca²⁺clock [5]. For example, a single gene therapy to overexpress a Ca²⁺-activated adenylyl cyclase (AC1)(that generates cAMP and activates PKA) has been sufficient to produce stable (for 7 days) biological pacemaking in experimental dogs[6]. Persistent biological pacemakers (for up to 8 weeks) have been also generated in intact myocardium of guinea pigs by reprograming (via Tbx18) of ventricular myocytes into SANC-like cells [7]. The reprogrammed cells also exhibited the LCRs and the integrated function of both clocks. Both AC1- and tbx18-derived pacemaking exhibited physiological flexibility, i.e. ability to increase and decrease the pacemaker rate in response to β-Adrenergic Receptor (β-AR) and Cholinergic Receptor (ChR) stimulation, respectively.

We have recently developed a novel, unique numerical model of the coupled-clock system (known as “Maltsev-Lakatta” model or ML model [8,9]) that reproduces a plethora of experimental data in SANC (particularly related to Ca²⁺ regulation and protein phosphorylation). The ML model, however, also includes formulations of 13 ion currents to describe the M-clock (Fig.1A), but which currents are fundamentally important for flexible pacemaker function remains unknown. Following the principle of Occam’s razor (i.e. principle of parsimony), the present study identifies and explores numerically minimal ensembles of electrogenic molecules that, together with the SR-based intracellular Ca²⁺clock, insure a robust and flexible pacemaker function. While the original ML model simulates function of rabbit SANC, our study identifies the new models for heart rates relevant to humans. Given the lack of human SANC data, our logic was to develop the “human-like” models by plugging in the same basic currents and fluxes as in the rabbit, since the molecular components are quite similar in mammals. The specific amounts of each component that are required to produce pacing rates appropriate for a human, can be determined by performing the systematic model evaluation. Thus this approach and resultant extended database of human-like models offer a novel framework and a useful tool to design robust and flexible cardiac bio-pacemakers. Indeed, designing bio-pacemakers (i.e. genetically engineered cells) requires selecting and manipulating specific molecular targets (explored numerically in the present study), rather than ion currents of the classical M-clock, some of which have no established molecular identity. A preliminary report of this study has been published as an abstract [10].

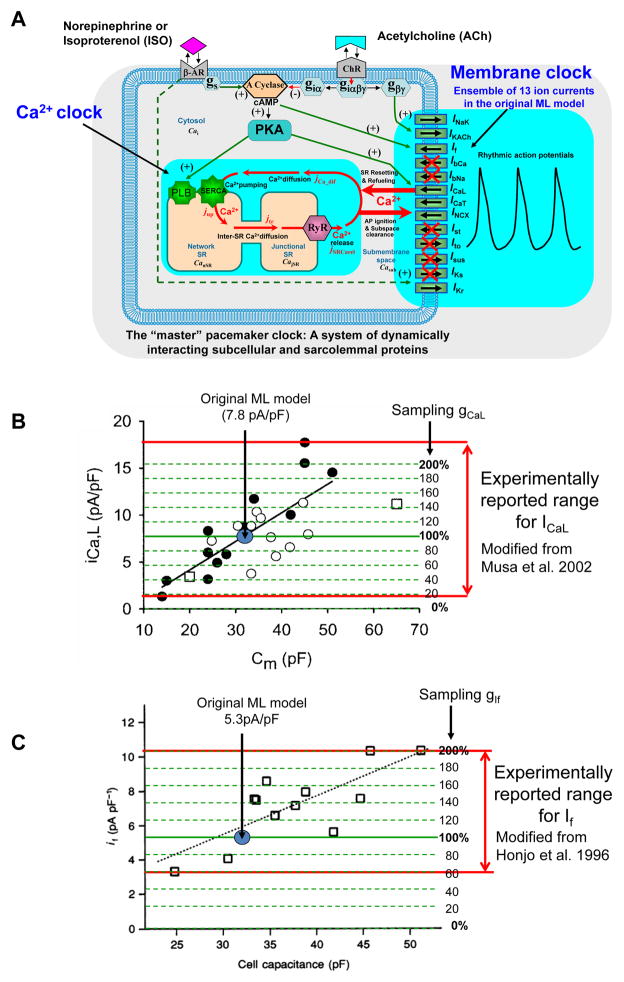
Fig. 1.

Our approach to devise and explore pacemaker cell models, featuring a minimal set of sarcolemmal electrogenic proteins and a Ca²⁺ clock. A: Schematic illustration of ML model that originally included 13 membrane currents. We tested a large variety of reduced models that included different combinations of major currents and Ca²⁺clock. Excluded currents are crossed by red lines (see Table 1 for all tested combinations). B,C: Experimentally measured intrinsic variability of I_CaL and I_f densities in rabbit SANC as a function of cell electric capacitance, C_m. Red double-headed arrows show the range of variability. The peak I_CaL of about 1.4 to 17.9 pA/pF density was measured at 0 mV from a holding potential of −40 mV. Modified from Musa et al. 2002[34]. The I_f density of about 3 to 11 pA/pF was measured 300 ms after a hyperpolarization step to −110 mV from a holding potential of −40 mV. Modified from Honjo et al. [35]. Blue circles show I_CaL and I_f densities predicted by original ML model with g_CaL = 0.58 nS/pF and g_If = 0.15 nS/pF. Our parameter sampling (from 20% to 200% of the original g_CaL and g_If) covers experimentally measured range for I_CaL and I_f as illustrated by dashed green lines.

Methods

Numerical SANC model

The present study used our previously published numerical model of rabbit SANC (ML model [8,9]) that describes the cardiac pacemaker function as a coupled-clock system. All model equations, initial conditions, and model parameters are given in the Online Supplement (section “Model equations”, Table S1, and Table S2). Simulations of previously published models were performed using their CellML format (http://models.cellml.org) and COR software (http://cor.physiol.ox.ac.uk/). Some simulations (Fig. S3) were taken from 2007 Wilders review [11].

General research strategy and terminology

1. “Model type” is a suite of mathematical equations that do not include specific parameter values. The specific aim of the present study was to identify and explore numerically several model types featuring minimal sets of electrogenic proteins that, together with Ca²⁺clock, comprise a robust, yet flexible, pacemaker system.

2. “Model set” (or “parameter set”): We sampled an extended range of key parameters in each model type. We call any combination of parameters as a model set (Table S2, third column). Figure 1 (Green dashed lines in panels B and C) illustrates our sampling procedure for two parameters, g_CaL and g_If. Thus, a model set is a specific combination of parameter values of a given model type.

3. “Non-failing set”: Each model set was numerically tested. We defined a set as a non-failing set if it generates rhythmic APs in the basal state (basal state test), in the presence of β-AR stimulation (ISO test), and in the presence of ChR stimulation (ACh test). Our computer algorithm classified AP generation as rhythmic when the relative change of simulated AP period from cycle to cycle remained within 0.0001.

4. “Robustness” (of a given model type) is a ratio of non-failing model sets to the total number of tested model sets.

5. “Flexibility”: ability of the pacemaker cell system (both numerical and real) to increase and decrease its rate by autonomic modulation, i.e. in response to β-AR and ChR stimulation.

6. The range of maximal and minimal rates: The maximum rate of the normal human heart varies with age from 140 to 210 bpm, and the normal minimum rate varies from 50 to 70 bpm depending on fitness level and age.

7. “Physiologically flexible set”: a model set that simulates rhythmic APs within the range of maximal and minimal rates, in ISO and ACh tests.

8. “Relative flexibility” of a non-failing set is defined as

   $$100\%·(\text{rate}\_\text{of}\_\text{ISO}\text{test}-\text{rate}\_\text{of}\_\text{ACh}\text{test})/\text{rate}\_\text{of}\_\text{ACh}\text{test}.$$

9. “Subset of the top ten sets”: a subset among all non-failing sets (of a given model type) which were the top ten with respect to maximal relative flexibility and also demonstrated a minimum rate of 50 to 70 bpm (in order to filter bradycardic sets) and AP amplitude of more than 80 mV. We used these sets as representative examples in our mechanistic analyses of flexibility in different model types.

Devising reduced model types

SANC electrophysiological properties in our original coupled-clock model [8] (with addition of I_KACh as in [9]) is described by a system of 13 ion currents (Fig.1A):

$${dV}_m/dt=({\mathrm{I}}_{\text{CaL}}+{\mathrm{I}}_{\text{Kr}}+{\mathrm{I}}_{\text{CaT}}+{\mathrm{I}}_{\text{Ks}}+{\mathrm{I}}_{\text{to}}+{\mathrm{I}}_{\text{sus}}+{\mathrm{I}}_{\mathrm{f}}+{\mathrm{I}}_{\text{NCX}}+{\mathrm{I}}_{\text{KACh}}+{\mathrm{I}}_{\text{NaK}}+{\mathrm{I}}_{\text{st}}+{\mathrm{I}}_{\text{bCa}}+{\mathrm{I}}_{\text{bNa}})/C_m$$

We chose and explored by parametric sensitivity analysis seven 4-parameter models and six 5-parameter models (Table 1). When constructing model types, our stringent inclusion criteria were based upon a general principle of “Occam’s razor” (the law of parsimony). Adopted to our quest, this principle translated into specific requirements for the desired numerical bio-pacemaker prototype to be comprised of ion currents with established molecular identity and these currents should be capable of (i) generating an AP (i.e. representing an excitable cell), (ii) diastolic depolarization (DD) (i.e. representing a pacemaker cell), and (iii) modulating AP firing rate within a physiologically relevant, broad range. Each ion current of the system was then examined using the aforementioned criteria as follows:

Table 1.

Components and major average characteristics of 13 pacemaker model types examined in the present study.

4 parameter model types
Components of model types								All non-failing model sets				Physiologically flexible sets
Model#	ICaL	IKr	INCX	Ca-clock	If	IKACh	ICaT	Fig.	#Non-failing/total %	Average relative flexibility %	Average Max. rate bpm	#Non-failing	Average relative flexibility %	Average Max rate bpm
1	Yes	Yes	Yes	Yes				2D	13.53	110.6	196.1	86	174.8	174.8
2	Yes	Yes	Yes		Yes			2C	20.29	51.7	141.4	None
3	Yes	Yes	Yes			Yes		2A	0.07	59.7	78.8
4	Yes	Yes	Yes				Yes	2B	20.85	13.7	85.2
5	Yes	Yes			Yes		Yes	All model sets failed
6	Yes	Yes				Yes	Yes
7	Yes	Yes			Yes	Yes
-	Yes	Yes		Yes	Yes			Not tested. These models with Ca2+ clock, but without NCX make no sense, because Ca2+ clock cannot interact with M clock
-	Yes	Yes		Yes		Yes
-	Yes	Yes		Yes			Yes
5 parameter model types
Components of model types								All non-failing model sets				Physiologically flexible sets
Model#	ICaL	IKr	INCX	Ca-clock	If	IKACh	ICaT	Fig.	#Non-failing/total %	Average relative flexibility %	Average Max. rate bpm	#Non-failing	Average relative flexibility %	Average Max rate bpm
8 INaK,max=0	Yes	Yes	Yes	Yes	Yes			3D	34.738	64.1	206.3	85	145.6	158.6
8b INaK,max= 0.9pA/pF	Yes	Yes	Yes	Yes	Yes			S4B	17.417	77.8	211.2	189	149.4	159.9
9	Yes	Yes	Yes	Yes		Yes		3F	1.281	101.7	216.4	23	174.8	178.3
10	Yes	Yes	Yes	Yes			Yes	3E	33.825	81.3	195.3	789	163.2	166.9
11	Yes	Yes	Yes		Yes	Yes		3B	7.313	68.6	148.5	166	127.9	146.8
12	Yes	Yes	Yes			Yes	Yes	3A	4.078	41	96	None
13	Yes	Yes	Yes		Yes		Yes	3C	25.694	34	153

• 1)I_CaL was included in all tested models as essential for cell excitability (AP upstroke), AP rate modulation, and Ca²⁺clock operation to supply Ca²⁺ to the system.
• 2)I_Kr was included in all tested models as essential for cell excitability (AP repolarization) and involved in AP rate modulation.
• 3)I_CaT was included only in some models (#4,5,6,10, 12,13 in Table 1), as a non-essential current, because it is present not in all SANC (only in 20% of SANC, in 5 of 25 cells tested [12]) and it is not crucial for rate modulation, cell excitability, and DD (at least in rabbit SANC).
• 4–6)I_Ks and 4-aminopyridine-sensitive K⁺ currents (I_to+I_sus) were excluded as non-essential currents: AP repolarization and DD can be generated in the absence of these currents [13]. While I_Ks is modulated by autonomic system, its expression is species-dependent and almost nonexistent in rabbit SANC. Therefore, following “Occam’s razor” principle, we kept I_Kr (see above) but omitted I_Ks.
• 7,8)Both I_f and I_NCX contribute to DD and are involved in AP rate modulation. I_NCX is also essential for coupling M-clock and Ca²⁺clock to substantiate a coupled-clock system [4]. Thus, both currents were included in our numerical investigation of different model types.
• 9)I_KACh was included only in some models (#3,6,7, 9,11,12 in Table 1), because a physiological (moderate) decrease of AP firing rate of SANC, can be achieved, at least in major part, without this current (i.e. via modulation of only I_f and Ca²⁺clock-I_NCX as previously demonstrated [9,14]). Specifically, tertiapin-Q, a selective blocker of I_KACh has no effect on AP firing rate reduction induced by 30 nM of carbachol [14]. Furthermore, the density of I_KACh was found negligible in the basal state (non-stimulated SANC) [14].
• 10)I_NaK was excluded as having no crucial importance for either AP, DD, AP rate modulation, or Ca²⁺clock, i.e. both APs and DD can be generated numerically in the absence of I_NaK [13] (but see Discussion about Na⁺ balance). We also insured that the most flexible and robust model type is preserved when it is adjusted for I_NaK (model #8a in Table 1). It is important to mention that intracellular K⁺ and Na⁺ concentrations were kept fixed in the minimal models.
• 11–13)I_bNa, I_st, and I_bCa were excluded because their molecular basis has not been established.

Thus, our tested model types were combinations of 7 components, including six major ion currents (I_CaL, I_Kr, I_NCX, I_f, I_KACh, I_CaT) and the SR-based Ca²⁺clock (Fig. 1A, Table 1). As we mentioned, we always kept I_CaL and I_Kr in all model types in order to generate AP upstroke and repolarization. Therefore, when considering 4-parameter model types, the number of possible parameter combinations of different couples among the remaining 5 components (I_NCX, I_f, I_KACh, I_CaT, and Ca²⁺clock) is given as 5!/[(5–2)!·2!] = 10. However 3 of these 10 possibilities include combinations of Ca²⁺clock but no I_NCX which were not tested (because Ca²⁺ would not interact with M-clock and cannot be balanced in the absence of Ca²⁺ efflux). Thus, we examined only seven 4-paramer models (#1–7 in Table 1). All examined 5-parameter model types had three components I_CaL, I_Kr, I_NCX. The number of possible combinations of couples among the remaining 4 components (I_f, I_KACh, I_CaT, and Ca-clock) is 6; and all 6 combinations were examined (models #8–13, Table 1).

Devising model sets

For each model type we constructed a large variety of parameter sets to be tested for robust and flexible pacemaker function. The following key model parameters were sampled to create these sets: 1) g_CaL,basal, the maximum conductance of I_CaL, mimicking expression of L-type Ca²⁺ channels; 2) g_Kr,basal, the maximum conductance of I_Kr, mimicking expression of the delayed-rectifier K⁺ channels; 3) k_NCX maximum NCX current, mimicking expression of NCX; 4) g_If, the maximum conductance of I_f, mimicking expression of funny channels; 5) P_up, the maximum SR Ca²⁺ pumping rate, mimicking expression of SERCA and its basal state activation by phospholamban. 6) g_KACh, the maximum conductance of I_KACh, mimicking expression of ACh-activated K⁺ channels; 7) g_CaT, the maximum conductance of I_CaT, mimicking expression of T-type Ca²⁺ channels.

Specifically, each parameter range was equally binned into 10 gradations, starting from 20% in 20% increments up to 200% of the value of the original ML model, yielding either 10,000 or 100,000 specific parameter combinations (i.e., specific model sets) for each 4- or 5-component model, respectively (Table S2, columns 1–3). Despite substantial computational expense, we chose the direct sequential, equally spaced sampling of model parameters in the sensitivity analysis, because in our study we want to find parameters for human heart pacemaker cells, natural or genetically engineered, which have not been measured or have not been created, yet. In the absence of strong guidance from experimental studies, our systematic sampling is reasonable, because otherwise a higher frequency sampling in one particular range would look arbitrary, but a rare sampling in the other range may miss combinations that exhibit desired properties (in our case, human heart rate modulation range). Moreover, experimental measurements of ion current densities in SANC in one species (traditionally rabbit) demonstrate substantial intrinsic (cell-to-cell) variations. For example, intrinsic variations of I_CaL density could be as much as 10 times and I_f density about three times (Fig.1B,C). The original ML model simulates the respective current densities close to the middle of their experimental ranges (shown by a blue circle in Fig.1B,C). Therefore our sampling strategy (from 20% to 200% of these values shown by green dashed lines) reasonably covers the extended range of intrinsic variations shown in Figure 1B,C (red double head arrows).

Sensitivity analysis in 4D or 5D parametric space

For each set (out of 10⁴ or 10⁵ total) we performed basal state test, ISO test, and ACh test. Based on these tests, we evaluated each model’s 1) robustness as the ratio of number of non-failing sets (i.e. those passed all three tests) to the total number of sets and 2) ability to simulate the range of autonomic modulation of human heart rate in ISO and ACh tests. Specific parameters and key characteristics of APs of the physiologically flexible sets are provided in Supplemental Excel files and summarized in Table S3 (the top ten sets, showing highest relative flexibility). Each model set was tested automatically using a computer algorithm of 4 or 5 nested “for”-loops (each loop for each graded parameter). For each specific model set our code executed a procedure to run three simulations: (i) at basal state, i.e. using a given set of parameters; (ii) in response to β-AR stimulation (ISO test); and (iii) in response to ChR stimulation. Specific changes of model parameters to simulate responses to β-AR and ChR stimulation were used as previously described [9] (summarized in Table S2, 4^th column, and in Online Supplement section “Model Equations”). The entire computation load was split and run in parallel using 6 Hewlett Packard xw8400 workstations (with two Quad-Core Intel® Xeon® 5355 processors 2.66 GHz in each).

Results

Examination of 4-parameter models

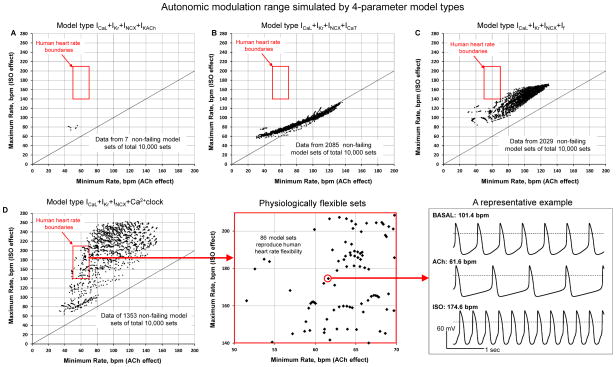
All model sets without NCX (Table 1 models #5,6,7) failed to generate rhythmic APs in at least one of the tests (basal state test, ISO test, or ACh test), confirming fundamental importance of this current for cardiac pacemaker function. Pure M-clock model sets (lacking Ca²⁺clock), but including I_NCX and I_KACh (model #3), exhibited only a few non-failing sets (7 out of 10,000 sets did not fail, Fig.2A). Other M-clock models featuring either I_f or I_CaT (models #2,4, Fig.2B,C) exhibited a substantial number of non-failing sets (20.29 and 20.85%). All these non-failing M- clock model sets, however, had a small or modest average relative flexibility (13.7, 59.7, and 51.7 %, for models #2,3, and 4, respectively); and they did not reproduce the variability of human heart rate, as their maximal rate always remained below the 140 bpm level.

Fig. 2.

Results of sensitivity analysis of different 4-parameter model types (indicated at the top of each plot). Each model type was tested in 10,000 parameter sets. Data points show maximum and minimum spontaneous AP firing rate (along Y and X axis, respectively) for all non-failing parameter sets (i.e. those passed basal state test, ISO test, and ACh test). Red square shows the boundaries of normal human heart operation (including different ages and level of fitness). The plot in panel D was extended to show a more detailed plot of all data points within the human heart rate boundaries and also to show an example of APs in basal state test, ACh test and ISO test.

A 4-parameter model featuring coupled function of M-clock and Ca²⁺clock (“I_CaL+I_Kr+I_NCX+Ca²⁺clock”, model #1 in Table 1) exhibited the highest relative flexibility of 110.6% on average combined with a substantial robustness of 13.53% (albeit slightly lower than that in M-clock models #2 and #4, with I_f and I_CaT, respectively). Furthermore, this was the only 4-parameter model type that exhibited physiologically flexible sets (black data points within the red square in Fig.2D) in a substantial number of physiological sets (86 out of 10,000).

Examination of 5-parameter models

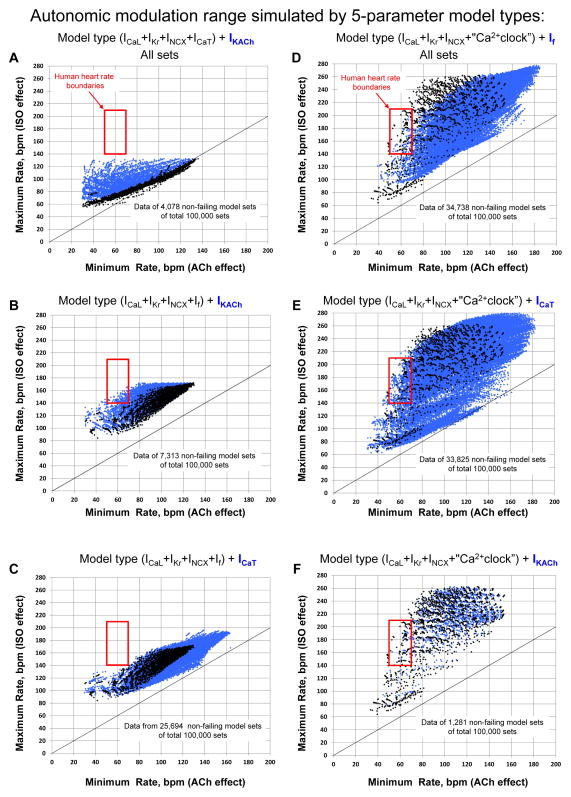
We tested and compared three pure M-clock model types (Table 1 models #11,12,13) and three model types featuring coupled-clock function of M-clock and Ca²⁺ clock (models #8,9,10). M-clock models #12 (“I_CaL+I_Kr+I_NCX+I_KACh+I_CaT”) and #13 (“I_CaL+I_Kr+I_NCX+I_f+I_CaT”) had no physiologically flexible sets at all (Fig.3A,C). Yet another M-clock model #11 (“I_CaL+I_Kr+I_NCX+I_f+I_KACh”) exhibited only “marginally” physiologically flexible sets [all those sets were located at the lower border of the maximum heart rate (140 bpm, Fig.3B)]. In contrast to the M-clock models, the most striking feature of coupled-clock models #8 (“I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f”) and #10 (“I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_CaT”) was a substantial number of sets reproducing autonomic modulation of human heart rate within almost entire range (Fig. 3D,E and 4A,B). Furthermore, the presence of I_f or I_CaT in these models substantially improved the model robustness if formally compared with that of the 4-parameter model without these currents (“I_CaL+I_Kr+I_NCX+Ca²⁺clock”, model #1 in Table 1): 34.738% and 33.825% vs. 13.53%. Another coupled-clock model #9 with I_KACh (“I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_KACh”, Fig. 3F and 4C) demonstrated the highest relative flexibility among the 5-parameter models tested, but again (as in case of 4-parameter model #3) the robustness of the I_KACh-including model was extremely low (1.281%).

Fig. 3.

Results of sensitivity analysis of different 5-parameter model types. Each model type was tested in 100,000 parameter sets. Data points show maximum and minimum spontaneous AP firing rate (along Y and X axis, respectively) for all non-failing parameter sets, i.e. those passed basal state test, ISO test, and ACh test. Each tested model type is written at the top of each plot. Black dots show data points of a simpler, 4-parameter model indicated in parenthesis of the model name, the blue dots show data points of the 5-parameter model.

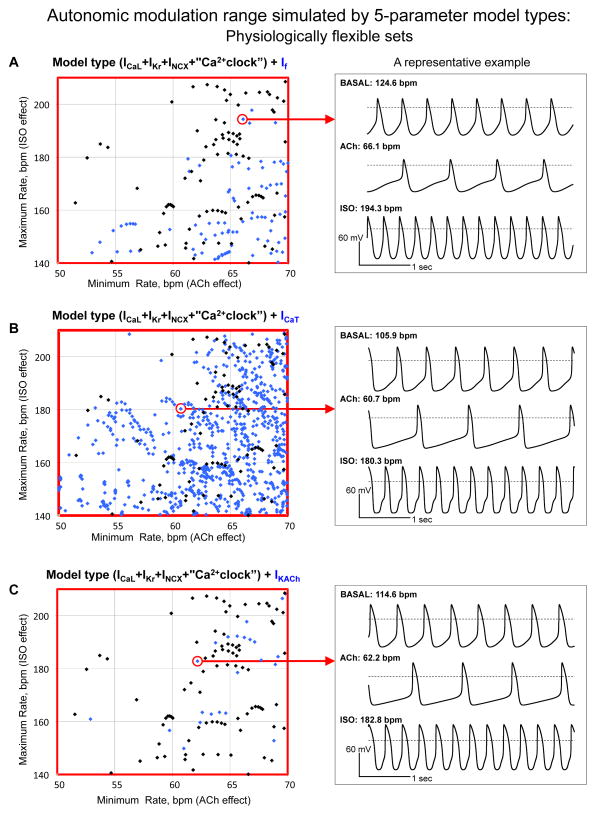
Fig. 4.

Detailed illustrations of physiologically flexible sets in three 5- parameter model types that have Ca²⁺ clock which shown in Fig. 3D,E,F (within red squares) and representative examples (within red circles) of simulations are shown in right-hand panels.

Component mechanism of robust and flexible pacemaking

To learn more about specific mechanisms that confer pacemaker flexibility, we simulated component mechanisms in three representative parameter sets of three different model types I_CaL+I_Kr+I_NCX+Ca²⁺clock”, “I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f” and “I_CaL+I_Kr+I_NCX+I_f”. Each representative parameter set was taken from the top ten sets of each model type (highlighted in Table S3).

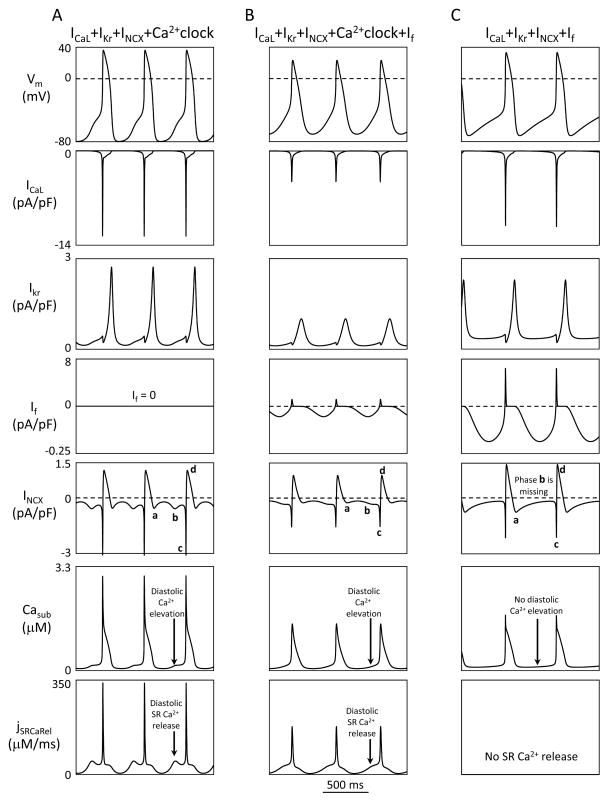
The presence of only 3 membrane ion currents, I_CaL+I_Kr+I_NCX, in M-clock is indeed sufficient to form a coupled-clock system with Ca²⁺clock, i.e. “I_CaL+I_Kr+I_NCX+Ca²⁺clock”, specifically: first phase of I_NCX activation is caused by membrane hyperpolarization (during AP repolarization) (Fig.5A, I_NCX panel, phase a). The diastolic Ca²⁺ release activates second, diastolic phase of I_NCX (phase b) and accelerates DD that prompts an AP occurrence. Once an AP upstroke is generated, Ca²⁺ influx via I_CaL generates Ca²⁺ transient [via Ca²⁺-induced Ca²⁺ release (CICR) mechanism] that increases I_NCX sharply further (phase c); but then I_NCX almost immediately reverses (phase d) due to AP overshoot (i.e. positive membrane potential). In turn, the I_CaL–induced Ca²⁺ release (i.e. Ca²⁺ transient) depletes the SR Ca²⁺ and hence resets the SR Ca²⁺ cycling (SR re-filling with Ca²⁺ starts from this depleted state). NCX depletes cell of Ca²⁺, during its phases a, b, and c; but Ca²⁺ influx via I_CaL and reverse mode NCX during AP (phase d) “refuels” the Ca²⁺clock, i.e. maintains the steady-state intracellular Ca²⁺ balance that is crucial for SR Ca²⁺ cycling.

Fig. 5.

Complete component mechanism of basal state AP firing in three different model types: two coupled-clock model types (panels A and B) and one pure M-clock model type (panel C). Simulations were performed using respective representative flexible sets for these models (highlighted in Table S3). Each model type is specified at the top of each column of panels.

The above described component mechanism of the coupled-clock system remains unchanged with the addition of I_f into the system (Fig.5B). It is important to note that both I_f and I_NCX are activated by AP repolarization (I_NCX phase a). In contrast to I_f, however, I_NCX activation occurs earlier and instantly follows changes in membrane potential and Ca_sub (I_NCX does not have activation or inactivation kinetics). Omitting Ca²⁺clock results in a qualitative change of the pacemaking mechanism (Fig.5C): the diastolic SR Ca²⁺ release and its associated diastolic phase (phase b) of I_NCX disappear that substantially limits autonomic modulation of AP firing rate.

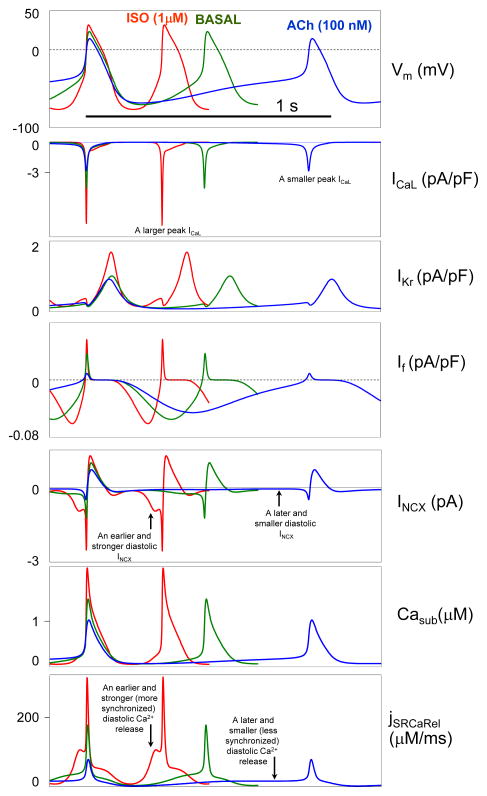
β-AR and ChR stimulation modulates the AP firing rate in the representative model set “I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f” via the coupled-clock mechanism (Fig.6), i.e. via a complex interactions of the clocks, including 1) NCX electrogenic coupling of diastolic SR Ca²⁺release to M-clock activation and 2) balancing Ca²⁺ influx and efflux during steady-state AP firing. Specifically, β-AR stimulation results in an earlier and more synchronized diastolic SR Ca²⁺ release and I_NCX (i.e. larger amplitudes are reached in a shorter time); and, vice versa, ACh stimulation results in a later and less synchronized diastolic SR Ca²⁺ release and I_NCX (Fig.6, vertical arrows). Also, β-AR stimulation increases (but ACh stimulation decreases) Ca²⁺ supply to Ca²⁺clock via both I_CaL and the reverse mode I_NCX.

Fig. 6.

Component mechanism of autonomic modulation of AP firing rate via a coupled function of M-clock and Ca²⁺clock in our new flexible and robust pacemaker models. The mechanism is illustrated using a representative model set of “I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f” model type. See text for details.

Next, we insured that each tested set is indeed representative of all model sets that perform well within its model type and there is no model sets that perform nearly as well as the representative set, but do so due to a different set of underlying mechanisms. Since I_NCX dynamics reflect the differences in underlying mechanisms, we simulated and examined the critical I_NCX phases for the top ten sets for each tested model (Fig. S1). All four phases of I_NCX (a, b, c, d) were indeed found in all examined sets with Ca²⁺clock; but phase b, linked to diastolic release, was absent in pure M-clock model “I_CaL+I_Kr+I_NCX+I_f”. We also noticed that all examined sets demonstrate a phase of reverse mode I_NCX, indicating that this is a common feature of these reduced models.

A fundamental limitation of M -clock flexibility

Since it is possible to over-express f-channel in a genetically engineered bio-pacemaker, we tested in-silico whether this simple approach would solve the aforementioned problem of the limited autonomic modulation range of M-clock in 4-parameter model type “I_CaL+I_Kr+I_NCX+I_f“ (Fig. S2). Specifically we tested whether the limited modulation range would be improved in our representative model set I_CaL+I_Kr+I_NCX+I_f“ (which has minimum and maximum rates of 63.8 and 131.9 bpm, respectively), if I_f conductance (g_If) is gradually increased to much higher values up to 0.9 nS/pF set, i.e. far beyond the range of reported values (0.09 to 0.375 nS/pF shown by double head arrow in Fig. S2 and Fig.1C). Larger I_f conductance, however, caused a simultaneous shift of the minimum rate and the maximum rate towards higher values, with the relative modulation range narrowing. As mentioned above, it is still possible to increase flexibility of the M-clock by addition of I_KACh as the 5^th system component (model #11, “I_CaL+I_Kr+I_NCX+I_f+I_KACh”), but the system robustness in this case substantially decreases from 20.29% to 7.313%.

Novel features of robust and flexible pacemaking (vs. prior models)

As described above, the highest balance of robustness and flexibility is achieved in our numerical coupled-clock systems that in addition to Ca²⁺clock and basic currents I_CaL+I_Kr+I_NCX also includes I_f (or I_CaT). Therefore, we continued to examine only the representative model set of this model type, i.e. “I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f”.

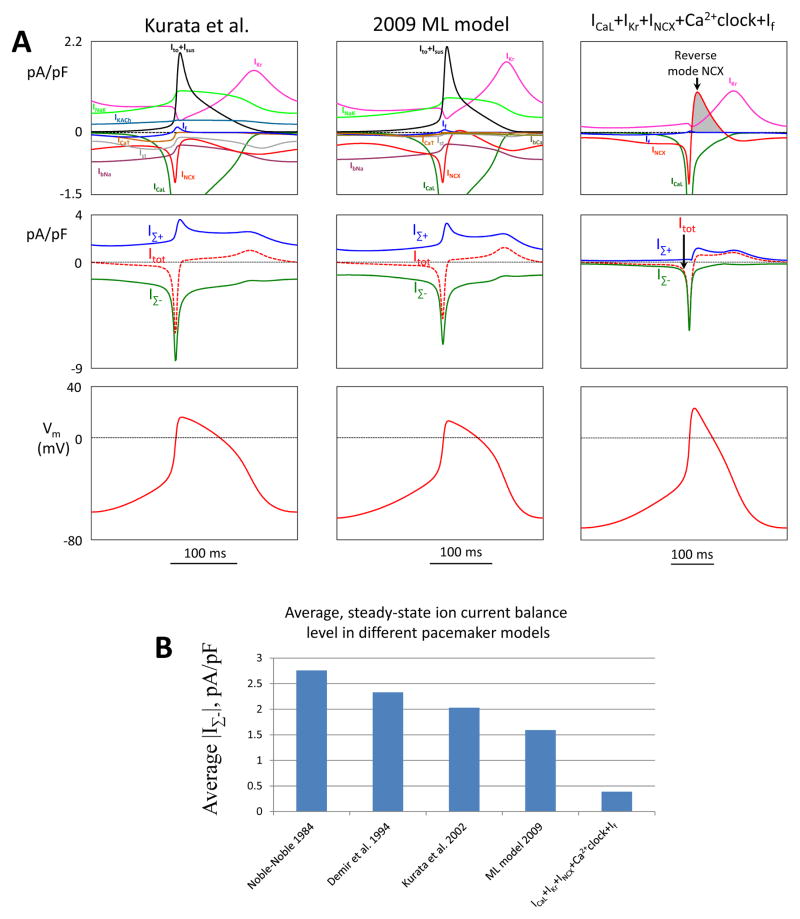
A low level of ion current balance

To quantitatively illustrate this new feature, we compared simulations made by Kurata et al. model, ML model, and a new model “I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f” (Fig.7A). For each model we calculated a sum I_Σ-(t) of instant values for all inward currents (for each time point t during an AP cycle) and the respective sum I_Σ+(t) for outward currents (Fig.7A, top and middle panels). The total current I_tot=I_Σ++I_Σ- (dashed curves) shapes the AP (bottom panels). While I_tot is about the same magnitude in three SANC models, our new model exhibits always (at any t) substantially smaller instant current balance level, i.e. the I_Σ-(t) curve is very close to the I_Σ+(t), especially during DD. The average ion current balance level for one AP cycle is the smallest in the minimal Model among 5 models tested (Fig.7B).

Fig. 7.

Our new flexible and robust pacemaker models feature a low balance level for inward and outward ion currents vs. prior models. A: Top panels show the entire ensemble of ion currents simulated by respective models for one AP cycle (MDP-to-MDP). Middle panels show sums I_Σ(t) of instant values for all inward currents in each model. I_Σ+(t) are respective sums of outward currents. The total current I_tot=I_Σ++I_Σ- (dashed curves) determines the AP shape in each model (bottom panels). B: Average steady-state ion current balance level, <|I_Σ-|>, is the smallest in I_CaL+I_Kr +I_NCX+Ca²⁺clock model vs. prior models.

Ca²⁺ influx via reverse mode phase NCX contributes to Ca²⁺clock “refueling”

Another important and unique feature of our new flexible models is a notable reverse mode phase of NCX. This phase is lacking in previously published pacemaker cell models (Fig. S3). As mentioned above, this phase provides additional Ca²⁺ influx and Na⁺ efflux during AP. For example, in simulations of “I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f” model, the net electrical charge of this phase amounts 1.225 picoCoulomb (pC) (i.e. I_NCX integral within gray area in Fig.7A). Taking into account 3Na⁺ to 1Ca²⁺ exchange ratio for NCX, it translates into 2.45 pC of Ca²⁺ influx (each Ca²⁺ transfers 2 elementary charges). This Ca²⁺ influx is substantial and comparable with I_CaL-mediated Ca²⁺ influx for one AP cycle (∫I_CaLdt=2.96 pC), indicating that Ca²⁺clock is “refueled” almost equally by I_CaL and the reverse mode NCX.

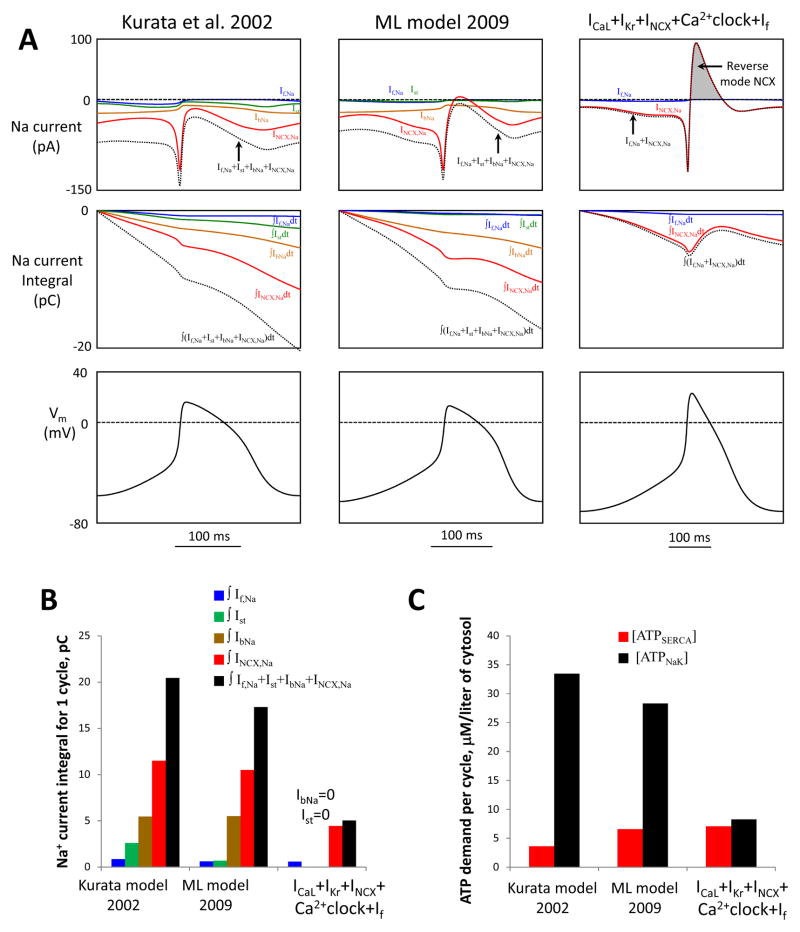
The reverse mode NCX and the lack of I_bNa and I_st insure a low steady-state Na⁺ influx

This new feature is illustrated in Figure 8. (Note I_NCX,Na=3·I_NCX). Specifically, the I_NCX–mediated Na⁺ efflux of 3.65 pC (grey area in Fig.8A) balances almost half of the NCX-mediated Na⁺ influx during the rest of the AP cycle (NCX phases a, b, c) of 8.1 pC. The total Na⁺ charge transferred via I_f during AP cycle is only 0.6 pC (see Online Supplement for I_f,Na formulation). Thus, only 8.1+0.6 −3.65=5.05 pC is left to be balanced (extruded) by ATPases. This is about 4 times smaller than in ML model or Kurata et al. model (black bars in Fig.8B), because the two prior models include substantial Na⁺ influx contributions via I_bNa and I_st, but lack Na⁺ efflux via the reverse mode I_NCX.

Fig. 8.

Our new flexible and robust pacemaker models feature a small steady-state influx of Na⁺ and is expected to be more energy-efficient in terms of Na⁺ balance regulation (i.e. Na⁺ extrusion) vs. prior models Kurata et al. [22] and ML [8]. A: Top panels show simulations of trans-membrane Na⁺ currents via different mechanisms (I_f,Na, I_st, I_bNa, I_NCX,Na) and their sum (dotted lines) in different models for one AP cycle (MDP-to-MDP, bottom panels). Middle panels: respective time-dependent integrals of Na⁺ currents of the top panels reflecting Na⁺ accumulation (during one AP cycle) in the absence of Na⁺ extrusion by ATPases. B: Respective integrals of Na⁺ currents in panel A calculated for one AP cycle. All three models have cell electric capacitance of 32 pF. C: Cell energy budget to maintain Na⁺ homeostasis [ATP_NaK] and to pump Ca²⁺ to the SR [ATP_SERCA] estimated by three models of SANC.

In SANC ATP is consumed not only to maintain cell ionic homeostasis in cytosol (including Na⁺ balance discussed above) but also to pump Ca²⁺ to the SR, to produce cAMP, and to support contraction [15]. It would be interesting to evaluate how much of the total energy budget can be saved if the cell indeed operates without aforementioned energy waste to balance Na⁺ leak due to I_bNa and I_st. Present numerical SANC models, however, do not describe all these components of the total energy budget. We can only evaluate and compare the parts of ATP consumption to pump Ca²⁺ to the SR via SERCA ([ATP_SERCA]) with that to balance Na⁺ influx via Na⁺/K-ATPase ([ATP_NaK]) using well-known equations[16]:

$$\begin{array}{c}d[{\text{ATP}}_{\text{SERCA}}]={\mathrm{I}}_{\text{SR}}/(4·\mathrm{F}·{\mathrm{V}}_{\mathrm{i}})=2·\mathrm{F}·j_{\text{up}}·{\mathrm{V}}_{\text{nSR}}/(4·\mathrm{F}·{\mathrm{V}}_{\mathrm{i}})=j_{\text{up}}·V_{\text{nSR}}/(2·{\mathrm{V}}_{\mathrm{i}})\text{and}\\ d[{\text{ATP}}_{\text{NaK}}]={\mathrm{I}}_{\text{NaK}}/(\mathrm{F}·{\mathrm{V}}_{\mathrm{i}}),\end{array}$$

where V_nSR and V_i are volumes of the network SR and cytosol, respectively, F is Faraday constant, j_up is SR Ca²⁺ uptake flux. Integrating these equations for one AP cycle and assuming for a steady-state AP firing that the integral of I_NaK must be equal to the integral of all Na⁺ currents (estimated above), we evaluated the respective ATP consumptions per cycle in Kurata et al. model, ML model, and in “I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f” model (Fig.8C). While in the two older models [ATP_NaK] substantially exceeds [ATP_SERCA] (by a factor of 9.2 and 4.3, respectively), in our new model [ATP_NaK] is substantially smaller, very close to [ATP_SERCA].

Since Na⁺/K⁺ ATPase exchanges 3Na⁺ to 2K⁺, it generates an outward current that can slow AP firing rate. Therefore we insured that our new robust and flexible pacemaking mechanism is preserved with the addition of I_NaK. We repeated our full sensitivity analysis for model type “I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f” but with the addition of I_NaK (Fig. S4). In these additional simulations the value of parameter I_NaK,max (that determines the density of I_NaK,) was set to 0.9 pA/pF, i.e. a 1/4 fraction of that in Kurata et al. model because the total Na⁺ influx per cycle in our reduced models is about 4 times smaller than in that the older model (Fig.8B, 5.03 vs. 20.45 pC). Our detailed examination showed that this additional I_NaK does not substantially change flexibility and robustness of the “I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f” model (see Table.1, model #8b vs. #8). At the same time the number of physiologically flexible sets substantially increased from 85 to 189, and average maximum diastolic potential (MDP) values in these sets became closer to those of SA node cells −64.0 mV vs. −69.6 mV for basal state AP firing (all key AP parameters of these sets are provided in supplemental Excel files and of the top ten sets in Table S3). The mechanism of flexibility of these model sets adjusted for I_NaK remained the same as in the original model, i.e. via an earlier and larger diastolic I_NCX (tested in the top 10 model sets, Fig. S5).

Discussion

The present study, for the first time, numerically investigated different types of pacemaker cell models to identify the minimum set of proteins that confer a robust and flexible pacemaker cell function. Only those models that include an intracellular Ca²⁺clock were able to reproduce the full range of human heart rate autonomic modulation. A minimal coupled-clock model for the flexible pacemaker cell function “I_CaL+I_Kr+I_NCX+Ca²⁺clock” includes only three ion currents. Further inclusion of I_f or I_CaT decreased flexibility, but increased robustness of the models. We also found that the new flexible models exhibit notable diastolic Ca²⁺ release, smaller ion current balance, and smaller Na⁺ influx.

Classical currents I_bNa and I_st were excluded from our numerical investigation because their molecular identity has not been established. A hypothetical I_bNa was introduced by Noble into his first (1960) theoretical model [3] as an essential current for cardiac pacemaker function and has always been present in every pacemaker model. I_st was discovered experimentally in 1995 [17] and remains a major pacemaker current in numerical modeling by Noma’s group [18]. To our surprise, however, our simulations show that the flexible and robust pacemaker function can be achieved without these currents. This could be explained by the fact that, in the absence of specific blockers, I_st properties are, in fact, a combination of I_CaL and I_NCX, so that I_st may not be a discrete entity[4]. I_bNa does not feature specific blockers, either, and could be also I_NCX (both I_bNa and I_NCX are inward going during DD and generate Na⁺ influx). Furthermore, the essence of the hypothetical I_bNa in the original 1960 model [3] was to balance I_K and to initiate DD, but I_NCX can (and does) also play this role. Indeed, being voltage-dependent, I_NCX is activated by AP repolarization (NCX phase a, Fig.5) and it is present (and fundamentally important) during the entire DD [19,20]. Thus, based on this reasoning and our simulation results, I_bNa could be actually generated by I_NCX.

The results of the present study are in line with ideas of DiFrancesco that numerical modeling of SANC must take into account energy conservation principle, i.e. that the natural system of ion currents and pumps is likely to be most energy-saving [21]. The problem with existing pacemaker models (including Kurata et al. model [22] and ML model [8,9]), however, is that they all have a relatively large balance of inward and outward currents (mainly due to presence of I_bNa and I_st, Fig.7) that implies a presence of a persistent Na⁺ influx and electric shunt of the cell membrane and, hence, inefficient energy use.

In contrast to prior models, our new minimal models (I_bNa=0 and I_st=0) feature a much smaller balance level of inward and outward currents (Fig.7), resulting in a much smaller steady-state Na⁺ influx (Fig.8). While our numerical (bio-)pacemaker prototype does not describe complex details of Na⁺, K⁺, H⁺, and Cl⁻ homeostasis (which will vary in specific bio-pacemaker designs or pacemaker models of different species), its predicted smaller steady-state Na⁺ influx is expected to demand less energy for the Na⁺ extrusion to keep the cell Na⁺ balance (Fig. 8B,C). Thus, by excluding I_bNa and I_st, the new model excludes the aforementioned persistent energy waste and thereby portrays a more energy-efficient and likely more realistic pacemaking mechanism in this regard. Further measurements of Na⁺ fluxes in SANC are required to test our new model prediction. These measurements are indeed important because predictions of Na⁺ handling in prior numerical pacemaker models may not be accurate; for example, in Kurata et al. model “the magnitude of I_NaK is linked to the influx of Na⁺ through I_bNa (and I_st)” (cited from [22]), but, as discussed above, I_bNa and I_st are likely contributed by I_NCX. Therefore, the same Na⁺ current (produced by same NCX molecules) is counted twice or even thrice in the numerical models of SANC featuring I_bNa and I_st.

Reverse mode NCX phase is yet another new feature of flexible and energy-efficient pacemaking revealed by our numerical investigation (Fig. S3, phase d in Fig.5). Our models have a fixed intracellular [Na⁺] of 10 mM as in Kurata et al. and ML models. Thus, the reverse NCX mode (and related Ca²⁺ influx) is higher in the new models due, in part, to its higher AP overshoot. For example, the overshoot in Kurata et al. model occurs at 16 mV, but in the new models at 37 mV and 26 mV, calculated for the average of the top ten models of “I_CaL+K_r+I_NCX+Ca²⁺clock” type or “(I_CaL+K_r+I_NCX+Ca²⁺clock)+I_f” type, respectively. In addition to the overshoot, the difference with older models (of 1980s and 1990s, Fig. S3) is also due to different NCX formulations, intracellular [Na⁺] (e.g. 7.3 mM in Noble-Noble 1984 model), and fundamentally different Ca²⁺ dynamics (Ca²⁺ is released from the SR only during the AP, like in ventricular myocytes). A strong, ventricular-cell-like Ca²⁺ transient peak in the absence of the Na⁺ channel current in SANC favors forward NCX mode, rather than the reverse mode. In contrast, in our models (those with Ca²⁺ clock) a notable diastolic Ca²⁺ release precede systolic Ca²⁺ transient, as discovered experimentally in SANC [4], with the peak systolic Ca²⁺ transient being smaller (1.5 μM vs. 3.5 μM in Noble-Noble model). While the reverse NCX mode is expected to aid I_CaL in its refueling Ca²⁺ clock with Ca²⁺ and also to extrude Na⁺ and save energy [see Results section “Novel features of robust and flexible pacemaking (vs. prior models)”], whether or not NCX actually operates in the reverse mode during AP in SANC requires further experimental elucidation.

Our broad sensitivity analysis revealed that the most flexible system (I_CaL+I_Kr+I_NCX+Ca²⁺clock) lacks I_f (Fig.2D). On the other hand, we show that I_f serves as an anti-bradycardic mechanism (Fig. S2) and improves the system robustness (Fig. 3D and Table 1). Therefore, a higher balance of flexibility and robustness is achieved in a 5-parameter model type that includes both Ca²⁺clock and I_f (i.e. I_CaL+I_Kr+I_NCX+Ca²⁺clock+I_f). While the I_f amplitude decreases upon ChR stimulation, the I_f contribution becomes more persistent at longer cycle lengths, thus acting as a “stabilizer” of the pacemaker rate (Fig.6)[23]. This interpretation is also in line with the findings in HCN4 knockout mice [24]. In stark contrast, five numerical models of M-clock alone (both 4- and 5-parameter models without Ca²⁺clock) cannot reproduce physiological range of autonomic modulation (Figs 2 and 3), even when I_f current is dramatically increased (Fig. S2). One exception is the model type I_CaL+I_Kr+I_NCX+I_f+I_KACh (Fig. 3B), but its physiologically flexible sets are located at the lower border of the maximum heart rate (140 bpm).

Interestingly, our sensitivity analysis also shows that I_f is not a unique current to increase the system robustness: a similar increase in robustness can be achieved with addition of I_CaT (Fig. 3D,E and Table 1) Another interesting result is that inclusion of I_KACh into the numerical system increases its flexibility, but dramatically reduces its robustness (Fig. 3F and Table 1). This result illustrates that addition of a current into the pacemaker cell system may not necessarily increase its robustness, i.e. a system of a larger number of components may be less robust than that with less number of components, and the outcome depends on which specific components are present in the system.

Based on our numerical examination of hundreds of thousand parameter sets of 13 model types, we found that at least 5 model types can reproduce human rate variability in a large variety of specific sets (n=1338, Table 1). Specific parameter values of these sets along with basic properties of APs they generate are provided in supplemental Excel files. The data for the top ten sets of the highest relative flexibility are also summarized in Table S3. This gives the idea and a starting point about qualitative and quantitative contents of a genetically engineered bio-pacemaker with desired properties. For example, using our new extended database of physiologically flexible models one can find a desired numerical model prototype, featuring a specific range of heart rate modulation (e.g. for patients of different ages), combined with maximal system robustness for that specific rate range. Numerical simulations might be also further extended to predict the properties not just a single pacemaker cell but the entire multicellular preparation including its interface with atria. Hence, this approach may guide and facilitate the practical implementation of bio-pacemakers with best predicted outcome and using minimal number of genetically manipulated components.

One specific biopacemaker design is to convert cardiac muscle cells into pacemaker cells [1]. But cardiac muscle cells, rather than pacemaker cells, do not exhibit Ca²⁺clock in the basal state function. One possibility to activate Ca²⁺clock and its coupling with M-clock is permanently activate Ca²⁺ cycling proteins via PKA (and/or CaMKII) -dependent phosphorylation [5], similar to that in SANC. The coupling can be established via expression of Ca²⁺-activated adenylyl cyclase (AC) type 1 and/or 8 [25,26]. This principle has been also recently supported by experimental studies of biopacemakers in dogs [6] and in vitro studies of spontaneously beating neonatal rat ventricular myocytes [27] and stem cell-derived cardiac cells [28]. Interestingly, the study in dogs [6] compared two types of bio-pacemakers with AC1 expression and combined expression of AC1 and I_f. This study showed that I_f is not required for bio-pacemaking, but the artificial increase in I_f results in a higher basal heart rate, i.e. very similar to results of the present study (Fig. S2). Our simulations demonstrated that by increasing I_f conductance beyond its physiological limit, it is still possible to reach the higher rate limit of the human heart (e.g. 207 bpm, Fig. S2), but the lower rate is then simultaneously increases to a non-physiological high level (155 bpm).

Finally, we believe that our new results are important not only for genetic engineering of biological pacemakers, but also provide a novel basis for general theory of cardiac cell pacemaker function. Indeed, the essential, robust mechanisms of the coupled-clock pacemaker system and its autonomic modulation are preserved after omitting 9 currents of the original model (“I_CaL+I_Kr+I_NCX+Ca²⁺clock”, Fig.2D). The minimal set of equations (i.e. ion currents) required and sufficient for a robust and flexible pacemaker cell prototype established in this study will be now much easier to theoretically analyze, e.g. by a bifurcation analysis [29], to gain new fundamental insights into pacemaker cell function. Furthermore, based on data of molecular biology, electrophysiology, and Ca²⁺ measurements, this minimal set of equations, representing interactions of only established molecules, can be further modified to reproduce robust and flexible pacemaking in different species. Development of numerical models with fully established molecular basis, in turn, will advance our knowledge of molecular mechanisms of the cardiac pacemaker function.

To our knowledge, this approach to identify physiologically relevant (i.e. robust and flexible) behavior in extended number of numerical models has not previously been applied to cardiac pacemaker cells. However, varying model parameters, systematically or randomly, has provided valuable insights in other cell types. For example, a similar strategy has been used in groundbreaking work in computational neuroscience by Marder and coworkers to generate large databases of model neurons[30,31]. A large variety of ventricular myocyte models with different properties have been also successfully examined to clarify importance of particular model parameters on AP properties [32] and different cell behaviors, including responses to drugs [33]. Thus, these prior studies and our present study demonstrate the importance of sensitivity analysis as a powerful method for the in-depth mechanistic analysis and searching for realistic numerical descriptions of cell functions, including now cardiac pacemaker function.