Abstract
Many of the solution phase properties of nanoparticles, such as their colloidal stability and hydrodynamic diameter, are governed by the number of stabilizing groups bound to the particle surface (i.e., grafting density). Here we show how two techniques, analytical ultracentrifugation (AUC) and total organic carbon analysis (TOC), can be applied separately to the measurement of this parameter. AUC directly measures the density of nanoparticle–polymer conjugates while TOC provides the total carbon content of its aqueous dispersions. When these techniques are applied to model gold nanoparticles capped with thiolated poly(ethylene glycol), the measured grafting densities across a range of polymer chain lengths, polymer concentrations, and nanoparticle diameters agree to within 20%. Moreover, the measured grafting densities correlate well with the polymer content determined by thermogravimetric analysis of solid conjugate samples. Using these tools, we examine the particle core diameter, polymer chain length, and polymer solution concentration dependence of nanoparticle grafting densities in a gold nanoparticle–poly(ethylene glycol) conjugate system.
Keywords: Grafting density, surface coating, nanoparticle, analytical ultracentrifugation, total organic carbon
INTRODUCTION
The number of bound polymers per unit surface area (i.e., the grafting density) is a critical feature to consider when designing nanoparticles for biological or environmental applications. This parameter directly affects the hydrodynamic diameter and colloidal stability of nanoparticles, factors that are crucial to biological and environmental applications.1–13 Liu et al., for example, found that 10 nm gold particles that were only partially capped with polymer aggregated in dilute salt solution; however, by increasing the grafting density to 50 chains/particle, samples stable in 1 M NaCl could be readily achieved.1 Biodistribution studies of poly(ethylene glycol) (PEG)-coated nanocapsules found a strong correlation between circulation time and polymer surface coverages.2,3 Fully capped materials, for example, had longer blood circulation times and reduced clearance by the liver, spleen, and kidneys as compared to materials with 20% less surface-bound polymer.3 Surface coverage and grafting density also influence a nanoparticle’s transport through environmental matrices such as soil and water. For example, only 1% of uncoated iron oxide nanoparticles were found in the effluent of a 30 cm long sand column however, greater than 50% were detected when the same samples were fully capped with poly(acrylic acid).4
In the majority of the aforementioned studies, investigators estimated ‘partial’ or ‘full’ surface coverage from the amount of polymer employed to functionalize the nanoparticle surface. Seldom are the number of polymers bound to a particle surface (i.e., the surface coverage) directly measured. One common estimate for surface coverage that is applicable only to saturated systems relies on a geometric argument that includes a consideration of the physical size of the free polymer and the known available particle surface area.4,9,14 Alternatively, grafting density can be experimentally derived from thermogravimetric analysis (TGA) of the carbon content in a solid nanoparticle–polymer sample. TGA is a general and widely used tool for quantitative analysis of polymer grafting densities. Conventional instrumentation however requires large volumes of solution to be evaporated in order to provide sufficient quantity (i.e., milligrams) of dried sample for analysis.7,9,15–18 Advances in TGA instrumentation, such as the implementation of quartz crystal microbalances, can reduce the required sample weight substantially.18 For some polymers, spectroscopic methods such as X-ray photoelectron spectroscopy (XPS) or nuclear magnetic resonance spectroscopy (NMR) can be effective in the measurement of surface coverage.11,19–21 Alternatively, fluorescence methods can be applied to either detect labeled polymers or the displacement of surface quenched fluorophores.22,23 Such approaches however can be highly specific to a particular polymer capping agent and less effective in the analysis of systems with low coverage owing to signal interference arising from the core of the nanoparticles under consideration.9
We herein separately apply two techniques, analytical ultracentrifugation (AUC) and total organic carbon analysis (TOC), to measure the grafting density of gold nanoparticle–poly(ethylene glycol) conjugates. Both approaches are well suited to the general problem of analyzing inorganic nanoparticle surfaces in solution. The results of each method agreed well for conjugate samples with nanoparticle diameters, polymer ligand molecular weights (MWt), and solution concentrations of capping polymer in the ranges of 8–11 nm, 1,000–20,000 g/mol, and 8.5–8.5 µM, respectively. Over this wide range of conditions, the grafting densities measured from AUC and TOC varied by less than 20%. The carbon content determined by the TGA of dried sample residues validated the measured solution phase grafting densities. As an example, we applied these tools and evaluated how the grafting density of partially coated and fully coated nanoparticles in solution correlated with their aggregation behavior in salt solution. For nanoparticles with complete surface coverage, we additionally demonstrate how the grafting densities depend on the molecular weight of the polymer capping agent and to a lesser extent on the diameter of the gold nanocrystal core.
MATERIALS AND METHODS
Nanoparticle Preparation
Citrate stabilized gold colloids (5, 10, 15, and 20 nm) purchased from Ted Pella were used as received or surface-modified with thiol-functionalized methyl-poly(ethylene glycol) (mPEG-SH) of 1, 2, 5, 10, or 20 K MWt purchased fresh from Creative BioChem and stored under inert gas. mPEG-SH may degrade under a variety of circumstances and, for these reasons, great care was taken to use materials within one to two weeks of preparation.24–26 All surface-coated gold samples were saturated with excess mPEG-SH, as described below, unless otherwise stated. For example, 10 nm gold particles at a particle concentration of 9.0 × 10−9 M were added to a solution of 2.5 × 10−5 M PEG (~2800 PEG/particle), covered, and subsequently stirred for 12 hours prior to purification. . We chose 12 hours for equilibration as studies of thiol-PEG bound to gold suggests that this time should be enough to allow for full equilibration.27,28 Samples with unsaturated polymer coating were prepared by reducing the polymer concentration in solution without change to nanoparticle concentration or stirring time. Unbound polymer was then removed by repeated (three times) centrifugal filtration (100 MWCO, EMD Millipore) at 4150 RPM for 10 min. TOC was used to verify that the cleaning method was sufficient to remove unbound polymer for each molecular weight. It was found that ~80 – 90% of the initial polymer could be removed in a single cleaning step, ~10% in the second and then there was less than 1% change for each additional round of centrifugation. No significant change in the carbon concentration was seen after the third centrifugation, so three cleaning steps were chosen for purification.
Transmission electron microscopy (TEM)
To determine the size of the gold nanoparticle core, a JEM-2100F JEOL field gun emission transmission electron microscope operating at 200 kV was used. Samples were prepared by drop casting ~20 µL of nanoparticle solution on an ultrathin carbon type-A 400 mesh copper grid (Ted Pella). ImagePro software was used to determine the sizes and distribution of over 500 particles.
Analytical ultracentrifugation (AUC)
Sedimentation velocity AUC experiments were run on a Beckman ProteomeLab XL-A ultracentrifuge equipped with a UV/Vis (monitored at 525 nm) scanning detection system and a AN-60 Ti 4-position rotor. Samples were housed in a 12 mm, charcoal-filled, dual channel, epon centerpiece with quartz windows. SEDFIT was used to find the sedimentation coefficient distributions using the ls-g*(s) analysis model with parameters set for the best fit and minimum residuals for each sample.29
Thermogravimetric analysis (TGA)
TGA was performed using TA Instruments Q-600 Simultaneous TGA/DSC. Approximately 10 mL of gold or PEGylated gold nanoparticle samples (~9.0 nM) were concentrated to a volume of 100 µL and then dried in the TGA furnace prior to analysis. Each sample was first dried at 100°C for 60 min to remove excess water and then held at 140°C for 60 min to remove residual water. The analysis was performed under a flow of 100 mL/min air while the change in mass was determined every 0.1°C over a temperature range of 150–1200°C. A stepwise isotherm method, which is designed to hold the temperature constant when the rate of weight loss is greater than 1 wt%/min and steadily ramp at 5°C/min at all other temperatures, was employed during evaluation. The organic component of the sample was found from the percent mass loss over the temperature range of 150–500°C, which for the gold nanoparticles was entirely attributed to the decomposition of surface-bound polymer. A pure PEG sample, analyzed for comparison, displayed a derivative peak at 229°C (FWHM, 65°C) and 96.5% mass loss between 150 and 500°C.
Total organic carbon (TOC)
A Shimadzu TOC-VWP was also used to determine the carbon content of the nanoparticle conjugates. The samples were run on a total non-purgeable organic carbon (NPOC) assay with triplicate 50 µL injection volumes. Following injection, the NPOC assay pretreats the sample with acid to remove and measure all inorganic carbon. The sample is then oxidized and analyzed to determine the remaining carbon content, which is again attributed to the polymer capping agent of the conjugates. Each sample was prepared by diluting 1 mL of purified nanoparticle solution to a total volume of 24 mL with Milli-Q 18 MΩ nanopure water. Concentration curves ranging from 0.02 to 50 ppm were prepared from a TOC standard solution (100 ppm) purchased from Sigma with a resulting R2 value of 0.998.
Dynamic light scattering (DLS)
DLS was performed on a Malvern Instruments ZEN-3600 Zetasizer Nano equipped with a HeNe 633 nm laser. Undiluted and as-purified half milliliter samples were analyzed (3 runs/measurement) in standard small volume disposable cuvettes (Fisher). The particle size was taken to be the first peak of the volume corrected data and the standard deviation was determined from triplicate measurements.
Flocculation assay
Flocculation assays were used to determine the critical coagulation concentrations (CCCs) of the gold nanoparticles in sodium chloride and calcium chloride solutions.1 Colorimetric determination of the CCCs were performed by evaluating the optical absorbance at 520 nm for non-aggregated and 595 nm for aggregated nanoparticle samples using a SpectroMax brand UV/Vis multiwell plate reader over a salt concentration range of 0.01 M to 2.5 M. The CCC for each sample corresponded to the lowest concentration of salt necessary to induce aggregation.
Grafting Density Calculations
TGA Grafting Density
The grafting density (σTGA) was calculated from TGA analysis using equation 1. First, the relative mass of the polymer (wt%shell) and the residual mass of the pure gold nanocrystal (wt%core) were found from the experimental TGA data at 500°C. The number of polymer units per total sample was then derived by taking the polymer mass (wt%shell) and dividing by the polymer mass per chain (i.e., polymer molecular weight/avogadro’s number). The denominator requires a measure of the total particle surface area in the sample, a value defined here to be the surface area per particle (4πr2) multipled by the total number of particles. Nanocrystal number was derived from the nanocrystal mass (wt%core) divided by the nanocrystal mass per particle, which corresponded to the product of the density of bulk gold (ρcore = 19.6 g/cm3) and the volume of a single particle (4/3πr3). Note that the radius of the particle was measured from TEM and both the surface area and volume calculations require the assumption that the particle assumes a spherical shape.
| (1) |
TOC Grafting Density
The grafting density (σTOC) was calculated from TOC data using equation 2. The non-purgeable organic carbon concentrations ([C]), reported in ppm (mg/L) from a typical TOC analysis, must first be converted to molarity (moles/liter) by dividing by the molar mass of carbon (12 g/mole) and multiplying by 1000 to convert the volume to liters (1000 mL/L). The molarity of carbon is then used to determine polymer concentration by applying the ratio of carbons per monomer unit (2 for PEG) and the number of monomers (n) in each polymer sample, which is given by the molecular weight divided by the molar mass of a single monomer unit (44 g/mole for PEG). To determine the number of PEG molecules per particle, the molar concentration of nanoparticles in solution ([NP]) must first be acquired; it can be determined based the optical absorbance of the gold nanoparticle solution.30 The molarity of PEG is then divided by the molarity of the nanoparticles, [PEG]/[NP]. The molar ratio of PEG molecules per particle once divided by the surface area of a single particle (using the radius found from TEM) results in a value of the grafting density.
| (2) |
AUC Grafting Density
This method takes a different approach to determining the surface coverage of particles. It relies on the change in density induced by the association of lower density particles with the very dense gold cores. In effect, particles become less dense as greater polymer capping agent is bound to their surfaces. This is quantified through measurement of the sedimentation coefficient (s), a value related to particle density (ρp) by equations 3 and 4. Other parameters that are pertinent to the definition of the sedimentation coefficient include the solvent viscosity (η) and density (ρs) as well as the particle’s hydrodynamic diameter (dh). While the first two parameters are easily obtained from the solvent itself (note that nanoparticle concentrations are too low to impact these values), dh is challenging to measure particularly for nanoparticle systems with unsaturated surface capping.
| (3) |
| (4) |
The volume of the polymer capping shell (Vshell) is the product of the polymer thickness and the nanoparticle surface area (4πrcore 2). The thickness of the polymer layer corresponds to the difference between the hydrodynamic radius (rh, from DLS) and the core radius (rcore, from TEM). The total density of the nanoparticle is given by the sum of the volume fraction of the core (Vcore, TEM) multiplied by the density of the core and the volume fraction of the shell multiplied by the density of the shell (equation 8). Given the density of the nanoparticle (equation 2) and the density of the core, which can be determined theoretically or by AUC analysis of an uncoated particle, equation 5 can be rearranged to solve for the density of the polymer shell (equation 6). The mass of polymer therefore corresponds to the product of the volume of the shell and the calculated shell density. The mass is related to the number of polymers per particle, obtained using Avogadro’s number (NA) and the known molecular weight. Finally, normalizing of the number of polymer molecules by the available surface area of the nanoparticle core (4πrcore 2) subsequently affords the desired grafting density (σAUC).
| (5) |
| (6) |
| (7) |
| (8) |
RESULTS AND DISCUSSION
In this work, the grafting densities of nanoparticle–polymer conjugates were derived from measurements of particle density using ultracentrifugation (AUC) as well as from total organic carbon content in solution (TOC). These tools only require small volumes of dilute nanoparticle dispersions for analysis and thus, are ideally suited for laboratory scale sample batches typically required for medical applications, environmental remediation, or reservoir analysis.5,9,18 Because these methods rely on different assumptions to arrive at the particle grafting density, a comparison of their results provides insight into the true value of the grating density as well as the magnitude of the methodological systematic error.
Analytical ultracentrifugation has been developed primarily as a tool for physical biochemists.31,32 Over the last ten years however, it has found increasing use in nanotechnology for the evaluation of the sizes and size distribution of various nanocrystal ensembles such as bioconjugates of gold nanoparticles. The surface structure and utility of various surfactant coating materials on carbon nanotubes have also been investigated with this methodology.33–40 AUC finds a sedimentation coefficient for a given nanoparticle–polymer sample, which significantly depends on the overall nanoparticle–polymer density. If the hydrodynamic diameter of the nanoparticle–polymer conjugate can be accurately measured, this density can then be used to determine the nanoparticle surface coverage.
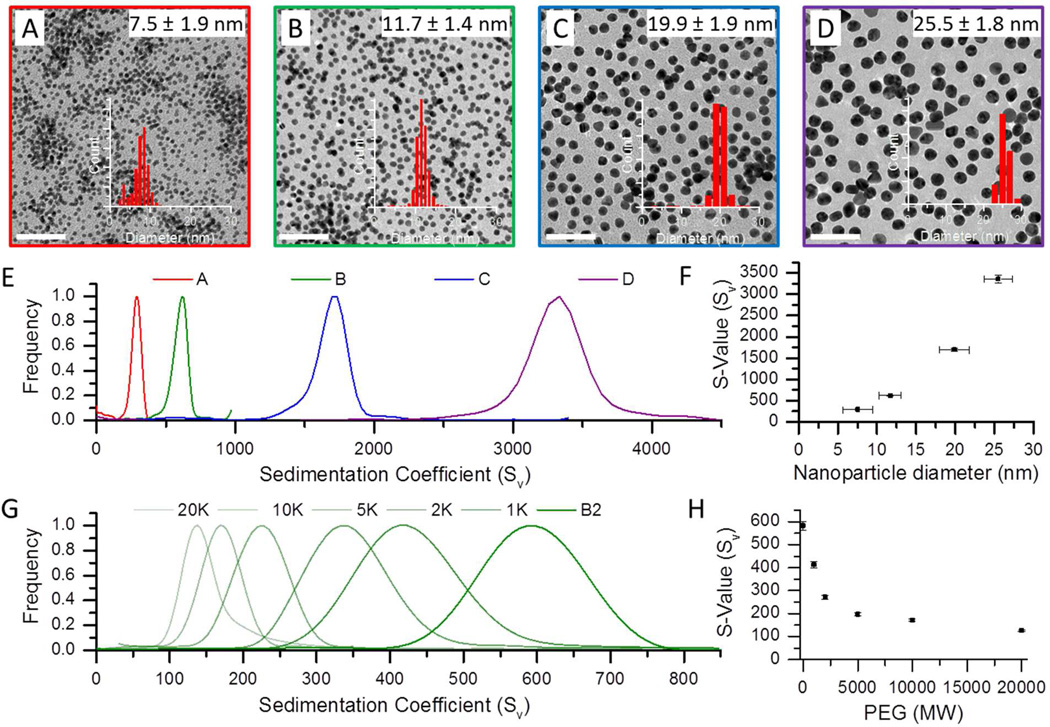
Figure 1 illustrates how the sedimentation coefficients (s-values) of the nanoparticle system bearing saturated surfaces varied with nanoparticle size and polymer thickness. Data was collected as a function of core nanoparticle size (7.5–25.5 nm, panels A–D) as well as polymer chain length (1 K to 20 K MWt, panels G–H). TEM micrographs provided in Figure 1 show gold particles of 7.5, 11.7, 19.9 and 25.5 nm diameter. AUC velocity sedimentation experiments run on each of these samples displayed increasing sedimentation coefficients (288 ± 7, 617 ± 15, 1697 ± 35 and 3359 ± 87 Sv) with increasing core diameter (Figure 1E). This trend is captured quantitatively in Figure 1F which illustrates the expected cubed dependence of sedimentation coefficient on core diameter, given its relationship to diameter and density in equation 3. Figure 1G illustrates that the addition of a polymer capping to the surface of a 9.1 nm batch of gold nanoparticles resulted in a decrease in their sedimentation coefficient. Figure 1H shows this relationship graphically as the sedimentation coefficient is plotted as a function of surface-bound polymer molecular weight over a range of 1–20 K. Longer capping polymers evidently exhibited greater effect on nanoparticle sedimentation.
Figure 1.
Analytical ultracentrifugation (AUC) characterization of nanoparticle conjugates as a function of conjugate size and density. Images A–D show transmission electron micrographs of four batches of gold nanoparticles (scale bars = 100 nm). Sedimentation coefficient distributions for the four sizes are shown in graphs E & F, which show there is an increase in s-value as a function of the particle diameter. A nanoparticle sample of 9.1 nm (B2) coated with PEG of increasing molecular weights, from 1K to 20K, show a decrease in the sedimentation coefficient distributions due to a decrease in the overall particle density (G and H).
The sensitivity of the sedimentation coefficient on the nanoparticle core size and the surface-bound polymer chain length derives from its relationship to both hydrodynamic diameter and overall conjugate density (see equation 3 above).34 By considering the hydrodynamic diameter (dh) determined from DLS along with known solution parameters such as solvent density and viscosity, the nanoparticle–polymer density can be readily obtained from equation 4. This data is reported in Table 1, which highlights that the nanoparticle–polymer conjugates had a lower density than bulk gold due to the presence of the organic capping groups. If the volume of the polymer shell is calculated from the hydrodynamic data, it is then possible to calculate the net mass of the polymer layer and thereby arrive at the number of surface-bound polymers.
Table 1.
Method based on nanoparticle density. Analytical Ultracentrifugation and DLS data.
| S-value (Sv) |
dh (nm) |
Density (g/cm3) |
Mass-polymer/NP (g) |
Grafting Density (PEG/nm2) |
Ligand Footprint (nm2) |
|
|---|---|---|---|---|---|---|
| AuNP_B2 | 586.3 | 9.9 | ||||
| AuNP_1KPEG | 418.1 | 13.9 | 4.9 | 1.37E-18 | 3.2 | 0.31 |
| AuNP_2KPEG | 337.4 | 17.5 | 3.0 | 1.67E-18 | 1.9 | 0.52 |
| AuNP_5KPEG | 225.4 | 25.3 | 1.6 | 2.39E-18 | 1.1 | 0.90 |
| AuNP_10KPEG | 170.2 | 34.6 | 1.3 | 3.51E-18 | 0.8 | 1.23 |
| AuNP_20KPEG | 138.5 | 79.9 | 1.0 | 9.41E-18 | 1.1 | 0.92 |
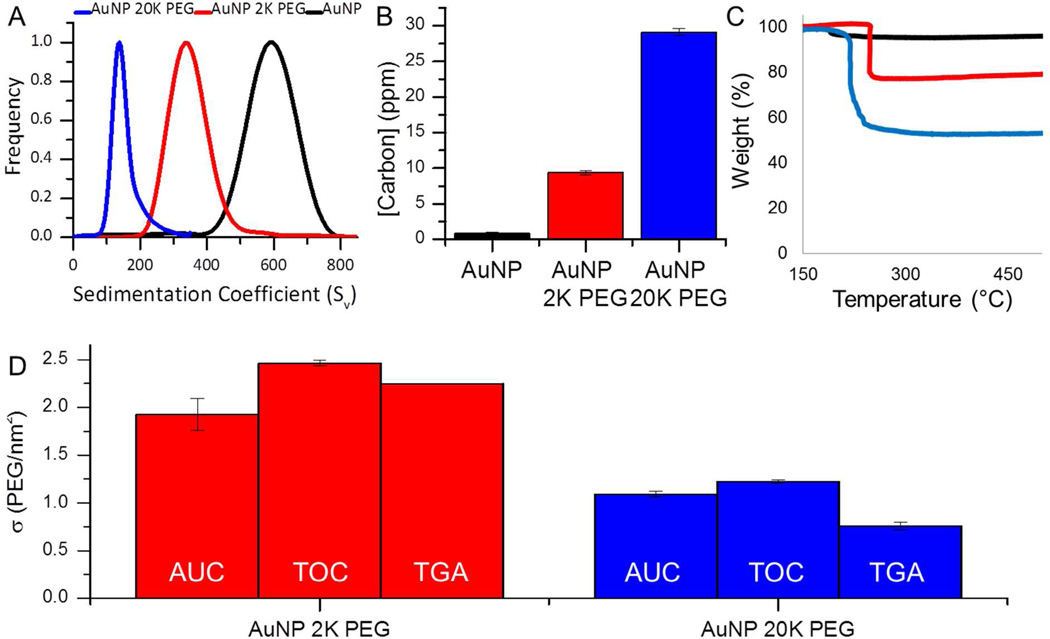
To demonstrate how the grafting density can be extrapolated from AUC analysis, consider the 2 K and 20 K PEG-coated gold nanoparticle samples (See AUC grafting density calculation provided in the experimental section). The core particle diameter selected here is 9.1 nm which possesses a sedimentation coefficient of 586 ± 19 Sv and hydrodynamic diameter of 9.9 nm. The slight increase in hydrodynamic diameter is attributed to the presence of citrate capping agents and solvent interactions at the particle surface. The 2 K PEG-coated sample shown in Figure 2A had a polymer shell thickness of 4.2 ± 0.4 nm (85.9% of the total volume). Using an overall particle density of 3.0 ± 0.3 g/cm3, this corresponds to a polymer mass of 1.7 ± 0.2 × 10−18 g and a grafting density of 1.9 ± 0.2 PEG/nm2. In contrast, the conjugate system prepared with a longer chain PEG had a coating thickness of 35.4 ± 0.5 nm (99.9% of the total volume). The overall density of this particle was 1.04 ± 0.03 g/cm3, which corresponds to a polymer mass of 9.41 ± 0.85 × 10−18 g and a grafting density of 1.09 ± 0.03 PEG/nm2.
Figure 2.
Poly(ethylene) glycol coatings of 2K (red) and 20K (blue) on ~10nm gold nanoparticles (A) decrease the density and lower the sedimentation coefficients measured on 400 µL of sample via analytical ultracentrifugation. Carbon present on the AuNP sample is due to the citrate molecules used as a stabilizer by the manufacturer. Polymer addition adds carbon to the sample which raises the carbon concentration found using (B) total organic carbon analysis and (C) thermogravimetric analysis, on 1 mL and 10 mL of sample, respectively. Each of these measurements can be used to quantify the polymer grafting densities, graph D shows a comparison of the values obtained using each of these techniques (Some error bars are not lager than the line).
Another approach to measuring grafting density relies on changes in the sample composition, which can be monitored by total organic carbon (TOC) analysis. This method is in principle very similar to thermogravimetric analysis however, TOC measurements can be performed on as little as 50 microliters of solution phase sample.41 In conventional TOC, phosphoric acid, an oxidant, and heat are used to catalyze and convert all carbon present to CO2 which is then quantified. Figure 2B shows that at equilibrium saturation (i.e. full coverage), the carbon concentration measured by TOC is minimal for the citrate coated gold nanoparticles and increased with addition of a surface coating and with increasing polymer chain length.
The carbon concentrations of the conjugates acquired from TOC measurements can be readily converted to the desired nanoparticle–polymer grafting densities. This first requires an accurate measure of nanoparticle concentration, derived here from the absorbance of the gold nanocrystal solutions.30 The grafting density is then given by the ratio of available surface area (per volume) to the number of PEG molecules derived from the carbon concentration and the PEG molecular weight (see TOC grafting density calculation provided in the experimental section). To illustrate, consider a 9.0 nM solution of 2 K MWt PEG-gold (9.1 nm core) with a measured carbon concentration of 9.4 ± 0.3 ppm. From equation 2, the corresponding grafting density is 2.46 ± 0.03 PEG/nm2. The most significant source of systematic error associated with the TOC method originates from the assumption that all measured carbon is derived from surface associated polymers. Careful sample purification ensures that carbon contamination is minimized however, it should be expected that this method will generally overestimate the carbon concentration at the nanoparticle–polymer interface.
To validate both the ultracentrifugation and TOC methods, we applied thermogravimetric analysis to powders derived from the nanoparticle solutions. This technique measures the total quantity of carbon in the solid phase as opposed to the liquid phase. Figure 2C shows that the percent mass loss between 150 and 500°C increases with increasing PEG molecular weight. The TGA-acquired weight percent of the carbonaceous material (polymer) and the core diameter of the particle determined from TEM, can then be used to determine the polymer grafting densities (See TGA grafting density calculation included in the experimental section). For the 2 K PEG-coated 8.5 nm gold, 20.8% of the sample weight was attributed to capping polymer and therefore, this system possessed a grafting density of 2.3 PEG/nm2. In contrast, the polymer component of the 20 K PEG-coated gold conjugate made up 47.0 ± 0.8% of the sample weight and thus, a resulting grafting density of 0.8 PEG/nm2. TGA, like TOC, is sensitive to organic contamination in the samples. However, with carefully purification this error can be minimized and the largest systematic error in TGA stems from the possibility that some carbonaceous materials will not be fully combusted, leaving behind graphitic soot, which subsequently contributes to the apparent weight of the inorganic fraction.
In this study, TGA provided a measure of polymer surface coverage that was in reasonable agreement; i.e., within 24% of the values determined from both AUC and TOC analyses (Figure 2D and Table 2). The TGA-determined surface coverage of the nanoparticle–polymer (2 K) conjugate was 2.2 PEG/nm2, which was greater than the AUC value of 1.9 PEG/nm2 and less than the TOC value of 2.5 PEG/nm2. The longest polymer studied, with a MWt of 20 K, afforded conjugates with a grafting density of 0.8 PEG/nm2 as measured by TGA which was less than both of the values obtained by TOC and AUC analyses (1.2 and 1.1 PEG/nm2 respectively). Interestingly, TGA measured carbon content consistently lower than the solution TOC methods. We attribute this to the systematic errors associated with TGA already discussed above.
Table 2.
Nanoparticle grafting density (PEG/nm2) determined by three methods. The errors provided reflect the standard deviation of the replicate error in triplicate measurements of the same sample.
| TOC | AUC | TGA | |
|---|---|---|---|
| σ | σ | σ | |
| AuNP_2KPEG | 2.46±0.03 | 1.93±0.17 | 2.25±0.01 |
| AuNP_20KPEG | 1.22±0.02 | 1.09±0.03 | 0.76±0.04 |
Also notable in Figure 2 was the consistent agreement between the grafting densities measured by AUC and TOC methods. The differences were most pronounced for the conjugates that contained shorter polymer chains as capping groups. For instance, AUC analysis of conjugates prepared with 2 K PEG yielded a grafting density of 1.9 PEG/nm2 as opposed to the 2.5 PEG/nm2 measured from TOC. The grafting densities for the conjugates that contained longer PEG chains (i.e., MWt = 20 K), were within 0.2 PEG/nm2 (1.0 to 1.2 PEG/nm2). Table 3 shows ~10 nm gold nanoparticles individually capped with five different molecular weight polymers within a range of 1–20 K were found to have average grafting densities that deviated by less than 22% between methods. Overall the agreement between the two methods was on average 20%, which is about four times the typical random error found in replicate studies using each technique alone.
Table 3.
Grafting density by TOC and AUC for five molecular weight polymer coatings on ~10 nm gold particles. The errors provided reflect the standard deviation between measurements of four batches. The column on the right is the average grafting density between the two methods and their agreement.
| Sample | TOC | AUC | Average of the two methods |
|---|---|---|---|
| σ | σ | σ | |
| AuNP_1KPEG | 3.62±0.37 | 4.61±1.69 | 4.12±0.70 |
| AuNP_2KPEG | 2.42±0.91 | 2.59±0.58 | 2.50±0.12 |
| AuNP_5KPEG | 2.07±1.26 | 1.46±0.31 | 1.77±0.43 |
| AuNP_10KPEG | 1.39±0.68 | 1.02±0.18 | 1.21±0.27 |
| AuNP_20KPEG | 1.19±0.36 | 0.93±0.14 | 1.06±0.18 |
Applications for grafting density measurements
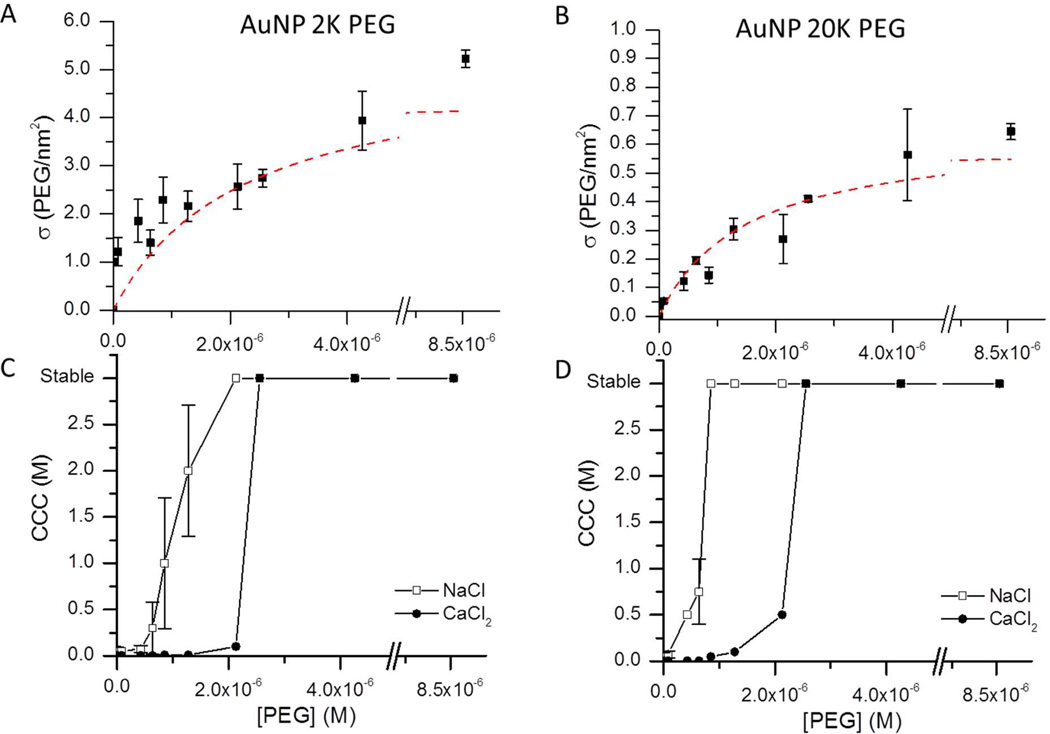
An advantage of both the AUC and TOC methods is that they are sufficiently sensitive to analyze conjugates with incomplete polymer surface coverage. We exploited this capability to examine how the grafting densities varied as the nanocrystals were exposed to increasing amounts of capping polymer. Figure 3 shows the systematic increase and eventual plateau in grafting densities as the polymer concentration was varied from 8.5 nM to 8.5 µM for 2 K and 20 K PEG-SH-coated gold nanoparticles. We note that samples were allowed to equilibrate for 12 hours before measurement, and studies of these dynamic surface exchange processes for fully coated particles indicates this is sufficient time to reach equilibrium.27,28 Still, it may be possible that if the dynamics are much slower for the undersaturated surfaces, then the data at the lower PEG treatment concentrations may reflect slower surface exchange rather than a true equilibrium state. For our purposes the trend allows us to illustrate that both measurements can detect changes in grafting density with less than a 10% increase in polymer concentration. The intersection of linear fits for the increase and plateau region of the respective samples were used to determine saturation of the surface of 8.2 nm gold nanoparticles at a solution concentration of 9.0 nM required concentrations of 4 µM and 3 µM PEG for 2 K and 20 K PEG, respectively. These saturation concentrations corresponded to surface coverages of 500 and 370 PEG/particle, respectively.
Figure 3.
Polymer grafting densities increase upon the addition of (A) 2 K or (B) 20 K PEG to a solution of ~10 nm gold nanoparticles (red dotted lines are added to guide the eye). Critical coagulation concentration (CCC) of (C) 2 K and (D) 20 K PEG-capped particles in sodium chloride (open squares) and calcium chloride (closed circles) solutions show that increased polymer concentrations improves the colloidal stability. Neither of the PEG coatings prevents nanoparticle aggregation in CaCl2 solutions below surface saturation.
As an indirect measure of the extent of particle surface capping, the critical coagulation behavior of the conjugates was also evaluated. The minimum NaCl or CaCl2 concentration that results in particle aggregation is known as the critical coagulation concentration (CCC).1 This analysis assumes that dispersions consisting of particles with saturated surface capping will remain colloidally stable irrespective of the salt concentration of the dispersion solution.1 Figure 3 compares the colloidal stability data for particles with surface coverages independently evaluated using TOC or AUC. The data demonstrates that even partially capped nanoparticles were resistant to aggregation in NaCl solutions. For example, samples treated with polymer concentrations of 2.1 µM 2 K PEG and 0.9 µM 20 K PEG (corresponding to grafting densities of 300 and 100 PEG/particle, respectively) were not yet fully saturated. However, these particles were resistant to aggregation as indicated by the flocculation assays. The Zeta potential measurements of these partially capped samples revealed that their surface charge was fully neutralized at polymer concentrations of 1.3 µM (150 PEG/particle) 2 K PEG and 0.6 µM (75 PEG/particle) 20 K PEG. These data illustrate that inferring the extent of nanoparticle surface coverage based on its stability in monovalent salt solutions or from its zeta potential can be misleading.
In contrast, when CaCl2 was employed as salt, much higher polymer grafting densities were required to achieve colloidal stability (Figure 3). For example, 2.6 µM PEG (i.e., 300 PEG/particle) treatments were not sufficient to stabilize the conjugates against aggregation. Only particles with the highest grafting densities were stable in CaCl2 solutions. Thus, measuring flocculation in a divalent salt solution is a significantly better approach for indirectly evaluating the extent of surface capping in a nanoparticle–polymer conjugate system.
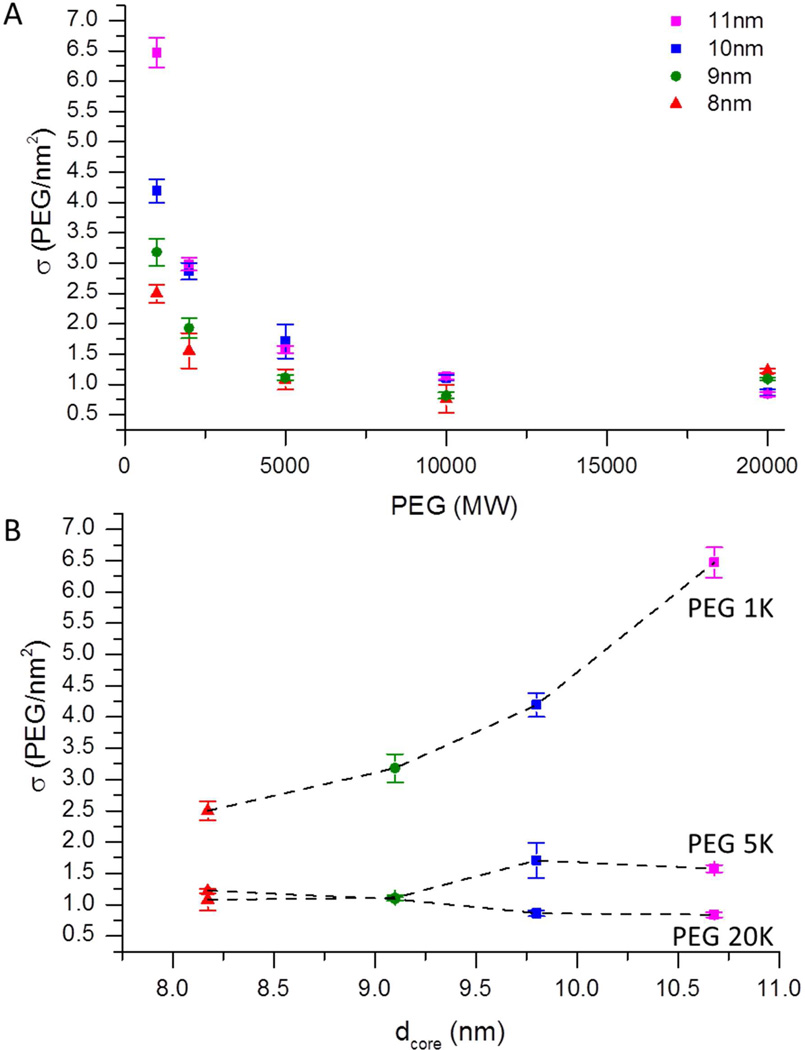
We also used these tools to study how the capping polymer chains packed in conjugates with complete surface coverage. As shown above, the grafting density of nanoparticle–polymer conjugates is sensitive to the polymer molecular weight as well as the curvature of the gold nanocrystal. Figure 4a shows how the grafting density of five polymers, with molecular weights ranging from 1 to 20 K, varied for four different gold nanocrystal diameters, ranging from 8 to 11 nm. As expected, the grafting densities decreased with increasing polymer molecular weight for all nanoparticle diameters tested (Table 3).27,28,42 For 1K PEG on the 9.1 nm particles the grafting density of 4.6 PEG/nm2 matches well with the ideal packing of helical PEG molecules with a cross-sectional area of 0.213 nm2 (4.7 PEG/nm2) expected from literature.27 Also, as the diameter of the core increased from 8 to 11 nm, a corresponding increase in grafting density from 2.5 to 6.5 PEG/nm2 (Figure 4B) exceeded the expected coverage for a monolayer of PEG in a helical conformation and suggests the polymers are further extended or additional material intercalated within the coating. This trend was only seen where the height of the polymer was equal to or less than the radius of the particle.43 The diameter dependence likely arises from the improved ability for short polymers to pack and optimize their interchain interactions on flatter surfaces of larger particles.44
Figure 4.
(A) AUC determination of PEG coverage as a function polymer molecular weight and nanoparticle core size. (B) Packing efficiency dependence of the 1K, 5K and 20K PEG-capped conjugates on the nanoparticle core diameter. (Most of the error bars are not larger than their corresponding data points).
This work presents two options for solution-based assays that can easily and reproducibly measure the polymer grafting densities of nanoparticle–polymer dispersions. Both AUC and TOC require liquid samples and use less than 1 mL (< 60 µg) of sample for a triplicate analysis. AUC requires specialized instrumentation, but is not affected by minor impurities in solution and offers a general approach for studying surface capped nanoparticles in both aqueous and organic solvents. It is noteworthy that by using 2D velocity sedimentation analysis, it may be possible to simultaneously obtain both the sedimentation coefficient and hydrodynamic diameter in a single scan.45 TOC, on the other hand, makes use of a simple bench-top instrument that requires no sample preparation or complicated data analysis. It is however less broadly applicable than AUC in that it cannot be used to analyze dispersions in organic solvents. Each technique presented comparable random error in the measurement of grafting density (typically 5 ± 3%). Nevertheless, over a broad range of experimental conditions, both methods provided measures of grafting density that agreed to within 20%.
CONCLUSION
Analytical ultracentrifugation (AUC) and total organic carbon (TOC) analyses are effective in the determination of the polymer grafting densities of solution phase nanoparticle– polymer conjugates. Both techniques were successfully used to evaluate a range of gold nanoparticle diameters coated with various molecular weights of thiol functionalized poly(ethylene glycol). Dilute (~10 nM) 1 mL samples were analyzed for polymer surface coverage; not only did each method independently agree, but their reported values were consistent with those derived from thermogravimetric analysis (TGA) of the carbon content of sample powders. AUC is best suited for samples with dense and uniform core nanoparticles, and it may be applied to nanoparticles in any type of solvent. It does however require specialized instrumentation capable of relatively intensive data analysis for extracting sedimentation coefficients. The TOC method, in contrast, uses a simple bench-top instrument and is the best choice for aqueous dispersions that have been carefully purified. These methods for measuring the polymer surface coverage of nanoparticle–polymer conjugates offer many advantages to researchers. These include routine tests to ensure batch-to-batch consistency in sample formulations, as well as quantitative assessments of the role of surface coverage on colloidal stability and transport in biological or environmental matrices.
Supplementary Material
ACKNOWLEDGEMENTS
This work was supported by a training fellowship from the Keck Center Nanobiology Training Program of the Gulf Coast Consortia (NIH Grant No. 5 T90 DK070121-04 & NIH Grant No. T32EB009379), the Center for Biological and Environmental Nanotechnology (Grant No. EEC- 0647452), and the EPA-UK Grant No. RD-83457501. We would like to thank Becca Barnes and the Masiello Lab for training and for use of their TOC instrument.
REFERENCES
- 1.Liu Y, Shipton MK, Ryan J, Kaufman ED, Franzen S, Feldheim DL. Anal. Chem. 2007;79:2221. doi: 10.1021/ac061578f. [DOI] [PubMed] [Google Scholar]
- 2.Stolnik S, Daudali B, Arien A, Whetstone J, Heald CR, Garnett MC, Davis SS, Illum L. B.B.A. Biomembranes. 2001;1514:261. doi: 10.1016/s0005-2736(01)00376-5. [DOI] [PubMed] [Google Scholar]
- 3.Mosqueira VCF, Legrand P, Morgat JL, Vert M, Mysiakine E, Gref R, Devissaguet JP, Barratt G. Pharm. Res. 2001;18:1411. doi: 10.1023/a:1012248721523. [DOI] [PubMed] [Google Scholar]
- 4.Jiemvarangkul P, Zhang Wx, Lien HL. Chem. Eng. J. 2011;170:482. [Google Scholar]
- 5.Darlington TK, Neigh AM, Spencer MT, Guyen OTN, Oldenburg SJ. Environ. Toxicol. Chem. 2009;28:1191. doi: 10.1897/08-341.1. [DOI] [PubMed] [Google Scholar]
- 6.Feng W, Brash JL, Zhu S. Biomaterials. 2006;27:847. doi: 10.1016/j.biomaterials.2005.07.006. [DOI] [PubMed] [Google Scholar]
- 7.Corbierre MK, Cameron NS, Sutton M, Laaziri K, Lennox RB. Langmuir. 2005;21:6063. doi: 10.1021/la047193e. [DOI] [PubMed] [Google Scholar]
- 8.Gessner A, Paulke BR, Muller RH, Goppert TM. Pharmazie. 2006;61:293. [PubMed] [Google Scholar]
- 9.Jokerst JV, Lobovkina T, Zare RN, Gambhir SS. Nanomedicine. 2011;6:715. doi: 10.2217/nnm.11.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Aggarwal P, Hall JB, McLeland CB, Dobrovolskaia MA, McNeil SE. Adv. Drug Del. Rev. 2009;61:428. doi: 10.1016/j.addr.2009.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kingshott P, Thissen H, Griesser HJ. Biomaterials. 2002;23:2043. doi: 10.1016/s0142-9612(01)00334-9. [DOI] [PubMed] [Google Scholar]
- 12.Takae S, Akiyama Y, Otsuka H, Nakamura T, Nagasaki Y, Kataoka K. Biomacromolecules. 2005;6:818. doi: 10.1021/bm049427e. [DOI] [PubMed] [Google Scholar]
- 13.Sun G, Hagooly A, Xu J, Nystro_m AM, Li Z, Rossin R, Moore DA, Wooley KL, Welch MJ. Biomacromolecules. 2008;9:1997. doi: 10.1021/bm800246x. [DOI] [PubMed] [Google Scholar]
- 14.Choi CHJ, Zuckerman JE, Webster P, Davis ME. Proc. Natl. Acad. Sci. 2011;108:6656. doi: 10.1073/pnas.1103573108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Maccarini M, Briganti G, Rucareanu S, Lui XD, Sinibaldi R, Sztucki M, Lennox RB. J. Phys. Chem. C. 2010;114:6937. [Google Scholar]
- 16.Zhu X, Su N, Li H, Liu X, Li Y. Mater. Lett. 2011;65:2816. [Google Scholar]
- 17.Corbierre MK, Cameron NS, Lennox RB. Langmuir. 2004;20:2867. doi: 10.1021/la0355702. [DOI] [PubMed] [Google Scholar]
- 18.Mansfield E, Kar A, Quinn TP, Hooker SA. Anal. Chem. 2010;82:9977. doi: 10.1021/ac102030z. [DOI] [PubMed] [Google Scholar]
- 19.Sofia SJ, Premnath V, Merrill EW. Macromolecules. 1998;31:5059. doi: 10.1021/ma971016l. [DOI] [PubMed] [Google Scholar]
- 20.Garcia-Fuentes M, Torres D, Martín-Pastor M, Alonso MJ. Langmuir. 2004;20:8839. doi: 10.1021/la049505j. [DOI] [PubMed] [Google Scholar]
- 21.Liu Q, de Wijn JR, de Groot K, van Blitterswijk CA. Biomaterials. 1998;19:1067. doi: 10.1016/s0142-9612(98)00033-7. [DOI] [PubMed] [Google Scholar]
- 22.Castelino K, Kannan B, Majumdar A. Langmuir. 2005;21:1956. doi: 10.1021/la047943k. [DOI] [PubMed] [Google Scholar]
- 23.Demers LM, Mirkin CA, Mucic RC, Reynolds RA, Letsinger RL, Elghanian R, Viswanadham G. Anal. Chem. 2000;72:5535. doi: 10.1021/ac0006627. [DOI] [PubMed] [Google Scholar]
- 24.Jurnak F. J. Cryst. Growth. 1986;76:577. [Google Scholar]
- 25.HamptonResearch. Old PEG & PEG Stability. Hampton Research: Website; 2012. [Google Scholar]
- 26.Ray WJ, Jr, Puvathingal JM. Anal. Biochem. 1985;146:307. doi: 10.1016/0003-2697(85)90544-5. [DOI] [PubMed] [Google Scholar]
- 27.Rundqvist J, Hoh JH, Haviland DB. Langmuir. 2005;21:2981. doi: 10.1021/la0471792. [DOI] [PubMed] [Google Scholar]
- 28.Xia X, Yang M, Wang Y, Zheng Y, Li Q, Chen J, Xia Y. ACS Nano. 2011;6:512. doi: 10.1021/nn2038516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schuck P, Rossmanith P. Biopolymers. 2000;54:328. doi: 10.1002/1097-0282(20001015)54:5<328::AID-BIP40>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- 30.Liu X, Atwater M, Wang J, Huo Q. Colloids Surf. B. Biointerfaces. 2007;58:3. doi: 10.1016/j.colsurfb.2006.08.005. [DOI] [PubMed] [Google Scholar]
- 31.Laue TM, Stafford WF., III Annu. Rev. Biophys. Biomol. Struct. 1999;28:75. doi: 10.1146/annurev.biophys.28.1.75. [DOI] [PubMed] [Google Scholar]
- 32.Lebowitz J, Lewis MS, Schuck P. Protein Sci. 2002;11:2067. doi: 10.1110/ps.0207702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Calabretta MK, Matthews KS, Colvin VL. Bioconjug. Chem. 2006;17:1156. doi: 10.1021/bc0600867. [DOI] [PubMed] [Google Scholar]
- 34.Jamison JA, Krueger KM, Mayo JT, Yavuz CT, Redden JJ, Colvin VL. Nanotechnology. 2009;20:355702. doi: 10.1088/0957-4484/20/35/355702. [DOI] [PubMed] [Google Scholar]
- 35.Jamison JA, Krueger KM, Yavuz CT, Mayo JT, LeCrone D, Redden JJ, Colvin VL. ACS Nano. 2008;2:311. doi: 10.1021/nn700144m. [DOI] [PubMed] [Google Scholar]
- 36.Falabella JB, Cho TJ, Ripple DC, Hackley VA, Tarlov MJ. Langmuir. 2010;26:12740. doi: 10.1021/la100761f. [DOI] [PubMed] [Google Scholar]
- 37.Cölfen H, Tirosh S, Zaban A. Langmuir. 2003;19:10654. [Google Scholar]
- 38.Calabretta M, Jamison JA, Falkner JC, Liu Y, Yuhas BD, Matthews KS, Colvin VL. Nano Lett. 2005;5:963. doi: 10.1021/nl047926f. [DOI] [PubMed] [Google Scholar]
- 39.Arnold MS, Suntivich J, Stupp SI, Hersam MC. ACS Nano. 2008;2:2291. doi: 10.1021/nn800512t. [DOI] [PubMed] [Google Scholar]
- 40.Backes C, Karabudak E, Schmidt CD, Hauke F, Hirsch A, Wohlleben W. Chem. Eur. J. 2010;16:13176. doi: 10.1002/chem.200903461. [DOI] [PubMed] [Google Scholar]
- 41.Leenheer JA. Environ. Sci. Technol. 1981;15:578. doi: 10.1021/es00087a010. [DOI] [PubMed] [Google Scholar]
- 42.Hershkovits E, Tannenbaum A, Tannenbaum R. The Journal of Physical Chemistry B. 2008;112:5317. doi: 10.1021/jp7097894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dukes D, Li Y, Lewis S, Benicewicz B, Schadler L, Kumar SK. Macromolecules. 2010;43:1564. [Google Scholar]
- 44.Aubouy M, Raphaël E. Macromolecules. 1998;31:4357. [Google Scholar]
- 45.Carney RP, Kim JY, Qian H, Jin R, Mehenni H, Stellacci F, Bakr OM. Nature Communication. 2011;2:335. doi: 10.1038/ncomms1338. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.