Cone-Beam CT of Traumatic Brain Injury Using Statistical Reconstruction with a Post-Artifact-Correction Noise Model

Abstract

Traumatic brain injury (TBI) is a major cause of death and disability. The current front-line imaging modality for TBI detection is CT, which reliably detects intracranial hemorrhage (fresh blood contrast 30-50 HU, size down to 1 mm) in non-contrast-enhanced exams. Compared to CT, flat-panel detector (FPD) cone-beam CT (CBCT) systems offer lower cost, greater portability, and smaller footprint suitable for point-of-care deployment. We are developing FPD-CBCT to facilitate TBI detection at the point-of-care such as in emergent, ambulance, sports, and military applications. However, current FPD-CBCT systems generally face challenges in low-contrast, soft-tissue imaging. Model-based reconstruction can improve image quality in soft-tissue imaging compared to conventional filtered backprojection (FBP) by leveraging high-fidelity forward model and sophisticated regularization. In FPD-CBCT TBI imaging, measurement noise characteristics undergo substantial change following artifact correction, resulting in non-negligible noise amplification. In this work, we extend the penalized weighted least-squares (PWLS) image reconstruction to include the two dominant artifact corrections (scatter and beam hardening) in FPD-CBCT TBI imaging by correctly modeling the variance change following each correction. Experiments were performed on a CBCT test-bench using an anthropomorphic phantom emulating intra-parenchymal hemorrhage in acute TBI, and the proposed method demonstrated an improvement in blood-brain contrast-to-noise ratio (CNR = 14.2) compared to FBP (CNR = 9.6) and PWLS using conventional weights (CNR = 11.6) at fixed spatial resolution (1 mm edge-spread width at the target contrast). The results support the hypothesis that FPD-CBCT can fulfill the image quality requirements for reliable TBI detection, using high-fidelity artifact correction and statistical reconstruction with accurate post-artifact-correction noise models.

1. Introduction

Traumatic brain injury (TBI) is a major cause of death and disability, with ∼2.2 million TBI-associated Emergency Department visits reported in the United States in 2010, and increasing by 70% during the period 2001-2010.¹ In the current clinical landscape, multi-detector CT (MDCT) is the front-line modality for diagnosis of fresh bleeds in acute TBI, providing reliable detection of fresh blood (contrast 30-50 HU, size 1-10 mm). While MDCT is well suited to the Emergency Department, a system with reduced cost, greater portability, and small footprint suitable to the point-of-care in sports, military, ambulance, urgent care, and ICU theatres could offer significant benefit to early detection and proper direction of therapy. Flat-panel detector (FPD) cone-beam CT (CBCT) has emerged in the past decade for a variety of specialty diagnostic applications, including imaging of the breast,² musculoskeletal extremities,³ and head and neck.⁴ However, current FPD-CBCT systems face major challenges to low-contrast soft tissue imaging performance, including higher noise, and a higher level of artifacts compared to MDCT.

Advanced model-based reconstruction (MBR) demonstrates major improvement in image quality over conventional 3D filtered backprojection (FBP) in FPD-CBCT imaging of the soft tissue.⁵ First, MBR makes better use of the measurements by incorporating a more sophisticated forward model of factors such as measurement noise, spectral effects, and complex system geometries. Moreover, the regularization terms in MBR allow incorporation of a wide spectrum of additional information to further improve image quality, ranging from general image roughness to incorporation of patient- specific prior images. Specifically in FPD-CBCT imaging of TBI, artifact corrections are essential to the challenging task of TBI detection; however, such corrections impart non-negligible noise amplification (e.g., increasing noise by more than a factor of 2) in FBP as shown in Fig. 1.⁶ Potential solutions include sinogram denoising by adaptive filtering techniques⁷ or by minimization of a cost function for the optimal sinogram.⁸

Figure 1.

Illustration of the artifact correction process for FPD-CBCT imaging of TBI. The colormaps show the difference image before and after correction (units HU). Images on the right show a head phantom with simulated TBI with and without artifact correction, illustrating the benefit to image uniformity but amplifying noise by greater than a factor of 2. (Grayscale window: with correction [0, 150] HU; without correction [-240, -160] HU). The correction process combined with model-based reconstruction (with corrected weights, detailed below) is hypothesized to provide both high-fidelity artifact correction and low noise images (high CNR) suitable to the challenging task of TBI detection.

Alternatively, we approach the problem with a MBR framework. Specifically, we extend a penalized weighted least-squares (PWLS) image reconstruction framework to include the effect of the two dominant artifact corrections (scatter and beam hardening) in FPD-CBCT imaging of TBI. We first model the underlying variations in the measurement noise characteristics through each correction, and then design novel weighting in PWLS to compensate for such variations. Huber regularization was used to maximize TBI detectability. Previous analogous work includes Zhu et al, who studied the change in measurement noise characteristics in scatter correction and built a PWLS image reconstruction objective with quadratic regularization, showing promising improvements in chest CT.⁹ In this work, experiments were performed on a CBCT test-bench using an anthropomorphic head phantom emulating intra-parenchymal hemorrhage in acute TBI. Measurement data with the two dominant corrections and all four corrections in Fig. 1 were used to compare the image quality of the proposed PWLS method, FBP, and PWLS using the traditional weights (i.e., raw measurements).

2. Methods

2.1 PWLS and artifact corrections

In this work, we consider a scenario where raw measurements are corrected for x-ray scatter and beam hardening before entering PWLS reconstruction.

As shown in Fig. 2, y, y^s, l^s, and l^bh denote a vector of the raw measurements, scatter-corrected measurements, scatter-corrected line integrals, and beam-hardening-corrected line integrals, respectively, g is a vector of measurement-dependent gains, and μ̂ is a vector representing the reconstructed image. We formulate the PWLS objective function as

Figure 2.

Workflow of the artifact corrections and PWLS reconstruction method investigated in this work.

$$\widehat{\mu }=\underset{\mu }{arg\; min}\frac{1}{2}{\parallel \mathbf{A}\mu -l\parallel }_{\mathbf{W}}^2+{\beta }_{R}R(\mu )$$ (1)

where the matrix A denotes the linear projection operator, l is a vector of all line integrals, W is the diagonal weighting matrix with the i^th diagonal element W_i the inverse of the variance of l_i, R(μ) is a Huber regularization term that penalizes first-order neighbor spatial differences in the image volume. Assuming Poisson noise in the measurements (i.e., no correction), the PWLS weights are originally chosen simply to be the raw measurements ( ${\mathbf{W}}_i^{\mathrm{O}}=y_i$).¹⁰ This weighting mechanism less heavily weights line integral errors associated with rays that pass through more dense objects and have lower signal-to-noise ratio, thereby reducing noise in the reconstructed image. We refer to the PWLS using these original weights as PWLS-O. However, the Poisson noise assumption no longer holds in the artifact-corrected measurements.

2.2 Modeling variance change in scatter correction

Most scatter correction algorithms essentially subtract an estimate of the scatter fluence from the raw measurements, estimated by either experimental measurements (e.g., beam blockers¹¹ or primary fluence modulators¹²) or simulations (e.g., analytical¹³ or Monte Carlo models¹⁴). We denote S̄, P̄, and n_y as the mean scatter, mean primary, and Poisson noise in the raw measurements y, and we assume y ∼ Poisson (S̄ + P̄) and thereby n_y = y − S̄ − P̄. The scatter-corrected line integrals can be written with a first-order Taylor approximation:

$$l_i^s=log\left(\frac{g_i}{y_i-{\overline{S}}_i}\right)=log\left(\frac{g_i}{{\overline{P}}_i+n_{y_i}}\right)=log(g_i)-log({\overline{P}}_i+n_{y_i})\approx log(g_i)-log({\overline{P}}_i)-\frac{1}{{\overline{P}}_i}{n}_{y_i}$$ (2)

One could also consider two additional sources of noise: 1) error between the true mean scatter S̄ and the scatter estimate S; and 2) variation associated with the gain g. These two noise sources are ignored in the current work, as they tend to be small compared to the measured quantum noise, given accurate scatter correction (e.g., the high-fidelity Monte Carlo correction¹⁴ in Fig. 1) and gain correction. The variance of the scatter-corrected line integrals can then be written as:

$$var(l_i^s)\approx var(-\frac{1}{{\overline{P}}_i}{n}_{y_i})=\frac{1}{{\overline{P}}_i^2}var(n_{y_i})=\frac{1}{{\overline{P}}_i^2}var(y_i)$$ (3)

Given the variance of the uncorrected line integrals, the ratio of the two sources of variance is written as follows:

$$var(l_i)\approx \frac{1}{{\overline{y}}_i^2}var(y_i),\frac{var(l_i^s)}{var(l_i)}\approx \frac{{\overline{y}}_i^2}{{\overline{P}}_i^2}={(1+{\text{SPR}}_i)}^2$$ (4)

This represents a dramatic variance change for measurements with high SPR (with SPR as high as 9 in the skull base, giving a 100-fold change in variance).

2.3 Modeling variance change in beam hardening correction

Beam hardening correction may include correcting water-induced artifacts (“water” correction) and / or bone-induced artifacts (“bone” correction).^15,16 In this preliminary work, the variance change due to water correction is first studied. While water correction alone substantially reduces cupping artifacts in the brain, bone correction could further reduce artifacts such as dark banding between bones, and modeling the variance change in bone correction is the subject of ongoing future work. Water correction can be regarded as a remapping of measured line integrals based on the calibration of the beam hardening response in water from either experimental measurements or an analytical model. The remapping can be modeled as a polynomial function (with coefficients α_m) and the beam-hardening-corrected line integrals could then be written as:

$$l_i^{bh}=\sum _{m=0}^M{\alpha }_m{(l_i)}^m={\alpha }_0+\sum _{m=1}^M{\alpha }_m{log}^m\left(\frac{g_i}{y_i}\right)\approx {\alpha }_0+\sum _{m=1}^M{\alpha }_m\left[{log}^m\right(\frac{g_i}{{\overline{y}}_i})-m{log}^{m-1}(\frac{g_i}{{\overline{y}}_i}\left)\frac{1}{{\overline{y}}_i}{n}_{y_i}\right]$$ (5)

Again, the small noise associated with the calibration estimate and gain correction are ignored. The variance of the beam-hardening-corrected line integrals can then be written as:

$$var(l_i^{bh})\approx var\left(\sum _{m=1}^M{\alpha }_{m}m{log}^{m-1}\right(\frac{g_i}{{\overline{y}}_i}\left)\frac{1}{{\overline{y}}_i}{n}_{y_i}\right)={\left[\sum _{m=1}^M{\alpha }_{m}m{log}^{m-1}\right(\frac{g_i}{{\overline{y}}_i}\left)\right]}^2\frac{1}{{\overline{y}}_i^2}var(y_i)$$ (6)

In our experiments, (6) yields an additional factor of up to 1.2 in variance changes of the line integrals.

2.4 Proposed PWLS method using corrected weights: PWLS-C

Considering the analysis above for scatter and beam hardening corrections to the raw measurements as in Fig. 2, the variance after both corrections is:

$$var(l_i^{s+bh})\approx {\left[\sum _{m=1}^M{\alpha }_{m}m{log}^{m-1}\right(\frac{g_i}{{\overline{y}}_i-{\overline{S}}_i}\left)\right]}^2\frac{1}{{({\overline{y}}_i-{\overline{S}}_i)}^2}var(y_i)$$ (7)

Using the relationship between the PWLS weights and the variance, the corrected PWLS weights can be derived as:

$${\mathbf{W}}_i^C=\frac{1}{var(l_i^{s+bh})}\approx \frac{{(y_i-{\overline{S}}_i)}^2}{{\left[\sum _{m=1}^M{\alpha }_{m}m{log}^{m-1}\right(\frac{g_i}{y_i-{\overline{S}}_i}\left)\right]}^2{y}_i}$$ (8)

by first replacing var(y) with ȳ (assuming Poisson noise in the raw measurements) and then approximating ȳ by y. Essentially, PWLS with corrected weights (denoted PWLS-C) adjusts the weights according to the variance changes imparted by artifact corrections, while PWLS-O weights the corrected-measurements according to the variance before corrections. One could perform the same analysis for scenarios other than in Fig. 2 (e.g., beam hardening then scatter correction, iterations of two corrections, etc.). Since the proposed objective function is convex and differentiable, it is solved via the ordered-subsets separable quadratic surrogates algorithm,¹⁷ which permits highly parallelizable image updates.

3. Results and Breakthrough Work

Imaging studies emulating intra-parenchymal hemorrhages were performed on a CBCT test-bench with a FPD (PaxScan 4343R, Varian, Palo Alto, CA) as shown in Fig. 3(a). A 580 mm source-to-axis distance (SAD) and an 800 mm source-to-detector distance (SDD) were used to resemble a typical configuration for compact head CBCT system¹⁸. A custom anthropomorphic head phantom was carefully prepared. The phantom was first filled with a gelatin mixture to provide contrast equivalent to brain. Ventricle models were then prepared from wax with contrast equivalent to cerebrospinal fluid and placed in the gelatin mixture within the central cranial vault. Finally, rows of plastic spheres were placed in the gelatin mixture with diameters ranging from 1.5 mm to 12 mm encompassing a pertinent range of imaging tasks for detection of intra-parenchymal hemorrhages in acute TBI. The preparation resulted in a gelatin-plastic contrast closely simulating that of brain to fresh blood (∼50 HU). The head phantom was scanned at 100 kVp, 0.4 mAs per projection with 720 projections (0.5° angular step), and 0.556 × 0.556 mm² pixel size. The raw projections were first corrected for scatter using a high-fidelity Monte Carlo correction,¹⁴ corrected for beam hardening using standard water correction,¹⁵ and then reconstructed using three methods: FBP, PWLS-O, and PWLS-C with 0.5 × 0.5 × 0.5 mm³ voxel size. Both PWLS methods used matched separable footprint projectors and backprojectors, and FBP used voxel-driven interpolating backprojector. To illustrate the different weighting mechanism in PWLS-O and PWLS-C, the ratio of the original weights to the corrected weights for an example projection (lateral) is shown in Fig. 3(b). Substantial variation in the weights can be seen throughout the head, with particularly large changes in the skull base (maximum ratio ∼400) where scatter and beam-hardening effects are most pronounced. Note that this image also shows the approximate variance changes through artifact corrections.

Figure 3.

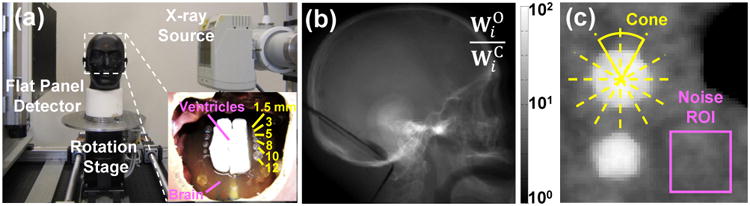
(a) Experimental setup on a FPD-CBCT test-bench and an anthropomorphic head phantom. (b) Ratio of the original weights to the corrected weights for a lateral projection. Note the logarithmic grayscale. (c) ROI for measuring image noise and the sphere (12 mm diameter simulated bleed) for edge-spread function analysis on an axial slice in the center of the head.

Both FBP and PWLS methods carry a tradeoff between spatial resolution and noise via a given parameterization-namely, the cutoff frequency of the smoothing kernel for FBP and the regularization control parameter β_R for PWLS. Therefore, images reconstructed by different methods were compared by first matching either spatial resolution or noise for fair comparison. Specifically, image noise was calculated as the standard deviation of the voxel values in a ROI (19 × 19 voxels) in a flat region of the brain (Fig. 3(c)) adjacent to a simulated structure of interest (simulated bleed; see Fig. 3). The axial spatial resolution and contrast were measured using a sphere (close to the noise ROI) using the method detailed in [5], involving a fit to the 3D edge spread function (ESF) averaged over a local cone and parameterized by the fit parameter σ (units mm, corresponding to the ESF “width”). Note that spatial resolution in the longitudinal (z) direction in FBP was also matched to PWLS methods by applying additional apodization in the z direction in FBP as in [5]. Figure 4(a) shows a clear reduction in noise with PWLS at matched spatial resolution; moreover, a further reduction of noise can be seen at all the spatial resolutions of interest after using the corrected weights. Similar results are found in the CNR-resolution tradeoff in Fig. 4(b), in which PWLS-C exhibited the best tradeoff among the three methods. Quantitative results are shown in Fig. 4(c), where PWLS-C exhibits the highest spatial resolution (e.g., at the edges of the spheres and ventricles) at matched CNR (∼12), and conversely, the lowest noise level at matched resolution (∼1 mm). The CNR was 9.6 (FBP), 11.6 (PWLS-O), and 14.2 (PWLS-C) for this matched resolution (∼1 mm).

Figure 4.

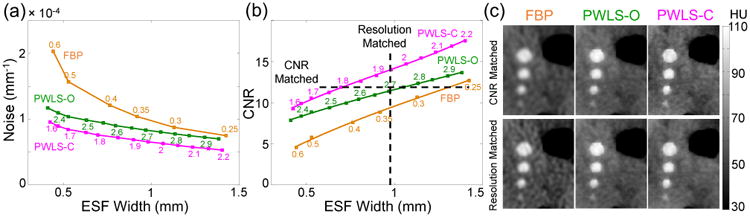
(a) Noise vs. spatial resolution for different reconstruction methods. Numbers on FBP curve and PWLS curves correspond to cutoff frequency and the exponents in β_R (base 10), respectively. (b) CNR vs. spatial resolution; (c) ROI of images reconstructed by different methods at matched CNR (∼12) or at matched spatial resolution (∼1 mm). Parameters in PWLS methods: 100 iterations, 20 subsets per iteration, ± 10^-4 mm^-1 quadratic neighborhood in Huber loss function.

The noise-resolution performance of the different methods was also examined for the full artifact correction process in Fig. 1 using the fully corrected projections (“bone correction” in beam hardening correction not considered in this preliminary work). This reduced the remaining artifacts from lag and veiling glare (e.g., “comet” artifacts). Figure 5 shows FBP and PWLS-C images with spatial resolution (∼0.5 mm) matched for the largest sphere (in the axial slice in Fig. 4). PWLS-C images exhibited lower noise overall, increased CNR across all spheres (3.0-12 mm diameter), as well as reduced cone-beam artifacts. The CNR was 5.1 (FBP), 8.7 (PWLS-O), and 10.4 (PWLS-C) for this matched resolution (∼0.5 mm). For resolution matched at ∼1 mm, the CNR was 9.7 (FBP), 11.7 (PWLS-O), and 14.8 (PWLS-C). Since lag and glare corrections also introduce some level of variance changes (small compared to scatter and beam hardening corrections), modeling the variance change in lag and glare corrections is expected to further improve image quality and is the subject of future work.

Figure 5.

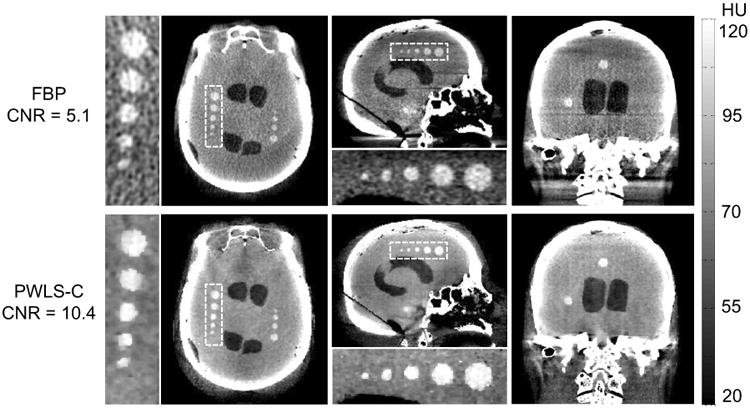
FBP images (top row) and PWLS-C images (bottom row) using projections with a full set of four corrections (spatial resolution matched at ∼0.5 mm). Each row from left to right shows the axial, sagittal, and coronal slice, respectively.

4. Conclusion

We have proposed a novel PWLS image reconstruction approach that: (1) provides accurate modeling of the underlying variations in measurement noise properties through the two dominant artifact corrections (scatter, beam hardening); and (2) utilizes a new weighting mechanism to compensate for correction-induced variations in the fidelity of the measurements. In test-bench experiments emulating intra-parenchymal hemorrhage in acute TBI, the proposed method demonstrated superior CNR-resolution tradeoffs in comparison to traditional methods including FBP and PWLS with traditional weights (raw measurements). Image quality obtained using the proposed method supports the hypothesis that FPD-CBCT can provide soft-tissue image quality suitable to TBI detection and motivates further investigation in development of a dedicated point-of-care system for diagnosis of acute TBI.