Abstract
This work introduces a task-driven imaging framework that incorporates a mathematical definition of the imaging task, a model of the imaging system, and a patient-specific anatomical model to prospectively design image acquisition and reconstruction techniques to optimize task performance. The framework is applied to joint optimization of tube current modulation, view-dependent reconstruction kernel, and orbital tilt in cone-beam CT. The system model considers a cone-beam CT system incorporating a flat-panel detector and 3D filtered backprojection and accurately describes the spatially varying noise and resolution over a wide range of imaging parameters and in the presence of a realistic anatomical model. Task-based detectability index (d') is incorporated as the objective function in a task-driven optimization of image acquisition and reconstruction techniques. The orbital tilt was optimized through an exhaustive search across tilt angles ranging ±30°. For each tilt angle, the view-dependent tube current and reconstruction kernel (i.e., the modulation profiles) that maximized detectability were identified via an alternating optimization. The task-driven approach was compared with conventional unmodulated and automatic exposure control (AEC) strategies for a variety of imaging tasks and anthropomorphic phantoms. The task-driven strategy outperformed the unmodulated and AEC cases for all tasks. For example, d' for a sphere detection task in a head phantom was improved by 30% compared to the unmodulated case by using smoother kernels for noisy views and distributing mAs across less noisy views (at fixed total mAs) in a manner that was beneficial to task performance. Similarly for detection of a line-pair pattern, the task-driven approach increased d' by 80% compared to no modulation by means of view-dependent mA and kernel selection that yields modulation transfer function and noise-power spectrum optimal to the task. Optimization of orbital tilt identified the tilt angle that reduced quantum noise in the region of the stimulus by avoiding highly attenuating anatomical structures. The task-driven imaging framework offers a potentially valuable paradigm for prospective definition of acquisition and reconstruction protocols that improve task performance without increase in dose.
Keywords: task-driven imaging, imaging task, detectability index, cone-beam CT, optimization, tube current modulation, automatic exposure control, reconstruction kernel, orbital tilt, image quality, noise-power spectrum, cascaded systems analysis
A Introduction
Cone-beam CT (CBCT) is an increasingly prevalent modality for image-guided procedures, including surgery, interventional radiology, and radiotherapy (Jaffray et al 2002, Siewerdsen et al 2005, Chen et al 2006, Fahrig et al 2006). In such procedures, images from pre-operative planning CT and/or previous intraoperative CBCT scans are often available and provide valuable information on patient-specific anatomy that can be used to specify locations of interest and the nature of the imaging task. Conventional imaging paradigms use such information indirectly or in a qualitative sense – e.g., specification of a “large” body habitus and “bone” or “soft tissue” reconstruction protocols. In this work, we introduce a framework for task-driven imaging that incorporates patient-specific prior images and a mathematical description of the imaging task to prospectively design task-specific and patient-specific acquisition and reconstruction techniques that maximize task performance.
Detectability index (d’) is a prevalent metric for task-based imaging performance that combines spatial resolution and noise characteristics of the imaging system, an observer model, and the imaging task. With roots in statistical decision theory, d’ (Green and Swets 1966) is commonly used as a metric for image quality assessment (Sharp et al 1996) and can be related to human observer performance in terms of the area under the curve (AUC) of the receiver operator characteristic (ROC) curve, as well as the proportion correct in alternative forced-choice (AFC) tests. Theoretical calculation of d’ has demonstrated good correspondence with observer performance in a number studies and provides a useful foundation for image quality assessment (Fiete et al 1987, Yao and Barrett 1992, Gang et al 2011, Richard et al 2011, Li et al 2012, Leng et al 2013, Yu et al 2013). In addition, d’ provides a basis for system design and optimization as an objective function that includes physical metrics of spatial resolution and noise in relation to the imaging task. Examples of such analysis can be found in application to tomosynthesis and CBCT in breast, chest, and musculoskeletal imaging as well as image-guided surgery, cardiovascular procedures, and radiotherapy (Frey et al 2002, Prakash et al 2011, Siewerdsen 2011, Gang et al 2012, Samei et al 2014, Sanchez et al 2014, Zhao et al 2014).
The task-driven framework presented below uses d’ to prospectively optimize the acquisition and reconstruction process – i.e., not as a metric of image quality assessment as in previous work, but as the objective function that drives specification of the acquisition and reconstruction process in a manner optimal to the task. An analytical relationship between d’ and CBCT imaging parameters (including gantry tilt, tube current modulation, and view-dependent reconstruction kernel) is derived from 3D cascaded systems analysis and used as the objective function to identify protocols that maximize task-performance. The current work involves reconstruction by 3D filtered backprojection (FBP), a method for which cascaded systems analysis has been shown to provide accurate predictions of local, nonuniform spatial resolution, noise, and task-based imaging performance (Tward and Siewerdsen 2008, Gang et al 2014). The method is applied in experiments involving anthropomorphic pelvis and head phantoms incorporating a variety of detection tasks to evaluate the performance of the task-driven approach in comparison to conventional unmodulated (i.e., fixed mA and kernel) and automatic exposure control (AEC) image acquisition methods.
B Methods
B.1 Framework for Task-Driven Imaging
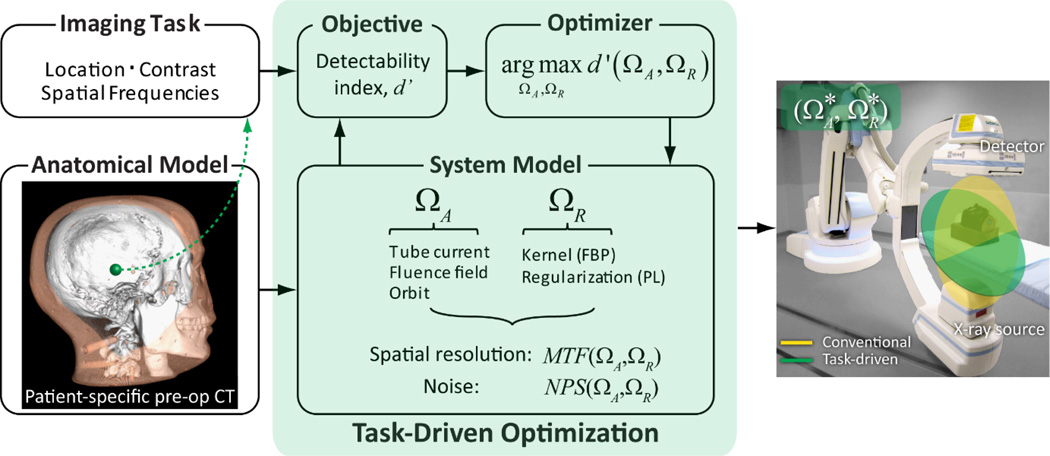
The task-driven imaging framework is illustrated in Fig.1. In this work, we obtain the patient-specific anatomical model from a preoperative CT within which we define the location, contrast, and spatial frequencies associated with the imaging task. The task-driven optimization can consider a broad range of imaging parameters, including those related to image acquisition (denoted ΩA) and reconstruction (denoted ΩR). In the work reported below, the latter is specifically the reconstruction kernel for FBP and could be extended to include (asymmetric) voxel size; furthermore, recent work supports extension of the framework to model-based reconstruction by penalized likelihood (PL) estimation.(Gang et al 2014) A system model based on 3D cascaded systems analysis establishes the functional relationship between (ΩA, ΩR) and the spatial resolution and noise characteristics in terms of the modulation transfer function (MTF) and noise-power spectrum (NPS) (Siewerdsen et al 1998, Tward and Siewerdsen 2008, Gang et al 2014). Combining the MTF, NPS, and imaging task within a given observer model, the detectability index (d’) is prospectively computed as a function of (ΩA, ΩR), providing the objective function in a multivariate optimizer for identifying the optimal acquisition and reconstruction parameters, .
Figure 1.
Task-driven imaging framework. Specification of imaging task includes the location, contrast, and spatial frequencies of interest. In this work, a patient-specific model is given by a previous CT scan. Imaging parameters ΩA and ΩR define the acquisition and reconstruction technique, respectively. Theoretical predictors of spatial resolution and noise are derived from cascaded systems analysis of the imaging chain. The parameters that maximize d’ are identified prospectively (i.e., before image acquisition) via multivariate optimization.
The objective function is given by the detectability index expressed as a function of optimization parameters ΩA and ΩR:
| (1) |
corresponding to a 3D non-prewhitening observer model, chosen to maximize the 3D signal to noise characteristics of the image without "prewhitening" of correlated noise (Wagner 1978). The terms T(ΩA,ΩR) and S(ΩA,ΩR) are the MTF and NPS, respectively, and (fx,fy,fz) denotes the 3D Fourier domain. As detailed below, characterization of the resulting image as assessed visually (but not within the optimization itself) considers d’ pertaining to a slice through the reconstruction and computed with the addition of an eye filter and internal noise (NPWEI), which has demonstrated reasonable agreement with human observer performance for simple imaging tasks (Gang et al 2011, Richard et al 2011). This distinguishes the forms for d’ associated with optimization of the intrinsic signal-to-noise characteristics of the image data (d’NPW) from that associated with retrospective image quality assessment (d’NPWEI).
The task function, denoted WTask, describes the contrast and spatial frequency characteristics associated with the imaging task. In a binary decision task such as detection, WTask is given by the Fourier transform of the difference between the “stimulus present” and “stimulus absent” hypotheses.(Sharp et al 1996) For example, for detection of a spherical stimulus on a uniform background, the task function is the Fourier transform of the sphere itself. Such calculation assumes the mean value (HU) of the stimulus (and background) to be known, and the imaging task is computed based on structures of interest in general (e.g., the contrast of blood and brain) or in a patient-specific sense (diagnostic reading of the preoperative image). The task function can either be constructed mathematically in the spatial domain then Fourier transformed, or be implemented in the Fourier domain directly. In addition to the task function, specification of the imaging task in this work includes its location, which affects performance because the spatial resolution and noise characteristics are considered to vary within the image.
Spatial resolution and noise are quantified in the spatial-frequency domain as the local MTF and NPS calculated from a 3D cascaded systems model established in previous work (Siewerdsen et al 1998, Tward and Siewerdsen 2008). The model yields accurate predictions of MTF and NPS for a broad range of acquisition techniques, detector configurations, system geometry, and reconstruction parameters. The model also accurately describes the spatially varying resolution and noise characteristics in terms of the “local” MTF and “local” NPS (Gang et al 2014) in a manner that includes view-dependent attenuation through the object. Such calculations require only the line integrals through the location of interest. The cascaded systems analysis model thus establishes the relationship between d’ and the imaging parameters (ΩA, ΩR) in a manner that is both task-specific and patient-specific. The relationship of Eq. (1) serves as the objective function in the optimization algorithm illustrated in Fig.1.
The framework is sufficiently general to optimize a wide range of imaging parameters. The work below focuses on a joint optimization of the orbit (viz., orbital tilt), tube current modulation, and view-dependent reconstruction kernel in FBP under a dose constraint specified by the total mAs. Parameterization of each within the optimization algorithm is detailed in Sec.B.2. Future work could expand the optimization to include fluence field modulation (Galvin et al 1993, Bartolac et al 2011, Szczykutowicz and Mistretta 2013), noncircular orbits, and regularization design in model-based iterative reconstruction (Gang et al 2013, 2014). We assume the patient anatomy to be known from a previous CT scan, requiring only a rigid registration of the prior image to the coordinates of the imaging system. Deformable registration and mismatch in image content are also subjects of future work. Uncertainties in the imaging task (e.g., location or orientation of the stimulus) could be incorporated into the d’ objective function under the signal-known statistically (SKS) or signal-known exactly but variable (SKEV) paradigms in statistical decision theory (Eckstein and Abbey 2001, Eckstein et al 2003).
B.2 Theoretical Methods
B.2.1 Tube Current Modulation
Conventional current modulation employs some form of automatic exposure control (AEC) to provide a constant signal level in a given region(s) of the detector (e.g., the center) or a heuristic sinusoidal modulation pattern associated with an oblate patient cross-section. Gies et al. (Gies et al 1999) introduced a scalar parameterization of the current modulation profile, α, which scales the mean fluence according to attenuation:
| (2a) |
where i and j denote arbitrary projection indices, denotes the mean bare beam fluence of the ith projection, and li is the line integral through the location of interest for the ith projection. Such parameterization yields a view-dependent fluence according to:
| (2b) |
and can be related to the following current modulation strategies:
Strategy 1: Unmodulated Tube Current
An unmodulated beam for which the tube current is constant in all projections corresponds to α = 0.
Strategy 2: Conventional AEC
This strategy enforces a mA modulation profile that yields constant fluence at the center of the detector and is denoted below as AEC. For simplicity, we assume the central ray (i.e., the ray orthogonal to the detector) to coincide with the center of the detector, corresponding to α = 1 and l computed for the isocenter.
Gies et al. also proved that the variance at the location of interest is minimized when α = 0.5. In general, while strategies based on Eq.(2) consider patient attenuation, they do not account for the effect of spatial resolution or noise correlation on task performance. For example, consider an imaging task for which the spatial frequencies of interest are asymmetric (e.g., striated or ductal stimuli with a certain directionality): intuitively, views with greater contribution to those spatial frequencies should be assigned greater fluence; conversely, views that do not contribute to the task power could be smoothed to reduce image noise. Such a modulation pattern would depend not only on patient attenuation and the location of the stimulus but also the imaging task and the local noise and resolution characteristics of the imaging system. Such consideration leads to the following case.
Strategy 3: Task-Driven Current Modulation
As derived in Appendix A, the tube current modulation that maximizes d' for a NPW observer model [Eq.(1)] is given by:
| (3a) |
where KQ and KE, defined in Eq. 8 of Appendix A, are view-dependent (but tube-current-independent) constants that include the imaging task and factors of system gain and blur associated with quantum and electronic noise, respectively. The view-dependent fluence, , was obtained by solving the following cubic equation from (3a) using a one-dimensional simplex search (Matlab R2014a, Natick, MA) for all projections relative to a fixed projection and fluence. For example, can be solved by setting j to 1 and to the fluence corresponding to a nominal mAs:
| (3b) |
This step is highly parallelizable and does not pose a computational burden. Since is directly proportional to mAs, the ratios obtained from Eq. 3(a) and (b) can be applied to mAs as well. The tube current modulation profile is thus obtained by normalizing the total mAs to the value specified in the dose constraint. The description above pertains to a fixed reconstruction kernel and orbital tilt, which are treated below.
B.2.2 View-Dependent Reconstruction Kernel
The FBP algorithm commonly uses a reconstruction kernel that is constant for each view, typically an apodization filter applied following the ramp filter to reduce high-frequency noise. Due to view-dependent attenuation and tube current modulation, each projection presents a varying level of quantum noise. For noisier views and/or views that do not contribute to the imaging task, application of a smoother reconstruction kernel could benefit detectability by reducing noise. Although increasing tube current could achieve the same effect, the range of mAs can be a strong constraint (especially for low-power CBCT systems) due to x-ray generator limits and detector saturation. Allowing the kernel to modulate along with mAs combines the noise reduction effects and could result in further improvement in imaging performance. The framework in Fig. 1 therefore allows the reconstruction kernel to vary view-to-view, permitting images with anisotropic spatial resolution. An interesting analogy can be made to model-based iterative reconstruction algorithms which tend to yield intrinsically anisotropic spatial resolution with increased blur along directions with decreased certainty (i.e., increased noise in the data) (Fessler 1996).
The reconstruction kernel is parameterized by the ratio of the cutoff frequency to the Nyquist frequency, denoted as c0, in the apodization filter, Twin:
| (4) |
where Δu is the pixel spacing along the u-direction in the projection domain and fu is the corresponding frequency axis. The apodization width, hwin, also affects the smoothness of the filter but was set to a fixed value of 0.5 (Hann filter) in this work.
Reconstruction kernel affects both the MTF and NPS - i.e., both the numerator and denominator of Eq. (1). An analytical derivation like Eq. (3) is therefore challenging, and an iterative optimization (interior point algorithm, Matlab 2014a) with a custom gradient vector, , was used to identify the task-driven kernel modulation profile that maximizes d’. Derivation of the gradient vector is given in Appendix B.
B.2.3 Orbital tilt
Many diagnostic CT scanners and interventional C-arms are capable of scanning with a source-detector trajectory in a plane that is tilted (by orbital tilt angle, ϕ) with respect to the axial plane defined by the anatomy. In head CT, for example, an orbital tilt of approximately 10–15° along the canthomeatal line is a common means of improving image quality by reducing noise and beam hardening associated with thick, dense areas of the temporal / petrous bones while reducing dose to the eyes. C-arm orbital tilt is common in obtaining optimal fluoroscopic view angles, and C-arms capable of 3D imaging can acquire data on such an inclined plane provided geometric calibration. In this work, optimization of orbital tilt along the cranio-caudal direction was investigated. A circular trajectory was adopted appropriate for FBP reconstruction. Extension to non-circular source-detector orbits and model-based reconstruction methods is in progress (Stayman and Siewerdsen 2013). Following the convention from Sec.B.2.1, Strategies 1 and 2 correspond to a conventional orbit with ϕ = 0°, while Strategy 3 adopts an orbital tilt from a task-driven optimization.
B.2.4 Joint Optimization of Current Modulation, View-Dependent Kernel, and Orbital Tilt
The joint optimization algorithm for tube current modulation, view-dependent reconstruction kernel, and orbital tilt is illustrated in Fig. 2. Tube current modulation and view-dependent kernel profiles are denoted as mAs(θ) and c0(θ), respectively, where θ indicates the view projection angle. The total number of elements in both equals the number of projections (set to 360 for all experiments below). Orbital tilt was optimized at discrete levels from −30° to +30° in 10° increments. Reconstruction kernel parameter, c0, ranged from 0.01 to 1.0. Tube current was calculated from Eq. 3(b) and discretized to the nearest mAs levels available on the x-ray tube control console (Sec. B.3.3).
Figure 2.

Flowchart for the joint optimization. Since only the line integrals are required to compute MTF and NPS from the cascaded systems analysis, one forward projection is required for each tilt angle.
A simple dose constraint was imposed such that the total mAs over all projections was equal to that of an unmodulated scan at a nominal mAs (e.g., 72 total mAs corresponding to 0.2 mAs per projection in a 360 projection scan). Other forms of dose constraint will be considered in future work – e.g., the total energy imparted or regional constraints upon radiosensitive organs.
As shown in Fig. 2, an exhaustive search of orbital tilt forms the outer loop of the algorithm. For each tilt angle, ϕ, the optimal combination of mAs(θ) and c0(θ) were identified through an alternating optimization. First, based on the current c0(θ), mAs(θ) was updated according to Eq. 3. Using the updated mAs(θ), c0(θ) was then identified through a gradient-based optimization. Detectability index (Eq. 1) was then calculated using the updated mAs(θ) and c0(θ) for the current iteration. The algorithm iterates until the improvement in d’NPW is less than 2% from the previous iteration. Finally, the optimal combination of [ϕ, c0(θ), mAs(θ)] was identified from the outer loop.
Since line integrals through the location of interest form the only input to the cascaded systems model, a single forward projection is required for each orbital tilt. To further improve computation speed, the MTF and NPS at different mAs and c0 were obtained from normalizing nominal values using the following relationships:
| (5a) |
where Tnom and Twin−nom were calculated for the maximum c0 of 1;
| (5b) |
where Twin−nom were calculated for c0 = 1; and
| (5c) |
where q̄ denotes the fluence at the detector (not to be confused with the bare-beam fluence q̄0). The MTF and NPS are denoted T and S, respectively, as in Eq. (1), and superscripts Q and E denote quantum and electronic components of the NPS, respectively.
B.3 Experimental Methods
B.3.1 Imaging Tasks and Phantoms
Investigation of task-driven tube current and kernel modulation was performed using the phantoms and imaging tasks illustrated in Fig. 3(a–b). As shown in Fig. 3(a), a spherical lesion detection task was investigated in a simulation study based on a pelvis phantom acquired at 120 kV, 362 mAs and reconstructed at a voxel size of 0.73×0.73×0.50 mm3 with a smooth B30f kernel (Siemens Healthcare, Forcheim Germany). The imaging task was formulated as the detection of a sphere against a uniform background. The task function is therefore the Fourier transform of the sphere itself, the central axial slice of which is illustrated in Fig. 3(a). The sphere was 4 mm in diameter with a contrast of ~550 HU to the soft tissue background. For this phantom, the CT scan provided the anatomical model input to the optimization (Fig. 1).
Figure 2.
Imaging tasks and phantoms for investigation of task-driven imaging performance. (a) Sphere detection task in a pelvis phantom. (b) Directional line pair detection task in a head phantom. Phantoms (a) and (b) were used to investigate the joint optimization of tube current and reconstruction kernel. (c) The spherical stimulus from (a) inserted posterior to a simulated embolization coil in a head phantom for investigation of optimal orbital tilt.
Figure 3(b) illustrates a line pair detection task within an anthropomorphic head phantom (ATOM, CIRS, Norfolk, VA). This task is an idealized representation of a directional, mid-high frequency task which can be generalized to the visualization of surgical devices, fractures, etc. The line pair pattern (CT Imaging QA kit for Atom, Model 700-QA, CIRS, Norfolk, VA) is 5×12.5×12 mm3, 6 line pairs/cm (line width ~0.83 mm), with ~350 HU contrast to the soft tissue-equivalent background. The imaging task was modeled as the discrimination of the line-pair pattern from a uniform block with attenuation equal to the average of the two materials. For this phantom, a high dose CBCT scan (acquired at 100 kV, 0.8 mAs per projection) provided the anatomical model input to the optimization process.
Investigation of orbital tilt was performed in a simulation study based on a CT scan of a head phantom as illustrated in Fig. 3(c) acquired at 120 kV, 350 mAs and reconstructed at a voxel size of 0.47×0.47×0.40 mm3 with a medium smooth U30u kernel (Siemens Healthcare, Forcheim Germany). A 9.2 mm diameter metal sphere (~15000 HU) was digitally inserted posterior to the skull base to simulate an embolization coil, and a range of stimuli were simulated at various locations. Results presented below pertain to a 4 mm diameter sphere of ~330 HU contrast located posterior to the embolization coil.
B.3.2 Image Simulation
From the two digital phantoms in Figs. 3(a) and (c), projections were simulated for a monoenergetic beam at 60 keV with a bare-beam fluence of 4.0×105 photons/mm2 at 1 mAs at the detector (approximating a 120 kV beam with 5 mm Al added filtration). Beam hardening effects associated with a polyenergetic beam were ignored in the current work. For the pelvis phantom, system geometry was set to a source-to-detector distance (SDD) ~150 cm and source-to-axis distance (SAD) ~120 cm to avoid truncation artifacts. For the head phantom in Fig. 3(c), system geometry was set to SDD ~120 cm and SAD ~80 cm, approximating the geometry of a Zeego interventional C-arm (Siemens Healthcare, Forcheim Germany). Forward projections were computed using a linear forward projectors implemented on GPU with independent Poisson noise added. Tube current modulation was achieved by scaling the bare beam fluence of each projection according to its mAs. Simulations involving a tilted orbit were achieved by an image transform specified with respect to the imaging system reference frame.
B.3.3 Physical Experiments
Experiments involving the head phantom in Fig. 3(b) were performed on an experimental CBCT imaging bench with components detailed in Zhao et el.(Zhao et al 2014) The bench included a PaxScan 4030CB flat-panel detector (FPD) with 2048×1536 pixels at 0.194 mm pixel pitch (Varian Medical Systems, Palo Alto CA). The FPD incorporated a 250 mg/cm2 CsI:Tl scintillator and was operated in 2×2 binning mode. System geometry was set to SDD ~120 cm and SAD ~80 cm. Each scan consisted of 360 projections acquired over a 360° rotation, with kV and mAs detailed below. To reduce x-ray scatter effects, the x-ray beam was collimated to a longitudinal extent of ~16 cm at isocenter. Neither a bowtie filter nor antiscatter grid was used.
Scans were performed at 100 kV with 4 mm Al and 0.2 mm Cu added filtration, giving a bare-beam exposure of 0.40 mR at the detector at the nominal 0.2 mAs per projection (72 mAs total for each scan). Ten scans were performed at different levels of constant mAs per projection (0.1, 0.13, 0.16, 0.2, 0.25, 0.32, 0.4, 0.5, 0.63, 0.80 mAs) without perturbing the phantom. The highest mAs level corresponded to ~80% of detector saturation. A given tube current modulation profile as described in Sec. B.2.1 was achieved by selecting projections from the closest available mAs level.
B.3.4 Image Reconstruction with View-Dependent Kernel
Filtered-backprojection reconstruction was performed using a GPU implementation of the FDK algorithm (Feldkamp et al 1984) modified to allow the reconstruction kernel to vary in each view. All reconstructions were performed at an isotropic voxel size of 0.73 mm for the pelvis phantom, 0.254 mm for the head phantom physical experiments, and 0.465 mm for the head phantom used in the simulations of orbital tilt. A linear backprojector was used to match the forward projector.
B.4 Image Quality and Dose
In addition to qualitative visual inspection of ROIs containing the stimuli associated with various imaging tasks, theoretically calculated MTF and NPS from were computed for each strategy to illustrate the spatial frequency characteristics of noise and resolution in relation to the task function. In addition, the detectability index for the NPWEI anthropomorphic observer model is presented as an assessment metric for image quality. Dose maps were also generated to examine the effect of current modulation on regional dose.
B.4.1 Detectability Index with an Anthropomorphic Observer Model
The 3D NPW observer model in Eq. (1) reflects the 3D signal and noise characteristics intrinsic to the reconstructed image and is therefore appropriate as the objective function for system optimization. As a measure of image quality as visualized in a single slice through the reconstruction, a 2D slice-based model incorporating anthropomorphic aspects of the eye filter and internal noise was used - specifically the 2D NPWEI model, which has demonstrated reasonable agreement with human observers for simple imaging tasks (Gang et al 2011, Richard et al 2011). Slice scrolling was not investigated in this work (Diaz et al 2013). Detectability index according to the 2D anthropomorphic observer model (denoted d’NPWEI) was calculated with the imaging task and NPS terms integrated along the direction orthogonal to the slice (fz for the extraction of a single axial slices):
| (6a) |
The eye filter, E, and internal noise, Ni, were based on previous work (Burgess 1994):
| (6b) |
| (6c) |
where c was 2.2 mm−1, giving peak response at 4 cycles/deg at a viewing distance, D, of 50 cm. The internal noise was modeled as a fraction of Seq, a white noise NPS equivalent in total power to the NPS of the ROI in the reconstruction. The scaling factor, ξ, was a free parameter selected to a value of 40 to roughly match the level of the observed conspicuity of the imaging task. The d’NPWEI analysis was not intended as a validation of the model compared to human observer performance but provided a metric complementary to the visual assessment of the resulting images.
B.4.2 Dose Maps
Dose maps for images resulting from each imaging strategy were computed by a GPU-accelerated Monte Carlo simulation detailed in previous work (Badal and Badano 2009, Sisniega et al 2013). Photon interaction models were adapted from PENELOPE 2006 (Salvat et al 2006), and trajectories of individual photons were computed by Woodcock tracking (Woodcock et al 1965). The energy for each interaction was assumed to be deposited locally, ignoring range effects associated with the photoelectron and Compton scatter. The calculations used the same polyenergetic beam model as that in the cascaded systems model (viz., the Spektr toolkit (Siewerdsen et al 2004)). Each phantom was represented as a simple voxelized model consisting of segmented materials: air, ICRP soft tissue, red marrow, and cortical bone. The energy imparted was calculated according to the tube current modulation profiles and converted to mGy by dividing the energy deposited in each voxel by the mass of material within the voxel. The total energy (in J) deposited in the central slice was also calculated as an analogue of integral dose.
C Results
C.1 Tube Current and Kernel Modulation
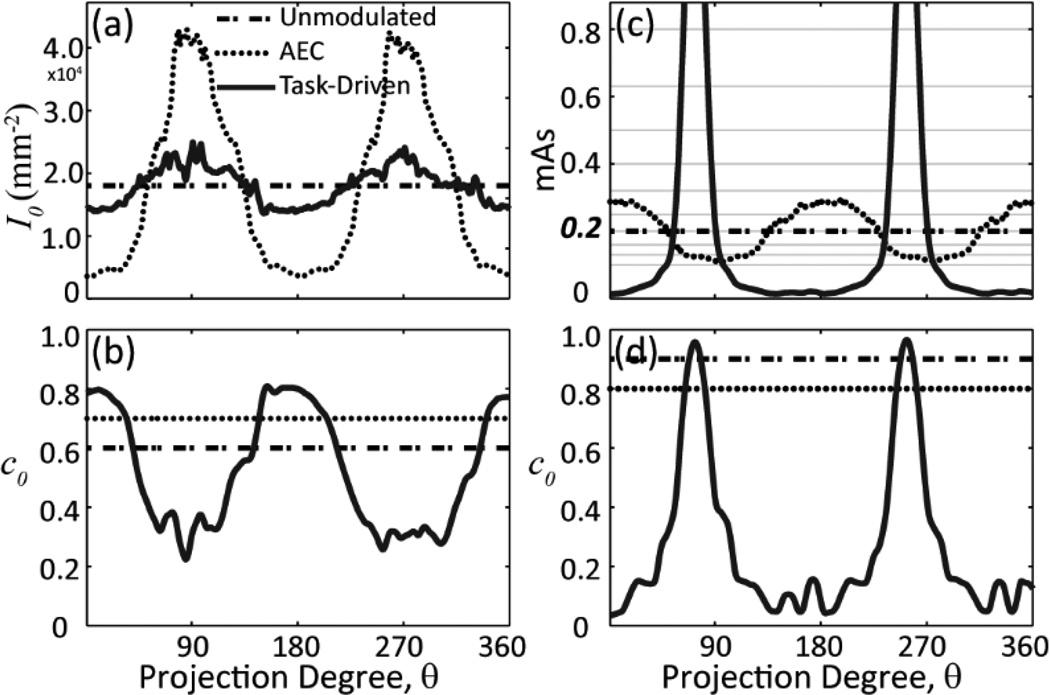
Figure 4 shows tube current [Fig. 4(a),(c)] and kernel [Fig. 4(b),(d)] modulation profiles for the sphere detection task [Fig. 4(a)–(b)] and the directional line pair detection task [Fig. 4(c)–(d)] illustrated in Fig. 3. Each plot includes the three imaging strategies introduced in Sec. B.2. The bare beam fluence values were presented for the simulation study in Fig. 4(a). For the unmodulated and AEC strategies, the kernel plots show the optimal constant c0 level that maximizes d’NPW.
Figure 4.
Tube current and kernel modulation for the (a–b) pelvis phantom + sphere detection task and (c–d) head phantom + line-pair detection task. Curves in each plot correspond to modulation profiles for the unmodulated, AEC, and task-driven imaging strategies. Bare beam fluence is shown in (a) for the simulation study. Gray lines in (c) correspond to the discrete mAs levels available on the x-ray control system.
For the sphere detection task, the AEC tube current profile assigns higher fluence to the noisier views lateral to the pelvis along θ = 90° and 270° in order to homogenize fluence at the center of the detector. The task-driven strategy employs kernel modulation to smooth over the lateral views, thus allowing more dose to be distributed to less noisy views in a manner that boosts overall detectability. For the directional task, the task-driven approach demonstrates modulation patterns dominated by the spatial frequencies of the line pair pattern – both mAs and kernel increase sharply in views around θ = 72° and 252° that contribute the most signal power associated with the imaging task.
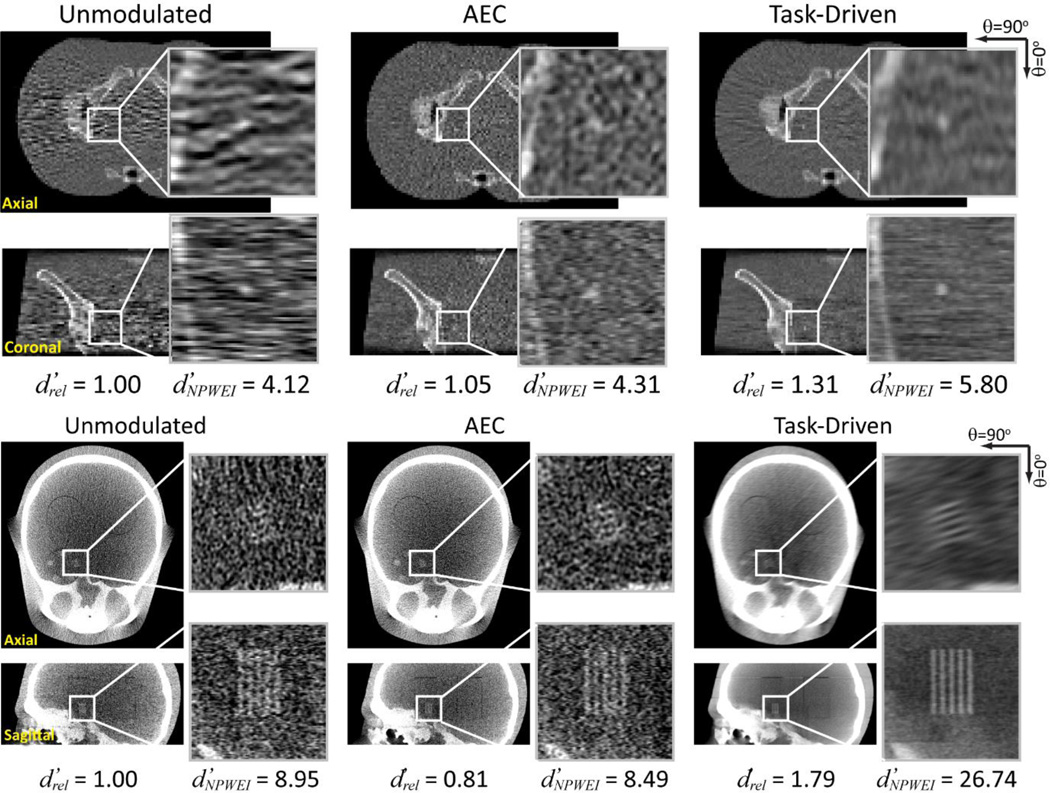
Figure 5 shows the image reconstructions associated with the tube current and kernel modulation profiles in Fig. 4. For each imaging strategy, the ratio of the value of to the unmodulated strategy, , and is presented. For the sphere detection task, strong correlated noise along the lateral views completely obscures the stimulus for the unmodulated strategy. The noise structure for the AEC case appears much more isotropic in the axial slice. The task-driven reconstruction has a much smoother appearance due to the lower cutoff frequencies along the lateral views. The stimulus shows improved conspicuity, with a ~30% increase in and ~40% increase in compared to the unmodulated case. For the directional line pair detection task, the task-driven strategy shows significantly improved conspicuity and a strong boost in d’ compared to both the unmodulated and AEC reconstructions. Interestingly, AEC performed worse than the unmodulated strategy in this case, since AEC adjusts modulation to maintain constant exposure at the center of the detector, but not in a manner that maximizes signal power with respect to the imaging task.
Figure 5.
Reconstructions of the (Top) pelvis and (Bottom) head phantoms corresponding to the (Left) unmodulated, (Middle) AEC, and (Right) task-driven imaging strategies.
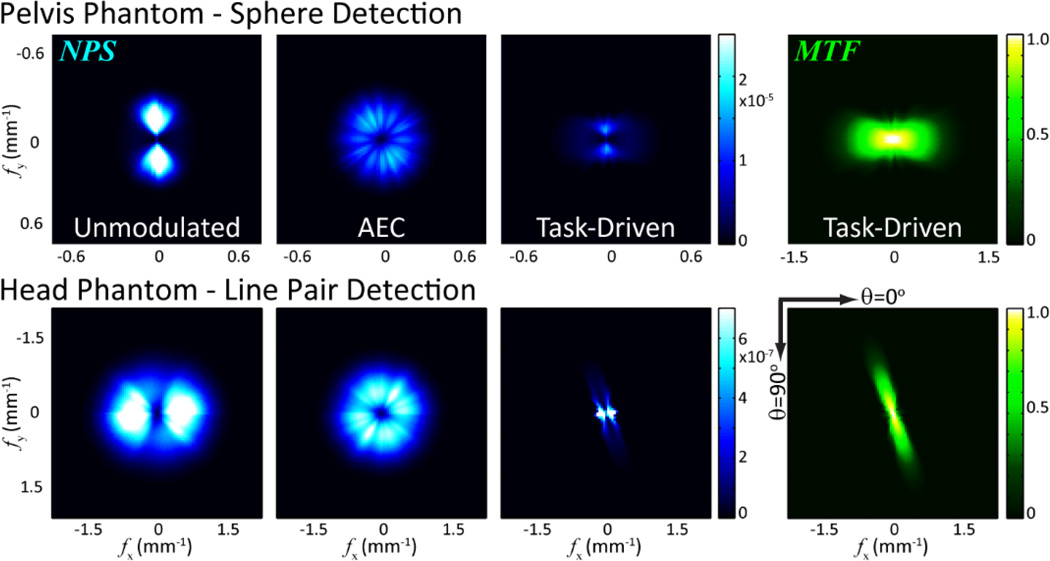
Figure 6 further illustrates the effect of tube current and kernel modulation in terms of the local NPS and MTF. The MTF for the unmodulated and AEC imaging strategies is isotropic and therefore not shown for brevity. The NPS for the unmodulated strategy is governed by the attenuation of the object. The local NPS for the AEC strategy is nearly isotropic due to proximity of the stimulus to the isocenter - i.e., the local NPS for AEC reconstructions is isotropic at the isocenter.
Figure 6.
Central slice through the local 3D NPS and MTF from the three imaging strategies and (Top) the sphere detection task and (Bottom) the line pair detection task. The MTF for the unmodulated and AEC strategies is isotropic and not shown for brevity.
For the sphere detection task, noisy views at θ = 90° and 270° are detrimental to imaging performance for the unmodulated case. The potential benefit of the task-driven strategy is clearly illustrated in the local MTF and NPS, for which such noisy views experience greater smoothing, while signal power [the numerator of Eq. (1)] is preserved for less noisy views coupled with decreased NPS [the denominator of Eq. (1)] through increased tube current.
The task-driven strategy for the line pair detection task preserves the task power through kernel modulation, resulting in an MTF that is closely matched to the task function illustrated in Fig. 3. At the same time, the NPS at such frequencies of interest is reduced by increased tube current. The peak noise power is observed in views mismatched with the imaging task – due both to longer pathlength and lower mAs – and mitigated by smoother reconstruction kernel.
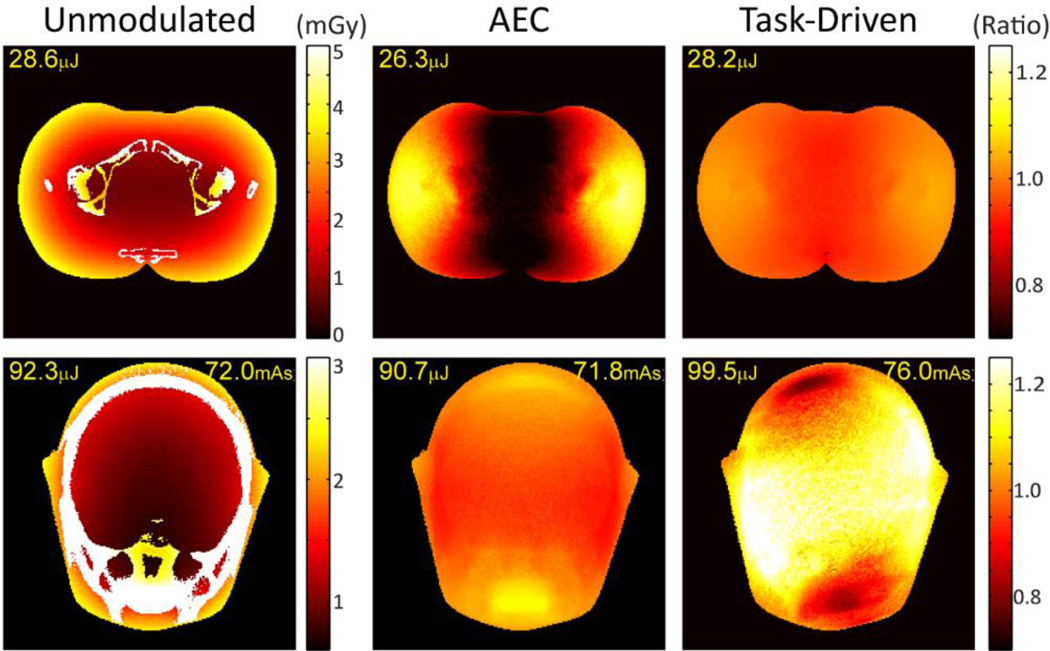
Figure 7 shows the effect of tube current modulation on dose distribution in the two anthropomorphic phantoms under the three imaging strategies. Dose maps in units of mGy are shown in the left column for the unmodulated strategy. The ratio of the dose maps to that of the unmodulated strategy is plotted for the other two strategies to better illustrate fractional change. The total energy deposited in the central slice of the reconstruction is indicated in each case (units µJ). For the physical experiments involving the head phantom, the total mAs after discretizing to experimentally available mA levels (~72 mAs) are also presented.
Figure 7.
Dose maps for the (Top) pelvis and (Bottom) head phantom corresponding to the (Left) unmodulated, (Middle) AED, and (Right) task-driven imaging strategies. The dose map for the unmodulated case (first column) is absolute dose (mGy), and the maps for the AEC and task-driven cases are each a ratio to that dose map.
Compared to the unmodulated case, the task-driven acquistion strategy effectively redistributes dose in a manner optimal to the imaging task, thereby reducing dose deposition in certain regions of the object. For the pelvis phantom, the dose distribution for the task-driven strategy shows a maximum increase of ~5% and maximum decrease of ~10% in local dose deposition compared to the unmodulated case. The total energy deposited is comparable. The AEC strategy shows a much more nonuniform dose distribution due to a more aggressive current modulation profile.
For the head phantom, the total mAs is slightly higher compared to the nominal level (~5.5%) due to discretization and is partly responsible for an 8% increase in total energy deposited. Such increase, however, is small compared to the improvement in imaging performance (~80% increase in d’NPW and ~200% increase in d’NPWEI). At constant total energy deposited for both the unmodulated and task-driven strategies (not shown), the latter would still lead to a 73.6% improvement in d’NPW for the line pair detection task.
C.2 Joint optimization of orbital tilt, mA, and kernel
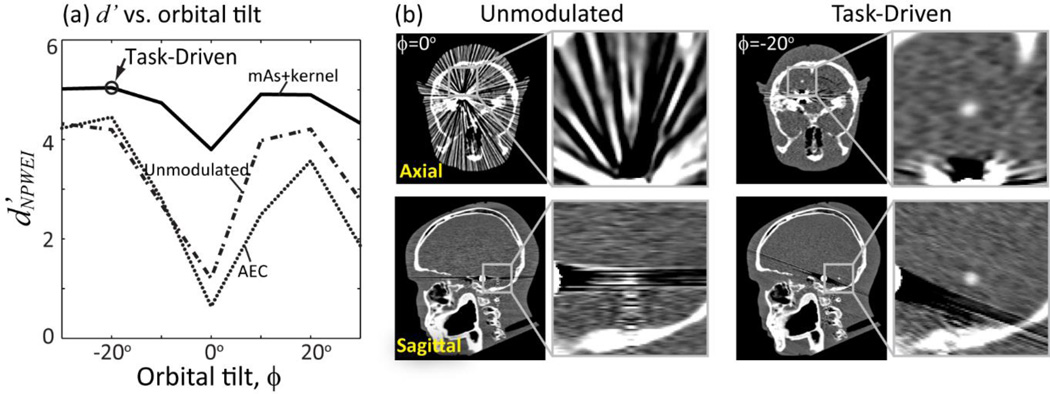
Joint optimization of orbital tilt, tube current modulation, and view-dependent kernel yields the results summarized in Fig. 8. Figure 8(a) shows d’NPWEI computed as a function of orbital tilt (ϕ) for the three imaging strategies, reaching a minimum for ϕ = 0° due to the highly attenuating embolization coil in plane with the stimulus. Detectability improves in each case for gantry tilts deviates from 0°, with the task-driven strategy reaching an optimum at ϕ = −20°. Detectability suffers from increased attenuation for more extreme tilt angles. Performance of the unmodulated and AEC strategies at all tilt angles are shown as well for comparison, but yield lower detectability compared to the task-driven strategy with combined current and kernel modulation.
Figure 8.
Task-driven imaging framework showing joint optimization of the orbital tilt, tube current modulation, and view-dependent reconstruction kernel. (a) Detectability index for the NPWEI observer model computed as a function of gantry tilt angle for the various imaging strategies. (b) Axial and sagittal reconstructions showing visibility of the spherical stimulus for conventional unmodulated acquisition (at 0° gantry tilt) and task-driven acquisition (with jointly optimized gantry tilt of −20°).
Figure 8(b) shows axial and sagittal reconstructions for the task-driven imaging strategy at ϕ = −20° compared to a conventional unmodulated acquisition at ϕ = 0°. The task-driven approach successfully avoids the highly attenuating embolization coil and surrounding bony structures and provides a strong improvement in conspicuity of the stimulus.
D Discussion
This work presents a framework for task-driven CBCT image acquisition and reconstruction predicated by a specification of the imaging task (i.e., the contrast, location, and spatial frequencies of interest) and a patient-specific anatomical model. While commonly used as a metric for image quality assessment, detectability index is directly incorporated as the objective function in a task-driven optimization framework to drive image acquisition and reconstruction. Utility of the framework was investigated in designing tube current modulation, orbital tilt, and view-dependent kernel in FBP reconstruction for a variety of imaging tasks and phantoms.
A joint optimization of both tube current and reconstruction kernel was found to yield improved imaging performance over conventional unmodulated and AEC strategies. For radially symmetric tasks, the algorithm yields a joint modulation profile that smooths noisy views and assign greater dose to the less noisy views in order to boost detectability. For directional tasks, the modulation patterns are dominated by the imaging task, with the mA and kernel peaking in views that contribute the greatest to spatial frequencies associated with the task function. The resulting MTF is strongly anisotropic and closely matched to the imaging task. It is important to acknowledge that varying reconstruction kernel for each view can accentuate data inconsistency and present artifacts in the reconstruction. In Fig. 5, streaks can be observed as a result of view-dependent smoothing of the projection data. For the detection of a known signal, however, these fluctuations do not diminish task performance, and detectability is improved. It is interesting to note that without considering the location or spatial frequencies of interest in the imaging task, the AEC case may perform worse than the unmodulated case.
Optimization of the orbital tilt yielded source-detector trajectories that avoid highly attenuating structures that introduce noise correlations and confound the imaging task. In studies involving an anthropomorphic head phantom, the method yielded a result analogous to the familiar strategy of gantry tilt in head CT, where the scanner is oriented along the canthomeatal line to avoid strong attenuation in the skull base. Other applications may benefit similarly – e.g., imaging of the upper thorax or cervical spine (where the shoulders can present a confounding influence) or the pelvis (avoiding strong attenuation in the femoral heads) – using C-arms that can vary the orbital inclination about any of three rotational axes. Generalization of the method to noncircular orbits is underway, incorporating task-based detectability index as the objective function within a model-based statistical reconstruction framework that intrinsically allow for reconstruction of non-standard orbits and geometries (Stayman and Siewerdsen 2013).
The alternating optimization of tube current and kernel typically converged after 2–3 iterations, requiring ~10 minutes on a Dell Precision T7610 Workstation with an Intel Xeon E5-2630 CPU at 2.60 GHz and 64 GB of RAM. The entire calculation therefore required ~70 min to loop through the seven orbital tilt angles. With respect to possible clinical workflow, the optimization could be incorporated in the preoperative planning process and could be performed as soon as the anatomical model becomes available - i.e., offline in advance of intraoperative imaging. Computation time in this case would therefore not diminish workflow. Should the need arise to update the imaging task or anatomical model during surgery, the optimization would need to be computed prior to the next CBCT acquisition. Further speedup of the algorithm is possible. The orbital tilt range could be further constrained based on experience or previous calculations. Investigation of more efficient gradient-based optimization algorithms with possibile implementation on GPU is underway and will lead to further improvement in speed.
A number of assumptions have been invoked in this work. The cascaded systems framework for signal, noise, and detectability index assumes the signal and noise characteristics of the imaging system to be linear, shift-invariant, and stationary within a local neighborhood. Note, however, that the model explicitly analyzes local metrics of MTF, NPS, and detectability and therefore does not assume such LSI properties to hold globally throughout the volume of reconstruction. Rather, such assumptions are invoked with respect to a region local to the stimulus, and errors associated with such assumption have been shown to be small – e.g., less than 10% difference in detectability index compared to a more computationally intense spatial domain approach that does not make such an assumption (Brunner et al 2012, Gang et al 2014) and with off-diagonal elements of the Fourier transform of the covariance matrix shown to be ~1% that of the diagonal (Pineda et al 2012). The effects of scatter and beam hardening were not explicitly considered in this work, although such effects can be readily incorporated in the cascaded systems model.(Prakash et al 2011) For example, if the scatter to primary ratio (SPR) at the detector corresponding to the projected location of the stimulus is constant in each view, then d’ simply scales by a factor of 1/(1 + SPR), and the optimal modulation profiles for tube current and reconstruction kernel would not be affected. Such assumption holds well when the stimulus is at the center of a cylindrical object. For oblate and complex objects, the SPR could be modeled separately for each projection as an additional view-dependent parameter in the cascaded systems model. Similarly, beam hardening effects can be modeled by using different input spectra and corresponding gain factors for each projection. Such effects will be included in future refinement of the system model.
The task-driven framework assumes prior knowledge of both the imaging task and a patient-specific anatomical model – the first defined in relation to a particular clinical objective and the second based on a previous scan. In image-guided interventions, the imaging task can be formulated fairly precisely in terms of the stimuli and location of interest. The anatomical model may require registration from the previous scan to the current coordinates of the imaging system, e.g., through a 3D-2D registration to radiographic scout images. However, it is important to note that the task-based optimization algorithm only requires information of the line integrals and can therefore tolerate moderate registration errors. In future adaptation of the framework to diagnostic imaging, a modified workflow may be employed to acquire the anatomical model – e.g., from an ultra-low-dose 3D scout image in place of conventional radiographic scouts. Again, since forward projection is a smoothing operation, the algorithm is robust against noisy anatomical models. The imaging task in this case could be reasonably well specified from the purpose of the examination (e.g., detection of blood in the brain or presence of a lesion in the liver) but would require uncertainties in task definitions, e.g., in the size, orientation, and/or location.
Extension of the task-driven imaging framework will incorporate specification of the imaging task with uncertainties, with detectability index derived following a signal-known statistically (SKS) or signal-known exactly but variable (SKEV) paradigm from statistical decision theory (Eckstein and Abbey 2001, Eckstein et al 2003). Also of interest is optimization with respect to multiple imaging tasks from the same image acquisition – e.g., detection of hemorrhage in one location and fracture in another. In such scenarios, it may be optimal to reconstruct separate images suited for different tasks or use spatially varying regularization in a model-based reconstruction method. The results presented above begin to demonstrate the potential of a task-driven paradigm by which combined image acquisition and reconstruction strategies optimized for the imaging task lead to improvements in image quality and reduction in radiation dose.
Acknowledgements
The authors would like to thank Dr. Yoshito Otake and Mr. Ali Uneri (Department of Biomedical Engineering and Department of Computer Science, Johns Hopkins University) for assistance with image reconstruction tools. Dr. Alejandro Sisniega and Dr. Wojciech Zbijewski (Department of Biomedical Engineering, Johns Hopkins University) advised on the MC GPU dose calculation. Thanks also to Mr. Thomas Reigel (Department of Biomedical Engineering, Johns Hopkins University) for help with data acquisition. This work was supported by NIH Grant No. 2R01-CA-112163, R01-EB-017226, U01-EB-018758, academic-industry partnership with Siemens Healthcare (Forcheim, Germany), and an AAPM Research Seed Funding Grant.
Appendix A. Derivation of current modulation to maximize d'
Previous work on cascaded system analysis yielded a view-dependent form of the MTF (denoted T) and NPS (denoted S) as follows:
| (7a) |
| (7b) |
where view-dependent terms are indicated by the subscript i, and the 3D frequency domain dependence (fx,fy,fz) is omitted for brevity The apodization filter is represented as Twin instead of T11. Notation is otherwise consistent with Tward and Siewerdsen, and Gang et. al. (Tward and Siewerdsen 2008, Gang et al 2014). Briefly, numbered subscripts indicate discrete stages corresponding to physical or mathematical processes of image formation. Notation T indicates stages resulting in spatial spreading of signal; ḡ indicates stages where signal is amplified or diminished; III indicates sampling; Sadd indicates electronic noise. The terms in Eq. 8(a) and (b) combine according to Eq. (1) for calculation of d’NPW.
To derive a tube current modulation profile that maximizes d’NPW for a given kernel modulation profile, we begin by noting that the numerator of Eq. (1) is independent of tube current and is thus a constant. Maximizing d’ therefore amounts to minimizing the denominator. The mean incident fluence at the detector, q̄i, is directly proportional to mAs and is the only term dependent on mAs. Furthermore, quantum and electronic noise have distinct dependence on q̄i and can be written separately as follows:
| (8a) |
| (8b) |
Separating the quantum and electronic noise components in the denominator and extracting the scalar q̄i out of the integral, the denominator can be written as:
| (9) |
where and are view-dependent, task-dependent, and mAs-independent constants, is the bare beam fluence of the ith projection, and l is the line integral through the location at which noise is computed.
In a manner similar to that in Gies et al. (Gies et al 1999) and under the dose constraint , the first derivative of the denominator with respect to yields the relationship between the bare beam fluence of projection j to any arbitrary projection k:
| (10) |
Setting to any fixed value, can then be solved numerically. The bare beam fluence for all projections can be normalized such that is equal to the level specified by the dose constraint.
Appendix B. Derivation of gradient vector
Since d′ is positive, maximizing d′2 also maximizes d′. The following derivation yields the gradient vector which can be used in a gradient-based optimization algorithm. The derivative of with respect to is:
| (11) |
The derivative of the numerator with respect to for a single projection is:
| (12) |
The derivative of the denominator can be obtained following the product rule:
| (13) |
Substituting (12) into (13) and (14), the gradient can be derived according to the quotient rule, and the gradient vector, , can be assembled for each projection.
Note that the derivative with respect to a variety of other imaging parameters (including ) could be derived in a similar manner and used in task-driven optimization.
References
- Badal A, Badano A. Accelerating Monte Carlo simulations of photon transport in a voxelized geometry using a massively parallel graphics processing unit. Med. Phys. 2009;36:4878. doi: 10.1118/1.3231824. Online: http://scitation.aip.org/content/aapm/journal/medphys/36/11/10.1118/1.3231824. [DOI] [PubMed] [Google Scholar]
- Bartolac S, Graham S, Siewerdsen J, Jaffray D. Fluence field optimization for noise and dose objectives in CT. Med. Phys. 2011;38(Suppl 1):S2. doi: 10.1118/1.3574885. Online: http://scitation.aip.org/content/aapm/journal/medphys/38/S1/10.1118/1.3574885. [DOI] [PubMed] [Google Scholar]
- Brunner CC, Abboud SF, Hoeschen C, Kyprianou IS. Signal detection and location-dependent noise in cone-beam computed tomography using the spatial definition of the Hotelling SNR. Med. Phys. 2012;39:3214–3228. doi: 10.1118/1.4718572. [DOI] [PubMed] [Google Scholar]
- Burgess AE. Statistically defined backgrounds: performance of a modified nonprewhitening observer model. JOSA A. 1994;11:1237–1242. doi: 10.1364/josaa.11.001237. [DOI] [PubMed] [Google Scholar]
- Chen G-H, Zambelli J, Nett BE, Supanich M, Riddell C, Belanger B, Mistretta CA. Design and development of C-arm based cone-beam CT for image-guided interventions: initial results. In: Flynn MJ, Hsieh J, editors. Medical Imaging. 2006. p. 614210–614210 – 12. (International Society for Optics and Photonics) Online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=1276504. [Google Scholar]
- Diaz I, Kobbe-Schmidt S, Verdun FR, Bochud FO. Characterization of human observer detection in AFC volumetric detection tasks. In: Abbey CK, Mello-Thoms CR, editors. SPIE Medical Imaging. 2013. p. 86730A. (International Society for Optics and Photonics) Online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=1673807. [Google Scholar]
- Eckstein MP, Abbey CK. Model observers for signal-known-statistically tasks (SKS) In: Krupinski EA, Chakraborty DP, editors. Medical Imaging 2001. 2001. pp. 91–102. (International Society for Optics and Photonics) Online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=907079&resultClick=1. [Google Scholar]
- Eckstein MP, Zhang Y, Pham B, Abbey CK. Optimization of model observer performance for signal known exactly but variable tasks leads to optimized performance in signal known statistically tasks. In: Chakraborty DP, Krupinski EA, editors. Medical Imaging 2003. 2003. pp. 123–134. (International Society for Optics and Photonics) Online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=758488. [Google Scholar]
- Fahrig R, Dixon R, Payne T, Morin RL, Ganguly A, Strobel N. Dose and image quality for a cone-beam C-arm CT system. Med. Phys. 2006;33:4541. doi: 10.1118/1.2370508. Online: http://scitation.aip.org/content/aapm/journal/medphys/33/12/10.1118/1.2370508. [DOI] [PubMed] [Google Scholar]
- Feldkamp LA, Davis LC, Kress JW. Practical cone-beam algorithm. JOSA A. 1984;1:612–619. [Google Scholar]
- Fessler JA. Mean and variance of implicitly defined biased estimators (such as penalized maximum likelihood): applications to tomography. IEEE Trans. Image Process. 1996;5:493–506. doi: 10.1109/83.491322. Online: http://www.ncbi.nlm.nih.gov/pubmed/18285134. [DOI] [PubMed] [Google Scholar]
- Fiete RD, Barrett HH, Smith WE, Myers KJ. Hotelling trace criterion and its correlation with human-observer performance. J. Opt. Soc. Am. A. 1987;4:945. doi: 10.1364/josaa.4.000945. Online: http://josaa.osa.org/abstract.cfm?URI=josaa-4-5-945. [DOI] [PubMed] [Google Scholar]
- Frey EC, Gilland KL, Tsui BMW. Application of task-based measures of image quality to optimization and evaluation of three-dimensional reconstruction-based compensation methods in myocardial perfusion SPECT. IEEE Trans. Med. Imaging. 2002;21:1040–1050. doi: 10.1109/TMI.2002.804437. Online: http://www.ncbi.nlm.nih.gov/pubmed/12564872. [DOI] [PubMed] [Google Scholar]
- Galvin JM, Chen X-G, Smith RM. Combining multileaf fields to modulate fluence distributions. Int. J. Radiat. Oncol. 1993;27:697–705. doi: 10.1016/0360-3016(93)90399-g. Online: http://www.sciencedirect.com/science/article/pii/036030169390399G. [DOI] [PubMed] [Google Scholar]
- Gang GJ, Lee J, Stayman JW, Tward DJ, Zbijewski W, Prince JL, Siewerdsen JH. Analysis of Fourier-domain task-based detectability index in tomosynthesis and cone-beam CT in relation to human observer performance. Med. Phys. 2011;38:1754–1768. doi: 10.1118/1.3560428. Online: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3069989&tool=pmcentrez&rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gang GJ, Stayman JW, Zbijewski W, Siewerdsen JH. Modeling and control of nonstationary noise characteristics in filtered-backprojection and penalized likelihood image reconstruction. 2013;8668:86681G – 86681G – 7. doi: 10.1117/12.2008408. Online: http://dx.doi.org/10.1117/12.2008408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gang GJ, Stayman JW, Zbijewski W, Siewerdsen JH. Task-based detectability in CT image reconstruction by filtered backprojection and penalized likelihood estimation. Med. Phys. 2014;41:081902. doi: 10.1118/1.4883816. Online: http://scitation.aip.org/content/aapm/journal/medphys/41/8/10.1118/1.4883816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gang GJ, Zbijewski W, Stayman JW, Siewerdsen JH. Cascaded systems analysis of noise and detectability in dual-energy cone-beam CT. Med. Phys. 2012;39:5145–5156. doi: 10.1118/1.4736420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gies M, Kalender WA, Wolf H, Suess C, Madsen MT. Dose reduction in CT by anatomically adapted tube current modulation. I. Simulation studies. Med. Phys. 1999;26:2235. doi: 10.1118/1.598779. Online: http://scitation.aip.org/content/aapm/journal/medphys/26/11/10.1118/1.598779. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal detection theory and psychophysics. Vol. 1. New York: Wiley; 1966. [Google Scholar]
- Jaffray DA, Siewerdsen JH, Wong JW, Martinez AA. Flat-panel cone-beam computed tomography for image-guided radiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 2002;53:1337–1349. doi: 10.1016/s0360-3016(02)02884-5. [DOI] [PubMed] [Google Scholar]
- Leng S, Yu L, Zhang Y, Carter R, Toledano AY, McCollough CH. Correlation between model observer and human observer performance in CT imaging when lesion location is uncertain. Med. Phys. 2013;40:081908. doi: 10.1118/1.4812430. Online: http://scitation.aip.org/content/aapm/journal/medphys/40/8/10.1118/1.4812430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li K, Bevins N, Zambelli J, Qi Z, Chen G-H. Detection performance study for cone-beam differential phase contrast CT. In: Pelc NJ, Nishikawa RM, Whiting BR, editors. SPIE Medical Imaging. 2012. p. 83131L. (International Society for Optics and Photonics) Online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=1284741. [Google Scholar]
- Pineda AR, Tward DJ, Gonzalez A, Siewerdsen JH. Beyond noise power in 3D computed tomography: The local NPS and off-diagonal elements of the Fourier domain covariance matrix. Med. Phys. 2012;39:3240–3252. doi: 10.1118/1.4705354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prakash P, Zbijewski W, Gang GJ, Ding Y, Stayman JW, Yorkston J, Carrino JA, Siewerdsen JH. Task-based modeling and optimization of a cone-beam CT scanner for musculoskeletal imaging. Med. Phys. 2011;38:5612–5629. doi: 10.1118/1.3633937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richard S, Li X, Yadava G, Samei E. Predictive models for observer performance in CT: applications in protocol optimization. 2011;7961:79610H – 79610H – 6. Online: http://dx.doi.org/10.1117/12.877069. [Google Scholar]
- Salvat F, Fernández-Varea JM, Sempau J. PENELOPE-2006: A code system for Monte Carlo simulation of electron and photon transport. Workshop Proceedings. 2006;4:7. [Google Scholar]
- Samei E, Richard S, Lurwitz L. Model-based CT performance assessment and optimization for iodinated and noniodinated imaging tasks as a function of kVp and body size. Med. Phys. 2014;41:081910. doi: 10.1118/1.4890082. Online: http://scitation.aip.org/content/aapm/journal/medphys/41/8/10.1118/1.4890082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez AA, Sidky EY, Pan X. Task-based optimization of dedicated breast CT via Hotelling observer metrics. Med. Phys. 2014;41:101917. doi: 10.1118/1.4896099. Online: http://scitation.aip.org/content/aapm/journal/medphys/41/10/10.1118/1.4896099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp PF, Metz CE, Wagner RF, Myers KJ, Burgess AE. ICRU Rep. 54 Medical imaging: the assessment of mage quality. Int. Comm. Radiol. Units Meas. (Bethesda, Md) 1996 [Google Scholar]
- Siewerdsen JH. Cone-beam CT with a flat-panel detector: From image science to image-guided surgery. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers, Detect. Assoc. Equip. 2011;648:S241–S250. doi: 10.1016/j.nima.2010.11.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siewerdsen JH, Antonuk LE, El-Mohri Y, Yorkston J, Huang W, Cunningham IA. Signal, noise power spectrum, and detective quantum efficiency of indirect-detection flat-panel imagers for diagnostic radiology. Med. Phys. 1998;25:614. doi: 10.1118/1.598243. Online: http://scitation.aip.org/content/aapm/journal/medphys/25/5/10.1118/1.598243. [DOI] [PubMed] [Google Scholar]
- Siewerdsen JH, Moseley DJ, Burch S, Bisland SK, Bogaards A, Wilson BC, Jaffray DA. Volume CT with a flat-panel detector on a mobile, isocentric C-arm: Pre-clinical investigation in guidance of minimally invasive surgery. Med. Phys. 2005;32:241. doi: 10.1118/1.1836331. Online: http://scitation.aip.org/content/aapm/journal/medphys/32/1/10.1118/1.1836331. [DOI] [PubMed] [Google Scholar]
- Siewerdsen JH, Waese AM, Moseley DJ, Richard S, Jaffray DA. Spektr: A computational tool for x-ray spectral analysis and imaging system optimization. Med. Phys. 2004;31:3057–3067. doi: 10.1118/1.1758350. [DOI] [PubMed] [Google Scholar]
- Sisniega A, Zbijewski W, Badal A, Kyprianou IS, Stayman JW, Vaquero JJ, Siewerdsen JH. Monte Carlo study of the effects of system geometry and antiscatter grids on cone-beam CT scatter distributions. Med. Phys. 2013;40:051915. doi: 10.1118/1.4801895. Online: http://scitation.aip.org/content/aapm/journal/medphys/40/5/10.1118/1.4801895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stayman JW, Siewerdsen JH. Proceedings of 12th International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine. Lake Tahoe, CA: 2013. Task-Based Trajectories in Iteratively Reconstructed Interventional Cone-Beam CT; pp. 257–260. [Google Scholar]
- Szczykutowicz TP, Mistretta CA. Design of a digital beam attenuation system for computed tomography: part I. System design and simulation framework. Med. Phys. 2013;40:021905. doi: 10.1118/1.4773879. Online: http://scitation.aip.org/content/aapm/journal/medphys/40/2/10.1118/1.4773879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tward DJ, Siewerdsen JH. Cascaded systems analysis of the 3D noise transfer characteristics of flat-panel cone-beam CT. Med. Phys. 2008;35:5510. doi: 10.1118/1.3002414. Online: http://scitation.aip.org/content/aapm/journal/medphys/35/12/10.1118/1.3002414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner RF. DECISION-THEORY AND DETAIL SIGNAL-TO-NOISE RATIO OF OTTO SCHADE. Photogr. Sci. Eng. 1978;22:41–46. [Google Scholar]
- Woodcock E, Murphy T, Hemmings P, Longworth S. Techniques used in the GEM code for Monte Carlo neutronics calculations in reactors and other systems of complex geometry. Proc. Conf. Applications of Computing Methods to Reactor Problems. 1965;557 [Google Scholar]
- Yao J, Barrett HH. Predicting human performance by a channelized Hotelling observer model. In: Wilson DC, Wilson JN, editors. San Diego ’92. 1992. pp. 161–168. (International Society for Optics and Photonics) Online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=999333. [Google Scholar]
- Yu L, Leng S, Chen L, Kofler JM, Carter RE, McCollough CH. Prediction of human observer performance in a 2-alternative forced choice low-contrast detection task using channelized Hotelling observer: impact of radiation dose and reconstruction algorithms. Med. Phys. 2013;40:041908. doi: 10.1118/1.4794498. Online: http://scitation.aip.org/content/aapm/journal/medphys/40/4/10.1118/1.4794498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Z, Gang GJ, Siewerdsen JH. Noise, sampling, and the number of projections in cone-beam CT with a flat-panel detector. Med. Phys. 2014;41:61909. doi: 10.1118/1.4875688. [DOI] [PMC free article] [PubMed] [Google Scholar]