Abstract
Regional intestinal effective permeability (Peff) values are key for the understanding of drug absorption along the whole length of the human gastrointestinal (GI) tract. The distal regions of the GI tract (i.e. ileum, ascending-transverse colon) represent the main sites for GI absorption when there is incomplete absorption in the upper GI tract, e.g. for modified release formulations. In this work, a new and pragmatic method for the estimation of (passive) intestinal permeability in the different intestinal regions is being proposed, by translating the observed differences in the available mucosal surface area along the human GI tract into corrections of the historical determined jejunal Peff values. These new intestinal Peff values or “intrinsic” Peff(Peff,int) were subsequently employed for the prediction of the ileal absorption clearance (CLabs,ileum) for a set of structurally diverse compounds. Additionally, the method was combined with a semi-mechanistic absorption PBPK model for the prediction of the fraction absorbed (fabs). The results showed that Peff,int can successfully be employed for the prediction of the ileal CLabs and the fabs. Peff,int also showed to be a robust predictor of the fabs when the colonic absorption was allowed in the PBPK model, reducing the overprediction of fabs observed for lowly permeable compounds when using the historical Peff values. Due to its simplicity, this approach provides a useful alternative for the bottom-up prediction of GI drug absorption, especially when the distal GI tract plays a crucial role for a drug’s GI absorption.
Electronic supplementary material
The online version of this article (doi:10.1208/s12248-015-9758-0) contains supplementary material, which is available to authorized users.
KEY WORDS: intestinal permeability, oral drug absorption, physiologically based pharmacokinetic modelling
INTRODUCTION
Human intestinal permeability is a key drug-related parameter governing the gastrointestinal (GI) drug absorption process. Due to the established correlation between human effective jejunal permeability (Peff) and the fraction of the administered oral dose that becomes absorbed in the GI tract (fabs or fa), Peff has been widely used for the a priori estimation of drug absorption in different stages of the drug development process (1–3). Peff is one of the fundamental biopharmaceutical parameters in the Biopharmaceutics Classification System (BCS) and has been extensively used in drug development (2,4,5). As a consequence, it has often been applied in mechanistic GI absorption models, i.e. GastroPlus™ (6), PK-Sim® (7,8), SimCYP® (9) and some in-house absorption models (10,11), for the “bottom-up” prediction of the rate and extent of oral drug absorption.
Human Peff is usually determined in single-pass perfusion experiments using open, semi-open or double-balloon (closed) perfusion systems (12), where the latter is considered to be the most accurate in vivo method for Peff determinations in humans (3,12). In the double-balloon technique, the drug is single-pass perfused in solution to conscious human volunteers employing a multilumen tube. The reader is referred to the following references for more details about the clinical procedure, the data analysis and the double-balloon technique (1,2,13–16).
The derived Peff values are a reflection of the intestinal membrane’s resistance to the passage of the drug across the apical membrane of the GI tract, regardless of the mechanisms involved, i.e. unstirred water layer (UWL) permeation, transcellular permeation, paracellular permeation and/or carried-mediated absorption/efflux (2,17–19). In addition, jejunal Peff can be affected by the experimental conditions and the physiological factors that the drug might encounter during its passage through the intestinal membrane in the upper jejunum (3,12,20).
Intestinal Peff is a time- and position-dependent parameter, and its magnitude is a function of the nature of the small-intestinal membrane and the luminal conditions (1–3,18,21). The latter is of special interest in the cases where jejunal Peff alone might not necessarily explain the drug absorption in certain regions of the human GI tract. This is the case of the distal ileum and/or the colon, where the luminal conditions and the structure of the intestinal membrane differ significantly with those of the upper jejunum (22,23). These distal intestinal sites play a key role in the absorption of drugs contained in modified release (MR) dosage forms, where due to the nature of the formulation and the prolonged colonic residence time, a great proportion of the given dose is designed to be absorbed in such regions (22,24). Regional permeability measurements are considered as an important parameter for the understanding and the mechanistic modelling of GI drug absorption. Nevertheless, the available regional Peff estimates are sparse and limited to a small set of compounds. Given that such values were determined mostly using open perfusion systems, their comparison with the ones obtained from the double-balloon technique is limited (4,5). Recent works have highlighted the necessity for regional Peff estimates in humans, which are of particular interest during early stages of drug and formulation development (4,5,21,25). Yet, due to the vast economic cost associated with clinical perfusion studies, further investigations on regional Peff determination might be limited in the near future.
Mechanistic absorption models can be employed as a complement for the understanding of drug permeation along the different segments of the GI tract. For instance, the majority of the aforementioned models can incorporate some of the physiological factors known to affect the drug’s regional absorption. Remarkable progress has been made in the field of solubility and dissolution, where factors such as the pH-dependent solubility for ionisable compounds, variable GI fluid volumes, supersaturation and precipitation, presence of bile micelles and bile salt-mediated solubility enhancement, to name a few, have already been incorporated in these models (6,7,26–30). Nevertheless, in terms of regional intestinal membrane permeability (once the intraluminal and intracellular processes have been accounted for), there is a need for improvements (6–8,26,28).
While in most of these mechanistic models, regional differences in the expression/abundance of intestinal transporters are already accounted to some extent (6–8,26,28), the approach with regard to the passive permeation along the GI tract is still not well defined. For example, in the physiologically based pharmacokinetic (PBPK) modelling of orally administered drugs, it is a common practice to assume that colonic absorption is insignificant compared to that in the small intestine. Thus, colonic absorption, by default, is not allowed in such models (10,11,31–34). However, based on the large number of MR dosage forms labelled for once-daily administration, absorption from the colon appears to be a very crucial and common process (22,35).
The aim of this study was to derive regional intestinal permeability estimates by translating the observed differences in intestinal mucosal surface area along the different segments of the human intestine (36,37) into the human Peff values and to evaluate the ability of the new permeability values to predict the GI absorption using a semi-mechanistic PBPK absorption model.
MATERIALS AND METHODS
Determination of the Mucosal Surface Area in the Small Intestine and the Colon
The human intestine has several structures known to increase the mucosal surface area (mSA) compared to that of a cylinder. In the small intestine (SI), the circular folds or plicae circularis (PC), villi (VL) and enterocyte microvilli (MV) are commonly believed to increase the surface area by factors of 3, 10, and 20, respectively (23,37,38). In the colon, the colonic haustra, the crypts and the colonic microvilli (MVcolon) perform a similar function (22). It has been shown, however, that the amplifications in mSA generated by the circular folds and villi decrease from the proximal SI to the distal SI. In addition, a decrease in mSA has been observed from the colonic microvilli compared to that of the small intestine (36,39).
For this work, three different methods for the estimation of the intestinal surface area were employed as follows: (a) method 1 (M1) or control assumes that the mSA of the intestine is that of a cylinder; (b) method 2 (M2) assumes that the mSA of the SI decreases exponentially, as per the work of Wilson (36); and (c) method 3 (M3) assumes that the mSA of the SI decreases gradually, based on recently published region-specific surface area expansion factors (SAEFs) (39). A detailed description of the three methods is given below, and they are illustrated in Fig. 1a.
Fig. 1.
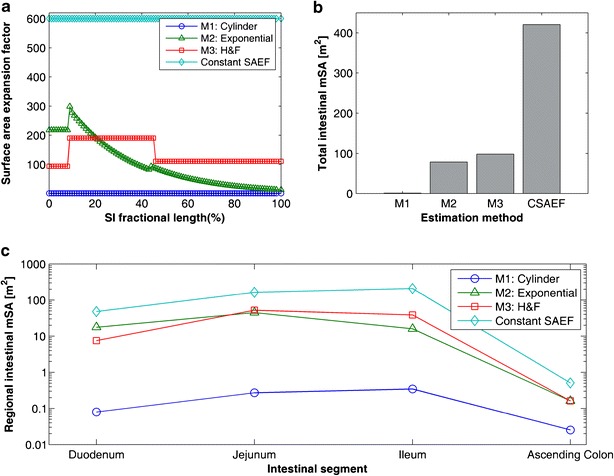
Illustrations of the changes on intestinal mucosal surface area estimated by the different methods. a Changes in the surface area expansion factors (SAEFs) along the length of the small intestine (as a percentage), the SAEF is defined as the ratio between the surface area estimated by a given method and the surface area of a cylinder. b Total mucosal surface area estimated from the different methods (M1 to M3), whereas CSAEF is the total mucosal surface area estimated by applying a constant SAEF of 600-fold along the small intestine. c An illustration of the total surface area estimated for each of the regions of the small intestine and the ascending colon, for the different methods (M1 to M3) and when using the CSAEF. The values were calculated assuming a reference human intestine (see main text for details on the anatomical values employed for the calculations)
M1: Cylindrical Surface Area (Control)
This method assumed that the surface area (SA) in all the intestinal segments was that of a cylinder (Fig. 1a), SAi = 2 × π × Ri × Li, where Ri and Li are the radii and lengths of the given intestinal segments (i), respectively. The anatomical parameters, i.e. lengths and radii, of the different intestinal segments were derived from the literature and were meant to represent the values of a “reference man” of 70 kg of weight and 170 cm of height (23,40).
The anatomical length of the small intestine (Lsi) was assumed as 670.7 cm (41), and the length of each small intestinal segment was calculated as a percentage of Lsi; 8, 37 and 55% for the duodenum, jejunum and ileum, respectively (23). The radius of the duodenum (rduo) was assumed to be 2.37 cm (23), whereas for the jejunum and the ileum, the radii were assumed to be 1.75 and 1.5 cm, respectively (5,15). With regard to the colon, the total length (Lcol) was assumed to be 104.34 cm, and it was calculated from Eq. 1 for the same reference man (40).
| 1 |
For this work, colonic absorption was assumed only to occur in the ascending colon (acol) and the length of the segment (Lacol) was considered to be a 16% of Lcol (22,23). The radius of the ascending colon was assumed to be 2.42 cm (42). The aforementioned anatomical parameters were also employed for the calculation of the mucosal surface area in M2 and M3.
M2: Exponential Decrease (Wilson)
This method was based on the work by Wilson (1967), who reported a correlation between the mSA and the longitudinal position between the beginning of the jejunum (duodenojejunal flexure, DJF) and the final portion of the ileum (ileocecal valve, ICV) (36). This method accounts for the amplification in SA product of the presence of circular folds and villi along the SI (Fig. 1a). Herein, Wilson’s data was digitized using GetData Graph Digitizer v2.26 (http://getdata-graph-digitizer.com/) and fitted by an exponential model (Eq. 2) using non-linear least squares regression with the “lsqnonlin” function of the Optimization Toolbox within Matlab 2014a (The Mathworks Inc., Natick, MA, USA)
| 2 |
where, y(xj + i) is the ratio of mSA per unit of serosal length (cm2/cm), xj + i is the longitudinal position (cm) along the segment comprised between the DJF and the ICV and Lj + i is the length (cm) of the jejunum plus the ileum (j + i) (0.92 × Lsi). The regression coefficients, λ1and λ2, were found to be 164.16 cm2/cm and −3.33 respectively. The coefficients of variation (CV) of the parameter estimates were found to be 0.65 and 35.03%, respectively. More details about the fitting process can be found in Section 1 of the Supplementary Material.
Equation 2 was integrated with respect to the longitudinal position (xi + j) between the DJF and the ICV in order to derive the cumulative mSA, as shown in Eq. 3
| 3 |
where mSAj + i is the cumulative mucosal surface area at any position of the aforementioned segment. To obtain the total mucosal surface area in the whole SI, a similar relationship for the duodenum was needed; however, no data for such a correlation was provided in Wilson’s work. This relationship was assumed to be proportional to the longitudinal position in the duodenal segment (xduo) and similar to that of the initial portion of the jejunum, i.e. the intercept (λ1) of the exponential relationship generated for the jejunum and ileum (Eq. 4).
| 4 |
Combining Eqs. 3 and 4 and accounting for the mSA expansion due to the intestinal microvilli (MVsi) of 20-fold (23,43), the cumulative mucosal surface area at any longitudinal position (x) of the SI is given by Eq. 5.
| 5 |
For the ascending colon, the only structure considered to effectively increase the mSA available for absorption was the colonic microvilli (MVcolon); its increase in colonic mSA was assumed to be 6.4-fold (39).
M3: Gradual Decrease (Helander and Fändriks, H&F)
This method was based on a recent work by Helander and Fändriks (2014) where they reported mean SA expansion factors generated by the different structures present in the SI and the colon (Fig. 1a) (39). The segmental cylindrical SA was calculated as per M1 and for each intestinal segment, the following SAEF were applied: (a) circular folds (for every segment in the SI), 1.57-fold; (b) duodenal villi and microvilli, 6.5- and 9.2-fold, respectively; (c) jejunal villi and microvilli, 8.6- and 14.1-fold, respectively; (d) ileal villi and microvilli, 4.5- and 15.7-fold, respectively, and (e) colonic microvilli, 6.4-fold (39).
The total intestinal mSA calculated for each of the methods described above was contrasted with the mSA resulting from the use of the classical amplification factors described in the literature; 3-fold for the circular folds, 10-fold for the villi and 20-fold for the intestinal microvilli (22,23,37) (Fig. 1b).
Analysis of the Differences in Regional Intestinal Permeability
A comparison between the reported human regional Peff values was performed in order to elucidate the possible impact that the mSA assumptions might have in the regional Peff determinations. This was done for a recently published dataset of 11 drugs whose in vivo absorption was measured in different segments of the human SI during single-pass open perfusion experiments (4,5). Regional Peff values were originally derived by Lennernäs by re-arranging the reported absorption data to a parallel tube model (4,5,12,18). Selection of this model was based on its ability to describe the hydrodynamics of the absorption process during open and/or semi-open single-pass perfusion experiments (12,18), as shown in Eq. 6
| 6 |
where the subscript i in Peff,i stands for either the upper jejunum or distal ileum, Qin is the perfusate flow rate (volume/time), Cin and Cout are the respective water transport-corrected concentrations of drug entering and leaving the test segment and SAi is the segment’s surface area.
Herein, the reported regional Peff,i values were re-calculated from the absorption data originally reported in the literature (44–49). This was done in order to allow the incorporation of the different mSA calculation methods for the estimation of the regional Peff values; the details of the re-calculation procedure can be found in Section 3 the Supplementary Material.
For the re-calculation, the value of the SA term in Eq. 6 depended upon which of the aforementioned mSA estimation methods were used. For M1, the mSA was calculated as described above for a cylinder of radius (ri) and length (Li), where ri was assumed either 1.75 cm (upper jejunum) or 1.5 cm (distal ileum) and Li was the length of the test portion of the perfusion tube (cm). For M2, the mSA available (Eq. 5) across the length of the test portion of the multiple lumen tube was employed (44–49). This mSA was defined as the difference in cumulative mucosal surface area between the distal (xfinal,i) and proximal (xinitial,i) collection orifices of the perfusion tube. The positions required to calculate the mSA according to M2, xfinal,i and xinitial,i, were assumed to be the same for all the experiments and were representative of the positions informed for the jejunal and ileal perfusion experiments (44–49). This was done due to the high variability reported in the positioning of the test segments of the multiple lumen tube or the lack of information about it in some of the references. For the jejunal experiments, xinitial, jejunum was assumed to be 10 cm distally from the DJF, whereas for the ileal experiments, xinitial, ileum, it was assumed to be 110 cm from the same intestinal landmark. The positions of the distal portions, xfinal, were estimated by adding the lengths of the test segments (Li) to both jejunal and ileal initial positions (xfinal, jejunum = xinitial, jejunum + Li and xfinal, ileum = xinitial, ileum + Li). Finally, for M3, the SA term was calculated using the cylindrical SA described above for M1 and the SAEF described in M3 for the jejunum and the ileum. The detailed regional estimates of the mSA derived from the aforementioned calculations methods are shown Table I.
Table I.
Segmental SA Employed for the Calculation of P eff,int from P eff Values (Open Perfusion System)
| Compounda | Segment Lengtha (cm) | x i, jejunum b (cm) | mSA jejunum (×104 cm2)c | x i, ileum d (cm) | mSA ileum (×104 cm2)e | Ratio (mSAjej/mSAile) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M1 | M2 | M3 | M1 | M2 | M3 | ||||
| Hydrocortisone | 15 | 10 | 0.0165 | 4.52 | 3.14 | 110 | 0.0141 | 2.89 | 1.57 | 1.26 | 1.56 | 2.00 |
| Triamcinolone acetonide | 15 | 10 | 0.0165 | 4.52 | 3.14 | 110 | 0.0141 | 2.89 | 1.57 | 1.26 | 1.56 | 2.00 |
| Paracetamol | 30 | 10 | 0.0330 | 8.71 | 6.28 | 110 | 0.0283 | 5.57 | 3.14 | 1.26 | 1.56 | 2.00 |
| Salicylic acid | 80 | 10 | 0.0880 | 20.6 | 16.7 | 110 | 0.0754 | 13.2 | 8.36 | 1.26 | 1.56 | 2.00 |
| Hydrochlorothiazide | 80 | 10 | 0.0880 | 20.6 | 16.7 | 110 | 0.0754 | 13.2 | 8.36 | 1.26 | 1.56 | 2.00 |
| Atenonol | 80 | 10 | 0.0880 | 20.6 | 16.7 | 110 | 0.0754 | 13.2 | 8.36 | 1.26 | 1.56 | 2.00 |
| Furosemide | 80 | 10 | 0.0880 | 20.6 | 16.7 | 110 | 0.0754 | 13.2 | 8.36 | 1.26 | 1.56 | 2.00 |
| Cimetidine | 80 | 10 | 0.0880 | 20.6 | 16.7 | 110 | 0.0754 | 13.2 | 8.36 | 1.26 | 1.56 | 2.00 |
| Talinonol | 30 | 10 | 0.0330 | 8.71 | 6.28 | 110 | 0.0283 | 5.57 | 3.14 | 1.26 | 1.56 | 2.00 |
| Griseofulvine | 20 | 10 | 0.0220 | 5.95 | 4.19 | 110 | 0.0188 | 3.81 | 2.09 | 1.26 | 1.56 | 2.00 |
| Ranitidine | 30 | 10 | 0.0330 | 8.71 | 6.28 | 110 | 0.0283 | 5.57 | 3.14 | 1.26 | 1.56 | 2.00 |
aLengths of the test segments during open perfusion experiments derived from references (4,5,44–49)
b,e x i, jejunum and x i, ileum, are the assumed positions (with respect to the DJF) of the proximal portion of the test segment of the tube employed during the single-pass open perfusion studies; this position was needed to calculate the mSA according to M2 (Eq. 5)
c,eFor the estimation of the mSA, the jejunal and ileal radii were assumed as 1.75 and 1.5 cm, respectively, as per references (4,5)
For the analysis, Peff,i values derived using the SA according to M1 were considered as the control values, whereas for the other two methods regional Peff values were considered as “intrinsic” values, Peff,int(i,k), where the subscript i stands for the region (jejunum or distal ileum) and the subscript k refers to the mSA calculation method. To support the hypothesis of the existence of a relatively similar Peff,int along the membrane of the GI tract, regional Peff values were contrasted in order to identify possible similarities between Peff along the SI, i.e. jejunal vs ileal. It is worth noting that Peff,int is not intended to represent pure membrane permeability (Pm) (50); instead, as for Peff, Peff,int is a lumped parameter involving several permeation mechanisms (2,17–19).
The evaluation of the agreement was done by visual inspection, i.e. comparing the plots between the regional Peff values for each method, and by calculation of error metrics such as: the average fold error (afe), for measuring bias (over/underprediction); the absolute average fold error (aafe), for measuring absolute spread between the values, and the concordance correlation coefficient (ccc), as a measure of their agreement. The metrics were calculated as described in a previous report (51), where a good agreement between Peff values was considered when both the afe and aafe were within the twofold error, i.e. afe between 0.5 and 2, and aafe less than 2. For the ccc, a moderate equivalence (ccc greater than 0.90 (52)) was considered as good agreement between regional Peff values.
The Use of Jejunal Peff,int(k) for the Prediction of Distal Absorption
In the same line as described above, the ability to predict the observed ileal absorption clearance (CLabs, ileal(observed)) using the aforementioned jejunal Peff, jejunum(k) values (derived from single-pass perfusion experiments) combined with ileal mSA data was also evaluated. The observed absorption clearance (CLabs, ileal(observed)) was derived from the absorption data reported in the original references of the single-pass perfusion experiments (44–49). This was calculated as per Eq. 7
| 7 |
where Qin is the perfusate flow rate (volume/time) and Cin,ileum and Cout,ileum are the water transport-corrected concentrations of drug entering and leaving the ileal segment. The detailed calculation method is shown in Section 3 of the Supplementary Material. The predicted ileal absorption clearance (CLabs, ileum(predicted)) was estimated according to Eq. 8
| 8 |
where Peff,int (jejunum, k) is the jejunal Peff,int, estimated by any of the aforementioned mSA calculation methods (k), and mSAileum(k) is the corresponding ileal mSA. The surface area values employed for such calculation are shown in Table I.
The predictions were evaluated, in terms or accuracy and precision, by visual inspection and by using the same error metrics, and criteria for success, as the one described above for the comparison between Peff values.
Development of a Semi Mechanistic-PBPK Model for the Prediction of the Regional Fraction Absorbed
To further explore the possibility of using Peff,int(k) for the predictions of the regional drug absorption, a semi-mechanistic PBPK model was developed. The new model, or minimal segmented absorption and transit (mSAT) model, is based on the compartmental absorption and transit (CAT) model developed by Yu and co-workers (31–33). However, the mSAT model describes the human GI tract by means of five physiologically defined GI compartments: stomach, duodenum, jejunum, ileum and ascending colon, as shown in Figure S2 of the Supplementary material. These five compartments are the minimal number of compartments required to represent the GI tract, considering all the small-intestinal segments involved in drug absorption following oral administration: hence the terms “minimal” and “segmented”.
Several assumptions were made for the estimation of GI drug absorption following oral dosing when using the mSAT model in this study, including: (a) no significant absorption can occur from the stomach (33); (b) the drug is emptied from the stomach by means of a first-order process (53–55); (c) drug release and dissolution are instantaneous (unless stated differently), and—as in the first development of the CAT model—no precipitation and/or changes in solubility due to differences in luminal pH or bile salts were included in this version of the mSAT model (31–33); (d) all the GI compartments are well mixed, and the drug concentration is homogenous within each GI compartment (31–33); (e) the lengths of each of the intestinal compartment are representative of their anatomy (23,40); (f) drug transit between the small-intestinal compartments is related to the segment’s anatomical length (23,40) and the mean small-intestinal transit time (SITT) (31,32,56); (g) drug absorption occurs only by means of non-saturable processes, where only the dissolved drug can be absorbed (2); (h) there is no drug degradation in the GI lumen and (i) the colonic transit is described as a first-order process (57,58). It is clear that these assumptions are valid to make when the regional differences in permeation is the main biopharmaceutical parameter affecting both rate and extend of drug absorption.
The mSAT model was implemented in Matlab 2014a as a system of 14 ordinary differential equations (9 in the case of assuming complete and instantaneous release/dissolution) to describe the drug transit and absorption in each of the GI segments. Mass balance equations were implemented in order to estimate the regional and overall fabs. The system was evaluated using Matlab’s ode15s solver for stiff differential equations. The most relevant details of the mSAT model are given below, and the detailed differential equations can be found in the Appendix 1.
The drugs used in the modelling and simulation (M&S) were assumed to be administered as solution. Within the luminal compartments of the mSAT model, the drug mass can be transferred along the segments with no possibility for precipitation. If required for simulations purposes, the drug can be modelled in the solid form (undissolved /unreleased), where the combined drug release and dissolution can be controlled by an empirical first-order release constant, krel. The first order gastric emptying rate constant (kge) was assumed to be 4 h−1, which is the inverse of the reported mean gastric residence time for liquids (53), whereas for the ascending colon, the first-order rate constant (kcol) was assumed to be 0.0667 h−1 (57).
Contrary to the CAT model, the mSAT model describes the SI by only three anatomically defined segments. Thus, in order to optimally describe the drug’s transit along the SI, a non-linear transfer between each of the small-intestinal segments was assumed. The mass (A(t)) transfer from an intestinal segment to its adjacent compartment was described by a Weibull function (Eq. 9)
| 9 |
where A0 is the initial amount of drug in said segment, β is the Weibull shape parameter and αn is a segment-dependent scale parameter. The scale parameter was defined for the nth small-intestinal segment as, an = fn × SITT × γ, where fn is the fractional length of the intestinal segment (with respect to Lsi), SITT is the mean small-intestinal transit time (3.32 h) (32) and γ is a dimensionless coefficient. Selection of the Weibull function for this process was based on its flexibility and similarity to the exponential model when β = 1. A representative differential equation describing the mass (An) transfer between the small-intestinal segments is shown in Eq. 10
| 10 |
where .
The coefficients, β and γ, were found to be 2.01 (CV = 5.6%) and 1.57 (CV = 2.90%), respectively. These were obtained by fitting the system described in Eq. 10 to the data on SITT’s distribution reported by Yu and co-workers (32). The fitting was done using the lsqnonlin function in Matlab 2014a. In addition, to evaluate the performance of the mSAT model to describe the SITT data, a comparison was performed by using different transit models, e.g. three compartment first order, CAT etc. More details about the fitting and the comparison with the alternative models can be found in the Section 4 of the Supplementary Material.
Finally, the segment-specific absorption rate constant (ka,n), necessary to describe the passage of the dissolved drug from the intestinal lumen across the intestinal wall, is shown in Eq. 11
| 11 |
where, Peff,int(k) is the intrinsic effective permeability, determined with the double-balloon technique and calculated as described below, mSAn(k) is the segment’s mSA, determined with any of the methods described previously (k), Vn is the segment’s cylindrical volume and DF is degree of flatness coefficient that accounts for the rather elliptical shape of the intestine compared to that a full cylinder (1.7) (59). All the aforementioned system-related input parameters for the mSAT model are summarized in Table S2 of the Supplementary Material.
Prediction of the fabs Using the mSAT Model and Peff,int(k)
The mSAT model was employed to evaluate the use of Peff,int (k) for the prediction of fabs, in particular when colonic absorption was considered. This approach also served as validation of the mSAT model for such predictions. The analysis was performed on 10 drugs whose Peff values were determined using the double-balloon technique (Table II) (3,33). Peff,int (k) was derived from Peff data, by multiplying it by the cylindrical SA of the jejunal segment where the double-balloon segment was positioned (SALoc-I-Gut), and then dividing it by the available jejunal mSA estimated by any of the methods (k) for the same segment. The length of the test segment (LLoc-I-Gut) was assumed 10 cm and the jejunal radius (rjej,Loc-I-Gut) was assumed as 1.75 cm. Thus, SALoc-I-Gut was estimated as 109.96 cm2 (2 × π × 1.75 cm × 10 cm), as shown in Eq. 12
| 12 |
Table II.
Intestinal Permeability Values (Double-Balloon Technique) Employed for the Prediction of f abs Using the mSAT Model
| Compound | BCS classa | P eff,int (M1) b(×10−4 cm/s) | P eff,int (M2) c(×10−4 cm/s) | P eff,int (M3) d(×10−4 cm/s) |
|---|---|---|---|---|
| Enalaprilat | 3 | 0.22 | 0.0008 | 0.0012 |
| Furosemide | 4 | 0.31 | 0.0010 | 0.0016 |
| Terbutaline | 3 | 0.50 | 0.0017 | 0.0026 |
| Atenolol | 3 | 0.53 | 0.0018 | 0.0028 |
| Metoprolol | 1 | 1.50 | 0.0052 | 0.0079 |
| Propranolol | 1 | 2.69 | 0.0093 | 0.014 |
| Fluvastatin | 1 | 2.81 | 0.0096 | 0.015 |
| Antipyrine | 1 | 5.61 | 0.019 | 0.029 |
| Naproxen | 1 | 8.00 | 0.027 | 0.042 |
| Ketoprofen | 1 | 8.50 | 0.029 | 0.045 |
aBCS classification extracted from reference (4)
b P eff values extracted from reference (33)
c P eff,int values re-calculated from the data in the third column (P eff,int (M1)) using Eq. 12 and the mSA estimated for the test segment used in double-balloon single-pass perfusion experiments; this value was estimated as 3.20 × 104 cm2, as per M2 (Eq. 5). The initial position of the test segment was assumed to be immediately after the DJF (14)
d P eff,int values re-calculated from the data in the third column (P eff,int (M1)) using Eq. 12 and the mSA estimated for the test segment used in double-balloon single-pass perfusion experiments; this value was estimated as 2.09 × 104 cm2, as per M3
Given the calculation method of mSA for the Loc-I-Gut segment according to M3, where SAEF are directly applied to the cylindrical SA, Eq. 12 can be reduced to the following expression (Eq. 13):
| 13 |
where rjej is the jejunal radius, LLoc-I-Gut is the length of the Loc-I-Gut segment and SAEFjejunum is the combined SAEF for the jejunal segment according to M3. Further details about this relationship can be found in Section 6 of the Supplementary Material.
The calculated Peff,int(k) values (Table II) were combined with the physiological parameters described previously in order to predict the overall and regional fabs using the mSAT model, where the main focus was to investigate the impact of allowing (ascending) colonic absorption for the fabs predictions. Due to the importance of the colon for the absorption of MR formulations, the investigation was performed assuming both the administration of a solution and a MR formulation. The MR profile was simulated by assigning a krel of 0.19 h−1 to the first-order release/dissolution model, i.e. 90% of the drug content is expected to be released and dissolved within 12 h of the administration of the dosage form.
The fabs predictions were evaluated by visual inspection and by using the same error metrics and criteria for success as the one described above for the prediction of the ileal CLabs. In addition, the theoretical relationship between fabs and Peff was evaluated for a wide range of simulated Peff values in order to validate the utility of the mSAT model for the prediction of the fabs from Peff data.
RESULTS
Intestinal Surface Area
The results of the total mSA involved in GI absorption are illustrated in Fig. 1b. For a representative human intestine, the surface area available for oral absorption was approximately 0.73, 79 and 98 m2, for M1, M2 and M3, respectively. However, when the classical SA expansion factors were applied to the cylindrical SA (600-fold), the available mSA was considerably greater (435 m2) than the ones estimated by M2 and M3 (Fig. 1b).
The regional variation in intestinal mSA according to all the methods is illustrated in Fig. 1c. Despite being shorter than the ileum, the jejunum displayed the largest mSA of all the small-intestinal segments. Depending on the method (M2 or M3), its mSA was around 35 to 280% higher than that of the ileum, the second biggest contributor in mSA for the SI. The detailed segmental mSA for all the methods can be found in Table S1 of the Supplementary Material.
Similarities in Regional Intestinal Permeability
The estimated jejunal and ileal Peff,int values are summarized in Table III. Due to differences in the mSA values, the magnitude of the Peff,int estimates varied between the estimation methods. However, for all the methods, only small differences between the jejunal and ileal Peff,int values were observed (Fig. 2a–c). This agreement was confirmed by the correlation concordance coefficient between the regional Peff, int values as follows: 0.93, 0.92 and 0.88 for M1, M2 and M3, respectively. The absolute average fold errors, on the other hand, varied between 1.60, 1.62 and 1.83, for M1, M2 and M3, respectively, whereas the average fold errors, varied between 0.95, 1.27 and 1.63, for M1, M2 and M3, respectively. The latter suggest that, for all the methods, the overall differences between jejunal and ileal Peff or Peff,int seems to be consistent and within the twofold error. Yet, when using M2 and M3, the ileal Peff,int tended to be slightly higher than the jejunal counterpart, where the differences were more marked for highly permeable compounds (BCS classes 1 and 2), as shown in Fig. 2(b, c).
Table III.
Regional P eff,int Values (Open Perfusion System) and Prediction of the Ileal Absorption Clearance Estimated by Three Different Methods
| Compound | BCS classa | P eff,int (jejunum) b (×10−4 cm/s) | P eff,int (ileum) b (×10−4 cm/s) | Observedc ileal CLabs (×10−4 cm3/s) | Predictedd ileal CL abs (×10−4 cm3/s) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M1 | M2 | M3 | M1 | M2 | M3 | |||
| Hydrocortisone | 2 | 8.79 | 0.032 | 0.046 | 5.57 | 0.027 | 0.050 | 787 | 1242 | 928 | 724 |
| Triamcinolone acetonide | 2 | 4.16 | 0.015 | 0.022 | 9.94 | 0.049 | 0.090 | 1405 | 588 | 439 | 343 |
| Paracetamol | 1 | 4.79 | 0.018 | 0.025 | 7.17 | 0.036 | 0.065 | 2028 | 1356 | 1012 | 790 |
| Salicylic acid | 1 | 2.67 | 0.011 | 0.014 | 4.12 | 0.024 | 0.037 | 3108 | 2010 | 1500 | 1171 |
| Hydrochlorothiazide | 4 | 0.18 | 0.00079 | 0.0010 | 0.16 | 0.00089 | 0.0014 | 117 | 139 | 104 | 81 |
| Atenonol | 3 | 0.38 | 0.0016 | 0.0020 | 0.27 | 0.0016 | 0.0025 | 206 | 283 | 211 | 165 |
| Furosemide | 4 | 0.48 | 0.0021 | 0.0025 | 0.22 | 0.0013 | 0.0020 | 166 | 365 | 272 | 213 |
| Cimetidine | 3 | 0.77 | 0.0033 | 0.0040 | 0.30 | 0.0017 | 0.0027 | 228 | 580 | 433 | 338 |
| Talinonol | 4 | 0.31 | 0.0012 | 0.0016 | 0.37 | 0.0019 | 0.0034 | 106 | 88 | 66 | 52 |
| Griseofulvine | 2 | 7.47 | 0.028 | 0.039 | 11.57 | 0.057 | 0.10 | 2181 | 1407 | 1051 | 820 |
| Ranitidine | 3 | 1.74 | 0.0066 | 0.0091 | 1.41 | 0.0072 | 0.013 | 400 | 492 | 367 | 287 |
aBCS classification extracted from references (4,5)
bOpen perfusion regional permeability values were re-calculated from references (4,5,44–49) and the mSA values shown in Table I
cObserved regional absorption clearances were re-calculated from references (4,5,44–49) employing a parallel tube model (Eq. 7); the details for the calculations can be found in the Section 2 of the Supplementary Material
dPredicted values from Eq. 8, using jejunal P eff data derived by the open perfusion system and ileal mSA data from Table I
Fig. 2.
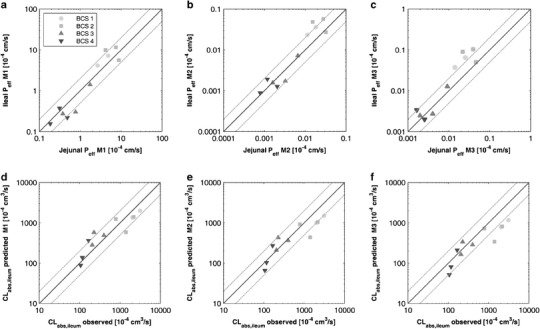
Upper panel, comparison between jejunal P eff,int calculated by: a M1 (cylindrical SA), b M2 (mSA according to Wilson’s method) and c M3 (mSA according to Helander and Fändriks’ method). Lower panel, prediction of ileal absorption clearance (permeability clearance) employing jejunal P eff and ileal surface area using: d M1, e M2 and f M3. Solid light circles, BCS class 1; solid light squares, BCS class 2; solid dark upper triangles, BCS class 3; and solid dark lower triangles, BCS class 4. Black solid line represents the line of unity, whereas the dashed grey lines represent the twofold error
Prediction of Ileal Absorption
The predictions of CLabs,ileal using jejunal Peff,int data and ileal mSA according to Eq. 8 are shown in Table III and Fig. 2d–f. There was good agreement between the observed and predicted CLabs,ileal values, especially for M1 and M2 (Fig. 2e, f). The absolute average fold error between observed and predicted CLabs,ileal was less than twofold for all the methods (1.60, 1.62 and 1.83 for M1, M2 and M3, respectively). However, a general trend towards the underprediction of CLabs,ileal was observed when using M2 and M3 (Fig. 2e, f). This was reflected in an afe of 0.78 and 0.61, for M2 and M3, respectively. In addition, for all the methods, the ccc was slightly less than when the Peff,int values were compared directly; the values varied between 0.88, 0.86 and 0.80, for M1, M2 and M3, respectively. In the same line as for the Peff,int comparisons, the differences between the observed and predicted values were more marked for highly permeable compounds (Fig. 2e, f). This was particularly pronounced when using M3 for the predictions (Fig. 2f). Nevertheless, the overall results suggest that jejunal Peff,int can be used for the prediction the CLabs,ileal, as long as the segment’s mSA is accounted for.
mSAT Model and fabs Predictions
The performance of different transit models to describe the mean SITT data is shown Fig. 3. Both the CAT model (seven transit compartment) and the mSAT model adequately described the mean SITT data. In contrast, the alternative three compartment transit model models showed to be inadequate to describe such data. This confirmed the necessity of introducing a non-linear transfer function, in this case Weibull, in order to adequately describe the mean SITT data when using a different number of transit compartments (other than 7).
Fig. 3.
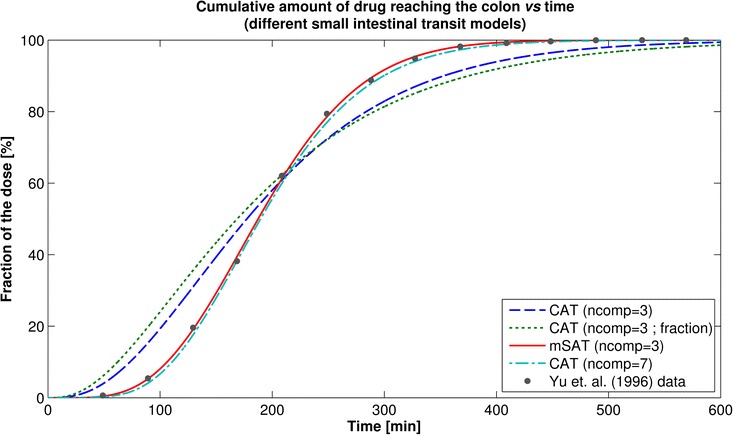
Comparison between different small-intestinal transit models to the describe SITT data. The lines represent the cumulative percentage of the dose reaching the colon for the different SITT models. Red solid line, mSAT model (Weibull transfer between segments); dot- dashed cyan line, full CAT model (seven transit compartments); dashed blue line, CAT model with only three compartments (same first-order transit rate constant for all the segments); dotted green line, CAT model with only three compartments, where the transit was fractionally divided for each segment (based on the segment’s length). The solid dots are the observed cumulative percentage of the dose reaching the colon, as per reference (32)
The fabs predictions using the mSAT model and Peff,int for the 10 drugs listed in Table II are summarized in Fig. 4 and Table IV. When colonic absorption was not allowed in the mSAT model, the predictions using Peff,int either calculated by M1 or M3 were in good agreement with the observed values (Fig. 4a, c). This was supported by the absolute average fold error, correlation concordance coefficient and average fold error as follows: 1.24, 0.90 and 1.21, for M1, and 1.19, 0.95 and 1.11, for M3, respectively. When using Peff,int calculated by M2, however, a general trend towards the underprediction of the fabs was observed (Fig. 4b); the corresponding aafe, ccc and afe were found to be 1.32, 0.88 and 0.83. Despite the aforementioned differences, for all the methods, the overall error (aafe) between the observed and predicted fabs remained less than 1.5-fold, thus confirming the utility of the mSAT model combined with Peff,int for fabs predictions.
Fig. 4.
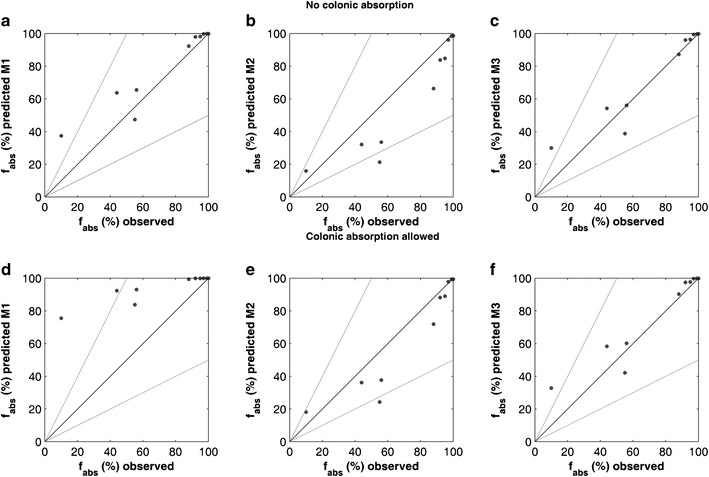
f abs (%) predictions using P eff values from Table II and the mSAT model. Upper panel, no colonic absorption allowed in the mSAT model: a M1 (cylindrical SA), b M2 (mSA according to Wilson’s method), c M3 (mSA according to Helander and Fändriks’ method). Lower panel, colonic absorption allowed in the mSAT model: d M1, e M2 and f M3. Black solid lines represent the line of unity, whereas the dashed grey lines represent the twofold error
Table IV.
Predicted f abs Using the mSAT Model and the P eff,int (Double-Balloon) Values from Table II
| Compound | BCS classa | f abs (%)b observed | Predicted f abs (%) mSAT model [no colonic absorption] | Predicted f abs (%) mSAT model [colonic absorption allowed] | ||||
|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M1 | M2 | M3 | |||
| Enalaprilat | 3 | 10 | 37.4 | 15.9 | 30.0 | 75.5 | 18.2 | 32.8 |
| Furosemide | 4 | 55 | 47.4 | 21.3 | 38.8 | 83.8 | 24.2 | 42.2 |
| Terbutaline | 3 | 44 | 63.7 | 32.1 | 54.2 | 92.4 | 36.2 | 58.3 |
| Atenolol | 3 | 56 | 65.5 | 33.5 | 56.0 | 93.1 | 37.7 | 60.2 |
| Metoprolol | 1 | 88 | 92.4 | 66.4 | 87.3 | 99.4 | 71.9 | 90.3 |
| Propranolol | 1 | 92 | 98.0 | 83.8 | 96.0 | 99.9 | 88.2 | 97.5 |
| Fluvastatin | 1 | 95 | 98.2 | 84.8 | 96.4 | 99.9 | 89.0 | 97.8 |
| Antipyrine | 1 | 97 | 99.7 | 96.1 | 99.4 | 100 | 97.9 | 99.7 |
| Naproxen | 1 | 99 | 99.9 | 98.4 | 99.8 | 100 | 99.3 | 99.9 |
| Ketoprofen | 1 | 100 | 99.9 | 98.7 | 99.8 | 100 | 99.4 | 99.9 |
The outcome changed dramatically when colonic absorption was allowed in the mSAT model (Fig. 4d, e). When employing Peff,int calculated by M1 (cylindrical surface area), the fabs was systematically overpredicted (Fig. 4d). This was reflected in the changes to the ccc (0.33), aafe (1.49) and afe (1.49). Using M2, the predictions were slightly improved compared to that in the previous scenario (Fig. 4bvs e); the ccc changed to 0.91, the aafe to 1.26 and the afe to 0.89. Using M3, however, the predictions remained almost invariant in terms of ccc (0.94), aafe (1.22) and afe (1.15). The simulated relationship between Peff,int and fabs using the mSAT model, for a wider range of Peff,int values, confirmed M3 as the most robust approach for fabs predictions, with and without allowing colonic absorption (Fig. 5).
Fig. 5.
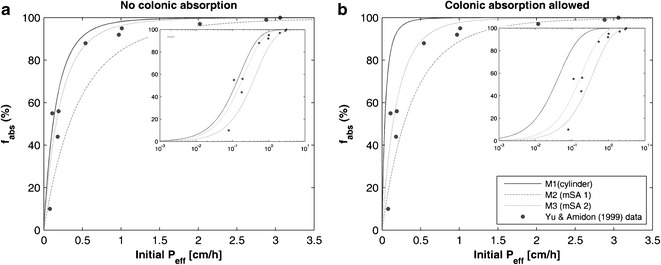
Simulated P eff * to f abs relationship for the mSAT model. a Colonic absorption not allowed. b Colonic absorption allowed. The lines represent different methods for the estimation of P eff,int. Black solid line, M1; grey long-dashed line, M2; and grey short-dashed line, M3. *For M2 and M3, P eff is re-calculated internally by the mSAT model according to the mSA available in the double-balloon segment. The insert shows the same plots in the semi logarithmic scale
Simulated Colonic Contribution to the fabs
The simulated regional intestinal contribution to the overall fabs is shown in Fig. 6a for a set of representative drugs (increasing in permeability): enlaprilat, metoprolol and ketoprofen. All the drugs listed in Table II are shown Figure S5 of the Supplementary Material. From Fig. 6a and Figure S5 it can be observed that for M1, the colonic absorption constituted a significant proportion of the total fabs, especially for lowly permeable drugs (enalaprilat, furosemide, terbutaline and atenolol). This was not the case of the predictions using either M2 or M3, where the colonic contribution to the total fabs remained relatively small compared to that of the overall SI. This was consistent with what is expected for the in vivo colonic fabs given the nature of the colon (35). For the simulated MR profiles, Fig. 6b and Figure S6, the colonic contribution to the total fabs increased gradually with the increase in permeability (for all the methods). For all the drugs listed in Table II, when using M1, the relative colonic contribution to the fabs was higher than for the whole SI combined (Fig. 6b and Figure S6), whereas for M2 and M3, this proportion was dependent upon the permeability value.
Fig. 6.
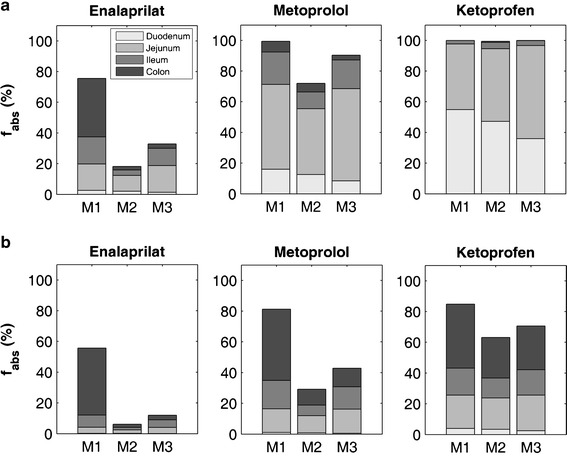
Bar chart of the predicted f abs (overall and regional) using the mSAT model and P eff,int for a subset of representatives drugs from Table II (colonic absorption was allowed). Upper panel (a), drugs assumed to be administered in solution; lower panel (b), drugs assumed to be administered as a MR formulation. Each bar represents a different method for the estimation of the absorption (M1, M2 and M3), whereas the shades of grey indicate the proportion of the contribution to the f abs from each intestinal segment
DISCUSSION
The work performed herein provides a mechanistically sound alternative to the bottom-up estimation of the regional intestinal absorption of drugs administered orally. This approach is based on the rationalization of Peff by the available mSA along the different regions of the human intestine.
As discussed earlier in this manuscript, Peff is an effective property related to the drug passage from the lumen and across the apical intestinal epithelium. Once the intraluminal and intracellular processes are accounted for, Peff itself implicitly encompasses several mechanisms involved in membrane permeation, such as: diffusion through the unstirred water layer, passive transcellular permeation, carrier mediated absorption/secretion and passive paracellular permeation (12,17,60). When Peff is experimentally determined from absorption data (e.g. luminal disappearance rate of the drug), its value is scaled by the SA available in the test segment, usually assuming a cylindrical SA (13). This SA does not reflect all available structures in the SI that might increase the surface area compared to a cylinder, i.e. circular folds, intestinal villi and intestinal microvilli (Fig. 1).
Despite this simplification, Peff, as it is, has been an effective predictor of both the rate and extent the GI absorption (2,16,61). This discrepancy can be explained by the following differential equation that describes the drug absorption from the SI (assuming the SI as single compartment) (1,2):
| 14 |
where Asi,lumen is the amount of drug in the SI’s lumen, SAsi is the SA of the SI and SALoc-i-Gut is the SA of the double-balloon segment. The total mSA of this segment can be represented as: 2 × π × rLIG × LLIG × SAEF. The term SAEF is the combined SA expansion factor due all the aforementioned intestinal structures. For the single compartment case, the main assumption is that the structure of the small-intestinal membrane is relatively the same across the whole length of the SI; therefore, its SA is given by: 2 × π × rsi × Lsi × SAEF. Under this assumption, the SAEF terms cancels out in Eq. 14, so that the intestinal absorption can be predicted from Peff, regardless of SA employed for its estimation (cylindrical vs mucosal). However, when the structure of the membrane is significantly different of that where Peff was measured, i.e. the colon, the latter assumption does not necessarily hold true, and the segment-dependent SAEF has to be considered for the estimation of the intestinal SA and absorption.
Based on this theoretical framework, we hypothesized that when using the mSA for the estimation of Peff, an “intrinsic Peff” (Peff,int) can be obtained which would remain relatively constant along the whole human intestine. Under the aforementioned assumption, the regional differences in absorption should be a product of the variable conditions along the GI tract and the variable nature of the intestinal membrane, where the differences in mSA are assumed to play a major role in defining such differences in absorption. This assumes however that the differences in the membrane composition are relatively small across the human intestine, which might not be necessary true as the small-intestinal and colon membrane have different physicochemical properties (62–64) as well as differences in the mucus layer and UWL composition (65).
To support the approach of employing the mSA differences along the intestine for the estimation of regional GI absorption, the first step was to provide good estimates of the changes in the available mSA along the GI tract. The data from Wilson [36] provided a good starting point for such an approach, whereas the data recently published by Helander and Fändriks (2014) served as an appropriate complement for such estimations (36,39). Both mSA estimation methods assume a decrease in the mSA from the proximal to the distal regions of the GI tract (Fig. 1a). This is consistent with the observed reduction in abundance and length of the circular folds and villi when moving from the proximal towards the distal SI (23,36,39). For instance, when using M2 and M3, the ileal mSA was estimated as 36 and 74% of that of the jejunum, respectively, whereas for M1, this relationship was estimated as 127% (Table S1). In the colonic case, due to the lack of circular folds and villi, the ratio between jejunal and ascending colonic surface area was reduced to 0.4 and 0.3%, for M2 and M3, respectively (Table S1). The total surface area for the SI was around 79 and 98 m2 when estimated using either M2 or M3, respectively. These values were in relatively good agreement with the value of 71 m2 reported by Willmann and co-workers (8). The reported value by Helander and Fändriks [39] was around 30 m2, due to the use of the physiological length of the small intestine in their calculations (291 cm), 43% of the small intestinal length employed in our study (670.7 cm) (39). In contrast, the value of 435 m2 obtained using the classical amplification factors (600-fold) seems to over-estimate the SA of the SI compared to the current estimates (36,39).
Further support for the possible use of Peff,int for the prediction of regional oral absorption was provided by the comparison between regional Peff,int values in Table III. Overall, there was good agreement between jejunal and ileal Peff,int (Fig. 2a–c), especially when using either M1 or M2 methods. A similar scenario was observed when the ileal absorption clearance was predicted using jejunal Peff, int and the ileal mSA (Fig. 2d, f), in line with our hypothesis of the existence of a relatively similar Peff,int along the membrane of the human intestine.
Since both M1 and M2 provided relatively similar results, to this point, the use of Peff,int instead of Peff did not provide any advantage (or disadvantage) for the estimation of regional absorption. The reason for the lack of difference can be explained from the ratio between jejunal and ileal mSA employed for the estimation of CLabs(ileum,k) (Eq. 8): 1.26, for M1, and 1.56, for M2 (Table I). These similarities can be also explained by the similar nature of the intestinal membrane along the human SI; while there are SA differences between the ileum and the upper jejunum, they are not as dramatic as when the SA is compared with, for instance, the colonic membrane. Yet, no direct colonic Peff data is available to perform such comparison (4,5). Further investigations were performed by evaluating the use of Peff,int compared to Peff for the predictions of fabs. This analysis was performed using the newly developed mSAT model. Contrary to the traditional CAT model, where the mass transfer along the SI is described by a series of (seven) transit compartments, all with the same mean residence time (31–33), the mSAT model performs a similar task using only three compartments. These three compartments, however, are physiologically sound, so that the lengths and radii are representative of each one of the small intestinal segments (Tables S1 and S2). In addition, the mean drug (mass) residence time is related to the segment’s length, where the longer the segment, the longer its residence time. This was implemented by assuming a non-linear mass transfer between the segments using a Weibull function (Eq. 10).
Alternative models were also considered in order to describe small-intestinal transit. For example, the data were also fitted by using an equally divided first-order transit rate constant (kt,si = 3 / SITT) in all the segments or by using a proportionally divided transit rate constant (kt,n = 1/fn × SITT), where fn is the fractional length of the small-intestinal segment. However, as shown in Fig. 3, none of these alternative models adequately described the mean SITT data (31). Therefore, the non-linear Weibull transfer implemented in the mSAT model was considered as the best alternative to the full CAT model (Fig. 3).
Under the same assumption as for the CAT model, i.e. no colonic absorption, the fabs predictions using the mSAT model were similar to that of the CAT model using the same validation dataset (33). The agreement between the observed and predicted fabs when using the mSAT model (Fig. 4a–c) suggests that both the mSAT model and Peff,int can be used for the prediction of GI absorption, especially when using the classical approach (Peff) and Peff,int estimated by M3. Yet, when using Peff,int calculated by M2, a systematic underprediction of fabs was observed for almost all the drugs and BCS classes (compared to M1 and M3, as shown in Fig. 4b and Table IV). This underprediction was probably due to the combination of two factors: (a) higher jejunal mSA estimated for the double-balloon segment in M2, and hence lower Peff,int values (Table II), and (b) a decreased mSA in the distal regions of the intestine in M2 when compared to M3 (Table S1).
The main differences between the two methods, classical Peffvs Peff,int, were observed when colonic absorption was included in the simulations (Table IV and Fig. 4d–f). It has been suggested that due to a reduced SA and higher abundance of tight junctions (i.e. assumed smaller paracellular area) in the colonic membrane, intestinal permeability and possibly absorption should be reduced compared to that in the SI (4,5,22,25,66,67). This was appropriately captured when the predictions were made using Peff,int, estimated by both M2 and M3, without affecting the overall fabs predictions (Figs. 4d–f and 6a and Figure S5). In fact, based on the aafe, ccc and afe, the predictions for M3 remained almost unaffected compared to that when colonic absorption was excluded (Fig. 4).
When employing the classical approach for permeability (M1), however, the overall fabs was systematically overestimated; the ccc was reduced by almost two thirds compared to that when colonic absorption was excluded. This overestimation might explain why it is a common practice to assume negligible colonic absorption during PBPK modelling of orally administrated drugs in solution, suspensions or IR formulations (31,33,34). When using Peff,int (M3), however, there is no need to make such assumptions, as the model seems to be able to capture such differences in absorption (Fig. 6a and Figure S5).
The aforementioned assumption has especial implications when it comes to the modelling of oral MR formulations. Current approaches for PBPK modelling of drugs formulated as oral MR involve either the need to perform a sensitivity analysis on the colonic permeability or to optimize it based on observed clinical data (34,68–71). Whereas some drugs have been successfully modelled using jejunal Peff (i.e. M1) as a fixed value along all the GI segments within the PBPK model (72), others might not necessarily benefit from such an approach, due to the inherent risk of overestimations in the fabs, especially for lowly permeable drugs (73). Thus, the use of Preff int seems to be an appropriate alternative during the bottom-up prediction of oral absorption of drugs administered as MR or at least a good starting point (Fig. 6b).
It is clear that reliable regional human intestinal permeability estimates are key for the successful prediction of drug absorption from the distal GI tract and to validate the approach presented herein. Due to the elevated cost of the clinical investigation of regional human Peff, the use of animal models and in vitro systems such as the Ussing chamber combined with excised human intestinal fragments can provide a reliable alternative for such estimates (3,60,65,66,74,75). In addition, one of the main goals of the Pan-European project Oral Biopharmaceutical Tools (OrBiTo), funded by the Innovative Medicines Initiative (IMI), is to provide the necessary information to improve our understanding of how orally administered drugs become absorbed from the GI tract and to generate better in vitro and in silico tools that allow a better prediction of their in vivo performance (http://www.orbitoproject.eu/objectives). Therefore, the aforementioned permeability investigations are part of the main goals of the project (76).
One of the major drawbacks of the newly proposed approach is its dependence on human jejunal in vivo Peff values for the prediction of regional intestinal absorption. Those jejunal Peff values are currently limited to only 30 drugs (3–5). Therefore, its application to drugs not listed in the current datasets depends on the availability of in vivo, in vitro or in silico methods for the prediction of jejunal Peff (59,60,77–82). Due to the use of Peff for this study, regional differences in the transport mechanisms of the drugs involved herein were not explicitly considered (e.g. UWL permeation, carrier-mediated transport, paracellular permeability). Instead, their impact was implicitly accounted for by the use of Peff to derive Peff,int. The latter might limit the application of this approach when such mechanisms are required to be explicitly accounted for the estimation of the overall rate and extent of drug absorption. However, the development of a fully mechanistic model to describe regional intestinal permeability was beyond the scope of this work.
Several simplifications were made during this analysis, one of the most relevant being the assumption of complete dissolution and no precipitation. This assumption might affect the predictions made for drugs whose solubility might limit their oral absorption, i.e. BCS class 2 and 4 drugs. For those drugs, accounting for the GI physiological factors affecting the solubility, dissolution and precipitation along the GI tract is absolutely necessary, especially when it comes to the prediction and understanding of their regional intestinal absorption (4,25,83–85). However, for our simulations, that assumption seemed reasonable as the majority of the drugs listed in Table II can be classified as highly soluble (BCS classes 1 and 3), with the exception of furosemide, which is poorly soluble weak acid (pKa = 3.9), yet its solubility is expected to be high at the intestinal pH range (6–7.4) (85,86).
One of the main advantages of the approach developed in this work (Peff,int) is that, given its simplicity, it can be readily implemented in the current intestinal mechanistic PBPK models. This can be done by means of applying the SAEF to the Peff values determined by the double-balloon technique; this will derive Peff (or Peff,int) values for each intestinal segment. The SAEF coefficients and an example of how to apply them can be found in Section 5 of the Supplementary Material.
CONCLUSION
A new approach for the prediction of regional intestinal absorption was proposed based on the scaling of in vivo-determined jejunal Peff by the available mSA along the human GI tract to derive an intrinsic Peff (Peff, int). This approach was successfully employed for the prediction of the ileal absorption of several structurally diverse compounds. Peff,int was combined with a newly developed semi-mechanistic absorption PBPK model for the prediction of fabs, where the predictions showed a good agreement with the observed data. In addition, the new approach showed to be robust when the colonic absorption was allowed in the PBPK model, by reducing the observed overprediction of fabs when using the classical Peff. Therefore, due to its simplicity, the new approach provides a useful alternative for the bottom-up prediction of oral drug absorption, especially when the distal GI tract plays a crucial role for a drug’s oral absorption.
Electronic supplementary material
(DOCX 2.88 mb)
ACKNOWLEDGMENTS
A.O-M. is recipient of a Ph.D. grant awarded by CONICYT Chile, Chilean Ministry of Education, and a President’s Doctoral Scholar Award from The University of Manchester. The authors would like to acknowledge the fruitful comments and discussions made with members of the Centre for Applied Pharmacokinetic Research (CAPKR) of The University of Manchester. This project is an associated (“sideground”) contribution to the IMI Oral Biopharmaceutical Tools (OrBiTo) project (http://www.imi.europa.eu/content/orbito).
Conflict of Interest
The authors declare no conflict of interest.
APPENDIX 1: mSAT MODEL EQUATIONS
Small-Intestinal Transit:
For the small-intestinal segments, the time-dependent transit rate for the duodenum (duo), jejunum (jej) and ileum (ile) was defined as per Eq. A1, a detailed explanation of the parameters and subscripts is given in the Materials and Methods section of the manuscript.
| A1 |
where kt,n is the time-dependent transit rate constant for the nth small-intestinal segment, defined by a Weibull transfer rate function, w(t)n, β is the Weibull’s shape parameter, fn is the fractional length (with respect to Lsi) of the nth small-intestinal segment, SITT is the mean small-intestinal transit time and γ is a dimensionless coefficient.
Mass transfer equations:
The general differential equations describing the amount of drug in each compartment () are described below (Eqs. A2-A12), where j stands for the drug’s state within the intestinal segment, i.e. solid in the lumen (), dissolved/released in the lumen () and/or absorbed in the intestinal wall (). However, for most of the analysis performed in this work, the drug was assumed to be administered as a solution with no possibility for precipitation.
Stomach (st):
| A2 |
| A3 |
Duodenum (duo), n = 1
| A4 |
| A5 |
| A6 |
Jejunum (jej) and ileum (ile) (n = 2, 3):
| A7 |
| A8 |
| A9 |
Ascending colon (acol):
| A10 |
| A11 |
| A12 |
Contributor Information
Andrés Olivares-Morales, Email: andres.olivaresmorales@manchester.ac.uk.
Hans Lennernäs, Email: hans.lennernas@farmaci.uu.se.
Leon Aarons, Email: leon.aarons@manchester.ac.uk.
Amin Rostami-Hodjegan, Phone: +44 161 3060634, Email: amin.rostami@manchester.ac.uk.
References
- 1.Sinko PJ, Leesman GD, Amidon GL. Predicting fraction dose absorbed in humans using a macroscopic mass balance approach. Pharm Res. 1991;8(8):979–88. doi: 10.1023/A:1015892621261. [DOI] [PubMed] [Google Scholar]
- 2.Amidon GL, Lennernas H, Shah VP, Crison JR. A theoretical basis for a biopharmaceutic drug classification: the correlation of in vitro drug product dissolution and in vivo bioavailability. Pharm Res. 1995;12(3):413–20. doi: 10.1023/A:1016212804288. [DOI] [PubMed] [Google Scholar]
- 3.Lennernas H. Intestinal permeability and its relevance for absorption and elimination. Xenobiotica. 2007;37(10–11):1015–51. doi: 10.1080/00498250701704819. [DOI] [PubMed] [Google Scholar]
- 4.Lennernas H. Human in vivo regional intestinal permeability: importance for pharmaceutical drug development. Mol Pharm. 2014;11(1):12–23. doi: 10.1021/mp4003392. [DOI] [PubMed] [Google Scholar]
- 5.Lennernas H. Regional intestinal drug permeation: biopharmaceutics and drug development. Eur J Pharm Sci. 2014;57:333–41. doi: 10.1016/j.ejps.2013.08.025. [DOI] [PubMed] [Google Scholar]
- 6.Agoram B, Woltosz WS, Bolger MB. Predicting the impact of physiological and biochemical processes on oral drug bioavailability. Adv Drug Deliv Rev. 2001;50(Suppl 1(0)):S41–67. doi: 10.1016/S0169-409X(01)00179-X. [DOI] [PubMed] [Google Scholar]
- 7.Thelen K, Coboeken K, Willmann S, Burghaus R, Dressman JB, Lippert J. Evolution of a detailed physiological model to simulate the gastrointestinal transit and absorption process in humans, part 1: oral solutions. J Pharm Sci. 2011;100(12):5324–45. doi: 10.1002/jps.22726. [DOI] [PubMed] [Google Scholar]
- 8.Willmann S, Schmitt W, Keldenich J, Lippert J, Dressman JB. A physiological model for the estimation of the fraction dose absorbed in humans. J Med Chem. 2004;47(16):4022–31. doi: 10.1021/jm030999b. [DOI] [PubMed] [Google Scholar]
- 9.Jamei M, Marciniak S, Feng K, Barnett A, Tucker G, Rostami-Hodjegan A. The Simcyp population-based ADME simulator. Expert Opin Drug Metab Toxicol. 2009;5(2):211–23. doi: 10.1517/17425250802691074. [DOI] [PubMed] [Google Scholar]
- 10.Sjogren E, Westergren J, Grant I, Hanisch G, Lindfors L, Lennernas H, et al. In silico predictions of gastrointestinal drug absorption in pharmaceutical product development: application of the mechanistic absorption model GI-Sim. Eur J Pharm Sci. 2013;49(4):679–98. doi: 10.1016/j.ejps.2013.05.019. [DOI] [PubMed] [Google Scholar]
- 11.Gertz M, Houston JB, Galetin A. Physiologically based pharmacokinetic modeling of intestinal first-pass metabolism of CYP3A substrates with high intestinal extraction. Drug Metab Dispos. 2011;39(9):1633–42. doi: 10.1124/dmd.111.039248. [DOI] [PubMed] [Google Scholar]
- 12.Lennernas H. Human intestinal permeability. J Pharm Sci. 1998;87(4):403–10. doi: 10.1021/js970332a. [DOI] [PubMed] [Google Scholar]
- 13.Lennernas H, Ahrenstedt O, Hallgren R, Knutson L, Ryde M, Paalzow LK. Regional jejunal perfusion, a new in vivo approach to study oral drug absorption in man. Pharm Res. 1992;9(10):1243–51. doi: 10.1023/A:1015888813741. [DOI] [PubMed] [Google Scholar]
- 14.Knutson L, Odlind B, Hallgren R. A new technique for segmental jejunal perfusion in man. Am J Gastroenterol. 1989;84(10):1278–84. [PubMed] [Google Scholar]
- 15.Knutson T, Fridblom P, Ahlstrom H, Magnusson A, Tannergren C, Lennernas H. Increased understanding of intestinal drug permeability determined by the LOC-I-GUT approach using multislice computed tomography. Mol Pharm. 2009;6(1):2–10. doi: 10.1021/mp800145r. [DOI] [PubMed] [Google Scholar]
- 16.Lennernas H, Lee ID, Fagerholm U, Amidon GL. A residence-time distribution analysis of the hydrodynamics within the intestine in man during a regional single-pass perfusion with Loc-I-Gut: in-vivo permeability estimation. J Pharm Pharmacol. 1997;49(7):682–6. doi: 10.1111/j.2042-7158.1997.tb06092.x. [DOI] [PubMed] [Google Scholar]
- 17.Sugano K, Kansy M, Artursson P, Avdeef A, Bendels S, Di L, et al. Coexistence of passive and carrier-mediated processes in drug transport. Nat Rev Drug Discov. 2010;9(8):597–614. doi: 10.1038/nrd3187. [DOI] [PubMed] [Google Scholar]
- 18.Amidon GL, Kou J, Elliott RL, Lightfoot EN. Analysis of models for determining intestinal wall permeabilities. J Pharm Sci. 1980;69(12):1369–73. doi: 10.1002/jps.2600691204. [DOI] [PubMed] [Google Scholar]
- 19.Fagerholm U, Lennernäs H. Experimental estimation of the effective unstirred water layer thickness in the human jejunum, and its importance in oral drug absorption. Eur J Pharm Sci. 1995;3(5):247–53. doi: 10.1016/0928-0987(95)00027-B. [DOI] [Google Scholar]
- 20.Dahan A, Miller JM, Hilfinger JM, Yamashita S, Yu LX, Lennernas H, et al. High-permeability criterion for BCS classification: segmental/pH dependent permeability considerations. Mol Pharm. 2010;7(5):1827–34. doi: 10.1021/mp100175a. [DOI] [PubMed] [Google Scholar]
- 21.Dahan A, Lennernas H, Amidon GL. The fraction dose absorbed, in humans, and high jejunal human permeability relationship. Mol Pharm. 2012;9(6):1847–51. doi: 10.1021/mp300140h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Watts PJ, Illum L. Colonic drug delivery. Drug Dev Ind Pharm. 1997;23(9):893–913. doi: 10.3109/03639049709148695. [DOI] [Google Scholar]
- 23.International Commission on Radiological Protection. Report of the Task Group on Reference Man: Pergamon Press; 1975.
- 24.Coupe AJ, Davis SS, Evans DF, Wilding IR. Nocturnal scintigraphic imaging to investigate the gastrointestinal transit of dosage forms. J Control Release. 1992;20(2):155–62. doi: 10.1016/0168-3659(92)90161-J. [DOI] [Google Scholar]
- 25.Tannergren C, Bergendal A, Lennernas H, Abrahamsson B. Toward an increased understanding of the barriers to colonic drug absorption in humans: implications for early controlled release candidate assessment. Mol Pharm. 2009;6(1):60–73. doi: 10.1021/mp800261a. [DOI] [PubMed] [Google Scholar]
- 26.Thelen K, Coboeken K, Willmann S, Dressman JB, Lippert J. Evolution of a detailed physiological model to simulate the gastrointestinal transit and absorption process in humans, part II: extension to describe performance of solid dosage forms. J Pharm Sci. 2012;101(3):1267–80. doi: 10.1002/jps.22825. [DOI] [PubMed] [Google Scholar]
- 27.Willmann S, Edginton AN, Kleine-Besten M, Jantratid E, Thelen K, Dressman JB. Whole-body physiologically based pharmacokinetic population modelling of oral drug administration: inter-individual variability of cimetidine absorption. J Pharm Pharmacol. 2009;61(7):891–9. doi: 10.1211/jpp.61.07.0008. [DOI] [PubMed] [Google Scholar]
- 28.Jamei M, Turner D, Yang J, Neuhoff S, Polak S, Rostami-Hodjegan A, et al. Population-based mechanistic prediction of oral drug absorption. AAPS J. 2009;11(2):225–37. doi: 10.1208/s12248-009-9099-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Woltosz WS, Bolger MB, Lukacova V. Modeling of absorption. Methods Mol Biol. 2012;929:313–36. doi: 10.1007/978-1-62703-050-2_13. [DOI] [PubMed] [Google Scholar]
- 30.Carlert S, Lennernas H, Abrahamsson B. Evaluation of the use of Classical Nucleation Theory for predicting intestinal crystalline precipitation of two weakly basic BSC class II drugs. Eur J Pharm Sci. 2014;53:17–27. doi: 10.1016/j.ejps.2013.12.004. [DOI] [PubMed] [Google Scholar]
- 31.Yu LX, Lipka E, Crison JR, Amidon GL. Transport approaches to the biopharmaceutical design of oral drug delivery systems: prediction of intestinal absorption. Adv Drug Deliv Rev. 1996;19(3):359–76. doi: 10.1016/0169-409X(96)00009-9. [DOI] [PubMed] [Google Scholar]
- 32.Yu LX, Crison JR, Amidon GL. Compartmental transit and dispersion model analysis of small intestinal transit flow in humans. Int J Pharm. 1996;140(1):111–8. doi: 10.1016/0378-5173(96)04592-9. [DOI] [Google Scholar]
- 33.Yu LX, Amidon GL. A compartmental absorption and transit model for estimating oral drug absorption. Int J Pharm. 1999;186(2):119–25. doi: 10.1016/S0378-5173(99)00147-7. [DOI] [PubMed] [Google Scholar]
- 34.Kesisoglou F, Wu Y. Understanding the effect of API properties on bioavailability through absorption modeling. AAPS J. 2008;10(4):516–25. doi: 10.1208/s12248-008-9061-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rubinstein A. Colonic drug delivery. Drug Discov Today Technol. 2005;2(1):33–7. doi: 10.1016/j.ddtec.2005.05.021. [DOI] [PubMed] [Google Scholar]
- 36.Wilson JP. Surface area of the small intestine in man. Gut. 1967;8(6):618–21. doi: 10.1136/gut.8.6.618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.DeSesso JM, Jacobson CF. Anatomical and physiological parameters affecting gastrointestinal absorption in humans and rats. Food Chem Toxicol. 2001;39(3):209–28. doi: 10.1016/S0278-6915(00)00136-8. [DOI] [PubMed] [Google Scholar]
- 38.Wilson TH. Intestinal absorption. Philadelphia: W.B. Saunders Company; 1962. [Google Scholar]
- 39.Helander HF, Fändriks L. Surface area of the digestive tract—revisited. Scand J Gastroenterol. 2014;49(6):681–9. doi:10.3109/00365521.2014.898326. [DOI] [PubMed]
- 40.Valentin J. Basic anatomical and physiological data for use in radiological protection: reference values. Ann ICRP. 2002;32(3–4):1–277. doi: 10.1016/S0146-6453(03)00002-2. [DOI] [PubMed] [Google Scholar]
- 41.Hounnou G, Destrieux C, Desme J, Bertrand P, Velut S. Anatomical study of the length of the human intestine. Surg Radiol Anat. 2002;24(5):290–4. doi: 10.1007/s00276-002-0057-y. [DOI] [PubMed] [Google Scholar]
- 42.Sadahiro S, Ohmura T, Yamada Y, Saito T, Taki Y. Analysis of length and surface-area of each segment of the large-intestine according to age, sex and physique. Surg Radiol Anat. 1992;14(3):251–7. doi: 10.1007/BF01794949. [DOI] [PubMed] [Google Scholar]
- 43.Sinclair TS, Jones DA, Kumar PJ, Phillips AD. The microvillus in adult jejunal mucosa—an electron microscopic study. Histopathology. 1984;8(5):739–46. doi: 10.1111/j.1365-2559.1984.tb02390.x. [DOI] [PubMed] [Google Scholar]
- 44.Gramatte T, Oertel R, Terhaag B, Kirch W. Direct demonstration of small intestinal secretion and site-dependent absorption of the [beta]-blocker talinolol in humans [ast] Clin Pharmacol Ther. 1996;59(5):541–9. doi: 10.1016/S0009-9236(96)90182-4. [DOI] [PubMed] [Google Scholar]
- 45.Gramatte T, Richter K. Paracetamol absorption from different sites in the human small intestine. Br J Clin Pharmacol. 1994;37(6):608–11. doi: 10.1111/j.1365-2125.1994.tb04312.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gramatte T, el Desoky E, Klotz U. Site-dependent small intestinal absorption of ranitidine. Eur J Clin Pharmacol. 1994;46(3):253–9. doi: 10.1007/BF00192558. [DOI] [PubMed] [Google Scholar]
- 47.Gramatte T. Griseofulvin absorption from different sites in the human small intestine. Biopharm Drug Dispos. 1994;15(9):747–59. doi: 10.1002/bdd.2510150903. [DOI] [PubMed] [Google Scholar]
- 48.Sutcliffe FA, Riley SA, Kaserliard B, Turnberg LA, Rowland M. Absorption of drugs from the human jejunum and ileum. Br J Clin Pharmacol. 1988;26(2):P206–7. [Google Scholar]
- 49.Schedl HP. Absorption of steroid hormones from the human small intestine. J Clin Endocrinol Metab. 1965;25(10):1309–16. doi: 10.1210/jcem-25-10-1309. [DOI] [PubMed] [Google Scholar]
- 50.Amidon GL, Sinko PJ, Fleisher D. Estimating human oral fraction dose absorbed: a correlation using rat intestinal membrane permeability for passive and carrier-mediated compounds. Pharm Res. 1988;5(10):651–4. doi: 10.1023/A:1015927004752. [DOI] [PubMed] [Google Scholar]
- 51.Musther H, Olivares-Morales A, Hatley OJ, Liu B, Rostami Hodjegan A. Animal versus human oral drug bioavailability: do they correlate? Eur J Pharm Sci. 2014;57:280–91. doi: 10.1016/j.ejps.2013.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.McBride G. A proposal for strength-of-agreement criteria for Lin’s concordance correlation coefficient. NIWA Client Report: HAM2005-062. 2005.
- 53.Yu LX, Amidon GL. Saturable small intestinal drug absorption in humans: modeling and interpretation of cefatrizine data. Eur J Pharm Biopharm. 1998;45(2):199–203. doi: 10.1016/S0939-6411(97)00088-X. [DOI] [PubMed] [Google Scholar]
- 54.Read NW, Al-Janabi MN, Holgate AM, Barber DC, Edwards CA. Simultaneous measurement of gastric emptying, small bowel residence and colonic filling of a solid meal by the use of the gamma camera. Gut. 1986;27(3):300–8. doi: 10.1136/gut.27.3.300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Davis SS, Hardy JG, Fara JW. Transit of pharmaceutical dosage forms through the small-intestine. Gut. 1986;27(8):886–92. doi: 10.1136/gut.27.8.886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Yu LX, Amidon GL. Characterization of small intestinal transit time distribution in humans. Int J Pharm. 1998;171(2):157–63. doi: 10.1016/S0378-5173(98)00174-4. [DOI] [Google Scholar]
- 57.Bouchoucha M, Devroede G, Dorval E, Faye A, Arhan P, Arsac M. Different segmental transit times in patients with irritable bowel syndrome and “normal” colonic transit time: is there a correlation with symptoms? Tech Coloproctol. 2006;10(4):287–96. doi: 10.1007/s10151-006-0295-9. [DOI] [PubMed] [Google Scholar]
- 58.Bouchoucha M, Thomas SR. Error analysis of classic colonic transit time estimates. Am J Physiol Gastrointest Liver Physiol. 2000;279(3):G520–7. doi: 10.1152/ajpgi.2000.279.3.G520. [DOI] [PubMed] [Google Scholar]
- 59.Sugano K. Estimation of effective intestinal membrane permeability considering bile micelle solubilisation. Int J Pharm. 2009;368(1–2):116–22. doi: 10.1016/j.ijpharm.2008.10.001. [DOI] [PubMed] [Google Scholar]
- 60.Lennernas H. Human jejunal effective permeability and its correlation with preclinical drug absorption models. J Pharm Pharmacol. 1997;49(7):627–38. doi: 10.1111/j.2042-7158.1997.tb06084.x. [DOI] [PubMed] [Google Scholar]
- 61.Fagerholm U, Johansson M, Lennernas H. Comparison between permeability coefficients in rat and human jejunum. Pharm Res. 1996;13(9):1336–42. doi: 10.1023/A:1016065715308. [DOI] [PubMed] [Google Scholar]
- 62.Brasitus TA, Dudeja PK. Regional differences in the lipid composition and fluidity of rat colonic brush-border membranes. Biochim Biophys Acta. 1985;819(1):10–7. doi: 10.1016/0005-2736(85)90189-0. [DOI] [PubMed] [Google Scholar]
- 63.Brasitus TA, Dudeja PK. Alterations in the physical state and composition of brush border membrane lipids of rat enterocytes during differentiation. Arch Biochem Biophys. 1985;240(1):483–8. doi: 10.1016/0003-9861(85)90054-2. [DOI] [PubMed] [Google Scholar]
- 64.Brasitus TA, Dudeja PK, Bolt MJ, Sitrin MD, Baum C. Dietary triacylglycerol modulates sodium-dependent D-glucose transport, fluidity and fatty acid composition of rat small intestinal brush-border membrane. Biochim Biophys Acta. 1989;979(2):177–86. doi: 10.1016/0005-2736(89)90433-1. [DOI] [PubMed] [Google Scholar]
- 65.Dahlgren D, Roos C, Sjogren E, Lennernas H. Direct in vivo human intestinal permeability (Peff) determined with different clinical perfusion and intubation methods. J Pharm Sci. 2014 doi: 10.1002/jps.24258. [DOI] [PubMed] [Google Scholar]
- 66.Sjoberg A, Lutz M, Tannergren C, Wingolf C, Borde A, Ungell AL. Comprehensive study on regional human intestinal permeability and prediction of fraction absorbed of drugs using the Ussing chamber technique. Eur J Pharm Sci. 2013;48(1–2):166–80. doi: 10.1016/j.ejps.2012.10.007. [DOI] [PubMed] [Google Scholar]
- 67.Ungell AL, Nylander S, Bergstrand S, Sjoberg A, Lennernas H. Membrane transport of drugs in different regions of the intestinal tract of the rat. J Pharm Sci. 1998;87(3):360–6. doi: 10.1021/js970218s. [DOI] [PubMed] [Google Scholar]
- 68.Johnson TN, Zhou D, Bui KH. Development of physiologically based pharmacokinetic model to evaluate the relative systemic exposure to quetiapine after administration of IR and XR formulations to adults, children and adolescents. Biopharm Drug Dispos. 2014;35(6):341–52. doi: 10.1002/bdd.1899. [DOI] [PubMed] [Google Scholar]
- 69.Watson KJ, Davis J, Jones HM. Application of physiologically based pharmacokinetic modeling to understanding the clinical pharmacokinetics of UK-369,003. Drug Metab Dispos. 2011;39(7):1203–13. doi: 10.1124/dmd.111.038224. [DOI] [PubMed] [Google Scholar]
- 70.Parrott N, Lukacova V, Fraczkiewicz G, Bolger MB. Predicting pharmacokinetics of drugs using physiologically based modeling–application to food effects. AAPS J. 2009;11(1):45–53. doi: 10.1208/s12248-008-9079-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Lukacova V, Woltosz WS, Bolger MB. Prediction of modified release pharmacokinetics and pharmacodynamics from in vitro, immediate release, and intravenous data. AAPS J. 2009;11(2):323–34. doi: 10.1208/s12248-009-9107-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Patel N, Polak S, Jamei M, Rostami-Hodjegan A, Turner DB. Quantitative prediction of formulation-specific food effects and their population variability from in vitro data with the physiologically-based ADAM model: a case study using the BCS/BDDCS Class II drug nifedipine. Eur J Pharm Sci. 2014;57:240–9. doi: 10.1016/j.ejps.2013.09.006. [DOI] [PubMed] [Google Scholar]
- 73.Olivares-Morales A, Kamiyama Y, Darwich AS, Aarons L, Rostami-Hodjegan A. Analysis of the impact of controlled release formulations on oral drug absorption, gut wall metabolism and relative bioavailability of CYP3A substrates using a physiologically-based pharmacokinetic model. Eur J Pharm Sci. 2015;67:32–44. doi: 10.1016/j.ejps.2014.10.018. [DOI] [PubMed] [Google Scholar]
- 74.Lennernäs H, Nylander S, Ungell AL. Jejunal permeability: a comparison between the Ussing chamber technique and the single-pass perfusion in humans. Pharm Res. 1997;14(5):667–71. doi: 10.1023/A:1012121632357. [DOI] [PubMed] [Google Scholar]
- 75.Lennernas H. Animal data: the contributions of the Ussing chamber and perfusion systems to predicting human oral drug delivery in vivo. Adv Drug Deliv Rev. 2007;59(11):1103–20. doi: 10.1016/j.addr.2007.06.016. [DOI] [PubMed] [Google Scholar]
- 76.Lennernas H, Aarons L, Augustijns P, Beato S, Bolger M, Box K, et al. Oral biopharmaceutics tools—time for a new initiative—an introduction to the IMI project OrBiTo. Eur J Pharm Sci. 2014;57:292–9. doi: 10.1016/j.ejps.2013.10.012. [DOI] [PubMed] [Google Scholar]
- 77.Stenberg P, Luthman K, Artursson P. Virtual screening of intestinal drug permeability. J Control Release. 2000;65(1–2):231–43. doi: 10.1016/S0168-3659(99)00239-4. [DOI] [PubMed] [Google Scholar]
- 78.Gertz M, Harrison A, Houston JB, Galetin A. Prediction of human intestinal first-pass metabolism of 25 CYP3A substrates from in vitro clearance and permeability data. Drug Metab Dispos. 2010;38(7):1147–58. doi: 10.1124/dmd.110.032649. [DOI] [PubMed] [Google Scholar]
- 79.Akamatsu M, Fujikawa M, Nakao K, Shimizu R. In silico prediction of human oral absorption based on QSAR analyses of PAMPA permeability. Chem Biodivers. 2009;6(11):1845–66. doi: 10.1002/cbdv.200900112. [DOI] [PubMed] [Google Scholar]
- 80.Tavelin S, Taipalensuu J, Soderberg L, Morrison R, Chong SH, Artursson P. Prediction of the oral absorption of low-permeability drugs using small intestine-like 2/4/A1 cell monolayers. Pharm Res. 2003;20(3):397–405. doi: 10.1023/A:1022699920043. [DOI] [PubMed] [Google Scholar]
- 81.Winiwarter S, Bonham NM, Ax F, Hallberg A, Lennernas H, Karlen A. Correlation of human jejunal permeability (in vivo) of drugs with experimentally and theoretically derived parameters. A multivariate data analysis approach. J Med Chem. 1998;41(25):4939–49. doi: 10.1021/jm9810102. [DOI] [PubMed] [Google Scholar]
- 82.Sun D, Lennernas H, Welage LS, Barnett JL, Landowski CP, Foster D, et al. Comparison of human duodenum and Caco-2 gene expression profiles for 12,000 gene sequences tags and correlation with permeability of 26 drugs. Pharm Res. 2002;19(10):1400–16. doi: 10.1023/A:1020483911355. [DOI] [PubMed] [Google Scholar]
- 83.Schiller C, Frohlich CP, Giessmann T, Siegmund W, Monnikes H, Hosten N, et al. Intestinal fluid volumes and transit of dosage forms as assessed by magnetic resonance imaging. Aliment Pharmacol Ther. 2005;22(10):971–9. doi: 10.1111/j.1365-2036.2005.02683.x. [DOI] [PubMed] [Google Scholar]
- 84.Sutton SC. Role of physiological intestinal water in oral absorption. AAPS J. 2009;11(2):277–85. doi: 10.1208/s12248-009-9087-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Fallingborg J, Christensen LA, Ingeman-Nielsen M, Jacobsen BA, Abildgaard K, Rasmussen HH. pH-profile and regional transit times of the normal gut measured by a radiotelemetry device. Aliment Pharmacol Ther. 1989;3(6):605–13. doi: 10.1111/j.1365-2036.1989.tb00254.x. [DOI] [PubMed] [Google Scholar]
- 86.Granero GE, Longhi MR, Mora MJ, Junginger HE, Midha KK, Shah VP, et al. Biowaiver monographs for immediate release solid oral dosage forms: furosemide. J Pharm Sci. 2010;99(6):2544–56. doi: 10.1002/jps.22030. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX 2.88 mb)


