Abstract
Early numerical proficiency lays the foundation for acquiring quantitative skills essential in today's technological society. Identification of cognitive and brain markers associated with long-term growth of children's basic numerical computation abilities is therefore of utmost importance. Previous attempts to relate brain structure and function to numerical competency have focused on behavioral measures from a single time point. Thus, little is known about the brain predictors of individual differences in growth trajectories of numerical abilities. Using a longitudinal design, with multimodal imaging and machine-learning algorithms, we investigated whether brain structure and intrinsic connectivity in early childhood are predictive of 6 year outcomes in numerical abilities spanning childhood and adolescence. Gray matter volume at age 8 in distributed brain regions, including the ventrotemporal occipital cortex (VTOC), the posterior parietal cortex, and the prefrontal cortex, predicted longitudinal gains in numerical, but not reading, abilities. Remarkably, intrinsic connectivity analysis revealed that the strength of functional coupling among these regions also predicted gains in numerical abilities, providing novel evidence for a network of brain regions that works in concert to promote numerical skill acquisition. VTOC connectivity with posterior parietal, anterior temporal, and dorsolateral prefrontal cortices emerged as the most extensive network predicting individual gains in numerical abilities. Crucially, behavioral measures of mathematics, IQ, working memory, and reading did not predict children's gains in numerical abilities. Our study identifies, for the first time, functional circuits in the human brain that scaffold the development of numerical skills, and highlights potential biomarkers for identifying children at risk for learning difficulties.
SIGNIFICANCE STATEMENT Children show substantial individual differences in math abilities and ease of math learning. Early numerical abilities provide the foundation for future academic and professional success in an increasingly technological society. Understanding the early identification of poor math skills has therefore taken on great significance. This work provides important new insights into brain structure and connectivity measures that can predict longitudinal growth of children's math skills over a 6 year period, and may eventually aid in the early identification of children who might benefit from targeted interventions.
Keywords: cognition, connectivity, development, longitudinal, pediatric, prediction
Introduction
Early numerical abilities provide the foundation for academic and professional success in an increasingly technological society (Reyna et al., 2009; Gerardi et al., 2013). Behavioral research has identified core numerical competencies necessary for mathematical skill acquisition (Siegler, 1998; Geary, 2000), but little is known about neurobiological factors that contribute to long-term gains in children's numerical abilities. Previous attempts to relate brain structure and function to numerical competency have focused on data acquired at a single time point (Rykhlevskaia et al., 2009; Matejko et al., 2013; Price et al., 2013; Rosenberg-Lee et al., 2015). Consequently, the brain bases of individual differences in growth trajectories are unknown. Crucially, establishing neuroanatomical and neurofunctional factors that predict cognitive gains can aid in timely diagnosis and treatment of children at risk for learning disabilities (Gabrieli et al., 2015). Longitudinal designs are essential for addressing this question (Geary, 2011), yet challenges of acquiring brain-imaging data at multiple time points in young children have largely precluded such investigations. Here, for the first time, we identify brain measures that prospectively predict children's longitudinal gains in numerical abilities.
Meta-analyses have identified multiple brain regions involved in numerical cognition (Arsalidou and Taylor, 2011; Menon, 2014): most prominently, the ventrotemporal occipital cortex (VTOC) and posterior parietal cortex (PPC). These posterior brain regions, spanning ventral and dorsal visual pathways, play critical roles in perceptual and semantic aspects of numerical-quantity representation and manipulation (Dehaene et al., 2003; Piazza et al., 2007; Ansari, 2008; Cohen Kadosh et al., 2008; Glezer et al., 2009). Additionally, multiple prefrontal cortex (PFC) regions, including the anterior insula, the ventrolateral PFC (VLPFC), and the dorsolateral PFC (DLPFC) have been implicated in effortful numerical calculation procedures (Kaufmann et al., 2011). Neurodevelopmental studies of numerical cognition have uncovered an anterior-to-posterior shift in brain activation from childhood to adulthood, characterized by decreased reliance on PFC and increased engagement of the VTOC and PPC with increased experience and proficiency (Rivera et al., 2005; Rosenberg-Lee et al., 2011). The cross-sectional nature of extant studies, however, leaves unclear the role of these brain areas in the prediction of long-term outcomes in children's numerical abilities.
We used a unique cohort of 43 children initially scanned at age 8 using structural and functional MRI, and subsequently assessed each child's behavior at multiple time points between ages 9 and 14, to investigate structural and intrinsic functional connectivity measures that predict individual differences in the longitudinal developmental trajectory of numerical skills. Based on prominent neurocognitive models emphasizing the roles of specific VTOC, PPC, and PFC regions in numerical cognition (Dehaene and Cohen, 1995; Ansari, 2008; Menon, 2014), we hypothesized that the structural integrity of these regions at age 8 would predict longitudinal gains in numerical abilities. We then used resting-state fMRI to investigate intrinsic functional circuits linking the regions identified in the structural MRI analysis, testing the hypothesis that the strength of the functional coupling within these regions, as well as the coupling of these regions with other brain circuitry, would also predict longitudinal gains in numerical abilities. We demonstrate that structural integrity and intrinsic functional connectivity of the VTOC, PPC, and PFC specifically predict children's gains in numerical abilities. In contrast, behavioral measures in children at age 8 did not predict longitudinal gains in numerical abilities.
Materials and Methods
Participants
Seventy-nine children (31 females) in second or third grade at entry participated in a longitudinal brain imaging study in which brain-imaging data were acquired at entry and behavioral–cognitive measures were assessed at multiple time points throughout childhood and early adolescence. All participants were right handed, had no history of neurological or psychiatric diseases, and were not taking any medications. Of these, 43 children (mean age, 8.69 years; SD = 0.77; 18 females) had high-quality structural brain-imaging data. Each participant underwent a full neuropsychological battery (see Behavioral assessments, below) as well as structural and resting-state MRI at their first visit. All 43 children returned for a second visit at ages 8–13, 12 children for a third visit at ages 9–13, and 7 children for a fourth visit at ages 11–14. Neuropsychological assessments were readministered at each subsequent visit.
Bilingual ability was not an exclusion criterion of our study. However, we assessed bilingualism via a parent questionnaire, and three of the children included in the behavioral and structural MRI analyses reported fluency in a language other than English (one Spanish, one German, and one Portuguese). None of these three bilingual children met inclusion criteria for the intrinsic functional connectivity analysis.
Behavioral assessments
IQ was assessed with the Wechsler Abbreviated Scale of Intelligence (WASI; verbal IQ: mean, 112.2; SD = 12.39; performance IQ: mean, 111.4; SD = 14.62; Wechsler, 1999). Standardized assessments of academic achievement (i.e., reading and mathematics) were performed using the Wechsler Individual Achievement Test, second edition (WIAT-II; Wechsler, 2001), including subtests in Word Reading (mean, 108.7; SD = 13.52), Reading Comprehension (mean, 106.7; SD = 11.87), Numerical Operations (mean, 102; SD = 15.04), and Math Reasoning (mean, 112.24; SD = 15.16). The Numerical Operations subscale of the WIAT-II was our main measure of interest as it assesses children's ability to identify numerals and solve written calculation problems and equations involving all four basic arithmetic operations (addition, subtraction, multiplication, and division). Our main control was reading, assessed via WIAT-II scores of Word Reading and Reading Comprehension. In addition, we provide further specificity to Numerical Operations by using an additional mathematical problem-solving measure, Mathematical Reasoning. Mathematical Reasoning presents a series of questions to assess children's ability to reason about word problems. Examples of Numerical Operations problems, our measure of interest, include the following: 8 + 5 = _, 7 × 6 = _. An example of a Mathematical Reasoning problem is as follows: “Jeff gave some cookies to five of his friends. He gave three cookies to each friend and had two left over for himself. How many cookies did Jeff have in the beginning?”
Working memory measures included the following subtests from the Working Memory Test Battery for Children (Pickering and Gathercole, 2001): Working Digit Recall (mean, 104.3; SD = 20.33), Block Recall (mean, 92.56; SD = 13.12), Count Recall (mean, 83.38; SD = 17.86), and Backward Digit Recall (mean, 94.14; SD = 16.63). Respectively, these subtests assess phonological loop, visuospatial sketchpad, and central executive components of working memory (Baddeley, 1992).
Growth rate of numerical-skill development
Standardized scores derived from the Numerical Operations subscore of the WIAT-II, which provides a measure of an individual's numerical abilities with performance adjusted for chronological age, were used to assess the rate of change specific to numerical skills. Annualized change (slope of regression line of standardized score vs age) in this measure was calculated based on scores from all neuropsychological assessments, which varied from two to four time points for each subject. The Math Reasoning subscore, which assesses mathematical problem solving, was used as a control measure within the domain of mathematics to ensure the specificity of our findings to basic skills in numerical computation.
Imaging data acquisition
High-resolution whole-brain structural images were obtained for each subject on a General Electric 3T Signa scanner using a 3D T1-weighted spoiled gradient recalled inversion recovery MRI sequence. The following parameters were used: TI = 300 ms; TR = 8.4 ms; TE = 1.8 ms; flip angle, 15°; 22 cm field of view; 132 slices in coronal plane; 256 × 192 matrix; number of excitations, 2; acquired resolution, 1.5 × 0.9 × 1.1 mm. Optimized parameters provided high-quality structural brain images for voxel-based morphometry (VBM) analysis.
During acquisition of resting-state fMRI data, children were instructed to keep their eyes closed and remain still for the duration of the 6 min scan. Whole-brain functional images were acquired using a custom-built head coil with a T2*-sensitive gradient echo spiral-in/spiral-out pulse sequence (based on blood oxygen level-dependent contrast) designed to increase signal-to-noise ratio and reduce signal dropout (Glover and Law, 2001).
Structural MRI data analysis
Voxel-based morphometry.
Structural brain images were visually inspected for quality control and artifact detection before processing. Qualified images were then manually aligned to the conventional anterior commissure–posterior commissure space and the midsagittal plane. Voxelwise cerebral volume was assessed by using an optimized VBM method (VBM8; University of Jena, Germany; http://dbm.neuro.uni-jena.de/vbm). Images were resliced, spatially normalized to the Montreal Neurological Institute (MNI) stereotactic space, and segmented into gray matter, white matter, and CSF. No tissue priors were used for segmentation, per the recommendation of Good et al. (2001) for children and elderly populations. Voxelwise values of gray and white matter images were modulated by the Jacobian determinants derived from spatial normalization and smoothed with a 5 mm isotropic Gaussian kernel.
Smoothed gray matter images were submitted to a second-level multiple-regression analysis to examine the relation between longitudinal trajectory of numerical-skill development and regional morphometry. Annualized change in Numerical Operations standardized score was modeled as the covariate of interest, while controlling for number of neuropsychological visits for each subject. The results were thresholded at a height threshold of p < 0.001 and an extent threshold of p < 0.05 with familywise error (FWE) correction using a nonstationary suprathreshold cluster-size approach based on Monte Carlo simulations (Nichols and Hayasaka, 2003).
Confirmatory cross-validation analysis.
A machine-learning approach with balanced fourfold cross-validation (CV) combined with linear regression (Cohen et al., 2010) was conducted to investigate the robustness of our GLM-derived brain-based predictors of individual differences in the developmental trajectory of numerical skills. Annualized change in Numerical Operations score as a dependent variable and gray matter volume in the regions identified in the VBM analysis as independent variables were treated as inputs to a linear regression algorithm. r(predicted, observed), a measure of how well the independent variable predicts the dependent variable, was first estimated using a balanced fourfold CV procedure. Data were divided into four folds so that the distributions of dependent and independent variables were balanced across folds (Cohen et al., 2010). A linear regression model was built using three folds leaving out the fourth, and this model was then used to predict the data in the left-out fold. This procedure was repeated four times to compute a final r(predicted, observed) representing the correlation between the data predicted by the regression model and the observed data. Finally, the statistical significance of the model was assessed using a nonparametric testing approach. The empirical null distribution of r(predicted, observed) was estimated by generating 1000 surrogate datasets under the null hypothesis that there was no association between changes in numerical skills and brain morphometry.
Intrinsic functional connectivity analysis
Preprocessing.
Resting state fMRI scans were acquired in 40 subjects. Given concerns about movement and data quality in pediatric resting-state fMRI studies (for review, see Power et al., 2015), we carefully examined scans from each participant to ensure high data quality. Ten participants were excluded because of excessive motion, defined as >5 mm maximum displacement. Ten other participants were excluded because of imaging artifacts—gray and white stripes were found in data from six participants and four had a physiological artifact due to respiration that resulted in ring artifacts near the sinus cavity. Functional images from the remaining 20 participants were preprocessed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm) and in-house Matlab scripts. The first eight volumes were discarded to allow for stabilization of magnetic resonance signal. Remaining images were realigned to correct for head motion, corrected for slice timing, resampled to 2 mm voxels, normalized to MNI space, and smoothed with a 6 mm FWHM 3D Gaussian kernel. Finally, voxelwise time series were bandpass filtered in the range of 0.008–0.1 Hz.
Regions of interest selection.
Regions of interest (ROIs) for functional connectivity analyses were generated by placing 6 mm spheres at the cluster peaks (most-significant voxels) from the structural VBM analysis. We also used a control seed within the default mode network (DMN) in the posterior cingulate cortex (PCC) at x = −2, y = −50, z = 28 in MNI coordinates. This location was selected using the peak coordinate in Neurosynth (neurosynth.org) for the search term “default mode.”
Intrinsic functional connectivity and prediction of numerical ability gains.
Intrinsic functional connectivity among ROIs was computed by extracting the mean time series from each ROI, regressing out the global signal computed from gray matter voxels, and computing Pearson correlations among pairwise ROI time series for each participant.
A support vector regression (SVR) analysis was then used to investigate the relationship between intrinsic functional connectivity among the structurally defined seed ROIs and individual trajectories of numerical skills (Vapnik, 1995; Hastie et al., 2009). In this analysis, pairwise resting-state functional connectivity (rsFC) data among all ROIs were entered as features into a linear-kernel SVR model with Numerical Operations slope as the dependent variable. We used a nested leave-one-out CV approach to select the penalty parameter, C, of the SVR model, and subsequently assess the model fit in an unbiased fashion (Varma and Simon, 2006). Under this procedure, each of N data points is held out in turn, and standard leave-one-out CV is performed on the remaining N − 1 samples. The optimal C is chosen based on minimum CV error and the model is trained using the full N − 1 samples then tested on the left-out sample. Model fit is assessed as the R2 between predicted and true values on these left-out samples.
We further investigated whether the intrinsic connectivity of any individual pair of ROIs was statistically predictive of longitudinal numerical skill trajectory using the same balanced fourfold CV procedure detailed above, now entering rsFC as the independent variable.
Seed-based whole-brain intrinsic functional connectivity and prediction of numerical gains.
Following preprocessing, a GLM was implemented in SPM8 to estimate seed-based, whole-brain rsFC maps in each individual for each of the ROIs, which were derived from the morphometric analysis.
Functional connectivity maps were then submitted to a second-level analysis in which connectivity strengths (β-weights estimated in GLM) were used to model longitudinal changes in numerical ability to examine whether the rsFC of these regions is predictive of children's developmental trajectory of numerical skills. Resulting maps were masked using a gray matter image and thresholded at a height of p < 0.01, with FWE corrections for multiple comparisons at the cluster level of p < 0.05 corrected.
Results
Individual variability of longitudinal growth in numerical abilities from ages 8–14
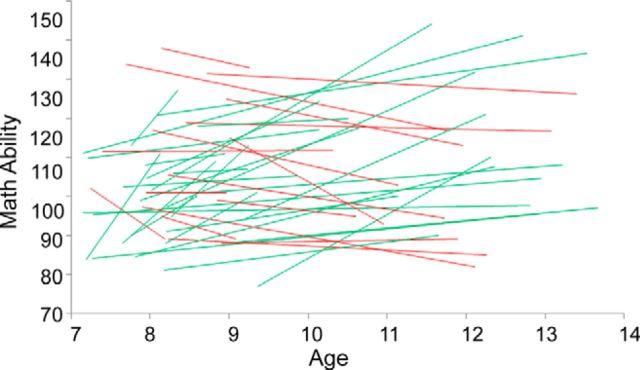
We first examined individual differences in the growth rate of numerical ability development. For each participant, we determined their individual growth rate as the slope obtained from regression analysis of the Numerical Operations subtest of the WIAT-II versus age. Figure 1 shows that children show considerable variation in growth rate of numerical abilities, with rates ranging from −13.79 to 29.07 (mean, 3.16; SD = 8.42).
Figure 1.
Growth curves for individual children's (n = 43) standardized score on the WIAT-II Numerical Operations subtest. Lines depict linear regression of Numerical Operations standardized score versus age across longitudinal visits for each child. Children who made gains relative to their peers over time are plotted in green. Those who declined or remained stable are plotted in red. The annualized change (slopes of individual regression lines) is used in subsequent regression and confirmatory cross-validation analyses.
Initial behavioral measures do not predict longitudinal growth in numerical abilities
We then investigated whether numerical abilities at Time 1 could predict individual longitudinal growth rates. The relationship between Time 1 behavioral measures and the growth rate of numerical abilities was first examined using a conventional correlation analysis. No significant correlations were found between the longitudinal growth in numerical abilities and Time 1 measures of Verbal IQ (r = 0.098, p = 0.534), Performance IQ (r = −0.166, p = 0.288), Word Reading (r = −0.203, p = 0.193), Reading Comprehension (r = −0.232, p = 0.134), Numerical Operations (r = −0.257, p = 0.096), or Math Reasoning (r = −0.287, p = 0.062). Working-memory measures also did not predict growth in numerical abilities (r = −0.1831, p = 0.7930). Although not statistically significant, our behavioral analysis resulted in trends toward negative correlations between Time 1 score in Numerical Operations and Math Reasoning and growth trajectory in Numerical Operations, an observation that might reflect regression to the mean in these measures.
Gray matter volume in the VTOC, PPC, and PFC predict longitudinal growth of numerical abilities
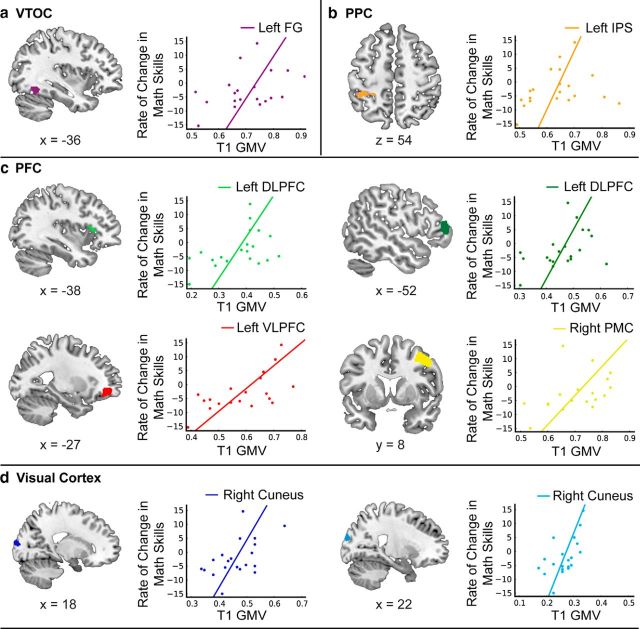
Next we investigated whether longitudinal gains in numerical abilities were associated with gray matter morphometry at the whole-brain level. Regression analysis revealed that higher gray matter volume in the VTOC, PPC, and PFC regions was associated with longitudinal growth of numerical skills. These regions included the left fusiform gyrus (FG), the left intraparietal sulcus (IPS), the left DLPFC, and the left VLPFC (Fig. 2, Table 1). Additionally, the right cuneus and premotor cortex showed a similar effect. Notably, gray matter volume in these regions at Time 1 was not correlated with Time 1 skill in mathematics (Numerical Operations, Math Reasoning), reading (Word Reading, Reading Comprehension), or IQ (Performance, Verbal). This highlights the specificity of our findings with respect to forecasting growth rate over time, and identifies a network of regions predictive of gains in numerical abilities, but not of current ability in any cognitive domain.
Figure 2.
a–d, Structural integrity in regions within (a) VTOC (FG), (b) PPC (IPS), (c) PFC [DLPFC, VLPFC, and pre/primary motor cortex (PMC)], and (d) visual cortex (cuneus) predicts longitudinal gains in numerical abilities. Children with higher volume in these regions at age 8 had steeper growth curves from childhood to adolescence. GMV, Gray matter volume.
Table 1.
Brain areas where structural integrity predicts longitudinal growth in numerical abilitiesa
| Region | Brodmann's area | Number of voxels (mm3) | Peak Z-score | Peak MNI coordinates (mm) |
Math Reasoning | Word Reading | Reading Comprehension | Working memory | ||
|---|---|---|---|---|---|---|---|---|---|---|
| x | y | z | ||||||||
| VTOC | ||||||||||
| Left FG | 37 | 97 | 3.62 | −36 | −58 | −12 | p = 0.14, r = 0.13 | p = 0.99, r = −0.34 | p = 0.14, r = 0.12 | p = 0.84, r = −0.2 |
| PPC | ||||||||||
| Left IPS | 39 | 161 | 3.78 | −42 | −40 | 54 | p = 0.78, r = −0.19 | p = 0.93, r = −0.24 | p = 0.67, r = −0.14 | p = 0.98, r = −0.29 |
| PFC | ||||||||||
| Left DLPFC | 46 | 215 | 3.97 | −52 | 41 | 13 | p = 0.54, r = −0.09 | p = 0.60, r = −0.11 | p = 0.84, r = −0.21 | p = 0.44, r = −0.04 |
| Left DLPFC | 45 | 92 | 3.5 | −40 | 27 | 6 | p = 0.97, r = −0.27 | p = 0.52, r = −0.07 | p = 0.92, r = −0.24 | p = 0.74, r = −0.18 |
| Left VLPFC | 10 | 516 | 4.10 | −27 | 45 | −8 | p = 0.22, r = −0.07 | p = 0.50, r = −0.06 | p = 0.84, r = −0.21 | p = 0.23, r = 0.07 |
| Right pre/primary motor cortex | 6 | 698 | 4.14 | 34 | 8 | 46 | p = 0.007, r = 0.34 | p = 0.32, r = 0.01 | p = 0.05, r = 0.22 | p = 0.67, r = −0.14 |
| Visual cortex | ||||||||||
| Right cuneus | 17 | 551 | 4.27 | 18 | −96 | 13 | p = 0.25, r = −0.05 | p = 0.45, r = −0.05 | p = 0.11, r = 0.16 | p = 0.95, r = −0.27 |
| Right cuneus | 18 | 116 | 3.79 | 22 | −94 | 25 | p = 0.08, r = −0.55 | p = 0.85, r = −0.19 | p = 0.93, r = −0.24 | p = 0.93, r = −0.24 |
aClusters in which gray matter volume is predictive of numerical gains. Math and reading measures are subtests from the WIAT-II. The Working Memory Test Battery for Children was used to measure working memory.
An identical whole-brain VBM analysis with the slope of raw Numerical Operations score with age as a covariate of interest yielded results consistent with these findings. We found the results to overlap with findings from the standardized Numerical Operations score analysis in all clusters—left FG, IPS, DLPFC, and VLPFC; and right cuneus and premotor cortex. Significant clusters from this analysis were also identified in the left DLPFC, insula, anterior temporal lobe, postcentral gyrus, precuneus, cuneus, middle/superior temporal gyrus extending into angular gyrus, and the bilateral superior temporal lobe. Since the aim of our study was to evaluate the trajectory of children's numerical ability relative to their peers, we focused on standardized scores in subsequent analyses. Our approach is identical to one used by Ramsden and colleagues (2011) to characterize individual differences in IQ (standardized scores) across adolescents relative to those of their peers.
We then conducted a confirmatory analysis using linear regression and a balanced fourfold cross-validation procedure to validate findings from the regression analysis. This analysis revealed that gray matter volume in the VTOC, PPC, PFC, and visual cortex clusters identified in the mass univariate analysis were all robustly predictive of longitudinal growth of numerical ability. Notably, gray matter volume in these regions was not predictive of individual gains in Math Reasoning, Word Reading, or working memory (p > 0.05) over time (with the exception of gray matter volume in the premotor cortex, which predicted gains in Math Reasoning; Table 1). Additionally, these findings held when gains in Math Reasoning, Word Reading, and working memory were added as covariates of no interest to the analyses, further highlighting the specificity of our findings with respect to numerical ability.
Intrinsic functional connectivity among the VTOC, PPC, and PFC predicts longitudinal gains in numerical abilities
To test the hypothesis that the integration of multiple cognitive systems is crucial for long-term success in mathematics, we investigated rsFC among all regions in which gray matter volume was associated with longitudinal gains in numerical abilities. In addition to the VTOC, PPC, and PFC regions, this included the cuneus and premotor cortex. Connectivity measures were entered into an SVR prediction model. We found that intrinsic functional connectivity among these structurally identified regions was predictive of individual gains in Numerical Operations (R2 = 0.4439, p = 0.0166), but not in Math Reasoning (R2 = 0.0022, p = 0.8656) or Word Reading (R2 = 0.0039, p = 0. 8152). Notably, balanced cross-validation combined with linear regression on the individual pairwise rsFC links revealed that no single link was predictive of long-term gains. These results highlight the importance of a network of distributed regions in supporting skill development specific to numerical abilities.
Intrinsic functional connectivity of the VTOC is a robust predictor of longitudinal gains in numerical abilities
Finally, we investigated the extent to which functional brain circuits associated with each of the brain regions identified above (FG, IPS, DLPFC, VLPFC, cuneus, premotor cortex) also predicted longitudinal gains. The left FG emerged as the region with the most widespread connectivity as measured by the number of connected target voxels that predicted gains in numerical skills (Fig. 3). Target areas connected to the FG included the left and right dorsolateral PFC, bilateral anterior temporal cortex, precuneus, right cuneus, and caudate (Table 2). Crucially, FG connectivity was not predictive of individual gains in verbally based Math Reasoning, Word Reading, or working memory. Additional control analyses using the PCC node of the DMN revealed that its connectivity with PPC, VTOC, or PFC clusters was not predictive of gains in Number Operations, again highlighting the specificity of the network identified here.
Figure 3.
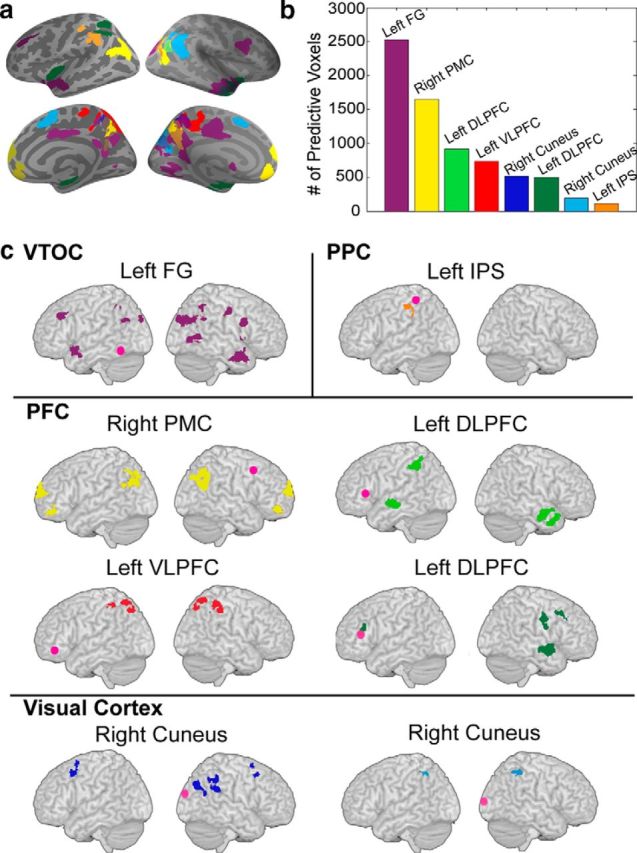
Intrinsic functional connectivity of brain regions identified in the structural MRI analysis predicts gains in numerical abilities. a, b, The FG connectivity map had the most predictive voxels, displayed here in (a) an overlay of all functional connectivity maps and (b) quantified in a bar graph. c, Individual connectivity maps of regions within the VTOC, PPC, PFC, and visual cortex are displayed with the seed shown in pink. ROIs for functional connectivity analyses were generated by placing 6 mm spheres at the cluster peaks (most-significant voxels) from the VBM-based predictive analysis. PMC, Premotor cortex.
Table 2.
Brain regions in which intrinsic functional connectivity with the FG is predictive of gains in numerical skills
| Region | Brodmann's area | Number of voxels (mm3) | Peak Z-score | Peak MNI coordinates (mm) |
||
|---|---|---|---|---|---|---|
| x | y | z | ||||
| VTOC | ||||||
| Right FG | 19 | 752 | 3.77 | 24 | −72 | −2 |
| PPC | ||||||
| Bilateral precuneus | 7 | 141 | 3.62 | 4 | −54 | 46 |
| PFC | ||||||
| Left DLPFC | 46 | 106 | 3.39 | −38 | 28 | 36 |
| Right DLPFC | 44 | 167 | 5.31 | 40 | 8 | 26 |
| Visual cortex | ||||||
| Right cuneus | 18 | 363 | 4.08 | 16 | −88 | 28 |
| Temporal cortex | ||||||
| Right anterior temporal cortex | 21 | 404 | 3.64 | 48 | 6 | −20 |
| Left anterior temporal cortex | 21 | 208 | 3.29 | −50 | 2 | −24 |
| Subcortical | ||||||
| Right basal ganglia (caudate) | 116 | 3.58 | 10 | 8 | 6 | |
| Medial | ||||||
| Mid-cingulate | 23 | 271 | 5.25 | 2 | −8 | 36 |
Discussion
Our study demonstrates that longitudinal cognitive gains in numerical skills from childhood through adolescence can be predicted by the structural integrity of specific regions within the VTOC, PPC, and PFC. Crucially, intrinsic functional connectivity among these regions also predicted gains in numerical skills, suggesting that these regions form a network that supports the development of numerical ability. Notably, these neuroanatomical and neurofunctional predictors were specific to numerical skills, but not reading skills, and no behavioral measure at age 8, including mathematics (Numerical Operations and Mathematical Reasoning), reading, IQ, and working-memory capacity, predicted longitudinal gains in numerical ability. Our findings provide novel evidence for the role of distributed brain structures and their interconnectivity underlying the development of numerical abilities in school-aged children.
Neuroanatomical basis of longitudinal gains in numerical skills
Consistent with our hypothesis, gray matter volume in the IPS subdivision of the PPC as well as the FG subdivision of the VTOC predicted numerical gains (Fig. 2). Interestingly, these effects were localized to the left hemisphere, suggesting that right hemisphere-based visuospatial processes (Pisella et al., 2011) may not be the main source of gains. In contrast to the IPS, the FG is thought to support perceptual representations and visual number form processing (Shum et al., 2013; Abboud et al., 2015). For example, a recent cross-linguistic fMRI study found that perceptual aspects of processing digits and ideographs were associated with FG activation, whereas semantic processing of both symbol types was associated with increased IPS response (Holloway et al., 2013). These results suggest that structural integrity of both VTOC number form-processing areas and PPC areas involved in semantic representations of quantity play crucial roles in guiding development. This finding suggests that structural abnormalities in more “low-level” perceptual-processing regions may play a more important role in the development of children's numerical skills than previously believed, similar to findings in the domain of reading, where children with dyslexia exhibit structural abnormalities in low-level auditory-processing and visual-processing regions preceding anomalies in language regions (Clark et al., 2014). DLPFC and VLPFC regions implicated in working memory and cognitive control were also predictive of gains in numerical skills. Crucially, the structural integrity of these brain areas was not predictive of gains in reading in these same children. Our results thus highlight the domain specificity of neurobiological predictors associated with long-term gains in numerical abilities.
Together these findings suggest that multiple distributed brain areas (Dehaene et al., 2003; Ansari, 2008; Menon, 2014), not just those isolated to the IPS, provide a structural scaffold that supports the development of numerical skills in elementary school children from age 8 into adolescence. The identification of structural biomarkers that predict the developmental trajectory of numerical skills is particularly useful because of its potential for identifying children at risk for developmental learning disabilities years in advance, independent of weaknesses in particular cognitive tasks.
Intrinsic functional connectivity of VTOC, PPC, and PFC gray matter clusters predicts longitudinal gains in numerical abilities
Intrinsic functional connectivity (Menon, 2013) provided novel evidence that a network of brain areas supports the longitudinal development of numerical abilities. We used resting-state fMRI to probe functional connectivity of VTOC, PPC, and PFC areas in which gray matter volume was associated with gains in numerical ability. Multivariate analysis revealed that intrinsic functional connectivity among these areas was strongly predictive of individual gains. Crucially, functional connectivity in this network of brain areas did not predict gains in other cognitive measures. Our findings provide novel evidence that the integrity of functional connections among multiple structurally relevant brain areas provides a supportive architecture for the development of numerical skills and is another potential biomarker of longitudinal numerical gains, independent of specific cognitive tasks. Importantly, our findings identify specific VTOC, PPC, and PFC regions (left FG, IPS, DLPFC, and VLPFC) that work in concert to support the development of numerical competence from an early age.
Multiple functional circuits, including those associated with the VTOC, support longitudinal gains in numerical skills
To further characterize functional circuits associated with gains in numerical abilities, we investigated nodewise connectivity of VTOC, PPC, and PFC areas in which gray matter integrity predicted gains in numerical ability. Intrinsic connectivity of the left FG, within the VTOC, identified the greatest number of voxels and distributed brain areas that predicted gains in numerical ability. This was followed by the three PFC areas—the DLPFC, VLPFC, and premotor cortex. Despite the known importance of the IPS in quantity processing, its whole-brain connectivity pattern identified the least number of voxels that predicted growth in numerical skills (Fig. 3). In contrast, left FG connectivity with multiple brain regions, including bilateral precuneus, anterior temporal cortex, ventrolateral PFC, and caudate showed strong effects, providing further evidence for a distributed brain network that supports individual gains in numerical ability. Left FG links with PPC are particularly noteworthy as numerical problem solving requires dynamic interactions among VTOC areas that support number-form recognition and PPC areas that support semantic aspects of quantity processing and manipulation (Cohen and Dehaene, 2004; Ansari, 2008; Menon, 2014).
It may be surprising that gray matter volume in the left FG and its connectivity to frontoparietal circuitry predicted numerical, but not reading, gains given the link that has been made between dyslexia and low-level perceptual processing regions. However there is evidence for object specificity for many categories (e.g., numbers, faces, places) in addition to words within the FG (Shum et al., 2013; Abboud et al., 2015) and much variability across individuals in the location of these populations of neurons (Glezer and Riesenhuber, 2013). Additionally, the precise location of preferential activity is not static with development (Olulade et al., 2013). Aberrant processing in the occipitotemporal cortex has also been associated with developmental dyscalculia (Rosenberg-Lee et al., 2015), a learning disability that impairs numerical processing, but not always language processing (Ashkenazi et al., 2013). Interestingly, previous work in the reading domain identified gray matter volume and activity (during a rhyme judgment task) of the right FG, but not the left FG, as predictors of later reading achievement (Hoeft et al., 2007).
Brain but not behavioral measures predict growth in numerical abilities
Our multimodal imaging approach revealed structural and functional brain measures predictive of growth in numerical abilities from childhood into adolescence. In contrast, behavioral measures, including mathematical (Numerical Operations and Mathematical Reasoning), reading, IQ, and working memory, did not predict individual trajectories, demonstrating the unique power of neurobiological approaches for forecasting future gains. Previous behavioral research has reported that IQ, processing speed, the central executive component of working memory (Geary, 2011), and proficiency in symbolic number comparison (Bartelet et al., 2014) can predict growth in children's mathematical skills. However, the larger sample sizes in these studies (n = 177 and n = 248, respectively) suggest that brain-imaging measures may be more sensitive predictors of growth in numerical abilities. Supporting this view are studies in the domains of reading and math indicating (1) that a combination model of brain and behavioral metrics is most predictive of language outcome after 6 months (Hoeft et al., 2007); (2) that brain, but not behavioral, metrics are predictive of 2.5 year reading gains in children with dyslexia (Hoeft et al., 2011); and (3) that brain activity during a working-memory task is a better predictor of arithmetic performance than behavior alone (Dumontheil and Klingberg, 2012). Similarly, short-term training studies designed to strengthen numerical and arithmetic skills have also found that neural, but not behavioral, measures predicted learning (Supekar et al., 2013). Extending these findings, our results point to brain measures that predict not just short-term but also long-term gains and have implications for early identification of children who may benefit from targeted cognitive intervention.
Conclusions
Here for the first time, we demonstrate the feasibility of forecasting long-term gains in children's numerical ability based on structural and intrinsic functional brain measures acquired at age 8. We found that the structural integrity of multiple distributed brain areas in the VTOC, PPC, and PFC specifically predicted long-term gains in numerical abilities. Intrinsic connectivity analysis provided strong evidence that the VTOC, PPC, and PFC form a network that works in concert to promote successful numerical-skill acquisition. Intrinsic functional circuits associated with the FG, within the VTOC, had the most extensively connected network that was predictive of gains in numerical ability. Our study identifies brain regions and functional circuits that are markers for the prospective development of numerical skills, and may be potentially relevant for identifying children at risk for learning disabilities.
Footnotes
This work was supported by a Stanford Clinical and Translational Science Award (UL1RR025744) and grants from the National Institutes of Health (HD047520, HD059205, and HD080367), the Child Health Research Institute at Stanford University, the Lucile Packard Foundation for Children's Health, and the Netherlands Organization for Scientific Research (NWO446.10.010). The authors acknowledge the contributions of Anna Swigart for her assistance with data management, and the anonymous reviewers for their valuable comments and suggestions.
References
- Abboud S, Maidenbaum S, Dehaene S, Amedi A. A number-form area in the blind. Nat Commun. 2015;6:6026. doi: 10.1038/ncomms7026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ansari D. Effects of development and enculturation on number representation in the brain. Nat Rev Neurosci. 2008;9:278–291. doi: 10.1038/nrn2334. [DOI] [PubMed] [Google Scholar]
- Arsalidou M, Taylor MJ. Is 2 + 2 = 4? Meta-analyses of brain areas needed for numbers and calculations. Neuroimage. 2011;54:2382–2393. doi: 10.1016/j.neuroimage.2010.10.009. [DOI] [PubMed] [Google Scholar]
- Ashkenazi S, Rosenberg-Lee M, Tenison C, Menon V. Weak task-related modulation and stimulus representations during arithmetic problem solving in children with developmental dyscalculia. Dev Cogn Neurosci. 2012;2(Suppl 1):S152–S166. doi: 10.1016/j.dcn.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashkenazi S, Black JM, Abrams DA, Hoeft F, Menon V. Neurobiological underpinnings of math and reading learning disabilities. J Learn Disabil. 2013;46:549–569. doi: 10.1177/0022219413483174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baddeley A. Working memory. Science. 1992;255:556–559. doi: 10.1126/science.1736359. [DOI] [PubMed] [Google Scholar]
- Bartelet D, Vaessen A, Blomert L, Ansari D. What basic number processing measures in kindergarten explain unique variability in first-grade arithmetic proficiency? J Exp Child Psychol. 2014;117:12–28. doi: 10.1016/j.jecp.2013.08.010. [DOI] [PubMed] [Google Scholar]
- Clark KA, Helland T, Specht K, Narr KL, Manis FR, Toga AW, Hugdahl K. Neuroanatomical precursors of dyslexia identified from pre-reading through to age 11. Brain. 2014;137:3136–3141. doi: 10.1093/brain/awu229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JR, Asarnow RF, Sabb FW, Bilder RM, Bookheimer SY, Knowlton BJ, Poldrack RA. Decoding developmental differences and individual variability in response inhibition through predictive analyses across individuals. Front Hum Neurosci. 2010;4:47. doi: 10.3389/fnhum.2010.00047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen Kadosh R, Lammertyn J, Izard V. Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Prog Neurobiol. 2008;84:132–147. doi: 10.1016/j.pneurobio.2007.11.001. [DOI] [PubMed] [Google Scholar]
- Cohen L, Dehaene S. Specialization within the ventral stream: the case for the visual word form area. Neuroimage. 2004;22:466–476. doi: 10.1016/j.neuroimage.2003.12.049. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Cohen L. Towards an anatomical and functional model of number processing. Math Cogn. 1995;1:83–120. [Google Scholar]
- Dehaene S, Piazza M, Pinel P, Cohen L. Three parietal circuits for number processing. Cogn Neuropsychol. 2003;20:487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- Dumontheil I, Klingberg T. Brain activity during a visuospatial working memory task predicts arithmetical performance 2 years later. Cereb Cortex. 2012;22:1078–1085. doi: 10.1093/cercor/bhr175. [DOI] [PubMed] [Google Scholar]
- Gabrieli JD, Ghosh SS, Whitfield-Gabrieli S. Prediction as a humanitarian and pragmatic contribution from human cognitive neuroscience. Neuron. 2015;85:11–26. doi: 10.1016/j.neuron.2014.10.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC. From infancy to adulthood: the development of numerical abilities. Eur Child Adolesc Psychiatry. 2000;9(Suppl 2):II11–II16. doi: 10.1007/s007870070004. [DOI] [PubMed] [Google Scholar]
- Geary DC. Cognitive predictors of achievement growth in mathematics: a 5-year longitudinal study. Dev Psychol. 2011;47:1539–1552. doi: 10.1037/a0025510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerardi K, Goette L, Meier S. Numerical ability predicts mortgage default. Proc Natl Acad Sci U S A. 2013;110:11267–11271. doi: 10.1073/pnas.1220568110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glezer LS, Riesenhuber M. Individual variability in location impacts orthographic selectivity in the “visual word form area.”. J Neurosci. 2013;33:11221–11226. doi: 10.1523/JNEUROSCI.5002-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glezer LS, Jiang X, Riesenhuber M. Evidence for highly selective neuronal tuning to whole words in the “visual word form area.”. Neuron. 2009;62:199–204. doi: 10.1016/j.neuron.2009.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover GH, Law CS. Spiral-in/out BOLD fMRI for increased SNR and reduced susceptibility artifacts. Magn Reson Med. 2001;46:515–522. doi: 10.1002/mrm.1222. [DOI] [PubMed] [Google Scholar]
- Good CD, Johnsrude IS, Ashburner J, Henson RN, Friston KJ, Frackowiak RS. A voxel-based morphometric study of ageing in 465 normal adult human brains. Neuroimage. 2001;14:21–36. doi: 10.1006/nimg.2001.0786. [DOI] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The elements of statistical learning: data mining, inference, and prediction. New York: Springer; 2009. [Google Scholar]
- Hoeft F, Ueno T, Reiss AL, Meyler A, Whitfield-Gabrieli S, Glover GH, Keller TA, Kobayashi N, Mazaika P, Jo B, Just MA, Gabrieli JD. Prediction of children's reading skills using behavioral, functional, and structural neuroimaging measures. Behav Neurosci. 2007;121:602–613. doi: 10.1037/0735-7044.121.3.602. [DOI] [PubMed] [Google Scholar]
- Hoeft F, McCandliss BD, Black JM, Gantman A, Zakerani N, Hulme C, Lyytinen H, Whitfield-Gabrieli S, Glover GH, Reiss AL, Gabrieli JD. Neural systems predicting long-term outcome in dyslexia. Proc Natl Acad Sci U S A. 2011;108:361–366. doi: 10.1073/pnas.1008950108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holloway ID, Battista C, Vogel SE, Ansari D. Semantic and perceptual processing of number symbols: evidence from a cross-linguistic fMRI adaptation study. J Cogn Neurosci. 2013;25:388–400. doi: 10.1162/jocn_a_00323. [DOI] [PubMed] [Google Scholar]
- Kaufmann L, Wood G, Rubinsten O, Henik A. Meta-analyses of developmental fMRI studies investigating typical and atypical trajectories of number processing and calculation. Dev Neuropsychol. 2011;36:763–787. doi: 10.1080/87565641.2010.549884. [DOI] [PubMed] [Google Scholar]
- Matejko AA, Price GR, Mazzocco MM, Ansari D. Individual differences in left parietal white matter predict math scores on the Preliminary Scholastic Aptitude Test. Neuroimage. 2013;66:604–610. doi: 10.1016/j.neuroimage.2012.10.045. [DOI] [PubMed] [Google Scholar]
- Menon V. Developmental pathways to functional brain networks: emerging principles. Trends Cogn Sci. 2013;17:627–640. doi: 10.1016/j.tics.2013.09.015. [DOI] [PubMed] [Google Scholar]
- Menon V. Handbook of mathematical cognition. Oxford: Oxford UP; 2014. Arithmetic in child and adult brain. [Google Scholar]
- Nichols T, Hayasaka S. Controlling the familywise error rate in functional neuroimaging: a comparative review. Stat Methods Med Res. 2003;12:419–446. doi: 10.1191/0962280203sm341ra. [DOI] [PubMed] [Google Scholar]
- Olulade OA, Flowers DL, Napoliello EM, Eden GF. Developmental differences for word processing in the ventral stream. Brain Lang. 2013;125:134–145. doi: 10.1016/j.bandl.2012.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazza M, Pinel P, Le Bihan D, Dehaene S. A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron. 2007;53:293–305. doi: 10.1016/j.neuron.2006.11.022. [DOI] [PubMed] [Google Scholar]
- Pickering SJ, Gathercole SE. Working memory test battery for children (WMTB-C) London: Psychological; 2001. [Google Scholar]
- Pisella L, Alahyane N, Blangero A, Thery F, Blanc S, Pelisson D. Right-hemispheric dominance for visual remapping in humans. Philos Trans R Soc Lond B Biol Sci. 2011;366:572–585. doi: 10.1098/rstb.2010.0258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Schlaggar BL, Petersen SE. Recent progress and outstanding issues in motion correction in resting state fMRI. Neuroimage. 2015;105:536–551. doi: 10.1016/j.neuroimage.2014.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price GR, Mazzocco MM, Ansari D. Why mental arithmetic counts: brain activation during single digit arithmetic predicts high school math scores. J Neurosci. 2013;33:156–163. doi: 10.1523/JNEUROSCI.2936-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsden S, Richardson FM, Josse G, Thomas MS, Ellis C, Shakeshaft C, Seghier ML, Price CJ. Verbal and non-verbal intelligence changes in the teenage brain. Nature. 2011;479:113–116. doi: 10.1038/nature10514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyna VF, Nelson WL, Han PK, Dieckmann NF. How numeracy influences risk comprehension and medical decision making. Psychol Bull. 2009;135:943–973. doi: 10.1037/a0017327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera SM, Reiss AL, Eckert MA, Menon V. Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cereb Cortex. 2005;15:1779–1790. doi: 10.1093/cercor/bhi055. [DOI] [PubMed] [Google Scholar]
- Rosenberg-Lee M, Barth M, Menon V. What difference does a year of schooling make? Maturation of brain response and connectivity between 2nd and 3rd grades during arithmetic problem solving. Neuroimage. 2011;57:796–808. doi: 10.1016/j.neuroimage.2011.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg-Lee M, Ashkenazi S, Chen T, Young CB, Geary DC, Menon V. Brain hyper-connectivity and operation-specific deficits during arithmetic problem solving in children with developmental dyscalculia. Dev Sci. 2015;18:351–372. doi: 10.1111/desc.12216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rykhlevskaia E, Uddin LQ, Kondos L, Menon V. Neuroanatomical correlates of developmental dyscalculia: combined evidence from morphometry and tractography. Front Hum Neurosci. 2009;3:51. doi: 10.3389/neuro.09.051.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shum J, Hermes D, Foster BL, Dastjerdi M, Rangarajan V, Winawer J, Miller KJ, Parvizi J. A brain area for visual numerals. J Neurosci. 2013;33:6709–6715. doi: 10.1523/JNEUROSCI.4558-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegler RS. Emerging minds: the process of change in children's thinking. New York: Oxford UP; 1998. [Google Scholar]
- Supekar K, Swigart AG, Tenison C, Jolles DD, Rosenberg-Lee M, Fuchs L, Menon V. Neural predictors of individual differences in response to math tutoring in primary-grade school children. Proc Natl Acad Sci U S A. 2013;110:8230–8235. doi: 10.1073/pnas.1222154110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vapnik V. The nature of statistical learning theory. New York: Springer; 1995. [Google Scholar]
- Varma S, Simon R. Bias in error estimation when using cross-validation for model selection. BMC Bioinformatics. 2006;7:91. doi: 10.1186/1471-2105-7-91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wechsler D. Wechsler Abbreviated Scale of Intelligence. San Antonio, TX: The Psychological Corporation; 1999. [Google Scholar]
- Wechsler D. Wechsler Individual Achievement Test. Ed 2. San Antonio, TX: The Psychological Corporation; 2001. [Google Scholar]