Abstract
Recently alpine skis with a wider waist width, which medially shifts the contact between the ski edge and the snow while turning, have appeared on the market. The aim of this study was to determine the knee joint kinematics during turning while using skis of different waist widths (65mm, 88mm, 110mm). Six highly skilled skiers performed ten turns on a predefined course (similar to a giant slalom course). The relation of femur and tibia in the sagital, frontal and coronal planes was captured by using an inertial motion capture suit, and Global Navigation Satellite System was used to determine the skiers’ trajectories. With respect of the outer ski the knee joint flexion, internal rotation and abduction significantly decreased with the increase of the ski waist width for the greatest part of the ski turn. The greatest abduction with the narrow ski and the greatest external rotation (lowest internal rotation) with the wide ski are probably the reflection of two different strategies of coping the biomechanical requirements in the ski turn. These changes in knee kinematics were most probably due to an active adaptation of the skier to the changed biomechanical conditions using wider skis. The results indicated that using skis with large waist widths on hard, frozen surfaces could bring the knee joint unfavorably closer to the end of the range of motion in transversal and frontal planes as well as potentially increasing the risk of degenerative knee injuries.
Key points.
The change in the skis’ waist width caused a change in the knee joint movement strategies, which had a tendency to adapt the skier to different biomechanical conditions.
The use of wider skis or, in particular, skis with a large waist width, on a hard or frozen surface, could unfavourably bring the knee joint closer to the end of range of motion in transversal and frontal planes as well as may potentially increase the risk of degenerative knee injuries.
The overall results of the abduction and internal rotation in respect to turn radii and ground reaction forces indicated that the knee joint movements are likely one of the key points in alpine skiing techniques. However, the skiing equipment used can still significantly influence the movement strategy.
Key words: Abduction, inertial sensor, rotation, ski turn, three-dimensional joint movements
Introduction
Alpine skiing is a popular winter sport on several continents and takes place in a complex natural environment. As in other sports, different injuries also occur in alpine skiing (from now on: skiing). In skiing, the knee is the most frequently injured joint (Brucker et al., 2014; Burtscher et al., 2008; Flørenes et al., 2009). The most common injuries are an injury of the anterior cruciate ligament and medial collateral ligament (Brucker et al., 2014; Flørenes et al., 2009; Paletta and Warren, 1994; Rust et al., 2013). Menisci (Duncan et al., 1995; Pressman and Johnson, 2003) and the lateral collateral ligament (Kim et al., 2012; Paletta and Warren, 1994) are injured less frequently. A correlation has been established in skiing between knee injuries and unexpected events, such as loss of balance, abrupt valgus-external rotation loading and abrupt internal rotational loading on the knee (Bere et al., 2011; Jarvinen et al., 1994; Pressman and Johnson, 2003; Rossi et al., 2003; Shea et al., 2014). For competitive and recreational skiing, the most commonly injured body part was also reported to be outer knee (Urabe et al., 2002). Despite this extensive knowledge about traumatic injuries, the connection between the degenerative changes in the knee joint and skiing under the influence of the varus/valgus malalignment has not yet been examined, although it is known that axial loadings with such malalignments cause such degeneration during walking and daily activities (Levine and Bosco, 2007; Sharma et al., 2001).
In a ski turn, compared to a normal upright posture and looking from the frontal plane perspective, the point of application of the ground reaction force in the more loaded (outside) leg (Vaverka and Vodickova, 2010) moves inwards from beneath the foot towards the ski edge in the medial direction (Figure 1 a-b). This shift of the point of application of the ground reaction force increases with the width of a ski on the assumption that the sinking of the ski edge into the snow is small and/or the snow surface is minimally compressible (Federolf et al., 2010). As the points of application of the ground reaction force acting to the ski-boot-shank system change with the ski width, this might either affect the knee joint loading, or force the subject to adapt the knee joint kinematics. A comparison can be made using a stance on one leg that has a varus deformity in the knee (Levine and Bosco, 2007). Compared to a stance on an anatomically normal leg, the compression force moves in the medial direction, which results in a higher loading on the joint cartilage of the internal compartment and exposes it to faster degeneration (Sharma et al., 2001). The shift of the point of application of the ground reaction force in skiing is particularly important, as the acting force is substantially greater than during normal walking. In a more dynamic type of recreational skiing using carving techniques, the magnitude of ground reaction force was shown to be in the range of 1.5 to 2 body weights (Scheiber et al., 2012), while these forces were substantially higher in competitive skiing (Supej et al., 2004). According to literature, in recreative skiing, the outside leg bears 60–75% of the total ground reaction force during turning (Klous et al., 2012; Scheiber et al., 2012; Spitzenpfeil et al., 2009; Vaverka and Vodickova, 2010).
Figure 1.
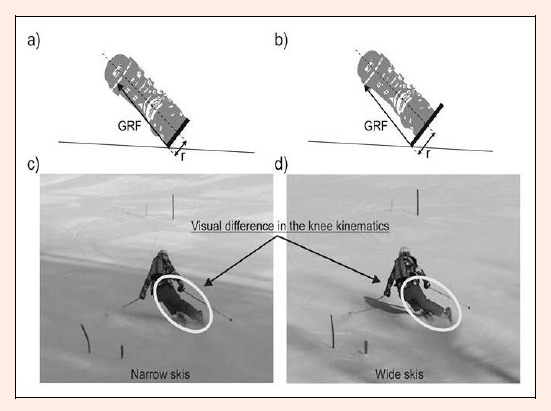
In a turn made on frozen snow, the point of application of the ground reaction force in the case of a wide ski, (b) moves more in the medio-lateral direction from the centre of the foot, compared to the narrow ski (a). The knee-joint kinematics with the wide ski (d) changes visually towards a stronger external rotation and abduction compared to the narrow ski (c).
It is known from the analysed examples of walking that a person adapts to anatomical impairments of the knee joint and the related changes in the position of body segments. One way of achieving that is to modify the movement kinematics, which also includes changing the mediolateral distance between the body’s centre of gravity and the knee joint so as to more favourably distribute the pressures between individual joint compartments (Mündermann et al., 2005). A shift of the knee joint in the mediolateral direction is possible mainly when the knee is flexed, because the loose position of the knee joint allows for some movement in both the valgus/varus direction and the direction of the internal/external rotation (Antolic, 1995; Grood et al., 1988). During skiing, the flexion angles in the knee joint typically range between 30° and 80° where joint abduction and external rotation are principally possible and have been suggested to occur during skiing with both classical and carving skis (Yoneyama et al., 2000).
Therefore, the aim of the study was to establish how the knee-joint kinematics changes during a skiing turn, using skis with different waist widths. More precisely, which knee joint angle movement strategy skiers do apply when the contact between the ski edge and the snow shifts inwards in the medial direction along with an increasing ski width? The hypothesis was that the wider the skis, the higher the occurrence of knee joint abduction and external rotation.
Methods
Subjects
The study sample included six healthy subjects aged between 20 and 30 years (M = 23.33, SD = 3.44), with body height between 1.66 and 1.76 m (M = 1.72, SD = 0.04), and body weight between 60 and 75 kg (M = 65.5, SD = 5.96) who were members of the Slovenian Demo Team as well as former competitors. None of them had ever sustained any knee injury or any other serious injury whatsoever. The study was conducted in compliance with the Helsinki Declaration and approved by the Regional Ethics Committee of the University of Ljubljana. All subjects volunteered for the measurements and had been informed before the measurements about the course of the study. They also signed an informed consent form.
Materials and testing procedures
The subjects used three different pairs of skis with a length of 1.76 m, a sidecut radius of 21.4 m and the same construction properties in terms of the material used and the layer composition. The first type of ski was ‘narrow’, with 65 mm of waist width, the second was ‘medium’ with 88 mm, and the third ‘wide’ with 110 mm (Figure 2, left). The narrowest waist width is in the range used in competitive as well as in recreational skiing while the other two are used only in recreational skiing. All three pairs were prepared identically with the use of computer-aided service machines. The terrain where the measurements took place was medium-demanding with an inclination of 14.5°. Based on a previous observation of the skiing of two of the six subjects using the selected skis, we determined the absolute distances and horizontal displacements of the gates on the terrain in order to ensure safe skiing with the carving technique. To ensure standardized conditions, a predefined course (similar to a giant slalom course) was set up, including 12 turns with horizontal displacements between the gates of 11 m and an absolute distance between the gates of 30 m (right pane of Figure 2). To ensure equal distances and displacements between the gates, the gates were set using a Leica Geosystems 1200 series geodetic high-resolution global satellite navigation system (Leica Geosystems AG, Heerbrugg, Switzerland) and the accompanying ‘Stakeout’ on-board programme. The first and last turns were not included in the analysis. A skier skied straight ahead into the first turn so that by the next turn (included in the analysis) he had already reached sufficient speed that for a technically well-performed carving turn was required (Lešnik and Žvan, 2010). A set of each consecutive three gates from the course setup was also used to assess the lateral inclinations of the slope (Gilgien et al., 2015) with the following outcome: mean lateral inclination was 0.91º (standard deviation (SD) = 3.75º ) with maximum lateral inclination of 5.4º; mean absolute lateral inclination was 3.3º (SD = 1.70º). As the terrain was only minimally inclined transversally, the default setting envisaged all characteristics of the 10 analyzed turns to be practically equal, with the exception of the direction.
Figure 2.
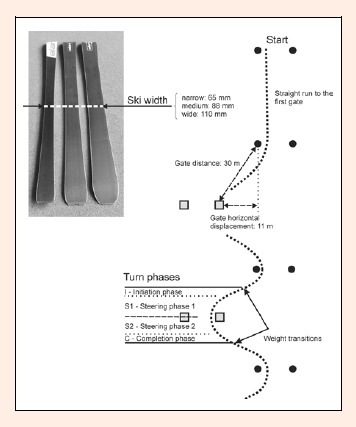
The skis of three different waist width used in the study (left). Gate setup, the scheme of the first turn and the division of the analysed turns in four phases (right).
Each subject made a run with the narrow, medium and wide skis in a random order. Despite the fact that all the skiers had previous experience with medium and wide skis, they also used the opportunity to familiarize themselves with the very same used later in the measurements. In total, 180 turns were captured and analysed. As ruts and grooves can occur on the course and influence the kinematic skiing parameters (Lešnik et al., 2013; Supej et al., 2005b), we divided the measurements into three successive days, with two subjects and a total of six runs per day. The snow surface was prepared every day. Specifically, the surface was compacted and frozen, and the course was fenced for safety reasons. The experimental days were chosen in line with the plan; specifically, it was necessary that the weather and snow conditions remained the same for all three days. Although the snow was hard and frozen, and only six runs were made on the course during a single day, the course was promptly arranged between individual runs by course slippers. Several reference points were additionally marked on the course, using a special snow-marking dye, to indicate the run between the gates. This ensured that the subjects skied along a trajectory that was as close as possible to the trajectories of the other subjects and those resulting from different types of skis.
Full-body three-dimensional motion of the subjects was captured using a fusion between an inertial measurement system and a high-definition and high-frequency Real Time Kinematics Global Navigation Sattelite system (RTK GNSS), similarly as in previous studies (Krüger and Edelmann-Nusser, 2010; Supej, 2010). The same RTK GNSS Leica Geosystems 1200 series (LeicaGeosystems AG, Heerbrugg, Switzerland) was used as in Supej (2010). In comparison to the previous study, in the current study a newer inertial system MVN Biomech. v3.4.1 (Xsens Technologies B.V., Enschede, the Netherlands) was used; it records data with a sampling rate of 120 Hz. The sensors in the newer version were not imbedded in the suit; they were fixed using special straps provided with the system. In addition, there was also a minor improvement in the comparison of the two measurement systems. The antenna position of the RTK GNSS was carefully measured relative to the hips and shoulders in the sagittal plane, similar as in Supej et al. (2013). These measures were thereafter used to model the position of the antenna relative to the trunk of the skier when measurements of the inertial motion capture and RTK GNSS system were combined. In order to facilitate the analysis, the subjects were recorded with a high-frequency Casio Exilim EX-F1 pro video camera (Casio Corp., Tokyo, Japan), capturing 60 images per second at full high-definition resolution.
The standard angles of the knee: flexion/extension, internal/external rotation and abduction/adduction were derived from the inertial motion capture system. The convention of positive signs used in the system was identical to e.g. (Lu et al., 2008; Wilson et al., 2000) where flexion, abduction and internal rotation were considered to be positive (Figure 3). According to previous studies (Cole et al., 1993; Grood and Suntay, 1983), the centre of rotation is assumed to be between the medial and lateral epicondyles. The same is used in the MVN Biomech with the difference that the lateral and medial epicondyles and lateral and medial malleoli are assumed to be at the same height.
Figure 3.
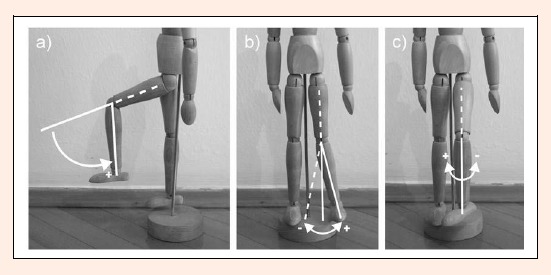
The scheme of knee flexion (a), abduction/adduction (b), and rotation (c). Note that in respect to flexion (a): The larger the number the higher the flexion. In respect to abduction/adduction (b): The positive value represents knee abduction. In respect to rotations (c): The positive value represents knee internal rotation.
The skiers’ paths of skiing using skis of different widths were analysed according to the radii of the curvature of the skis trajectory. They were calculated by fitting arcs and their radii at each point of observation of the outside ski’s trajectory, as explained in previous studies (Supej et al., 2005a; Supej et al., 2008). The difference from previous studies was that for the skis’ trajectory, the heights of the ski, the ski plate, the ski binding and the ski boot were included in the calculations to better derive the actual track of the skis on the snow (i.e. skis trajectory). The ground reaction forces were calculated using the same analogy as presented in an earlier study (Supej et al., 2011). The difference was how the skier’s centre of mass was derived. First, the full-body kinematics was measured with inertial motion capture and an RTK GNSS as described earlier. Second, the segments’ centres of mass were defined by the anthropometric model described by Zatsiorsky et al. (1990) and modified by de Leva (1996). Third, the weights of the ski and measurement equipment have been calculated in the model as follows:
the ski boot’s weight was added to the centre of the mass of each foot,
the weights of the skis, ski plates and ski bindings were added under each foot and centred longitudinally as well as laterally to the midfoot position,
The ski pole’s weight was attached to each hand, where the origin of the ski pole was in the centre of the mass of the hand and thereafter oriented using hand orientation, and
the backpack’s weight (carrying the RTK GNSS system) was added parallel to the trunk with antenna position as described earlier.
The rest of the skiing equipment (i.e. ski clothes) and measurement equipment (i.e. inertial sensors) were weighed for this procedure together with the skier and used as if they were part of the skier’s body weight. The magnitudes of ground reaction forces in the current study are expressed in multiples of body weight (BW).
Using the analogy presented by Müller et al. (1998), the analysed turns were divided into initiation and steering phases (Figure 2), with the subdivisions further described by Supej and Holmberg (2010): First, the initiation phase was restricted to the area where the ski turn radius was above 21.4 m, which was the ski’s sidecut radius. Second, the initiation phase was divided into two consecutive phases (completion and initiation) based on the mean weight transition point, defined as the mean cross-section of the centre of the mass trajectory and the skis’ trajectory, orthogonally projected onto the snow surface. Third, the steering phase was divided based on the turn’s gate position into two parts, namely steering phase 1 and 2 (S1 and S2).
As the duration of a turn and its phases differ with every skier, data on the turns had to be aligned appropriately. To enable a direct and accurate comparison of the motor tasks in individual phases, each of the four phases was separately cubically interpolated instead of being temporally aligned throughout the turn, and then combined in the entire cycle of the turn, from 0% to 100%. For this purpose, the average duration of individual phases of the turn was first calculated based on all measured turns of all runs. This enabled a synchronized comparison of turns in 300 points.
Statistical analysis
The mean and standard deviations of the parameters were calculated at each point of observation along the turn cycle and were thereafter presented in diagrams. The mean and the peak values of these parameters for the turn phases and for the different types of skis were also calculated and were thereafter used for further statistical analysis. The Shapiro-Wilk test was used to test the normality of distributions. In three cases, the samples were not normally distributed. These were remedied with the Box-Cox power transformation. In order to test the differences among the paramaters, one-way ANOVA with repeated measures has been used. Mouchly’s W test indicated that the assumption of sphericity had been violated in all cases. Therefore, the correction was made, according to the epsilon value, with either the Huynh-Feldt or the GreenHouse-Geisser method. For the post hoc analysis, paired sample t-tests were made to test the differences in parameters between separate pairs of skis. The false discovery rate of a family of hypotheses was controlled with the Benjamini–Hochberg–Yekutieli procedure (Benjamini and Yekutieli, 2001). The level of statistical significance was set at p < 0.05. The statistical and kinematic data processing was carried out in the Matlab 7.5 software environment (MathWorks, Natick, MA, USA).
Results
Skiing radius
The mean skiing radii and their standard deviations for all three different pairs of skis are shown in Figure 4. The mean turn radii ranged from 9.1 to 21.4 m in the steering phases and were practically identical using skis of different widths. The shortest mean turn radii were observed between 60% and 70% of the turn cycle. The mean turn radii were kept below 10.5 m between 30 and 80% of the turn cycle. At the same interval, the standard deviations (SD) of the turn radii were around 0.5 m. The SD of the turn radii dropped to zero at the point of the beginning of S1 and at the point of the end of S2 as the consequence of turn phases’ definitions.
Figure 4.
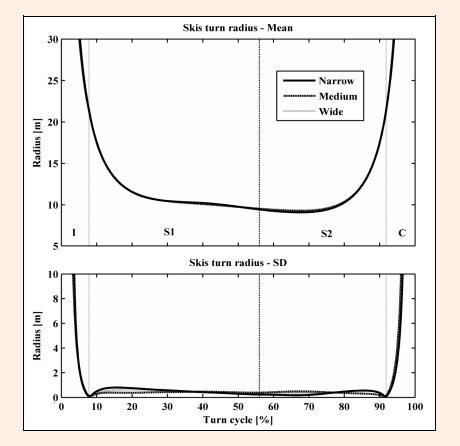
Mean radii of skis along with the standard deviations of three different widths in four phases of the turn: I – initiation phase, S1 – steering phase 1, S2 – steering phase 2, and C – completion phase.
Knee kinematics
The mean knee joint angles in three anatomical planes and their standard deviations are presented in Figures 5-7 for each ski width. In addition, the mean and peak values along with the statistical analysis for each turn phase of these knee joint angles are represented in Tables 1 and 2.
Figure 5.
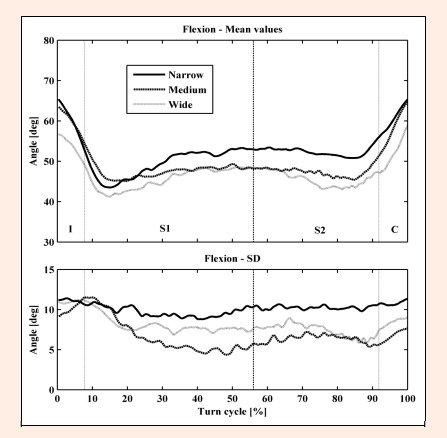
Mean knee flexion on the outside ski along with the standard deviations in four phases of the turn: I – initiation phase, S1 – steering phase 1, S2 – steering phase 2, and C – completion phase.
Figure 6.
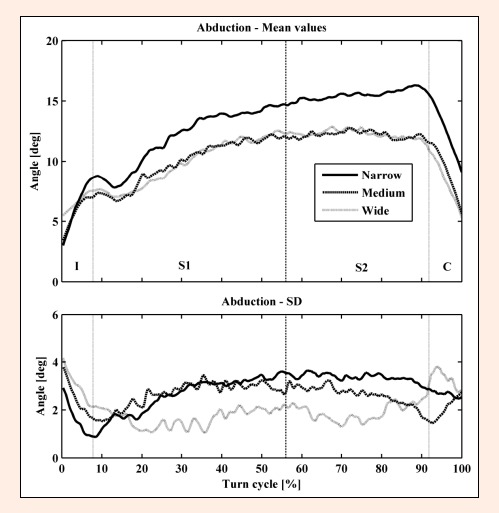
Mean knee abduction on the outside ski along with the standard deviations in four phases of the turn: I – initiation phase, S1 – steering phase 1, S2 – steering phase 2, and C – completion phase. Note: Positive values represent abduction.
Figure 7.
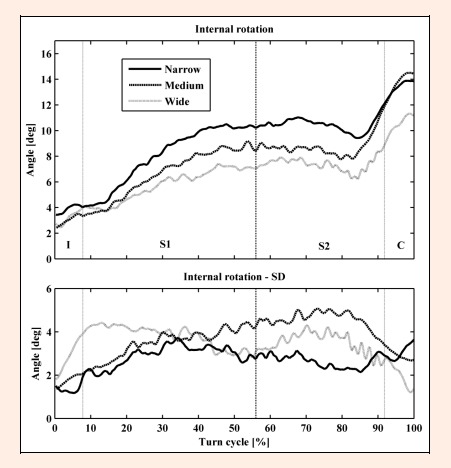
Mean internal rotation of the knee on the outside ski along with the standard deviations in four phases of the turn: I – initiation phase, S1 – steering phase 1, S2 – steering phase 2, and C – completion phase. Note: Positive values represent internal rotation.
Table 1.
Comparison between mean values of all three knee joint angles in four turn phases using skis of three different waist widths. Means and standard deviations (in parentheses) by groups of skis, ANOVA results and paired sample t-tests are presented.
| Joint motion | Turn phases | N angle(°) n=6 | M angle(°) n=6 | W angle(°) n=6 | ANOVA, F statistics | p-sph‡ | Paired sample t-tests§ |
|---|---|---|---|---|---|---|---|
| Abduction | I | 6.3 (1.5) | 5.8 (2.5) | 6.6 (2.9) | 0.94 | 0.38 | NA |
| S1 | 12 (2.6) | 9.9 (2.6) | 9.9 (1.2) | 11.34 | 0.003* | 1,2 | |
| S2 | 15.5 (3.3) | 12.2 (2.6) | 12.3 (1.9) | 18.3 | <0.001* | 1,2 | |
| C | 12.6 (2.6) | 9.3(2) | 8.4 (3.3) | 43.26 | <0.001* | 1,2 | |
| Int. rotation | I | 3.9 (1.2) | 3 (1.8) | 3.2 (2.8) | 1.1 | 0.37 | NA |
| S1 | 8.1 (2.6) | 6.6 (3.4) | 5.7 (3.7) | 7.7 | 0.01* | ||
| S2 | 10.4 (2.6) | 8.7 (4.6) | 7.4 (3.5) | 9.62 | 0.005* | 2,3 | |
| C | 13.3 (3.0) | 13.7 (2.9) | 10.4 (1.9) | 29.7 | <0.001* | 2,3† | |
| Flexion | I | 60 (11.1) | 59.8 (10.1) | 53.7 (10.9) | 6.54 | 0.02* | 2 |
| S1 | 49.5 (9.5) | 47.6 (6.6) | 45.6 (7.9) | 4.9 | 0.06† | 2†,3† | |
| S2 | 52.3 (10.2) | 47.3 (6.3) | 45.6 (7.2) | 12.01 | 0.009* | 1†,2 | |
| C | 60.3 (10.1) | 57.9 (6.3) | 51.8 (7.3) | 8 | 0.024* | 2,3 |
N, narrow skis; M, medium skis; W wide skis
°, degrees; n, numbers of subjects skiing on each skis; I, initiation phase; S1, steering phase 1; S2, steering phase 2; C, completion phase; Int, internal.
*significant (p<0.05) difference,
† trend (0.05≤p≤0.1) of difference
p-sph‡ p-sphericity adjusted (GG:Eps<0.75 HF:Eps>0.75)
§ significance level of p<0.05. Significant difference between three pairs of skis is indicated by numeral: 1, narrow versus medium; 2, narrow versus wide; 3, medium versus wide; NA, not applicable when ANOVA p>0.05
Table 2.
Comparison between means of peak values of all three knee joint angles in four turn phases using skis of three different waist widths. Means and standard deviations (in parentheses) by groups of skis, ANOVA results and paired sample t-tests are presented.
| Joint motion | Turn phases | N angle(°) n=6 | M angle(°) n=6 | W angle(°) n=6 | ANOVA, F statistics | p-sph‡ | Paired sample t-tests§ |
|---|---|---|---|---|---|---|---|
| Abduction | I | 8.6 (.9) | 7.2 (1.7) | 7.7(2) | 7.67 | 0.011* | 1 |
| S1¶ | 15 (3.5) | 12.3 (2.9) | 12.8(2) | 1.71 | 0.232 | NA | |
| S2¶ | 16.9 (3.2) | 13.2 (2.7) | 13.3 (1.8) | 4.92 | 0.034* | ||
| C | 15.6 (2.9) | 11.6 (1.5) | 11.1 (3.1) | 43.48 | <0.001* | 1,2 | |
| Int. rotation | I | 4.7 (1.2) | 3.5(2) | 4.2 (3.7) | 1.1 | 0.352 | NA |
| S1 | 10.8 (3.1) | 9.2 (4.4) | 7.8 (3.4) | 12.07 | 0.008* | ||
| S2 | 12.3 (2.8) | 11.7 (3.5) | 9.2 (3.2) | 16.62 | 0.003* | 2,3 | |
| C | 14.1 (3.3) | 14.8 (2.5) | 11.9 (1.5) | 12.5 | 0.008* | 2†,3 | |
| Flexion | I | 65.4 (11.2) | 63.6 (9.1) | 56.7 (10.9) | 9.06 | 0.002* | 3 |
| S1 | 55.4 (10.3) | 55.2 (9.5) | 50.9 (10.6) | 5.16 | 0.063† | 3 | |
| S2 | 56.7 (10.5) | 51.5 (5.3) | 49.7 (7.2) | 6.97 | 0.031* | 2† | |
| C | 65.3 (11.3) | 64.9 (7.7) | 58.9(9) | 5.91 | 0.05* | 3 |
N, narrow skis; M, medium skis; W wide skis
°, degrees; n, numbers of subjects skiing on each skis; I, initiation phase; S1, steering phase 1; S2, steering phase 2; C, completion phase; Int, internal.
*significant (p<0.05) difference,
† trend (0.05≤p≤0.1) of difference,
p-sph‡, p-sphericity adjusted (GG:Eps<0.75 HF:Eps>0.75),
§ significance level of p<0.05. Significant difference between three pairs of skis is indicated by numeral: 1, narrow versus medium; 2, narrow versus wide; 3, medium versus wide; NA, not applicable when ANOVA p>0.05.
¶ Box – Cox power transformation was performed
The knee flexion of the outside leg ranged between ~ 42° and ~ 66° on average in the case of all ski widths in the analysed turns (Figure 5). Regardless of the waist width, an extension in phase I, a slight flexion in phase S1 and a slightly pronounced flexion in phase C were observed. The standard deviation in the steering phases for flexion ranged from ~ 5 to ~ 11°. The highest standard deviation was demonstrated with the narrow skis. In the phase I, the average knee flexion with the narrow skis was significantly higher than with the wide ones (Table 1). In phase S1, there was a trend of higher flexion with narrow and medium skis in comparison to wide ones. The average knee flexion for the outside narrow ski in phase S2 was significantly higher than that with the wide one. Moreover, there was a trend of higher flexion with narrow skis in comparison to medium ones. In phase C, the average knee flexion was significantly higher with the narrow and medium skis in comparison to the wide ones. The mean peak value of flexion was the highest with narrow skis in phases I and C, where it reached the value of ~ 65° (Table 2). There was statistically significant higher flexion with medium skis in comparison to wide ones in phases I, S1 and C, while there was a trend of higher flexion with narrow skis compared to wide ones in phase S2.
In all phases of the turn, with all skis, the outside knee was on average in abduction (Figure 6). In phase I, the mean abduction first increased and then decreased slightly and then continued to increase through S1-2 until phase C. In phase C, abduction decreased rapidly. The change in the mean abduction was ~ 7° for the wide and medium and ~ 12° for the narrow skis. The standard deviation in the steering phases for abduction ranged from ~1 to ~3.5°. The lowest standard deviation was demonstrated with the widest skis. The mean abduction was significantly lower with the medium and the wide skis in comparison to narrow ones in phases S1, S2 and C (Table 1). The differences between the medium and wide skis were not significant. The mean peak value of abduction was highest (~17°) with narrow skis in phase S2 (Table 2). There was significantly higher abduction with narrow skis compared to the medium ones in phases I and C. In phase C there was also significantly higher abduction with narrow skis compared to the wide ones.
Throughout all the turn phases, with all the skis the outside knee joint was rotated internally (Figure 7). The internal rotation started at ~ 3° in phase I and increased almost throughout the entire turn cycle to ~ 14° (narrow and medium skis) and ~ 11° (wide skis). The standard deviation in the steering phases for internal rotation ranged from ~ 2 to ~ 4°. The lowest standard deviation was demonstrated with the narrow skis. In phases S2 and C, the average knee internal rotation with the wide ski was significantly lower compared to the one with narrow ski (Table 1). In phase C, there was also trend of less internal rotation with wide skis compared to medium ones. The differences in knee rotations between skis in phases I and S1 were not significant. The average maximal values of the outside knee internal rotation of all the skiers in phase S2 was ~ 12° with the narrow skis and ~ 9° with the wide ones (Table 2). The mean peak value of internal rotation was significantly higher with narrow and medium skis compared to the wide ones in phase S2 (Table 2). The mean peak value of internal rotation in the completion phase was also significantly higher with medium skis in comparison to wide ones, while there was a trend of higher internal rotation with narrow skis in comparison to wide ones in the phase C.
Ground reaction forces
The mean values for magnitudes of ground reaction forces (GRF) for each of the ski throughout the turn are represented in Figure 8. In the phases I and C, the weakest GRF were present. At the beginning of phase S1, the GRF rapidly increased and achieved the highest values in S2. From 20–80% of the turn cycle (the majority of phase S1 and S2), the GRF ranged from 1.5–2 times body weight (BW). The mean values in separate phases of the turn for each of the ski along with the statistical analysis are represented in Table 3. There were no statistically significant differences in GRF among different types of skis.
Figure 8.
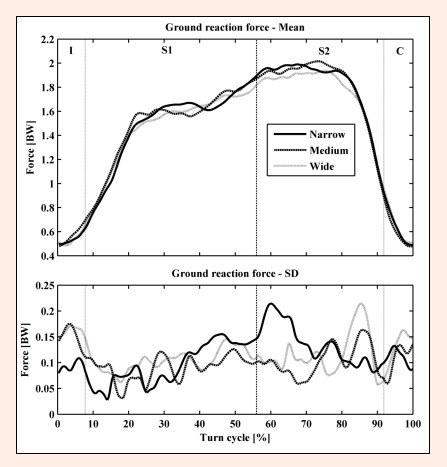
The mean values for magnitudes of ground reaction forces (GRF) for each of the ski throughout the turn along with the standard deviations in four phases of the turn: I – initiation phase, S1 – steering phase 1, S2 – steering phase 2, and C – completion phase. Note: There were no statistically significant differences in GRF among different types of skis.
Table 3.
Mean values of ground reaction force in separate turn phases with three different ski widths. Means and standard deviations (in parentheses) by groups of skis, ANOVA results and paired sample t-tests are presented.
| Turn phases | GRF N (BW) n=6 | GRF M (BW) n=6 | GRF W (BW) n=6 | ANOVA, F statistics | p-sph‡ | Paired sample t-tests§ |
|---|---|---|---|---|---|---|
| I¶ | .54 (.08) | .57 (.15) | .54 (.15) | .36 | .731 | NA |
| S1 | 1.48 (.07) | 1.5 (.03) | 1.47 (.06) | 2.06 | .205 | NA |
| S2 | 1.83 (.1) | 1.83 (.04) | 1.78 (.08) | 3.95 | .044* | |
| C | .64 (.1) | .61 (.09) | .66(1) | 2.1 | .136 | NA |
GRF, ground reaction force; N, narrow skis; BW, body weight; M, medium skis; W, wide skis; n, number of subjects skiing on each skis; I, initiation phase; S1, steering phase 1; S2, steering phase 2; C, completion phase.
*significant (p<0.05) difference,
p-sph‡, p-sphericity adjusted (GG:Eps<0.75 HF:Eps>0.75)
§ significance level of p<0.05. Significant difference between three pairs of skis is indicated by numeral: 1, narrow versus medium; 2, narrow versus wide; 3, medium versus wide; NA, not applicable when ANOVA p>0.05.
¶ Box – Cox power transformation was performed
Discussion
The main finding of the study was that the kinematics of the knee joint in the turn while skiing on a hard snow surface depended on the ski width. More specifically, significantly decreased mean abduction was observed with the medium and wide skis in comparison with the narrow skis in steering phases (S1 and S2) and the completion phase, as well as significantly decreased mean internal rotation when using wide skis in comparison to medium and narrow skis in steering phase S2 and in the completion phase. Generally, over the turn cycle the flexion and abduction of the medium skis behaved similarly to the wide ones, whereas with rotation their value was between the narrow and the wide ones. Neither of the two hypotheses were confirmed directly. However, as it will be explained in the following, the knee joint movement can be argued to behave as initially expected when considering the predicted neutral positions of the abduction and rotation at certain flexion from the literature (Lu et al., 2008; Wilson et al., 2000).
The analysis of the mean turn radii along the turn cycle revealed that there were practically no differences when using skis of different waist widths (Figure 4). This was assured by the pilot study and the consequent selection of the appropriate gate setup as well as additional measures during the experiment, such as marking the track along the course. These similarities guaranteed to a high degree that the measured differences in the knee joint kinematics were mainly the consequence of adaptation to the position to the different ski widths and not because the skiers skied on different trajectories when using the different skis. Furthermore, there were no statistically significant differences in the magnitude of the GRF (normalized to their body mass) between skiers using different skis, which further confirmed the equality of the conditions for all skis (Figure 8).
The analysis of the knee joint movement focused on the outside ski as the bulk of the ground reaction force is applied to it (Scheiber et al., 2012; Vaverka and Vodickova, 2010); furthermore, the outside ski is considered by skiing professionals to be the leading leg while making a turn (Barth, 2011; Held et al., 2002; Howe, 2001; LeMaster, 2009; Lešnik and Žvan, 2010) The relation of femur against tibia in all three planes of the left and right knees of the outside leg in the turn was almost identical in the case of the same skier. Therefore, for every subject in the sample, the outside knee in left and right turns was taken into account so as to obtain a larger and more relevant sample of movement of the knee joint. In contrast, the kinematics of the inside and outside knee in the turn differ (at the last point of the turn, the outside ski is in the phase of shifting to the inside side), which is why it is understandable that the values of the angles in the completion phase of the turn vary from the initial values. Therefore, the values of the first and last points on the graphs of knee angles do not correspond (Figures 5-7).
The flexion of the knee joint was the largest especially in the steering phases when the narrow skis were used (Figure 5). This can be explained by the fact that the skiers avoided the position of deep flexion when using the wide skis because this could further intensify the loading on the thigh muscles by increasing the torques in the joint (Zatsiorsky, 2002). In contrast, with the wide skis since lowering the body’s centre of mass is one way of achieving a more balanced position, the opposite could also be expected (Winter et al., 1990). The lower position (higher flexion) with the narrow skis, which in terms of geometry resembles junior-men competition skis, can be explained by the fact that the skiers assumed such a tuck position to take maximum advantage of the competitive technique, e.g. in an attempt to reduce the air resistance (Gilgien et al., 2013; Supej et al., 2013).
The abduction analysis showed that the skiers, when skiing on all three different skis that were used in our study, had their knee joint in abduction throughout all phases of the turn (Figure 6). These results should be discussed carefully because, in morphological terms, the knee behaves in such a way that its adduction actually increases with flexion (Lu et al., 2008). In the middle of the turn (the second part of phase S1 and the first part of phase S2), where the knee flexion was between ~48° and 53°, knee adduction of about 3–5° could be expected, unless the knee joint is abducted intentionally or by external forces (Lu et al., 2008; Moglo and Shirazi-Adl, 2005; Wilson et al., 2000). Since we measured abduction (valgus) in the turn, it can be concluded that the skiers adopted their knee position due to the skiing technique and equipment used. Contrary to the hypothesis of the study, abduction was greatest with the narrow skis and not with the wide skis where the point of application of the ground reaction force moves inwards (in the medial direction). A possible explanation is that, in both cases, while moving in the direction of abduction, the knee joint reached the end range of motion, which is slightly higher in the area of greater flexion (Grood et al., 1988) as measured with the narrow skis. Another explanation for the measured higher abduction with the narrow skis is that the skier cannot fully resist the probable consequential larger torque with medium and wide skis, which have larger lever arms compared to narrower skis on a hard snow base. Perhaps it is also more difficult for a skier, when using medium and wide skis, to force the knee through muscle activation into abduction, given all external disturbances, i.e. uneven terrain and vibrations on the snow (Mester, 1997).
The analysis of the rotation demonstrated the occurrence of an internal rotation in the turn, which was observed for all ski widths (Figure 7). The internal rotation does not correspond to the computer video analysis and Figure 1 c–d, where an external knee rotation in the turn can be perceived. However, the evaluation of rotations in the knee joint is also quite complicated because the coupled degrees of freedom of the knee-joint motion must be considered (Lu et al., 2008; Moglo and Shirazi-Adl, 2005; Wilson et al., 2000). These accompanying movements are defined by the shape of the joint surfaces and the tension in the ligaments, especially with more extended knee positions. For example, Lu et al. (2008) reports an internal rotation increment of about 10° if flexion is increased from 0° to 30° as well as a further internal rotation increment of 8.8° when flexion is further increased from 30° to 114°. The latter values can be understood as the knee joint neutral positions at certain flexion angles, while the same flexion angle defines the possible range of motion for abduction/adduction and rotation under the influence of the muscle activity and external forces acting on the joint (Antolic, 1995; Grood et al., 1988). Consequently, a higher internal rotation than those measured with the skiers using all three ski types would be expected. In the area of flexion, between approximately 45 and 52° measured in the steering phases (Table 1) the internal rotation would be expected to be 15° (Lu et al., 2008), whereas in our measurements (Table 1) they were substantially lower (ranging between, 5.5 and 10.5 °).
As rotation in the knee joint must be discussed in relative terms due to the mechanism of coupled degrees of freedom of motion, the lower than expected internal rotation to the neutral position can thus be (with some speculation) considered as the actual occurrence of the relative external rotation. Thus, rotation in the external direction increased with the width of the ski in our study. In the area of about 50° of flexion, the knee joint allows a considerably active changing of the rotation (up to 40° of the external rotation and up to 20° of the internal rotation) (Grood et al., 1988; Platzer, 2004) and it seems that the skiers actively performed less internal rotation that can be understood as a relative external knee rotation to the neutral position. The occurrence of such relative external rotation in skiing coincidentally concurs with the previous study (Yoneyama et al., 2000) in which the directly measured absolute external rotation in skiing can be ascribed to the measurement method, since the rotation of the femur was measured against the ski boot and not the rotation between the shinbone and femur as is the case in the current study and comonly used in other studies (Lu et al., 2008; Wilson et al., 2000).
When inspecting the forms of graphs for internal rotation and abduction compared to turn radii and ground reaction forces, very similar patterns were observed. Increasing and decreasing intervals as well as the areas of high and maximum values almost completely coincided regardless of which skis have been used. It only needs to be taken into account that that turn radii had an inverse behavior. This observed phenomena indicated that these movements of the knee joint are likely one of the key points in controlling the turning in alpine skiing, which concurs with previous findings (Müller et al., 1998).
Following the aforementioned considerations, the changes in knee joint angles in frontal and sagittal planes with the different skis can be considered in the perspective of the adaptation of the skier to the shift in point of application of the ground reaction force. Probably the requirements of controlling the skis in the turn were different with different waist widths, as the torque acting on the skis was most likely different. This adaptation of the skier in the knee abduction, especially using narrow skis, seems to be an important strategy throughout the time when the ski is set on its edge, i.e. from mid of phase I to the end of phase C (Figure 6, knee abduction). It seems that in the case of wider skis another adaptation came into play more prominently: changing the knee rotation into an external (less internal) direction (Figure 7, knee rotation). Perhaps the combined movement of changed abduction as well as rotation was needed in the turn with wider skis where the point of application of the ground reaction force was displaced further away from the middle of the foot as with the narrower skis.
When evaluating the correlation between the measured positions in the current study and the risk of knee joint injury, it can be concluded that the increment of abduction and external rotation mainly increased the tension of the medial collateral ligament and, to some extent, the anterior cruciate ligament (Bendjaballah et al., 1997; Pressman and Johnson, 2003). This might increase the risk of injury of these two structures with wider skis in the case of an abrupt additional force. However, as it is not known how close to the end of range of motion the knee joint actually reached and as the kinematics at the very moment of the injury might entirely differ to the measured positions, such a conclusion is rather speculative.
Perhaps a more interesting result in the scope of the adverse loading of cartilage surfaces was the change of varus/valgus alignment. In phase S2, where the ground reaction force was highest the mean difference in the abduction was in the range of 3° and the difference between peak values was in the range of 4°. Previous studies demonstrated that only a few degrees of change of alignment in the frontal plane in the stance position can enormously hasten the degenerative process of the knee joint during daily activities (Sharma et al., 2001). In the situation of varus/valgus malalignment as recorded in the current study, muscle forces may importantly increase compression forces and thus negatively influence the degenerative process. As the ground reaction forces were practically the same with each type of ski in our study, it can be speculated that the knee joint torques might differ predominantly due to changes in kinematics (Klous et al., 2014). In the case of high skiing volume and during a longer period, different lower extremity alignments with wider skis could, speculatively, have some adverse effect on joint cartilage. However, due to the influence of knee joint flexion on varus/valgus and rotatory alignment and as the amount of flexion was changing during the turns, the statement about different joint loadings with different ski widths needs further confirmation.
The main limitation of the study was the relatively small sample, which meant that many differences were observed only ‘as a trend’ and were not always statistically significant. However, 180 turns in total were analysed, i.e. 10 turns per subject using each type of skis, which is one of the largest full-body three-dimensional kinematics sample size published in alpine skiing to date. Collecting large samples are problematic in the science of alpine skiing because it is extremely difficult to conduct field measurements with a large number of subjects while ensuring the same or comparable conditions for all, e.g. the problem of ruts on the ski course (Lešnik et al., 2013; Supej et al., 2005b). For this purpose, the field measurements in this study were conducted over three consecutive days, which required us to carefully monitor the weather forecast and consider the snow conditions as well as to place the gates exactly at the same locations every day using the geodetic equipment.
As a large sample and a large quantity of input data was desired, a measurement system that uses inertial sensors and a high-resolution RTK GNSS system (Krüger and Edelmann-Nusser, 2010; Supej, 2010) was employed. A laboratory study with an instrumental gimbal demonstrated that the errors of inertial sensors for three-dimensional joint kinematics were around 3° for all three anatomical axes (Brennan et al., 2011). Whether these accuracy values, particularly those for adduction/ abduction and internal/external rotation angles, are transferable to in-filed measurements and the application in skiing has not been assessed so far. Another study (Zhang et al., 2013) demonstrated that the inertial system differed from the optical considerably more than that, mainly in the knee rotations and in knee abduction/adduction. However, it should be noted that the level of errors in stereophotogrammetry for rotations and abduction/adduction angles reported in the laboratory conditions (Della Croce et al., 2005) were at the same level as the differences found between stereophoto-grammetry and MVN (Zhang et al., 2013). To conclude, bearing in mind the limitations and the accuracies for knee joint angles of both systems (Brennan et al., 2011; Della Croce et al., 2005; Zhang et al., 2013) as well as the need to collect a large sample size, it can be presumed that the system used in the current study was the equipment of choice, despite its potential limitations.
The question that needs to be addressed is whether the accuracy of the system used was sufficient for the measured differences. In terms of knee angles, the differences between knee flexions using different skis were at the limits of the accuracy of the system. However, a part of the knee joint angles error was shown to be related to the placement of the sensors (Brennan et al., 2011; Zhang et al., 2013). Because the skiers in the current study were using the same placement of sensors when skiing with skis of different widths, this part of error only increased the standard deviation among skiers and should not have affected the statistics used in the study.
The accuracy of skis trajectory and consequently turn radii can be estimated from the inclination accuracy of the inertial motion capture system and the position accuracy of the RTK GNSS. According to Brennan et al. (2011), the joint angles have errors of up to approximately 3.5º deg. It can be assumed that half of this error corresponds to each segment. If a rounded value of 2º is thereafter used as an error of inclination of the skier’s body from the antenna to the ground (ski), the relative position error of the ski would be approximately 5 cm. Adding the error of an identical RTK GNSS system used during alpine skiing (Supej and Holmberg, 2011), a maximum absolute position error of the skis trajectory of approximately 8 cm can be expected, which is more than sufficient for the needs of the current study.
Deriving the GRF using kinematical data is accompanied with larger errors, but still usable in alpine skiing, as previously demonstrated (Lüthi et al., 2005). The position error in the current study was comparable to the measurement error of a previous study (Supej et al., 2011) and in principle the same analogy of calculation of GRF has been used. Therefore, the same GRF estimation error of approximately 0.25 BW can be assumed. Since the GRF were solely used as a supplementary parameter, such accuracy was considered to be adequate.
In the future, in order to facilitate a more accurate definition of the biomechanical parameters of the knee joint while using skis of different widths and in order to better establish the risk of overuse injury, the measurement system should be supplemented with a measurement of the ground reaction force and muscular activity. It would also be meaningful to include skiers of different levels of performances and the sample of skiers should preferably be increased. Furthermore, different snow conditions should be tested, because wide skis are primarily built for backcountry or so-called off-piste skiing where softer snow conditions or powder snow is often present. In such conditions, a ski sinks into a soft snow surface (Federolf et al., 2010), which can cause the point of application of the ground reaction force to move in the lateral direction (outward) as the pressure on the ski is distributed along the entire width of the contact with the snow. Consequently the effect of wider skis found in the current study might diminish.
Conclusion
The changed biomechanical conditions that occurred in the transition to a different ski width caused a change in the knee joint kinematics, and it appears that two different motion strategies were formed depending on the ski width. The strategy using narrow skis was a more pronunced knee abduction, while using medium and wider skis caused progresively increased knee external rotation (less internal). Both of these strategies most probably occurred due to the changed point of application of the ground reaction force. Furthermore, based on the results of the current study, it can be plausibly argued that the use of wider skis or, in particular, skis with a large waist width, on a hard or frozen surface as was the case in this study, could force the knee joint closer to the end of range of motion in transversal and frontal planes. In addition, using wider skis on a hard frozen snow may increase the potential risk of degenerative knee injuries; however the latter needs further justification. Such hard snow conditions are characteristic for most prepared ski slopes, especially in recent times when natural snow is lacking and has to be substituted with considerably more compact artificial snow. Finally, the overall results of the abduction and internal rotation in respect to turn radii and ground reaction forces indicated that the knee joint movements are likely one of the key points in alpine skiing technique.
Acknowledgments
This study was supported financially by the Foundation for Financing Sport Organisations in Slovenia, the Slovenian Research Agency, Elan d.d. and ŠC Pohorje d.d. The authors would like to thank sincerely the subjects for their participation, as well as Prof. Zlatko Matjačić and Prof. Vojko Strojnik for their valuable comments on the project.
Biographies

Martin ZORKO
Employment
University Medical Centre Ljubljana, Clinical Institute of Occupational, Traffic and Sports Medicine, Ljubljana, Slovenia
Degree
MD
Research interest
Sensory motor integration in rehabilitation, biomechanics of alpine skiing.
E-mail: martin.zorko@kclj.si

Bojan NEMEC
Employment
Research associate in the Department for Automatics, Biocybernetics and Robotics, Jozef Stefan Institute, Ljubljana, Slovenia
Degree
PhD
Research interests
Robot control, robot learning, service robotics, and sports biomechanics.
E-mail: bojan.nemec@ijs.si

Jan BABIČ
Employment
Senior researcher in the Department of Automation, Biocybernetics and Robotics, Jožef Stefan Institute, Ljubljana, Slovenia
Degree
PhD
Research interests
Whole-body human motor control, and design of biologically plausible robot controllers that achieve similar robustness and adaptation to the environment as found in humans.
E-mail: jan.babic@ijs.si

Blaž LEŠNIK
Employment
University of Ljubljana, Faculty of sport, Department of alpine skiing, Ljubljana, Slovenia.
Degree
PhD
Research interest
Motor development, methodics and technique in alpine skiing, biomechanics of alpine skiing.
E-mail: blaz.lesnik@fsp.uni-lj.si

Matej SUPEJ
Employment
Head of Laboratory of Biomechanics, Faculty of Sport, University of Ljubljana, Ljubljana, Slovenia & Associate professor University of Primorska, Faculty of Mathematics, Natural Sciences and Information Technologies, Koper, Slovenia.
Degree
Associate professor, PhD
Research interests
Biomechanics of sport (mechanical modelling of different sport disciplines and human movement, elite athletes performance, computer simulation, sport equipment development and testing…), methodology and technology of measurement in biomechanics of sport (GNSS technology, camcorder based systems kinematic systems, motion trackers and full body inertial motion capture, accelerometers, force sensors…) and their combinations.
E-mail: Matej.Supej@fsp.uni-lj.si
References
- Antolic V. (1995) Osnove klinicne biomehanike kolena. Medicinski razgledi 34, 263-268. (In Slovenian: English abstract). [Google Scholar]
- Barth K. (2011) Ich Lerne Skifahren. Meyer + Meyer Fachverlag, Aachen. (In German) [Google Scholar]
- Bendjaballah M. Z., Shirazi-Adl A., Zukor D. J. (1997) Finite element analysis of human knee joint in varus-valgus. Clinical Biomechanics 12, 139-148. [DOI] [PubMed] [Google Scholar]
- Benjamini Y., Yekutieli D. (2001) The control of the false discovery rate in multiple testing under dependency. Annals of Statistics 29, 1165-1188. [Google Scholar]
- Bere T., Florenes T. W., Krosshaug T., Koga H., Nordsletten L., Irving C., Müller E., Reid R.C., Senner V., Bahr R. (2011) Mechanisms of anterior cruciate ligament injury in World Cup alpine skiing: a systematic video analysis of 20 cases. The American Journal of Sports Medicine 39, 1421-1429. [DOI] [PubMed] [Google Scholar]
- Brennan A., Zhang J., Deluzio K., Li Q. (2011) Quantification of inertial sensor-based 3D joint angle measurement accuracy using an instrumented gimbal. Gait & Posture 34, 320-323. [DOI] [PubMed] [Google Scholar]
- Brucker P.U., Katzmaier P., Olvermann M., Huber A., Waibel K., Imhoff A.B., Spitzenpfeil P. (2014) Recreational and competitive alpine skiing: Typical injury patterns and possibilities for prevention. Der Unfallchirurg 117, 24-32. (In German: English abstract). [DOI] [PubMed] [Google Scholar]
- Burtscher M., Gatterer H., Flatz M., Sommersacher R., Woldrich T., Ruedl G., Hotter B., Lee A., Nachbauer W. (2008) Effects of modern ski equipment on the overall injury rate and the pattern of injury location in Alpine skiing. Clinical Journal of Sport Medicine 18, 355-357. [DOI] [PubMed] [Google Scholar]
- Cole G.K., Nigg B.M., Ronsky J.L., Yeadon M.R. (1993) Application of the joint coordinate system to three-dimensional joint attitude and movement representation: a standardization proposal. Journal of Biomechanical Engineering 115, 344-349. [DOI] [PubMed] [Google Scholar]
- de Leva P. (1996) Adjustments to Zatsiorsky-Seluyanov's segment inertia parameters. Journal of Biomechanics 29, 1223-1230. [DOI] [PubMed] [Google Scholar]
- Della Croce U., Leardini A., Chiari L., Cappozzo A. (2005) Human movement analysis using stereophotogrammetry. Part 4: assessment of anatomical landmark misplacement and its effects on joint kinematics. Gait & Posture 21, 226-237. [DOI] [PubMed] [Google Scholar]
- Duncan J. B., Hunter R., Purnell M., Freeman J. (1995) Meniscal injuries associated with acute anterior cruciate ligament tears in alpine skiers. The American Journal of Sports Medicine 23, 170-172. [DOI] [PubMed] [Google Scholar]
- Federolf P., Roos M., Lüthi A., Dual J. (2010) Finite element simulation of the ski–snow interaction of an alpine ski in a carved turn. Sports Engineering 12, 123-133. [Google Scholar]
- Flørenes T.W., Bere T., Nordsletten L., Heir S., Bahr R. (2009) Injuries among male and female World Cup alpine skiers. British Journal of Sports Medicine 43, 973-978. [DOI] [PubMed] [Google Scholar]
- Gilgien M., Crivelli P., Spörri J., Kröll J., Müller E. (2015) Characterization of Course and Terrain and Their Effect on Skier Speed in World Cup Alpine Ski Racing. PLOS ONE 10, e0118119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilgien M., Spörri J., Chardonnens J., Kröll J., Müller E. (2013) Determination of External Forces in Alpine Skiing Using a Differential Global Navigation Satellite System. Sensors 13, 9821-9835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grood E.S., Stowers S.F., Noyes F.R. (1988) Limits of movement in the human knee. Effect of sectioning the posterior cruciate ligament and posterolateral structures. Journal of Bone and Joint Surgery 70, 88-97. [PubMed] [Google Scholar]
- Grood E.S., Suntay W.J. (1983) A joint coordinate system for the clinical description of three-dimensional motions: application to the knee. Journal of Biomechanical Engineering 105, 136-144. [DOI] [PubMed] [Google Scholar]
- Held F., Kaiser W., Deutscher Verband für das Skilehrwesen. (2002) Ski-Lehrplan perfect: Für fortgeschrittene Skifahrer und Carver. Blv, München. (In German) [Google Scholar]
- Howe J. (2001) The new skiing mechanics: including the technology of short radius carved turn skiing and the claw ski. McIntire, Waterford. [Google Scholar]
- Jarvinen M., Natri A., Laurila S., Kannus P. (1994) Mechanisms of anterior cruciate ligament ruptures in skiing. Knee Surgery, Sports Traumatology, Arthroscopy 2, 224-228. [DOI] [PubMed] [Google Scholar]
- Kim S., Endres N. K., Johnson R. J., Ettlinger C. F., Shealy J. E. (2012) Snowboarding injuries: trends over time and comparisons with alpine skiing injuries. The American Journal of Sports Medicine 40, 770-776. [DOI] [PubMed] [Google Scholar]
- Klous M., Muller E., Schwameder H. (2012) Three-dimensional knee joint loading in alpine skiing: a comparison between a carved and a skidded turn. Journal of Applied Biomechanics 28, 655-664. [DOI] [PubMed] [Google Scholar]
- Klous M., Muller E., Schwameder H. (2014) Three-dimensional lower extremity joint loading in a carved ski and snowboard turn: a pilot study. Computational and Mathematical Methods in Medicine 2014, 340272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krüger A., Edelmann-Nusser J. (2010) Application of a full body inertial measurement system in alpine skiing: A comparison with an optical video based system. Journal of Applied Biomechanics 26, 516-521. [DOI] [PubMed] [Google Scholar]
- LeMaster R. (2009) Ultimate Skiing. Human Kinetics, Champaign. [Google Scholar]
- Lešnik B., Axelsson E. P., Supej M. (2013) Influence of the start number on elite alpine skiing competitors'results. Kinesiologia Slovenica 19, 17-27. [Google Scholar]
- Lešnik B., Žvan M. (2010) A turn to move on : alpine skiing - Slovenian way: theory and methodology of alpine skiing : a university textbook and official syllabus developed for training courses for levels 1, 2 and 3 ski instructors. Faculty of Sport, Ljubljana. [Google Scholar]
- Levine H.B., Bosco J.A., 3rd. (2007) Sagittal and coronal biomechanics of the knee: a rationale for corrective measures. Bulletin of the NYU Hospital for Joint Diseases 65, 87-95. [PubMed] [Google Scholar]
- Lu T.W., Tsai T.Y., Kuo M.Y., Hsu H.C., Chen H.L. (2008) In vivo three-dimensional kinematics of the normal knee during active extension under unloaded and loaded conditions using single-plane fluoroscopy. Medical Engineering & Phys 30, 1004-1012. [DOI] [PubMed] [Google Scholar]
- Lüthi A., Federolf M., Fauve M., Oberhofer K., Rhyner H., Ammann W., Stricker G., Shiefermüller C., Eitzlmair E., Schwameder H., Müller E. (2005) Determination of forces in carving using three independent methods. In: Science and skiing III. Ed: Müller E., Bacharach D., Klika R., Lindinger S., Schwameder H. Oxford: Meyer & Meyer Sport; 96-106. [Google Scholar]
- Mester J. (1997) Movement regulation in alpine skiing. In: Science and skiing. Ed: Müller E. London: E & FN Spon. 333-348. [Google Scholar]
- Moglo K.E., Shirazi-Adl A. (2005) Cruciate coupling and screw-home mechanism in passive knee joint during extension--flexion. Journal of Biomechanics 38, 1075-1083. [DOI] [PubMed] [Google Scholar]
- Müller E., Bartlett R., Raschner C., Schwameder H., Benko-Bernwick U., Lindinger S. (1998) Comparisons of the ski turn techniques of experienced and intermediate skiers. Journal of Sports Sciences 16, 545-559. [DOI] [PubMed] [Google Scholar]
- Mündermann A., Dyrby C. O., Andriacchi T.P. (2005) Secondary gait changes in patients with medial compartment knee osteoarthritis: Increased load at the ankle, knee, and hip during walking. Arthritis & Rheumatology 52, 2835-2844. [DOI] [PubMed] [Google Scholar]
- Paletta G.A., Warren R.F. (1994) Knee injuries and Alpine skiing. Treatment and rehabilitation. Sports Medicine 17, 411-423. [DOI] [PubMed] [Google Scholar]
- Platzer W. (2004) Color Atlas of Human Anatomy: Locomotor system. 5th edition Thieme, Stuttgart. [Google Scholar]
- Pressman A., Johnson D.H. (2003) A review of ski injuries resulting in combined injury to the anterior cruciate ligament and medial collateral ligaments. Arthroscopy 19, 194-202. [DOI] [PubMed] [Google Scholar]
- Rossi M.J., Lubowitz J.H., Guttmann D. (2003) The skier's knee. Arthroscopy 19, 75-84. [DOI] [PubMed] [Google Scholar]
- Rust D.A., Gilmore C.J., Treme G. (2013) Injury patterns at a large Western United States ski resort with and without snowboarders: the Taos experience. The American Journal of Sports Medicine 41, 652-656. [DOI] [PubMed] [Google Scholar]
- Scheiber P., Seifert J., Müller E. (2012) Relationships between biomechanics and physiology in older, recreational alpine skiers. Scandinavian Journal of Medicine & Science in Sports 22, 49-57. [DOI] [PubMed] [Google Scholar]
- Sharma L., Song J., Felson D.T., Cahue S., Shamiyeh E., Dunlop D.D. (2001) The role of knee alignment in disease progression and functional decline in knee osteoarthritis. JAMA 286, 188-195. [DOI] [PubMed] [Google Scholar]
- Shea K.G., Archibald-Seiffer N., Murdock E., Grimm N.L., Jacobs J. C., Willick S., Van Houten H. (2014) Knee Injuries in Downhill Skiers: A 6-Year Survey Study. Orthopaedic Journal of Sports Medicine 2, 2325967113519741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spitzenpfeil P., Huber A., Waibel K. (2009) Mechanical load and muscular expenditure in alpine ski racing and implications for safety and material considerations. In: Science and skiing IV. Ed: Mueller E., Lindinger S., Stöggl T. Maidenhead: Meyer & Meyer Sport; 479-486. [Google Scholar]
- Supej M. (2010) 3D measurements of alpine skiing with an inertial sensor motion capture suit and GNSS RTK system. Journal of Sports Sciences 28, 759-769. [DOI] [PubMed] [Google Scholar]
- Supej M., Holmberg H.C. (2010) How gate setup and turn radii influence energy dissipation in slalom ski racing. Journal of Applied Biomechanics 26, 454-464. [DOI] [PubMed] [Google Scholar]
- Supej M., Holmberg H.C. (2011) A new time measurement method using a high-end global navigation satellite system to analyze alpine skiing. Research Quaterly for Exercise and Sport 82, 400-411. [DOI] [PubMed] [Google Scholar]
- Supej M., Kipp R., Holmberg H.C. (2011) Mechanical parameters as predictors of performance in alpine World Cup slalom racing. Scandinavian Journal of Medicine & Science in Sports 21, e72-e81. [DOI] [PubMed] [Google Scholar]
- Supej M., Kugovnik O., Nemec B. (2004) Modelling and simulation of two competition slalom techniques. Kinesiology 36, 206-212. [Google Scholar]
- Supej M., Kugovnik O., Nemec B. (2005a) Advanced analysis of alpine skiing based on 3D kinematic measurements. In: Science and skiing III. Ed: Müller E., Bacharach D., Klika R., Lindinger S., Schwameder H. Oxford: Meyer & Meyer Sport. 216-227. [Google Scholar]
- Supej M., Kugovnik O., Nemec B. (2008) DGPS Measurement System in Alpine Skiing Track and Center of Mass Estimation. In: Proceedings of First Joint International Pre-Olympic Conference of Sports Sciences and Sports Engineering. Vol. 1, Computer Science in Sports. Ed: Jiang Y., Baca A., Zhang H. Liverpool: World Academic Union; 120-125. [Google Scholar]
- Supej M., Nemec B., Kugovnik O. (2005b) Changing conditions on the slalom ski course affect competitors' performances. Kinesiology 37, 151-158. [Google Scholar]
- Supej M., Sætran L., Oggiano L., Ettema G., Šarabon N., Nemec B., Holmberg H.C. (2013) Aerodynamic drag is not the major determinant of performance during giant slalom skiing at the elite level. Scandinavian Journal of Medicine & Science Sports 23, e38-e47. [DOI] [PubMed] [Google Scholar]
- Urabe Y., Ochi M., Onari K., Ikuta Y. (2002) Anterior cruciate ligament injury in recreational alpine skiers: analysis of mechanisms and strategy for prevention. Journal of Orthopaedic Science 7, 1-5. [DOI] [PubMed] [Google Scholar]
- Vaverka F., Vodickova S. (2010) Laterality of the lower limbs and carving turn. Biology of Sport 27, 129-134. [Google Scholar]
- Wilson D.R., Feikes J.D., Zavatsky A.B., O'Connor J.J. (2000) The components of passive knee movement are coupled to flexion angle. Journal of Biomechanics 33, 465-473. [DOI] [PubMed] [Google Scholar]
- Winter D.A., Aftab E.A., James S.F. (1990) Assessment of balance control in humans. Medical Progress Through Technology 16, 31-51. [PubMed] [Google Scholar]
- Yoneyama Kagawa, Okamoto and Sawada. (2000) Joint motion and reacting forces in the carving ski turn compared with the conventional ski turn. Sports Engineering 3, 161-176. [Google Scholar]
- Zatsiorsky V.M. (2002) Kinetics of Human Motion. Human Kinetics, Champaign. [Google Scholar]
- Zatsiorsky V.M., Seluyanov V.N., Chugunova L.G. (1990) Methods of determining mass-inertial characteristics of human body segments. In: Contemporary Problems of Biomechanics. Ed: G.G. C., S.A. R. Mishawaka: Better World Books; 272-291. [Google Scholar]
- Zhang J.T., Novak A. C., Brouwer B., Li Q. (2013) Concurrent validation of Xsens MVN measurement of lower limb joint angular kinematics. Physiological Measurement 34, 0967-3334. [DOI] [PubMed] [Google Scholar]


