Abstract
Visible light optical coherence tomography (vis-OCT) has demonstrated its capability of measuring vascular oxygen saturation (sO2) in vivo. Enhanced by OCT angiography, the signal from microvasculature can be further isolated and directly used for sO2 extraction. In this work, we extended the theoretical formulation for OCT angiography-based oximetry by incorporating the contribution from motion contrast enhancement. We presented a new method to eliminate the associated confounding variables due to blood flow. First, we performed in vitro experiments to verify our theory, showing a stable spectral derivative within the selected wavelength bands for sO2 extraction. Then, we tested our method in vivo to measure retinal sO2 in rats inhaling different gas mixtures: normal air, 5% CO2, pure O2, and 10% O2. Absolute sO2 values in major arterioles and venules in the retinal circulation can be accurately measured. In addition, we demonstrated the relative changes of sO2 can be measured non-invasively from choriocapillaris immediately underneath the retinal pigmented epithelium (RPE) in rodents.
OCIS codes: (110.4500) Optical coherence tomography; (170.1460) Blood gas monitoring; (170.2655) Functional monitoring and imaging; (170.6480) Spectroscopy, speckle
1. Introduction
Optical coherence tomography (OCT) demonstrated tremendous success in imaging three dimensional (3D) tissue anatomy with micrometer-level spatial resolution on a macroscopic length scale [1]. In the past two decades, the technique has been translated into various clinical practices [2]. In particular, OCT has joined the standard of care in ophthalmology, providing rich 3D anatomical images from, for example, various retinal layers, choroid, and optic nerve head. Besides the technical advances on high-speed and high-resolution retinal imaging, functional imaging of various hemodynamic parameters has emerged as an invaluable supplement to anatomical OCT imaging. Perhaps the most important developments of functional OCT in retinal imaging are the measurement of retinal blood flow [3–9], and label-free retinal OCT microangiography (OMAG) [10–12]. Because the neuroretina has a high metabolic demand, the blood flow in the retinal circulation can be an excellent indicator of the viability of the retina and has been associated to various retinal diseases [13–15].
Another important hemodynamic parameter of the retinal circulation is the hemoglobin oxygenation saturation or sO2. The sO2 difference between the arterial and venous blood vessels indicates oxygen extraction from the circulation. When combined with blood flow measurements, oxygen metabolism in the retina can be quantified by gas volume of oxygen consumed per unit time [16, 17]. The attempts of using OCT to measure blood oxygenation dated back more than a decade ago, where the spectroscopic contrast around the isosbestic point around 800 nm from oxy- and deoxy-hemoglobin was characterized [18–21]. Since then, several groups also explored the oxygenation dependent scattering coefficient to create contrast for oxygenated or deoxygenated whole blood. However, none of the efforts has progressed into successful measurements of absolute sO2 in vivo. The reason is that the absorption contrast around 800 nm was overwhelmed by the wavelength-dependent scattering coefficient of red blood cells/whole blood, which have later been theoretically and numerically demonstrated [22, 23]. Knowing that hemoglobin has much higher absorbing contrast within visible-light spectral range than within NIR range, Yi et. al. and Robles et. al. explored the feasibility of using visible-light OCT (vis-OCT) to quantify sO2 from ex vivo and in vitro samples, respectively [24, 25]. They further showed in vivo measurement of blood oxygenation [26], and the first demonstration of in vivo retinal oximetry in rodents using vis-OCT combing with the spatially-resolved spectroscopic analysis [27]. Later, to isolate the blood signal from the static tissue in OCT signal, we proposed to combine the speckle contrast and the spectroscopic contrast of blood simultaneously [28] to calculate sO2 in microvasculature. We demonstrated that sO2 could be directly calculated from wavelength-dependent OCT angiography without the cumbersome image processing previously needed to locate blood vessels. A similar strategy was recently adapted for both exposed cortical imaging and optical-power-cancelled retinal imaging in rodents [29]. However, the theoretical treatment did not consider the complication of blood flow to the angiography signal, which could confound the blood oxygenation calculation in vivo.
Here, we expanded our theoretical formulation by taking blood flow contrast into account in OCT angiography-based oximetry. Experimental verification was conducted by pumping anticoagulated whole bovine blood through a capillary tube. We tested the influence of different flow rates to the spectral derivative (i.e. the first-order partial derivative of spatially resolved OCT spectrum against wavelength). Further, we proposed a new data processing algorithm to normalize different flow rate and yield a robust sO2 calculation. We tested our method in rat retina in vivo and detected sO2 variation upon inhaling different gas mixtures. Moreover we demonstrated, for the first time, a non-invasive measurement of the relative sO2 changes in choriocapillaris using vis-OCT.
2. Theory
In this section, we described the extended theoretical formulation for the spectroscopic analysis on vis-OCT angiography-based oximetry. The following motion-enhanced dynamic scattering model is to demonstrate that a linear relationship can be established between sO2 and OCT angiographic derived spectrum measurements. Without loss of generality, we can start the formulation from a wavelength-dependent A-line signal from OCT angiogram , where z defines the axial coordinate and λ denotes the wavelength. Note that we will omit the finite axial resolution and sensitivity roll-off for simplicity purpose. At any given point along the A-line,
| (1) |
where is incidence intensity. is the wavelength-dependent back scattering coefficient of local tissue, which can be further expressed by a power law under the first Born approximation. is a scaling constant while the value of depends on the tissue type and has been previously characterized to be ~1 with variations around ± 0.2 [30, 31]. The term is a non-negative scalar representing the dynamic contrast enhancement caused by random phase variation due to motion. The value of G is assumed to be 0 only if the tissue is static. is the cumulative attenuation when light double passes the tissue,
| (2) |
where is the total attenuation coefficient of local tissue attributed to both optical absorption and scattering. For whole blood, it is a linear combination of absorption coefficient , scattering coefficient , and a packing factor W, [22, 32]. For other retinal tissue, reduced total attenuation coefficient, may be used, where g denotes the anisotropy factor of the scattering process.
After normalizing by the source spectrum , the resulted image is analogous to the wavelength-dependent optical density (OD) mapping used in traditional fundus retinal oximetry, except for one additional motion enhancement term . Hence we use the same notation and denote the normalized as ,
| (3) |
or
| (4) |
As we take the partial derivative of OD against wavelength (spectral derivative), we have
| (5) |
If we assume that the wavelength is much smaller than the motion displacement of the blood cells, the phase variation becomes random and the enhancement factor loses wavelength dependence. The spectral derivative of could be considered to be zero and the equation becomes
| (6) |
Now let us consider the attenuation contribution from the whole blood and the static tissues. As light propagates in tissue, the cumulative attenuation is
| (7) |
or
| (8) |
where and denote the total attenuation coefficients of whole blood and averaged attenuation coefficient of static retinal tissue, respectively; and denote the cumulative optical path length within the blood vessel and in other retinal tissues, respectively.
Based on the previous characterization of and , we found that the spectral derivative of was close to zero [32, 33]. As a result, the spectral derivative of Eq. (7) is
| (9) |
We can further express with respect to sO2 as
| (10) |
where and are the total attenuation coefficients for fully oxygenated and deoxygenated whole blood, respectively. For simplicity, we define the following two constants, and and plug Eqs. (8)-(10) into Eq. (6) so that
| (11) |
It is clear that Eq. (11) establishes a linear relationship between the spectral derivative of the OD function and sO2, while serves as a constant scaling factor. During our experiment, lb is a constant determined by the choice of ROI. Its exact value can be estimated by measuring the mean optical path on the OCT angiograph.
3. Methods
3.1 Animal preparation
We anesthetized wild-type Long Evans rats using Ketamine/Xylazine cocktail solution (11.45 mg Ketamine and 1.71 mg Xylazine per milliliter of solution, respectively). The solution was administrated via intraperitoneal injection (IP) at a dosage of 87 mg Ketamine and 13 mg Xylazine per kilogram of body weight. A supplementary dose (30% of the original volume) was administrated after 30 minutes of the initial injection to maintain the animal at deep anesthesia. We applied 0.5% Tetracaine hydrochloride ophthalmic solution for local eye anesthesia and 1% Tropicamide ophthalmic solution for pupil dilation. During the entire period of anesthesia, we maintained the core body temperature at 37 °C using an electronic heating pad with feedback control (FHC Inc). The animal was held on a custom-made imaging stage and properly immobilized. A pulse oximeter attached to the rear limb of the animal provided real-time monitoring of its heart rate and systemic arterial oxygen saturation.
The animal was first ventilated with normal air (21% O2, 79% N2) at 4.2 Standard Liter per Minute (SLPM). Then we supplied the following gas mixtures in the order of: (1) 5% carbon dioxide (21% O2, 74% N2, and 5% CO2); (2) pure oxygen (100% O2); and (3) 10% oxygen (10% O2 and 90% N2). For each gas inhalation, the animal was allowed to stabilize for at least 3 minutes before the measurement was taken. Additional time was allowed if the pulse oximeter reading showed large fluctuation (>2% deviation over 10 seconds). We supplied normal air for 3 minutes between changes. We took one additional measurement after the sequence with normal air ventilation. For each OCT measurement, the corresponding oximeter readings were also recorded simultaneously.
All the experimental procedures were approved by the Northwestern University IACUC and conformed to the Association for Research in Vision and Ophthalmology Statement on Animal Research.
3.2 Image acquisition
We developed a spectral-domain vis-OCT system to image rodent retina in vivo. A supercontinuum laser source (SuperK EXTREME EXW-6, NKT Photonics) provided broadband illumination. The output beam was delivered to the input arm of a free-space Michaelson interferometer via fiber optics. The beam splitter (CM1-BS013, Thorlabs) of the interferometer divided and redirected the beam to the reference arm and the sample arm. In the reference arm, a set of carefully chosen glass plates compensated for dispersions created by the unbalanced optical components. A continuously adjustable ND filter (NDC-50C-2M, Thorlabs) attenuated the beam intensity to enhance the dynamic range of the interference signal. The sample arm consists of a pair of scanning galvanometer mirror (Nutfield Technology) and a Keplerian telescope (0.2 × magnification) to project rectangular raster scanning pattern on the rat fundus. The spectrometer covered a spectrum range from 520 nm to 630 nm. We estimated the transverse and axial resolutions of our vis-OCT system to be 15 μm and 1.7 μm, respectively. A fast CMOS line scan camera (spL2048-140km, Basler) digitized the interference spectrum for image reconstruction. All acquisition sequence and recording were synchronized by a customized LabView (National Instrument) virtual instrument program.
We adopted uni-directional scans in our OCT angiography. Here we denote the fast-scan direction as the x axis and slow scan direction as the y axis. During one B-scan, we translated the laser spot along the positive x axis at 50-kHz A-line rate and a total of 400 A-lines were recorded. Immediately after each B-scan, we returned (flied back) the laser spot to the x axis origin without acquiring any signal. The returning speed was limited to four times the forward scanning speed, which was constrained by the mechanical properties of the galvanometer. We repeated the process five times at each y location before moving to the next one. For one vis-OCT angiography image stack, we had 5 × 512 = 2560 B-scans at 512 different y locations, each B-scan consisted of 400 A-lines. The entire OCT image stack took 25.6 seconds to acquire.
3.3 Vis-OCT imaging of retinal microvasculature
We generated vis-OCT angiography using phase-sensitive decorrelation algorithm [11, 28, 34]. The contrast originated from the flowing blood cells inside vessels as they randomly change the phase and amplitude of back-scattered light. The random phase shift caused decorrelation in OCT signal and can be enhanced via high-pass filtering. However, such enhancement may be confounded by bulk motion, which also contributed to the signal via the same mechanism. These motion originated from normal physiological movements (e.g. heart beat and breathing) and the rotating galvanometer mirrors, both of which were inevitable. We must take measures to minimize their effects so as not to interfere with vis-OCT angiography. We adopted a three-step approach to correct the aforementioned bulk motion decorrelation within each y location: (1) Bulk image shift; (2) Axial global phase fluctuations (AGPF) correction; and (3) Lateral global phase fluctuations (LGPF) correction [35]. Without loss of generality, we used the notation to represent the recovered complex vis-OCT signal of the five consecutive B-scans at a given y location; x and z represents the lateral and axial location, respectively; t indicates the specific B-scan in time order, whose value ranges from 1 to 5 in our case.
The first step was to co-register the five real-valued OCT structure image at each y location, so that motion shift greater than the imaging resolution can be corrected. We calculated the cross-correlation function between the two adjacent B-scan images (t + 1 and t). We identified the maximum value of the cross-correlation function along x and z directions, which indicates when the two images were properly aligned. The second image was then shifted back so the two images were properly registered.
The second step was to correct the global phase fluctuations with two phase modifiers AGPF and LGPF on the co-registered OCT images. The AGPF can be estimated by integrating the phase variation along the A-line axial direction (z axis) as
| (12) |
while the LGPF can be estimated by integrating the phase variation along the x axis as
| (13) |
We multiplied the two phase modifiers AGFP and LGFP to the corresponding complex OCT signal pixel-wise. The corrected complex valued vis-OCT signal is denoted . The B-scan angiography cross-section at location y can then be calculated by
| (14) |
where represents the expected value; and represents the modulus operation. We iterated the process at each y location and generated a three dimensional image stack .
At last, en face angiogram was generated by integrating the first 15 pixels of the highest motion contrast along z direction.
3.4 sO2 estimation
We performed spectroscopic angiography to obtain the spectral profile of motion enhanced contrast of blood vessels [10, 11, 28], which was used to calculate the absolute blood sO2. Instead of using the full spectrum, we employed short-time Fourier transform (STFT) to perform spatial-spectral dual-domain analysis. We empirically chose four Gaussian-shaped STFT windows centered at 565 nm, 568 nm, 571 nm, and 574 nm, each with 10 nm full-width-half-maximum (FWHM) bandwidth. The full spectrum was windowed using these narrow-band STFT windows, respectively. For each center wavelength chosen, we generated the corresponding narrow-band OCT angiography using the method described in the above section. The calculated wavelength-dependent OCT angiography is denoted . For any given vessel at depth z, we first performed image segmentation to isolate a thin layer containing the vessel. To project the image stack into a two-dimensional en face angiograph , we integrated the first 15 superficial pixels within the blood vessel. The integration interval of 15 was empirically chosen to optimize signal-to-noise ratio. We then calculated the mean value of within the x-y plane inside the vessel region. The value was then assigned to to characterize one designated vessel, as in Eq. (1). The process is repeated for all four center wavelength windows.
Next, we normalized using the corresponding source spectrum I0(λ) to calculate the localized . We performed a linear regression to calculate the slope of the straight line that went through the center of the four OD points. We used this slope to estimate the partial derivative of the OCT angiograph spectrum against wavelength.
To convert the spectral derivative into absolute sO2 values, we performed a calibration based on pulse oximetry spO2 readings where we assumed that the major retinal arteries had the same sO2 as systemic arterial sO2. Based on the calibration on each animal, we can measure the absolute sO2 values in the major retinal arteries and venules around the optic disk.
We summarized the data processing steps in Table 1.
Table 1. Summary of data processing procedures to extract sO2.
| Operations procedure to extract sO2 for any given blood vessel | ||
|---|---|---|
| 1 | To generate wavelength-dependent OCT angiography using STFT and motion enhanced dynamic scattering contrast according to Eq. (14) | |
| Input: Raw interference spectrum, STFT window; Output: | ||
| 2 | To choose a region of interest within a vessel from en face OCT image and average the signal over x, y extents. | |
| Input: , ROI of a vessel (x, y); Output: | ||
| 3 | To calculate localized optical attenuation function according to Eq. (4) | |
| Input: , source spectrum I0(λ); Output: | ||
| 4 | To calculate partial derivative on against wavelength according to Eq. (5) | |
| Input: , λ; Output: (spectral derivative) | ||
| 5 | To calculate average long the z axis and to calibrate all the major retinal arteries against systemic spO2 | |
| Input: spO2, ; Output: calibration curve | ||
| 6 | To convert to sO2 according to Eq. (11) | |
| Input: of selected vessel, calibration curve; Output: absolute sO2 | ||
4. Results
4.1 Phantom experiment verification
To demonstrate that the spectral derivative method is not affected by flow velocity, we designed and performed the following in vitro experiment. We fabricated a capillary phantom using a polystyrene tube (inner diameter: 125 µm) filled with anticoagulated bovine whole blood (Quad Five). We fully oxygenated the blood by exposing it to normal air at room temperature for 1 hour prior to the experiment. The phantom was embedded beneath 2.5% agarose gel to mimic a blood vessel in the retina. We controlled the blood flow rate in the tube using a syringe pump (PHD 2000 Infusion, Harvard Apparatus) at various pre-set values within physiological range.
In order to image the in vitro sample, we slightly modified our OCT system. An objective lens (LSM03-VIS, Thorlabs) replaced the telescope system to create a focusing spot about 5.5 µm in diameter. The same data acquisition and processing protocols were applied.
Figure 1(a) compares the cross-sectional view of OCT structural images and motion-enhanced images. It can be clearly seen that surrounding agarose gel has strong scattering background in conventional OCT. In comparison, the motion-enhanced images largely suppressed the static background, while the moving blood within the tube was enhanced due to dynamic scattering. Even when the flow rate was set to zero, intrinsic random Brownian motion was sufficient to enhance the contrast (the left most images in Fig. 1(a)). On the sectioned en face view of the OCT angiograph showing the capillary phantom, we took four rectangular region of interest (ROI’s) of equal size along its longitudinal axis (Fig. 1(b)). We extracted the wavelength-dependent motion contrast spectrum within the selected ROI’s to evaluate the influence of flow velocity. As expected, the shapes of these spectra were comparable, showing characteristic absorption spectrum of oxygenated whole blood. The spectrum calculated from zero-flow phantom is shown in Fig. 1(c).
Fig. 1.
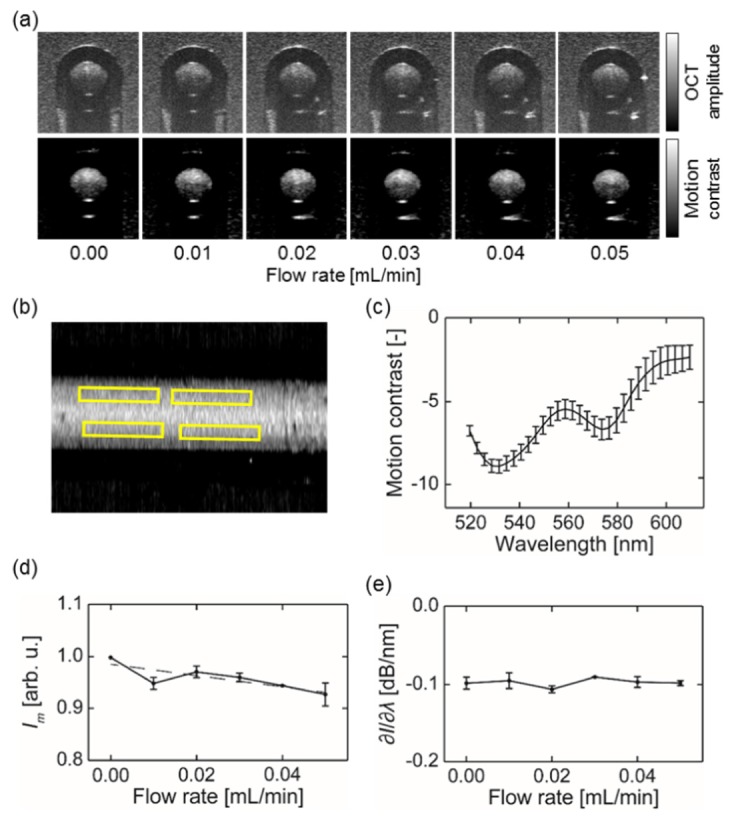
Spectroscopic analysis of in vitro phantom experiment. (a) Cross-sectional images of the tube based on direct (top row) and motion-enhanced dynamic scattering (bottom row) contrasts; (b) En face OCT angiography image of the tube. The yellow rectangles indicate the ROI used; (c) Representative motion contrast spectrum calculated from selected ROI’s, flow rate = 0.00 mL/min; (d) Averaged intensity Im taken from four ROI’s within the capillary tube; (d) The spectral derivative of motion contrast spectrum obtained within the capillary tube with varying flow rates from 560 to 580 nm. Error bar = S.D.
We extracted two parameters to characterize the obtained motion contrast spectrum, the averaged intensity (Im) and spectral derivative (∂I/∂λ) from 565 nm to 574 nm. Their values were plotted against increasing flow rate in Figs. 1(d) and 1(e), respectively. We performed liner regressions to estimate the slopes of both curves. Im showed a clear decreasing trend with a negative slope, which is statistically significant (p < 0.001). On the contrary, the slope of the ∂I/∂λ curve did not deviate from zero (p = 0.74). The result showed that ∂I/∂λ was flow-independent across the tested range, suggesting that sO2 estimation based on ∂I/∂λ would not be affected by different flow rate.
4.2 Measuring rat retinal sO2 in vivo
Figure 2 compares the cross-section view of the OCT images in rat retina in vivo. Figure 2(a) is the conventional structural OCT image. The anatomical features of the retina can be clearly distinguished. The cross sectional OCT angiogram is shown in Fig. 2(b). We further overlaid the structure image with the angiography in Fig. 2(c), showing locations of each vessel within the retina. Besides the vasculatures in retinal circulation, we also found strong blood motion contrast directly beneath the RPE, which suggested the existence of blood flows in choriocapillaris. Beyond that, visible light attenuated rapidly.
Fig. 2.

(a) Example of cross-sectional images of conventional OCT in rat retina in vivo using vis-OCT. Anatomical layers are labeled including, NFL/GCL-nerve fiber layer/ganglion cell layer, IPL-inner plexiform layer, INL-inner nuclear layer, OPL-outer plexiform layer, ONL-outer nuclear layer, ELM-external limiting membrane, IS/OS-inner segments/outer segments, and RPE-retinal pigment epithelium. (b) The corresponding OCT microangiograph generated using motion contrast. Vessels in retinal circulation and choroicapillaries are identified. Artifacts created by the hyper-reflective layers in IS/OS and RPE are indicated with a blue arrow. (c) Overlaid image from (a) and (b). The choroicapillaris lay beneath RPE layer.
We then compared the en face view of rat fundus obtained by two OCT modality. Figure 3(a) illustrates the conventional structural OCT image. Although the superficial vessels can be clearly observed, we cannot distinguish the microvasculature. In comparison, Fig. 3(b) showed motion-enhanced dynamic scattering contrast of the same data set, where the hyper-reflective signals from the static tissues are largely suppressed. Due to limited lateral resolution, choriocapillaris appeared as a single bright layer and was excluded through segmentation. Further, we calculated the sO2 of the major retinal vessels in the retinal circulation during normal oxygen inhalation, as the color-encoded angiographic image in Fig. 3(b). We can clearly distinguish the arteries and veins based on their individual sO2. Finally, we rendered the 3D vascular structure in Fig. 3(c). Besides the dominating brunches of central retinal arteries and veins, laminated structures of micro-vasculatures within nerve fiber layer (NFL) and outer plexiform layer (OPL) are also distinguishable. The fly-through en face microangiogram is shown in the movie.
Fig. 3.
In vivo imaging of a rat retina using vis-OCT. (a) and (b) are en face projection of amplitude and motion enhanced microangiography, respectively. In the microangiography map, each major retinal arterioles and venules are color-encoded based on the measured sO2 value. (c) A three dimensional rendering of rat retinal microvasculature. See Visualization 1 (4.8MB, AVI) for the fly-through en face microangiogram.
4.3 Absolute sO2 measurement in retinal circulation
We next performed in vivo verification of our spectral derivative method. We calibrated the absolute sO2 values from the major retinal arteries against a pulse oximeter readings under different ventilation conditions (normal air, 5% CO2, pure O2, and 10% O2), as shown in Fig. 4(a). The calibration process corresponded to the Step 5 in Table 1. The result shows a strong positive correlation (R2 = 0.87) between the two independent measurements, indicating that the calibration offered reasonably good estimation of the true sO2.
Fig. 4.
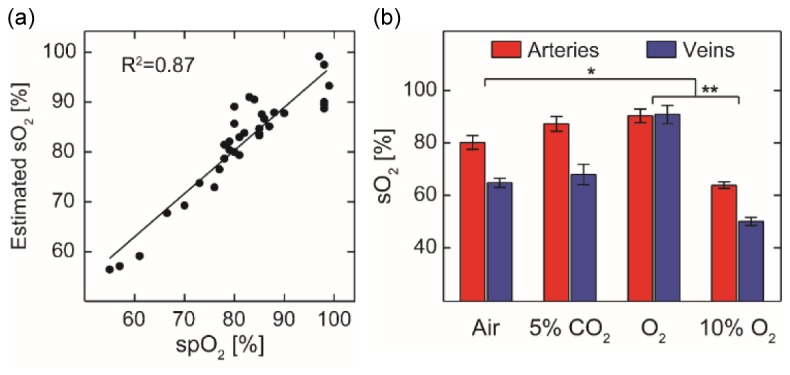
Measurement of absolute sO2 values in the retinal circulation in vivo. (a) Measured arterial sO2 calibrated against pulse oximetry readings (R2 = 0.87) from n = 8 rats. Black line is the linear regression of the data (b) Measured sO2 of major retinal arteries and venues upon changes of inhalation gas mixtures (n = 8 for each bar). Error bar = S.E.M. *: p < 0.05. **: p < 0.01.
Based on the established calibration curve, we measured the major retinal arterial and venous sO2 in respond to the change of inhalation gases. In the course of the experiment, we changed the inhalation gases in the order of normal air, 5% CO2, pure oxygen, and 10% oxygen. As shown in Fig. 4(b), the arterial and venous sO2 were significantly different (p < 0.05), except when pure oxygen was inhaled and the shunting between arterioles and venules elevated the venous sO2. Besides the arteriovenous sO2 difference, we observed a moderate increase (p = 0.06) in both arterial and venous sO2 when we supplied 5% CO2 gas. This increased sO2 is expected because 5% CO2 has the effect of vasodilation, which improves tissue oxygenation [36, 37]. Both the arterial and venous sO2 increased significantly (p < 0.05) under pure O2 and decreased significantly (p<0.01) under 10% O2.
4.4 Relative sO2 change in choriocapillaris
Given the fact that we had strong flow-contrast enhanced signals from choriocapillaris directly underneath the RPE, we attempted to measure the relative changes of sO2 in choriocapillaris. Due to limited lateral resolution, we could not distinguish individual choriocapillaris; instead, we averaged the signal over the entire area of choriocapillaris. We performed image segmentation to remove any area shadowed by superficial blood vessels, and yielded one averaged spectrum , where zc was the axial position in the choroid.
In order to eliminate the contamination from the retinal circulation in the inner retina, we normalized the choriocapillaris OCT angiograph spectrum by the intensity spectrum from the layer directly above RPE and calculated the spectral derivative. We used the same calibration curve obtained from retinal circulation to obtain the relative change of sO2 with respect to normal air breathing, as in Fig. 5. When we supplied 5% CO2 gas mixture, the average sO2 in choriocapillaris was observed to increase moderately by 2% (p = 0.29). When we supplied pure O2 and 10% O2 gas mixture, the average sO2 was observed to increase by 3.5% (p < 0.001) and decreased by 5% (p < 0.001), respectively.
Fig. 5.
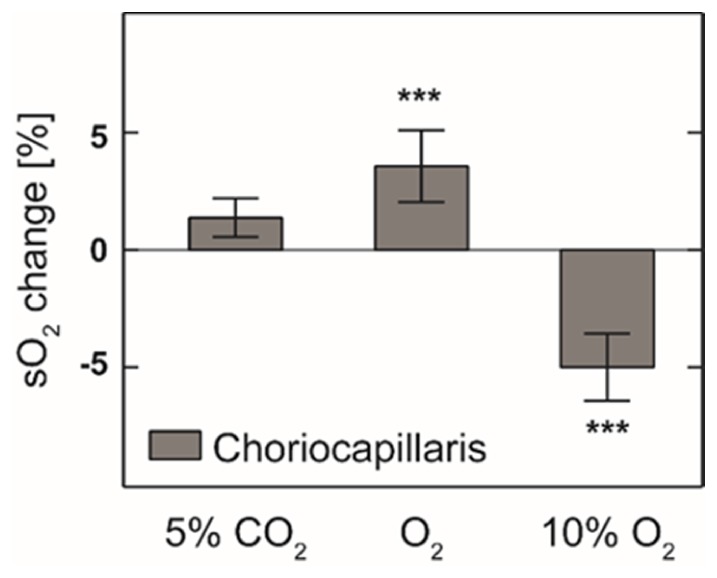
Measured relative choriocapillaris sO2 change comparing to normal air breathing (n = 6). ***: p < 0.0001.
4. Discussion
In this work, we presented an extended theoretical formulation for OCT angiography-based oximetry. This method used the flow contrast in OCT angiography, based on which we normalized the wavelength-dependent angiography and provided a robust measurement of sO2. The approach differs from our previous vis-OCT oximetry publication [27], where only static OCT amplitude information was used. The introduction of dynamic contrast eliminates the need for cumbersome vessel segmentation, and has arguably higher sensitivity and noise resistance than our previous method. More importantly, the new approach also enables us to measure the relative change of sO2 in chororiocapillaries, which are generally inaccessible in structural vis-OCT images. We observed the change of sO2 in both retinal circulation and choriocapillaris under different inhaling gas mixtures, which include normal air, 5% CO2, 100% O2, and 10% O2. Our in vivo measurements were verified by independent and concurrent pulse oximetry.
In our dynamic scattering model, we assumed that the motion enhancement term (G) is wavelength-independent. The assumption requires that the phase fluctuation is random between 0 to 2π without any preference. The condition is automatically satisfied when the displacement of scattering particles during the scanning dwell time are much larger than the wavelength. In our case, the red blood cell travels about 0.13 mm during the 0.01 s dwell time, which suffices the requirement.
We calculated the first derivative of the spectral range from 560 nm to 580 nm to establish its correlation with sO2. It differs from the least square fitting method over much larger wavelength range (530 nm-600 nm) as previously reported by our and other groups [28, 29]. The major benefit is that the permitted incidence power in the current study could be reduced by about 2/3, which is ~0.3mW in the current experiments. By removing unnecessary exposure, the safety margin for vis-OCT for human can be significantly improved and the discomfort can be dramatically reduced. By sacrificing the spectral information from the absorption contrast, our method requires independent oxygenation measurements for calibration purpose. Fortunately, pulse oximetry utilizes the pulsatile profile and provides the reading of the overall arterial oxygen saturation, which should be equal to the values in the major retinal arterioles immediately exiting optic nerve head. This allows us to calibrate our spectral derivatives as we showed in Fig. 4(a) in every experiment. Such a calibration is easily achievable using a pulse oximetry that is widely available in the clinical settings.
Interestingly, we were also able to measure sO2 variations in choriocapillaris right beneath the RPE under different inhalation conditions. The choroidal circulation is very different from retinal circulation, both anatomically and functionally [38]. The choroidal blood is supplied through posterior ciliary arterioles and drained through vortex vein. To our concern, the major difference between the two circulations is that the choroidal circulation has very small arteriovenous sO2 difference, whereas the retinal circulation has a large arteriovenous sO2 difference [39, 40]. This results in an almost uniform sO2 level in the choriocapillaris under normal physiology conditions, which allows us to measure sO2 over a relatively large area of choriocapillaris.
However, there are a few complications that prevent us providing absolute sO2 measurements in choriocapillaris. First, the true sO2 level in choriocapillaris is still unknown. The most accurate reference is the direct measurement of oxygen tension using an invasive oxygen sensitive microelectrode [38]. Although it is commonly assumed that the choroidal circulation has the systemic oxygenation as in the arterioles, the microelectrode measurements turned out to be lower than expected [38]. Without a reliable reference, we were not able to calibrate our spectral derivative as we did for the retinal vessels. Alternatively, one might consider using the least square fitting method with the full spectral range of the hemoglobin absorption contrast to characterize choriocapillaris sO2. However, the optical properties of dispersed single blood cells in capillary network are not entirely clear, which would bring another uncertainty in the least square fitting method. Second, light passes through entire retina before choriocapillaris. The accumulated attenuation is also wavelength dependent, which would affect the spectral derivative. Nonetheless, we found that this is the first time a non-invasive measurement can be implemented to measure relative choriocapillaris sO2 variations.
5. Conclusion
In summary, we presented a new theoretical formulation for vis-OCT angiography-based oximetry. The flow contrast was used and characterized by in vitro experiments. After proper spectral normalization, we demonstrated, for the first time, robust in vivo measurements of absolute sO2 variation in the retinal circulation and relative sO2 variation in the choriocapillaris. The new method requires much reduced illumination power, which greatly benefits clinical applications of vis-OCT.
Acknowledgments
We would like to acknowledge the following funding resources: National Institute of Health 1R01EY019951 and 1R24EY022883 and National Science Foundation grants CBET-1055379, CBET-1066776, and DBI-1353952. J. Yi is supported in part by a postdoctoral fellowship award from the Juvenile Diabetes Research Foundation. H. F. Zhang has financial interests in Opticent Health Inc., which, however, did not support this work.
References and links
- 1.Fujimoto J. G., “Optical coherence tomography for ultrahigh resolution in vivo imaging,” Nat. Biotechnol. 21(11), 1361–1367 (2003). 10.1038/nbt892 [DOI] [PubMed] [Google Scholar]
- 2.Zysk A. M., Nguyen F. T., Oldenburg A. L., Marks D. L., Boppart S. A., “Optical coherence tomography: a review of clinical development from bench to bedside,” J. Biomed. Opt. 12(5), 051403 (2007). 10.1117/1.2793736 [DOI] [PubMed] [Google Scholar]
- 3.White B., Pierce M., Nassif N., Cense B., Park B., Tearney G., Bouma B., Chen T., de Boer J., “In vivo dynamic human retinal blood flow imaging using ultra-high-speed spectral domain optical coherence tomography,” Opt. Express 11(25), 3490–3497 (2003). 10.1364/OE.11.003490 [DOI] [PubMed] [Google Scholar]
- 4.Wang Y., Bower B. A., Izatt J. A., Tan O., Huang D., “In vivo total retinal blood flow measurement by Fourier domain Doppler optical coherence tomography,” J. Biomed. Opt. 12(4), 041215 (2007). 10.1117/1.2772871 [DOI] [PubMed] [Google Scholar]
- 5.Baumann B., Potsaid B., Kraus M. F., Liu J. J., Huang D., Hornegger J., Cable A. E., Duker J. S., Fujimoto J. G., “Total retinal blood flow measurement with ultrahigh speed swept source/Fourier domain OCT,” Biomed. Opt. Express 2(6), 1539–1552 (2011). 10.1364/BOE.2.001539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhi Z., Yin X., Dziennis S., Wietecha T., Hudkins K. L., Alpers C. E., Wang R. K., “Optical microangiography of retina and choroid and measurement of total retinal bloodflow in mice,” Biomed. Opt. Express 3(11), 2976–2986 (2012). 10.1364/BOE.3.002976 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhi Z., Cepurna W., Johnson E., Shen T., Morrison J., Wang R. K., “Volumetric and quantitative imaging of retinal blood flow in rats with optical microangiography,” Biomed. Opt. Express 2(3), 579–591 (2011). 10.1364/BOE.2.000579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Werkmeister R. M., Dragostinoff N., Palkovits S., Told R., Boltz A., Leitgeb R. A., Gröschl M., Garhöfer G., Schmetterer L., “Measurement of Absolute Blood Flow Velocity and Blood Flow in the Human Retina by Dual-Beam Bidirectional Doppler Fourier-Domain Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 53(10), 6062–6071 (2012). 10.1167/iovs.12-9514 [DOI] [PubMed] [Google Scholar]
- 9.Dai C., Liu X., Zhang H. F., Puliafito C. A., Jiao S., “Absolute Retinal Blood Flow Measurement With a Dual-Beam Doppler Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 54(13), 7998–8003 (2013). 10.1167/iovs.13-12318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.An L., Wang R. K., “In vivo volumetric imaging of vascular perfusion within human retina and choroids with optical micro-angiography,” Opt. Express 16(15), 11438–11452 (2008). 10.1364/OE.16.011438 [DOI] [PubMed] [Google Scholar]
- 11.Jia Y., Tan O., Tokayer J., Potsaid B., Wang Y., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kim D. Y., Fingler J., Zawadzki R. J., Park S. S., Morse L. S., Schwartz D. M., Fraser S. E., Werner J. S., “Optical imaging of the chorioretinal vasculature in the living human eye,” Proc. Natl. Acad. Sci. U.S.A. 110(35), 14354–14359 (2013). 10.1073/pnas.1307315110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang Y., Fawzi A. A., Varma R., Sadun A. A., Zhang X., Tan O., Izatt J. A., Huang D., “Pilot Study of Optical Coherence Tomography Measurement of Retinal Blood Flow in Retinal and Optic Nerve Diseases,” Invest. Ophthalmol. Vis. Sci. 52(2), 840–845 (2011). 10.1167/iovs.10-5985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jia Y., Bailey S. T., Wilson D. J., Tan O., Klein M. L., Flaxel C. J., Potsaid B., Liu J. J., Lu C. D., Kraus M. F., Fujimoto J. G., Huang D., “Quantitative Optical Coherence Tomography Angiography of Choroidal Neovascularization in Age-Related Macular Degeneration,” Ophthalmology 121(7), 1435–1444 (2014). 10.1016/j.ophtha.2014.01.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Srinivas S., Tan O., Wu S., Nittala M. G., Huang D., Varma R., Sadda S. R., “Doppler Fourier-domain optical coherence tomography measured Retinal blood flow in Chinese American adults: The Chinese American Eye Study,” Invest. Ophthalmol. Vis. Sci. 55(5), 214 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Song W., Wei Q., Liu W., Liu T., Yi J., Sheibani N., Fawzi A. A., Linsenmeier R. A., Jiao S., Zhang H. F., “A combined method to quantify the retinal metabolic rate of oxygen using photoacoustic ophthalmoscopy and optical coherence tomography,” Sci. Rep. 4, 6525 (2014). 10.1038/srep06525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yao J., Maslov K. I., Zhang Y., Xia Y., Wang L. V., “Label-free oxygen-metabolic photoacoustic microscopy in vivo,” J. Biomed. Opt. 16(7), 076003 (2011). 10.1117/1.3594786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Faber D. J., Mik E. G., Aalders M. C. G., van Leeuwen T. G., “Light absorption of (oxy-)hemoglobin assessed by spectroscopic optical coherence tomography,” Opt. Lett. 28(16), 1436–1438 (2003). 10.1364/OL.28.001436 [DOI] [PubMed] [Google Scholar]
- 19.Lu C.-W., Lee C.-K., Tsai M.-T., Wang Y.-M., Yang C. C., “Measurement of the hemoglobin oxygen saturation level with spectroscopic spectral-domain optical coherence tomography,” Opt. Lett. 33(5), 416–418 (2008). 10.1364/OL.33.000416 [DOI] [PubMed] [Google Scholar]
- 20.Faber D. J., Mik E. G., Aalders M. C. G., van Leeuwen T. G., “Toward assessment of blood oxygen saturation by spectroscopic optical coherence tomography,” Opt. Lett. 30(9), 1015–1017 (2005). 10.1364/OL.30.001015 [DOI] [PubMed] [Google Scholar]
- 21.Kagemann L., Wollstein G., Wojtkowski M., Ishikawa H., Townsend K. A., Gabriele M. L., Srinivasan V. J., Fujimoto J. G., Schuman J. S., “Spectral oximetry assessed with high-speed ultra-high-resolution optical coherence tomography,” J. Biomed. Opt. 12(4), 041212 (2007). 10.1117/1.2772655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Faber D. J., Aalders M. C. G., Mik E. G., Hooper B. A., van Gemert M. J. C., van Leeuwen T. G., “Oxygen Saturation-Dependent Absorption and Scattering of Blood,” Phys. Rev. Lett. 93(2), 028102 (2004). 10.1103/PhysRevLett.93.028102 [DOI] [PubMed] [Google Scholar]
- 23.Chen S., Yi J., Liu W., Backman V., Zhang H., “Monte Carlo Investigation of Optical Coherence Tomography Retinal Oximetry,” IEEE Trans. Biomed. Eng. (Accepted). [DOI] [PMC free article] [PubMed]
- 24.Robles F. E., Chowdhury S., Wax A., “Assessing hemoglobin concentration using spectroscopic optical coherence tomography for feasibility of tissue diagnostics,” Biomed. Opt. Express 1(1), 310–317 (2010). 10.1364/BOE.1.000310 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yi J., Li X., “Estimation of oxygen saturation from erythrocytes by high-resolution spectroscopic optical coherence tomography,” Opt. Lett. 35(12), 2094–2096 (2010). 10.1364/OL.35.002094 [DOI] [PubMed] [Google Scholar]
- 26.Robles F. E., Wilson C., Grant G., Wax A., “Molecular imaging true-colour spectroscopic optical coherence tomography,” Nat. Photonics 5(12), 744–747 (2011). 10.1038/nphoton.2011.257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yi J., Wei Q., Liu W., Backman V., Zhang H. F., “Visible-light optical coherence tomography for retinal oximetry,” Opt. Lett. 38(11), 1796–1798 (2013). 10.1364/OL.38.001796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yi J., Chen S., Backman V., Zhang H. F., “In vivo functional microangiography by visible-light optical coherence tomography,” Biomed. Opt. Express 5(10), 3603–3612 (2014). 10.1364/BOE.5.003603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chong S. P., Merkle C. W., Leahy C., Radhakrishnan H., Srinivasan V. J., “Quantitative microvascular hemoglobin mapping using visible light spectroscopic Optical Coherence Tomography,” Biomed. Opt. Express 6(4), 1429–1450 (2015). 10.1364/BOE.6.001429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yi J., Backman V., “Imaging a full set of optical scattering properties of biological tissue by inverse spectroscopic optical coherence tomography,” Opt. Lett. 37(21), 4443–4445 (2012). 10.1364/OL.37.004443 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rogers J. D., Radosevich A. J., Yi J., Backman V., “Modeling Light Scattering in Tissue as Continuous Random Media Using a Versatile Refractive Index Correlation Function,” IEEE J. Sel. Top. Quantum Electron. 20(2), 173–186 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bosschaart N., Edelman G. J., Aalders M. C., van Leeuwen T. G., Faber D. J., “A literature review and novel theoretical approach on the optical properties of whole blood,” Lasers Med. Sci. 29(2), 453–479 (2014). 10.1007/s10103-013-1446-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hammer M., Roggan A., Schweitzer D., Müller G., “Optical properties of ocular fundus tissues-an in vitro study using the double-integrating-sphere technique and inverse Monte Carlo simulation,” Phys. Med. Biol. 40(6), 963–978 (1995). 10.1088/0031-9155/40/6/001 [DOI] [PubMed] [Google Scholar]
- 34.Srinivasan V. J., Jiang J. Y., Yaseen M. A., Radhakrishnan H., Wu W., Barry S., Cable A. E., Boas D. A., “Rapid volumetric angiography of cortical microvasculature with optical coherence tomography,” Opt. Lett. 35(1), 43–45 (2010). 10.1364/OL.35.000043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lee J., Srinivasan V., Radhakrishnan H., Boas D. A., “Motion correction for phase-resolved dynamic optical coherence tomography imaging of rodent cerebral cortex,” Opt. Express 19(22), 21258–21270 (2011). 10.1364/OE.19.021258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Akça O., Doufas A. G., Morioka N., Iscoe S., Fisher J., Sessler D. I., “Hypercapnia improves tissue oxygenation,” Anesthesiology 97(4), 801–806 (2002). 10.1097/00000542-200210000-00009 [DOI] [PubMed] [Google Scholar]
- 37.Dorner G. T., Garhoefer G., Zawinka C., Kiss B., Schmetterer L., “Response of retinal blood flow to CO2-breathing in humans,” Eur. J. Ophthalmol. 12(6), 459–466 (2002). [DOI] [PubMed] [Google Scholar]
- 38.Wangsa-Wirawan N. D., Linsenmeier R. A., “Retinal oxygen: Fundamental and clinical aspects,” Arch. Ophthalmol. 121(4), 547–557 (2003). 10.1001/archopht.121.4.547 [DOI] [PubMed] [Google Scholar]
- 39.Alm A., Bill A., “Blood flow and oxygen extraction in the cat uvea at normal and high intraocular pressures,” Acta Physiol. Scand. 80(1), 19–28 (1970). 10.1111/j.1748-1716.1970.tb04765.x [DOI] [PubMed] [Google Scholar]
- 40.Wang L., Törnquist P., Bill A., “Glucose metabolism in pig outer retina in light and darkness,” Acta Physiol. Scand. 160(1), 75–81 (1997). 10.1046/j.1365-201X.1997.00131.x [DOI] [PubMed] [Google Scholar]



