Resolution enhancement in integral microscopy by physical interpolation

Abstract

Integral-imaging technology has demonstrated its capability for computing depth images from the microimages recorded after a single shot. This capability has been shown in macroscopic imaging and also in microscopy. Despite the possibility of refocusing different planes from one snap-shot is crucial for the study of some biological processes, the main drawback in integral imaging is the substantial reduction of the spatial resolution. In this contribution we report a technique, which permits to increase the two-dimensional spatial resolution of the computed depth images in integral microscopy by a factor of √2. This is made by a double-shot approach, carried out by means of a rotating glass plate, which shifts the microimages in the sensor plane. We experimentally validate the resolution enhancement as well as we show the benefit of applying the technique to biological specimens.

1. Introduction

Three-dimensional (3D) live imaging is important for a better understanding of some biological processes. There are different techniques that can acquire 3D information of samples as they provide optical sections of the specimen [1–4]. In these techniques, obtaining 3D information of samples is time limited as, typically, two-dimensional sensors are only capable of recording one “in-plane” image per shot. The volumetric information is then obtained by axially scanning the sample. The main drawback of the latter is that the inertia of the scanning can be the bottleneck when high-speed acquisition is required. In order to avoid the mechanical scanning, electrically addressable liquid lenses have been proposed as a solution [5,6]. In this case, the acquisition time depends on the speed response of the liquid to the voltage, but still requires several shots for taking a z-stack of images.

However, there are different techniques for recovering 3D information of a sample by means of a single shot. One of them is off-axis digital holographic microscopy [7,8] in which a hologram of the sample is recorded. From it, the phase information of the sample can be computationally retrieved, permitting the numerical refocusing the complex amplitude of the sample to different planes. Notwithstanding, this is a coherent technique and the main drawback is the amount of coherent noise, especially when imaging dispersive samples. A solution to this problem is the use of incoherent light, either in the illumination or in the response of the sample to the light, as occurs in the case of fluorescence. In the latter case, 3D information of samples can be extracted from a single frame by using a double-helix point spread function [9]. In this technique, the distorted point spread function suffers a rotation depending on the depth, permitting to accurately determine the axial position of different parts of a single image. Since it based on a highly aberrated point spread function, this technique produces a 3D map of particle localizations, but not an image. One possible solution to this problem is the technique named as multi-focus microscopy (MFM) in which different axial positions are spatially multiplexed in a sensor by using diffractive optics [10]. MFM permits to recover a z-stack of 9 images with high lateral resolution by a single frame.

Integral-imaging (InI) technology offers the possibility of calculating depth images from the image of an incoherently illuminated scene recorded after a single shot. Lippmann proposed the InI concept in 1908 [11]. The main idea of the technique is the recording of a set of micro-images provided by an array of microlenses (MLA). Adding a camera lens before the MLA [12] allows the imaging of far scenes, constituting the so-called plenoptic camera [13–17]. Since each microimage represents a different perspective of the scene, spatio-angular information can be extracted from the recorded field. This information can be used for displaying a 3D image or for extracting 3D information by means of image processing. The latter is made by the definition of the plenoptic function [13], which describes the radiance of each light-ray as a function of spatial and angular coordinates. Computing this function from the captured microimages, orthographic views and depth images can be reconstructed. Taking these characteristics into account, InI is a promising technique when applying it to microscopy, especially when there is the need for recording high-speed volumetric information. The InI microscope was firstly proposed by Jang and Javidi [18], but only with the aim of displaying microscopic images. Later on, Levoy et al. [19] showed the applicability of this kind of microscope for recovering 3D information of microscopic samples. However, there is a trade-off between the spatial resolution and the angular information in every InI system. As a result, the spatial resolution obtained in the reconstructed images, even after applying deconvolution algorithms [20], is far away from the microscopy standards. In order to improve the resolution, Lim et al. [21] reported an InI Microscope working in Plenoptics 2.0 mode and proposed the use of a movable microlens array. Despite they synthesized a radiance map from 25 images, most of the benefit was in terms of angular resolution and therefore the improvement of lateral resolution was modest. More recently, an interpolation procedure over the micro-images has been reported [22], which, although it improves the visual aspect, does not increase the resolution as this is limited by the previously existing information. Although this kind of microscopy has been named in different ways, like lightfield microscopy, or plenoptics microscopy, we would like to acknowledge the importance of Lippmann in the inception of this technology and coin the name integral microscopy. Therefore, the instrument is named here as the integral microscope (IMic).

In this paper we propose to enhance the lateral resolution of IMic by means of a physical interpolation of two shifted radiance maps. This interpolation generates a synthetic radiance map with doubled spatial-frequency sampling. This shifting, which corresponds to a half of the microimages diagonal period, is performed by use of a tilting glass plate. It should be pointed out that this element is present in other microscopes, as the Apotome from Zeiss© [23], and its actuation can be implemented for high-speed acquisition. So that, although we perform a time-multiplexing technique that requires of two shots, it is worth it as the final resolution is closer to the conventional microscopy and it is still faster than performing an axial scanning. The reconstruction algorithm is based on the overlapping of mutually shifted microimages [24], but applying it over the orthographic views calculated by the transposition of the synthetic radiance map instead of over the microimages acquired directly by the IMic.

The paper is organized as follows. In Section 2, we introduce the principles of the IMic. In Section 3, we show theoretically the working principle of time-multiplexing IMic, as well as the improvement in resolution is experimentally demonstrated. Section 4 summarizes the achievements of this work.

2. The integral microscope: basic theory

The InI camera, also known as plenoptic camera, can be constructed from a conventional photographic camera by inserting an array of microlenses (MLA), of focal length $f_L$ and pitch $p$, at the sensor position. Then the sensor is shifted backwards, to a distance g, in such a way that a collection of small 2D microimages of the 3D scene is acquired. In order to avoid the overlapping between neighboring microimages, the pupil plane of the camera lens must be conjugated with the sensor through the microlenses. Besides, the f-number of the microlenses must be smaller or equal than the f-number of the camera lens in the image space. The filling factor is optimized, that is, the fields of view of the microimages are tangent, when both f-numbers match each other.

From the collection of microimages it is possible to build a radiance map with the spatial and the angular information of rays coming from the3D scene. A sketch of such map is shown in Fig. 1. Points aligned over the abscissa direction of the radiance map contain the information regarding to the field captured by a single microlens. In the same way, points aligned over a single straight-line in the ordinate direction correspond to an orthographic view of the 3D scene. Depth images in the neighborhood of the object plane can be calculated by propagating the radiance map, that is, performing an horizontal shearing of it, and then calculating the Abel transform of the resulting map [25].

Fig. 1.

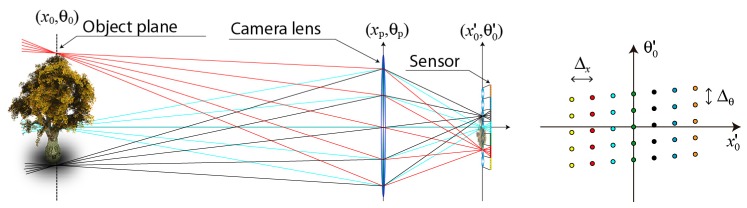
Scheme of an InI camera and sketch of the sampled radiance map captured with it. The spatial sampling period is ${\Delta }_x=p$. The angular sampling period, ${\Delta }_{\theta }$, is the angular size of pixels as seen from the MLA

The resolution of reconstructed depth images depends on the selected reconstruction plane [26]. The resolution limit can be expressed in terms of cutoff frequency, ${\rho }_C$, giving rise to values within the range

$${\rho }_{\mathrm{C}}\in [M{p}^{-1},2M{p}^{-1}],$$ (1)

being M the lateral magnification of the camera lens. The Eq. (1) can be easily deduced when applying the transposition relationship between the microimages and the orthographic views. Concretely, the properly scaled pitch of the microlenses defines the pixel size in the transposed space.

The main problem when applying the InI concept to microscopy is the reduction of the native resolution provided by the host microscope, whose limit is given by the diffraction cutoff frequency

$${\rho }_{\mathrm{C}}^{nat}=\frac{2NA}{\lambda }.$$ (2)

A schematic of the IMic is shown in Fig. 2. In this system a telecentric arrangement between an infinity-corrected microscope objective (MO) and a tube-lens (TL) performs the image of a 3D sample in the proximity of the MLA with a magnification given by the quotient of their focal-lengths, $M=-f_{TL}/f_{MO}$. The sensor is placed at a distance $g=f_L$ from the MLA. In this system, the condition for optimizing the filling factor is fulfilled when the numerical aperture (NA) of the microscope in the image space, $NA\text{'}=NA/\left|M\right|$, matches the numerical aperture of the microlenses, $N{A}_L=p/2f_L$.

Fig. 2.

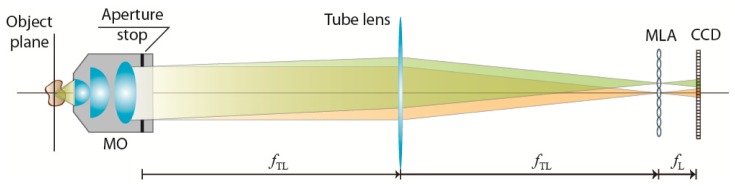
Scheme of an IMic, which is the result of inserting a MLA in the optical path of the host microscope.

To show the utility of this instrument, we built a IMic by coupling a $20x/0.40$ MO, a tube lens of $f_{TL}=200 mm$, and an array composed by 113x113 microlenses with pitch $p=110 \mathrm{\mu }\text{m}$ and $N{A}_L=0.01$ (MLA #12-1192-106-000 from SUSS MicroOptics). Note that in the experiments we did not use a customized MLA, but a commercial one. Due to this fact there was a mismatch between the $NA\text{'}=0.02$ and the $N{A}_L$. In order to avoid the overlapping between microimages we inserted an additional aperture at the pupil plane in such a way that the $NA\text{'}$ reached the effective value $NA{\text{'}}_{eff}=0.01$, and consequently $N{A}_{eff}=0.20$. It should be pointed out that this reduced the resolution capability of the system, but allowed us to perform proof-of-concept experiments. In our experimental setup, the sensor was not placed directly behind the MLA. Instead of this, we used a digital camera (Canon 450D, with a CMOS sensor of 4272x2848 pixels with 5.2 μm of size) coupled to a macro-objective of 1:1 for recording the microimages.

The image of a High Resolution USAF 1951 resolution chart in negative (groups of the test are transparent and the background is chrome-coated) performed by the host microscope, that is, the same arrangement as in the IMic but replacing the MLA by the sensor, is shown in Fig. 3(a).

Fig. 3.

Image of a USAF 1951 test by using a microscope with 20x, NA = 0.2. (a) Collection of 113x113 microimages, with 17x17 pixels each, of the USAF chart obtained with the IMic.

We captured the equivalent image of the USAF 1951 test target by means of the IMic (see Fig. 3(b)). This image contains a set of 113x113 microimages of 17x17 pixels each one. For reconstructing an in-focus image, we applied an algorithm based on the conventional one, but after making a transposition of the microimages, which prevents the apparition of artificial periodic patterns [28]. As a result of the transposition, we have a set of 17x17 orthographic views of 113x113 pixels, shown Fig. 4(a).

Fig. 4.

(a) Orthographic views obtained by applying the transposition to the microimages (b) Image reconstructed from the radiance map extracted from (a).

In the applied algorithm, the orthographic images were mutually shifted and summed. The position of the reconstruction depth plane depends on the amount of shifted pixels. The algorithm also includes intensity normalization by means of the resulting image after applying the procedure to a white matrix. To allow a larger number of reconstructed planes, the orthographic views were resized to 678x678 pixels through a nearest neighbor interpolation. Note that this upscaling does not affect the resolution of the system. The algorithm was implemented in C + + with computing times in the order of 1 second for computing the 14 depth images. After applying the reconstruction algorithm to the orthographic views of the USAF 1951 test target, we obtained the image shown in Fig. 4(b).

According to Eq. (1), the cutoff frequency of reconstructed images must be in the range ${\rho }_C(m{m}^{-1})\in [181,362]$, or, in terms of the spatial resolution, within the values $r(\mathrm{\mu }m)\in [2.7,5.5]$. The element marked with the white square in Fig. 4(b) (Group 7, element 4) corresponds to a spatial frequency of ${\rho }_C=181 m{m}^{-1}$, or a spatial resolution of $r=5.5 \mathrm{\mu }\text{m}$, which are within the theoretical prediction. As expected, this performance is poor in terms of resolution when comparing it to the host microscope. The measurement in the latter gives a cutoff frequency of ${\rho }_{\mathrm{C}}^{nat}=670 {\text{mm}}^{\text{-1}}$, which means that the spatial resolution is $r=1.5 \mathrm{\mu }\text{m}$.

3. The time-multiplexing integral microscope

As reported in the previous section, the main disadvantage of applying InI to microscopy is the lack of suitable resolution. In order to improve the resolution performance of the IMic, we propose a method based on the physical interpolation of two shifted radiance maps. These are captured sequentially and, with the proper shifting, they can be interlaced for creating a synthetic radiance map that doubles the number of sampling points, in such a way that the resolution of the reconstructions is enhanced. This idea was successfully applied to InI in our previous paper [30]. Nevertheless the method presented here is markedly different to this work, especially, from the experimental point of view. In the new approach, all the optical elements of the IMic remain static. For shifting the radiance map, we introduce a transparent plate that can be tilted, between the tube lens and the MLA, see Fig. 5. This element produces a displacement of the field that can be controlled with high accuracy, and it considerably reduces the inertia introduced to the system in comparison with the previous reported methods, that need an assembled movement of the MLA and the sensor. This is an important advantage to take into account, especially for microscopy, due to the fact that high stability is normally required. For this reason, there are other microscopes that perform a lateral shifting by means of rotating elements. This is the case of the confocal microscope in which the lateral scanning is made with lightweight ultra-precise galvanometers, which can work at repetition rates above 1 kHz [31]. Other interesting case is the ApoTome, in which also a glass plate is tilted at high speed for shifting the illumination grid pattern [23].

Fig. 5.

Single-frame excerpted from a video that shows the functioning of the time-multiplexing IMic (Visualization 1 ^{(178.1KB, AVI)} ).

In our case, when introducing the glass plate with a certain angle $\gamma$, considering low incident angles of light-rays, the outgoing optical field suffers a shifting that can be calculated by geometrical optics, given by

$$d=e\gamma \frac{n-1}{n},$$ (3)

where e is the plate thickness and n its refractive index.

As illustrated in the Fig. 5, the controlled tilting of the plate allows to laterally shift the beams coming from the tube lens while preserving their propagating angle. With this system, multiple acquisitions of shifted radiance maps can be done to improve the spatial resolution. Instead of this, our idea is to obtain the maximum benefit from the minimum number of shots. On this basis, although performing four shots (with shifting of $d=p/2$ over both transverse directions) would provide a better spatial sampling for the physical interpolation, we perform a two-shot acquisition in which the rays are laterally shifted by $d=\sqrt{2}p/2$ along the diagonal of the MLA unit cell. The two collections of microimages are interlaced for building a new synthetic collection in which the pitch is reduced, and therefore the spatial cutoff frequency of reconstructed images is enlarged.

To demonstrate our proposal we inserted, in the experimental IMic described in the previous section, a parallel plate of thickness $e=1.0 \text{mm}$ and refractive index $n=1.5$. The plate was mounted on a goniometer stage with an accuracy of 0.1°. According to Eq. (3) the required rotation angle was $\gamma =13.4°$.

With this instrument we obtained two images of the USAF chart, with 113x113 microimages each one. A close-up region of the images is shown in Fig. 6, panels (a) and (b). Figure 6(c) shows the result of interlacing them into a new synthetic set of 226x226 microimages, but it shows a chessboard-like arrangement, meaning that one half of microimages are empty. However, this structure does not affect the resolution of the reconstructed image as long as the microlens image plane is avoided during the reconstruction. The reconstructed image after applying the algorithm described in the previous section is shown in Fig. 7(c). The resolution is determined by the element marked with the white square (Group 8, element 1), which corresponds to a cutoff frequency of ${\rho }_{\mathrm{C}}=256 {\text{mm}}^{\text{-1}}$, or, in terms of the lateral resolution a value of $r=3.9 \mathrm{\mu }\text{m}$.

Fig. 6.

Panel (a) and (b) show the two images, colored in red and green, taken for the composition shown in panel (c).

Fig. 7.

(a) and (b), Microimages obtained after one-shot for two different axial positions of the USAF 1951 test target, and (c) and (d) their respective reconstruction when applying the physical interpolation.

For taking into account the 3D resolution, the experiment was repeated for different axial positions of the USAF 1951 test target within the depth of focus of the system, that is, a range of motion of 60 μm. Since InI technique does not provide 3D isotropic resolution [26], we found axial positions of the USAF test in which the resolution is reduced. The resolution loss was in only one element, see Fig. 7 (d). In that case the measured cutoff frequency for the double-shot reconstruction is ${\rho }_{\mathrm{C}}=228 {\text{mm}}^{\text{-1}}$, which corresponds to $r=4.4 \mathrm{\mu }\text{m}$. As expected, the time-multiplexing IMic improves the lateral resolution by a factor $\sqrt{2}$, and therefore the resolution of the system is about 2/5 of the native one.

Finally, we used the time-multiplexing IMic for imaging a seaweed thallus sample. Again we obtained two collections of microimages (similar to the one shown in Fig. 8(a)), and interlaced them to obtain the synthetic collection of microimages shown in Fig. 8(b). As in the previous experiment, the synthetic collection has a chessboard structure in which half of the microimages are empty.

Fig. 8.

(a) Set of 113x113 microimages of a seaweed thallus captured by the IMIC. (b) Corresponding set of 226x226 microimages of the specimen obtained by interlacing the microimages images captured with the time-multiplexing IMic. (c) Orthographic views calculated by the transposition of microimages.

After making the transposition to orthographic views, Fig. 8(c), we obtain a chessboard structure. But now the orthographic views have a half of the pixels empty. These black pixels are very inconvenient when observing the orthographic views of the sample. To overcome this problem we applied a bilinear interpolation over the views. The resulting orthographic views are shown in Fig. 9(a) and 9(c). Direct comparison between Visualization 2 ^{(1.1MB, AVI)} and Visualization 3 ^{(894.3KB, AVI)} demonstrate the superior performance of the time-multiplexing microscope. Finally we calculated the depth images, see Fig. 9(b) and 9(d). Also in this case the direct comparison between the Visualization 4 ^{(488.9KB, AVI)} and Visualization 5 ^{(838.9KB, AVI)} shows the utility of the proposed time-multiplexing IMic.

Fig. 9.

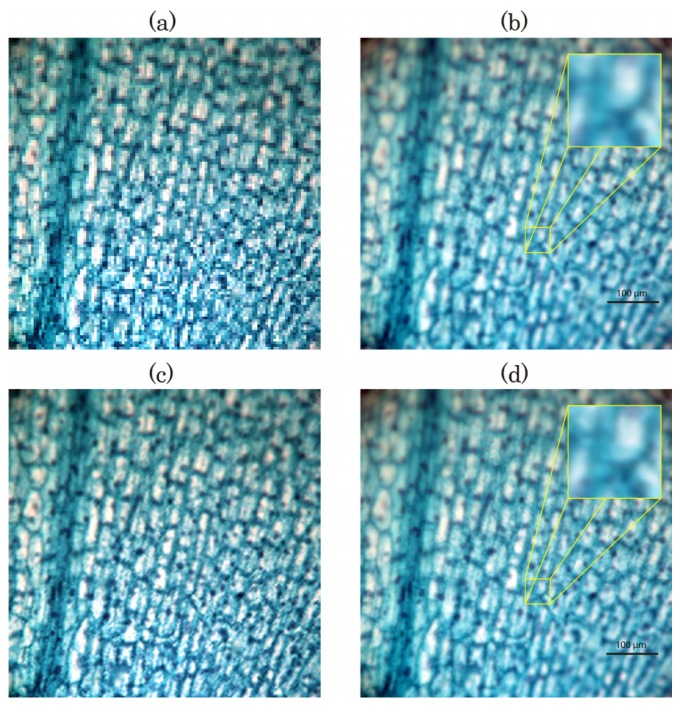
Orthographic views of the seaweed thallus obtained by the IMic for (a) single-shot (Visualization 2 ^{(1.1MB, AVI)} ), and (c) physical interpolation (Visualization 3 ^{(894.3KB, AVI)} ). Single frame extracted from the depth reconstruction for (b) single shot (Visualization 4 ^{(488.9KB, AVI)} ) and (d) physical interpolation (Visualization 5 ^{(838.9KB, AVI)} ).

It is important to remark that time-multiplexing technique is useful only in integral microscopes working in the Plenoptic 1.0 mode, that is, in which the plane of the microlenses is conjugated with front focal plane of the microscope objective. In the case of microscopes working in the 2.0 mode (in which the sensor is conjugated with the object plane) the time multiplexing gives rise to benefits that are shared by the spatial and the angular direction. Taking this into account, the application of the same method to Plenoptics 2.0 provides non-significant improvements in terms of the lateral resolution.

Conclusion

In this paper we have proposed a new method for the application of InI to microscopy, which improves the resolution of the reconstructed depth images. The method, name here as the time-multiplexing IMic, is based on the physical interpolation along the spatial direction of the radiance map. In order to make this interpolation at high speed while avoiding vibration and inertia effects, we have proposed the use of a tilting glass plate. We have demonstrated that this procedure, together with the application of the adequate reconstruction algorithm, permits to implement IMic with 2/5 the resolution of the host microscope.