Simple wavefront correction framework for two-photon microscopy of in-vivo brain

Abstract

We present an easily implemented wavefront correction scheme that has been specifically designed for in-vivo brain imaging. The system can be implemented with a single liquid crystal spatial light modulator (LCSLM), which makes it compatible with existing patterned illumination setups, and provides measurable signal improvements even after a few seconds of optimization. The optimization scheme is signal-based and does not require exogenous guide-stars, repeated image acquisition or beam constraint. The unconstrained beam approach allows the use of Zernike functions for aberration correction and Hadamard functions for scattering correction. Low order corrections performed in mouse brain were found to be valid up to hundreds of microns away from the correction location.

1. Introduction

Two-Photon Excited Fluorescence (2PEF) microscopy is widely used in the field of neuroscience, owing to its large penetration depth compared to confocal microscopy. Despite this, wavefront error introduced by the sample ultimately limits the achievable 2PEF signal to noise ratio (SNR) and resolution with increasing depth in the sample.

This degradation is caused primarily by aberration and scattering of the excitation beam. Aberrations can be introduced not only by the sample’s inhomogeneous refractive index but also by imperfections and misalignment of the optical system as well as the refractive index mismatch between the immersion medium and the sample. High numerical aperture (NA) systems, common in 2PEF microscopy, are especially prone to aberrations.

Wavefront correction, as it is applied to 2PEF microscopy, represents a set of techniques that attempt to compensate for light scattering and aberrations. Since most 2PEF systems use a non-descanned detector to collect all emitted fluorescent light, the effects of aberrations on the emission light are minimal compared to the effects on the excitation light. While many different wavefront correction schemes have been reported, the common goal is to find a correction for the wavefront of the excitation beam that yields an optimally focused beam.

One way of estimating the optimal wavefront involves directly measuring the wavefront of fluorescent light originating from a localized fluorescent object using a wavefront-sensor. While this approach has been demonstrated in relatively non-scattering samples like zebrafish [1] or drosophila embryo [2], the emitted fluorescent light is in the visible wavelength band and is prone to scattering effects and hence this approach is not well suited for highly scattering samples such as mouse brain.

This limitation of direct wavefront sensing can be overcome by using wavefront-sensorless methods to determine the optimal wavefront. In these methods, the wavefront of the incident beam is modulated in a systematic way and either the 2PEF signal [3, 4] or some image property such as the mean intensity [5] or image displacement [6, 7] is used as feedback to drive an algorithm that determines the optimal wavefront. In addition to being compatible with highly scattering samples, wavefront-sensorless methods offer the further advantage that no new optics need to be implemented on the detection arm of the microscope. However, wavefront-sensorless methods demonstrated so far have suffered from limitations such as requiring serial image acquisition [6], requiring the introduction of fluorescent beads to measure image displacement [7], long optimization times [3, 7] or have generated corrections that are valid over only a small volume [4].

Here, we present a simple 2PEF signal-based wavefront correction scheme that does not require image acquisition or beam constraint, can use intrinsic structures in the brain as signal sources for optimization and has modest hardware requirements. The scheme is especially suited for microscope setups that utilize liquid crystal spatial light modulators (LCSLMs) for patterned illumination and can be implemented on microscopes that already utilize an LCSLM for beam-shaping [8, 9] without additional modification.

Our scheme is distinct from several other previously demonstrated wavefront-sensorless in-vivo schemes [3, 4, 7] in that it uses a modal rather than a zonal approach. In zonal schemes, measurements are used to determine the optimal value at each pixel or a subset of pixels of the modulator. In modal approaches, the correction is determined across the whole pupil at each iteration, which speeds up the optimization. Even though modal schemes have been demonstrated before [5, 10], and have been shown to be useful for in-vivo imaging [11], the model free approach we present exploits the non-linear dependence of two-photon excitation to optimize focal quality based only on the measured 2PEF intensity [12, 13] to achieve correction without the need for beam constraint or image acquisition. The scheme we present can also compensate for scattering by using the Hadamard basis in addition to the commonly used Zernike basis. We present results of optimizations performed in various phantoms and biological samples including in-vivo mouse brain.

The optimization scheme we present progressively increases the 2PEF signal at each iteration, and hence requires a signal source that is not only stable but is also relatively immune to photobleaching. We demonstrate that Sulforhodamine 101 labeled astrocytes have these properties and can be effectively used as intrinsic guide-stars throughout the rodent cortex for signal-based optimization.

2. Methods

2.1 Corrections based on the two-photon signal

The peak intensity of a focused, pulsed laser beam is given by:

$$I_{peak}=\frac{2P_{ave}}{{\tau }_{p}f\pi w_0^2}$$ (1)

Where P_ave is the average laser power, τ_p is the pulse duration, f is the pulse repetition rate and w₀ is the Gaussian beam-width. 2PEF emission scales as the square of incident intensity, such that the signal should be optimized when both τ_p and w₀ have minimum possible values, as would be achieved when all beamlets forming the focus are both spatially and temporally aligned [12]. This property would not be true for single-photon excitation, which has no dependence on pulse duration, and a linear dependence on incident intensity.

These 2PEF dependencies on beam properties allow the use of the 2PEF signal as a feedback for beam optimization, under the constraint that decreasing the beam size doesn’t cause a compensating reduction in the number of fluorescent molecules in the excited volume. This condition only breaks down when the object generating the signal is much thicker than the Rayleigh range of the excitation beam $z_R=n\pi w_0^2/\lambda$ (in which case the 2PEF signal becomes independent of the beam-width [14]). Thus, by selecting structures that are of the same order as Z_R, the 2PEF signal can be used as a feedback signal for optimization.

2.2 Modal optimization without beam constraint

In modal optimization, the optimal wavefront φ_corr is expressed as a superposition of basis functions F_i so that ${\phi }_{corr}=\sum b_i{F}_i(x,y)$. Each iteration of the algorithm attempts to determine one of the coefficients b_i. Previous modal implementations of wavefront correction for 2PEF microscopy [5, 10] have relied on a constrained beam approach. In such an approach, the correction functions used for optimization are either derived [5] or experimentally calibrated [10] so that wavefront modulation does not translate the focus. Experimental calibration involves measuring the amount of translation introduced by different basis functions and adding tip, tilt or defocus to each basis function in order to prevent beam translation. This approach prevents apparent signal improvement due to simply moving the focus to a shallower depth. However, in practice, when the beam is constrained in this way, the 2PEF signal is not reliable for feedback since it can sometimes be increased by expanding the focal volume, if the new volume includes a nearby region of higher fluorophore concentration [15]. We demonstrate that it is possible to achieve corrections without any kind of beam constraint. Also, the need for image acquisition exposes a large field of view to excitation light while the optimization is being performed, which can cause photobleaching in the entire region that is being imaged.

In our scheme, we have found that beam constraining is unnecessary if a discrete object can be used as a signal source for the optimization process. This recognizes that optimization will both translate the beam to find the point of highest fluorescence, and then optimize spatiotemporal focusing on this point [13]. Since the 2PEF signal itself can be used as a measure of beam quality, we eliminate the need for both image acquisition and experimental function calibration or special functions. This model-free approach also allows us to freely vary the functions used for optimization. While previously demonstrated modal schemes have used Zernike functions to correct low-order aberrations, our scheme can achieve corrections in highly-scattering samples through the use of Hadamard functions.

In addition, our approach provides the versatility of being able to perform optimization in either a dwelling beam or a sweeping beam configuration, where the beam either dwells at a single point, or is swept across a small (~10 μm x 10 μm) region during optimization. The dwelling beam approach delivers superior SNR, while the sweeping beam approach is useful for avoiding photobleaching a single point. We note that it is important for the sweeping beam to scan only a small area encompassing a single cell to avoid unpredictable beam translation effects and that the laser power used is much less than that used in wavefront correction schemes that require sequential acquisition of clear images. On a practical note, since repeated image acquisition and analysis is not required, the microscope software itself does not need to be modified and the wavefront correction system interacts with the microscope only through the signal from one of the photomultiplier tube detectors (PMTs).

2.3 Optical setup

An existing home-built 2PEF microscopy platform [16–18] was modified to permit modulation of the excitation beam wavefront by a reflective LCSLM (Pluto, Holoeye). A schematic of the beam path is shown in Fig. 1. The x and y galvanometer mirrors (Cambridge Technologies), the LCSLM and the back aperture of the objective are all on conjugate image planes. This prevents beam motion on the LCSLM or the back aperture of the objective during scanning. The beam is expanded to fill the vertical extent of the modulator and de-magnified to fill the back aperture of the objective (Olympus LUMPlan FLN 60x, NA = 1.0, water immersion).

Fig. 1.

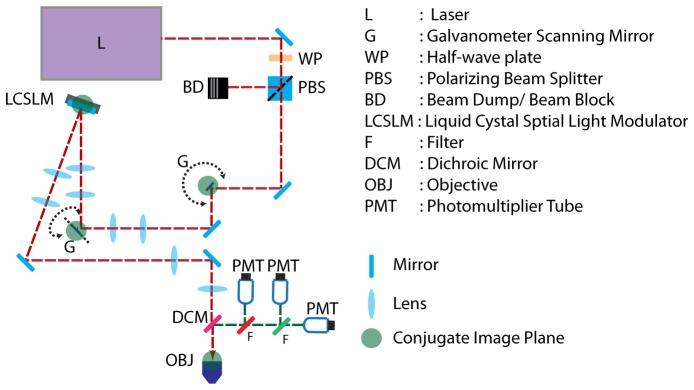
Optical Setup. The x and y galvanometer mirrors (G), the spatial light modulator (LCSLM) and the back aperture of the objective (OBJ) are in conjugate planes.

Excitation light is provided by a mode-locked Ti:Sapphire laser (Mai Tai HP DeepSee, Spectra Physics). The pulse repetition rate is ~80 MHz with a pulse width of ~100 fs. Emitted fluorescence signal is detected using three PMTs (R3896, Hamamatsu) separated by dichroic filters to detect three spectral bands (<505 nm, 505-560 nm and 560-690 nm). The signal from each PMT is converted to a voltage and filtered using a transimepdence amplifier (SR570, Stanford Research), and digitized via an analog to digital converter (PCI 6133, National Instruments).

The LCSLM has a total of 1920x1080 pixels, a bit depth of 8 bits and a refresh rate of 60 Hz. The beam is centered so that a 1080 pixel diameter circular region is used for modulation. The wavefront correction system runs independently of the microscope on a separate computer (Intel Core2 Duo with 4 GB of RAM). The LCSLM is addressed using a video signal from a graphics board (GeForce 9500 GT, Nvidia). All software is implemented as custom-written code in MATLAB (Mathworks). Reliable addressing of the LCSLM was achieved using Psychophysics toolbox extensions for MATLAB [19–21]. The optimization feedback signal was digitized using a data-acquisition board (PCIe-6359, National Instruments).

2.4 Optimization scheme

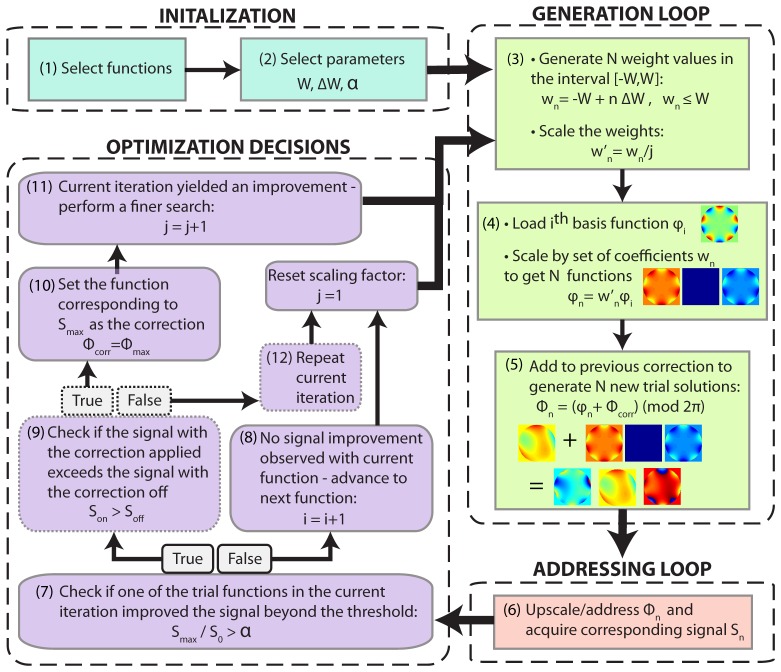
In our optimization scheme, the system starts off with a flat wavefront as the first estimate for the correction. Each new iteration of the algorithm perturbs the previous correction to generate several new trial wavefronts. The scheme decides whether to accept one of these trial wavefronts as the new correction by comparing the 2PEF signal associated with the new wavefronts with that of the previous correction. This scheme is shown in Fig. 2.

Fig. 2.

Wavefront Optimization Scheme. At the beginning, the basis index i and the scale factor j are set to 1. Steps 1,2: A set of correction functions and parameters W (maximum weight), ∆W (step size), and α (acceptance threshold are chosen). Step 3: N weight values w_n (which includes 0) are generated based on the parameters set in step 2. These weight values are scaled by an integer j based on the results of the previous iteration. Step 4: The i^th basis function is loaded and scaled by the weight values generated above to generate N functions. Step 5: The N functions generated in the previous step are summed with the correction of the previous iteration and phase wrapped to generate N trial solutions Φ_n. Step 6: The functions are up-scaled and addressed one by one and the corresponding 2PEF signal S_i is recorded. Step 7: The ratio between the maximum signal S_max to the signal S₀ corresponding to a weight of 0 is compared to α. Step 9: (optional) attempts to detect incorrect decisions caused by signal fluctuations. Step 10-11: If step 7 yielded a positive result, the function corresponding to the maximum signal is set as the current correction and the scaling factor j is incremented by 1. This causes the scheme to perform another optimization cycle using the same basis function but with the weight values scaled by 1/j. Step 8: If step 7 did not yield a positive result, the variable i is incremented and the scale-factor j is reset so that the scheme moves on to the next basis function.

The acceptance threshold (α) is an important feature of the scheme presented here. The 2PEF signal, while being a suitable feedback signal, does suffer from signal fluctuations. These are more pronounced during in-vivo experiments due to breathing and heart-beat. One strategy to deal with fluctuations involves increasing integration time to average them out. However, large integration times slow down the optimization process. Inclusion of an acceptance threshold allows the wavefront correction system to discard steps that do not measurably improve the solution, and thus ignore signal fluctuations. Only signal changes greater than α are considered valid. For best corrections, α is set to the percentage of fluctuation expected on the measured signal. Inclusion of this allows the scheme to achieve corrections in-vivo based on the signal alone without long signal integration times. To experimentally determine α, a number of 2PEF signal measurements are performed without changing the wavefront addressed to the LCSLM, and the maximum fluctuation compared to the mean is set equal to α.

2.5 Phase-wrapping

Wavefront correction has been demonstrated using LCSLMs [6, 7, 12, 13, 22], deformable mirrors (DMs) [4, 5, 10] or a combination of both [3]. While having slow refresh rates compared to DMs, LCSLMs offer a large number of pixels and are typically used in the field of neuroscience to perform photo-stimulation by holographic light shaping [8, 9]. We designed our optimization scheme to be compatible with such light patterning applications.

The optimization scheme operates sequentially, so that the best known wavefront from the previous cycle is carried forward to the next cycle. Since the LCSLM only offers ~2.7π of maximum phase modulation at 8-bit resolution, the number of wavefronts that can be directly summed is limited. Implementing phase-wrapping can solve this problem, permitting a large number of corrections to be summed, but is computationally intensive to calculate for all 1920 x 1080 pixels on the LCSM. Instead, we found that corrections could still be achieved if calculations were performed at lower pixel resolutions. Previous studies have achieved corrections using various numbers of distinct segments of a phase modulator ranging from 256 to 1200 [4, 12, 13, 22]. In our scheme, we performed computations using 64, 256 or 10,000 segments. These wavefronts were then up-sampled to match the modulator resolution as they are being addressed. This approach lowers the computation time by a factor of ~140.

2.6 Optimization functions

While it is possible to optimize a large number of basis functions to generate corrections, fast corrections can be achieved by matching the functions to the expected shape of the correction wavefront. As will be shown in the results section, if the correction functions are chosen judiciously, using only a small number (5-20) functions can yield significant improvements in beam focusing.

While our optimization scheme can adaptably use any chosen basis functions, our current demonstration focuses on Zernike and Hadamard bases. Zernike functions are commonly used to describe wavefront aberrations induced by optical systems and sample geometries [23, 24] and have been previously used in modal schemes [5, 10]. Reported results of zonal optimization schemes in mouse brain contain symmetries that might be easily represented using simpler Zernike functions [7]. Scattering has a more random effect on wavefront shape [12, 13] which is better represented by Hadamard basis functions [22]. Our choice of basis function was determined by the expected type of aberration in each sample. Function definitions and indexing schemes are provided in Appendix 1.

2.7 Sample preparation

Various phantoms were used in this study to characterize the performance of our optimization scheme. The epoxy resin phantom was created by adding titanium dioxide (PM-1 pigment, Alec Tiranti Ltd) at a concentration of 1 µL of pigment per 1 mL of two-part epoxy [25] to yield an approximate μ_s’ of 1 mm⁻¹ at 800 nm. 4 µm diameter fluorescent beads (Invitrogen F-8859, Life Technologies) were suspended in the epoxy prior to hardening. Tape (Transpore, 3M) and raw chicken tissue were also used as scattering samples. For the agar phantoms, the fluorescent beads were suspended in a 0.5% agarose solution and placed on a glass slide with a coverslip on top.

For in-vivo experiments, adult C57BL/6J mice weighing 20-30 g were anesthetized with isoflurane, then IP urethane, secured in a stereotaxic frame, and a small section of the skull was removed to expose the cortex. With the dura intact, Sulforhodamine 101 (12 µM in artificial cerebrospinal fluid) was applied using gelfoam for 5-20 minutes and rinsed. In some cases, 4 µm fluorescent beads were applied to the surface of the dura. A #1.5 glass coverslip was then placed over a drop of 0.5% agarose in ACSF on the brain and sealed with dental acrylic to the surrounding skull. During 2PEF imaging, the mouse’s head was held in place using a metal bar glued to the back of the skull. All procedures detailed here were approved by the Columbia University Institutional Animal Care and Use Committee.

3. Results

In order to evaluate our optimization scheme, experiments were performed in a range of different samples. In all experiments, axial image stacks were acquired with and without the correction applied and the 2PEF intensity of discrete objects was compared in each case.

Optimization and imaging were performed at the same excitation wavelength. An improvement in beam focusing is expected to yield an increase in the 2PEF intensity, thus signal enhancement percentage was computed as SE = $100\times (S_{on}-S_{off})/S_{off}$, where S_on and S_off refer to the 2PEF intensity measured with and without the correction applied respectively.

3.1 In and out-of-focus corrections

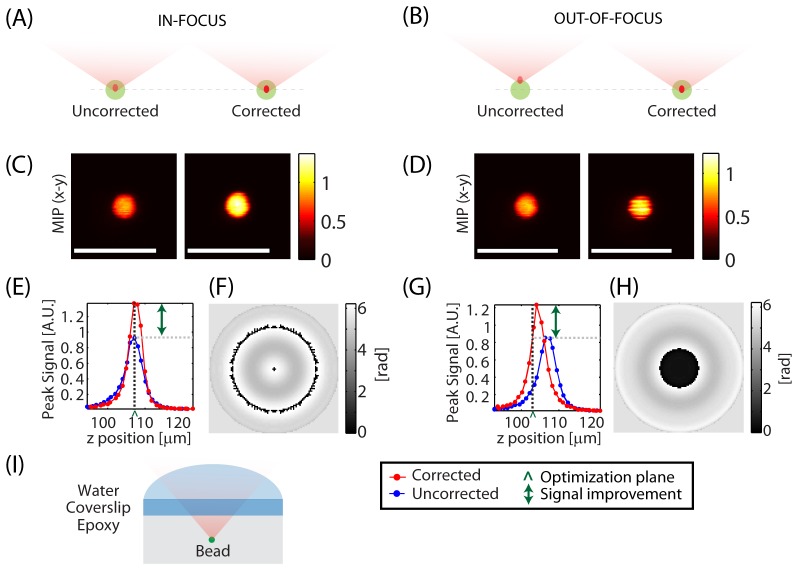
Figure 3 shows optimization performed for both an in-focus and an out-of-focus object. The sample was a scattering epoxy resin phantom with embedded 4 μm beads, imaged through a glass coverslip as shown in (I). Aberrations are thus expected due to scattering and refractive index differences between water used for immersion, glass and the epoxy material (refractive index ≈1.55) [26–28]. Zernike functions were chosen for optimization.

Fig. 3.

In and out-of-focus corrections: Aberration correction performed on a 4 micron diameter bead embedded in a scattering epoxy phantom at a depth of ~100 μm with the bead initially in-focus (left panel) and out-of-focus (right panel). Axial stacks were acquired with and without the correction applied. Optimization was achieved for both the in-focus and out-of-focus bead. In both cases, the optimized focus was formed near the center of the bead. (A,B) Schematics showing the optimization process. (C,D) Max intensity projections of the axial stack to the x-y plane (MIP-xy). (E,G) Peak signal measured at each plane with and without the correction applied as a function of depth. ‘^’ marks the approximate location of the focus prior to optimization. (F,H) Final correction applied to the LCSLM. (I) Schematic of the sample. Scale bars = 10 µm. λ = 755 nm. Configuration: Sweeping Beam.

Optimizations were performed for the same bead, but starting from either a point at the approximate center of the bead (A) or slightly above the bead (B). In both cases, axial image stacks were acquired to monitor for axial shift as well as signal improvement. Max intensity projections to the x-y plane (MIP-xy) with and without the correction applied are shown in (C) and (D) for the in-focus and out-of-focus case respectively. As shown in the axial peak-signal plots (E,G), when optimization was started on an object that was not within the same axial plane as the focus, wavefront optimization both adjusted the depth of the focal point to coincide with the center of the bead, and optimized and improved peak signal similarly to the case where optimization was started at the correct axial position. The differences seen in the final corrections (F) and (H) can be accounted for by the fact that in the out-of-focus case, the wavefront adds axial translation in addition to performing correction. This result shows that optimization can be achieved without beam-constraints so long as a discrete object is present. In all subsequent experiments, the reference object used for optimization was brought into focus before starting the optimization process.

3.2 Comparing Zernike and Hadamard functions

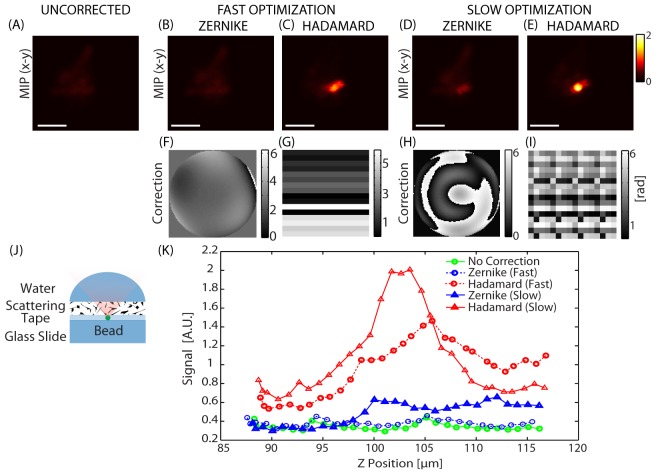
To test whether our signal-based scheme can be utilized to correct for the effects of heavy scattering, the coverslip in the above experiment was replaced with a piece of scattering tape as shown Fig. 4(J). As can be seen in (A), in this case, the heavy scattering makes the bead difficult to resolve. As described previously, Hadamard functions would be expected to better represent the wavefront compared to Zernike functions in a scattering sample. Figure 4 thus compares corrections obtained with Zernike and Hadamard functions. In both cases, both a fast optimization (16 functions) and a slower optimization (60 functions) were performed for comparison (see Appendix 1 for function details).

Fig. 4.

Comparing bases for scattering corrections: Comparing optimization performed with Zernike vs. Hadamard functions on a scattered excitation beam. Short optimization: Correcting function set Z16 (Zernike) and H256-16 (Hadamard). Long Optimization: Correcting function set Z60 (Zernike) and H256-60 (Hadamard). (A-E) are maximum intensity projections to the x-y plane (MIP-xy). (A) Uncorrected. (B) After fast optimization using Zernike and (C) Hadamard functions. (D) After slow optimization with Zernike and (E) Hadamard functions. (F-I) are the corrections corresponding to (B-E) respectively. (J) shows the sample setup and (K) shows the axial peak signal variation with depth before and after correction. λ = 850 nm. Configuration: Standing Beam. Scale bars = 10 µm.

For the fast correction, Zernike function optimization took ~24 seconds, but shows no significant improvement in the image (B). However, Hadamard function optimization, which took 22 seconds, yielded a SE≈230% (C). For a slower correction, optimizing with 60 Zernike functions yielded noticeable enhancement (SE≈50%) as seen in (D), which took 73 seconds while a 70 second Hadamard function optimization yielded a superior enhancement (SE≈357%) as shown in (E). When comparing the corrections (F-I), it can be seen that Hadamard functions are able to capture the randomness of the wavefront better than the Zernike functions. The Hadamard optimization was performed using low order functions represented by only 256 distinct segments on the LCSLM. This is consistent with other studies which show that measurable enhancement can be achieved even when using a small number of segments [22, 29]. While using higher order Hadamard functions is likely to yield better results, optimizing over a larger number of functions will increase computation time.

3.3 Sample-specific correction functions

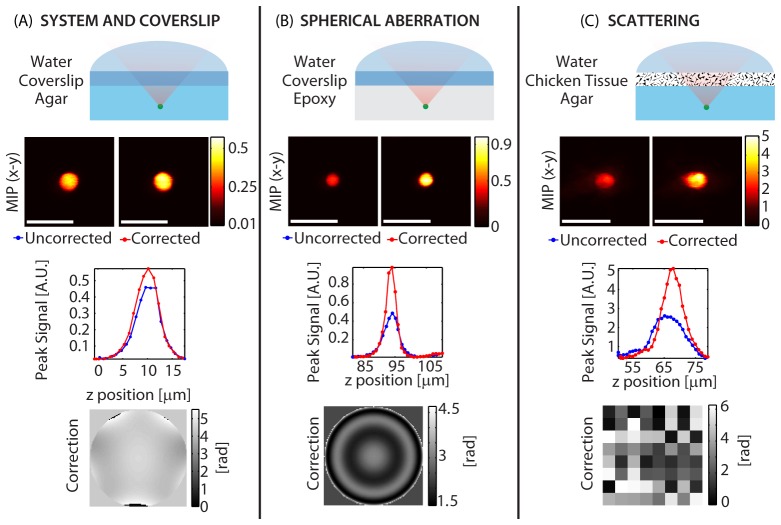
One advantage of using a modal approach is that specific types of wavefront error can be targeted by choosing specific optimization functions. Figure 5 shows three cases where optimization functions have been chosen based on the sample. (A) shows an agar and glass composite sample that mimics a typical window used for in-vivo brain imaging experiments. (B) shows a case where high refractive index mismatch is present while (C) shows corrections achieved when imaging through scattering chicken tissue. Sets of Zernike functions were used for the first two samples, while Hadamard functions were used for the final sample (function sets Z16, ZR and H64 respectively, as defined in Appendix 1). Both the optimization time and the final enhancement vary by sample.

Fig. 5.

Comparison of optimizations performed on 4 micron diameter beads embedded in various samples: The functions were picked to match the expected wavefront error. (A) System and coverslip correction. (B) Spherical aberration correction. (C) Scattering induced by chicken tissue. Axial stacks were acquired with and without the correction applied. Each column shows the sample schematic (row 1), maximum intensity projection to the x-y plane (MIP-xy) (row 2), peak signal variation with depth (row 3) and the correction applied to the LCSLM (row 4). λ = 755 nm (A, B) and λ = 850 nm (C). Configuration: Sweeping Beam (A,B) and Standing Beam (C). Scale bars = 10 µm.

The system and coverslip correction yielded an enhancement of SE≈25%. The spherical aberration correction yielded an enhancement of SE≈100%, and the chicken tissue scattering correction yielded an enhancement of SE≈95% as measured using a 4 micron diameter bead. The optimization time in each case was 16.1 seconds, 4.5 seconds and 96 seconds respectively. One important result here is that for samples where spherical aberration is present, significant improvements can be achieved in a short (~5 second) correction using the function set ZR. This is in agreement with Booth et al. [27], who have shown computationally that the wavefront error introduced by refractive index mismatch can be well approximated by several orders of Zernike spherical aberration functions.

3.4 In-vivo corrections

Our correction method does require the presence of some fluorescent contrast that is physically constrained. Ideally, these sources of signal should be well distributed in all areas that are being imaged. In addition, they should provide a stable 2PEF signal. While fluorescent beads can be used for this purpose, introducing beads requires injection, which can disturb the brain, or in-utero surgery [7].

Rather than introduce external sources, we focused on utilizing structures already present in the brain as signal sources. We identified both astrocytes and blood vessels as possible candidates. We first attempted to use blood vessels carrying dextran-conjugated FITC (Fluorescein isothiocyanate), however the movement of red blood cells resulted in high levels of signal fluctuations. Instead, we chose to use astrocytes, which are distributed widely in the cortex, and can be easily loaded with a cell-specific red fluorophore (Sulforhodamine, SR101) via simple topical, or even intraperitoneal labeling [30–32]. Since SR101 is distributed via astrocytic gap junctions, it can spread to astrocytes > 500 microns deep into the brain within 30-60 minutes of application. The excitation and emission spectrum of SR101 are complementary to GFP, GCaMP or Oregon Green labeling of neurons [33].

3.4.1 Window-only corrections

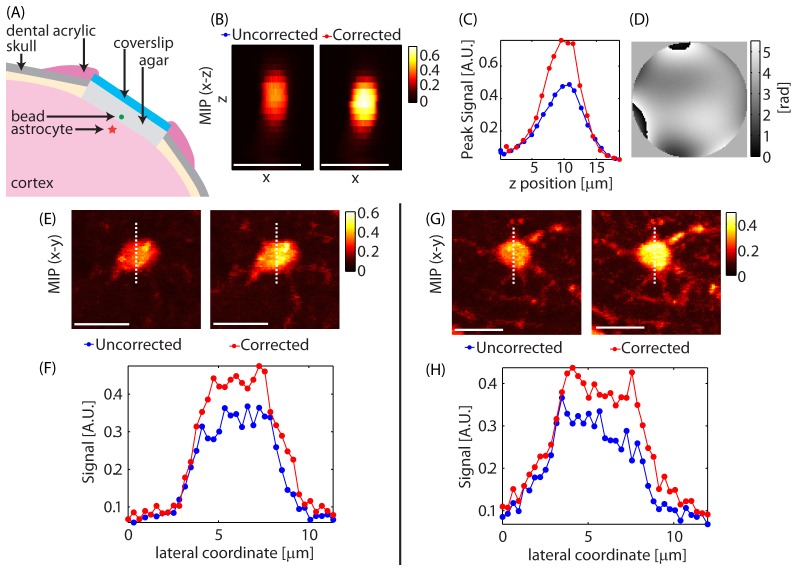
As previously shown in Fig. 5(A), performing a correction using a bead imaged through a coverslip yielded ~25% improvement in signal, corresponding to correction of system and coverslip aberrations. Since the windows used for in-vivo imaging were made using a single coverslip, as shown in Fig. 6(A), it was expected that performing such a correction would also yield improved signal in-vivo. To test this correction, we introduced 4 µm diameter beads onto the surface of the dura, under the cranial window during its construction. When comparing the axial image stacks with and without correction, the window correction itself shows improved 2PEF signal as seen in (B) and (C).

Fig. 6.

Cranial window corrections: A correction was performed using a 4 µm diameter bead placed underneath the window on the surface of the dura. The correction obtained using the bead was applied to image astrocytes near the surface of the brain. Axial stacks were acquired with and without the correction applied. (A) Schematic showing the sample setup. (B) Maximum intensity projections to the x-z plane of the bead used for optimization. (C) Peak signal variation with depth for the bead. (D) The final correction applied to the LCSLM. (E,G) Max intensity projections to the x-y plane of astrocytes at a z≈65 µm with and without correction. (F,H) Signal variation along the dashed lines in (E) and (G). Optimization time was 18 seconds. λ = 850 nm. Configuration: Sweeping Beam. Scale bars = 10 µm.

The correction shown in (D), was achieved in ~18 seconds and yielded enhancement of SE≈56% as measured on the bead (F). When the same correction was applied to two astrocytes at a depth of z = 65 µm in the brain, enhancement values of SE≈22% and SE≈15% were obtained compared to an uncorrected excitation beam as shown in (E-H).

3.4.2 Brain and window corrections using intrinsic guide-stars

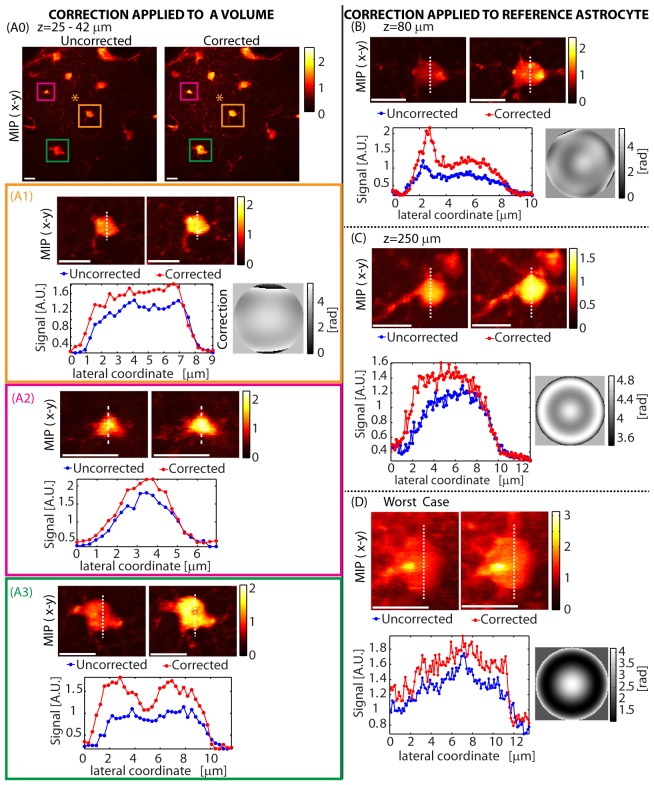
While just correcting for aberrations related to the cranial window is seen to be beneficial, next we set out to perform wavefront corrections to account for both window and brain induced aberrations. Figure 7 shows corrections achieved using astrocytes at various depths as the reference object. In each case, an astrocyte was chosen as an intrinsic guide-star and optimization was run to maximize the two-photon signal. In all cases, the optimized focus of the beam remained on the chosen astrocyte despite dense labeling of local somata and processes. Figures 7(A1-3) demonstrate that a single correction can improve imaging of astrocytes throughout the imaged volume. Figures 7(B)-7(D) show corrections optimized on single astrocytes. The correction shown in (C) on an astrocyte at a depth of z = 250 µm was achieved using the function set ZR, which targets spherical aberration and is seen to improve both signal as well as the visibility of processes. (D) shows a worst case scenario. Even though the astrocyte is weakly labeled and is barely discernible over the background, the optimization process still provided some improvement in both signal and image quality.

Fig. 7.

In-vivo corrections using astrocytes at various depths: (A) A correction was performed using the astrocyte at the center of the field of view (indicated by a ‘*’ in A0). An axial stack of this field of view (approximately 120x120x19 µm) was then acquired with and without this correction. (A0) shows the max-intensity projection to the x-y plane (MIP-xy). (A1-A3) shows the MIP–xy and signal cross sections of three astrocytes in the volume located at z≈35 µm, z≈40 µm and z≈25 µm respectively, showing that the correction remains valid across the volume. In (B,C,D), a correction was performed on the same astrocyte as imaged, for a range of astrocytes at different depths. The final LCSLM correction pattern is shown next to the signal variation plot. Function sets used for optimization were: (A) Z16, (B) Z16 followed by ZR, (C) ZR and (D) ZR. Optimization time was (A) 19 seconds, (B) 37 seconds, (C) 6 seconds and (D) 6 seconds. λ = 850 nm. Configuration: Sweeping Beam. Scale bars = 10 µm.

3.5 Physical extent of in-vivo correction applicability

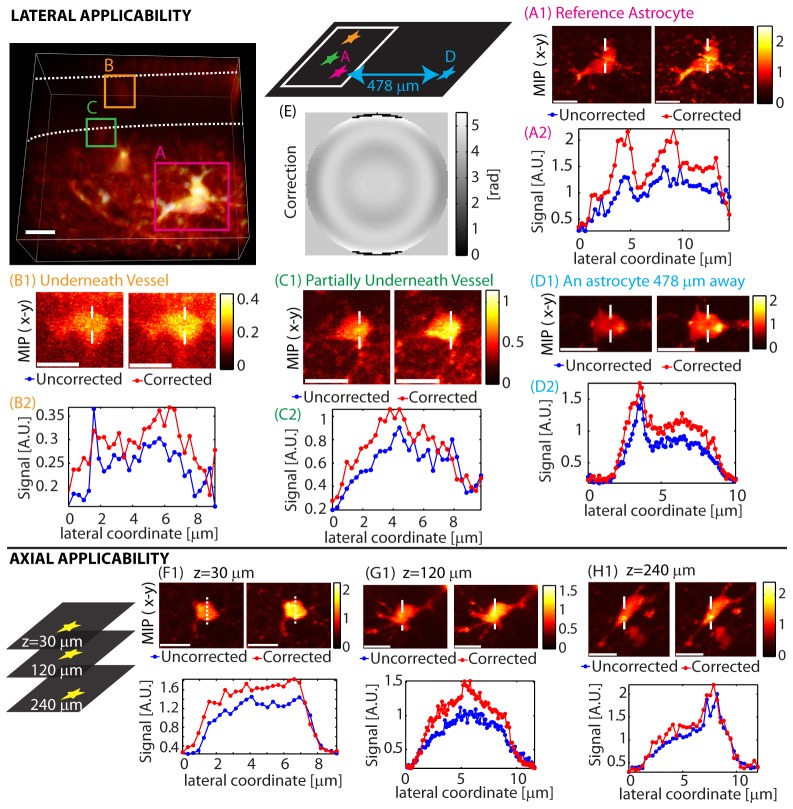
Figure 7(A) demonstrated our ability to improve signal and image quality for objects within the same field of view as the astrocyte used for optimization. However, broader applicability of a correction optimized at one location over the surrounding volume will reduce the number of repeated corrections that need to be calculated during in-vivo imaging.

The extent of validity of a correction can depend on sample properties as well as the type of correction performed. Figure 7(A) showed how a correction performed on an astrocyte at the center of the field of view remains valid over a of volume. Figure 8(A), 8(B), 8(C) shows a similar situation where a correction made using one astrocyte provides some improvement when applied to two nearby astrocytes hidden by a vessel. When the same correction was applied to another astrocyte 478 µm away as shown in (D), image quality improved and yields SE≈40%. Re-optimizing at the same location yielded a higher enhancement of SE≈60% as previously shown in Fig. 7(B). These results show that while local structure can have an effect on corrections, they can remain valid laterally for hundreds of microns.

Fig. 8.

Spatial applicability of a single correction. Lateral: The image on the top left is a 3-D rendering showing the imaged volume indicating three astrocytes and a blood vessel (outlined in dashed white lines). A correction generated using an astrocyte (A) was applied to the same astrocyte (A), two nearby astrocytes (hidden by a vessel) (B,C), and another astrocyte ~478 µm away laterally (D). The corresponding correction is (E). Optimization time was 22 seconds. Axial: A correction generated at z = 30 µm was applied at two other depths (G,H). The corresponding correction is shown in Fig. 7(A). λ = 850 nm. Configuration: Sweeping Beam. Scale bars = 10 µm.

Figure 8 also shows the axial validity of a correction generated at z≈30 µm. The correction is still found to be valid at z≈120 µm and z≈240 µm, but is seen to become less effective with increasing depth. These in-vivo corrections were achieved in a relatively short amount of time of 5-37 seconds.

4. Discussion

We have demonstrated a simple in-vivo two-photon wavefront correction scheme which generates corrections quickly, without image acquisition or beam constraint. The function type used for correction can be freely varied to match the sample, so the scheme can correct both aberrations as well as scattering. Low order corrections performed in in-vivo mouse brain were found to be valid over hundreds of microns from the point of optimization.

The benefits of our approach make it well suited for in-vivo brain imaging, where adaptive optics promises to improve penetration depth and resolution without requiring greatly increased laser power. In-vivo brain imaging studies focusing on functional recording of neuronal activity require multiple regions to be surveyed within a given experiment. Animals are either anesthetized or, increasingly, awake and head fixed, both of which impose constraints on the duration of imaging experiments. Both of these factors make it inconvenient to utilize wavefront correction schemes that take a long time to optimize.

Another concern when performing adaptive optimization is that the process requires additional sample exposure to the excitation light. In our approach, corrections can be generated at much lower excitation power levels than are typically used for imaging: in most cases the power was lowered during optimization so that the 2PEF signal was 2-10 times lower than for imaging. In addition, since corrections are valid over hundreds of microns, and because optimization is performed without image acquisition, additional light exposure can be localized to small regions, potentially outside of the required field of view. Thus, while our scheme does not provide orders of magnitude improvements in signal, its ability to be recalculated at different sites in less than 60 seconds, yielding up to 100% signal improvements makes it feasible for routine in-vivo use.

In exploring the types of aberrations affecting signal and the effects of each correction, we note that in many cases, just correcting for spherical aberration can produce marked improvements, and can be achieved in around 5 seconds using a simple object at the surface of the brain. Rather than utilize a single spherical aberration correction, we found it useful to correct up to five orders of spherical aberration with the function set ZR. This recognizes that the standard optical window configurations used in in-vivo brain microscopy cause marked aberrations that are well suited to Zernike function correction. For example, we have found that wavefront corrections performed on thicker windows made of two coverslips yielded >100% enhancement when correcting only for the coverslips. Hence spherical aberration should be the first aberration to be corrected for. In cases where an objective with a correction collar is used, adjusting the collar will reduce spherical aberration, before starting the optimization process. In addition to spherical aberration, we performed corrections using 16 low order Zernike functions. We found Hadamard functions to be useful when there were obvious signs of scattering as seen in Fig. 4(A), where the image of a single bead appears as many beads. In the case of Hadamard functions, we did not choose specific functions. In principal, it is also possible to combine multiple types of bases, such as Hadamard and Zernike to correct for both aberrations and scattering.

In our in-vivo results, we did not explicitly single out the wavefront error coming from the microscope and the window itself, however for the results shown in Figs. 7 and 8, Zernike functions were used, with minimal improvements being seen with Hadamard functions, suggesting that the dominating effects were aberrations. This is consistent with the fairly long range validity of our corrections within the brain, since the correction for aberrations within the microscope and the cranial window will be valid independent of the location within the sample. However, the smaller variations in the validity of corrections shown in Fig. 8 do highlight some sample-location specificity in our corrections suggesting that brain induced wavefront error was also corrected. In terms of limitations, the corrections generated by our optimization scheme depend on its acceptance threshold, which in turn is based on signal fluctuations. Because setting a high acceptance threshold only picks out the corrections that contribute strongly to signal improvement, the optimization scheme might not achieve the best possible correction for a given location. On the positive side, only picking out the most dominant parts of the correction seems to yield corrections that are valid over a large volume.

In the scheme presented here, optimization times of 5-37 seconds are demonstrated to provide useful corrections over large field of view in in-vivo mouse brain. While a 2-photon signal-based optimization scheme that can achieve higher order corrections in around 5 seconds has been demonstrated previously in fixed mouse brain tissue [4], these corrections were valid for only small fields of view, increasing the number of times optimization needed to be performed to image a larger volume. Comparing to image and scanning-beamlet based segmented pupil approaches demonstrated previously for in-vivo mouse brain imaging [3, 7], our faster modal approach achieves similar corrections while also requiring a less complex experimental setup.

In conclusion, we have demonstrated a simple signal-based wavefront correction scheme that uses the 2PEF signal as the feedback. The optimization scheme has modest hardware requirements and can be implemented on a single LCSLM in a configuration compatible with standard patterned photo-activation [8, 9].

Appendix 1. Function definitions

The correction functions used in our scheme were generated using the definitions presented below and in both cases the minimum and maximum value of each function was mapped to the lowest and the highest phase retardation value of the modulator.

Zernike functions $Z_n^m$ as defined by Thibos et al. [24] were used. The definitions are reproduced below:

$$Z_n^m=\{\begin{array}{c}{N}_n^m{R}_n^{\left|m\right|}(\rho )\cos (m\theta );m\ge 0\\ -N_n^m{R}_n^{\left|m\right|}(\rho )\sin (m\theta );m<0\end{array}$$ (2)

$$R_n^{\left|m\right|}(\rho )={\displaystyle \sum _{s=0}^{(n-\left|m\right|)/2}\frac{{(-1)}^s(n-s)!}{s![0.5(n+\left|\mathrm{m}\right|-s]![0.5(\mathrm{n}-\left|\mathrm{m}\right|)-\mathrm{s}]!}}{\rho }^{n-2s}$$ (3)

$$k=\frac{n(n+2)+m}{2}$$ (4)

Here, ρ and θ are the radial and angular coordinates. Each Zernike function $Z_n^m$ is described by an order n and an azimuthal frequency m. The order n takes integer values with 0 being the minimum. For a given order n, the only allowed values of m vary from –n to n in steps of 2. Since each function is described by two indices n and m, the index k used to describe the functions using a signal index. We set the normalization constant N = 1 for all functions in order to avoid phase-wrapping the initial set of functions used for optimization.

The n^th order Hadamard matrix is defined by the relation [34]:

$$H_n{H}_n^T=n{I}_n$$ (5)

where all the elements of H are either +1 or −1.

Relevant orders of Hadamard matrices can be generated using:

$$H_{2n}=\left[\begin{array}{cc}{H}_n& H_n\\ H_n& -H_n\end{array}\right]$$ (6)

To generate the Hadamard correction functions with n discrete elements, The n^th order Hadamard matrix was generated and each column was rearranged into a 2-dimensional matrix of dimensions $\sqrt{n}$ x $\sqrt{n}$ to represent wavefronts. Functions were indexed so that the k^th column of the Hadamard matrix formed the k^th correction wavefront.

Since various functions were used, they are identified in Table 1

Table 1. Functions used for optimization.

Identifier	Basis	Segments	Functions
ZR	Zernike	10,000	k = (12,24,40,60,84)
Z16	Zernike	10,000	k = 5 to 20
Z60	Zernike	10,000	k = 1 to 60
H64	Hadamard (order = 64)	64	k = 1 to 60
H256-60	Hadamard (order = 256)	256	k = 1 to 60
H256-16	Hadamard (order = 256)	256	k = 5 to 20

below. The number of segments used to compute the wavefronts is indicated in the ‘Segments’ column.

In the case of Zernike functions, specific sets of functions were chosen based on the sample. For Hadamard functions, no special functions were selected.