Automated stereo vision instrument tracking for intraoperative OCT guided anterior segment ophthalmic surgical maneuvers

Abstract

Microscope-integrated intraoperative OCT (iOCT) enables imaging of tissue cross-sections concurrent with ophthalmic surgical maneuvers. However, limited acquisition rates and complex three-dimensional visualization methods preclude real-time surgical guidance using iOCT. We present an automated stereo vision surgical instrument tracking system integrated with a prototype iOCT system. We demonstrate, for the first time, automatically tracked video-rate cross-sectional iOCT imaging of instrument-tissue interactions during ophthalmic surgical maneuvers. The iOCT scan-field is automatically centered on the surgical instrument tip, ensuring continuous visualization of instrument positions relative to the underlying tissue over a 2500 mm² field with sub-millimeter positional resolution and <1° angular resolution. Automated instrument tracking has the added advantage of providing feedback on surgical dynamics during precision tissue manipulations because it makes it possible to use only two cross-sectional iOCT images, aligned parallel and perpendicular to the surgical instrument, which also reduces both system complexity and data throughput requirements. Our current implementation is suitable for anterior segment surgery. Further system modifications are proposed for applications in posterior segment surgery. Finally, the instrument tracking system described is modular and system agnostic, making it compatible with different commercial and research OCT and surgical microscopy systems and surgical instrumentations. These advances address critical barriers to the development of iOCT-guided surgical maneuvers and may also be translatable to applications in microsurgery outside of ophthalmology.

1. Introduction

Intraoperative optical coherence tomography (iOCT) enables cross-sectional imaging of tissue-instrument interactions and surgical dynamics. Over the last decade, various technologies have been developed to aid in intraoperative visualization during ophthalmic surgery, including intraocular fiber probes [1, 2], integrated instruments [3, 4], and modified OCT scan-heads [5–13]. More recently, surgical microscope-integrated iOCT systems [14, 15] have successfully demonstrated real-time OCT imaging concurrent with ophthalmic surgical maneuvers [16, 17]. However, limitations in data acquisition and processing speeds remain critical barriers to real-time volumetric visualization of instrument-tissue interactions and iOCT-guided ophthalmic surgery. Recent developments in swept-source technology have significantly increased imaging speeds over current-generation OCT systems to multi-megahertz line-rates [18–21]. While these novel light sources have demonstrated video-rate volumetric imaging, many remain research prototypes with limited availability and require complex scanning and acquisition systems. Moreover, there remain fundamental trade-offs between imaging speed, optical power incident on the sample, and SNR; and between field-of-view (FOV) and sampling density, which are approaching limits of current-generation detector and digitizer bandwidths. Finally, real-time surgical guidance using iOCT requires precision feedback on the three-dimensional position of surgical instruments relative to adjacent tissue microstructures. Despite previous work using complex ray casting and projection methods to help distinguish subsurface features in volumetric iOCT data sets [22–24], three-dimensional renderings remain difficult to manipulate and interpret in real-time as compared to individual cross-sectional images.

Spatial compounding is a method for cross-sectional visualization of instrument-tissue interactions during surgical maneuvers at video-rates using iOCT [25, 26]. A fixed three-dimensional region-of-interest (ROI) is imaged using densely sampled B-scans and sparsely sampled C-scans. Here, the ROI is set such that the B-scan dimension is aligned with the trajectory of the surgical instrument and sparse C-scans span the width of the surgical instrument. Adjacent B-scans are then averaged, which ensures the surgical instrument cross-section is visible as surgical maneuvers are performed within the ROI. This technique provides several advantages, including SNR enhancement and mitigation of shadowing artifacts as a result of averaging, and enables video-rate visualization of surgical dynamics at the modest imaging speeds of current-generation clinical OCT systems (~10-50 kHz line-rate). However, spatial compounding trades temporal resolution for FOV, which generally limits video-rate visualization to small ROIs at the tip of surgical instruments. Another limitation is that the spatial compounding FOV must be precisely aligned with the surgical instrument such that the B-scan dimension is parallel to its projected trajectory, which constrains the types of surgical maneuvers able to be imaged and adds additional complexity and delays to standard surgical workflow. While the implementation of heads-up display has aided the alignment and localization of spatial compounding FOVs relative to surgical ROIs [15, 27], the potential for iOCT-guided surgery using spatial compounding remains limited.

Real-time visualization of surgical dynamics requires tracking both the orientation and tip position of surgical instruments and using this information to dynamically control the OCT scan-field in real-time. While documentation cameras, which are integrated in all surgical microscopes, may be used to track instrument positions, image processing of live surgical video frames suffers from several drawbacks. Complex image processing algorithms are needed for high-accuracy tracking. These methods are computationally expensive and trade tracking performance for temporal resolution, therefore, making video-rate operation not readily achievable [28–32]. Several methods for video-rate instrument-tracking using a video feed have been developed specifically for retinal microsurgery and are based off of machine learning and data fusion [28–32]. However, these methods rely on offline training models, which are susceptible to large errors when encountering complex features not included in their training set [26]. As a solution, recent approaches have employed online-learning with a continuously adaptive model [29]. While this has improved performance over previous methods, the tracking accuracy of both approaches remains highly dependent on properties of the video feed and generally achieves 70-90% accuracy at a 15-pixel error threshold [29]. Instrument modifications to increase the contrast of the working-tip may help reduce the computational complexity of tracking algorithms but poses potential safety hazards. For example, placing LEDs at the instrument working-tip in conjunction with wavelength-specific imaging may provide enhanced contrast and easier instrument detection using image processing. However, any modification to the working-tip of conventional surgical instruments raises significant safety concerns, such as alterations to the ergonomics and performance of the instruments, potential sterilization complexities, electrical shock hazards, and chemical and light toxicity. Magnetic tracking methods may cause fewer safety concerns, but are susceptible to noise from ferromagnetic and electromagnetic interference caused by objects placed near the tracking volume, such as surgical instrumentation and clinical monitoring equipment [33].

We propose an alternative approach by tracking the free-tip of the instrument and computing the position of the working-tip using prior information on instrument geometry. This allows for a wider range of instrument modifications by using active or passive markers with minimal safety concerns. A larger FOV needs to be tracked using this approach because small motions at the working-tip will result in a larger range of motions at the free-tip assuming that the instrument is held closer to the working-tip for optimal control and stability. Moreover, while only two-dimensional positional information is needed for lateral tracking, the three-dimensional pose of the instrument needs to be unambiguously determined to accurately compute the working-tip position in the lateral plane. Similar tracking methods for image-guided surgery have been previously demonstrated for fMRI and CT [34]. Similarly, a manual OCT-integrated scanning probe has also been reported [35] that implements known computer vision and photogrammetry algorithms for three-dimensional position estimation from two-dimensional images at video-rates [36, 37]. However, using a single camera for three-dimensional pose estimation requires large tracking features and imaging distance (51 cm), which are impractical in a surgical setting.

Binocular stereo vision is a well-known method for three-dimensional metrology using computer vision. Information about the mathematical model of a fixed camera-pair setup is used to compute the three-dimensional position of points within the overlapping FOV of two cameras. The main bottleneck in these systems is stereo matching or correspondence, in which pixel locations in an image from one camera have to be mapped to corresponding locations in the image acquired by the second camera to create an accurate disparity map. However, if prior information is available about the scene, then the stereo matching problem can be significantly constrained and reduced to a sorting step, which costs virtually no computational overhead. Here, we implement a stereo vision tracking system using infrared markers and two CMOS area sensors for real-time tracking of the free-tip of surgical instruments. The tracking information is then used to calculate the three-dimensional position of the working-tip which is used to automatically align the iOCT scan-field. The proposed system is agnostic to the surgical instrument, OCT system, and surgical microscope. This design is suitable for tracking surgical maneuvers in the anterior segment. For posterior segment tracking, the calculated tip positions may need to be offset in proportion to the refractive power and axial length of the eye. This may potentially be resolved by employing methods for measuring the intraocular lens power and the axial length [38, 39] and using this information to apply a forward correction of the measured tip positions in real-time.

2. Methods

2.1 Design specifications

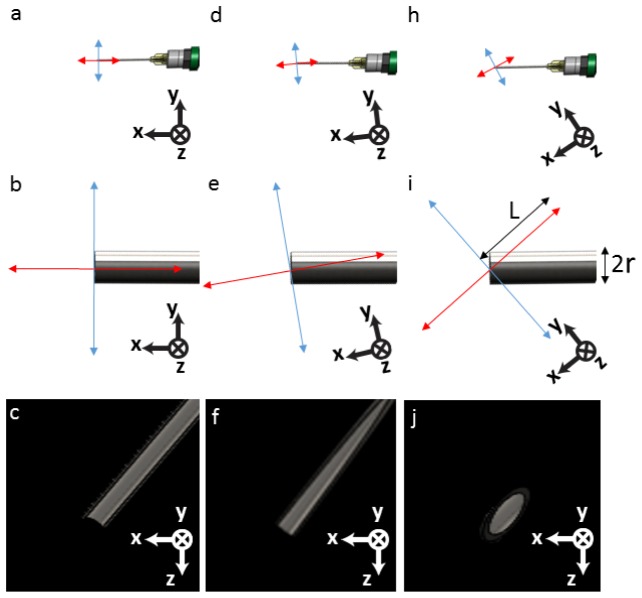
The lateral tracking resolution was determined by the range of working-tip thicknesses for different ophthalmic surgical instruments. The optimal lateral tracking resolution was set at 150 μm to accommodate the diameter of a 40 G instrument such that the instrument tip will be continuously visible in iOCT cross-sections. The orientation resolution (δθ) (Fig. 1) was set such that a full instrument cross-section was visible across half of each B-scan. For a maximum iOCT scan length of 10 mm and a 40 G instrument tip, the desired orientation resolution is 0.9° (Fig. 2). The tracking update rate was chosen to be at least video rate (~30 Hz) to avoid the instrument moving out of plane in sequential cross-sections and reduce blurring artifacts.

Fig. 1.

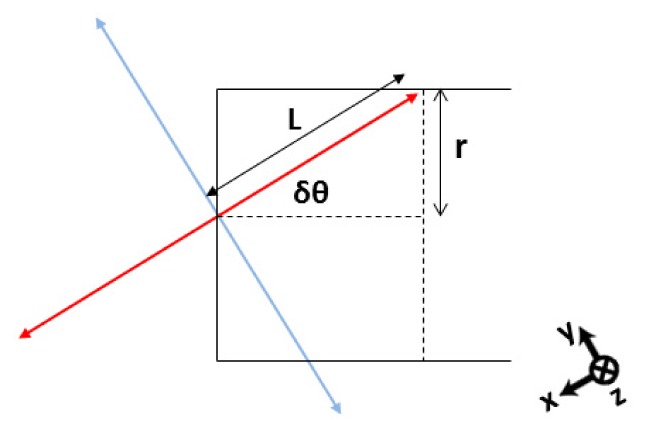
Orientation resolution criterion. The solid black outline is a schematic representation of the en face view of an instrument tip with radius r. The red and blue lines represent orthogonal iOCT scan beams with length 2L. For a maximum iOCT scan length of 10 mm and a 40 G instrument tip, δθ is ~0.9°. x-, y-, and z-axes denote B-scan, C-scan, and A-scan directions, respectively.

Fig. 2.

Simulated iOCT cross-sectional images relative to instrument orientation tracking error. (a) En face view of the instrument, (b) magnified view of the instrument tip, and (c) simulated iOCT cross-sectional image along the instrument axis (red line) with no orientation error. (d)-(f) Small orientation error resulting in a slightly rotated iOCT field relative to the instrument, but the entire instrument cross-section remains visible on iOCT. (h)-(j) Large orientation error resulting in a partial instrument cross-section on iOCT. Red and blue lines denote orthogonal iOCT cross-sectional scans and x-, y-, z-axes denote B-scan, C-scan, and A-scan directions, respectively.

2.2 Binocular stereo vision setup and camera calibration

We implemented a binocular stereo vision system to track active markers at the free-tip of surgical instruments. Binocular stereo vision relies on triangulation to calculate the three-dimensional position of a point based on the disparity in its projection in the image planes of two cameras (Fig. 3). The FOV overlap between the cameras represents the “stereo field”. The stereo vision tracking system was comprised of two CMOS area detectors (PixArt Imaging, Inc.), each with 128 x 96 pixel density and 8X sub-pixel sampling resulting in a 1024 x 768 pixel image. Each camera had a 40° x 30° FOV and on-board processing, which reported the pixel positions of the 4 brightest points in the image plane.

Fig. 3.

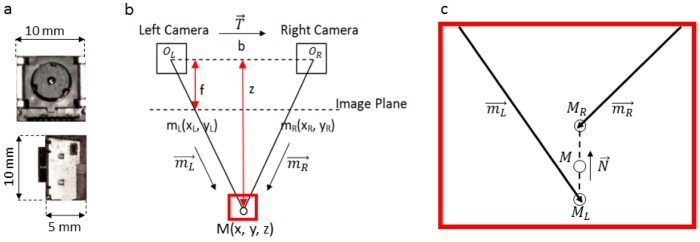
Bionocular stereo vision setup. (a) CMOS area sensor. (b) Stereo vision triangulation with two cameras with optical centers, O_L,R; baseline, b; focal length, f; and imaging distance, z. m_L.R are projections of M at the camera image plane. c) Stereo vision noise may result in non-coplaner calculated three-dimensional rays. Here, the midpoint between M_R and M_L is used to approximate the three-dimensional intersect, M.

The stereo vision setup was calibrated using methods described in [40] and Bouguet’s camera calibration toolbox for MATLAB [41]. The calibration yields a 3 x 4 matrix of extrinsic parameters,

$$[R|t]=\left(\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}|\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right),$$ (1)

which is used to describe the relative pose between the cameras, and an intrinsic parameter matrix for each camera,

$$A=\left(\begin{array}{ccc}{S}_x& (\tan \theta )S_y& x_o\\ 0& S_y& y_o\\ 0& 0& 1\end{array}\right).$$ (2)

Here, S_x and S_y are the x- and y-dimension scaling factors, respectively, and $\theta$ is the pixel skew angle. The skew was set to zero in the calibration process for rectangular pixels. x_o and y_o denote the positions of the principal point, which is defined as the intersection of the optical axis of the camera and image plane. The three-dimensional coordinates of a point, M, and its two-dimensional projection in the camera image plane, m_L,R, are linearly related in homogeneous coordinates by $z{m}_{L,R}=A[RT]M$ [40], where m_L,R is defined up to a scalar, z, which is the distance along the optical axis (Fig. 3(b)). From this equation, it is immediately clear that using a pair of cameras provides a well-defined system of linear equations, allowing us to compute the three-dimensional position, M, from its projection. Depth resolution in stereo vision, $\Delta \text{z}$, is directly proportional to the square of the imaging distance and inversely proportional to both the focal length of and separation distance between the cameras, conventionally defined as the baseline,

$$\Delta \text{z}=\frac{{\text{z}}^2}{bf}.$$ (3)

For a fixed imaging distance and focal length, the baseline can be maximized in order to achieve optimal depth resolution. In our setup, the upper limit of the baseline was set to 100 mm as not exceed the body width of the iOCT system. The cameras were pointed inwards in a converging stereo setup with a tilt that maximized the stereo vision FOV overlap at a desired imaging distance of approximately 19 cm. This imaging distance was set by the axial distance between the bottom of the iOCT chassis and ophthalmic surgical microscope focal plane. This allowed for a depth resolution that was <0.5 mm, suitable for accurate pose estimation.

A model square with 4 IR LEDs (center wavelength: 940 nm) separated by 50 mm was used to calibrate the cameras. The model was manually moved in front of the cameras and 1500 frames were captured at different lateral positions and rotations and used to minimize uncertainty in camera parameter estimation. Information about the model and the captured frames were used by the calibration toolbox to estimate the intrinsic and extrinsic parameters of the stereo system and four orders of lens distortion coefficients in post-processing.

A separate triangulation calibration step was necessary for three-dimensional tracking. Similar to the previous stereo vision calibration, this step only needs to be performed once assuming the relative positions of the stereo vision cameras remain unchanged. First, the pixel coordinates from each camera were normalized using their respective intrinsic parameters (Eq. (2)) and lens distortion coefficients. Direct triangulation uses the three-dimensional intersect between rays ${\overrightarrow{m}}_L$ and ${\overrightarrow{m}}_R$ to find M (Fig. 3(b)) [41]. However, noise in localizing the pixel position of the active marker and errors in the estimated camera parameters may cause the rays to be non-coplanar and nonintersecting (Fig. 3(c)). To account for these noise sources, we employed a triangulation method that computed the midpoint of the shortest line segment connecting both rays [42]. In Fig. 3(b) and 3(c), O_L and O_R denote the optical centers of both cameras. Three-dimensional rays connecting O_L and O_R to normalized pixel coordinates M_L and M_R, respectively, are represented in homogenous coordinates as

$${\overrightarrow{m}}_L=\left(\begin{array}{c}{x}_L\\ y_L\\ 1\end{array}\right),{\overrightarrow{m}}_R=\left(\begin{array}{c}{x}_R\\ y_R\\ 1\end{array}\right).$$ (4)

Using our triangulation method, we can define

$$\begin{array}{l}a{\overrightarrow{m}}_L+b\overrightarrow{N}-c{\overrightarrow{m}}_R=\overrightarrow{T}\\ \overrightarrow{N}={\overrightarrow{m}}_L\times {\overrightarrow{m}}_R.\end{array}$$ (5)

This results in a system of three linear equations with three unknowns (a, b, and c). By applying the intrinsic and extrinsic parameters from the camera calibration, we solve this system of linear equations to calculate the midpoint of the line connecting M_L and M_R using

$$\begin{array}{l}{M}_L=O_L+a{\overrightarrow{m}}_L\\ M_R=O_R+c{\overrightarrow{m}}_R\\ M=\frac{1}{2}(M_L+M_R).\end{array}$$ (6)

The resulting three-dimensional point, M, is our triangulated point.

2.3 Camera-to-world coordinate transformation matrix

The three-dimensional positions from the stereo system are computed with respect to the frame of reference of one camera. In our implementation, the left camera was used as the reference. A transformation matrix is then used to convert these coordinates to the desired “world” coordinate system. To compute this transformation, a single IR LED was mounted on a three-axis motorized stage with 25 mm travel in each direction (Thorlabs, MTS25-Z8). The stage was software controlled and moved in preprogrammed trajectories in the x- and y-axes at 200 μm steps over 6 different z planes separated by 4 mm steps. The starting position of the stage was designated as the “world” coordinate origin. 1500 points were triangulated at known stage positions and used to compute the transformation matrix between the camera and “world” coordinate systems. The computed matrix was then applied to all triangulated coordinates to evaluate the triangulation error in “world” coordinates.

2.4 Active markers and mathematical model

Three IR LEDs (center wavelength: 940 nm) with 160° beam angle were attached to collars and placed on the instrument body in the arrangement shown in Fig. 4. The LEDs were used as active stereo vision markers and the three-dimensional positions of all three LEDs were continuously updated at the frame-rate of the camera. The coordinates of the markers were triangulated and used to calculate the working-tip position and orientation of the instrument.

Fig. 4.

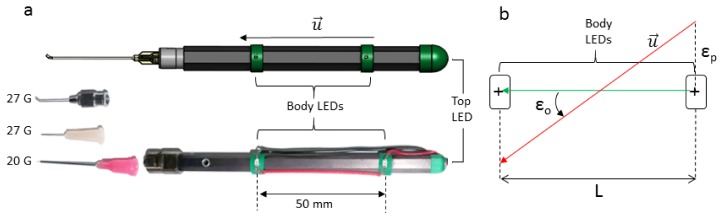
Active stereo vision tracking markers. (a) Solidworks model and photo of the instrument with LED active marker collars attached. The instrument body included a Luer lock termination and was used with three detachable tips: 27 G blunt canula, 27 G needle tip, and 20 G silicone soft-tip. (b) Shematic showing computed orientation error (ε_o) based on LED separation distance, L, and triangulation position error (ε_p).

To calculate the working-tip position, a directional vector, $\overrightarrow{u}$, which was defined by the two body LEDs. These LEDs were positioned such that $\overrightarrow{u}$ would be parallel to instrument axis. The tip was then defined as a point along a vector parallel to $\overrightarrow{u}$ that intersected the top LED. The two body LEDs were radially offset from the axis of the instrument and an LED at the free-tip of the instrument was needed to compensate for the thickness of the instrument at each body LED position. Instrument orientation was defined as the angle between $\overrightarrow{u}$ and the y-axis of the “world” coordinate.

Triangulation position error of each active marker and the desired orientation resolution determines the separation distance between the body LEDs. Thus, for ε_o < δθ, where δθ = 0.9°, and a measured triangulation position error, ε_p, set by the desired resolution of 150 μm, the minimum LED separation distance, L, would have to be 19.1 mm. To compensate for additional error sources, such as variability in the placement of each LED, a separation distance of approximately 2.5 times the calculated minimum was used (Fig. 4).

2.5 Control of the scanning mirrors drive signal

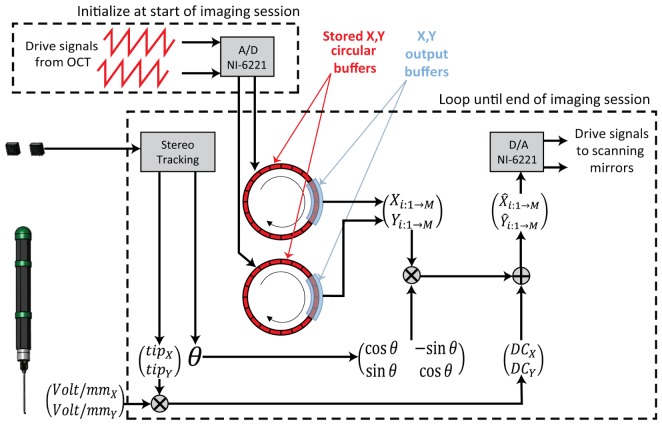
For optimal cross-sectional visualization of tissue-instrument interactions, we chose to continuously acquire sequential B-scans aligned parallel and perpendicular to the instrument axis and centered at the instrument tip. To maintain an OCT agnostic platform, we relayed conventional sawtooth scanner drive waveforms, generated from our iOCT system, through a DAQ board (National Instruments, PCI-6221) to add voltage and field rotation offsets calculated from our stereo vision system to track the tip position and orientation of surgical instruments. At the beginning of each imaging session, one second of the drive signal for each galvanometer was sampled at 100 KS/s on two analog channels and stored in internal buffers. Custom software was developed to find the zero-crossings in the stored sampled signals to identify the start of each scan trajectory. For each channel, the corresponding output buffer output contiguous chunks of samples from the stored drive signal corresponding to a single B-scan. The output buffer looped over the stored signal circularly, starting and ending at a zero-crossing to avoid discontinuities in the output signal. The output buffer size was determined based on the selected sampling rate and desired update rate (30 Hz was used), where

$$bufsiz{e}_{output}=\frac{\text{sampling rate}}{\text{update rate}}\cdot$$ (7)

The calculated tip position and orientation of the tracked instrument were translated to the following transformation matrices, which were applied to the output samples,

$$\left(\begin{array}{c}{\hat{X}}_i\\ {\hat{Y}}_i\end{array}\right)=R\left(\begin{array}{c}{X}_i\\ Y_i\end{array}\right)+\left(\begin{array}{c}D{C}_x\\ D{C}_y\end{array}\right).$$ (8)

Here, DC_x,y denoted the position of the tip and R was a 2D rotation matrix defined as

$$R=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right).$$ (9)

The modified output signals were then output to their respective galvanometer scanner drivers such that sequential orthogonal scan trajectories were centered at the tracked instrument tip and oriented parallel and perpendicular to the instrument axis. A schematic of the stereo vision tracking iOCT system is illustrated in Fig. 5.

Fig. 5.

Schematic of stereo vision tracked iOCT. Drive signals from iOCT were sampled for 1 s and stored in circular buffers. Output buffers were continuously read from circular buffers at ~30 Hz. The output samples were rotated and translated by the computed instrument pose from the stereo vision system by applying voltage and field rotation offsets. Finally, tracked scanner trajectories were output to each corresponding galvanometer scanner.

3. Results

3.1 Performance of stereo vision setup

The setup described in Section 2.3 was used to assess the lateral resolution error in the stereo vision system. Since the stereo vision system reports measurements relative to the coordinate system of the left camera, a coordinate transformation from the camera coordinate system to that of the three-axis stage was performed. The coordinate transformation consisted of a three-dimensional translation and rotation. The translation vector was computed directly by using the starting position of the stage as the origin. Half of the collected points were used to compute the rotation matrix by $X_{motor}=R\times X_{stereo}$, where X_motor and X_stereo were 3-by-M matrices that represented the position of the stage and measured position of the LED, respectively. Here, M represented the number of points collected and R was a 3-by-3 rotation matrix that was the product of rotation matrices about the x-, y-, and z-axis:

$$\begin{array}{c}{R}_x(\theta )=\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \theta & -\sin \theta \\ 0& \sin \theta & \cos \theta \end{array}\right),R_y(\theta )=\left(\begin{array}{ccc}\cos \theta & 0& \sin \theta \\ 0& 1& 0\\ -\sin \theta & 0& \cos \theta \end{array}\right),R_z(\theta )=\left(\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right)\\ R=R_x\times R_y\times R_z.\end{array}$$ (10)

A least squares optimization (Mathworks, Matlab) was used to solve for R. The rotation angles ${\left(\begin{array}{ccc}{\theta }_x& {\theta }_y& {\theta }_z\end{array}\right)}^T$were recovered from R using a Rodrigues transform and plotted to verify convergence (Fig. 6).

Fig. 6.

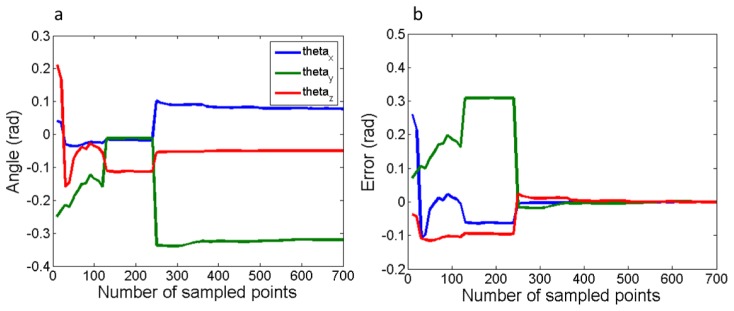
Convergence of coefficients of rotation angles between camera and world coordinates. (a) Calculated rotation angles and (b) error of the calculated angles relative to final converged values.

The rotation matrix converged to the following:

$$R=\left(\begin{array}{ccc}0.9726& 0.0325& -0.3039\\ -0.0635& 1.0235& -0.0540\\ 0.3331& 0.1006& 0.9551\end{array}\right).$$ (11)

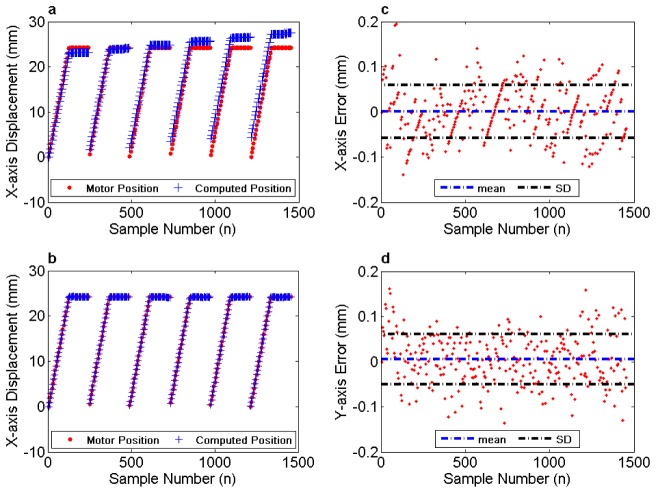
Figure 7 shows the x-axis trajectory before and after coordinate transformation. The error in the calculated positions relative to those reported by the motor controller is shown in Figs. 7(c) and 7(d).

Fig. 7.

x- and y-axis triangulation error of a single IR LED. The traveled trajectory along the x-axis over 6 z-plans at 4 mm increments (a) before and (b) after coordinate transformation. The flat regions correspond to motion in y-axis only. Similar curves were obtained for y-axis (not shown). Triangulation error in (c) x-axis (mean = 0.001 mm, SD = 0.058 mm) and (d) y-axis (mean = 0.005 mm, SD = 0.055 mm).

To evaluate errors in measured orientation, a surgical instrument modified with active markers was mounted on a rotational stage. The stage was manually rotated through 180° at 10° increments 4 times, twice clockwise and twice counter-clockwise. Measurements from this experiment show that orientation accuracy is well within the desired range (Fig. 8).

Fig. 8.

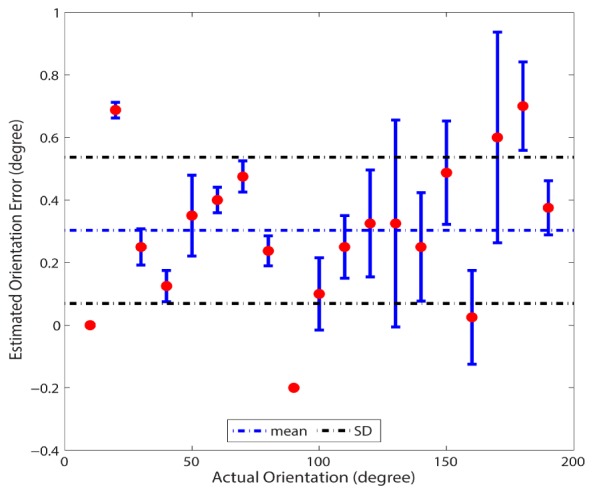
Orientation error measured by manual rotation of a surgical instrument instrument through 180° clockwise and counterclockwise. Mean error = 0.3°, SD = 0.23°.

3.2 Freehand motion error

To assess how tracking errors scaled to the calculated working-tip position during freehand motion, a 0.5 mm mechanical pencil was fitted with LEDs and used in place of the surgical instrument. The tracking system was used to compute the pencil tip as it wrote on paper. The writing was then scanned and compared with the computed tip coordinates to analyze the tracking error. The computed tip trajectory, actual writing, and measured error are shown in Fig. 9. Two experiments were performed, one using raw calculated tracking coordinates and the other with filtered tracking coordinates. In the filtered version, a non-weighted, digital moving-average filter with a 2-frame window was implemented in the tracking software and used to filter out noise due to pixel jitter introduced by sub-pixel sampling on the camera. The filter had a tracking frequency cut-off of 50 Hz and decreased the tracking update rate to 15 Hz. The filtered coordinates were smoother than the raw data due to averaging of jitter noise, but the tracking errors for both experiments were comparable. This data served to verify that the tracking resolution was dominated by the sampling density of the stereo vision imaging system rather than pixel jitter.

Fig. 9.

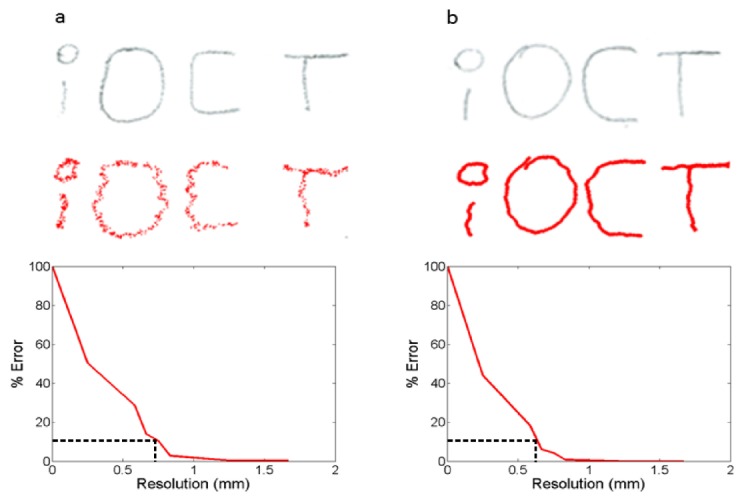
Freehand motion error. Pencil writing (grey) and calculated working-tip coordinates (red) for (a) raw and (b) moving average filtered tracking results. Error plots show relative error between actual and computed positions for different tracking accuracies. Dotted black lines show resolution at 10% error.

Freehand motion was also used to demonstrate automated tracking and control systems running in real-time. A green laser was used as an iOCT aiming beam. A two-axis galvanometer scanner was driven by alternating sawtooth scan trajectories to simulate the cross-hair scan pattern used for subsequent instrument tracking studies. Figure 10 shows the iOCT scan-field tracking the mechanical pencil at various positions and orientations.

Fig. 10.

Freehand motion tracking. (a) Green laser tracking instrument tip at different (b) positions and (c) orientations. Scale bar: 10 mm (Visualization 1 ^{(1.1MB, MP4)} ).

3.3 iOCT integration

We integrated our stereo vision tracking system with our previously described prototype iOCT system [15, 27]. The iOCT was programmed to scan a cross-hair pattern with a length of 5 mm sampled with 1024 x 500 pixels (axial x lateral) at 36 kHz line-rate. Our modified Luer lock instrument handle was used with a 20 G soft-tip, 27 G blunt cannula, and 27 G needle tip (Fig. 4) to demonstrate tracking of conventional surgical instruments (Figs. 11–13). Continuous visualization is demonstrated with each surgical tip with some out of field errors resulting from bending of non-rigid instrument tips (Fig. 11(d)) and tracking errors (Fig. 12(c), 13(b)).

Fig. 11.

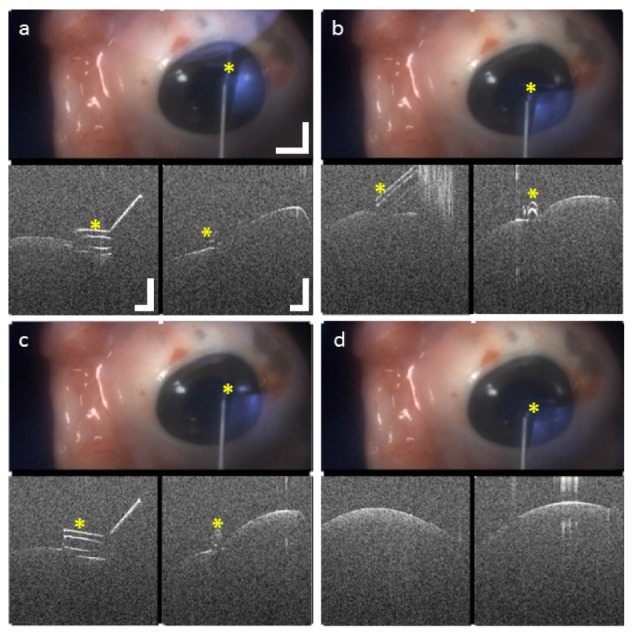
20 G silicone soft-tip on enucleated porcine eye. (a)-(c) Corneal compressions and scraping with the tip visible in both cross-sections. (d) Tip out of field in both cross-sections due to bending of the non-rigid instrument tip. Video scale bar: 5 mm, OCT scale bar: 0.5 mm (Visualization 2 ^{(1.5MB, MP4)} ).

Fig. 13.

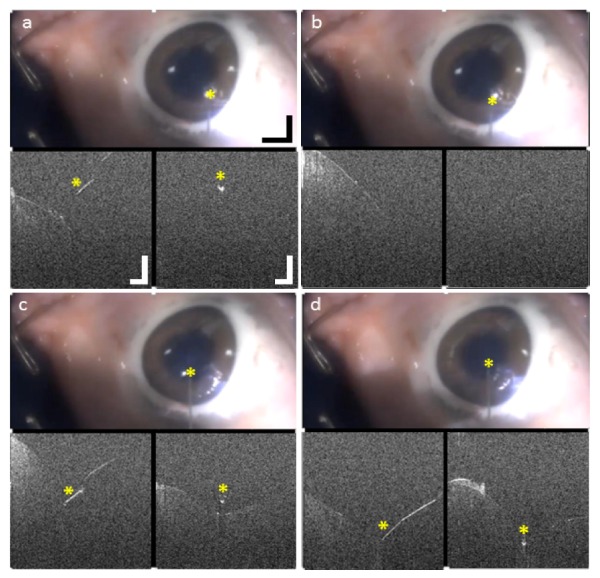
27 G needle tip on enucealated porcine eye. (a) Needle approaching cornea and (b) out of field both cross-sections due to tracking error. (c) Needle starts perforating the cornea and (d) needle visualized inside the cornea after perforation. Video scale bar: 5 mm, OCT scale bar: 0.5 mm (Visualization 4 ^{(4.4MB, MP4)} ).

Fig. 12.

27 G blunt canula on enucealated porcine eye. (a) Scraping corneal surface and (b) near edge of a corneal wound. (c) Instrument out of field in one cross-section due to tracking error. (d) Canula initiates corneal dissection at wound site. Video scale bar: 5 mm, OCT scale bar: 0.5 mm (Visualization 3 ^{(4.6MB, MP4)} ).

4. Discussion

The design considerations for our automated instrument tracking iOCT system were motivated by the need for live visualization of tissue-instrument interactions during ophthalmic surgical maneuvers. The results from our current proof-of-concept tracking system demonstrate the utility of automated instrument tracking for imaging surgical dynamics by relaxing constraints on both data acquisition speed and volumetric visualization methods. The use of active fiducial markers provides higher contrast tracking features as compared to two-dimensional video feeds, which reduces the computational complexity of real-time image processing and enhances tracking accuracy. Placing the markers on the free-tip of instruments minimizes safety concerns, but requires three-dimensional pose estimation to enable accurate working tip tracking. As described in the Introduction, while three-dimensional pose estimation from a single camera is possible, it is not suitable for a surgical setting. Using stereo vision allows for compact tracked features and shorter imaging distances, which benefits surgical ergonomics and clinical translation. The stereo vision tracking system described here allows for high-speed, computationally efficient tracking of the lateral position and orientation of surgical instruments, and may be combined with precision axial position feedback using OCT for three-dimensional instrument tracking. Moreover, this approach decouples lateral instrument tracking from the underlying OCT technology, which is advantageous in several ways. First, the tracking speed is not limited by the speed of the OCT system. The CMOS sensors used can run at up to 100 frames/second. With sparse stereo processing, three-dimensional position information is available at that rate without affecting OCT resolution or SNR. Second, decoupling of instrument tracking and OCT imaging enables our tracking method to be adapted to current-generation clinical OCT systems, which operate at modest 20-50 kHz line-rates and lag behind research system speeds by more than an order of magnitude. Finally, the processing used in our tracking system is less computationally intensive as compared to processing OCT volumes and completely independent of OCT image quality, which may be partially or completely obscured by ocular opacities as a result of pathology or surgical trauma. Additional system enhancements may be made to further improve tracking speed and accuracy for future stereo vision tracking implementations.

4.1 Resolution requirements and temporal performance

The tracking resolution of our stereo vision system was described in Section 2.3 and set to accommodate continuous tracking of 40 G ophthalmic surgical instruments with 150 μm tip diameter. Our single LED tracking results showed lateral tracking accuracies of <60 μm (Fig. 7), thus satisfying our design criterion. However, during tracking of ophthalmic surgical instrument tips under freehand operation, we observed tracking errors of <1 mm for ~90% of tracked frames (Fig. 9), which only allows for continuous tracking of >21 G instrument tips. When tracking smaller diameter instruments, tracking errors resulted in the instrument moving out of field in OCT cross-sections (Fig. 12(c), Fig. 13(b)). This discrepancy in tracking accuracy is because any errors in triangulating the positions of body and free-tip LEDs scale when used to calculate working-tip positions. For example, the triangulation position error, ε_p, scales at the instrument tip by a factor that is proportional to the instrument length (Fig. 4). Since the errors scale linearly between the free-tip and working-tip, the single LED tracking accuracy provides a useful performance metric for the final accuracy of tracking system. Modifications to the placement of instrument body LEDs may further enhance the accuracy of instrument free-tip tracking. Similarly, the mathematical model used to calculate the working-tip position is another source of position and orientation errors. From the model described in Section 2.4, we see that errors when calculating $\overrightarrow{u}$ would result in a directional vector that is not parallel with the instrument axis. This error would then propagate to the calculated working-tip position when projecting the triangulated free-tip LED position by the instrument length along $\overrightarrow{u}$. Both of these sources of error may be addressed by increasing the separation distance between body LEDs. However, body LED positions are limited by ergonomic constraints that may differ between surgical instruments and surgeons. An alternative solution would be to explore different mathematical models that relax the collinearity constraint on the body LEDs, which would provide a more robust computational method. Furthermore, a quantitative comparison of different triangulation methods with regard to computational efficiency and triangulation accuracy, within the context of this tracking problem would also provide better insight into whether a more accurate triangulation algorithm may be employed. Finally, since both of these error sources are limited by the sampling resolution of the stereo vision cameras in our current setup, increasing the pixel density of the cameras would improve triangulation accuracy and allow for a more compact configuration of active markers by decreasing the minimum separation distance required between body LEDs.

The relatively large variance in the calculated orientation error (Fig. 8) is likely due to repeatability errors of the manually actuated rotation stage used (Thorlabs, PR01 high-precision rotational mount with 5 arcmin resolution). Even so, the error range is well within the design specifications. The non-zero mean in the orientation error measurements is a result of manual alignment errors between the zero degree position of the rotational stage and coordinate system of the tracking system. Since all subsequent orientation changes were calculated as an offset from an arbitrarily set starting position, a non-zero mean orientation error is not attributable to system performance.

Our stereo vision tracking system is designed to calculate the working-tip position based on the assumption that the tip is coaxial with the instrument axis for (Section 2.4). Thus, instruments with curved or non-rigid tips are more challenging to track continuously. As shown in the en face video frame of Fig. 11(d), bending of the flexible silicone soft-tip during corneal compression results in the instrument moving out of frame in the tracked iOCT cross-sections. These tracking challenges may be addressed by integrating image processing of the documentation camera video feed with our stereo vision setup to further refine tracked instrument working-tip positions. Similarly, due to absence of feedback on the actual position of the iOCT beam, the current system is designed for open-loop control of the iOCT scanning mirrors. However, additional real-time processing of iOCT cross-sections may be used to provide closed-loop feedback to the tracking system to ensure instruments are always within the tracked iOCT FOV. However, both of these solutions would increase computational overhead and system complexity.

A 2500 mm² lateral field-of-view was imaged by the stereo vision setup at 100 frames/second. The maximum trackable inter-frame translation was 70 mm, corresponding to the diagonal of the field. The scanning galvanometer mirrors used were Cambridge Technology model 6210H with 0.1 ms small angle step response. The tip tracking velocity was ultimately limited by the allowable update rate on the National Instruments DAQ board used (PCI-6221). The DAQ application programming interface sets an upper limit for the number of software interrupts per second, which limited iOCT drive signal updates to a rate of 30 Hz. This resulted in a maximum tip tracking velocity of 2100 mm/s with a 33.3 ms latency as a consequence of both the open-loop control design and DAQ update rate. It should be noted that the data points collected for Figs. 6 and 7 were not indicative of the temporal performance of our tracking system. Both positional and rotational accuracy measurements were recorded at low temporal frequencies to avoid confounding tracking errors with the settling time of the motorized translation and rotation stages.

4.2 Active markers and design feasibility

The active markers used in this study were designed to be safe, compact, easy to build, and detachable so that they could accommodate different surgical instrumentation. The use of off-the-shelf surface-mount IR LEDs significantly reduced fabrication costs with the intention of demonstrating an inexpensive and disposable tracking add-on that may be easily integrated into the ophthalmic surgical framework. Moreover, the LEDs were driven at 65 mA DC and mounted to the surgical instrument in an insulated package to minimize any potential shock hazards to patients. Similarly, the LEDs (0.8 mW, NA = 0.98) may be considered extended sources, are oriented away from the eye, and any stray reflections incident at the pupil would pose minimal eye hazard risk. Additionally, longer wavelength IR LEDs may be used to further reduce potential eye hazards. In our study, the active markers were wired to a power supply, however, tethering the surgical instrument to a power supply may affect surgical ergonomics and raise additional concerns over preserving a sterile surgical field. Thus, wireless battery operation may be desirable. The LEDs used were rated at 130 mW (electrical power), which would allow for continuous wireless battery-powered operation for over an hour with a 1000 mAh battery. Similarly, the stereo vision cameras in our setup were battery powered and communicated wirelessly with our computer via Bluetooth. These design considerations demonstrate the potential for simple clinical translation of our tracking technology.

4.3 Tracking posterior segment surgical maneuvers

Our current stereo vision tracking system was only tested during anterior segment surgical maneuvers. Tracking in the posterior segment is confounded by an additional 4-f imaging relay formed by the optics of the eye and a widefield aspheric ophthalmic lens used to magnify retina features under ophthalmic surgical microscopy. It may be possible to measure the refractive power of the eye and pupil position relative to the iOCT field to compensate for position offsets in the calculated tip position. Alternatively, if image processing of the documentation video feed is integrated with the tracking system (Section 4.1), then the stereo vision system can be used to approximate the instrument tip position, limit the search-space, and reduce the computational complexity of any video feed image processing algorithms used.

5. Conclusion

Automated tracking of surgical instruments in microscope-integrated iOCT can provide real-time feedback for image-guided ophthalmic surgery. This may help guide surgery decision-making, enhance clinical outcomes, and enable novel surgical techniques requiring precision access to specific tissue layers and microstructures. We demonstrated a stereo vision instrument tracking implementation that allowed automated tracking of a wide range of surgical instrumentations. Our proof-of-principle system was agnostic to both the underlying iOCT technology and surgical microscopy system used, which will facilitate integration with commercially available iOCT systems and benefit clinical translation. Our current stereo vision system achieved a lateral tracking resolution that was able to continuously track >21 G surgical instrument tips, but the use of higher pixel density cameras and alternative triangulation algorithms may further improve tracking accuracies. We presented a design for active tracking markers using IR LEDs that allowed for simple and cost-effective fabrication and is disposable, sterilizable, and wireless. Finally, our stereo vision tracking system addressed critical barriers to the development of iOCT-guided surgical maneuvers and may be translatable to applications in microsurgery outside of ophthalmology.