Diversity in pathogenicity can cause outbreaks of meningococcal disease

Abstract

Neisseria meningitidis, the meningococcus, is a major cause of bacterial meningitis and septicemia worldwide. Infection in most cases leads to asymptomatic carriage and only rarely to disease. Meningococcal disease often occurs in outbreaks, which are both sporadic and highly unpredictable. The occurrence of disease outbreaks in a host population in which the etiological agent is widely carried is not well understood. A potential explanation lies in the fact that meningococci are diverse with respect to disease-causing potential. We formulated a stochastic mathematical model to investigate whether diversity of the bacterial population is related to outbreaks of meningococcal disease. In the model, strains that occasionally cause the disease appear repeatedly in a population dominated by a nonpathogenic strain. When the pathogenicity, i.e., the disease-causing potential, of the pathogenic lineage was low, the model shows distinct outbreaks, the size distribution of the outbreaks follows a power law, and the ratio of the variance to the mean number of cases is high. Analysis of notification data of meningococcal disease showed that the ratio of the variance to the mean was significantly higher for meningococcal diseases than for other bacterial invasive diseases. This result lends support to the hypothesis that outbreaks of meningococcal disease are caused by diversity in the pathogenicity of meningococcal strains.

Meningococcal disease is the collective name for the pathological syndromes caused by Neisseria meningitidis. Despite the notoriety of meningococcal disease, the meningococcus is essentially a human commensal, and the great majority of infections result in harmless colonization of the nasopharynx. Asymptomatic meningococcal carriage is common and has been detected throughout the world. In temperate climates, meningococci are carried by 5–25% of individuals (1–3).

Meningococcal disease occurs on the rare occasions that the colonizing bacteria penetrate the mucosal tissue of the nasopharynx and invade the bloodstream. The presence of meningococci in the bloodstream can lead to invasion of the cerebrospinal fluid and meninges, resulting in meningitis, and the release of highly active meningococcal endotoxins into the bloodstream, which causes fulminant septicemia. These disease syndromes normally develop within a few hours of initial colonization and can occur either separately or together. Fulminant meningococcal septicemia is especially dangerous because it has been associated with mortality rates >30%, and survivors frequently suffer from disabling sequelae (4).

Reported incidence of meningococcal disease varies widely from 1 to 1,000 per 100,000 with the disease following several distinct epidemiological patterns (5–7). Sporadic endemic disease is the predominant epidemiology, with annual incidence rates of 1 to 5 per 100,000, whereas localized disease outbreaks, with incidence between 20 and 30 per 100,000, occur worldwide. These are demographically, temporally, and geographically limited, often being confined to a particular population, such as the members of an educational or military institution, and lasting up to a few weeks. The most serious epidemiological manifestations of meningococcal disease are large-scale pandemic or epidemic outbreaks with incidence that can rise as high as 1,000 per 100,000 and last for several years.

Meningococci isolated from asymptomatic carriers are highly diverse (8, 9). This diversity is structured into clonal complexes, or lineages, identified by genetic characteristics: either electrophoretic type, determined by multilocus enzyme electrophoresis (10); or, more recently, by sequence type, determined by multilocus sequence typing (11). Members of some of these clonal complexes are isolated more frequently from cases of invasive meningococcal disease than would be anticipated from their prevalence among carriage isolates (7, 12). Approximately 10 of these “hyperinvasive lineages” have been responsible for the majority of meningococcal disease reported during the 20th century. Particular lineages are associated with particular types of disease outbreak, but it is not known which bacterial features are responsible for the different epidemiologies.

The unpredictable nature of meningococcal disease, combined with its rapidly progressing and dangerous symptoms, leads to difficulties in disease management and high levels of public concern. Here we investigate the potential of a mathematical model to describe features of meningococcal disease epidemiology and to find out how and why outbreaks of the disease can occur if the disease-causing organism is continuously present. We will demonstrate that the occurrence of meningococcal disease outbreaks is inconsistent with the continuous presence of the homogeneous population of etiological agents at a high density and hypothesize that an explanation for outbreaks lies in the heterogeneity of disease-causing potential of meningococci. We test our hypothesis by analyzing notification data for several invasive diseases.

A Model for Meningococcal Disease

To study the effect of a heterogeneous population on the epidemiology, our model describes the situation of a population consisting of two bacterial strains. One of these strains, which we will call benign, can cause asymptomatic carriage but does not cause invasive disease. The second strain, which we will refer to as invasive, causes as many new infections as the benign strain but, upon acquisition, occasionally causes meningococcal disease. This distinction between a completely benign and an invasive strain is motivated by the observation that the disease-causing potential of N. meningitidis on average is very low, in the order of 0.0001 (13). The pathogenicity of certain lineages, although still small in absolute terms, appears to be at least an order of magnitude higher than this. For instance, the hyperinvasive lineage known as the sequence type 32 (electrophoretic type 5) complex causes invasive disease with a probability of ≈0.01 per acquisition (3), whereas members of the sequence type 11 (electrophoretic type 37) complex cause disease with a probability of between 0.05 and 0.0025 (2). This difference justifies the assumption of a completely benign and invasive strain in our model. A model with more strains is described in ref. 14. Meningococcal disease normally develops shortly after acquisition of the bacterium (2, 4). We, therefore, assumed that if disease develops it does so immediately upon acquisition. We assume that there is no tradeoff between pathogenicity and transmission. It is well known that such a positive tradeoff leads to the evolution of pathogen with intermediate virulence (15). The fact that the pathogenicity is, on average, very low is a clear indication that there is no positive tradeoff between the pathogenicity and transmission.

We assumed that carriage of one strain partially protects against co- and superinfection with a second strain. This assumption is supported by the following observations. First, carriage of the meningococcus induces antibodies, and these antibodies reduce subsequent colonization (16). Second, there are no reported cases of meningococcal disease caused by more than a single lineage, and coinfection is rarely documented in carriage studies. Third, the prevalence of carriage of Neisseria lactamica, a close relative of the meningococcus, is negatively correlated to the prevalence of carriage of N. meningitidis and invasive disease (17, 18), suggesting that carriage of N. lactamica protects against coinfection with N. meningitidis. For mathematical simplicity we have assumed that carriage gives complete protection from co- and superinfection; however, partial protection leads to qualitatively similar results.

To describe the population biology of N. meningitidis we subdivide the host population into classes. We follow standard models (15) by describing the number of susceptible individuals, S, carriers colonized by the benign strain, I, and individuals that have recovered from colonization and are immune, R. In addition, our model describes the number of hosts that asymptomatically carry the invasive strain by Y. The number of hosts with meningococcal disease is given by X. We assume that on the time-scale relevant to disease epidemiology the total host population is constant and has size N = S + I + R + Y + X.

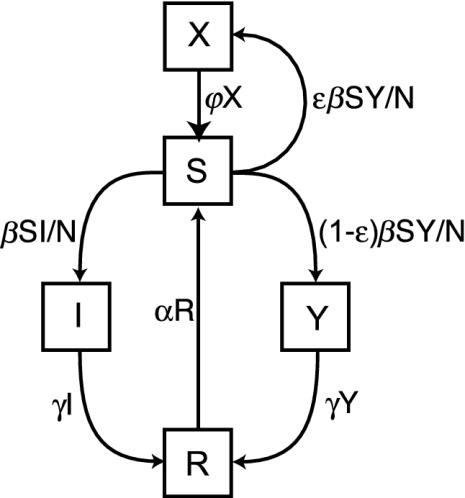
Susceptible hosts acquire the meningococcus through close contact with other hosts carrying the bacterium. The force of infection depends on the fraction of hosts carrying the bacterium and the transmission parameter β (15). We assume a constant average number of contacts per host so that the force of infection for the benign strain is given by β(I/N) and for the invasive strain by β(Y/N). Hosts who develop meningococcal disease do not transmit because of the debilitating and potentially fatal consequences of the disease. Acquisition of the benign strain always leads to asymptomatic carriage, whereas acquisition of the invasive strain can result in either asymptomatic carriage or disease. The pathogenicity, ε, is the probability of disease to develop upon acquisition, hence, the probability per unit of time of acquiring the invasive strain and developing the disease is given by εβ(Y/N). Upon acquisition, asymptomatic carriage develops with probability 1 - ε, hence the probability of acquiring the bacterium and developing asymptomatic carriage per unit of time is (1 - ε)β(Y/N). Hosts who carry the bacterium lose the bacterium and become immune to further infection with probability γ. Hosts lose their immune state and become susceptible again with probability α. Hosts who developed meningococcal disease can recover (or die and be replaced by a susceptible host) with rate Ψ. Fig. 1 depicts these transitions.

Fig. 1.

A diagrammatical representation of the model. The boxes represent the different classes, and arrows indicate transitions between the different classes. In a well mixed population the ensemble means of the stochastic model obey the differential equations (14): dS/dt = αR + ΨX - βS(I + Y)/N, dI/dt = βS(I/N) - γI, dR/dt = γ(I + Y) - αR, dY/dt = β(1 - ε)S(Y/N) - γY, dX/dt = βεS(Y/N) - ΨX.

We modeled the sporadic appearance of invasive strains in the population. Although strains can appear through introduction from another locality, mutation, or recombination, a mechanism that could lead to the repeated appearance of invasive strains with a relatively high rate is the switching on of contingency genes through phase shifting (13, 19, 20). We, therefore, added a transition to our model that lets a very small fraction, μ << ε, of infections with the benign strain result in carriage of the invasive strain and, to keep the population size constant, adjusted the force of infection of the benign strain to β(1 - μ)(I/N). The stochastic transitions (Table 1) define a continuous time Markov process.

Table 1. Transition rates for the Markov process.

Type of transition	Rate	Event
S → S – 1, I → I + 1	β(1 – μ)S(I/N)	Acquisition benign strain
S → S – 1, Y → Y + 1	β(1 – ε)S(Y/N)	Acquisition invasive strain, carriage
S → S – 1, X → X + 1	βεS(Y/N)	Acquisition invasive strain, disease
I → I – 1, R → R + 1	γI	Loss of benign strain
Y → Y – 1, R → R + 1	γY	Loss of invasive strain
R → R – 1, S → S + 1	αR	Loss of immunity
X → X – 1, S → S + 1	ψX	Replacement/recovery diseased
S → S – 1, Y → Y + 1	βμS(I/N)	Appearance invasive strain

Results

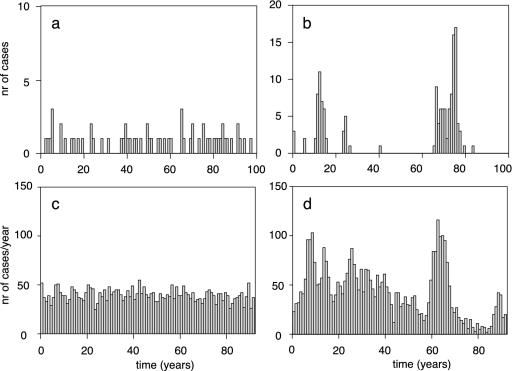
Previous models for meningococcal disease (17, 21) assumed that the bacterial population is homogeneous with respect to pathogenicity, and that all meningococci have the same propensity to cause disease. This scenario is recovered in our model by setting the number of carriers of the benign strain, I, to zero. Under this scenario large outbreaks are unlikely as is confirmed by numerical simulations (Fig. 2a). The number of outbreaks is variable but never strongly clustered.

Fig. 2.

Numerical simulations of the model defined in Table 1. (a) A homogeneous meningococcal population. Parameters γ = α = 10, β = 12.5, Ψ = 1,000, ε = 0.0008, N = 1,000. (b) A heterogeneous bacterial population. Parameters as in a but with μ = 0.0008 and ε = 0.04. (c) A homogeneous bacterial population with a sinusoidal transmission rate with a period of 1 year. Parameters are γ = α = 13, β = 16.25 ± 4.875, Ψ = 15,600, ε = 0.0000192, N = 5,000,000. (d) A heterogeneous bacterial population with sinusoidal transmission rates. Parameters as in c but with μ = 0.0000192 and ε = 0.016.

Fig. 2b shows the number of cases of invasive disease in a heterogeneous bacterial population. The simulation shows a highly variable disease incidence in which outbreaks of different sizes occur. In all simulations the number of hosts carrying the benign strain was essentially constant. The number of cases are clustered in time, and outbreaks follow the appearance of invasive strains in the population. These results show that heterogeneity with respect to pathogenicity can lead to outbreaks.

Outbreaks of meningococcal disease have been associated with high contact rates of hosts (1). Changes in contact rates could potentially explain outbreaks of the disease. We used our model to investigate in how far this mechanism can lead to the clustering of cases of meningococcal disease and large-scale outbreaks. Meningococcal disease rates often show a marked seasonal variation (1). We, therefore, varied the contact rates by assuming that the transmission parameter β changes sinusoidally with a period corresponding to 1 yr. We first investigated the effect of varying contact rates in a homogeneous bacterial population. We found that a periodic change in transmission leads, not surprisingly, to a corresponding periodic change in disease incidence but does not lead to large disease clusters or outbreaks in the number of cases per year, which is fairly constant (Fig. 2c). If, however, we varied the transmission rate in a heterogeneous bacterial population, we found that the behavior is very different. As in the homogeneous case there is a noticeable periodicity in the number of cases within a year (data not shown); in contrast with the homogeneous population, the variation and clustering in the annual number of cases are considerable (Fig. 2d).

We will next quantify the clustering to compare it with epidemiological data. We start with observing that if we set the appearance rate of the invasive strain, μ, to 0, the invasive strain invading a population dominated by the benign strain has a reproductive number (15) equal to 1 - ε. This can be seen as follows: If the population is sufficiently large, the dynamics will be virtually deterministic and the number of susceptibles will converge to the equilibrium of the Susceptibles, Infected, and Recovered model, i.e., S = N(γ/β) (22); the reproductive number of the invasive strain is then Sβ(1 - ε)/γN = 1 - ε. It follows that the invasive strain cannot establish itself in this population and is bound to disappear (15).

Before an invasive strain disappears, it can cause a highly variable and potentially large number of cases of the disease. Under assumption that the number of individuals carrying the invasive strain is small compared with the total population size, the probability of an outbreak to be of size X, p(X), can be found by reducing the transmission dynamics from a continuous time branching process to a discrete, event-based, description (22, 23).

To do so we reformulated this stochastic process by considering a rare invasive strain in a large population dominated by a benign strain. The number of susceptibles is kept at its deterministic equilibrium by the benign strain, so we did not further consider the dynamics of the benign strain. We, therefore, considered only the following events: acquisition of the invasive strain leading to asymptomatic carriage, acquisition of the invasive strain leading to disease, and the removal of an asymptomatic carrier of the invasive strain. Because we were interested only in the total number of cases after the strain had disappeared, we did not consider the time that elapsed between these events. The probability per unit of time of at least one of these events occurring is γ(1 - ε)Y + γεY + γY = 2γY. The probability that the next event is acquisition leading to carriage is (1 - ε)γY/2γY = (1 - ε)/2. Similarly, the probability that the next event is acquisition leading to disease is εγY/2γY = ε/2, and removal through recovery occurs with probability γY/2γY = 1/2. If the number of individuals carrying the invasive strain, Y, reaches 0, the process reaches an absorbing state and stops. The event-based stochastic dynamics are a discrete time branching process, a random walk, for which the transition probabilities do not depend on the state variables.

This random walk can be solved in closed form (22). We found that the total number of cases of disease in an outbreak is given by

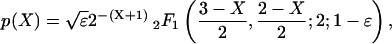where ₂F₁ is the hypergeometric function (24). Note that this distribution depends only on the pathogenicity, ε, and none of the other model parameters. However, the duration of an outbreak is proportional to the average duration of carriage, 1/γ. The epidemiological behavior of an invasive strain can therefore be characterized by the pathogenicity, ε, and the average duration of carriage, 1/γ.

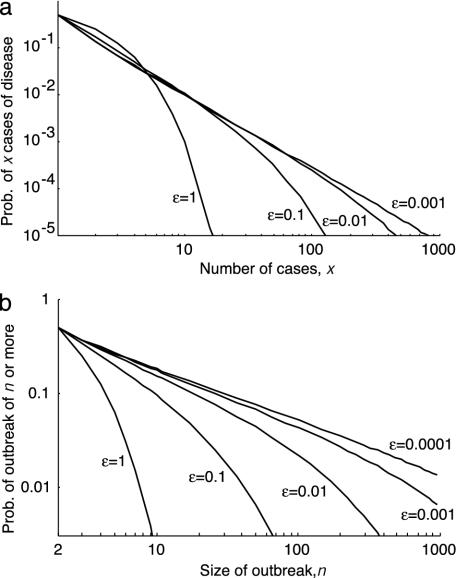
Following the introduction of an individual carrying the invasive strain on average a total of 1/ε carriers will result, and because the probability of contracting the disease is ε, on average one case of meningococcal disease will occur (see Appendix). The average number of cases is therefore independent of the pathogenicity of the invasive strain. The variance in the outbreak size does depend on pathogenicity and is 2/ε (see Appendix). Large outbreaks occur with a much higher probability if the pathogenicity is small. The distribution of the number of observed cases (p(X|X ≥ 1)) is approximately exponential for high pathogenicities. For low pathogenicity, the distributions have tails that are overexponential (Fig. 3a). In the limit of ε tending to 0 we find that the distribution gives rise to a power law with exponent -3/2 (22). Fig. 3b depicts the probability of an outbreak to be at least of size n, in which case we find a power law with exponent -1/2 for large n. This power law leads to clusters of cases of meningococcal disease following the appearance of invasive strains.

Fig. 3.

Probability distributions of observable outbreaks. (a) The probability distribution of the number of cases given that at least one case occurs, p(X|X ≥ 1) = p(X)/[1 - p(0)] = [(1 + √ε)/√ε]p(X), for various pathogenicities. For ε = 1, p(X|X ≥ 1) = 2^-X), and for ε = 0, lim_ε→0 p(X|X ≥ 1) ≈ X^-3/2/2√π (22), i.e., a power law with exponent -3/2. (b) The probability of an outbreak of at least n cases for various pathogenicities. The probabilities are computed as 1 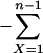p(X|X ≥ 1). For large n and ε tending to 0, the logarithm of the probability scales with the logarithm of the minimum outbreak size and the scaling factor is -1/2.

In the model, invasive strains appear with rate μβS(I/N). Assuming that S and I are given by the equilibrium of the Susceptibles, Infected, and Recovered model, this rate is proportional to the size of the population (see Appendix). If we assume that the strains appear at random, the number of appearances is Poisson distributed. If the number of cases per appearance follows the distribution p(X), the variance in the number of cases per year is (2/ε + 1) × the mean (see Appendix). The ratio of the variance to the mean, therefore, is large if the pathogenicity is small. In a homogeneous bacterial population, in which disease can follow any acquisition with the same probability, the total number of cases will be distributed according to a Poisson distribution, for which the ratio of the variance to the mean will be unity (see Appendix).

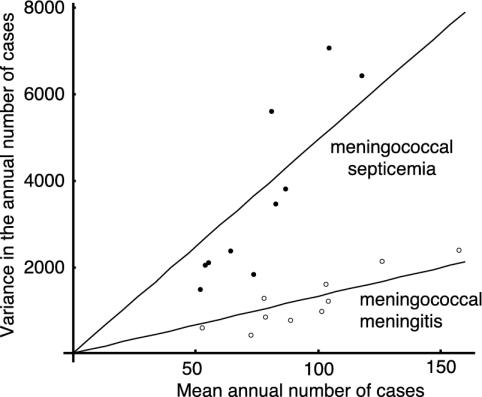
This observation leads to the prediction that the variance and the mean of the number of recorded cases should show a linear relationship for populations of different size. Fig. 4 shows the variance and the mean for meningococcal meningitis and meningococcal septicemia for the different health regions of England and Wales. The gradient of this line offers a way to estimate the ratio of the variance to the mean of the annual number of cases of meningococcal disease. This result allows us to distinguish between two hypotheses: if the bacterial population is homogeneous with respect to pathogenicity, the gradient of this line is predicted to be 1. If the bacterial population is heterogeneous, the gradient of this line should exceed 3.

Fig. 4.

The variance in the annual number of notified cases of meningococcal disease against the mean over the years 1982–1999 (meningococcal meningitis) and 1989–1999 (meningococcal septicemia) for the 10 health regions of England and Wales.

We calculated this gradient for a number of other pathogens that cause invasive disease (Table 2). We found that the ratio of the variance to the mean for all these invasive diseases differs significantly from 3. However, for meningitis caused by Haemophilus influenzae b (Hib) and pneumococcal meningitis we found much lower values than for meningococcal disease, which indicates that for N. meningitidis the diversity of the bacterial population is of particular importance. It is worth noting that the ratio of the variance to the mean was much higher for meningococcal septicemia than for meningococcal meningitis, possibly because hyperinvasive lineages of N. meningitidis are more likely to cause septicemia (25).

Table 2. The clustering of cases in several invasive diseases in England and Wales.

Disease	Variance to mean	Confidence interval
Meningococcal septicemia	49.44	36.56–53.97
Meningococcal meningitis	13.25	10.00–14.83
Hib meningitis	6.61	4.87–7.27
Pneumococcal meningitis	4.91	3.87–5.48

Clustering of cases, which is measured as the ratio of the variance to the mean of the annual incidence and based on the number of notified cases of the disease per year per health region, and 90% bootstrap confidence intervals are given. The data spanned the years 1982–1999 (meningococcal meningitis), 1989–1999 (meningococcal septicemia), 1982–1992 (H. influenzae b meningitis), and 1989–2002 (pneumococcal meningitis). Data source, Health Protection Agency Communicable Disease Surveillance Centre.

Discussion

The genetic characterization of meningococci isolated from carriage and disease has demonstrated that distinct clonal complexes or lineages are associated with particular levels of pathogenicity and types of disease outbreaks (7, 12). We have shown theoretically that the size and duration of outbreaks are determined by the pathogenicity and the average duration of carriage of hyperinvasive strains. Outbreaks are unlikely to result from the introduction of new meningococcal variants that are highly pathogenic, because such meningococci will disappear quickly from the population. Outbreaks are, however, likely to be caused by meningococci that are only marginally pathogenic. The low probability of invasive strains of meningococci causing disease, of the order of 1 per 100 infections, is consistent with this observation. We have shown that the clustering of cases caused by the repeated appearance of mildly pathogenic variants results in a high ratio of the variance to the mean of the annual number of cases. For the England and Wales notification data for meningococcal disease, this ratio was much higher than can be expected by chance and lends support to the hypothesis that outbreaks are caused by members of hyperinvasive lineages that exist in a background of bacteria of lower pathogenic potential. Our model predicts distinct patterns in relatedness between bacteria that cause disease and bacteria that cause carriage in the general population. With the advent of genomic analysis this hypothesis will be testable.

We have shown here that seasonal variation in transmission leads to a seasonal variation in carriage and, thus, disease incidence; however, variation in transmission does not lead to variation in the yearly incidence unless the meningococcal population is diverse with respect to disease-causing potential. Alternative explanations for the variation in the annual incidence would therefore have to include factors that vary on this time scale. One possible explanation would be an association between meningococcal disease and another infectious disease. Several other pathogens have been postulated to be associated with meningococcal disease, yet there is little evidence to substantiate most of these claims. Only for influenza A has it been shown that infection with the virus is a risk factor for meningococcal disease (1). Because influenza A generally predisposes the hosts to infection with bacteria, this is unlikely to be the main explanation for the high variation in meningococcal disease relative to the variation in pneumococcal and H. influenzae b meningitis.

For disease outbreaks caused by bacteria with low pathogenicity, the number of cases of disease is distributed by a power law with exponent -3/2. Power laws are a general property of critical systems, and the exponent of -3/2 occurs generally in branching processes at criticality (see theorem 13.1 in ref. 26). Our theoretical results corroborate previous findings that criticality, and the accompanying power laws, occur naturally in epidemiological situations (23, 27, 28). Distributions that obey power laws have been associated with events such as forest fires and earthquakes (29). Such distributions have overexponential tails and are perceived as being disastrous, in that most frequently only small realizations are observed, but occasionally a large realization occurs. In the case of meningococcal disease, the small realizations would be equivalent to sporadic cases with large disease outbreaks representing large events.

Our findings have a number of implications for the management of meningococcal-disease outbreaks. First, the fact that we detected the signature of clustered outbreaks in notification data gathered at a national scale suggests that outbreaks of meningococcal disease occur commonly. This finding implies that many of these outbreaks will go undetected, and that the association of meningococcal disease with semiclosed environments is due primarily to the ease of detection. Second, if outbreaks are mainly caused by mildly pathogenic strains, the number of individuals who are exposed to invasive meningococci will be large. It is unlikely that carriers of invasive meningococci are confined to the primary and secondary contacts of the diseased individuals. This observation may explain the mixed success of chemoprophylaxis in the control of meningococcal outbreaks (30), which aims to control a disease outbreak by eliminating the invasive meningococcus from the population. This approach will work best in situations where the invasive meningococcus is confined to a small group of contacts. Under our model this situation will obtain in the case of meningococcal disease outbreaks caused by more pathogenic variants that will, in any case, be self-limiting. The measure will be less effective in the case of meningococci of lower pathogenicity, which are likely to cause larger outbreaks. This reasoning leads us to conclude that chemoprophylaxis will be least effective in those instances where it is most needed. A further confounding factor is that chemoprophylaxis does not protect against subsequent reacquisition of N. meningitidis (31), therefore, widespread prophylactic treatment can fuel the outbreak by creating pockets of susceptible individuals in a population in which the invasive meningococcus is circulating.

Vaccination against the meningococcal strain responsible for an outbreak is potentially a more effective control measure. Although a policy of local vaccination is unlikely to eradicate the meningococcal strain immediately, it will reduce the availability of susceptible individuals and should therefore reduce the longevity of the outbreak. Whereas vaccines against serogroup C and serogroup A capsular polysaccharide are available, and have been used successfully in outbreak control, there is currently no vaccine against the serogroup B polysaccharide, and meningococci expressing this capsule are responsible for the majority of cases of invasive disease in many countries (32). Whereas the coverage of protein-containing outer membrane vesicle (OMV) vaccines is compromised by the high antigenic variability of these cell-surface components (32), each hyperinvasive meningococcal lineage tends to be associated with particular combinations of protein antigens. Outer membrane vesicle vaccines based on outbreak strains have been shown to be effective in the context of hyperinvasive meningococcal disease outbreaks (33, 34), and in the absence of comprehensive meningococcal vaccines, the preparation of outbreak-specific vaccines against common hyperinvasive meningococci may be an effective disease-control strategy. This strategy is being adopted to deal with the hyperendemic outbreak of meningococcal disease caused by members of the sequence type 41/44 complex (lineage III) in New Zealand, but it does rely on the provision of lineage-specific vaccines (35).

Appendix

The generating function of the outbreak distribution is 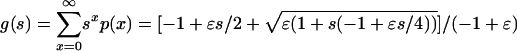. The mean number of cases is g′(1) = 1, and the variance is g″(1) + g′(1) - g′(1)² = 2/ε. If the number of appearances of invasive strains is Poisson distributed with parameter c, the generating function of the number of appearance is f(s) = e^{cN (s-1)}. In a large population the parameter c = μβ(S/N)(I/N), if S and I are at equilibrium c = μ(αγ/β)(β - γ)/(α + γ). The generating function of the number of cases per unit of time is f(g)(s). The mean number of cases per unit of time is therefore f′(1)g′(1) = cN. The variance in the number of cases per unit of time is cN[(2/ε) + 1]. Note that both the mean and the variance scale with cN and the ratio of the variance to the mean is (2/ε) + 1, which is independent of the population size or the rate of appearance of invasive strain. This calculation assumes that outbreaks follow an introduction instantaneously, and therefore, overestimates the variance to mean ratio, especially for small pathogenicity.

If, in contrast, we assume that the bacterial population is homogeneous and that cases of meningococcal disease occur upon infection with a constant probability, the number of cases per unit of time is Poisson distributed. If we take the mean number of cases per unit of time to be cN, the variance in the number of cases is also cN, and the ratio of the variance to the mean is unity, independent of the size of the population.