Season and preterm birth in Norway: A cautionary tale

Abstract

Background: Preterm birth is a common, costly and dangerous pregnancy complication. Seasonality of risk would suggest modifiable causes.

Methods: We examine seasonal effects on preterm birth, using data from the Medical Birth Registry of Norway (2 321 652 births), and show that results based on births are misleading and a fetuses-at-risk approach is essential. In our harmonic-regression Cox proportional hazards model we consider fetal risk of birth between 22 and 37 completed weeks of gestation. We examine effects of both day of year of conception (for early effects) and day of ongoing gestation (for seasonal effects on labour onset) as modifiers of gestational-age-based risk.

Results: Naïve analysis of preterm rates across days of birth shows compelling evidence for seasonality (P < 10⁻¹⁵²). However, the reconstructed numbers of conceptions also vary with season (P < 10⁻³⁰⁷), confounding results by inducing seasonal variation in the age distribution of the fetal population at risk. When we instead properly treat fetuses as the individuals at risk, restrict analysis to pregnancies with relatively accurate ultrasound-based assessment of gestational age (available since 1998) and adjust for socio-demographic factors and maternal smoking, we find modest effects of both time of year of conception and time of year at risk, with peaks for early preterm near early January and early July.

Conclusions: Analyses of seasonal effects on preterm birth are demonstrably vulnerable to confounding by seasonality of conception, measurement error in conception dating, and socio-demographic factors. The seasonal variation based on fetuses reveals two peaks for early preterm, coinciding with New Year’s Day and the early July beginning of Norway’s summer break, and may simply reflect a holiday-related pattern of unintended conception.

Key Messages

• Analyses of preterm rates based on births across the seasons are subject to confounding by seasonal patterns of conception, and a fetuses-at-risk approach is needed for interpretable analysis.

• Factors associated with nondifferential errors in assigning the date of the last menstrual period (LMP) will be confounders in studies of the aetiology of preterm birth that rely on the LMP to assess gestational duration.

• With proper avoidance of those two problems, an analysis of a registry-based large set of births reveals scant evidence for any effect of seasons on preterm birth.

Introduction

Preterm birth imposes a considerable global public health burden,^1,2 with substantial costs for families and health care systems and adverse impacts on the quality of life of babies who survive.³ Despite its significance, much is still unknown about the causes, and preventive strategies remain largely ineffective.

Some potential risk factors vary with season, such as maternal vitamin D levels,⁴ influenza, flu vaccination, ambient temperature and air pollution. Therefore, the question naturally arises whether season could confound the evaluation of putative risk factors. In addition, if effects of season can be identified, they could suggest potentially avoidable environmental causes.

A recent review considered 28 studies⁵ that examined season in relation to gestational length. The evidence from five studies that analysed time of year of conception (the largest of which was based on US data) suggested that spring conceptions have shorter gestations. In a separate analysis based on five studies that instead considered season of birth (in the northern hemisphere), the authors also found a relation between season and rate of preterm birth.⁵ The monthly rates (dividing by total births) revealed a bimodal pattern, based on more than 63 million births,⁵ with a peak in January and another in June.

Such birth-based analyses neglect that it is fetuses and not newborns who are at risk of preterm birth. By definition, risk continues up until 36 weeks and 6 days, after which birth is ‘term.’ Darrow et al. pointed out⁶ that, if family planning results in a seasonal pattern of conceptions, then there will be seasonal variation in both the numbers of fetuses at risk of preterm birth and the gestational age distribution of the at-risk fetuses. Such variation can produce artefacts when births are erroneously treated as the risk sets. The likelihood of conception may vary with season and many economic and social factors influence family planning. Studies of preterm birth in relation to seasonally-varying factors could be sensitive to such forms of confounding.

Norway offers a valuable resource for exploring seasonality: a well-managed registry has captured births since 1967,^7,8 and its geography guarantees seasonal extremes, in both temperature and hours of daylight. In addition to the benefits of its geography, its low rate of preterm birth and population with universal access to prenatal medical care make Norway an ideal natural experiment for exploring effects associated with season. We begin by demonstrating that confounding can seriously distort birth-based analyses of seasonality. We then carry out a fetuses-at-risk analysis, using event-time Cox regression with harmonic (trigonometric) analysis to assess effects on preterm birth of both season of conception and season of ongoing gestation.

Methods

The Medical Birth Registry of Norway includes data for 2 321 652 pregnancies from 1967 through 2010, after excluding multiple births, babies conceived through assisted reproductive technologies such as in vitro fertilization and implausibly light or heavy babies that differed by more than four standard deviations from the Norwegian-standardized mean weight for gestational age. In total, 113 876 (4.9%) of those births were preterm.⁷ In our fetuses-at-risk analysis we included pregnancies ending in stillbirth in the fetal risk sets but treated them as statistically censored just before birth (i.e. a stillbirth between weeks 22 and 37 was not considered a preterm birth). The registry also records the date of the last menstrual period preceding conception (LMP), the mother’s smoking status (included since 1999) and whether she was married to / cohabiting with the father at the end of the pregnancy. Mother’s education was retrieved by linkage to the education registry in Norway. This study was approved by the internal review board of the Medical Birth Registry of Norway and by the regional ethics committee, REK Vest, Norway (2009/1868).

Periodic outcomes, whether circadian and cycling across the 24 h of the day or seasonal and cycling across the 365 days of the year, can be modelled by representing times as points on a circle. For example, one can transform days of the year to directional data, i.e. angles, by θ = 2π (day/365) in radians, and then model a continuous outcome or an event probability using regression, using trigonometric functions of the angles as predictors. Any smooth periodic function of day of the year can be approximated as a weighted sum of trigonometric components, where each component harmonic is a sine function with data-determined phase and amplitude.⁹ The first harmonic cycles once each year; the second harmonic cycles twice each year, being a function of 2θ; and so on. Each desired harmonic is entered into the regression by including both a sine and a cosine to capture both period and phase (shift). Accordingly inclusion, for example, of 12 harmonics, requires estimation of 24 coefficients. For a useful introduction to harmonic analysis, see the didactic paper by N.J. Cox.¹⁰

We first carried out a naïve analysis, applying harmonic logistic regression¹¹ to assess whether the rate of preterm birth varied with date of birth or was constant across the year. Such an analysis assumes (inappropriately) that the risk set for each day is all births. We then estimated dates of conception, approximated by adding 2 weeks to the LMP, and assessed whether, for pregnancies delivering after 22 weeks, the timing of their conception was seasonal. We used harmonic Poisson regression to model the counts of conceptions in relation to the day of the year, with days 1 to 365 (or 1 to 366 for leap years) converted to angles, testing for uniformity in the count data across the year.

Particularly if there is seasonality in the timing of conception, a fetuses-at-risk approach is needed: on any given day only those fetuses who are in a designated interval of gestational time are at risk of preterm, and that risk rises sharply with gestational age. Accordingly, we applied harmonic Cox regression to assess possible effects of day (of year) of conception on the hazard of preterm birth. We left-truncated gestational time prior to completion of gestational week 22, and then allowed the birth hazard to be positive for the next 15 weeks, up to completion of day 6 of week 36. We did not include the very small number of births between week 16 and 22, most of which would not be viable. We included up to 12 harmonics, i.e. frequencies from 1 a year up to 12 a year, to develop a fitted function that was reasonably smooth and repeated with a period of 1 year.

Given the unexpected appearance of a 12th harmonic, indicating within-monthly cycling, we further explored the possible roles of monthly patterns of behaviours, error related to digit preferences in reporting the day of the month for the starting date of the last menstrual period (LMP), and social correlates of those digit preferences. One such correlate could be unintended pregnancy, which would be associated with uncertainties about the LMP and also with adverse exposures (e.g. prescription drugs) experienced by women who are unaware that they are pregnant.

To assess possible inaccuracies in the recorded LMP, we enumerated the frequencies of reporting specific days between 1 and 31. We then examined whether the digit preference we observed was predictive of preterm birth, as it could reflect either measurement error in reporting the date or other social factors (such as educational level) that influence both reporting and risk. We examined the influence of education and smoking status during pregnancy on the digit-preference pattern.

Given that the probability of birth increases steeply towards the end of pregnancy, non-differential errors in reporting the date of the last menstrual period will cause differential misclassification of term births as ‘preterm’. To see why this paradox arises, suppose, for example, an error is equally as likely to be + 1 week as to be - 1 week, producing equal probabilities that a given 37-week pregnancy will be mis-recorded as 36 (‘term’ designated ‘preterm’) as that a given 36-week pregnancy will be mis-recorded as 37 (‘preterm’ designated ‘term’). Because there are many more 37-week pregnancies than 36-week pregnancies,⁶ the net effect of this error mechanism will be to bias upward the proportion categorized as preterm. Consequently, factors associated with non-differential errors in LMP (e.g. those associated with unplanned pregnancy) will appear to be risk factors for preterm birth even if they are not.

Because a digit-preference pattern associated with preterm risk might only reflect errors in reporting the date of the LMP (and consequent differential misclassification of term births as preterm), we next restricted the analysis to pregnancies after 1998, when dating of pregnancies was routinely based on fetal size as determined by ultrasound (usually around week 18–19). Using this restricted population of 610 352 births (with 31 071 preterm babies), we explored whether risk was still associated with LMP digit-preference, which could still act as a marker for unintended conception and possibly associated exposures.

Day of year of conception determines the seasonal timing of each successive later phase of pregnancy; thus the risk of preterm birth could be influenced either by events around the time of conception (e.g. causing abnormal placentation) or by effects of season of the year on the later stages of pregnancy (e.g. triggering early labour). Accordingly we also extended the Cox periodic regression model to allow for possible effects of day of the year of ongoing gestational time (as a time-dependent ‘exposure’) on risk.

Smoking, educational attainment and whether the mother was married/cohabiting might be associated with season of conception and also with pregnancy planning, reporting errors and risk of preterm birth. Consequently, we assessed whether those factors acted as predictors of LMP digit preference. We then introduced social factors as possible confounders in the periodic regression model to reassess the possible contributions of the two seasonal predictors, day of year of conception and day of year of ongoing pregnancy. We also carried out a sensitivity analysis focusing on spontaneous onset of labour by treating as censored any births that followed caesarean section or medical induction.

Because we found a seasonal pattern that appeared to link risk of preterm delivery with two major holidays in Norway, January 1 and the start of summer break in early July, we carried out additional subset-based analyses to further explore the possible role of unintended pregnancy. We did this by identifying a subpopulation likely at increased risk for unintended pregnancy. This subpopulation included women who were not married/cohabiting; women under age 23 who were having their first birth; and women over age 40 who were not having their first birth.

Results

Naïve analysis

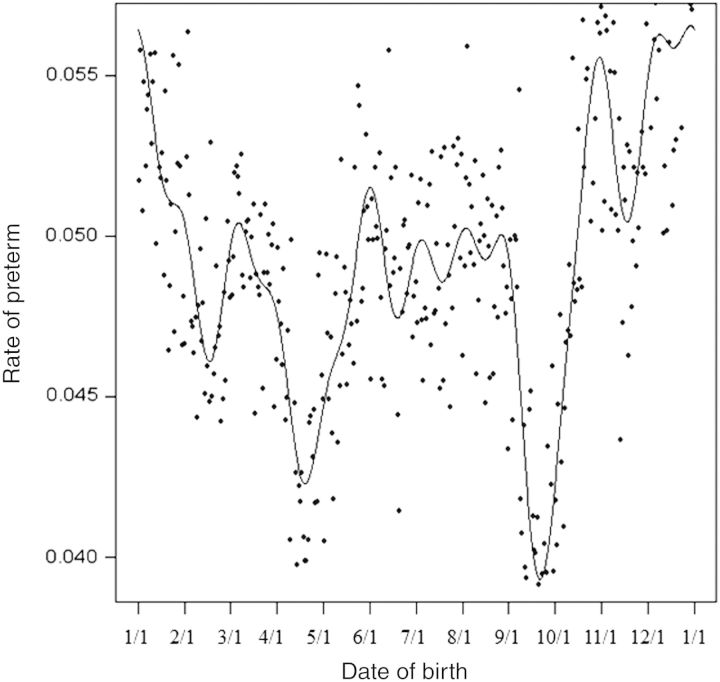
The initial naïve analysis considered preterm rates in relation to time of year of birth, using all births of babies after 22 weeks as the risk set. The fitted regression curve, based on logistic regression including the first 12 harmonics, is shown in Figure 1.The pattern shows a peak in summer and a second peak in winter, closely resembling the seasonality described in the recent review.⁵

Figure 1.

The observed rate of preterm delivery shown by day of the year of birth for all 2 321 652 singleton births in the Norwegian Medical Birth Registry. The smooth curve is fitted based on including the first 12 harmonics, which are shown separately in Figure 2; that is, the smooth curve in Figure 1 is the sum of the 12 curves shown in Figure 2.

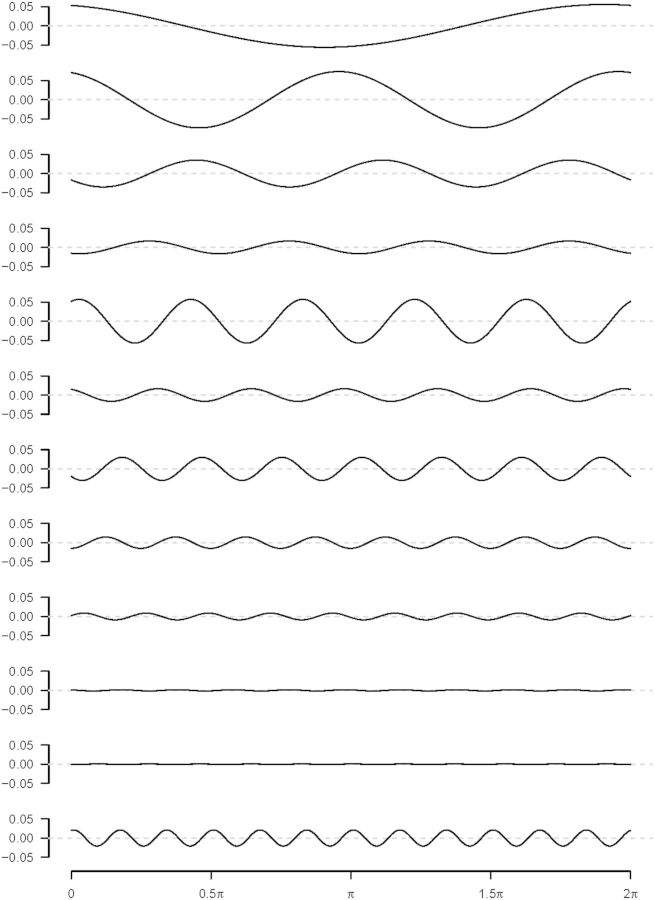
The likelihood ratio statistic for a test of uniformity of those rates across the year yielded a χ² (with 24 degrees of freedom) of 798 (P < 10⁻¹⁵²)_, providing compelling evidence that the rate of preterm birth was not uniform across time of year of birth. The 12 orthogonal harmonic functions that, when summed, comprise the fitted curve of Figure 1, are shown separately in Figure 2. Whereas the likelihood ratio statistic provides a valid test for constancy of rate of preterm birth across the year, seasonality of conception induces confounding by producing seasonal changes in the number and the gestational age distribution of fetuses at risk. For example, suppose conceptions often occur in July. Then the rate of preterm based on births would be increased the subsequent March, as conceptions from that large July cohort reach week 36.

Figure 2.

The12 harmonic components whose sum produces the fitted curve are shown in Figure 1, with the first harmonic shown at the top. Note the substantial contribution of the 12th harmonic, suggesting a cause that acts within each month.

Assessing seasonality of conceptions

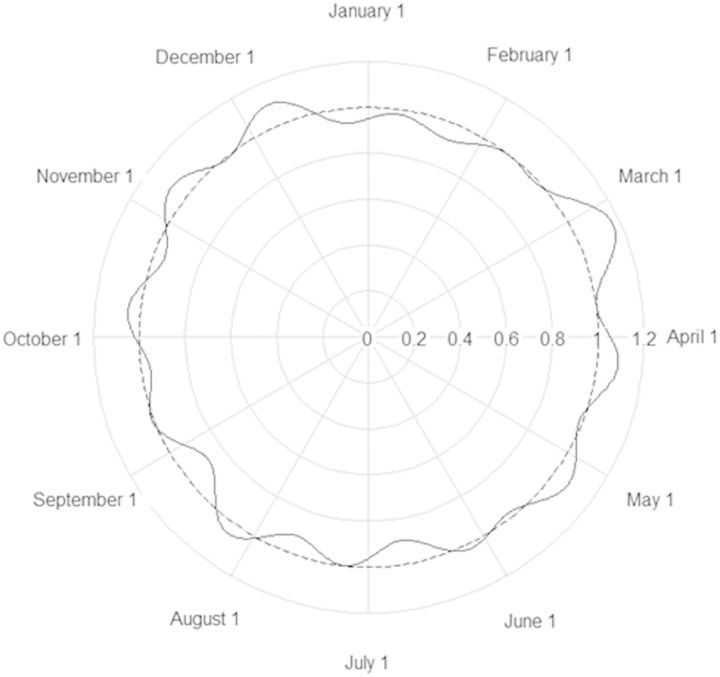
The weighted-average smoothed fit for the numbers of conceptions by day of the year is shown radially in the circular plot in Figure 3a. The fitted curve based on a harmonic Poisson regression that includes the first 12 harmonics is shown in Figure 3b. The corresponding likelihood ratio test (LRT) for uniformity of conception times yielded a chi-squared value of 12 815 with 24 degrees of freedom (DF) (P < 10⁻³⁰⁷). Thus, conceptions in Norway are much more likely to occur in the summer months than in the first quarter of the year. This observed seasonal pattern in conceptions underscores the need for a fetuses-at-risk analysis.

Figure 3.

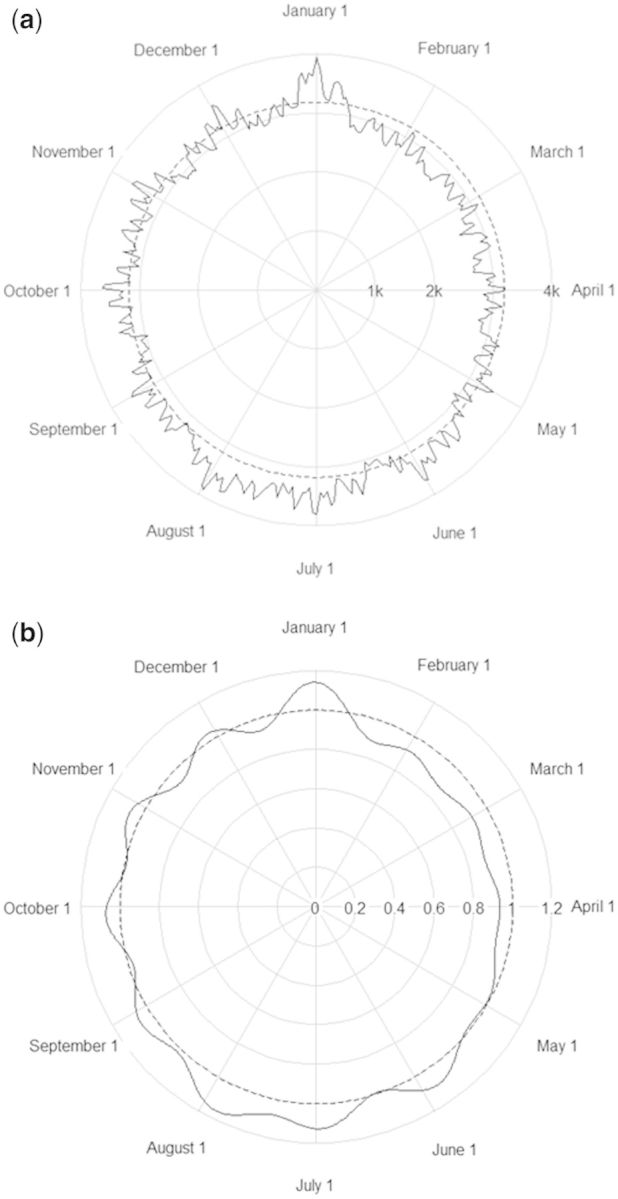
a. The 7-day moving averages of the number of conceptions by day of the year, based on the reported last menstrual period plus 14 days for the 2 321 652 births. The concentric circles mark the scale for the number of conceptions (where 1 k is 1000, etc). The dashed circle shows the average, and the excursions above and below it indicate a strong surplus in late December and during the summer months with a corresponding deficit during the first quarter of the year, presumably caused by pregnancy planning. b. The fitted curve for the relative number of conceptions by day of the year, with 1.0 corresponding to the average number, based on periodic Poisson regression.

Fetuses at risk in relation to timing of conception

We explored effects of time of year of conception on risk, based on fetuses at risk, accounting for effects of their ongoing gestational age (as the primary time scale), using a Cox model for the hazard of birth. When, using the Cox model with the first 12 harmonics, the estimated time of year of conception (instead of time of birth) was considered as the predictor, there was compelling evidence for seasonality, with a χ² for uniformity of 374 (24 DF) and P < 10⁻⁶³. The fitted curve is shown in Figure 4, revealing large repeating perturbations due to the12th harmonic, which makes a major contribution, with a χ² of 131 (2 DF, P < 10⁻²⁸).

Figure 4.

Estimated hazard ratio for preterm birth as a function of time of year of conception for the 2 321 652 births, revealing strong monthly cycling.

Trying to understand the monthly pattern

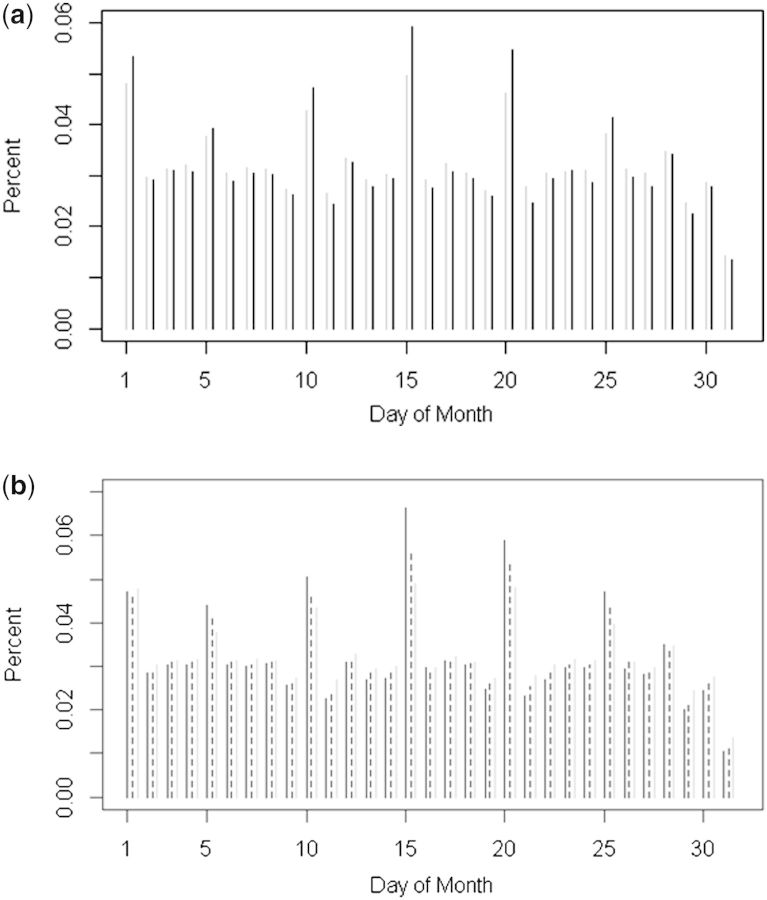
The puzzling within-month cycling (measured by the12th harmonic) could reflect any (or all) of three distinct phenomena. The first involves measurement error: digit preference for a favoured day in the month could cause monthly cycling in the fitted model and also be a marker for uncertainties in reporting of the LMP date which, (even if the mean error is 0) as previously mentioned, will result in differential misclassification of term births as preterm,⁶ as previously mentioned. In fact, there was highly significant over-reporting of day 15 as the LMP date, a date presumably favoured by pregnant women (or data coders) who did not know the LMP (see Figure 5a and b). Day 15 was indeed associated with increased risk of preterm birth, even in a model including all 12 harmonics. In fact there was increased risk associated with identifying any multiple of 5 as the day of the LMP [hazard ratio 1.15; confidence interval (CI) = (1.14, 1.17)]. A second mechanism may involve true effects, as there could be deleterious exposures associated with reporting the LMP to have begun on day 15 (or some other multiple of 5). Some of those exposures may also be actual risk factors for preterm birth, e.g. having an irregular menstrual cycle, drug use or unintended conception. Thirdly, certain exposures might tend to follow a monthly pattern, e.g. increased alcohol consumption on certain days (e.g. early in July or 1 January), producing increased risk through actual effects on the pregnancy.

Figure 5.

a. Digit preference by smoking status for 507 873 pregnancies. Grey bars show nonsmoker proportions and black bars show smoker proportions reporting particular days of the month as the start of their last menstrual period. b. Digit preference by education for the 2 321 652 pregnancies: black bars are for women with up to 9 years of schooling, dashed bars are for women with10 to 14 years, grey bars are for women with15 or more years of schooling.

We explored possible confounding effects of smoking status (as of the beginning of pregnancy) and educational status on the digit-preference effects by counting the number of women declaring various days from 1 to 31 as their LMP date. Figure 5a shows results for smokers and nonsmokers and Figure 5b shows results for three strata of educational attainment (less than high school, high school, more than high school). Whereas the patterns of digit preference are strikingly similar across the categories, the detected excess at multiples of 5 appears more pronounced for smokers and for women with lower educational attainment—consistent with the possibility of more unintended pregnancies in smokers and less-educated women.

We analysed the propensity to digit preference in LMP as follows. We reasoned that the day in a given month when menstruation begins is biologically equally likely to be the first, the second, etc. Thus, for example, for LMPs that begin in January the odds that the onset day falls on a multiple of 5 should be 6/25 (there being 6 multiples of 5 in January). We accordingly fit a logistic model for reporting the LMP day as a multiple of 5, using month-specific offsets equal to the logarithm of the calculated odds for the month reported, and tested the intercept against 0. Overall, the evidence for digit preference was overwhelming (P < 10⁻³⁰⁷). More importantly, the tendency varied with smoking status and education level. The odds of reporting a multiple of 5 were related to smoking with an odds ratio of 1.10 (1.08, 1.12), and to education level with odds ratios of 1.21 (1.19, 1.24) and 1.07 (1.06, 1.09) for less than 10 and 11–14 years, compared with 15 or more years of education, respectively. One way to control for digit preference would have been to simply omit the 12th harmonic, which would smooth the bumps away. However, our concern was not with bias directly due to digit preference, but with the confounding as described above that is caused by measurement errors in assigning the time of conception, for which digit preference serves as a telltale marker.

Restricting to ultrasound-based data

To better control the contribution of measurement error to the 12th harmonic, we next restricted attention to the data after late 1998, when use of ultrasound to assess gestational age became routine in Norway (610 352 pregnancies) and likely resulted in more accurate assessment of gestation age. When timing of conception and length of gestation were calculated based on ultrasound measures, the first two harmonics for time of conception remained significant as determinants of preterm birth, but the 12th harmonic was no longer important (P > 0.1). Nonetheless, in a model with the first two harmonics the risk of preterm was still elevated in women who reported that their LMP had started on day 15 (P = 0.013), even though in this analysis LMP was not being used to define time of conception or preterm birth. These results suggest that uncertainty about the date of LMP is itself actually predictive of risk of preterm.

Additionally allowing for effects of time of year on initiation of labour

Thus far, the only seasonal contribution we had accounted for in our modelling was time of year of conception; a second source of possible seasonal effects also needed to be considered, namely the passage through the seasons during pregnancy. Accordingly we entered the time of year of the ongoing pregnancy by including in the model the first 12 harmonics in an analysis that, along with the two remaining harmonics for time of conception, now comprehensively allowed all three time scales. When we also included smoking and educational level as potential confounders, both time of year of conception and time of year of ongoing gestation showed patterns that were adequately captured by the first two harmonics.

Results for a fully-adjusted model

The model fit changed somewhat with additional inclusion of possible confounding effects of social and demographic factors, marriage/cohabitation, parity (nulliparous versus multiparous), health region of Norway and maternal age (under 30 versus 30 and older), as well as interactions between education and, in turn, parity, maternal age and smoking. (We did not adjust for calendar year of conception, as it was not itself important, nor did it have an effect on the other coefficients in the model.) With adjustment for the above covariates, there remained only modest evidence for seasonality, involving the first two harmonics for time of conception and the first two for time of ongoing pregnancy (LRT χ² of 18.4, DF = 8, P < 0.02). The evidence for seasonality was further reduced by treating medical interventions as censoring events, restricting outcomes to spontaneous preterm birth (LRT χ² of 15.0, DF = 8, P < 0.06). Because the comprehensive model includes two season variables, the hazard ratio representing estimated effects of season lives on a surface. The estimated hazard ratio surface as a function of both time of year of conception and time of year of ongoing gestation is shown by the shading in Figure 6, as in the key provided. Most of the seasonal pattern seems confined to risk of early preterm, whereas toward the end of the 37th week (the upper edge of the band in the figures) the risk becomes independent of season (monochromatic near the upper edge across the band). The risk amplitude is modest (ratio of highest to lowest hazard ratio 1.18/0.85 = 1.39), with the highest hazard ratio for preterm birth experienced by conceptions that occur during the Christmas/New Year holiday season.

Figure 6.

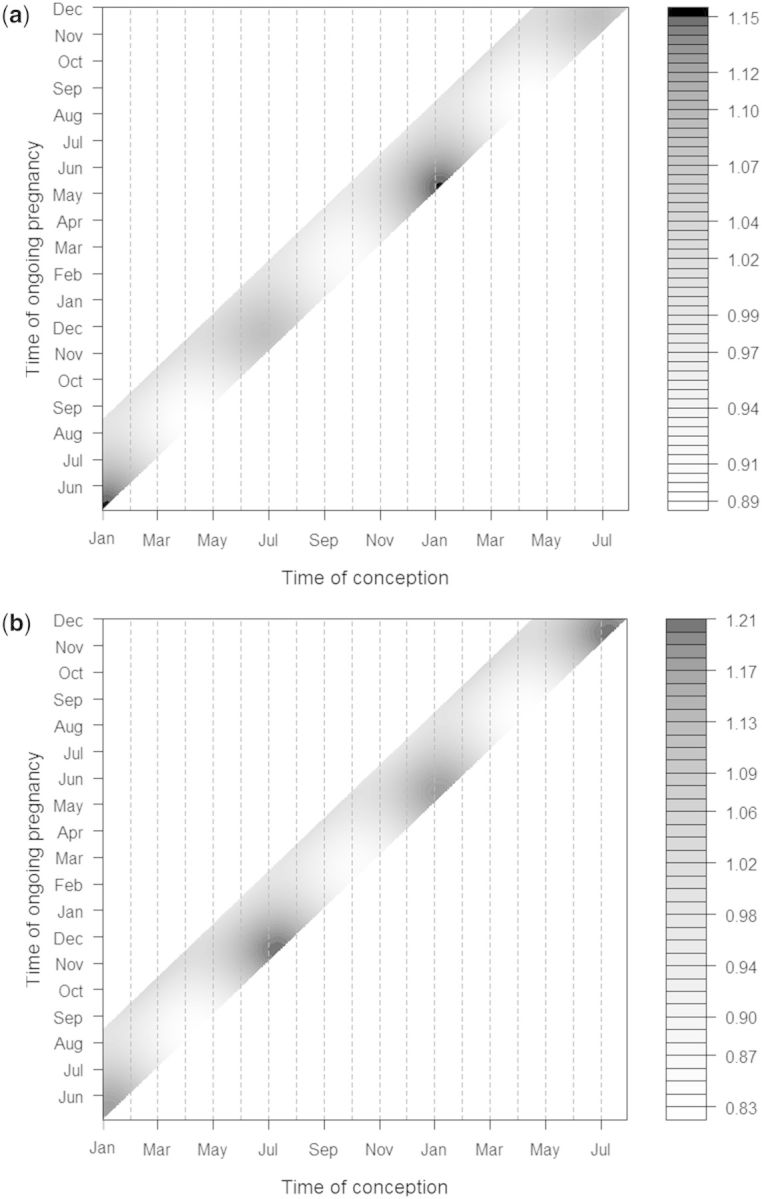
a Fitted seasonal hazard ratios as a function of time of year of conception and time of year of ongoing pregnancy, with adjustment for smoking, parity, relationship status, age, education and interactions between education and smoking, parity and relationship status. The shading indicates the magnitude of the fitted hazard ratio for birth, as shown in the shading key. The axes show dates of conception as horizontal and dates of ongoing pregnancy as vertical. These results are based on restricting analysis to time since 1998 when more accurate assessment of gestational age was routinely based on ultrasound and smoking status was known (n = 443 566). The bands are narrow because for each day of the year of conception the pregnancy is at risk of preterm for only 15 weeks. b. As for a, except that medical interventions to end the pregnancy are treated as censoring events.

Discussion

When studying seasonality of preterm birth, there are many ways to get it wrong. First, the individuals at risk are not births but fetuses, and only those within a specific range of gestational ages. Additionally, as pointed out by Darrow et al.,^6,12 confounders, including social and behavioural factors such as education and smoking, can induce outcome misclassification and apparent seasonality by causing seasonal variation in the size and the gestational age distribution of the population of ongoing at-risk pregnancies. The extraordinarily strong statistical significance we observed in our first analysis, based on modelling seasonality of rates across dates of birth, primarily reflected artefacts caused by seasonality of conception, misclassification of gestational durations and confounding by socio-demographic factors and smoking.

Our time-to-event analysis was able to handle three different time scales simultaneously: gestational age, reflecting strong biological effects of maturation on the risk of delivery; time of year of conception, which could be related to factors that influence implantation and placentation; and time of year of ongoing pregnancy, which could reflect later effects on initiation of labour. These three time scales are statistically highly interdependent, because knowing any two determines the third. In this respect, the problem of distinguishing effects of all three time scales is related to the analytical problems associated with attempting to distinguish effects of age, period and birth cohort¹³ in population studies. However, the analytical problem becomes more tractable in analyses of seasonality in pregnancy complications, because two of the time scales involve directional (angular) data, and their joint effects are consequently inherently nonlinear, hence statistically identifiable.

The role of confounding needs to be thought of in a slightly different way in the context of Cox-based analysis of season. As we have seen, factors that are not actual risk factors for preterm birth but are associated with measurement error in assigning gestational age (even nondifferentially) and that are also associated with season of conception can be de facto confounders.

The modest seasonal pattern that remained evident after harmonic analysis with adjustment for socio-demographic factors could reflect effects of such unmeasured confounders. The most likely confounders may be factors associated with unplanned pregnancy, a phenomenon not recorded by the birth registry. The apparent second-harmonic increase in risk that corresponds to holiday conceptions is consistent with that possibility, suggesting a possible role for exposures that may be experienced by Norwegians at risk of an unintended New Year’s or summer holiday conception. There is evidence from the Danish birth cohort that alcohol consumption may be associated with very early preterm birth,¹⁴ which offers another hypothesis that could be consistent with the patterns observed in Figure 6.

To further investigate the possibility that unintended conceptions might explain the observed bimodal holiday-related pattern, we carried out additional exploratory analyses. We identified a subpopulation of mothers we considered likely to be pregnancy nonplanners: those who were neither married nor living in a stable relationship with the father; or were under 23 and nulliparous; or were over 40 and parous (N = 61 445, with 3811 preterm, 6.2%). The remaining mothers we considered relatively more likely to be pregnancy planners (N = 382 118, with 18 129 preterm, 4.7%). A bimodal risk pattern similar to the one shown in Figure 6 was evident in both groups, but was very weak in the larger, likely-planner group, with a risk amplitude of 1.25 and P = 0.24 for seasonality. By contrast, the smaller likely-nonplanner group showed a risk amplitude of 2.21 and P = 0.014. If we treated medical interventions (i.e. inductions and caesarean sections) as censoring events, the contrast became 1.34 (P = 0.43) and 2.6 (P = 0.011) for likely planners and likely nonplanners, respectively. These data suggest that there is little if any effect of season per se, and the risk pattern we see may instead be a behaviour-mediated effect of seasonal holidays on unintended conceptions in Norway.

In summary, this analysis illustrates that assessment of seasonal influences on preterm birth is subject to strong biases unless one uses a fetuses-at-risk approach and a time-to-event model, which inherently accounts for the time-dependent gestational-age structure of the population of fetuses at risk. One must also adjust for factors that can influence accuracy of estimation of conception timing and hence the preterm classification.

Funding

This research was supported by the Norwegian Research Council and in part by the Intramural Research Program of the NIH, National Institute of Environmental Health Sciences, under project Z01 AES 040006-18.