Contemporary considerations for constructing a Genetic Risk Score: An Empirical Approach

Abstract

Genetic Risk Scores are an increasingly popular tool for summarizing the cumulative risk of a set of SNPs with disease. Typically only the set of the SNPs that have reached genome-wide significance compose these scores. However recent work suggests that including additional SNPs may aid risk assessment. In this paper, we used the Atherosclerosis Risk in Communities Study (ARIC) cohort to illustrate how one can choose the optimal set of SNPs for a GRS. In addition to p-value threshold, we also examined linkage disequilibrium, imputation quality and imputation type. We provide a variety of evaluation metrics. Results suggest that p-value threshold had the greatest impact on GRS quality for the outcome of coronary heart disease, with an optimal threshold around 0.001. However, GRSs are relatively robust to both linkage disequilibrium and imputation quality. We also show that the optimal GRS partially depends on the evaluation metric and consequently the way one intends to use the GRS. Overall the implications highlight both the robustness of GRS and a means to empirically choose the best set of GRSs.

Introduction

Genome wide association (GWA) studies and follow-up meta-analyses have identified a plethora of susceptibility loci for many different common diseases (Welter et al., 2014). While the number of polymorphisms reaching genome wide significance remains modest, typically < 100 per disease, simulation and empirical studies suggest that many more common susceptibility variants remain to be discovered (Stahl et al., 2012; Visscher et al., 2012; Welter et al., 2014; Wray et al., 2011). These discoveries will undoubtedly result in a better understanding of the pathophysiology of chronic diseases and the development of novel therapeutic options over the long term. However, great interest exists in leveraging these findings to better predict the occurrence of chronic diseases over the short term particularly for diseases that have therapeutic options that can reduce risk irrespective of the source of excess genetic risk (Jostins and Barrett, 2011; Thanassoulis and Vasan, 2010). Such is the case for coronary heart disease (CHD) where a combination of optimal modifiable risk factors can virtually eradicate the probability of developing disease (Stamler et al., 1999; Yusuf et al., 2004).

Currently the most practical way to leverage recent GWAS findings for risk prediction is through the use of genetic risk scores (GRS) (Amin et al., 2009). To date, GRSs have been created for many complex diseases, including cardiovascular disease (Thanassoulis et al., 2012), schizophrenia (Purcell et al., 2009) and multiple sclerosis (De Jager et al., 2009). GRSs combine the modest effects of multiple SNPs into a single variable. They are typically calculated as a weighted sum of the number of high risk alleles, where the GRS for person i is:

$${\mathit{GRS}}_i=\sum _{j\in \mathit{GRS}}{w}_j\sum _{k=1}^2{RA}_{jk}$$

RA is an indicator for the presence of risk alleles at allele k at SNP j (0 – 1) and w_j is the weight of each risk allele, generally derived from the estimated log odds ratio for that allele from either a large GWAS or a meta-analysis involving multiple case-control studies. However, these weights can also be derived from the hazard ratio or relative risk of one or more cohort studies. Since the weights are based off of marginal associations, the two implicit assumptions in such a construction are that (1) the effect each SNP is independent and (2) the marginal effects capture the full effect for a given SNP, indicating the SNP does not interact with any other SNP in the GRS. While adjacent SNPs are expected to be in linkage disequilibrium (LD), one can remove such SNPs through LD pruning. While there may be interactions, main effects are likely to dominate overall (Hemani et al., 2014; Hill et al., 2008). Thus, while these assumptions may be violated, the impact is likely minimal. The range of GRS values is determined by both the number of SNPs involved and the sign (positive or negative) of the weight (based on the direction of effect of the coded allele). Since the raw value of the GRS itself is not particularly meaningful, standardizing it to a mean of 0 and variance of 1 facilitates its interpretation.

Recent work has focused on combining GRSs with clinical risk scores to demonstrate incremental value in risk prediction (Goldstein et al., 2014). While most investigators have tested scores that include only the few SNPs that have met GWA significance – typically p < 5 ×10⁻⁸ – others have constructed more expansive GRSs using many more SNPs (Purcell et al., 2009; Simonson et al., 2011), showing that doing so explains a greater percentage of the variance in the outcome. Others have considered the impact of study sample size (Chatterjee et al., 2013) and LD (Wu et al., 2013). Building off these, and other considerations, the aim of this analysis is to illustrate how one could empirically determine which SNPs to include in a GRS using the most reliable genetic association data available. We present our approach for the outcome of CHD using a large scale, publicly available GWAS but it can be easily applied to other chronic diseases and to association data that more reliably survey the lower frequency spectrum of mutations. However, we emphasize that our goal here is to illustrate which factors should be considered understanding that the specific findings in this study are not necessarily generalizable to other cohorts or to other outcomes. Instead, the optimal GRS depends on a number of factors including the true genetic architecture of the disease and the strength of the corresponding genetic association studies.

Methods

SNP Selection & Weighting

An important consideration in constructing a GRS is selecting the study from which the association results (i.e. weights) will be derived. We constructed our GRSs using SNPs from the most recent and largest GWAS for coronary artery disease conducted by the CARDIoGRAM. The GWAS included 22,233 cases and 64,762 controls of white/European ancestry (Schunkert et al., 2011).

Prospective Cohort for testing Genetic Risk Scores

We selected the Atherosclerosis Risk in Communities Study (ARIC) study to test the various GRSs we constructed. The ARIC Study is an ongoing prospective investigation of atherosclerosis and its clinical sequelae involving 15,792 white and black persons aged 45–64 years at recruitment (1987–1989). Detailed descriptions of the study designs, IRB consent process, sampling procedures, methods, definitions of cardiovascular outcomes, and approach to statistical analyses is published elsewhere (1989; White et al., 1996). ARIC is an ideal testing cohort for several reasons including the availability of individual level genome wide data for all participants through the National Institutes of Health (NIH) controlled access database of Genotypes and Phenotypes (dbGaP) (Mailman et al., 2007), a prolonged follow up with > 1000 incident outcomes of interest among participants of European descent, and no overlap of incident cases with prevalent cases that were included in the CARDIoGRAM consortium study.

All white/Europeans without a history of CHD, myocardial infarction, or heart failure at baseline were included. Incident CHD was defined by the recording for the first time of either non-fatal or fatal myocardial infarction (“mi04”, “fatchd04”), CHD related revascularization procedure (“in_by04p”), or silent MI detected by ECG (“in_04s”). The outcome of interest was incident CHD within 10 years. Those without a positive event who died or were lost to follow up prior to their 10th year anniversary of follow up were removed from analysis. All others were deemed event free at 10-years regardless of whether they developed incident CHD sometime after their 10 year anniversary of follow up.

Genotyping and 1000 genomes Imputation

The Affymetrix 6.0 array was used to genotype all participants of the ARIC study. We used MACH and Minimac to phase and impute the individual level genotype data from ARIC to the latest build of the 1000 genomes project to minimize the need to search for and use proxies used in the construction of the GRS (Howie et al., 2012; Li et al., 2010). We used GTOOL (Genetics Software Suite, (c) 2007, The University of Oxford) to convert Minimac dosage files to best guess genotype calls.

GRS Construction

We considered four different choices for choosing SNPs to be part of the GRS. These were: p-value for the marginal association (8 p-values: ≥ 5 × 10⁻⁸, ≥ 1 × 10⁻⁵, ≥ 0.001, ≥ 0.01, ≥ 0.05, ≥ 0.1, ≥ 0.2, and ≥ 0.5), LD between SNPs, (4 values ≤ 0.2, ≤ 0.5, ≤ 0.8 and ≤ 1.0 (all)), imputation quality (5 values: ≥ 0.9, ≥ 0.8,. ≥ 0.5, ≥ 0.3, and ≥ 0 (all)) and allele coding of imputed SNPs (genotype or probabilities). P-values were derived from the CARDIoGRAM GWAS. We used the PLINK software (Purcell et al., 2007) to calculate pairwise unphased correlation (LD) between SNPs and obtained the imputation quality score from MACH. To choose SNPs for the GRS we:

1. Removed all SNPs below the imputation quality score

2. Rank ordered the SNPs based on p-value

3. Chose the top SNP from the list

4. Removed any SNPs that were in LD with that SNP based on the LD threshold

5. Repeated steps 3 & 4 until the p-value threshold was reached.

6. Constructed the GRS using either genotype calls or dosages of the imputed SNPs

7. Standardized the GRS to have mean 0 and variance 1.

We performed a grid search assessing each permutation of GRS construction for a total of 256 GRSs per person.

Analysis

We first assessed the degree of similarity between the various GRSs by calculating their pairwise correlations. Next, we assessed the performance of each GRS by testing it as a predictor of CHD within 10 years in the ARIC cohort using log-linear regression to estimate the relative risk (RR) for a 1-unit change in the GRS. In the regression, we controlled for all clinical risk factors that are part of the Framingham Risk Score: age, gender, blood pressure, cholesterol (Total and HDL), smoking status and diabetes (Wilson et al., 1998). Using 10-fold cross-validation, we calculated the c-statistic and calibration slope for predicting CHD from each GRS. A calibration slope of 1.00 indicates perfect calibration while values less than 1.00 suggest over-fitting and above 1.00 less than perfect calibration (Crowson et al., 2014). Finally we calculated the change in the c-statistic using 2000 bootstrap replications (Obuchowski & Lieber, 1998).

All statistical analyses were performed in R version 3.01 (R Core Team, 2012).

Results

ARIC cohort

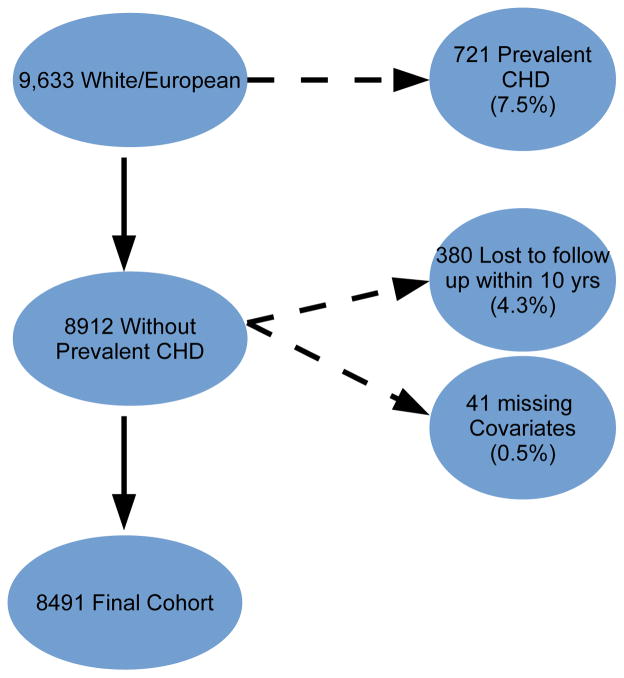
Of the 12,771 from the ARIC cohort with phenotypic and genotypic data, 9,633 (75%) were white/European (Figure 1). Among the remaining subjects, 721 (7.5%) had a history of CHD or CHF at baseline and were excluded from further analysis. Lastly, we excluded 380 people who were lost to follow-up or died of non-CHD related factors within 10 years and 41 people with missing covariate information, comprising a final cohort of 8,491 (Figure 1). Summary statistics of baseline characteristics for the ARIC subcohort used in our analyses are shown in Table 1.

Figure 1.

Flow diagram for inclusion of subjects in the study cohort

Table 1.

Characteristics of the ARIC subcohort used in analyses (n = 8491)

	mean (IQR)
Age (years)	54 (49, 59)
SBP (mm/Hg)	116 (106, 128)
DBP (mm/Hg)	71 (65, 78)
HDL (mg/dL)	48 (39, 61)
TC (mg/dL)	211 (187, 238)
	count (%)
white/European	8491 (100)
Male	3848 (45)
Diabetes	626 (7.4)
Smoking status
Current	2010 (24)
Former	2914 (34)
Never	3567 (42)

IQR = inter-quartile range, SBP = Systolic Blood Pressure, DBP = Diastolic Blood Pressure, HDL = High-Density Lipoprotein Cholesterol, TC = Total Cholesterol

SNP Data

Overall, 2,430,359 SNPs were in the CARDIoGRAM GWAS. Of these, 841,820 (35%) were directly genotyped within ARIC. Our 1,000 genomes imputation allowed us to imputed 30, 061,896 SNPs in ARIC, providing coverage of 2,393,551 (98%) of the CARDIoGRAM SNPs. Of these, 2,101,223 (88%) were common SNPs with MAF > 0.05 in ARIC.

GRS Scores and Improvement in Risk Prediction

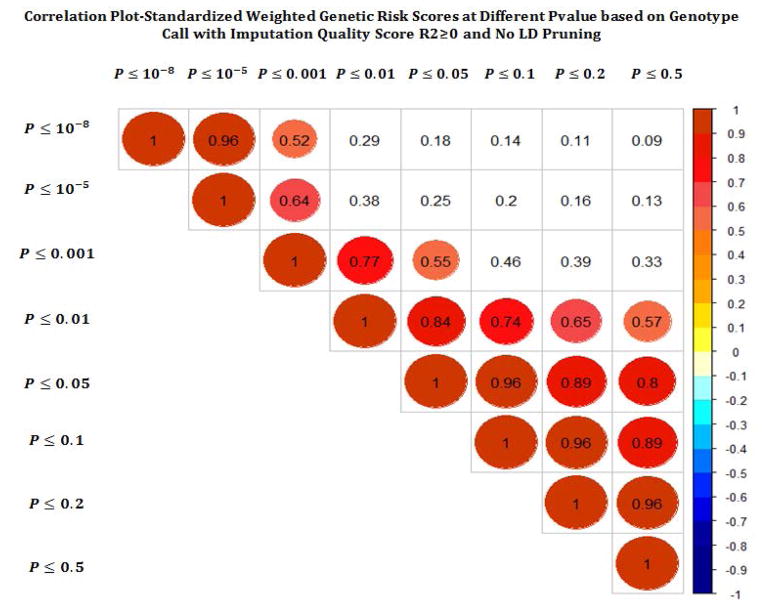
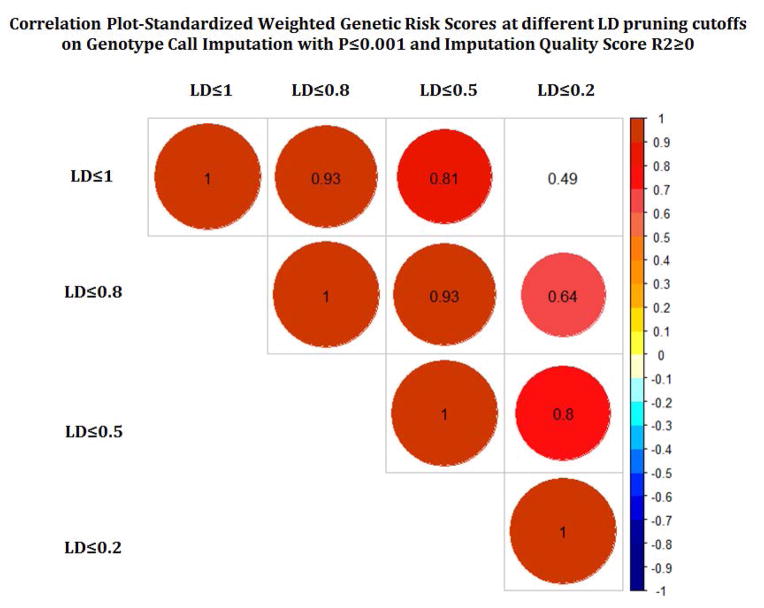
We created and compared a total of 256 GRS scores. Figures 2a–c show the correlation between different GRS scores based on different p-value, LD and imputation quality thresholds. While the correlation across different LD thresholds and different imputation quality scores were quite high, we observed more variability in correlations across the different p-value thresholds.

Figure 2.

Pairwise correlation across different GRS across while varying p-value threshhold (a), linkage disequilibrium (b), and imputation quality (c).

The predicted 10-year risk of developing CHD based on the FRS in this subcohort is 7.4% (interquartile range 4.3% to 12.3%), which coincides very well with the observed proportion that actually developed CHD (7.3%). The c-statistic and calibration slope for the prediction of CHD within 10-years using clinical factors alone was 0.774 (0.758, 0.791) and 3.12 (2.55, 3.69), respectively, suggesting moderately strong discrimination but suboptimal calibration. Table 2 shows the RR of CHD for a 1-standard deviation change in GRS for select models that we tested. Results for all models tested can be found in the supplement (Table S1). The RR for CHD varied from 1.08 to 1.28 for each standard deviation in GRS, with better performing GRSs having higher estimated RRs. Using 10-fold cross validation, we calculated the c-statistic for predicting CHD. The optimal GRSs improved the c-statistic by 0.009, while the worst did not improve the statistic at all. Most GRS constructions led to a significant improvement in discrimination compared to the baseline model with just clinical factors. All of the GRSs led to improved calibration, with a maximal improvement observed of 0.96 units translating to a 56% improvement of calibration. Not surprisingly there was some discrepancy between the optimal calibration and discrimination (Cook, 2007).

Table 2.

Select Results of GRS quality across different tuning parameters

Parameters	#SNPs	Relative Risk	AUC	Calibration Score
Pvaluea
≤ 5E-08	166	1.180(1.096, 1.270)	0.777(0.761, 0.794)*	2.684(2.067, 3.302)
≤ 0.00001	525	1.231(1.143, 1.325)	0.780(0.763, 0.797)**	2.563(1.905, 3.222)
≤ 0.001	7387	1.277(1.186, 1.375)	0.783(0.766, 0.800)***	2.888(2.311, 3.465)
≤ 0.01	41017	1.213(1.126, 1.306)	0.780(0.763, 0.796)**	2.369(1.710, 3.028)
≤ 0.05	156193	1.215(1.127, 1.309)	0.780(0.763, 0.796)**	2.257(1.623, 2.891)
≤ 0.1	287398	1.201(1.114, 1.296)	0.779(0.763, 0.796)**	2.367(1.734, 3.001)
≤ 0.2	535188	1.179(1.090, 1.275)	0.778(0.761, 0.794)*	2.350(1.702, 2.998)
≤ 0.5	1244367	1.157(1.068, 1.253)	0.777(0.760, 0.793)*	2.473(1.806, 3.141)
Imputation Quality-R2b
≥ 0	7387	1.277(1.186, 1.375)	0.783(0.766, 0.800)***	2.888(2.311, 3.465)
≥ 0.3	7205	1.272(1.181, 1.370)	0.783(0.766, 0.799)***	2.915(2.346, 3.484)
≥ 0.5	6959	1.273(1.183, 1.371)	0.783(0.766, 0.799)***	2.921(2.342, 3.501)
≥ 0.8	6015	1.264(1.174, 1.361)	0.782(0.766, 0.799)**	2.921(2.322, 3.520)
≥ 0.9	5055	1.252(1.162, 1.348)	0.782(0.765, 0.798)**	2.990(2.379, 3.602)
Ldc
No LD prunning	7387	1.277(1.186, 1.375)	0.783(0.766, 0.800)***	2.888(2.311, 3.465)
Prunned with LD R2≥ 0.8	2267	1.267(1.175, 1.368)	0.782(0.765, 0.798)**	2.350(1.781, 2.919)
Prunned with LD R2≥ 0.5	1711	1.227(1.137, 1.324)	0.780(0.763, 0.796)**	2.340(1.746, 2.935)
Prunned with LD R2≥ 0.2	1406	1.173(1.089, 1.264)	0.777(0.761, 0.794)*	2.377(1.825, 2.930)

Baseline c-stat 0.774(0.758, 0.791) and calibration score is 3.121(2.548, 3.693)

^*p < 0.05,

^**p < 0.01,

^***p < 0.001 compared to base model

^aR2 ≥ 0; no LD pruning

^bp-value ≤ 0.001; no LD pruning

^cp-value ≤ 0.001; R2 ≥ 0

We observed the greatest impact in GRS performance across different p-values. For discrimination, the optimal performance was observed at a threshold of 0.001. This threshold also corresponded to the largest estimated RR. A p-value cut point of 0.001, would correspond to a Benjamini-Hochberg false discovery rate (FDR)of 0.323 (Yoav Benjamini and Yosef Hochberg), beyond typical standards for statistical significance. On the other hand, calibration was optimized at a p threshold of around 0.01 – 0.05. Both showed decreased performance at very stringent and liberal thresholds. The least amount of variability in GRS quality was observed across different imputation metrics, with also little difference between dosage and genotype based calls. For LD, increasing the pruning threshold led to a slight deterioration in quality, with the relative risk and discrimination dropping with more pruning, but the calibration being slightly higher with some LD pruning.

Discussion

We illustrate an approach to empirically determining the optimal set of SNPs for a GRS. The focus is on performing a grid-search across the various tuning parameters (p-value, LD, imputation quality, and imputation type) and using cross-validation to select the optimal combination. The primary conclusions are that the addition of a GRS improves the overall model and that the GRSs are relatively robust to different specifications. Aside from extreme values, the results were relatively similar.

For 10 year risk prediction of CHD in the ARIC cohort using SNPs derived from the CARDIoGRAM consortium GWAS of ~2.5 M HapMap SNPs, we found optimal discrimination was achieved using a GRS that included all SNPs in CARDIoGRAM with a p < 0.0001 without a need to remove SNPs in high LD and without a need to filter by low imputation quality. Since each disease is likely to have a varying degree of evidence supporting the set of SNPs useful for risk prediction, we emphasize that our optimal parameterization is not generalizable to other outcomes. Moreover, even within a given a disease (such as CHD) it is possible that results will be different among different cohorts since they will each have different case mixes. However, our findings suggest, instead of arbitrarily selecting different cut-points an empirical evaluation is warranted to select the optimal cut-points.

Investigators have carefully considered how best to select a set of SNPs for a GRS. Wu et al.(Wu et al., 2013) examined this question in the context of a single study, where one wants to perform both discovery and prediction and found that estimating the effect size of SNPs was a critical part of the process, an issue we did not need to struggle with because we simply applied the weights from the CARDIoGRAM GWAS. Others (Purcell et al., 2009; Simonson et al., 2011) have suggested that the typical approach of using genome wide significance may not be sufficient, a finding that is somewhat confirmed in our analysis, though not to the extent that they report. In our case we found the optimal p-value threshold when considering RR to be 0.001. This corresponded to a Benjamin-Hochberg FDR of 0.323, suggesting there is value in incorporating what are still likely false associations. We anticipate that the optimal p-value threshold will strongly depend on the supporting data to create the GRS and the underlying genetic architecture of the trait of interest with a more polygenic trait benefiting from the addition of a larger fraction of the top SNP associations. In studies based on smaller studies, where the effects are less stable, it may be necessary to go further down the list to capture more of the genetic variability, where larger studies will be able to better estimate the true relationships. Ultimately the question of how far “down-the-list” is an important one that has implications beyond simply the optimal GRS. Our optimal score incorporated 7,387 SNPs. For a GRS computed off of a full genome chip, this is not a challenge. However, we can also envision a scenario where hospital systems may choose to create custom chips for their patients to capture a variety of GRSs. In this case, the slight loss in prediction quality may be worth creating a smaller, custom chip.

Imputation quality and LD level were less important determinants of GRS quality. The LD finding is counter to the findings of Wu et al, who noted LD pruning was beneficial. Theoretically, one would expect LD pruning to improve a GRS since LD violates one of the assumptions of the GRS construction: the independence of marginal effects. An increasingly important consideration is the role of imputation. In our data, 60% of the SNPs eligible for the GRS were imputed using 1000 genomes data. It is possible that as the percentage of the dataset that needs to be imputed increases, the imputation quality will matter more. Overall, the results suggested that we did not need to filter on imputation quality, as measured by r². Similarly using genotype calls or dosages did not make a noticeable in quality. We note that over the long term, the need for imputation will diminish as more individuals undergo whole genome sequencing.

A very challenging matter is the evaluation of the clinical utility of a GRS. We considered only three potential evaluation metrics: relative risk, c-statistic, and calibration slope. These three metrics are interconnected. It has been noted that the Wald test on an odds ratio is a more powerful test than testing the increase in AUC (Demler et al., 2012; Pepe et al., 2013). While comparing GRSs are not technically nested tests, we did observe high correlation between the AUC and RR, with the RR showing more variability across constructions, Moreover, as noted previously, an increase in discrimination can often lead to a decrease in calibration (Cook, 2007), observed in our own results. Ultimately the choice of evaluation metric is an important consideration and partially depends on how the GRS will be used. If the goal is simply to estimate the strength of association of the GRS then RR is probably the best metric. However if one will be using the GRS as part of a clinical risk tool to group patients then discrimination should be considered. Calibration is most useful if one wants to give an individual accurate information about his or her risk of disease. Of course these metrics do not speak specifically to clinical utility, something that will ultimately need to be shown prospectively.

The process we suggest has implication both within analytic and clinical settings. As more genetic data becomes readily available researchers are using GRS in different ways. This includes assessing heritability (Chatterjee et al., 2013; Purcell et al., 2009), Mendelian Randomization studies (Palmer et al., 2012), and risk prediction (Weijmans et al., 2015). Having a means to optimally develop a GRS within a specific research context is important. In addition to the research context, the clinical environment is increasingly becoming “a learning environment.” With the proliferation of electronic health records and declining cost of genotyping, the incorporation of genetic data into clinical practice becomes more likely (Kannry and Williams, 2013). In such a setting it becomes important for the clinical system to properly validate the optimal scoring system to use, for their patient population.

Our analysis has several strengths and weaknesses. We took advantage of large GWAS data to get robust estimates of SNP association with CHD. Using an independent cohort we calculated a GRS and evaluated with cross-validation to minimize overfitting. While our results point out important considerations for creating a GRS it is important to note that this is only in one cohort and one disease. Our results will not necessarily directly translate to other diseases or even other cohorts. Instead, we suggest that others can be guided by our approach when constructing and testing their own GRS. Moreover, we have only considered GRS construction based on marginal associations. While this was necessary based on the use of outside source data, it is possible that approaches that used multivariable associations would provide additional insights (Goldstein et al., 2010).

Overall, our work helps to add an empirical approach to the construction and evaluation of a GRS. We suggest different criterion that one can assess and means to perform that assessment. As GRSs become more commonplace there will be more of a need for each user to determine the optimal set of parameters for their specific analysis.