Integrated Simulation Framework for Toxicity, Dose Intensity, Disease Progression, and Cost Effectiveness for Castration-Resistant Prostate Cancer Treatment With Eribulin

Abstract

Quantitative model-based analyses are helpful to support decision-making in drug development. In oncology, disease progression/clinical outcome (DPCO) models have been used for early predictions of clinical outcome, but most of such approaches did not include adverse events or dose intensity. In addition, cost-effectiveness evaluations of investigational compounds are becoming increasingly important. Here, we developed an integrated model-based framework including relevant treatment effects for patients with castration-resistant prostate cancer treated with the anticancer agent eribulin. The framework included (i) a DPCO model relating prostate-specific antigen (PSA) dynamics to survival; (ii) models for adverse events including dose-limiting neutropenia and other graded toxicities; (iii) a model for Eastern Cooperative Oncology Group (ECOG) performance score; (iv) a model for dropout; (v) the consideration of cost effectiveness. The model allowed simulation of realistic treatment courses. Subsequently, simulations evaluating alternative treatment protocols or patient characteristics were performed in order to derive inferences on expected efficacy and cost effectiveness.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC? ☑ Cost-effectiveness analyses are becoming increasingly important in the field of oncology, but are currently only conducted during late-stage development. Models for disease progression in oncology can be used to predict clinical outcome, but these have not yet been applied for making predictions of cost effectiveness, or for predicting clinical outcome while considering key aspects such as toxicities, dose adjustments, and clinical treatment protocols. • WHAT QUESTION DID THIS STUDY ADDRESS? ☑ How can early predictions of clinical outcome and cost effectiveness at early stages of oncology drug development be generated? • WHAT THIS STUDY ADDS TO OUR KNOWLEDGE ☑ This model-based approach represents a tool for integration of knowledge related to disease progression, clinical outcome, dose-limiting toxicities, quality of life, and cost effectiveness, in order to evaluate different potential treatment strategies at early stages of drug development. • HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY AND THERAPEUTICS ☑ The described approach can be considered for generating informative inferences on clinical outcome and cost effectiveness at early stages of drug development and associated decision-making processes.

Integration of toxicity and efficacy models in oncology

Quantitative model-based analyses are helpful to inform and support drug development.1–4 In oncology, such approaches have initially focused on the development of models describing (dose-limiting) toxicities.5–10 Quantitative understanding of toxicity profiles is of key importance for most cytotoxic drugs, as often the maximum tolerated dose is assumed to be related to treatment efficacy.11 Increasingly, models with system-, drug-, or disease-specific properties are being developed, which are more informative for predictive purposes. For instance, the semiphysiological model for hematological toxicity proposed by Friberg et al.12 has been demonstrated to have consistent system-specific parameters. More recently, a paradigm has been proposed to link quantitative models describing cancer disease progression, or tumor growth inhibition, to models describing clinical outcome (e.g., overall survival).1 Such disease progression/clinical outcome (DPCO) models may provide reasonable predictions of clinical outcome based on the observed dynamics of disease progression biomarkers, as was initially demonstrated for colorectal cancer13 and non-small cell lung cancer.14 DPCO models are potentially disease-specific, and as such, a DPCO model developed for a specific indication can be used to extrapolate expected clinical outcome for new drugs in early clinical development based on their early biomarker response in patients

Thus, overall, quantitative models for toxicity and efficacy can be considered highly relevant and informative in trial design optimization and associated decision-making prior to the conduct of phase III studies. However, ideally these approaches should be applied in an integrated fashion to allow for their interaction, as toxicity-induced dose reductions may potentially impact efficacy.

Integration of pharmacology and pharmacoeconomics

With rapidly rising healthcare costs, cost-effectiveness analyses (CEA) are becoming more important. CEAs are usually conducted after approval based only on pivotal registration trials supplemented with additional sources of evidence. Growing interest exists to further integrate CEAs with the process of regulatory evaluation15 to include cost-effectiveness assessments at early stages of development. As these CEAs are mostly conducted at a late stage of clinical development, few opportunities exist to evaluate and potentially impact clinical development strategies. However, during early phases of drug development informative datasets on all aspects of drug effects are being collected. By integrating pharmacological and pharmacoeconomical models, earlier assessment of expected clinical utility and cost effectiveness can be obtained, which can be useful to estimate cost effectiveness and clinical utility a priori, rather than to only assess these important aspects post hoc.16,17 However, only one such example has been reported to date.18 Finally, as many novel anticancer agents may only show a marginal difference in efficacy, additional metrics allowing differentiation between other comparator agents may be of value.

Proof-of-concept analysis for castration-resistant prostate cancer

The overall aim of this study was to develop an integrated simulation framework for toxicity, dose intensity, disease progression, and cost effectiveness for castration-resistant prostate cancer treatment with eribulin as a proof-of-concept. This work builds further upon the previous development of a semiphysiological model for neutropenia, the major dose-limiting toxicity of eribulin,8 and second on the previous development of a DPCO model for patients with castration-resistant prostate cancer (CRPC) treated with eribulin, which related prostate-specific antigen (PSA) dynamics to overall survival (companion article). The work consists of two parts. In the first part, we developed additional models to support the framework. Here, we developed new models for: (i) graded nonhematological adverse events; (ii) the change in Eastern Cooperative Oncology Group (ECOG) performance scores; and (iii) dropout. In the second part of this analysis, these models were integrated to allow for trial simulations including preliminary CEA. Here, the previously developed models for neutropenia and DPCO were integrated into a single stochastic simulation framework that was used to evaluate a number of proof-of-concept simulation scenarios.

METHODS

The schematic structure of this simulation framework is presented in Figure 1. The figure accounts for the causal relationships between dose, exposure, toxicity, efficacy, and cost effectiveness. First, the interaction between dose, pharmacokinetics (PK), and toxicities results in a realized dose regimen for each patient that includes dose reductions. Then, the patient-specific PSA response is predicted, together with its relation with expected overall survival. Finally, the ECOG performance score was included as a surrogate metric for quality-of-life, and finally dropout was considered. Ultimately, this framework was developed to provide predicted efficacy and cost-effectiveness metrics including life-years gained (LYG), incremental cost-effectiveness ratios (ICERs), and quality-adjusted life years across a population of patients. Where possible, models included interindividual variability on parameters and associated predictors for this variability, to evaluate with flexibility different potential treatment scenarios.

Figure 1.

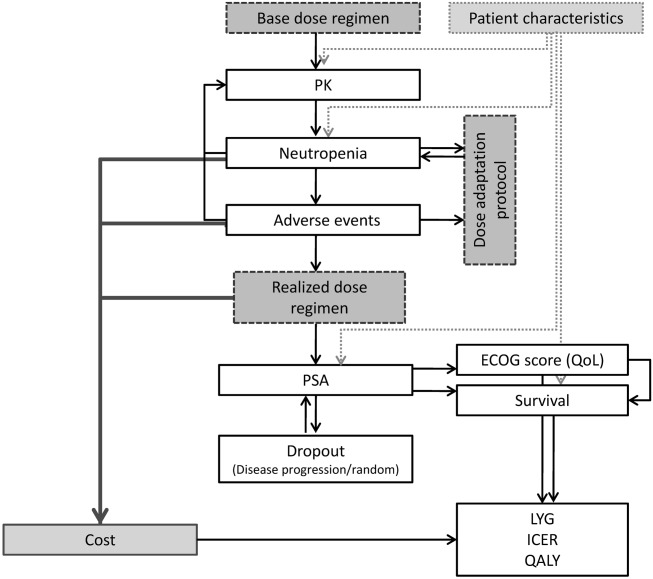
Schematic representation of the integrated simulation framework that was developed. PSA, prostate-specific antigen; LYG, life years gained; ICER, incremental cost-effectiveness ratio; QALY, quality-adjusted life years; PK, pharmacokinetics.

Part I. Model development

Study data

Phase II data from a clinical trial (n = 108) of eribulin mesilate in CRPC patients20 was used for the development of models for (i) the ECOG performance score; (ii) nonhematological adverse events; and (iii) patient dropout. Data from this study were also used for the development of the DPCO model for PSA dynamics and its relation with clinical outcome.19 The previously developed pharmacodynamic model for eribulin-induced neutropenia, which was also integrated in the simulation framework, was based on a much larger pooled dataset from multiple phase I, II, and III studies including a total of 1,579 patients8 who were predominantly treated for breast cancer.

Drug exposure

The approved dose of eribulin for treatment of breast cancer is 1.4 mg/m², administered on day 1 and day 8 of a 21-day cycle.20 This dosing regimen was also used in the current analysis, unless otherwise specified. Pharmacokinetics (PK) were described using a previously developed model based on data from several phase I and II studies, which included a systematically developed covariate model describing the impact of various patient characteristics on drug exposure.8 The model was a 3-compartmental PK model with linear elimination with albumin, alkaline phosphatase, bilirubin as covariates on clearance,21 and in addition a dose–effect on intercompartmental clearance.

PSA DPCO

The previously developed DPCO model in patients with CRPC was used to describe the dynamics of PSA and its association with clinical outcome (overall survival). The model for PSA dynamics was a compartmental tumor growth model with parameters for baseline PSA (PSA₀), PSA growth rate (K_G), drug-induced PSA inhibition (KD₀), and a term for resistance development. In the model, the predicted area under the concentration–time curve (AUC) was used as the exposure metric in this model. Prior docetaxel treatment was identified as a covariate on baseline PSA and on drug-induced PSA inhibition. The second component of the DPCO model described overall survival using a parametric Weibull function, which included the following covariates: (i) patient-specific ECOG-performance state; (ii) treatment-induced time to nadir (TTN) of PSA; and (iii) the disease-specific PSA growth rate (K_G).

Neutropenia

Neutropenia is the main dose-limiting toxicity for eribulin. The time course of absolute neutrophil counts (ANC) was described using a semiphysiological model for neutropenia previously developed by us,8 which included a systematically developed covariate model explaining part of the between-subject variability observed in the pharmacodynamic response. The model included parameters for baseline ANC, maturation time, feedback, and drug effect (ANC_SLOPE).

Other adverse events

For adverse events (AEs) other than neutropenia, we developed models for AEs with an incidence of more than 20 events (2.1% incidence), which were: nausea, fatigue, peripheral neuropathy, paresthesia, diarrhea, asthenia, and anemia. The occurrence of these AEs was modeled using separate Markov-transition models. We considered three toxicity states: no adverse event (state 0), nondose-limiting adverse event with CTCAE grade 1 or 2 (state 1), and dose-limiting adverse event with CTCAE grade 3 or 4 (state 2). Only transition rates between bordering states (e.g., between 0 and 1 or 1 and 2) were considered.

ECOG performance score

A Markov-transition model was used to describe the probability of experiencing different ECOG performance scores. Furthermore, we evaluated whether PSA dynamics could be included as a covariate on transition rates, in order to consider treatment effects on ECOG score dynamics. In the simulation framework, the ECOG model was used to derive a summary metric for quality of life.

Dropout

A model for random informative dropout was developed using the time of dropout, defined as the time after start of treatment until stop of treatment. Different parametric survival models were fit to the time to event data, namely, Weibull, exponential, normal, lognormal, logistic, and log-logistic models. Based on visual model fit and the −2 log likelihood, we selected the base parametric model. Thereafter, we evaluated the inclusion of patient-specific covariates as predictors for dropout (P < 0.05, likelihood ratio test). The following covariates were considered: PSA₀, TTN, relative and absolute change from PSA baseline, individual predicted PSA growth rate, individual predicted PSA inhibition rate, and age. All covariates were log transformed prior to inclusion.

Patient characteristics covariate distribution

Based on the observed body surface area (BSA) distribution in the original phase II study for eribulin in CRPC, we assumed a mean BSA of 1.93 m² distributed according to a truncated normal distribution with a standard deviation of 0.23 and truncated between 1.3–3 m². The BSA values were used to derive absolute dose amounts for each simulated patient. Unless otherwise specified, we assumed that patients were not pretreated with taxanes, as this was a significant covariate in the DPCO model. The neutropenia model included biochemical markers for liver function (bilirubin, albumin, lactate dehydrogenase (LDH)), assuming typical values.8

Dose adaptation and disease progression

A dose adaptation model defined when and how doses should be adjusted after toxicities. Unless otherwise specified, we assumed single 25% and 50% dose reductions after experiencing any grade 3 or 4 toxicity, respectively. For neutropenia, we defined grade 3 and 4 toxicities for absolute neutrophil counts (ANCs) <1.0·10⁹ and <0.5·10⁹ cells/L, respectively. In addition, no drug administration was performed when the pre-dose ANC was below 1.5·10⁹ cells/L.

The disease progression criterion (e.g., stop treatment due to rise in PSA) was defined as an increase in PSA levels of >25% from PSA nadir values, and an absolute PSA level >5 ng/mL, which remained consistent after 14 days.

An overview of dose adjustment and disease progression rules is provided in Table 1.

Table 1.

Simulation characteristics of the base scenario (B)

Description	Specification
Dose regimen
Dose	1.4 mg/m2
Dose times (days)	0, 7
Cycle length (days)	21
Dose reduction after AE	Single (nonrepeated dose reduction) Grade 3: 25% of dose; Grade 4: 50% of dose
Progression criterion	25% increase from nadir + PSA > 5 ng/mL (after 2 weeks)
Patient characteristics
Baseline PSA (mean) [ng/mL]	23.2
Baseline ECOG	0
Body surface area (mean, SD)	1.73 (0.3)
Baseline ANC (mean) [109 cells/L]	4.03
Prior taxane treatment	—
Costs
Dose (U/mg)	100*	Direct cost of drug and drug administration visit
Neutropenia, grade 4 (U/day)	100	Average costs for hospitalization, growth factors etc.
Peripheral neuropathy, any grade (U/day)	5	Medication, contact physician
Paresthesia, any grade (U/day)	5	Medication, contact physician
Diarrhea, any grade (U/day)	5	Medication, contact physician
Asthenia, any grade (U/day)	1	Contact physician
Anemia, any grade (U/day)	5	Medication, contact physician

Part II. Simulation framework development

Overall structure

A schematic overview of the developed framework is depicted in Figure 1. In the framework, individual patient characteristics were generated from the covariate distribution model, and associate absolute doses were derived. Individual time courses for neutrophils, PSA, nonhematological adverse events and ECOG score were generated using the developed models. These profiles were simulated for each patient in iterative fashion, in order to allow for potential dose reduction after each administration, according to the specified treatment protocol.

Summary metrics

The individual time courses of the different parameter summary metrics were computed as summarized in Table 2.

Table 2.

Overview of summary evaluation metrics

Metric	Description
Dose intensity	Fraction of the dose compared to the maximum unreduced dose.
Neutropenia	Incidence and duration of grade 3 and 4 neutropenia.
Efficacy: survival	Median individual predicted overall survival based on PSA disease progression model and other covariates.
Life-years gained (LYG)	Median individual differences in overall survival between two competing treatments
Total treatment costs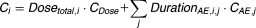
Incremental cost-effectiveness ratio (ICER)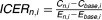
Quality-of-life (QOL)
Quality-adjusted life years (QALY)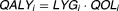

i = individual i.

Dose intensity

Dose intensity was defined as the fraction of the dose compared to the maximum unreduced dose.

Neutropenia incidence and duration

The incidence and duration of grade 3 and 4 neutropenia were computed to provide insight in the impact of dose regimen alterations on the most important toxicity of this agent.

Efficacy: survival

A total of 1,000 overall survival times were simulated based on the individual values for TTN, PSA growth rate, and ECOG baseline score of each simulated patient. Subsequently, the median survival time for each patient was computed.

Life years gained

Life years gained (LYG) was defined as the median differences in overall survival between two competing treatments for each simulated patient.

Costs

The cost model defines the assignment of costs to various events that may contribute to the total overall treatment costs (Eq. 1, for which we considered two types: (i) direct drug costs and (ii) adverse event-related costs. Direct costs were computed as the dose costs (C_dose) multiplied by the received absolute cumulative dose (Dose_total) for each individual, i. The adverse event-related costs were computed by multiplying the duration of each adverse event j for individual i with its associated costs (C_AE,j) (Eq. 1. Hypothetical costs and cost units (CU) were assumed, and are provided in Table 1.

1

ICER

We computed the incremental cost-effectiveness ratio (ICER) as follows for each scenario, compared to the base treatment scenario, as follows:

2

Here, the reference costs (C_base,i) are substracted from the total costs C for scenario n in individual i are subtracted from the reference costs (C_base,i) for the corresponding individuals, and divided by the difference in corresponding effectiveness metrics E, which could either be median survival or TTN.

QALYs

The ECOG performance score was used to calculate a surrogate marker for mean quality-of-life (QOL) during the observation period. Individual QOL value was computed using the individual ECOG profile as follows:

3

where t_EOT represents the end-of-treatment time for individual i, max(ECOG) represents the maximum possible ECOG score (e.g., ECOG = 2 for this example), and finally QOL_i represents the quality of life metric for individual i. Thus, QOL was bounded between 0 and 1, where 1 represents optimal quality of life. Subsequently, quality-adjusted life years (QALY) for each individual i were computed as follows:

4

where QOL represents the individual QOL metric as computed from the ECOG time course.

Part III. Simulations

Base and “no-treatment” reference simulation scenarios were first defined. The base scenario assumes typical values for all of the different models. An overview of characteristics of the base scenario is provided in Table 1. The no-treatment scenario represents the case where no drug has been administered, and was used to compare efficacy metrics. Subsequently, alternative simulation scenarios were evaluated, addressing specific aspects of treatment and patient characteristics, while keeping other characteristics equal to the base scenario. For each scenario, 500 patients were simulated for a duration of seven treatment cycles (i.e., 147 days), unless patients would dropout earlier.

Dosing regimen

Two alternative dosing regimens were defined. The first scenario evaluated a lowered dose of 1.0 mg/m², at the default dose administration timepoints of day 1 and 8. The second scenario considered the default dose of 1.4 mg/m²; however, only administered at day 1 of each cycle.

Alternative disease progression criterion

An alternative PSA-based disease progression criterion of 50% instead 25% increase from PSA nadir was considered.

Dose-reduction rules

Here we either assumed a scenario with no dose reductions at all, in order to assess how this would influence toxicity profiles, or, for the second scenario, we considered more strict dose reductions of −50% and −65% for grade 3 and 4 toxicities, respectively.

Patient population

In the first scenario, patients with a low disease burden were considered, assuming a typical baseline PSA of 5 ng/mL. In the second scenario we assumed the alternative case where patients were significantly pretreated with taxanes.

Comparator agents and uncertainty assessment

Here we modified the parameters of the underlying model for toxicity and efficacy (PSA dynamics) models for two purposes. First, it may be desirable to profile comparator agents to a drug under investigation in terms of expected toxicity, efficacy, and/or cost-effectiveness metrics. In such cases, knowledge related to toxicity and/or efficacy may be available for these comparator agents. We considered three scenarios: (i) a comparator agent with an expected 3-fold increased PSA inhibition drug effect parameter; (ii) a comparator agent with an increased drug effect (3*KD₀), but also a higher toxicity parameter (1.5*ANC_SLOPE, the drug-effect parameter in the neutropenia model); and (iii) a comparator agent with a decreased drug effect (0.5*KD₀), and lower toxicity parameter (0.5*ANC_SLOPE).

Second, during early clinical development, uncertainty related to toxicity or efficacy profiles may still be relatively high, and in such cases sensitivity analysis could be considered to quantify the impact of uncertainty in toxicity parameters on any inference derived from an integrated simulation framework. For this application, we considered (i) an increased drug effect parameter for neutropenia by a factor of 1.5, and (ii) a transition rate to higher toxicity scores for peripheral neuropathy increased by a factor of 3.

Software

The Markov-transition models for AEs and ECOG score were developed using NONMEM (v. 7.2), with the first-order conditional estimation method. The parametric survival model was estimated using the survreg function in R (v. 3.0).22 The overarching simulation framework, as well as simulations for different submodels, were conducted using R together with the R packages deSolve23 and MASS. For implementation of integrated cost-effectiveness analyses in R, we refer to our previous work on this as described by Frederix et al. 24,25

RESULTS

Model development

ECOG score

The Markov-transition model adequately described the ECOG transitions between neighboring ECOG states (Figure 2). Transition rates could be estimated with a relative standard error (RSE) of <27%. The baseline ECOG score distribution was 51, 48, and 1% for ECOG scores of 0, 1, and 2, respectively. Most transitions were occurring within the same state (0 to 0, 1 to 1). The number of events of an ECOG score of 3 or 4 was low. Therefore, we pooled ECOG scores of 2, 3, and 4 into one state. We also estimated an effect of PSA disease progression on transition rates towards higher ECOG states. When >50% inhibition of the PSA was observed, the transition rates to higher ECOG scores decreased by a factor of 0.704 (RSE 36%). The parameter estimates of the Markov-transition model are provided in Table S1. When >50% inhibition of the PSA was observed, the transition rates to higher ECOG scores decreased by a factor of 0.704 (RSE 36%). When comparing these groups with >50% inhibition vs. <50%, the overall proportions of ECOG 0 and 1 were 75% and 23% vs. 44% and 48%, and was also consistent with observed transition frequencies. Nonetheless, the amount of ECOG data available was relatively limited, so the certainty and magnitude of the identified effect should be interpreted with caution.

Figure 2.

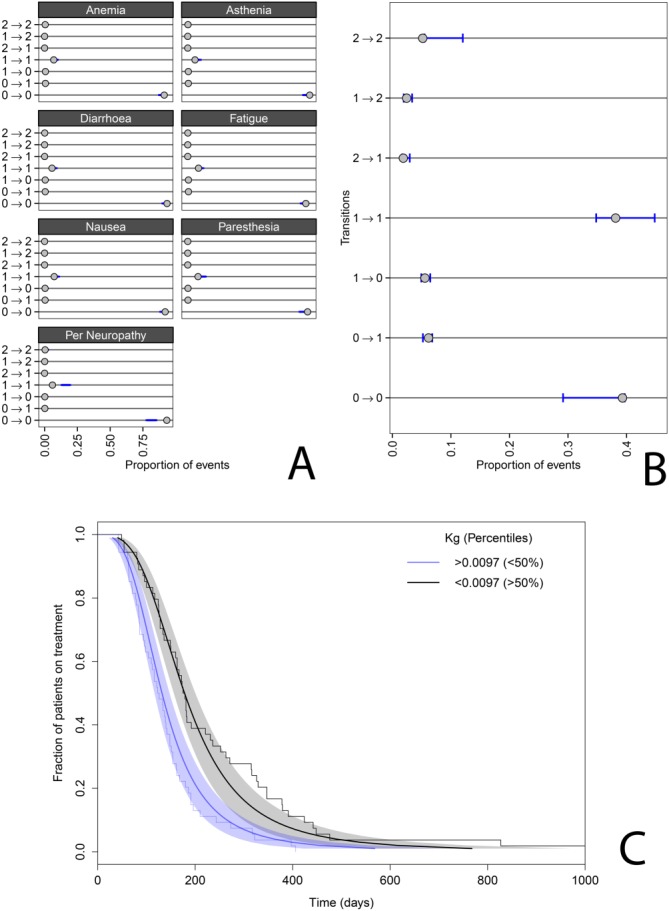
(A) Model predictions (95% prediction intervals) and observed incidence of transitions for the Markov-transition models for the other adverse events model and (B) ECOG performance score model. (C) Dropout model simulated median (thick solid lines) and 95% confidence intervals (areas) and observed (thin solid lines), stratified by patients above (blue) and below (gray) the median estimate for the PSA growth rate (K_G).

AE model

AEs other than neutropenia were described using a series of Markov-transition models. The overall distribution of different toxicity grades for each toxicity are provided in Table S2. Of all nonhematological toxicities, anemia showed the largest incidence of dose-limiting (grade >3) toxicities. Because no individual PK data were available for this specific study, we were not able to establish a direct exposure–response relationship. The parameter estimates of the Markov-transition models for the different AEs are provided in Table S1. For nausea and diarrhea, not enough observations for grade 3 and 4 toxicities were present to estimate their respective transition probabilities. Predicted and observed transition frequencies are depicted in Figure 2, and indicated an overall adequate description, with a limited discrepancy observed for transition rates of peripheral neuropathy.

Dropout

A log-logistic model best described dropout. A limited part of the observed dropout patterns falls outside the predicted curve. Alternative functions (other than log-logistic) only resulted in further deviations of the observed dropout pattern. Possibly, the observed deviation can also be related to the limited size, especially at later times with only a limited number of events occurring. For the purpose of simulations, this was found to be not very relevant. The individual predicted PSA growth rate (K_G) was found as the most significant predictor (dOFV -11.4). PSA inhibition rate (KD₀) and age were also significant (ΔOFV = −4.3 and −4.05). However, in the multivariate model only K_G remained significant. For the final dropout model, the intercept was estimated at 2.212 (RSE 24.6%), scale was estimated at 0.3178 (RSE 7.0%), and a coefficient of −0.6102 (RSE 19.4%) was estimated for log(K_G). A visual predictive check is depicted in Figure 2, indicating adequate description of the data.

Simulations

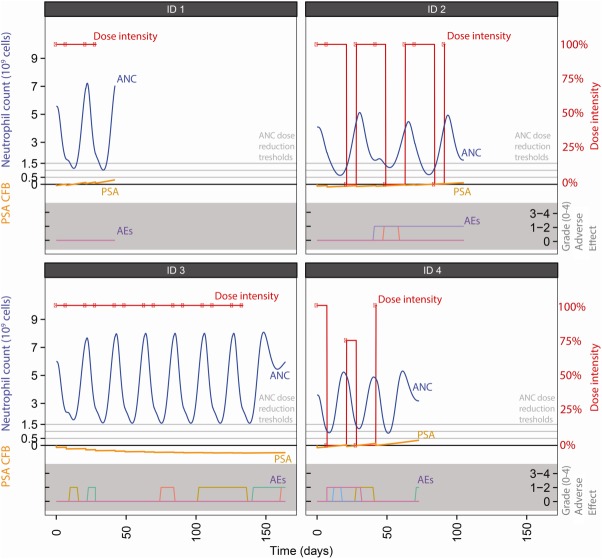
Typical time courses for neutrophil count, incidences of other AEs, PSA time courses, and the fractions of the full doses received at each dose event are depicted in Figure 3.

Figure 3.

Typical simulated time courses for dose reductions (red symbols and lines), neutrophils (dashed line), PSA (dotted orange line) and other adverse events (colored lines in bottom gray area) in four simulated patients. Neutropenia dose reductions thresholds are at 1.5*10⁹ (predose threshold), 1.0*10⁹ (grade 3), and 0.5*10⁹ (grade 4) cells/L.

Results of the simulated scenarios are summarized in Table 3. Throughout these scenarios, changes in summary metrics (Tables 2, 3) were compared to either the no-treatment scenario for values related to efficacy (i.e., LYG), or to the base scenario for values of ICER and QALYs.

Table 3.

Outcome metrics for simulation scenarios evaluated

				Neutropenia duration (d) [median, 95% PI]		Efficacy (days) [median, 95% PI]	Ci (CU) [median, 95% PI]			Compared to the No Treatment Scenario [median, 95% PI]	Comparison to the Base Scenario [median, 95% PI]
Scenarios		Dose intensity (%) [median, 5th–95th percentiles]	Neutropenia incidence (grade 3, 4)	Grade 3	Grade 4	Survival	Dose	AEs	Total	Life years gained (days)	ICER (CU)	QALY (CU/QOL)
B	Base	0.77 (0.39 – 1)	(63.4, 34.9)	4 (0 – 28)	0 (0 – 19)	517 (100 – 2081)	1418.9 (400.15 – 4024.58)	299 (0 – 2300.45)	1985.5 (501.95 – 4856.3)	29 (0 – 401)	–	–
S2	Dose regimen – 1.0 mg/m2 at t=[1,8] days	0.96 (0.44 – 1)	(45.4, 17.7)	0 (0 – 25)	0 (0 – 10)	512 (99 – 2069)	1161.8 (325.89 – 2971.67)	189 (0 – 1256.3)	1469 (374.95 – 3520.45)	25 (0 – 391)	18.9 (–12.93 – 140.91)	0 (–45 – 37.1)
S3	Dose regimen – 1.4 mg/m2 at t=1 days	0.96 (0.75 – 1)	(40.8, 17.8)	0 (0 – 19)	0 (0 – 8)	491 (97 – 2033)	747.94 (294.25 – 2053.36)	180.5 (0 – 1037.35)	1042 (303.8 – 2752.4)	3 (0 – 377)	32.71 (6.91 – 858.51)	–2.51 (–120.7 – 0)
S4	Progression after 50% increase from nadir (instead of 25%)	0.77 (0.38 – 1)	(65.9, 38.8)	6 (0 – 29)	0 (0 – 21)	517 (100 – 2081)	1918 (513.99 – 4063.7)	390.5 (10 – 2395.6)	2735.5 (734.7 – 4964.95)	30 (0 – 401)	19.05 (–22.66 – 243.59)	0 (0 – 0)
S5	Dose reductions – No dose reductions	1 (1 – 1)	(66.8, 45.4)	6 (0 – 39)	0 (0 – 53)	539 (103 – 2123)	2806.26 (597.39 – 4478.2)	511.5 (0 – 5687.05)	3770 (618.55 – 9847.2)	69 (1 – 420)	59.37 (12.28 – 403.31)	0 (0 – 112.15)
S6	Dose reductions – Permanent dose reduction (instead of single)	0.69 (0.36 – 1)	(63.2, 32.8)	3.5 (0 – 27)	0 (0 – 9)	514 (100 – 2073)	1285.92 (400.15 – 3870.67)	280 (0 – 1259.05)	1760.5 (501.95 – 4349.9)	25 (0 – 395)	24.43 (–23.51 – 161.33)	0 (–18.57 – 0)
S7	Changed dose reduction for grade 3 (50%) and 4 (65%) toxicity	0.75 (0.39 – 1)	(63.2, 34.5)	4 (0 – 26)	0 (0 – 17)	515 (100 – 2077)	1364.21 (361.82 – 3986.15)	322.5 (0 – 2007.8)	1927.5 (472.8 – 4716.65)	26 (0 – 399)	13.14 (–71.73 – 203.26)	0 (–5.07 – 0)
S8	Patient population – Lower PSA baseline (5 ng/mL)	0.78 (0.39 – 1)	(63.8, 35)	4 (0 – 30)	0 (0 – 22)	644.5 (125 – 2594)	1685.45 (400.15 – 4074.53)	344 (0 – 2408.65)	2366.5 (503.9 – 5060.85)	165 (27 – 902)	0.23 (–2 – 8.26)	127.68 (47 – 397)
S9	Patient population – Taxane pre–treated (200 days) patients	0.78 (0.39 – 1)	(63.3, 34.7)	4 (0 – 27)	0 (0 – 19)	433 (84 – 1750)	1366.2 (398.76 – 3986.74)	274 (0 – 2212.05)	1884 (503.9 – 4914.1)	–22 (–130 – 96)	0 (–2.99 – 6.1)	–84 (–253.5 – 30)
S10	Comparators – Increased drug effect (3*KD0), and equal toxicity	0.79 (0.39 – 1)	(64.1, 35.9)	5 (0 – 30)	0 (0 – 22)	555 (106 – 2131)	2037.97 (408.65 – 4157.49)	355.5 (1 – 2689.25)	2949.5 (545.4 – 5123)	86 (1 – 430)	7.94 (–9.58 – 56.11)	21.75 (0 – 118.07)
S11	Comparators – Increased drug effect (3*KD0), higher toxicity	0.59 (0.34 – 1)	(84.3, 60.7)	8.5 (0 – 31)	4 (0 – 34)	547 (104 – 2127)	1554.39 (391.65 – 3807.68)	682.5 (3 – 3712.65)	2793 (499.7 – 5831.45)	79 (1 – 427)	13.25 (–28.47 – 89.21)	13.35 (0 – 113.58)
S12	Comparators – Decreased drug effect (0.5*KD0), and lower toxicity	1 (0.5 – 1)	(24.9, 6.2)	0 (0 – 15)	0 (0 – 3)	503 (99 – 2053)	1588.91 (495.7 – 4236.81)	145 (0 – 877.45)	1804.5 (530 – 4716.35)	5 (0 – 380)	9.54 (–26.05 – 107.82)	0 (–69.37 – 23.34)
S13	Uncertainty – Increased neutropenia (1.5*ANCSLOPE)	0.71 (0.45 – 1)	(86.4, 68.8)	6 (0 – 26)	4 (0 – 36)	524 (101 – 2090)	1312.78 (497.43 – 3626.11)	890 (1 – 3966.8)	2398.5 (587.85 – 6219.9)	52 (1 – 398)	21.04 (–124.28 – 261)	0 (–35.07 – 66)
S14	Uncertainty – Increased peripheral neuropathy (3*kn+1)	0.78 (0.39 – 1)	(63.4, 34.9)	4 (0 – 27)	0 (0 – 19)	517 (100 – 2081)	1418.9 (400.15 – 4027.44)	400 (0 – 2445.55)	2103 (512.8 – 4981.35)	30 (0 – 401)	–9.48 (–23.85 – 45.28)	0 (0 – 0)

NDLT = non dose–limiting toxicity (grade 1 or 2); DLT = Dose–limiting toxicity (grade 3 or 4); LYG = Life–years gained; QALY = Quality adjusted life years gained; ICER = Incremental cost–effectiveness ratio.

^*Other adverse events (pooled): U = Cost unit; TTN = Time to PSA nadir; QOL = Quality of life metric; Ci = Total costs per individual i.

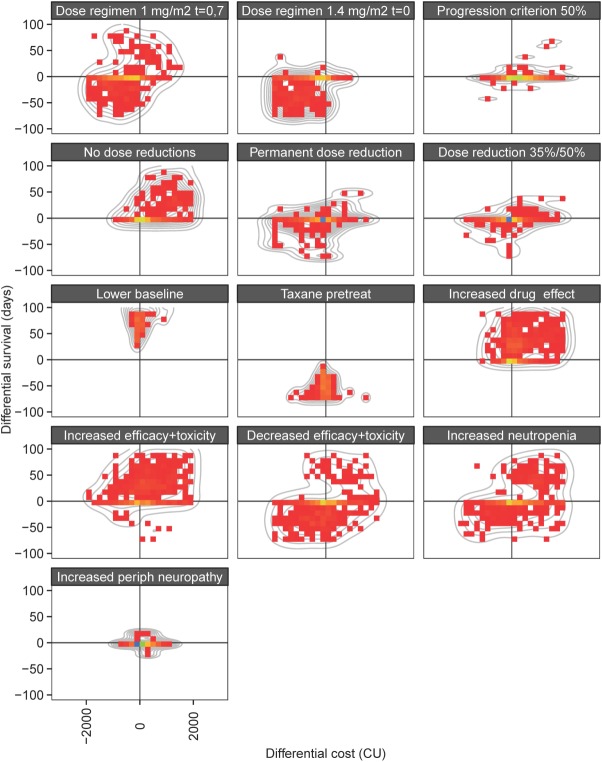
Finally, the individual differences in costs and effects for the different simulation scenarios vs. placebo treatment are represented in Figure 4. This figure depicts for each simulated individual the expected costs and expected efficacy, taking into consideration simulated values derived from toxicity and efficacy models and associated dose reductions, in comparison with the base scenario. These types of differential cost-effectiveness plots are commonly used in the field of CEA to evaluate different CEA scenarios, and, the effect of parameter uncertainty. In this case, however, the interindividual variability is thus depicted.

Figure 4.

Distribution of difference in cost (CU) vs. effect (overall survival, days) for the different simulation scenarios vs. the base scenario. The color intensity represents the relative density of cost-effectiveness pairs across individuals. The gray lines represent 2D density smoothers.

Dose regimen

In Scenarios S2 and S3, alternative dosing regimens were evaluated in which a lower dose (1.0 mg/m² instead of 1.4 mg/m²) was administered (S2), or, where only a dose at day 1 of the 21-day cycle was administered (S3). Because in these dosing regimens lower doses were used, they were associated with less toxicity and thus with higher dose intensities. Consequently, costs for both dose (as a lower total dose was administered) and toxicity were lower.

Alternative disease progression criterion

Design of CRPC trials is still strongly debated26 and therefore the implications of altering the disease progression criterion were evaluated. If the disease progression criterion was increased by >50% after reaching PSA nadir (S4), instead of the more commonly used 25%, the costs due to toxicities increased, as did the dose costs due to the longer treatment duration.

Dose reduction rules

In Scenario S5, no dose reductions were allowed. As expected, this led to increased neutropenia accompanied by increased costs. Scenario S6 evaluated permanent, instead of single-event dose reductions. This led to further decreased dose intensities, a decrease in the median duration of neutropenia, and overall decreased drug and toxicity-associated costs. In Scenario S7, in which larger dose reductions of 50% and 35% for grade 3 and 4 toxicities were used, no substantial differences in outcome metrics or costs were observed.

Patient population

Patients with low typical PSA baselines (5 ng/mL) (S8), i.e., with less progressed disease, clearly benefited when looking at efficacy metrics, with a median increase in survival of 124 days. However, drug-associated costs were increased since patients could be treated longer until disease progression occurred.

When patients were pretreated with taxane (a significant covariate in the PSA model (S9)), median survival benefit again changed considerably, compared to the base scenario with a median decrease of survival of 80 days. Clear decreases in QALYs were also predicted for these patients, based on a higher probability of reaching higher ECOG scores.

Comparators and uncertainty assessment

We demonstrated how expected changes in toxicity or efficacy profiles for a hypothetical comparator could be evaluated in terms of efficacy and cost metrics. In Scenario S10, drug effects were higher while toxicity was equal, which led to substantially increased drug costs, but with the expected survival benefit, the ICER was only marginally reduced. In Scenario S11, increased toxicity and drug effect led to increased median survival, although this benefit was associated with increased drug and toxicity-related costs. For Scenario S12, for a comparator with an expected lower efficacy and toxicity, decreased toxicities and associated costs were observed, but in terms of cost effectiveness, the expected ICER was substantially increased, indicating that this inferior treatment was not cost-effective. Finally, Scenarios S13 and S14 considered a sensitivity analysis for toxicity parameter values on outcome metrics.

DISCUSSION

We have developed and integrated several models into an overarching simulation framework that allowed early assessment of toxicity, efficacy, and cost effectiveness in CRPC patients treated with eribulin. This work serves as a proof-of-concept example on how trial design and decision making in oncology can be further informed using a model-based approach in early clinical drug development. The major novelty of the current study was a full integration of the realized dosing regimen, toxicity, efficacy, and quality of life in CRPC. While we acknowledge the ideas that we present are not new, the full integration of all different components has not been presented for CRPC before.

Currently conducted CEAs mainly use empirical models to predict the incidence of toxicity and clinical outcome, which are based on late-stage clinical trials only. As such, they are mainly of relevance during late-stage evaluation of treatments for which pivotal registration trials have been conducted, and which may have already obtained regulatory approval. These approaches do not allow for drawing inferences related to expected cost effectiveness during early clinical development. In contrast, integrated simulation approaches that take into account relevant properties such as drug exposure, dose reductions, toxicities, biomarker response, dropout, and efficacy do allow for the development of much more comprehensive approaches that can be used to address “what if” scenarios during clinical development, as we have attempted to demonstrate in the current work. We evaluated various factors related to drug treatment regimens and patient characteristics (e.g., dose regimens, dose reductions rules, progression criteria), patient characteristics, comparator agents, and model uncertainty, which may be present during early development, and related these to a range of clinical utility and cost-effectiveness metrics (Table 3, Figure 4).

Pharmacokinetic-pharmacodynamic models typically evaluate patient characteristics that are predictors for observed interindividual variability. Such patient characteristics can be leveraged into an integrated simulation framework to assess the specific impact of, for example, increased probability to experience toxicities, or decreased probability for treatment response. For instance, in Scenario S9 we specifically evaluated the previously identified covariate effect of prior taxane treatment on PSA dynamics, and its subsequent impact on cost effectiveness. These simulations are of relevance, as an increasing interest exists for the evaluation of cost effectiveness in subgroups of patient populations.27

Typically, CEAs use plots of the difference in cost vs. effectiveness to assess the impact of parameter uncertainty. Here, we extended this type of visualization specifically for interindividual variation (Figure 4), and such a figure can be considered to visually identify subgroups of patients who are treated cost-effectively (or the opposite).

In oncology, pharmacological quantitative toxicity or efficacy models are becoming increasingly mechanistic. Potentially, these developments allow for further sharing and integration of knowledge with clinical development programs of different drugs. Such integration was also demonstrated in the current analysis, as we used a neutropenia model that was based on patient data for the same drug but in different indications (mainly breast cancer). Likewise, disease-specific DPCO models may become available that potentially allow informing an efficacy model across different drugs, as was demonstrated for colorectal cancer.13

Previously, Claret et al.28 developed a DPCO model for thyroid cancer that included an empirical model for the first time considering the probability of dose reduction in the context of DPCO frameworks. However, to our knowledge, the current analysis is the first example of a simulation framework for efficacy evaluation that integrated dose reductions in a somewhat more explicit and mechanistic fashion, potentially allowing more flexible use when evaluating alternative scenarios.

In 2001, Poland et al.16 and Hughes et al.17 suggested the potential value of integrated model-based approaches that also include pharmacoeconomical features. However, to date only one example has been published in which pharmacological models have been leveraged into an otherwise conventional health economical model.18 This particular example included a previously developed model linking rituximab pharmacokinetics to progression-free survival in patients with follicular lymphoma, which was subsequently integrated in a conventional cost-effectiveness framework. However, this implementation may still be viewed as an empirical approach, as for any new drug the relation between drug exposure and clinical outcome has yet to be determined empirically. As such, the approach described by Pink et al.18 cannot be implemented in the context of early drug development of a novel investigational agent. In addition, this approach did not include features such as model-based descriptions key to dose-limiting toxicities and associated dose reductions, and biomarkers for disease progression. Thus, this analysis demonstrates the relevance of utilizing more mechanism-based modeling approaches with system, disease, and drug-specific properties that more easily allow transfer of knowledge across drugs (e.g., using DPCO models) or indications (e.g., toxicity profiles such as neutropenia). It should be noted that not all of the models included in our simulation framework are of a mechanistic nature themselves (e.g., the categorical AE models). Nonetheless, in our view the overall framework may be referred to as a mechanistic framework, meaning it includes clinical and pharmacological causality to various factors that ultimately relate to efficacy or costs.

Although from a pharmacoeconomical modeling perspective various interactions and causalities were considered, this approach was not carried forward for the characterization of correlations between different types of toxicities and efficacy, by performing joint modeling. This could be of relevance, since the occurrence of one type of toxicity may be informative for the risk for other toxicities and potentially also efficacy. This was, however, not performed since part of the datasets originated from a different population, and also because of the technical challenges for implementing such joint models. Nonetheless, the development of joint models for toxicity and efficacy would be of substantial relevance for further advances such as integrated simulation frameworks.

As our research was a proof-of-concept analysis, some limitations and assumptions should be acknowledged. Although PSA is the primary biomarker for disease progression, patients may in some cases develop progression of disease due to development of (bone) metastases while PSA levels do not indicate such disease progression. This is a well-known limitation of PSA as a biomarker for disease progression of prostate cancer in general.29 In the current framework, we did not specifically model other reasons for disease progression, although implicitly other reasons for disease progression were at least partially captured by the dropout model.

We were not able to identify an exposure–response relationship for AEs other than neutropenia, as no PK data were available from the phase II study in patients with prostate cancer. For this specific example, these AEs did not play a significant role, as dose reductions were mostly related to eribulin-induced neutropenia, for which the exposure–response relationship was accurately characterized.

The ECOG score, which was included as a metric for quality-of-life, is not a widely used metric to describe QoL and most likely does not fully capture QoL in patients. Metrics such as the EQ5D score may have been more suitable, but these were not available for this example. Nonetheless, it is clear that any other metric describing QoL dynamics may replace the currently used ECOG score without issues.

The cost-effectiveness model was hypothetical and was kept relatively simple, as only drug and direct AE-related costs were considered. Moreover, the implementation of both drug- and AE-related costs was fully hypothetical, since we only aimed to demonstrate a proof of concept. Typically, CEAs include additional cost considerations, for instance, costs for follow-up hospital visits or background mortality rates. Of course, such cost considerations can easily be included in the current framework, but as all costs where hypothetical we did not consider this of additional value, since these costs are typically not directly related to pharmacological action.

Although our framework can provide inferences that may be relevant to inform decision making in drug development in CRPC, it remains crucial to be aware of the impact of the various assumptions made. For instance, the DPCO model was based on a selected CRPC patient population; other CRPC patient populations may have further or less advanced disease, with potential implications on expected PSA dynamics and associated clinical outcome predictions. Such considerations may be important to consider when performing simulations using this framework or similar frameworks. Another example is the neutropenia model, which was developed in a population of female breast cancer patients. While on the one hand the sharing of knowledge between therapeutic indications for toxicities can be considered a highly relevant exercise, also here it remains important to explicitly assess if potential differences in, for instance, baseline risk, or sensitivity, to certain toxicities may be expected. In our case this was considered justified because of the availability of various covariates related to sensitivity for neutropenia, and the fact that clear gender differences have not been reported for neutropenia. Nonetheless, when applying such frameworks in drug development, a careful consideration and quantitative evaluation of all possible assumptions is of critical importance.

Although this framework applies to CRPC and for the treatment with eribulin, components of this model can also be used for simulation purposes of other anticancer agents in patients with CRPC. This work is a first proof-of-concept example of an integrated model-based approach for evaluation of toxicity, efficacy, and cost effectiveness during early clinical development. Specifically, this approach can be considered for the evaluation, and associated decision making, of different possible treatment protocols for anticipated clinical trials, and to assess the impact of potentially relevant patient characteristics.

CONFLICT OF INTEREST

A.D.R.H., J.H.B. and J.H.M.S. did not have financial relationships with any organizations that might have an interest in the submitted work. The PhD program of JGCvH was financially supported by Eisai Ltd. AG and ZH are paid employees of Eisai Ltd.

AUTHOR CONTRIBUTIONS

J.G.C.v.H., A.D.R.H. and Z.H. designed the analysis. J.G.C.v.H. performed the analysis. J.G.C.v.H., A.G., Z.H., J.H.B. and A.D.R.H. wrote the article.

Supporting Information

Additional Supporting Information may be found in the online version of this article.