Disease Progression/Clinical Outcome Model for Castration-Resistant Prostate Cancer in Patients Treated With Eribulin

Abstract

Frameworks that associate cancer dynamic disease progression models with parametric survival models for clinical outcome have recently been proposed to support decision making in early clinical development. Here we developed such a disease progression clinical outcome model for castration-resistant prostate cancer (CRPC) using historical phase II data of the anticancer agent eribulin. Disease progression was captured using the dynamics of prostate-specific antigen (PSA). For clinical outcome, overall survival (OS) was used. The model for PSA dynamics comprised parameters for baseline PSA (23.2 ng/ml, relative standard error (RSE) 16.5%), growth rate (0.00879 day⁻¹, RSE 12.6%), drug effect (0.241 µg·h·l⁻¹ day⁻¹, RSE 32.6%), and resistance development (0.0113 day⁻¹, RSE 44.3%). OS was modeled according to a Weibull distribution. Predictors for survival included model-predicted PSA time to nadir (TTN), PSA growth rate, Eastern Cooperative Oncology Group (ECOG) score, and baseline PSA. The developed framework can be considered to support informative design and analysis of drugs developed for CRPC.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC? ☑ Prostate-specific antigen (PSA) is an important biomarker for prostate cancer disease progression and PSA-derived metrics are key endpoints in prostate cancer trials. • WHAT QUESTION DID THIS STUDY ADDRESS? ☑ Can metrics derived from a model for PSA dynamics be of use to predict overall survival in prostate cancer patients? • WHAT THIS STUDY ADDS TO OUR KNOWLEDGE ☑ This is the first disease progression-clinical outcome framework for castration-resistant prostate cancer, describing both the dynamics of PSA and its relationship with overall survival. • HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY AND THERAPEUTICS ☑ This model may be of use to support early clinical development of cancer therapeutics for castration-resistant prostate cancer based on observed PSA dynamics.

Prostate cancer

Prostate cancer (PC) is one of the most common malignancies in men in Europe1 and the United States.2 Local PC is potentially curable with radiation therapy, hormone therapy, and/or radical prostectomy.3–5 However, up to 40% of the patients who are diagnosed with localized disease ultimately develop advanced PC, even after initial treatment of local disease.5,6 In advanced PC, androgen deprivation is the standard first-line therapy,7 which has been shown to improve quality of life and survival.8 Ultimately, however, disease progression to castration-resistant PC (CRPC) occurs, which is associated with a high mortality rate.7

Approved treatments of CRPC include docetaxel,9 cabazitaxel,10 enzalutamide,11 the immunotherapeutic vaccine sipuleucel-T,12 and abiraterone,13 the latter two being approved only for minimally symptomatic CRPC. These treatments, however, are not curative, so the need exists to develop novel treatment options14–17 and a range of new agents are still in development.18 Combination treatments with docetaxel are currently not approved, although several studies investigating such combination treatments have been performed.19

Quantifying treatment response

Disease progression of PC can be monitored by measuring the serum levels of prostate-specific antigen (PSA), which have been associated with survival.15,20,21 Indeed, the use of PSA as a biomarker for disease progression is associated with a number of advantageous properties—compared to imaging-based disease progression markers—as it is easily quantifiable, reproducible, and inexpensive.22 PSA-based endpoints, however, are associated with some challenges.21,23 First, in some cases, inconsistent relationships between PSA-derived endpoints and clinical outcome measures have been reported.22 Second, in the case of bone-targeting agents, PSA may not be a relevant marker of disease activity.19 Nonetheless, PSA-derived study endpoints are still considered as a primary biomarker for efficacy.21

The Response Evaluation Criteria in Solid Tumors (RECIST)24 are widely used to evaluate treatment response in solid tumors. The RECIST criteria, however, do not adequately capture some key properties of PC.21 In 1999, the Prostate Specific Antigen Working Group (PSWG1) provided a number of recommendations for the design and conduct of clinical trials in PC,25 focusing specifically on trial design in patients with CRPC.25 More recently, new recommendations for design of PC studies have been published by the Prostate Cancer Working Group (PCWG2), which included further guidance on some important issues in PC drug development such as assessment of posttherapy changes in PSA and bone scans.21

Quantitative models to support prostate cancer drug development

For hormone-sensitive PC, several mathematical models have been developed describing the dynamics of PSA in response to androgen ablation therapy.26,27 Furthermore, for CRPC, Stein et al.14,15 developed a basic mathematical model that included growth and inhibition parameters to describe individual PSA timecourses in patients under treatment with anticancer agents.

Quantitative integrated disease-specific models describing the relationship between biomarkers of disease progression (DP) and clinical outcome (CO), such as overall survival, have been developed for various malignancies including colorectal cancer28 and nonsmall-cell lung cancer.29 These models typically consist of two components: a DP model describing the timecourses of a disease progression biomarker for each individual, and a parametric survival model for CO which includes metrics derived from the DP model as covariates. For the DP model, the sum of longest tumor diameters (e.g., derived from computed tomography (CT) or positron emission tomography (PET) scans) is typically used as a disease progression biomarker, although any other biomarker for disease progression can also be considered. In the case of tumor size-based biomarkers, such DP models are mostly referred to as tumor growth inhibition (TGI) models.

Previous approaches relating PSA dynamics as DP metric to CO metrics include time-to-event models that studied prognostic30 and diagnostic31 purposes in early PC. Moreover, a number of correlative analyses between PSA metrics and overall survival have been described.14,15,32 In addition to previously described approaches studying PSA dynamics to various outcome metrics (Table 1), a quantitative DP-CO model consisting of a dynamical DP model and a parametric survival model for CO, such as established for other indications,28,29 has, to our knowledge, not been established yet for CRPC. Such a DP-CO model may be useful to support decision making during drug development of CRPC agents.

Table 1.

Overview of studies investigating the relationship between PSA and clinical outcome metrics

Patient population	Model	Purpose	Reference
Localized PC patients	Joint latent class model PSA, risk of recurrence	Prognosis prediction	30
No PC + early PC patients	Joint latent class model PSA, risk of PC	Diagnosis of PC onset	31
Metastatic CRPC	Logistic regression model of PSA metrics and survival	Prognosis prediction for application as primary trial endpoint	32
Metastatic CRPC	Correlation analysis PSA metrics and survival	Prognosis prediction	14,15
Metastatic CRPC	Cox regression analysis PSA metrics and survival	Prognosis prediction	50

PC, prostate cancer; CRPC, castration-resistant prostate cancer.

Objectives

The aim of the current analysis was to develop an integrated quantitative DP-CO model for CRPC, using individual PSA timecourse data and overall survival of patients included in a phase II trial of the anticancer agent eribulin mesilate,33 which can be used to further support informative design and analysis of clinical studies in CRPC.

METHODS

Clinical study

The analysis was performed using data from 108 patients from a phase II clinical trial investigating the efficacy of eribulin mesilate in CRPC patients who were either pretreated with docetaxel- (n = 50) or taxane-naïve (n = 58).³³ Further details on the included patient population and trial design are described by de Bono et al.33 Key demographic and treatment information is provided in Supporting Table S1. The study was approved by an Institutional Review Board or Independent Ethics Committee and conducted in accordance with International Conference on Harmonization guidelines and the Declaration of Helsinki. All patients signed written informed consent.

Disease progression model

Pharmacokinetic model

No PK data were available for this study. In order to obtain estimates of drug exposure, a previously developed systematically covariate population PK model, based on pooled PK data from multiple other clinical studies, was used together with the individual dosing histories to predict typical area under the curve (AUC) values, taking individual patient characteristics into account. The model used in this analysis was a 3-compartment PK model with linear elimination with albumin, alkaline phosphatase, and bilirubin as covariates on clearance.34,35 Our analysis used an earlier version of this model, but this had no relevant impact for the current data.

The individual AUC value after each dose administration (not the cumulative AUC) was used as input to the DP model, i.e., using a K-PD approach.36 The use of patient characteristic-based AUC was preferred above using dose (e.g., a classical K-PD model), as it somewhat better reflects interindividual variability (IIV) in exposure (see Table S1).

Structural model

We considered a DP turnover model with a factor accounting for resistance development to describe the PSA dynamics as previously described by Claret et al.28 for other malignancies. First, in the drug effect compartment D the predicted AUC enters the system after each dose event. Subsequently, with a rate K_P, the drug effect washes out again (Eq. 1).

1

Subsequently, the PSA dynamics is described by Eq. 2, which comprises a first-order PSA growth rate K_G, a PSA inhibition rate K_D, an exponential resistance development term exp(-λt₀), where t₀ represents the time after start of treatment, and λ represents the resistance development coefficient, and a relationship with the drug effect D(t), described by Eq. 1.

2

with PSA_0,i representing the individual estimate of pretreatment baseline PSA for individual i. If several pretreatment PSA values were available, these were all included in the analysis to support estimation of baseline PSA as well as PSA growth rate.

Observed PSA concentrations were log-transformed prior to model fitting and were analyzed using a log-transform both-sides approach.37

Statistical model

IIV random effects were considered for all fixed effect parameters, and were implemented as follows:

3

where P_i represents the individual estimate of P for the i^th individual, P_g represents the fixed effect parameter, which can be corrected by patient-specific characteristics (see next section), and η_i was considered to be distributed according to N(0,ω2).

For residual unexplained (RUV) random effects, additive, proportional, and combined models were considered to account for deviations between individually predicted and observed PSA values.

The criteria for the selection of random effects including off-diagonal elements was based on a combination of evaluation of the magnitude of decrease in the minimum objective function value (OFV) of at least 3.84 points for IIV variances, by the assessment of parameter standard errors, by assessment of shrinkage, by assessment of their magnitude (e.g., magnitudes near 0), and by assessment of trends in residual plots for the RUV.

Covariates model development

Selection of covariates was based on a statistical significance of P < 0.01 (likelihood ratio test), a relevant decrease in the variance of IIV, and adequate estimation precision. Inclusion and selection of parameter–covariate relationships was also strongly guided by clinical and biological relevance.

The following covariate–parameter relationships were considered to be potentially relevant to the PSA dynamics: age on PSA₀, body weight on PSA₀, and prior taxane treatment on all model parameters.

Continuous covariates were scaled by their median values and were evaluated as both linear and power functions. Specifically, the covariate prior taxane treatment was included either as a dichotomous covariate, but in addition was also parameterized using a continuous function based on the number of cycles of prior taxane treatment (NCYCL) and as the number of days of prior taxane treatment (NTRT) for each individual i as follows, normalized by their respective median values, e.g., 720 treatment days or 30 cycles.

4

5

where P_g represents the patient-characteristic scaled fixed-effect parameter estimate, and θ_P represents the unscaled fixed effect estimate for parameter P.

Model evaluation

Throughout model building, models were evaluated by the assessment of goodness-of-fit and residuals diagnostic plots, by assessment of parameter standard errors, and based on the change in OFV. Covariates and structural model parameters were included based on the likelihood ratio test (P < 0.01).

Clinical outcome model

Base parametric survival model

Normal, log-normal, Weibull, logistic, exponential, and log-logistic parametric survival models were fitted to the observed survival data. A base parametric survival model was selected based on visual assessment of goodness of fit.

Covariate model development

A univariate covariate analysis was conducted evaluating covariates predictive for survival. We distinguished between covariates related to treatment effect, disease-specific effects, patient-specific characteristics, and effects potentially related to combinations of these previously identified to be relevant to survival.

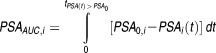
The following individual predicted treatment effect covariates from the DP model were considered: (i) TTN; (ii) relative maximum change from PSA baseline prior to start of treatment CFB; (iii) AUC above the PSA inhibition curve (PSA_AUC); (iv) PSA inhibition rate K_D.

The PSA_AUC for individual i was computed as the difference between the baseline PSA₀ and area under the individual predicted PSA time–curve, until time t where the individual predicted PSA becomes larger than PSA₀ (Eq. 6), e.g., the area above the PSA curve with an upper constraint of baseline PSA across time.

The following patient-specific covariates were considered: (i) prior taxane treatment PTAX; (ii) age; (iii) observed Eastern Cooperative Oncology Group (ECOG) score. Finally, the following disease-specific covariates were considered: (1) baseline PSA prior to start of treatment PSA₀, (2) PSA growth rate K_G.

6

All continuous covariates, except for age, were log-transformed prior to inclusion in order to obtain more symmetric distributions. When the covariate could contain zero (T_nadir, CFB), they were log-transformed as log(n+1).

For the multivariate model, a treatment effect parameter was included first, as it was considered of key relevance for this analysis. Subsequently, the multivariate survival model was further developed in a stepwise fashion according to the rank order of the level of significance (P < 0.05) and only covariates which remained significant were retained in the model.

Model evaluation

Survival models were evaluated based on visual assessment of predicted survival curves stratifying for covariate levels, and using the likelihood ratio test.

External evaluation

External evaluation of the final multivariate model was performed using previously published patient-level data from Stein et al.,15 from which relevant covariates (i.e., baseline PSA, growth rates, time to PSA nadir, survival) could be extracted. Patients had CRPC and were treated with alendronate plus ketoconazole and hydrocortisone (AKH), ketoconazole and hydrocortisone (KH), docetaxel and thalidomide (DT), or docetaxel (D) only. Since the ECOG score (a covariate in this analysis) was not available, we assumed an ECOG score of 1. Visual evaluation was performed comparing the observed and predicted survival–time curves. Predictions were depicted as the median prediction and the standard error derived from the uncertainty in survival model parameter estimates. Uncertainties in individual covariates derived from the DP model were not included.

Software

The PK and DP models were fit using NONMEM v. 7.2³⁸ using first-order conditional estimation. The survival model was fit using the parametric survival analysis function survreg in the R package Survival using R v. 3.0.39

RESULTS

Disease progression model

Structural model

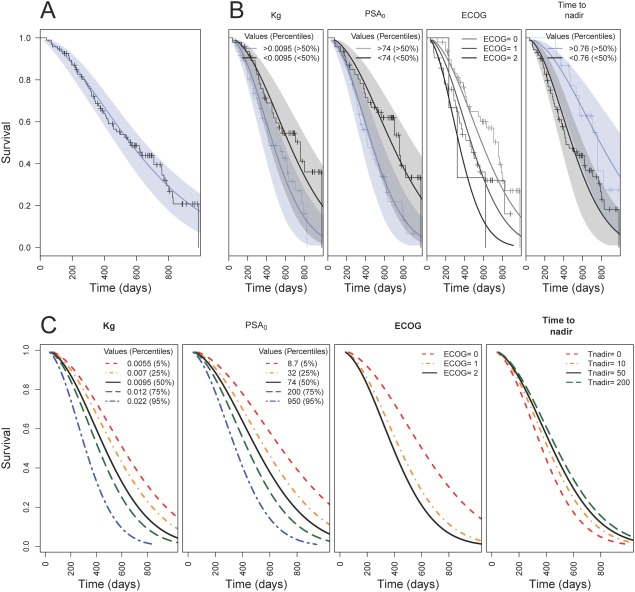
The structure of the PSA DP model is depicted in Figure 1. The final model parameter estimates for the DP model are provided in Table 2. Structural model parameters could be estimated with adequate precision (RSE < 44.3%). The optimal value of the drug exposure parameter (K_P) was selected based on evaluation of different fixed values in the model. We selected a large value of 6,000 to allow for a nearly instantaneous dosing event. Similar large values resulted in the same parameter estimates. The only relevance of this parameter was to include variability in predicted exposure. The baseline PSA (PSA₀) was estimated at 23.2 ng/mL (RSE 16.5%), the growth rate parameter was estimated at 0.00879 day⁻¹ (RSE 12.6%), the drug-induced inhibition parameter (K_D) was estimated at 0.241 µg·h·l⁻¹ day⁻¹ (RSE 32.6%), and the drug resistance development parameter (λ) was estimated at 0.0113 day⁻¹ (RSE 44.3%).

Figure 1.

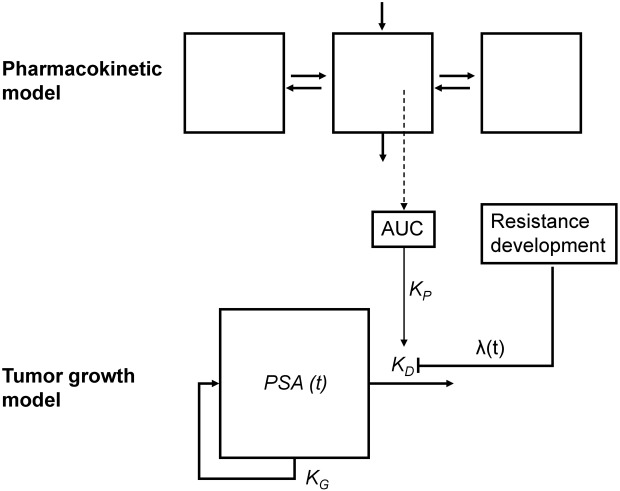
Schematic diagram of the disease progression model for the dynamics of prostate-specific antigen (PSA). K_G, growth rate; K_D, inhibition rate; λ, drug resistance development; AUC, predicted area-under-the-concentration-time curve.

Table 2.

Parameter estimates for the PSA disease progression model

Description	Parameter	Units	Estimate (RSE) [Shrinkage, %]	Bootstrap (n = 1,000)
Fixed effect parameters				Median	95% PI
Drug effect	θKP	day−1	6000‡	—
Drug inhibition	θKD0	ng·h·l−1 day−1	0.241 (32.6)	0.260	0.136–0.472
~ Days pretreated taxanes*	θKD0-NTRT	—	-4.00 (52.5)	-3.21	-8.96–0.123
Resistance development	θλ	day−1	0.0113 (44.3)	0.00949	0.00341-0.0262
Growth rate	θKG	day−1	0.00879 (12.6)	0.00941	0.00731–0.0112
Baseline PSA	θPSA0	ng/mL	23.2 (16.5)	23.1	17.3–31.6
~ Prior taxane†	θPSA0-PTAX	—	3.23 (27.6)	3.09	1.84–5.33
Interindividual variability variances
Inhibition rate	ωKD0	CV%	127.3 (14) [26]	132	99.5–175
Resistance development a	ωλ	CV%	88.3 (37.5) [40]	110	62.9–189
Growth rate b	ωKG	CV%	53.7 (13.5) [18]	56.3	40.9–70.8
Baseline PSA c	ωPSA0	CV%	130.4 (8.8) [1.0]	128	110–153
Residual variability variance
Proportional error	σprop	CV%	34.2 (27.5) [14]	24.8	18.8–43.4

^*Power relationship

^†proportional relationship

^‡estimate fixed.

^aCorrelation coefficient ωλ∼ω_KD0 = 0.802

^bcorrelation coefficient ω_KG∼ω_KD0 = -0.293; ω_KG∼ω_λ = -0.111

^ccorrelation coefficient ω_PSA0∼ω_λ = -0.094; ω_PSA0∼ω_KG = -0.032.

Individual parameters were defined as: K_D0 = θ_KD0^* (1+(θ_KD-NTRT/720)) ^*exp(η_KD0); K_P = θ_KP ^* exp(η_KP); λ = θ_λ^* exp(η_λ); K_G = θ_KG ^*exp(η_KG); PSA₀= θ_PSA0 ^*θ_PSA0-PTAX ^*exp(η_PSA0); with η_P distributed according to N(0,ω²_P) for parameter P.

Statistical model

Variances for IIV could be estimated for all structural model parameters (Table 2). Covariances between IIV random effects could be estimated for all model parameters, except for the correlation between the drug effect parameter K_D and PSA₀, which approached zero in the final obtained estimate. The individual η-distributions appeared reasonably symmetric. Shrinkage was <26% except for the drug resistance development parameter λ (40%). The proportional residual error variance was considerable, with 34.2 CV%. However, there were no trends that suggested model misspecification.

Model evaluation

Based on inspection of observed and predicted individual PSA timecourse plots (Figure 2) and goodness-of-fit diagnostic plots (Figure S2), the model was able to adequately capture the dynamics of the PSA–time profiles (Figure 2). The visual predicted check (Figure S3) suggested adequate description of the PSA–time profiles in the first part of the dataset, where most patients were still included in the trial. At later stages, there was a divergence observed for observed and simulated PSA profiles due to disease progression-related dropout. The incorporation of dropout mechanisms in the simulation based on either protocol criterion defined dropout, or based on parametric survival models for dropout (including either last observed PSA, individual predicted PSA at time of dropout, or individual predicted PSA growth rate), did not result in relevant improvements of the VPC.

Figure 2.

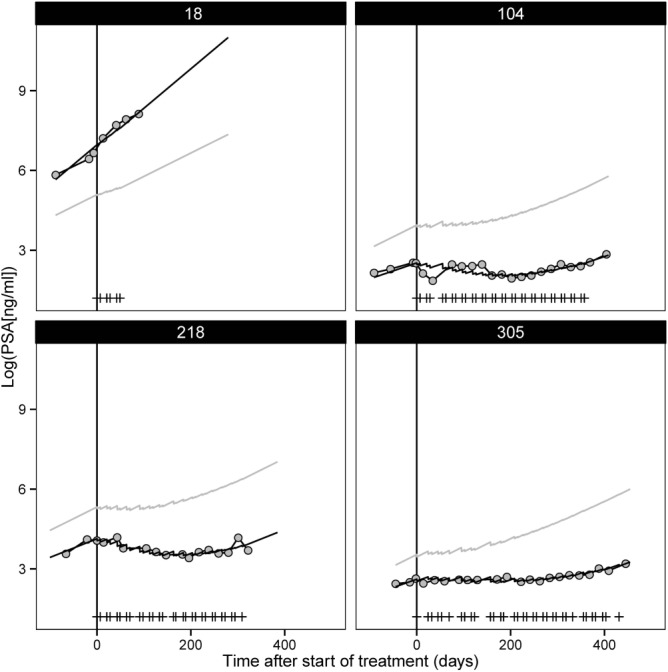
Selected individual plots for log-transformed prostate-specific antigen (PSA) vs. time after start of treatment (days) for observed values (gray circles), individual model predictions (black solid line), population model predictions (solid gray line), and dose events (vertical lines).

Covariate model

Age and weight were not significant covariates for predicting IIV of PSA₀ (dOFV < –0.4). Prior taxane treatment as dichotomous covariate was only significant for PSA₀ and K_D. When parameterizing prior taxane treatment as a continuous covariate in terms of either number of days of prior taxane treatment (NTRT) or number of prior taxane cycles received (NCYCL), only the relationship with K_D was found significant, with a dOFV of −10 and −8, respectively, and was considered preferable over a dichotomous covariate. Although the change in OFV was relatively limited, the clinical relevance of taxanes as covariate was also confirmed by previous identification of taxanes as predictor for survival in the original study analysis.33

The precision of the estimate for the effect on K_D was relatively low (RSE 52.5%), while the precision of the dichotomous effect of taxanes on PSA0 was adequate (RSE 27.6%). Patients with prior taxane treatment had lower drug growth inhibition rates. The final covariate DP model included prior taxane treatment (yes/no) related to PSA₀, and NTRT related to K_D (Table 2).

Survival model

A Weibull function best described the survival curve (Figure 3A). The parameter estimates of the base survival model are provided in Table 3, and could be estimated with good precision (RSE <23.1%). Subsequently, in the univariate covariate survival analysis we identified the following covariates as significant (P < 0.05): ECOG score, individual predicted values for time to PSA nadir (T_nadir), baseline (PSA₀), relative maximum change from PSA baseline (CFB), areas under the PSA-time curve (PSA_AUC), and PSA growth rate (K_G).

Figure 3.

Observed and predicted survival vs. time (days). (a) Observed (Kaplan-Meier), median predicted (blue line) with associated 95% confidence interval (blue area). (b) Observed (Kaplan-Meier) and model predictions (median and 95% prediction interval) stratified below and above the 50^th percentile for covariates (ECOG, time to PSA nadir [days], K_G [days⁻¹], PSA₀ [ng/ml]) in the final covariate survival, or stratified for different ECOG scores. C: Model predictions for different values of the covariates in the final survival model.

Table 3.

Parameter estimates of parametric Weibull survival models

Description	Estimates (RSE)			P-value*
	Intercept	Coefficient	log(Scale)
Base model	6.556 (1.3)	—	-0.483 (23.1)	—
Univariate models [unit]
Prior taxanes [0,1]	6.622 (1.7)	-0.149 (110)	-0.484 (22.9)	0.3632
ECOG score [0, 1, 2]	6.711 (1.7)	-0.344 (46.8)a -0.681 (52.9)b	-0.528 (21.1)	0.0130
Age [years]	7.535 (8.1)	-0.014 (60.3)	-0.489 (22.6)	0.0936
log (TTN) [days] + 1)	6.433 (1.4)	0.091 (45.1)	-0.507 (21.7)	0.0265
log (PSA0 [ng/mL])	7.352 (3.6)	-0.186 (29.1)	-0.560 (19.9)	0.0006
log (CFB [%])	6.880 (3.1)	0.206 (56.7)	-0.505 (21.9)	0.0779
log (PSAAUC [ng*h/ml]+ 1)	6.349 (1.9)	0.050 (49.9)	-0.494 (22.2)	0.0486
log (KG [day−1])	6.798 (2.1)	0.155 (42.9)	-0.492 (22.3)	0.0198
log (KD [day−1])	6.798 (2.1)	0.429 (42.9)	-0.492 (22.3)	0.0145
Multivariate model [unit]
log(kG [day−1])	4.987 (16.1)	-0.482 (34.7)	-0.644 (16.8)	<0.0001
log(PSA0 [ng/ml])		-0.144 (36.8)
ECOG [0, 1, 2]		-0.313 (46.2)* -0.428 (75.3)*
log (Tnadir [days] + 1)		0.049 (75.2)

^*Likelihood ratio test, compared to base model.

^aECOG = 1

^bECOG = 2.

RSE, relative standard error (%); PSA, prostate-specific antigen; PSA₀, predicted individual predicted baseline level of PSA; PSA_AUC, AUC under the PSA-time curve; CFB, relative maximum change from baseline (%); TTN, time (days) to PSA nadir; K_D, PSA growth inhibition rate. The survival function S is given by: S=1-(shape/scale)^*(t/scale)^(shape-1) with scale=(exp(Intercept+β_n^*cov_n +(..) + β_n^*cov_n)) for covariate n and its associate regression coefficient β_n.

The individual estimate for T_nadir was selected as best treatment effect covariate. In addition to T_nadir, the final multivariate model (Table 3) included individual estimates for K_G and PSA₀ as disease-specific parameters, and the patient-specific ECOG performance score.

In Figure 3C, the relative impact of each of the covariates in the multivariate model is illustrated. T_nadir showed the smallest effect, although it was a significant parameter. The significance was expected to be related to differentiation between patients dropping out quickly due to disease progression, who consequently also had poor subsequent survival. Other variables such as growth rate and PSA₀ showed wider ranges of variation with respect to impact on overall survival.

Model evaluation

Visual predictive checks of the separate covariate effects identified in the final covariate survival model are depicted in Figure 3B and indicated adequate description of the empirical survival curves.

External evaluation

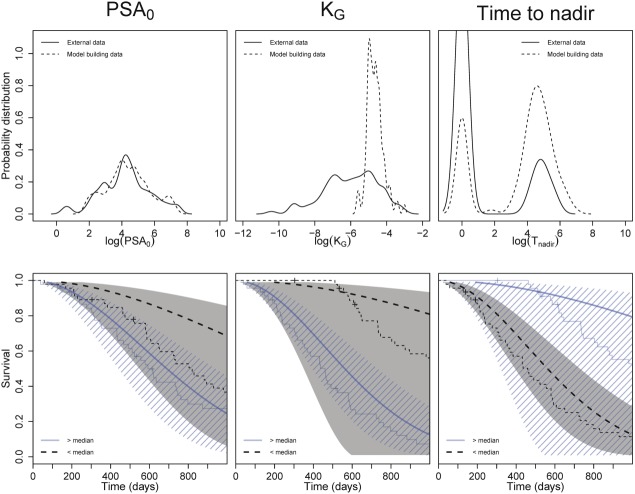
An external evaluation of the DP-survival model was performed by predicting the reported overall survival of previously reported15 individual values of PSA₀, K_G, and T_nadir for two external clinical studies in patients with CRPC investigating (i) docetaxel with and without thalidomide and (ii) ketoconazole plus hydrocortisone with and without alendronate (Figure 4). The predicted survival without stratification is depicted in Figure S4. A high level of uncertainty in the predictions was present, with some systematic overprediction of overall survival. The largest deviation was seen for the most favorable covariate values (e.g., patients with low growth rates and low PSA₀ values).

Figure 4.

Distribution of observed baseline PSA (PSA₀) and PSA growth rates (K_G) for the model building (dashed line) and external dataset (solid line) (top). Model-predicted (areas and bold solid lines) and observed (normal solid lines) in survival in external dataset, stratified for PSA₀ and K_G.

DISCUSSION

We successfully developed a model for PSA dynamics and subsequently related PSA dynamics to overall survival in patients with CRPC receiving eribulin mesilate.

The DP model for PSA dynamics in CRPC adequately described the individual and typically observed PSA–time profiles. Alternative dynamic models for PSA could also have been considered, such as a more simplified dose–effect model, which is also supported by the use of a high KP value for the decay of eribulin AUC. Nonetheless, the developed DP model for PSA was merely developed to provide acceptable individual PSA predictions, and hence the chosen model is justified for the aims of this project.

We identified prior taxane treatment as a significant covariate for both baseline PSA level (PSA₀), and drug-induced PSA inhibition rate (K_D). The effect of prior taxane treatment on PSA₀ was expected, considering that taxane pretreated patients may have more advanced disease. The effect of prior taxane treatment on K_D could be interpreted as development of resistance, as both docetaxel and eribulin act by inhibition of microtubule dynamics.33 Even after inclusion of the taxane covariate in the model, the resistance parameter remained significant.

The current PSA DP model included a number of important features not included in a previously described model for PSA dynamics in CRPC patients.15 First, PSA–time curves were analyzed using an NLME approach in contrast to Stein et al. This allowed for simultaneous quantification of both parameters describing the typical PSA response, as well as estimates for IIV in these parameters, thereby describing the individual PSA responses. NLME models allow “sharing” of information between individuals; hence, the parameter estimates derived in the current analysis are likely to be more informative. Second, in our analysis drug exposure was included in the model, whereas the model by Stein et al. did not consider an exposure–response relationship, and therefore did not allow for differences in dosing schedules between patients or treatments. Third, the model by Stein et al. did not consider the development of drug resistance, individual patient-specific covariates in the TGI model, or a formal relationship between PSA dynamics and a parametric survival model, which were all included in the current analysis.

The final multivariate survival model included T_nadir (treatment effect covariate), PSA₀ and K_G (disease-specific covariates), and ECOG score (patient-specific covariates). We consider the explicit separation of drug-, disease-, and patient-specific covariates as a very relevant approach in the development of DP-CO models. The use of T_nadir represents the net effect of a combined drug-induced inhibition of PSA and the development of drug resistance, and was therefore considered as a reasonable representation of treatment effects. Moreover, from the different evaluated treatment effect parameters, T_nadir was the most significant. Inclusion of the PSA₀ level was considered plausible, as PSA is widely accepted as the marker for disease progression, and patients with more progressed disease can be expected to show inferior survival benefit. The currently identified relevance of PSA growth rate (K_G) was also confirmed by Stein et al., while the PSA inhibition rate K_D was not identified as a relevant covariate in both the current analysis and by Stein et al. Finally, DP-CO models for other malignancies have shown that time to progression, baseline tumor (biomarker) levels, tumor growth rates, and ECOG score were identified as significant covariates in the respective survival models, further supporting the clinical relevance of the identified covariates.40

Although the current model was developed on a rather large phase II dataset, still the number of patients included might be relatively small to estimate all the parameters with high precision. This should be appropriately acknowledged if the model is implemented for simulation purposes.

In our analysis we did not perform joint continuous-categorical modeling between PSA and overall survival, as our aim was to identify DP-model-derived predictors for overall survival only, i.e., not to identify a more accurate drug effect. The justification for not performing such joint modeling has been commented on before by Claret & Bruno.41

Relatively high shrinkage (<15%) was identified for some of the estimates of the PSA DP model. As such, individual predictors derived from this model may not be informative when they are evaluated for their ability to predict overall survival. The alternative would have been not to include covariates with high shrinkage, but this would have greatly limited our ability to identify any clinically relevant predictors for survival in this population, e.g., the whole aim of this analysis. One should be aware, however, that it may not be possible to obtain informative individual estimates for all patients regardless of the available study design, due to the very nature of this advanced CRPC population in which a subset of patients are expected to progress in disease (and drop out) quickly, and in which it is known that not all patients who drop out will show increases in PSA. Such lack of information will also be a reality when either predicting or designing clinical trials in another CRPC population. In addition, the final multivariate model contains the parameter TTN, which is expected to account for the effect where patients drop out quickly, which may be indicative of their probability of survival. In summary, it is important to be aware of the shrinkage in individual estimates, but the current inclusion of individual estimates will result in a model that has superior clinical and practical relevance despite shrinkage.

We did not perform joint modeling with dropout in this work because the mechanism of such dropout was unclear. Dropout may be either completely at random of observed or unobserved dependent variable (MCAR), depending on the observed dependent variable (MAR), or depending on the unobserved dependent variable (MNAR). In the case of MNAR dropout, joint modeling is important in order to obtain unbiased estimates. Based on the evaluation of different dropout mechanisms during the generation of the VPC (see Results section, Figure S3), none of the informative dropout mechanisms related to PSA dynamics appeared to result in relevant improvements of VPC, suggesting that informative dropout may not play a major role in the dropout mechanism. The small size of the dataset together with a small number of patients that stay in the trial much longer is another potential reason why it was not possible to replicate the mechanism of dropout. Nonetheless, for the initial part of the PSA–time curves, the VPC indicated adequate model performance. When dropout mechanisms are complex, such as in our case, the VPC may not be a very suitable diagnostic to assess model performance.

The external model evaluation (Figure 4) showed high uncertainty of overall survival predictions based on the reported estimates of PSA₀ and K_G, with relevant deviations between observations and predictions. The high uncertainty and deviations between observations and predictions could relate to differences in covariate distributions. Another potential cause could be the different drugs (see Methods) used in this dataset, which partly have a different mechanism of action. Therefore, when this model is applied to predict outcome based on PSA dynamics of other drugs than eribulin and related mitotic inhibitors such as taxanes, or when extrapolating outside the covariate range of the current analysis, predictions should be handled with caution. Nonetheless, previously, Stein et al. demonstrated how PSA growth rates consistently related to survival across different drugs, thus supporting the overall relevance of the current analysis.

Specifically for PC drug development, the use of the DP-CO model is considered to be of relevance. The aforementioned robustness of PSA as biomarker for disease progression is debateable,22 which can be a challenge in CRPC drug development. The DP-CO model provides a tool to address this challenge to some extent, as it provides a formal quantitative framework that allows integration of multiple predictors which could be potentially relevant to clinical outcome. Furthermore, the demonstrated disease-specific nature of these models allows continuous updating of these models, i.e., allowing for leveraging knowledge obtained across clinical development programs of different drugs.

Increasingly, targeted therapies are or will be developed in the area of PC.42 These therapies may have different mechanisms of action, and as such these drugs might have a different relationship between DP (as measured by PSA) and CO. Therefore, the developed model may need to be updated for targeted anticancer agents in CRPC. Potentially, with the rapidly increasing knowledge of disease heterogeneity in PC,43,44 further improvements could be gained in the development of predictive disease progression models, by implementation of systems pharmacology-based modeling approaches45 to describe CRPC disease progression in a mechanistic fashion, such as was recently developed for hormone-sensitive PC²⁷ or a model which considered also immune system contributions.46

In conclusion, we successfully developed an integrated model quantifying the dynamics and variability of PSA disease progression and its relationship with overall survival in CPRC. The identified patient characteristics as covariates in the DPCO model could be used to assess the implications for specific patient groups. The developed model can potentially be applied also for other drugs in CRPC to either generate expected phase III clinical outcomes based on phase II results, or to assess potential clinical trial designs47–49 with respect to expected PSA dynamics and associated clinical outcome. However, given the observed uncertainty in the external evaluation this may require further model optimization.

Conflict of Interest

A.D.R.H., J.H.B. and J.H.M.S did not have financial relationships with any organizations that might have an interest in the submitted work. The PhD program of JGCvH was financially supported by Eisai Ltd. AG and ZH are paid employees of Eisai Ltd.

Author Contributions

J.G.v.H., A.D.R.H., A.G. and Z.H. designed the analysis. J.G.v.H. performed the analysis. J.G.v.H., A.G., J.H., J.H.M.S., J.H.B., and A.D.R.H. wrote the article.

Supporting Information

Additional Supporting Information may be found in the online version of this article.