iGWAS: Integrative Genome-Wide Association Studies of Genetic and Genomic Data for Disease Susceptibility Using Mediation Analysis

Abstract

Genome-wide association studies (GWAS) have been a standard practice in identifying single nucleotide polymorphisms (SNPs) for disease susceptibility. We propose a new approach, termed integrative GWAS (iGWAS) that exploits the information of gene expressions to investigate the mechanisms of the association of SNPs with a disease phenotype, and to incorporate the family-based design for genetic association studies. Specifically, the relations among SNPs, gene expression, and disease are modeled within the mediation analysis framework, which allows us to disentangle the genetic effect on a disease phenotype into two parts: an effect mediated through a gene expression (mediation effect, ME) and an effect through other biological mechanisms or environment-mediated mechanisms (alternative effect, AE). We develop omnibus tests for the ME and AE that are robust to underlying true disease models. Numerical studies show that the iGWAS approach is able to facilitate discovering genetic association mechanisms, and outperforms the SNP-only method for testing genetic associations. We conduct a family-based iGWAS of childhood asthma that integrates genetic and genomic data. The iGWAS approach identifies six novel susceptibility genes (MANEA, MRPL53, LYCAT, ST8SIA4, NDFIP1, and PTCH1) using the omnibus test with false discovery rate less than 1%, whereas no gene using SNP-only analyses survives with the same cut-off. The iGWAS analyses further characterize that genetic effects of these genes are mostly mediated through their gene expressions. In summary, the iGWAS approach provides a new analytic framework to investigate the mechanism of genetic etiology, and identifies novel susceptibility genes of childhood asthma that were biologically meaningful.

Introduction

Given the rapid increase of the available data on genetic variants, genome-wide association studies (GWAS) have been a common practice for investigating the associations of single nucleotide polymorphisms (SNPs) with complex diseases [Amos et al., 2008; Ferreira et al., 2008; Hung et al., 2008; Moffatt et al., 2007; Thorgeirsson et al., 2008; Wallace et al., 2008]. The success of these studies in numerous discoveries of new disease susceptibility loci further popularized the usage of GWAS, which, on the other hand, also incurred challenges and limitations. A well-acknowledged limitation is its agnostic style [Hunter and Chanock, 2010]: none of the biological knowledge was encoded in standard GWAS analyses. Multimarker analyses have been advocated to integrate the biological information into statistical learning and to decrease the number of tests. Successful examples are multiple SNP analyses or SNP-set analyses [Kwee et al., 2008; Liu et al., 2008; Wu et al., 2010] that have been shown to have better performance than the standard single SNP analyses in reanalyzing breast cancer and Alzheimer’s disease GWAS datasets [Cruchaga et al., 2014;Wu et al., 2010].

To move beyond GWAS for disease risk, gene expression can also be construed as a molecular phenotypic trait. Such a type of genetic association studies focusing on identifying SNPs that are associated with gene expression or namely expression quantitative trait loci (eQTL) are so-called eQTL studies. As both GWAS and eQTL studies become popular in genetic research, considerable interest emerges in integrating the two. Studies that substantiate the notion have been conducted in many diseases, including asthma [Cusanovich et al., 2012; Moffatt et al., 2007], osteoporosis [Hsu et al., 2010], type 2 diabetes [Zhong et al., 2010], skin cancer [Zhang et al., 2012], glioblastoma, and Crohn’s disease [Xiong et al., 2012]. These studies consider SNP-disease and SNP-expression associations separately. For example, the most commonly used two-stage approach is to identify the top GWAS SNPs that are also eQTL SNPs. This type of analyses was supported by the evidence that trait-associated SNPs are more likely to be functional and thus eQTL [Nicolae et al., 2010]. The role of gene expression in the biological process from SNPs to disease phenotype remains unclear. Even though eQTL studies may be helpful in reranking or filtering the top SNPs to enrich true positives, whether the association of those eQTL SNPs with gene expression can be translated into a mechanistic contribution to the disease risk is rarely addressed.

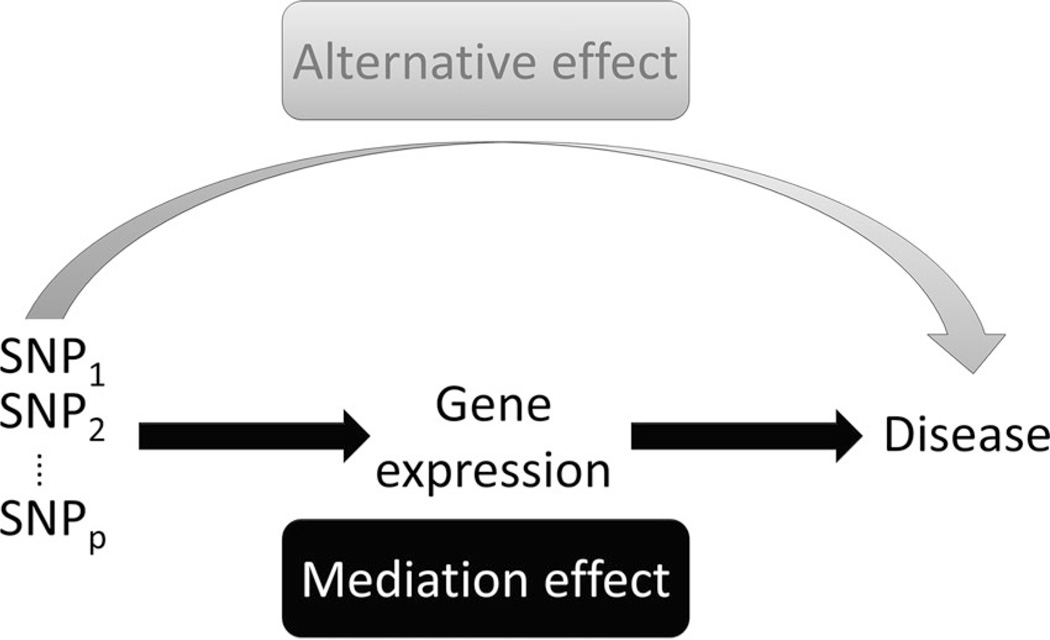
This article ismotivated by a family-based GWAS of childhood asthma, in which the association between SNPs at the ORMDL3 gene and the risk of childhood asthma was discovered in an MRCA (Medical Research Council Asthma) dataset, a family-based case-control study, and validated in many other datasets [Moffatt et al., 2007]. In the MRCA study, mRNA expression data were also collected, and it was reported that SNPs at the ORMDL3 gene were highly associated with its expression value in an eQTL study [Dixon et al., 2007;Moffatt et al., 2007]. The association of the GWAS SNPs and expression of the ORMDL3 gene has also been validated in a molecular study [Berlivet et al., 2012]. Based on these work, we propose an integrative approach to conduct GWAS, termed iGWAS (integrative GWAS) where we jointly analyze SNPs and gene expression on disease risk as a biological process, illustrated by a mediation model (Fig. 1). Moreover, we are interested in studying whether the effect of genes on asthma risk is mediated through gene expression, or though alternative biological mechanisms.

Figure 1.

Directed acyclic diagram (DAG) of the mediation model. The gray path indicates the alternative effect, and the black path indicates the mediation effect.

The iGWAS approach is developed within the framework of causal mediation modeling [MacKinnon, 2008; Robins and Greenland, 1992] using counterfactuals [Rubin, 1978]. The model can be illustrated as a directed acyclic graph (DAG) [Robins, 2003], which provides intuitive interpretation of how SNPs and gene expression coordinate to influence on the development of diseases (Fig. 1). Rather than focusing on agnostic associations, the iGWAS approach considers the coordinated biological process from genetics to gene transcription and then to disease outcome. In particular, we decompose the etiological mechanism for the total genetic effect (TE) into the genetic effect on disease risk mediated through gene expression (mediation effect, ME) and the genetic effect through other biological pathways or environmental risk factors (alternative effect, AE). We developed previously a testing procedure for the TE of SNPs and gene expression in population-based case-control studies [Huang et al., 2014]. However, this method focuses only on the TE.

In this paper, we are primarily interested in examining ME and AE. The characterization of the ME and AE is critical in understanding the etiological mechanisms of genetic effects, and will in turn assist in generating new hypotheses that are more biologically plausible. Inclusion of gene expression data can also better explain the heterogeneity of the human genome that genetic data alone are not able to capture and thus increase statistical power of identifying disease susceptibility genes. Furthermore, the existing method for TE was developed under population-based studies that study subjects are independent, and failed to accommodate the family design of the MRCA data. To bridge these gaps, we develop in this paper a general analytic framework, iGWAS, that integrates genetic and genomic data to examine ME, AE, as well as TE and incorporates the family design.

This paper makes both methodological and scientific contributions. Methodologically, we propose a new analytic framework, iGWAS, that facilitates to study the ME (eQTL genetic effect on a phenotype mediated through gene expression) and the AE (genetic effect through other biological pathways or environment-mediated mechanisms), and incorporates the family design. Moreover, we develop robust tests for ME and AE of SNPs using both SNP and gene expression data. Scientifically, our proposed iGWAS approach identifies novel susceptibility genes of childhood asthma and characterizes their mechanisms through gene expression.

Methods

Integrative Genome-Wide Association Studies (iGWAS)

Causal Mediation Model and Null Hypotheses

We utilize the causal mediation model to investigate the etiologic mechanism of genetic effect. We jointly model the effect of a set of SNPs associated with expression of a gene (i.e., eQTL SNPs) and the corresponding gene expression on occurrence of a disease using a logistic regression model, adjusting for covariates. For subject i, the probability of having a dichotomous outcome (e.g., Y = 1/0 for case/control) is associated with q covariates (X_i, with the first covariate to be 1, i.e., the intercept), p SNP genotypes (S_i, e.g., cis-eQTL SNPs of a gene), one mRNA expression of a gene (G_i), and p cross-product interactions between the SNPs and gene expression as:

$$\text{logit}\{P(Y_i=1|{\mathit{S}}_i,G_i,X_i)\}={\mathit{X}}_i^T{\mathit{\beta }}_X+{\mathit{S}}_i^T{\mathit{\beta }}_S+G_i{\beta }_G+G_i{\mathit{S}}_i^T{\mathit{\beta }}_C,$$ (1)

where β_X = (β_X1, …, β_Xq)^T, β_S = (β_S1, …, β_Sp)^T, β_G and β_C = (β_C1, …, β_Cp)^T are regression coefficients for the covariates, SNP genotypes, gene expression, and interactions of the SNP genotypes and gene expression, respectively. We next consider another regression model for the gene expression (G_i), which depends on the q covariates (X_i) and p SNP genotypes (S_i):

$$G_i={\mathit{X}}_i^T{\mathit{\alpha }}_X+{\mathit{S}}_i^T{\mathit{\alpha }}_S+{\epsilon }_{Gi},$$ (2)

where α_X = (α_X1, …, α_Xq)^T and α_S = (α_S1, …, α_Sp)^T are the regression coefficients for the covariates and SNP genotypes, respectively; and ε_Gi follow a normal distribution with mean 0 and variance ${\sigma }_G^2$. We here focus on eQTLs by restricting analyses to SNPs that are associated with the gene expression, i.e., α_S ≠ 0.

Assuming confounding effects are properly controlled after accounting for the covariates, the TE of comparing two genotypes of the SNPs s₁ vs. s₀ is defined as: TE = logit{P (Y = 1|S = s₁, X)} − logit{P (Y = 1|S = s₀, X)}. Under the rare disease assumption for a binary disease phenotype, the TE of the SNPs on the log odds ratio (OR) of disease risk comparing two genotype values s₁ vs. s₀ can be expressed using the regression coefficients in models (1) and (2) as [Huang et al., 2014]:

$$TE={({\mathit{s}}_1-{\mathit{s}}_0)}^T\{{\mathit{\beta }}_S+{\beta }_G{\mathit{\alpha }}_S+{\mathit{\beta }}_C({\mathit{X}}^T{\mathit{\alpha }}_X+{\mathit{s}}_0^T{\mathit{\alpha }}_S+{\beta }_G{\sigma }_G^2+{\mathit{s}}_1^T{\mathit{\alpha }}_S\left)\right\}+\frac{1}{2}{\sigma }_G^2{({\mathit{s}}_1+{\mathit{s}}_0)}^T{\mathit{\beta }}_C{({\mathit{s}}_1-{\mathit{s}}_0)}^T{\mathit{\beta }}_C.$$

We can also express the ME (indirect effect) of the SNP set (s₁ vs. s₀)mediated by the gene expression G, and AE (direct effect) of the SNP set through other biological pathways, on the log OR of disease risk as [Huang et al., 2014]:

$$AE={({\mathit{s}}_1-{\mathit{s}}_0)}^T\{{\mathit{\beta }}_S+{\mathit{\beta }}_C({\mathit{X}}^T{\mathit{\alpha }}_X+{\mathit{s}}_0^T{\mathit{\alpha }}_S+{\beta }_G{\sigma }_G^2\left)\right\}+\frac{1}{2}{\sigma }_G^2{({\mathit{s}}_1+{\mathit{s}}_0)}^T{\mathit{\beta }}_C{({\mathit{s}}_1-{\mathit{s}}_0)}^T{\mathit{\beta }}_C,$$ (3)

$$ME={({\mathit{s}}_1-{\mathit{s}}_0)}^T({\beta }_G{\mathit{\alpha }}_S+{\mathit{\beta }}_C{\mathit{s}}_1^T{\mathit{\alpha }}_S).$$ (4)

Note that the TE can be decomposed into ME and AE. Although direct and indirect effects have been defined and used in the causal mediation literature [Robins and Greenland, 2012], we rename them here as AE and ME to better reflect their biological interpretation. The indirect effect or ME of an SNP set S in our setting is the effect of eQTL SNPs on disease risk mediated through gene expression (the black path in Fig. 1), whereas the direct effect or AE is the effect on disease risk independent of expression of the gene, but perhaps through other genes or other mechanisms (the gray path in Fig. 1). We have shown that identification of the TE requires a weaker assumption than those required for the ME and AE [Huang et al., 2014].

As we focus on the eQTL SNPs, the SNPs with nonzero association with the gene expression, or equivalently, α_S ≠ 0, it can be easily shown that

$$H_0:AE=0\leftrightarrow H_0:{\mathit{\beta }}_S=\mathbf{0},{\mathit{\beta }}_C=\mathbf{0},$$ (5)

$$H_0:ME=0\leftrightarrow H_0:{\beta }_G=0,{\mathit{\beta }}_C=\mathbf{0},$$ (6)

provided that there does not exist a perfect cancellation for effects with β_S ≠ 0, β_G ≠ 0, and β_C ≠ 0. It follows that the equivalence for TE under the null would be:

$$H_0:TE=0\leftrightarrow H_0:{\mathit{\beta }}_S=\mathbf{0},{\beta }_G=0,{\mathit{\beta }}_C=\mathbf{0}.$$ (7)

Note different genetic models (dominant, recessive, or additive) follow the same null hypotheses (5)–(7): no effects for subjects carrying two different genotypes. Regardless of the genetic models, the above equivalence applies. However the coefficients may have different interpretations under different models. For example, under the additive models, β_s is the log OR comparing between subjects carrying two minor alleles and those with one allele, as well as between one and zero minor allele; and β_s under the dominant models is the log OR between the presence and absence of a minor allele. For implementation, different genetic models can be easily incorporated by altering the genetic coding in S, e.g., 0, 1, 2 for zero, one, and two minor alleles, respectively, under additive model.

Testing Procedure for the AE Under Family Design

As the number of SNPs (p) in a gene can be large and some may be highly correlated due to linkage disequilibrium, the conventional test such as the likelihood ratio test that uses large degrees of freedom has limited power. We resort to an empirical Bayes approach [Lin, 1997] by assuming the regression coefficients of individual SNP effects, β_Sj (j = 1, …, p), follow an arbitrary distribution with mean 0 and variance τ_S, and the SNP-by-expression interaction coefficients β_Cj follow another arbitrary zero-mean distribution with variance τ_C. The resulting model (1) becomes a logistic mixed model [Breslow and Clayton, 1993]. The null hypothesis of no AE (5) hence is equivalent to a joint test of the two variance components, τ_S and τ_C, in the induced logistic mixed model:

$$H_0:{\tau }_S={\tau }_C=0.$$

For family data, one can obtain the scores for τ_S and τ_C under the induced logistic mixed model: U_τS = (Y − μ̂_{0, AE})^T R^*−1SS^TR^*−1(Y − μ̂_{0, AE}) and U_τC = (Y − μ̂_{0, AE})^T R^*−1CC^T R^*−1(Y − μ̂_{0, AE}), where Y = (Y₁, …, Y_n)^T, S = (S₁, …, S_n)^T, C = (C₁, …, C_n)^T = (G₁S₁, …, G_nS_n)^T; the outcome risk under the null ${\hat{\mathit{\mu }}}_{0,AE}={({\hat{\mathit{\mu }}}_{0,AE,1}^T,\dots ,{\hat{\mathit{\mu }}}_{0,AE,m}^T)}^T,{\hat{\mathit{\mu }}}_{0,AE,i}=\text{exp}({\mathit{X}}_i^T{\hat{\mathit{\beta }}}_{X0}+G_i{\hat{\beta }}_{G0})/\{1+\text{exp}({\mathit{X}}_i^T{\hat{\beta }}_{X0}+G_i{\hat{\beta }}_{G0})\}$ (element-wise calculation), and β̂_X0 and β̂_G0 are the estimators of β_X and β_G, respectively, under the null model: $\text{logit}\{P({\mathit{Y}}_i=1|{\mathit{S}}_i,G_i,{\mathit{X}}_i)\}={\mathit{X}}_i^T{\mathit{\beta }}_X+G_i{\beta }_G;{\mathit{R}}_i^{*}(i=1,\dots ,m)$, an n_i by n_i covariance matrix represents the within-family correlation with n_i being the number of subjects within family i and m being the number of families, and ${\mathit{R}}^{*}=\mathit{\text{diag}}\{{\mathit{R}}_1^{*},\dots ,{\mathit{R}}_m^{*}\}$. With scores for the parameters of interest, τ_S and τ_C, we propose a test statistic $(Q_{SGC}^{AE})$ as a weighted sum of the two scores, w₁U_τS + w₂U_τC:

$$Q_{SGC}^{AE}=m^{-1}{(\mathit{Y}-{\hat{\mathit{\mu }}}_{0,AE})}^T{\mathit{R}}^{*-1}(w_1\mathit{S}{\mathit{S}}^T+w_2\mathit{C}{\mathit{C}}^T){\mathit{R}}^{*-1}(\mathit{Y}-{\hat{\mathit{\mu }}}_{0,AE}),$$

where the weights (w₁ and w₂) are chosen to be the inverse of their respective standard deviation of U_τS and U_τC to make them comparable on the same scale. The unknown true covariance R^* can be replaced by a working covariance R, which leads to a sum of L 2 norms of two estimating equations for β_s and β_c:

$$Q_{SGC}^{AE}=m^{-1}{(\mathit{Y}-{\hat{\mathit{\mu }}}_{0,AE})}^T{\mathit{R}}^{-1}(w_1\mathit{S}{\mathit{S}}^T+w_2\mathit{C}{\mathit{C}}^T){\mathit{R}}^{-1}(\mathit{Y}-{\hat{\mathit{\mu }}}_{0,AE}).$$

Examples of possible working covariance structures include a sample covariance matrix, a diagonal matrix assuming working independence or a kinship matrix.

The test statistic $Q_{SGC}^{AE}$ is derived according to the outcome model (1) where the disease risk is determined by SNPs, gene expression, and their cross-product interactions (i.e., the full model). We may specify a parsimonious model with only main effects by assuming that the disease risk depends on SNPs and gene expression without interactions (β_C = 0). Following the same development as described above, we obtain a similar test statistic under the main effect model:

$$Q_{SG}^{AE}=m^{-1}{(\mathit{Y}-{\hat{\mathit{\mu }}}_{0,AE})}^T{\mathit{R}}^{-1}(w_1\mathit{S}{\mathit{S}}^T){\mathit{R}}^{-1}(\mathit{Y}-{\hat{\mathit{\mu }}}_{0,AE}).$$

Testing Procedure for the ME Under Family Design

The null hypothesis of no ME (6) in the induced logistic mixed model is equivalent to:

$$H_0:{\beta }_G={\tau }_C=0.$$

We construct the test statistics for the ME for the above null hypothesis under model (1) as a weighted sum of L2 norms of estimating equations for β_G and β_C:

$$Q_{SGC}^{ME}=m^{-1}{(\mathit{Y}-{\hat{\mathit{\mu }}}_{0,ME})}^T{\mathit{R}}^{-1}(w_1\mathit{G}{\mathit{G}}^T+w_2\mathit{C}{\mathit{C}}^T){\mathit{R}}^{-1}(\mathit{Y}-{\hat{\mathit{\mu }}}_{0,ME}),$$

and under the main effect model, one can obtain the test statistic:

$$Q_{SG}^{ME}=m^{-1}{(\mathit{Y}-{\hat{\mathit{\mu }}}_{0,ME})}^T{\mathit{R}}^{-1}(w_1\mathit{G}{\mathit{G}}^T){\mathit{R}}^{-1}(Y-{\hat{\mathit{\mu }}}_{0,ME}),$$

where ${\hat{\mathit{\mu }}}_{0,ME}={({\hat{\mathit{\mu }}}_{0,ME,1}^T,\dots ,{\hat{\mathit{\mu }}}_{0,ME,n}^T)}^T,{\hat{\mathit{\mu }}}_{0,ME,i}=\text{exp}({\mathit{X}}_i^T{\hat{\mathit{\beta }}}_{X0}+{\mathit{S}}_i^T{\hat{\mathit{\beta }}}_{S0})/\{1+\text{exp}({\mathit{X}}_i^T{\hat{\mathit{\beta }}}_{X0}+{\mathit{S}}_i^T{\hat{\mathit{\beta }}}_{S0})\}$ (element-wise), and β̂_X0 and β̂_S0 are the estimators of β_X and β_S, respectively, under the null model:

$$\text{logit}\{P({\mathit{Y}}_i=1|{\mathit{S}}_i,G_i,{\mathit{X}}_i)\}={\mathit{X}}_i^T{\mathit{\beta }}_X+{\mathit{S}}_i^T{\mathit{\beta }}_S.$$ (8)

However, the maximum likelihood estimators of (β_x, β_s) may not be stable in the presence of a large number of SNPs and high correlations due to linkage disequilibrium. Thus, we estimate (β_x, β_s) by fitting the null model (8) using ridge regression via the penalized log-likelihood: $l_p({\mathit{\beta }}_X,{\mathit{\beta }}_S)={\sum }_{i=1}^n{l}_i({\mathit{\beta }}_X,{\mathit{\beta }}_S)-\frac{1}{2}\lambda {\mathit{\beta }}_S^T{\mathit{\beta }}_S$, where l_i is the estimating equation for the null model (8) constructed as log-likelihood of Y_i assuming working independence for subjects Y_ij (j = 1, …, n_i) within unit i, and λ is a tuning parameter. The tuning parameter λ can be selected using cross-validation or generalized cross-validation (GCV) [O’Sullivan, 1994]. Using the asymptotic distribution of $Q_{SGC}^{ME}$ and $Q_{SG}^{ME}$ and the GCV function presented in the supplementary material, one can construct a perturbation procedure (discussed in the following) to calculate P-values of $Q_{SGC}^{ME}$ and $Q_{SG}^{ME}$.

Testing Procedure for the TE Under Family Design

The null hypothesis of no total SNP effect (7) is equivalent to a joint test of the two variance components, τ_S and τ_C, and the scalar regression coefficient for gene expression effect, β_G in the induced logistic mixed model:

$$H_0:{\tau }_S={\tau }_C={\beta }_G=0.$$

With scores for the three parameters of interest, τ_S, τ_C, and β_G, we propose a test statistic $(Q_{SGC}^{TE})$ as a weighted sum of L 2 norms of three estimating equations for β_S, β_G, and β_C:

$$Q_{SGC}^{TE}=m^{-1}{(\mathit{Y}-{\hat{\mathit{\mu }}}_0)}^T{\mathit{R}}^{-1}(w_1\mathit{S}{\mathit{S}}^T+w_2\mathit{G}{\mathit{G}}^T+w_3\mathit{C}{\mathit{C}}^T){\mathit{R}}^{-1}(\mathit{Y}-{\hat{\mathit{\mu }}}_0).$$ (9)

Again, test statistics can be derived under other parsimonious models, e.g., the main effect model by assuming that the disease risk depends on SNPs and gene expression without interactions (β_C = 0), or the SNP-only model by assuming that the disease risk depends only on SNPs (β_G = 0, β_C = 0). Following the same development, we obtain similar test statistics for the two simpler models, denoted as $Q_{SG}^{TE}$ and $Q_S^{TE}$:

$$Q_{SG}^{TE}=m^{-1}{(\mathit{Y}-{\hat{\mathit{\mu }}}_0)}^T{\mathit{R}}^{-1}(w_1\mathit{S}{\mathit{S}}^T+w_2\mathit{G}{\mathit{G}}^T){\mathit{R}}^{-1}(\mathit{Y}-{\hat{\mathit{\mu }}}_0),$$

$$Q_S^{TE}=m^{-1}{(\mathit{Y}-{\hat{\mathit{\mu }}}_0)}^T{\mathit{R}}^{-1}(w_{1}S{S}^T){\mathit{R}}^{-1}(\mathit{Y}-{\hat{\mathit{\mu }}}_0),$$

where μ̂₀ = (μ̂₀₁, …, μ̂_0n)^T, ${\hat{\mathit{\mu }}}_{0i}=\text{exp}({\mathit{X}}_i^T{\hat{\mathit{\beta }}}_{Xo})/\{1+\text{exp}({\mathit{X}}_i^T{\hat{\mathit{\beta }}}_{X0})\}$, and β̂_X0 is the maximum likelihood estimator of β_X under the null model: $\text{logit}\{P({\mathit{Y}}_i=1|{\mathit{S}}_i,G_i,{\mathit{X}}_i)\}={\mathit{X}}_i^T{\mathit{\beta }}_X$.

Perturbation Procedure and Omnibus Test Under Family Design

In this section, we develop perturbation procedure for AE, ME, and TE. For illustration, we focus on the TE, and stress that procedures for AE and ME can be constructed following the same development. Under the null model that there is no effect of a gene on disease, i.e., under the null hypothesis (7), tests under the full model $(Q_{SGC}^{TE})$, main effect model $(Q_{SG}^{TE})$, and SNP-only model $(Q_S^{TE})$ are all valid tests. If there indeed exists an effect of the gene, the test assuming the correct model is expected to perform optimally with the highest power, while a test under the mis-specified model is likely to lose power. However, we do not know which model is the true underlying model, so it is desirable to develop an omnibus test that maximizes testing power by searching all three candidate models. Specifically, we calculate the P-values under each of the three models, and construct an omnibus test statistic using the minimum of the three P-values. We then calculate the P-value of the omnibus test statistic using a perturbation procedure [Cai et al., 2000; Huang et al., 2014; Parzen et al., 1992].

With the asymptotic distribution derived for $Q_{SGC}^{TE}$ in the supplement material (III. Asymptotics of Q statistics), we construct a perturbation procedure to perform hypothesis tests. Let $\hat{\mathit{\epsilon }}=m^{-\frac{1}{2}}{\sum }_{i=1}^m{\mathit{U}}_i({\mathit{Y}}_i-{\hat{\mathit{\mu }}}_{0i})Z_i$, where ${\mathit{U}}_i^T=({\mathit{X}}_i^T,\sqrt{w_1}{\mathit{R}}_i^{-1}{\mathit{S}}_i^T,\sqrt{w_2}{\mathit{R}}_i^{-1}{\mathit{G}}_i^T,\sqrt{w_3}{\mathit{R}}_i^{-1}{C}_i^T)$, X_i, S_i, G_i, C_i are q by n_i, p by n_i, 1 by n_i, p by n_i matrices, respectively; Y_i = (Y_i1, …, Y_ini)^T, ${\hat{\mathit{\mu }}}_{0i}=\text{exp}({\mathit{X}}_i^T{\hat{\mathit{\beta }}}_{X0}){(1+\text{exp}({\mathit{X}}_i^T{\hat{\mathit{\beta }}}_{X0}))}^{-1}$ are the corresponding estimates under the null, β̂_X0 is the estimator of β_X under the null model for the correlated family data, and Z_i are independent standard normal random variables. By generating independent Z = (Z₁, …, Z_m) repeatedly, the perturbed realization of $Q_{SGC}^{TE}$ in (9) under the null can be obtained, {$Q_{SGC}^{TE(b)}$, b = 1, …, B} where $Q_{SGC}^{TE(b)}={\Vert \mathit{A}\hat{\mathit{\epsilon }}\Vert }^2$ expression of A can be found in supplement material (III), and B is the number of perturbations. The P-value of Q_SGC can then be approximated using the tail probability of the perturbed realizations $\{Q_{SGC}^{TE(b)}\}$ by comparing $\{Q_{SGC}^{TE(b)}\}$ and the observed $Q_{SGC}^{TE}$. Similar perturbation procedures can be constructed for ME with the asymptotic distribution of Q_ME (see supplement material) or AE. The advantage of our proposed method is that we account for the within-family correlation by introducing a working correlation matrix R. Furthermore, our method does not require a correct specification of R. Through the perturbation procedure, our method protects the type I error under any structure of R, and gains power if the structure is close to the truth. The family design can also introduce ascertainment bias: families are not randomly selected from population, but instead ascertained according to disease status. Previous studies have shown that the bias in type I error rate is negligible using variance component tests based on estimating equations [Schifano et al., 2012]. We also account for ascertainment in our simulation studies.

Using the perturbation procedure, we can also calculate the P-value of the omnibus test statistic. Specifically, denote by p_S, p_SG, and p_SGC, the P values of the test statistics $Q_S^{TE},Q_{SG}^{TE}$, and $Q_{SGC}^{TE}$, respectively; we define the minimum P-value of p_S, p_SG, and p_SGC as the test statistic for the omnibus test. With the perturbed realization of the distribution for the three statistics $Q_S^{TE},Q_{SG}^{TE}$, and $Q_{SGC}^{TE}$, the underlying distribution of this minimum P-value can then be approximated [Huang et al., 2014]. By comparing the observed minimum P-value with the approximated distribution, the omnibus P-value can be calculated as the tail probability of the distribution. One can also use the perturbation procedure to calculate the P-value of the omnibus test for ME (or AE) constructed using the minimum of the P-values of $Q_{SGC}^{ME}$ and $Q_{SG}^{ME}$ (or $Q_{SGC}^{AE}$ and $Q_{SG}^{AE}$). R codes that implement the proposed testing procedures for the TE, ME, and AE are available upon request.

Simulation and Asthma Data Analysis

We detailed the simulation and data analysis in the supplement material (I. Numerical Simulation, and II. Asthma iGWAS Data Analysis). Briefly, we randomly simulated SNPs and gene expression from chromosome 10 for 100 cases and 100 controls, mimicking the family design of the MRCA data and accounting for ascertainment. We simulated 500,000 datasets to estimate size of the test and 2,000 datasets to estimate statistical power. We conducted an integrative GWAS using the MRCA asthma dataset [Moffatt et al., 1986]. The MRCA asthma dataset is a GWAS for childhood asthma with a family design where both genome-wide SNP and gene expression data are available. The MRCA data were collected from families of the British descent and consists of 378 subjects: 266 cases and 112 controls. Control subjects are either siblings or parents of the cases. Genome-wide SNP genotypes were obtained using the Illumina 300K SNP array and gene expressions were measured using the Affymetrix HU133A 2.0 expression array. Our analyses focused on the SNPs that are associated with the nearby gene within 1 Mb on the same chromosome (cis-eQTL) with false discovery rate (FDR) [Benjamini and Hochberg, 1995] less than 1%, which has been published using similar datasets [Liang et al., 2008]. We then grouped these eQTL SNPs with their corresponding gene expression as an SNPs-expression set. The iGWAS analyses were applied to a total of 11,198 such sets. P-values were calculated with 5,000 resampling perturbation and approximated with the method based on the mixture of normal distributions [Cai et al., 2012].

Results

Detail simulation results were provided in the supplement material (IV. Numerical Results for AE, ME, and TE; supplementary Table S1, and Figs. S1 and S2). In summary, numerical simulation showed that under the null, the iGWAS for ME, AE, and TE protect the small type I error (e.g., 5 × 10⁻⁵); and under the alternative, the omnibus tests are robust to different underlying models and approach the optimal power from tests with correct model specification.

Family-Based iGWAS of Childhood Asthma

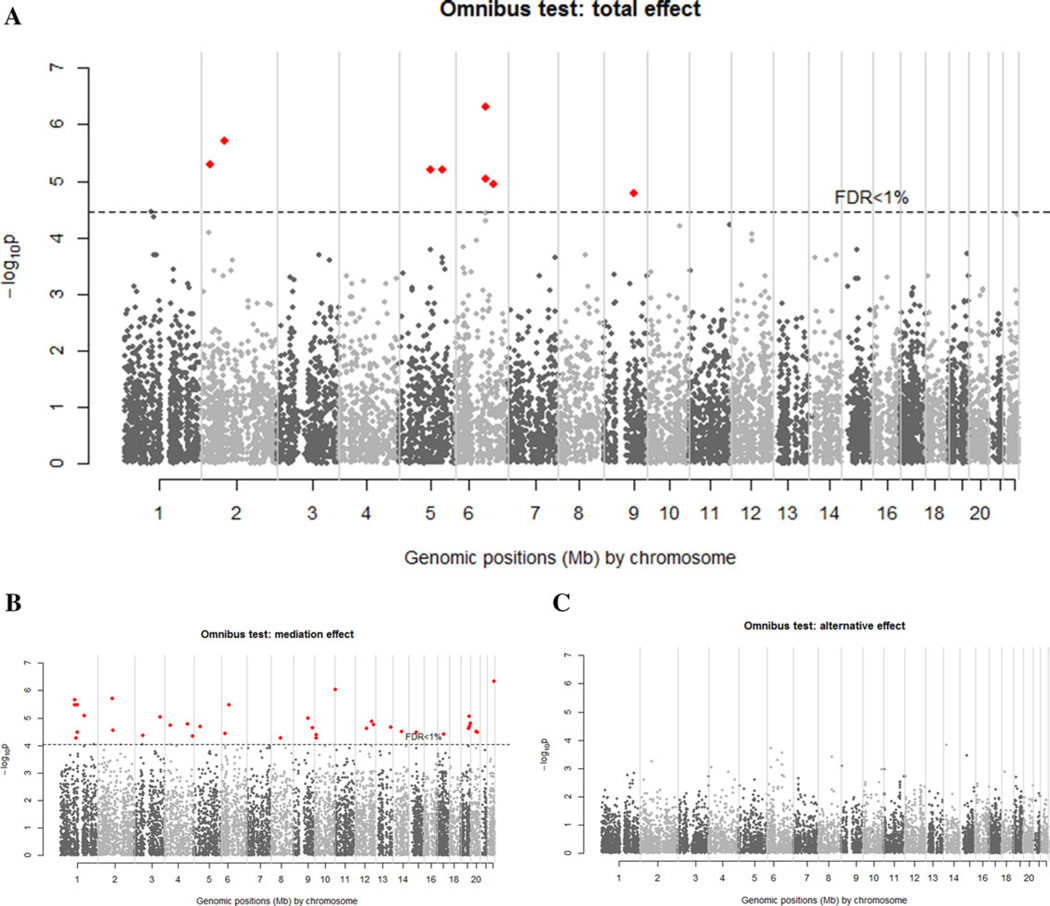
We grouped eQTL SNPs and their corresponding gene expression probes into 11,198 sets and then performed the proposed gene-centric iGWAS analyses on these sets one at a time. We first focused on examining 11,198 TEs of SNPs and gene expression. For the SNP-only analyses, the set contained only eQTLs without gene expression. We used 1% of FDR as the cut-off for genome-wide statistical significance. For the SNP-only analyses, there were no gene or transcript with FDR < 1% (supplementary Fig. S3A). There were 14 transcripts, 2 transcripts, and 8 transcripts with FDR < 1% in genome wide analyses using the main effect model (Q_SG), full model with interaction (Q_SGC), and omnibus test (Q_omb), respectively (supplementary Figs. S3B and S3C, and Fig. 2A). The genome-wide results were consistent with our findings from numerical simulations: the omnibus test (Q_omb) and main effect model (Q_SG) that incorporated the information of gene expression were more powerful tests compared to the conventional SNP-only approach (Q_S).

Figure 2.

Manhattan plots of genome-wide scan of the asthma data using SNPs and gene expression data with the gene-centric iGWAS approach. Analysis is restricted to eQTLs. (A) Omnibus P-values for total effects; (B) omnibus P-values for mediation effects; (C) omnibus P-value for alternative effects. Red dots indicate the transcripts found from the omnibus test with FDR < 1%.

In addition to increasing power of identifying susceptibility genes, a more important advantage of the iGWAS approach is that it facilitates to unravel the mechanism of genetic effects. Specifically, we investigated the mechanistic contribution of SNPs and gene expression to asthma risk by studying the ME of eQTL SNPs on asthma risk through gene expression and the AE of eQTL SNPs on asthma risk through other mechanisms. To study the ME and AE, we investigated the main effect model and full model. The P-values of omnibus tests for MEs and AEs in scanning the genome are presented in Figures 2B and C, and those of main effect models and full models are presented in supplementary Figures S4 and S5. There are 36 genes with significant MEs at FDR < 1%, but no gene with AE survives the same cut-off. The results indicated that the effect of most asthma susceptibility genes may be mediated through their own gene expressions. The 36 genes with significant MEs (FDR < 1%) and the top 10 genes with the most significant AEs are presented in supplementary Tables S2 and S3.

iGWAS Results for Candidate Genes

The nominal P-values of the eight transcripts with FDR < 1% in omnibus tests for TEs are presented in Table 1. The eight transcripts corresponded to six unique genes and an RNA transcript not within a gene (229319_at). The MANEA gene showed up twice in the list because the eQTL SNPs-expression set was grouped for each expression probe, and genes with multiple probes may be grouped into different sets. For the TEs of the eight transcripts, the model with main effects of SNPs and gene expression (Q_SG) performed the best, except for MRPL53 and MANEA (219003_s_at) where the full model (Q_SGC) performed even better. The omnibus P-values were very close to the smallest P-values among the three candidate models (Q_S, Q_SG, and Q_SGC). The SNP-only effect of PTCH1 was not significant (P = 0.32), but its SNP-expression joint effect was very significant (P = 8.5 × 10⁻⁶). Even with the conservative Bonferroni adjustment for the 11,198 sets (P < 4.5 × 10⁻⁶), MANEA (219003_s_at) (P = 4.8 × 10⁻⁷) and MRPL53 (P = 1.9 × 10⁻⁶) were still statistically significant.

Table 1.

P-values of alternative effect, mediation effect, and total effect for genes with most significant total effect (FDR < 1%) using the asthma data. Ch, chromosome; Q_S, test with only SNP-set, the SNP-only model; Q_SG, test with both SNP set and gene expression (without interaction), the main effect model; Q_SGC, test with SNP set, gene expression, and their cross-product interactions, the full model; Q_omb, omnibus test for Q_S (if applicable), Q_SG, and Q_SGC

				Alternative effect			Mediation effect			Total effect
Probe	Gene	Ch	Number of eQTL	$Q_{omb}^{AE}$	$Q_{SG}^{AE}$	$Q_{SGC}^{AE}$	$Q_{omb}^{ME}$	$Q_{SG}^{ME}$	$Q_{SGC}^{ME}$	$Q_{omb}^{TE}$	$Q_S^{TE}$	$Q_{SG}^{TE}$	$Q_{SGC}^{TE}$
219003_s_at	MANEA	6	159	2.9 × 10−4	2.6 × 10−4	2.8 × 10−4	0.0079	0.0076	0.0082	4.8 × 10−7	2.1 × 10−6	2.9 × 10−7	2.8 × 10−7
225523_at	MRPL53	2	175	5.7 × 10−4	5.8 × 10−4	6.2 × 10−4	0.055	0.053	0.060	1.9 × 10−6	1.0 × 10−5	5.2 × 10−6	1.0 × 10−6
226996_at	LYCAT	2	193	0.19	0.18	0.18	4.7 × 10−4	4.6 × 10−4	5.0 × 10−4	5.2 × 10−6	0.0065	4.0 × 10−6	6.0 × 10−5
230261_at	ST8SIA4	5	185	0.012	0.012	0.013	1.9 × 10−4	2.0 × 10−4	2.0 × 10−4	6.3 × 10−6	0.0020	4.1 × 10−6	1.4 × 10−4
222422_s_at	NDFIP1	5	48	0.11	0.11	0.11	0.0011	0.0010	0.0012	6.4 × 10−6	0.0031	4.0 × 10−6	4.1 × 10−5
1554193_s_at	MANEA	6	67	0.0017	0.0018	0.0020	0.012	0.011	0.012	9.0 × 10−6	6.0 × 10−5	4.8 × 10−6	1.4 × 10−5
229319_at	—	6	148	0.29	0.29	0.28	2.9 × 10−4	3.0 × 10−4	3.0 × 10−4	1.2 × 10−5	0.018	7.5 × 10−6	6.70 × 10−5
209815_at	PTCH1	9	13	0.92	0.91	0.93	1.0 × 10−5	1.8 × 10−5	1.3 × 10−5	1.6 × 10−5	0.32	8.5 × 10−6	2.2 × 10−4

As shown in Table 1, all except MRPL53 had very significant ME, no matter under the main effect model or full model, and the omnibus P-values were very close to smallest P-values. The AE was significant in MANEA (P = 2.9 × 10⁻⁴ and 0.0017), MRPL53 (P = 5.7 × 10⁻⁴), and ST8SIA4 (P = 0.012), which indicated that eQTL SNPs of these genes may act through other mechanisms in addition to mRNA expression of the genes, to affect the asthma risk.

Nominal P-values for genes containing SNPs reported in previous asthma GWAS [Ferreira et al., 2011; Moffatt et al., 2007; Ober et al., 2008; Torgerson et al., 2011] are presented in Table 2. The iGWAS approach confirmed the significant TEs from ORMDL3 (P = 0.0081), CHI3L1 (P = 0.0055), and IL6R (P = 0.040). The effects of CHI3L1 and IL6R were mostly through gene expression (P = 0.0013 and 0.018, respectively), while the effect of ORMDL3 gene seemed to be mainly through alternative biological mechanisms (P = 0.023). Of note, the strategy used in previous GWAS to identify these genes was single SNP analysis, while our reanalysis utilized the proposed gene-centric approach.

Table 2.

Nominal P-values of alternative effect, mediation effect, and total effect for genes reported in previous GWAS of asthma risk

				Alternative effect			Mediation effect			Total effect
Probe	Gene	Ch	Number of eQTL	$Q_{omb}^{AE}$	$Q_{SG}^{AE}$	$Q_{SGC}^{AE}$	$Q_{omb}^{ME}$	$Q_{SG}^{ME}$	$Q_{SGC}^{ME}$	$Q_{omb}^{TE}$	$Q_S^{TE}$	$Q_{SG}^{TE}$	$Q_{SGC}^{TE}$
223259_at	ORMDL3	17	209	0.027	0.028	0.027	0.037	0.037	0.040	0.094	0.065	0.11	0.068
235136_at	ORMDL3	17	93	0.023	0.023	0.022	0.31	0.30	0.35	0.053	0.034	0.12	0.058
240701_at	ORMDL3	17	36	0.048	0.050	0.047	0.11	0.11	0.12	0.0081	0.015	0.0052	0.0080
209395_at	CHI3L1	1	14	0.20	0.19	0.19	0.0013	0.0011	0.0019	0.0055	0.48	0.0030	0.018
209396_s_at	CHI3L1	1	14	0.24	0.23	0.25	0.0081	0.0074	0.0090	0.025	0.47	0.015	0.053
226333_at	IL6R	1	23	0.67	0.70	0.66	0.018	0.017	0.021	0.040	0.76	0.021	0.072
205945_at	IL6R	1	29	0.89	0.88	0.90	0.71	0.65	0.87	0.94	0.88	0.92	0.94
206618_at	IL18R1	2	66	0.66	0.68	0.64	0.98	0.95	1.0	0.81	0.68	0.91	0.85
209349_at	RAD50	5	12	0.84	0.82	0.85	0.83	0.74	0.99	0.92	0.84	0.95	0.95

Abbreviation and notations are the same as Table 1.

Single-Locus Analyses

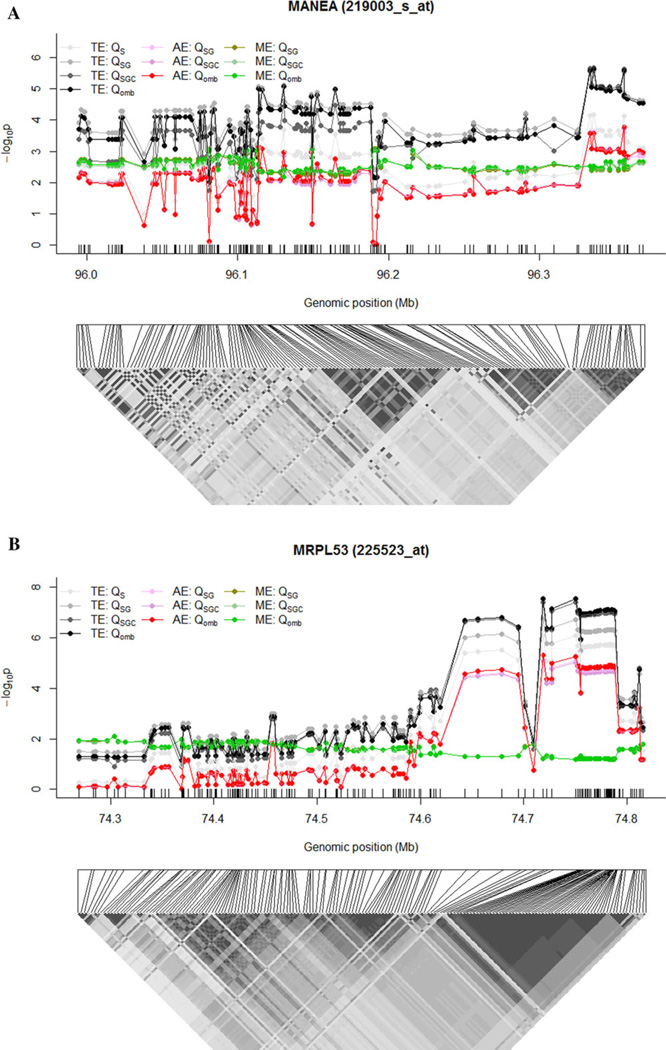
We also conducted single-locus analyses for the top eight transcripts as well as the candidate genes identified from previous GWAS. In the single-locus analyses, we analyzed each single SNP and the gene expression associated with the SNP, studying AEs, MEs, and TEs. Again, AEs and MEs were studied under the main effect model and full model, whereas TEs were investigated under the SNP-only model, main effect model, and full model. We present the P-values from different tests for AEs, MEs, and TEs of MANEA (219003_s_at) and MRPL53, the two most significant genes in Fig. 3. Results of the remaining six transcripts are shown in supplementary Figures S6–S11. The ME or AE was prominent in certain linkage disequilibrium blocks, in particular, for MRPL53, MANEA, and ST8SIA4. The median (first quartile-third quartile) of the proportion (%) of mediation for all eQTL SNPs was 11.9% (8.8–13.6%) for MANEA (219003_s_at), 3.9% (1.0–4.4%) for MANEA (1554193_s_at), 8.7% (3.8–13.7%) for MRPL53, 50.6% (31.6–53.7%) for LYCAT, 17.7% (13.7–20.7%) for ST8SIA4, 54.1% (33.6–54.5%) for NDFIP1, 95.0% (78.8–100.0%) for 229319_at, and 48.4% (25.9–100.0%) for PTCH1. The high proportions of mediation observed in NDFIP1, PTCH1, LYCAT, and 229319_at were consistent with their highly significant MEs and nonsignificant AEs (Table 1, supplementary Figs. S6, S8, S10, and S11). Detailed results from single-locus analyses are presented in supplementary Tables S4–S11, and the patterns support the findings of gene-centric analyses presented in Table 1. The results of single-locus analyses for the genes identified from the previous GWAS (ORMDL3, CHI3L1, IL6R, IL18R1, and RAD50) are presented in supplementary Tables S12–S20. The findings from single-locus analyses are consistent with the results using the iGWAS approach.

Figure 3.

Plots of P-values of AE, ME, and TE in single-locus analyses for MANEA (219003_s_at) (A) and MRPL53 (B). Lower panel represents the linkage disequilibrium structure for SNPs within each gene, measured as r² ranging from 0 (white) to 1 (black). Q_S, tests assuming an SNP-only model; Q_SG, tests assuming a model with main effects of SNPs and gene expression; Q_SGC, tests assuming a model with main effects and their interactions; Q_omb, omnibus tests.

Discussion

We proposed in this paper an integrative approach, iGWAS, that is able to analyze multiplatform genomic data under the family-based design. The model can be presented as a causal diagram (Fig. 1), which was set up based on the central dogma of molecular biology that DNA can be transcribed to mRNA expression and mRNA can then be translated to be protein to affect the phenotypic trait such as disease risk. The mediation diagram provides an intuitive illustration of our hypothesis. The iGWAS approach is integrative in different aspects. The model not only integrates different types of genomic data, i.e., SNP and gene expression data, but also incorporates different types of genetic/genomic association studies to delineate clinical outcome rather than perform a GWAS, an expression microarray study, and an eQTL study separately. Moreover, the iGWAS approach integrates biological knowledge into the computational model, as illustrated in the causal mediation diagram.

The iGWAS approach has several advantages. First, with the enriched genomic information compared to single one alone, a better statistical power has been illustrated in both numerical studies and a family-based GWAS of childhood asthma using the family-based MRCA data. The iGWAS outperforms the SNP-only approach and identifies novel genes for asthma susceptibility that have not been reported. Second, the iGWAS approach makes an analytic investigation into the biological mechanism of genetic effects possible. The ME represents a cis-regulating effect that SNPs regulate expression of a nearby gene; and possible mechanisms behind the AE include a trans-regulating effect that SNPs affect expression of a distant causal gene, or a structural related effect that SNPs alter the biochemical structure of their gene product instead of their expression level. Third, although the iGWAS was developed under the family design, it can accommodate a wide range of study designs such as nonfamily-based case-control studies, cohort studies, or longitudinal studies with repeat measurement. Finally, the iGWAS approach may have translational utilities. For example, for genes with significant MEs, the expression levels may serve as diagnostic biomarkers to screen and prevent the disease. Moreover, potential therapeutic agents such as small RNAs that can repress expressions of the specific genes may be developed to counteract the MEs.

Because our method is developed under the framework of mediation modeling based on causal inference, we need to make untestable no-unmeasured confounding assumptions to draw conclusions beyond association. If we are interested in studying the TE, the only assumption is that there is no unmeasured confounding for the effect of eQTL SNPs on the outcome after adjusting for the covariates, which is the same as that made in the conventional SNP-only GWAS. However, if we are interested in the ME and AE, stronger assumptions are required [Huang et al., 2014].

The iGWAS approach confirmed the genes that have been reported to be associated with asthma risk such as ORMDL3 (P = 0.0081), CHI3L1 (P = 0.0055), and IL6R (P = 0.040) [Ferreira et al., 2011;Moffatt et al., 2007]. In addition to confirming their overall genetic effects, we also found that the genetic effects of CHI3L1 and IL6R were mediated by gene expression (Table 2) and that genetic loci of ORMDL3 may have alternative mechanisms independent of acting through its gene expression (P = 0.023). Our approach also identified six novel genes (MANEA, MRPL53, LYCAT, ST8SIA4, NDFIP1, and PTCH1). NDFIP1 has been reported to be a candidate susceptible gene in asthma GWAS but with weak effect, OR = 1.11 [Ferreira et al., 2011]. As we found that most of the genetic effect of NDFIP1 was through gene expression, the heterogeneity due to not accounting for gene expression may explain the modest effect in the previous study. NDFIP1 mediates peripheral immune tolerance by inducing cell cycle exit in CD4 T lymphocytes [Altin et al., 2014]. PTCH1, patched homolog 1, has been found to be associated with lung function in the general population and lung function abnormalities in white and African Americans with asthma [Li et al., 2011]. ST8SIA4, sialyltransferase, is predominantly expressed in immune cells [Kolker et al., 2012]. It plays an important role in substrate recognition that modulates cell adhesion and signaling [Zapater and Colley, 2012]. MANEA, α-endomannosidase, has been reported to be associated with psychiatric disorders including substance dependence and anxiety disorders [Farrer et al., 2009; Jensen et al., 2014; Yu et al., 2008]. Studies in nonpsychiatric disorders, however, are very limited. Consistent with our findings, a 3′UTR SNP, rs113503, has been shown to be related to mRNA expression of MANEA [Jensen et al., 2014]. LYCAT, lysocardiolipin acyltransferase 1, is expressed in developing lung of mouse [Wang et al., 2010], but its association with asthma or other immune-related disorders has not been reported. MRPL53, mitochondrial ribosomal protein L53, is involved in a ribonucleotide complex [Wessels et al., 2013]. The molecular mechanism of these candidate genes in relation to the development of asthma warrants further examination.