Constant-complexity stochastic simulation algorithm with optimal binning

Abstract

At the molecular level, biochemical processes are governed by random interactions between reactant molecules, and the dynamics of such systems are inherently stochastic. When the copy numbers of reactants are large, a deterministic description is adequate, but when they are small, such systems are often modeled as continuous-time Markov jump processes that can be described by the chemical master equation. Gillespie’s Stochastic Simulation Algorithm (SSA) generates exact trajectories of these systems, but the amount of computational work required for each step of the original SSA is proportional to the number of reaction channels, leading to computational complexity that scales linearly with the problem size. The original SSA is therefore inefficient for large problems, which has prompted the development of several alternative formulations with improved scaling properties. We describe an exact SSA that uses a table data structure with event time binning to achieve constant computational complexity with respect to the number of reaction channels for weakly coupled reaction networks. We present a novel adaptive binning strategy and discuss optimal algorithm parameters. We compare the computational efficiency of the algorithm to existing methods and demonstrate excellent scaling for large problems. This method is well suited for generating exact trajectories of large weakly coupled models, including those that can be described by the reaction-diffusion master equation that arises from spatially discretized reaction-diffusion processes.

I. INTRODUCTION

Traditional differential equation models of chemically reacting systems provide an adequate description when the reacting molecules are present in sufficiently high concentrations, but at cellular scales, biochemical reactions occur due to the random interactions of reactant molecules that are often present in small numbers. These processes display behavior that cannot be captured by deterministic approaches. Under certain simplifying assumptions, including spatial homogeneity, these systems can be modeled as continuous-time Markov jump processes. The evolution of the probability of the system being in any state at time t is described by the Chemical Master Equation (CME).^1,2 The invariant distribution and the evolution can be found for certain classes of reaction networks,^3–5 but for many realistic problems, the state space and the CME are too large to solve directly. Gillespie’s Stochastic Simulation Algorithm (SSA) generates exact trajectories from the distribution described by the CME,^6,7 but one must generate an ensemble of trajectories to estimate the probability distribution.

Consider a well-mixed (spatially homogeneous) biochemical system of S different chemical species with associated populations N(t) = (n₁(t), n₂(t), …, n_S(t)). The population is a random variable that changes via M elementary reaction channels $\left\{R_1,R_2,\dots ,R_M\right\}$. Each reaction channel R_j has an associated stoichiometry vector ν_j that describes how the population N changes when reaction R_j “fires.” The CME (and the SSA) are derived by assuming that each reaction channel R_j is a non-homogeneous Poisson process whose intensity is determined by a propensity function, a_j, which is defined as^6–8

$${\displaystyle a_j\left(N\right)dt\equiv \text{probability that reaction }{R}_j\text{will occur once in }[t,t+dt).}$$ (1)

The definition in (1) describes a property of an exponential distribution. The time τ and index j of the next reaction event, given the current state N and time t, can therefore be characterized by the joint probability density function

$${\displaystyle p(\tau ,j|N,t)=e^{-\sum _{i=1}^M{a}_i\left(N\right)\tau }{a}_j\left(N\right).}$$ (2)

Equation (2) combined with the fact that the process is Markovian — a consequence of the well-mixed assumption — leads naturally to the SSA.

We will refer to as any simulation algorithm that generates trajectories by producing exact samples of τ and j from the density in (2) as an “exact SSA.” Note that when other sources describe “the SSA” or “the Gillespie algorithm,” they are often implicitly referring to the direct method variant of the SSA (see Section II A).^6,7 However, many other SSA variants have been proposed that achieve different performance and algorithm scaling properties by utilizing alternate data structures to sample density function (2).^9–18 Many of these methods apply random variate generation techniques described in Devroye¹⁹ to the SSA. Among the most popular of these alternate formulations of the SSA for large problems is the Next Reaction Method (NRM) of Gibson and Bruck.⁹ We discuss this and other formulations in detail in Secs. II–IV. Many authors have also described approximate methods that sacrifice exactness in exchange for computational efficiency gains, including the class of tau-leaping algorithms and various hybrid approaches.^20–30,51 In this paper, we restrict our attention to exact methods.

An important class of problems that leads to large models arises from spatially discretized reaction diffusion processes. The assumption underlying the CME and SSA that the reactant molecules are spatially homogeneous is often not justified in biological settings. One way to relax this assumption is to discretize the system volume into N_s subvolumes and assume that the molecules are well-mixed within each subvolume. How to choose the subvolume size to ensure this is discussed elsewhere.³¹ Molecules are allowed to move from one subvolume to an adjacent one via diffusive transfer events. This setting can also be described as a Markov jump process and leads to the reaction-diffusion master equation (RDME).^32,33 In simulating the RDME, reaction events within each subvolume are simulated with the standard SSA and diffusive transfers are modeled as pseudo-first order “reactions.” The resulting simulation method is algorithmically equivalent to the SSA (see Gillespie et al.³³ for an overview). However, the state space and the number of transition channels grow rapidly as the number of subvolumes increases, since the population of every species must be recorded in every subvolume. The number of transition channels includes all diffusive transfer channels, and in addition, each reaction channel in the homogeneous system is duplicated once for each subvolume. In a spatial model, M is the total number of reaction and diffusion channels. Several exact and approximate algorithms and software packages designed specifically for simulating the RDME have been proposed.^34–39

In this paper, we present an exact SSA variant that is highly efficient for large problems. The method can be viewed as a variation of the NRM that uses a table data structure in which event times are stored in “bins.” By choosing the bin size relative to the average simulation step size, one can determine an upper bound on the average amount of computational work per simulation step, independent of the number of reaction channels. This constant-complexity NRM is best suited for models in which the fastest time scale stays relatively constant throughout the simulation. Optimal performance of the algorithm is sensitive to the binning strategy, which we discuss in detail in Section IV A.

The remainder of the paper is organized as follows. In Sec. II, we discuss the standard direct and NRM methods in more detail. In Section III, we demonstrate how alternate methods with various scaling properties can be derived by modifying the standard methods. Section IV presents the constant-complexity NRM algorithm and the optimal binning strategy. The performance and scaling of several methods is presented in Section V. Section VI concludes with a brief summary and discussion.

II. STANDARD METHODS FOR SPATIALLY HOMOGENEOUS MODELS

The majority of exact SSA methods are based on variations of the two standard implementations: the direct method and the NRM. Here, we review these standard methods in more detail.

A. Direct method

The direct method variant of the SSA is the most popular implementation of the Gillespie algorithm.^6,7 In the direct method, the step size τ is calculated by generating an exponentially distributed random number with rate parameter (or intensity) equal to the sum of the propensities. That is, τ is chosen from the probability density function

$${\displaystyle f\left(\tau \right)=\left(\sum _{i=1}^M{a}_i\left(N\right)\right)e^{-\sum _{i=1}^M{a}_i\left(N\right)\tau },\tau \ge 0.}$$ (3)

The index of the next reaction, j, is an integer-valued random variable chosen from the probability mass function

$${\displaystyle f\left(j\right)=\frac{a_j}{\sum _{i=1}^M{a}_i\left(N\right)},j\in \{1,2,\dots ,M\}.}$$ (4)

The original direct method is implemented by storing the propensities in a one-dimensional data structure (e.g., an array in the C programming language). Generating the reaction index j as described in (4) can be implemented by choosing a continuous, uniform random number r between 0 and the propensity sum and choosing j such that

$${\displaystyle j=\text{smallest integer satisfying }\sum _{i=1}^j{a}_i\left(N\right)>r.}$$ (5)

This “search” to find the index of the next reaction proceeds by iterating over the elements in the array until condition (5) is satisfied. After the time of the next event and the reaction index are determined, the simulation time t and system state N are updated as t = t + τ and N = N + ν_j. Changing the population N will generally lead to changes in some propensities, which are recalculated and the propensity sum is adjusted accordingly. The algorithm repeats until a termination condition is satisfied. Typically, an ensemble of many simulation trajectories is computed.

An analysis of the scaling properties for a single step of the direct method, or any SSA variant, can be done by considering the computational work required for the two primary tasks of the algorithm: (1) searching for the next reaction index and (2) updating the reaction generator data structure (see Ref. 40). If the propensities are stored in random order in a one-dimensional array, the search will take approximately M/2 steps on average. Utilizing static or dynamic sorting can reduce the search to a smaller fraction of M.^41,42 The average cost of the update step will be the number of dependencies for each reaction, weighted by the firing frequencies of the reactions. The update cost is at worst O(M), making the direct method an O(M) algorithm overall. The SSA direct method is easy to implement with simple data structures that have low overhead, making it a popular choice that performs well for small problem sizes.

B. Next reaction method

In his 1976 paper,⁶ Gillespie also proposed the first reaction method (FRM), which involves generating a tentative next reaction time for every reaction channel and then finding the smallest value to determine the next event that occurs. The NRM is a variation of the FRM that uses a binary min-heap to store the next reaction times.⁹ The search for the next reaction in the NRM is a constant-complexity, or O(1), operation because the next reaction is always located at the top of the heap. However, updating the binary min-heap data structure when a propensity changes is computationally expensive. For each affected propensity, the propensity function has to be evaluated, the reaction time has to be recomputed based on this new propensity, and the binary min-heap must be updated to maintain the heap property.

Maintaining the heap structure generally requires O(log₂(M)) operations for each affected event time, implying that the total computational cost of the update step is DO(log₂(M)) = O(log₂(M)), where D is the average number of propensity updates required per step.⁹ In practice, the actual update cost will depend on many factors, including the extent to which the fastest reaction channels are coupled and whether or not the random numbers are “recycled.”^9,17 For what we later call strongly coupled reaction networks, where D is O(M), the update step is O(Mlog₂(M)). The interested reader should consult Gibson and Bruck⁹ for a detailed analysis.

The work estimates for the update step of these algorithms (O(M) for the direct SSA and O(Mlog₂M) for the NRM) are worst-case estimates that apply when a large fraction of the propensities must be updated after every reaction event. This is an extreme case, and when it obtains we call the underlying network strongly coupled. Well-established examples of such networks are known in the biological realm and include the yeast protein interaction network⁴³ and the metabolic network in E.coli.⁴⁴ The former has a “hub” that connects to several hundred nodes, but typical copy numbers of proteins are at least O(10²) and usually O(10⁴).^45,46 In the latter case there are 473 metabolites and 574 links (as of 2005⁴⁴), and while adenosine triphosphate (ATP) and adenosine diphosphate (ADP) are reactants or products of many reactions, or are involved in the control of numerous enzymes, their concentration is typically in the millimolar range. Thus in either case, the copy numbers are large enough that a deterministic description of the dynamics is often appropriate, though exceptions may certainly occur.

Typical applications of stochastic models in biology are to enzyme-catalyzed reactions and signal transduction or gene control networks that have relatively few reacting components (≤100) in which the reactions are at most bimolecular and which produce at most three product species. In these cases the reactions are weakly coupled in the sense that there is a fixed constant upper bound D to the number of propensities that must be updated after each reaction step. We call these weakly coupled networks and note that they apply to discretized reaction-diffusion equations with a reaction network that satisfies the above constraints, since each diffusive step only affects two subvolumes. As we show later, this class of networks leads to constant complexity SSAs.

In this work, we assume the reaction network is weakly coupled and that D is bounded above independent of M, leading to O(log₂(M)) scaling overall for the original NRM formulated with a binary min-heap. The original NRM is therefore superior to the direct method for large, weakly coupled networks. For strongly coupled networks, methods utilizing partial propensities, equivalence classes, or rule-based modeling may be more efficient.^14,47,48

III. ALTERNATIVE FORMULATIONS

There are two main techniques for improving the scaling properties of an exact SSA implementation. The first is to use different data structures, as in the binary tree utilized for the NRM min-heap implementation. The other technique is to split the search problem into smaller subproblems by partitioning the reaction channels into subsets. The two techniques are complementary and in some cases conceptually equivalent. By utilizing different combinations of data structures and partitioning schemes, it is possible to define an infinite number of alternate SSA formulations with varying performance and scaling properties.

To fix ideas, consider a simple variation of the direct method. Instead of storing all M propensities in a single array, one could partition the reaction channels into two subsets of size M/2 and store them using two arrays. If we label the propensity sums of the two subsets a_S1 and a_S2, respectively, then the probability that the next reaction will come from subset i is a_Si/(a_S1 + a_S2). Conditioned on the next reaction coming from subset i, the probability that the next reaction is R_j will be a_j/a_Si, for all j in subset i. These statistical facts follow from the properties of exponential random variables and lead naturally to a simulation algorithm. We select the subset i from which the next reaction will occur by choosing a continuous uniform random number r₁ between 0 and the propensity sum and using a linear search as in the direct method to choose i,

$${\displaystyle i=\text{smallest integer satisfying }\sum _{k=1}^i{a}_{S_k}\left(N\right)>r_1.}$$ (6)

We have written (6) in a generic way to accommodate more than two subsets. After selecting the subset i, we can use the linear search from (5) again to select the reaction j from within subset i, but choosing the uniform random number between 0 and a_Si and iterating over the elements in the array corresponding to subset i.

The resulting algorithm can be viewed as a “2D” version of the direct method. The (unsorted) algorithm requires, on average, a search of depth 1.5 to choose the subset and an average search depth of M/4 to select the particular reaction within the chosen subset. The algorithmic complexity of this variation is still O(M), so the NRM will still outperform this method for sufficiently large problems. Below we show how more sophisticated partitioning and data structures can be used to achieve improved scaling properties.

A. Alternate direct formulations

One can expand on the idea above to create other direct method variants. If each of the two subsets is then split into two more subsets, a similar procedure can be applied to derive a method with M/8 scaling. If this processes is repeated recursively, the resulting partitioning of the reaction channels can be viewed as a binary tree.^9,12,18 This logarithmic direct method has O(log₂(M)) cost for the search and update steps. If the reaction channels were partitioned into $\sqrt{M}$ subsets each containing $\sqrt{M}$ channels, the search for the subset and the search within the subset are both $O\left(\sqrt{M}\right)$ operations, leading to $O\left(\sqrt{M}\right)$ algorithmic complexity. This is the theoretically optimal “2D search” formulation. Similarly, one can define a three-dimensional data structure, leading to a “3D search” which scales as $O\left(\sqrt[3]{M}\right)$, and so on.^12,18

Slepoy et al.¹⁰ proposed a constant-complexity (O(1)) direct method variant that uses a clever partitioning strategy combined with rejection sampling. The reaction channels are partitioned based on the magnitude of their propensities with partition boundaries corresponding to powers of two. That is, if we number the partitions using (positive and negative) integers, partition i contains all of the reaction channels with propensities in the range [2ⁱ, 2ⁱ⁺¹). (We note that this partitioning strategy, referred to as “binning” in Slepoy et al.,¹⁰ is unrelated to the binning strategy we employ in the constant-complexity NRM presented in this work.) The partition g from which the next reaction will occur is chosen exactly via a linear search, which is assumed to have a small average search depth, independent of M. A rejection sampling technique is employed to select the particular channel within the subset g. An integer random number r₁ is chosen between [1, M_g], where M_g is the number of reaction channels in subset g. This tentatively selects the reaction channel j corresponding to the r₁-th channel in the subset. Then a continuous random number r₂ is chosen between [0, 2^g+1). If r₂ < a_j(x), reaction channel j is accepted as the next event, otherwise it is rejected and new random numbers r₁ and r₂ are chosen. The process is repeated until a reaction is accepted. Since the subsets have been engineered such that all propensities in subset g are within the range [2^g, 2^g+1), it takes fewer than two samples on average to select the next reaction, independent of the number of reaction channels. Updating the data structures for each affected propensity is also an amortized constant-complexity operation leading to O(1) algorithmic complexity independent of M for weakly coupled networks.

B. Next subvolume method (NSM)

The preceding methods are general formulations that can be applied to any model that can be described by the CME or RDME. In this subsection, we describe the NSM (not to be confused with the NRM), which is formulated specifically for simulating processes described by the RDME. The NSM is a variation of a 3D search method.³⁴ The NSM partitions on subvolumes and uses the NRM (implemented using a binary min-heap) to select the subvolume in which the next event occurs. Within each subvolume, the diffusion channels and reaction channels are stored and selected using two arrays, similar to the two-partition direct method scheme from the beginning of this section. Among the favorable properties of the NSM is that organizing the events by subvolume tends to keep the updates local in memory. Partitioning by subvolume ensures that an event affects at most two subvolumes (which occurs when the event is a diffusive transfer); therefore, at most two values in the binary min-heap need to be updated on each step of the algorithm. The NSM scales as O(log₂(N_s)) for weakly coupled reaction networks, where N_s is the number of subvolumes.

Recently, Hu et al. presented a method in which the NSM search is effectively reversed.¹⁸ First, the type of event is selected, then the subvolume is chosen using a binary, 2D, or 3D search, leading to algorithmic complexity that is O(log₂(N_s)), $O\left(\sqrt{N_s}\right)$, or $O\left(\sqrt[3]{N_s}\right)$, respectively. Improved scaling can be achieved by using the NRM partitioning strategy in a direct method variant and utilizing the O(1) composition-rejection method to select the subvolume.³⁸ We note that for strongly coupled reaction networks, the within-subvolume search can be replaced with a partial-propensity method as in the partial-propensity stochastic reaction-diffusion method (PSRD) method.^15,38 Although methods with better scaling exist, the original NSM remains popular in practice and performs well on weakly coupled spatial models over a wide range of problem sizes.

IV. CONSTANT-COMPLEXITY NEXT REACTION METHOD

The NRM was derived by taking the basic idea of the FRM and utilizing a different data structure to locate the smallest event time. The abstract data type for this situation is known as a priority queue and in principle any correct priority queue implementation can be used. Here, we present an implementation of the next reaction method that uses a table data structure comprised of “bins” to store the event times for the priority queue. If the propensity sum, and therefore the expected simulation step size, can be bounded above and below, then the average number of operations to select the next reaction and update the priority queue will be bounded above, independent of M, resulting in a constant-complexity NRM.

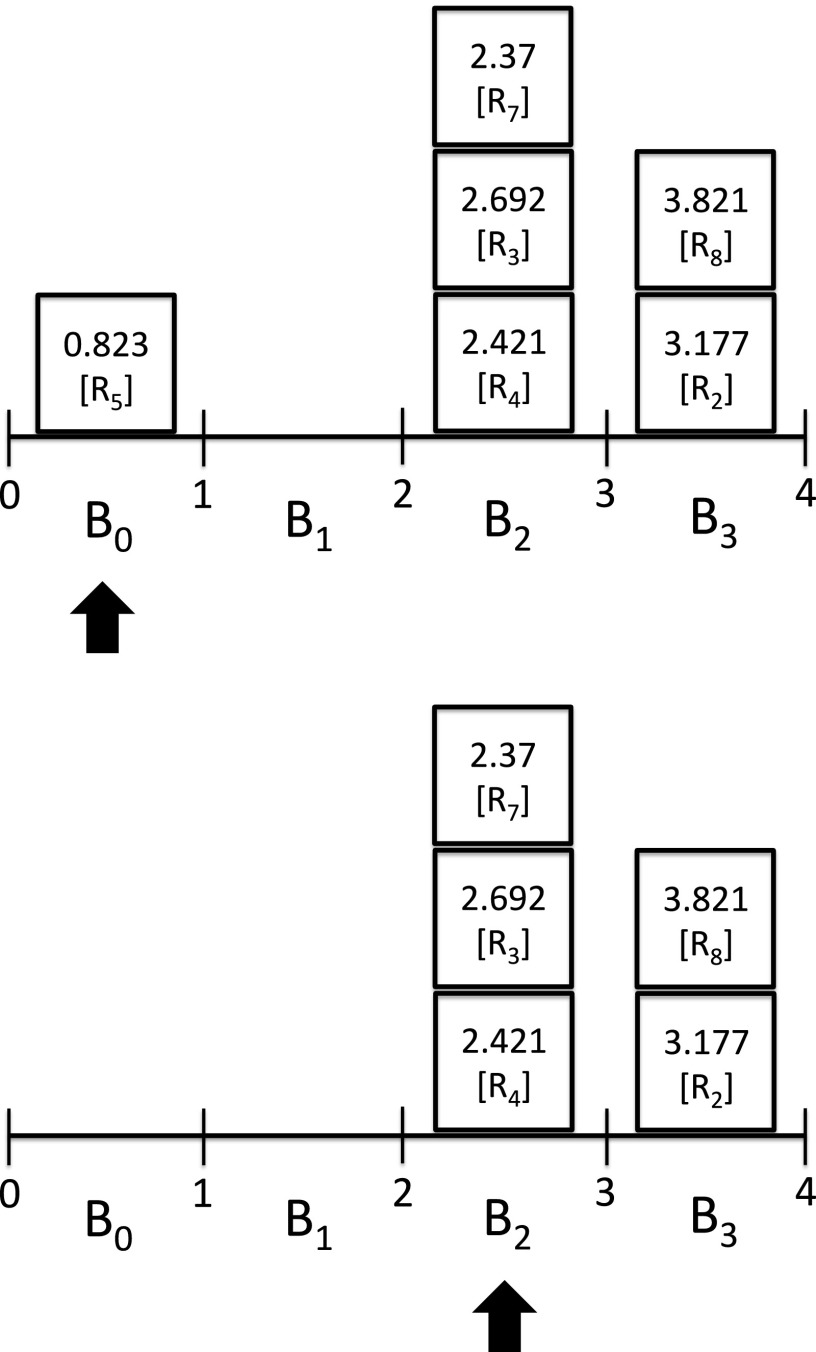
To implement a constant-complexity NRM, we partition the total simulation time interval, from the initial time t = 0 to final time t = T_f, into a table of K bins of width W. For now, we will let WK = T_f. Bin B_i will contain all event times in the range [iW, (i + 1) W). We generate putative event times for all reaction channels as in the original NRM, but insert them into the appropriate bin in the table instead of in a binary min-heap. Events that fall outside of the table range are not stored in the table. Values within a bin are stored in a 1D array, although alternative data structures could be used. To select the next reaction, we must find the smallest element. Therefore, we must find the first nonempty bin (i.e., the smallest i such that B_i is not empty). To locate the first non-empty bin, we begin by considering the bin i from which the previous event was found. If that bin is empty, we repeatedly increment i and check the ith bin until a nonempty bin is found. We then iterate over the elements within that bin to locate the smallest value (see Figure 1). The update step of the algorithm requires computing the new propensity value and event time for each affected propensity. In the worst case, the new event time will cause the event to move from one bin to another, which is an O(1) operation. Therefore, the update step will be an O(D) operation, where again D is the average number of propensity updates required per simulation step. When the reaction network is weakly coupled, D will be bounded above independent of M. Therefore, if the propensity sum is bounded above and below independent of M, the overall complexity of the algorithm is O(1) for weakly coupled networks. In Sec. IV A, we consider the optimal bin width to minimize the cost to select the next reaction.

FIG. 1.

Priority queue using binning. The next reaction in a simulation is the event with the smallest event time. Locating the smallest event time requires first locating the smallest non-empty bin, then finding the smallest element within that bin. Elements in the bins contain the event time and the event (reaction) index. Bin boundaries are integers here for simplicity. Elements within a bin are unsorted. Elements with zero propensity or with an event time beyond the last bin are not stored in the queue. In the top figure, the first bin, B₀, contains the smallest element as indicated by the arrow. After that event occurs, the search for the next nonempty bin begins at the current bin and, if empty, the bin pointer is incremented until the next nonempty bin is located, as indicated by the arrow under bin B₂ in the bottom figure. Here, the next event is “R₇.” In a real simulation, the update step may cause elements to move from one bin to another.

A. Optimal bin width

Storing the elements within a bin using a 1D array is similar to the chaining approach to collision resolution in a hash table (see Appendix B). However, unlike a hash table, targeting a particular “load factor” (the ratio of elements to bins) can lead to good or bad performance depending on the distribution of the propensities, because the key to efficiency is choosing the appropriate bin width relative to the mean simulation step size. If the bin width is too small, there will be many empty bins, and if the bin width is too large, there will be many elements within each bin.

In considering the search cost and optimal bin width, it is helpful to consider two extreme cases. For the first case, suppose one reaction channel is “fast” and the rest are slow. For the second case, suppose all reaction channels have equal rates (propensities). For simplicity of analysis we can rescale time so that the propensity sum equals one and we assume T_f ≫ 1. Then in the first case, if the propensity of the fast channel is much larger than the sum of the slow propensities (i.e., the fast propensity is approximately equal to one), we can choose the bin width to be large on the scale of the fast reaction but small on the scale of the slow reactions. For example, choosing W ≈ 6.64 (corresponding to the 99th percentile for a unit rate exponential distribution) ensures that the fast reaction will initially be in the first bin with approximately 99% probability. By assumption, there is a small probability that any of the slow reactions will also appear in the first bin. Upon executing the simulation, the fast reaction will repeatedly appear in the first bin and be selected during the next step, until it eventually appears in the second bin (with probability <1% of landing beyond the second bin). If it takes on average approximately 6.6 steps before the fast reaction appears in the second bin, then the average search depth to locate the first nonempty bin is about $1+\frac{1}{6.6}\approx 1.15$ and the average search depth within a bin is approximately one. The “total search depth” will be approximately 2.15. The slow reactions contribute a relatively small additional cost in this scenario. If, however, the slow reactions are not negligible, then the fast reaction plays a less important role in the search cost and the situation can be viewed as similar to the second case, which we consider next.

Here, we suppose that all reaction channels have equal propensities and the propensity sum equals one. In this case, the number of elements that will initially be placed in the first bin will be approximately Poisson distributed with mean W. As the simulation progresses, elements will be removed from the first bin until it is emptied and the simulation will move on to the second bin where the process repeats. If the number of events per bin is Poisson distributed with mean W, the average search depth to locate the first nonempty bin is 1/W + 1 and the average search depth within a bin is W/2 + 1. The total search depth is minimized when $W=\sqrt{2}$, leading to a total search depth of $2+\sqrt{2}\approx 3.41$. That is, it takes an average of about 3.41 operations to select the next reaction, independent of the size of the model. If the propensity sum does not equal one, this minimum total search depth will be achieved with a bin width of $W=\sqrt{2}{\left(\sum _{i=1}^M{a}_i\left(x\right)\right)}^{-1}$.

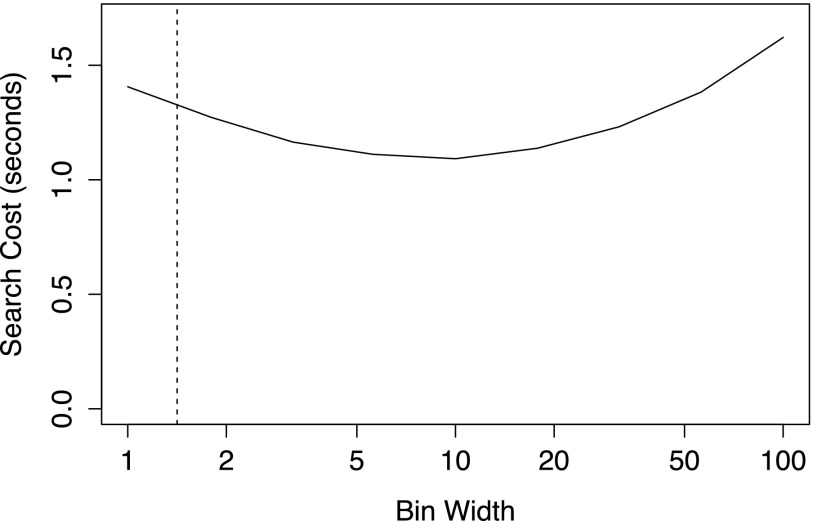
The theoretical optimal relative bin width $W=\sqrt{2}$ does not minimize the search cost in an actual implementation. Figure 2 shows that the search cost is minimized at a bin width much larger than $\sqrt{2}$. One reason for this is that accessing consecutive items within a bin is generally faster than traversing between bins because items within a bin are stored in contiguous blocks of memory. In our experience, a bin width of approximately 16 times the mean simulation time to the next event performs well across a wide range of problem sizes. Widths between 8 and 32 times the step size perform well, making the choice of 16 robust to modest changes in the propensity sum. However, it is possible that the optimal values may vary slightly depending on the system architecture. More importantly, if the propensity sum varies over many orders of magnitude during a simulation, a static bin width may be far from optimal during portions of the simulation.

FIG. 2.

Search cost for various bin widths. In this example, M = 10⁷ and every propensity =10⁻⁷ (the propensity sum equals one). The theoretical optimal bin width for minimizing the total search depth corresponding to $W=\sqrt{2}$ is shown as a dashed vertical line. In practice, the true optimal bin width is larger than $W=\sqrt{2}$. A bin width of 16 times the mean simulation step size performs well over a wide range of problem sizes. Search cost is measured in seconds for 10⁷ simulation steps.

B. Optimal number of bins and dynamic rebuilding

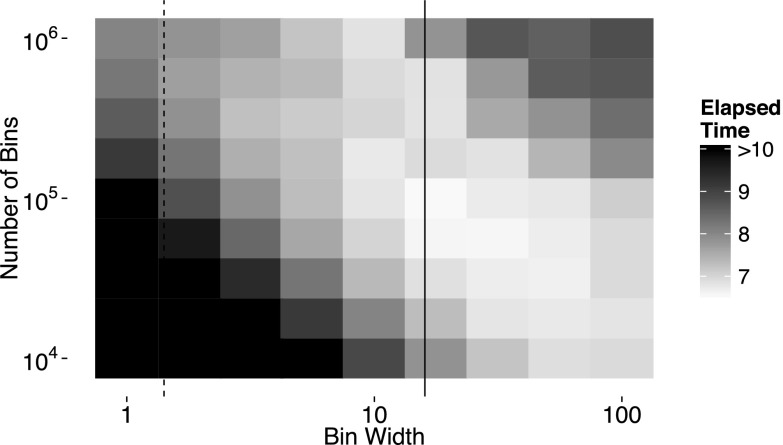
It is not necessary to choose the number of bins K such that WK ≥ T_f, where again T_f is the simulation end time. If for a chosen K, W(K − 1) > T_f, then the table is larger than necessary, which is inefficient as larger memory use leads to slower simulations. However, it is less obvious that a choice of K such that WK < T_f can lead to improved performance. When WK < T_f, the table data structure must be rebuilt when the simulation time exceeds WK. A tradeoff exists between choosing K large, which is less efficient because it uses more memory, and choosing K small, which requires more frequent rebuilding of the table data structure. The propensity and reaction time “update step” also benefit slightly from a smaller table because fewer reaction channels will be stored in the table leading to fewer operations required to move reactions from one bin to another. Figure 3 shows the elapsed time to execute simulations for varying bin widths and numbers of bins.

FIG. 3.

Simulation time for various bin widths and number of bins. In this example, M = 10⁷ and every propensity = 10⁻⁷ (the propensity sum equals one). The dashed line corresponds to the theoretical optimal bin width $W=\sqrt{2}$ that minimizes the total search depth. The solid line corresponds to W = 16, which is the target bin width used in practice. The algorithm performs well over a fairly wide range of bin widths and number of bins. As the problem size increases, the optimal number of bins increases roughly proportional to $\sqrt{M}$.

As the problem size increases, the optimal number of bins gets larger due to the increased rebuild cost. We have found that the optimal number of bins scales roughly proportional to the square root of the number of reaction channels. In practice, choosing $K=20\sqrt{M}$ leads to good performance across a wide range of problem sizes, though the optimal value may vary across different system architectures. In the case where many of the reaction channels have zero propensity, it is more efficient to use the average number of nonzero propensity channels instead of M in computing the number of bins. To facilitate rebuilding the table, we record the number of steps since the last rebuild. This allows for the bin width to be chosen adaptively based on the simulation step sizes used most recently. This adaptive bin sizing strategy partially mitigates the problem of suboptimal bin widths that may arise due to changing propensity sums. Overall, the constant-complexity NRM algorithm with the bin width determined by the propensity sum and dynamic rebuilding strategy exhibits excellent efficiency across a wide range of problem sizes as demonstrated in Sec. V.

V. NUMERICAL EXPERIMENTS

In this section, we demonstrate the performance and scaling of the constant-complexity NRM (“NRM (constant)”) relative to other popular methods. Among the other methods considered are the constant-complexity direct method (referred to as “direct (constant)” here but sometimes labeled “SSA-CR” in other work) of Slepoy et al.,¹⁰ the original NRM (“NRM (binary)”) of Gibson and Bruck,⁹ and the NSM of Elf and Ehrenberg³⁴ (“NSM (binary)”). We also consider a direct method variant that uses the NSM’s partitioning strategy and that uses the composition-rejection algorithm to select the subvolume (i.e., the PSRD’s subvolume selection procedure³⁸) and the direct method to select the event within the subvolume (“direct (CR+DM)”) see discussion in Section III B). The algorithms were implemented in C++, using code from StochKit2⁴⁹ and Cain⁵⁰ were possible. Pseudocode that outlines the constant-complexity NRM is given in Appendix A. All timing experiments were conducted on a Macbook Pro laptop with a 2.4 GHz Core i5 processor and 8 GB of memory.

A. Reaction generator test

Most exact SSA variants can be viewed as either a direct method or NRM implementation with varying data structures used to select the next reaction. The performance of the reaction generator data structure is the primary determinant of the overall algorithm performance. In this section, we test the efficiency of several reaction generator data structures, independent of the rest of the solver code, by simulating the “arrivals” of a network of M Poisson processes. We note that the NSM and other methods that partition on subvolumes are different from the methods considered here in that information about the spatial structure is built in to the algorithm. Therefore, we only consider direct method and NRM variants in this section. Additional methods, such as the NSM, are included in Sec. V B.

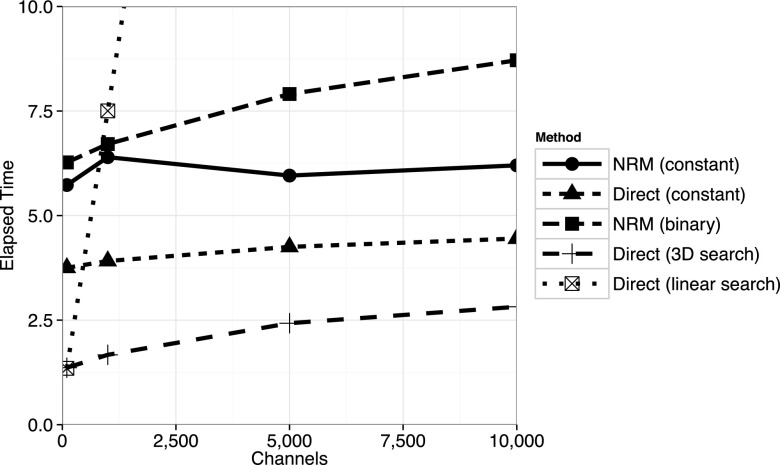
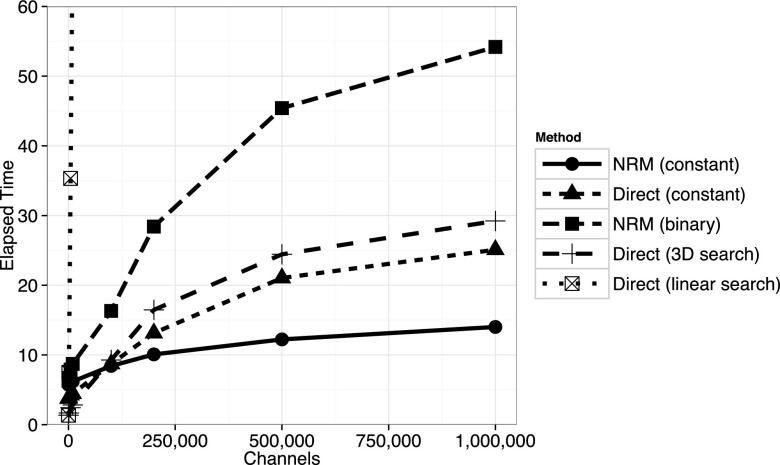
As shown in Figure 4, methods utilizing simple data structures with low overhead perform best on small to moderate sized problems. For extremely small problems, the original direct method performs best, but as the problem size increases, methods with better algorithmic complexity become advantageous. The example in Figure 4 used a random network model of unit-rate Poisson processes with a relatively high degree of connectivity (10 updates required for each step; note that the data structure updates were performed as if the propensities were changing, even though they were always set to unit rates). The original NRM, implemented with a binary min-heap, would perform better relative to the others if fewer updates were required at each step. The constant-complexity NRM exhibits small timing fluctuations due to the method being tuned for much larger problems. In Figure 5, we see that the constant-complexity direct method and constant-complexity NRM method outperform the others on large problems, with the constant NRM performing best. However, we see that the O(1) scaling is not exactly constant across large problem sizes, due to the effects of using progressively larger amounts of memory. Running the same experiments on a different system architecture could lead to differences in crossing points between methods, but the overall trends should be similar.

FIG. 4.

Scaling on small problems. Elapsed time in seconds to generate the reaction index and update the data structure 10⁷ times for various reaction generators. Each reaction channel has a unit rate propensity and a random network in which 10 updates are required was generated. For models where M < 100 or so, the original direct method with linear search performs best. As the problem size increases, the direct method with a 3D search is optimal. Not shown is the direct method with 2D search, which slightly outperforms 3D search when M < 5000. The constant-complexity NRM performance exhibits some fluctuations because the implementation was not optimized for small problems.

FIG. 5.

Scaling on large problems. Under the same conditions as Figure 4 with larger problem sizes, the constant-complexity methods outperform the others. Although the O(1) algorithms scale roughly constant across a wide range of moderate problem sizes, as the problem size becomes large, the increased memory demands lead to a slightly increasing scaling.

B. 3D spatial model

Here, we compare the constant-complexity NRM to several other methods on a model using a 3D geometry comprised of equal sized cubic subvolumes with periodic boundary conditions. The reactions and parameters are³⁴

$${\displaystyle \begin{array}{cc}\hfill E_A& \stackrel{k_1}{⟶}{E}_A+A,\hfill \\ \hfill E_B& \stackrel{k_1}{⟶}{E}_B+B,\hfill \\ \hfill E_A+B& \underset{k_d}{\overset{k_a}{\rightleftharpoons }}{E}_{A}B,\hfill \\ \hfill E_{A}B+B& \underset{k_d}{\overset{k_a}{\rightleftharpoons }}{E}_A{B}_2,\hfill \\ \hfill E_B+A& \underset{k_d}{\overset{k_a}{\rightleftharpoons }}{E}_{B}A,\hfill \\ \hfill E_{B}A+A& \underset{k_d}{\overset{k_a}{\rightleftharpoons }}{E}_B{A}_2,\hfill \\ \hfill A& \stackrel{k_4}{⟶}0̸,\hfill \\ \hfill B& \stackrel{k_4}{⟶}0̸.\hfill \end{array}}$$

$${\displaystyle k_1=150{\mathrm{s}}^{-1},k_a=46.2{\left(\mu \mathrm{M}\right)}^{-1}{\mathrm{s}}^{-1},}$$

$${\displaystyle k_d=3.82{\mathrm{s}}^{-1},k_4=6{\mathrm{s}}^{-1},}$$

$${\displaystyle D=10^{-8}{\mathrm{cm}}^2{\mathrm{s}}^{-1},}$$

$${\displaystyle \left[E_A\right]\left(0\right)=\left[E_B\right]\left(0\right)=12.3\mathrm{nM}.}$$

The diffusion constant D is equal for all species. The rate constant for all diffusive transfer events is therefore D/l², where l is the subvolume side length.³⁴ We note that the first two reaction channels are a common motif used to model processes such as protein production for an activated gene or, in this case, enzyme-catalyzed product formation in the presence of excess substrate, where the rate constant k₁ implicitly accounts for the effectively constant substrate population.

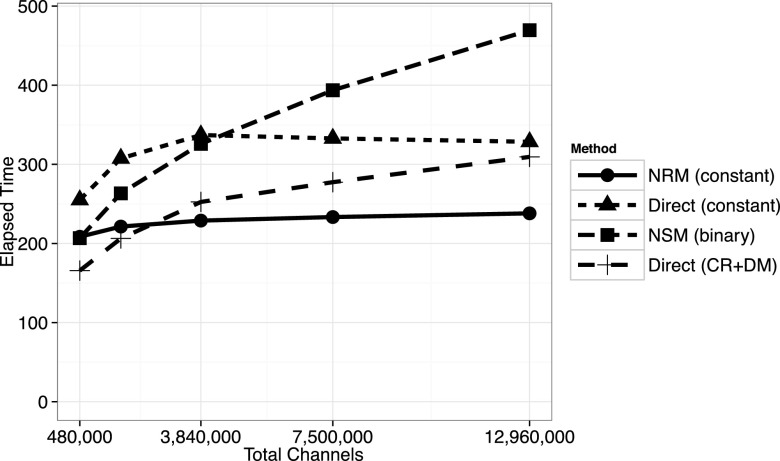
It is possible to scale up the number of transition (reaction and diffusion) channels by changing the system volume or changing the subvolume side length. First, we consider a large volume, with domain side length 12 μm and subvolume side lengths ranging from 0.6 μm to 0.2 μm, corresponding to a range of 8000–216 000 subvolumes, respectively (see Fig. N1C in the supplementary material of Elf and Ehrenberg³⁴). As shown in Figure 6, the constant-complexity NRM performs well for very large problems arising from fine mesh discretizations.

FIG. 6.

3D spatial model with system volume V = 12³ μm³. Plotted is the elapsed time in seconds to execute 10⁸ simulation steps. Below M = 480 000 channels, the NSM is more efficient than the constant-complexity methods. The direct method variant that partitions on subvolumes and uses the composition-rejection algorithm to select the subvolumes (“direct (CR+DM)”) outperforms the other methods below about M = 1 620 000 channels. At the largest problem size considered here, the constant-complexity NRM is about 20% faster than the other methods.

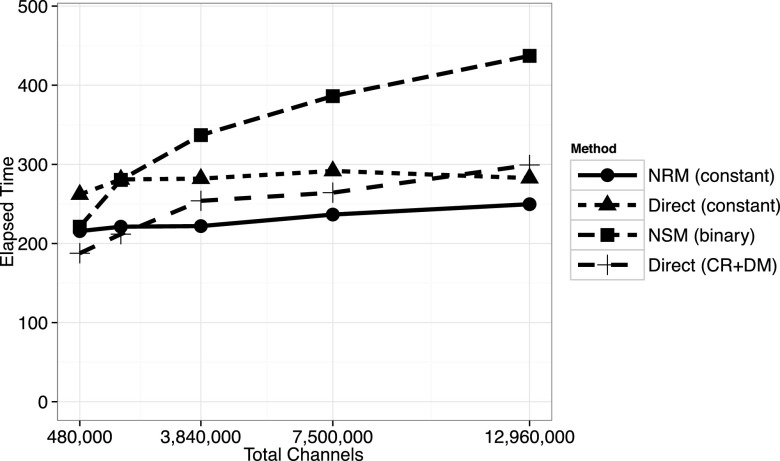
We next consider the same 3D model with system volume V = 6³ μm³. As shown in Figure 7, the constant-complexity NRM still achieves a benefit over the other methods for large problems, albeit a smaller improvement. In this example, there are approximately 28 000 molecules in the system after the initial transient. At the finest resolution in Figure 7, there are 216 000 subvolumes, of which most contain no molecules. Therefore, the majority of the reaction channels are effectively switched off, or inactive, with propensity zero. In this example at the finest resolution, typically fewer than 2 × 10⁵ of the nearly 1.3 × 10⁷ channels have nonzero propensities. The constant-complexity (composition-rejection) direct method and the NSM exclude zero propensity reactions from their reaction selection data structures, effectively reducing the problem size to the number of nonzero channels. The constant-complexity NRM does not benefit much from having many zero propensity channels.

FIG. 7.

3D spatial model with system volume V = 6³ μm³. At this smaller system volume, when the mesh is highly refined, most subvolumes are empty. Hence, many of the reaction channels have zero propensity. The constant-complexity direct method and the NSM exclude all events with propensity zero from their data structures. The constant-complexity NRM uses the number of active (nonzero propensity) reactions to determine the number of bins K to use, but this algorithm does not benefit much from having many zero-propensity reaction channels.

Changing the spatial discretization influences the rates of zeroth order and bimolecular reactions within each subvolume. The former scales proportional to the volume while the latter scales inversely with the volume. Furthermore, using a finer discretization increases the frequency of diffusion events, which means that more simulation steps are required to reach a fixed simulation end time. Changing the relative frequencies of different reaction channels influences simulation performance, though the effect is typically small for all methods. In the NSM, for example, increasing the relative frequency of diffusion events may improve performance slightly if there are fewer diffusion channels than reaction channels for each subvolume because the average “search depth” will be weighted more heavily toward the smaller diffusion event search. In any method of solution of the RDME, choosing the optimal compartment size is important. See, for example, Kang et al.³¹ and the references therein for details on how to choose the subvolume size in practice.

VI. DISCUSSION AND CONCLUSIONS

We have shown that it is possible to formulate a constant-complexity version of the NRM that is efficient for exact simulation of large weakly coupled discrete stochastic models by using event time binning. We optimized the performance by choosing the bin width based on the average propensity sum (and, therefore, step size) of the simulation. The examples in Section V demonstrate the advantages and some of the disadvantages of the constant-complexity NRM. The algorithm is not well suited for small models due to the overhead of the data structures. However, for models with a large number of active channels and time scales that do not vary too rapidly, the constant-complexity NRM is often more efficient than other popular methods.

For models with many inactive (zero propensity) channels, the performance of some SSA variants depends on the number of active channels rather than the total number of channels. The original NSM scales proportional to the logarithm of the number of subvolumes containing active channels. The constant-complexity direct and NRM methods scale O(1) in algorithmic complexity, but their performance does depend on the amount of memory used. Both constant-complexity methods have memory requirements for their reaction generator data structures that scale roughly proportional to the number of active channels. However, the table rebuild step in the constant-complexity NRM method scales as O(M). This typically constitutes a small fraction of the total computational cost (e.g., <3% for the largest problem in Figure 4). However, in the case of extremely large M and an extremely small number of active channels, the relative cost of rebuilding the table in the constant-complexity NRM becomes more significant. In an extreme case, other methods such as the constant-complexity direct method, NSM, and original NRM may be more efficient.

It may be possible to modify the constant-complexity NRM to make it less sensitive to changes in the average simulation step size and number of active channels. The current dynamic table rebuilding strategy handles this well in many cases. However, in the case of extreme changes, one could implement a “trigger” that initiates a table rebuild if changes in the time scale or number of active channels exceed a threshold. One could also envision utilizing step size data from previous realizations to guide the binning strategy, possibly even utilizing unequal bin sizes, to further improve performance. The underlying data structure presented here is amenable to use in other simulation methods that utilize a priority queue.

Performance comparisons are inherently implementation, model, and system architecture dependent. While we have attempted to present a fair comparison and the general algorithm analysis is universal, the exact simulation elapsed times may vary in different applications. The constant-complexity NRM presented here is an efficient method in many situations but inappropriate in others. As modelers develop larger and more complex models and as spatial models become more common, this algorithm provides a valuable exact option among the large family of exact and approximate stochastic simulation algorithms.

APPENDIX A: ALGORITHM PSEUDOCODE

The following pseudocode is representative of an implementation of the constant-complexity method with optimal binning.

Model: propensities, ν, dependencyGraph

DataStructure: table, lowerBound, binWidth, bins

procedure NRM(x0, tFinal)

t←0

x←x0

buildDataStructure()

while t < tFinal do

event←selectReaction()

t←event.time

x←x + ν(event.index)

updateDataStructure(event.index)

% store output as desired

end while

end procedure

procedure selectReaction

% return min event time and index

% first, locate bin index of smallest event

while table(minBin).isEmpty() do

minBin←minBin + 1

if minBin > bins then

buildDataStructure()

end if

end while

% smallest event time is in table(minBin)

% find and return smallest event time and index

return min(table(minBin))

end procedure

procedure buildDataStructure

lower Bound←t

% default 20*sqrt(ACTIVE channels)

bins←20∗sqrt(propensities.size)

% default 16*step size

% in practice, an approximation to

% sum(propensities) is used

binWidth←16/sum(propensities)

for i = 1 : propensities.size do

rate←propensities(i)

r←exponential(rate)

eventTime(i)←t + r

table.insert(i, eventTime(i))

end for

minBin←0

end procedure

procedure updateDataStructure(index)

for i in dependencyGraph(index) do

oldTime←eventTime(index)

oldBin←ComputeBinIndex(oldTime)

rate←propensities(i)

r←exponential(rate)

eventTime(i)←t + r

bin←ComputeBinIndex(eventTime(i))

if bin≠oldBin then

table(oldBin).remove(i)

table.insert(i, eventTime(i))

end if

end for

end procedure

procedure table.insert(i, time)

bin←computeBinIndex(time)

% insert into array

table(bin).insert(i, time)

end procedure

procedure ComputeBinIndex(time)

offset←time − lowerBound

range←lowerBound∗binWidth∗bins

bin←integer(offset/range∗bins)

return bin

end procedure

APPENDIX B: HASH TABLE OVERVIEW

A hash table is a data structure in which values are mapped to bins using a hash function. Since there are generally more possible values than total bins, collisions, where multiple values are mapped to the same bin, are possible. Chaining (or “closed addressing”) is a collision resolution strategy where multiple values that map to the same bin are stored in a linked list. A well-designed hash table typically has amortized constant time insertion and retrieval. Interested readers should consult an introductory computer science data structures textbook. An important difference between our data structure and a hash table implementation is that hash tables are typically designed to have a particular load factor. The load factor is defined as the number of elements stored in the table divided by the number of bins. For a hash table with a good hash function, a low load factor ensures that each bin will contain a small number of elements, on average. However, we are effectively using the reaction event times as a hash function. Whereas a good hash function distributes elements uniformly amongst the bins, the reaction times are not uniformly distributed, they are exponentially distributed. Therefore, the load factor is not a good measure of performance of our table data structure.