Abstract
Purpose:
To develop an automatic segmentation algorithm integrating imaging information from computed tomography (CT), positron emission tomography (PET), and magnetic resonance imaging (MRI) to delineate target volume in head and neck cancer radiotherapy.
Methods:
Eleven patients with unresectable disease at the tonsil or base of tongue who underwent MRI, CT, and PET/CT within two months before the start of radiotherapy or chemoradiotherapy were recruited for the study. For each patient, PET/CT and T1-weighted contrast MRI scans were first registered to the planning CT using deformable and rigid registration, respectively, to resample the PET and magnetic resonance (MR) images to the planning CT space. A binary mask was manually defined to identify the tumor area. The resampled PET and MR images, the planning CT image, and the binary mask were fed into the automatic segmentation algorithm for target delineation. The algorithm was based on a multichannel Gaussian mixture model and solved using an expectation–maximization algorithm with Markov random fields. To evaluate the algorithm, we compared the multichannel autosegmentation with an autosegmentation method using only PET images. The physician-defined gross tumor volume (GTV) was used as the “ground truth” for quantitative evaluation.
Results:
The median multichannel segmented GTV of the primary tumor was 15.7 cm3 (range, 6.6–44.3 cm3), while the PET segmented GTV was 10.2 cm3 (range, 2.8–45.1 cm3). The median physician-defined GTV was 22.1 cm3 (range, 4.2–38.4 cm3). The median difference between the multichannel segmented and physician-defined GTVs was −10.7%, not showing a statistically significant difference (p-value = 0.43). However, the median difference between the PET segmented and physician-defined GTVs was −19.2%, showing a statistically significant difference (p-value =0.0037). The median Dice similarity coefficient between the multichannel segmented and physician-defined GTVs was 0.75 (range, 0.55–0.84), and the median sensitivity and positive predictive value between them were 0.76 and 0.81, respectively.
Conclusions:
The authors developed an automated multimodality segmentation algorithm for tumor volume delineation and validated this algorithm for head and neck cancer radiotherapy. The multichannel segmented GTV agreed well with the physician-defined GTV. The authors expect that their algorithm will improve the accuracy and consistency in target definition for radiotherapy.
Keywords: multimodality segmentation, Gaussian mixture model, target definition, head and neck cancer
1. INTRODUCTION
Defining the true target volume in an accurate and consistent way remains a major challenge in radiotherapy,1–3 particularly in head and neck, for which variability in interobserver contouring of the target volume definition can be substantial.4–8 Incorrect identification of the target volume during treatment planning can lead to marginal misses9,10 that ultimately compromise local disease control, the main goal of radiotherapy. Moreover, variability among physicians in contouring the target volume makes evaluating the effectiveness of new treatments challenging and interinstitutional comparisons challenging.
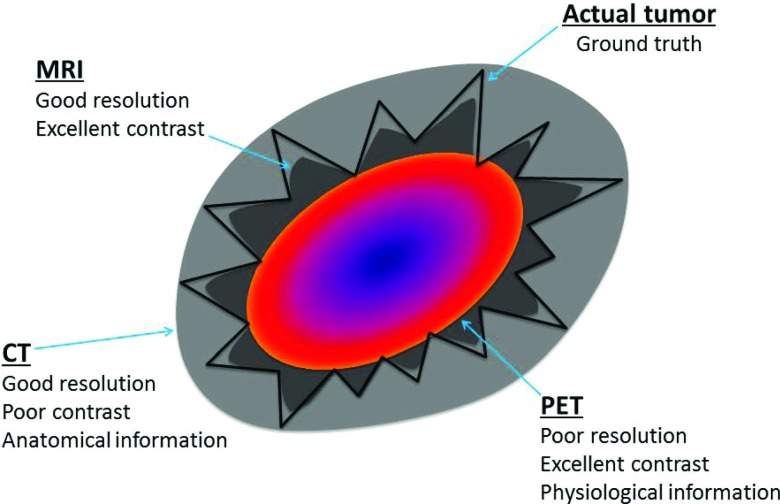
In the absence of pathological information, the best estimate of the extent of disease is derived from imaging data. Fortunately, nowadays, we often have multiple imaging modalities available to incorporate into radiotherapy treatment planning. Computed tomography (CT), which provides excellent anatomical information, has traditionally been the imaging modality of choice for contouring the tumor volume and organs at risk. Other imaging modalities have also shown promise in this area, particularly in reducing interobserver variability in contouring.5,6,11–13 For example, Riegel et al.6 showed that, compared with CT alone, positron emission tomography (PET)/CT helped physicians define gross disease more consistently while planning head and neck and lung radiotherapy. Geets et al.11 showed that magnetic resonance imaging (MRI) could identify the boundaries between different tissues in the head and neck. However, using each of these modalities individually may provide an incomplete picture of the disease extent and an inaccurate definition of the target volume. Theoretically, combining the superb resolution and soft tissue contrast of magnetic resonance (MR) image, the anatomical information of CT image, and the strong physiological signal of PET image would provide a robust estimation of the disease extent and reduce the interobserver variability in defining the target volume (Fig. 1).
FIG. 1.
A diagram highlighting that different imaging modalities provide different types of information about the tumor volume and surrounding structures.
To help physicians more accurately define tumor volume, many researchers have worked to develop automatic segmentation techniques based on different imaging modalities.14–18 For a given imaging modality, various image features, such as gradients or textures, have been used for classification to achieve automatic segmentation. However, most of these approaches have not exploited the potential capabilities of multiple modalities concurrently and thus possibly miss important information from the segmentation (e.g., lack of anatomical information on PET). Limited work19–22 has been done in automating the segmentation on multiple modalities simultaneously.
In this study, we developed an automatic segmentation algorithm that integrates MRI, CT, and PET information to define the target volume for head and neck cancer radiotherapy. While in previous work,21,22 either PET/CT or CT/MR has been used for multimodality segmentation, it is the first time to combine all three modalities to segment head and neck targets. On the other hand, previous multimodality segmentation using active contours22 or graph-cut approach21 by simply combining the objective functions from each modality into one might limit the expansion of including more modalities. Therefore, we were motivated to develop a multimodality segmentation algorithm, which formulates multichannel data into a Gaussian mixture model15 for segmentation. Our algorithm is essentially a classification approach based on the expectation–maximization (EM) algorithm.23 The algorithm also takes advantage of our experience with these modalities and knowledge about how they complement each other. We validated our algorithm on a cohort of head and neck cancer patients who received definitive radiotherapy at our institution. These patients’ physician-contoured gross tumor volumes (GTVs) served as the ground truth for validating our approach.
2. METHODS AND MATERIALS
2.A. Patient data
Twenty-two patients who had primary squamous cell carcinomas in the base of tongue (BOT) or tonsil were included in this study. These patients underwent both MRI and PET/CT for diagnosis and staging within 2 months prior to the start of chemoradiotherapy or radiotherapy alone. The primary tumor stages of these patients ranged from T1 to T4. This study has been approved by the Institutional Review Board of MD Anderson Cancer Center.
Treatment planning CT images had an in-slice resolution of 1 × 1 mm and slice spacing of 2.5 mm. For PET/CT, the CT images had a resolution of 1 × 1 × 3.3 mm, whereas the PET images had a resolution of 5.5 × 5.5 × 3.3 mm. We used T1-weighted MRI with contrast for this study because this protocol provides better tumor visibility than other MRI protocols. The MR images had a high in-slice resolution of 0.6 × 0.6 mm and a slice spacing of 6.5 mm.
2.B. Multimodality segmentation framework
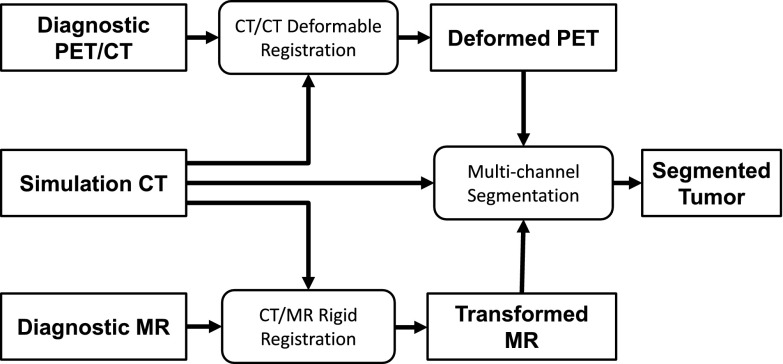
The overall framework of our proposed multimodality segmentation approach, which is the implementation of our vision described previously,24 is illustrated in Fig. 2. Briefly, a deformable image registration between the diagnostic CT and planning CT brings the PET image to the simulation CT space; a rigid registration between the diagnostic MRI and planning CT brings the MR image to the simulation CT space; and finally, a multichannel segmentation is applied to the simulation CT, PET, and MR images to segment the tumor volume. Although image registration was included, the focus of this paper was to develop the multichannel segmentation algorithm.
FIG. 2.
Overall framework of our multimodality segmentation algorithm for target volume delineation.
2.B.1. Image registration
Coregistration between PET, CT, and MR images is the prerequisite of the multichannel segmentation. To perform image registration, we used the Velocity AI software program (Velocity Medical Systems, Atlanta, GA), whose registration accuracy has been validated previously.25 The deformable registration in Velocity AI is accomplished by a modified B-spline registration algorithm,26 which was used to register the CT image of the PET/CT scan to the planning CT image. The resulting deformation vector field was then used to deform the PET image to the planning CT space. We performed a rigid registration between the MR and planning CT images in Velocity AI because the deformable registration between the diagnostic MR and simulation CT images performed inferior to the rigid registration and was not robust or accurate, which was possibly due to the large slice spacing of MR images resulting to large unreasonable distortion. In performing the MR-CT registration, we investigated three MRI sequences consistently available for all patients for registration: T1-weighted without contrast, T1-weighted with contrast, and T2-weighted. The T1-weighted MRI without contrast was found to give the best registration. The rigid registration in Velocity used the Mattes mutual information metric27 to correct a transformation of 6 degrees of freedom that included rotation and translation. This transformation was then used to resample the T1-weighted MRI with contrast to the planning CT space. Both the resampled PET and MR images had the same resolution and geometry as the planning CT image.
We quantified the registration accuracy using a registration score (RS) ranging from 1 to 5. Contours of bony anatomy and organs at risk in the vicinity of the tumor were overlaid on the registered image for evaluation. We observed that the deformable registration of PET/CT was less than 2 mm for all cases; therefore, we considered scoring the registration of planning CT and MR images only. We measured the distance of the structures (e.g., the mandible, parotids, and cord) as seen on the registered MRI to the contours from planning CT. The registration score was assigned to 1 for a distance less than 2 mm, 2 for a distance of 2–4 mm, 3 for a distance of 4–6 mm, 4 for a distance of 6–8 mm, and 5 for a distance greater than 8 mm. In addition, we estimated the maximal diameter of the GTV manually delineated by the radiation oncologist and compared it with that reported by the diagnostic radiologist. The ratio of these two diameters, termed diameter ratio (DR), was used to quantify the accuracy of the GTV manually delineated by the radiation oncologist as compared with that independently measured by the radiologist. A dataset quality index (QI) was then defined as
| (1) |
The dataset QI combines the evaluation of the registration and contouring uncertainties into a single metric. The square of DR is to bring the DR evaluation into a similar scale as the RS evaluation. We used dataset QI to exclude cases with inaccuracy mostly resulting from inaccurate registration and cases of inaccurate manual contours with inconsistency between radiation oncologists and radiologists.
2.B.2. Multichannel segmentation
The multichannel segmentation algorithm described herein is an extension of our previous work on single-channel automatic segmentation for PET (Ref. 15) and is based on the Gaussian mixture modeling of the tumor region from multichannel data. Formally, let denote the vector of the observations at voxel location i, with entries of the intensity values of PET, CT, and MR images at location i, respectively, and let i = 1, 2, …, N with N as the total number of voxels in the regions under consideration, assuming that a number of K classes exist and each class follows a Gaussian distribution. The probability of voxel location i belonging to class k ∈ {1, 2, …, K} can be characterized by the probability density function (PDF) as
| (2) |
where d is the dimension of the observation vector (d = 3 in this example) and Θk = {μk, Σk} denotes the parameters for class k, with μk as the mean and Σk as the covariance matrix for the Gaussian distribution. Thus, the PDF for xi can be written as a Gaussian mixture model as
| (3) |
where λk is the mixing proportion satisfying 0 ≤ λk ≤ 1 and , and Φ = {λ1, λ2, …, λK; Θ1, Θ2, …, ΘK} is the collection of all parameters.
Essentially, the solution to the segmentation problem is to estimate the parameters in the Gaussian mixture model. This is a typical parameter estimation problem that can be solved using the EM algorithm.23,28 Briefly, the EM algorithm iterates between an expectation step (E-step) and a maximization step (M-step). In E-step, the algorithm computes the conditional probability of the segmentation for each voxel based on the estimated parameters in the last iteration and observation. Formally, let a random variable Λi be a binary indicator vector for voxel i of dimension K, with only one component being 1 and the others being 0, and let ek denote a K-dimensional binary vector with the kth component being 1. Thus, P(Λi = ek) denotes the probability of voxel i belonging to class k. The E-step computes the conditional probability for k = 1, 2, …, K and i = 1, 2, …, N as
| (4) |
where the superscript (n) is the number of iterations. The E-step actually performs an average over the complete data {Λi, xi : i = 1, 2, …, N}, conditioned upon the incomplete data , to produce a log-likelihood function. In the M-step, the EM algorithm estimates the parameters Φ by maximizing the log-likelihood function and produces the following parameter update functions:
| (5) |
| (6) |
| (7) |
The EM algorithm continues to iterate between an E-step and a M-step until convergence or a maximum number of iterations is reached. The classification of voxel i is characterized by the converged conditional probability . Equation (4) also implies that .
2.B.3. Markov random fields (MRFs)
In the multichannel segmentation approach described above, the probability of segmentation at any given voxel is assumed to be independent of the segmentation of the neighboring or adjacent voxels. However, in a practical scenario, this assumption is generally not true and there is underlying spatial homogeneity. To account for this spatial homogeneity, we introduced a MRF model into our segmentation framework.23,29 In the MRF model, the conditional dependence of a given voxel is restricted to the voxels in a local neighborhood. Let Λ = {Λi : i = 1, 2, …, N}. The MRF model can be characterized by a Gibbs distribution30,31 with a probability mass function for Λ defined as
| (8) |
where Z is a normalization factor satisfying , and α is a preset constant. is an energy function that decreases when neighboring voxels are assigned to the same class. We use the same model as that used in previous studies,30,31 i.e.,
| (9) |
where γ is a constant that takes values from interval (0, 1), and Ni denotes the set of the neighbors of voxel i. We use a 26-neighbor system for our algorithm.
The MRF model enables us to incorporate a model of the spatial homogeneity of the segmentation into our estimation framework. However, direct MRF estimation is difficult. One common alternative approach that has low computational complexity is mean field approximation.32,33 Instead of using the conditional probability in Eq. (4) to update the parameters in Eqs. (5)–(7), we used an estimated mean value of the conditional probability at iteration n, denoted by , to update the parameters. The mean values in a vector format, , were calculated by an embedded iteration process, which was initialized with the voxelwise independent estimate using Eq. (4) and then iterated the following relation until convergence:
| (10) |
where Ni is the collection of neighboring voxels. The mean values satisfy . This MRF approximation is computationally efficient and enforces the current voxel under consideration to be consistent with its neighboring voxels in terms of the classification, thus accounting for the spatial homogeneity in the iterative segmentation estimation. In Eq. (10), the parameter, αγ, controls the level of spatial homogeneity. It is set to 0.1 based on experience.
2.B.4. Implementation remarks
Our proposed multichannel segmentation algorithm for PET, CT, and MR images was briefly summarized in Fig. 3. Below are the implementation details of this algorithm.
FIG. 3.
Summary of our PET/CT/MR multimodality segmentation algorithm.
2.B.4.a. Preprocessing.
To make our segmentation algorithm robust and efficient, we restricted the algorithm to run in a small rectangular region that encompassed the primary target and adjacent areas with moderate to high FDG avidity.
2.B.4.b. Initialization.
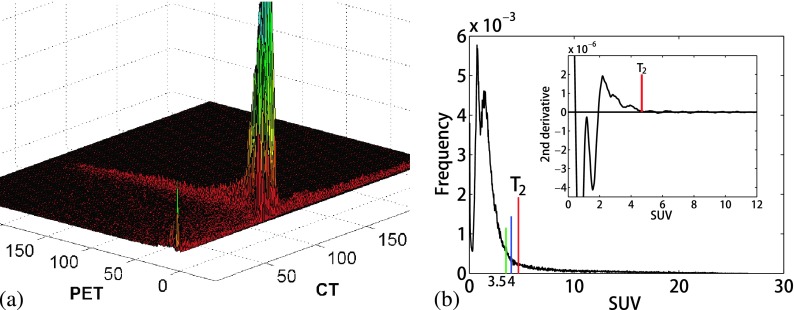
We relied on our prior knowledge of the mixture model-based segmentation from PET images15 and an analysis of joint image intensity histograms from several patients for optimal algorithm initialization. First, we performed a two-channel segmentation of the PET and CT images. The class means were initialized by examining the areas of high data concentration on joint PET-CT histograms, as shown in Fig. 4(a). We initialized 15 classes for the algorithm because we found that the segmentation result was not sensitive to the assigned class number when a sufficient number of classes were used. In addition, we assumed that the PET image had a threshold standardized uptake value (SUV) intensity that separated the tumor from background. On several image intensity histograms of SUVs, we consistently identified a point at which the second derivative of the PET image intensity histogram converged at zero at higher SUVs, as shown in the embedded plot in Fig. 4(b). We assumed that this was the point of transition (T2) on the histogram, where the numerous background voxel intensities end and the higher SUV tumor intensities begin. The algorithm automatically identified the T2 point, as shown in Fig. 4(b). This two-channel segmentation was run for five iterations to obtain an initial estimate of the class means. Next, the mean and standard deviation (SD) of the MR image intensities for the 15 classes from the first step were calculated. Each of the 15 classes was then further split into one or two additional classes by adding and/or subtracting one SD from the mean MR intensity in each class. We chose to further separate classes on the MR image because it has the richest soft tissue details of the three modalities. This process typically resulted in a total of 32 classes as input to the 3-channel run of the algorithm.
FIG. 4.
(a) An example of a joint PET-CT image intensity histogram showing areas of data concentration. (b) An example of a PET image intensity histogram with the second derivative of the high SUVs showing the threshold selection (inset).
2.B.4.c. Stopping criteria.
The algorithm was stopped if (1) the difference of conditional probability from the last iteration was less than a threshold value; (2) the sum of difference of the mixing proportion, mean, and variance from the last iteration was less than a threshold value; or (3) a maximum number of iterations was reached. In most cases, we used the first criterion, and the threshold value was set to 0.3% of its value at first iteration. This criterion shortened the time necessary to run the algorithm, as the change in classification beyond the stopping point was not significant. The maximum number of iterations was set to 180, which was enough for the algorithm to converge in most cases.
2.B.4.d. Postprocessing.
The tumor classes were determined automatically and combined together to generate the GTV in three steps. First, classes with mean PET values greater than the computed histogram threshold [the T2 point in Fig. 4(b)] were included if those classes had MRI and CT means within two SDs of their original mean and SD estimates. These original estimates were made by selecting the image intensities in the MR and CT images that corresponded to 50% of the maximum SUV threshold on PET. The selected tumor classes were combined to one class and the means and SDs of the MR and CT images for this class were calculated for the next two steps. Second, classes with a PET SUV greater than 4 were included if the corresponding CT and MRI means were within two SDs of the updated mean estimates. Third, classes with a PET SUV mean of as low as 3.5 were included if the corresponding CT and MRI means were within one SD of the updated mean estimates. After determining the tumor volume, we performed thresholding to remove regions with mean SUVs of less than 3.3 and morphological operations to remove small areas and smooth the boundary.
2.C. Quantitative evaluation
We quantitatively evaluated the accuracy of the resulting multichannel autosegmented GTV (GTVmc) and compared it with the autosegmented GTV using only PET images (GTVpet).15 The physician-defined primary GTV (GTVman) was used as the ground truth. We computed the volume difference between the GTVmc and GTVman (VDmc) and that between the GTVpet and GTVman (VDpet),
| (11) |
where x represents mc or pet. The difference between the manual and automatic segmentation was tested for statistical significance using a two-tailed, paired, t-test, evaluated at the 0.05 significance level. In addition, we used set theory operators to obtain the Dice similarity index (DSI) and sensitivity between two volumes R and T,
| (12) |
| (13) |
where TP is the true positive volume and FN is the false negative volume. We also measured two types of surface distances for the quantitative evaluation. First, a symmetric 3D mean surface distance (MSD) between two surfaces R and T was calculated as
| (14) |
Second, the Hausdorff distance (HD) that measures the maximum Euclidean distance between two surfaces R and T was calculated as
| (15) |
The DSI, MSD, and HD were calculated between GTVmc and GTVman and between GTVpet and GTVman, respectively, for comparison. Again, the difference between the manual and automatic segmentations in terms of DSI, MSD, and HD was tested for statistical significance using the aforementioned t-test. Further, we utilized the QI to compute and assess the correlation between the different parameters and the dataset quality.
3. RESULTS
Of the 22 patients selected for this study, three were excluded because they had no identifiable primary tumor or the primary tumor boundary was ill-defined. Of the remaining 19 patients, 11 who had a dataset QI of less than 2 were included in the study. The patient information and the dataset QI are shown in Table I.
TABLE I.
Patient information and dataset quality index (QI). The data of the patients included in the present study are highlighted in bold. Abbreviations: SUVmax, maximum standardized uptake value; RS, registration score; DR, diameter ratio; SCC, squamous cell carcinoma; BOT, base of tongue; GP, gingivobuccal.
| Patient | Sex | Diagnosis | T stage | SUVmax | RS | DR | QI |
|---|---|---|---|---|---|---|---|
| 1 | M | SCC Rt BOT | T1 | 13.1 | 2 | 1.06 | 1.50 |
| 2 | M | SCC BOT | T2 | 10.4 | 2 | 2.18 | 3.08 |
| 3 | F | SCC bilateral tonsil | T3/T1 | 19.8 | 2 | 1.18 | 1.67 |
| 4 | M | SCC Lt tonsil | T2 | 17.6 | 1 | 1.07 | 1.07 |
| 5 | F | SCC BOT | T2 | 7.0 | 2 | 2.17 | 3.06 |
| 6 | M | SCC BOT | T3 | 18.8 | 2 | 1.22 | 1.72 |
| 7 | M | SCC Rt BOT | T3 | 10.3 | 1 | 1.13 | 1.13 |
| 8 | M | SCC BOT | T3 | 14.0 | 3 | 1.52 | 2.62 |
| 9 | M | SCC BOT | T4 | 15.1 | 3 | 1.30 | 2.25 |
| 10 | M | SCC Lt BOT | T4 | 19.5 | 2 | 1.02 | 1.45 |
| 11 | M | SCC Rt BOT | T4 | 26.6 | 1 | 1.36 | 1.36 |
| 12 | M | SCC Rt BOT | T4 | 22.0 | 3 | 1.45 | 2.52 |
| 13 | M | SCC pharyngeal wall | T3 | 16.0 | 5 | 1.47 | 3.28 |
| 14 | M | SCC Rt tonsil/GP sulcus | T2 | 13.5 | 2 | 1.26 | 1.78 |
| 15 | M | SCC BOT | T3 | 10.8 | 2 | 1.06 | 1.50 |
| 16 | M | SCC GP sulcus | T2 | 14.5 | 2 | 1.05 | 1.48 |
| 17 | M | SCC BOT | T2 | 13.5 | 2 | 1.52 | 2.15 |
| 18 | M | SCC Lt tonsil | T2 | 14.7 | 3 | 1.07 | 1.86 |
| 19 | M | SCC Rt BOT | T2 | 15.9 | 3 | 1.35 | 2.33 |
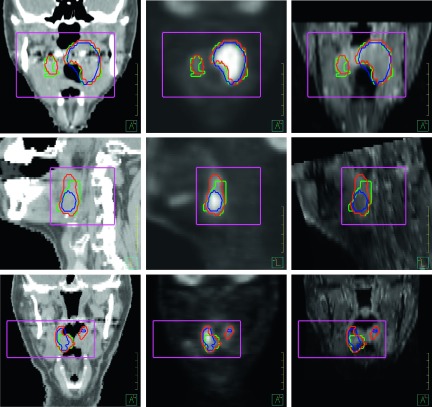
The proposed segmentation algorithm was applied to the imaging data of the 11 selected patients. A comparison of the autosegmentation and the manual segmentation for three patients showed that autosegmented contours are close to the manually segmented contours, although inconsistency exists (Fig. 5).
FIG. 5.
The multichannel segmented contours (red) and the PET-based segmented contours (blue) were compared with the physician-defined manual contours (green). The rectangular boxes manually drawn in the preprocessing step define a small region for the segmentation. Left to right: contours overlaid on CT, PET, and MR images. Top to bottom: coronal, sagittal, and coronal views of the target volumes for patients 3, 16, and 1, respectively.
The comparison of the three GTV estimates is shown in Table II. The median volume of GTVman was 22.1 cm3 (range, 4.2–38.4 cm3), the median volume of GTVmc was 15.7 cm3 (range, 6.6–44.3 cm3), and the median volume of GTVpet was 10.2 cm3 (range, 2.8–45.1 cm3). The median VDmc was −10.7% and the median VDpet was −19%, showing that the autosegmented GTVs from both segmentation approaches tended to be smaller than the manually segmented GTVs. However, the difference between GTVmc and GTVman was not statistically significant (p-value = 0.44), while the difference between GTVpet and GTVman was statistically significant (p-value = 0.0037).
TABLE II.
Comparison of the physician-defined gross tumor volume (GTVman), multichannel autosegmented tumor volume (GTVmc), and the PET-based autosegmented tumor volume (GTVpet). Abbreviation: VDmc, volume difference between the GTVman and GTVmc; VDpet, volume difference between the GTVman and GTVpet.
| Patient | GTVman (cm3) | GTVmc (cm3) | GTVpet (cm3) | VDpet (%) | VDmc (%) |
|---|---|---|---|---|---|
| 1 | 4.2 | 6.6 | 2.8 | −33.3 | 57.1 |
| 3 | 24.5 | 21.3 | 16.3 | −33.5 | −13.1 |
| 4 | 12.3 | 11.6 | 10.0 | −18.7 | −5.7 |
| 6 | 36.2 | 32.3 | 22.4 | −38.1 | −10.8 |
| 7 | 38.4 | 44.3 | 45.1 | 17.5 | 15.4 |
| 10 | 35.8 | 40.6 | 29.4 | 17.9 | 13.4 |
| 11 | 36.9 | 40.3 | 24.1 | −34.7 | 9.2 |
| 14 | 20.6 | 11.9 | 8.9 | −56.8 | −42.2 |
| 15 | 18.4 | 15.7 | 10.2 | −44.6 | −14.7 |
| 16 | 12.9 | 10.4 | 5.8 | −55.0 | −19.4 |
| 18 | 22.1 | 13.7 | 6.3 | −71.5 | −38.0 |
Table III shows the results of the quantitative evaluation of the multichannel autosegmentation and PET-based autosegmentation. The DSI, MSD, and HD were computed between the autosegmented contours and the manual contours. For the 11 patients, the multichannel autosegmentation resulted in a DSI of 0.74 ± 0.09, a MSD of 2.8 ± 1.0 mm, and a HD of 16.3 ± 7.3 mm. These values showed a reasonable volume overlap of the GTVmc and GTVman, although at some location, the surface distance was still large (as shown by HD). On the other hand, the PET-based autosegmentation resulted in a DSI of 0.65 ± 0.11, a MSD of 3.4 ± 0.8 mm, and a HD of 15.3 ± 5.6 mm. The t-test results showed that the DSI had statistically significant difference (p-value = 0.002), the MSD had a distinct trend toward significant difference (p-value = 0.070), and the HD had no statistically significant difference (p-value = 0.466) between the multichannel autosegmentation and the PET-based autosegmentation. In comparison, the largest discrepancy between autosegmented contours and the manual contours shown by the HD values was similar for both segmentation approaches, but the multichannel autosegmentation showed a better overall agreement than the PET-based autosegmentation did, as shown by the DSI and MSD values.
TABLE III.
Quantitative comparison between the multichannel autosegmentation and PET-based autosegmentation. Abbreviations: DSI, Dice similarity index; MSD, mean surface distance; HD, Hausdorff distance.
| Multichannel autosegmentation | PET-based autosegmentation | |||||
|---|---|---|---|---|---|---|
| Patient | DSI | MSD (mm) | HD (mm) | DSI | MSD (mm) | HD (mm) |
| 1 | 0.55 | 4.2 | 25.0 | 0.49 | 3.3 | 19.4 |
| 3 | 0.84 | 1.4 | 7.0 | 0.76 | 2.3 | 8.9 |
| 4 | 0.75 | 4.2 | 25.8 | 0.74 | 3.5 | 26.7 |
| 6 | 0.86 | 1.4 | 6.2 | 0.72 | 2.9 | 12.0 |
| 7 | 0.82 | 2.3 | 21.5 | 0.79 | 2.8 | 18.5 |
| 10 | 0.69 | 4.1 | 25.5 | 0.72 | 3.7 | 21.1 |
| 11 | 0.76 | 3.1 | 16.7 | 0.65 | 4.1 | 10.7 |
| 14 | 0.70 | 2.8 | 11.2 | 0.58 | 3.8 | 14.0 |
| 15 | 0.76 | 2.1 | 11.1 | 0.67 | 2.8 | 11.7 |
| 16 | 0.73 | 2.4 | 16.6 | 0.60 | 2.8 | 9.3 |
| 18 | 0.68 | 3.1 | 12.7 | 0.44 | 5.1 | 15.9 |
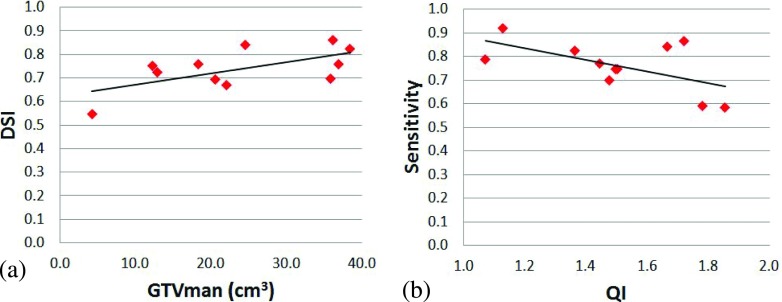
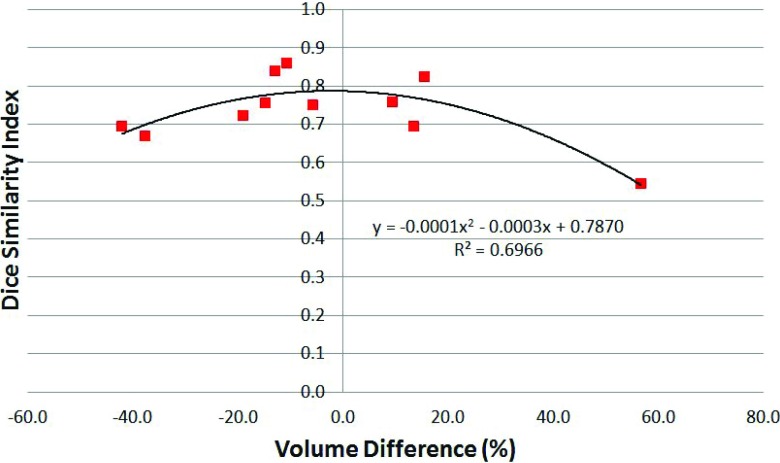
The DSI values were plotted against the GTVman, and a linear function was fitted to the data, as shown in Fig. 6(a). We found that the DSI increased with the GTVman: for each 10 cm3 increase in the GTVman, the DSI increased about 0.05. The QI (i.e., the registration and contouring quality measure) also affected the accuracy of the segmentation. We plotted the sensitivity against the QI, as shown in Fig. 6(b), and found that higher QI values (representing worse registration and/or contouring quality) resulted in lower sensitivity. Finally, to investigate the relationship between the spatial and absolute agreements between GTVman and GTVmc, we plotted the DSI against the volume difference (Fig. 7). A second order polynomial was fitted to the data and showed that the peak DSI of approximately 0.79 occurred at a volume difference of −2.3%. Thus, the best spatial agreement between the GTVman and GTVmc does not occur at a volume difference of zero.
FIG. 6.
(a) The Dice similarity index (DSI) was positively correlated with the physician-defined gross tumor volume (GTVman). (b) The sensitivity was negatively correlated with the quality index (QI).
FIG. 7.
The Dice similarity index (DSI) plotted against the volume difference between GTVmc and GTVman for all 11 patients. The second order polynomial fit to the data is also shown.
4. DISCUSSION
Utilizing multiple imaging modalities to define the true extent of disease has become common practice in radiation therapy. Each modality has its own advantages and disadvantages, and only when used synergistically, the strengths of each modality can complement each other to provide the best and most complete picture of the target volume. However, in clinical practice, the use of multiple modalities in the target definition is often suboptimal. To date, few attempts have been made to bring different modalities together into a single segmentation framework for tumor volume segmentation.21,22
In our approach, accurate image registration is a prerequisite to accurate segmentation. Misregistration causes ill-posed feature vectors to feed into the segmentation algorithm, resulting in the omission of tumor parts or the inclusion of a larger-than-expected background in the tumor segmentation. Because of this, we needed to score the registration accuracy and exclude datasets that could not be correctly registered. The misregistration occurred mostly between the simulation CT and MR images because the immobilization mask used during CT simulation can result in deformations of the anatomy from its normal resting stage. In addition, different neck flexions in two scans may cause deformation as well. These deformations could not be corrected using the rigid registration between simulation CT and MR images. In our routine clinic, we need to register the T1-weighted MRI with contrast to the planning CT for physicians to draw the GTV contours. In all the clinical cases we experienced, we have not had one satisfactory MR-to-CT deformable registration. This partially drove us to opt for rigid registration in this study. This clinical experience also directed us to use the T1-weighted sequence with contrast for multichannel segmentation. However, our investigation found that the T1-weighted sequence without contrast gave the best MR-to-CT registration; therefore, this sequence acted as an intermediate role for the registration purpose. Nevertheless, there is an imperative need to develop robust deformable registration between CT and MR images, which will be a subject of our future study.
To correctly evaluate the segmentation accuracy, we also needed to ensure that the physician-delineated contour is a reasonable representation of the gross disease as seen on imaging. In many cases, physicians have pathological information, clinical information, and/or previous experience that can influence them to contour beyond what is visible on a scan. Incorrect registration at the time of the contouring for treatment planning (not the same registration as we performed) can also affect the extent of the disease that the physician contours. For that reason, we decided to evaluate the accuracy with which the physician contoured radiographically visible disease, since comparing the algorithm-defined contour with a contour that includes anything other than what can be seen on imaging would provide an inaccurate estimation of the algorithm’s performance. At our institution, radiologists examining diagnostic scans, particularly diagnostic CT scans, estimate the maximum tumor diameter. Therefore, we compared the maximum diameter of the GTV defined by the radiation oncologist to that estimated by the diagnostic radiologist as a measure of the manual GTV delineation accuracy. We then selected GTVs whose estimations by the radiation oncologist and radiologist were consistent.
The dataset QI was devised specifically for this study to select cases for evaluation of our segmentation algorithm. It was formulated in such a way so that only datasets with a QI less than 2 would be included. It works generally fine for most cases but not perfect. One exception is the inclusion of patient 18 (Table I). The small difference between the physician diameter estimates resulted in the inclusion of patient 18 despite its relatively low registration accuracy (RS = 3). However, other 10 patients that were selected had a RS less than or equal to 2, which was what we expected.
In the postprocessing, the decision on the different thresholds for inclusion of a class in the tumor volume was based on our own experience, reports of common thresholds in the literature, and reports of typical uptake values in common normal tissues in the head and neck region. Threshold SUVs in the range from 2.5 to 3.5 are commonly reported34,35 to decide benign or malignant diseases. At the same time, normal tissue SUVs in the head and neck region can average over 3 for organs such as the palatine tonsil, base of tongue, and palatine mucosa.36 From our observation, the T2 point in Fig. 4(b) was typically greater than 4. Since we wanted to include regions with lower SUVs that had image intensities consistent with disease as observed on CT and/or MR images, lower secondary thresholds of 4, 3.5, and 3.3 were chosen. The chosen thresholds provide a compromise between including the entire tumor and minimizing the false positives. The most common false positive in our results was in the contralateral tonsil tissue (as illustrated in the bottom row of Fig. 5).
We also observed that perhaps not surprisingly, PET dominates the segmentation. PET provides a much stronger signal than CT or T1-weighted MR with contrast. On CT without contrast, boundaries are evident at anatomical landmarks such as bony anatomy and air cavities, but soft tissues are difficult to delineate; therefore, tumor surrounded by muscle has no clear boundary in most cases. In addition, even with contrast, T1-weighted MRI does not provide distinct image intensities inside the tumor, despite the fact that the tumor seems visually obvious. On MRI, tumor is easy to delineate from surrounding structures because of the heterogeneous image intensities that comprise the tumor and the clearly identifiable normal structures in the vicinity. However, tumor image intensities on MRI can be similar to other image intensities in the tumor background, which makes it difficult for an image intensity-based algorithm, such as the one developed with this work, to separate tumor from background. Therefore, the algorithm relies mostly on the PET signal to perform the segmentation and distinguish tumor from background. The role of the CT and MRI signals in the algorithm is 2-fold. In the high PET intensity region, they provide regularization, by instructing the algorithm to avoid obvious normal structures such as air and bone. For example, in the top and bottom rows of Fig. 5, the multichannel autosegmented contour avoids the air cavity in the pharynx, despite having to exclude high uptake regions as seen on PET. At intermediate PET intensities, CT and MR can be the deciding factor in determining whether to include certain regions in the segmented tumor. For example, if the PET SUV intensity in a region continuous with known tumor is moderate (around 3–5 SUVs) and both CT and MR signals in that region are similar to those in the tumor, then that moderate SUV region could be included as part of the tumor. Alternatively, if the PET intensity in a region is on the borderline and the CT or MRI signals do not show good agreement with the intensities in the tumor then this region would be excluded. For example, in the top row of Fig. 5, it can be seen that the contralateral right tonsil area is correctly included in the GTV despite having moderate SUV intensity on PET as a result of the similarity of the CT and MR intensities.
As one might expect, the moderate correlation we observed between the DSI and GTV implies that larger tumors had a larger DSI value, which indicated that DSI was affected by the volume of the structure under evaluation. At the same time, the moderately negative correlation between sensitivity and the QI suggests that the dataset QI can affect the evaluation results. We also found a strong polynomial relationship between the DSI and volume difference. The fitted polynomial function was centered in negative volume difference territory, as would be expected based on the overall underestimation of the tumor volume observed with the algorithm (median of −10.7%). This relationship also suggests that even if the absolute volume difference is 20%, the spatial agreement can still be high. Therefore, to correctly evaluate the segmentation, one may need to take into account the tumor volume, the volume difference, and the DSI simultaneously. On the other hand, a dosimetric evaluation of the difference of dose volume histogram (DVH) between the autosegmented GTV and the manual GTV may provide insight into the clinical benefits of the proposed approach. In a future study, we will evaluate how much volume difference or spatial disagreement may produce significant dosimetric impact.
Although our algorithm shows great promise in defining target volumes for head and neck radiotherapy, this study had certain limitations. Varied sources of uncertainties may contribute to the segmentation errors. A major contribution might come from the image registration inaccuracies, which are further associated with the limited image resolution in MR and PET images, CT image slice thickness, and image resampling issues, etc. The multichannel segmentation algorithm is also subject to the impact of image noise. In addition, uncertainties in manual contours might affect the evaluation. Due to the lack of ground truth (e.g., the pathological size), we chose to evaluate the segmentation using contours that were manually defined by a physician for clinical use. At our institution, all tumor contours are peer-reviewed by three or more head and neck physicians in so called planning clinics. The resulting GTVs represent “consensus” contours, which implicitly include the knowledge of multiple observers. However, as discussed earlier, factors other than imaging information may have influenced their contouring and therefore may not be limited to actual gross disease. Quantifying the manual contouring uncertainty will be a future study where the GTV segmentation can be evaluated within the context of interobserver contouring uncertainty. Furthermore, although anatomical information is implicitly taken into account by utilizing the CT scan in the segmentation, the algorithm is still essentially an image intensity based method. More explicit approaches of including anatomical information could be explored in future studies to improve the robustness of the algorithm. For this application of the algorithm, we focused on segmenting primary tumors. The variability in uptake of nodal disease with, in many cases, negative PET appearance makes it difficult to have an accurate nodal volume estimate from this method that was as discussed earlier heavily dependent on PET images. In addition, tumors with heterogeneous FDG uptake can also potentially have a compromised segmentation performance, since they can exhibit regions with low FDG uptake (e.g., necrotic areas). However, with the inclusion of contrast CT or alternative MRI sequences (such as DWI) with stronger tumor to background ratios, the algorithm could become less dependent on PET and therefore more robust when it comes to uptake inhomogeneity. Future studies will be necessary to assess the robustness of the algorithm under these conditions. Finally, imperfect registration may negatively affect the segmentation accuracy. A more sophisticated segmentation approach may involve using segmentation results to correct registration errors and iterate between registration and segmentation, similar to the single-modality approach described by Lu et al.37
5. CONCLUSIONS
We developed an automatic segmentation approach that takes into account information from multiple imaging modalities simultaneously to segment an optimal tumor volume encompassing all radiographically visible disease. The autosegmented contours compared favorably with the physician-defined contours. We expect that this algorithm will reduce interobserver contouring variability, a major source of uncertainty in head and neck cancer radiotherapy. With further validation, this algorithm could become a clinically useful tool for more consistent target definition.
ACKNOWLEDGMENTS
This work was partially supported by a sponsored research grant from Varian Medical Systems and the National Institutes of Health through Cancer Center Support Grant No. P30CA016672. The authors would like to thank Dr. Eduard Schreibmann from Emory University for discussing the registration algorithms in the Velocity Software and Joseph Munch from the Department of Scientific Publication at MD Anderson Cancer Center for reviewing the paper.
This work was partially presented at the 56th American Association of Physicists in Medicine meeting in July 2014.
REFERENCES
- 1.Njeh C. F., “Tumor delineation: The weakest link in the search for accuracy in radiotherapy,” J. Med. Phys. 33, 136–140 (2008). 10.4103/0971-6203.44472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Weiss E. and Hess C. F., “The impact of gross tumor volume (GTV) and clinical target volume (CTV) definition on the total accuracy in radiotherapy theoretical aspects and practical experiences,” Strahlenther. Onkol. 179, 21–30 (2003). 10.1007/s00066-003-0976-5 [DOI] [PubMed] [Google Scholar]
- 3.Njeh C. F., Dong L., and Orton C. G., “Point/Counterpoint. IGRT has limited clinical value due to lack of accurate tumor delineation,” Med. Phys. 40, 040601 (4pp.) (2013). 10.1118/1.4789492 [DOI] [PubMed] [Google Scholar]
- 4.Mukesh M., Benson R., Jena R., Hoole A., Roques T., Scrase C., Martin C., Whitfield G. A., Gemmill J., and Jefferies S., “Interobserver variation in clinical target volume and organs at risk segmentation in post-parotidectomy radiotherapy: Can segmentation protocols help?,” Br. J. Radiol. 85, e530–e536 (2012). 10.1259/bjr/66693547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ashamalla H., Guirgius A., Bieniek E., Rafla S., Evola A., Goswami G., Oldroyd R., Mokhtar B., and Parikh K., “The impact of positron emission tomography/computed tomography in edge delineation of gross tumor volume for head and neck cancers,” Int. J. Radiat. Oncol., Biol., Phys. 68, 388–395 (2007). 10.1016/j.ijrobp.2006.12.029 [DOI] [PubMed] [Google Scholar]
- 6.Riegel A. C., Berson A. M., Destian S., Ng T., Tena L. B., Mitnick R. J., and Wong P. S., “Variability of gross tumor volume delineation in head-and-neck cancer using CT and PET/CT fusion,” Int. J. Radiat. Oncol., Biol., Phys. 65, 726–732 (2006). 10.1016/j.ijrobp.2006.01.014 [DOI] [PubMed] [Google Scholar]
- 7.Berson A. M., Stein N. F., Riegel A. C., Destian S., Ng T., Tena L. B., Mitnick R. J., and Heiba S., “Variability of gross tumor volume delineation in head-and-neck cancer using PET/CT fusion, part II: The impact of a contouring protocol,” Med. Dosim. 34, 30–35 (2009). 10.1016/j.meddos.2007.08.003 [DOI] [PubMed] [Google Scholar]
- 8.Breen S. L., Publicover J., De Silva S., Pond G., Brock K., O’Sullivan B., Cummings B., Dawson L., Keller A., Kim J., Ringash J., Yu E., Hendler A., and Waldron J., “Intraobserver and interobserver variability in GTV delineation on FDG-PET-CT images of head and neck cancers,” Int. J. Radiat. Oncol., Biol., Phys. 68, 763–770 (2007). 10.1016/j.ijrobp.2006.12.039 [DOI] [PubMed] [Google Scholar]
- 9.Wang K., Heron D. E., Flickinger J. C., Rwigema J. C., Ferris R. L., Kubicek G. J., Ohr J. P., Quinn A. E., Ozhasoglu C., and Branstetter B. F., “A retrospective, deformable registration analysis of the impact of PET-CT planning on patterns of failure in stereotactic body radiation therapy for recurrent head and neck cancer,” Head Neck Oncol. 4, 12(10pp.) (2012). 10.1186/1758-3284-4-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chen A. M., Farwell D. G., Luu Q., Chen L. M., Vijayakumar S., and Purdy J. A., “Misses and near-misses after postoperative radiation therapy for head and neck cancer: Comparison of IMRT and non-IMRT techniques in the CT-simulation era,” Head Neck 32, 1452–1459 (2010). 10.1002/hed.21343 [DOI] [PubMed] [Google Scholar]
- 11.Geets X., Daisne J. F., Arcangeli S., Coche E., De Poel M., Duprez T., Nardella G., and Gregoire V., “Inter-observer variability in the delineation of pharyngo-laryngeal tumor, parotid glands and cervical spinal cord: Comparison between CT-scan and MRI,” Radiother. Oncol. 77, 25–31 (2005). 10.1016/j.radonc.2005.04.010 [DOI] [PubMed] [Google Scholar]
- 12.Paulino A. C., Koshy M., Howell R., Schuster D., and Davis L. W., “Comparison of CT- and FDG-PET-defined gross tumor volume in intensity-modulated radiotherapy for head-and-neck cancer,” Int. J. Radiat. Oncol., Biol., Phys. 61, 1385–1392 (2005). 10.1016/j.ijrobp.2004.08.037 [DOI] [PubMed] [Google Scholar]
- 13.Nishioka T., Shiga T., Shirato H., Tsukamoto E., Tsuchiya K., Kato T., Ohmori K., Yamazaki A., Aoyama H., Hashimoto S., Chang T. C., and Miyasaka K., “Image fusion between (18)FDG-PET and MRI/CT for radiotherapy planning of oropharyngeal and nasopharyngeal carcinomas,” Int. J. Radiat. Oncol., Biol., Phys. 53, 1051–1057 (2002). 10.1016/S0360-3016(02)02854-7 [DOI] [PubMed] [Google Scholar]
- 14.Li H., Thorstad W. L., Biehl K. J., Laforest R., Su Y., Shoghi K. I., Donnelly E. D., Low D. A., and Lu W., “A novel PET tumor delineation method based on adaptive region-growing and dual-front active contours,” Med. Phys. 35, 3711–3721 (2008). 10.1118/1.2956713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Aristophanous M., Penney B. C., Martel M. K., and Pelizzari C. A., “A Gaussian mixture model for definition of lung tumor volumes in positron emission tomography,” Med. Phys. 34, 4223–4235 (2007). 10.1118/1.2791035 [DOI] [PubMed] [Google Scholar]
- 16.Hsu C. Y., Liu C. Y., and Chen C. M., “Automatic segmentation of liver PET images,” Comput. Med. Imaging Graphics 32, 601–610 (2008). 10.1016/j.compmedimag.2008.07.001 [DOI] [PubMed] [Google Scholar]
- 17.Belhassen S. and Zaidi H., “A novel fuzzy C-means algorithm for unsupervised heterogeneous tumor quantification in PET,” Med. Phys. 37, 1309–1324 (2010). 10.1118/1.3301610 [DOI] [PubMed] [Google Scholar]
- 18.Zaidi H. and El Naqa I., “PET-guided delineation of radiation therapy treatment volumes: A survey of image segmentation techniques,” Eur. J. Nucl. Med. Mol. Imaging 37, 2165–2187 (2010). 10.1007/s00259-010-1423-3 [DOI] [PubMed] [Google Scholar]
- 19.Menze B. H., Van Leemput K., Lashkari D., Weber M. A., Ayache N., and Golland P., “A generative model for brain tumor segmentation in multi-modal images,” Med. Image Comput. Comput.-Assisted Intervention 6362, 151–159 (2010). 10.1007/978-3-642-15745-5_19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bredno J., Lehmann T. M., and Spitzer K., “A general discrete contour model in two, three, and four dimensions for topology-adaptive multichannel segmentation,” IEEE Trans. Pattern Anal. Mach. Intell. 25, 550–563 (2003). 10.1109/TPAMI.2003.1195990 [DOI] [Google Scholar]
- 21.Song Q., Bai J., Han D., Bhatia S., Sun W., Rockey W., Bayouth J. E., Buatti J. M., and Wu X., “Optimal co-segmentation of tumor in PET-CT images with context information,” IEEE Trans. Med. Imaging 32, 1685–1697 (2013). 10.1109/tmi.2013.2263388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.El Naqa I., Yang D., Apte A., Khullar D., Mutic S., Zheng J., Bradley J. D., Grigsby P., and Deasy J. O., “Concurrent multimodality image segmentation by active contours for radiotherapy treatment planning,” Med. Phys. 34, 4738–4749 (2007). 10.1118/1.2799886 [DOI] [PubMed] [Google Scholar]
- 23.Zhang Y., Brady M., and Smith S., “Segmentation of brain MR images through a hidden Markov random field model and the expectation maximization algorithm,” IEEE Trans. Med. Imaging 20, 45–57 (2001). 10.1109/42.906424 [DOI] [PubMed] [Google Scholar]
- 24.Sharp G., Fritscher K. D., Pekar V., Peroni M., Shusharina N., Veeraraghavan H., and Yang J., “Vision 20/20: Perspectives on automated image segmentation for radiotherapy,” Med. Phys. 41, 050902 (13pp.) (2014). 10.1118/1.4871620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kirby N., Chuang C., Ueda U., and Pouliot J., “The need for application-based adaptation of deformable image registration,” Med. Phys. 40, 011702(10pp.) (2013). 10.1118/1.4769114 [DOI] [PubMed] [Google Scholar]
- 26.Stapleford L. J., Lawson J. D., Perkins C., Edelman S., Davis L., McDonald M. W., Waller A., Schreibmann E., and Fox T., “Evaluation of automatic atlas-based lymph node segmentation for head-and-neck cancer,” Int. J. Radiat. Oncol., Biol., Phys. 77, 959–966 (2010). 10.1016/j.ijrobp.2009.09.023 [DOI] [PubMed] [Google Scholar]
- 27.Mattes D., Haynor D. R., Vesselle H., Lewellen T. K., and Eubank W., “PET-CT image registration in the chest using free-form deformations,” IEEE Trans. Med. Imaging 22, 120–128 (2003). 10.1109/TMI.2003.809072 [DOI] [PubMed] [Google Scholar]
- 28.Blum R. S. and Yang J., “Image fusion using the expectation–maximization algorithm and a Gaussian mixture model,” in Multisensor Surveillance Systems, edited byForesti G. L., Regazzoni C. S., and Varshney P. K. (Springer, Norwell, MA, 2003), pp. 81–95. [Google Scholar]
- 29.Warfield S. K., Zou K. H., and Wells W. M., “Simultaneous truth and performance level estimation (STAPLE): An algorithm for the validation of image segmentation,” IEEE Trans. Med. Imaging 23, 903–921 (2004). 10.1109/TMI.2004.828354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Geman S. and Geman D., “Stochastic relaxation, Gibbs distributions, and Bayesian restoration of images,” IEEE Trans. Pattern Anal. Mach. Intell. PAMI-6, 721–741 (1984). 10.1109/tpami.1984.4767596 [DOI] [PubMed] [Google Scholar]
- 31.Lakshmanan S. and Derin H., “Simultaneous parameter-estimation and segmentation of Gibbs random-fields using simulated annealing,” IEEE Trans. Pattern Anal. Mach. Intell. 11, 799–813 (1989). 10.1109/34.31443 [DOI] [Google Scholar]
- 32.Zhang J., “The mean field-theory in EM procedures for Markov random-fields,” IEEE Trans. Signal Process. 40, 2570–2583 (1992). 10.1109/78.157297 [DOI] [PubMed] [Google Scholar]
- 33.Kapur T., “Thesis model-based three-dimensional medical image segmentation,” Ph.D. dissertation,Massachusetts Institute of Technology, Cambridge, MA, 1999. [Google Scholar]
- 34.Nguyen N. C., Kaushik A., Wolverson M. K., and Osman M. M., “Is there a common SUV threshold in oncological FDG PET/CT, at least for some common indications? A retrospective study,” Acta Oncol. 50, 670–677 (2011). 10.3109/0284186X.2010.550933 [DOI] [PubMed] [Google Scholar]
- 35.Murakami R., Uozumi H., Hirai T., Nishimura R., Tomiguchi S., Oya N., Katsuragawa S., and Yamashita Y., “Impact of FDG-PET/CT imaging on nodal staging for head-and-neck squamous cell carcinoma,” Int. J. Radiat. Oncol., Biol., Phys. 68, 377–382 (2007). 10.1016/j.ijrobp.2006.12.032 [DOI] [PubMed] [Google Scholar]
- 36.Shreve P. and Townsend D. W., Clinical PET-CT in Radiology: Integrated Imaging in Oncology (Springer, New York, NY, 2011). [Google Scholar]
- 37.Lu C., Chelikani S., Papademetris X., Knisely J. P., Milosevic M. F., Chen Z., Jaffray D. A., Staib L. H., and Duncan J. S., “An integrated approach to segmentation and nonrigid registration for application in image-guided pelvic radiotherapy,” Med. Image Anal. 15, 772–785 (2011). 10.1016/j.media.2011.05.010 [DOI] [PMC free article] [PubMed] [Google Scholar]