Abstract
A method to transform the impedance measured in the ear canal, ZEC, to the plane of the eardrum, ZED, is described. The portion of the canal between the probe and eardrum was modeled as a concatenated series of conical segments, allowing for spatial variations in its cross-sectional area. A model of the middle ear (ME) and cochlea terminated the ear-canal model, which permitted estimation of ME efficiency. Acoustic measurements of ZEC were made at two probe locations in 15 normal-hearing subjects. ZEC was sensitive to measurement location, especially near frequencies of canal resonances and anti-resonances. Transforming ZEC to ZED reduced the influence of the canal, decreasing insertion-depth sensitivity of ZED between 1 and 12 kHz compared to ZEC. Absorbance, A, was less sensitive to probe placement than ZEC, but more sensitive than ZED above 5 kHz. ZED and A were similarly insensitive to probe placement between 1 and 5 kHz. The probe-placement sensitivity of ZED below 1 kHz was not reduced from that of either A or ZEC. ME efficiency had a bandpass shape with greatest efficiency between 1 and 4 kHz. Estimates of ZED and ME efficiency could extend the diagnostic capability of wideband-acoustic immittance measurements.
I. INTRODUCTION
This study introduces a technique to compensate for contributions from ear-canal geometry to the impedance measured in the canal, thereby yielding viable estimates of (1) the input impedance at the eardrum and (2) the efficiency of the middle ear (ME) in delivering sound power to the cochlea. Deriving the impedance at the eardrum is important as the effects of different ME pathologies on the resistive and reactive components of the ME impedance can be assessed. An objective estimate of sound transmission through the ME is expected to improve the diagnostic power of test-batteries using wideband-acoustic immittance measures (i.e., quantities such as power reflectance derived from the acoustic impedance or admittance measured in the ear canal over a broad frequency range).
Wideband-acoustic ear-canal measures of the input impedance measured in the ear canal (ZEC) are sensitive to the residual canal space between the plane of the measurement probe and the eardrum (e.g., Zwislocki, 1962; Rabinowitz, 1981; Voss and Allen, 1994; among others). Specifically, standing-wave cancellation between the forward- and reverse-propagating sound pressure waves produces an impedance resonance at the frequency with 1/4-wavelength approximating the residual canal's length. In addition, anti-resonance is generated at the frequency with a 1/2-wavelength approximating the residual canal's length. The sensitivity of ear-canal impedance measurements to the length of the residual canal limits the use of ZEC as a diagnostic tool for assessing ME pathology.
Measurement of ZEC is necessary, however, to derive the reflectance of the ear canal (), which is dominated by reflection from the ME. quantifies the portion of forward-propagating sound pressure reflected by the eardrum and, unlike ZEC, has magnitude that is relatively insensitive to the residual canal space (at least between 1 and 5 kHz; Voss et al., 2008; Souza et al., 2014). Therefore, is commonly converted to power reflectance , which retains only its magnitude. Absorbance (A) describes the portion of sound power absorbed by the ME and is derived from according to . Expressing in terms of A is conceptually useful as it focuses on the effect of ME pathology on sound transmission from the canal to the ME. Both A and have potential clinical value as these measures exhibit patterns specific to various pathologies including perforation of the eardrum, disarticulation of the ossicles, fixation of the stapes, fluid in the ME cavity, and dehiscence of the superior semi-circular canal (Feeney et al., 2009; Voss et al., 2012; Nakajima et al., 2012).
Despite their potential clinical utility, A and provide only an indirect assay of the impedance at the eardrum, ZED (which includes the impedance of the ME and cochlea). Specifically, although these measures describe the impedance mismatch between the canal and ME (including the cochlea), they do not contain sufficient information to derive ZED. The diagnostic power of ZED may be expected to be greater than that of either A or as ZED includes additional phase information, which is lost in the calculation of A and . As such, the effects of different pathologies on the resistive and reactive components of the ME (e.g., Zwislocki, 1962) cannot be ascertained from A or . Unfortunately, the measurement of ZED is not trivial, being complicated by the residual space between the measurement probe and eardrum.
Knowing ZED, as well as A and , may still not take full advantage of the diagnostic power of ear-canal measurements without some additional measure describing the efficiency of the ME in delivering sound to the cochlea (i.e., ME efficiency, Rosowski et al., 1986; Rosowski, 1991; Ravicz and Rosowski, 2013). For instance, in ears with large eardrum perforations can approximate normal ears despite the likely presence of a conductive hearing loss (Voss et al., 2001a; Voss et al., 2012; Mehta et al., 2006). Moreover, test batteries that combine either A or with the air-bone gap–a measure of sound transmission through the ME–have been shown to perform better than those relying on either A or alone (Shahnaz et al., 2009; Nakajima et al., 2012). An objective, non-invasive estimate of ME efficiency could improve the clinical utility of wideband-acoustic immittance measures.
In an effort to extend the diagnostic power of wideband-acoustic immittance measures, the current study describes a technique to transform the impedance measured in the ear canal to the plane of the eardrum, and estimate the efficiency of the ME. Previous work transforming ZEC to ZED have relied on a model of the residual canal space where the cross-sectional area was fixed (Rabinowitz, 1981; Voss and Allen, 1994; Margolis et al., 1999; Withnell and Gowdy, 2013). However, the area of the canal changes across its length (e.g., Stinson and Lawton, 1989; Farmer-Fedor and Rabbitt, 2002; Rasetshwane and Neely, 2011) with the effect that a portion of the forward-propagating sound pressure may be reflected before reaching the eardrum (as occurs in an acoustic horn, Rasetshwane et al., 2012). Attributing these reflections to the ME as opposed to the canal is likely to introduce error in estimates of ZED. Such reflections may also explain probe placement sensitivity observed in reflectance measurements above 5 kHz (Voss et al., 2008; Souza et al., 2014). In light of the potential for distributed reflections occurring in the ear canal, a model of the residual canal space was developed that allows for variations in the cross-sectional area.
To estimate ZED and ME efficiency, a simple model of the ME and cochlea was developed based on previous work by Zwislocki (1962), Matthews (1983), and Kringlebotn (1988). ZEC was measured at two locations in the ear canal and the resulting ZED estimates were compared to determine the effectiveness of the transform in removing ear-canal contributions to ZED. Because this is a preliminary study designed to determine the efficacy of the proposed impedance transform, measurements were restricted to subjects with normal auditory function. However, viability of this method in non-pathologic ears could justify future work that will extend the method to ears with dysfunction.
II. METHODS
A. Subjects
Fifteen subjects (ages 21 to 45; 11 females) participated in the study. Data were collected from the right ears of all subjects. All subjects had normal hearing at the octave and inter-octave frequencies between 0.25 and 8 kHz (pure-tone audiometric thresholds ≤15 dB hearing level), normal ME function (226 Hz tympanometry; peak static pressure between −100 and +50 daPa, compliance between 0.3 and 2.5 mmhos), and a normal otoscopic inspection. Subjects were compensated for participation. The experimental protocol was approved by the Boys Town National Research Hospital Institution Review Board and informed consent was obtained from all participants.
B. Sound-delivery and data-acquisition
Two-channel digital stimuli were generated at a sampling rate of 48 kHz using custom software and a personal computer running Windows XP. The two-channel electrical output from a 24-bit Layla3G (Echo Digital Audio Corporation, Santa Barbara, CA) sound card was routed to a pair of custom-designed sound sources made from 1 cm polymer-dome tweeters (TW010F1, Audax, France). The output from each sound source was directed to a sound tube of a low-noise microphone probe assembly (ER10B+, Etymotic Research, Elk Grove, IL), using plastic tubing. (The sound-delivery hardware design was developed at Northwestern University by J. H. Siegel.) The probe assembly was coupled to the measurement cavity (either an ear canal or calibration tube) using an ER10-14 foam eartip. Cavity sound pressure was transduced to an electrical voltage by the ER10B+ microphone, amplified 20 dB, and routed back to the soundcard. Recordings were stored for offline analysis.
C. Transducer calibration
The Thévenin-equivalent source characteristics (Psource and Zsource) for each channel of the probe assembly were calculated using a variation of the techniques proposed by Allen (1986) and Keefe et al. (1992). (A detailed description of the calibration procedure is provided in Scheperle et al., 2008 and Lewis et al., 2009.) Briefly, five cylindrical brass tubes (inner diameter, d = 0.8 cm) of varying lengths (L1 = 6.74, L2 = 4.5, L3 = 3.29, L4 = 2.54, L5 = 1.64 cm) served as calibration cavities. The sound pressure generated in each cavity (PC; frequency-domain) was recorded for 8 repetitions of a 1.71 ms, 60 dB sound pressure level (SPL) chirp (linear frequency sweep from 0 to 24 kHz). Each tube has an impedance (Zcav) approximated by
| (1) |
where z0 is the characteristic impedance and is the cavity reflectance for cavities (cav) 1 through 5. The characteristic impedance is calculated as where ρ = 1.18 × 10−3 g cm−3, c = 3.46 × 104 cm s−1, and . The cavity reflectance is calculated as . A lossless tube with 100% reflection at its rigid termination would be represented by setting rcav = 1 and . Instead, we fit rcav ≤ 1 to the cavity measurements and represent kcav with equations developed by Keefe (1984) that approximate lossy propagation. Allowing rcav to be less than unity yields agreement between the theoretical Zcav and measured Zcav. Zsource and Psource were calculated using an over-determined set of five linear equations with
| (2) |
and
| (3) |
An optimization procedure was used to adjust cavity lengths to minimize an (arbitrarily scaled) error function across frequency (see Scheperle et al., 2011). The calibration procedure was repeated until the error was ≤0.1. Calibrations of each channel were conducted on a daily basis with the probe at room temperature. Although the source calibration accounted for propagation losses within the calibration cavities, the modeling detailed in the subsequent sections assumes lossless propagation with the ear canal.
D. Ear-canal measurements
Ear-canal sound-pressure measurements were made for two probe-insertion depths (deep and shallow). For the deep insertion, the probe was inserted so that the lateral surface of the foam surrounding the sound tubes and microphone inlet was flush with the concha bowl at the entrance to the canal. The shallow insertion was achieved by withdrawing the probe approximately 2 mm from the initial insertion. For each insertion depth (and transducer channel), 64 repetitions (4 sets of 16 sweeps) of a 1.71 ms, 60 dB SPL chirp (linear frequency sweep from 0 to 24 kHz) were presented to the ear canal and the ear canal sound-pressure responses were recorded. Artifact rejection was performed on the sound-pressure recordings for each stimulus set to identify and discard recordings contaminated by high-level, transient noise. When necessary, additional stimulus sets were presented to achieve a total of 64 artifact-free recordings.
Recordings were synchronously averaged in the time domain to yield the mean ear-canal sound-pressure response (pEC), which was transformed to the frequency domain (PEC) via discrete fast Fourier transform. The acoustic input impedance in the ear canal (ZEC) was calculated as
| (4) |
Reflectance () was calculated as
| (5) |
where z0 was the characteristic impedance of the ear canal. z0 was initially estimated from the cross-sectional area of the calibration tubes. was subsequently transformed to the time domain using methodology outlined in Rasetshwane and Neely (2011). The estimate of z0 was then refined by determining the z0 that minimized the absolute value of the time-domain reflectance at time = 0. Time-domain reflectance is essentially the reflected-pressure response to a forward-pressure impulse at time = 0. The equivalent interpretation in the frequency domain is that reflectance is the transfer function between forward pressure and reflected pressure. Time-domain reflectance is required to be zero at time = 0 (e.g., Claerbout, 1985). Surge impedance is defined by the time-domain impedance at time = 0.
For each insertion depth and channel, the absorbance was inspected for evidence of a sound leak. Sound leaks are a result of an air leak between the coupling of the foam eartip and ear canal that is sufficiently large to provide a low-impedance pathway for sound to escape from the canal to the outside environment. Sound leaks are problematic primarily at frequencies below 1 kHz and may confound interpretation of absorbance (Rosowski et al., 2012; Groon et al., 2015). A change in the amount of sound leaking out of the ear canal between insertion depths will also introduce variability to the measured impedance and absorbance that is unrelated to ear-canal geometry. Therefore, it was necessary to identify and exclude data contaminated by sound leaks. Based on findings from Groon et al., a sound leak was defined as being present whenever the mean absorbance between 0.1 and 0.2 kHz was greater than 0.29 and/or the mean admittance phase () between 0.1 and 0.2 kHz was less than 44°. When a sound leak was identified, the probe was removed from the canal, reinserted, and measurements for both insertion depths were repeated. For one of the subjects, ear-canal measurements could not be achieved for the shallow-insertion depth without a sound leak being detected. Therefore, data from this subject were excluded from further analysis.
The sound leak criteria adopted for inclusion in the study was sensitive to air leaks with effective diameters ≳0.5 mm (0.02 in Groon et al., 2015). [The term effective is used to describe the diameters of possible air leaks in the current study because Groon et al. (2015) introduced air leaks by inserting stiff plastic tubing of varying diameters into the foam of the eartip surrounding the probe. However, air leaks in the current study would likely be non-cylindrical and occur at the coupling between the outer edge of the eartip and the canal wall. An air leak at the coupling between the eartip and canal wall is expected to result in changes in the absorbance and admittance approximating those from a cylindrical air leak with a given diameter; therefore, the former are described in terms of having an effective diameter.] Air leaks of smaller diameters can also result in sound leaking from the canal and introduce variability in the impedance and absorbance. Therefore, subjects who passed the initial screening were categorized into two groups: Data for the first group were suggestive of a sound leak resulting from an air leak with an effective diameter no larger than ∼0.5 mm, whereas data for the second group were suggestive of no air leak (mean low-frequency absorbance less than 0.2 and mean low-frequency admittance phase greater than 61°; see Fig. 8 in Groon et al., 2015). Different line styles in several of the subsequent figures will be used to identify data from the two groups.
E. Model
1. Model components
a. Ear canal. The occluded ear canal (space between the terminating edge of the probe eartip and eardrum) was represented as a concatenated sequence of seven rigid-walled, conical segments. Each section was modeled as a lossless two-port network using an ABCD transmission matrix (; Peres et al., 2003) of the form
| (6) |
where P and U are the sound pressure and volume velocity, respectively, at the entrance (in) and exit (out) of the cone. The equations governing wave propagation through a conical waveguide are provided by Beranek and Mellow (2012) and reproduced here [note that these are for lossless propagation and differ from the equations for lossy propagation provided by Keefe (1984) used for the Thévenin-source calibration],
| (7) |
| (8) |
| (9) |
and
| (10) |
where S is the cross-sectional area (cm2) at the entrance (in) and exit (out) of the conical segment, x is the distance (cm) from the entrance (in) and exit (out) of the cone to the cone's apex, is the wavenumber and l is the length of the conical segment (cm; ).
Initial estimation of Sin and Sout for each segment of the canal model was based on an estimate of the cross-sectional area of the canal (SEC), determined from the canal's characteristic impedance,
| (11) |
For each of the seven segments (n = 1:7), and were initially constrained to be identical. An optimization process was used to refine estimates of the cross-sectional areas (described below). For these estimates, Sin and Sout between adjacent segments were constrained to be identical, i.e., ; however, and were allowed to differ, thereby permitting conical segments.
The lengths of the seven conical segments (l1,l2, …, l7) were constrained to be equal to one-seventh of the total length of the occluded ear canal (lEC),
| (12) |
An initial estimate of lEC was obtained from the time-domain reflectance. The time index associated with the peak of the time-domain reflectance (tEC, s) was used to estimate the time required for the stimulus sound pressure to travel from the probe to the eardrum and back (i.e., the round-trip travel time in the ear canal). The length of the canal (lEC) was calculated as
| (13) |
tEC was included in the optimization algorithm alluded to earlier with the effect that the final estimate of lEC (as well as ln) deviated from the initial estimates just described.
The transmission matrix of each ear-canal segment () was calculated from Eqs. (7)–(10). The transmission matrix describing wave propagation across the total length of the ear canal () was calculated as the product of those matrices,
| (14) |
b. ME and cochlea. A simplified version of Kringlebotn's (1988) ME model was formulated for use in the current study. Our method of fitting model parameters to individual measurements required that fewer parameters be allocated to the ME. An initial simplification of the Kringlebotn model included elimination of the ME cavities, the eardrum inertance, and the eardrum suspension, yielding a new model with 10 parameters [as opposed to the 20 parameters in Kringlebotn (1988)]. The model parameter corresponding to the capacitance of the malleus, incus, ligaments, and tensor tympani was also eliminated (Kringlebotn's value for this parameter, Co, is ∞), yielding a new model with nine parameters. Not including the ME cavities likely compromises the resultant model's capacity to represent subject-specific ME resonances in ZED (Stepp and Voss, 2005; Voss et al., 2008; Keefe, 2015) and sensitivity to eardrum perforations (Voss et al., 2001a,b). Exclusion of the eardrum inertance and suspension may limit the model's sensitivity to pathologic-specific changes in the eardrum's mass (e.g., resulting from myringitis) and ME static pressure (Voss et al., 2012), respectively.
Three additional parameters from the Kringlebotn model were excluded from the simplified model including the resistance of the malleus, incus, ligaments and tensor tympani [Ro in Kringlebotn (1988)], the mass of the stapes, stapedial tendon, cochlea and cochlear windows [Lc in Kringlebotn (1988)], and the capacitance of the coupling between the incus and stapes [Ci in Kringlebotn (1988)]. These parameters were eliminated based on pilot work in which non-linear optimization was used to determine the best-fit values of the nine parameters by fitting the model to each subject's pressure reflectance. Across subjects, the best-fit values for Ro and Lc were frequently close to 0, whereas the inter-subject range of the best-fit values for Ci was much broader compared to the ranges of the other model parameters.
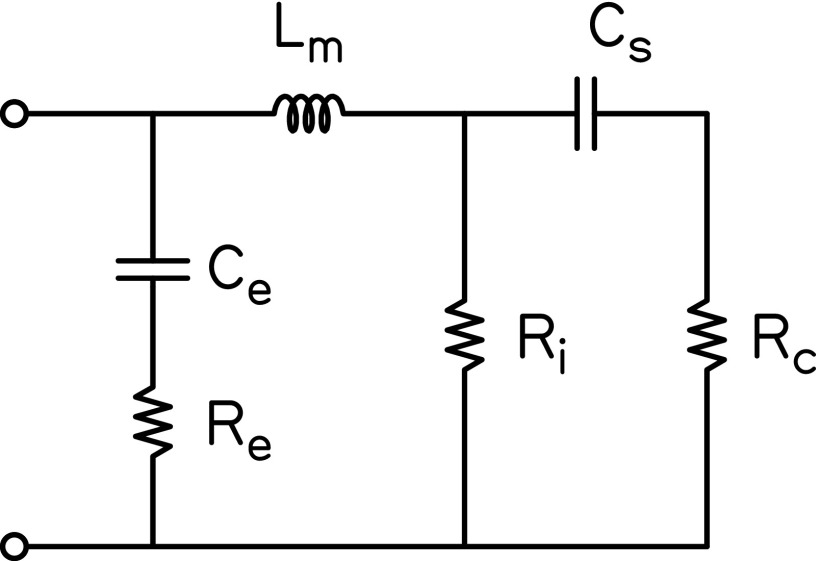
Figure 1 provides the electrical analogue of the resultant six-parameter ME model. Initial values for all components were taken from Kringlebotn (1988) and are provided in the caption of Fig. 1. The specific ME components represented in the model included the coupling between the eardrum and manubrium (Ce and Re), the malleus (and incus, Lm), the incudostapedial joint (Ri), and the stapes (Cs). The cochlea was represented as a purely resistive element, Rc. Although the model parameters are named according to specific ME structures and the cochlea, the simplicity of the model likely limits the extent to which the values of these parameters are representative of the physical characteristics of those structures. For instance, the incudostapedial joint was cast as a pure resistance even though this structure has a large compliance component (e.g., Zwislocki, 1962). Consequently, the effect of this compliance on ZED may be either absorbed by other model parameters or not captured by the current model. From the model components, the modeled impedance at the eardrum, ZED_M, was calculated as
| (15) |
where f is in Hz and || indicates a parallel combination of element impedances. The modeled reflectance () was calculated according to Eq. (5) with z0 set equal to that estimated from the measured time-domain reflectance and ZEC equal to the modeled ZEC (ZEC_M),
| (16) |
The relationship defined in Eq. (16) is derived by solving Eq. (6) in terms of the input and output impedances ( and , respectively), using linear algebra.
FIG. 1.
Electrical analogue of the ME and cochlea. Each subscript indicates a specific component of the model: e = coupling between eardrum and manubrium, m = malleus, i = incudostapedial joint, s = stapes, c = cochlea. Initial values were taken from Kringlebotn (1988): Ce = 0.38 × 10−6, Re = 120, Lm = 22 × 10−3, Ri = 6000, Cs = 0.56 × 10−6, Rc = 330.
2. Model-based impedance transforms
For each probe-insertion depth, ZEC was transformed to remove contributions from the ear canal, yielding an estimate of the input impedance at the eardrum,
| (17) |
Equation (17) is obtained by solving Eq. (16) (replacing ZEC_M with ZEC and ZED_M with ZED) for ZED. From the ME and cochlear model, ME efficiency (; Rosowski et al., 1986; Rosowski, 1991; Ravicz and Rosowski, 2013) was calculated as
| (18) |
where ZC is equal to the model parameter Rc. The expression quantifies the ratio of sound pressure at the input to the cochlea to that at the input to the ME. and are calculated by representing the ME model as an ABCD transmission matrix using parameters for shunt and series impedances,
| (19) |
| (20) |
| (21) |
| (22) |
The estimation of ME efficiency is thus derived entirely from the model parameters.
3. Determination of final model parameter values
A two-step optimization process was used to find the best-fit ear-canal and ME model parameter values for each subject. Step 1 determined the best-fit ME model parameters and step 2 determined the best-fit ear-canal model parameters. Each step used the Matlab function fminsearch to minimize an error function. To reduce the risk of fminsearch converging to a local minimum of the error function, after a single function call of fminsearch yielded a set of best-fit parameters, those same parameters served as new starting values for a subsequent call to fminsearch. This process repeated until the change across all best-fit parameters between successive calls to fminsearch was less than 1%. Across subjects, between 3 and 18 calls to fminsearch (mean = 7.71) were required to achieve the stopping criteria when determining the best-fit ME model parameters (fewer were typically required when determining the best-fit ear-canal model parameters); each call to fminsearch did converge to a minimum of the error function. Although this procedure kept fminsearch from converging to the first local minimum it encountered using the ME model parameter starting values provided in Fig. 1, given the number of parameter values, more exhaustive search methods may be required to determine the best-fit model parameters that correspond to the global minimum of the error function.
During step 1, the six ME and nine ear-canal parameters (eight for cross-sectional areas and one for canal length) were allowed to vary in order to minimize the error (ε1) function
| (23) |
where was the measured reflectance, was the modeled reflectance, was the probe-insertion depth measurement index (deep and shallow), was the total number of probe-insertion depth measurements (2), was the frequency index, and was the total number of frequencies. The frequency range extended from 0.1 to 12 kHz (0.1-kHz steps from 0.1 to 1 kHz and 1/6-octave steps from 1 to 12 kHz). The parameter values from Kringlebotn (1988) were used as the starting values for the ME parameters; starting values for ear-canal length and cross-sectional area were determined from the time-domain reflectance and surge impedance (averaged across insertion depths), respectively.
During step 2, the ME parameters determined from step 1 were held fixed and only the ear-canal parameters were allowed to vary. The ear-canal parameter values determined from step 1 were used as starting values for step 2. The error (ε2) function was defined as
| (24) |
In contrast to step 1, minimization of Eq. (24) was performed individually for each probe-insertion depth measurement, yielding a unique set of best-fit ear-canal parameters for each measurement.
The following constraints were placed on the values that the ear-canal cross-sectional areas could assume (for both steps 1 and 2):
| (25) |
The first two constraints limited the amount of change in the cross-sectional area over adjacent segments of the canal model. The third constraint specified that the canal diameter at the plane of the measurement probe must be less than 1 cm. The fourth constraint limited changes in the cross-sectional area in the immediate vicinity of the eardrum.
The only constraint placed on the ME parameters was that the peak of the modeled ME efficiency had to be between 0.5 and 4 kHz. Killion's (1978) minimum audible pressure curve demonstrates that the human auditory system is most sensitive to detection of sound around 1 kHz, on average. Assuming that detection relies, in part, on the efficiency of the ME in delivering sound to the cochlea, the peak of should also be close to 1 kHz, on average. The selected constraints of 0.5 to 4 kHz for the peak of allow for inter-subject variability.
The result of the two-step optimization process was that the two probe-insertion depth measurements for a given subject shared a common set of ME parameter values (determined from step 1) but had unique ear-canal parameter values (determined from step 2). Forcing both measures to share the same set of ME parameter values assumed that the ME did not change between insertion depths.
III. RESULTS
A. Ear-canal measurements of impedance and absorbance
Figures 2(A) and 2(B) plot ZEC magnitude and phase, respectively, measured at the deep and shallow probe-insertion depths for a single representative subject. ZEC was characterized by a series of resonances and anti-resonances, as evidenced by magnitude minima and maxima accompanied by ∼1/2-cycle phase shifts. For the subject in Figs. 2(A) and 2(B), the first resonance occurred at 3.02 kHz for the deep insertion and 3.12 kHz for the shallow insertion, corresponding to the 1/4-wavelength standing-wave null frequencies in the ear-canal sound-pressure responses. A second resonance occurred at 9.9 kHz for the deep insertion and 9.42 kHz for the shallow insertion, corresponding to the 3/4-wavelength standing-wave null frequencies in the ear-canal sound-pressure responses. An anti-resonance in the magnitude response occurred at 8.12 kHz for the deep insertion and 6.96 kHz for the shallow insertion, corresponding to the 1/2-wavelength ear-canal sound-pressure response peak.
FIG. 2.
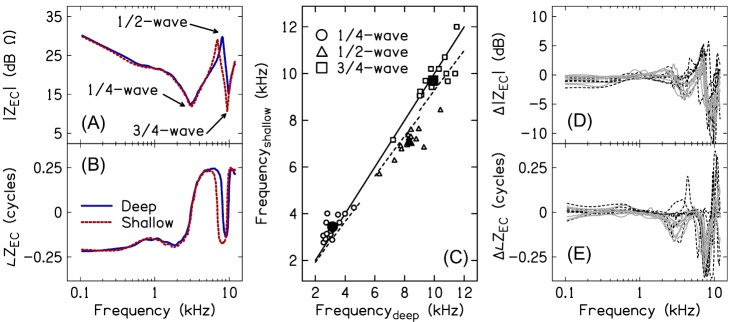
(Color online) Effect of probe insertion-depth on ZEC. (A) and (B) plot the magnitude and phase of ZEC for subject S9 measured at the deep (solid lines) and shallow (dashed lines) insertion depths. Arrows in (A) identify the 1/4-wavelength resonance, the 1/2-wavelength anti-resonance, and the 3/4-wavelength resonance. (C) plots the resonant and anti-resonant frequencies measured for the shallow insertion depth against the resonant and anti-resonant frequencies measured for the deep insertion depth, for all subjects (small open markers) and averaged across subjects (large filled markers). The solid line corresponds to a 1:1 relationship between the shallow and deep frequencies. The dashed lines illustrate the expected relationships between deep and shallow frequencies based on a 2 mm change in residual canal length between the deep and shallow insertion depths. (D) and (E) plot magnitude and phase differences, respectively, between ZEC measured at the shallow and deep insertion depths. Solid gray lines show data for the subjects with an air leak effective diameter ≤0.5 mm. Dashed black lines show data for the subjects with no air leak.
Figure 2(C) plots the ZEC resonances (1/4- and 3/4-wavelength frequencies, f1/4 and f3/4) and anti-resonances (1/2-wavelength frequency, f1/2) for all subjects and both insertion depths. The solid line describes a 1:1 relationship between the deep and shallow insertion depth resonant and anti-resonant frequencies. If the change in probe placement had no effect on the resonant and anti-resonant frequencies in ZEC, all data points would fall on the solid line. The dashed lines describe the expected relationships between the deep and shallow insertion depth resonant and anti-resonant frequencies when the distance between the probe and terminating end of a cylindrical cavity with a rigid termination is increased by 2 mm (this difference approximates the difference in the residual canal length between the deep and shallow insertions). In contrast to predictions, f1/4 either increased or remained nearly constant as the distance between the probe and eardrum increased (mean f1/4_deep = 3.15 kHz, mean f1/4_shallow = 3.44 kHz). f3/4 exhibited the expected decrease for the shallow insertion depth for several subjects; however, f3/4 remained approximately unchanged for the remaining subjects (mean f3/4_deep = 9.92 kHz, mean f3/4_shallow = 9.7 kHz). Only f1/2 decreased in all subject ears for the shallow insertion relative to the deep insertion (mean f1/2_deep = 8.3 kHz, mean f1/2_shallow = 7.11 kHz).
Figures 2(D) and 2(E) plot the subject-specific magnitude and phase differences and , respectively, between ZEC measured at the two insertion depths [ and ]. Data for the subject group without an air leak (based on low-frequency absorbance and admittance phase) is shown by the dashed black lines and data for the subject group with an air leak effective diameter ≤ ∼0.5 mm is shown by the solid gray lines. Differences associated with probe placement were largest at the 3/4-wavelength resonant frequencies and approached 15 dB in some subjects. Smaller differences occurred near the 1/2-wavelength anti-resonant frequencies (differences approaching 5 dB) and near the 1/4-wavelength resonant frequencies (differences approaching 4 dB). Differences in phase accompanied the magnitude differences and often exceeded a 1/4-cycle at the 1/2- and 3/4-wavelength frequencies. Changing probe-insertion depth had the smallest effect at frequencies below 2 kHz (differences ≤2 dB). There were no obvious differences between the two subject groups categorized by the predicted size of the air leak.
Figure 3(A) plots absorbance (10th-, 50th-, and 90th-percentiles) for deep and shallow probe insertions. A increased with frequency through approximately 1.5 kHz, before decreasing to a local minimum near 6 kHz. Above 6 kHz, a local maximum occurred at 8.6 kHz for the shallow insertion and at 9.1 kHz for the deep insertion, on average. Despite all ears having normal ME function, high inter-subject variability in A was apparent, an observation that has been reported previously (e.g., Voss et al., 2008).
FIG. 3.
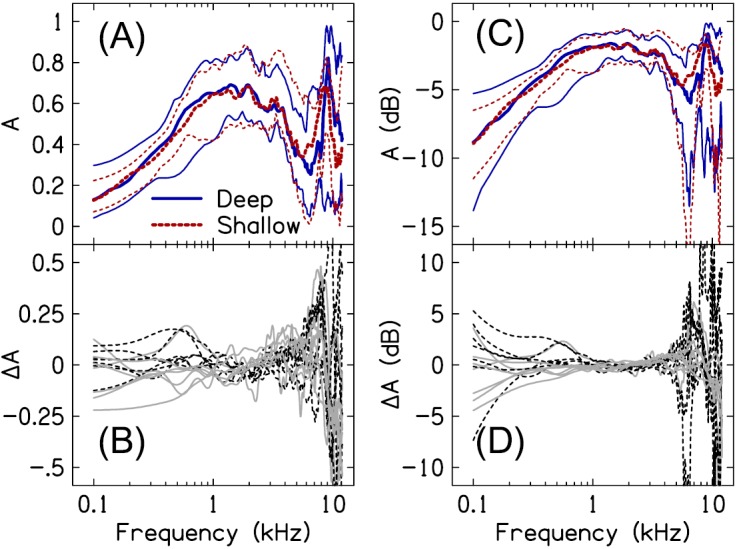
(Color online) Effect of probe-insertion depth on absorbance. (A) and (C) plot the absorbance in linear and dB units, respectively, for deep (solid lines) and shallow (dashed lines) insertion depths. The thick lines correspond to the 50th-percentile of the data; the thin lines above and below the 50th-percentile represent the 90th- and 10th-percentiles of the data, respectively. (B) and (D) plot the difference in A between probe placements in linear and dB units, respectively. Data from subjects with an air leak effective diameter ≤0.5 mm are shown by the solid gray lines; data from subjects with no air leak are shown by the dashed black lines.
Absorbance is often described as being independent of probe placement in the canal, at least for frequencies through 5 kHz (e.g., Rosowski et al., 2013). The data in Fig. 3 similarly suggest a frequency region over which absorbance is insensitive to probe placement. Figure 3(B) plots the difference in absorbance between the two insertion depths (). Between 1 and 3 kHz, the difference between measures was within ±0.05, for most subjects. As frequency decreased below 1 kHz, increased for several subjects to values around ±0.2; however, for most subjects, the difference between measures was within ±0.1. Above 5 kHz, differences between the measures frequently approached ±0.5. As shown in Fig. 3(A), differences in A above 5 kHz were primarily a result of the absorbance peak shifting to lower frequencies when the distance between the probe and eardrum increased. As was the case for ZEC, ΔA was similar between the subject group with no apparent air leak (dashed black lines) and the subject group with an air leak effective diameter ≤5 mm (solid gray lines).
Figures 3(C) and 3(D) also plot A and ; however, units are now in dB. When A is plotted in dB, 0 dB corresponds to the case where the ME absorbs all of the incident power. In the case that A is negative, the absorbed power is attenuated relative to the incident power. Expressing in dB [] is useful because it (1) provides a more direct interpretation of how insertion depth presumably affects the amount of sound power entering the ME and (2) facilitates comparison with the probe-insertion depth sensitivity of ZED. Over the frequency range spanning 1 to 5 kHz, differences in the amount of sound power absorbed by the ME between the deep- and shallow-insertion depths were often less than 2 dB. Below 1 kHz, ranged from approximately −6 to +6 dB, the difference between the two insertion-depth measures increased as frequency decreased through 0.1 kHz. Above 5 kHz, often exceeded ±10 dB around the frequencies of the absorbance peak.
B. Model-based transformation of ZEC to ZED
1. Estimation of the ear-canal diameter profile
To transform ZEC to the plane of the eardrum and remove ear-canal contributions from the impedance, it was first necessary to estimate the length of the canal and the diameter of the canal over its length. Figure 4 plots the modeled ear-canal diameter profiles for deep and shallow insertion depths, in all subjects. The average length of the occluded canal (determined from the model) was 17.4 mm for the deep probe placement and 19.1 mm for the shallow placement, an average difference of 1.7 mm between insertions. In some subjects, the estimated insertion-depth difference was either larger or smaller than the targeted 2 mm. This may have been due to imprecision in the physical manipulation of the probe by the experimenter and allowing the canal length to vary during the optimization process in order to best-fit the data. The diameter profiles in most subjects exhibited an increase in diameter across the initial 5–10 mm near the probe before reaching a plateau over the next 5–10 mm. Beyond the plateau region, diameters tapered, indicative of the tapering of the canal in the vicinity of the eardrum (Stinson and Lawton, 1989). The largest differences between the deep and shallow canal-diameter profiles occurred within the initial 5–10 mm beyond the plane of the probe. The significance of the differences between the deep and shallow diameter profiles is further addressed in Sec. IV.
FIG. 4.
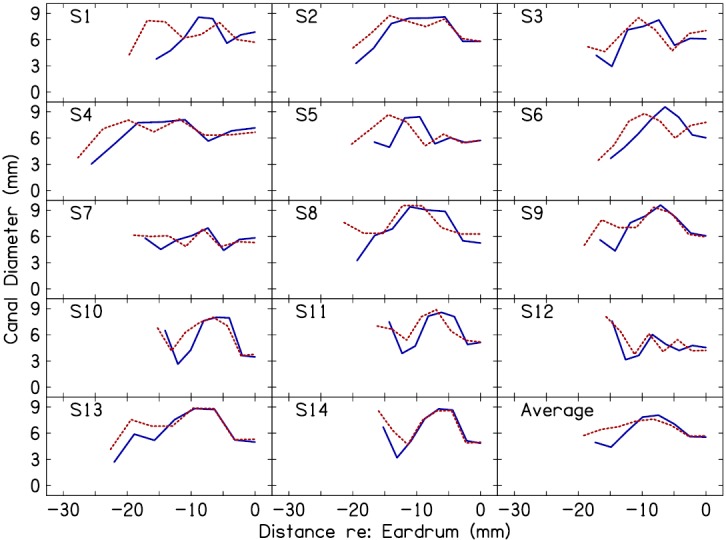
(Color online) Ear-canal diameter profiles for deep (solid lines) and shallow (dashed lines) probe insertions as estimated from the seven-conical segments of the ear-canal model. Each panel plots data for an individual subject (subject identifier in upper left corner). The panel in the lower right corner plots the mean data. Along the x axis, 0 mm corresponds to the plane of the eardrum; negative values indicate distance in the canal from the eardrum.
2. Modeled versus measured ZEC and A
Figure 5 plots measured and modeled ZEC, A, and group delay () for one representative subject. The modeled impedance [magnitude and phase, Figs. 5(A) and 5(B)] captured the dominant characteristics of the measured impedance including the 1/4- and 3/4-wavelength resonances and the 1/2-wavelength anti-resonance. More subtle variations in the measured ZEC, such as the ripples in the magnitude and phase spectra between 1 and 4 kHz, were not well represented by the modeled ZEC. Additionally, the modeled ZEC did not accurately fit the measured ZEC below 1 kHz for the shallow-insertion measure and below 0.5 kHz for the deep-insertion measure.
FIG. 5.
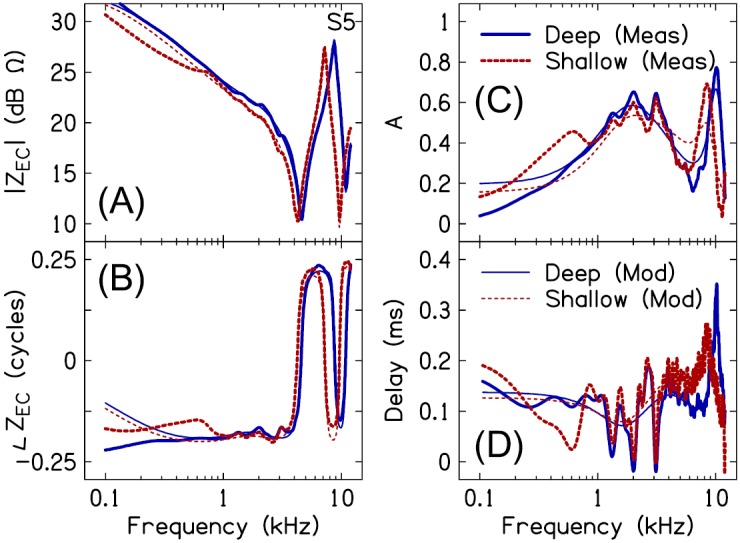
(Color online) Measured versus modeled ear-canal impedance (ZEC) magnitude (A) and phase (B), absorbance (C), and delay (D) for deep (solid lines) and shallow (dashed lines) insertion depths, for a single representative subject (S5). Measured data are indicated by the thick lines, model fits are indicated by the thin lines.
The modeled absorbance approximated a smoothed version of the measured absorbance [Fig. 5(C)]. As was the case for ZEC, the absorbance fine-structure was not well described by the modeled absorbance. The modeled absorbance did capture the high frequency changes in the measured absorbance associated with probe insertion depth. For instance, the differences in measured absorbance between the two insertion depths apparent at frequencies above 5.6 kHz were also evident in the modeled absorbance. However, the low frequency differences between Adeep and Ashallow were often not accurately fit by the model.
Similar to the modeled ZEC and A, the modeled provided a smoothed version of the measured delay [Fig. 5(D)]. The fluctuations that characterize between 1 and 4 kHz are presumably a result of reflections arising from ME structures beyond the eardrum. Note that a change in the vertical direction of is associated with either a local maximum or minimum in the absorbance. Unlike the frequencies of the maxima and minima in between 1 and 4 kHz, which did not vary with insertion depth, the frequencies of the maxima in above 6 kHz were specific to probe-insertion depth.
3. Impedance transformed to the plane of the eardrum
ZEC was transformed to the plane of the eardrum (ZED) using Eq. (17). Figure 6 plots the estimated and modeled ZED magnitude, phase, resistance, and reactance for deep and shallow insertion depths, in the same subject from Fig. 5. ZED lacked the resonances and anti-resonances that characterized ZEC. Multiple magnitude fluctuations accompanied by small phase shifts were evident in ZED, especially between 1 and 5 kHz. Presumably, these magnitude and phase fluctuations are associated with the acoustics of the ossicles and/or middle-ear air space (Stepp and Voss, 2005; Withnell and Gowdy, 2013). ZED was stiffness dominated through at least 12 kHz.
FIG. 6.
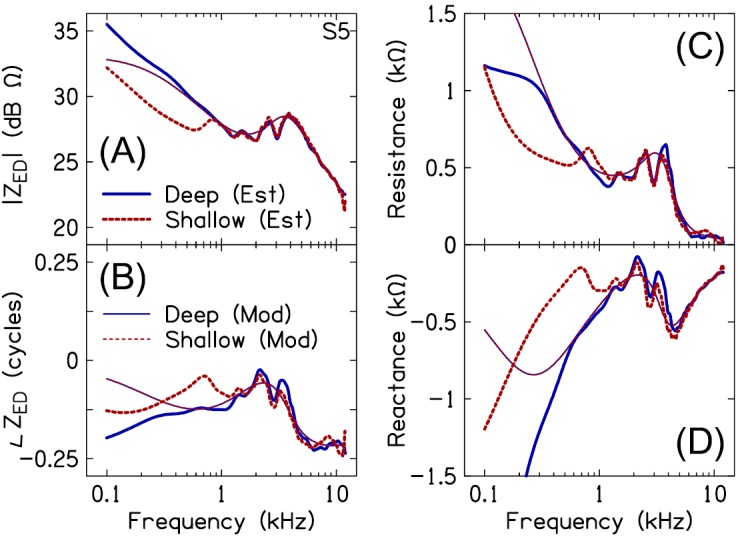
(Color online) Measured versus modeled eardrum impedance (ZED) magnitude (A), phase (B), resistance (C), and reactance (D) for deep (solid lines) and shallow (dashed lines) insertion depths, in a single subject (S5). Note that the model fits for the deep and shallow probe placements are identical.
As was the case for the modeled ZEC and absorbance, the modeled ZED approximated a smoothed version of the estimated ZED [including magnitude, phase, resistance, i.e., , and reactance, i.e., ]. In contrast to the magnitude and phase fluctuations observed in the estimated ZED between 1 and 5 kHz, the modeled ZED exhibited more gradual changes in magnitude and phase. In many subjects, the modeled resistive and reactive components of ZED did a poor job of approximating the estimated resistive and reactive components at frequencies below 1 kHz. Table I provides the best-fit ME model parameters for all subjects. These parameter values can be used in conjunction with Eq. (15) to derive the modeled ZED.
TABLE I.
The ME and cochlear model parameters (cgs units) are provided for each subject. Mean and standard deviations of the parameter values are highlighted in bold at the bottom.
| Subject | Re | Ce (× 10−6) | Lm (× 10−3) | Ri (× 103) | Cs (× 10−6) | Rc |
|---|---|---|---|---|---|---|
| 1 | 23.6 | 0.170 | 18.8 | 2.53 | 0.314 | 364 |
| 2 | 6.78 | 0.150 | 13.0 | 3.02 | 0.266 | 526 |
| 3 | 23.2 | 0.148 | 12.2 | 4.08 | 0.824 | 366 |
| 4 | 32.9 | 0.149 | 17.9 | 2.53 | 0.626 | 297 |
| 5 | 31.1 | 0.082 | 28.9 | 2.03 | 0.167 | 697 |
| 6 | 10.1 | 0.196 | 9.51 | 3.82 | 0.451 | 421 |
| 7 | 27.0 | 0.136 | 13.1 | 3.79 | 0.450 | 409 |
| 8 | 0.44 | 0.153 | 5.76 | 3.81 | 0.392 | 600 |
| 9 | 6.98 | 0.296 | 18.4 | 11.5 | 0.889 | 371 |
| 10 | 0.79 | 0.167 | 0.01 | 2.48 | 0.373 | 574 |
| 11 | 17.2 | 0.283 | 13.0 | 3.11 | 0.878 | 450 |
| 12 | 43.8 | 0.183 | 15.0 | 1.83 | 0.300 | 372 |
| 13 | 32.1 | 0.125 | 16.0 | 2.76 | 0.594 | 405 |
| 14 | 12.2 | 0.235 | 0.78 | 3.78 | 0.566 | 612 |
| Mean | 19.2 | 0.177 | 13.0 | 3.65 | 0.506 | 462 |
| S. Dev. | 13.4 | 0.059 | 7.52 | 2.38 | 0.232 | 119 |
Figure 7 plots the 10th-, 50th- and 90th-percentiles of ZED magnitude [Fig. 7(A)], phase [Fig. 7(B)], resistance [Fig. 7(C)], and reactance [Fig. 7(D)], estimated across all subjects for the deep and shallow probe-insertion depths. The two estimates of ZED were similar between 1 and 12 kHz. Figures 8(A) and 8(B) plot the magnitude and phase differences Δ|ZED| and Δ∠ZED, respectively, between ZED_shallow and ZED_deep. [ and ]. For 12 of the 14 subjects, |ZED_shallow| was within 1.5 dB of |ZED_deep| and ∠ZED_shallow was within 0.075 cycles of ∠ZED_deep between 1 and 10 kHz (for the remaining 2 subjects, the two estimates of |ZED| and ∠ZED were within 3 dB and 0.15 cycles of each other, respectively). Below 1 kHz, |ZED_shallow| was often lower than |ZED_deep| and ∠ZED_shallow less negative than ∠ZED_deep [e.g., Fig. 6(B)]. The apparent presence of an air leak (solid gray lines) did not have an obvious effect on either Δ|ZED| or Δ∠ZED.
FIG. 7.
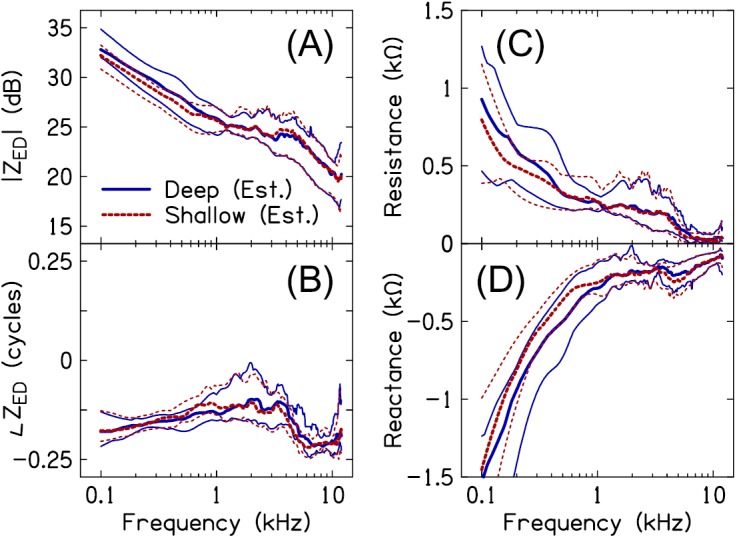
(Color online) ZED magnitude (A), phase (B) and resistive (C) and reactive (D) components for deep (solid lines) and shallow (dashed lines) insertion depths, across subjects. The thick lines in each plot represent the 50th-percentile of the data. The thin lines above and below the median indicate the 90th- and 10th-percentiles of the data, respectively.
FIG. 8.
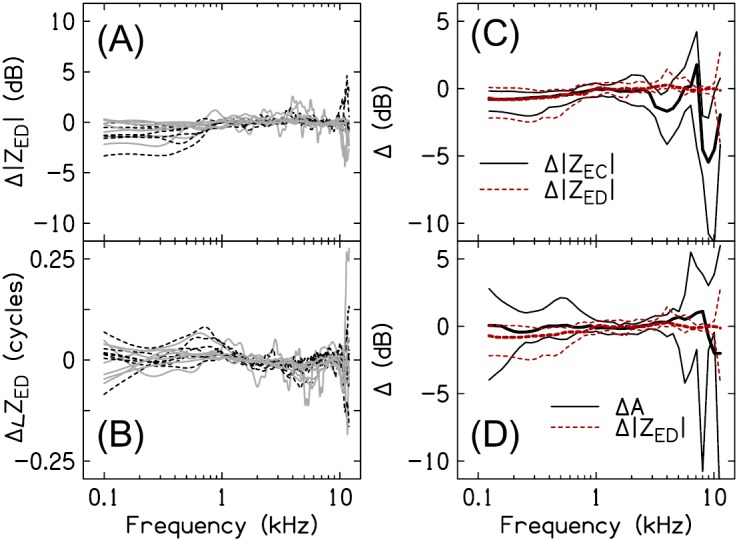
(Color online) Probe insertion-depth sensitivity of ZED. (A) and (B) plot magnitude and phase differences, respectively, between ZED estimated from the shallow and deep insertion depths. Data from subjects with an air leak of ≤0.5 mm are shown by the solid gray lines; data from subjects with no air leak are shown by the dashed black lines. (C) and (D) compare the insertion-depth sensitivity (10th-, 50th-, and 90th-percentiles) of ZED to that of ZEC and A, respectively.
Figure 8(C) compares the 10th-, 50th-, and 90th-percentiles of Δ|ZED| and Δ|ZEC|. The magnitudes of ZED and ZEC exhibited a similar dependence on probe-insertion depth across the frequency range of 0.1–1.5 kHz. ZEC was actually less sensitive to insertion depth than ZED at low frequencies, evidenced by the 10th-percentile of Δ|ZEC| being closer to 0 dB than that for Δ|ZED|. In other words, the impedance transformation did not reduce probe-insertion depth differences in the data at low frequencies; rather, for some subjects the impedance transform increased these differences (this was most apparent for subject S5 where Δ|ZED| below ∼0.7 kHz was −3.5 dB compared to −2 dB for Δ|ZEC|). Above 1.5 kHz, insertion-depth differences between the magnitudes of ZED_shallow and ZED_deep were smaller than those between ZEC_shallow and ZEC_deep. Additionally, in contrast to Δ|ZEC|, which exhibited a characteristic frequency-dependency resulting from shifts in the resonant and anti-resonant frequencies between probe placements, Δ|ZED| was approximately constant across frequency. Although not shown, the pattern of differences between Δ∠ZED and Δ∠ZEC was similar to that between Δ|ZED| and Δ|ZEC|.
Figure 8(D) compares the 10th-, 50th-, and 90th-percentiles of Δ|ZED| and ΔA. Below 1 kHz, the median of ΔA was closer to 0 dB than the median of Δ|ZED|; however, both quantities exhibited similar degrees of inter-subject variability (2–3 dB between the 10th- and 90th-percentiles) at all but the lowest frequencies (0.1 kHz) where ΔA ranged from +3 to −4 dB compared to 0 to −2 dB for Δ|ZED|. Δ|ZED| and ΔA were similar between 1 and 5 kHz and consistent with only small changes to A and ZED resulting from the measurement location in the canal. Above 5 kHz, differences between Adeep and Ashallow exceeded those between ZED_deep and ZED_shallow, consistent with the latter being less sensitive to probe-insertion depth than the former.
4. ME efficiency
An advantage of modeling the ME (terminated by the input impedance of the cochlea) is that it provides a non-invasive means to estimate the efficiency of the ME in transmitting sound power to the cochlea (). Figure 9 plots the estimated for each subject and the mean . resembled a bandpass filter. Across subjects, the peak occurred between 0.9 and 4 kHz (mean = 2.09 kHz) and ranged from 0.67 to 0.95 (mean = 0.83). For most subjects, decreased rapidly below 1 kHz and above 4 kHz such that only 10%–15% of sound power absorbed by the ME was transmitted to the cochlea at 0.1 and 10 kHz. In this regard, estimated for subjects S8, S9, and S10 was unusual: For subjects S8 and S10, remained high (between 0.75 and 0.85) through 10 kHz, whereas for subject S9, was high through 0.1 kHz.
FIG. 9.
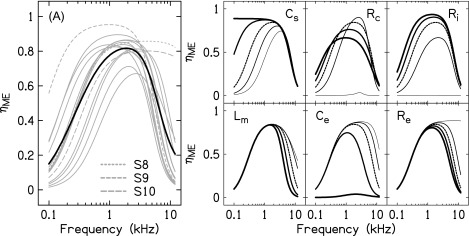
ME efficiency (. (A) plots the modeled for the different subjects (thin gray lines) and averaged across subjects (thick black line). The dashed gray lines show for subjects S8, S9, and S10 (see text). The six smaller panels plot for conditions where the mean value of a particular model parameter (indicated in the upper left or right corner of each plot) was scaled by factors of 0.0005, 0.325, 1, 2, and 3.5 (line thickness increases with scaling factor). The dashed line corresponds to a scaling factor of 1 and the calculated from the mean parameter values in Table I.
To determine which ME parameters were responsible for limiting at high and low frequencies, was re-calculated after applying a range of scaling factors to each of the mean parameter values from Table I (a single parameter was scaled for each calculation, holding all other parameter values fixed at their mean values). The range of the scaling factors was 0.0005–3.5 and was based on the largest variation in parameter values across subjects (note, however, that not all parameter values in Table I exhibited this range of variability). The six panels in Fig. 9, each of which is identified by a unique model parameter, demonstrate the effects of changing the parameter value on . Parameters Ce, Lm, and Re affected at high frequencies: Decreasing each parameter increased and shifted the peak to higher frequencies. Subjects S8 and S10 both had especially low best-fit values for the model parameters Re and Lm, which likely accounted for in these ears remaining relatively high through 10 kHz. Parameters Cs and Ri primarily affected at low frequencies: Increasing each parameter increased and shifted the peak to lower frequencies. Cs for subject S9 was similar to other subjects and presumably not responsible for the relatively high at lower frequencies; however, Ri was approximately 3× higher than the mean, and likely accounted for this subject's unusually high low-frequency . The effect of changing Rc on was more complex than for the other model parameters. For the smallest scaling factor, was close to 0. As Rc initially increased, the peak also increased but then decreased with subsequent increases in Rc. In addition to the non-monotonic changes in the peak , became less frequency-specific (i.e., the transmitted frequency range broadened) as Rc increased.
IV. DISCUSSION
A. Impedance transformed to the plane of the eardrum
A goal of the present study was to reduce the influence of the ear canal on the measured impedance, ZEC, by transforming this impedance to the plane of the eardrum, ZED. The sound-pressure distribution along the length of the residual canal, lEC, is non-uniform with the effect that ZEC exhibits a series of resonances and anti-resonances. The frequency dependence of these features on lEC results in sometimes-large differences between ZEC measured at different locations in the canal, as illustrated in Fig. 2. As such, ZEC exhibits greater dependence on the geometric properties of the canal as an acoustic waveguide than the mechanics of the ME. Using models of the ear canal and ME, the current work transformed ZEC to the plane of the eardrum, ZED. ZED was free of the resonances and anti-resonances found in ZEC and, consequently, less sensitive to changes in probe placement compared to ZEC (see Fig. 8).
In contrast to predictions from a cylindrical cavity with a rigid termination, the impedance resonance in ZEC resulting from the 1/4-wavelength standing-wave null frequency (f1/4) did not decrease in frequency as the length of the residual canal increased, but, rather, tended to increase in a number of ears [see Fig. 2(C)]. It is not clear as to why f1/4 would increase as lEC is increased; however, the compliance of the eardrum may be a contributing factor to the unexpected findings. Specifically, the compliance of the eardrum can increase the effective length of the residual canal (Voss and Allen, 1994), thereby causing the 1/4-wavelength frequency to be less sensitive to probe insertion depth.
Figure 10 compares ZED estimated from the present work (averaged across subjects and insertion depths) to data from Margolis et al. [1999—Fig. 5(B) without viscothermal losses], Voss et al. (2001b—Fig. 2 ), and O'Connor and Puria [2008—Fig. 6(A) ]. The data from Margolis et al. (1999) are from living ears, whereas the data from Voss et al. (2001b) and O'Connor and Puria (2008) are from cadaveric preparations (both of which do not include the impedance of the ME air space). Data from all studies are consistent with the ME being stiffness dominated through 1 kHz, as evidenced by |ZED| decreasing at a rate of ∼3 dB/octave (power units) and a negative ∠ZED. Other work has similarly demonstrated the stiffness dominance of ZED at low frequencies in humans and other mammals (Zwislocki, 1962; Shaw and Stinson, 1981; Rabinowitz, 1981; Lynch et al., 1994; Voss and Allen, 1994; Huang et al., 2000a; Withnell and Gowdy, 2013).
FIG. 10.
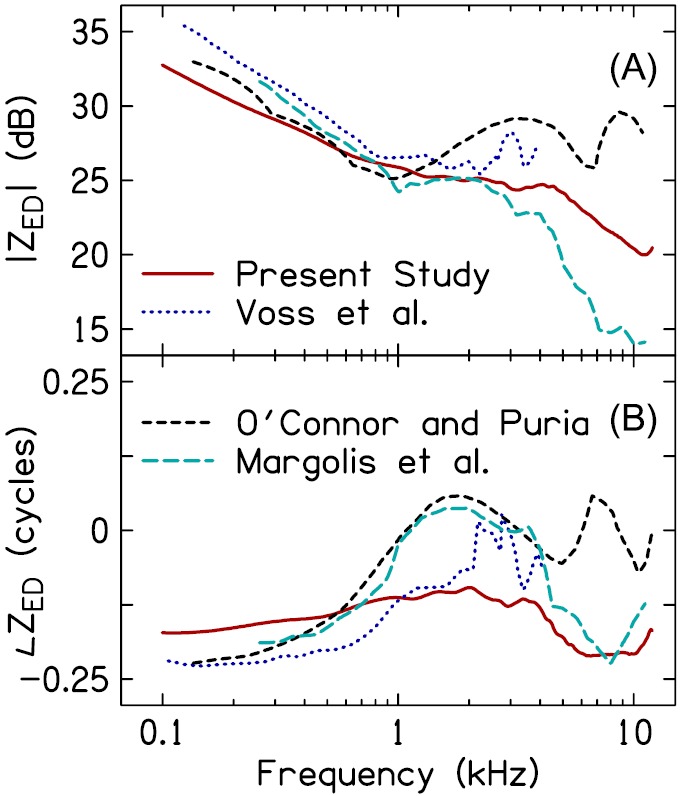
(Color online) Comparison of ZED across studies. (A) plots the magnitude of ZED and (B) plots the phase of ZED. Data for the comparison studies were taken from Voss et al. (2001b), O'Connor and Puria (2008), and Margolis et al. (1999). ZED from Voss et al. (2001b) and O'Connor and Puria (2008) was based on measures in cadaver ears whereas ZED from Margolis et al. (1999) was from living ears. The present study's estimate represents the average across subjects and probe-insertion depths.
In the frequency range between 1 and 4 kHz, differences between the data sets shown in Fig. 10 become more apparent. Data from Margolis et al. (1999), Voss et al. (2001b), and O'Connor and Puria (2008) exhibit resonances and anti-resonances, as evidenced by the minima and maxima in |ZED| and the shifts in ∠ZED between positive and negative values. The present study's mean estimate of ZED lacked both resonances and anti-resonances; however, ∠ZED did show some evidence of interplay among the mass and stiffness elements of the ME, as did data from individual subjects (e.g., S5 Fig. 6). The resonances and anti-resonances in ZED from Margolis et al. (1999) are likely due to the impedances of the ossicles (Withnell and Gowdy, 2013) and ME air space (Zwislocki, 1962; Stepp and Voss, 2005; Keefe, 2015), whereas those in ZED from Voss et al. (2001b) and O'Connor and Puria (2008) may be due primarily to the ossicles (as these studies subtracted the impedance of the ME air space from ZED). Had the ME model used in the current work been extended to include either the ME air space or additional mass-elements for the ossicles, the estimated ZED might have more closely approximated that from the other studies. However, inclusion of these features would have required additional model parameters, thereby not only increasing the complexity and time of the iteration process, but also risking non-convergence of the iteration. An extension of the present work that includes additional ME elements could be beneficial for estimating ZED in pathologic ears; for example, those with tympanic-membrane perforations (Voss et al., 2001a,b; Stepp and Voss, 2005).
Above 4 kHz, ZED from Margolis et al. (1999) is consistent with the ME becoming stiffness-dominated and agrees with the current study (also see Zwislocki, 1962 and Hudde, 1983). In contrast, data from O'Connor and Puria (2008) suggest additional interactions between mass and stiffness elements of the ME. Data from Voss et al. (2001b) was obtained only to 4 kHz and so further comparison with that study is not possible. Recent modeling work in living ears from Withnell and Gowdy (2013) suggests that ZED becomes mass-dominated above 4 kHz (also see Shaw, 1977 and Kringlebotn, 1988). Indeed, the form of ZED above 4 kHz remains an area of uncertainty and likely is influenced by the particular ME model used to derive the estimate.
B. Probe-placement sensitivity of A and ZED below 1 kHz
Transforming ZEC to the plane of the eardrum did not reduce probe-placement differences below 1 kHz. Probe-placement related differences below 1 kHz were apparent in both A and ZED. Specifically, in many subjects the magnitude of ZED was reduced, the phase lag decreased, and A increased for the shallow insertion depth, compared to the deep insertion. One potential explanation for these findings is that a greater portion of the low-frequency sound energy was absorbed by the canal walls (Huang et al., 2000b; Voss et al., 2008; Withnell and Gowdy, 2013) for the shallow probe-insertion, given the longer residual canal length. In several cadaver ears, Voss et al. (2008) observed changes in resulting from probe placement that were similar to the changes in A reported in the current work: decreased (analogous to an increase in A) as measurement distance from the eardrum increased. Modeling work by Voss et al. (2008) suggested that the decrease in below 1 kHz was due, at least in part, to sound energy absorbed by non-rigid canal walls (as occurs in infant canals, Keefe et al., 1993). Extending the current canal model to include non-rigid canal walls may provide a means to reduce the probe-placement sensitivity of ZED.
Alternatively, the changes in ZED and A between probe-insertion depths may be explained by a change in the impedance of the ME. Such a change could have arisen between probe placements if the static pressure of either the ear canal or ME changed. Although this may be possible, the lack of a hermetic seal at the coupling of the probe and ear canal, combined with the action of adjusting the probe to achieve a shallower insertion from the initial deep insertion, may have provided a sufficient air leak to preclude pressurization of the canal. Changes in ME static pressure may also be unlikely given the short time period across which measurements were made (1–2 min).
A difference in the amount of sound leaking from the canal to external environment at the coupling between the probe and ear canal could have also contributed to the probe-placement sensitivity of A and ZED. Greater sound leakage from the canal would have been more likely for the shallower insertion depth as a portion of the foam eartip often extruded from the canal, thereby increasing the likelihood and/or size of an air leak between the foam eartip and canal wall. Effects of a sound leak include increasing the absorbance and reducing the phase lag in the impedance below 1 kHz (Rosowski et al., 2012; Groon et al., 2015), both of which were evident in the shallow probe-insertion data compared to the deep probe-insertion data. Although a difference in the amount of sound leaking out from the canal between deep and shallow probe depths could explain the probe-placement related changes in A and ZED for a subset of the subjects, it likely does not explain the changes observed for all subjects. Recall that subjects were categorized into two groups based on whether their low-frequency absorbance and admittance phase were suggestive of either no air leak (black dashed lines in Figs. 2, 3, and 8) or an air leak effective diameter <0.5 mm (solid gray lines in Figs. 2, 3, and 8). Despite the former group lacking an air leak, probe-placement changes in A and ZED were similar to those observed in the group with a small air leak. Consequently, some other factor is likely responsible for the probe-placement changes in the group of subjects where sound leakage from the canal was unlikely due to the apparent absence of an air leak.
Regardless of the origin of the probe-placement sensitivity in ZED and A below 1 kHz, the findings suggest that it is overly simplistic to assume that the canal behaves as a lossless waveguide. To minimize losses (and variability) associated with either an acoustic leak or non-rigid canal walls, achieving a deep placement of the probe, preferably within the bony-portion of the canal (as noted by Withnell and Gowdy, 2013) seems advisable. Static pressurization of the canal may also be advantageous, as this necessitates a hermetic seal between the probe and canal.
C. The contribution of spatial variations in the cross-sectional area of the ear-canal model to A and ZED
1. Varying vs uniform canal diameter
The sensitivity of A and above 5 kHz to the measurement location of the probe in the canal has been documented previously (Farmer-Fedor and Rabbitt, 2002; Voss et al., 2008; Souza et al., 2014). Above 5 kHz, the primary difference in A between deep and shallow insertions was in the frequency of a local maximum. Specifically, the absorbance peak often shifted to a lower frequency as the distance from the eardrum increased (see Figs. 3 and 5). data from Souza et al. (2014) also exhibited this trend (although for a local minimum instead of a maximum). This feature of A and appears to depend, in part, on the acoustics of the residual canal space.
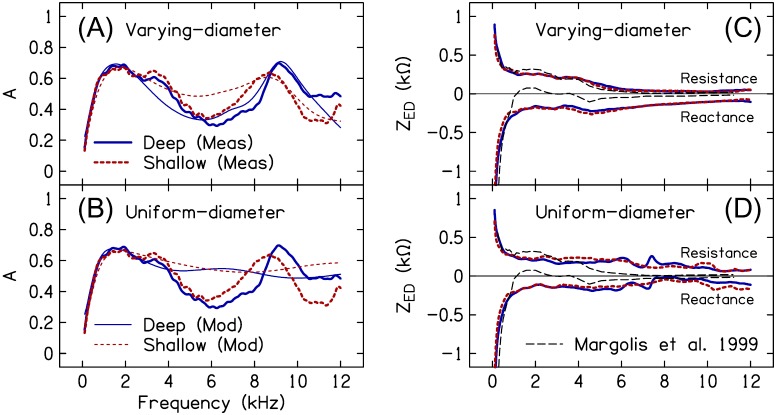
Figure 11 plots the measured and modeled Adeep and Ashallow (averaged across subjects) using the varying-diameter ear-canal model described previously [Fig. 11(A)] and an ear-canal model with a uniform diameter over its length [Fig. 11(B)]. The ME and ear-canal model parameters for the uniform-diameter model were determined using the same two-step optimization procedure outlined in Sec. II E 3 with the exception that there were only two ear-canal model parameters (canal length and area). Through 3 kHz, both models yielded similar estimates of A for both insertion depths. Between 3 and 4 kHz, the uniform-diameter canal model more closely approximated the measured data, compared to the varying-diameter model. Above 4 kHz, only the varying-diameter canal model approximated the features of the measured A, namely, the peaks at 8.7 and 9.2 kHz in the shallow and deep measures, respectively.
FIG. 11.
(Color online) Modeled and measured A and estimated ZED resistance and reactance in a varying-diameter canal model compared to a uniform-diameter canal model. Mean modeled (thin lines) and measured (thick lines) A for the deep (solid lines) and shallow (dashed lines) probe placements are shown in (A) for the varying-diameter canal model and in (B) for the uniform-diameter canal model. Mean estimated ZED resistance and reactance for the two probe placements are shown in (C) for the varying-diameter canal model and in (D) for the uniform-diameter canal model. The thin dashed black lines in (C) and (D) are data from Margolis et al. (1999). Note that the frequency axis is linear to emphasize the high-frequency portion of the data.
Also seemingly consistent with contributions from the residual canal space on at high frequencies, data from Voss and Allen (1994) exhibited a minimum, but at a higher frequency (between 10 and 15 kHz) than the analogous feature in the present work (between 6 and 11 kHz). Inspection of ZEC from Voss and Allen (1994) reveals that the 1/2-wave anti-resonance was regularly above 10 kHz and higher than that achieved in the present study [between 6 and 11 kHz, see Fig. 2(C)], suggestive of a deeper probe placement and shorter residual canal length. Thus, the length of the residual-canal space combined with distributed reflections occurring within the canal due to cross-sectional area changes may be responsible for the placement sensitivity observed in A and above 5 kHz.
Concerning ZED, Figs. 11(C) and 11(D) plot the mean resistive and reactive components of ZED_deep and ZED_shallow for the varying- and uniform-diameter ear-canal models, respectively. The varying-diameter model provided estimates of ZED resistance and reactance from the deep and shallow probe placements that were in closer agreement than those from the uniform-diameter model, especially above 3 kHz. However, although the data in Fig. 11 suggest that estimation of ZED necessitates accounting for potential spatial variations in the canal's diameter, this may not necessarily be the case. For instance, Margolis et al. (1999) estimated ZED using a cylindrical model of the canal and obtained results that exhibited frequency-dependency more similar to that in the current work estimated from the varying-diameter compared to the uniform-diameter model [i.e., the decrease in resistance and the reactance notch near 4 kHz; the thin dashed black lines in Figs. 11(C) and 11(D) show the data from Margolis et al. (1999)]. Unlike the current study's measurements, from Margolis et al. (1999) did not show evidence of a high-frequency minimum (at least through ∼10 kHz), perhaps due to a deeper probe placement. It is plausible that the presence of this feature (and/or the frequency where it occurs) in is a limiting factor in obtaining a reliable estimate of ZED at higher frequencies when using a cylindrical canal model.
2. Probe-placement differences in the canal-diameter profiles
Recall from Fig. 4 that the canal's cross-sectional diameters determined for the deep and shallow probe-insertion depths were not identical when compared at equal distances from the eardrum. This was especially evident over the length of the canal in the vicinity of the measurement probe, although differences also occurred closer to the eardrum. These differences suggest that the estimated diameters may not necessarily be physically meaningful and that the fitting process is using these parameters to explain variations in the data that are not directly related to the physical properties of the canal. However, some of the differences may have only small effects on the modeled and derived data. Additional analysis was therefore performed to determine the importance of the diameter differences between the two canal-diameter profiles in accurately modeling A and reducing differences between ZED_shallow and ZED_deep.
For each subject, the best-fit ear-canal diameter profile for the shallow insertion-depth measure (BFs) was shortened by a length ΔlEC (ΔlEC = lEC_shallow − lEC_deep) to equal the estimated length of the canal for the deep insertion-depth measure. The modeled Adeep and ZED_deep were subsequently calculated using the shortened shallow canal-diameter profile (this profile is hereafter referred to as profile 0). The modeled Adeep and ZED_deep were also calculated for additional diameter profiles in which a subset of the canal diameters from profile 0 were allowed to vary in order to provide a better fit to the measured Adeep. Eight such profiles (1–8) were created. For profile 1, the best-fit value for the diameter at the plane of the probe was determined using non-linear optimization [minimization of Eq. (24)], holding the ME model parameters, ear-canal length parameter (for the deep probe placement) and remaining seven canal diameters (from profile 0) fixed. For profile 2, best-fit values were determined for the diameter at the plane of the probe and the diameter immediately adjacent. For profile 3, best-fit values were determined for the diameter at the plane of the probe and the two adjacent diameters. This process continued until, for the final profile (i.e., profile 8), best-fit values were determined for all eight diameters. Figure 12 illustrates the process of shortening the shallow ear-canal diameter profile and the formation of the additional diameter profiles from which Adeep and ZED_deep were calculated.
FIG. 12.
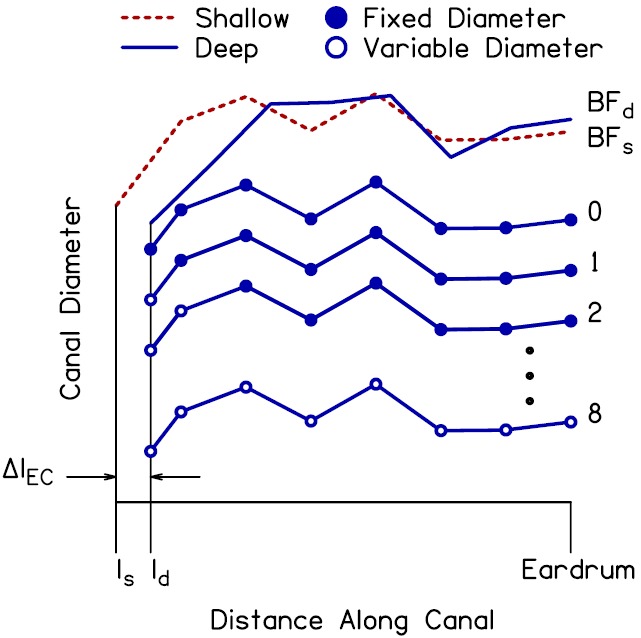
(Color online) Illustration of the method used to create variations of the shallow ear-canal diameter profile, from which Adeep was calculated. The best-fit diameter profiles determined from step 2 of the optimization procedure for the shallow and deep probe placements (BFs and BFd) are shown by the dashed and solid lines, respectively, at the top of the panel. The shallow profile was shortened by a length ΔlEC to create the deep diameter profile 0. The filled symbols identify the resulting entrance and exit diameters of the seven conical segments of the canal model. Diameter profile 1 had the same diameters as profile 0 (indicated by the filled markers) with the exception of the diameter at the plane of the probe (ld). Optimization was used to determine the value of this diameter that best fit the measured Adeep (the open marker indicates that the final value of this diameter was determined using optimization–note that the final value is not shown in the figure). Similarly, diameter profile 2 had the same diameters as profile 0 with the exception of both the diameter at the plane of the probe and the adjacent diameter. Optimization was used to determine the final values of these diameters that best fit the measured Adeep. This pattern continued until optimization was used to determine the final values of all eight diameters, i.e., profile 8, to better fit the measured Adeep.
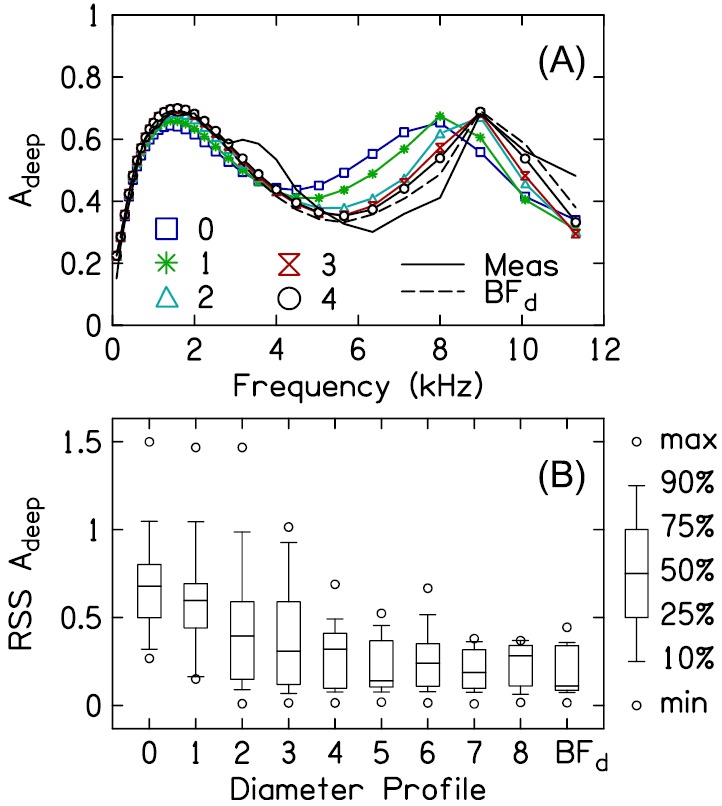
Figure 13(A) plots the measured Adeep (averaged across subjects) and the modeled Adeep (averaged across subjects) from the diameter profiles 0–4. The modeled Adeep using the best-fit deep canal-diameter profile is also shown (BFd, thin dashed line). Note that the x axis uses a linear scale in order to facilitate visualization of the high-frequency range of the data. Compared to the modeled Adeep using the BFd profile, the modeled Adeep using the shortened shallow canal-diameter profile, i.e., profile 0, did a poorer job of approximating the measured Adeep. Most notably, Adeep for profile 0 exhibited a peak at 7.9 kHz whereas the peak in Adeep for the BF profile occurred at 8.9 kHz–the same frequency as the peak in the measured Adeep. However, as the number of cross-sectional diameters in the vicinity of the probe that were allowed to deviate from profile 0 increased, e.g., profiles 1–4, the modeled Adeep more closely approximated the measured Adeep and the modeled Adeep for the BFd profile.
FIG. 13.
(Color online) Modeled compared to measured Adeep for the different diameter profiles. (A) plots the average measured Adeep (solid line without symbols) and modeled Adeep for a subset of the diameter profiles, including the best-fit profile BFd (dashed line). (B) plots the distribution (across subjects) of the RSS between the measured Adeep and modeled Adeep for each diameter profile.
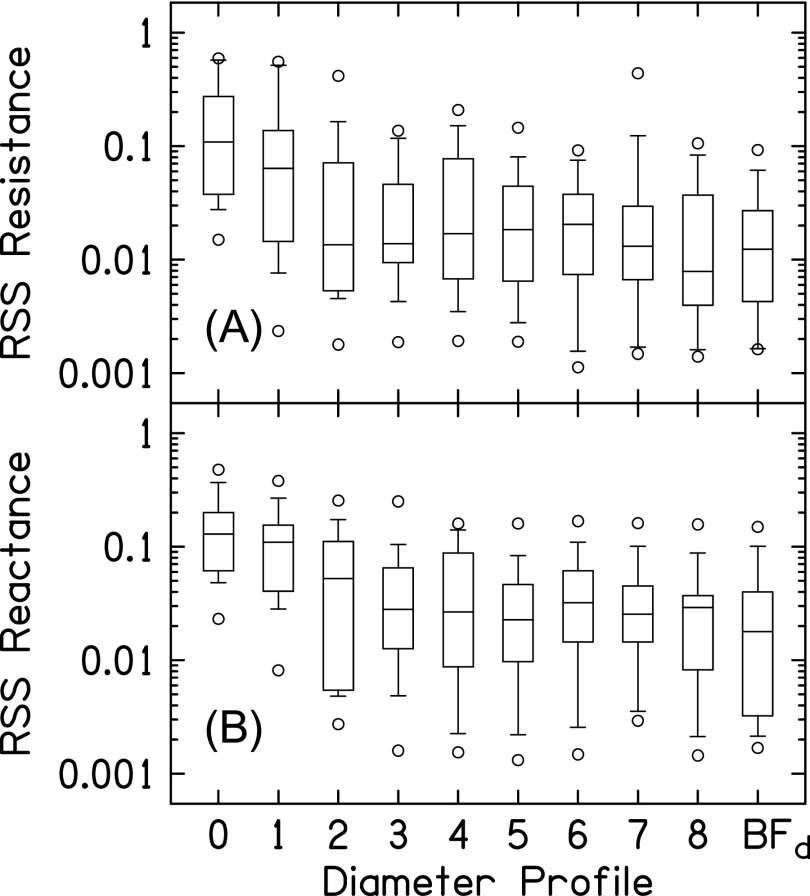
Figure 13(B) plots the distributions (across subjects) of the residual sum-of-squares (RSS) between the measured Adeep and modeled Adeep for the different diameter profiles (, where indicates the diameter profile and is the frequency index for the frequency range between 1 and 12 kHz in 1/6-octave steps). The differences between the measured and modeled Adeep were highest for profile 0. As more of the canal diameters were allowed to deviate from those in profile 0, differences between the measured and modeled Adeep decreased, at least through profile 4. Allowing more than four of the diameters to deviate from those in profile 0 had a smaller effect on the difference between the measured and modeled Adeep than that observed between profiles 0 and 4. These findings demonstrate that the insertion-depth specific differences between the deep and shallow ear-canal diameter profiles nearest to the probe are most important in accurately modeling the measured A at high frequencies (i.e., minimizing the RSS between the measured and modeled A).
A similar analysis was performed to examine how the diameter differences between the shallow and deep canal-diameter profiles contributed to reducing differences between ZED_shallow and ZED_deep. Figure 14(A) plots the distributions (across subjects) of the RSS between the estimated resistive components of ZED_shallow and ZED_deep for the different diameter profiles (, where indicates the diameter profile and is the frequency index for the frequency range between 1 and 12 kHz in 1/6-octave steps). Increasing the number of diameters that were allowed to deviate from profile 0 reduced the differences between the estimated resistive components of ZED_shallow and ZED_deep, especially for the diameters in closest vicinity to the plane of the measurement probe. Figure 14(B) plots the distributions of the RSS between the estimated reactive components of ZED_shallow and ZED_deep for the diameter profiles (). As for the resistive components in Fig. 14(A), the difference between the reactive components of ZED_shallow and ZED_deep decreased as the number of diameters in the vicinity of the probe that were allowed to deviate from those in profile 0 increased.
FIG. 14.
Differences between resistive and reactive components of ZED_shallow and ZED_deep for the deep diameter profiles. (A) plots the distributions (across subjects) of the RSS between the resistive component of ZED_shallow and ZED_deep. (B) plots the distributions of the RSS between the reactive component of ZED_shallow and ZED_deep. The key to the box-and-whisker plot is shown in Fig. 13.
The necessity of preserving the differences between the deep and shallow ear-canal cross-sectional area profiles in the vicinity of the probe to accurately model the high-frequency A and reduce differences between ZED_shallow and ZED_deep demonstrates that the estimated areas in this region do not represent the physical dimensions of the canal. One hypothesis is that these area estimates may be the model's attempt to account for non-planar wave propagation in the vicinity of the probe. Non-planar wave propagation near the plane of the probe might be expected given the sudden diameter change encountered by the incident sound pressure wave as it propagates from the probe sound tube into the ear canal (e.g., Huang et al., 2000a). However, although the canal-diameter profiles typically exhibited a noticeable change in diameter over the initial 5 to 10 mm beyond the plane of the probe, the direction of change was not always indicative of an increase in diameter (e.g., subjects S10, S11, S12, and S14). Further understanding of how non-planar wave propagation in the vicinity of probe affects the measured absorbance and impedance could be gained by comparing measurements made in physical models (e.g., horns, artificial ears, etc.) to the theoretical absorbance and impedance of those models, which would then facilitate refinement of the proposed ear-canal model and impedance transform.
Whereas allowing the diameter of the ear canal model to vary over the canal region in the vicinity of the probe is important, it is not clear whether variations in the diameter must also be included over regions of the canal closer to the eardrum. In other words, could similar results be obtained using a model of the canal that allows for diameter variations in the vicinity of the probe but casts the remaining portion of the canal as a uniform-diameter cylinder? This type of model would be attractive as it would require fewer parameters, thereby reducing the processing time and/or allowing additional parameters to be devoted to the ME model.
D. Clinical utility of ZED and ME efficiency
At the group level, both A and show patterns specific to various pathologies. However, both measures also exhibit high inter-subject variability with the effect that neither A nor in a pathologic ear may be significantly different from either a normal ear or an ear with a different pathology, at the individual level (Voss et al., 2012; Nakajima et al., 2012). A portion of the variability seems to be associated with differences in transmission of sound through the ME to the cochlea (Nakajima et al., 2012). The estimated ME efficiency (see Fig. 9) may therefore be clinically useful. Unfortunately, the inter-subject variability associated with ME efficiency was high, not unlike that for A and ; additional work is needed to determine the extent to which this variability is indicative of behavioral differences in sound detection between subjects versus inadequacies with the underlying ME model.
It is important to note that the derived ME efficiency suggests that between 50% and 80% of the energy absorbed by the ME is delivered to the cochlea, at least for a frequency range spanning 0.25–5 kHz. This estimate is higher than what has been directly measured in other mammals, where ME efficiency typically does not exceed 50% (Rosowski, 1991; Ravicz and Rosowski, 2013). The damping afforded by different structures within the ME reduces the amount of sound power delivered to the cochlea. As such, it is probable that the exclusion of certain structures including the ME air space, eardrum suspension, and damping of the ossicular chain from the current work's ME model biased the efficiency estimate toward higher values. It is also possible that the model parameter used to represent cochlear resistance, Rc, included some damping that might otherwise have been attributed to ME losses in a more detailed ME model. By attributing this ME damping to the cochlea, the power absorbed by the ME decreases whereas the power absorbed by the cochlea increases, resulting in overestimation of ME efficiency.
ZED may also have diagnostic power and be complementary to either A or . In addition to not providing information concerning sound transmission through the ME to the cochlea, A and provide only a general description of ME impedance. Specifically, changes in the resistive and reactive components of the ME cannot be directly analyzed from either A or as phase information is discarded in the requisite calculation. Measurements of ZED and ME efficiency (or other descriptors of sound transmission through the ME) in pathologic ears are necessary to determine whether either measure, as described in the present study, offers any diagnostic value.
V. CONCLUSIONS
The input impedance of the ME can be estimated by applying an impedance transform to the impedance measured at a location in the ear canal remote from the eardrum. Necessary to the transform was development of a model of the ear canal, ME, and cochlea. Compared to the impedance measured at the plane of the probe, the impedance transformed to the plane of the eardrum was less sensitive to the acoustics of the residual canal space for frequencies between 1 and 12 kHz. By modeling both the ME and cochlea, the efficiency of the ME in delivering sound power to the cochlea was estimated.
ACKNOWLEDGMENTS
Research was supported by grants from the National Institutes of Health [Grant No. NIH-NIDCD R01 DC008318 (S.T.N.); Grant No. NIH-NIDCD P30 DC004662 (Michael P. Gorga)]. The authors thank Judy G. Kopun and Sara Fultz for their help with subject recruitment and data collection, Lindsay Reuter and David Raybine for their help with the preparation of figures, and Michael P. Gorga for helpful comments on an earlier version of this manuscript.
Portions of this work were presented at the 2014 Annual Meeting of the American Auditory Society, Scottsdale, AZ, March 2014.
References
- 1. Allen, J. B. (1986). “ Measurement of eardrum acoustic impedance,” in Peripheral Auditory Mechanisms, edited by Allen J. B., Hall J. L., Hubbard A., Neely S. T., and Tubis A. ( Springer-Verlag, New York: ), pp. 44–51. [Google Scholar]
- 2. Beranek, L. L. , and Mellow, T. (2012). Acoustics: Sound Fields and Transducers ( Academic Press, New York). [Google Scholar]
- 3. Claerbout, J. F. (1985). Imaging the Earth's Interior ( Blackwell Science, New York: ), p. 287. [Google Scholar]
- 4. Farmer-Fedor, B. L. , and Rabbitt, R. D. (2002). “ Acoustic intensity, impedance and reflection coefficient in the human ear canal,” J. Acoust. Soc. Am. 112, 600–620. 10.1121/1.1494445 [DOI] [PubMed] [Google Scholar]
- 5. Feeney, M. P. , Graint, I. L. , and Mills, D. M. (2009). “ Wideband energy reflectance measurements of ossicular chain discontinuity and repair in human temporal bone,” Ear Hear. 30, 391–400. 10.1097/AUD.0b013e3181a283ed [DOI] [PubMed] [Google Scholar]
- 6. Groon, K. A. , Rasetshwane, D. M. , Kopun, J. G. , Gorga, M. P. , and Neely, S. T. (2015). “ Air-leak effects on ear-canal acoustic absorbance,” Ear Hear. 36, 155–163. 10.1097/AUD.0000000000000077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Huang, G. T. , Rosowski, J. J. , Puria, S. , and Peak, W. T. (2000a). “ A noninvasive method for estimating acoustic admittance at the tympanic membrane,” J. Acoust. Soc. Am. 108, 1128–1146. 10.1121/1.1287024 [DOI] [PubMed] [Google Scholar]
- 8. Huang, G. T. , Rosowski, J. J. , Puria, S. , and Peak, W. T. (2000b). “ Tests of some common assumptions of ear-canal acoustics in cats,” J. Acoust. Soc. Am. 108, 1147–1161. 10.1121/1.1287025 [DOI] [PubMed] [Google Scholar]
- 9. Hudde, H. (1983). “ Measurement of the eardrum impedance of human ears,” J. Acoust. Soc. Am. 73, 242–247. 10.1121/1.388855 [DOI] [PubMed] [Google Scholar]
- 10. Keefe, D. H. (1984). “ Acoustical wave propagation in cylindrical ducts: Transmission line parameter approximations for isothermal and nonisothermal boundary conditions,” J. Acoust. Soc. Am. 75, 58–62. 10.1121/1.390300 [DOI] [Google Scholar]
- 11. Keefe, D. H. (2015). “ Acoustical transmission-line model of the middle-ear cavities and mastoid air cells,” J. Acoust. Soc. Am. 137, 1877–1887. 10.1121/1.4916200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Keefe, D. H. , Bulen, J. C. , Arehart, K. H. , and Burns, E. M. (1993). “ Ear-canal impedance and reflection coefficient in human infants and adults,” J. Acoust. Soc. Am. 94, 2617–2638. 10.1121/1.407347 [DOI] [PubMed] [Google Scholar]
- 14. Keefe, D. H. , Ling, R. , and Bulen, J. C. (1992). “ Method to measure acoustic impedance and reflection coefficient,” J. Acoust. Soc. Am. 91, 470–485. 10.1121/1.402733 [DOI] [PubMed] [Google Scholar]
- 15. Killion, M. C. (1978). “ Revised estimate of minimum audible pressure: Where is the ‘missing 6 dB?,’ ” J. Acoust. Soc. Am. 63, 1501–1508. 10.1121/1.381844 [DOI] [PubMed] [Google Scholar]
- 16. Kringlebotn, M. (1988). “ Network model for the human middle ear,” Scand. Audiol. 17, 75–85. 10.3109/01050398809070695 [DOI] [PubMed] [Google Scholar]
- 17. Lewis, J. D. , McCreery, R. W. , Neely, S. T. , and Stelmachowicz, P. G. (2009). “ Comparison of in-situ calibration methods for quantifying input to the middle ear,” J. Acoust. Soc. Am. 126, 3114–3124. 10.1121/1.3243310 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Lynch, T. J. III , Peak, W. T. , and Rosowski, J. J. (1994). “ Measurements of the acoustic impedance of cat ears: 10 Hz to 20 kHz,” J. Acoust. Soc. Am. 96, 2184–2209. 10.1121/1.410160 [DOI] [PubMed] [Google Scholar]
- 19. Margolis, R. H. , Saly, G. L. , and Keefe, D. H. (1999). “ Wideband reflectance tympanometry in normal adults,” J. Acoust. Soc. Am. 106, 265–280. 10.1121/1.427055 [DOI] [PubMed] [Google Scholar]
- 20. Matthews, J. W. (1983). “ Modeling reverse middle ear transmission of acoustic distortion signals,” in Mechanics of Hearing, edited by de Boer E. and Viergever M. A. ( Springer, Netherlands: ), pp. 11–18. [Google Scholar]
- 21. Mehta, R. P. , Rosowski, J. J. , Voss, S. E. , O'Neil, E. , and Merchant, S. N. (2006). “ Determinants of hearing loss in perforations of the tympanic membrane,” Otol. Neurotol. 27, 136–143. 10.1097/01.mao.0000176177.17636.53 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Nakajima, H. H. , Pisano, D. V. , Roosli, C. , Hamade, M. A. , Merchant, G. R. , Mahfoud, L. , Halpin, C. F. , Rosowski, J. J. , and Merchant, S. N. (2012). “ Comparison of ear-canal reflectance and umbo velocity in patients with conductive hearing loss: A preliminary study,” Ear Hear. 33, 35–43. 10.1097/AUD.0b013e31822ccba0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. O'Connor, K. N. , and Puria, S. (2008). “ Middle-ear circuit model parameters based on a population of human ears,” J. Acoust. Soc. Am. 123, 197–211. 10.1121/1.2817358 [DOI] [PubMed] [Google Scholar]
- 24. Peres, P. L. D. , de Souza, C. R. , and Bonatti, I. S. (2003). “ ABCD matrix: A unique tool for linear two-wire transmission line modelling,” Int. J. Elec. Eng. Educ. 40, 220–229. 10.7227/IJEEE.40.3.5 [DOI] [Google Scholar]
- 25. Rabinowitz, W. M. (1981). “ Measurement of the acoustic input immittance of the human ear,” J. Acoust. Soc. Am. 70, 1025–1035. 10.1121/1.386953 [DOI] [PubMed] [Google Scholar]
- 26. Rasetshwane, D. M. , and Neely, S. T. (2011). “ Inverse solution of ear-canal area function from reflectance,” J. Acoust. Soc. Am. 130, 3873–3881. 10.1121/1.3654019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Rasetshwane, D. M. , Neely, S. T. , Allen, J. B. , and Shera, C. A. (2012). “ Reflectance of acoustic horns and solution of the inverse problem,” J. Acoust. Soc. Am. 131, 1863–1873. 10.1121/1.3681923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Ravicz, M. E. , and Rosowski, J. J. (2013). “ Middle-ear velocity transfer function, cochlear input immittance, and middle-ear efficiency in chinchilla,” J. Acoust. Soc. Am. 134, 2852–2865. 10.1121/1.4818745 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Rosowski, J. J. (1991). “ The effects of external- and middle-ear filtering on auditory threshold and noise-induced hearing loss,” J. Acoust. Soc. Am. 90, 124–135. 10.1121/1.401306 [DOI] [PubMed] [Google Scholar]
- 30. Rosowski, J. J. , Carney, L. H. , Lynch, T. J. III , and Peake, W. T. (1986). “ The effectiveness of external and middle ears in coupling power into the cochlea,” in Peripheral Auditory Mechanisms, edited by Allen J. B., Hall J. L., Hubbard A., Neely S. T., and Tubis A. ( Springer-Verlag, New York: ), pp. 3–12. [Google Scholar]
- 31. Rosowski, J. J. , Nakajima, H. H. , Hamade, M. A. , Mafoud, L. , Merchant, G. R. , Halpin, C. F. , and Merchant, S. N. (2012). “ Ear-canal reflectance, umbo velocity and tympanometry in normal hearing adults,” Ear Hear. 33, 19–34. 10.1097/AUD.0b013e31822ccb76 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Rosowski, J. J. , Stenfelt, S. , and Lilly, D. (2013). “ An overview of wideband immittance measurements techniques and terminology: You say absorbance, I say reflectance,” Ear Hear. 34(1), 9S–16S. 10.1097/AUD.0b013e31829d5a14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Scheperle, R. A. , Goodman, S. S. , and Neely, S. T. (2011). “ Further assessment of forward pressure level for in situ calibration,” J. Acoust. Soc. Am. 130, 3882–3892. 10.1121/1.3655878 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Scheperle, R. A. , Neely, S. T. , Kopun, J. G. , and Gorga, M. P. (2008). “ Influence of in situ, sound-level calibration on distortion-product otoacoustic emission variability,” J. Acoust. Soc. Am. 124, 288–300. 10.1121/1.2931953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Shahnaz, N. , Bork, K. , Polka, L. , Longridge, N. , Bell, D. , and Westerberg, B. D. (2009). “ Energy reflectance and tympanometry in normal and otosclerotic ears,” Ear Hear. 30, 219–233. 10.1097/AUD.0b013e3181976a14 [DOI] [PubMed] [Google Scholar]
- 36. Shaw, E. A. G. (1977). “ Eardrum representation in middle-ear acoustical networks,” J. Acoust. Soc. Am. 62(1), S12. 10.1121/1.2016028 [DOI] [Google Scholar]
- 36. Shaw, E. A. G. , and Stinson, M. R. (1981). “ Network concepts and energy flow in the human middle-ear,” J. Acoust. Soc. Am. 69(S1), S43. 10.1121/1.386273 [DOI] [Google Scholar]
- 37. Souza, N. N. , Dhar, S. , Neely, S. T. , and Siegel, J. H. (2014). “ Comparison of nine methods to estimate ear-canal stimulus levels,” J. Acoust. Soc. Am. 136, 1768–1787. 10.1121/1.4894787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Stepp, C. E. , and Voss, S. E. (2005). “ Acoustics of the human middle-ear air space,” J. Acoust. Soc. Am. 118, 861–871. 10.1121/1.1974730 [DOI] [PubMed] [Google Scholar]
- 39. Stinson, M. R. , and Lawton, B. W. (1989). “ Specification of the geometry of the human ear canal for the prediction of sound-pressure level distribution,” J. Acoust. Soc. Am. 85, 2492–2503. 10.1121/1.397744 [DOI] [PubMed] [Google Scholar]
- 40. Voss, S. E. , and Allen, J. B. (1994). “ Measurement of acoustic impedance and reflectance in the human ear canal,” J. Acoust. Soc. Am. 95, 372–384. 10.1121/1.408329 [DOI] [PubMed] [Google Scholar]
- 41. Voss, S. E. , Horton, N. J. , Woodbury, R. R. , and Sheffield, K. N. (2008). “ Sources of variability in reflectance measurements on normal cadaver ears,” Ear Hear. 29, 651–665. 10.1097/AUD.0b013e318174f07c [DOI] [PubMed] [Google Scholar]
- 42. Voss, S. E. , Merchant, G. R. , and Horton, N. J. (2012). “ Effects of middle-ear disorders on power reflectance measured in cadaveric ear canals,” Ear Hear. 33, 195–208. 10.1097/AUD.0b013e31823235b5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Voss, S. E. , Rosowski, J. J. , Merchant, S. N. , and Peake, W. T. (2001a). “ Middle-ear function with tympanic-membrane perforations. I. Measurements and mechanisms,” J. Acoust. Soc. Am. 110, 1432–1444. 10.1121/1.1394195 [DOI] [PubMed] [Google Scholar]
- 44. Voss, S. E. , Rosowski, J. J. , Merchant, S. N. , and Peake, W. T. (2001b). “ Middle-ear function with tympanic-membrane perforations. II. A simple model,” J. Acoust. Soc. Am. 110, 1445–1452. 10.1121/1.1394196 [DOI] [PubMed] [Google Scholar]
- 46. Withnell, R. H. , and Gowdy, L. E. (2013). “ An analysis of the acoustic input impedance of the ear,” J. Assoc. Res. Otolaryngol. 14, 611–622. 10.1007/s10162-013-0407-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Zwislocki, J. (1962). “ Analysis of the middle-ear function. Part I: Input impedance,” J. Acoust. Soc. Am. 34, 1514–1523. 10.1121/1.1918382 [DOI] [Google Scholar]