Characterization of trabecular bone plate-rod microarchitecture using multirow detector CT and the tensor scale: Algorithms, validation, and applications to pilot human studies

Abstract

Purpose:

Osteoporosis is a common bone disease associated with increased risk of low-trauma fractures leading to substantial morbidity, mortality, and financial costs. Clinically, osteoporosis is defined by low bone mineral density (BMD); however, increasing evidence suggests that trabecular bone (TB) microarchitectural quality is an important determinant of bone strength and fracture risk. A tensor scale based algorithm for in vivo characterization of TB plate-rod microarchitecture at the distal tibia using multirow detector CT (MD-CT) imaging is presented and its performance and applications are examined.

Methods:

The tensor scale characterizes individual TB on the continuum between a perfect plate and a perfect rod and computes their orientation using optimal ellipsoidal representation of local structures. The accuracy of the method was evaluated using computer-generated phantom images at a resolution and signal-to-noise ratio achievable in vivo. The robustness of the method was examined in terms of stability across a wide range of voxel sizes, repeat scan reproducibility, and correlation between TB measures derived by imaging human ankle specimens under ex vivo and in vivo conditions. Finally, the application of the method was evaluated in pilot human studies involving healthy young-adult volunteers (age: 19 to 21 yr; 51 females and 46 males) and patients treated with selective serotonin reuptake inhibitors (SSRIs) (age: 19 to 21 yr; six males and six females).

Results:

An error of (3.2% ± 2.0%) (mean ± SD), computed as deviation from known measures of TB plate-width, was observed for computer-generated phantoms. An intraclass correlation coefficient of 0.95 was observed for tensor scale TB measures in repeat MD-CT scans where the measures were averaged over a small volume of interest of 1.05 mm diameter with limited smoothing effects. The method was found to be highly stable at different voxel sizes with an error of (2.29% ± 1.56%) at an in vivo voxel size as compared to the original ex vivo voxel size. Tensor scale measures derived from imaging under in vivo and ex vivo conditions with significantly different modulation transfer function, i.e., difference in “true resolution,” showed strong linear correlation (r = 0.92). The study of healthy volunteers shows that, after adjustment for height and weight, males have a 14% higher mean TB plate-width as compared to females (p < 0.05). SSRI-treated patients have 12.5% lower mean TB plate-width (p = 0.052) as compared to age-similar and sex-, height-, and weight-matched healthy controls. In contrast, the observed group difference in dual-energy x-ray absorptiometry (DXA)-derived hip BMD was 10.5% between males and females and only 5.04% between healthy controls and patients on SSRIs.

Conclusions:

Tensor scale analysis of MD-CT images yields accurate and reproducible characterization of TB plate-rod microarchitecture that may be more sensitive than DXA-derived BMD to sex differences and to the skeletal changes associated with medical conditions or their treatments.

1. INTRODUCTION

Osteoporosis is associated with an increased risk of low-trauma fractures. Its incidence increases progressively with age.^1–3 In the United States, about eight million women and two million men have osteoporosis⁴ with medical costs estimated at twenty two billion dollars in 2008.⁵ Clinically, osteoporosis is defined by low bone mineral density (BMD). BMD only accounts for approximately 60% to 70% of the variability in bone strength.⁶ The remaining variability is due to the cumulative and synergistic effects of various factors, including trabecular bone (TB) microarchitecture.^7–9 Thus, reliably measuring TB microarchitecture could be of clinical significance, particularly as trabecular bone may be more susceptible to hormonal, pharmacological, and toxic effects.

The conventional tool for assessing TB structure is two-dimensional (2D) cross-sectional histomorphometry from bone biopsies.¹⁰ More recently, direct three-dimensional (3-D) analysis of biopsy specimens using micro-computed tomography (μ-CT) has gained interest.^11,12 μ-CT instruments have maximum resolution on the order of 8 μm isotropic voxels, providing detailed insight into TB microarchitecture. Although it provides the highest resolution while being nondestructive, μ-CT requires bone biopsy, which is rarely indicated clinically and is not suited for monitoring treatment response. Recent advancements in volumetric bone imaging, such as magnetic resonance (MR),^6,13,14 high resolution peripheral quantitative computed tomography (HR-pQCT),^15,16 and multirow detector computed tomography (MD-CT),^17,18 allow characterization of bone microarchitecture without the need for biopsy.

Various topologic and geometric analytic approaches have been reported^19–23 to characterize TB architecture using ex vivo and in vivo bone imaging technologies. Parfitt et al.¹⁹ conceived a parallel interconnected plate model of trabeculae yielding TB area and volume fractions, and trabecular spacing and number from 2-D histomorphometric sections. Vesterby et al.²⁰ conceived a new stereologic parameter, called star volume, which is the average volume of an object region that can be seen from a point inside that region unobscured in all directions. Hahn et al.²¹ introduced the “trabecular bone pattern factor” which captures TB connectivity in terms of the convexity property of the TB surface defined as the ratio of the differences in perimeter and area under dilation. Hildebrand and Rüegsegger²² developed a 3-D structure model index, a function of global plate-to-rod ratio, based on the observation that the rate of volume change with respect to half thickness (or the radius) for plate-like elements is different from that for rod-like elements. Feldkamp et al.²³ showed that the makeup of TB networks can be expressed in terms of topological entities such as the 3-D Euler number.

A large number of histologic studies^8,9 have confirmed the relationship between erosion of trabeculae from plates to rods and fracture risk. Kleerekoper et al.⁸ found lower mean TB plate density in individuals with osteoporotic vertebral compression deformities compared with a BMD-matched control group without fractures. Recker⁹ observed reduced trabecular connectivity in patients with vertebral crush fractures as compared to healthy controls for identical TB volume. Saha and colleagues developed the digital topological analysis (DTA)^24–27 to characterize topological plates, rods, and junctions at individual TB voxels, which has been adopted by others.^14,28–30 A major limitation of the DTA method is that resulting classifications are inherently discrete, failing to distinguish between narrow and wide plates. The balance between plates and rods during bone formation at younger ages, as well as during bone loss or antiresorptive treatment, changes gradually and, therefore, demands classification of TB microarchitecture along the continuum between a perfect plate and a perfect rod. Recently, Saha et al.¹⁸ developed a volumetric topological analysis (VTA) algorithm characterizing the topology of individual trabeculae on the continuum between a perfect plate and a perfect rod. Although VTA provides an effective measure of TB microarchitecture from in vivo images, its premise is built upon digital topology and path propagation approaches, making it more susceptible to cumulative errors incurred during digital path propagation. Also, VTA ignores information related to structure orientation and anisotropy.

This paper presents an accurate and robust algorithm for computation of plate/rod classification and orientation of individual trabeculae using tensor scale³¹ and examines the algorithm’s effectiveness to characterize the quality of TB microarchitecture from in vivo MD-CT imaging. An improved and robust algorithm for computation of 3-D tensor scale for fuzzy digital objects with significant partial voluming is presented. The optimal ellipsoidal representation of a local structure in the tensor scale model is used to quantitatively characterize the microarchitecture of individual trabeculae. The accuracy and robustness of derived TB measures were examined in cadaveric studies and the results are presented. Sex- and body size dependence of TB microarchitecture was assessed in healthy volunteers from MD-CT imaging. Finally, TB plate/rod microarchitectural differences in patients treated with selective serotonin reuptake inhibitors (SSRIs) as compared to sex-weight-height-matched controls were characterized using the new algorithms applied to MD-CT imaging of the distal tibia. Treatment with SSRIs was selected as preclinical and clinical studies have shown SSRIs to interfere with bone metabolism.^32,33 A preliminary and shorter version of this work was published in a conference paper.³⁴ Compared to the conference version, this paper includes the following new contributions—(1) major expansion of the theory and algorithm section, (2) characterization of “representative points” for computing different TB measures using the tensor scale, (3) addition of the new location optimization technique for axial points, (4) new experiments and results on accuracy and stability of the method at different voxel sizes, and (5) new in vivo human pilot investigations and results for sensitivity of tensor scale measures to sex differences and to the possible effects of SSRIs on TB plate-rod microarchitecture.

2. THEORY AND ALGORITHMS

Tensor scale computation is applicable to fuzzy digital objects (e.g., TB network imaged at a relatively low resolution). For the current application, the membership value at a given voxel is interpreted as the partial occupancy of bone within the voxel, termed the bone volume fraction (BVF). To characterize the local TB microarchitecture, the proposed algorithm finds the largest ellipsoid fitting within the local trabecular structure. Let R denote the set of real numbers and Z denote the set of integers. In the remainder of this section, we will use R³ to denote the Euclidean 3-space and Z³ to denote the underlying digital voxel grid; let BVF : Z³ → [0, 1] be the function providing the BVF value at each voxel.

2.A. Tensor scale computation

The tensor scale, at a point p inside an object O ⊂ R³, is the parametric representation of the maximally included ellipsoid centered at p, where the maximization of the three semiprincipal axes is accomplished in the reverse order of their lengths. This definition of the tensor scale may be understood as follows. First, a ball is isotropically grown from its center p until it hits the boundary of O, thus defining the first semiaxis of the tensor scale; then the circle, the intersection of the ball in the orthogonal subspace, is allowed to grow until it hits the boundary of O in the subspace; and so on. Saha³¹ presented a computational solution for the tensor scale using radial sample line tracing, while Xu et al.³⁵ presented a computationally efficient algorithm using differential geometric approaches. Here, we leverage the original sample line-based approach, since it alleviates digitization effects at low resolutions by ellipsoid fitting on a relatively large number of boundary points along sample lines. The process of tensor scale computation at point p is schematically illustrated in Fig. 1. For simplicity, 2-D illustrations are used, while the method is described in 3-D. The method is based on tracing pairs of radially opposite sample lines that emanate from a candidate point p and locate the closest object boundary or edge on each sample line (pink or darker points). The edge points are repositioned to ensure axial symmetry (yellow or lighter points). Finally, the tensor scale at p is determined by computing the best-fit ellipsoid to the repositioned edge points [Figs. 1(b) and 1(c)]. The following steps describe this process in detail.

FIG. 1.

Steps of tensor scale computation. (a) Original edge points (pink or darker) on radial sample lines and repositioned edge points (yellow or lighter) for a candidate point. (b) Bounding box (dotted) and the best-fit ellipse (white) after rotating the repositioned edge points (grey) using PCA. (c) Final tensor scale ellipsoid.

2.A.1. Edge Detection along sample lines

First, m pairs of mutually opposite sample lines are pseudo-uniformly selected over the entire 3-D angular space ensuring that the computed tensor scale is not skewed along any direction. Forty pairs of sample lines at an approximate 22.5° of angular separation were used. This choice was made by analyzing the trade-off between computation time and accuracy performance; the current computation time for human bone data over a volume of interest (VOI) of 200 × 200 × 200 voxels is approximately 40 min. Two other parameters, namely, the sampling interval δ and the sample line length L, are also relevant. L defines the maximum possible length of individual trabeculae; here, we use L = 5 mm. δ defines the step-size between two successive sample points on a sample line and its value is set as the scale of the finest detectable structure. Assuming that the image resolution is appropriate for the target application, we recommend choosing δ between “1” and “0.5” times the smallest dimension of a pixel. Following the Nyquist theorem of sampling, δ = 0.5 is sufficient for reconstruction of a signal and, therefore, setting δ < 0.5 offers no additional benefit. On the other hand, if δ > 1 is used, it clearly misses one voxel thick structures in an image. In this paper, we chose to use δ = 0.5.

The ith sample line ${\gamma }_p^i$ emanating from a point p ∈ R³ is defined as a sequence of sample points ${\gamma }_p^i\left[0\right],{\gamma }_p^i\left[1\right],\dots ,{\gamma }_p^i\left[M_L\right]$, where, ${\gamma }_p^i\left[0\right]=p$ and M_L = L/δ. The BVF value at each sample point ${\gamma }_p^i\left[j\right]$ is computed by tri-linear interpolation of BVF values at the eight image voxels on the 2 × 2 × 2 bounding box of ${\gamma }_p^i\left[j\right]$. Finally, the edge on the sample line ${\gamma }_p^i$ is located at a distance ${\nu }_p^i$ from p,

$${\displaystyle {\nu }_p^i=\sum _{j=0}^{\underset{p}{\overset{i}{e}}-1}\delta \times \left(\text{BVF}\left[{\gamma }_p^i\left[j\right]\right]+\text{BVF}\left[{\gamma }_p^i\left[j+1\right]\right]\right)/2,}$$ (1)

where $e_p^i$ is the first sample point on ${\gamma }_p^i$ with interpolated BVF as zero indicating a full-background location. In the above equation, the term $\left(\text{BVF}\left[{\gamma }_p^i\left[j\right]\right]+\text{BVF}\left[{\gamma }_p^i\left[j+1\right]\right]\right)/2$ represents the average density over the interval between the two successive sample points ${\gamma }_p^i\left[j\right]$ and ${\gamma }_p^i\left[j+1\right]$. The multiplication of the average density with step-size δ accounts for partial voluming.

2.A.2. Repositioning edge points

The edge points obtained as above describe the boundary of the local object centered at the candidate point p. Following the axial symmetry of an ellipsoid, as demonstrated by Saha,³¹ for each pair of opposite sample lines, the two edge points should be equidistant from p, which is the center of the tensor scale ellipsoid. However, the detected edge points on a local structure do not necessarily satisfy this property. For example, in Fig. 1(a), the edge locations colored pink or darker on the lower-right sample lines tend to be farther from the candidate point p than the corresponding opposite sample lines. Therefore, the edge points need to be repositioned by analyzing the edge points on every pair of sample lines. Specifically, between the two edge points on a pair of sample lines, the one closer to p is selected and reflected on its complementary sample line. The edge locations colored yellow or lighter are obtained using this repositioning algorithm. In the rest of this section, “edge point” will refer to “repositioned edge point.”

2.A.3. Tensor scale ellipsoid fitting

The last step in tensor scale computation is to fit an ellipsoid to the repositioned edge points. The literature on ellipsoid fitting is quite mature, with several established approaches.³⁶ All ellipsoid-fitting approaches essentially minimize the error between the observed data (here, the edge points) and the computed ellipsoid. These methods primarily differ with respect to the nature of these errors. When errors are defined using algebraic distance, a canonical solution can be derived leading to a computationally efficient solution. However, the solution may not be stable for highly anisotropic data sets, and in our application such situations may frequently occur. The geometric distance approach generates stable solutions for most ellipsoids and uses a more natural Euclidean distance metric. Unfortunately, it is difficult to derive a canonical form solution for ellipsoid fitting that optimizes geometric distance error, and therefore, a geometric distance-based approach commonly needs an optimization step. Here, the geometric distance error is used and the fitting algorithm is summarized as follows [Fig. 1(b)].

Step 1:

Translate all edge points, moving the candidate point p to the origin.

Step 2:

Apply principle component analysis (PCA) to edge points computing eigenvectors ${\mathbf{i}}_1\left(p\right),{\mathbf{i}}_2\left(p\right),{\mathbf{i}}_3\left(p\right)$ of the point-distribution.

Step 3:

Rotate the edge points to align i₁(p), i₂(p), and i₃(p) with the three coordinate axes.

Step 4:

Determine the smallest box enclosing all edge points and use it to determine the eigenvalues for the initial guess of the best-fit ellipsoid.

Step 5:

Compute the final ellipsoid by applying iterative minimization of the sum of geometric distance errors using Newton’s optimization algorithm. Let ${\lambda }_1\left(p\right),{\lambda }_2\left(p\right),{\lambda }_3\left(p\right)$ be the length of the three semiprincipal axes of the final ellipsoid.

Step 6:

Set the tensor scale at the point p as the ellipsoid with the three semiprincipal axes—${\lambda }_i\left(p\right){\mathbf{i}}_i\left(p\right)$ for i = 1, 2, 3.

2.B. Characterization of individual trabeculae using the tensor scale

As described in Sec. 2.A, the tensor scale at a point p is represented by three orthogonal unit vectors ${\mathbf{i}}_1\left(p\right),{\mathbf{i}}_2\left(p\right),{\mathbf{i}}_3\left(p\right)$ and the lengths ${\lambda }_1\left(p\right),{\lambda }_2\left(p\right),{\lambda }_3\left(p\right)$ of corresponding semiprincipal axes, which are used to define geometric properties of the local structure. It is important to understand how the representative points are chosen while characterizing a specific geometric property of a local structure. An elongated plate-like structure can be represented by its surface- and arc-skeletons as shown in Fig. 2. Three different local geodesic measures are defined on such a structure—(1) thickness, i.e., the smallest dimension, (2) width, the second largest dimension, and (3) length, the largest dimension. To obtain accurate measures of these three classical structure dimensions, their values must be sampled at the midpoint of the respective dimension. Thus, on the surface-skeleton (e.g., the point r in Fig. 2) of a structure, the smallest semiprincipal axis of the tensor scale provides the correct measure of local thickness. However, the tensor scale at r may not be used to define the width of the local structure. To accurately compute the width of the local structure, it is important to reduce another dimension of freedom for representative points. In other words, the local width should be defined by the second largest semiprincipal axis of the tensor scale at a point (e.g., a point q in Fig. 2) on the arc skeleton of the structure. The length of the structure should be measured from the tensor scale of the mid-point p (see Fig. 2) on the arc-skeleton. Here, the tensor scale is used to define the orientation and plate-width of individual trabeculae and, thus, both measures are sampled at arc-skeletal points using the tensor scale; such points will be referred to as “axial points.” Finally, the measures at nonaxial points are inherited from the nearest axial point. This step is solved using the feature propagation scheme established by Liu et al.³⁷

FIG. 2.

Illustration of the choice of representative points for different TB measures using the tensor scale. To obtain accurate descriptions of local dimensions, these measures must be derived from the midpoint of the respective dimension. See text for details.

Spatial discretization of voxels in a digital image produces yet another hurdle in that the axial voxel may not coincide with the true axial point of the object in the continuous space. This hurdle is solved by optimizing the location of the target axial point a_p from a digitally computed axial voxel a_v using the tensor scale as follows.

Algorithm I.

Location optimization for axial points.

for each axial voxel av

initialize an axial point ap = av

repeat

compute the tensor scale at ap with eigenvectors

${\mathbf{i}}_1\left(a_p\right),{\mathbf{i}}_2\left(a_p\right),{\mathbf{i}}_3\left(a_p\right)$

compute local structure intercepts v2 and v3 at ap along ${\mathbf{i}}_2\left(a_p\right)$

and ${\mathbf{i}}_3\left(a_p\right)$

corresponding to the shorter semiaxes

reposition ap at the middle of the intercepts v2 and v3

until convergence of the axial point ap or a maximum of three

iterations

In the rest of this section, representative tensor scales at nonaxial voxels are inherited from axial points using the principle established by Liu et al.;³⁷ the points are used for characterization of microarchitectural properties at individual TB voxels. The orientation of the individual trabeculae at p, denoted by TS_O(p), is defined by the cosine of the angle θ between the eigenvector ${\mathbf{i}}_1\left(p\right)$, corresponding to the largest eigenvalue, and the longitudinal axis of the while bone, here, the distal tibia. The local plate-width at p, denoted by TS_W(p), is twice the length of the second largest eigenvalue ${\lambda }_2\left(p\right)$. The normalized plateness measure in the [0,1] scale, denoted by TS_P(p), is defined as the square of the classical measure of anisotropy between the length of the second longest semiprincipal axis ${\lambda }_2\left(p\right)$ and the shortest semiprincipal axis ${\lambda }_3\left(p\right)$ as follows:

$${\displaystyle {\text{TS}}_P\left(p\right)=1-{\left(\frac{{\lambda }_3\left(p\right)}{{\lambda }_2\left(p\right)}\right)}^2.}$$ (2)

This plateness measure provides a characterization of individual trabeculae between a perfect plate and a perfect rod without requiring any threshold values for min and max plate-widths as needed for VTA.¹⁸ The normalized rodness measure TS_R(p) is defined as

$${\displaystyle {\text{TS}}_R\left(p\right)=1-{\text{TS}}_P\left(p\right).}$$ (3)

The entire process of tensor scale-based characterization of TB microarchitecture can be summarized in the following steps.

Step 1:

Compute the set A of axial voxels representing the arc-skeleton of the fuzzy representation of a TB network using fuzzy skeletonization.^38,39

Step 2:

For each axial voxel a_v ∈ A, derive the optmized location of the axial point a_p.

Step 3:

At each axial point a_p, compute the tensor scale and derive TB measures-TS_W(a_p), TS_O(a_p), TS_P(a_p), and TS_R(a_p).

Step 4:

At each nonaxial voxel q, inherit the TB measures from the axial points following the principle of Liu et al.³⁷

Finally, several statistical TB measures defined over a VOI, V. $\text{BMD}\left(p\right)$ and BVF(p) are used to indicate bone mineral density (mg/cm³) and bone volume fraction at a given voxel p. Let $\left|\cdot \right|$ denote the cardinality of a set and let O denote the set of voxels in V with nonzero BVF; thus, O ⊂ V. The following TB measures were used for our investigation:

$${\displaystyle \text{plate-width: }{\text{PW}}_{\text{TS}}=\frac{\sum _{p\in O}{\text{TS}}_W\left(p\right)\text{BVF}\left(p\right)}{\sum _{p\in O}\text{BVF(}p\text{)}},}$$

$${\displaystyle \text{plate-to-rod ratio: }{\text{PRR}}_{\text{TS}}=\frac{\sum _{p\in O}{\text{TS}}_P\left(p\right)\text{BVF}\left(p\right)}{\sum _{p\in O}{\text{TS}}_R\left(p\right)\text{BVF}\left(p\right)},}$$

$${\displaystyle \text{Transverse bone mineral density: }{\text{tBMD}}_{\text{TS}}=\frac{\sum _{p\in O}\left(1-{\text{TS}}_O\left(p\right)\right)\text{BMD}\left(p\right)}{\left|V\right|}.}$$

In addition to the above measures of TB, for the purpose of comparison, two other measures, namely, mean plate-width PW_VTA and plate-to-rod ratio PRR_VTA were computed using the VTA algorithm as described by Saha et al.¹⁸ Also, the structure model index (SMI) was computed using the algorithm described by Hildebrand and Rüegsegger.²²

3. EXPERIMENTAL PLANS AND METHODS

The 3-D tensor scale algorithm was applied to estimate average plate-width (PW_TS), plate-to-rod ratio (PRR_TS), and transverse BMD (tBMD_TS) measures for TB networks acquired using MD-CT imaging of human in vivo and cadaveric distal tibia. Also, the VTA-based measures of average trabecular plate-width (PW_VTA) and plate-to-rod ratio (PRR_VTA), as well as SMI,²² were computed. After MD-CT imaging, the cadaveric specimen underwent further removal of soft tissue and dislodgement of distal tibia from the ankle joint, followed by μ-CT imaging. The experimental study was designed as follows.

• 1.Accuracy: Computer-generated phantoms with known measures of local structure width were used as the gold standard to evaluate the method’s accuracy.
• 2.Stability at different voxel sizes: Stability of the method was assessed using μ-CT images of cadaveric distal tibia specimens down-sampled at different voxel sizes spanning 28.5 to 199.5 μm; covering the range between ex vivo and in vivo imaging.
• 3.Relationship of TB measures computed from ex vivo and in vivo imaging: The relationship between TB plate-width measures computed from μ-CT and MD-CT imaging of the cadaveric specimens under ex vivo and in vivo conditions, respectively, was examined. The goal was to assess how TB plate-width measures derived using in vivo imaging relate to the corresponding measures from ex vivo μ-CT imaging, which yields high-resolution images with little fuzziness and well-defined microstructures.
• 4.Method reproducibility: Reproducibility of the method was examined using three repeat MD-CT scans of cadaveric distal tibia specimens with repositioning after each scan. The intraclass correlation coefficient (ICC) for each TB measure was computed using observed values from matching VOIs from the three repeat scans. The method’s reproducibility was further studied as a function of VOI size.
• 5.Sensitivity of in vivo TB measures to sex differences and to the possible effects of SSRIs on TB plate-rod microarchitecture: The method’s potential to detect and characterize sex differences and skeletal changes in SSRI-treated patients was examined using MD-CT imaging of the distal tibia in 97 healthy controls and 12 SSRI-treated participants. Of note, this in vivo study was primarily designed to examine the performance of the new analytical method rather than disentangle the effect of SSRIs from that of the underlying psychiatric condition on the skeleton.

3.A. Computerized phantoms with known truths

Three-dimensional binary phantoms with known structure widths were generated at 50 μm isotropic voxel resolution over an array of 512 × 512 × 512. The simulation began with sinusoidal mathematical surfaces with known widths in the continuous 3-D space, R³, constituting different cross-structures (see Fig. 3). The ideal mathematical surface cross-structure was densely and quasiuniformly sampled; let S_T be the set of N_T sampled points. A distance transform⁴⁰ map DT_T : Z³ → R⁺ was computed from S_T. To generate a binary volumetric object, a thickness threshold of 200 μm, or, equivalently a DT_T threshold of 100 μm was applied. The bone volume fraction or BVF (fuzzy) representation of test phantom images was generated by down-sampling binary phantoms at 150 μm isotropic resolution and by adding Gaussian noise at signal-to-noise ratios (SNR) of 12. Altogether, ten phantom images were generated. Each phantom image was generated at a given plate width and the plate width range was varied from 150 to 2000 μm covering the ranges of human trabecular bone plate-width as observed in our previous studies.^18,34

FIG. 3.

Illustration of computer-generated phantom images of sinusoidal cross-plates at 150, 750, and 2000 μm plate-widths.

3.B. Cadaveric specimens

Fifteen fresh-frozen human cadaveric ankle specimens were removed at midtibia from 11 body donors (age at death: 82.3 ± 12.5 yr). The bodies were collected under the Deeded Bodies Program, The University of Iowa, Iowa City, IA. Exclusion criteria were evidence of previous fracture or knowledge of bone tumor or bone metastasis. The specimens were kept frozen until MD-CT imaging using the protocol described in Sec. 3.D.

3.C. Healthy participants and SSRI-treated patients for in vivo studies

Studies involving human subjects were approved by The University of Iowa Institutional Review Board and all participants provided written informed consent. MD-CT distal tibia bone scans were obtained for 46 healthy males and 51 healthy females (age: range 19 to 20 yr; mean ± SD 19.4 ± 0.4 yr) as part of the ongoing Iowa Bone Development Study (IBDS).^41,42 In general, observed heights and weights for male participants (height 180.4 ± 8.0 cm, weight 83.6 ± 14.8 kg) were greater than female participants (mean ± SD height 165.2 ± 6.8 cm, weight 67.9 ± 21.0 kg). MD-CT scans were obtained on the left lower leg using the MD-CT protocol described in Sec. 3.D. Sex differences and associations with body size for trabecular bone characteristics were tested by fitting a multivariable linear regression model that included sex, height, and weight.

In addition, six male and six female patients (age: 19 to 21 yr; 20.2 ± 1.0 yr) on continuous treatment with a SSRI for at least 1 yr (duration: 3.3 ± 3.0 yr; fluoxetine-equivalent dose: 36 ± 13 mg/day) were recruited. In order to examine potential differences in cortical and trabecular bone measures, the SSRI-treated patients (male: height mean ± SD 180.1 ± 3.5 cm weight 86.0 ± 16.1 kg; female: height 163.3 ± 7.7 cm, weight 70.1 ± 13.6 kg) were matched with an age-similar group of healthy IBDS cohort members (controls) by sex, height, and weight using a variable optimal matching algorithm with two to four controls/patient (total 36 controls).⁴³ Mean values were calculated for each patient-matched control subgroup, and student’s paired t-test and the Wilcoxon nonparametric matched pairs signed rank test were used to compare patients and controls. In addition, group differences between SSRI patients and all 97 healthy controls were also tested by fitting a multivariable linear regression model that included group (patients/controls), weight, and height as independent variables; least squares (LS) group means were estimated and tests of mean differences were performed. The sample sizes of 46 male and 51 female IBDS controls provided 80% power to detect an effect size of 0.58 SD using a two-sided 0.05-level test. The sample sizes of 12 SSRI patients and 97 IBDS controls provided 80% power to detect an effect size of 0.86 SD using a two-sided 0.05-level test. The paired analysis of 12 SSRI patients and paired subgroups of 1 to 4 IBDS controls provided 80% power to detect and effect size of 0.89 SD using a two-sided 0.05-level test.

3.D. MD-CT, μ-CT, and dual-energy x-ray absorptiometry (DXA) imaging

High resolution MD-CT scans of the distal tibia were acquired at The University of Iowa Comprehensive Lung Imaging Center on a 128 slice SOMATOM Definition Flash scanner (Siemens, Munich, Germany) using the following CT parameters: single tube spiral acquisition at 120 kV, 200 effective mAs, 1 s rotation speed, pitch factor: 1.0, nominal collimation: 16 × 0.3 mm, scan length of 10 cm beginning at the distal tibia end-plateau, and total effective dose equivalent: 17 mrem ≈20 days of environmental radiation in the US. One AP projection scout scan of the entire tibia was acquired to locate the field of view (FOV) for the CT scan. High resolution MD-CT scan mode: The Siemens Flash scanner has two 64 rows of equal 0.6 mm detectors under two x-ray guns allowing operation in both single and dual source scan modes. The highest resolution single gun scan mode was used, which activated 16 of the most inner 0.6 detectors to maximize beam quality. Siemens double z sampling allowed for a dual sampling of the 0.6 mm detectors, splitting the signal so that each detector created a 0.3 mm slice in the z plane.⁴⁴ As specified by the manufacturer, the z-UHR scan mode within the Siemens Flash scanner enabled high spatial resolution with 14.0 line-pairs/cm at 10% modulation transfer function (MTF) and thus provided a more accurate slice profile and lowered partial volume artifact allowing for better separation of TB structures [Fig. 4(a)]. After scanning in a helical mode with a 0.4 mm slice thickness, data were reconstructed at 0.2 mm slice thickness using a normal cone beam method with a special U70u kernel achieving high structural resolution. A calibration phantom was scanned once per scan to calibrate CT Hounsfield units into BMD (mg/cm³). The same MD-CT scan protocol was applied for cadaveric ankle specimens as well as for human participants and the images were reconstructed at 0.2 mm isotropic voxel-size.

FIG. 4.

Matched axial image slices from postregistered MD-CT (a) and μ-CT (b) images of a cadaveric specimen.

Three repeat MD-CT scans of each distal tibia specimen were acquired after repositioning the specimen on the CT table. Following MD-CT repeat scans, each specimen was further scanned on a Micro-cat II (Siemens Pre-Clinical, Tennessee) cone beam μ-CT scanner after removing soft tissue and dislocating the tibia from the ankle joint to fit the specimen in the scanner. The following μ-CT parameters were used: 100 kV, 200 mAs, 720 projections over 220°, exposure 1 s/projection, 2 mm Al filter for beam hardening. The images were reconstructed using filtered back-projection: image size 1536 × 1536, 1024 slices at 28.8 μm isotropic voxel size [see Fig. 4(b)].

All human participants also underwent a DXA scan of the proximal femur on a Hologic QDR 4500A unit (Waltham, MA), performed by a certified densitometry technologist.

3.E. VOI Selection for in vivo studies

VOI was computed for the in vivo pilot study to adjust the VOI for individual-specific tibial length and width. The following protocol was adopted—(1) determination of tibial length by locating distal and proximal end plateaus on the MD-CT scout scan; all proximal sites are defined as percentage of tibial length in reference to the distal end plateau, (2) reorientation of the tibial image to align its axis with the coordinate z-axis using the same protocol described in Sec. 3.D, (3) location of the distal end plateau in the MD-CT volume scan, (4) determination of the ROI at the 5% proximal site of the distal tibia covering 2% of the tibial length, (5) determination of the inner trabecular region after applying a 60% peel on each cross-sectional slice of the ROI and defining the outer trabecular region as the annular section between 60% peel and 30% peel on each cross-sectional slice.

3.F. Image processing

Each image dataset was processed through the following step sequence—(1) computation of BMD at each voxel using a step-up ramp function, (2) resampling of BMD images at 0.15 mm isotropic voxel using a linear interpolation method, (3) computation of surface and arc skeletons,²⁶ (4) computation of tensor scale and bone measures at axial points, and (5) propagation of TB measures from axial points to the entire bone volume. The MD-CT Hounsfield number at each voxel was converted to a BMD (mg/cm³) value using average MD-CT values in three calibration rods in the INTable™ Calibration Phantom at concentrations of 0, 75, and 150 mg/cm³ of calcium hydroxyapatite (CaHA) homogeneously blended into the CT-Water™ compound; the Gammax™ calibration phantom was used for in vivo scans. Finally, the bone volume fraction of BVF at each voxel was computed as follows:

$${\displaystyle \text{BVF}\left(p\right)=\left\{\begin{array}{cc}\hfill 0,\hfill & \hfill \text{if BMD}\left(p\right)<940\text{ mg}/{\text{cm}}^3,\hfill \\ \hfill \frac{\text{BMD}\left(p\right)-940}{2184-940}\hfill & \hfill \text{if BMD}\left(p\right)\ge 940\text{ mg}/{\text{cm}}^3\text{ and }<2184\text{ mg}/{\text{cm}}^3,\hfill \\ \hfill 1\hfill & \hfill \text{othewise}.\hfill \end{array}\right.}$$

In the above equation, 940 mg/cm³ was used as the bone marrow density, while 2184 mg/cm³ was used as the density of fully mineralized bone as determined following the results observed by Hernandez et al.⁴⁵

4. RESULTS AND DISCUSSION

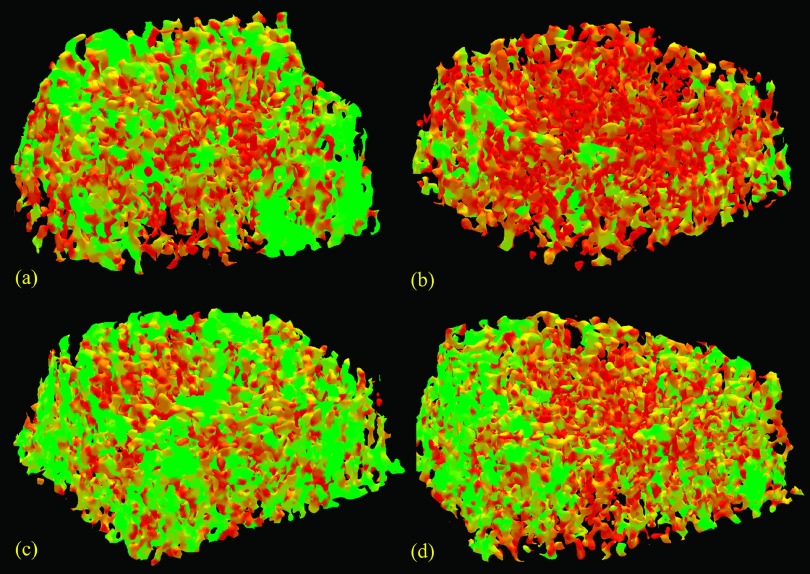
Results of tensor scale-based assessment of orientation and plate-width of individual trabeculae on a μ-CT image of a cadaveric ankle specimen are illustrated in Fig. 5. As observed in Fig. 5(b), tensor scale-based orientation successfully distinguishes between the longitudinal (orientation close to 90°) and transverse (orientation close to 0°) trabeculae. The tensor scale-based local plate-width measure on the same μ-CT image is presented in Fig. 5(c), while the analogous measure using the VTA method¹⁸ is presented in Fig. 5(d). There is strong visual agreement between tensor scale- and VTA-based plate/rod classifications of individual trabeculae. However, at several locations [indicated by arrows in Figs. 5(c) and 5(d)], the gradation of TB plate width along individual trabeculae is smoother as compared to VTA-based results. As discussed earlier, the sharp changes in VTA-based assessment of TB plate width are possibly caused by digitization errors acquired during path propagation. Also, skeletonization error affects VTA measures more severely as compared to tensor scale-based measures. The former method is primarily based on topologic and geometric analysis of the skeleton. In contrast, the new method uses the skeleton to determine representative locations where microarchitectural properties are sampled.

FIG. 5.

Tensor scale based analysis of TB microarchitecture. (a) A TB region selected from a μ-CT image of a human ankle specimen. (b) Color coded illustration of TB orientation at individual trabeculae. (c) and (d) Characterization of individual trabeculae on the continuum between a perfect plate (large plate-width) and a perfect rod (small plate-width) using the tensor scale (c) and VTA (d); the common color-coding bar for plate-width measures in (c) and (d) is shown on the right. Two regions with visual differences between the tensor scale- and VTA-based measures are indicated with arrows.

4.A. Accuracy analysis

To quantitatively examine the accuracy of the method, 3-D phantoms were computer-generated at 150 μm isotropic resolution with known plate-width as described in Sec. 3.A. These phantoms were generated with significant partial voluming and noise to simulate in vivo image quality. The average plate-width measures, PW_TS and PW_VTA, were computed from a given test phantom with the known true plate-width. The deviation of these measures from the ideal line is shown in Fig. 6. To examine the accuracy of the method, an error function was defined using the known plate-width of the structure. At each voxel with nonzero BVF, the error was defined as the difference between the true and computed measures of plate-width. Each data point in Fig. 6 was derived from one image. Finally, the mean and standard deviation of error measures from individual images at different plate widths were estimated and normalized by the average true plate-width from all images. The observed mean and standard deviation of errors for tensor scale-based plate-width PW_TS was 3.2% ± 2.0% as compared to 6.1% ± 4.6% for the VTA-based measure PW_{V TA}; this difference was statistically significant based on a paired t-test (p = 0.03).

FIG. 6.

Relationships between the true surface width and measures obtained using tensor scale- and VTA-based methods as observed using computer-generated phantoms. Error values are shown for the two methods.

4.B. Robustness under different conditions

Two experiments were undertaken to assess the robustness of TB microarchitectural measures. The stability of VTA- and tensor scale-based TB measures at different voxel sizes was evaluated using μ-CT images of cadaveric specimens. These images were down-sampled at different voxel sizes covering ex vivo and in vivo regimes. Specifically, ten μ-CT images with original isotropic voxel size of 28.5 μm were down-sampled at six isotropic voxel sizes of 57.0, 85.5, 114.0, 142.5, 171.0, and 199.5 μm. The variability in measured values of different TB measures, namely, PW_VTA, PW_TS, PRR_VTA, PRR_TS, tBMD_TS, and SMI at different voxel sizes, is shown in Figs. 7(a)–7(f). For a given measure and a down-sampled image, the error was computed as the difference between the observed value of the measure from the down-sampled image and that from the corresponding image at the original μ-CT voxel size. Finally, the mean and standard deviation of errors from ten μ-CT images across all down-sampled voxel sizes were computed and the results are reported in Fig. 8. As observed in Fig. 7, in general, the tensor scale-based measures show little voxel-size dependent bias in computed values, while the VTA-based measures show some signs of upward bias with larger voxel size, and the trend is magnified for SMI. This observation is confirmed in the results of quantitative error analysis presented in Fig. 8. Despite a wide range of down-sampling voxel sizes covering ex vivo to in vivo regimes, the average error was less than 6% for all three tensor scale-based TB measures and the average error observed for the tensor scale-based surface width measure PW_TS was 2.29%. Voxel size dependent errors in the VTA-based measures as well as SMI were higher as compared to the tensor scale-based measures. The VTA-based algorithm accumulates geodesic distance errors during path propagation and, also, the accuracy of the computed plate-width measure is further compromised by digitization of skeletal location. In principle, the computation of SMI is based on the binary representation of a TB network; therefore, it fails to incorporate any partial voxel voluming information at larger voxel sizes. The tensor scale-based algorithm minimizes these errors by directly computing the local plate-width in a volumetric object representation using an optimal ellipsoidal model that involves no digital path propagation. The observed results in Fig. 8 demonstrate the effectiveness of the fundamental methodological difference of the tensor scale approach for computing local plate-width.

FIG. 7.

Results of stability analysis for VTA- and tensor scale-based TB measures and SMI across different voxel sizes. (a) Observed values of the surface-width measure PW_VTA at different voxel sizes generated by down-sampling μ-CT images. The distribution of observed values for an individual specimen is assigned a unique color. (b)–(f) Same as (a) but for PW_TS, PRR_VTA, PRR_TS, tBMD_TS, and SMI measures, respectively.

FIG. 8.

Errors in observed values of different TB microarchitectural measures over a range of isotropic voxel-sizes of 57.0, 85.5, 114.0, 142.5, 171.0, and 199.5 μm as compared to their values obtained at the original voxel size of 28.5 μm.

To examine the performance of the algorithm under true loss of resolution by different imaging modalities with widely different characteristics of the MTF, the correlation of each TB measure computed from ex vivo μ-CT and in vivo MD-CT imaging was examined. The purpose of this experiment differed from the previous experiment where different voxel-sizes were obtained computationally, and the results showed that the proposed algorithm produces highly stable values for different measures across a wide range of resolution. On the other hand, the current experiment aimed to examine the relationship between observed values of a given measure from images acquired using ex vivo and in vivo imaging modalities with widely different MTF. As observed in Fig. 4, the trabecular structures are thicker and some small holes are filled in with MD-CT imaging due to a larger MTF. Therefore, the two widely different imaging modalities should not be expected to generate identical trabecular plate-width measures. Rather, the objective of this experiment was to assess the proportion of the variability in observed values of a specific measure based on MD-CT imaging that is “explained” by the values observed based on μ-CT imaging.

The correlation coefficients (r) representing the linear association between TB measures computed from postregistered μ-CT and MD-CT images are presented in Table I. For PW_TS, PRR_TS, and tBMD_TS, the linear regression line passed near the origin. Thus, the results of this experiment reveal that the tensor scale-based TB measures computed using two distinctly different modalities are strongly correlated, albeit not identical. Although, comparable results were observed for VTA-based measures, the correlation coefficients were marginally lower than those of tensor scale-based measures (Table I). The SMI measure showed worse performance in the linear regression analysis of computed measures from postregistered μ-CT and MD-CT images.

TABLE I.

Descriptive measures from linear regression analysis of the observed values of different TB measures computed from MD-CT and μ-CT imaging of cadaveric specimens.

	Tensor scale			VTA
TB measures	PWTS	PRRTS	tBMDTS	PWVTA	PRRVTA	SMI
Slope	0.89	0.87	0.88	0.83	0.84	0.33
Intercept (% of the mean value)	8.25	6.21	9.56	11.57	8.68	67.5
Correlation coefficient	0.92	0.91	0.91	0.89	0.88	0.72

4.C. Reproducibility analysis

Ten spherical VOIs were randomly selected in the first MD-CT scan of each cadaveric specimen (a total of 150 VOIs). Each VOI was located at least 8 mm proximal to the distal endplate. A postregistration algorithm was used to locate the matching VOIs in the second and third repeat scans. Reproducibility was tested at increasing VOI sizes. The relationship between the method’s reproducibility and VOI size is presented in Fig. 9. The average plate-width measure PW_TS at a VOI diameter of 1.05 mm or greater has an ICC that exceeds 0.95. In contrast, PW_VTA requires a VOI diameter of 3.15 mm to achieve equivalent reproducibility in terms of the ICC. For plate-to-rod ratio measures, both methods reach an ICC value of 0.95 with a VOI diameter of 3.15 mm or larger. The parameter tBMD_TS reaches an ICC value of 0.95 with a VOI diameter of 5.85 mm or larger; SMI reaches the ICC value of 0.95 with a VOI diameter of 4.35 mm or larger. Of note, the VOI diameter that achieves an ICC value of 0.95 represents the smallest region over which the measures can be reliably computed. In the case of surface width, the tensor scale algorithm proved to be considerably more reliable as the value stabilized at a much smaller VOI diameter.

FIG. 9.

Repeat MD-CT scan reproducibility of three TB measures as a function of VOI size. (a) At a VOI diameter of 1.05 mm or greater, the ICC value of plate surface width PW_TS using the tensor scale exceeded 0.95, while the same measure using VTA requires a VOI diameter of at least 3.15 mm to achieve a similar degree of reproducibility. (b) At a VOI diameter of 3.15 mm or greater, the ICC value of plate-to-rod ratio measures using both tensor scale and VTA exceeded 0.95. (c) The ICC value of longitudinal bone volume fraction tBMD_TS exceeded 0.95 at a VOI diameter of 5.85 mm or greater. (d) The ICC value of SMI exceeded 0.95 at a VOI diameter of 4.35 mm or greater.

4.D. In vivo pilot study results

An example of tensor scale-based assessment of individual trabecular plate-width for age-similar and height- and weight-matched female and male healthy controls is illustrated in Fig. 10. Observed PW_TS and PRR_TS measures for both the inner (i) and outer (o) trabecular regions were significantly lower for females; however, these differences were less pronounced for VTA- than for tensor scale-based measures (Table II). Using both methods, the difference in trabecular plate-width between males and females is greater at the outer region as compared to the inner region. Similar results were observed using SMI. This suggests that the difference in TB plate-rod microarchitecture between normal young adult males and females is more pronounced at outer TB regions as compared to inner regions. A large number of histologic studies^8,46 have confirmed the relationship between conversion of trabeculae from plates to rods and increased fracture risk. The results observed in this study present in vivo evidence that females have reduced TB plates as compared to males placing females at higher risk for osteoporotic fractures with bone loss due to aging or other clinical conditions.

FIG. 10.

An example of tensor scale-based assessment of individual trabecular plate-width for age-similar and height- and weight-matched female (a) and male (b) healthy controls. The female control had more rod-like trabeculae as compared to the matching male control.

TABLE II.

Tensor scale- and VTA-based trabecular bone measures (4% to 6% slice): comparisons by sex and association with body size measures in multivariable linear regression models.

	Males (N = 46)	Females (N = 51)		Associations with weight and heighta
(i)-inner ROI (o)-outer ROIb	mean ± SD	mean ± SD	Difference (%)c	β (SE) for weight, per 10 kg	β (SE) for height,per 5 cm	R2
PWTS (o) (μm)	1352 ± 313	1161 ± 257	14.1***	59 (17)***	30 (14)**	0.24
PWTS (i) (μm)	932 ± 189	853 ± 169	8.5**	35 (11)***	17 (9)*	0.21
PRRTS (o)	3.71 ± 0.65	3.36 ± 0.55	9.4***	0.04 (0.04)	0.08 (0.03)**	0.12
PRRTS (i)	3.14 ± 0.74	2.81 ± 0.60	10.5**	0.09 (0.04)**	0.08 (0.04)**	0.17
tBMDTS (o) (mg/cm3)	436.3 ± 39.4	427.7 ± 41.4	2.0	9.25 (2.55)***	−4.16 (2.11)*	0.12
tBMDTS (i) (mg/cm3)	407.5 ± 32.7	405.9 ± 31.3	0.4	7.78 (1.99)***	−3.02 (1.65)*	0.14
PWVTA (o) (μm)	1061 ± 191	942 ± 160	11.2***	28 (11)**	23 (9)**	0.22
PWVTA (i) (μm)	813 ± 155	743 ± 128	8.6**	20 (9)**	17 (7)**	0.18
PRRVTA (o)	3.71 ± 0.46	3.51 ± 0.37	5.4**	0.06 (0.03)**	0.04 (0.02)*	0.15
PRRVTA (i)	3.22 ± 0.36	3.09 ± 0.29	4.0*	0.04 (0.02)**	0.04 (0.02)**	0.17
SMI (o)	1.13 ± 0.75	1.57 ± 0.52	−38.9***	−0.08 (0.04)**	−0.10 (0.03)***	0.21
SMI (i)	2.06 ± 0.42	2.21 ± 0.32	−7.3*	−0.04 (0.02)*	−0.04 (0.02)**	0.14
Hip aBMD (DXA)	1.14 ± 0.16	1.02 ± 0.12	10.5***	0.04 (0.01)***	0.02 (0.01)***	0.46

^aMultivariable linear regression models with height and weight as independent variables, sex is not included as it does not show a statistically significant association with any of the bone outcomes in the presence of the anthropometric measures. β and (SE) are the parameter estimate associated with a10 kg increase in weight (5 cm increase in height), and its standard error from the fitted TB bone measure model.

^bInner ROI (i) corresponds to the inner region of trabecular bone (60% from the outer edge), outer ROI (o) corresponds to the outer region of trabecular bone (30% to 60% from the outer edge).

^cUnadjusted comparison of male and female IBDS cohort members: *p-value < 0.10; **p-value < 0.05; ***p-value < 0.01 from two sample t-tests.

A unique feature of the tensor scale algorithm is its ability to detect the transverse trabeculae (Fig. 5) in vivo which are used to define the transverse trabecular BMD or tBMD_TS. For most TB measures, height and weight were positively with them (Table II) and this might account for the fact that sex was correlated as well. For example, increases in both height and weight resulted in an increase in average plate-width and plate-to-rod ratio measures. Hip areal BMD (aBMD) from DXA scans of the healthy controls was significantly higher in males than females in unadjusted analysis (p < 0.01), but the difference became not significant with adjustment for body size; again suggesting that hip aBMD increased with increasing height and weight. The same was not true for tBMD_TS which was positively associated with weight but negatively associated with height. This opposite association with height and weight may explain why there appeared to be no significant difference in tBMD_TS between male and female controls in the unadjusted analysis, since females on average are both lighter and shorter than males. To the best of our knowledge, this result is the first in vivo observation related to the comparison of transverse trabecular BMD in males and females. There is evidence suggesting that reductions in the number of transverse trabeculae are associated with marked reduction in bone strength leading to failure due to buckling of longitudinal trabeculae.⁴⁷ This observation indicates that taller people may be at higher risk of fractures induced by buckling of longitudinal trabeculae. However, this early observation on the new measure of transverse BMD or tBMD_TS requires further investigation before a conclusion may be drawn.

The group of 12 SSRI-treated patients showed somewhat lower values for all trabecular measures than the healthy controls, with the exception of the SMI-based measures which were slightly higher. Trabecular plate-rod microarchitecture at the distal tibia in a male and a female SSRI-treated patient and matched male and female IBDS cohort members is illustrated in Fig. 11. In matched-pairs analysis, the largest difference was found for PW_TS − 12.5% for the outer region (p = 0.052, effect size 0.69) and 6% for the inner region (p = NS, effect size 0.43), corresponding differences for VTA-based measures were 7.2% (p = NS, effect size 0.49) and 3.2% (p = NS, effect size 0.25), and for SMI-based measures, they were 0.8% (p = NS, effect size −0.10) and 0.8% (p = NS, effect size −0.03), respectively (Table III). Patients also had 3% to 4% lower tBMD_TS (for comparison, the difference in DXA-based hip aBMD was approximately 5%). Multivariable linear regression models that compared SSRI-treated patients to the entire group of healthy controls showed similar results (data not shown). These results suggest that tensor scale-based measurements of TB plate-rod microarchitecture are more sensitive to differences associated with the extended use of SSRIs than either DXA-, SMI, or VTA-based measures. Major depressive disorder has been associated with low bone mass.^48,49 Furthermore, both animal and human studies have implicated SSRI use in low bone mass.^32,50 The present findings contribute to this growing literature despite not being able to disentangle the effect of SSRIs from that of the underlying psychiatric condition on the skeleton.

FIG. 11.

The same as Fig. 10, but comparison between age-sex-BMI-similar IBDS cohort members (a) and (c) and SSRI patients (b) and (d). A matching male pair (a) and (b) and a matching female pair (c) and (d) are shown.

TABLE III.

Tensor scale- and VTA-based trabecular bone measures: comparisons of SSRI-treated patients and matched IBDS controls.

	SSRI-treated patients (N = 12)	IBDS controls (N = 36)a
(i)-inner ROI (o)-outer ROIb	mean ± SD	mean ± SD	difference SSRI-control (%)c	Effect size (in SD units)
PWTS (o)	1092 ± 272	1245 ± 184	−12.5c*	0.69
PWTS (i)	790 ± 134	851 ± 127	−6.20	0.43
PRRTS (o)	3.46 ± 0.68	3.50 ± 0.48	−0.44	0.05
PRRTS (i)	2.74 ± 0.66	2.83 ± 0.55	−1.68	0.14
tBMDTS (o)	422.3 ± 49.8	435.0 ± 17.3	−2.94	0.27
tBMDTS (i)	395.2 ± 41.6	414.6 ± 21.3	−4.31	0.37
PWVTA (o)	918 ± 184	992 ± 124	−7.23	0.49
PWVTA (i)	714 ± 120	743 ± 102	−3.16	0.25
PRRVTA (o)	3.50 ± 0.47	3.58 ± 0.28	−2.00	0.18
PRRVTA (i)	3.04 ± 0.33	3.08 ± 0.27	−1.00	0.13
SMI (o)	1.50 ± 0.62	1.45 ± 0.50	0.80	−0.10
SMI (i)	2.24 ± 0.31	2.23 ± 0.27	0.81	−0.03
Hip aBMD (DXA)	1.02 ± 0.16	1.08 ± 0.11	−5.04	0.44

^aA total of 36 controls from the Iowa Bone Development Study, 1 to 4 controls per SSRI patient (subgroup), mean values from subgroups were used as paired values for comparisons with matched SSRI patients. Values in this column are the mean of the control subgroup means.

^bInner ROI (i) corresponds to the inner region of trabecular bone (60% from the outer edge), outer ROI (o) corresponds to the outer region of trabecular bone (30% to 60% from the outer edge).

^c*p-value < 0.05 from paired t-test (results were verified using nonparametric Wilcoxon matched pairs signed rank test).

5. CONCLUSIONS

A new method for characterization of individual TB microarchitecture on the continuum between a perfect plate and perfect rod is presented using tensor scale analysis of MD-CT imaging at the distal tibia. A comprehensive set of experiments using computer-generated phantoms and MD-CT distal tibia imaging of fifteen cadaveric ankle specimens, as well as human participants, was conducted to examine the performance of the new algorithm and the results are presented. Observed results demonstrate high accuracy and robustness of tensor scale measures across a wide range of voxel sizes covering ex vivo and in vivo imaging modalities. Also, high repeat MD-CT scan reproducibility of the new tensor scale computation method was observed in the cadaveric ankle imaging. Tensor measures for TB derived from ex vivo μ-CT and in vivo MD-CT imaging with significantly different resolution were found to be strongly correlated. Results from two pilot human studies suggest that tensor scale-based TB measures derived from MD-CT imaging are superior to DXA or even VTA-based methods with regard to detecting sex differences in TB microarchitecture as well as differences associated with extended SSRI treatment. Tensor scale provides a unique measure of transverse BMD contributed by transverse trabeculae which stop buckling failure of bones. The observed data suggest that transverse BMD may be positively associated with weight but negatively associated with height, putting taller people at risk for fractures induced by buckling. However, this early observation on the new measure of transverse BMD requires further validation before a definitive conclusion can be drawn. While the observed result is important, it will be useful to answer whether the same would be also true in older adults, who are at highest risk for osteoporosis and fractures. Overall, the results provide initial evidence that the tensor scale-based method represents an improvement over the VTA-based method and may be more sensitive than traditional DXA-based measures to TB changes due to hormonal, physiological, health-related, or environmental changes. As compared to SMI, tensor scale-based measures demonstrate improved stability at different voxel sizes and image resolutions. As observed from in vivo pilot studies, compared to tensor scale-based measures, SMI produced similar results in identifying sex differences in TB microarchitecture; however, SMI underperformed when detecting TB microarchitectural differences associated with extended SSRI treatment. Finally, it should be mentioned that SMI is a global measure over a ROI and it fails to capture localized bone loss or conversion of individual trabecular plates into rods.

One drawback of the current tensor scale computation algorithm is its high computational complexity. Every time the tensor scale is computed at a given point, it requires BVF interpolations at several sample points on each of multiple star-lines. Also, repeated computation of the tensor scale is needed at each axial point during its location optimization. Current implementation of the tensor scale computation algorithm on a desktop with a 2.53-GHz Intel(R) Xeon(R) CPU and Linux OS requires approximately 3–4 h for a typical MD-CT image analysis of human TB over a 300 × 300 × 300 voxel array at an isotropic resolution of 150 μm.