Measuring retinal blood flow in rats using Doppler optical coherence tomography without knowing eyeball axial length

Abstract

Purpose:

Doppler optical coherence tomography (OCT) is widely used for measuring retinal blood flow. Existing Doppler OCT methods require the eyeball axial length, in which empirical values are usually used. However, variations in the axial length can create a bias unaccounted for in the retinal blood flow measurement. The authors plan to develop a Doppler OCT method that can measure the total retinal blood flow rate without requiring the eyeball axial length.

Methods:

The authors measured the retinal blood flow rate using a dual-ring scanning protocol. The small and large scanning rings entered the eye at different incident angles (small ring: 4°; large ring: 6°), focused on different locations on the retina, and detected the projected velocities/phase shifts along the probing beams. The authors calculated the ratio of the projected velocities between the two rings, and then used this ratio to estimate absolute flow velocity. The authors tested this method in both Intralipid phantoms and in vivo rats.

Results:

In the Intralipid flow phantom experiments, the preset and measured flow rates were consistent with the coefficient of determination as 0.97. Linear fitting between preset and measured flow rates determined the fitting slope as 1.07 and the intercept as −0.28. In in vivo rat experiments, the measured average total retinal blood flow was 7.02 ± 0.31μl/min among four wild-type rats. The authors’ measured flow rates were consistent with results in the literature.

Conclusions:

By using a dual-ring scanning protocol with carefully controlled incident angle difference between the two scanning rings in Doppler OCT, the authors demonstrated that it is feasible to measure the absolute retinal blood flow without knowing the eyeball axial length.

1. INTRODUCTION

Abnormal retinal blood flow is associated with many blinding diseases such as diabetic retinopathy (DR), glaucoma, branch retinal vein occlusion (BRVO), and others.^1–3 In the early stage of DR, the loss of pericytes⁴ can progress into capillary dropout and lead to abnormal retinal blood flow rate.⁵ In glaucoma, elevated intraocular pressure is associated with reduced blood flow rate around the optic nerve head.² In BRVO, lower blood flow in retinal arterioles is also reported.³ Thus, the precise measurement of retinal blood flow rate is important for detecting and treating these blinding diseases.

There have been promising experimental investigations to measure retinal blood flow rate with spectral domain optical coherence tomography (SD-OCT).⁶ To measure blood flow, both the vessel size and the blood velocity must be quantified. In SD-OCT, retinal vessel size is normally extracted from a cross-sectional B-scan image, because the axial resolution is higher than the lateral resolution. Several techniques have been proposed to extract retinal blood flow velocity: (1) the indirect method by first calculating the phase shift variance or light intensity within vessels,⁷ then calibrating the measured results using well-controlled phantoms; and (2) the mean phase shift method,^8,9 in which the phase shift between two adjacent A-lines can directly quantify axial flow velocity. However, this method requires the Doppler angle (i.e., the angle between the probing beam and retinal vessels) to measure absolute velocity.¹⁰

Researchers have introduced different approaches to measure or circumvent the Doppler angle by using either a multiple-beams scanning scheme^8,10,11 or the en face Doppler approach,^12–14 but such methods require the eyeball axial length. The multiple-beams scanning approach requires the eyeball axial length in order to access the geometrical information of the retinal vessels, which thus enables the Doppler angle calculation. The en face Doppler method requires the eyeball axial length to calibrate a transverse scanning dimension to measure flow rate. Instead of measuring the eyeball axial length for every subject, a more commonly applied approach is a universal empirical eyeball axial length for flow quantification. In reality, however, eyeball axial length varies with age (e.g., the aged eye has a significantly shorter eyeball¹⁵) and other eye conditions. In myopia, for instance, the eyeball axial length of subjects with −4.36 D nearsightedness was reported to be 5.2 mm shorter than subjects with −6.00 D.¹⁶ Therefore, the ability to quantify retinal blood flow without knowing the eyeball axial length has yet to be developed.

Recently, Blatter et al. proposed an angle-independent flow assessment,¹⁷ in which they simultaneously illuminated the retina with two beams at different incident angles. The corresponding mean phase shifts detected by the two illumination beams can extract the absolute flow rate without knowing the eyeball axial length. Despite promising aspects of the angle-independent method, it requires perfect alignment of the two illuminating beams, which complicates the system and exposes the eye to high laser intensity.

In the current study, we demonstrate an eyeball axial length independent flow measurement using dual-ring scanning Doppler SD-OCT. First, we consecutively scanned a few pairs of small and large rings on the retina around the optic disc, then acquired parameters such as the mean phase shifts and vessel cross-sectional sizes from both the small and large scanning rings. Finally, we used the detected phase shifts, vessel sizes, and preset scanning angles between the small and large scanning rings to quantify the absolute blood flow rate. Since the real eye optical system is complex,^18,19 factors such as multiple refracting surfaces from the cornea and ocular lens, among others, complicate the blood flow rate calculation. As a preliminary study, we employed a simplified optical model of the eye as used by other groups.^11,13,18 We simplified the multiple refracting ocular surfaces into a single ocular lens, and assumed the single ocular lens can focus a collimated beam perfectly onto the retina. We also assumed that the simplified ocular lens would not modify the preset incident angles.

We tested the proposed method in both phantoms and in vivo rat eyes. The Intralipid phantom experiments demonstrated the accuracy of the proposed flow measurement. In vivo rat experiments showed the consistency of the measured retinal blood flow between our approach and other reported results.¹⁴ Compared with other dual-ring Doppler SD-OCT investigations,^10,11 our method does not require, and thus is less sensitive to, the eyeball axial length. Furthermore, we illuminated only a single beam into the eye at one time, which reduced the alignment complexity and lowered the laser exposure to the retina.

2. METHODS AND MATERIALS

2.A. Experimental setup

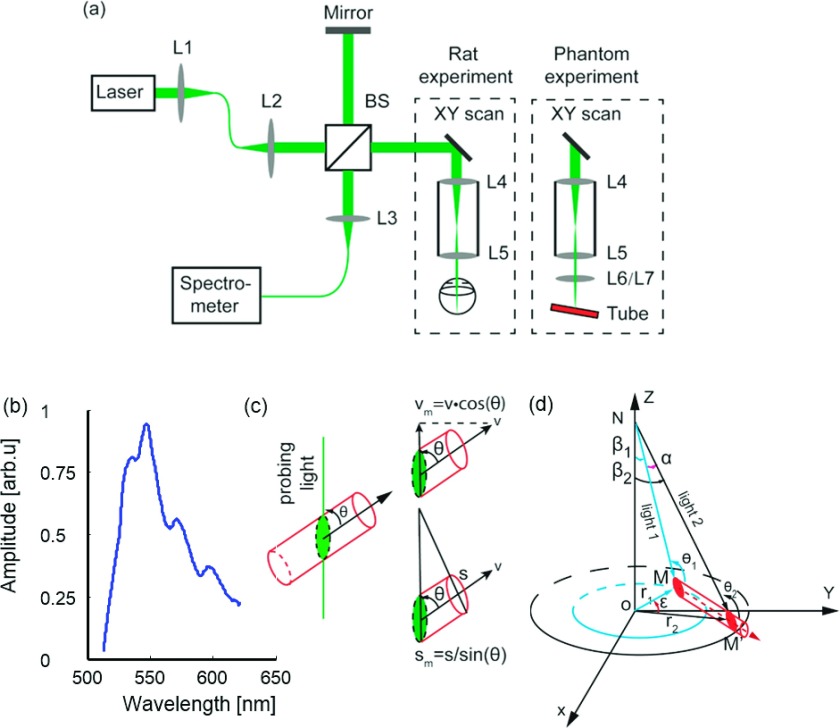
Our experimental system is described briefly here; more details can be found in our previous paper.¹⁹ We implemented a free-space SD-OCT, as shown in Fig. 1(a), where a supercontinuum laser [SuperK NKT photonics; center wavelength: 568.5 nm; bandwidth: 107 nm; spectrum of the laser source shown in Fig. 1(b)] light was collimated and split into the sample arm and the reference arm. In the sample arm, the laser beam was scanned by a 2D galvanometer (QS-7, Nutfield Technology) and relayed to the eye/phantom through a telescope system (f_L4 = 75 mm, f_L5 = 15 mm). The reflected light from the sample arm and the reference arm was combined and detected by a homemade spectrometer (spectral resolution: 0.0522 nm). The measured axial resolution of the SD-OCT is 1.7 μm in air, which gives a 1.25 μm axial resolution in the retina, considering the refractive index of the retina is 1.36.²⁰ The lateral resolution of the SD-OCT is around 15 μm. The imaging speed was 70 kHz for in vivo rat experiments and 25 kHz for phantom experiments. The signal-to-noise ratio (SNR) of the SD-OCT was measured at 95 dB with 70 kHz A-line rate. In the present study, the laser power was set at 0.8 mW for in vivo rat experiments, which is considered safe based on the American National Standards Institute for the safe use of lasers (ANSI Z136.1-2014); see supplementary material²¹ for more details.

FIG. 1.

(a) Schematic of the experimental setup for in vivo rodent and phantom imaging; L1–L7 are lenses and BS is the beam splitter. (b) Light source spectrum. (c) Dependence of measured velocity and measured cross-sectional vessel size on the Doppler angle. (d) Geometry to quantify the retinal blood flow rate from the dual-ring scanning.

2.B. Principles of flow measurement without eyeball axial length

Within one retinal vessel, the absolute flow rate F (μl/min) is the product of the absolute flow velocity V (mm/s) and the perpendicular cross-sectional vessel size S (μm²). Alternatively, as illustrated in Fig. 1(c), F also can be quantified from the detected projected mean velocity V_m and the measured vessel size area S_m as

$${\displaystyle F=VS=\frac{V_m}{cos\left(\theta \right)}{S}_m\hspace{0.17em}sin\left(\theta \right)=V_m{S}_{m}tan\left(\theta \right),}$$ (1)

where θ (°) is the Doppler angle. In Eq. (1), V_m can be calculated by

$${\displaystyle V_m=\frac{f_{\text{sample}}{\lambda }_0\mathrm{\Delta }\varphi }{4\pi n}=\frac{f_{\text{sample}}{\lambda }_0}{4\pi n}\frac{\int \varphi d{S}_m}{S_m},}$$ (2)

where f_sample (kHz) is the SD-OCT A-line rate, λ₀ (nm) is the center wavelength of the SD-OCT light source, and Δϕ (rad) is the flow-induced mean phase shift within the vessel. S_m can be measured within the cross-section B-scan as

$${\displaystyle S_m=\pi {\left(\frac{\text{Dia}}{2}\right)}^2=\pi {\left(\frac{N\_P\times P\_L}{2}\right)}^2,}$$ (3)

where Dia is the vessel diameter along the axial direction, N_P is the number of pixels in Dia, and P_L is the pixel size in the axial dimension of the image. N_P can be obtained from the B-scan image, and P_L in the current system is 0.62 μm. Combining Eqs. (1)–(3), we can calculate F as

$${\displaystyle F=\frac{f_{\text{sample}}{\lambda }_0\int \varphi d{S}_m}{4\pi n}tan\left(\theta \right)=\frac{f_{\text{sample}}{\lambda }_0\mathrm{\Delta }\varphi \pi {\left(\frac{N\_P\times P\_L}{2}\right)}^2}{4\pi n}tan\left(\theta \right).}$$ (4)

According to Eq. (4), F can be calculated once the Doppler angle θ is known.

To assess the Doppler angle θ without the eyeball axial length, we employed a dual-ring scanning protocol.²² As shown in Fig. 1(d), we consecutively scanned several pairs of small and large rings on the retina with different preset angles (β₁ and β₂). The small and large scanning rings intersect the centerline of one retinal vessel at positions M and M′. For the small and large rings, (θ₁, θ₂) and (r₁, r₂) are the corresponding Doppler angles and radiuses, respectively. During experiment, the angle difference between β₁ and β₂ was set to be small (2°) to ascertain the same depth locations of the small and the large rings on the retina (around 30 μm deviation in depth location). Assuming the absolute blood velocity within the sample vessel is V, the corresponding velocities detected by the probing beam NM′ and NM are

$${\displaystyle V_s=Vcos\left({\theta }_1\right),}$$ (5)

$${\displaystyle V_b=Vcos\left({\theta }_2\right)=Vcos({\theta }_1+a),}$$ (6)

where a is the angle between the two probing beams. Combining Eqs. (5) and (6), we have

$${\displaystyle \frac{V_b}{V_s}=\frac{Vcos({\theta }_1+a)}{Vcos\left({\theta }_1\right)}=\frac{cos\left({\theta }_1\right)cos\left(a\right)-sin\left({\theta }_1\right)sin\left(a\right)}{cos\left({\theta }_1\right)}=cos\left(a\right)-tan\left({\theta }_1\right)sin\left(a\right).}$$ (7)

The Doppler angle θ₁ can then be derived from Eq. (7) as

$${\displaystyle tan\left({\theta }_1\right)=\frac{cos\left(a\right)-\frac{V_b}{V_s}}{sin\left(a\right)}.}$$ (8)

According to Eq. (8), we can obtain the Doppler angle θ₁ if the angle a is known. To obtain a, we denote the eyeball axial length (NO) as h, the geometrical path lengths (NM and NM′) of the two probing beams are l₁ and l₂, respectively, as shown in Fig. 1(d). We can calculate the length of r₁, r₂, l₁, and l₂ by

$${\displaystyle r_1=htan\left({\beta }_1\right),}$$

$${\displaystyle r_2=htan\left({\beta }_2\right),}$$

$${\displaystyle l_1=h/cos\left({\beta }_1\right),}$$

$${\displaystyle l_2=h/cos\left({\beta }_2\right).}$$ (9)

Within the triangle M′OM, we denote the length of M′M as l₃, and we have

$${\displaystyle {l_3}^2={r_1}^2+{r_2}^2-2r_1{r}_{2}cos\left(\epsilon \right),}$$ (10)

where ε is the angle between OM and OM′, which can be directly obtained from B-scan images of the large and small scanning rings. Within the triangle M′NM, the angle a can be calculated by

$${\displaystyle cos\left(a\right)=\frac{l_1^2+l_2^2-l_3^2}{2l_1{l}_2}=\frac{h^{2}sec{\left({\beta }_1\right)}^2+h^{2}sec{\left({\beta }_2\right)}^2-h^{2}tan{\left({\beta }_1\right)}^2-h^{2}tan{\left({\beta }_2\right)}^2+2h^{2}tan\left({\beta }_1\right)tan\left({\beta }_2\right)cos\left(\epsilon \right)}{2h^{2}sec\left({\beta }_1\right)sec\left({\beta }_2\right)}=cos\left({\beta }_1\right)cos\left({\beta }_2\right)+sin\left({\beta }_1\right)sin\left({\beta }_2\right)cos\left(\epsilon \right).}$$ (11)

With calculated angle α, the Doppler angle θ is then obtained from Eq. (8), and the retinal flow rate can be calculated further from Eq. (4) without requiring the eyeball axial length.

2.C. Phantom experiment

Figure 1(a) shows the schematic diagram of the phantom experiment. One additional lens (either L6 or L7) was placed on the focal plane of the telescopic system (L4 and L5) to mimic the ocular lens. To simulate different eyeball axial lengths, the focal lengths of L6 and L7 were selected to be 10 and 12 mm, respectively, which focused the probing light onto a capillary tube (Paradigmoptics, CTPS125-250; inner diameter: 125 μm). The capillary tube was connected to a syringe pump (A-99, Razel). We set the Doppler angle of the capillary tube at approximately 82°, which is close to the Doppler angle obtained from in vivo rat experiments.⁹ A 1% Intralipid suspension was pumped through the capillary tube, with flow rate changing from 1 to 8 μl/min. We scanned eight consecutive pairs of small and large rings on the capillary tube, with the scanning angles β₁ and β₂ at 4° and 6°, respectively. Each scanning ring contained 4096 A-lines, and the A-line rate was 25-kHz. The maximum flow-induced mean phase shift in our experiments was around 1.28 rad, which prevented phase wrap.

2.D. Animal preparation

We imaged Long Evans rats (Charles River, 300 g) in our in vivo experiments. The rat was first anesthetized with a mixture of 2% isoflurane and 3 l/min regular air flow for 10 min, then anesthetized with 1.5% isoflurane and 2 l/min regular air for 5 min. During imaging, the isoflurane rate and regular air flow rate were kept constant at 1.5% and 2 l/min, respectively. We dilated the rats’ pupils with 1% tropicamide ophthalmic solution and paralyzed the iris sphincter muscles with 0.5% tetracaine hydrochloride ophthalmic solution. We applied artificial tear drops (Systane, Alcon Laboratories) every minute to prevent corneal dehydration during imaging. We also monitored the rats’ electrocardiogram (ETH-256 Amplifier, Iworx) during imaging. To measure the retinal blood flow, we scanned eight consecutive pairs of small and large rings on the rat retina, with scanning angles β₁ and β₂ at 4° and 6°, respectively. To sample the pulsatile blood flow profile, all scanning rings (small and large) contained 4096 A-lines at 70-kHz A-line rate.

All experimental procedures complied with the ARVO Statement for the Use of Animals in Ophthalmic and Vision Research, and the laboratory animal protocol was approved by the Institutional Animal Care and Use Committee at Northwestern University.

3. RESULTS

3.A. Phantom experiment results

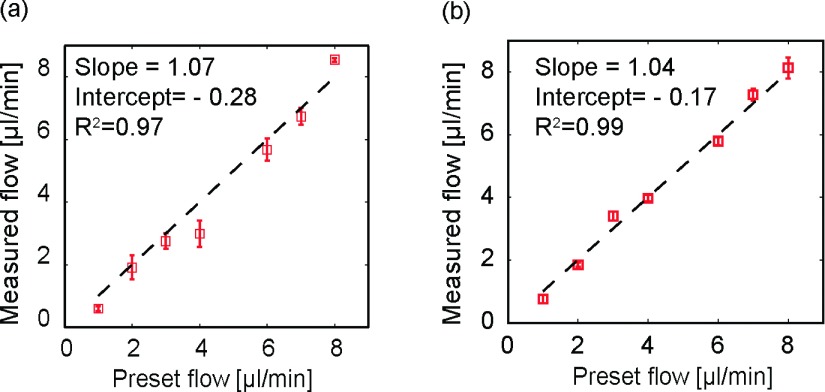
We used two lenses with different focal lengths to mimic different eyeball axial lengths in the Intralipid flow phantom experiments. L6 had a focal length of 10 mm, L7 had a focal length of 12 mm. Figure 2(a) shows that the measured flow rate was consistent with the preset values (linear fitting slope: 1.07; R² = 0.97, where R² is the coefficient of determination) using L6. We then replaced L6 with L7 to test the stability of our flow measurement without the eyeball size. The measured flow results are shown in Fig. 2(b), in which the preset flow rates were consistent with measured flow rates (linear fitting slope: 1.04; R² = 0.99). By comparing Fig. 2(a) with Fig. 2(b), we found a higher standard deviation in Fig. 2(a) (L6), which was probably caused by slight misalignment of the system using L6 (i.e., the tube may not have been perfectly placed in the focal plane of L6).

FIG. 2.

Validation of the flow measurement in phantom experiments. (a) Comparison of measured and preset flow rates using L6. (b) Comparison of measured and preset flow rates using lens L7.

We further tested the accuracy in the Doppler angle measurement. Using L6, the detected Doppler angles were 82.4° ± 0.4° and 84.6° ± 0.45°; using L7, the angles were 82.6° ± 0.45° and 85° ± 0.3°. The measured Doppler angles were consistent with but slightly larger than the preset values (82° and 84°). The relatively enlarged measurements of the Doppler angles may be caused by the imprecision of our preset angles.

3.B. Animal experiment results

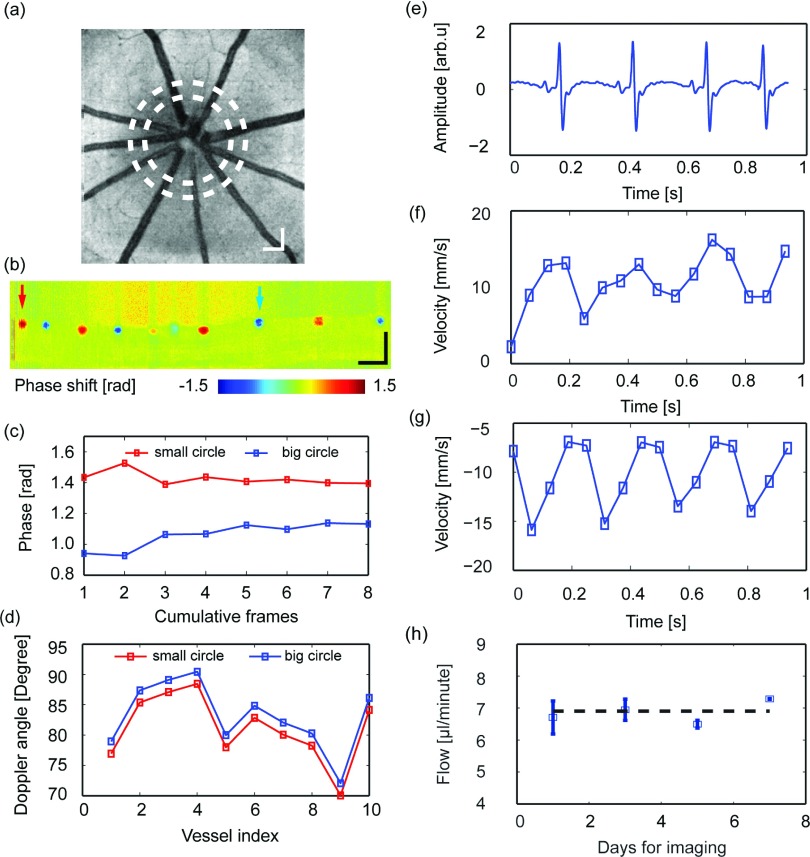
We further tested the flow quantification without eyeball axial length in rats in vivo. Figure 3(a) shows the OCT fundus image of one sample rat eye, where two dashed circles highlight the trajectories of the dual-ring scanning. Figure 3(b) shows one sample Doppler SD-OCT B-scan from the inner scanning ring; the left and right arrows highlight an artery and a vein, respectively. We scanned eight consecutive dual-ring pairs and tested the mean phase stability across a different number of cumulative Doppler B-scans. We considered the mean phase shift stable if it was identical between the adjacent cumulative B-scans (defined as a difference less than 0.05 rad). In our study, the stable mean phase shift was achieved after seven B-scan data averaging (0.006 rad difference from sixth averaging to seventh averaging), as shown in Fig. 3(c). With the stable phase shift from both small and large scanning rings, the Doppler angle θ was then retrieved [shown in Fig. 3(d)].

FIG. 3.

In vivo imaging of retinal blood flow in rodents. (a) Fundus imaging of a rat eye; the two dashed circles indicate where the dual-ring scans were performed. (b) The phase image from the inner-circle scan. (c) Phase stability across a different number of cumulative frames for a sample vessel, indicated by the left arrow in panel (b). (d) Estimated Doppler angles for all the vessels from both small and large scanning locations. (e) Recorded rat electrocardiogram during imaging. (f) Measured pulsatile flow from one retinal artery, highlighted by the left arrow in panel (b). (g) Measured pulsatile flow from one retinal vein, highlighted by the right arrow in panel (b). (h) Consistency in flow imaging of the same rodent subject over seven days. Bar: 200 μm.

After extracting the Doppler angles, we quantified the pulsatile flow velocities in both artery and vein. Figures 3(f) and 3(g) show sample arterial and venous pulsatile flow velocities, respectively. The retinal arterial and venous pulsatile blood flow were synchronized with the electrocardiogram, with the venous pulsatile flow profile delayed by 0.15 s. We also quantified the absolute retinal flow rate. In this particular rat, the total retinal blood flow was around 7 μl/min, which is consistent with other reported flows in rats under the same anesthesia condition.^9,14 The measured average total retinal blood flow was 7.02 ± 0.31 μl/min among four different wild-type rats. Furthermore, the stability of the flow measurement without the eyeball axial length was confirmed when we repeatedly monitored the rats for one week. We expected the rats’ total retinal flow to have minimal variation within such a short period. We can see from Fig. 3(h) that the four independent measuring retinal flow rate results were consistent: the standard deviation of the measured mean flow rate across four independent measuring points was 0.34 μl/min or 4.86%.

4. DISCUSSION

Most existing Doppler OCT studies required the eyeball axial length to measure retinal blood flow,^10,13,14 in which empirical eyeball axial length values are often used because the retinal blood vessel size and flow velocity are calculated separately. However, variations in the interindividual eyeball axial length were expected to induce biased retinal blood flow rate measurement.⁸ By adopting the traditional dual-ring scanning Doppler OCT, we tested the dependence of the blood flow measurement on eyeball axial length in rats.¹¹ When we intentionally increased the eyeball axial length from 5 to 7 mm (the empirical rat eyeball axial length reported is 6 mm) in Doppler OCT flow measurement, the calculated total rat retinal blood flow rate changed from 6.3 to 9.1 μl/min. A 2 mm variation in the eyeball axial length induced a 2.8 μl/min fluctuation in the calculated flow rate, which clearly demonstrated the dependence of the eyeball axial length and retinal blood flow measurement in existing dual-ring Doppler OCT. For comparison, our method’s absolute flow rate was 7.02 μl/min.

In this work, building on the dual-ring scanning protocol, we directly calculated retinal blood flow without separating the retinal vessel size and blood velocity measurements. We scanned dual rings on the retina consecutively, and detected the flow-induced mean phase shifts from both the small and large scanning rings, respectively. The mean phase shifts were used to measure projected blood flow velocity along the OCT probing beams; the phase shift ratios between the small and large scanning rings were used to extract the Doppler angles. The vessel diameters in the cross-section B-scan image were measured along the axial direction. In this way, we measured the absolute blood flow rate without knowing the eyeball axial length, and validated the measurement accuracy through Intralipid phantom experiments by using lenses with different focal lengths to mimic different eyeball axial lengths (Fig. 2).

According to Eqs. (8) and (11), accurate retinal blood flow measurement depends on factors such as preset scanning angles β₁ and β₂, and the angles α and ε. Among these factors, the most critical are the preset scanning angles β₁ and β₂. If the preset scanning angles are too small, the Doppler angles between the OCT probing beams and the blood vessels will be close to 90°, which can greatly reduce the contrast of the mean phase shifts in Doppler OCT and degrade the accuracy of the retinal flow measurement. On the other hand, the difference in the scanning angles between the small ring (β₁) and the large ring (β₂) needs to be selected carefully. The principle of the angle-difference selection is that it should be small enough to ensure comparable SNR of the phase shifts between the two scanning rings, as well as to ensure the same depth position of the two scanning rings on the retina. A scanning step greater than 1.4 μm between adjacent A-lines can reduce the SNR in phase shift measurement.¹¹ In the current study, there were 4096 A-lines within each scanning ring; the 1.4 μm scanning step determines the largest scanning angle to be 8.65° for rat eyes (6 mm in axial eyeball length). Furthermore, the difference in the scanning angles should be large enough to detect the phase shift difference between the small and large scanning rings. Since the acquired mean Doppler angle is around 80° in rat eyes,⁹ according to Eqs. (7) and (11), the 2° angle difference can lead to up to a 20% phase shift difference between the small and large rings. Therefore, we set the scanning angle of the small and large rings as 4° and 6°, and the scanning angle difference was 2°.

Since the proposed method does not require eyeball axial length, it is less sensitive to the eyeball size variation and can measure retinal flow with greater accuracy. Another advantage of our method is its simplicity: no additional hardware is required and it can be easily implemented in almost any commercial OCT device on the market.

There are several challenges in our axial-eyeball-free flow quantification. In the current method, the backscattered light signals from the small and large scanning rings are detected sequentially by one spectrometer. Despite results averaging across multiple B-scans, the pulsatile flow and eye motion may cause variations in the phase shift ratio between the small and the large rings. The best solution is to use dual-beam OCT with two spectrometers, as demonstrated by other groups,^8,17 because it collects the signals from the small and large scanning rings simultaneously. The disadvantages of employing the dual-beam OCT come from stricter laser safety limits and much higher instrumentation costs. Furthermore, the acquired vessel cross-sections may not be perfect circles in B-scans. Measuring the vessel cross-sectional areas as ellipses would be more accurate; however, this requires the lateral sizes of retinal vessels, and determining vessel lateral size requires the eyeball axial length for proper dimension calibration. To completely circumvent eyeball axial length, we assumed that vessel areas are circular and measured only the vessel diameter in axial direction; the circular assumption, however, may cause biased results.

The second aspect to consider is the SNR of the acquired phase shift. Since we quantified the retinal flow directly from the phase shift ratio between the small and large scanning rings, the acquired phase shift signals with low SNR can induce biased flow measurement. Also, when the flow rate is low or the Doppler angle is close to 90°, the contrast of phase shift is greatly reduced and thus compromises the proposed flow measurement. Further investigation is necessary to determine how to measure blood flow without the eyeball axial length when low flow rate or the 90° Doppler angle is present.

Finally, we reported 0.15 s venous pulsatile flow delay related to arterial flow; however, the measurement accuracy needs attention. In the present study, the ring sampling rate is 70 kHz/4096 = 17 Hz, and the time interval between two adjacent sampling B-scans on the same retinal vessel is 1/17 = 0.0588 s, implying that the precision in pulsatile flow detection is 0.0588 s. Since the corresponding cardiac cycle duration for a sample rat is around 0.2288 s [Fig. 3(e)], our current imaging protocol may not be able to precisely detect the time interval between the venous and arterial pulsatile flow. To detect the pulsatile flow profile with higher accuracy, a higher A-line rate is required.

In conclusion, we demonstrated retinal flow measurement without the need for the eyeball axial length based on dual-ring scanning protocol. In both flow phantom and in vivo rodent experiments, we showed that the proposed method can help to eliminate the influence of eyeball axial length variation in retinal flow quantification. Future research will focus on the limitations described above.