Micro-elastometry on whole blood clots using actuated surface-attached posts (ASAPs)

Abstract

We present a novel technology for microfluidic elastometry and demonstrate its ability to measure stiffness of blood clots as they form. A disposable micro-capillary strip draws small volumes (20 μL) of whole blood into a chamber containing a surface-mounted micropost array. The posts are magnetically actuated, thereby applying a shear stress to the blood clot. The posts’ response to magnetic field changes as the blood clot forms; this response is measured by optical transmission. We show that a quasi-static model correctly predicts the torque applied to the microposts. We experimentally validate the ability of the system to measure clot stiffness by correlating our system with a commercial thromboelastograph. We conclude that actuated surface-attached post (ASAP) technology addresses a clinical need for point-of-care and small-volume elastic haemostatic assays.

INTRODUCTION

Rheology is used throughout industry and academic research to study a wide range of materials, from the mouth-feel of ice cream1 to the mechanics of individual cells.^2,3 However, typical rheometers require large specimen volumes, extensive pre-analytical processing, and highly-trained operators. The last two decades have seen the emergence of micro-rheology, the field of small-volume visco-elastic measurements.⁴ Micro-rheology has been dominated by micro-bead rheology, but new microfluidic devices and micro-cantilever technologies have also been developed.^5–11 Lab-on-a-chip rheometers simplify data collection and expand the reach of viscoelastic measurements. Potential applications exist in medical diagnostics, process monitoring in manufacturing, and mobile or field environments.

Numerous microfluidic systems have been shown to successfully characterize viscoelastic materials. Many rely on a flowing fluid^6,12; these are not appropriate systems for materials that are primarily elastic. These systems have had success in measure changes in visco-elastic properties of whole blood¹², but are not suitable to measuring the elastic properties of blood clots. Passive^7–9 and resonant^10,11,13 techniques have measured viscoelastic fluids using surface-attached. However, these techniques have very high operating frequencies (10² -10⁴ Hz), limiting their utility when the specimen's low-frequency modulus is of interest.

In this paper we demonstrate qualitative elastometry using an array of actuated surface-attached posts (ASAPs, Fig. 1B). We have previously shown that ASAPs can operate as microfluidic pumps and mixers¹⁴. Here we show that by monitoring the post motion while controlling the applied torque, we can measure the elastic properties of a blood clot as it forms. The ASAPs are magnetically actuated, and their tilt angle is detected by optical transmission. The physical dimensions and number of posts per unit area is tightly controlled to allow consistent results across different ASAP elements. Aside from the microposts themselves, the system has no moving parts or fluid pumps.

Figure 1.

A) A summary of the ASAP manufacturing process. (i) A polycarbonate membrane (ii) is partially filled with nickel tubes, (iii) filled with PDMS and mounted on glass, then (iv) dissolved away to produce free-standing posts. B) A scanning electron micrograph of the final ASAP structure. The flexible PDMS region (dark grey) is visible at the base while the magnetic nickel (light grey) shell covers the top half of the posts.

ASAP technology could enable elastic measurements in a wide range of natural and synthetic materials. Here we focus on the application of ASAP to the in-vitro testing of blood coagulation and specifically on a novel micro-fluidic implementation of a viscoelastic hemostatic assay (VHA). VHAs are a type of in vitro diagnostic test for blood coagulation that measures over time the stiffness of a blood clot as it forms(or clotting) inside a chamber. It has been shown that VHAs such as Thromboelastography (TEG) can guide transfusion therapy^15,16 and may diagnose other acute bleeding conditions such as trauma-induced coagulopathy.^17–21 VHAs are distinct from traditional coagulation tests, which measure the kinetic activity of the pro-coagulant cascade, often in platelet poor plasma. By contrast, VHAs measure clot initiation, formation, mechanical stability, and lysis in whole blood. The result is a global view of a patient’s overall hemostatic function, from which clinical insight can be gained, as shown in both preclinical17,18 and clinical studies.^19–22

Trauma centers increasingly use treatment algorithms that include hemostasis testing based on elastometry.²³ These algorithms improve survival²⁴ and reduce costs by limiting blood product use.^15,16,25 Surgical suites see similar benefits.²⁶ While VHAs provide valuable clinical insight, they suffer from the typical issues that affect rheometers. In the clinic VHAs suffer from standardization, portability and usability issues²⁷. In the scientific community, VHAs use large volumes of blood (up to 1 mL), which make non-terminal studies on mice difficult. Ultrasound based methods for measuring clot properties but like conventional VHAs uses large volumes of blood (~400 μL or more).^28–30 Clot elasticity can be measured in smaller volumes (150 μL) using acoustic spectroscopy with optical vibrometry (RASOV), but the technique currently does not perform kinetic measurements such as clotting time.³¹

Here we report on a novel technique for measuring the time dependent elastic properties of microliter quantities (20 uL) of material and demonstrate its utility as a blood coagulation diagnostic tool.

Methods and Materials

ASAP Manufacturing

The actuated surface-attached posts (ASAPs) were fabricated by Rheomics, (Chapel Hill, Inc. NC) using a modified version of the procedure developed by Fiser.³² The ASAP elements are core-shell structures where a nickel shell encapsulates the top half of an elastomeric rod (core) made of polydimethylsiloxane (PDMS). The PDMS rod is flexible, with an elastic modulus of approximately 1MPa³³, allowing the core-shell structure to bend in response to magnetic fields.

ASAP fabrication is summarized in Figure 1. ASAP arrays were made using a template-based process that utilizes a polycarbonate track etched membrane (it4ip™, S.A., product number #100M25) as a mold for the core-shell structures. First, the nickel “shell” of the structure was created by coating one side of the track etched membrane with a 200nm thick layer of gold that served as the cathode for electrodeposition of nickel into the pores. Electrodeposition was performed in a custom electrolytic cell with an all-sulfate plating bath. Upon completion, the nickel containing track etched membranes were rinsed with DI water and dried. The “core” of the structures was made by filling the membrane with PDMS (Dow Corning, Sylgard 184) at a 10:1 base to cross linker ratio. Prior to curing the PDMS, a 22×22mm coverslip (Corning, 2870-22) was pressed into the uncured elastomer to provide a rigid substrate for the array. After curing the PDMS, the gold layer (cathode) was removed using a nickel compatible gold etchant (Aldrich, 651842) and the posts were released by dissolving the polycarbonate template using dichloromethane (ACROS Organics, 610300010). Released posts were then stored in ethanol until they were dried using a critical point drier (Balzers Union, CPD 020).

ASAP arrays were prepared for data collection by plasma cleaning the dry arrays (Harrick Plasma, PDC-001) for 30 seconds to render all surfaces hydrophilic. A flow cell consisting of a double-sided adhesive and a lid (with input/output ports) was then assembled around the ASAP array (Figure 2)

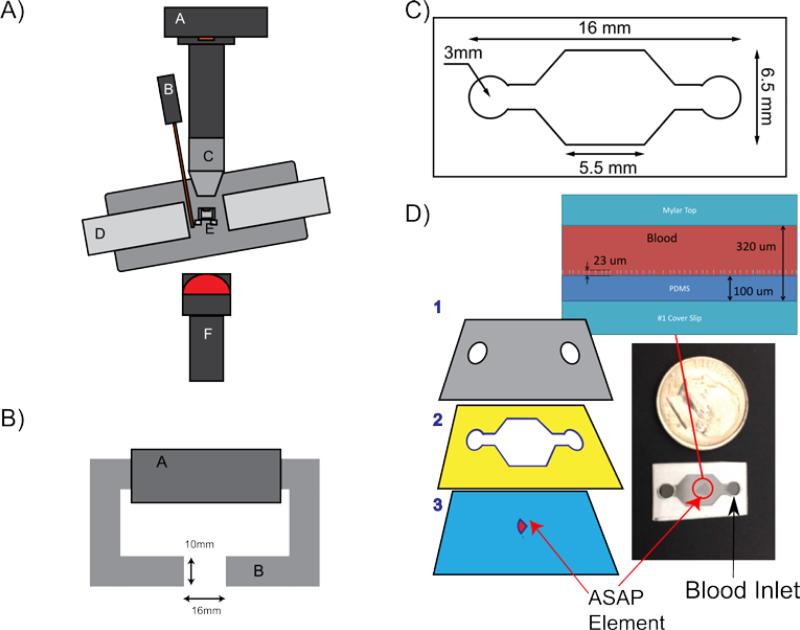
Figure 2.

A) Diagram of the experimental setup, where: A is the 120 fps Pulnix camera; B is a gauss probe; C is a 10x Plan Nikon lens; D is the soft iron electromagnet; E is the heated holder for the ASAP element; and F is the diffuse near-infrared LED. B) Top down view of the electromagnet. A is the magnetic coil, and B is a silicon steel tape wound core. The gap is 16 mm wide and the faces are 10 by 10 mm. C) Diagram of the micro-fluidic chamber used for the blood experiments. The entire channel is 200 μm tall. D) A schematic showing the layers used in constructing the micro-fluidic chamber, where: 1 is a Mylar top with air vents cut out; 2 is an adhesive spacer that defines the chamber dimensions; 3 is a #1 18x18mm coverslip with the post array mounted in the center. These layers are adhered to produce the final device as shown in the bottom-right. The blood droplet is put on one of the two ports and wicks into the device through capillary action. A side view of the post array in a channel filled with blood is shown above channel.

Experimental Setup

ASAP actuation was performed with an opto-magnetic system as shown in Figure 2. The posts were imaged using a 10x, 0.3 NA, Plan DL, Nikon objective mounted 160 mm from a Pulnix TM-6710CL (648x484 pixels) camera, capable of up to 120 fps. A collimated 780nm high intensity LED from Thor labs (Cat# M780L3), with a polycarbonate diffuser, was used as the light source. The noise level of the camera and LED system was less than 0.03% of the average image intensity.

To actuate the posts, an electromagnet consisting of a soft iron C-shaped core with a 10 × 10 mm cross-section and a 16 mm gap was constructed. Magnetomotive force was produced by two magnet coils, each with 680 turns, connected in parallel for a total of 1,380 turns. The magnetic field varies less than 10% within 3mm of the gap center, confirmed experimentally and with COMSOL simulations. The electromagnet was driven by a transconductance amplifier³⁴. The amplifier and magnets had a combined bandwidth greater than 50Hz. The amplifier magnet combo was able to reproducibly produce a field within the 1% precision of the gauss probe used to measure the signal. The amplifier has a noise level as a function of frequency of approximately 1 nA/Hz^1/2.

The transconductance amplifier was driven by a NI-Instruments PCI-6713 analog output board with 12-bit resolution over the range −5 to 5 V and 1 MS/s update rate, using custom software written in MATLAB. The output DAQ has a reported absolute accuracy of 7 mV. The dominate uncertainty, by an order of magnitude, in the magnetic field is in the uncertainty in registering the ASAP array with respect to the magnetic field.

Blood Sample Preparation

Human venous blood was collected from healthy consenting volunteers using butterfly needles (BD Vacutainer, BD Safety-Lok, Cat # 367283BD, Franklin Lakes, NJ) and stored in 4.5 mL citrated tubes (BD Vacutainer, Buffered Cit. Na., Cat # 366415), and kept at 22 °C Blood sample procurement protocols were approved by IRB of the University of North Carolina at Chapel Hill (IRB # 12-1592). Blood samples were used within 24h of collection and run as split specimens on the ASAP system and a TEG 5000 analyzer (Heomentics, Inc). For the dilution experiments, isotonic saline (0.90% w/v NaCl) was added to the blood and mixed by gently inverting the tube. Streptokinase, purchased from Sigma-Aldrich (product # S3134-10KU), was diluted to a final concentration of 9.6 U/ml for the high dose lysis experiment (Figure 4, blue circles) and 1.2 U/mL for the low dose lysis experiment (Figure 4, green squares). Immediately prior to data collection, all specimens were re-calcified by adding 1 μL of 0.2M CaCl per 17 μL of specimen volume. A 20 μL droplet of blood was pipetted onto the opening of the micro-fluidic device, and the blood wicked into the channel. The final, as tested, specimen volumes for the ASAP and TEG systems were 20 μL and 360 μL, respectively. The TEG was run according to standard operating procedures.

Figure 4.

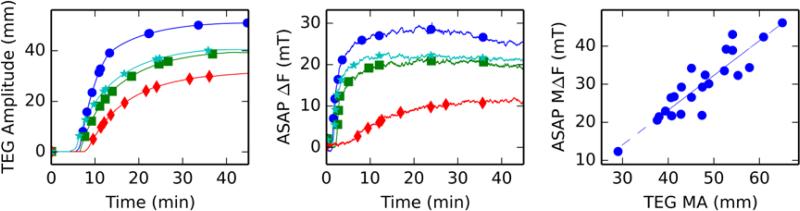
Coagulation measurements performed by ASAPs. Results are reported as magnetic field (mT), which is related to clot stiffness through equation 4. Three specimens are shown: normal blood (red diamonds), blood spiked with a low streptokinase concentration (green squares), and blood spiked with a high streptokinase concentration (blue circles). Streptokinase interference provides a model of clot lysis. In low dose, the clot forms normally before collapsing. In high dose, the clot never forms, resulting in a flat curve.

SEM Sample Pep

Clotted specimens for SEM imaging were harvested from micro-fluidic devices approximately 45 minutes after the initialization of clot formation. At that time, the top half of the flow cell was removed to expose the clot and the ASAP array. The sample was then fixed by adding 4μL of 0.2% glutaraldehyde directly onto the array and incubating at 37°C and 100% humidity for 30 minutes. The water in the sample was serially diluted in mixtures of increasing ethanol-to-phosphate buffered saline, ending in 100% ethanol. The sample was critically point dried, then sputter coated with 7nm of 80:20, Au:Pd before imaging in a Hitachi S-4700 scanning electron microscope.

ASAP Control and Analysis

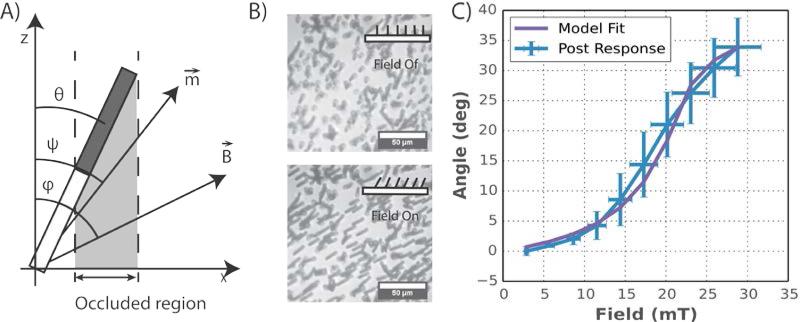
An initial field of 10 mT was applied to the posts, and the post response was measured. The magnet was then turned off, and the posts returned to their initial upright position. This on/off pulsing was repeated. As the blood clot formed and restricted the post motion, the deflection of the post would decrease if the applied field were held constant. Instead, we used discrete-time proportional feedback control of the magnetic field to maintain constant post deflection during the magnet-on periods throughout clot formation. The feedback maintained a constant ratio of mean image brightness between the magnet-on and magnet-off condition through control of the magnet drive current. The set point was determined (as described above) by the initial response of the posts. The gain was set to maximize responsiveness without inducing instability. The use of the ratio of the two most recent magnet-off and magnet-on image intensities makes the system insensitive to slow changes in overall image intensity (which can be induced by increasing turbidity during clotting). This assumed that the overall intensity is proportional to the product rather than the sum of the contributions of the post deflection and the overall clot intensity. We hypothesized that the nickel posts act like a shutter below the blood clot, blocking a percentage of the light depending on their deflection (Figure 3A), which was consistent with the multiplicative assumption.

Figure 3.

Parameters used in modeling ASAP behavior are: theta (θ) is the deflection angle of the posts; Psi (ψ) is the angle of the induced magnetic moment; and Phi (φ) is the angle of the applied magnetic field. B) Representative images showing ASAP response to magnetic fields. As the post tilt over, the average intensity of the image decreases. Scale bar = 50 μm. C) Measurements of ASAP deflection compared against the theoretical model (equations 4-6). The purple line is the deflection predicted by our model with a two parameter fit, the PDMS stiffness and the remanent magnetization. The blue line represents the average response of 6 different post arrays. The y error bars are the standard deviation of the post arrays, and the x error bars represent the uncertainty of the magnetic field. All other inputs were determined from independent measurement or known material properties.

The field required to maintain the post deflection was a measure of the mechanical resistance of the post/clot system. Because the mechanical properties of the posts remained constant over the course of the experiment (see Figure 4 blue curve) the change in applied field represented a change in the clot stiffness. The maximum applied magnetic field is similar to the maximum amplitude measurement in a TEG system.

As a reference instrument, a TEG 5000 Thromboelastograph Hemostasis Analyzer from Haemonetics was used. Blood samples were run on the TEG according to standard operating procedures provided by Haemonetics.

Results

In the system described above, a force is applied to the blood by the posts through an applied magnetic field. Converting this applied field to an applied force requires a model of the magnetic response of the posts, which is developed here. The torque on the posts is calculated using the model of axial symmetric soft magnetic bodies described in Abbott et al. 2007.³⁵ According to this model, as long as the magnetic susceptibility is large, X >> 1, the induced moment is dominated by the geometry of the post. COMSOL modeling and experiments on the magnet setup suggests that the gradient terms in the post region are negligible. Using the Abbott model without the gradient term, the torque on the magnetic posts is:

$$\mid \tau \mid =\{\begin{array}{cc}\frac{v\mid n_r-n_a\mid }{2{\mu }_0{n}_a{n}_r}{\mid \mathit{B}\mid }^{2}sin\left(2(\theta -\varphi )\right),\hfill & \mid \mathit{B}\mid <{\mid \mathit{B}\mid }_{sat}\hfill \\ \frac{{\mu }_{0}v\mid n_r-n_a\mid }{2}{m}_s^{2}sin\left(2(\theta -\psi )\right),\hfill & \mid \mathit{B}\mid >{\mid \mathit{B}\mid }_{sat}\hfill \end{array}\phantom{\}}$$ (1)

where: ν is the volume of nickel; η^a and η^r are geometric demagnetization factors³⁶; μ₀ is the permability of free space; B is the magnetic field vector; Θ and Φ are the angle of the magnetic field and the angle of the post from the vertical; ms is the saturation point of the nickel; and Ψ is the angle of the induced magnetic moment, see Figure 3A. The magnetic field at which material saturation occurs, |B|_sat, is determined using the following equation

$${\mid \mathit{B}\mid }_{sat}=\frac{m_s{n}_a{n}_r}{{\mu }_0\sqrt{n_a^{2}si{n}^2(\theta -\varphi )+n_r^{2}co{s}^2(\theta -\varphi )}}$$ (2)

The angle of the magnetic moment while saturated, ψ, is calculated by minimizing the following equation for an ellipsoid magnetic field domain using a Stoner-Wohlfarth model.

$$(n_r-n_a)m_{s}sin\left(2(\theta -\psi )\right)=2\mid \mathit{H}\mid sin(\varphi -\psi )$$ (3)

The nickel posts are not perfectly paramagnetic, so there is some remanent moment. We account for this remanence by adding a linear correction to the torque model from Abbott et al. (2007).³⁵ Assuming the remanent moment is along the long axis of the rod, the equation for the magnetic torque then becomes:

$$\mid {\tau }_{mag}\mid =m_{rem}\mid \mathit{B}\mid sin\left(2(\theta -\varphi )\right)+\{\begin{array}{cc}\frac{v\mid n_r-n_a\mid }{2{\mu }_0{n}_a{n}_r}{\mid \mathit{B}\mid }^{2}sin\left(2(\theta -\varphi )\right),\hfill & \mid \mathit{B}\mid <{\mid \mathit{B}\mid }_{sat}\hfill \\ \frac{{\mu }_{0}v\mid n_r-n_a\mid }{2}{m}_s^{2}sin\left(2(\theta -\psi )\right),\hfill & \mid \mathit{B}\mid >{\mid \mathit{B}\mid }_{sat}\hfill \end{array}\phantom{\}}$$ (4)

Assuming the absence of a surrounding material (such as blood), deflections were calculated numerically using the quasi-static assumption and solving the torque balance equation between magnetic and deflection torque contributions.

$${\tau }_{mag}+{\tau }_{post}=0$$ (5)

where the torque due to bending, τ_post, is calculated using an Euler-Bernulli Beam Model. Because the magnetic field applies a pure torque, it is assumed that the PDMS portion of the posts bends with a constant radius of curvature. This has been shown to introduce an error of less than 30%.³⁷ The torque is therefore:

$${\tau }_{post}=\frac{d{U}_E}{d\theta }=\frac{\pi E{r}^4\theta }{L_{pdms}}$$ (6)

where E is the elastic modulus of PDMS, r is the radius of the post and L_pdms is the length of the PDMS portion of the rod. For the geometry of the model we assumed a nickel shell thickness of 200 nm, a nickel shell length 13±1 μm and a post diameter of 2 μm. For material properties, the elastic modulus of PDMS was fitted to be 0.85+-.07MPa³³ and the permanent moment of the rod was fitted to the measured post response (see below). The fitted permanent moment of the nickel shell was (4+-1)e-13 A*m². The predicted deflection of the posts can be seen in Figure 3C.

Magnetic Response of Posts

To determine the tilt response of the ASAP posts to the applied field, the magnetic field was applied in pulses of increasing magnitude. Images of the posts were taken before and during each magnetic pulse. The deflection angles were estimated through analysis of the imaged posts by measuring the projected length of the nickel shell (Figure 2A-B), and using a measured nickel shell length of 13±1 μm . The precision of this method degrades at small post deflection, so we extend the field-angle mapping by extrapolating the large angle deflection results (Figure 2C). 6 post arrays were used to get an average response and a measure of the post variability. The nickel shell length was measured using SEM images as seen in Figure 1B.

Demonstration of ASAP as VHA

In a standard VHA measurement, clot stiffness vs. time is plotted, and the clotting time, clot stiffness, and lysis are extracted from the curve shape. In TEG, a cup and bob style rheometer, the clot stiffness is plotted as the amplitude of rotation of the inner bob over time for a constant cup rotation amplitude. In the ASAP system, the magnetic field is pulsed on and off and the post deflection is monitored. As the clot forms around the posts, the posts deform the clot as they deflect. Feedback is used to maintain a constant post deflection by increasing the magnetic field. The blood clot experiences shear, compressive, and tensile stress because of the post motion. The readout of the ASAP system is the required magnetic field as a function of time. We studied the ASAP system’s ability to detect coagulation and lysis of normal whole blood, with and without streptokinase, a known mimic for hyperfibrinolysis18 (Figure 4). The forming clot restricts the post motion such that the feedback loop increases the applied field to maintain a constant deflection. The normal blood shows a sudden increase in the applied field, indicating the clotting time (called R time in TEG). As expected, normal blood does not show lysis over the course of 30 minutes, in contrast with blood dosed with streptokinase. At low streptokinase concentration the clot forms normally, but subsequently breaks down, as shown by the drop in applied field. We note that this demonstrates that ASAP is a reversible elastometer: it can measure both increases and decreases in stiffness. Blood with high-dose streptokinase never clots, as indicated by the unchanged applied field over the course of the experiment, and as confirmed by TEG.

ASAP system noise is 0.1 mT, calculated by subtracting a smoothed curve (moving average with a one minute window) from the raw data, and taking the standard deviation of the resulting signal. The maximum error signal seen in the feedback loop is 0.3%. The two largest limitations on the devices precision are the applied field, and post material properties. Posts have variations in magnetic response are up to 20% between post arrays (see Figure 3C), and are the single largest limitation on the instruments precision. We suspect that the main source of variability in ASAP properties is the geometry of the nickel shell, which could be made more consistent by implementing the electro-deposition process in a higher-quality system.

To compare ASAP and TEG measurements, we performed serial dilutions of normal blood with saline. In both ASAP and TEG systems (Figure 5A-B), clot stiffness varies with dilution as expected. The primary effect of increasing dilution is a drop in maximum clot stiffness, along with slightly delayed clotting initiation and a slower clotting rate.18 All of these features are apparent in both the ASAP and TEG results. Additional dilution results are summarized in the correlation plot shown in Figure 5C. The samples were a collection of diluted specimens and whole blood specimens from multiple draws. The R value of the linear fit is 0.91, indicating good agreement between the two systems.

Figure 5.

Serial dilutions of blood were used to modify clot stiffness and compare the Haemonetics TEG 5000 with ASAP measurements using split specimens. A) Output of TEG on representative blood samples: normal blood (blue circles), 33% dilution (cyan stars), 50% dilution (green squares), and 66% dilution (red diamonds). Note the noiseless curves, which are the result of intense smoothing by the TEG software. B) ASAP results for the same four specimens show the same features seen in TEG: as dilution increases, clotting time are rate are slightly reduced, while clot stiffness is dramatically reduced. No smoothing was applied to the ASAP results. C) ASAP and TEG systems show excellent correlation (r=0.91). Clot stiffness is plotted on the x-axis in TEG maximum amplitude and on the y-axis in terms of ASAP maximum applied field. The consistency across platforms is surprising given that the ASAP system has a much higher surface area to volume ration than TEG.

Discussion

Validity of Magnetic Model

The experimental deflection vs. field results agree well with the predicted results from the model (see Figure 3C). The model curve was calculated by numerically solving equation 6 using equations 4 and 5 for the magnetic and post torque. The only parameter that was fitted was the permanent moment term, and the post stiffness. The rest of the model parameters were based off of known and measured values for the posts, including the material properties of nickel, the post dimensions, length of the nickel rods, and volume of the nickel shells.

The fitted permanent moment, 2e-13 A*m², was consistent with remanence from a previous exposure to a magnetic field, as it was less than the predicted moment generated under the largest applied fields (~50 mT). Prior to experiments with blood or angle vs. field tests, ASAPs were pulsed with varying magnetic fields over the full range of a typical experiment to test actuation. This initial exposure to the magnetic field likely introduced the permanent magnetic moment. Additionally, because the magnetic susceptibility of a high ratio structure is dominated by the geometry and not by the material properties, the equations for the induced magnetic moment should not change significantly.

The blood clot forms around the ASAP posts (see Figure 6). As the posts deflect they deform the clot around them causing shear, compressive, and tensile forces. While we can model the torque applied to the posts, and therefore the forces applied to the clot, the calculation of a clot's bulk elastic modulus is not supported by this model; this would require modeling the mechanical interaction between the micro posts and the surrounding clot. Establishing the nature of this interaction represents an intriguing di

Figure 6.

Scanning electron micrograph of a clot formed on the ASAP posts. The long strands are fibrin fibers and the biconcave discs are red blood cells. The posts interact with the clot by deform the clot formed around the posts as they deflect. The stiffer the blood clot the more force is required to deflect the posts and clot system.

Comparing ASAP and TEG

Figure 5A shows that the broad features of clot stiffness over time are identified by both the ASAP and TEG systems, and both produce the expected result for serial dilution of blood: the maximum clot stiffness decreases as the saline concentration increases.¹⁸

The TEG curves are essentially noiseless, while ASAP data show acceptable but noticeable noise. This comparison is misleading, because the TEG software uses an unknown smoothing algorithm that is easily confounded by vibration or other physical disturbance. We have elected to report ASAP output in raw data format. The rotation period of the TEG instrument is about 10 seconds. The ASAP data are sampled at a rate of 1 Hz and assuming TEG samples once every half rotation or every 5 seconds, then significant smoothing of the ASAP curves should be possible while maintaining adequate time resolution. Finally, the clotting rate in the ASAP system is considerably faster than in the TEG system. The faster clotting rate could have numerous causes, shear from the posts, differences in the scale of the measurement (micro vs. macro), and or differences in the surface to volume ratio of the between the sample chamber in the two devices. Surfaces are well known to initiate the clotting cascade, even though the mechanism is not well understood.³⁸ The two devices, ASAP and TEG, have a well-correlated measurement of stiffness (r=0.91). This agreement is surprising: ASAPs are 2 μm in diameter and deflect on the order of 1-5 μm. At this scale ASAPs might well detect heterogeneities in fibrin cross-linking density or platelet concentration. We hypothesize that ASAP correlates with the bulk measurement because of the large number of posts over which the measurement is performed: a 1 mm² patch of posts has roughly 14,000 posts. To provide a context for relative length scales in the ASAP system, we show an SEM image of a clot formed around the posts in Figure 6. TEG has a well known dependence on hematocrit, as the red blood cell concentration increases the clot stiffness decreases. ^39,40 While the ASAP system correlates well with TEG in this dilution study it is conceivable that because of the microstructure of the device the hematocrit dependence would differ between the devices.

Applications of ASAP Technology

The ASAP technology can perform tests on very small samples of blood and can be further miniaturized. No pumps were used in this experimental setup, the imaging requirements can be easily met with compact optical components, and the active area is under 1mm² electromagnet is the largest single component and can fit within a 100 cm³ A) when on, the duty cycle is low and the overall power draw time-averages to about 2 W. These properties bode well for the potential use of ASAP as a point-of-care or mobile diagnostic system. In addition, our model indicates that it is possible to tune the torque using a constant magnetic field and adjusting the field angle. This could enable the use of rotating permanent magnetic systems. A one cubic centimeter rare earth permanent magnet (e.g. neodymium) could produce the required field and dramatically reduce the device size and power requirements.

Because of the small volumes required, ASAP would be useful in small animal model research. There is currently no convenient system for small animal blood coagulation testing. Some TEG assays use multiple reagents, requiring up to four simultaneous measurements and nearly 2 mL of blood. Yet sacrificing a laboratory mouse produces only ~1 mL of whole blood or 0.5 mL of plasma. Weekly blood draws are limited to the 20% of the total blood volume, 300 uL for a 25 gram mouse, which is not enough for standard TEG experiments.⁴¹ An ASAP measurement only uses 20 uL of blood sample allowing for multiple tests on a single draw, or the remaining blood to be used in parallel experiments. This dramatic reduction in blood sample volume requirements opens the door to non-lethal time course studies in mice.” Finally, we have demonstrated that ASAP elements easily integrate into simple micro-fluidic systems. This implies that ASAP elements may be useful as an element in a panel of blood tests, as has been shown elsewhere, on a single chip.⁴² Additionally, tests could be performed on platelet rich or platelet poor plasma that has been filtered on a disposable test element using one of the many blood filtering micro-fludic technolgoies.^43–46

Conclusions

We have demonstrated the design and use of a post-array elastometer that operates on micro-liter quantities of blood. The posts’ behavior under an applied magnetic field could be described by our magneto-mechanical modeling. We demonstrated that the ASAP posts measure the elasticity of a blood clot over time, and that the maximum amplitude correlates well with a commercial blood elastometer (TEG). We also show demonstration curves that show that the lysis can and clotting kinetics can be measured on the ASAP arrays. The ASAP array system uses dramatically less blood, 20 μL vs. 360 μL per test, making the system applicable for small animal studies, where conventional blood elastometry is currently impractical, such as experiments that require multiple tests and time course studies in mice. The ASAP device has the potential to be made into a compact portable POC device for trauma or critical care. Finally the ASAP element of the device is currently mounted in a small micro-fluidic chamber that could easily be integrated into more complex micro-fluidic devices that perform sample preprocessing. Micro-fluidic devices have had recent success in reducing volumes in numerous blood applications, such as devices that perform panels of tests⁴⁷, separate blood components^43–46, or mimic blood vasculature for the study of thrombus formation.^48–52 The ASAP technology presented here could be combined with many of these technologies to perform panels of tests on a single device, and/or preprocessing of the blood sample prior to testing.