Statistical Reconstruction for Cone-Beam CT with a Post-Artifact-Correction Noise Model: Application to High-Quality Head Imaging

Abstract

Non-contrast CT reliably detects fresh blood in the brain and is the current front-line imaging modality for intracranial hemorrhage such as that occurring in acute traumatic brain injury (contrast ~40-80 HU, size > 1 mm). We are developing flat-panel detector (FPD) cone-beam CT (CBCT) to facilitate such diagnosis in a low-cost, mobile platform suitable for point-of-care deployment. Such a system may offer benefits in the ICU, urgent care/concussion clinic, ambulance, and sports and military theatres. However, current FPD-CBCT systems face significant challenges that confound low-contrast, soft-tissue imaging. Artifact correction can overcome major sources of bias in FPD-CBCT but imparts noise amplification in filtered backprojection (FBP). Model-based reconstruction improves soft-tissue image quality compared to FBP by leveraging a high-fidelity forward model and image regularization. In this work, we develop a novel penalized weighted least-squares (PWLS) image reconstruction method with a noise model that includes accurate modeling of the noise characteristics associated with the two dominant artifact corrections (scatter and beam-hardening) in CBCT and utilizes modified weights to compensate for noise amplification imparted by each correction. Experiments included real data acquired on a FPD-CBCT test-bench and an anthropomorphic head phantom emulating intra-parenchymal hemorrhage. The proposed PWLS method demonstrated superior noise-resolution tradeoffs in comparison to FBP and PWLS with conventional weights (viz., at matched 0.50 mm spatial resolution, CNR = 11.9 compared to CNR = 5.6 and CNR = 9.9, respectively) and substantially reduced image noise especially in challenging regions such as skull base. The results support the hypothesis that with high-fidelity artifact correction and statistical reconstruction using an accurate post-artifact-correction noise model, FPD-CBCT can achieve image quality allowing reliable detection of intracranial hemorrhage.

1. Introduction

Traumatic brain injury (TBI) is a major cause of death and disability, with causes including falls, motor vehicle accidents, contact and collision sports, and blast exposure. The total number of TBI-associated emergency department visits in the United States increased by 70% during the period 2001-2010 and reached ~2.2 million in 2010 (Centers for Disease Control and Prevention 2010). TBI is often associated with intracranial hemorrhage (ICH), cranial fracture, and/or increased intracranial pressure. Non-contrast-enhanced multi-detector CT (MDCT) is the current first-line modality for reliable diagnosis of acute TBI and provides a high degree of sensitivity in detection of ICH (attenuation value of fresh blood in brain ranging from 40 HU to 60 HU immediately after bleed and rapidly increasing to ~80 HU in the following hours due to serum extraction and clot formation with lesions of size ranging from >10 mm down to ~1 mm) (Dublin et al 1977, Parizel et al 2001, Greenberg and Arredondo 2006, Adams et al 1989). Accurate detection of ICH is also important in monitoring other clinical conditions including bleeding occurring in the ICU following surgery or due to hemorrhagic stroke. While multi-detector CT (MDCT) is well suited for the emergency department, a system with lower cost, greater portability, and smaller footprint optimal for point-of-care use in the ICU, urgent care / concussion clinic, ambulance, and sports and military theatres may offer significant advantages for the immediate detection of bleeding and choice of treatment.

Cone-beam CT (CBCT) with a flat-panel detector (FPD) has emerged in the past decade as an invaluable tool for a variety of specialty diagnostic applications, including imaging of the breast (Boone et al 2001, Yang et al 2007), musculoskeletal extremities (Zbijewski et al 2011, Koskinen et al 2013), and head and neck (Xu et al 2012, Penninger et al 2011). While CBCT systems can be well suited to point-of-care applications (offering a small footprint, open adaptable geometry, and relatively low cost), current CBCT systems face significant challenges with respect to image quality in low-contrast, soft tissue imaging tasks such as ICH. Among factors limiting soft-tissue image quality are increased levels of image artifacts and noise when compared to MDCT.

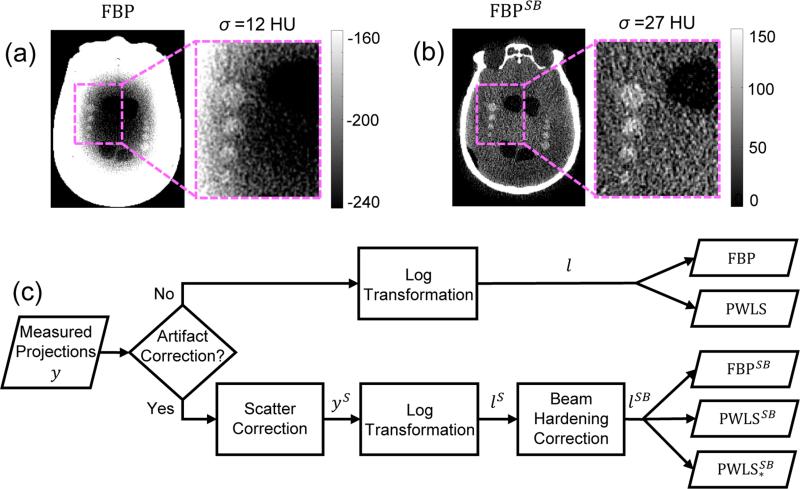
Recent work (Sisniega et al 2015) has demonstrated a promising framework for artifact correction in CBCT of the head and brain, including correction of x-ray scatter, beam hardening, image lag, and low-frequency glare/off-focal radiation. The artifact correction framework overcomes major sources of image non-uniformity and streaks and provides a level of image quality potentially suitable to detection of ICH; however, such corrections also cause an amplification of noise in images reconstructed by conventional 3D filtered backprojection (FBP). As shown in Fig. 1(a-b), although the artifact correction framework removes >300 HU of deterministic bias (cupping and streaks primarily associated with scatter and beam hardening) in a head phantom emulating intra-parenchymal hemorrhage, the image noise increases by more than a factor of two (Sisniega et al 2015). Potential solutions for noise reduction include sinogram denoising by adaptive filtering techniques (Kachelrieß et al 2001) and estimation of the ideal sinogram by minimizing a cost function (La Rivière et al 2006). Alternatively, the problem can be approached with a model-based reconstruction (MBR) framework, which has demonstrated major improvements in CBCT image quality over conventional FBP for low-contrast, soft tissue imaging tasks (Wang et al 2014a). In general, MBR makes better use of the measurements by leveraging a more sophisticated forward model including factors such as measurement noise, the x-ray spectrum, and system geometry. Moreover, MBR approaches can include various image regularization approaches to further improve noise-resolution tradeoffs.

Figure 1.

Artifact corrections in CBCT of the head. (a) CBCT image reconstructed using FBP without artifact corrections. (b) CBCT image with artifact corrections (scatter and beam hardening, denoted by the superscript SB) showing a strong improvement in image uniformity but an amplification of noise by more than a factor of 2. (c) Flowchart of the artifact correction process and image reconstruction methods (FBP and PWLS) investigated in this work.

In the work presented here, we develop an MBR approach that includes the effects of artifact corrections on the underlying noise model, thereby maintaining the benefit of artifact corrections while overcoming the associated noise penalty. The underlying variations in measurements are integrated into a penalized weighted least-squares (PWLS) reconstruction approach, and the noise characteristics following each data correction are accounted by modified weights. Regularization with a Huber penalty on image roughness was used to further improve noise-resolution tradeoffs. Previous analogous work (Zhu et al 2009) investigated a PWLS objective that included the variations in measurement noise characteristics with scatter correction and quadratic regularization, showing improved image quality in chest CT. In this work, we build on previous studies that modeled noise after scatter and a single material (“water-only”) beam hardening correction (Dang et al 2015) and propose a general framework for modeling the effect of data corrections on the noise model. The framework is then applied to the two dominant correction factors required for high-quality CBCT of the head – scatter and beam hardening (using bone and water segmentation). Image quality is evaluated in CBCT images of a head phantom emulating intra-parenchymal hemorrhage. The proposed PWLS method using modified weights is compared to FBP as well as PWLS using conventional weights, and the improvements to image noise and/or spatial resolution are quantified.

2. Theoretical methods

2.1 PWLS image reconstruction with a noise model for generalized data transformation

The PWLS method (Sauer and Bouman 1993) weighs the residual error for each measurement by the fidelity of that measurement – specifically an estimate of the inverse of the variance of each measurement, thereby reducing the contributions of low-fidelity measurements and consequently reducing noise in the reconstructed image. We formulate the PWLS objective function as:

$$\widehat{\mu }=\underset{\mu }{\arg \min }\frac{1}{2}{\Vert \mathbf{A}\mu -l\Vert }_{\mathbf{w}}^2+{\beta }_{R}R\left(\mu \right)$$ (1)

where the matrix A denotes the linear projection operator, μ is a vector representing the image estimate, l is a vector of measured line integrals, and W is the diagonal weighting matrix with the i^th diagonal element W_i representing the fidelity of the i^th measurement. We chose a regularization term R(μ) that penalizes first-order neighborhood differences in the image μ using the Huber penalty function (Huber 1981), which is quadratic within a neighborhood ([−δ, δ]) and linear for larger differences. The strength of regularization is controlled by the scalar β_R.

The line integrals in Eq. (1) are typically derived from the raw measurements through a number of steps. Such steps include a log transformation to convert from the raw measurement domain to the line integral domain. In many situations, the measured data are also processed to correct for effects such as x-ray scatter (Boone and Seibert 1988, Ning et al 2004, Siewerdsen et al 2006, Zhu et al 2006, Sisniega et al 2013) and beam hardening (Joseph and Spital 1978, Hsieh et al 2000) and/or to reduce noise in the measurements (e.g., sinogram smoothing (Li et al 2004)). Such processes lead to potential changes in the noise characteristics of the measurements, which need to be accommodated in the PWLS weighting terms. We first model the processing of the measured data (including log transformation and processes associated with artifact correction) as a general function f, giving processed line integrals expressed as:

$$l_i=f\left(y_i\right)$$ (2)

under the common assumption of independent measurements y_i. The variance of the line integrals can be derived using first-order Taylor expansion assuming the function f is differentiable at mean measurements (Benaroya et al 2005) and the second and higher order terms in the Taylor expansion are negligible:

$$\mathrm{var}\left(l_i\right)=\mathrm{var}\left[f\left(y_i\right)\right]=\mathrm{var}[f\left({\stackrel{‒}{y}}_i\right)+\stackrel{.}{f}\left({\stackrel{‒}{y}}_i\right)(y_i-{\stackrel{‒}{y}}_i)+O\left(y_i^2\right)]$$ (3a)

where ḟ is the derivative of the function f and ȳ is a vector of the mean measurements. The approximation in Eq. (3a) can be simplified by removing the terms that have zero variance:

$$\mathrm{var}\left(l_i\right)\approx \mathrm{var}\left[\stackrel{.}{f}\left({\stackrel{‒}{y}}_i\right)y_i\right]$$ (3b)

Since the term ḟ(ȳ_i) is a constant, it can be taken out of the variance to yield the final expression of the variance:

$$\mathrm{var}\left(l_i\right)\approx {\left[\stackrel{.}{f}\left({\stackrel{‒}{y}}_i\right)\right]}^2\mathrm{var}\left(y_i\right)$$ (3c)

Eq. (3c) shows that applying a number of operations (modeled as the function f) on the raw measurements results in a scaling of the variance by a factor [ḟ(ȳ_i)]². The PWLS weights can be computed as the inverse of the variance given in Eq. (3c):

$${\mathbf{W}}_i=\frac{1}{\mathrm{var}\left(l_i\right)}\approx \frac{1}{{\left[\stackrel{.}{f}\left({\stackrel{‒}{y}}_i\right)\right]}^2}\frac{1}{\mathrm{var}\left(y_i\right)}$$ (4)

which includes the changes in variance associated with the processing operations, f.

2.2 Effect of log transformation on variance

First consider a scenario in which no artifact correction is applied. Assuming Poisson noise in the raw measurements, we write the forward model in this scenario as:

$$y_i\sim Poisson\left({\stackrel{‒}{y}}_i\right),{\stackrel{‒}{y}}_i=g_i\exp (-{\left[\mathbf{A}\mu \right]}_i)$$ (5)

where g_i represents measurement-dependent gains. In this scenario, the line integrals in Eq. (1) can be computed from the raw measurements simply by log transformation. This process can be simply modeled as:

$$f_l\left(y_i\right)=\log \left(\frac{g_i}{y_i}\right)$$ (6a)

$$l_i=f\left(y_i\right)=f_l\left(y_i\right)$$ (6b)

where the log transformation is modeled as function f_l(y_i) and the general form for f in Eq. (2) is taken in this section to refer specifically to log transformation. Using Eq. (3c), and since ḟ(ȳ_i) = –1/ȳ_i, the variance of the line integrals is:

$$\begin{array}{cc}\hfill \mathrm{var}\left(l_i\right)& \approx {\left[\stackrel{.}{f}\left({\stackrel{‒}{y}}_i\right)\right]}^2\mathrm{var}\left(y_i\right)\hfill \\ \hfill & =\frac{1}{{\stackrel{‒}{y}}_i^2}\mathrm{var}\left(y_i\right)\hfill \end{array}$$ (7)

where we have ignored variations associated with g and assumed accurate measurement-dependent gains (Kwan et al 2006). Thus, log transformation simply scales the variance by a factor $1∕{\stackrel{‒}{y}}_i^2$, giving:

$${\mathbf{W}}_i=\frac{1}{\mathrm{var}\left(l_i\right)}\approx \frac{{\stackrel{‒}{y}}_i^2}{\mathrm{var}\left(y_i\right)}={\stackrel{‒}{y}}_i\approx y_i$$ (8)

which are the conventional PWLS weights equal to the mean measurements under the usual Gaussian approximation of a Poisson noise model as in (Sauer and Bouman 1993, Thibault et al 2007). In practice, actual measurement values are typically used in place of the mean measurement values. With additional processing of the measurements, however, the above assumption may no longer hold, as shown in the following sections that apply the general form of Eq. (3c) to the specific cases of scatter correction and beam hardening correction.

2.3 Effect of scatter correction on variance

Scatter correction typically involves subtraction of a scatter fluence estimate from the measurements, where the scatter fluence may be estimated from the measurements (Siewerdsen et al 2006, Ning et al 2004, Zhu et al 2006), by analytical models (Boone and Seibert 1988), and/or by Monte Carlo (MC) calculation (Sisniega et al 2013, 2015). Assuming Poisson noise in the raw measurements and including mean scatter fluence as part of the mean measurements, we write the forward model in this scenario as:

$$y_i\sim Poisson\left({\stackrel{‒}{y}}_i\right),{\stackrel{‒}{y}}_i=g_i\exp (-{\left[\mathbf{A}\mu \right]}_i)+{\stackrel{‒}{S}}_i$$ (9)

where S̄_i represents the mean scatter fluence. In this scenario, the line integrals in Eq. (1) can be computed by subtracting a scatter fluence estimate from the raw measurements followed by log transformation. Assuming ideal scatter estimation in which the scatter estimate equals the mean scatter fluence, the process can be modeled as:

$$l_i^S=f\left(y_i\right)=f_l(y_i-{\stackrel{‒}{S}}_i)=\log \left(\frac{g_i}{y_i-{\stackrel{‒}{S}}_i}\right)$$ (9)

where the superscript S denotes scatter-corrected line integrals, and the function f from the general form of Eq. (2) refers in this section specifically to scatter correction followed by log transformation. As in the previous section we assume negligible variation associated with g, and we assume the error in the scatter fluence to be negligible compared to the quantum noise (i.e., a high-fidelity scatter fluence estimate as obtained by accurate MC calculation).

The variance of the scatter-corrected line integrals can therefore be computed from Eq. (3c), and since ḟ(ȳ_i) = –1/(ȳ_i – S̄_i), we have:

$$\begin{array}{cc}\hfill \mathrm{var}\left(l_i^S\right)& \approx {\left[\stackrel{.}{f}\left({\stackrel{‒}{y}}_i\right)\right]}^2\mathrm{var}\left(y_i\right)\hfill \\ \hfill & =\frac{1}{{({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)}^2}\mathrm{var}\left(y_i\right)\hfill \end{array}$$ (10)

This form shows that the noise is scaled as a result of scatter correction, but the scale factor is different from that in Eq. (7). Taking the ratio of the post-correction variance to the pre-correction variance, we have:

$$\frac{\mathrm{var}\left(l_i^S\right)}{\mathrm{var}\left(l_i\right)}\approx \frac{{\stackrel{‒}{y}}_i^2}{{({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)}^2}=\frac{{({\stackrel{‒}{P}}_i+{\stackrel{‒}{S}}_i)}^2}{{\stackrel{‒}{P}}_i^2}={(1+{\mathrm{SPR}}_i)}^2$$ (11)

where P̄_i is mean primary fluence and SPR is the scatter-to-primary ratio. This analytical result is consistent with previous work (Zhu et al 2009) but is derived as a special case of the general form in Sec. 2.1. In CBCT systems, where the SPR is often greater than unity (Siewerdsen and Jaffray 2001) and can be as high as ~5-10 in highly attenuated regions of the projection (e.g., the skull base, as shown below), this implies a substantial modification from the conventional PWLS weights – e.g., a 9-fold increase in variance for a SPR of 2.

2.4 Effect of beam hardening correction on variance

Beam hardening correction typically includes a so-called water correction that compensates for the beam hardening error (e.g., cupping) introduced by soft tissue. When many bony structures are present in addition to soft tissue in a scanned object, a so-called bone correction is often used after water correction to compensate for bone-induced artifacts such as blooming or shading between bones (Joseph and Spital 1978, Hsieh et al 2000). Since ICH can present anywhere throughout the intracranial space (both deep in the parenchyma and immediately adjacent to the cranium), both corrections are needed for high-quality CBCT of the head. We model the beam hardening correction as a two-step process of water correction followed by bone correction (Joseph and Spital 1978):

$$l_i^B=f\left(y_i\right)=l_i^{Bw}+l_i^{Bb}$$ (12a)

where the superscript B denotes beam hardening correction, and the superscripts B_w and B_b more specifically denote water and bone correction, respectively. The function f from the general form in Eq. (2) refers in this section specifically to log transformation followed by the two-step beam hardening correction. The water-corrected line integrals can be regarded as a 1-dimensional remapping of measured line integrals based on the calibration of the beam hardening response in water (e.g., from a measured calibration or an analytical model). This 1-dimensional remapping is denoted as f_w and approximated using polynomial functions of the log transformed data:

$$l_i^{Bw}=f_w\left(f_l\left(y_i\right)\right)\approx \sum _{u=0}^U{\alpha }_u{\left[f_l\left(y_i\right)\right]}^u=\sum _{u=0}^U{\alpha }_u{\left[\log \left(\frac{g_i}{y_i}\right)\right]}^u$$ (12b)

where U and α_u are the order and coefficients of the water correction polynomial function, respectively. The bone correction can be regarded as a 2-dimensional remapping of water-corrected line integrals and the line integrals of bony structures, which can also be approximated using polynomial functions. We denote this 2-dimensional remapping as f_b and model the bone correction based on Eq. (16) in (Joseph and Spital 1978) (polynomials not written out for simplicity):

$$l_i^{Bb}=l_i^{bone}[{\lambda }_0-f_b(f_w\left(f_l\left(y_i\right)\right),l_i^{bone})]$$ (12c)

where l^bone denotes the line integrals of the bony structures, and λ₀ represents the ratio of the bone mass attenuation coefficient to the water mass attenuation coefficient. The error associated with the calibration of the remapping functions, segmentation of the bony structures, and computation of the measurement-dependent gains are assumed to be small.

The variance of the beam-hardening-corrected line integrals can be derived from Eq. (3c):

$$\begin{array}{cc}\hfill \mathrm{var}\left(l_i^B\right)& \approx {\left[\stackrel{.}{f}\left({\stackrel{‒}{y}}_i\right)\right]}^2\mathrm{var}\left(y_i\right)\hfill \\ \hfill & ={\left[{\stackrel{.}{f}}_w\left(f_l\left({\stackrel{‒}{y}}_i\right)\right){\stackrel{.}{f}}_l\left({\stackrel{‒}{y}}_i\right)-l_i^{bone}\frac{\partial f_b(f_w\left(f_l\left({\stackrel{‒}{y}}_i\right)\right),l_i^{bone})}{\partial f_w\left(f_l\left(y_i\right)\right)}{\stackrel{.}{f}}_w\left(f_l\left({\stackrel{‒}{y}}_i\right)\right){\stackrel{.}{f}}_l\left({\stackrel{‒}{y}}_i\right)\right]}^2\mathrm{var}\left(y_i\right)\hfill \end{array}$$ (13a)

where ḟ_w(f_l(ȳ_i)) represents the derivative of the function f_w with respect to f_l(y_i) evaluated at f_l(ȳ_i), ḟ_l(ȳ_i) represents the derivative of the function f_l evaluated at mean measurement ȳ_i, and ∂f_b(f_w(f_l(ȳ_i)), ·)/∂f_w(f_l(y_i)) represents the partial derivative of the function f_b with respect to the first operand f_w(f_l(y_i)) evaluated at f_w(f_l(ȳ_i)). Rearranging the terms and replacing ḟ_l(ȳ_i) with $1∕{\stackrel{‒}{y}}_i^2$ in Eq. (13a) yields:

$$\mathrm{var}\left(l_i^B\right)\approx {\left[{\stackrel{.}{f}}_w\left(f_l\left({\stackrel{‒}{y}}_i\right)\right)\right]}^2{\left[l_i^{bone}\frac{\partial f_b(f_w\left(f_l\left({\stackrel{‒}{y}}_i\right)\right),l_i^{bone})}{\partial f_w\left(f_l\left(y_i\right)\right)}-1\right]}^2\frac{1}{{\stackrel{‒}{y}}_i^2}\mathrm{var}\left(y_i\right)$$ (13b)

showing that the variance is scaled by two terms corresponding to the variance change in water and bone corrections, respectively. For simplicity, these two terms are denoted as:

$$\begin{array}{cc}\hfill {\eta }_w\left({\stackrel{‒}{y}}_i\right)=& {\left[{\stackrel{.}{f}}_w\left(f_l\left({\stackrel{‒}{y}}_i\right)\right)\right]}^2\hfill \\ \hfill {\eta }_b\left({\stackrel{‒}{y}}_i\right)=& {\left[l_i^{bone}\frac{\partial f_b(f_w\left(f_l\left({\stackrel{‒}{y}}_i\right)\right),l_i^{bone})}{\partial f_w\left(f_l\left(y_i\right)\right)}-1\right]}^2\hfill \end{array}$$ (13c)

where the functional argument ȳ_i in η_w(ȳ_i) and η_b(ȳ_i) denotes that the derivative of the function f_w is taken at f_l(ȳ_i) and the partial derivative of the function f_b is taken at f_w(f_l(ȳ_i)), respectively. The ratio of the variance after and before beam hardening correction is therefore:

$$\frac{\mathrm{var}\left(l_i^B\right)}{\mathrm{var}\left(l_i\right)}\approx {\eta }_w\left({\stackrel{‒}{y}}_i\right){\eta }_b\left({\stackrel{‒}{y}}_i\right)$$ (14)

These analytical results of the variance following water and bone beam hardening correction were derived as a special case of the general form in Sec. 2.1. However, the results can also be applied to other scenarios of beam hardening correction in which only the water correction is applied simply by removing the η_b(ȳ_i) term in Eq. (13) and (14).

2.5 Effect of both scatter and beam hardening corrections and modified PWLS weights

We propose a PWLS image reconstruction method that accounts for the changes in variance resulting from artifact correction. Modified weights associated with the post-correction variance are derived to account for both scatter and beam hardening corrections as illustrated in Fig. 1. The post-correction variance is derived from the analysis of scatter and beam hardening in the previous two sections, yielding:

$$\mathrm{var}\left(l_i^{SB}\right)\approx \frac{1}{{({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)}^2}{\eta }_w({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i){\eta }_b({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)\mathrm{var}\left(y_i\right)$$ (15a)

where the superscript SB denotes both scatter and beam hardening corrections and

$$\begin{array}{cc}\hfill {\eta }_w({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)=& {\left[{\stackrel{.}{f}}_w\left(f_l({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)\right)\right]}^2\hfill \\ \hfill {\eta }_b({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)=& {\left[l_i^{bone}\frac{\partial f_b(f_w\left(f_l({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)\right),l_i^{bone})}{\partial f_w\left(f_l(y_i-{\stackrel{‒}{S}}_i)\right)}-1\right]}^2\hfill \end{array}$$ (15b)

The ratio of the variance after and before both corrections is therefore:

$$\frac{\mathrm{var}\left(l_i^{SB}\right)}{\mathrm{var}\left(l_i\right)}\approx {(1+{\mathrm{SPR}}_i)}^2{\eta }_w({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i){\eta }_b({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)$$ (16)

showing the change in variance as a result of scatter correction (by a factor (1+SPR_i)²), water correction (by a factor η_w(ȳ_i – S̄_i)), and bone correction (by a factor η_b(ȳ_i – S̄_i)).

The modified PWLS weights can therefore be written as the inverse of the post-correction variance, replacing mean measurements ȳ_i with actual measurement values y_i:

$${\left[{\mathbf{W}}_{\ast }^{SB}\right]}_i=\frac{1}{\mathrm{var}\left(l_i^{SB}\right)}\approx \frac{{({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)}^2}{{\eta }_w({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i){\eta }_b({\stackrel{‒}{y}}_i-{\stackrel{‒}{S}}_i)\mathrm{var}\left(y_i\right)}\approx \frac{{(y_i-{\stackrel{‒}{S}}_i)}^2}{{\eta }_w(y_i-{\stackrel{‒}{S}}_i){\eta }_b(y_i-{\stackrel{‒}{S}}_i)y_i}$$ (17)

In the methods and results below, we denote PWLS image reconstruction with conventional weights simply as PWLS, and PWLS image reconstruction with modified weights as PWLS_*.

2.6 Optimization approach for PWLS image reconstruction with a noise model for generalized data transformation

Because the objective function for PWLS_* is equivalent to the conventional PWLS formulation (with modification to the diagonal weights), PWLS_* can employ well established PWLS optimization algorithms. In this work, we used the separable quadratic surrogate with ordered subsets (OS-SQS) method (Erdoğan and Fessler 1999) for solving PWLS_*, due in part to its suitability for parallelizable image updates (i.e., using parallel computation on GPU), with OS selected to further speed convergence. The OS-SQS algorithm used in this work for solving PWLS_* differs from the OS-SQS algorithm for solving penalized-likelihood reconstruction (Erdoğan and Fessler 1999) on the following two points. First, instead of the log-likelihood data fit term for which the optimal curvatures change over the course of iterations, the optimal curvatures of the data fit term in PWLS_* are constants that can therefore be precomputed. Furthermore, the term corresponding to the optimal curvature of the data fit term (d_j in Table 1) in the update equation can also be precomputed; however, because this term is subset-dependent (and carries a large computation time to calculate for every subset), we precompute an approximation using all projections (found to be a good approximation in the data reported below).

Table 1.

Pseudocode for solving PWLS_* using OS-SQS.

Precompute optimal curvatures

$c_i\left({\widehat{l}}_i\right)={\left[{\left[{\mathbf{W}}_{\ast }\right]}_i\right]}_{+}{\widehat{l}}_i\ge 0$

Precompute approximate dj term $d_j={\sum }_{i=1}^{N_y}{a}_{ij}{\gamma }_i{c}_i\left({\widehat{l}}_i\right)$

for each iteration n = 1, ..., niter

for each subset m = 1, ..., M

${\widehat{l}}_i={\sum }_{j=1}^{N_{\mu }}{a}_{ij}{\widehat{\mu }}_j{\stackrel{.}{h}}_i=w_i(l_i-{\widehat{l}}_i)\forall i\in S_m$

for j = 1, ..., Nμ

${\stackrel{.}{L}}_j=M{\sum }_{i\in S_m}{a}_{ij}{\stackrel{.}{h}}_i$

${\widehat{\mu }}_j={\left[{\widehat{\mu }}_j+\frac{{\stackrel{.}{L}}_j-{\beta }_R{\sum }_{k=1}^K{\left[{\Psi }_R\right]}_{kj}\stackrel{.}{H}\left({\left[{\Psi }_R\widehat{\mu }\right]}_k\right)}{d_j+2{\beta }_R{\sum }_{k=1}^K{\left[{\Psi }_R\right]}_{kj}^2{\omega }_H\left({\left[{\Psi }_R\widehat{\mu }\right]}_k\right)}\right]}_{+}$

end

end

end

Table 1 presents pseudocode for solving PWLS_* using OS-SQS. The notation [·]₊ denotes the nonnegativity constraint, N_y and N_μ are the size of the measurements and the image, respectively, γ_i is the i^th projection of an image of all ones, a_ij is the (i, j) element of the matrix A, n_iter is the maximum number of iterations, M is the number of subsets, l̂_i is the projection of the current image estimate $\widehat{\mu }$, and S_m denotes all the projections in the m^th subset. In the regularization part, Ψ_R computes the first-order neighborhood difference, K is the number of neighboring voxels, and Ḣ and ω_H are the gradients and curvatures of the Huber penalty function H, respectively. The exact form for H can be written as:

$$H\left(x\right)=\{\begin{array}{cc}\frac{1}{2\delta }{x}^2\hfill & \mid x\mid <\delta \hfill \\ \mid x-\frac{\delta }{2}\mathrm{sgn}\left(x\right)\mid \hfill & \mid x\mid \ge \delta \hfill \end{array}\phantom{\}}$$ (18)

where x is a scalar input and sgn(·) is the sign function. The gradients Ḣ are straightforward to compute and the curvatures ω_H are defined as ω_H(x) = Ḣ(x)/x.

The computational complexity of PWLS_* (solved by OS-SQS) can be characterized by the number of projection operations needed (forward projections and backprojections), which is the dominant factor in computation time. Execution of PWLS_* as expressed in Table 1 requires 2 × n_iter projection operations on all the projections. The PWLS_* method was implemented in Matlab (The Mathworks, Natick MA), with the major part of the computation (i.e., projection and arithmetic operations) executed on GPU using CUDA-based libraries.

3. Experimental methods

3.1 Experiments on a CBCT Test-Bench and Head Phantom

Experiments were performed on a CBCT test-bench with a FPD (PaxScan 4343R, Varian, Palo Alto CA) as shown in Fig. 2(a). A custom anthropomorphic head phantom was scanned at 100 kVp, 0.4 mAs per projection with 720 projections (0.5° angular steps), and a 0.556 × 0.556 mm² pixel size (after 2 × 2 binning). The system used a 580 mm source-to-axis distance (SAD) and a 800 mm source-to-detector distance (SDD), resembling a typical configuration for compact head CBCT system (Zbijewski and Stayman 2009). As shown in Fig. 2(b-c), the head phantom was filled with a gelatin mixture carefully prepared to provide contrast equivalent to brain. The phantom was equipped with ventricle models prepared from wax with contrast equivalent to cerebrospinal fluid, and rows of plastic spheres with diameters ranging from 1.5 mm to 12 mm that were included to encompass a pertinent range of imaging tasks for the detection of intra-parenchymal hemorrhages in acute TBI. The resulting gelatin-plastic contrast closely simulated that of brain to fresh blood (~50 HU) (Parizel et al 2001, Greenberg and Arredondo 2006).

Figure 2.

Experimental methods. (a) Benchtop CBCT system with the x-ray source and FPD in a geometry emulating a compact head scanner. (b) Anthropomorphic head phantom incorporating simulated intracranial hemorrhage. The occipital portion can be removed to access inside the interior of the cranium. (c) A photograph inside the head phantom during assembly, showing the gelatin mixture (brain), wax (ventricles), and plastic spheres (hemorrhage).

The performance of the PWLS_* method was evaluated using a variety of CBCT scan conditions and correction methods. First, a narrow-beam scan was performed with longitudinal collimation reduced to a ~10 mm field of view covering only the skull base region. The narrow-beam scan provided projection data with a low contribution of x-ray scatter. As such, these data were only corrected for beam hardening using the Joseph and Spital approach (Joseph and Spital 1978) mentioned above, referred to as the beam-hardening-corrected dataset. Second, a wide collimation scan was performed covering the entire cranium and incurring the substantial effects of both scatter and beam hardening. The projections were corrected for scatter using a high-fidelity Monte Carlo correction method (Sisniega et al 2015) to form a scatter-corrected dataset, and then corrected for beam hardening to form a fully-corrected dataset. All projection data were offset-corrected and gain-normalized by mean dark and flood field calibrations and corrected for detector lag and veiling glare (Sisniega et al 2015) prior to scatter and/or beam hardening corrections. Since the latter two effects are small in comparison to scatter and beam hardening, they were not explicitly considered in the current work.

For each dataset, images were reconstructed using three methods: FBP, PWLS, and PWLS_*. The same regularization parameters, number of iterations (100), and subsets (20) were used for both PWLS methods. Similarly, both PWLS methods used matched separable footprint projectors and backprojectors (Long et al 2010), and FBP used voxel-driven interpolating backprojection. All images were reconstructed with 0.5 × 0.5 × 0.5 mm³ voxel size on a workstation equipped with one Nvidia GeForce GTX TITAN graphics card. The main parameters in the OS-SQS algorithm for PWLS_* along with the nominal values or range used in the experiments are summarized in Table 2. The execution of OS-SQS over one subset in one iteration took about 10 seconds, and the total execution time over all 20 subsets and 100 iterations was about 5.5 hours. Since the current work mainly focused on evaluation of image quality for the proposed method (rather than computation speed), acceleration of the algorithm was not fully investigated in the current implementation and will be the subject of future work. For example, the projection/backprojection step was implemented using the separable footprint method. Replacing that with faster methods (such as a combination of ray-driven Siddon (Siddon 1985) and voxel-driven interpolating method (Peters 1981)) is expected to reduce time by a factor of ~5 while achieving similar image quality, according to previous work in (Wang et al 2014b). Major reduction in execution time may also be achieved (beyond the scope of this paper) by methods including acceleration techniques compatible with OS-SQS such as spatially non-uniform updates (Kim et al 2013) and Nesterov's method (Kim et al 2015). For example, previous work (Wang et al 2014b) showed that Nesterov-accelerated penalized-likelihood reconstruction by OS-SQS with simplified forms of projection/backprojection reduced reconstruction time of C-arm CBCT data from ~100 min to as little as ~2 min.

Table 2.

Summary of major parameters in the OS-SQS algorithm for PWLS_*.

Symbol	Description	Nominal values or range
Ψ R	Sparsifying operator in image regularization	First-order neighborhood difference
β R	Parameter controlling strength of image regularization	101 ~ 103
δ	Size of quadratic region in Huber penalty	5 HU
niter	Number of iterations	100
M	Number of subsets	20
Ny	Number of measurements	668 × 668 × 720
Nμ	Number of voxels in reconstructed image	412 × 512 × 512

3.2 Evaluation of Image Quality

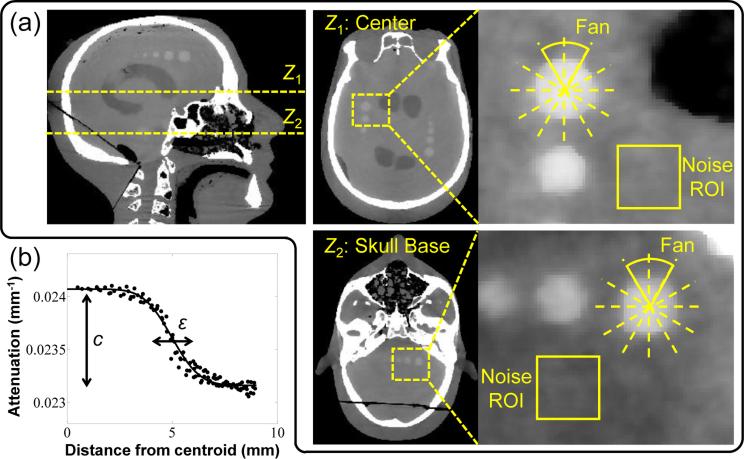
Both FBP and PWLS permit control of the tradeoffs between spatial resolution and noise through adjustment of algorithm parameters: for FBP, via the cutoff frequency of the apodization (smoothing) kernel; for PWLS, via the regularization strength, β_R, and the Huber distance, δ. For fair comparison, images reconstructed by different methods were matched in terms of either the spatial resolution or the image noise by adjusting the apodization kernel in FBP and the regularization strength β_R in PWLS and PWLS_*. The Huber distance δ was fixed and chosen to be the same between PWLS and PWLS_*, and the selection of its value is discussed in Sec. 4.2. Spatial resolution was assessed using the method detailed in (Wang et al 2014a) in terms of the edge spread function (ESF) of a sphere of contrast equal to the structure of interest (i.e., fresh blood). The ESF was fit to a sigmoid parameterized by width, ε, as shown in Fig. 3(b). The ESF width was computed using all voxels within 60° fans centered on the sphere, and spatial resolution was characterized as the average ε computed over all the fans. The contrast of the sphere was given by a second fit parameter c (mm⁻¹) and was also averaged over all the fans. Image noise was calculated as the standard deviation of voxel values in a region-of-interest (ROI) (19 × 19 voxels) in a homogeneous region of gelatin (brain) immediately adjacent to the sphere. Contrast-to-noise ratio (CNR) was computed using the contrast of the sphere and image noise mentioned above.

Figure 3.

Illustration of image quality metrology. (a) Two axial slices in which the spatial resolution, noise, and contrast-to-noise ratio (CNR) were computed. The spatial resolution and contrast were computed by fitting an edge spread function (ESF) to voxel values in 60° fans centered on a sphere of contrast equivalent to blood. Noise was computed as the standard deviation of voxel values in a homogeneous ROI immediately adjacent to the sphere. (b) Example sigmoid fit to the measured ESF, from which spatial resolution was characterized in terms of the ESF width, ε, and contrast was given by the parameter c.

Figure 3(a) shows two axial slices (Z₁ and Z₂) in which the image quality metrics were evaluated. For the beam-hardening-corrected dataset, the metrics were computed in axial slices about the Z₂ region in the skull base. For the scatter-corrected dataset and fully-corrected dataset, the metrics were computed in axial slices about the Z₁ region of central brain parenchyma. Note that for fair comparison, the spatial resolution in the longitudinal (z) direction in FBP reconstructions was also matched to that in PWLS reconstructions by additional apodization in the z direction in the FBP smoothing kernel as in (Wang et al 2014a). Conversion of voxel values to HU assumed a constant value of water attenuation (0.0219 mm⁻¹).

4. Results

4.1 Effect of Artifact Corrections on Variance

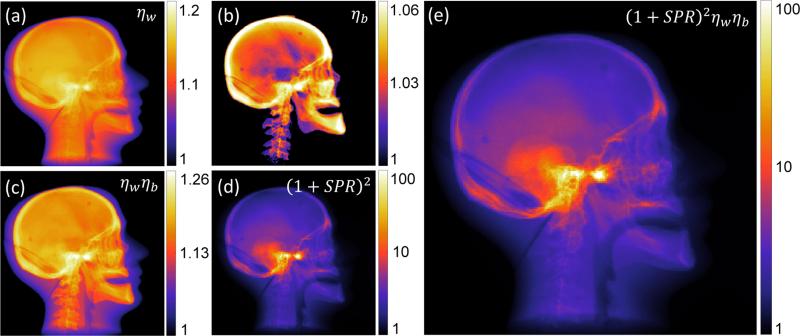
The change in variance associated with each step of the artifact correction was computed using the test-bench data as shown in Fig. 4. An increase in variance throughout the head was observed in every step of the artifact correction. For the beam hardening correction, such changes are seen to vary spatially throughout the head for the water (η_w) correction (Fig. 4(a)) and was more highly concentrated in the bony regions in bone (η_b) correction (Fig. 4(b)), consistent with the particular correction applied in each case. The combined beam hardening correction (η_w η_b) gives a maximum change in variance by ~30% (Fig. 4(c)). For scatter correction, the change in variance also depended strongly on location (Fig. 4(d)) with a maximum change as high as two orders of magnitude in dense bone regions, where scatter fractions are highest. The total variance change after applying all corrections (Fig. 4(e)) was dominated mainly by the scatter correction part, indicating scatter correction to be the dominant factor affecting the variance in this case. The substantial changes in variance throughout the head suggests the importance of the proposed modified weighting terms to compensate for such variations.

Figure 4.

Example illustration (in a lateral projection view) of the change in variance associated with each step of artifact correction. The change in variance is shown for corrections associated with: (a) beam hardening correction for water (η_w); (b) beam hardening correction for bone (η_b); (c) total beam hardening correction (η_w η_b); (d) scatter correction (1+SPR)²; and (e) all scatter and beam hardening corrections.

4.2 Selection of Image Regularization Parameters

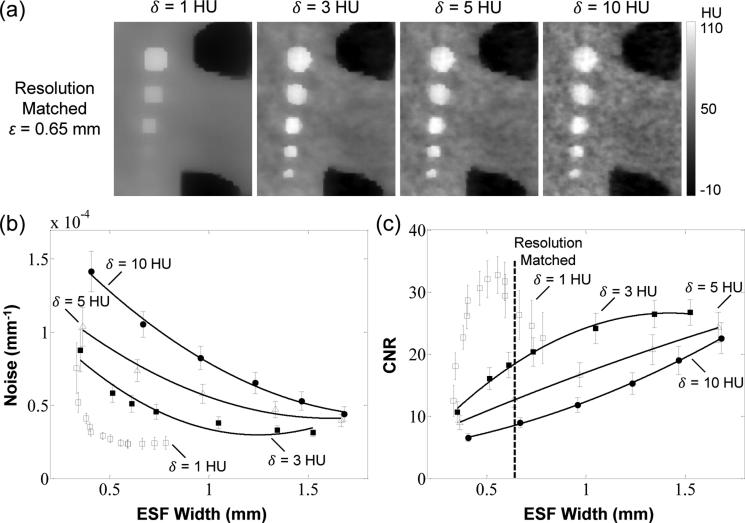
Fair comparison of image quality for different reconstruction methods requires a justification of parameter settings suitable to the imaging task as well as evaluation of noise and spatial resolution on equal footing. The PWLS_* and PWLS methods used a Huber penalty function to reduce noise in a manner governed by the range of the quadratic neighborhood δ. Previous work showed that a small value of δ (relative to the contrast of structures of interest) should be selected to provide edge preservation and noise reduction (Wang et al 2014a, Stayman et al 2013), but selection of δ too small tends to over-regularize the image and lead to unrealistic, piecewise-constant images. To find a reasonable value of δ, the PWLS_* images were reconstructed using a fully-corrected dataset over a range of δ values (1, 3, 5, and 10 HU). A region-of-interest from images resulting from PWLS_* reconstructions at various values of δ are shown in Fig. 5(a) with spatial resolution matched at a level of ε = 0.65 mm. The image with δ = 10 HU exhibits a high degree of noise with little benefit from the linear region of the Huber penalty, and noise reduces for smaller values of δ. However, reduction of δ to 1 HU leads to an unrealistic patchy texture and decreased contrast, suggesting over-regularization. Figures 5(b-c) summarize the performance in terms of the noise and CNR over a broad range of spatial resolution for different δ values. Consistent with the images in Fig. 5(a), the quantitative analysis shows that reducing δ from 10 HU to 3 HU reduces the noise and increases the CNR at any level of spatial resolution, whereas at δ = 1 HU the CNR exhibits a ‘kink’ in the noise-resolution tradeoff, suggesting over-regularization and contrast degradation. Together, these results suggest a reasonable value of δ in the range ~3-5 HU. Considering the narrow range of suitable values (3~5 HU) for δ, its value was fixed for both PWLS and PWLS_* at a level that avoided under-regularization or over-regularization. In the results reported below, we selected δ = 5 HU as a conservative choice balancing noise reduction and edge preservation for both the PWLS_* and PWLS methods and all three datasets.

Figure 5.

Selection of regularization parameters with respect to noise-resolution tradeoffs. (a) PWLS_* images in a ROI in the Z₁ axial slice using different δ values. Images were reconstructed using the fully-corrected dataset with spatial resolution matched at ε = 0.65 mm. (b-c) Noise-resolution tradeoff and CNR-resolution tradeoff for PWLS_* using different δ values. The error bars are based on the standard deviation of the noise in 6 neighboring axial slices. The solid curves are second-order polynomial fits intended merely as a guide to trends evident in the underlying data points. A value of δ = 5 HU was selected as a conservative choice giving a reasonable level of noise reduction and edge preservation without introducing an unnatural appearance of patchy over-regularization.

4.3 Image Reconstruction with Beam Hardening Correction

The narrow-beam collimation case strongly reduced x-ray scatter effects (SPR less than ~10%) and provided data that largely isolated beam hardening effects. FBP, PWLS, and PWLS_* reconstructions were performed following water and bone beam hardening correction to quantify and visualize the effects of the correction algorithm on image variance and the potential improvements in image quality with modified PWLS weights. Figure 6 shows reconstructions for each case within a ROI in the axial slice Z₂, where beam hardening effects were severe due to the presence of thick, dense bone in the skull base. FBP reconstruction without beam hardening correction (Fig. 6(a)) exhibits fairly severe artifacts and a nominal level of quantum noise σ = 9.3 HU, whereas the same data with beam hardening correction (denoted FBP^B in Fig. 6(b)) shows a substantial reduction in artifacts but a ~13% increase in noise. PWLS reconstruction with conventional weights provides a strong (~43%) reduction in noise (at matched spatial resolution) as shown in Fig. 6(c). A further (~12%) reduction in noise is obtained using modified weights as shown in Fig. 6(d), demonstrating the benefits of the proposed method in preserving the fidelity of artifact corrections and reducing noise by nearly a factor of 2 compared to FBP^B .

Figure 6.

Reconstructions with beam-hardening correction. (a) FBP reconstruction with no corrections. (b) FBP reconstruction of beam-hardening-corrected data. (c) PWLS reconstruction of beam-hardening-corrected data with conventional weights. (d) PWLS_* reconstruction of beam-hardening-corrected data with modified weights. The proposed method (${\mathrm{PWLS}}_{\ast }^B$) maintains the quality of artifact correction and gives a factor of ~2 improvement in noise compared to FBP^B. (Resolution was matched at ε = 0.70 mm for fair comparison.)

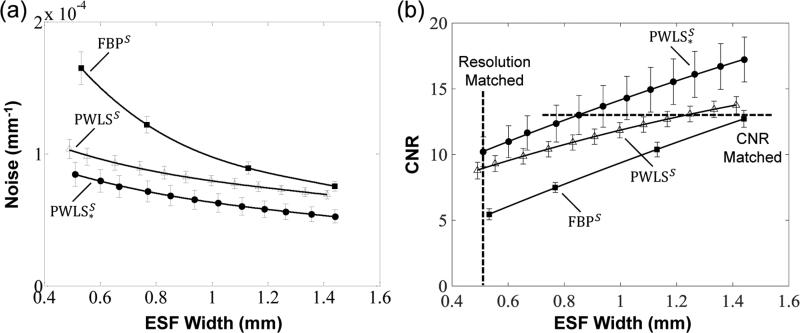
4.4 Image Reconstruction with Scatter Correction

Full field-of-view (wide-collimation) projection data were reconstructed using FBP, PWLS, and PWLS_* following scatter correction by a Monte Carlo method (Sisniega et al 2015). Figure 7 shows reconstructions for each case in a ROI in the Z₁ axial slice at matched spatial resolution (ε = 0.50 mm, top row) and at matched contrast-to-noise ratio (CNR = 13, bottom row). In Fig. 7a (matched spatial resolution images), we observe FBP reconstruction without scatter correction to exhibit severe cupping artifacts, reduced contrast, and inaccurate HU (but relatively low noise). FBP reconstruction of the scatter-corrected data (denoted FBP^S) shows a strong reduction in artifacts but an increase in noise by ~72%. This dramatic increase in noise is consistent with the large change in variance associated with scatter correction shown in Fig. 4. PWLS reconstruction of the scatter-corrected data (using conventional weights, denoted PWLS^S) reduced the noise by ~41%, and use of the modified weights further reduced noise by an additional ~26%, denoted ${\mathrm{PWLS}}_{\ast }^S$. In Fig. 7b (matched CNR images), we observe complementary improvement in spatial resolution for the proposed method, with the ESF width improving from ε = 1.44 mm for FBP^S to 1.25 mm for PWLS^S with conventional weights to and to 0.85 mm for ${\mathrm{PWLS}}_{\ast }^S$ with modified weights.

Figure 7.

Reconstructions with scatter correction - top row at matched spatial resolution and bottom row at matched CNR. From left to right: FBP reconstruction of uncorrected and scatter-corrected projection data; PWLS of scatter-corrected data with conventional weights; and PWLS_* reconstructions of scatter-corrected data with modified weights.

Figure 8 quantifies the noise-resolution tradeoffs among the three reconstruction methods with scatter correction. As expected, both the PWLS and PWLS_* methods show improved noise (and CNR) compared to FBP at any level of spatial resolution. The proposed PWLS_* method shows a further improvement in noise and CNR compared to PWLS with conventional weights - for example, a 34% improvement in CNR at a spatial resolution of ε = 0.50 mm.

Figure 8.

Noise-resolution tradeoffs for the FBP, PWLS, and PWLS_* reconstruction methods operating on scatter-corrected projection data. The levels of matched spatial resolution and CNR used in Fig. 7 are marked by the dashed lines in (b).

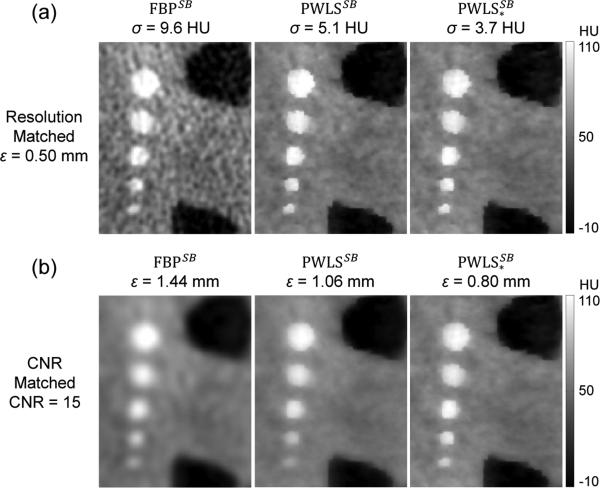
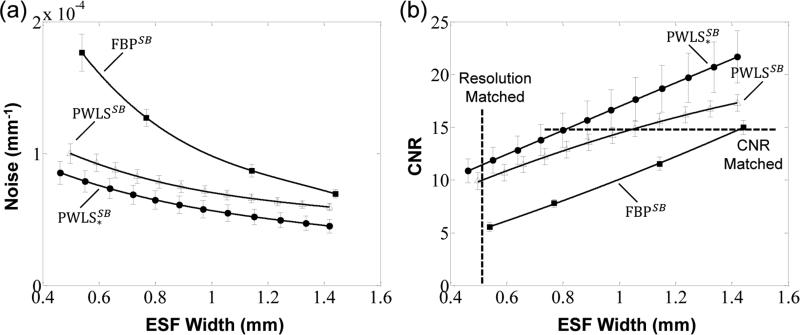
4.5 Image Reconstruction with Scatter and Beam Hardening Corrections

Finally, we evaluated the combined effects of scatter and beam hardening corrections in FBP, PWLS, and PWLS_* reconstructions. Similar to Fig. 7, the results in Fig. 9 show images from full field (wide collimation) scans in a ROI in the Z₁ axial slice. Reconstruction of the fully corrected (scatter and beam hardening) projection data are denoted by the superscript SB. Considering the top row of Fig. 9 (images at matched spatial resolution), we see a progressive reduction in noise for the FBP^SB, PWLS^SB, and ${\mathrm{PWLS}}_{\ast }^{SB}$ reconstructions, with the last providing a ~40% reduction in noise compared to the first. Considering the bottom row of Fig. 9 (images at matched CNR), we see that the PWLS_* method also exhibits the highest spatial resolution (ε = 0.50 mm). Moreover, the PWLS_* images show reliable detection of simulated intracranial hemorrhages as small as 3 mm diameter. The corresponding noise-resolution tradeoffs among the three methods are quantified in Fig. 10, with PWLS_* demonstrating an improvement in each respect. Note also the increased CNR of all three methods in Fig. 10 compared to Fig. 8, owing to the additional correction (beam hardening).

Figure 9.

Reconstructions with scatter and beam hardening corrections - top row at matched spatial resolution and bottom row at matched CNR. As in Fig. 7, from left to right: FBP, PWLS, and PWLS_* reconstructions of fully corrected projection data.

Figure 10.

Noise-resolution tradeoffs for the FBP, PWLS, and PWLS_* reconstruction methods operating on fully-corrected (scatter and beam hardening) projection data. The levels of matched spatial resolution and CNR used in Fig. 9 are marked by the dashed lines in (b).

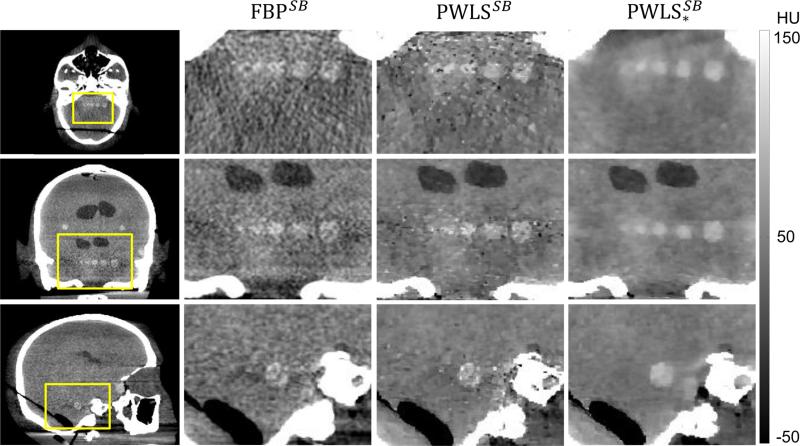
Visual assessment is further illustrated in Fig. 11, showing FBP, PWLS, and PWLS_* reconstructions of the fully-corrected data in regions about the skull base, where scatter and beam hardening effects are strongest. Axial, coronal, and sagittal slices are shown with spatial resolution matched at ε = 0.40 mm. Uncorrected images (not shown) are severely degraded by artifact and are not suitable for detection of ICH in this region. The fully corrected FBP^SB reconstruction yields strong reduction of artifact but exhibits a high level of noise, particularly in the region between the temporal bones. Interestingly, the PWLS^SB reconstruction with conventional weights does not provide a reduction in noise due to gross mismatch between the presumed noise model with the fully corrected data. The proposed PWLS_* reconstruction with modified weights substantially reduced the noise at a fixed level of spatial resolution, which may improve detection of low contrast intracranial hemorrhage. These results in a challenging region demonstrated the importance of incorporating an accurate noise model in MBR. The bias in the ${\mathrm{PWLS}}_{\ast }^{SB}$ reconstruction surrounding the spheres was most likely caused by under or over correction of image artifacts in this challenging region. Such bias may be reduced by methods including more accurate bone segmentation in beam hardening correction and performing the “two-step” beam hardening correction multiple times.

Figure 11.

Axial (top row), coronal (middle row), and sagittal (bottom row) CBCT images of the head phantom with scatter and beam hardening corrections, reconstructed by FBP, PWLS, and PWLS_*. The skull base presents a challenging region for which proper account of scatter and beam hardening corrections is essential to high-quality reconstruction. The spatial resolution in each case was matched (ε = 0.40 mm) at the largest sphere in the axial slice Z₁.

5. Discussion and conclusion

This work has developed and evaluated a novel PWLS image reconstruction method with a generalized framework for accommodating accurate noise models for artifact-corrected CBCT data. We considered the specific scenario where the two dominant artifact correction methods essential to high-quality CBCT - scatter and beam hardening corrections – are applied. The resulting reconstruction method (denoted PWLS_*) utilizes modified weights to compensate for noise amplification imparted by each step of the artifact correction. Experiments included physical data acquired on a FPD-CBCT test-bench using an anthropomorphic head phantom emulating intra-parenchymal hemorrhage as in acute TBI. A conservative level of regularization in the Huber penalty was selected to improve the conspicuity of simulated hemorrhages while not resulting in an unnaturally patchy, over-regularized image. The proposed PWLS_* method demonstrated superior noise-resolution tradeoffs in comparison to traditional methods, including FBP and PWLS with conventional statistical weights (and noise models).

The theoretical and practical contributions of the current work include: (i) development of a novel PWLS image reconstruction method with a noise model that includes modeling of the noise characteristics associated with different processes and incorporates modified weights to account for the changes in noise characteristics; (ii) derivation of analytical expressions for the change in variance arising from scatter and standard beam hardening corrections; (iii) illustration and quantitation of the high degree of changes in variance (more than two orders of magnitude) after artifact corrections; (iv) validation of the assumptions on the benefits of incorporating variance changes into PWLS in the presence of artifact corrections through test-bench experiments emulating ICH detection; (v) evaluation of image quality for the proposed PWLS_* method in support of the hypothesis that FPD-CBCT can provide soft-tissue image quality suitable to reliable detection of ICH and supporting the development of a dedicated system for point-of-care diagnosis of acute TBI.

The work suggests a number of interesting points meriting future investigation. The first is that the current model of variance change focuses on Poisson noise propagated through each correction. While this is a valid starting point, assuming accurate scatter and beam hardening estimates and gain normalization, the model could be extended to consider other sources of noise, including error in the MC scatter estimate, uncertainties in the segmentation of bony structures in the beam hardening correction, and incomplete correction of detector gain variations. For example, in the Monte Carlo estimation of the scatter fluence, noise could be introduced in steps that require random sampling from a known distribution (e.g., photon energy, direction, path length before interaction, etc.), and the effects could be exaggerated when only a small number of photons are simulated (Sisniega et al 2013). Incorporating such additional sources of variation is the subject of future work.

A second area for future study is to account of other sources of image artifacts in FPD-CBCT, such as the effects of image lag and low-frequency glare / off-focal radiation. These effects are included within the comprehensive artifact correction framework of Sisniega et al. (Sisniega et al 2015) but were not included in the current work. Since lag and veiling glare corrections also introduce variance changes (although measurably small compared to scatter and beam hardening effects), the noise changes associated with these corrections could also be included in further modification of the PWLS weights - for example, derived from the known relationship between noise and image lag (Siewerdsen et al 1997, Siewerdsen and Jaffray 1999) and low-frequency blur. Note that the assumption of independent measurements no longer holds in the case of lag and veiling glare corrections, due to the existence of temporal (lag) or spatial (veiling glare) correlations between measurements. Therefore, Eq. (2) and (3) need to be re-written for consideration of correlations when dealing with these corrections and a generalized reconstruction model as in (Stayman et al 2014, Tilley et al 2014) may be required.

A third topic for additional investigation is the recognition and challenge associated with spatially varying spatial resolution effects in MBR (Fessler and Rogers 1996) including the PWLS_* method detailed in this paper, which could potentially degrade detectability of ICH. For example, in a PWLS_* image with a fixed image roughness strength, β_R, and for a given size and contrast of sphere (simulated hemorrhage), lower spatial resolution characteristics were observed in the central region of the head, while higher spatial resolution was evident adjacent to the cranium. This problem could be at least partly addressed by methods that encourage space-invariant spatial resolution, such as the certainty-based method (Fessler and Rogers 1996). Preliminary results showed that the use of certainty-based method achieved a more uniform spatial resolution across the image, thereby enabling similar noise-resolution tradeoffs between the simulated hemorrhages in different regions of the head. Moreover, intentional use of spatially varying regularization may be beneficial to the imaging task(s) - for example, sharper resolution (via reduced penalty strength) in regions of the cranium for detection of fracture, simultaneous with stronger noise reduction (via higher penalty strength) within the brain parenchyma for detection of intracranial hemorrhage. Among the possible methods for achieving such a space-varying noise-resolution characteristic is a space-varying β_R map (Gang et al 2014) optimized for CBCT imaging of the head.

Another point worth further investigation is the assessment of image quality with respect to specific clinical tasks. In this work, simple imaging performance metrics were used to quantify spatial resolution, contrast, noise, and CNR. These metrics provide useful preliminary insight on the improvements obtained with the proposed reconstruction method, and future work will include assessment with respect to task-based measures such as detectability index, various observer models, and human observer studies. For example, detection of a low-contrast, low-frequency lesion (analogous to the clinical task of intracranial hemorrhage detection) and/or a higher-contrast, high-frequency abnormality (analogous to the clinical task of fracture detection) can be analyzed via statistical decision theory hypothesis testing in terms of task-based detectability index and various model observers (Siewerdsen and Antonuk 1998, Tward et al 2007, Tward and Siewerdsen 2008, Gang et al 2014, Wunderlich and Noo 2008, Barrett and Myers 2004). Application of such methods in a manner that accounts for the complexities of nonlinear reconstruction methods is an area of active research, and such work will necessarily account not only for the clinical task but also complexities associated with nonlinear, nonstationary characteristics of the 3D image reconstruction. The results reported above suggest imaging performance consistent with the clinical task of visualizing a 3 mm intracranial hemorrhage (e.g., CNR = 11.9 in images with ESF width = 0.50 mm, also evident in Fig. 9). This may be sufficient for detection of a broad spectrum of acute injuries (subject to validation in future clinical studies) and suggest the possibility for further improvement allowing detection of mm-scale micro-hemorrhage in diffuse axonal injury after concussion (Adams et al 1989).

Finally, certain application scenarios present an opportunity to leverage a patient-specific head image from a previous scan to improve image quality and/or reduce dose in a subsequent scan. Examples include longitudinal monitoring of brain hemorrhage in the intensive care unit (ICU) (where acquisition of multiple head CT scans over the course of ICU monitoring is common) and populations at high risk of head injury in sports and military theatres. Such patient-specific prior images can be incorporated into the PWLS_* reconstruction in the form of previously developed prior image regularization (Stayman et al 2013, Dang et al 2014) to maximize the conspicuity of low-contrast hemorrhages and increase the sensitivity to subtle anatomical changes. The previously developed methods (Stayman et al 2013, Dang et al 2014) also jointly register the patient-specific prior image to the current anatomy in the course of image reconstruction so that the corresponding anatomical structures are well aligned for correct prior image regularization. The joined registration might be performed in a rigid fashion (which is often a good approximation of the motion of the head) or in a deformable fashion (Dang et al 2014) if soft tissue deformation is present in the head (e.g., midline shift, ventricular compression).