Capturing the energetics of water insertion in biological systems: The water flooding approach

Abstract

Consistent description of the effect of internal water in proteins has been a major challenge for both simulation and experimental studies. This effect has been particularly important and elusive in cases of charges in protein interiors. Here we present a new microscopic method that provides an efficient way for simulating the energetics of water insertion. Instead of performing explicit Monte Carlo (MC) moves on the insertion process, which generally involves an enormous number of rejected attempts, our method is based on generating trial configurations with excess amount of internal water, estimating the relevant free energy by the linear response approximation (LRA) and then using a postprocessing MC treatment to filter out a limited number of configurations from a very large possible set. Our approach is validated on particularly challenging test cases including the pK_a of the V66D mutation in Staphylococcal Nuclease (SNase), Glu286 in Cytochrome c Oxidase (CcO) and the energetics of a protonated water molecule in the D channel of CcO. This approach allows us to reproduce the relevant energetics of highly unstable charges in protein interiors using fully microscopic calculations and provides a very substantial improvement over regular microscopic free energy estimates. This establishes the effectiveness of our water insertion strategy in challenging cases that have not been addressed successfully by other microscopic methods. Furthermore, our study provides a new exciting view on the crucial effect of water penetration in key biological systems as well as a new view on the nature of the dielectric in protein interiors.

I. Introduction

Water molecules are integral parts of proteins, membranes and other biological systems [1]. The presence of internal water as well as the effect of water penetration plays a major role in determining the energetics of biological processes, ranging from catalysis [2], redox reactions [3], ligand binding [4–7], ion channel selectivity [8], to proton transport in membrane proteins [9, 10] and ionization of deeply buried protein residues [11, 12]. While this fact is now appreciated on a qualitative level, computationally practical strategies for quantitative estimates of the water insertion energy have not yet been developed. In earlier attempts to capture the energetics of water in and around proteins the Protein Dipole Langevin Dipole (PDLD) model has been quite successful [13–15]. The very early realization of the challenges in treating internal water molecules by all-atom models has led to the development of the PDLD type models, whose simplified dipolar representation has appeared to be very powerful (for a review see ref. [15]). Attempts to consider the water molecules around the protein implicitly in continuum models have not been so successful due to the problem of ill-defined dielectric constant [15, 16]. The earliest attempts to include water molecules in fully microscopic free energy calculations of charges in proteins were reported in ref. [17], using the surface constrained all-atom solvent (SCAAS) model [18, 19], which emerged from our earlier surface constrained soft sphere dipole (SCSSD) model [20] and countless other studies that consider water molecules in and around the proteins in free energy calculations have followed. The SCAAS approach involved an initial generation of a water grid followed by deletion of the grid points that are too close to the protein atoms and subsequent relaxation runs. In some cases we tried to generate denser initial grid to allow for larger number of initial internal water molecules. Various adaptations of the above surface constraint ideas have emerged and used by other groups (e.g. ref. [21]) and eventually have focused on proper electrostatic boundaries [22, 23].

Both the PDLD and the all-atom models have been used in studies of the energetics of many biological processes (e.g. binding, redox reactions, catalysis, ion channel selectivity, proton transport etc.) and they have often provided encouraging results [15]. However, key problems started to emerge in several of these systems. Arguably, the most serious problem has been the apparent overestimate of the solvation penalty of charges in non-polar sites of proteins, where a very glaring case have been provided by the energetics of protonated water molecules in Cytochrome c Oxidase (CcO) [9, 23], where standard free energy perturbation (FEP) calculations can overestimate the actual stabilization by more than 15 kcal/mol (see also section III). Similar problems have been exhibited in the impressive set of benchmarks of ionizable residues provided by Garcia-Moreno and coworkers [11, 12, 24]. In these cases one obtains major overestimates of the penalty of moving the relevant charges from water to the protein interiors by simple free energy perturbation (FEP) microscopic calculations (see [9, 25]). This problem could be overcome by using a semimacroscopic model such as the PDLD/S-LRA with a relatively high dielectric for the self-energy in the problematic sites (around 6–8) [25]. However, such a knowledge-based treatment may not be fully justified. An alternative approach has been provided by the instructive overcharging strategy that forces the protein to undergo partial unfolding with accelerated water penetration [25], but this approach has been quite computationally demanding. Another field where the water insertion issue has become a major problem is the calculation of binding free energies. In this case it has been pointed out [4] that performing free energy perturbation (FEP) or linear response approximation (LRA) may not allow for proper water equilibration, and a specialized systematic approach of mutating internal water molecules to dummy molecules (that do not interact with the environment) has been examined in a preliminary way [4].

Several alternative strategies have been proposed by others as well. For example, approaches emphasizing on formal rigor have focused on grand canonical Monte Carlo (GCMC) based methods for insertion of water molecules into the protein cavities [26–28]. These class of methods are analogous to Widom’s pioneering test particle insertion method which is aimed at determination of the chemical potential in fluid systems [29]. Similar test particle insertion based approaches have also been used to calculate pK_a values in bulk water quite early [30]. The GCMC approach allow, in principle, water molecules to exchange in and out of cavities with solvent. Unfortunately, although these methods are formally appealing, they turn out to be computationally quite expensive, as insertion/deletion moves of entire water molecules are infrequent. Attempt to develop approximate faster methods has been reported by Jorgensen and coworkers [5] who developed a method called “Just Add Water Molecules” (JAWS), where “θ-water” molecules can appear/disappear from the system based on a scaling parameter θ, which is the fractional occupancy of a certain hydration site. However, this method also involves a multistage refinement using explicit MC moves on the effective water potential. Moreover, the primary intention of such methods have been focused on reproducing the hydration sites observed in high resolution crystal structures, rather than actual energetics of water penetration. An interesting water clustering (WaterMap) approach has been introduced by Berne, Friesner and coworkers [6, 31] and the combination of this approach with empirical scaling parameters seems to improve the results of binding calculations. However, we are not aware of a full validation of the above models in particular to the level of quantitative evaluation of the solvent entropic contributions to ligand binding as was done in our study of binding entropy [32]. Moreover, to the best of our knowledge none of these methods explore the difference in the water penetration energies when the relevant protein residue is charged and uncharged. Thus there remains a potential risk of using an incorrect thermodynamic cycle, while inserting water using only the charged state, and not accounting for the corresponding energetics at the uncharged state.

Regardless of the potential of the above approaches they have been used mainly in exploring the ability to predict structural water. However, it seems to us that the above MC approaches have not proven to provide a major quantitative improvement of the calculated binding free energies and their practical advantage remains to be established. In fact, the most important way to establish the validity of water insertion approaches is to explore the performance of the given approach in electrostatic calculations where the effect of the water can be enormous and thus the error in the method can be fully quantified.

In view of the above discussion it is clear that the water insertion process is a very important phenomenon that deserves to be treated efficiently and quantitatively to achieve reliable energetics of many key biological processes. Thus we introduce here a new “water flooding” approach where we completely avoid the need to perform any explicit MC simulation during the energy evaluation step. Instead we determine the energy of rationally inserted (rather than blindly inserted) water molecules using the LRA approach and then sort the energetics by post-processing MC approach, which becomes extremely fast. Our new approach is explored here considering major validation tests and shown to be quite effective. The corresponding studies provide exciting new insights about the major role of internal water molecules in stabilizing charges in relatively non-polar protein sites and in promoting key biological processes.

II. Methods and systems

II.1 General direction

Since the types of problems that we would like to address here are quite general, we would like to formulate a formally rigorous, yet effective and reliable treatment of the internal water molecules. This can be applied to binding problems as illustrated in Fig. 1, and more importantly to studies of the energetics of internal charges (e.g. pK_a, redox potential etc.) as illustrated in Fig. 2.

Figure 1.

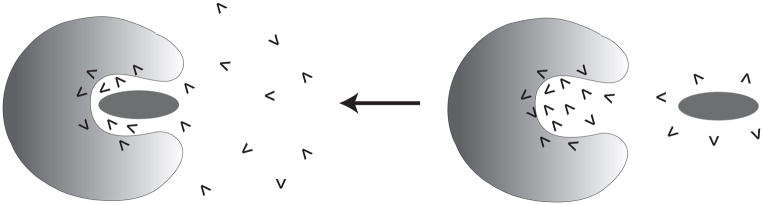
A schematic diagram of binding of a ligand in protein and associated water penetration.

Figure 2.

A schematic diagram of moving a charge from solvent water to protein interior and associated water penetration.

In both cases our primary challenge is to find the most favorable configurations by moving the optimal number of water molecules from the solvent to the protein interior, where the solvent and the protein are part of a single system, with a large number of water molecules (see Fig. 2). Our aim is to develop a practical procedure for finding the lowest free energy of the system (or the free energy at the end of the equilibration of the water molecules between the solvent and the protein) and to focus on the configurations that contribute most to the free energy of the equilibrium ensemble. It should be noted that seemingly more rigorous formal approaches such as the grand canonical Monte Carlo based methods for insertion of water molecules into the protein cavities [26–28] consider moving the water molecules from a solvent, which is around the simulation system rather than a part of this system. However, our treatment, which can be considered as a canonical treatment (although it can also be related to a grand canonical treatment), has a simpler physics that makes it more manageable and practical.

II.2 Outline of the water insertion strategy

As outlined in the introduction we are trying to develop a reasonable rigorous approach for generating the microscopic effects of internal water molecules without the use of any expensive random insertion approaches. Our goal is to first obtain an effective strategy for evaluating the insertion energy (which will be further simplified subsequently) and then to deal with the formation of solvent configurations by a post-processing MC approach. Here the key point is not to perform any explicit MC water insertion simulation, since this will involve an enormous number of rejected insertion attempts. Thus we start by generating a reasonable approximation for the free energy of each configuration and only then we post-process the available free energy data using a MC procedure to estimate the minimum free energy configurations. In order to better clarify our strategy and figure out the important quantities to be evaluated, we first consider the simplified test case of a protein with a few possible sites for internal water molecules near an ionizable residue and a surrounding sphere of solvent water. Our task is to determine the final equilibrium population of the system (that includes exchange of water molecules between different sites). Since it would be usually impractical to run infinitely long MD simulation and to let the system reach a full equilibrium, we look for a simpler approach.

In developing our strategy we consider a system composed of a protein with M sites for internal water molecules surrounded by a deformable sphere of N solvent water molecules. As a start we evaluate the standard free energy of moving any single water molecule from the gas phase to each of the protein sites and to a water site. This can be done by the following steps as shown in the cycle of Fig. 3: (i) we start with a molar volume in the gas phase (by using a constraint of 0.026 kcal/mol.Ų), (ii) the constraint is increased to 0.3 kcal/mol.Ų (our standard cage constraint that corresponds to a volume of a water molecule), (iii) the water molecule is mutated from a full polar water to nonpolar water, and (iv) the non-polar water is mutated to a non-interacting “dummy” water, (v) releasing the constraint to 0.026 kcal/mol.Ų, (vi) moving to the site in the protein (or solvent water), (vii) changing the constraint to 0.3 kcal/mol.Ų and then (viii) regenerating the polar water and finally releasing the constraint to 0.026 kcal/mol.Ų. We also generate the free energy, ΔG_ij, of the interaction between the water molecules inside the protein by evaluating the insertion energy when there is only one water in the protein and then considering the effect of additional sites (see below). Note that the evaluation of ΔG_ij using the FEP approach is very demanding.

Figure 3.

The thermodynamic cycle for insertion energy.

With the free energy of insertion in each site available, we can now explore the free energy of equilibration. That is, we ask what is the free energy of starting with all the N water molecules in water and ending up in the equilibrated system where we have water molecules in L interior protein sites. Our computational approach uses MC procedure to find the free energy of moving water molecules between the water (solvent) sphere and the protein. In doing so it is assumed that removing a water molecule from the solvent to i-th protein site leads to a ( $\mathrm{\Delta }{G}_i^p-\mathrm{\Delta }{G}^w$) change in the free energy of the system and moving a water molecule from the protein to the solvent leads to a ( $-\mathrm{\Delta }{G}_i^p+\mathrm{\Delta }{G}^w$) change in free energy. This treatment implies that the water sphere is deformed to retain a constant density of the solvent. The occupancy of the protein site can be determined by MC procedure that uses the effective potential

$$U_{(\underset{\sim }{m})}=\sum _{i(\underset{\sim }{m}(w))}\mathrm{\Delta }{G}^w{\delta }_i(\underset{\sim }{m})+\sum _{i(\underset{\sim }{m}(p))}\mathrm{\Delta }{G}_i^p{\delta }_i(\underset{\sim }{m})+\sum _{i(\underset{\sim }{m}(p))}\sum _{j(\underset{\sim }{m}(p))<i(\underset{\sim }{m}(p))}\mathrm{\Delta }{G}_{ij}^p{\delta }_i(\underset{\sim }{m}){\delta }_j(\underset{\sim }{m})$$ (1)

where $\mathrm{\Delta }{G}_{ij}^p$ is the interaction between the water molecules at the i-th and j-th sites. The function δ_i(m̰) describes the occupancy of the n sites in the current m̰-th configuration. Thus, δ_i(m̰) =1 when the i-th site in the m̰-th configuration is occupied and δ_i(m̰) = 0 otherwise.

The above MC approach can also be simplified by using

$$U_{(\underset{\sim }{m})}^{\prime }=\sum _{i(\underset{\sim }{m}(p))}(\mathrm{\Delta }{G}_i^p-\mathrm{\Delta }{G}^w){\delta }_i(\underset{\sim }{m})+\sum _{i(\underset{\sim }{m}(p))}\sum _{j(\underset{\sim }{m}(p))<i(\underset{\sim }{m}(p))}\mathrm{\Delta }{G}_{ij}^p{\delta }_i(\underset{\sim }{m}){\delta }_j(\underset{\sim }{m})$$ (2)

where we only consider moves on the protein sites and subtract the cost of moving water from the solvent to these sites.

Our canonical strategy is directly related to what would be obtained by taking a SCAAS sphere and running extremely long MD simulation with a fixed number of water molecules while using the surface constraint to maintain constant density. Note in this respect that practically such runs almost never provide any conclusive quantitative estimate even for MD runs longer than tens of nanoseconds. Basically it is nearly impossible to obtain sufficient statistics in reasonable computer time using brute force molecular dynamics simulations.

Now most studies of related problems have been performed by a grand canonical MC (GCMC) approach (e.g. [33, 34]) where the system (in our case protein plus the solvent sphere) can accept or transfer water molecules to the bulk. In the traditional approach one must wait for many insertion attempts until the water region has a large enough opening to accept the insertion of an external water molecule. In this respect it seems that our philosophy of processing the LRA insertion free energy may also be used as a general way for accelerating GCMC approaches. That is, we can generate a model that is in some respect isomorphic to the GCMC, where the simplest version will have only the protein as the explicit system. In this model we can consider M sites in the protein with the LRA insertion energies, and attempt to transfer water molecules to or from the bulk. In this case the penalty for insertion in the protein comes from the ( $\mathrm{\Delta }{G}_i^p-\mathrm{\Delta }{G}^w$) and $\mathrm{\Delta }{G}_{ij}^p$ terms and from having restricted number of sites. The potential and the justifications for such an approach will be considered in the future.

At any rate our approach allows one to evaluate the population of water molecules in the protein and turn to the evaluation of the free energy of charging the specific ionized group (for example, in the case depicted in Fig. 2) in the protein, following the thermodynamic cycle of Fig. 4. Here we need to consider the fact that the lowest free energy configuration may have different number of water molecules for the charged and uncharged species.

Figure 4.

The thermodynamic cycle used to describe the process of water insertion associated with moving a charge from solvent water to protein interior.

To clarify the strategy of Fig. 4, let’s consider the lowest free energy configurations corresponding to the charged (A⁻) and uncharged (AH) species, where the corresponding number of water molecules is N and M (with N>M and L=N-M), respectively. To obtain the relevant free energy of the combined process of charging and the associated water penetration (ΔG^p(Mw, AH → Nw, A⁻)), we use:

$$\mathrm{\Delta }{G}^p(Mw,AH\to Nw,A^{-})=\mathrm{\Delta }{G}_{\mathit{sol}}^{p(Nw)}(AH\to A^{-})+\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},Lw}^{w\to p(AH,Mw)}$$ (3)

Here, the $\mathrm{\Delta }{G}_{\mathit{sol}}^{p(Nw)}(AH\to A^{-})$ term is evaluated by first finding the value of N (by the above MC procedure) and then evaluating the charging free energy of A⁻ in the presence of the N water molecules, by a FEP procedure. The $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},LW}^{w\to p(AH,MW)}$ term signifies the free energy cost of insertion of extra (N-M) water molecules at the uncharged state, which is evaluated by determining the free energy difference of both the N and M water clusters. The free energy of the N water cluster at the uncharged state is evaluated directly using Eq.2, without going through the MC minimization. On the other hand, the free energy of insertion of the equilibrium value of M water molecules is obtained by first running the LRA/MC screening process at the uncharged state to find the minimum free energy configuration. The difference between these insertion energies gives us the insertion energy of the extra (N-M) waters, i.e. $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},LW}^{w\to p(AH,MW)}$.

II.3 Exploiting the LRA Approach

Although the above approach is much faster than a GCMC insertion strategy, it is still very demanding. Thus we further accelerate the selection of the most important configurations. That is, we start with an excess amount of water inside the protein cavity, and then perform a screening by an iterative combination of linear response approximation (LRA) [35] and postprocessing by a MC procedure of Eqs. 1 or 2, in order to obtain the lowest free energy configurations. Our approach involves the following steps:

1. We start by generating a series of water configurations by using the MOLARIS standard grid insertion method [36]. The number of water molecules (N) generated within the cavity/channel is varied by changing the van der Waals cut-off distance (r_cut) between the protein atoms and the inserted water molecules. Thus, we can push in more water molecules by using a smaller r_cut, say 2Å. This approach allows us to forcefully insert more water molecules than would be normally accepted (by default, r_cut=2.8Å). This special insertion is performed only within a sphere of radius 6Å from the protein residue of interest (defined as region I atoms in MOLARIS), and outside of this sphere the water molecules are added using the default r_cut=2.8Å.

2. For each of the water configurations we run a 200ps long equilibration trajectory. Note that we do not need very long equilibration trajectories at this stage as we put a weak position constraint (0.3 kcal/mol) on each water molecule and our primary intention is to achieve a rapid MC screening based on LRA estimate of free energy. At a later stage we can always run longer FEP calculations to obtain accurate charging free energy for all screened configurations. After equilibration we continue the production run of 200ps to estimate the free energy of each water molecule (still maintaining the weak position constraint for better convergence) within 6Å distance using the leading term of the LRA treatment [35] for the electrostatic contribution and writing:

   $$\begin{array}{c}\mathrm{\Delta }{G}_i=\frac{1}{2}{\langle U_q^i-U_0^i\rangle }_{U_q}+\mathrm{\Delta }{G}_{\mathit{ins},0}^i=\frac{1}{2}{\langle \sum _{k\notin \text{WAT}}(U_q^{ik}-U_0^{ik})\rangle }_{U_q}+\mathrm{\Delta }{G}_{\mathit{ins},0}^i,\text{where}i\in \text{WAT}\\ \mathrm{\Delta }{G}_{ij}=\frac{1}{2}{\langle U_q^{ij}-U_0^{ij}\rangle }_{U_q}+\mathrm{\Delta }{G}_{\mathit{ins},0}^{ij},\text{where}i,j\in \text{WAT}\end{array}$$ (4)
   where, $U_q^i$ is the total energy of the ith water molecule corresponding to its normal charge distribution and $U_0^i$ corresponds to a non-polar water molecule with 0 charge on all atoms. The ensemble average is done for trajectories over the potential U_q that corresponds to the case where all the water molecules are in their regular polar states. As an approximation, here we ignore the LRA contribution from the average 〈U_q − U₀〉_U0 to be performed over the non-polar state due to the difficulty of evaluating this term for the whole cluster rather than for each water molecule. Note that in the first equation, the self-energy term ΔG_i does not include the contributions from other inserted water molecules added by our procedure (as indicated by molecule type WAT in Eq. 4). The pairwise contributions are stored separately in ΔG_ij, where the pairwise interaction energy between each pair of water molecules of type WAT is averaged over the LRA trajectory as shown in Eq.4. Here $U_q^{ij}$ indicates the average interaction energy between ith and jth WAT molecules at their polar state (normal charge distribution) and $U_0^{ij}$ indicates the corresponding value when both of them are non-polar. The term $\mathrm{\Delta }{G}_{\mathit{ins}.0}^i$ is the free energy of creating the cavity corresponding to the ith water molecule, whereas $\mathrm{\Delta }{G}_{\mathit{ins},0}^{ij}$ is the contribution to the pairwise term from the nonpolar insertion energy. This can be computed by converting a non-polar water molecule to dummy atoms within a FEP approach, but a practical and fast estimate can be obtained by using the Linear Interaction Energy (LIE) approximation [37, 38]] (see also [36]) given by:

   $$\mathrm{\Delta }{G}_{\mathit{ins}.0}^i=\beta {\langle U_{\mathit{vdw}}^i\rangle }_{U_q}$$ (5)
   where $U_{\mathit{vdw}}^i$ is the van der Walls interaction between the ith water molecule and its surroundings. The scaling parameter β has been estimated to be in the range of 0.3–0.5 by comparing explicit FEP calculations with the approximation of Eq.5 Thus, we can rewrite Eq.5 as:

   $$\begin{array}{c}\mathrm{\Delta }{G}_i=\frac{1}{2}{\langle U_q^i-U_0^i\rangle }_{U_q}+\beta {\langle U_{\mathit{vdw}}^i\rangle }_{U_q}=\frac{1}{2}{\langle \sum _{k\notin \text{WAT}}(U_q^{ik}-U_0^{ik})\rangle }_{U_q}+\beta {\langle U_{\mathit{vdw}}^i\rangle }_{U_q},\text{where}i\in \text{WAT}\\ \mathrm{\Delta }{G}_{ij}=\frac{1}{2}{\langle U_q^{ij}-U_0^{ij}\rangle }_{U_q}+\beta {\langle U_{\mathit{vdw}}^{ij}\rangle }_{U_q},\text{where}i,j\in \text{WAT}\end{array}$$ (6)

   The above approach is referred to here as the LRA/β approach.

   At any rate, while computing the LRA/β free energy of each of the N water molecules using Eqs. 4–6, we compute two separate contributions, namely the self-energy (ΔG_i), which contain interactions with all the whole system, accept other (N-1) water molecules, and the pairwise interactions ΔG_ij for all pairs of water molecules. The above approximation will be demonstrated to work reasonably well in the validation study reported below

3. After the LRA trajectory is completed, we employ the post-processing MC procedure described above. Note that our MC postprocessing procedure is almost instant and does not involve any appreciable computer time.

4. The above procedure is repeated for different water configurations generated with different initial number of water molecules (N).

At the end of the above procedure we select the configurations with the lowest free energy (typically 10 configurations) and repeat the LRA calculation separately on each of these configurations iteratively (see Fig. 5 for a flowchart of our algorithm). We finally select the lowest free energy configuration (or configurations) for the subsequent calculation of solvation free energy or a related property using microscopic FEP.

Figure 5.

A flowchart of the water insertion algorithm.

The molecular dynamics simulations are performed using the polarizable ENZYMIX force field [36] with a 0.5fs time step with the solute parameters described in Refs. [39, 40]. The free energy perturbation (FEP) calculations of creating a charge in solvent water and protein interior are performed over 21 frames with each of them being 40 ps long. The simulations included the use of 22Å of the SCAAS spherical constraints and the local reaction field (LRF) long-range treatment (see [36]). The simulation system represented the membranes by a grid of induced dipoles (e.g., see ref. [40]) which are treated explicitly in our polarizable model.

III. Results and discussion

The aim of this work is to develop a practical and reliable way of estimating the free energy of internal water. Here we take a pragmatic view, which is based on our belief (and experiences) that the main issue is not the formal elegance (e.g. being ascribed to a given ensemble) but the effectiveness of the given formulation and this can and must be checked by the performance of the method.

Our first validation study considered the evaluation of the pK_a of the V66D mutant of SNase. This mutant constructed by Garcia-Moreno and coworkers [11, 12, 24] has much lower pK_a than that obtained by oversimplified macroscopic calculations, and more importantly from the perspective of the present work, regular microscopic free energy calculations also drastically underestimate the stability of the ionized form by the surrounding “non-polar” protein site. Apparently the charging of Asp66 leads to some local unfolding and water penetration that involves significant barrier and cannot be captured within standard simulation time. Our specialized overcharging method [25] could overcome this problem by artificially charging the ionized acid up to −2, thus forcing the relevant solvation process and then returning the charge to −1 and thus completing the charging thermodynamic cycle. However, the overcharging approach is very demanding and might also be problematic in deeper protein interiors where the forced partial unfolding coordinate may be very complex. Thus we have here an ideal test case for our water insertion approach.

Before examining the effect of water penetration on the pK_a of V66D, we used this system to explore and demonstrate and examine the key aspects of the model. We started by considering the Asp66 system with two internal water molecules comparing energetics of inserting two water molecules. In this simple case we can easily evaluate the relevant energetics by both the LRA and the FEP approach. The corresponding results are summarized in Table I. Overall we find a reasonable agreement between the two set of calculated values as demonstrated in the table. For example, the first water molecule in Table I has an LRA free energy of −13.2 kcal/mol, whereas the FEP procedure gives −16.3 kcal/mol for the charged state of Asp66 (A⁻). The corresponding value with the uncharged state (AH) is −9.2 kcal/mol from LRA and −8.7 kcal/mol from FEP, respectively. We have also compared the non-polar cavity formation free energy $\mathrm{\Delta }{G}_{\mathit{ins},0}^i$ obtained using explicit FEP conversion of a non-polar water molecule to dummy atoms, and the approximate LIE formulation as given by Eq.3. The obtained values are in general very small, and in the range of −0.5 to 1.0 kcal/mol.

Table I.

Comparison of free energy values obtained by partial LRA approach of Eq.6 with FEP approach for the simple test case of two water molecules (W1 and W2) near the V66D mutation of SNase for both charged and uncharged stated of the Asp66 residue.

	Asp66 charged (A−)		Asp66 uncharged (AH)
	FEP	LRA/β	FEP	LRA/β
W1 (elec)	−16.3	−13.2	−8.7	−9.2
W1 (vdw)	0.8	0.3	1.2	−0.7
W2 (elec)	−14.0	−14.4	−9.1	−9.7
W2 (vdw)	0.9	0.7	−0.3	−0.9
ΔGij (elec)	3.2	1.8	2.0	1.2
ΔGij (vdw)	−0.6	−0.2	−1.4	−0.3

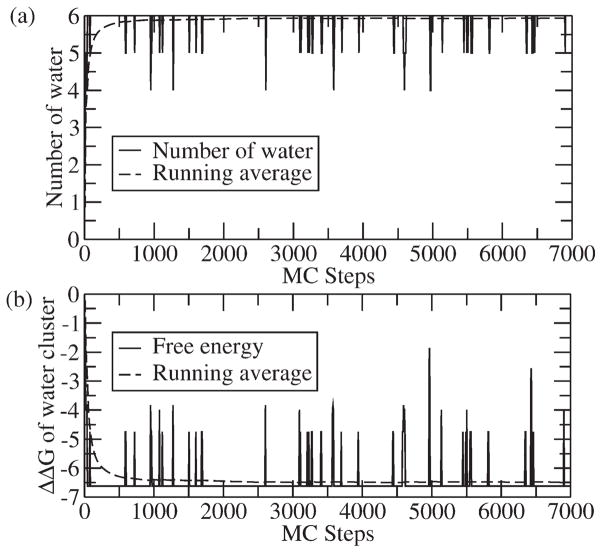
Next we use the V66D to demonstrate the evaluation of the energetics of water configurations generated by the above water flooding approach. This is done first in Fig. 6 where we describe the convergence of the LRA/MC evaluation of the number of water molecules and the corresponding free energy. In this particular case we obtain about 6 water molecules within a 6A radius from the Asp66 residue for the charged system. As demonstrated in Fig. 6 we achieve very rapid convergence in our MC cycles. The LRA energies for these water molecules at both charged and uncharged states of Asp66 are summarized in the Table II. As clearly demonstrated in Fig. 7, our MC screening converges very rapidly within a few thousand MC cycles. Obviously our approach is very effective only because the energy in the selected sites has been evaluated before the MC procedure (by the LRA approach) rather than by a MC insertion approach.

Figure 6.

Representative convergence of the MC/LRA approach for the SNase system with charged Asp66: (a) evolution of the number of water molecules (solid line) and running average (dashed line) with MC cycles, (b) the free energy of transfer of the water cluster (solid line) and running average (dashed line) with MC cycles. Starting with an initial 7-water cluster, the MC cycles rapidly converges to an average of 6 water molecules.

Table II.

The energetics of the internal water molecules at the optimal penetration configuration near the V66D mutation of SNase^a

Index	Charged Asp66 (A−)		Uncharged Asp66 (AH)
	Distance from Asp66	$\mathrm{\Delta }{G}_{(i)}^p$	Distance from Asp66	$\mathrm{\Delta }{G}_{(i)}^p$
1	2.8	−11.5 (−5.5)	3.2	−9.2 (−3.2)
2	2.9	−9.5 (−3.5)	3.6	−8.4 (−2.4)
3	3.0	−10.1 (−4.1)	4.9	−6.1 (−0.1)
4	3.8	−10.9 (−4.9)	5.0	−10.0 (−4.0)
5	5.6	−12.4 (−6.4)	5.8	−8.5 (−2.5)
6	6.4	−8.2 (−2.2)	7.9	−10.2 (−4.2)
7	9.2	−8.5 (−2.5)	8.4	−4.2 (1.8)

^aThe calculated energies (in kcal/mol) are reported for both charged (A⁻) and uncharged (AH) stated of the Asp66 residue. The term $\mathrm{\Delta }{G}_{(i)}^p$ signifies the LRA total energy of a water molecule in the i-th protein site (this should not be confused with the self energy ΔG_i of Eq 5). The values in bracket indicate the relative energy with reference to being in water, i.e. $\mathrm{\Delta }{G}_i^p-\mathrm{\Delta }{G}^w$, where ΔG^w = −6 kcal/mol. These energies have been obtained using the partial LRA equation as described in Eqs. 4–6. Note that all of the selected water molecules do not always remain within the 6 angstrom water sphere, e.g. in this table 6^th and 7^th water molecules are quite far apart. Thus, these water molecules have exchange equilibrium with the surrounding bulk water molecules.

Figure 7.

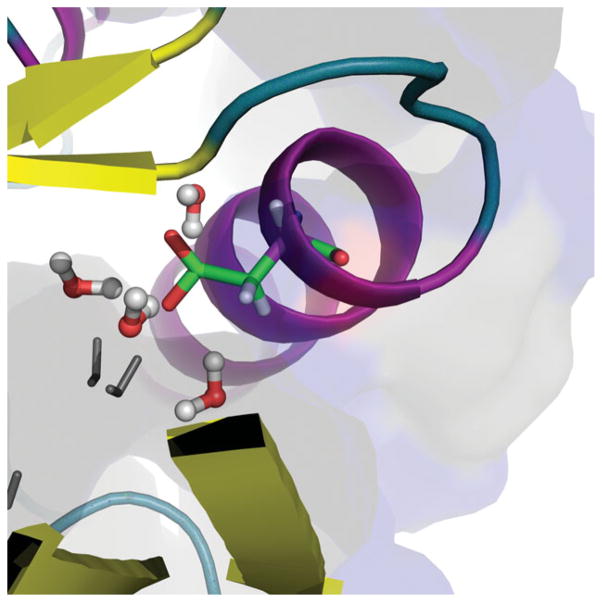
Representative snapshots of water insertion in the surrounding of the V66D site in SNase using our water flooding LRA/MC screening approach. Here only the water molecules within 3.5A of the charged carboxylate group of Asp66 have been marked in color. Note that all of the marked water molecules have been inserted into the protein interior (marked by the coarse solvent accessible surface).

Next we considered the effect of the selected water molecules on the pKa of Asp66. This was done by a FEP calculation of the free energy of charging of Asp66, where the basic workflow has been clarified in Fig. 5. The actual pK_a results are summarized in Table III as well as Figs.7–8. In this particular case, we find the water insertion penalty term, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},lW}^{w\to p(AH,mW)}$, to be zero, since the number of water molecules obtained in the charged and uncharged state is almost equal, i.e. ~6. Our study compared two procedures, namely, Procedure A: using standard solvation approach while including the water molecules resolved by X-ray, and Procedure B: using exclusively our water flooding LRA/MC screening approach without using the X-ray resolved water molecules. The comparisons clearly established that our water insertion approach leads to a major improvement in reducing the free energy penalty of moving a charge from solvent water to protein site. The calculated pK_a values are in excellent agreement with the observed values in this test case. Of course, it is also possible that the protein configurations with more significant unfolding will give similar pK_a with different number of water molecules, but clearly the water insertion approach allows us to come much closer to the observed pK_a without a major unfolding. It should be noted that X-Ray studies have successfully located the water molecules near Glu66 in SNase [11]. Moreover, 10ns long MD simulations [41] have also provided interesting and useful information on the radiance of water molecules near this Glu66.

Table III.

The dependence of the calculated pK_a of the V66D mutant of SNase on the method used ^(a)

	ΔGnp→crg	ΔΔGw→p	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},LW}^{w\to p(AH,MW)}$	pKa (4.0+ ΔΔGw→p/1.37)
In water (ΔGw)	−81.0	---
In protein (ΔGp) (procedure A)	−46.0	35.0		29.5
In protein (ΔGp) (procedure B)	−72.6	8.4	0.0	10.1

^(a)Energy values are reported in kcal/mol. A weak constraint of 0.3 kcal/mol was used to keep the LRA/MC generated water molecules in place. Procedure A corresponds to using standard solvation approach while including water molecules resolved by X-ray, whereas Procedure B corresponds to using our water flooding LRA/MC screening approach. All of these molecular dynamics simulations are performed using the polarizable ENZYMIX force field [36].

Figure 8.

The convergence of the pK_a of V66D in SNase as a function of the procedure used. The open bar depicts the results obtained using a standard solvation approach while including the X-ray resolved structural water. The solid bar depicts the results obtained using our new LRA/MC screening approach followed by FEP.

The subsequent test case has been the ability to reproduce the pK_a of Glu286 in CcO. This functionally important pK_a has been explored very systematically in previous studies [42, 43], including the complications associated with the fact that the observed pK_a also reflects a kinetic component [43]. However, the actual pK_a in several states of the CcO cycle are well known and it lies in the range of 9–11. Reproducing such pK_a values by semimacroscopic calculations with a dielectric in the range of 4 to 6 is trivial, but doing so by microscopic simulations is extremely challenging. Our previous study using the SCAAS method with overcharging and/or adding local water molecules could obtain the pK_a value of 13.6 [9]. Cui and coworkers have used the so called QM/MM-GSBP approach [23]. The GSBP method has been basically an adaptation of our SCAAS model by Roux and coworkers [22], where our idea of spherical boundary conditions, polarization surface constraints and completion by solvent [18, 19] has been reimplemented. However, the GSBP has tried to emphasize the rather trivial effect of the solvent rather than the crucial treatment of the surface polarization and have not yet been subjected to size dependence validation studies [44]. At any rate the GSBP approach obtained pK_a in the range of 14.8–16.4 [23].

Before exploring more challenging cases it is useful to consider the energetics of the inserted water molecules. This is done here by providing in Table II a representative set of data for LRA free energies of the excess water molecules both in presence of the charged species ${\mathrm{A}}^{-}(\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},lW}^{w\to p(A^{-},mW)})$ and the uncharged species $\text{AH}(\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},lW}^{w\to p(AH,mW)})$. Here we clearly see that in the presence of the charge (A⁻), the free energy values of the water molecules are indeed much lower than the corresponding value in solvent water (about −6 kcal/mol). Thus they are more stable in the protein sites. This opens up the possibility that in the process of moving the charge from solvent to protein, a significant number of water molecules spontaneously penetrate even the relatively hydrophobic environments. In the same table, we also report the corresponding LRA free energy values with the uncharged species (AH). These values are used in Eq.3 to obtain the overall insertion penalty term of additional L water molecules, i.e. $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},lW}^{w\to p(AH,mW)}$. This term, which is typically around 2–5kcal/mol, is added to the FEP charging free energy ( $\mathrm{\Delta }{G}_{\mathit{sol}}^{p(n\mathrm{w})}(AH\to A^{-})$), as shown in the thermodynamic cycle of Fig. 4.

The performance of our approach in obtaining the pK_a of Glu286 in CcO is summarized in Table IV and Figs. 9–10. Clearly our method shows a major advantage over conventional water addition procedure. Here we obtain the pK_a 15.0, which is higher than what we obtained with the overcharging strategy [9], but yet significantly lower than the results without adding water. We must mention that it is possible that the pK_a of Glu 286 represent a conformation that was not explored here. We also note that our semimacroscopic PDLD/S-LRA calculations (e.g. ref. [43]), which are arguably among the most consistent calculations of their type, produce a reasonable pK_a for Glu 286. It is, however, possible that the apparent pK_a reflects a more complex situation than that explored by the present study, including complications of the type explored in our detailed semimacroscopic study [43]. Finally, it is possible that we have here a concerted PT with a proton at the D channel which has been considered in some of our earlier works (e.g. ref. [39, 45]). These types of complications and challenges highlight the importance of elucidating the microscopic nature of the ionization of Glu 286 (which will be explored further in our lab).

Table IV.

The dependence of the pK_a of E286 in CcO on the method used ^(a)

	ΔGp	ΔΔGw→p	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},LW}^{w\to p(AH,MW)}$	pKa (4.5+ ΔΔGw→p/1.37)
In water	−79.3	---
In protein (procedure A)	−59.1	20.2		19.2
In protein (procedure B)	−68.1	11.2	3.2	15.0

^(a)Energy values are reported in kcal/mol. A weak constraint of 0.3 kcal/mol was used to keep the LRA/MC generated water molecules in place. Procedure A corresponds to using standard solvation approach while including water molecules resolved by X-ray, whereas Procedure B corresponds to using our water flooding LRA/MC screening approach. All of these molecular dynamics simulations are performed using the polarizable ENZYMIX force field [36].

Figure 9.

Representative snapshots of water insertion in the surrounding of the E286 (Glu) site in CcO. Here we marked in color only the water molecules within 3.5A of the charged carboxylate group of Glu286.

Figure 10.

The convergence of the pK_a of E286 (Glu) in CcO as a function of the procedure used. The open bar depicts the results obtained using a standard solvation approach while including the X-ray resolved structural water. The solid bar depicts the results obtained using our new LRA/MC screening approach followed by FEP.

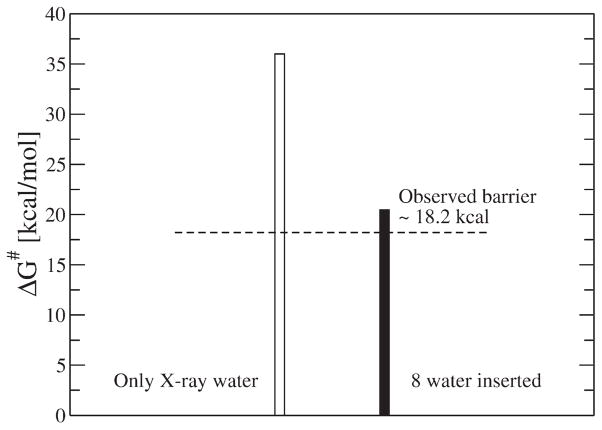
To explore an additional major challenge we have examined our ability to evaluate the free energy of an internal proton in the D channel of CcO. In this case we know the overall barrier for some mutants (e.g. D132N) that make the transport through the D channel rate limiting (e.g. for the D132N mutant the barrier is ~18.2kcal/mol). However, the energy of forming a proton is given by [9]:

$$\mathrm{\Delta }{G}^{\ne }=1.38(pH-{pK}_a[H_3{O}^{+}])+\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol}}^{w\to p}+\mathrm{\Delta }{G}_{\mathit{ins}}$$ (7)

where, the first term is the free energy of forming the proton in the solvent and it is already ~12 kcal/mol at pH = 7.0. Thus the second and the third term (which represent the change in solvation energy upon transfer from water to the given protein site and the stabilization by the protein ionized groups) cannot be larger than ~6.2 kcal/mol. Obtaining such a small reduction in solvation energy means that the protein/internal water system must provide a major stabilization which is clearly not obtained by standard microscopic simulations even with induced dipoles and with very careful considerations of the stabilization by the flanking water molecules in the D channel. As shown in Table V and Fig. 11, only the insertion of water molecules brings the barrier for proton transport through the D channel to a reasonable range.

Table V.

Calculation of the free energy cost of moving a protonated water from solvent water to the highest point (barrier) in the proton translocation pathway (D channel) of the D132N mutant of CcO ^(a).

	ΔGnp→crg	ΔΔGw→p	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},LW}^{w\to p(AH,MW)}$	ΔG#=12.0+ ΔΔGw→p
In water (ΔGw)	−92.9	---
In protein (ΔGp) (procedure A)	−68.9	24.0		36.0
In protein (ΔGp) (procedure B)	−86.7	6.2	2.3	20.5

^(a)Energy values are reported in kcal/mol. A weak constraint of 0.3 kcal/mol was used to keep the LRA/MC generated water molecules in place. The results reported were obtained from microscopic FEP calculations using two different procedures. Procedure A corresponds to using standard solvation approach while including water molecules resolved by X-ray, whereas Procedure B corresponds to using our water flooding LRA/MC screening approach. All of these molecular dynamics simulations are performed using the polarizable ENZYMIX force field [36].

Figure 11.

The convergence of the energetics of a protonated water near the D132N mutation site of the D channel of the mutated CcO. This location corresponds to the highest point in the proton translocation free energy surface along the D channel for the D132N mutant. The open bar depicts the results obtained using a standard solvation approach while including the X-ray resolved structural water. The solid bar depicts the results obtained using our new LRA/MC screening approach followed by FEP.

IV. Conclusion

The effect of internal water is one of the least quantifiable issues in the field of computer simulations of biological molecules and the situation is similar as much as direct experimental studies are concerned. Previous attempts have not provided quantitative approaches. The problem is that water penetration processes may take very long time that cannot be captured by regular simulations. In some cases one may try to simulate the actual process (e.g. binding or proton transfer) by very long brute force PMF calculations, but it is not clear a priori what is the sufficient trajectory length needed for convergence. In most cases FEP calculations seem like the most effective approach [15], but in such cases we might not capture the water penetration effect properly, since the insertion process is likely to involve significant barrier and thus likely to be not sampled well during a typical charging process. Forcing the water penetration by the overcharging approach is sometimes a reasonable strategy, but it is far from being general. Alternative approaches (e.g. [5, 28]) have explored various options but have not provided clear evidences for quantitative results or full convergence. A part of the problem has been that validations on binding calculations are much less discriminative than calculations of charging free energies, which have never been explored by the alternative approaches.

Of course, in principle one could have developed a formally correct approach, such as Bennett Acceptance Ratio (BAR) approach [46] but implementing such approaches is at present unpractical strategy for exploring biophysical problems. Our current strategy is aimed at providing a practical route, which is sufficiently reliable. Here the use of the LRA estimates and the MC post processing is the key innovation of our strategy. Of course, the only way of judging a practical approach is by careful validations, which have been performed in this work. The remarkable success of our validations seems to indicate that the correct physics is being reproduced.

The present study seems to indicate that the internal charges are stabilized by internal water, including water molecules that only enter the protein when the charged state is being formed. This means that we have here a time-dependent solvation process [47] (see also ref. [43]) which can be sometimes longer than the microsecond time scale). At any rate, exploring the full validity of our findings may require significant experimental and theoretical effort.

The entropic contributions of ordering of the water molecules have been expressed in terms of elegant extension terms in ref. [6]. However, we are not aware of any careful quantitative validation of such treatments of entropy as done within our restraint release (RR) treatment [32]. It seems to us that at present there is no fast approach that can provide reliable estimate of the water entropic contributions. Thus the real issue is adoption of a practical approach that can capture the entropic effects of the insertion process. Fortunately the LRA does provide an estimate of the free energy of converting the nonpolar water to polar water, which is the main part of the water orientational effect. Of course, ignoring the missing term (the average over trajectories that do not experience the force of the water residual charges) in the LRA calculation might mean that our approximation can be improved by the evaluation of the missing term. This however would require significantly more expensive calculations, including FEP calculations that were done here in selective cases.

This work has explored the performance of our approach in studies of the energetics of internal charges in proteins and ligand binding. It would be interesting if this approach can also work in studies of internal charges in membranes where very long time brute force simulations have provided an interesting insight [48].

Our finding that the water penetration effect is larger in the charged state is of major significance as much as charge transport processes are concerned. It presents a new view on the requirements from microscopic calculations and the way to obtain reliable results from such calculations without extremely long runs. Interestingly, the present study predicts a time lag between the formation of the charged state and its stabilization by water penetration. This time scale should be considered in studies of charge transfer processes and it depends on the conformational motions that are coupled to the penetration process. Experimental elucidation of the times of the water penetration process are of particular interest and in this respect it is exciting to note the experiments of Brzezinski and coworkers [49], who found that the exchange of H₂O and D₂O in the mitochondrial CcO (linked to ET to the catalytic site) occurs over time scales up to ~1s.