In silico model-based inference: an emerging approach for inverse problems in engineering better medicines

Abstract

Identifying the network of biochemical interactions that underpin disease pathophysiology is a key hurdle in drug discovery. While many components involved in these biological processes are identified, how components organize differently in health and disease remains unclear. In chemical engineering, mechanistic modeling provides a quantitative framework to capture our understanding of a reactive system and test this knowledge against data. Here, we describe an emerging approach to test this knowledge against data that leverages concepts from probability, Bayesian statistics, and chemical kinetics by focusing on two related inverse problems. The first problem is to identify the causal structure of the reaction network, given uncertainty as to how the reactive components interact. The second problem is to identify the values of the model parameters, when a network is known a priori.

1. Introduction

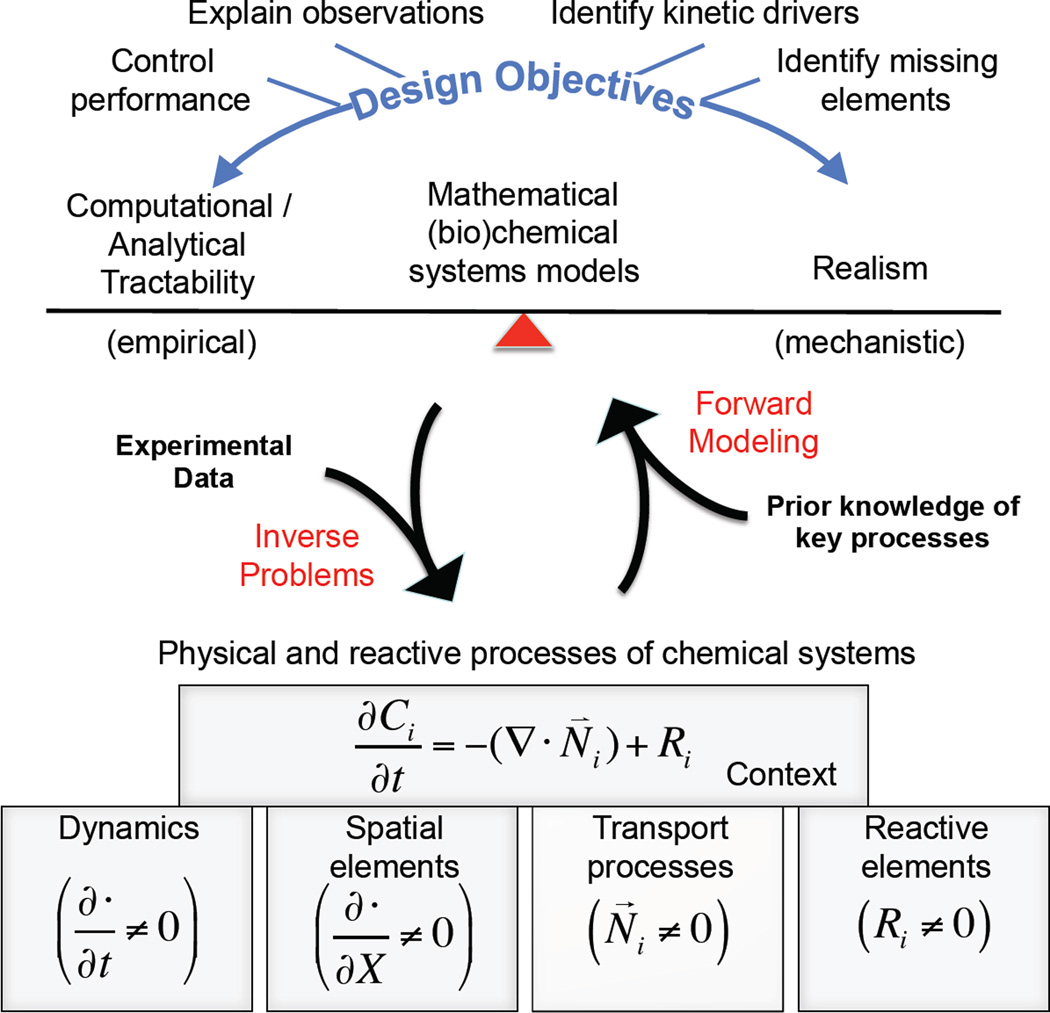
Chemical engineering has a rich history in using mathematical modeling to describe chemical systems [1, 2]. As summarized in Figure 1, mathematical models aim to capture our understanding of the underlying mechanisms associated with a variety of reactive and physical processes that govern the behavior of chemical systems. The particular formulation of the mathematical model represents a trade-off between computational or analytical tractability and realism. The art of modeling is finding the right level of abstraction appropriate for the task at hand. The mathematical models are used in one of two scenarios. The first scenario is forward modeling, where a mathematical model is used to predict future behavior based on changing operating conditions. The second scenario is for inverse problems, where mathematical models are used to interpret observations of a chemical system as a way to identify the governing physical and reactive processes.

Figure 1. Overview of the role of mathematical modeling in the context of reactive systems.

The behavior of reactive systems can be described in mathematical terms that represent the underlying physical, kinetic, and reactive processes. The specific mathematical relationships incorporated into a model reflect a trade-off between computational and analytical tractability and realism that relate to the specific design objectives associated with how the mathematical model will be used. Modeling applications can be categorized into one of two applications. The first application, called forward modeling, predicts the behavior of the system based on prior knowledge of the relative importance of the physical, kinetic, and reactive processes. The second application is to identify aspects of reactive system that govern the behavior of the process using experimental observations of the system. This second application is called an inverse problem.

Predictions derived from a mathematical model depend on the relationships specified between the interacting species modeled, which is expressed generally as a reaction network, and the speed of information transfer by a modeled interaction, which is captured by a model parameter. Conceptually, there are then two types of inverse problems. The first type of inverse problem, which is more frequently encountered, is parameter inference. Parameter inference involves selecting a set of parameter values or initial conditions that enable the mathematical model to capture the observed data, where the reaction network is known a priori. The second type of inverse problem is network inference, which is more challenging. Network inference involves selecting an appropriate set of interactions among a set of plausible interactions based on the limited information available about the reactive and physical phenomena contained within the chemical system. In dynamic systems, the reaction network alone provides constraints as to how the model species could potentially evolve in time. The goal of network inference is then to see if the postulated reaction network can capture the observed data given any plausible combination of model parameters and initial conditions.

Historically, these two types of inverse problems have been treated similarly. However, changes in the scientific landscape and advances in technology motivate approaches specifically tailored to the specific inverse problem at hand. The focus of this review is as follows. First, we will discuss pharmaceutical drug discovery and development as a pressing area of inverse problems. Second, we will discuss some of the conceptual and technological advances that have enables a more tailored approach towards inverse problems that focus on either network inference or parameter inference, especially in cases where significant prior information exists.

2. Improving confidence in target selection is a important class of inverse problems in pharmaceutical RnD

One important application of mechanistic mathematical models is to help in the discovery and development of therapeutic drugs. Using pharmacologic agents to treat disease underpins many of the clinical successes in modern medicine. While these successes encourage an optimistic outlook, there remain unmet medical needs despite decades of intense scientific effort. The emergence of multi-drug resistant bacteria, infectious disease outbreaks, and mixed progress in the war on cancer highlight some of these unmet medical needs and the complexity of a constantly changing therapeutic landscape. Engineering better medicines to fulfill these unmet medical needs is one of the grand challenges of engineering [3]. To address these needs, new therapies are discovered and developed by a multi-stage process that relies initially on model experimental systems and then testing in humans using clinical trials. With costs associated with bringing a new therapy to market exceeding $1 billion and the high level of attrition during the research and development process, there is significant concern over sustainability of the current model for innovation in the industry [4, 5, 6].

In a recent NIH white paper, an industrial and academic working group found that the source of attrition had shifted over the last couple of decades from Phase I clinical trials, which focus on toxicology, to Phase II clinical trials [7]. The objective of a Phase II clinical trial is to test the therapy in patients diagnosed with the disease. A Phase II success is to improve clinical outcome relative to the current standard of care. To illustrate the challenges of demonstrating efficacy, a recent retrospective analysis of clinical trials in patients with acute myeloid leukemia found that, of the 37 therapies that received positive indications in early phase clinical trials, only 1 drug actually made it to clinical use [8]. This NIH working group observed that the failures in demonstrating efficacy stem from an incomplete understanding of clinical importance of a specific biological mechanism that was targeted by the therapy. Understanding how a drug interacts with a target is challenging as many diseases of therapeutic interest (e.g., cancer, heart disease, and diabetes) are multi-genic, progressive, and heterogeneous in that each case may have a different mechanism of origin. While pre-clinical studies using model systems supported the clinical trials, the failure in translation suggests that the model systems have unclear fidelity in capturing the complexity of human disease.

One of the main recommendations to improve innovation was to focus on a network-centric view of biology to balance the “one-gene, one-receptor, one-mechanism” (OGRM) paradigm prevalent within the industry [9]. In short, methods developed under the OGRM paradigm select drugs that modulate a specific therapeutic target in experimental systems that have been taken out of context. From the network-centric perspective, a drug target resides within a complex network of interactions that responds in dynamic and non-linear ways to therapeutic modulation. Moreover, these networks can be altered in disease such that the importance of a particular target in regulating phenotype can be quite different in health and disease. Beyond this, current multi-genic and progressive diseases are the result of a multi-variate pathology such that drug efficacy is poorly predicted by only considering a drug’s primary target. For example, most so-called ”targeted” tyrosine kinase inhibitors for cancer therapy actually have broad spectrum activity against several kinases, and in fact some of the ”dirtiest” drugs that target multiple kinases are some of the most effective [10].

Upon this network-centric foundation, mechanistic modeling and simulation are integrated with quantitative wet lab studies to advance the systems-level understanding of the pathophysiology relevant for drug discovery and development. While the mechanistic modeling and simulation aspects are more aligned with the discipline of chemical engineering than pharmacology, the strong focus on translational medicine motivated the group to coin a new field called quantitative and systems pharmacology.

3. Quantitative and systems pharmacology versus systems biology: What’s the diff?

On a simplistic level, one may view quantitative and systems pharmacology (QSP) as a simple extension of systems biology with the addition of drug dynamics. However, they are motivated by two different objectives and are orthogonal approaches to organize data and knowledge about biological systems [9, 7]. QSP is motivated by applied translational research questions that require vertical integration. To inform drug discovery, the structure of the model tends to be focused around the targeted pathways and disease mechanisms. Mathematics is used to integrate vertically data and mechanistic knowledge that span multiple levels of biological organization thereby linking molecular targets to clinical read-outs. For instance, a team of 3 PhD-level engineers and 3 PhD-level immunologists worked for 2 years to build a mechanistic model of the NOD mouse model of type 1 diabetes [11]. To predict changes in blood glucose levels, cellular immune responses in the endocrine pancreas and a secondary lymphoid organ and the trafficking of cells between these two locations were modeled. In addition to these tissue- and organism-level phenomena, cytokines and cellular decision-making processes were also represented, as these are potential points of therapeutic intervention. The model was used to evaluate alternative strategies to induce tolerance to insulin, such as the optimal dose, frequency of administration, or stage of disease progression [12, 13]. Representing drug pharmacology adds an additional layer of complexity as drugs exhibit multi-organ dynamics that are important for their clinical performance and that can vary significantly from patient to patient. In contrast, systems biology studies tend to be motivated by a desire for deep understanding of a biological network. Mathematics is used to integrate horizontally data and knowledge focused at a particular scale of biological organization. For instance, Covert and coworkers developed a model of the obligate intracellular pathogen Mycoplasma genitalium [14]. To capture an archtypical cell between cell division events, 28 different cellular processes were modeled including metabolism, transcriptional regulation and repair of DNA, synthesis and processing of RNA, and post-translational modification and macromolecular assembly of proteins. The model was then used to relate genotype to cellular phenotype. While one could envision a future where these two approaches lead to similar models that link genotype to clinical read-outs, these two different approaches are tailored to achieve the research aims given current limitations in biological knowledge and experimental methods.

While systems biology may receive more attention from academic circles, mechanistic modeling and simulation represents ”dark matter” within the pharmaceutical industry, given the financial incentives for keeping competitive advantages secret. In recent years, many of the major pharmaceutical companies have created QSP teams. Yet, there are few tangible case studies illustrating how mechanistic modeling and simulation financially impact the drug discovery process. Related examples include developing monoclonal antibodies against ErbB3 for treating cancers addicted to Epidermal Growth Factor signaling [15, 16]. This target is interesting as a OGRM approach would not have selected ErbB3 as a target, since it is a catalytically inactive kinase. By focusing on the network, ErbB3 was found to be an obligate dimerization partner to other ErbB receptors targeted by trastuzumab (i.e., ErbB2) or lapatinib (i.e., ErbB1/ErbB2) [17]. In assessing toxicity, QSP approaches have yielded better classifiers for arrhythmia risk [18] and predictive models for hepatic injury [19].

4. Biological systems present unique challenges in contrast to more traditional chemical processes

The conceptual toolkit developed to analyze and design chemical systems provides a rich framework to aid in understanding how biological networks function in health and disease. The focus on how cells process information is a natural point of focus as the transfer of information with a cell involves the reactive conversion and intracellular transport of a number of biochemical species, as described in Box 1. Moreover, decades of detailed biochemical and molecular biology studies have identified the major components of these intracellular signaling networks. This prior information can significantly reduce the set of possible networks that can explain observed behavior. For instance, candidate networks can be obtained by mining the published literature[20, 21]. However, this prior information can also significantly bias how we interpret experimental observations, given the limited observability of biological systems.

Translating cartoons to mechanistic models: A case study of the JAK-STAT pathway.

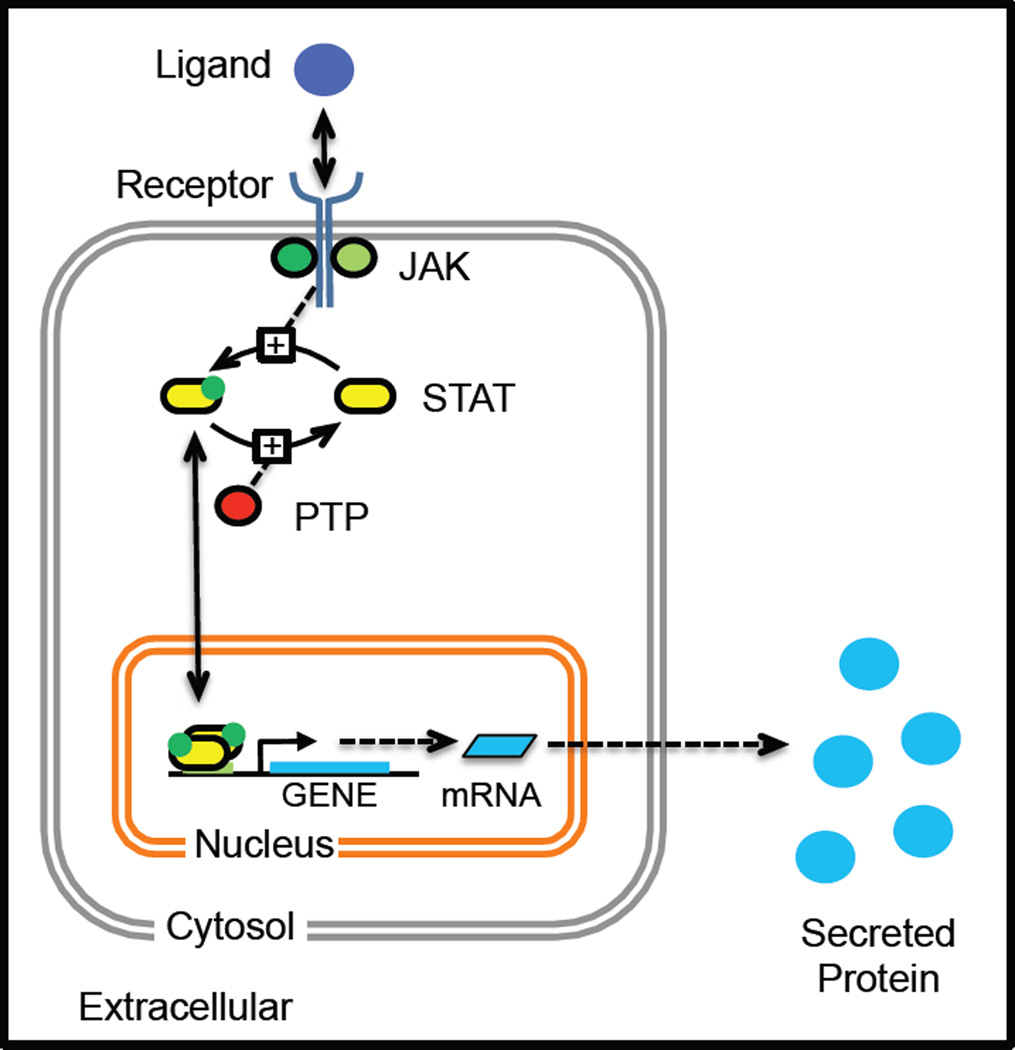
In contrast to more traditional chemical systems, the analysis of reaction networks associated with biological systems is characterized by lumped reactions and poor observability. To illustrate this point, consider the canonical Janus kinase (JAK)-signal transducer and activator of transcription (STAT) signaling pathway, which is highly conserved across eukaryotic organisms. As summarized in Figure 2, this compact signaling pathway transmits extracellular polypeptide signals, through transmembrane receptors, to control gene expression in a variety of fundamental cellular processes, including innate and adaptive immunity [24], regulation of cell growth and apoptosis [25], and control of embryonic stem cell self-renewal [26].

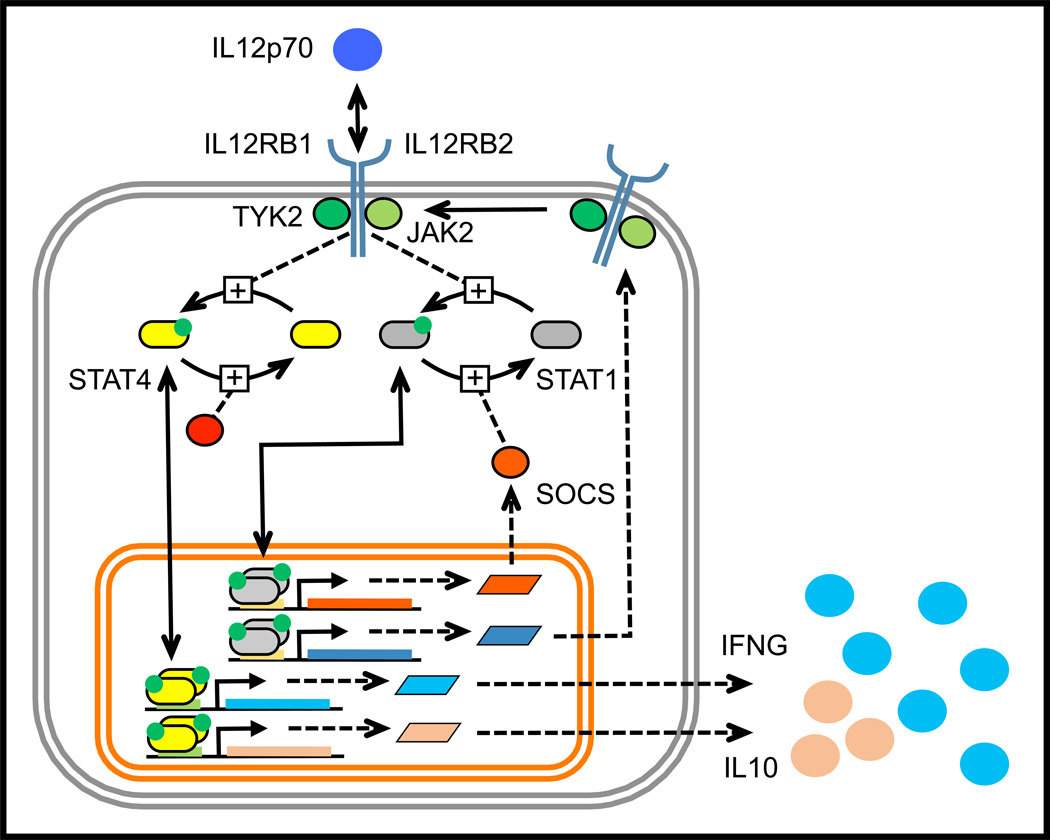
While cartoons like Figure 2 summarize the flow of molecular information down particular pathways within cells, identifying the network associated with a specific JAK-STAT signaling pathway within a specific cell type is more challenging. To illustrate this point, we will consider how Interleukin-12 (IL12) activates a JAK-STAT signaling pathway in type 1 CD4+ T helper cells [27, 28, 29]. In the case of IL12, the integrated use of modeling, simulation, and experimentation identified that multiple STAT proteins (STAT4 and STAT1) can become activated in response to receptor ligation and the activity of these STAT proteins are differentially regulated through uncharacterized negative feedback mechanisms, as summarized in Figure 3. The relationships between the abundance of activated STAT4 in the nucleus and de novo protein production and release are unique for each secreted protein, such as Interferon-γ (IFNG) and IL10 [29]. In addition, IL12 stimulation also enhances cell survival, which suggests that receptor ligation activates additional signaling pathways like the phosphoinositide-3-kinase-protein kinase B/Akt (PI3K-PKB/Akt) pathway [30]. Given the emerging complexity of the IL12 signaling pathway, experimental observability of this pathway is a challenge. For instance, flow cytometry can be used to obtain multiplex single-cell measures of protein phosphorylation, protein copy numbers, and mRNA abundance. Assuming that bench skills and reagents are up to the task, an experiment to monitor intracellular signaling activation and a functional response as a function of time in a cell line can cost $10,000.¹ Inevitably, limitations in bench skills, reagents, or financial resources impose a suboptimal experimental design. The mathematical models then aid in interpreting the acquired data in light of our current understanding of how a cell interprets IL12 to orchestrate a response.

Experimental observability is probably one of the biggest differences between traditional chemical processes and biological systems. Cellular decision making is regulated by the spatial localization and post-translational modification of proteins within a cell. Given technical limits in detecting small numbers of proteins, many assays measure cellular decision making indirectly or using significant assumptions. Given that nucleotides can be easily amplified using PCR, changes in gene expression is used as a surrogate measure of nuclear localization of a signaling protein. Assuming that a large population of cells (e.g., 1 × 10⁶ cells) behave identically, protein abundance and post-translational modifications can be quantified by western blot [22]. In practice, these experimental limitations imply that multiple approaches must be used and the resulting data should provide a self-consistent picture of cellular decision making. As described in the next section, math models aid in testing whether these data are self-consistent and consistent with what we currently know about the biology. For example, single-cell biochemical and imaging measurements acquired over time and in different cell types in response to different perturbations were used to identify the dynamic regulation of adhesive contacts between adjacent cells [23].

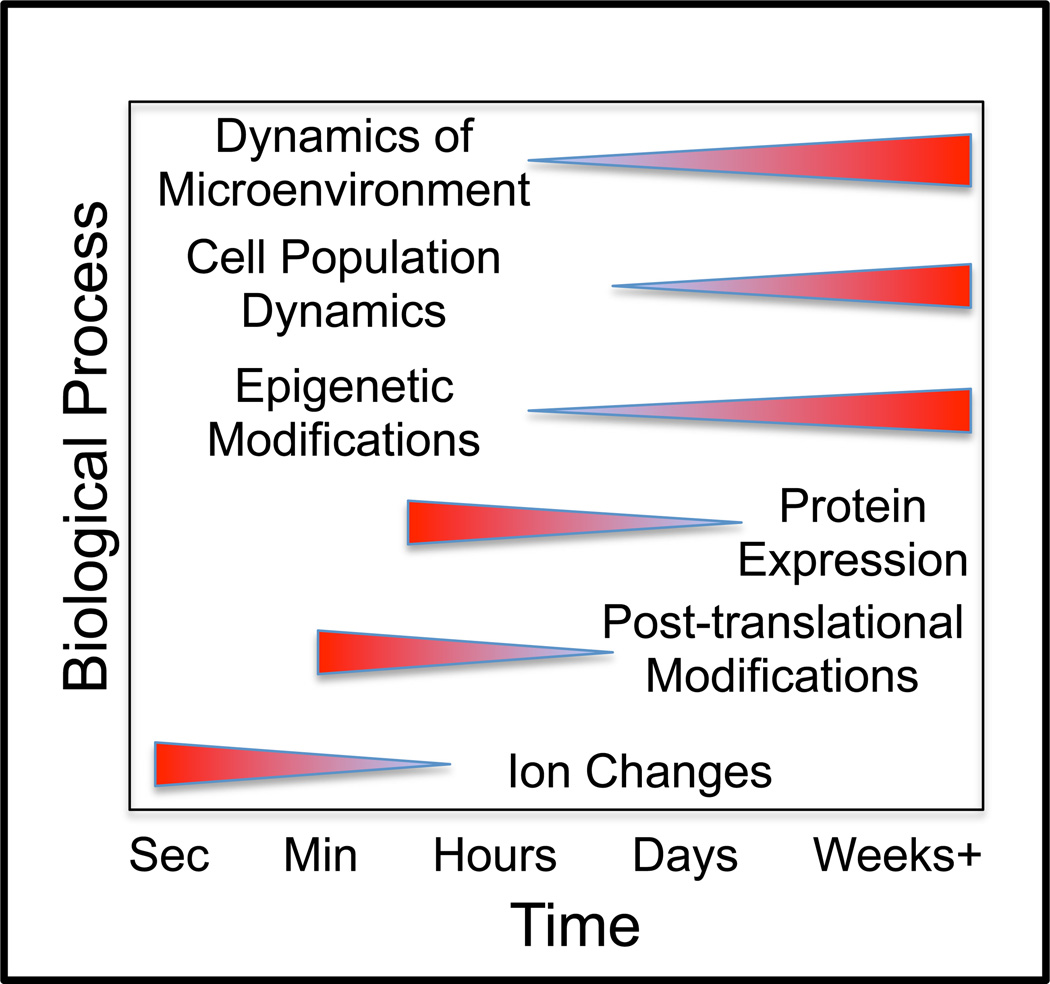
In addition, biological systems contain a number of complex biological processes that confound identifying the underlying physical and reaction processes from experimental observations of cellular behavior. Cellular responses to extracellular cues are governed by a variety of biological processes that can influence protein structure, protein abundance, the functional response to signaling protein activation, and other contextual cues present within the local microenvironment of the cell (Figure 4). Each of these biological processes also have associated time scales in which a change can be observed in response to a perturbation. Introducing a time delay between an experimental perturbation and assaying a cellular response implies that many of these different biological processes can become involved in influencing the cellular response. The challenge in improving our understanding of biological systems comes from deconvoluting the contributions of these different biological processes, which remains a pressing problem in identifying the networks that regulate cellular responses [31].

Figure 4. Besides the physical and reactive processes typically associated with chemical systems, a variety of additional biological processes influence how cells respond to extracellular cues.

A sampling of biological processes that orchestrate the cellular responses to an extracellular cue (ligand) are shown as a function of their associated kinetic time scales. With the fastest time scales, ion changes in the cytosol and post-translational modifications influence protein structure. Changes in protein structure alter the affinity of protein interactions. Protein abundance can be altered due to signaling-induced changes in abundance via de novo synthesis, degradation, or dilution within an expanding cell population. Epigenetic changes influence the relationship between transcription factor activation and the resulting protein synthesis by altering promoter binding sites, mRNA stability, or translation. Finally, cellular response can be modified by additional secreted or metabolic cues present within the local microenvironment that can, in turn, be shaped by the cell populations themselves.

5. Bayesian Statistics and Markov Chain Monte Carlo methods are reshaping how we approach inverse problems in reactive networks where prior knowledge exists

In part, these two types of inverse problems reflect a distinction between concepts associated with statistics and causality [32]. Statistical concepts are applied to quantify uncertainty, which is captured through the use of distributions [33]. In contrast, causality concepts are used to identify how observable events are structured into independent and dependent variables, which implies that the value of one variable is conditioned on the value of another variable. Causality can be depicted as a directed graph, where the variables comprise the vertices, such as the ligand and receptor in Box 1, and causal relationships are depicted as directed edges, such as an arrow that indicates that a ligand binds to the receptor to form a multi-protein complex. A directed edge is a generalization of a reactive event that can range from elementary steps to lumped reactions, which is more common in biology. The key idea drawn from chemical kinetics is that causality among reactive species is determined based on how the variables dynamically respond to perturbations [34]. For instance, observed species can be rank ordered into primary, that is those species impacted directly by the perturbation, and secondary, that is those species impacted indirectly by the perturbation through intermediates, based on their kinetic responses [35, 36, 37]. Given the uncertainty associated with experimental observations, the statistical and causal concepts are integrated through the use of conditional probability: P(Y|X, M), which is the probability of observing the value of a dependent variable (Y), given the value of the independent variable (X) and the causal model (M) that captures our understanding of the relationship between X and Y.

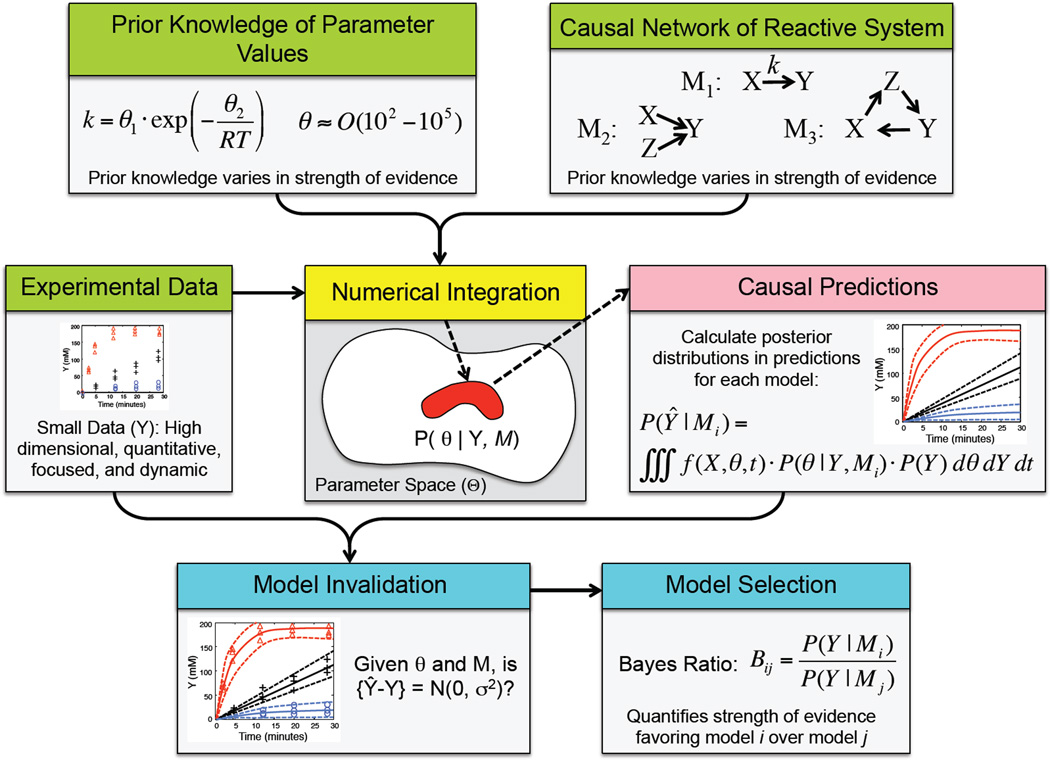
In silico model-based inference is an emerging approach that can be applied to inverse problems especially where prior knowledge exists [38], as summarized in Figure 5. To test the implications of the causal structure of a network model, the posterior distributions in the model predictions (P(Ŷ|M)) need to be established, which also depend on the available data (Y) and the uncertainty in the model parameters (P(Θ|M)). To account for these confounding influences, we can formulate the problem as an integral:

$$P(Ŷ|M)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }P(Ŷ|\mathrm{\Theta },M)·P(\mathrm{\Theta }|M,Y)·P(Y)d\mathrm{\Theta }dY.$$ (1)

As P(Θ|M, Y) is difficult to obtain directly, Bayes theorem is used to re-express this in terms of quantities that we can calculate,

$$P(\mathrm{\Theta }|M,Y)·P(Y)=P(Y|\mathrm{\Theta },M)·P(\mathrm{\Theta }|M),$$ (2)

to give:

$$P(Ŷ|M)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }P(Ŷ|\mathrm{\Theta },M)·P(Y|\mathrm{\Theta },M)·P(\mathrm{\Theta }|M)d\mathrm{\Theta }dY.$$ (3)

In equation 3, P(Θ|M) is the probability of sampling a point (Θ_i) in parameter space Θ prior to any knowledge about data Y (i.e., the prior for Θ) and P(Y|Θ_i, M) is the conditional probability of observing data similar to the simulated response Y when Θ_i and M are given (i.e., the likelihood of Y, given Θ_i and M). Generally, P(Ŷ|Θ, M) represents how the modeled variables will evolve in time, based on a set of parameter values and a mathematical model. In the case of a deterministic model, this conditional probability collapses down to a single path that describe how the variables evolve in time for a single set of parameter values.

Figure 5. A schematic of an emerging approach for inverse problems that use mechanistic mathematical models of reactive systems.

This approach leverages concepts from Bayesian statistics, probability, and advances in computational power to test competing hypotheses regarding causal structure of the reaction network. A mechanistic model of the reactive system, prior knowledge of parameter values, and experimental data are inputs to a computational filter. If prior knowledge of the key processes that govern the behavior of the reactive systems is weak, multiple competing hypotheses could be pro-posed as a reaction network. If prior knowledge of the parameter values is also weak, the computational filter uses this information as it searches parameter space to select a statistically-based ensemble of parameter values (red region of parameter space), given the uncertainty in the experimental data and model. This ensemble of parameter values are then used to generate a corresponding ensemble of predictions that describe probabilistically how the system evolves in time from the initial values, given the specific data and network model. A model invalidation step involves testing whether the difference between the model pre-dictions (Ŷ) and experimental data (Y) do not have systematic differences (i.e., {Ŷ − Y} ≠ N(0, σ²)). Finally, a Bayes Ratio can be used to select among competing hypothesis as to the governing processes associated with the reactive system.

To solve for P(Ŷ|M), integration over the finite discrete set of experimental observations (Y) is equivalent to a sum over the comparisons between each model prediction, Ŷ, and the corresponding observation, Y, as represented by the likelihood term: P(Y|Θ, M). Integrating with respect to the parameters, Θ, is more difficult. Exponential leaps in computational power have enabled Markov Chain Monte Carlo (MCMC) methods to integrate Equation 3. Given the explosion of MCMC methods in general, resources for MCMC integration are abundant, including reference texts [39, 40], stand-alone software [41, 42, 43, 44, 45], and R packages [46]. While MCMC algorithms are relatively simple to program, they can be a challenge to implement correctly such that the results provide an estimate of P(Ŷ|M). For instance, the criteria to assess convergence of the Markov Chains should be applied to the model predictions and not the model parameters due to the presence of kinetic slaving in dynamic systems [47, 28]. Kinetic slaving means that the overall speed of information transfer within a network is slaved to the slowest step within the network. Other steps in the network are either near equilibrium or are kinetically unimportant.

5.1. Applications to network inference

To achieve meaningful learning, one must first identify and address misconceptions that are specific to a scientific domain (i.e., prior knowledge) [48]. In the context of network inference in biology, a discrepancy between our model and an observation identifies flaws in our current understanding of the modeled system. Historically, the models most frequently used are mental models, which are communicated as cartoons (see Box 1). However, biological systems, like cell signaling networks, exhibit characteristics that make it extremely difficult to test our mental models, namely embedded dynamics, feedback regulation, or competing pathways. Dynamic mathematical models, like systems of coupled ordinary differential equations, provide a quantitative framework for encoding our causal knowledge about systems [32]. Predictions derived from the models can be used to test our models against data. Historically, these predictions are a single dynamic trajectory that is dependent on the values of the underlying model parameters. However, uncertainty in the model predictions is convoluted with the uncertainty of the model parameters. Thus, it is impossible to make confident statements about model inadequacy, given our ignorance of the underlying parameter values and the biology (e.g., protein-protein interaction energies or protein abundance) that they represent.

In a network inference context, in silico model-based inference methods can be used to encode competing hypotheses regarding the causal network and then generate posterior distributions in the model predictions by statistically sampling over all parameter values that give predictions that are consistent with the observed data. As the error between a model prediction and observed data should be normally distributed with a zero mean value, competing hypotheses can be rejected if they systematically deviate from the observed experimental data. Competing hypotheses that pass model invalidation criteria can then be evaluated using a Bayes Ratio, which quantifies the strength of evidence that favors one model over another, as illustrated in [49, 45]. Alternatively, a number of other model selection criteria, like the Akaike Information Criterion, have been proposed, as reviewed in [50]. These criteria quantify the perceived trade-off between predictive power, as commonly quantified by the summed squared error between the observations and model predictions, and a penalty term associated with model complexity, which can be related to the number of parameters. While these model selection criteria provide a simple metric, there are a number of underlying assumptions in developing these relationships that are not commonly encountered in biology. First, these criteria are applied in the asymptotic limit of empirical clarity, which means that the states of the system are all observed and all of the model parameters can be identified. Second, the penalty terms are ad hoc, which makes the criteria qualitative as a different weighting scheme would select a different winner among similarly scoring models [51]. In biology, the complexity of the model is influenced heavily by prior knowledge of the reactive network and observability is limited. A biologically realistic model inevitably includes many parameters that can not be identified in practice. To improve parameter identifiability, timescale analysis of reactive networks provides a data-based approach to select the appropriate complexity [28].

As all models are abstractions of reality, the value of the model ultimately depends on the fitness-of-purpose of the model for aiding inductive/deductive reasoning. The goal, then, is not necessarily to confirm our existing knowledge, but to use mathematical models to capture our cognitive understanding of the system and challenge these models with experimental data to identify flaws in our current understanding, as discussed in [38]. One example of the approach is mentioned in Box 1, where the differential regulation of STAT1 versus STAT4 phosphorylation, an indirect measure of activity, in response to IL12 stimulation was identified after an initial data set was unable to distinguish between competing hypotheses [29]. Another example focuses on the dynamic regulation of adherens junctions [23], which maintain the integrity of epithelial tissues through extracellular homotypic bonds. Experimentally, quantitative single-cell and population-level in vitro assays were used to quantify the endogenous pathway dynamics following the proteolytic disruption of the adherens junctions. Using prior knowledge of isolated elements of the overall network, these data were interpreted using in silico model-based inference to identify the topology of the regulatory network. While not previously recognized as playing a role in this network, an endocytic recycling pathway was essential to capture the observed data. Collectively, the data suggest that the regulatory network contains interlocked network motifs consisting of a positive feedback loop, which is used to restore the integrity of adherens junctions, and a negative feedback loop, which is used to limit beta-catenin-induced gene expression.

5.2. Applications to parameter inference

The parameters of a model can include rate parameters that quantify the propensity of a reaction to proceed, initial values of the model, and nuisance parameters that are required to map a mathematical model onto experimentally observed values. By integrating equation 3 using a MCMC approach, the predictions contained within the converged segments of the Markov Chains represent samples from posterior distribution in the model predictions, P(Ŷ|M). In addition, the corresponding parameter values from the converged segments of the Markov Chains represent samples from the posterior distributions in the parameters (P(Θ|Y, M)):

$$P(\mathrm{\Theta }|M,Y)=\frac{P(Y|\mathrm{\Theta },M)·P(\mathrm{\Theta }|M)}{P(Y)},$$ (4)

where P(Θ|M) is the prior for the model parameters and P(Y) serves effectively as a normalization constant.

In implementing a MCMC approach for parameter inference using mechanistic models of dynamic systems, there are a couple of points to keep in mind. First, the parameter priors should have heavy tails, meaning that prior probability for a particular set of parameter values (P(Θ|M)) should be greater than the posterior probability. In traditional chemical kinetic systems, the priors for parameters may be well defined in thermodynamic terms and calculated using ab initio methods (e.g., [52]). In models where multiple kinetic processes are grouped together as a lumped reaction, the prior distribution may be broad as possible values of the parameters are known only within a couple of orders of magnitude. Second, the data should “swamp” the prior, which means that the posterior distribution should reflect the combination of the data and the model used to interpret the data rather than an arbitrary choice of prior distributions for the parameters. Although in practice, this is difficult to diagnose, which leads to the last point. Finally, the structure of mechanistic models of biological systems are created based on the prior knowledge of the key variables involved in a system. In creating a more realistic model of the biology, additional parameters become incorporated into the model. However, the available data may only constrain a subset of the parameters through a process described as kinetic slaving.

In kinetic slaving, parameters associated with reactions that are fast, such as pre-formed multi-protein complexes, or that are kinetically unimportant, such as stationary reactions, exhibit one-sided distributions.[28]. This means that parameters associated with fast (or stationary) reactions are only constrained such that the value has to provide a time scale that is faster (or slower) than the observable time scales associated with the rate-limiting steps. This is a subtle but important point as many studies that apply statistical inference methods to inverse problems related to dynamic biological networks provide distributions in the model parameters that have bounds all supposedly informed by data (i.e., a posterior distribution) but that are in the form of a multivariate Gaussian distribution (i.e., all the parameters are bounded). Distributions in parameters of dynamic system models that are inconsistent with kinetic slaving is an indication that distributions do not reflect the experimental data but are constrained by the prior or that the model has been overly simplified to achieve an empirical fit.

6. Conclusion

In understanding traditional chemical processes and in engineering better medicines, making mechanistic models of these reactive systems involve similar challenges, which involve establishing causal relationships among reactive components of a system based on their observed dynamics. Moreover our existing knowledge of these systems is incomplete, as we have some prior knowledge of the likely reactive components and how they influence system response, and our ability to observe the system is limited. Nonetheless, these mechanistic models aim to assist our natural intuition and facilitate communication by providing a concrete realization of how we think the system works. While mathematics and simulation play central roles in addressing these problems, advances in computational power have enabled more sophisticated methods that provide a solid statistical and probabilistic foundation to test our mechanistic understanding against data.

Here, we provide an overview of some of the emerging model-based inference tools that leverage Markov Chain Monte Carlo methods enabled by increases in computational power and concepts drawn from Bayesian statistics, probability, and chemical kinetics. We have focused on applications related to cellular signal transduction networks, which transmit molecular information within a cell to regulate a functional response. Given the importance of understanding cellular behavior to engineer better medicines, cellular systems are particularly challenging as limited observability of these intracellular networks is more acute and potential reactive components of these systems are being discovered at an increasing pace. Computational approaches built upon solid statistical and causal foundations, as described here, will be increasingly used to help think more clearly about the dynamic relationships among the components of reactive networks.

Figure 2. A cartoon illustrating the canonical JAK-STAT signaling pathway that initiates a cellular response, as depicted by secreted protein production, in response to stimulation with an extracellular ligand.

An extracellular soluble cue binds to a multi-protein complex that is comprised of transmembrane receptor proteins and associated Janus kinases. Upon ligand binding, the receptor changes conformation enabling the JAKs to phosphorylate STAT binding sites within the cytoplasmic tails of the receptors. The STAT proteins then associate with the activated receptor complex and sub-sequently become phosphorylated by the JAKs, as indicated by the green dot. The phosphorylated STAT proteins dimerize and migrate to the nucleus to initiate the transcription and translation of the corresponding STAT-responsive genes, which include cytokines that are released by the cell to help coordinate cellular response. STAT proteins become deactivated following dephosphorylation by a number of different phosphatases, including protein tyrosine phosphatases (PTP), that are present within the cell.

Figure 3. The emerging JAK-STAT pathways associated with IL12 signaling in type 1 T helper cells.

IL12 binds to a multi-protein receptor complex comprised of two transmembrane receptor proteins, IL12RB1 and IL12RB2, that are bound to the Janus kinases TYK2 and JAK2, respectively. Binding of the receptor complex by IL12 results in the phosphorylation of both STAT1 and STAT4. STAT1 plays a role in the expression of IL12RB2 while STAT4 promotes the transcription and translation of Interferon-γ (IFNG) and Interleukin-10 (IL10). While initially activated by IL12, STAT1 becomes dephosphorylated through an unclear mechanism that may involve the inducible expression of a phosphatase, like a Suppressor of Cytokine Signaling (SOCS). The intracellular transport of the receptor complex (i.e., receptor trafficking), dilution of proteins due to cell proliferation, and signaling pathways that connect IL12 stimulation to enhanced cell viability are some of the biological processes not depicted in this diagram.

Highlights.

• Discovering new drugs requires knowing the flow of information within networks.

• Identifying the causal structure of a network from data is a type of inverse problem.

• Computational solutions use ideas from Bayesian statistics and chemical kinetics.

• Methods use prior knowledge of network and tolerate limited observability.

• While easy to implement, obtaining useful results requires critical analysis.