Abstract
Compressed sensing (CS) has been used in dynamic cardiac MRI to reduce the data acquisition time. The sparseness of the dynamic image series in the spatial and temporal-frequency (x-f) domain has been exploited in existing works. In this paper, we propose a new k-t Iterative Support Detection (k-t ISD) method to improve the CS reconstruction for dynamic cardiac MRI by incorporating additional information on the support of the dynamic image in x-f space based on the theory of CS with partially known support. The proposed method uses an iterative procedure for alternating between image reconstruction and support detection in x-f space. At each iteration, a truncated ℓ1 minimization is applied to obtain the reconstructed image in x-f space using the support information from the previous iteration. Subsequently, by thresholding the reconstruction, we update the support information to be used in the next iteration. Experimental results demonstrate that the proposed k-t ISD method improves the reconstruction quality of dynamic cardiac MRI over the basic CS method in which support information is not exploited.
Keywords: Compressed sensing, dynamic MRI, k-t Iterative Support Detection (k-t ISD), partially known support, truncated ℓ1 minimization
INTRODUCTION
Dynamic cardiac cine magnetic resonance imaging (MRI) is a technique to acquire a time series of images from cardiac motion at a high frame rate. The acquired data in dynamic cardiac MRI is in the spatial-frequency and temporal domain, the so-called k-t space. The acquisition time is an important factor to minimize so that cardiac function can be accurately evaluated in a clinical workflow. Accelerating the acquisition speed by undersampling k-space may compromise spatial resolution, temporal resolution, signal-to-noise ratio (SNR), or introduce image artifacts. A range of techniques have been developed to reconstruct a high-quality image series from the undersampled MRI data by exploiting spatial and/or temporal correlations in the dynamic image series. Typical methods for the reconstruction from undersampled single-coil measurements include RIGR (1), keyhole (2), view-sharing (3), UNFOLD (4), Partially Separable Function (PSF) (5–7), Kalman filter (8, 9), PARADIGM (10–12), and k-t BLAST (13).
Among many advanced techniques to reduce the amount of measured data while preserving the quality of the image sequence, the emerging theory of compressed sensing (CS) (14, 15) holds great potential for significant data reduction. In most existing CS-based dynamic cardiac MRI methods, the basic CS formulation is used which mostly exploits only the prior that the dynamic image series is sparse in the spatial and temporal-frequency domain (x-f space). Since additional prior information about the unknown MR images may be available for certain applications, it is advantageous to incorporate this information into the CS reconstruction.
In this paper, based on a recent theory on compressed sensing with partially known support, we study how to obtain and exploit the support information to improve CS reconstruction in dynamic cardiac MRI applications. A new method, named k-t Iterative Support Detection (k-t ISD), is proposed. The method alternates between image reconstruction and support detection in x-f space iteratively. Within each iteration, the dynamic image in x-f space is reconstructed through a truncated ℓ1 minimization implemented using a FOCal Underdetermined System Solver (FOCUSS) algorithm. Specifically, the truncated ℓ1 minimization excludes the signal at the known support (detected from the previous iteration) from the cost function of the ℓ1 minimization. Once the image is reconstructed in this iteration, the support information is updated by thresholding the reconstruction and used in the next iteration of image reconstruction. Improvement of the proposed method over the basic CS approaches is demonstrated using retrospectively undersampled in vivo cardiac cine MR experiments.
THEORY
Summary on Dynamic MRI Using Compressed Sensing
The application of CS in dynamic MRI is made possible by the fact that dynamic MRI satisfies the two conditions of CS (16): the image series is sparse in a certain transform domain due to the spatial and temporal correlations, and the sampling in k-t space can be designed to be incoherent. In the CS framework, a dynamic image series is reconstructed in the x-t domain by
| [1] |
where Fx is the Fourier transform matrix in the spatial domain, m is a vector representing the signal in the x-t domain, d is the vector for the reduced data in k-t space, and Ψ denotes the sparsifying transform.
Several methods have been proposed to apply CS in dynamic MRI (16–23). In terms of the sparsifying transform employed to make the image series sparse, these methods can be categorized as using (a) spatial correlation only, (b) temporal correlation only, and (c) both spatial and temporal correlations. When only the spatial correlation is exploited, the image in each frame is reconstructed individually using approaches similar to those in (24, 25), where the sparsifying transform such as wavelet transform is applied along the spatial domain only (17). Exploiting the temporal correlation is more useful to take advantage of the dynamic characteristics. One way to exploit the temporal correlation is to subtract the image at each frame by that from a reference frame (18–21). Due to the slow motion of dynamic features, the difference image is usually sparse. Another way is to apply Fourier transform along the temporal direction (20–23). The slow motion suggests the image series is sparse in the temporal-frequency domain. Exploiting both the spatial and temporal correlations is more appealing to sparsify the image series. k-t SPARSE (16) exploits the temporal correlation by Fourier transform in time domain and the spatial correlation by wavelet transform in spatial domain. Three-dimensional CS (17) exploits the temporal and spatial correlations using a three-dimensional wavelet transform.
Theory on Compressed Sensing with Partially Known Support
Recently, an extension of CS — CS with partially known support (CS-PKS) has been studied in (26–30) to incorporate the partial support information of a sparse signal into the CS reconstruction, where support is defined as the locations of non-zero elements in the sparse domain. It is shown through theoretical analysis and numerical study that, this new technique can effectively reduce the number of measurements required by basic CS to achieve a given reconstruction quality or improve the quality of CS reconstruction given the same number of measurements.
In basic CS, the solution is the one with the minimum number of nonzero among infinite data-consistency candidates, or equivalently the one satisfying data consistency constraint among infinite enumeration of all possible combinations for the nonzero locations in the signal. Now we consider the CS reconstruction of an s-sparse signal x with partial known support from measurements y. The support of x, denoted as S, can be represented as S = T ∪ Δ, where T is the known part with size |T| and Δ is the unknown part with size |Δ|. With partially known support T, the candidates for the s-sparse signal x are restricted in a signal space smaller than that in basic CS. We use a simple example to demonstrates the difference between CS-PKS and basic CS. Suppose x is a three dimensional signal (x1, x2, x3) with a sparsity of two (i.e., two out of three dimensions are nonzero). Basic CS needs to search for solutions in three possible two-dimensional subspaces (x1, x2, 0), (x1, 0, x3), and (0, x2, x3). If the support is partially known such that x1 is known to be nonzero, we only need to search for solutions in two possible two-dimensional subspaces (x1, x2, 0) and (x1, 0, x3). Clearly, the search space is reduced when the support is partially known. The reduction is even more when the dimension of signal x is higher and/or the more the support is known. Since the signal x is known to be nonzero at some locations (denoted as support T), CS-PKS allows us to minimize the number of nonzeros at other locations (outside the support T) only when searching for a sparse solution to Φx = y. This procedure can be formulated as
| [2] |
or, more practically (considering computational complexity and robustness)
| [3] |
where xΔ denotes the signal outside the known support. This problem is referred to as the truncated minimization because the cost function to be minimized is not related to the entire signal, but a truncated version of the signal that leaves out the part with known support. This formulation suggests that, in order to find a sparse solution that satisfies the data consistency constraint, it is sufficient to consider a much smaller signal space that always has nonzero elements at the known support. In other words, truncated minimization favors a solution with more zeros outside T (26), and thus it may recover the signal more accurately than basic CS does for signals whose support includes T. Once the non-zero locations outside the known support are determined, the value of the entire signal can be obtained from the data consistency term.
The sufficient conditions for CS-PKS have been studied theoretically and independently from the view of restricted isometry property (RIP) and null space property (NSP), respectively (27, 28). It follows from these conditions that the number of measurements required for CS-PKS is less than that for basic CS, and the more the support is known, the fewer the measurements are needed. The robustness of truncated ℓ1 minimization under noisy measurements has been demonstrated in (27–29) using an upper bound.
In practical conditions, the partially known support may not be exactly a subset of the true support. There may be some false locations (assumed nonzero but actually zero) in the known support. In this case, we define the known support as T = Tc + Tf, where Tc is a subset of true support with size |Tc|, and Tf is the set of false support with size |Tf |. Numerical simulations in Ref. (26, 28) show that the truncated minimization with some false support can still reconstruct the underlying signals provided the size of correct support is larger than that of false support (i.e., |Tc|>|Tf |). In addition, it has also been proved in (28) that as long as |Tc|>|Tf |, CS-PKS requires fewer measurements than basic CS. The more accurate the support is, the fewer measurements are needed for exact reconstruction.
Proposed k-t Iterative Support Detection (k-t ISD) Method
Based on the above theory, we propose a k-t ISD method which adaptively and iteratively learns and utilizes the support information in compressed sensing for dynamic MRI such that the images are reconstructed more accurately. The method alternates between CS reconstruction with partially known support and adaptive learning of support knowledge, which are elaborated below.
A. Compressed Sensing for Dynamic MRI with Partially Known Support
Among the two methods to sparsify dynamic images, we consider the Fourier transform along the temporal direction as the sparsifying transform (20–23, 31). This is based on a recent work (31) that demonstrates the temporal Fourier transform can achieve a higher degree of sparsity than that achieved by the temporal difference in cardiac imaging. With signal representation in x-f domain, the data consistency constraint becomes
| [4] |
where F denotes the two-dimensional Fourier transform in both k-t directions and ρ is the signal vector in x-f domain. According to the theory on CS-PKS, reconstruction of the signal ρ in x-f domain can be formulated as a truncated ℓ1 minimization problem
| [5] |
when the support of the signal ρ in x-f domain has a known part T and an unknown part Δ.
In our implementation, we rewrite [6] as a weighted ℓ1 minimization problem and reconstruct the signal ρ by
| [6] |
where W is a diagonal weighting matrix whose diagonal element equals 0 if the corresponding element in x-f space belongs to the known support T, and 1 otherwise. Here we apply the FOCUSS algorithm (32, 33) to solve Eq.[6], although many other algorithms are also applicable. The solution to the weighted ℓ1 minimization problem is computed by iteratively solving a reweighted ℓ1 minimization problem defined as
such that q is the solution to
| [7] |
and D is a diagonal weighting matrix that is updated iteratively. The above constrained ℓ2 optimization problem can be converted into an unconstrained optimization problem,
| [8] |
which has a closed-form solution:
| [9] |
Conjugate gradient (CG) [34] is used to solve Eq.[9] to avoid direct inversion of a large matrix, and the regularization parameter λ is selected by solving Eq.[9] with different values of λ and choosing one so that . Then the x-f space image is given by
| [10] |
In the l-th iteration, the diagonal elements of the matrix Dl are the square root of the absolute value of the solution ρl−1 in the previous iteration. Specifically,
| [11] |
where is the n-th element of ρl−1.
It can be seen that the regularized term of ℓ2 norm in [8] is equivalent to , which has the following asymptotic behavior
| [12] |
where the property WHW = W is used. It implies that the solution to [7] asymptotically approaches the solution to the truncated ℓ1 minimization [5] with infinite iterations. In practice, the iteration terminates when the normalized difference between the consecutive solutions is less than a threshold (e.g., 1×10−2).
B. Adaptive Learning of Support Knowledge
It is usually difficult to obtain the exact x-f support of unknown cardiac images a priori because the signal support is patient and scan dependent (12). The support information in x-f space has been studied and used in prior works outside the CS context. Aggarwal and Bresler (10–12) have used the x-f support to develop a patient-adapted reconstruction and acquisition dynamic imaging method (PARADIGM). They suggested that the support in x-f space for cardiac imaging should have the following features (12): (a) The highly dynamic region (e.g., the heart region) should have a small support in the spatial domain x, but its exact location depends on the specific imaging experiment. (b) Other regions of the body may also vary temporally due to slow non-cardiac motion, but should have narrow temporal bandwidth. (c) Due to the approximately periodic heart motion, the highly dynamic region should have a banded temporal spectrum with the bands located at the multiples of the heart rate, but the width of each band is patient dependent. In order to exploit accurate x-f support information in the design of the time-sequential acquisition scheme, PARADIGM uses a pre-scan to obtain the support. Brinegar et al (7) also explores the x-f support obtained empirically to improve the reconstruction using the partially separable function model.
1) Iterative support detection
To avoid pre-scan or empirical estimate, we propose to learn the support in x-f space from the reconstructions iteratively. The idea of iterative support detection is based on a new CS algorithm by Wang and Yin (28). In k-t ISD, we start with a basic CS reconstruction without any support information. Because fewer k-t data are acquired than those required for perfect recovery, the initial reconstruction using basic CS is poor. We then learn the support in x-f space using the locations whose values are above a predefined threshold. This support is held fixed and used in truncated ℓ1 minimization for an updated reconstruction. The support detection and signal reconstruction steps are then repeated alternately until convergence.
The above two steps can be mathematically represented as follows. In the reconstruction step of the i-th iteration in k-t ISD, the intermediate reconstruction ρi is obtained by solving a truncated ℓ1 minimization problem
| [13] |
with a known support Ti−1 (Δi−1 denotes the nonzero locations outside the known support). As we introduced above, ρi is reconstructed by rewriting [13] as the weighted ℓ1 minimization problem
| [14] |
and solved using FOCUSS algorithm. In the support detection step, the support is obtained by thresholding the above reconstructed signal ρi in x-f space
| [15] |
where is the z-th element of ρi.
2) Choice of thresholds in k-t ISD
The threshold τi largely affects the performance of k-t ISD. Small τi will result in too many false locations in the detected support, which may not be corrected in subsequent iterations of reconstruction. On the other hand, large τi will result in too few locations in the detected support and hence a large number of iterations is required for converge. Strategies on the choice of τi were discussed and applied in (28). One is to find the “first significant jump” in the ascending sequence of the magnitude of the reconstructed signal. However, another threshold to tell this “jump” is different for different decay rate, which is difficult to accurately estimate from undersampled measurements. Another simple but quite effective one is to set with an increasing sequence of δ(i) > 0. We find this strategy works well for our study on many cardiac datasets when δ(i) is chosen as an exponential function of the number of outer iteration i. The choice of exponential function is based on the definition of compressible signals that CS primarily deals with in practice. Compressible signals are usually approximated by an exponential law , or alternately by a power law , where is the magnitude of the sorted signal x, b and r can be regarded as decay rates, with a and C being positive constant (31).
The complete k-t ISD algorithm is summarized in Algorithm 1.
|
| |
| Algorithm 1. Pseudocode for k-t ISD | |
|
| |
| 1. | Initialize W0 |
| 2. | For i = 1,2,⋯, do following until convergence |
| [1] Reconstruct ρi based on Wi−1 using [14], which is implemented by the following steps of FOCUSS: | |
| a. Initialize D0 | |
| b. For i = 1,2,⋯, do the following until convergence | |
| i. Reconstruct ρi using ℓ2 minimization in [10] | |
| ii. Update Dl using [11] | |
| c. Use ρl for ρi after convergence | |
| [2] Update detected support Ti and Wi based on ρi using thresholding in [15] | |
|
| |
C. Applicability of k-t ISD
Numerical studies in (28) showed that ISD is applicable to signals with a fast decaying rate. The nonzero components of such signals have relatively large magnitude. This property ensures that even when the initial reconstruction is poor (due to insufficient measurements), the signal magnitude at the nonzero locations within the true support is likely to remain large, and thus these locations can be detected correctly by thresholding. In subsequent iterations, the magnitude at the detected nonzero locations will be corrected with the aid of improved support information through ISD. In the event that some of the zero locations outside the true support also present large magnitude in the initial reconstruction, resulting in false locations to be included in the detected support, we have claimed in previous section that the ISD still converges as long as the number of false locations is less than the number of correct locations by a certain amount (28).
The development of k-t ISD for cardiac cine MRI is made possible by the fact that signals in x-f space rapidly decay in magnitude. This characteristic has been claimed in Ref.(31) and demonstrated in Fig.1 using five cardiac cine datasets.
Fig. 1.
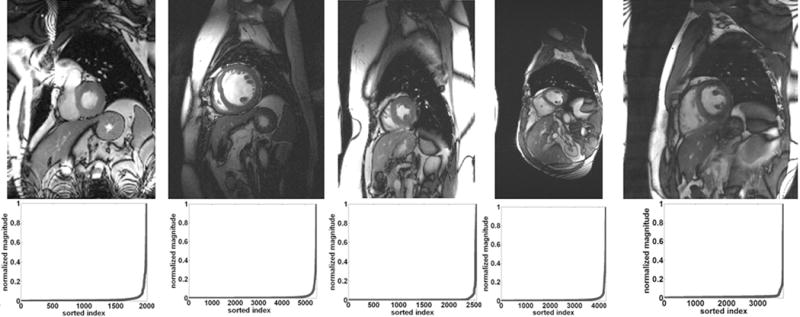
Top row shows a single frame reconstructed from the fully sampled data. The bottom row shows plots of the magnitude of the normalized and sorted signals in x-f space for a given position in the frequency-encoding direction. Three different datasets with five coils (left), a single coil (middle), and four coils (right) were used.
METHODS
The feasibility of k-t ISD was validated on five fully sampled sets of dynamic cardiac cine data, each covering an entire cardiac cycle. The imaging parameters are provided in Table 1. Informed consent was obtained from all volunteers in accordance with the institutional review board policy. The fully sampled data were undersampled retrospectively and used to compare the proposed k-t ISD method with other reconstruction methods. Similar to existing methods that apply CS to dynamic MRI, the phase encoding direction is undersampled and an incoherence undersampling pattern is used to acquire the signal in k-t space. In our work, we generate a random sampling pattern using a zero-mean Gaussian distribution whose density tapers off toward the outer k-space. Other incoherent sampling schemes (22, 35) that impose additional constraints on the sampling patterns can also be applied to the proposed k-t ISD. The central 8 phase encoding lines were fully sampled to obtain a low-resolution image for FOCUSS algorithm. The matrix W, representing the detected support information, was initialized to an identity matrix before the first reconstruction when no support knowledge was available. For all datasets, the threshold follows , where we empirically set δ(i) = 5 ~8i+1 based on our experiments. Note the threshold only depends on the image reconstructed in the previous iteration and its selection does not need knowledge of fully sampled original image.
Table 1.
Data acquisition parameters for imaging experiments
| Data 1 | Data 2 | Data 3 | Data 4 | Data 5 | |
|---|---|---|---|---|---|
| Scanner | 3T Siemens | 1.5T Philips | 3T Siemens | 3T Siemens | 3T Siemens |
| Sequence | SSFP | SSFP | SSFP | SSFP | SSFP |
| Flip angle (degree) | 44 | 50 | 50 | 44 | 50 |
| TE/TR (msec) | 1.5/3.0 | 1.7/3.45 | 1.7/3.45 | 1.22/42.5 | 1.89/56.6 |
| Matrix size (FE × PE × frame × coil) | 160×133×15×5 | 256×220×25 | 256×150×17×4 | 304×165×26×12 | 256×225×17×15 |
| FOV (mm× mm) | 350 × 262 | 345 × 270 | 340 × 277 | 340 × 276 | 340 × 287 |
| Slice thickness (mm) | 7 | 10 | 8 | 6 | 6 |
| Heart beats (bpm) | 54 | 66 | 60 | 62 | 61 |
The proposed k-t ISD, k-t FOCUSS (20), and the two-step OMP methods (22) were used to reconstruct the desired image series. The same sampling pattern was used for all methods when the reduction factor and dataset are fixed. All methods were implemented in MATLAB and the code for k-t FOCUSS was obtained from http://bisp.kaist.ac.kr/research_02.htm. For the dataset acquired using multiple coils, we reconstructed images for each coil separately, and then combined them using square-root of sum-of-squares (SoS). The image series reconstructed from the full k-t data were used as the reference for comparison. The top row of Fig. 1 shows a single frame reconstructed from fully sampled measurements of the first to the fifth datasets (from left to right) for reference. The bottom row shows the corresponding normalized and sorted signals in x-f space for a given position in the frequency-encoding direction. It is seen that all of these signals in x-f space are compressible with a fast decaying rate.
RESULTS
Reconstruction Quality of k-t ISD
The reconstructions with a net reduction factor of R = 3 and the corresponding difference images with the reference at the 6th frame of the 5-coil dataset are shown in Fig. 2. The difference images were scaled appropriately to better reveal the distinctions between reconstructions. Rows show different methods with the first row for two-step OMP, the second for k-t FOCUSS, and the third for k-t ISD. The result of the k-t ISD method is after two iterations of support detection. It is seen in Fig. 2 that compared to k-t ISD, the k-t FOCUSS presents more undersampling artifacts along the phase encoding direction and the two-step OMP presents more noise as indicated by arrowheads. The superiority of k-t ISD is clearly seen in the difference images. Figure 3 shows the reconstructions of the 11th frame at R=4 as well as the corresponding difference images for the single-coil dataset. Three iterations of support detection were used in k-t ISD. The results of the single-coil data lead to the same conclusion that the k-t ISD is able to suppress more artifacts and preserve more details than k-t FOCUSS. To quantify the improvement of k-t ISD over k-t FOCUSS and two-step OMP, the normalized mean-squared error (MSE) (24) between the reconstruction and the reference were calculated for four datasets and plotted as a function of time frame in Fig. 4(a)–(d) respectively. The solid lines are for k-t ISD, dotted lines for k-t FOCUSS, and dashed lines for two-step OMP, respectively. The k-t ISD is seen to have a lower MSE than the other two methods for all frames.
Fig. 2.
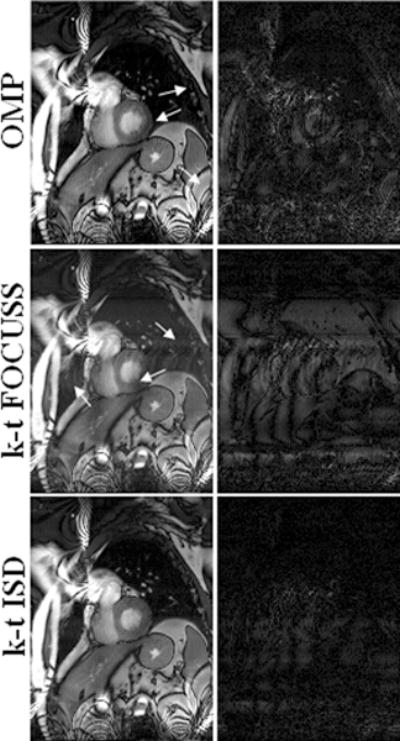
Reconstructions (left) of the 6th frame using two-step OMP (top), k-t FOCUSS (middle) and k-t ISD (bottom), and the corresponding difference images (right) with a reduction factor of 3 from the 5-coil dataset.
Fig. 3.
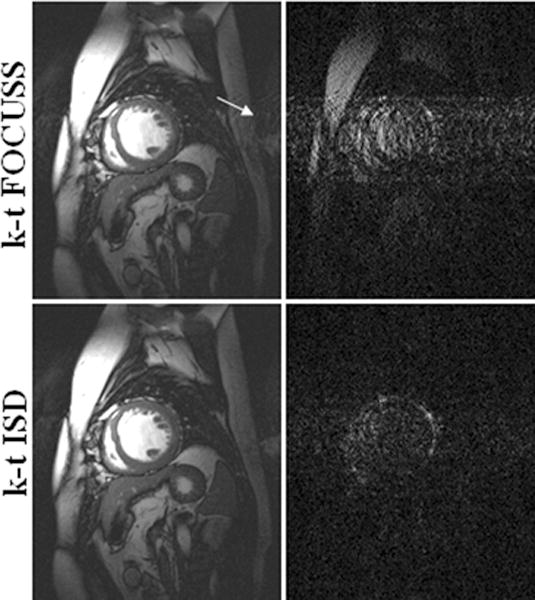
Reconstructions (left) at the 11th frame using k-t FOCUSS (top) and k-t ISD (bottom), and their corresponding difference images (right) with a reduction factor of 4 for the single-coil dataset.
Fig. 4.

Frame-by-frame plots of MSE for two-step OMP, k-t FOCUSS, and k-t ISD with R = 3 for the 5-coil dataset (top left), R = 4 for the single-coil dataset (top right), R = 8 for the 12-coil dataset (bottom left), and R = 8 for the 15-coil dataset (bottom right). The solid lines are for k-t ISD, dotted lines for k-t FOCUSS, and dashed lines for two-step OMP.
Due to its importance in clinical diagnosis, the heart region with highly dynamic motion is considered as the region of interest (ROI) to further evaluate the proposed method. Figure 5 shows the ROI reconstructions for the 5-coil dataset with R=3, the 4-coil dataset with R=4, the 12-coil dataset with R=8, and the 15-coil with R=8 from left column to right column. Rows show the reference, k-t FOCUSS, and k-t ISD from top to bottom. It is evident that k-t FOCUSS presents larger aliasing artifacts than k-t ISD in the heart region. We note that the success of k-t ISD is based upon the fast-decaying property of dynamic cardiac images in the x-f space and the ability of ISD to learn the true support from poor reconstructions for such images.
Fig. 5.
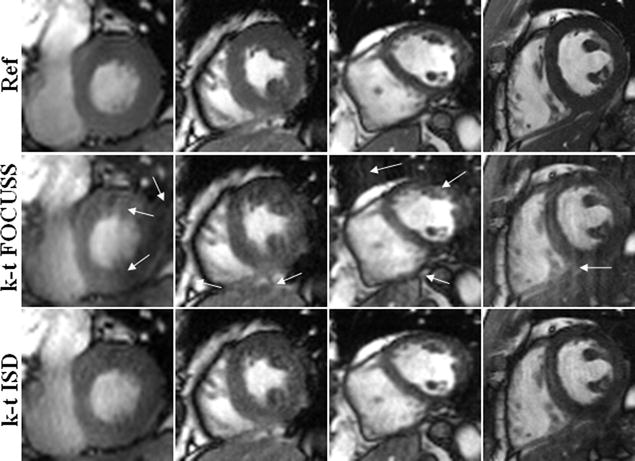
ROI of reference (top), k-t FOCUSS (middle), and k-t ISD (bottom) for the 5-coil dataset with R = 3 (first column), the 4-coil dataset with R = 4 (second column), the 12-coil dataset with R = 8 (third column), and the 15-coil dataset with R = 8 (fourth column).
The ability to catch the dynamic motion along temporal direction is very important for dynamic reconstruction methods. To evaluate the temporal fidelity in k-t ISD, for a fixed position in the frequency-encoding direction, we show in Fig. 6 the reconstructions in x-t plane for the 5-coil dataset with R=3 and 12-coil dataset with R=8. It is seen that the two-step OMP smoothes out the rapid temporal variations and k-t FOCUSS shows some loss of contrast. In comparison, the proposed k-t ISD preserves more temporal variations than other methods especially in regions indicated by arrows.
Fig. 6.

The temporal profiles in x-t plane of different reconstruction methods for the 5-coil dataset with R = 3 (top row) and the 15-coil dataset with R = 6 (bottom row).
Support-detection Fidelity of k-t ISD
To evaluate the fidelity of the detected support in k-t ISD, Fig. 7 compares the support maps detected after different iterations of k-t ISD, with the “true” support maps of the fully sampled reference signal in x-f space (with a fixed position in the frequency-encoding direction). In addition, the false detection maps are also shown. Although the “true” support is not available when the fully sampled original image is unknown in practice, it is used here only to verify that our threshold-selection method can detect the support rather accurately. The single-coil dataset with a reduction factor of 4 was used as an example. Because the reference signal is compressible but not exactly sparse in x-f space, the “true” support here refers to locations with relatively large magnitude (i.e., above a threshold). To facilitate the comparison with k-t ISD, an iterative approach is also used to choose a decreasing sequence of thresholds from which a sequence of “true” support maps are obtained by thresholding the x-f space of the fully sampled reference. The largest threshold used for the first iteration is set to be the signal value at the corner of the sorted reference signal (shown on the lower left of Fig.1). This curve is then truncated by excluding the portion above the threshold, and then the corner of the truncated curve is identified and set to be the threshold for the next iteration. This procedure is repeated so that the corners of each truncated curve of the sorted reference are used to determine the sequence of decreasing thresholds for the generation of the “true” support maps in Fig. 7. It is worth noting that these thresholds are (and should be) different from those in k-t ISD because the latter are selected to detect the support from imperfect reconstructions instead of from the reference signal. The “true” support map after the first iteration shows that the most significant elements dominate the low temporal-frequency region. As the threshold decreases over iterations, the support begins to include locations of smaller elements and thus spreads from the low temporal-frequency region to other regions.
Fig. 7.

The “true” (top), detected (middle) and false (bottom) support maps (support shown in white) in x-f space. The true maps are obtained with decreasing thresholds and the detected maps are obtained from different iterations of support detections (shown on the bottom). The single-coil dataset with a reduction factor of 4 was used.
Recall that the detected support maps for k-t ISD are also generated by thresholding each reconstruction using a threshold that decreases over iterations. For the first two iterations, the detected support maps (size of 204 and 611 respectively) are very similar to the first two “true” support maps, and the false support maps are very sparse (only 2 and 107 respectively). This suggests that k-t ISD is able to accurately detect the low temporal-frequency locations with significant elements. Because the number of correct detections is significantly more than that of the false ones, CS-PKS should perform better than CS. As the iterations proceed, even if the number of false detections increases (582, 743, 626 for the 3rd, 4th, and 5th iterations, respectively) due to the difficulty to detect small elements using k-t ISD, the number of correct detections also increases (1242, 2612, 4028 for the 3rd, 4th, and 5th iterations, respectively) and always takes a larger part in detected supports. According to Ref. (28), as long as the numbers of correct detections is sufficiently more than those of false detections, further iterations using CS-PKS still improve the reconstruction quality. It has been noted that the detected support is not necessarily always increasing. This is demonstrated by the decrease in the number of false detection from the 4th to 5th iterations.
Convergence of k-t ISD and effect of threshold
The convergence behavior is an important factor in evaluating the performance of k-t ISD. Although ISD is known to converge under certain conditions (28), these conditions are difficult to verify in practice. In addition, the convergence behavior is largely affected by the parameter δ(i) in k-t ISD. Hence, we opt to study the convergence of k-t ISD and its dependence on δ(i) using MSE-iteration curves. Three different values δ(i) = 15i+1, 8i+1 and 2i+1 were used where i is the iteration number. The corresponding MSE-iteration plots are shown in Fig. 8 when R=3 for the 5-coil dataset. The plots for other reduction factors and other datasets have the same behavior. Since strict convergence is not observed, a stopping criterion is needed to terminate iterations. We calculate the normalized difference between the adjacent iterations and terminate iterations once its value is below a threshold (10−2 used here).
Fig. 8.
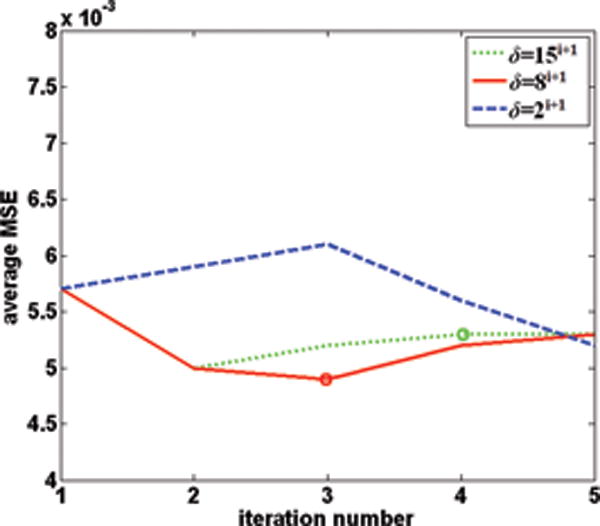
The plots of MSE (averaged over all frames) versus the number of iterations for different choices of δ with R=3 for the 5-coil data.
It can be seen that when threshold changes fast with iterations, the MSE initially decreases but then increases with more iterations. The initial decrease is because the detected support improves over iterations and so does the reconstruction quality. The subsequent increase with more iterations is due to the increased number of false locations in support detection as δ gets too large. For δ(i) = 15i+1, k-t ISD stops after 4 iterations to an MSE value that is greater than the lowest MSE. On the other hand, slowly-changing δ will result in too few locations detected in support and thus slow convergence. For δ(i) = 2i+1, k-t ISD does not terminate even after 5 iterations. A moderate changing rate with δ(i) = 8i+1 needs only 3 iterations to stop which corresponds to the lowest MSE.
To demonstrate the improvement of k-t ISD on image quality over iterations, we show in Fig. 9 the intermediate reconstructions, the corresponding difference images, and the temporal profiles for the first, second, and fourth iterations (from top to bottom) using the 12-coil datasets with R = 8. The first iteration has no knowledge on support and the reconstruction shows some smoothing and artifacts due to insufficient measurements. As the number of iterations increases, the resolution improves and fine details become clearer. The improvement is better demonstrated in the regions indicated by arrows and in the difference images.
Fig. 9.
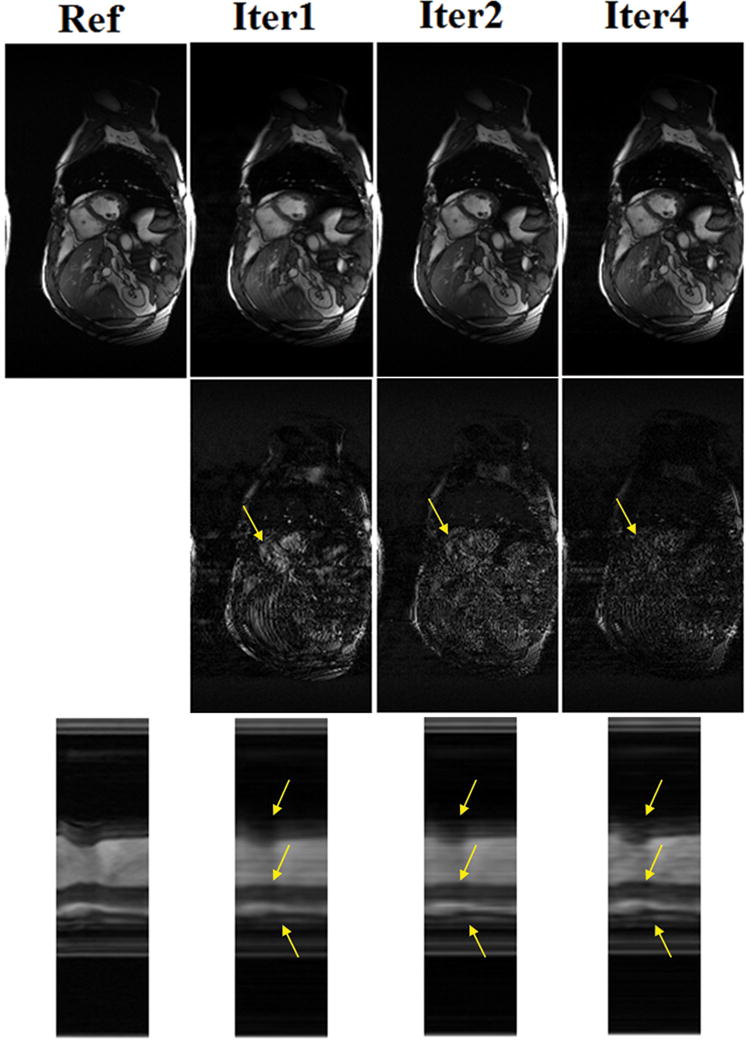
The reconstructions (top), corresponding difference images (middle), and temporal profiles (bottom) at the first, second, and fourth iteration of k-t ISD for the 12-coil dataset with R=8.
Robustness of k-t ISD to Noise
All datasets tested here contain noise. In order to demonstrate the robustness of k-t ISD to even noisier measurements, different levels of white Gaussian noise were simulated and added to the acquired data, and the undersampled noisy data were used to reconstruct the dynamic images. The amount of noise added was qualified by an SNR index that was calculated as the ratio between the average intensity of selected signal region and the standard deviation of the background region in the SoS reconstruction from full measurements.
Figure 10 shows the plots of frame-by-frame MSE on ROI with different reduction factors R for the 4-coil dataset when the SNR are 30 and 15. The solid lines are for k-t ISD and dotted lines for k-t FOCUSS. Compared to the scanned data with SNR of 30, the MSE curve of SNR=15 preserves a similar shape but with larger values. A similar trend was also observed for other SNRs and other datasets. It suggests that the reconstruction quality degrades gracefully with reduced SNR for both methods, and k-t ISD still outperforms k-t FOCUSS at low SNRs. This agrees with the theoretical results for CS and CS-PKS that the reconstruction error is upper bounded by a linear function of measurement noise level.
Fig. 10.

The frame-by-frame MSE plots of k-t ISD and k-t FOCUSS at SNR = 30 (scanned data), and 15 (noise added manually) for the 4-coil dataset. The solid lines are for k-t ISD and dotted lines for k-t FOCUSS.
In addition, we also observed that fewer iterations should be used in k-t ISD at low SNRs to prevent the threshold from being too small. This is because a higher threshold is less sensitive to noise and thus reduces false support detections for noisier data.
DISCUSSION
Relationship to Other Methods
Both k-t FOCUSS and the two-step OMP also use support information, but in different ways. In k-t FOCUSS, the temporal DC (f=0) component is predicted as and subtracted during reconstruction (20). If the temporal DC is considered as the known support in x-f space at f=0 and excluded from the cost function, then k-t FOCUSS is equivalent to a single iteration of truncated ℓ1 minimization with partially known support. In essence, the first iteration of the proposed k-t ISD is equivalent to k-t FOCUSS without DC subtraction. Although we find that k-t FOCUSS without DC subtraction can perform better than that with DC subtraction (for example, first iteration of k-t ISD in Fig. 9 is seen to be better than k-t FOCUSS with DC subtraction in Fig.5), further iterations in the proposed k-t ISD still improves the reconstruction. It suggests that the improvement of the proposed k-t ISD over k-t FOCUSS is not simply due to the lack of DC subtraction, but the multiple iterations of truncated ℓ1 minimizations in which the known support is iteratively updated.
In the two-step OMP (22), the OMP algorithm is used twice for the reconstruction of the signal in x-f space and the support is detected iteratively within each OMP step, as well as after the first of the two-steps. However, the detected support sets obtained within each OMP step always increase over iterations, which is not necessarily true for the k-t ISD. This explains why k-t ISD is robust to false detections in x-f space and has a strong self-correcting capability (28). In addition, for the two-step OMP, although the support in x-f space is updated again after the first-step by finding the significant components, method excludes the elements that are known to be insignificant/zero in the second iteration of minimization.. This is in contrast to the proposed k-t ISD, which follows the theoretical principle of CS with partially known support to perform signal reconstruction by excluding the elements that are known to be significant/nonzero in minimization. These differences contribute to the superior performance of k-t ISD over the two-step OMP in dynamic cardiac cine MRI.
Computational Complexity
The proposed k-t ISD typically requires two nested iteration loops. The outer loop (step 2 in Algorithm 1) is for support detection based on the outcome of truncated ℓ1 minimization. An inner loop is within the FOCUSS algorithm (step b in Algorithm 1) to approximate the solution to the ℓ1 minimization through iteratively reweighted ℓ2 minimization. In general, at most 4 iterations for the outer loop and 3 iterations for the inner loop are sufficient to achieve good performance empirically. When we ran our MATLAB programs on a Hewlett-Packard workstation with Xeon 2.33GHz CPU and 2GB RAM, each outer iteration took about 154s to reconstruct a series of 256 × 220 × 25 dynamic complex MR images. This execution time of a single outer iteration is comparable to the time of 143s for k-t FOCUSS for the same dataset. Although the computational complexity of k-t ISD is higher than that of the basic CS algorithms such as k-t FOCUSS, due to solving a truncated ℓ1 minimization problem repeatedly, the number of iterations is usually small (≤4).
Empirical Support Knowledge
The k-t ISD is more effective when the signal in x-f space has a fast decaying rate. Otherwise, a rectangle window at the center of x-f space (entire FOV but low temporal-frequency locations) can be assumed as the known support (9, 37). This is based on the fact that the low temporal-frequency region usually has significant values in dynamic MRI, as observed in the “true” support map in Fig. 7. The quality of signal reconstruction largely depends on the width of the support window. A small width guarantees inclusion of the true support, but may also miss a good portion of the true support. On the other hand, a large width would include locations outside the true support. Both can lead to degraded reconstructions. The choice of width was studied in (37) and performance comparable to that of k-t ISD can be achieved when the width is selected properly.
Extensions
Although in this work we have tested k-t ISD using only dynamic cine MRI data, the framework is expected to be useful in other dynamic imaging applications, such as dynamic contrast-enhanced (DCE) MRI (17, 18, 38), dynamic MR angiography, and functional MRI (fMRI) to improve the spatio-temporal resolution. The specific procedure should be application dependent in order to accommodate the unique characteristics of the signals in each application. For instance, in order to use iterative support detection, the requirement of a large decay rate needs to be satisfied for the signal in the domain of sparse representation. However, the x-f space of the fMRI images might not have a large decay rate. In this case, Karhunen-Loeve transform (KLT) or principal component analysis (PCA) (39) may be preferred as the sparsifying transform (20) to meet the fast-decay requirement.
It is also applicable to non-Cartesian trajectories such as radial trajectory by incorporating regridding (40, 41) or nonuniform FFT (42). An interesting direction for future work is to investigate truncated ℓp(p <1) minimization for CS-PKS to further reduce sampling requirements in dynamic MRI. In addition, optimization of sampling pattern as a function of cardiac phase is interesting and may be investigated in our future study.
The proposed k-t ISD can be easily integrated with parallel imaging using sensitivity encoding to further reduce data acquisition (43). There are two ways to conduct this integration. One commonly used way is to simply replace Fourier encoding matrix F in Eq.[5] with sensitivity encoding matrix which consists of both Fourier encoding and sensitivity weighting (22).
| [16] |
where is the undersampled data from all channels. This kind of integration can deal with any trajectory. However, the major issue is that the incoherence between the sensitivity encoding matrix and any sparsifying basis such as the identity or wavelet has not yet been explored. In our previous work (26), we have integrated Cartesian SENSE and compressed sensing in a cascade manner without compromising the incoherence requirement. This method can be easily incorporated in k-t ISD with Cartesian trajectory. In this case, Eq.[5] is used to reconstruct the aliased images in x-f domain for each channel and Cartesian SENSE is applied to get the image with full FOV:
| [17] |
where is the aliased image in x-f domain at jth coil, and dj is the undersampled data at jth coil.
CONCLUSION
In this paper, we have demonstrated the support information improves the CS reconstruction in dynamic cardiac cine imaging. A method named k-t ISD is developed. This method iteratively learns and exploits the support knowledge in x-f space to improve CS reconstruction. The learned support is incorporated in CS reconstruction by excluding part of the signal at the known support from the cost function in the constrained minimization process. The method is shown to accurately detect the support in the x-f space through iterations and also converge fast. Experiments using dynamic cardiac cine data show that the proposed method is able to suppress more artifacts and preserve more details of dynamic images and more temporal variations than existing CS methods such as OMP and k-t FOCUSS.
Acknowledgments
This work was supported in part by the UWM Research Foundation Research Fellow Awards to Liang, the National Science Foundation CBET-0846514 and a grant from The Lynde and Harry Bradley Foundation to Ying, and the National Institute of Health EB00615 to DiBella. The authors would like to thank Jong Chul Ye for making available the in vivo data set and k-t FOCUSS code at http://bisp.kaist.ac.kr/research_02.htm and the anonymous reviewers for their helpful comments.
References
- 1.Liang ZP, Lauterbur PC. An efficient method for dynamic magnetic resonance imaging, IEEE Trans Med Imaging. 1994;13(4):677–686. doi: 10.1109/42.363100. [DOI] [PubMed] [Google Scholar]
- 2.van Vaals JJ, Brummer ME, Dixon WT, Tuithof HH, Engels H, Nelson RC, Gerety BM, Chezmar JL, den Boer JA. “Keyhole” method for accelerating imaging of contrast agent uptake. J Magn Reson Imaging. 1993;3(4):671–675. doi: 10.1002/jmri.1880030419. [DOI] [PubMed] [Google Scholar]
- 3.Riederer SJ, Tasciyan T, Farzaneh F, Lee JN, Wright RC, Herfkens RJ. MR fluoroscopy: technical feasibility. Magn Reson Med. 1988;8(1):1–15. doi: 10.1002/mrm.1910080102. [DOI] [PubMed] [Google Scholar]
- 4.Madore B, Glover GH, Pelc NJ. Unaliasing by Fourier-encoding the overlaps using the temporal dimension (UNFOLD), applied to cardiac imaging and fMRI. Magn Reson Med. 1999;42(5):813–828. doi: 10.1002/(sici)1522-2594(199911)42:5<813::aid-mrm1>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 5.Liang ZP. Spatiotemporal imaging with partially separable functions; Proceedings of 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro; Washington DC. 2007. pp. 988–991. [Google Scholar]
- 6.Brinegar C, Wu L YJ, Foley LM, Hitchens TK, Ye Q, Ho C, Liang ZP. Real-time cardiac MRI without triggering, gating or breath holding; Proceedings of the 30th Annual International Conference of the IEEE EMBS; Vancouver, Canada. 2008. pp. 3381–3384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brinegar C, Zhang H, Wu L YJ, Foley LM, Hitchens TK, Ye Q, Pocci D, Lam F, Ho C, Liang ZP. Real-time cardiac MRI using prior spatial-spectral information; Proceedings of the 31st Annual International Conference of the IEEE EMBS; Minneapolis, MN. 2009. pp. 4383–4386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sümbül U, Santos JM, Pauly JM. Improved time series reconstruction for dynamic MRI. IEEE Trans Med Imaging. 2009;28(7):1093–1104. doi: 10.1109/TMI.2008.2012030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sümbül U, Santos JM, Pauly JM. A practical acceleration algorithm for real-time imaging. IEEE Trans Med Imaging. 2009;28(12):2042–2051. doi: 10.1109/TMI.2009.2030474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Aggarwal N, Zhao Q, Bresler Y. Spatio-temporal modeling and minimum redundancy adaptive acquisition in dynamic MRI; Proceedings of 1st IEEE International Symposium on Biomedical Imaging: From Nano to Macro; Washington DC. 2002. pp. 737–740. [Google Scholar]
- 11.Aggarwal N, Bandyopadhyay S, Bresler Y. Spatio-temporal modeling and adaptive acquisition for cardiac MRI; Proceedings of 2nd IEEE International Symposium on Biomedical Imaging: From Nano to Macro; Arlington, VA. 2004. pp. 628–631. [Google Scholar]
- 12.Aggarwal N, Bresler Y. Patient-adapted reconstruction and acquisition dynamic imaging method (PARADIGM) for MRI. Inverse Problems. 2008;24(4):045015-1–045015-29. [Google Scholar]
- 13.Tsao J, Boesiger P, Pruessmann KP. k-t BLAST and k-t SENSE: dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magn Reson Med. 2003;50:1031–1042. doi: 10.1002/mrm.10611. [DOI] [PubMed] [Google Scholar]
- 14.Candès EJ, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory. 2006;52(2):489–509. [Google Scholar]
- 15.Donoho D. Compressed sensing. IEEE Trans Inf Theory. 2006;52(4):1289–1306. [Google Scholar]
- 16.Lustig M, Santos JM, Donoho DL, Pauly JM. k-t SPARSE: high frame rate dynamic MRI exploiting spatio-temporal sparsity; Proceedings of the 14th Annual Meeting of ISMRM; Seattle, WA. 2006. p. 2420. [Google Scholar]
- 17.Bilgin A, Trouard TP, Altbach MI, Raghunand N. Three-dimensional compressed sensing for dynamic MRI; Proceedings of the 16th Annual Meeting of ISMRM; Toronto, Canada. 2008. p. 337. [Google Scholar]
- 18.Lang T, Ji J. Accelerating dynamic contrast-enhanced MRI using compressed sensing; Proceedings of the 16th Annual Meeting of ISMRM; Toronto, Canada. 2008. p. 1481. [Google Scholar]
- 19.Fischer A, Breuer F, Blaimer M, Seiberlich N, Jakob PM. Accelerated dynamic imaging by reconstructing sparse differences using compressed sensing; Proceedings of the 16th Annual Meeting of ISMRM; Toronto, Canada. 2008. p. 341. [Google Scholar]
- 20.Jung H, Ye JC, Kim EY. Improved k-t BLAST and k-t SENSE using FOCUSS. Phys Med Biol. 2007;52(11):3201–3226. doi: 10.1088/0031-9155/52/11/018. [DOI] [PubMed] [Google Scholar]
- 21.Jung H, Sung K, Nayak KS, Kim EY, Ye JC. k-t FOCUSS: a general compressed sensing framework for high resolution dynamic MRI. Magn Reson Med. 2009;61(1):103–116. doi: 10.1002/mrm.21757. [DOI] [PubMed] [Google Scholar]
- 22.Gamper U, Boesiger P, Kozerke S. Compressed sensing in dynamic MRI. Magn Reson Med. 2008;59(2):365–373. doi: 10.1002/mrm.21477. [DOI] [PubMed] [Google Scholar]
- 23.Vitanis V, Manka R, Gamper U, Boesiger P, Kozerke S. Compressed sensing cardiac perfusion imaging; Proceedings of the 16th Annual Meeting of ISMRM; Toronto, Canada. 2008. p. 2937. [Google Scholar]
- 24.Lustig M, Donoho DL, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182–1195. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 25.Liang D, Liu B, Wang JJ, Ying L. Accelerating SENSE using compressed sensing. Magn Reson Med. 2009;62(6):1574–1584. doi: 10.1002/mrm.22161. [DOI] [PubMed] [Google Scholar]
- 26.Miosso CJ, von Borries R, Argàez M, Velazquez L, Quintero C, Potes CM. Compressive sensing reconstruction with prior information by iteratively reweighted least-squares. IEEE Trans Signal Process. 2009;57(6):2424–2431. [Google Scholar]
- 27.Jacques L. A short note on compressed sensing with partially known signal support. Signal Process. 2010;90(12):3308–3312. [Google Scholar]
- 28.Wang Y, Yin W. Sparse signal reconstruction via iterative support detection. SIAM J Imaging Science. 2010;3(3):462–491. [Google Scholar]
- 29.Lu W, Vaswani N. Modified basis pursuit denoising (Modified -BPDN) for noisy compressive sensing with partially known support; Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing; Dallas, TX. 2010. pp. 3926–3929. [Google Scholar]
- 30.Vaswani N, Lu W. Modified-CS: Modifying compressive sensing for problems with partially known support; Proceedings of IEEE International Symposium on Information Theory; Seoul, Korea. 2009. pp. 488–492. [Google Scholar]
- 31.Usman M, Batchelor PG. In signal processing with adaptive sparse structured representations (SPARS) Saint-Malo, France: 2009. A quantitative criterion for selecting the optimal sparse representation of dynamic cardiac data in compressed MRI. [Google Scholar]
- 32.Gorodnitsky IF, George JS, Rao BD. Neuromagnetic source imaging with FOCUSS: a recursive weighted minimum norm algorithm. Electroencephalogr Clin Neurophysiol. 1995;95(4):231–251. doi: 10.1016/0013-4694(95)00107-a. [DOI] [PubMed] [Google Scholar]
- 33.Gorodnitsky IF, Rao BD. Sparse signal reconstruction from limited data using FOCUSS: A re-weighted minimum norm algorithm. IEEE Trans Signal Process. 1997;45(3):600–616. [Google Scholar]
- 34.Chong EKP, Zak SH. An Introduction to Optimization. New York: Wiley-Interscience; 1996. [Google Scholar]
- 35.Lustig M, Alley MT, Vasanawala S, Donoho DL, Pauly JM. L1 SPIR-iT: Autocalibrating parallel imaging compressed sensing; Proceedings of the 17th Annual Meeting of ISMRM; Honolulu, HI. 2009. p. 379. [Google Scholar]
- 36.Reykowski A. Tim matrix modes. MAGNETOM Flash. 2005;1(30):80–85. http://www.medical.siemens.com/siemens/en_US/gg_mr_FBAs/files/Articles/Tim/Tim_Matrix_Modes.pdf. [Google Scholar]
- 37.Liang D, Ying L. Compressed-Sensing Dynamic MR Imaging with Partially Known Support; Proceedings of the 32nd Annual International Conference of the IEEE EMBS; Buenos Aires, Argentina. 2010. pp. 2829–2832. [DOI] [PubMed] [Google Scholar]
- 38.Chen L, Schabel MC, DiBella EV. Reconstruction of dynamic contrast enhanced magnetic resonance imaging of the breast with temporal constraints. Magn Reson Imaging. 2010;28(5):637–645. doi: 10.1016/j.mri.2010.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Poor HV. An Introduction to Signal Detection and Estimation. 2nd. New York: Springer; 1994. [Google Scholar]
- 40.Jackson JI, Meyer CH, Nishimura DG, Macovski A. Selection of a convolution function for Fourier inversion using gridding. IEEE Trans Med Imaging. 1991;10(3):473–478. doi: 10.1109/42.97598. [DOI] [PubMed] [Google Scholar]
- 41.Beatty P, Nishimura D, Pauly JM. Rapid gridding reconstruction with a minimal oversampling ratio. IEEE Trans Med Imaging. 2005;24(6):799–808. doi: 10.1109/TMI.2005.848376. [DOI] [PubMed] [Google Scholar]
- 42.Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans Signal Process. 2003;51(2):560–574. [Google Scholar]
- 43.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]


