Abstract
Although adhesive interactions between cells and nanostructured interfaces have been studied extensively1–6, there is a paucity of data on how nanostructured interfaces repel cells by directing cell migration and cell-colony organization. Here, by using multiphoton ablation lithography7 to pattern surfaces with nanoscale craters of various aspect ratios and pitches, we show that the surfaces altered the cells’ focal-adhesion size and distribution, thus affecting cell morphology, migration and ultimately localization. We also show that nanocrater pitch can disrupt the formation of mature focal adhesions to favour the migration of cells toward higher-pitched regions, which present increased planar area for the formation of stable focal adhesions. Moreover, by designing surfaces with variable pitch but constant nanocrater dimensions, we were able to create circular and striped cellular patterns. Our surface-patterning approach, which does not involve chemical treatments and can be applied to various materials, represents a simple method to control cell behaviour on surfaces.
Attempts to control cell behavior at cell-material interfaces have employed surface chemical and physical properties, such as surface chemistry8–11, topography3–6,12–15, stiffness16,17, and combinations of these properties18,19. Regarding topographical cues, it is well known that interfaces with nanoscale and microscale topographical features strongly modulate cell behavior including adhesion3,4,12, migration13,14, proliferation15 and differentiation5,6. Although topographical cues on the microscale have been shown to be powerful to control cell behavior, they are limited by the inability to independently control physical inputs to cells on the length scale of focal contacts (e.g., ~ 100–200 nm depending on maturity). Furthermore, it is recognized that the extracellular matrix surrounding cells possesses complex nanoscale topographic features20. Despite over a decade of intense research addressing the interaction between cells and nanotopography, nanotopographical interface design to control cell migration has not been extensive studied, mainly due to the limitations of fabrication processes.
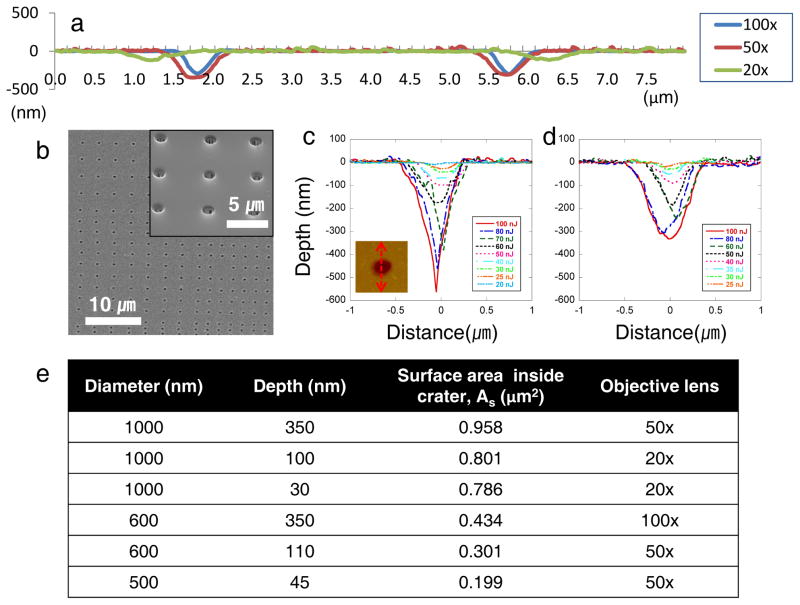
The present study uses multiphoton ablation lithography to create spacing-gradient nanocrater patterned interfaces that control focal adhesion formation and cell migration, rendering surfaces cell repellant under specific conditions. We fabricated nanoscale topographical patterns by exploiting the optical breakdown of dielectric materials induced by femtosecond laser pulses (Supplementary Fig. S1). Intense femtosecond laser pulses can incur damage in transparent dielectrics through nonlinear absorption processes such as multiphoton initiated avalanche ionization21. The femtosecond laser induced ablation process is stable and reproducible, since there is no heat exchange during the femtosecond laser pulse irradiation (~100 fs), minimizing thermal stress and collateral damage. We fabricated nanometer length scale features in quartz with various aspect ratios (depth versus diameter) by adjusting the pulse energies and focusing with objective lenses of different numerical apertures (N.A.) (Fig. 1a,e). For quartz samples, there was no evidence of melting or capillarity assisted material movement around the periphery of the crater, since thermal exposure was minimized during the short pulse regime (Fig. 1b,c,d). This attribute allowed us to fabricate nanocraters in quartz without the addition of a rim of material surrounding the ablated areas. Minimizing positive topography allowed our cell studies to eliminate roughness effects on their cell mechanobehavior.
Figure 1.
Nanoscale craters were fabricated by direct-write laser ablation lithography. a, AFM contour scans presenting cross sectional images for three different nanocrater dimensions fabricated by 100×, 50×, and 20× objective lenses. There was no evidence of melting or capillarity assisted material movement around the periphery of the crater, since the thermal process exposure was minimized over the short pulse regime. Depending on magnitude of the objective lens, different aspect ratio nanocraters were achieved. b, SEM image of the patterned craters. The inset shows an enlarged patterned surface. c, Cross sectional profiles at the center-line of the ablated nanocraters depending on pulse energies using the 100× objective. Inset image is an AFM top view of a crater showing sectioning line. d, Cross sectional profile of the nanocraters by the 50× objective. e, Dimensions of nanocraters for creating the gradient patterns. Six different dimensions of nanocrater gradient patterns were fabricated by using 100×, 50× and 20× objective lenses. The surface area inside crater was calculated based on diameter and depth with assuming the craters are conical shape.
Features and spatial distribution of the nanoscale craters in quartz affected cell morphology, migration, and spatial organization. We observed cellular (NIH3T3 fibroblast) adhesion and spreading on isometric patterned surfaces with craters of 1 μm in diameter, 350 nm in depth, and 2, 4 and 8 μm pitch of nanocraters (Supplementary Figs. S2, S3). After cells were allowed time to migrate, areas of low pitch exhibit smaller cell densities than larger pitched nanocrater surfaces or unablated areas. Cells on the smaller pitched surfaces also appeared refractile and weakly attached (Supplementary Fig. S3). Furthermore, the morphology and focal adhesion distribution was altered for cells depending on pattern pitch, where cells on surfaces with the smaller pitches had decreased and less pronounced focal adhesions that were primarily distributed at either the leading or trail edge of the cell. These cells also appeared to have a greater degree of polarization and fewer multiaxial protrusions.
We further compared the repellant efficiency of the isometric striped patterns with a stripe with a spacing-gradient. When cells were cultured on multiple arrays of nanoscale topographical patterns with 800-nm diameter and 300-nm depth nanocraters, they moved away from the patterned surfaces and migrated towards planar areas, forming “lines” of cell colonies between the patterned zones (Fig. 2a and Supplementary Movie S1). Since the width of the patterned area was 160 μm, cells on the patterned zones can interrogate the planar surface during random directional migration. Once the cells sensed the planar surface, they tended to translocate their body on the new regions. On the spacing-gradient patterns, the cell-repelling effect was more pronounced (Fig. 2b), since the cells migrated towards larger pitch areas, i.e. from the center to the periphery of the patterned lines, which provided the cells greater probability to contact the “nanocrater-free” surface. Most of the cells on the spacing-gradient pattern migrated towards borders without dramatically shifting their migration direction (Supplementary Fig. S4).
Figure 2.
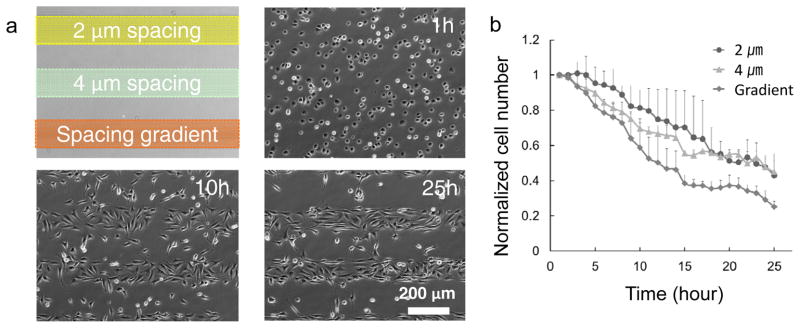
a, Time-lapse phase-contrast images of NIH3T3 cells cultured on isometric pitch (2 and 4 μm) patterns and a spacing-gradient (2, 3, and 4 μm) pattern with 800-nm diameter and 300-nm depth nanocraters. b, A plot of the normalized cell number (cell number/initial cell number) shows the repellent effect of each pattern. After 25 hours from the cell seeding, the normalized cell numbers are 0.43±0.08 (normalized value ± standard deviation, for 2-μm spacing pattern), 0.45±0.10 (for 4-μm spacing pattern), and 0.25±0.03 (for spacing-gradient pattern), respectively. The normalized cell numbers of 2-μm and 4-μm spacing patterns were similar; however, the cell number of the spacing-gradient pattern was 55% of those values.
We next prepared a different spacing-gradient pattern of nanoscale craters in quartz (Supplementary Fig. S5), and subsequently observed cell morphology, migration, and spatial organization (Fig. 3). The distance between nanocraters varied between 1 and 10 μm (i.e., pitch), and each patterned area with the same pitch was approximately 20 ~ 40-μm wide. Hence, attached cells can spread and subsequently sense the neighboring crater features with differential pitch. The spacing-gradient pattern effectively guided cell migration and created cell repellant interfaces. By spatially defining nanocrater patterns over a large substrate area, cells migrated to avoid areas of the surface with high nanocrater density, i.e. small pitch (Supplemental Movies S2–S4). High densities of the nanocraters perturbed the coordination of leading edge protrusion, cell body translocation, and trailing edge retraction during migration. Cells on the small pitch regions therefore migrate to regions of the surface where normal two-dimensional coordination of these events can occur.
Figure 3.

Time-lapse phase-contrast images of NIH3T3 cells cultured on a patterned surface. a, Schematic diagram showing the full pattern design representing the pitch gradient. The distance between features varied between 1 and 10 μm, detailed dimensions are shown in Supplementary Fig. S5. The gradient was patterned on an area of 700 × 700 μm2 with crater diameter and depth of 1000 nm and 350 nm, respectively. b, At 1hr most cells are able to attach to the surface and spread even on the 1~2 μm spacing patterned area. c–f, However, the cells tend to migrate towards regions with greater pitch between the nanocraters. One day after cell seeding, clear boundary lines define a cell repellent region.
To understand how the nanoscale interface affects cell patterning, we fabricated six different nanoscale topographical patterns using 100×, 50× and 20× objective lenses (Fig. 1e). At the early stage of cell spreading, within 1~2 hours after cell seeding, no significant difference was observed between patterned and the non-patterned surfaces, even though cells at the center of spacing-gradient patterns did not spread compared to cells at the perimeter. However, approximately 5 hours after cell seeding, the cell density at the center of the pattern decreased, an observation that was most pronounced for the larger diameter nanocraters (1000 nm in diameter and 350 nm in depth). After 10 hours, cells clearly migrated from the highest density of nanocraters, small pitch, creating a region on the surface that repelled cell colonization (Supplementary Movies S2–S4). After 25 hours, the formed boundary lines of the repellent region did not show significant changes.
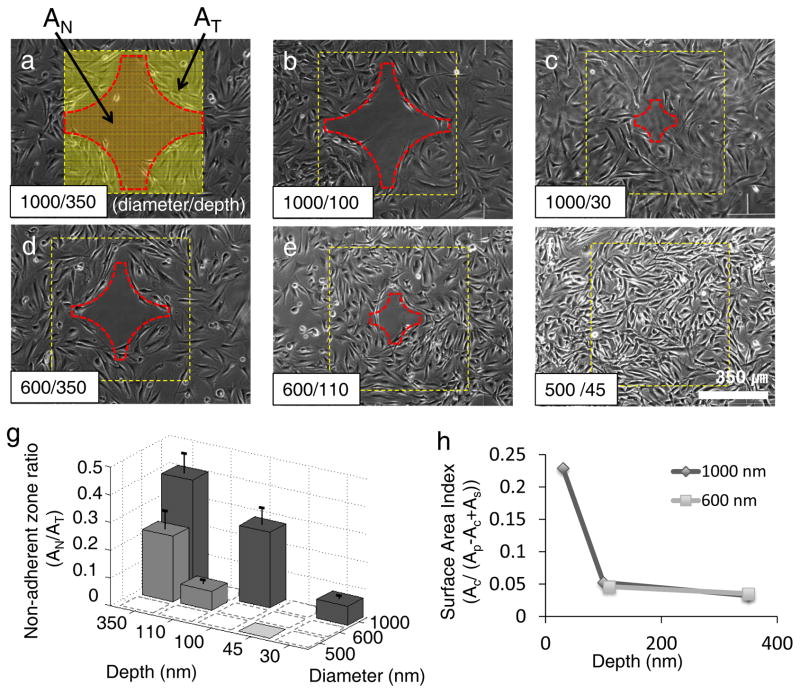
The nanocraters’ depth and diameter affected the area of the cell repellent zone: the area increased with larger craters and decreased with the smaller features (Fig. 4). Guided migration, and ultimately cell repellence, was not observed for the smallest patterns of 500/45 nm in diameter/depth (Fig. 4f). For quantitative analysis, we defined a “non-adherent zone ratio” representing the area of cell repelling zone (AN) to the total area of spacing-gradient patterns (AT) (Fig. 4a). The non-adherent zone ratio decreased with decreasing depth and diameter (Fig. 4g). Within nanocraters of constant diameter, the deeper craters had significantly greater areas of the surface that repelled cells.
Figure 4.
Effect of nanocrater size on cell migration and formation of a cell repellant zone. a–f, Phase-contrast images of cell migration 25 hours after cell seeding on spacing-gradient patterns with 6 different nanocrater dimensions (diameter nm/ depth nm): 1000/350, 1000/100, 1000/30, 600/350, 600/110 and 500/45. The squares represent the patterned region, and the cross medal shaped region at the center of the patterned area represents the cell repellant zone. The area of the repelling zone was dependent on the nanocrater dimensions. Clear boundary lines of the repellent region formed for all samples except f, the sample of 500 nm in diameter and 45 nm in depth. g, Non-adherent zone ratio was defined as “the area of repelling zone (AN) / the total area of patterned surface (AT) (See Fig. 4a).” The non-adherent zone ratio decreased with decreasing nanocrater diameter and depth. Dashed-line squares mean no experimental data, and error bars represent standard deviations of repeated experiments. h, Surface Area Index (SAI) is defined as a ratio of the crater area versus surface area (Ac/(Ap-Ac+As) at the boundary of cell-adhesion repellent zone (See Supplementary Fig. S6). The SAI changes depending on crater depth: increasing with increasing depth. However, nanocrater diameters above 600 nm do not show significant differences in SAI depending.
To determine the effect of the nanocrater dimension on the cell repellant region of the spacing-gradient patterns, we also defined a “Surface Area Index” (SAI) as the ratio of crater area versus exposed surface area (i.e., the area of a crater opening (AC) / (area of a unit plane surface (AP) - area of a crater opening (AC) + surface area inside the crater (As)) from images taken 25 hours after cell seeding (Supplementary Fig. S6). The boundary line of the repelling zone resembles an arc. Along this arc, the ratios of planar surface versus nanocraters area are constant (Supplementary Fig. S7), which shows that the repelling effect from the nanocraters is independent of the distribution of the planar surface. The SAIs at the repellent boundary depends on the depth of the craters (Fig. 4h), suggesting a critical depth for the bottom of the crater to be inaccessible for cellular interrogation. For example, the critical SAIs for 350-nm deep patterns with 1000- and 600-nm diameters were 0.033 and 0.035, respectively, while the critical SAIs for 100-nm deep and 1000-nm diameter patterns and 110-nm deep and 600-nm diameters were approximately 0.052 and 0.046, respectively. The 1000- and 600-nm diameter patterns with 350-nm depth had similar SAIs (Fig. 4h), but yielded a large difference in the non-adherent zone ratio (Fig. 4g). These observations support the hypothesis craters of a critical depth, i.e. ~100 nm in this study, prevent cells from reaching the crater bottom to form stable focal adhesions.
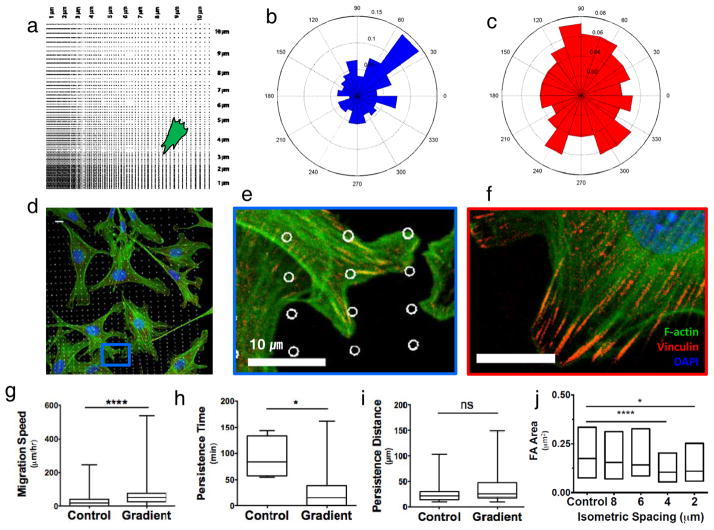
We hypothesized that the nanocraters disrupt formation of mature focal adhesions and encourage cell migration to regions that allow more and larger two-dimensional focal adhesions (Fig. 5e,f and Supplementary Fig. S3). To characterize the cell migration on the spacing-gradient pattern, we calculated directionality, migration speed, persistence time, and persistence distance. By separating the spacing-gradient pattern (Supplementary Fig. S5) into four quadrants based on the patterned lines of 1-μm spacing, the upper-right quadrant can represent the other three quadrants (Fig. 5a). The cells on the patterned surface tend to migrate toward to favorable regions of larger pitch patterns from smaller pitch patterns. Specifically, near 45° the directionality shows higher frequency than that of other angles (Fig. 5b), while cells on planar surface do not show preferential migration (Fig. 5c). Focal adhesions of the cells located on small pitch area or near the nanocraters look nascent, while elongated and mature focal adhesions were observed on non-ablated controls (Fig. 5d–f). Regarding cell migration speed, cells on the spacing-gradient pattern showed significantly higher migration speed compared to those on the non-ablated surface (p≤0.0001) (Fig. 5g). Comparing the persistence time, cells on the non-ablated pattern shows longer persistence time than cells on the gradient-spacing pattern (Fig. 5h). In contrast to this, persistent distance wasn’t significant for the conditions tested (Fig. 5i). Finally, we quantified focal adhesion maturity by the focal adhesion size, which moderately predicts cell speed and persistence22. Cells were seeded on both gradient and isometric patterns with 2, 4, 6, and 8-μm spacing. After 1 hour of cell seeding, cells were able to form focal adhesions and spread on all patterns, but on 4-μm (p≤0.0001) and 2-μm (p≤0.05) spacing patterns the focal adhesion area was significantly smaller (Fig. 5j).
Figure 5.
Focal adhesion size distribution correlates with migration descriptors. a, Schematic showing approximate location of representative immunofluorescence staining. b, The angular graph on the right shows a higher frequency of migration direction at 45°±15. c, The angular graph shows no preferential migration directionality on unablated regions. d, Immunofluorescence image of cells on spacing-gradient pattern coated with fibronectin fixed 1 hour after seeding. e, Blue inset from d showing small focal adhesions imaged through vinculin staining. f, On unablated control substrates, cells are able to form large focal adhesions. g, Migration speed is significantly higher on gradient patterns, h, whereas persistence time was significantly smaller, and i, persistence distance is not significantly different (non-parametric T-test). j, Focal adhesion interquartile distributions on 4μm and 2μm isometrically spaced patterns were significantly different from the unablated control, but 8μm and 6μm showed focal adhesion distributions similar to control samples. Cells were fixed after 1 hour seeding. ns =p>0.05,*p≤0.05,**p≤0.01, ***p≤0.001, ****p≤0.0001 (Kruskal-Wallis). F-actin in green, Vinculin in red, DAPI in blue.
To test if integrin activation could re-stabilize focal adhesion formation disrupted by patterned nanocraters, cells were transfected with DNA plasmids encoded with Talin-1(405)/GFP. Talin is a focal adhesion protein that regulates integrin affinity for ligands in the extracellular matrix (ECM) during cell adhesion, migration, and assembly23. The first 405 N-terminal amino acids of Talin-1 are sufficient to activate both the α5β1 and α5β3 integrins 24. Cells overexpressing Talin-1(405) are capable of forming stable and mature focal adhesions with a smaller adhesive pad area compared to wild type cells through Talin’s ability to increase integrin affinity for adhesion ligands25. Cells transfected with Talin-1(405)/GFP overcame the 4-μm pattern disruption and exhibited focal adhesion size distributions similar to unpatterned control samples (Supplemental Fig. S8). Most important, the Talin-1(405) transfected cells on a spacing-gradient pattern do not show any directional migration, and have larger focal adhesion areas compared to their respective wild type controls (Supplemental Fig. S9), suggesting cell patterning is critically dependent on cell migration.
To explore the effect of cell migration on cell patterning in more detail, cells were treated with the small molecule inhibitor blebbistatin, which has high affinity to myosin II and hinders binding of myosin II to actin. This interference of binding results in inhibition of myosin II contractility and cell migration26. In the presence of blebbistatin, dendritic extensions appeared with deficient stress fibers and focal adhesions, resulting in lower cell motility, and directional cell migration was not observed (Supplemental Fig. S10).
To demonstrate the generality of our observations, we also evaluated the directional cell migration with another substrate that is widely used for cell culture, tissue culture polystyrene (TCPS). Using the same fabrication technique as for quartz, similar nanocraters were fabricated in TCPS. The polymer-laser interactions, however, complicated thermal absorption processes. Atomic force microscopy (AFM) revealed a rim of ablated material surrounding the craters that was not formed on quartz substrates (Supplementary Fig. S11). Although we did minimize the rim dimensions, it was not possible to prevent it entirely leading to some deviations of the cell behavior compared to quartz. However, we were able to successfully reproduce the cell repellant effect on the patterned TCPS (Supplementary Fig. S12). To investigate cell behavior on the patterned TCPS, we again used immunofluorescence staining of vinculin to characterize focal adhesion size on isometric patterns (Supplementary Fig. S13). Focal adhesions located on 2-μm pitch isometric pattern were distributed at the leading and trailing edges of cells, and appeared less mature compare to those on larger pitch patterns. These results are similar to those in Figure 5 for quartz surfaces, but the 2-μm pitch patterns on TCPS seem more mature, which we attribute to surface topography of a rim formed during laser ablation (Supplementary Fig. S11). To characterize the protein adsorption to both surfaces, we performed quartz crystal microbalance with dissipation monitoring (QCM-D) experiments. The protein adsorption studies to quartz and model TCPS surfaces (e.g., oxidized polystyrene) did not show pronounced differences in the adsorption kinetics or total mass for fibronectin (Supplementary Fig. S14).
Our results suggest that nanocrater patterns can be effectively designed to generate cell repellant interfaces and induce guided cell migration into a desired shape or area. The spacing-gradient patterns can provide stable and external stimuli to cells in order to control their migration, and can be easily fabricated compared to other gradient stimuli platforms for directional cell migration (i.e. chemotaxis27, durotaxis16 and haptotaxis28). We could exploit the induced migration phenomenon to demonstrate the formation of cell colonies of different shapes. We demonstrated the organization of cell colonies in shapes of not only parallel lines (Supplementary Fig. S15), but also “circular” cell patterns (Supplementary Fig. S16; Supplementary Movie S5).
The nanocrater patterning by direct-write laser nanofabrication technique is of general applicability and amenable to fabrication on any biomaterial such as glass, ceramics, metals, and polymers, and even onto complex geometries under ambient processing conditions. We conclude that the cell repellant effect is dependent on disrupting focal adhesion maturation, and this observation is robust and generic, but can be influenced by the surface topography surrounding the nanocraters. We anticipate our findings will be useful for surface patterning of biomaterials, controlling tissue formation with desired shapes or patterns, and understanding fundamental mechanisms of cell migration and sensing.
Methods
Laser fabrication of nanoscale craters
We used a Ti:Sapphire regeneration amplifier system (Spectra-physics, US) and patterned sub-micrometer scale features by user-designed rastering of the sample across the beam path while applying laser pulses synchronized with the sample translation. The laser ablation experiments were performed in ambient air using the amplified Ti: Sapphire femtosecond laser with 100 fs pulse length [at full width half maximum (FWHM)] and a wavelength of ~400 nm that was obtained by frequency-doubling a fundamental 800 nm wavelength laser beam using a nonlinear crystal. The experimental apparatus is shown in Figure S1. We adjusted the laser fluence with an attenuator comprised of a half wave plate (λ/2) and a polarizing beam splitter (PBS). As the laser pulse energy required to ablate high-resolution features is extremely low, we inserted a neutral density (ND) filter into the beam path. To generate user-designed patterns, we loaded samples on a precise three-dimensional motorized stage with a synchronized laser firing system controlled by a programmable computer. The scanning stage (ANT130, Aerotech Inc., US) was driven by its own driver (NDrive ML) and software (A3200, Aerotech Inc., US) controlled by a computer. The driver has digital input and output ports that can generate TTL signal configured by the software. The sample was precisely aligned perpendicular to the incident laser beam by adjusting the tilting angle of the sample. To fabricate various aspect ratio nano-craters, we used long working distance objective lenses with three different numerical aperture sizes: 20× Mitutoyo M Plan Apo (N.A.= 0.45), 50× Mitutoyo M Plan Apo (N.A.= 0.55) and 100× Nikon CFI 60 LU Plan Epi ELWD Infinity-Corrected (N.A.= 0.8). We ablated bare quartz samples with single pulses using the computer-controlled system. The ablation craters were examined by atomic force microscopy (AFM, Nanoscope IIIa, Bruker) with high aspect ratio tips (Nanosensors, AR5-NCHR, Aspect ratio ≥ 5:1) in tapping mode. To analyze the relationship between the ablated crater dimensions and the laser energy, we generated craters with various energies and scanned a 3×3 μm2 area of the substrate with the AFM. We performed a parametric study with 20×, 50×, and 100× objective lenses. Figure 1c,d shows graphs for 50× and 100× objective lenses. Since the interaction of the laser with TCPS is significantly different from that on quartz, we conducted an independent parametric analysis on TCPS to optimize the laser parameters for fabrication of the nanocraters for this new material. We optimized the laser ablation parameters by changing the laser power and number of laser pulses. For TCPS ablation, the required power for a single laser pulse is significantly lower than for quartz. We used a 50× Mitutoyo M Plan Apo (N.A, = 0.55) to fabricate the small diameter craters on TCPS. The craters were also analyzed using AFM and FEI-scanning electron microscopy (FEI-SEM; Zeiss) (Fig. S11a). The cross-section profiles of ablation pattern were obtained via the AFM software (Nanoscope analysis; Bruker) (Fig. S11b,c). For characterization of the ‘lip’ features adjacent to the crater, we measured their height and FWHM. We observed wider (larger FWHM) and taller lips as the laser power increased, and similarly with increasing number of laser shots (Fig. S11d). To generate nanocraters matching the size on quartz, we used single laser pulses with 3 nJ via 50× objective lens. Thereby, the width and height of the lip was kept relatively small compared to the diameter, depth, and pitch of the craters. We created patterns in TCPS similar to those in the previously studied quartz substrates.
Cell culture sample preparation
Fused silica (fused quartz) glass and TCPS were used as cell culture substrates. For quartz, square pieces with 8 mm by 8 mm dimensions were prepared for the experiment by dicing a 0.5-mm thick 4-inch quartz glass wafer. We cleaned the quartz substrates ultrasonically with acetone for 1 hour before and after ablation processing and with Methanol for 1 hour additionally after the processing. Finally, the substrates were dipped in 70% Ethanol for sterilization and rinsed with buffered saline. Before cell seeding, the samples were coated with 20 μg/mL fibronectin (Sigma Aldrich) in phosphate buffered saline (PBS, Gibco, Invitrogen) for 1 hour, and rinsed with PBS three times. TCPS samples were sonicated in DI water for 30 min after patterning, subsequently exposed to 70% ethanol for 1hr under UV light, and finally dried in 60°C oven for 30 min prior to cell seeding.
Cell culturing and imaging of the cell migration
NIH3T3 cells were maintained in Dulbecco’s Modified Eagle Medium (Gibco Invitrogen), with 10% fetal bovine serum (FBS) (Gibco Invitrogen) and 100 units/ml penicillin (Gibco Invitrogen) in 75-cm2 culturing flask (Corning) at 37 °C and 5% CO2 culture incubator. Before experimentation, confluent cells were detached from the flask through treatment with 0.05% Trypsin-EDTA (Gibco Invitrogen) and seeded onto the patterned substrate in sterile polystyrene well plates with CO2-independent media (Gibco Invitrogen), 10% FBS, 100 units/ml penicillin, and 1% GlutaMAX (Gibco Invitrogen) and placed on an inverted fluorescence microscope (IX71, Olympus) that was covered by a chamber to maintain temperature and humidity. Phase-contrast images were taken every 5 minutes with a digital CCD camera (Retiga 2000R cooled, Qimaging) for about 2–3 days.
Immunofluorescence
Samples were fixed 1 hour and 12 hours post seeding with 4% paraformaldehyde (Santa Cruz Biotech) for 15 minutes. Cell were permeablized using 0.2% Triton X (Sigma) in dPBS. Blocking and fixation were done with a solution of 2% bovine serum albumin (Sigma), 0.3 M glycine (Sigma), 0.2% Tween-20 (Sigma) in dPBS for at least 30 minutes. Samples were incubated with a primary mouse-anti-vinculin antibody (1:200) (Sigma) overnight at 4°C then washed. Anti-mouse 633 secondary (1:100) (molecular probes) and Actistain-555 (1:500) (Cytoskeleton, Inc.) were incubated for 1.5 hours at room temperature then washed. The nucleus was stained with DAPI (Molecular Probes) for 5 minutes and washed. Samples were inverted onto coverslips just before imaging. Images were acquired using the Zeiss 710 Axio-Observer with 40× oil immersion objective. For immunofluorescence imaging of fibroblast cells on TCPS ablation patterns, a 40× water immersion objective was used.
Focal Adhesion Analysis
Vinculin fluorescent images were analyzed using ImageJ to measure focal adhesion size. Vinculin is a focal adhesion protein recruited slightly after initiations of focal adhesion formation. First, background fluorescence was removed by subtracting background with a 4 pixel rolling ball radius. Only cells completely on patterns at the time of fixation were used for measurements. Kruskal-Wallis tests were performed using Graphpad Prism.
Talin over-expression
Over-expression of the first 405 amino acid sequence of the globular N-terminus of Talin-1 was accomplished using the Lonza Nucleofector 2B. GFP/Talin-1(1-405) plasmids described by Bouaouina and others include the entire FERM domain and were shown to over-activate the α5β1 and α5β3 integrins in transfected cells. For each transfection, approximately 10 million cells were suspended in 100 μL of Nucleofector 2 Solution R with 8 μg of plasmid and transfected using program U-030. Immediately after transfection, 500 μL of Dulbecco’s Modified Eagle Medium (ATCC) supplemented with 10% Fetal Calf Serum (ATCC) was added to the cell solution. The sample was then incubated at 37° C for 15 minutes. Cells were gently transferred into culture flasks and seeded at ~90% confluency in normal growth medium. After 24 hours, transfected cells were sorted using flow cytometry for GFP fluorescence. Cells were seeded on patterned samples 48 hours after transfection.
Persistence random walk model
To quantitatively study cell migration we used a persistence random walk model. First, the number of cells in a 160-μm × 2000-μm area of the patterned surface was counted from three independently repeated experiments. For every hour, we calculated the normalized cell number (the number of currently residual cells / the number of initially attached cells) (Fig. 2b). Subsequently, ten or more cells, spatially isolated from each other, were randomly selected for quantitative analysis (15 cells for 2- and 4-μm isometric spacing samples, 10 cells for spacing gradient samples and 20 cells for a control flat surface). Cell migration was examined by cell tracking and fitted using a persistence random walk model as described previously13. From each image, specific cells were tracked and matched, and relative cell displacement (dx and dy) between the matched nuclei centers of the cells were measured for each time step. Trace lines were plotted by connecting the positions of single cells at subsequent time points during migration whereby the initial position of each cell was assigned to a common origin (Fig. S4). From the measured displacements, migration speeds were calculated. For the persistence random walk modeling, mean squared displacement, <d2>, versus time increment was calculated by using the overlapping time interval sample method and averaging all the squared displacements29:
where x and y are the coordinates of each position, and N is the total number of time intervals over the entire cell migration track. Persistent time (P) and random migration coefficient (μ) were obtained by fitting the mean squared displacement data acquired from cell tracking experiments to the following theoretical equation:
where n represents the number of dimensions, which is 2 in this study. Persistent time (P) represents the average time length between drastic changes in the direction of the cell migration. The random motility coefficient (μ) is a quantitative measurement of random migration of the cell population. It is defined as:
with cell speed (S) and the number of dimensions (n). To reduce calculation error, the experimental data for time up to tmax/3 (one third of the entire time period of the cell migration) were used to calculate the values of P and μ since the true path of cell movement cannot be observed at longer time period29,30.
To calculate persistence distances, persistent movement was defined by the migration length exceeding 10 μm before a cell changes direction significantly (over 70°). If the migration distance was shorter than 2 μm between two images, that data was neglected.
Calculation of directionality
To calculate directionality of the cell migration, we took the symmetry of the patterns into account. On the ablated pattern, we defined the center featuring 1 μm spacing as the origin (0, 0) of a Cartesian coordinate system with X- and Y-axis through the symmetry axis of the pattern. Thereby, four quadrants are created featuring bilateral symmetry. In other words, if a cell moves from the center to the left in the 2nd quadrant, it has the same migration properties as a cell moving from the center to the right in the 1st quadrant. Within each quadrant, there is an additional symmetry about the |y|=|x| axis. Hence, we can map the entire pattern on the region between the positive Y-axis and the y=x axis, which we define as a unit region. To calculate the persistent time and distance mapped on this unit region, two position mappings were necessary: First, we replaced the position data with their respective absolute values thereby flipping all quadrants onto the 1st quadrant. Second, we mirrored the resulting position data along the |y|=|x| axis.
Cell migration is composed of persistent and non-persistent migration segments. To calculate directionality of cell, we differentiated between persistent and non-persistent migration, and only considered the persistent motion. By assigning the starting point of the persistent migration segment to the origin (0, 0), we obtained directionality metrics such as the angle between X-axis and persistent migration distance. By normalizing the occurrence frequency of each angle with the total number of persistent segments, we then obtained the angular frequency.
Blebbistatin treatment
To explore the effect of cell migration on cell patterning, cells were treated with 50 μM blebbistatin, which inhibits the binding of myosin II to actin and therefore interferes with myosin II contractility and cell migration. Treatment solutions were prepared by suspending (−)-blebbistatin (Sigma) in dimethyl sulfoxide (Sigma). This solution was added to the cell media immediately after cell seeding.
Quartz Crystal Microbalance with Dissipation (QCM-D)
The adsorption kinetics of fibronectin (bovine, Sigma Aldrich) to TCPS and SiO2 sensor crystals was characterized using the standard flow module of a Q-Sense E1 QCM-D (Biolin Scientific, Sweden). To create the TCPS interfaces, polystyrene sensor crystals were activated by an oxygen plasma treatment (Plasmatic Systems) at 1 Torr and 150 W for 1 min. Adsorption to both SiO2 and TCPS surfaces was determined by recording the frequency shift of the fifth and seventh overtone at 23°C for a fixed time interval (50min). The QCM-D was set up and calibrated in buffer (1X PBS, pH 7.4, flow rate = 100 μl/min). After obtaining a stable signal (Δf = 0), the peristaltic pump was stopped and the protein sample (20 μg/ml in DMEM) was introduced (flow rate = 100 μl/min). 50 min after injection, the sensor was rinsed with 1×PBS for 10 minutes to remove non-specifically-bound protein.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health grants GM085754 and HL096525. We thank Dr. Young Jun Kim of KIST Europe for QCM-D measurements.
Footnotes
Supplementary information is available in the online version of the paper.
Competing financial interests
The authors declare no competing financial interests.
Author contributions
C.P.G., K.E.H. and H.J. conceived and designed the sample fabrication and cell migration experiments; C.P.G. supervised the laser fabrication; K.E.H. supervised the biological experiments and analysis; H.J. and S.K. fabricated the samples, performed the cell adhesion and migration experiments; S.K. and P.L. analyzed cell migration; W.M.R. performed focal adhesion experiments and analysis. H.J. and K.E.H. wrote the manuscript with discussions and improvements from all authors. C.P.G. and K.E.H. designed and funded the study.
References
- 1.Bettinger CJ, Langer R, Borenstein JT. Engineering Substrate Topography at the Micro- and Nanoscale to Control Cell Function. Angewandte Chemie-International Edition. 2009;48:5406–5415. doi: 10.1002/Anie.200805179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Biggs MJP, Richards RG, Dalby MJ. Nanotopographical modification: a regulator of cellular function through focal adhesions. Nanomedicine-Nanotechnology Biology and Medicine. 2010;6:619–633. doi: 10.1016/J.Nano.2010.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Curtis ASG, et al. Cells react to nanoscale order and symmetry in their surroundings. Ieee Transactions on Nanobioscience. 2004;3:61–65. doi: 10.1109/Tnb.2004.824276. [DOI] [PubMed] [Google Scholar]
- 4.Karuri NW, Porri TJ, Albrecht RM, Murphy CJ, Nealey PF. Nano- and microscale holes modulate cell-substrate adhesion, cytoskeletal organization, and -beta 1 integrin localization in SV40 human corneal epithelial cells. Ieee Transactions on Nanobioscience. 2006;5:273–280. doi: 10.1109/Tnb.2006.886570. [DOI] [PubMed] [Google Scholar]
- 5.Dalby MJ, et al. The control of human mesenchymal cell differentiation using nanoscale symmetry and disorder. Nature Materials. 2007;6:997–1003. doi: 10.1038/Nmat2013. [DOI] [PubMed] [Google Scholar]
- 6.McMurray RJ, et al. Nanoscale surfaces for the long-term maintenance of mesenchymal stem cell phenotype and multipotency. Nature Materials. 2011;10:637–644. doi: 10.1038/Nmat3058. [DOI] [PubMed] [Google Scholar]
- 7.Perry MD, et al. Ultrashort-pulse laser machining of dielectric materials. J Appl Phys. 1999;85:6803–6810. doi: 10.1063/1.370197. [DOI] [Google Scholar]
- 8.Jeon H, et al. Chemical Patterning of Ultrathin Polymer Films by Direct-Write Multiphoton Lithography. Journal of the American Chemical Society. 2011;133:6138–6141. doi: 10.1021/ja200313q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tourovskaia A, et al. Micropatterns of chemisorbed cell adhesion-repellent films using oxygen plasma etching and elastomeric masks. Langmuir. 2003;19:4754–4764. doi: 10.1021/La0267948. [DOI] [Google Scholar]
- 10.Keselowsky BG, Collard DM, Garcia AJ. Surface chemistry modulates focal adhesion composition and signaling through changes in integrin binding. Biomaterials. 2004;25:5947–5954. doi: 10.1016/J.Biomaterials.2004.01.062. [DOI] [PubMed] [Google Scholar]
- 11.Chen CS, Mrksich M, Huang S, Whitesides GM, Ingber DE. Geometric control of cell life and death. Science. 1997;276:1425–1428. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
- 12.Park J, et al. TiO(2) Nanotube Surfaces: 15 nm - An Optimal Length Scale of Surface Topography for Cell Adhesion and Differentiation. Small. 2009;5:666–671. doi: 10.1002/Smll.200801476. [DOI] [PubMed] [Google Scholar]
- 13.Jeon H, Hidai H, Hwang DJ, Healy KE, Grigoropoulos CP. The effect of micronscale anisotropic cross patterns on fibroblast migration. Biomaterials. 2010;31:4286–4295. doi: 10.1016/J.Biomaterials.2010.01.103. [DOI] [PubMed] [Google Scholar]
- 14.Doyle A, Wang F, Matsumoto K, Yamada K. One-dimensional topography underlies three-dimensional fibrillar cell migration. The Journal of cell biology. 2009;184:481–490. doi: 10.1083/jcb.200810041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Richert L, et al. Surface nanopatterning to control cell growth. Advanced Materials. 2008;20:1488–1492. doi: 10.1002/Adma.200701428. [DOI] [Google Scholar]
- 16.Discher DE, Janmey P, Wang YL. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. doi: 10.1126/Science.1116995. [DOI] [PubMed] [Google Scholar]
- 17.Engler AJ, Sen S, Sweeney HL, Discher DE. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. doi: 10.1016/J.Cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 18.Le Saux G, Magenau A, Boecking T, Gaus K, Gooding JJ. The Relative Importance of Topography and RGD Ligand Density for Endothelial Cell Adhesion. Plos One. 2011;6:ARTN e21869. doi: 10.1371/journal.pone.0021869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Charest JL, Eliason MT, Garcia AJ, King WP. Combined microscale mechanical topography and chemical patterns on polymer cell culture substrates. Biomaterials. 2006;27:2487–2494. doi: 10.1016/J.Biomaterials.2005.11.022. [DOI] [PubMed] [Google Scholar]
- 20.Stevens MM, George JH. Exploring and engineering the cell surface interface. Science. 2005;310:1135–1138. doi: 10.1126/Science.1106587. [DOI] [PubMed] [Google Scholar]
- 21.Grigoropoulos CP. Transport in Laser Microfabrication: Fundamentals and Applications. Cambridge University Press; 2009. [Google Scholar]
- 22.Kim DH, Wirtz D. Focal adhesion size uniquely predicts cell migration. Faseb J. 2013;27:1351–1361. doi: 10.1096/Fj.12-220160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tadokoro S, et al. Talin binding to integrin beta tails: A final common step in integrin activation. Science. 2003;302:103–106. doi: 10.1126/science.1086652. [DOI] [PubMed] [Google Scholar]
- 24.Bouaouina M, Lad Y, Calderwood DA. The N-terminal domains of talin cooperate with the phosphotyrosine binding-like domain to activate beta 1 and beta 3 integrins. J Biol Chem. 2008;283:6118–6125. doi: 10.1074/jbc.M709527200. [DOI] [PubMed] [Google Scholar]
- 25.Coyer SR, et al. Nanopatterning reveals an ECM area threshold for focal adhesion assembly and force transmission that is regulated by integrin activation and cytoskeleton tension. Journal of Cell Science. 2012;125:5110–5123. doi: 10.1242/Jcs.108035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rhee S, Jiang H, Ho CH, Grinnell F. Microtubule function in fibroblast spreading is modulated according to the tension state of cell-matrix interactions. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:5425–5430. doi: 10.1073/pnas.0608030104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Park S, et al. Motion to form a quorum. Science. 2003;301:188–188. doi: 10.1126/science.1079805. [DOI] [PubMed] [Google Scholar]
- 28.Carter SB. Haptotaxis and mechanism of cell motility. Nature. 1967;213:256. doi: 10.1038/213256a0. [DOI] [PubMed] [Google Scholar]
- 29.Stokes CL, Lauffenburger DA, Williams SK. Migration of individual microvessel endothelial cells stochastic model and parameter measurement. Journal of Cell Science. 1991;99:419–430. doi: 10.1242/jcs.99.2.419. [DOI] [PubMed] [Google Scholar]
- 30.Dimilla PA, Stone JA, Quinn JA, Albelda SM, Lauffenburger DA. Maximal migration of human smooth-muscle cells on fibronectin and type-IV collagen occurs at an intermediate attachment strength. J Cell Biol. 1993;122:729–737. doi: 10.1083/jcb.122.3.729. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.