Structure Alignment of Membrane Proteins: Accuracy of Available Tools and a Consensus Strategy

Abstract

Protein structure alignment methods are used for the detection of evolutionary and functionally related positions in proteins. A wide array of different methods are available, but the choice of the best method is often not apparent to the user. Several studies have assessed the alignment accuracy and consistency of structure alignment methods, but none of these explicitly considered membrane proteins, which are important targets for drug development and have distinct structural features. Here, we compared 13 widely-used pairwise structural alignment methods on a test set of homologous membrane protein structures (called HOMEP3). Each pair of structures was aligned and the corresponding sequence alignment was used to construct homology models. The model accuracy compared to the known structures was assessed using scoring functions not incorporated in the tested structural alignment methods. The analysis shows that fragment-based approaches such as FR-TM-align are the most useful for aligning structures of membrane proteins. Moreover, fragment-based approaches are more suitable for comparison of protein structures that have undergone large conformational changes. Nevertheless, no method was clearly superior to all other methods. Additionally, all methods lack a measure to rate the reliability of a position within a structure alignment. To solve both of these problems, we propose a consensus-type approach, combining alignments from four different methods, namely FR-TM-align, DaliLite, MATT and FATCAT. Agreement between the methods is used to assign confidence values to each position of the alignment. Overall, we conclude that there remains scope for the improvement of structural alignment methods for membrane proteins.

Introduction

The alignment of two protein structures allows for the identification of evolutionarily related protein segments, and helps with the prediction of protein function and the classification and identification of folds. The correct detection and assignment of evolutionarily and functionally homologous residues or fragments is strongly correlated with the accuracy of the method being used, and dozens of methods have been developed in attempts to solve this problem¹. A few studies^2-5 have compared available structural alignment methods on large data sets of water-soluble protein structures, and these studies indicate that no single method outperforms all others. Moreover, none of these studies explicitly considered the classes of integral membrane proteins. Membrane proteins represent ~30 % of genes in a genome^6-8 and constitute the targets for over half of approved drugs⁹. Integral membrane proteins have a number of distinct evolutionary and structural properties from water-soluble proteins as a result of their interaction with the hydrophobic membrane bilayer (see e.g. Refs 10-12). On a global level, this environment limits membrane protein structures to two major folds: α-helical and β-barrel¹³. Their folds are assigned by the Structural Classification of Proteins (SCOP) classification scheme¹⁴ into a distinct class from their water-soluble counterparts. Although it is generally assumed that structure alignment programs that perform well on general protein data sets will also be the most suitable for membrane proteins, to our knowledge no evidence exists to support that assumption. For example, membrane proteins have a higher propensity for secondary structure within the membrane region, which could be an advantage for structure alignment programs such as SKA¹⁵, which focus on aligning secondary structure elements. Some membrane proteins also have lower density packing, due to the intercalation of lipids between helices or due to the presence of pores and pathways¹⁶, which may be an advantage for programs that consider intra-structural distances, such as DALI^17,18. In part, the lack of studies into alignments of membrane protein structures probably reflects the limited availability of structural data, which constitute only ~2% of the entire Protein Data Bank (PDB)¹⁹. However, recent increases in the rate of membrane protein structure determination²⁰ (http://blanco.biomol.uci.edu/mpstruc/) mean that available reference sets are now sufficient to make such comparisons possible.

Here, we update an earlier data set of homologous membrane protein structures²¹ (HOMEP2) compiled in 2010, that includes both α-helical and β-barrel membrane proteins, neither of which has been addressed specifically in previous studies of structure alignments^2-5. We use this dataset to compare the accuracy of 13 different structure alignment methods, focusing on the question of whether the methods find the optimal solution between two structures, rather than the related question of whether they can identify similar folds. For each protein pair, sequence alignments are extracted from the structure alignment outputs. Assuming that residues placed in the same column arise from an ancestral residue, we use these pairwise sequence alignments to build homology models; any two aligned residues will therefore be in the same position in space. The accuracy of the structural alignments is then assessed by calculating the similarity between the model and the known structure using both superposition-dependent and superposition-independent (packing-based) scores. The assessment scores also differ from those optimized in the structural alignment methods.

We find that although no single method outperforms all others, several methods perform well on average. Based on these results, we propose a consensus-based approach for increasing the odds of identifying the most reasonable alignment, which simultaneously provides a confidence score for each position in the alignment.

Materials and Methods

HOMEP3 reference data set

Since the construction of the HOMEP2 data set²¹, over 700 annotations have been added to the PDB_TM database²² of membrane protein structures. Similar to the procedure used to construct HOMEP2, individual membrane protein structure chains were taken from the PDB_TM database^22,23, release date 01 Feb 2013, if their resolution was <3.5 Å. The protein chains were then separated according to their primary fold type (α or β) and the number of membrane spanning segments, according to the TMDET assignments²⁴. Two fast structural alignment methods, SKA¹⁵ and TM-align²⁵, were used to align all pairs of proteins within each group for the purpose of clustering their folds into families. Applying two structural alignment methods with distinct scoring schemes reduces the chances that the clustering of homologous structures is biased by the choice of quality measure or alignment procedure. We followed a relatively conservative strategy for identifying homologs, since we wished to assess the ability of the methods to generate the optimal alignment for proteins that are known to have the same fold, rather than to search for remote relationships. Therefore, all protein pairs with a protein structure distance (PSD) score <1.2 (according to SKA¹⁵) and a TM-score >0.6 (see below, computed using TM-align²⁵) were assigned to a common structural family. When only one of these two criteria was met for a given pair, their alignment was assigned to a family after a manual assessment of the alignment quality. Using this clustering approach, we identified 159 α-helical protein chains in 37 families corresponding to 354 protein pairs (Table S1), plus 68 β-barrels in 8 families corresponding to 319 alignments (Table S2), for a total of 673 alignments. See Fig. 1 for an analysis of the composition of the HOMEP3 data set.

Figure 1. Composition of the HOMEP3 data set of homologous membrane protein structures.

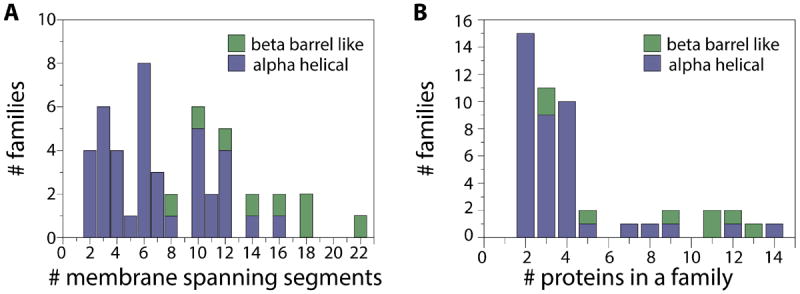
A. Distribution of family size for a given number of membrane-spanning segments for α-helical (blue) and β-barrel proteins (green). B. Distribution of families with different numbers of proteins. Most families of α-helical proteins (blue) contain 2-4 known protein structures, whereas the β-barrel families (green) contain more proteins per family.

Generation of pairwise structural alignments

Thirteen structure alignment methods differing in their superimposition approaches, internal scoring schemes, and handling of flexible regions were tested (see overview in Table I): CE²⁶, SAP^27,28, DaliLite v3.3 ^17,18, SHEBA²⁹, SKA¹⁵, MAMMOTH³⁰, FATCAT^31,32, TM-align²⁵, LovoAlign³³, SABERTOOTH³⁴, FR-TM-align³⁵, MATT³⁶, and PPM³⁷. These methods were all available for local installation, commonly used, and/or previously shown to out-perform other available methods. For each method, pairwise structure alignments were generated for all pairs of proteins within each family of HOMEP3. Because some methods produce different alignments depending on which protein is listed first, alignments were generated using both combinations of each pair of proteins.

Table I.

Overview of pairwise structural alignment methods

Method	aFragments	Score	Alignment
CE	8-residue	RMSD	Combinatorial extension of locally aligned fragment pairs using intra-structural distances
DaliLite	6-residue	Dali	Joins optimally-matched fragments based on Monte Carlo search
FATCAT	8-residue	Σ	Flexible chaining of aligned fragment pairs allowing for twists
FR-TM-align	Y	TM-score	Matching aligned fragment pairs
LovoAlign		STRUCTAL & RMSD	“Low Order Value Optimization” using dynamic programming
MAMMOTH		RMSD	Matching molecular models obtained from theory
Matt	5-8 residue	RMSD	Aligning fragment pairs allowing temporarily for twists and translations
PPM		PPM	Phenotypic plasticity applied to measure the cost of morphing structures
SABERTOOTH			Matching profiles of vectorial representations of two protein structures
SAP		Intra RMSD	Iterated double dynamic programming of matrix of intra-structure residue-residue distance differences
SHEBA			Comparing a list of primary, secondary and tertiary structural profiles
SKA		PSD	Double dynamic programming to align secondary structure alignments
TM-align		TM-score	Optimize intra-structure residue-residue distance matrix using dynamic programming

Methods are listed in alphabetical order. TM-score: template modeling score.

^aFor methods that use fragments in the optimization phase, the fragment length is provided. The DALI score measures the difference between intra-structure residue-residue distances. Methods also differ in the construction of initial alignments, which are then refined to identify better-scoring alignments. Flexible aligners typically use a sum of the similarities of all aligned fragment pairs, to which a penalty is added for each breakage between fragments.

If a method provided a sequence alignment for a given pair then that alignment was used for the subsequent analysis. Otherwise, the underlying sequence alignment was constructed based on the reported assignment of matched residues, with any missing C- or N-terminal residues aligned to gaps. For FATCAT, alignments were generated either using the fragment-based mode, or not, by setting the “–flexible” flag to true or false, respectively.

Evaluation of alignment accuracy

The major challenge in assessing structural alignment accuracy is the lack of a standard score that ranks the quality of structural alignments. Although efforts have been made to address this issue recently³⁸, those strategies are not yet publicly available. Here, we rely on the fact that a homology model built using the ideal alignment should provide sufficient information to reconstruct the structure of the other protein. Thus, for each pair of sequences, each sequence was modeled using the other as a template, and vice versa. Models were generated using five cycles of optimization in Modeller v9.10 ³⁹, and the best of these five models was selected for comparison based on the GDT_TS score of the model relative to the known structure (see below).

Structural Similarity Scores

Assessment of the structural similarity of two protein structures is necessary both for the optimization of structure alignments by the tested methods, as well as in our analysis of the accuracy of the homology models. Here, we describe two common structural similarity measures used in the tested structure alignment methods, namely the root mean squared deviation (RMSD) and TM-score. We then describe four related distance-based model accuracy scores (AL0, AL4, GDT_TS, and GDT_HA), and a packing-based model accuracy score (CAD), which we used for comparing two structures (or models) of the same protein sequence.

RMSD

The RMSD between Cα atom coordinates (ν_i and w_i) of two superimposed structures (of alignment length L_aln) is defined as⁴⁰:

$$\mathit{RMSD}(\nu ,w)=\sqrt{\frac{1}{{\mathit{L}}_{\mathit{aln}}}{{\sum }_{i=1}^{{\mathit{L}}_{\mathit{aln}}}({\nu }_i-w_i)}^2}$$

This score is used as the optimization value in two of the tested methods: CE and SAP. The squaring term makes the RMSD score very sensitive to large local deviations and to differences in the lengths of the template^41,42. Therefore, the RMSD score is most useful for closely related protein structures, but less useful for more distantly related structures, especially if there are regions that have no equivalents, i.e., insertions and deletions. For the comparison in Table II, RMSD values were calculated after a least squares fit of all equivalent Cα atoms, computed using the LGA package⁴³.

Table II.

Correlation between structural similarity scores

		β-barrels
		RMSD	TM-score	GDT_HA	GDT_TS	AL0	AL4	CAD
α-helical proteins	RMSD		-0.48	-0.37	-0.43	-0.44	-0.56	-0.42
	TM-score	-0.60		0.88	0.94	0.96	0.86	0.90
	GDT_HA	-0.60	0.85		0.98	0.93	0.76	0.97
	GDT_TS	-0.57	0.91	0.98		0.98	0.86	0.97
	AL0	-0.60	0.92	0.90	0.96		0.90	0.93
	AL4	-0.67	0.91	0.68	0.79	0.83		0.79
	CAD	-0.56	0.79	0.90	0.90	0.85	0.71

Pearson’s correlation coefficients (PCC) between structural similarity scores were calculated for a set of homology models of β-barrels (upper right), or α-helical proteins (lower left). RMSD and TM-score values are optimized in several of the structure alignment methods, whereas GDT, AL and CAD scores are used for assessment. Entries in bold indicate scores that are highly correlated with each other (PCC >0.9). Note that the RMSD values are negatively correlated with all other scores, because the RMSD has a maximum value of zero, whereas all other scores are inverted and rescaled to have a maximal value of 1.

TM-score

The TM-score⁴⁴, used in the programs TM-align and FR-TM-align, accounts for large outliers by using a distance-dependent weighting scheme:

$$\mathit{TM–score}=\max \left[\frac{1}{L_{\mathit{target}}}{\sum }_i^{{\mathit{L}}_{\mathit{aln}}}\frac{1}{1+{\left(\frac{d_i}{d_0}\right)}^2}\right],$$

where L_target is the number of residues in the target and d_i is the distance between the ith pair of residues. The d₀ term normalizes the match difference to make the TM-score length-independent:

$$d_0=1.24·\sqrt[3]{L_{\mathit{target}}-15}-1.8.$$

The TM-score ranges between 0 (no relationship) and 1 (perfect match).

Distance threshold-based measures

The AL0 ⁴⁵, AL4 ⁴⁶, GDT_TS and GDT_HA scores are all designed to assess the correctness of a homology model, albeit at different levels of precision. None of the structure alignment methods uses these similarity measures for optimization and therefore these scores are not biased toward a particular method. These four scores apply the same assumptions in order to identify the most structurally similar regions between the model and template. Specifically, they assume that the two structures have identical sequences (which is not the case in the structural alignment exercise), and that the similarity between the structures is a function of the largest segments (i.e., the number of Cα atoms), G(c) that can be fitted within a given cut-off distance, c. The identification of those largest similar (and not necessarily continuous) segments involves an iterative superposition procedure carried out using the LGA⁴³ or CAD-score⁴⁷ programs. The iterative procedure starts with a diverse set of initial alternative alignments (i.e., every 3-residue segment, plus the three longest continuously related segments within cut-off distances of 1, 2 and 5 Å), to improve the chances of finding the largest set of similar residues. The AL0 and AL4 scores identify the largest subset of Cα atoms of the model that can be superimposed with the reference structure below a cut-off distance of either 3.8 Å or 10 Å, respectively:

$$\mathit{AL}(\%)=\frac{G(c)}{L_{\mathit{target}}}\times 100.$$

The GDT_TS, or global distance test (total score)⁴³, and GDT_HA (high-accuracy)⁴⁵ scores also identify the number of structurally-equivalent pairs of atoms, but instead use an average over four different cutoff distances:

$$\begin{array}{l}\mathit{GDT}\_\mathit{TS}(\%)=\frac{1}{4}{\sum }_{c=1,2,4,8}\left[\frac{G(c)}{L_{\mathit{target}}}\times 100\right]\mathrm{or}\\ \mathit{GDT}\_\mathit{HA}(\%)=\frac{1}{4}{\sum }_{c=0.5,1,2,4}\left[\frac{G(c)}{L_{\mathit{target}}}\times 100\right].\end{array}$$

Packing-based score

The contact area difference (CAD) score⁴⁷ relies on the computation of residue-residue contact surface areas using Voronoi tessellation, for both the target model (M) and the template reference structure (T). Let G denote the set of pairs of residues (i,j) in the target structure with a non-zero contact surface area, T(_i,j). For the same set of pairs, the contact surface areas are also computed for the model, M_(i,j). The difference in the contact area between the model and the template for that residue pair CAD_(i,j) is computed as:

$$\mathit{CA}{D}_{(i,j)}=\min \left(\left|T_{(i,j)}-M_{(i,j)}\right|,T_{(i,j)}\right),$$

and the CAD-score of the model is defined as:

$$\mathrm{CAD–score}=1-\frac{{\sum }_{(i,j)\in G}\mathit{CA}{D}_{(i,j)}}{{\sum }_{(i,j)\in G}{T}_{(i,j)}}.$$

A CAD-score of 1 indicates that all the residues in the model have the same orientation as in the reference structure, whereas a score of zero indicates that no contacts have been suitably reproduced. Here we use the surface area of all atoms (AA-CAD) based on the results of Olechnovic et al⁴⁷. Note that this score can be computed without requiring a structural superposition.

Ranking of methods

For each of the tested structural similarity measures, each structure alignment method was assigned a mean score, S_mean over the scores S_m of all models m in the set of M models, i.e., all aligned pairs of structures. Subsequently, each method was assigned a rank R_mean (similar to the AR score⁴⁸) based on the value of S_mean. The R_mean ranking therefore reflects the relative overall accuracy of a method.

An alternative ranking called R_reliability (also known as the RA score⁴⁸) was used to identify whether a method produces significant outliers, both positive and negative, compared to the other methods, and therefore provides a measure of its self-consistency. First, for every model m (each alignment pair), the score S_m of the model produced by each method was compared, and each method was given a ranking R_rank based on those scores. These rankings were then averaged over all M models to obtain R_reliability for each method, reflecting the frequency that the method produces an outlier.

Model selection

As mentioned above, for each alignment pair, five models were generated using the Modeller optimization routine. To identify the most reasonable model, we considered the GDT_TS, AL4, and AA-CAD scores relative to the known structure, as well as the DOPE score, which is a statistical energy function. In each case, the selected models were used to compute the R_mean and R_reliability rankings for each method. Comparison of the four scoring schemes indicated that this choice has a minimal effect on the results; R_mean values were identical in 83.7% and 88.9% of cases for α-helical and β-barrel proteins, respectively, and the R_mean rankings for a given method never deviated by more than three positions. Similarly, the R_reliability values were identical in 70.7% and 77.4% of all cases for α-helical and β-barrel proteins, respectively, and also never deviated more than three positions. We therefore selected the best out of the five models according to their GDT_TS scores relative to the known structure.

Consistency

Accurate structural alignment methods should match evolutionarily related positions. Consequently, an attribute of an accurate method is that the alignment denoted AB of a pair of homologs (protein A with protein B) can be deduced from alignments of the two proteins with a third homolog (AC and BC). Based on the alignments AC and BC, an alignment of AB’ can be derived using protein C as a reference sequence. Comparison of each amino acid pair in the derived alignment AB’ with those in the original alignment AB, provides a count of the number of consistent positions. The average self-consistency of the alignment between A and B is then defined as an average over the sum of L_A and L_B. This procedure is repeated for all combinations of A, B and C.

Another potentially interesting metric is the “average shift error” of the inconsistent positions, which is zero for a perfectly consistent set of alignments. In inconsistent positions (i.e., B_i aligned to C_j with j differing between the derived and original alignments: j^derived != j^original), the difference between the aligned positions is calculated: |j^derived - j^original|. Here, we considered only ungapped positions. To obtain the average shift error E(AB∣C) for the alignment AB, relative to AC and BC, the shift error is summed over all inconsistent positions, and divided by the sum of L_A and L_B.

Consensus alignments and confidence scores

Results from four different structure alignment methods were collected and merged using an in-house script. The confidence of each column was computed with the same script according to the degree of consensus between the methods. This script is available from www.bioinfo.mpg.de/AlignMe/download/ConsensusAlignment.zip.

Statistical analysis

Due to the diversity of the HOMEP3 data set²¹, the structural similarity scores of the homology models are not normally distributed. Therefore, we cannot use, for example, a paired Student’s t-test or ANOVA for statistical analysis. Instead, to test whether a given method was statistical significantly better than any of the other methods, we used the non-parametric Wilcoxon signed ranked test⁴⁹; differences were deemed to be significant when p<0.05.

Results

Modeling scores

To facilitate an efficient and effective comparison of the different structure alignment methods, we first analyzed the available approaches for scoring the accuracy of a structural alignment. In our case, that meant comparing the methods for scoring the structural similarity of the alignment-based models to the native structures, namely GDT_HA, GDT_TS, AL0, AL4, and CAD. Specifically, we identified which of these scores contained complementary information, by calculating the Pearson’s correlation coefficient (PCC) between each pair of scores for a test set of models. We also compared those scores with RMSD and TM-score values; however, since RMSD and TM-score are optimized by several of the structural alignment programs, these two scores were not used for assessing accuracy.

The distance-threshold based scores GDT_TS, GDT_HA, AL0 are strongly correlated with one another for both α-helical and β-barrel proteins (Table II, 0.90 < PCC < 0.98), reflecting the fact that all three scores consider short-range similarity, in a length-independent manner. The AL4 score is less well correlated with the other three threshold-dependent scores (0.68 < PCC < 0.90), because the AL4 score also considers long-range differences up to a 10 Å cut-off.

All four threshold-based GDT and AL scores are strongly correlated with the TM-score measure (0.85 < PCC < 0.96), which also uses a threshold, but they are poorly correlated with the RMSD (-0.37 < PCC < -0.67), which does not involve a distance threshold. Therefore, rankings based on GDT or AL scores could potentially be biased toward methods that optimize structure alignments using the TM-score.

The packing-based CAD score is computed without any structural superposition or distance-threshold component (aside from atom contact), and only relies on the consistency between local packing interactions in the two structures. Therefore, any strong correlation between the CAD score and the threshold-based scores should indicate that the latter are good measures of the local similarity of two structures. Interestingly, the CAD scores are better correlated with the threshold-based modeling scores GDT_TS and GDT_HA that focus on highly-accurate positions (< 2Å; 0.90 < PCC < 0.97) than with the AL0 (cut-off of 4 Å) or AL4 score (cut-off of 10 Å), both of which consider longer-range differences (0.71 < PCC < 0.93). Notably, the CAD score is very poorly correlated with the RMSD (PCC ~-0.5), and less well correlated with the TM-score than all other measures tested except the AL4 score (Table II).

Based on these results, we opted to assess the structure alignment methods using only the three least mutually-correlated scores, i.e. GDT_TS, AL4 and CAD, although there may be some overlap between the conclusions according to the CAD and GDT_TS scores.

Fragment-based approaches gave the best overall performance

The top-ranking methods for α-helical membrane proteins were fragment based methods (FR-TM-align, FATCAT, MATT; Table III). Comparison of the results obtained for α-helical proteins using the TM-align and FR-TM-align methods (Table III) clearly demonstrates the increased accuracy obtained by fragmenting the structure, since all other aspects of these methods, including the scoring function, are the same.

Table III.

Ranking of structural alignment methods for the subset of α-helical membrane proteins

Score	Type	FR-TM-align	TM-align	FATCAT rigid	FATCAT	Matt	LovoAlign	SKA	DaliLite	SABERTOOTH	SHEBA	CE	SAP	PPM	MAMMOTH
CADa	Rmean	1	4	3	2	5	8	10	9	7	6	11	12	13	14
	Rreliability	1	2	4	3	8	5	7	6	11	10	12	9	13	14
	mean (%)	63.3	63.3	63.3	63.3	63.3	62.8	62.4	62.7	62.8	62.9	62.3	62.0	60.7	59.7
	stdev (%)	0.08	0.08	0.08	0.08	0.09	0.09	0.09	0.09	0.09	0.09	0.09	0.10	0.09	0.09
AL4	Rmean	2	1	3	6	4	9	5	11	7	10	8	14	12	13
	Rreliability	1	2	4	6	7	5	3	8	10	11	9	12	14	13
	mean (%)	94.8	94.8	94.5	93.9	94.2	93.1	94.2	92.8	93.6	92.9	93.4	90.0	90.9	90.4
	stdev (%)	7.0	6.9	7.2	9.3	8.1	12.9	8.3	11.2	8.3	9.2	8.3	17.0	10.9	14.7
GDT	Rmean	1	2	3	5	4	9	10	8	6	7	11	12	13	14
	Rreliability	1	2	7	8	6	3	4	5	10	11	9	12	13	14
	mean (%)	71.1	71.0	70.6	70.1	70.4	69.5	69.7	69.7	70.0	69.6	69.4	67.2	66.2	63.3
	stdev (%)	14.8	14.8	14.8	16.0	15.8	17.9	16.1	16.5	15.6	15.8	15.9	19.6	16.7	18.4
aveb	Rmean	1.3	2.3	3.0	4.3	4.3	8.7	8.3	9.3	6.7	7.7	10.0	12.7	12.7	13.7
	Rreliability	1.0	2.0	5.0	5.7	7.0	4.3	4.7	6.3	10.3	10.7	10.0	11.0	13.3	13.7

The structural alignment methods are sorted according to the sum of their average R_mean and R_reliability rankings, with the most accurate alignments on the left side of the table. The mean and standard deviation (stdev) of each score over all pairs of alignments are given.

^aCAD score multiplied by 100.

^bMean ranking over all three scores. Entries in bold indicate the highest or best scores in that column and those that are not significantly different from the highest/best score, according to the Wilcoxon signed rank test, with p < 0.05.

Similar results as for the α-helical membrane proteins were obtained for the β-barrels (Table IV). Again, fragment-based approaches (FR-TM-align, FATCAT, DaliLite) were generally ranked higher than methods that apply a rigid superimposition, with FR-TM-align again the best choice among all methods.

Table IV.

Ranking of structural alignment methods for the subset of β-barrel membrane proteins

Score	Type	FR-TM-align	TM-align	DaliLite	FATCAT rigid	FATCAT	MATT	SKA	LovoAlign	SHEBA	SABERTOOTH	CE	PPM	SAP	MAMMOTH
CAD	Rmean	2	4	1	5	3	6	8	9	7	10	11	12	14	13
	Rreliability	1	2	5	3	4	7	6	8	9	10	12	13	11	14
	mean	54.4	54.1	54.4	54.1	54.2	54.1	53.1	52.6	53.6	52.6	51.5	47.5	46.9	47.1
	stdev	0.09	0.10	0.09	0.09	0.09	0.09	0.11	0.11	0.10	0.11	0.11	0.10	0.15	0.11
AL4	Rmean	1	2	4	3	6	5	8	9	7	10	11	12	14	13
	Rreliability	1	2	7	3	5	8	4	6	11	10	9	13	12	14
	mean	90.5	90.1	89.3	89.8	88.9	89.1	87.0	86.1	87.7	85.7	85.7	82.7	66.8	79.9
	stdev	10.5	11.2	11.2	11.0	12.6	11.5	17.6	17.6	12.4	16.9	15.5	14.7	35.9	17.7
GDT_TS	Rmean	1	3	2	4	6	5	8	10	7	9	11	12	14	13
	Rreliability	1	2	3	4	5	6	8	7	10	11	9	13	12	14
	mean	63.9	63.1	63.4	62.9	62.0	62.6	59.5	58.7	61.0	59.0	58.3	50.4	46.1	47.4
	stdev	14.9	15.7	15.3	15.5	16.6	15.9	19.4	20.9	16.4	19.3	19.2	19.0	30.3	20.3
ave.	Rmean	1.3	3.0	2.3	4.0	5.0	5.3	8.0	9.3	7.0	9.7	11.0	12.0	14.0	13.0
	Rreliability	1.0	2.0	5.0	3.3	4.7	7.0	6.0	7.0	10.0	10.3	10.0	13.0	11.7	14.0

See legend to Table III for details.

Length-independent scoring schemes result in better alignments

Aside from the choice of rigid-body or fragment-based fitting, the next most significant characteristic of a structure alignment method is the internal scoring scheme used for selecting the optimal superimposition of the structures. Broadly speaking, the incorporation of scores that down-weight the contribution of incorrectly modeled fragments (e.g., TM-score in TM-align, Dali score in DaliLite) resulted in methods that were more accurate and higher ranking than methods that use a score that squares the differences between the two superimposed structures (e.g., URMS in MAMMOTH, RMSD in CE and SAP; Tables III and IV). The influence of length-dependent scoring on the alignment quality is exemplified by CE, which applies simultaneously a fragment-based approach, that we found to be advantageous, as well as an RMSD score. This results in the least accurate and worst ranked (11^th place) alignments of the fragment-based approaches for both α-helical (Table III) and β-barrel proteins (Table IV).

Interestingly, the Template Modeling score (TM-score) seems to be most useful for aligning α-helical membrane proteins, since both methods that use the TM-score (FR-TM-align and TM-align) were the highest-ranking and most accurate methods for α-helical proteins in general (Table III). This result could in principle reflect a bias because two of the scoring schemes (GDT_TS and AL4) use related threshold-based distance measures. Nevertheless, even when assessed using the CAD score, FR-TM-align and TM-align are ranked among the top four methods for both accuracy and reliability (Tables III and IV).

Finally, the Dali score used in DaliLite appears to be better suited to β-barrel proteins than to α-helical proteins, since its ranking jumps from 8^th to 3^rd position (Tables III and IV). We speculate that this is because the Dali score compares the intra-structural Cα distance matrices of two proteins: the distance matrices of β-barrel proteins are likely to be a distinctive mixture of small and large distances, unlike the matrix of many short distances that would be characteristic of α-helical proteins.

Fragment-based methods are suitable for alternate conformational states of membrane proteins

Some membrane proteins are extremely dynamic, and adopt distinct conformations during their function, for example, during transmembrane transport or signaling. One example in the HOMEP3 data set is the Major Facilitator Superfamily (MFS) of solute transporters, including two structures (PDB codes 1PW4 and 2CFQ) of inward-facing states, and two structures (PDB codes 3OYQ and 4GC0) of outward-facing states. The differences in these states mainly arise from the repositioning of two six-transmembrane-helix domains relative to one another, so as to open a pathway into the membrane from one or other side of the membrane (Fig. 2).

Figure 2. Alternate conformations in the family of major facilitator superfamily transporters.

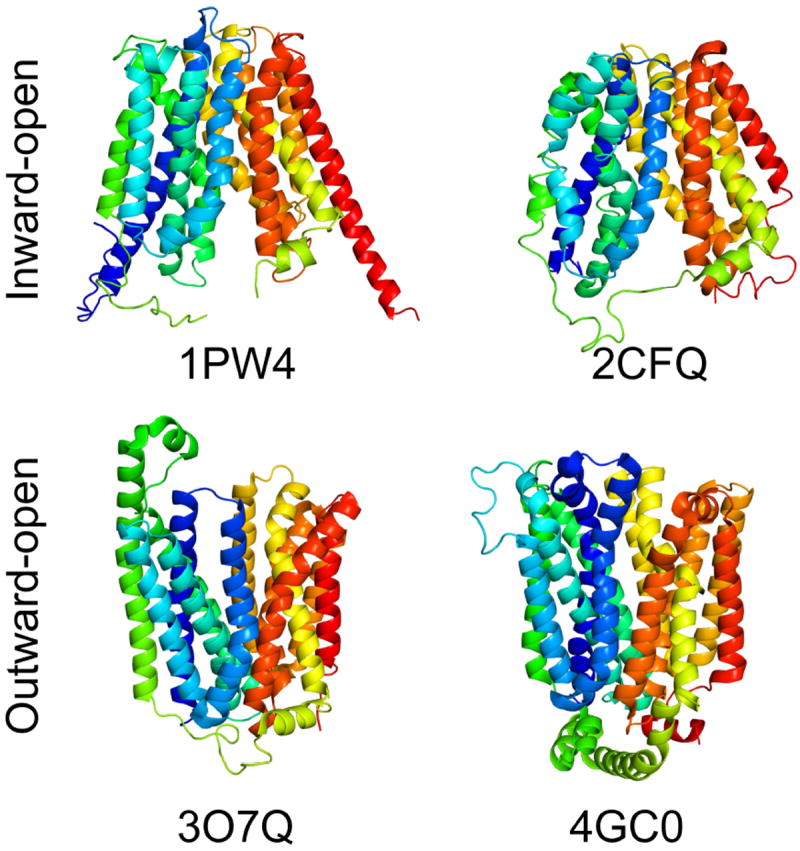
Two structures reflect inward-facing conformations (GlpT and LacY; PDB codes: 1PW4 and 2CFQ) and two reflect outward-facing conformations (FucP and XylE; PDB codes: 3O7Q and 4GC0). The proteins are shown as cartoon helices, viewed from along the plane of the membrane with the outside of the cell toward the top, and colored according to a rainbow, from blue (N-terminal) to red (C-terminal).

The results obtained when aligning these MFS protein structures indicate that the effectiveness of a method depends on the question being asked. We demonstrate this by comparing the results obtained using FATCAT with the rigid-body fitting option with those obtained when using its ‘flexible’ (fragment-based) mode. For comparison of structures in the same conformation, using FATCAT with the rigid-body fitting option resulted in more accurate models (46.4% < GDT_TS < 56.0%) than using FATCAT in ‘flexible’ mode (42.3% < GDT_TS < 51.0%; Table V(a)). For those cases, we also found that the distance-threshold based GDT_TS scores and the packing-based CAD score both described the results well, and were consistent with one another (Table V(a)).

Table V.

Comparison of models in the MFS transporter family based on alignments generated using FATCAT in flexible and rigid-body fitting modes for structures in similar or different conformational states.

a) same states		GDT_TS (%)		CAD (%)
template	model	rigid	flexible	rigid	flexible
1PW4	2CFQ	48.5	44.3	49.8	48.8
2CFQ	1PW4	46.4	42.3	49.3	48.2
3O7Q	4GC0	50.1	45.5	50.3	49.6
4GC0	3O7Q	56.0	51.0	54.2	53.4
b) different states
1PW4	3O7Q	37.3	40.2	47.5	50.9
1PW4	4GC0	38.8	32.4	45.8	46.7
2CFQ	3O7Q	34.9	37.3	46.5	49.8
2CFQ	4GC0	33.2	30.9	45.0	45.2
3O7Q	1PW4	36.1	38.3	49.0	50.2
3O7Q	2CFQ	36.3	35.3	46.9	50.3
4GC0	1PW4	41.5	33.7	50.1	50.1
4GC0	2CFQ	38.9	34.6	48.4	49.2

Structural similarity scores for MFS transporter proteins that have been reported in an inward-facing conformation (GlpT and LacY; PDB codes: 1PW4 and 2CFQ) or an outward-facing conformation (FucP, and XylE; PDB codes: 3O7Q and 4GC0). Entries in bold indicate the best score of the flexible or rigid-body mode. Chain A is used in all cases.

For comparison of structures in different conformations, however, the distance-dependent measures may be misleading, whereas the CAD score might be expected to better capture the changes inherent in repositioning large domains relative to one another. Consistent with this expectation, the models are ranked differently when using the GDT_TS and CAD scores (Table V(b)). According to the CAD scores, the flexible mode of FATCAT results in more accurate alignments of structures in different conformations than the mode of FATCAT that relies on rigid-body fitting.

This example illustrates that fragmentation is a useful feature of structure alignment tools for aligning protein structures in different conformations, whereas rigid-based superimposition is more suitable for comparing structures in a similar state. Unfortunately, to date, none of the programs includes an option for identifying which of the two approaches may be more useful for a given pair of structures, and this decision must currently be made ad hoc.

Poor performance is reflected in over- or under-alignment

The accuracy of structural alignment methods is directly related to their ability to correctly insert gaps at evolutionarily unrelated positions, i.e., to identify insertions or deletions. Thus, structural alignment methods that are not able to identify the correct relationships may align too many residues that are evolutionarily unrelated (overalign) and thereby produce an unrealistically short alignment, or they might fail to identify relationships between positions and instead insert too many gaps (underalign). To test whether the different methods tend to over- or underalign, we computed the coverage, and the percentage of the two structure lengths that are aligned for each method. We then assessed these values relative to the most accurate method, which in this case is FR-TM-align. For both α-helical and β-barrel proteins, SAP and PPM tended to significantly underalign membrane protein structures, whereas MAMMOTH and SHEBA tended to overalign them (Table VI), which explains their overall poor to average performance in terms of model accuracy (see Tables III and IV).

Table VI.

Alignment coverage in the alignments generated using different structure alignment programs

α-helical proteins			β-barrels
	%aln	length		%aln	length
MAMMOTH	85.4%	333.8	MAMMOTH	79.0%	455.2
SHEBA	84.8%	336.0	SHEBA	76.0%	461.7
FATCAT	84.3%	336.8	LovoAlign	75.5%	462.9
LovoAlign	84.1%	337.3	FATCAT	75.5%	463.2
FATCAT rigid	83.9%	337.9	FATCAT rigid	75.2%	463.8
TM-align	82.5%	340.5	FR-TM-align	73.4%	468.2
FR-TM-align	82.5%	340.5	TM-align	73.2%	468.6
SABERTOOTH	79.4%	346.9	SABERTOOTH	73.8%	468.6
SKA	78.4%	349.1	DaliLite	69.4%	481.0
CE	78.1%	350.0	Matt	66.2%	489.8
Matt	77.7%	351.3	SKA	66.4%	490.2
DaliLite	78.5%	356.8	CE	65.6%	496.8
SAP	82.7%	359.2	PPM	59.1%	512.0
PPM	70.5%	366.6	SAP	57.5%	602.4

%aln: percentage of structure that is aligned. Length: average alignment length. Values of FR-TM-align used as a reference are shown in bold. Results are sorted in order of coverage (length).

Self-consistency

To assess whether self-consistency would be a useful measure of a structure alignment program, we first asked whether a method that produces accurate alignments also produces self-consistent alignments, or not. Specifically, we tested whether consistency was correlated with model quality. This correlation was assessed using either the CAD, AL4 or GDT_TS scores for a triplet of proteins; the consistency of their alignments was measured as the percentage of positions that are consistent, and the correlation was moderately high, both for α-helical proteins (PCC of 0.80, 0.66, and 0.78, for the three scores, respectively) and for β-barrels (PCC of 0.79, 0.67, and 0.78, respectively).

Given this moderate correlation between accuracy and consistency, we therefore proceeded to analyze the self-consistency of the structure alignments generated for the membrane proteins in the HOMEP3 set. For the α-helical membrane proteins, interestingly, alignments generated using DALILITE contained the highest proportion of self-consistent positions (88.7%; Table VII) even though these alignments scored poorly in terms of absolute accuracy (R_mean ranking >8; see Table III). This discrepancy can be explained by the observation that in the rare cases that there are inconsistencies, the error in their position tends to be large, with a mean shift error, E = 1.05 (Table VII), which is relatively high for the α-helical proteins. Interestingly, several methods that produced the most accurate alignments according to the model scores (e.g., FR-TM-align and FATCAT rigid, which ranked among the top five methods; Tables III and IV) also exhibited low shift errors (E <0.6) compared to, e.g., MAMMOTH, SKA and CE (E >1.3; Table VII). This analysis suggests that even though there are inconsistencies between the alignments by the top-ranking methods, these errors are relatively small, with the correct residue only 1-4 positions away. In α-helical proteins, such errors may reflect a subtle shift in the pitch of individual helices, since the repetitive nature of a helix may lead to multiple similar solutions with the helix shifted up and down by a turn.

Table VII.

Self-consistency of non-gapped positions in the alignments generated using different structure alignment programs.

α-helical proteins			β-barrels
	% correct	E		% correct	E
SABERTOOTH	85.9%	0.59	DaliLite	74.2%	2.84
FR-TM-align	87.2%	0.60	FR-TM-align	71.9%	2.95
TM-align	87.2%	0.60	FATCAT	72.0%	3.32
SHEBA	87.7%	0.60	Matt	71.0%	4.46
FATCAT rigid	88.4%	0.61	SHEBA	69.5%	4.68
SAP	88.5%	0.76	PPM	48.2%	4.79
Matt	86.7%	0.84	TM-align	68.8%	5.19
DaliLite	88.7%	1.05	FATCAT rigid	68.1%	5.23
FATCAT	87.4%	1.09	MAMMOTH	51.6%	5.59
SKA	80.6%	1.36	LovoAlign	59.6%	9.17
PPM	79.4%	1.46	SAP	45.5%	9.79
MAMMOTH	69.4%	1.54	SKA	58.6%	10.06
CE	76.7%	1.79	SABERTOOTH	57.1%	10.60
LovoAlign	79.2%	2.25	CE	43.6%	26.57

Results are sorted according to the average shift error, E. Entries in bold indicate the highest scores in that column.

For the β-barrel proteins, the overall rankings were similar, although interestingly, DaliLite gives the most consistent alignments of all methods, with 74.2% of positions correctly aligned, and with the smallest shift error (E = 2.84).

Comparing the two fold types, it is clear that the set of β-barrel proteins were harder to align consistently than the α-helical proteins, and the average shift error was significantly higher (Table VII). These differences between the two folds may be explained by the higher number of loosely-packed residues in β-barrels, because the reduced number of constraints on their positions means that they tend to be less consistently aligned than those that are well-packed or buried, as noted previously⁴. Moreover, the internal pseudo-symmetry of a β-barrel could lead to many possible solutions that are shifted by one or two β-strands, resulting in large shift errors.

Combining results from four structure alignment methods

Structural alignments of membrane proteins have been used as reference data sets for assessing various computational approaches, such as sequence alignment methods^21,46,50. In all these studies, a single structural alignment method was used to generate the reference data set. However, our comparisons indicate that none of the structure alignment methods performs significantly better than all others (Tables III and IV), consistent with observations for water-soluble proteins⁴. Selecting a single method to generate a reference set may therefore skew the results for such assessments. Specifically, incorrectly assigned positions would be treated as correct (false positives) and correctly-aligned positions would be treated as incorrect (false negatives).

To overcome such errors, we propose a consensus-type approach, similar to that used for transmembrane helix prediction in, e.g. TOPCONS ⁵¹, in which we collect the results from four structural alignment methods that produced some of the most accurate alignments. We selected the structural alignment methods that performed best according to the GDT_TS and CAD-score, namely FR-TM-align, FATCAT (rigid-body mode), MATT and DaliLite. TM-align was excluded because the underlying algorithm and score is similar to that of FR-TM-align, and because the models obtained from FR-TM-align and TM-align alignments are not significantly different (p >0.5). TM-align therefore does not introduce any significant additional information to the alignment that is already contained within FR-TM-align. Similarly, for FATCAT, the rigid-body mode was chosen instead of the flexible mode, because the former produced slightly more accurate alignments overall.

Unlike the transmembrane prediction consensus approach, we do not propose that the information from the four alignments be flattened into a single ‘consensus’ alignment. Rather by collecting the results of four different methods together we increase the odds that the correct alignment is identified.

Confidence scores provide a measure of reliability of aligned positions

The use of four different methods as described above also allows the assignment of a confidence value to each alignment position (Fig. 3). We assume that the more methods that place two residues in the same column, the more reliable the position. Therefore we assign the confidence score to be 1 when only one method predicts that alignment; 3, when two methods agree; 6 when three methods agree; and 9 when all four methods agree.

Figure 3. A consensus-type structure-based alignment fragment with confidence values.

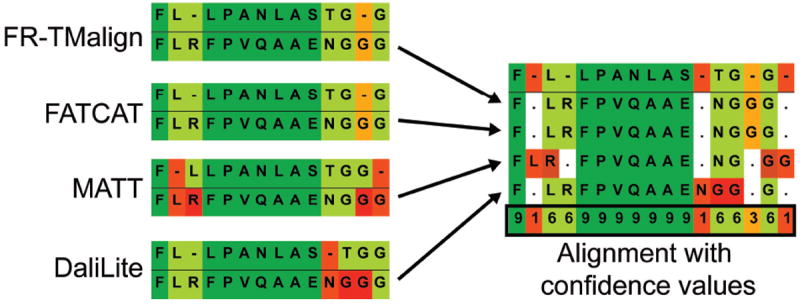
Two protein structures were aligned with four different structural alignment methods, FR-TM-align, FATCAT, MATT and DaliLite. The resulting alignments were then fused using the sequence of one of the protein structures as a reference. Depending on the agreement between the four methods, confidence values were assigned as very strong (i.e., all methods concur, confidence value of 9, dark green), strong (three methods agree, confidence value of 6, pale green), moderate (two methods agree, confidence value of 3, orange), and weak (only one method found this solution, confidence value of 1, red).

We note that agreement between methods is not necessarily a good reflection of the accuracy of a position, since all four methods could be incorrect. However, correlating the different confidence levels with the position-specific model accuracy of the corresponding positions shows that alignment positions with the highest agreement between the four methods typically correspond to accurately modeled positions, with an error in position <4 Å (Fig. 4). Moreover, as the confidence level decreases, so does the model accuracy (Fig. 4). Thus, positions with a high confidence level are indeed the most reliable. Alignment positions with low confidence values, by contrast, should be treated with caution and potentially checked manually for their correctness.

Figure 4. Correlation of residue accuracy with confidence values based on the consensus between FR-TM-align, FATCAT, MATT and DaliLite alignments.

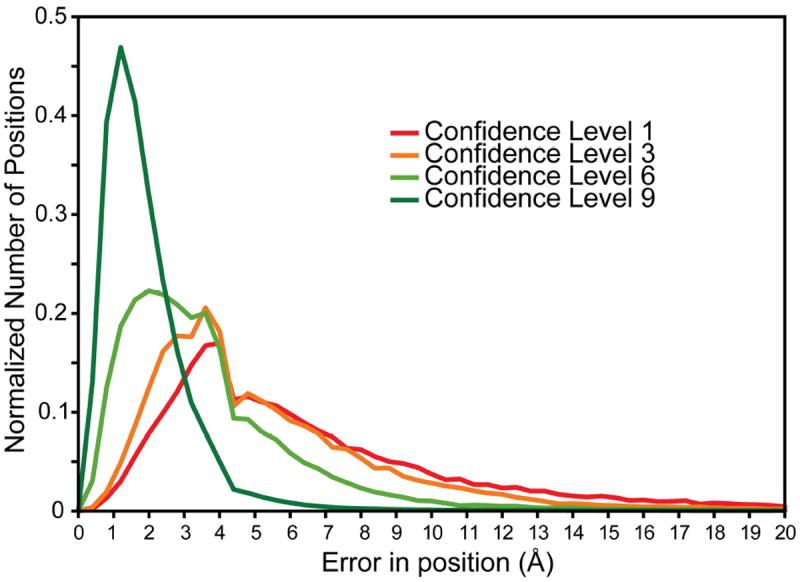
From all consensus alignments of the α-helical subset of HOMEP3, the position-specific confidence level was extracted for positions in which amino acids were aligned, i.e., excluding gapped positions. For each considered position, the distance (in Å) of the corresponding Cα-atom in the homology model to that in the native X-ray structure was calculated. This value then was averaged over the models built based on each of the alignments from the four structural alignment methods. The plot contains the normalized distribution of averaged Cα distances for each of the confidence levels (see Fig. 3).

Discussion

In this study we attempted to identify a method for reliably aligning structures of membrane proteins, which should be useful for many studies of membrane protein structure prediction or analysis. Overall, and in agreement with studies on more general data sets, no single method produced more accurate alignments than all other methods.

In comparing the different methods, however, several trends became clear. First, the methods that use length-independent scores such as TM-score for optimizing their superpositions produced the most accurate alignments of membrane proteins. We note that this observation could be biased by the use of GDT_TS and AL4 scores for assigning the accuracy of the different methods, because these two scores use threshold-dependent distance metrics and are quite strongly correlated with the TM-score (Table II). However, the TM-score based methods are also highly ranked when assessed using the CAD score, which is independent of any fitting procedure and therefore unbiased.

A second striking observation is that the fragment-based approaches typically resulted in overall more accurate alignments than the rigid-body fitting methods. This was particularly clear when comparing FR-TM-align with TM-align. FATCAT, in contrast, typically gave slightly more accurate alignments when used in “rigid” mode, rather than “flexible mode”. Importantly, the fragment-based flexible mode of FATCAT was most useful for comparing structures with very large conformational differences, such as the inward- versus outward-facing conformations of the major facilitator superfamily transporters, whereas the rigid-body mode resulted in more accurate alignments when comparing structures of similar conformational states.

We conclude that, as discussed previously for globular proteins³⁸, there is room for improvement in structure alignment programs, both in terms of alignment accuracy and alignment consistency⁴. Introducing membrane information within the superimposition procedure of membrane proteins might be one approach to improving the alignment quality. For example, for each structure, the membrane-spanning segments could be identified (e.g. using OPM⁵² or TMDET²⁴), and used as an additional criterion in the fitting.

In the meantime, we designed a consensus-type approach that collects the results from four diverse methods: FR-TM-align, FATCAT, MATT, and DaliLite, to identify the most accurate possible alignments of membrane protein structures. This approach simultaneously allows the assignment of a confidence score for each position. The collected alignments and confidence scores could be useful in a number of ways. For example, when used as “gold standard” reference alignments for evaluations of other bioinformatic methods, one could compare the test alignments only against the most confident regions of the reference set.

Another interesting application of the collected alignments and confidence scores is as input for homology modeling. Although typically the structure of the target protein is not known when building a homology model, there is at least one exception, namely when modeling alternate protein conformations⁵³. One such method relies on the observation that internal repeats in membrane transport proteins adopt distinct conformations, lending that structure functionally relevant features (e.g., opening a pathway to one side of the membrane; see Fig. 2). It has been shown that alternate conformations of a protein can be modeled by using each repeat as a template for the other^54,55. In such cases, confidence values would be useful primarily for the low-scoring, least reliable regions, and could be used in different ways, as follows.

First, consider regions with two alternative alignments of the same two sequences, e.g., where two of the four methods suggest one alignment, and the other two methods suggest another alignment. Two different models could be built, one for each of the alternate alignments, and the best model could be selected based on some independent score of the models (such as ProQM⁵⁶). Note that this strategy would become combinatorially expensive if there are many regions of uncertainty in the alignments. Alternatively, the same template could be used twice but with different alignments; with Modeller, for example, restraints could be derived automatically that consider both alignments simultaneously, and the optimization routine would attempt to find the model that best fits the two alternative alignments. Finally, the least confident regions, e.g., where all four structure alignment methods disagree, could be modeled without any template if only a few residues in length, such as a short loop, or omitted from the model if longer than a few residues, as in a terminal segment.

Interestingly, a couple of structural alignment methods (SymD⁵⁷ and CE-symm⁵⁸) have been designed to detect internal repeats such as those described above, and analyses with those programs suggest that internal repeats are more common in membrane proteins than in water-soluble proteins^58,59. In future, therefore, it will be interesting to compare the ability of different structural alignment methods to detect repeats in membrane proteins, as well as to detect distant relationships between known membrane protein structures.

In conclusion, we present a novel approach to the use of structural alignments, which leverages the available technology to the greatest degree possible, compensating for the fact that no single method outperforms all others, while also providing important information about alignment reliability.