Test–retest reliability of freesurfer measurements within and between sites: Effects of visual approval process

Abstract

In the last decade, many studies have used automated processes to analyze magnetic resonance imaging (MRI) data such as cortical thickness, which is one indicator of neuronal health. Due to the convenience of image processing software (e.g., FreeSurfer), standard practice is to rely on automated results without performing visual inspection of intermediate processing. In this work, structural MRIs of 40 healthy controls who were scanned twice were used to determine the test–retest reliability of FreeSurfer‐derived cortical measures in four groups of subjects—those 25 that passed visual inspection (approved), those 15 that failed visual inspection (disapproved), a combined group, and a subset of 10 subjects (Travel) whose test and retest scans occurred at different sites. Test–retest correlation (TRC), intraclass correlation coefficient (ICC), and percent difference (PD) were used to measure the reliability in the Destrieux and Desikan–Killiany (DK) atlases. In the approved subjects, reliability of cortical thickness/surface area/volume (DK atlas only) were: TRC (0.82/0.88/0.88), ICC (0.81/0.87/0.88), PD (0.86/1.19/1.39), which represent a significant improvement over these measures when disapproved subjects are included. Travel subjects’ results show that cortical thickness reliability is more sensitive to site differences than the cortical surface area and volume. To determine the effect of visual inspection on sample size required for studies of MRI‐derived cortical thickness, the number of subjects required to show group differences was calculated. Significant differences observed across imaging sites, between visually approved/disapproved subjects, and across regions with different sizes suggest that these measures should be used with caution. Hum Brain Mapp 36:3472–3485, 2015. © 2015 Wiley Periodicals, Inc.

INTRODUCTION

The outermost layered structure of neural tissue of the brain, the cortex, is known to have important connections to higher intellectual processing, such as judgment, having a sense of purpose, and imagination [Desikan et al., 2006b; Haines and Ard, 2013]. As such, differences in brain morphology—such as regional volume, surface area, and thickness—of the cortex may indicate structural deficits that could shed light on neurodegenerative and psychiatric disorders [Desikan et al., 2006b]. For example, patients diagnosed with major depressive disorder (MDD) have been shown to exhibit reduced cortical thickness [Bremner et al., 2002; Frodl et al., 2008; Tu et al., 2012; van Eijndhoven et al., 2013]. Importantly, a landmark study suggests that cortical thinning is an endophenotype, characterizing those at high genetic risk for MDD, independent of their having developed the syndrome [Peterson et al., 2009]. Cortical thinning has also been observed in other diseases such as Parkinson's disease [Pagonabarraga et al., 2013], Schizophrenia [Cobia et al., 2011], Alzheimer's disease [Lerch et al., 2008], and Huntington's disease [Rosas et al., 2002] in different brain areas. Taken together, these findings imply that cortical thinning may be regional and potentially used to differentiate diseases. This makes the accuracy of the tools we use to map cortical thinning critically important to the field for diagnosis, exploration of endophenotypes, and the possible use as a moderator to predict differential treatment outcome [Trivedi et al., 2013].

Traditional cortical thickness calculations are the result of postmortem observations, but Magnetic Resonance Imaging (MRI) allows for in vivo measurements to be made. Using MRI, regional measures can then be either determined manually [Hermoye et al., 2004; Hutton et al., 2009; Jou et al., 2005; Peterson et al., 2009] or automatically [Dale et al., 1999; Hutton et al., 2009; Liem et al., 2015; Reuter et al., 2012; Sereno et al., 1995; Storsve et al., 2014; Tustison et al., 2014]. As the human cortex consists of many layers and folds of sheets of neurons, manual estimation is challenging and time consuming. Using an automated method, data from large sample sizes can be analyzed using standardized analysis algorithms with minimal time and monetary cost. These algorithms utilize either volume‐based [Ardekani et al., 2005; Gholipour et al., 2007; Klein et al., 2009; Tustison et al., 2014] or surface‐based [Davatzikos et al., 1996; Fischl et al., 1999; Hinds et al., 2009; Khan et al., 2011; Liem et al., 2015; Storsve et al., 2014; Tosun and Prince, 2008] registrations. Volume‐based registrations have been shown to result in high intersubject variability as their use of intensities to define cortical regions causes poor anatomical delineation [Ghosh et al., 2010]. Developed to improve cortical registration accuracy, the surface‐based approach provides better alignment of cortical landmarks than volume‐based registration, and is now used ubiquitously [Ghosh et al., 2010; Mills and Tamnes, 2014; Winkler et al., 2010].

FreeSurfer (http://surfer.nmr.mgh.harvard.edu/) is a popular and publicly available software package for studying cortical and subcortical anatomy [Colloby et al., 2011; Han et al., 2006; Jovicich et al., 2009; Lyoo et al., 2011; Reuter et al., 2012]. A PubMed search for publications using FreeSurfer (“FreeSurfer” in any field) yields over 500 published papers in the last 5 years alone. Using a surface‐based approach, FreeSurfer can automatically segment the brain into different cortical regions of interest, and calculate average thickness—along with other closely related measures, such as surface area and volume—in the defined regions. FreeSurfer's main cortical reconstruction pipeline begins with registration of the structural volume with the Talairach atlas [Talairach and Tournoux, 1988]. After bias field estimations and the removal of bias, the skull is stripped and subcortical white and gray matter structures are segmented [Fischl et al., 2002]. Next, tessellation, automated topology correction, and surface deformation routines—the first steps of the surface‐based stream—create white/gray (white) and gray/cerebrospinal fluid (pial) surface models [Fischl et al., 2001]. These surface models are then inflated, registered to a spherical atlas, and used to parcellate the cortical mantle according to gyral and sulcal curvature [Desikan et al., 2006a]. The closest distance from the white surface to the pial surface at each surface's vertex is defined as the thickness [Desikan et al., 2006b]. Average cortical thickness, surface area, and total volume statistics corresponding to each parcellated region can then be computed.

When using any automated method to examine neurobiology, it is important to properly validate the results. As such, several studies have analyzed the reliability of automated cortical thickness measurements using test–retest studies [Desikan et al., 2006b; Dickerson et al., 2008; Han et al., 2006; Jovicich et al., 2013; Liem et al., 2015; Schnack et al., 2010; Wonderlick et al., 2009]. For example, Eggert et al. investigated the reliability and the accuracy of different segmentation algorithms in SPM8 (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/), VBM8 (http://dbm.neuro.uni-jena.de/vbm/), FSL (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/), and FreeSurfer on real and simulated brain images. They concluded that FreeSurfer had very high reliability between scans, particularly on a test–retest basis but it had the lowest accuracy (quantified by Dice coefficient) among all software packages tested [Eggert et al., 2012]. However, they mentioned that these results should be interpreted cautiously as FreeSurfer segments the gray matter volumes of structures as a whole whereas the other algorithms segment images voxel‐wise into tissue classes, making it difficult to directly compare results. Tustison et al. compared Advanced Normalization Tools (ANTs, http://stnava.github.io/ANTs/) and FreeSurfer in terms of reliability and prediction performance and showed that both ANTs and FreeSurfer had high cortical thickness reliability. Nevertheless, ANTs had a better age and gender prediction accuracy [Tustison et al., 2014]. As they did not have the ground truth (i.e. post‐mortem measurements), they reported accuracies based on prediction performances. Liem et al. evaluated the reliability of cortical and subcortical measures of healthy elderly subjects. They concluded that the intraclass correlation coefficient (ICC) of these measures was high. They also examined the effect of surface‐based smoothing on the reliability and provided a tool for performing power and sensitivity analysis [Liem et al., 2015].

Although studies such as those mentioned above examined the reliability of FreeSurfer measures, to our knowledge, none report on the percentage of FreeSurfer results containing artifacts, or the effect of these artifacts on subsequent calculations or estimation of group differences. Therefore, in this work, each image processed through FreeSurfer was thoroughly evaluated for artifacts as well as errors in FreeSurfer surface detection or segmentation, resulting in an “approved” and “disapproved” datasets. After that, the effects of using disapproved data on test–retest reliability of FreeSurfer‐derived cortical thickness, cortical surface area, and cortical volume were calculated.

Study subjects were recruited for the Establishing Moderators and Biosignatures of Antidepressant Response for Clinical Care (EMBARC) study (NIMH1U01 MH092250, http://embarc.utsouthwestern.edu/), designed to address the need for biosignatures of treatment outcome and to advance personalized care of major depressive disorder. The main goal of this study is to search for a biomarker (e.g., pretreatment regional cortical thickness) of antidepressant treatment response. To be considered as valid, test–retest reliability of these biomarkers was first validated by healthy controls, assessed twice over one week. T1‐weighted (T1w) MRIs were acquired twice on 40 healthy control subjects at one of four different imaging locations, using three different brands of magnet and software (General Electric (GE), Philips, and Siemens) with standardized acquisition protocols. This sample size (N = 40), is comparable to ([Jovicich et al., 2013], N = 40) or larger (N = 6–30 [Desikan et al., 2006b; Dickerson et al., 2008; Han et al., 2006; Schnack et al., 2010; Wonderlick et al., 2009]) than the other studies that analyzed the test–retest reliability, except two recent studies (N = 1205 [Tustison et al., 2014]; N = 189 [Liem et al., 2015]).

After assessing the variability in approved and disapproved data, we performed a power analysis to estimate the required number of subjects needed for group comparisons of cortical thickness data, based on the measured standard errors [Han et al., 2006]. This type of calculation is important because it reveals the increased number of subjects required to compensate for the increased variability that results from including disapproved data in the analyses. (As many users of automatic techniques do not visually approve their data, these subjects are included in analyses by default.) Because this analysis was performed on T1w MRIs acquired at multiple sites, with a range of reliability estimates, it is likely generalizable to all 3T structural MRI acquisitions.

METHODS

Data Acquisition

Forty healthy control individuals (age 18–65) enrolled in the Establishing Moderators and Biosignatures of Antidepressant Response for Clinical Care (EMBARC) project were scanned at least twice, one week apart, using a 3T MRI scanner, at one of four sites: University of Texas Southwestern Medical Center (TX: Philips Achieva, 8‐channel [ch.] head coil), University of Michigan (UM: Philips Ingenia, 15‐ch.), Massachusetts General Hospital (MG: Siemens Trio, 12‐ch.), and Columbia University Medical Center (CU: GE Signa HDx, 8‐ch.). Three subjects at each site, totaling 12 of the 40 control subjects (travel group), also traveled to another EMBARC site and were scanned for the third time to evaluate inter‐site variability. Site pairs for the travel group comprised CU‐MG (2), CU‐TX (2), MG‐TX (2), MG‐UM (2), UM‐CU (2), and UM‐TX (2).

IR‐FSPGR (CU) and MPRAGE (TX, UM, MG) sequences were used to acquire T1w images over 4.4–5.5 min with following parameters: TR (repetition time): 5.9–8.2 ms, TE (echo time): 2.4–4.6 ms, Flip Angle: 8° to 12°, slice thickness: 1 mm, FOV (field of view): 256 × 256 mm², voxel dimensions: 1 × 1 × 1 mm³, acquisition matrix: 256 × 256 or 256 × 243, acceleration factor: 2, and 174–78 sagittal slices.

These parameters were selected to be as consistent across sites while accommodating for different scanner types. We aimed to obtain a spatial resolution of 1 mm, as previous multisite studies such as the Alzheimer's Disease Neuroimaging Initiative (ADNI) study [Jack et al., 2008] have suggested that a spatial resolution of 1 mm is desired for brain morphometric examinations. Furthermore, although the ADNI study used a slice thickness of 1.2 mm to accommodate sites with 1.5T scanners (1 mm thickness would yield very low SNR at 1.5T), all of the sites in our study are equipped with 3T MRI systems. We therefore used an isotropic voxel size of 1 × 1 × 1 mm³ for optimal results. The shortest TR and TE values are commonly used in an MPRAGE or IR‐FSPGR sequence, as they allow a fast acquisition of the k‐space data. However, as the MRI systems used in our study were manufactured by different venders (GE, Philips, and Siemens) and have slightly different hardware (e.g., gradient strength and slew rate), the shortest possible TR and TE were slightly different. The flip angle is accordingly different based on the actual TR value in order to achieve the maximum signal (so‐called Ernst angle). A larger flip angle is used when the TR is longer.

Processing

Cortical thickness, cortical surface area, and cortical volume were calculated using FreeSurfer version 5.1 (http://surfer.nmr.mgh.harvard.edu/) and two different atlases: Desikan‐Killiany (DK, 34 regions per hemisphere) [Desikan et al., 2006b] and Destrieux (74 regions per hemisphere) [Destrieux et al., 2010]. FreeSurfer outputs were “approved” or “disapproved” by a trained technician using a systematic visual inspection process described below, and summarized in Figure 1.

Figure 1.

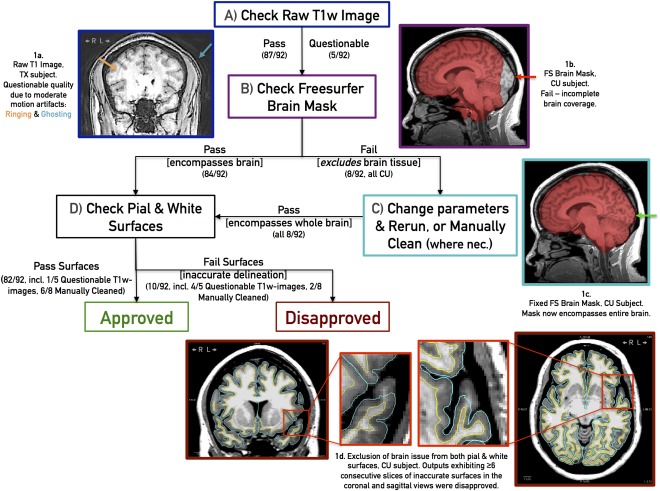
Flowchart summarizing the inspection process and pass/fail criteria, with example cases. Boxes represent image processing steps and examples of proper and inaccurate brain exaction outputs. See text for details. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Raw T1w images were first examined for common MR T1w imaging artifacts, which can undermine FreeSurfer's segmentation accuracy. These include smearing/blurring, ringing/rippling/striping, ghosting, and radiofrequency leak, which are caused by subject motion, scanner setup, signal interference, and soforth [Bellon et al., 1986; Morelli et al., 2011]. Raw T1w images exhibiting moderate/severe artifacts were flagged (Fig. 1a) for later assessment but nonetheless processed through FreeSurfer. Next, the accuracy of FreeSurfer's brain mask (brainmask.mgz) was assessed visually across sagittal, coronal, and axial sections. Brain masks excluding brain tissue (Fig. 1b) were corrected, either by rerunning FreeSurfer's “skullstrip” routine with the “no‐wsgcaatlas” flag or manually cleaning using the Freeview application (Fig. 1c), and reprocessed through later steps. As an under‐cropped brain mask (i.e., one encompassing extra‐cerebral anatomy such as the dura mater, eyes, and neck in addition to the brain) still permitted accurate surface delineation, under‐cropped images were not manually corrected. Following cropping, the FreeSurfer‐generated pial and white surfaces (directly used to calculate cortical thickness and surface area, and divide cortical and subcortical domains for label propagation) were visually inspected in 2D coronal and axial sections (Fig. 1d). Based on an empirical process, we deemed inaccurate surface delineations at the same region for ≥6 consecutive coronal and axial slices enough to invalidate outcome measures and consequently “disapproved” such outputs. Another candidate for “disapproval” is an output with subthreshold delineation issues but whose raw T1w weighted images are excessively blurry and noisy, leading to no apparent tissue contrast in certain regions and consequently touching white/pial surfaces. We observed that when acceptable raw T1w images gave rise to poor segmentations, these “disapproved” FreeSurfer outputs could not be reliably or consistently rectified using FreeSurfer 5.1's documented white‐matter or control‐point intervention procedures. Editing the white matter volume (i.e., filling in unrecognized white matter voxels) proved ineffective at repositioning surface boundaries, while adding white‐matter control points (i.e., marking unrecognized white matter voxels to renormalize white matter intensity globally) changed surface boundaries, and consequently outcome measures, at almost all regions, including regions whose surfaces were originally deemed acceptable. Given these complications, only brain mask errors were corrected. After this correction, disapproval rate dropped from 16/92 (17%) to 10/92 (11%) scans.

As our visual inspection protocol requires examining FreeSurfer's generated surfaces slice by slice in coronal and axial view for each subject, this methodology is time‐consuming (5–25 min per scan, depending on the number and ambiguity issues requiring attention).

Subjects were categorized into groups based on the result of visual inspection and scan sites:

1. Approved (App): Both test and retest data are approved (Scanned in the same site).

2. Disapproved (Dis): Either test or retest data are disapproved (Scanned in the same site).

3. Combined (App+Dis): Test and retest data are approved or disapproved.

4. Travel: Only approved test and retest data were used (Scanned in different sites).

The subjects were distributed over the four sites as in Table 1.

Table 1.

The number of the approved (App) and the disapproved (Dis) subjects over sites

	Before brain mask intervention		After brain mask intervention
Site	App	Dis	App	Dis	Total
Columbia University (CU)	3	7	8	2	10
Massachusetts General Hospital (MG)	9	1	9	1	10
University of Texas (TX)	7	3	8	2	10
University of Michigan (UM)	6	4	8	2	10
Travel Group	10	2	11	1	12

Test–Retest Reliability

Three different measures were used to evaluate the reliability of FreeSurfer measures:

1. Test–retest correlation (TRC): Sample Pearson correlation coefficient [Eq. (1)] was calculated between test ( $T$) and retest ( $R$) data with the following formula for each region.

   $${TRC}_j=\frac{{\sum }_{i=1}^n(T_{i,j}-{\overline{T}}_j)(R_{i,j}-{\overline{R}}_j)}{\sqrt{{\sum }_{i=1}^n(T_{i,j}-{\overline{T}}_j{)}^2}\sqrt{{\sum }_{i=1}^n(R_{i,j}-{\overline{R}}_j{)}^2}} n:\hspace{0.17em}\# \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{s}; j:\hspace{0.17em}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n}\hspace{0.17em}\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x};\hspace{0.17em}i:\hspace{0.17em}\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t} \mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}$$ (1)

   In (1), ${TRC}_j$ represents the correlation coefficient between the cortical thickness, surface area, or volume of a specific region (j) in the test and the retest scan. ${\overline{T}}_j$ and ${\overline{R}}_j$ are the arithmetic means of $T_j$ and $R_j$ respectively. The TRC calculation evaluates the linear correlation dependence between the first ( $T$) and second ( $R$) scans. Values can range from −1 to +1. Zero indicates no association, ${TRC}_j$ > 0 indicates a positive association, and ${TRC}_j$ < 0 indicates a negative association. For the travel subjects, ${TRC}_j$ accounts for scanner differences as well as inter‐session variability.

2. Intraclass Correlation Coefficient (ICC): ICC, which is a measure of within‐subject variability relative to between‐subject variability was calculated to quantify the reliability of FreeSurfer measures [Gudmundsson et al., 2012].

   $${ICC}_j=\frac{{MS}_{j\left(\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n}\right)}-{MS}_{j\left(\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n}\right)}}{{MS}_{j\left(\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n}\right)}+\left(k-1\right){MS}_{j\left(\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n}\right)}} \mathrm{k}: \# \mathrm{o}\mathrm{f} \mathrm{r}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}$$ (2)
   In Eq. (2), ${MS}_{j\left(\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n}\right)}$ and ${ MS}_{j\left(\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n}\right)}$ are the mean square error between and within the subjects respectively for the given region j. In the case of test and retest data, k = 2 and these measures are defined in eq. (3).

   $${MS}_{j\left(\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n}\right)}=\frac{1}{2n}\sum _{i=1}^n{\left(T_{i,j}-{MW}_{i,j}\right)}^2+{\left(R_{i,j}-{MW}_{i,j}\right)}^2 {MW}_{i,j}=\frac{T_{i,j}+R_{i,j}}{2}$$ (3)

   $${MS}_{j\left(\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n}\right)}=\frac{1}{n}\sum _{i=1}^n{\left({MW}_{i,j}-{\overline{MW}}_j\right)}^2 {\overline{MW}}_j: \mathrm{a}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c} \mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n} \mathrm{o}\mathrm{f} {MW}_j$$

   An ICC value of 1 is the ideal case when there is no difference between measurements ( ${MS}_{j\left(\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n}\right)}$=0). When ${MS}_{j\left(\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n}\right)}$= ${MS}_{j\left(\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n}\right)}$, the ICC value becomes zero. Negative ICC values occur when ${MS}_{j\left(\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n}\right)}< {MS}_{j\left(\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n}\right)}$. ICC value of −1 occurs when there is no difference between the measurements of different subjects ( ${MS}_{j\left(\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n}\right)}$=0). For the travel subjects, scanner differences will affect both ${MS}_{j\left(\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{n}\right)}$ and ${MS}_{j\left(\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n}\right)}$. As such comparison of ICC values between test–retest and travel subjects sheds light on the contribution of scanner differences to between subject comparison.
3. Percent difference (PD): PD of FreeSurfer measures of a specific region (j) between test ( $T$) and retest ( $R$) data was calculated with the following formula for each region.

   $${\mathrm{P}\mathrm{D}}_j= \frac{2}{n}\sum _{i=1}^n|\frac{T_{i,j}‐R_{i,j}}{T_{i,j}+R_{i,j}}|\times 100$$ (4)

   All of these measures provide unique information. TRC shows how much the test and retest data vary together. However, it does not give any information about the difference between these two sets. Percent difference gives us this missing information in TRC. However, neither TRC nor percent difference is sufficient to compare the within‐subject variability and between‐subject variability. In this case, ICC completes this information.

Power Analysis

Sample size determination is an important step in planning a statistical study or clinical trial. Enrolling more subjects than necessary is not desirable due to the increased cost, time, and necessary subject burden. Using less than the required subjects will result in poor statistical power. Therefore, to estimate the required sample size for detecting changes in cortical thickness between groups, a power analysis was performed using a two‐sided t‐test with a significance level of 0.05. Standard deviation (std) of the measurement error was calculated as given in [Han et al., 2006] for the approved and the combined (approved plus disapproved) groups. Using this analysis, one can determine the additional number of subjects required to compensate for increased variance when using data that has not been approved. In other words, one can estimate the trade‐off between person‐hours to approve cortical thickness data and costs incurred from additional subjects needed when using data that may have FreeSurfer errors.

All methods were performed in Matlab (http://www.mathworks.com) version (R2012b). In power analysis, G*Power [Faul et al., 2007] was used.

RESULTS

Cortical Thickness

In Figure 2, a histogram of cortical thickness values calculated by FreeSurfer 5.1 shows the distribution of mean cortical thickness values across all regions in the approved subjects for regions defined by the Destrieux atlas.

Figure 2.

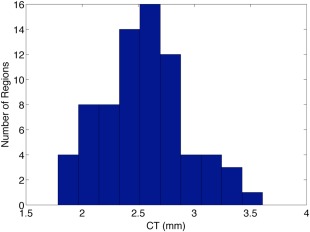
Histogram of cortical thickness for Destrieux atlas. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The histogram was similar for regions of the DK atlas. The range of cortical thickness values (1.58–3.72 mm) is consistent with both previous postmortem findings and a FreeSurfer‐based analysis [Desikan et al., 2006b]. Cortical thickness values range from 1 and 4.5 mm (average = ∼2.5 mm) in both automated and postmortem studies [Desikan et al., 2006b].

Test–Retest Reliability

To calculate test–retest reliability, we used the subject groups before brain mask intervention (Table 1), as this represents a sample with no intervention. In other words, these are the outputs that would exist in studies without a visual inspection system. Therefore, there are 25 Approved (App), 15 Disapproved (Dis), and 40 combined (App+Dis) subjects. For the travel group, we used only the 10 approved subjects and did not include the two disapproved subjects in the analysis. Eight subjects were subsequently approved after brain mask intervention. We analyzed the reliability of these subjects separately, before and after intervention in Supporting Information: Table 1.

In approved subjects, there was no statistical difference between PD values of left vs. right for cortical thickness (P = 0.76), cortical surface area (P = 0.95), and cortical volume (P = 0.84) for Destrieux atlas. Similarly, no statistical difference in PD values of left vs. right for cortical thickness (P = 0.88), cortical surface area (P = 0.97), and cortical volume (P = 0.79) for DK atlas. For this reason, left and right hemispheres were combined for all analyses. In Tables 2, 3, 4, means and standard deviations of regional TRC, ICC, and PD of cortical thickness, surface area and volume are given for the specified atlas.

Table 2.

Mean and standard deviation (std) of test–retest correlation (TRC) values of cortical thickness (CT), surface area (CS), and volume (CV).

FreeSurfer 5.1		Atlas 1 (Destrieux)						Atlas 2 (DK)
	N	TRC (CT)	Std (CT)	TRC (CS)	Std (CS)	TRC (CV)	Std (CV)	TRC (CT)	Std (CT)	TRC (CS)	Std (CS)	TRC (CV)	Std (CV)
App.	25	0.78***	0.14	0.86***	0.13	0.85**	0.12	0.82***	0.10	0.88*	0.13	0.88	0.14
App+Dis	40	0.72	0.13	0.80	0.14	0.80	0.13	0.75	0.12	0.83	0.14	0.84	0.14
Dis.	15	0.62	0.20	0.71	0.21	0.73	0.21	0.65	0.21	0.75	0.23	0.77	0.24
Travel	10	0.63	0.26	0.85	0.17	0.84	0.16	0.65	0.22	0.89	0.16	0.87	0.16

Significant differences are presented for App vs. App+Dis (*P < 0.05, **P < 0.01, ***P < 0.001). N: Number of subjects.

Table 3.

Mean and std of ICC values of cortical thickness (CT), surface area (CS), and volume (CV).

FreeSurfer 5.1		Atlas 1 (Destrieux)						Atlas 2 (DK)
	N	ICC (CT)	Std (CT)	ICC (CS)	Std (CS)	ICC (CV)	Std (CV)	ICC (CT)	Std (CT)	ICC (CS)	Std (CS)	ICC (CV)	Std (CV)
App.	25	0.77***	0.15	0.84***	0.13	0.84**	0.12	0.81**	0.11	0.87*	0.14	0.88	0.15
App+Dis	40	0.71	0.13	0.79	0.14	0.79	0.13	0.75	0.12	0.82	0.15	0.83	0.14
Dis.	15	0.59	0.21	0.67	0.24	0.68	0.22	0.62	0.21	0.72	0.25	0.73	0.25
Travel	10	0.56	0.27	0.82	0.19	0.80	0.18	0.57	0.24	0.87	0.19	0.85	0.17

Significant differences are presented for App vs. App+Dis (*P < 0.05, **P < 0.01, ***P < 0.001). N: Number of subjects.

Table 4.

Mean and standard deviation (std) of PD of cortical thickness (CT), surface area (CS), and volume (CV).

FreeSurfer 5.1		Atlas 1 (Destrieux)						Atlas 2 (DK)
	N	PD (CT)	Std (CT)	PD (CS)	Std (CS)	PD (CV)	Std (CV)	PD (CT)	Std (CT)	PD (CS)	Std (CS)	PD (CV)	Std (CV)
App.	25	1.06**	0.49	1.91*	1.38	2.17*	1.36	0.86*	0.35	1.19*	0.76	1.39*	0.77
App+Dis	40	1.24	0.50	2.24	1.36	2.53	1.36	1.00	0.41	1.49	0.76	1.74	0.82
Dis.	15	1.53	0.62	2.78	1.61	3.13	1.60	1.24	0.57	1.99	1.08	2.32	1.13
Travel	10	1.34	0.69	1.94	1.42	2.31	1.36	1.13	0.47	1.21	0.89	1.56	0.93

Significant differences are presented for App vs. App+Dis (*P < 0.05, ** P < 0.01). N: Number of subjects.

For all three measurements (cortical thickness, surface area and volume), approved (App) subjects exhibited significantly higher TRC and ICC and lower PD than disapproved (Dis) subjects. When we compared approved vs. all (App+Dis), approved subjects also exhibited significantly higher TRC and ICC, and lower PD than all subjects. (For cortical volumes, TRC and ICC differences were significant only in the Destrieux atlas.)

To detect variation in reliability across ROIs, regional reliability results are given in Supporting Information tables for Destrieux (Supporting Information: Tables II–IV) and DK (Supporting Information: Tables V–VII) atlases. Cortical color maps illustrating PD across each outcome measure are provided in Figure 3. Color maps for TRC and ICC are given in Supporting Information Figures 1 and 2, respectively.

Figure 3.

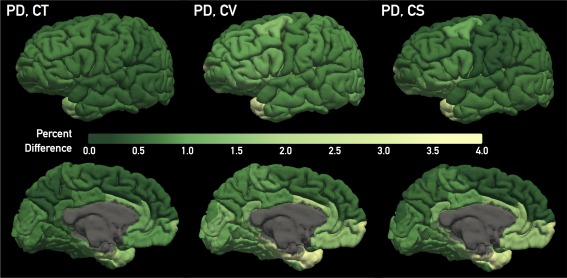
Percent difference (PD) map for (from left to right) regional cortical thickness (CT), cortical volume (CV), and cortical surface area (CS), across the Desikan–Killiany atlas regions. Depicted PD values were averaged across the “approved” group subjects. Each column provides lateral (top) and medial (bottom) views. A green color scale was applied to convey the high reliability across these three outcome measures, evidenced by a relatively small and narrow range of PD values. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

For cortical thickness, regions defined by the DK atlas had higher TRC (P = 0.032) and ICC (P = 0.035), and lower PD (P = 0.002) than those of the Destrieux atlas in the approved subjects. For cortical surface/volume, this was not the case, that is, TRC and ICC of cortical surface/volume measures did not significantly differ between atlases. (However, TRC and ICC of cortical volume for the DK atlas was higher on a trend level (P = 0.069 TRC, P = 0.064 ICC) than the Destrieux atlas.) However, in these measures, the DK atlas regions had lower PD (P < 0.001) than Destrieux atlas regions in the approved subjects.

Travelling subjects showed the lowest ICC values in cortical thickness measurements for both atlases. However, ICC values for cortical surface area and volume were closer to the approved (App) group than the combined and Dis groups. TRC and PD values of travel group were better than the Dis group for cortical thickness. Again, these measures were closer to the App group for cortical surface area and volume.

In the Supporting Information: Table 1, test–retest reliability of the eight subjects, before (disapproved) and after (approved) brain mask intervention is given. Here in cortical thickness measurements, approved (App) subjects exhibited significantly higher TRC and ICC (both P < 0.05 for Destrieux atlas) than the previously disapproved subjects. No significant difference was observed between these two groups for PD. In cortical surface area and volume measurements, approved (App) subjects exhibited significantly higher TRC and ICC and lower PD than previously disapproved (Dis) subjects for both atlases.

Volume and Surface Area Dependency

To investigate the observed cortical thickness differences between atlases, the effect of cortical surface area and cortical volume on reliability estimates was examined. (Regions of the DK atlas have greater surface area and volume than those of the Destrieux atlas.)

In Figure 4, PD of cortical thickness is presented vs. cortical surface area (CS) and cortical volume (CV), respectively for DK atlas in the App group for 68 (34 left and 34 right) regions. A relationship was observed between the percent difference (PD) of cortical thickness and cortical surface area (CS). A power law fit (mean square error [mse] = 0.047) generated the best fit among logarithmic (mse = 0.051), exponential (mse = 0.075), and linear (mse = 0.077) fits. Same relationship was observed between the percent difference (PD) of cortical thickness and regional volume (CV). Again, power law fit (mean square error [mse] = 0.061) generated the best fit among logarithmic (mse = 0.062), exponential (mse = 0.078), and linear (mse = 0.080) fits.

Figure 4.

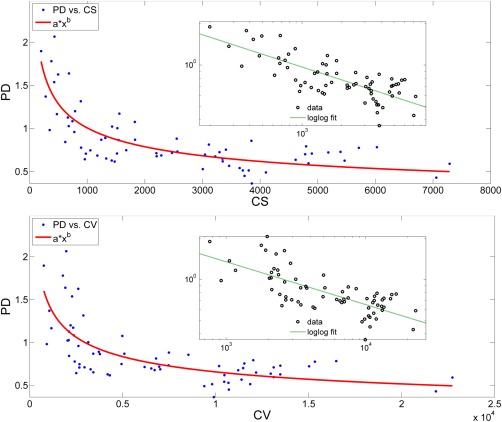
(Top): Variation of percent difference (PD) of cortical thickness with respect to the mean cortical surface area (CS) across regions of DK atlas. Fit equation: ax^b, coefficients with confidence intervals: a = 11.46 (6.49, 16.43), b = −0.35 (−0.41, −0.29). Adjusted R ² of the fit = 0.63. (bottom): Variation of percent difference (PD) with respect to the mean cortical volume (CV) across regions of DK atlas. Fit equation: ax^b, coefficients with confidence intervals: a = 15.99 (5.47, 26.51), b = −0.35 (−0.43, −0.27). Adjusted R ² of the fit = 0.51. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Site Differences

As the data were acquired from four different imaging sites, reliability measures of cortical thickness, cortical surface area, and cortical volume were calculated for each site in the approved group segmented by DK atlas.

In Figures 5, 6, 7, median and the comparison intervals of TRC, ICC and PD measures are given respectively for cortical thickness, cortical surface area, and cortical volume.

Figure 5.

Median and the comparison intervals of TRC for cortical thickness (CT) (P = 0.003), cortical surface area (CS) (P < 0.001), and cortical volume (CV) (P = 0.041) in different sites. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 6.

Median and the comparison intervals of ICC for cortical thickness (CT) (P < 0.001), cortical surface area (CS) (P = 0.008), and cortical volume (CV) (P = 0.405) in different sites. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 7.

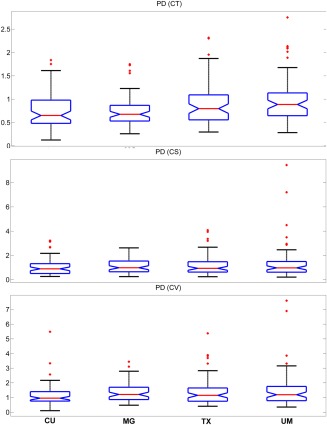
Median and the comparison intervals of PD for cortical thickness (CT) (P < 0.001), cortical surface area (CS) (P = 0.203), and cortical volume (CV) (P = 0.172) in different sites. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Cortical thickness, cortical surface area, and cortical volume values are considered as outliers when they are larger than Q3+W*(Q3 − Q1) or smaller than Q1 − W*(Q3 − Q1). Here, Q1 and Q3 are the 25th and 75th percentiles, respectively. W stands for whisker length (W = 1.5).

Power Analysis

To estimate the required sample size (per group) for observing a potential predefined percent difference (e.g., 1%, 2%, 5%) in cortical thickness values between two groups, a power analysis was performed. For comparison, this analysis was performed using the standard measurement errors of cortical thickness from either the approved or approved plus disapproved control subjects (40 subjects, 80 total scans) for each region in DK atlas. As the measurement error is variable across regions, and this error greatly affects the number of subjects required, results are given for the ranges in addition to the mean std of errors.

In Table 5, for a power of 0.9, two‐sided t‐test and a detectable difference of 1%, required number of subjects for Approved versus All (Approved+Disapproved) subjects were 155 (41–945) and 231 (96–1357) per comparison group respectively. These numbers were reduced to 2 (2–4) and 3 (2–5) for a difference of 20%. Differences in the effect sizes were significant (P < 0.001).

Table 5.

Sample size (N) estimations to detect certain percent differences (significance level = 0.05, two‐sided, power = 0.9) in cortical thickness (CT) for different subject groups.

		Required sample size (N) per comparison group for detectable % difference (mean CT = 2.6 mm)
Group	Std of measurement error (mm)	1%	2%	3%	4%	5%	10%	20%
App	0.081(0.033–0.231)	155(41–945)	40(11–237)	19(6–106)	11(4–60)	8(3–39)	3(2–11)	2(2–4)
App+Dis	0.097(0.047–0.275)	231(96–1357)	59(25–341)	27(12–152)	16(8–86)	11(5–56)	4(3–15)	3(2–5)

The results are given for the mean std of measurement error. The ranges are given in parenthesis.

DISCUSSION

Although the ground truth for cortical thickness, surface area, and volume estimates is not available, the reliability of these FreeSurfer‐derived measures could be estimated using a test–retest paradigm. Based on study results, we confirm the high reliability of FreeSurfer‐derived measures. We report a mean standard measurement error <0.1 mm for cortical thickness in approved studies. This is slightly lower than the 0.12 mm reported in [Han et al., 2006].

In this work, approved subjects had significantly higher test–retest correlation (TRC) (Table 2) and intraclass correlation coefficient (ICC) (Table 3) and lower percent difference (PD) (Table 4) as compared with the disapproved subjects. Moreover, we observed that the test–retest reliability, across all three reliability measures, was higher when using regions defined by the DK atlas rather than the Destrieux atlas. Although the percent difference of all groups was low, percent difference of approved subjects using the DK atlas was the lowest (<1%). Further investigation revealed that this difference was related to differences in the sizes of the regions defined by each atlas. (The regions in the DK atlas are mostly larger than those defined by the Destrieux atlas.) As Figure 4 shows, there is a (nonlinear) relationship between percent difference of cortical thickness and regional volume/surface area. Power coefficients were the same (b = 0.35) for both cases, indicating that the power law relationship between percent difference vs. cortical volume and percent difference vs. cortical surface area are similar. As expected, regions with smaller sizes have measures with lower reliability (as their boundaries are harder to define reliably). Although it has been pointed out that a relationship between reliability and region size exists [Tustison et al., 2014], none of the previous studies have directly examined the relationship between the reliability and the regional surface area/volume.

In Supporting Information Table 1, test–retest reliability was evaluated for the eight subjects before and after brain mask intervention to determine the effect of the intervention. Consistent with previous results, approved (i.e., after intervention) subjects had significantly higher TRC, ICC, and lower PD as compared with the disapproved (i.e., before intervention) subjects. Brain mask cleaning (i.e., manually cleaning using the Freeview application) was the only type of manual intervention that reliably improved surface delineation accuracy in this study. However, the pre/post intervention comparison indicates that these types of manual interventions can improve FreeSurfer‐based results and should therefore be encouraged. As with the initial images, post‐intervention results must be also carefully reviewed.

In Supporting Information Tables (II–VII), the great difference in the regional reliability is worth mentioning. The difference in the four subject groups can be seen clearly for each region. As presented in Figure 4, regional cortical thickness measures are sensitive to regional volume. In the Destrieux atlas, negative TRC and ICC values were observed for cortical thickness in the temporal pole, occipital pole and fronto‐marginal gyrus and sulcus in Supporting Information Tables 3, 4. However, the negative results were observed only for the Travel Group, which showed the lowest ICC among four groups. For the other groups, TRC and ICC remained positive in the same site scans even for the regions with small volumes. It has been pointed out that the boundaries of the temporal pole and occipital lobe were not defined precisely and that variation across individuals in these regions is often observed [Destrieux et al., 2010]. This may also affect within‐subject measurements. With the additional variation resulting from the scanner differences, this might explain the negative TRC and ICC values. However, reliability of cortical surface area and volume appeared unaffected by the between‐site comparisons, suggesting that cortical thickness is more susceptible to scanner differences than cortical surface area and volume.

Figures 5, 6, 7 show that test–retest reliability of cortical thickness differs across sites. This may be due variability in scanner characteristics. Cortical surface area TRC (Fig. 5) and ICC (Fig. 6) measures were also susceptible to site differences. However, they were not as susceptible to site differences as cortical thickness measures. Estimations of cortical volume were more robust to site differences and did not exhibit significant differences except TRC (Fig. 5) measure. Despite the great variability in cortical thickness reliability across sites, approved subjects showed consistently higher TRC and lower PD than the combined group within the same site. These results indicate that, in this sample, regardless of scanner characteristics, the approval process improves reliability. It is therefore, likely a finding generalizable to most sites.

TRC and ICC of cortical surface area and cortical volume were higher than cortical thickness. In the literature, a similar tendency was reported for ICC (CT: ICC = 0.87, CS: ICC = 0.97, CV: ICC = 0.97) by Liem et al. [2015] when there was no surface‐based smoothing. As Winkler et al. [2010] explains, in a surface‐based representation, volume is more highly correlated with area because volume is a quadratic function of surface distance and only a linear function of thickness. They also added that cortical thickness has low genetic, environmental, and phenotypic correlation with cortical surface area, which supports the hypothesis that these two measures have different genetic origins. They found no significant correlations between cortical thickness and surface area for most of the cortical regions. Similarly, Liem et al. showed that surface‐based smoothing can increase the reliability of cortical thickness (ICC = 0.91), but at the expense of cortical surface area (ICC=0.87) and volume (ICC=0.94) reliability for a smoothing kernel=20 mm [Liem et al., 2015]. They concluded that smoothing reduced the variance of cortical thickness less than surface area or volume.

Liem et al.'s reliability results were higher than the results presented here, likely due to their use of Freesurfer's longitudinal pipeline, which was designed to improve consistency and reliability in processing and analysis of intra‐subject scans. The longitudinal pipeline was not used in this work because the goal of our study was not to identify reliability in the ideal case, but rather to use the test–retest analysis to estimate variability that is not due to anatomical differences (i.e., within subject variability). Further, we wanted to be consistent with the analysis performed in a standard cross‐sectional study, in which multiple MR images of the same individual are not usually acquired.

The variance in measurements such as cortical thickness will affect the total number of subjects required to observe differences between groups (such as depressed versus controls). Based on estimates of variance from this work, the required number of subjects to distinguish groups with a desired power was calculated (see Table 5). A similar approach was performed by Han et al. [2006]. Their sample size estimation showed that cortical thickness differences of 0.2 mm (10%) could be identified with only 7 subjects (per group) whereas difference of 0.1 mm (5%) could be detected with 26 subjects (significance level = 0.05, one‐sided, statistical power = 0.9). In this case, the measurement error was 0.09 mm, which is comparable to our study. Similarly, their estimated values, though based on a one‐sided analysis, are within the range of required subjects estimated in this work. In our study, we give a range of required subjects that, as observed in Table 5, is highly dependent on the variation in the regional cortical thickness measurement (which is dependent on region size). A similar approach was performed by Liem et al. [2015]. They showed the number of required subjects (α = 0.05 (two‐tailed), statistical power = 0.8) to detect a difference of 10% in Freesurfer measures using different smoothing options (0, 10, and 20 mm). The results showed that smoothing decreases the number of required subjects, though the range of the required number of subjects needed to detect differences is similar to ours. Unique to our study, we provide a comparison of increased number of subjects needed to compensate for use of data that has not been visually inspected (approved+disapproved). As Table 5 shows, the visually approved group requires fewer subjects to detect a predefined percent cortical thickness difference compared to using all subjects. This is especially dramatic when the expected group difference decreases. This type of calculation may be important for those trying to balance the costs of time‐consuming FreeSurfer approvals versus using uninspected data.

CONCLUSION

The purpose of this work was to understand the reliability of automated measures of cortical volume, surface area, and thickness extracted by FreeSurfer. Establishing this reliability is essential for designing and interpreting studies that evaluate differences in these measures between groups. This study was performed on test–retest MRI data acquired at four different sites—providing a robust test bed for analysis. Further, a unique aspect of this study was that key intermediate processing outputs (segmentation, parcellation) of FreeSurfer were all carefully visually inspected for accuracy. The results indicate that the approval process results in more reliable thickness, surface area and volume estimates. This holds true within each site tested, despite the dependence of reliability measures on the site of acquisition. The reduced variance of the approved subjects allows between‐group comparisons to be made with fewer subjects (for the same expected difference and power). Other general trends include the robustness of the cortical volume measure over cortical thickness, and the dependence of reliability on the volume and the surface area of the region. Given the role of the cortical thinning in psychiatric and neurodegenerative diseases, and the increasing use of automated calculation of these measures, this type of study is important to establish reliability and need for manual assessment of automated outputs. We concur with others that FreeSurfer performs well for cortical thickness and even better for cortical surface and cortical volumes, but its performance is significantly improved by the addition of visual screening approval, which enhances precision and therefore power, and may be considered to be cost effective for some applications. Our data may be useful for precision estimation and power calculations, including in the increasingly common situation where multiple scanner platforms are used in collaborative studies.

Supporting information

Supporting Information Figure 1

Supporting Information Figure 2

Supporting Information Table 1

Supporting Information Table 2

Supporting Information Table 3

Supporting Information Table 4

Supporting Information Table 5

Supporting Information Table 6

Supporting Information Table 7