Dead-End Elimination with a Polarizable Force Field Repacks PCNA Structures

Abstract

A balance of van der Waals, electrostatic, and hydrophobic forces drive the folding and packing of protein side chains. Although such interactions between residues are often approximated as being pairwise additive, in reality, higher-order many-body contributions that depend on environment drive hydrophobic collapse and cooperative electrostatics. Beginning from dead-end elimination, we derive the first algorithm, to our knowledge, capable of deterministic global repacking of side chains compatible with many-body energy functions. The approach is applied to seven PCNA x-ray crystallographic data sets with resolutions 2.5–3.8 Å (mean 3.0 Å) using an open-source software. While PDB_REDO models average an R_free value of 29.5% and MOLPROBITY score of 2.71 Å (77th percentile), dead-end elimination with the polarizable AMOEBA force field lowered R_free by 2.8–26.7% and improved mean MOLPROBITY score to atomic resolution at 1.25 Å (100th percentile). For structural biology applications that depend on side-chain repacking, including x-ray refinement, homology modeling, and protein design, the accuracy limitations of pairwise additivity can now be eliminated via polarizable or quantum mechanical potentials.

Introduction

The Protein Data Bank (PDB; http://www.rcsb.org/pdb/home/home.do) (1) now contains biomolecular structural models derived from >90,000 x-ray diffraction experiments conducted over the last half century. More than 80,000 of these structures have been deposited with their original diffraction data, which permits the experiments to be more fully interpreted as biomolecular refinement programs improve (2,3). Only a small fraction of PDB structures result from diffraction data to atomic resolution (i.e., ∼1 Å). Mid- to low-resolution data sets, such as those for proliferating-cell nuclear antigen (PCNA) studied here, are much more common (Fig. 1). For these data, attainment of high-quality models relies heavily on the use of both systematic validation tools such as MOLPROBITY (4) and the prior chemical knowledge contained in molecular mechanics force fields (5). It is also possible to leverage previously solved structures to parameterize restraints based on elastic networks (6,7), although this level of coarse-graining is incapable of repacking side chains as networks deform or come together to form the interface of a complex.

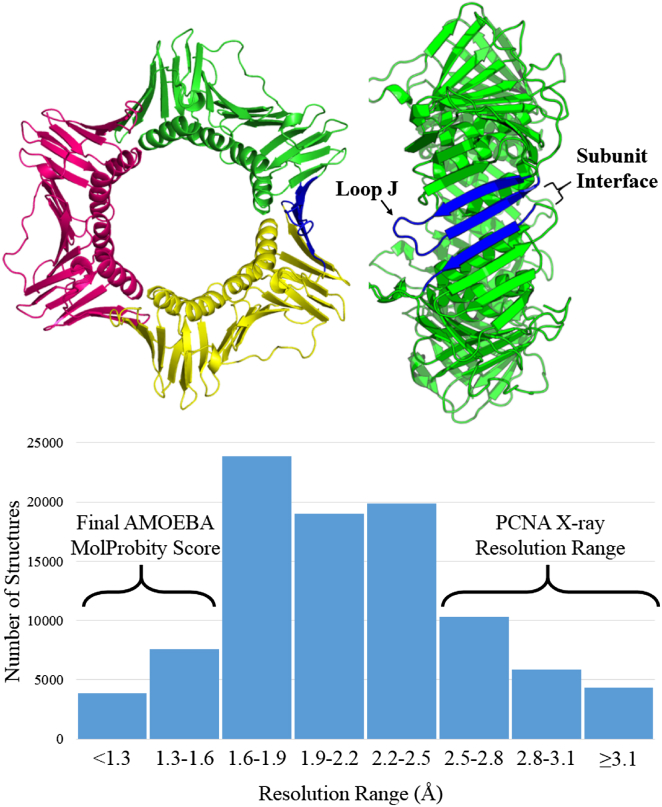
Figure 1.

The biological unit of PCNA (above) is a trimeric ring with a central hole for binding double-strand DNA. Viewing PCNA from the side shows the subunit interface between two PCNA monomers (blue). Histogram (below) showing the number of x-ray diffraction data sets within resolution bins for structures deposited in the PDB as of January 20, 2015. The experimental resolution and deposited MOLPROBITY scores for the PCNA data sets used in this study averaged 2.96 and 2.86 Å, respectively. Structures determined by the algorithm described here yielded a mean MOLPROBITY score of 1.25 Å.

To address the protein side-chain repacking problem, a brute force search over discrete conformations is computationally intractable for even small proteins due to a combinatorial explosion of conformational possibilities. However, by considering the relative energetics of discrete side-chain conformations (rotamers) for a single residue in the context of its interactions with the rest of the protein structure, unfavorable rotamers can be eliminated by proving that they cannot be part of the global minimum energy conformation (GMEC). The eliminated conformations are dead-ends in the search; therefore, the algorithm used to eliminate rotamers, rotamer pairs, and so on, is known as dead-end elimination (DEE).

The combination of low-energy side-chain rotamer libraries (8–10) with DEE (11,12) global optimization has been widely used for protein electrostatic network optimization and sequence design (13–17). However, rotamer elimination criteria have only been defined for pairwise-additive energy functions such as the OPLS-AA (18), AMBER (19), and CHARMM (20) families of fixed partial-charge force fields and pairwise decomposable continuum solvents (21–23). Explicit inclusion of many-body effects has been neglected such that the strength of the interaction between two residues must be independent of their mutual environment. Therefore, important molecular driving forces such as the hydrophobic effect (24) and electronic polarization (25), which are fundamentally many-body in nature, have been implicitly approximated or neglected entirely (Fig. 2). Here we overcome the restriction to pairwise energy functions by showing that both the DEE criteria (11) and more-stringent Goldstein criteria (12) can be derived in the context of many-body energy functions such as polarizable force fields (25,26) as well as quantum mechanical potentials and continuum solvents (27–30).

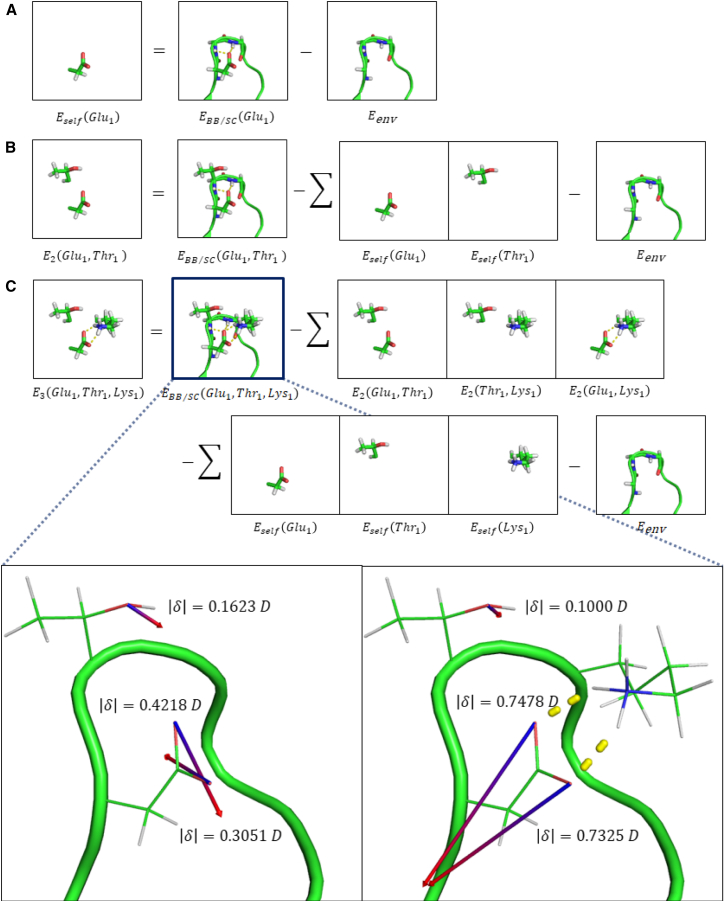
Figure 2.

This diagram explains energy terms used in Eq. 1 including the (A) self-energy, (B) two-body energy, and (C) three-body energy. The induced dipole vectors for three side-chain oxygen atoms in wild-type PCNA are shown in the absence of Lys¹⁰⁷ (left) and in its presence (right). A vector length of 7 Å corresponds to 1 Debye. Changes in induced dipole direction and magnitude reflect the AMOEBA electronic polarization response to the total electrostatic field, which results in polarization energy that is not pairwise. For this example, the three-body energy is 1.55 kcal/mol.

Rotamer and rotamer pair elimination criteria compatible with many-body energy functions are given below and their derivations supplied in the Supporting Material. For a pairwise decomposable energy function, the new expressions simplify to the established elimination criteria. The approach is used to refine a series of PCNA structures in the context of a many-body x-ray crystallographic target function E_tot = E_chem + w_Aex-ray. Here E_chem is a parallelized implementation of the polarizable AMOEBA force field that supports space group symmetry (31), E_x-ray is a real-space electron density function (32,33), and w_A is used to weight the importance of the force field and x-ray terms (33). The resulting AMOEBA structures are compared to PDB_REDO (34) and pairwise DEE refinements based on the OPLS-AA/L(18) fixed charge force field.

Finally, functional insights into changes in PCNA stability due to single amino-acid mutations are discussed. PCNA plays an essential role in the maintenance of genome stability. It is a replication accessory factor that interacts with and regulates the activities of proteins involved in DNA replication, DNA repair, DNA recombination, chromatin modifications, sister chromatid cohesion, and cell-cycle control (35). Each PCNA subunit consists of two domains, which interact in a head-to-tail arrangement to form a ring-shaped homo-trimer possessing pseudo-sixfold symmetry (Fig. 1) (36). The PCNA trimer binds double-stranded DNA through the central pore of the ring. PCNA function is regulated in part by posttranslational modifications. For example, ubiquitylation of PCNA on Lys¹⁶⁴ promotes translesion synthesis (TLS), which is the replicative and generally mutagenic bypass of damaged DNA (37). Several separation-of-function mutations in PCNA have been identified that inhibit various cellular processes including DNA mismatch repair as well as TLS (38,39). X-ray structures of wild-type PCNA, ubiquitin-modified PCNA, SUMO-modified PCNA, two separation-of-function mutant PCNA proteins that block mismatch repair, and two separation-of-function mutant proteins that block TLS have been determined (40–42).

Materials and Methods

Theory

Side-chain repacking with a pairwise potential

For a potential energy function that approximates nonbonded interactions as being a pairwise sum over residues, the total energy of a protein E(r) is given by

$$E\left(\mathbf{r}\right)=E_{\text{env}}+\sum _i{E}_{\text{self}}\left(r_i\right)+\sum _i\sum _{j>i}{E}_2\left(r_i,r_j\right),$$ (1)

where E_env is the energy of the environment (i.e., the protein backbone and residues that are not being optimized), E_self(r_i) is the self-energy of residue $i$ including its intramolecular bonded energy terms and nonbonded interactions with the backbone, and E₂(r_i, r_j) is the two-body nonbonded interaction energy between residues i and j with other residues turned off. The self-energy and two-body terms, diagrammed in Fig. 2, are calculated as

$$E_{\text{self}}\left(r_i\right)=E_{BB/SC}\left(r_i\right)-E_{\text{env}},$$ (2)

$$E_2\left(r_i,r_j\right)=E_{BB/SC}\left(r_i,r_j\right)-E_{\text{self}}\left(r_i\right)-E_{\text{self}}\left(r_j\right)-E_{\text{env}},$$ (3)

where E_BB/SC(r_i) is the energy of the protein backbone with only the side chain of residue i attached. Likewise, E_BB/SC(r_i,r_j) is the energy of the backbone and only side chains i,j. E_env is subtracted from each self and two-body term to avoid double counting. The original elimination criteria for rotamers and rotamer pairs (11), respectively, under the approximation of a pairwise decomposable force field, are

$$E_{\text{self}}\left(r_i^{\alpha }\right)+\sum _{j^{\prime }}\underset{\gamma }{\text{min}}{E}_2\left(r_i^{\alpha },r_j^{\gamma }\right)>E_{\text{self}}\left(r_i^{\beta }\right)+\sum _{j^{\prime }}\underset{\gamma }{\max }{E}_2\left(r_i^{\beta },r_j^{\gamma }\right),$$ (4)

$$E_{\text{pair}}\left(r_i^{\alpha },r_j^{\beta }\right)+\sum _{k^{\prime }}\underset{\epsilon }{\text{min}}\left[E_2\left(r_i^{\alpha },r_k^{\epsilon }\right)+E_2\left(r_j^{\beta },r_k^{\epsilon }\right)\right]>E_{\text{pair}}\left(r_i^{\gamma },r_j^{\delta }\right)+\sum _{k^{\prime }}\underset{\epsilon }{\max }\left[E_2\left(r_i^{\gamma },r_k^{\epsilon }\right)+E_2\left(r_j^{\delta },r_k^{\epsilon }\right)\right],$$ (5)

$$E_{\text{pair}}\left(r_i^{\alpha },r_j^{\beta }\right)=E_{\text{self}}\left(r_i^{\alpha }\right)+E_{\text{self}}\left(r_j^{\beta }\right)+E_2\left(r_i^{\alpha },r_j^{\beta }\right),$$ (6)

where r_i^α and r_i^β are different rotamers of the same residue i. The prime notation indicates that the summation occurs over all residues i ≠ j; similarly, k′ implies k ≠ i, k ≠ j.

Side-chain repacking with a many-body potential

Under a many-body potential, the total energy of a protein E(r) can be defined to arbitrary precision using the expansion

$$E\left(\mathbf{r}\right)=E_{\text{env}}+\sum _i{E}_{\text{self}}\left(r_i\right)+\sum _i\sum _{j>i}{E}_2\left(r_i,r_j\right)+\sum _i\sum _{j>i}\sum _{k>j}{E}_3\left(r_i,r_j,r_k\right)+\sum _i\sum _{j>i}\sum _{k>j}\sum _{l>k}{E}_4\left(r_i,r_j,r_k,r_l\right)+\dots ,$$ (7)

where the three- and four-body contributions, respectively, are given by

$$E_3\left(r_i,r_j,r_k\right)=E_{BB/SC}\left(r_i,r_j,r_k\right)-E_{\text{self}}\left(r_i\right)-E_{\text{self}}\left(r_j\right)-E_{\text{self}}\left(r_k\right)-E_2\left(r_i,r_j\right)-E_2\left(r_i,r_k\right)-E_2\left(r_j,r_k\right)-E_{\text{env}},$$ (8)

$$E_4\left(r_i,r_j,r_k,r_l\right)=E_{BB/SC}\left(r_i,r_j,r_k,r_l\right)-E_{\text{self}}\left(r_i\right)-E_{\text{self}}\left(r_j\right)-E_{\text{self}}\left(r_k\right)-E_{\text{self}}\left(r_l\right)-E_2\left(r_i,r_j\right)-E_2\left(r_i,r_k\right)-E_2\left(r_j,r_k\right)-E_2\left(r_i,r_l\right)-E_2\left(r_j,r_l\right)-E_2\left(r_k,r_l\right)-E_3\left(r_i,r_j,r_k\right)-E_3\left(r_i,r_j,r_l\right)-E_3\left(r_i,r_k,r_l\right)-E_3\left(r_j,r_k,r_l\right)-E_{\text{env}}.$$ (9)

The DEE rotamer and rotamer pair elimination equations, respectively, can be extended to arbitrary order as follows:

$$E_{\text{self}}\left(r_i^{\alpha }\right)+\sum _{j^{\prime }}\underset{\gamma }{\text{min}}\left\{E_2\left(r_i^{\alpha },r_j^{\gamma }\right)+\sum _{k^{\prime }}\underset{\delta }{\text{min}}\left[E_3\left(r_i^{\alpha },r_j^{\gamma },r_k^{\delta }\right)+\dots \right]\right\}>E_{\text{self}}\left(r_i^{\beta }\right)+\sum _{j^{\prime }}\underset{\gamma }{\max }\left\{E_2\left(r_i^{\beta },r_j^{\gamma }\right)+\sum _{k^{\prime }}\underset{\delta }{\max }\left[E_3\left(r_i^{\beta },r_j^{\gamma },r_k^{\delta }\right)+\dots \right]\right\},$$ (10)

$$E_{\text{pair}}\left(r_i^{\alpha },r_j^{\beta }\right)+\sum _{k^{\prime }}\underset{\epsilon }{\text{min}}\left\{E_2\left(r_i^{\alpha },r_k^{\epsilon }\right)+E_2\left(r_j^{\beta },r_k^{\epsilon }\right)+E_3\left(r_i^{\alpha },r_j^{\beta },r_k^{\epsilon }\right)+\sum _{l^{\prime }}\underset{\eta }{\text{min}}\left[E_3\left(r_i^{\alpha },r_k^{\epsilon },r_l^{\eta }\right)+E_3\left(r_j^{\beta },r_k^{\epsilon },r_l^{\eta }\right)+E_4\left(r_i^{\alpha },r_j^{\beta },r_k^{\epsilon },r_l^{\eta }\right)+\dots \right]\right\}>E_{\text{pair}}\left(r_i^{\gamma },r_j^{\delta }\right)+\sum _{k^{\prime }}\underset{\epsilon }{\max }\left\{E_2\left(r_i^{\gamma },r_k^{\epsilon }\right)+E_2\left(r_j^{\delta },r_k^{\epsilon }\right)+E_3\left(r_i^{\gamma },r_j^{\delta },r_k^{\epsilon }\right)+\sum _{l^{\prime }}\underset{\eta }{\max }\left[E_3\left(r_i^{\gamma },r_k^{\epsilon },r_l^{\eta }\right)+E_3\left(r_j^{\delta },r_k^{\epsilon },r_l^{\eta }\right)+E_4\left(r_i^{\gamma },r_j^{\delta },r_k^{\epsilon },r_l^{\eta }\right)+\dots \right]\right\},$$ (11)

where the ellipses signify the presence of further higher-order terms up to n-body (see the Supporting Material for the derivation).

Although terms based on interactions between three or more residues are zero for pairwise decomposable energy functions such as OPLS-AA/L, for the polarizable AMOEBA force field the three-body term E₃(r_i, r_j, r_k) captures energetic changes due to mutual polarization between the three residues and their environment (Fig. 2). In the context of continuum solvation, higher-order terms additionally capture energetic changes that result from modifications to the protein-solvent dielectric boundary.

Goldstein elimination

More stringent elimination criteria were introduced by Goldstein (12), which for a pairwise energy function are given by

$$E_{\text{self}}\left(r_i^{\alpha }\right)-E_{\text{self}}\left(r_i^{\beta }\right)+\sum _{j^{\prime }}\underset{\gamma }{\text{min}}\left[E_2\left(r_i^{\alpha },r_j^{\gamma }\right)-E_2\left(r_i^{\beta },r_j^{\gamma }\right)\right]>0,$$ (12)

and

$$E_{\text{pair}}\left(r_i^{\alpha },r_j^{\beta }\right)-E_{\text{pair}}\left(r_i^{\gamma },r_j^{\delta }\right)+\sum _{k^{\prime }}\underset{\epsilon }{\text{min}}\left[E_2\left(r_i^{\alpha },r_k^{\epsilon }\right)+E_2\left(r_j^{\beta },r_k^{\epsilon }\right)-E_2\left(r_i^{\gamma },r_k^{\epsilon }\right)-E_2\left(r_j^{\delta },r_k^{\epsilon }\right)\right]>0,$$ (13)

for rotamer and rotamer pair elimination, respectively. The Goldstein elimination criteria, extended to include higher-order energy components for rotamers and rotamer pairs, respectively, are given by

$$E_{\text{self}}\left(r_i^{\alpha }\right)-E_{\text{self}}\left(r_i^{\beta }\right)+\sum _{j^{\prime }}\underset{\gamma }{\text{min}}\left\{E_2\left(r_i^{\alpha },r_j^{\gamma }\right)-E_2\left(r_i^{\beta },r_j^{\gamma }\right)+\sum _{k^{\prime }}\underset{\delta }{\text{min}}\left[E_3\left(r_i^{\alpha },r_j^{\gamma },r_k^{\delta }\right)-E_3\left(r_i^{\beta },r_j^{\gamma },r_k^{\delta }\right)\dots \right]\right\}>0,$$ (14)

and

$$E_{\text{pair}}\left(r_i^{\alpha },r_j^{\beta }\right)-E_{\text{pair}}\left(r_i^{\gamma },r_j^{\delta }\right)+\sum _{k^{\prime }}\underset{\epsilon }{\text{min}}\{E_2\left(r_i^{\alpha },r_k^{\epsilon }\right)+E_2\left(r_j^{\beta },r_k^{\epsilon }\right)+E_3\left(r_i^{\alpha },r_j^{\beta },r_k^{\epsilon }\right)-E_2\left(r_i^{\gamma },r_k^{\epsilon }\right)-E_2\left(r_j^{\delta },r_k^{\epsilon }\right)-E_3\left(r_i^{\gamma },r_j^{\delta },r_k^{\epsilon }\right)+\sum _{l^{\prime }}\underset{\eta }{\text{min}}{E}_3\left(r_i^{\alpha },r_k^{\epsilon },r_l^{\eta }\right)+E_3\left(r_j^{\beta },r_k^{\epsilon },r_l^{\eta }\right)+E_4\left(r_i^{\alpha },r_j^{\beta },r_k^{\epsilon },r_l^{\eta }\right)\left[-E_3\left(r_i^{\gamma },r_k^{\epsilon },r_l^{\eta }\right)-E_3\left(r_i^{\delta },r_k^{\epsilon },r_l^{\eta }\right)-E_4\left(r_i^{\gamma },r_j^{\delta },r_k^{\epsilon },r_l^{\eta }\right)+\dots \right]\}>0.$$ (15)

Many-body x-ray refinement function

Pairwise molecular mechanics force fields have been used in tandem with experimental x-ray diffraction data to refine protein structural models for more than two decades (43,44). To quantify agreement between the experimental and model electron densities, and avoid overfitting, both R and R_free values are monitored (45). To measure agreement between the structural model and prior chemical knowledge, the MOLPROBITY structure validation tool (4) compares van der Waals contacts, hydrogen-bond distances, side-chain rotamers, and peptide backbone conformation with tabulated values from high-resolution protein structures. The overall MOLPROBITY score was calibrated against the PDB to reflect the x-ray diffraction resolution that, on average, is needed to produce a structure of a given quality. For example, the average MOLPROBITY score for the original seven PCNA models indicates structure quality consistent with 2.86 Å diffraction data, which is near the actual 2.96 Å experimental resolution of the data. MOLPROBITY clash scores were corrected based on experimental evidence (46) and quantum mechanical calculations for the optimal CH…O hydrogen-bond distance (47). Although the ideal distance is reported to be 2.3 Å, MOLPROBITY incorrectly reports this separation as a clash (31). The corrected scores are denoted uwith a footnote as MOLPROBITY^a.

The optimization procedure used here operates on a hybrid target function based on maximum-likelihood principles (48). The target function (E_Tot) is composed of a weighted sum of force-field (25,49,50) (E_chem) and x-ray (E_x-ray) energy terms, where the latter is a measure of the agreement between a real-space map and the electron density of the model:

$$E_{\text{Tot}}=E_{\text{chem}}+w_A{E}_{\text{x}\text{-}\text{ray}}.$$ (16)

Calculation of real-space density maps followed the formalism of Read (51) and implementation of Cowtan (52) to compute σ_A and figure-of-merit coefficients for structure factors. Real-space density values at specific coordinates were computed using a Catmull-Rom spline (τ = 0.25). OPLS-AA/L and AMOEBA electrostatics were evaluated using particle-mesh Ewald summation as described previously in Schnieders et al. (31).

Methods

The rotamer elimination criteria were implemented in the FORCE FIELD X (FFX) molecular biophysics software package (http://ffx.biochem.uiowa.edu) (31,33) and applied in an iterative fashion, such that rounds of rotamer and rotamer-pair elimination were performed until no new eliminations were produced. The target function for all remaining permutations was then evaluated to determine the GMEC. For all AMOEBA stages of this work, the electron density and potential energy terms were weighted equally (33). The electron density weight was doubled for OPLS-AA/L refinements (w_A = 2) as this was observed to yield output structures with a better balance between R and other quality metrics.

Seven structures of PCNA were optimized according to the following protocol: input structures were first minimized (in coordinates and temperature factors) to remove clashes, and then the coordinates of each side chain were recorded. Each unit cell was divided into subvolumes with axis lengths of 4 Å that were placed with 3 Å overlap between neighboring subvolumes. Residues were placed into any box containing their C_α atom. Side-chain optimization via DEE was performed on each box using the Richardson rotamer library augmented by the initial coordinates of each residue as an additional rotameric choice (Ponder and Richards (8)). Pairwise DEE was applied for OPLS-AA/L, while many-body DEE truncated after trimer interactions was used for AMOEBA. After another round of minimization in both coordinates and temperature factors, residues that remained in poor rotameric positions were optimized individually using the same criteria, but without using the initial coordinates as a rotameric choice. This final step was performed iteratively until no further improvement in structure quality metrics was achieved, which accounted for <5% of the final side-chain positions.

A conservative approximation was employed to significantly reduce the computational expense of applying the elimination criteria. All rotamers whose self-energy was 30 kcal/mol larger than that residue’s self-energy minimum were pruned before continuing on to two- and three-body calculations. This approach is based on the observation that rotamers with self-energy disparities of this magnitude, which often arise from side-chain van der Waals clashes with the protein backbone, are inconsistent with a well-packed GMEC (11). Such prunable rotamers are also eliminated during application of the rotamer elimination criterion; however, removing them immediately after self-energy calculation drastically reduces the required number of two- and three-body energies. This pruning strategy produced even more benefit under a hybrid target function because in many cases the density map is well fit by only a handful of rotamers.

Results and Discussion

Atomic-resolution quality from mid- to low-resolution diffraction

PCNA data sets (Table 1) are ideal for demonstrating the ability of the refinement approaches described above to achieve atomic-resolution structural quality from mid- to low-resolution diffraction data. Overall, many-body DEE with the AMOEBA polarizable force field yielded higher quality PCNA models than PDB_REDO, local minimization, or traditional two-body DEE using OPLS-AA/L (Table 2). Although each strategy was able to improve the original PDB models, many-body DEE displayed the most significant gains across all major quality metrics. Mean improvement in R_free was 3.0 for AMOEBA DEE versus 2.5 for pairwise OPLS-AA/L DEE and almost no reduction for PDB_REDO. The locally minimized structures were used as a baseline for comparing force-field energy, against which both OPLS-AA/L and AMOEBA DEE models were favored by an average of >200 kcal/mol per structure. These large increases in stability may favorably affect downstream computational methods such as molecular-dynamics simulations, which generally begin from a crystal structure after local optimization using a chosen force field, but without side-chain repacking. A more targeted analysis on the effects of the three-body term is available in Table S3 in the Supporting Material, which compares structure quality for the two- versus three-body approximation under AMOEBA. Three-body optimization under AMOEBA is shown to yield additional improvements not obtained by any other combination.

Table 1.

The PDB ID, resolution, R/R_free values, and MOLPROBITY analyses for the deposited PCNA models

Data Set	Resolution (Å)	Reported		FFX		MOLPROBITYa		Clasha		Ramachandran		Poor
		R	Rfree	R	Rfree	Score	%	Score	%	Out (%)	Favorable (%)	Rotamer (%)
3F1W	2.90	22.8	25.5	23.5	25.9	2.81	81	35.3	65	0.4	95.2	3.9
3GPM	3.80	27.5	31.2	35.4	34.3	3.43	73	52.9	51	4.0	89.3	7.5
3GPN	2.50	23.6	27.3	23.8	27.3	2.19	91	11.8	92	0.0	98.0	6.2
3L0W	2.80	27.9	31.4	31.5	33.2	3.57	23	51.0	20	0.0	92.3	15.8
3L0X	3.00	24.4	26.7	24.3	25.7	2.79	86	15.0	97	0.0	94.4	9.2
3L10	2.80	27.9	31.4	31.8	34.4	3.56	23	51.8	20	0.0	92.3	15.1
WT	2.95	24.6	27.3	24.9	27.3	1.65	100	5.5	100	0.4	94.9	0.9
Mean	2.96	25.5	28.7	27.9	29.7	2.86	68	31.9	64	0.7	93.8	8.4

^aSee main text for explanation.

Table 2.

The R/R_free values, change in force-field potential energy, and MOLPROBITY analyses for the PCNA data sets are given for PDB_REDO, OPLS-AA/L, and AMOEBA refinement methods

Data Set	Model	R	Rfree	EFF	MOLPROBITYa		Clasha		Ramachandran		Poor
					Score	%	Score	%	Out (%)	Favorable (%)	Rotamer (%)
3F1W	PDB_REDO	27.01	29.28		1.98	99	3.7	100	0.0	96.0	5.2
	OPLS-AA/L	23.78	26.86		1.78	100	1.0	100	0.8	93.3	5.2
	+ DEE	23.99	26.21	133	1.67	100	1.2	100	0.8	93.7	3.5
	AMOEBA	21.94	26.11		1.39	100	0.5	100	0.4	96.4	4.4
	+ DEE	22.12	26.25	−129	1.03	100	1.2	100	0.4	96.4	0.4
3GPM	PDB_REDO	30.14	32.01		2.68	96	8.5	97	4.8	86.9	6.1
	OPLS-AA/L	26.35	28.25		1.94	100	0.5	100	4.8	84.5	6.1
	+ DEE	23.88	26.32	40	1.51	100	0.5	100	3.2	85.3	1.8
	AMOEBA	29.53	30.43		2.13	99	1.3	100	5.6	84.9	6.6
	+ DEE	24.42	27.25	−110	1.33	100	0.0	100	4.4	85.7	1.8
3GPN	PDB_REDO	23.60	27.24		2.02	95	2.8	100	0.4	96.0	7.9
	OPLS-AA/L	21.26	25.60		1.86	97	1.8	100	0.4	95.6	6.6
	+ DEE	21.65	26.04	−242	1.41	100	1.3	100	0.8	95.6	2.2
	AMOEBA	20.75	25.19		2.07	94	2.3	100	0.0	96.4	12.3
	+ DEE	20.98	25.59	−351	1.28	100	0.5	100	0.0	96.4	3.1
3L0W	PDB_REDO	28.58	32.45		3.14	53	30.1	70	4.0	86.7	5.4
	OPLS-AA/L	30.07	31.50		1.99	99	1.0	100	1.2	93.2	10.1
	+ DEE	28.17	30.80	−316	1.86	99	0.8	100	1.9	92.3	7.1
	AMOEBA	27.09	29.71		2.29	96	2.9	100	1.2	92.3	9.4
	+ DEE	27.12	29.60	−260	1.17	100	1.0	100	0.6	94.7	1.7
3L0X	PDB_REDO	22.26	23.53		2.71	89	8.2	97	1.6	91.2	9.6
	OPLS-AA/L	21.33	24.27		2.05	99	1.3	100	1.6	93.6	10.9
	+ DEE	20.47	24.78	−334	1.51	100	0.8	100	1.6	92.8	2.6
	AMOEBA	20.92	24.10		2.22	98	3.0	100	0.8	92.4	7.4
	+ DEE	20.98	24.43	−125	1.25	100	1.8	100	1.6	92.8	0.4
3L10	PDB_REDO	28.01	32.04		3.35	37	43.8	33	5.0	84.2	5.4
	OPLS-AA/L	30.41	33.08		1.79	100	0.4	100	2.2	92.9	8.4
	+ DEE	27.04	30.65	−281	1.67	100	0.6	100	1.6	91.0	4.0
	AMOEBA	27.58	30.20		2.25	97	3.3	100	0.6	92.0	7.1
	+ DEE	26.82	29.56	−360	1.59	100	1.0	100	0.6	91.6	3.4
WT	PDB_REDO	28.71	30.15		3.06	68	14.6	96	0.8	92.1	15.6
	OPLS-AA/L	23.89	27.22		1.69	100	0.5	100	1.6	92.9	5.6
	+ DEE	23.21	25.57	−664	1.69	100	1.5	100	2.0	93.3	3.0
	AMOEBA	22.64	25.89		1.73	100	2.0	100	0.8	94.9	3.5
	+ DEE	21.63	24.24	−760	1.09	100	0.7	100	1.2	94.9	0.9
Mean	PDB_REDO	26.90	29.53		2.71	77	16.0	85	2.4	90.1	7.9
	OPLS-AA/L	25.30	28.11		1.87	99	0.9	100	1.8	92.3	7.6
	+ DEE	24.06	27.20	−238	1.62	100	0.9	100	1.7	92.0	3.5
	AMOEBA	24.35	27.38		2.01	98	2.2	100	1.3	92.8	7.2
	+ DEE	23.44	26.70	−299	1.25	100	0.9	100	1.3	93.2	1.7

All R/R_free values were calculated in FFX for consistency. Potential energy (E_ff) after DEE repacking is reported relative to the energy after local minimization (kcal/mol).

^aSee main text for explanation.

The MOLPROBITY score was improved by ∼1.0 using local minimization alone, by 1.24 using pairwise OPLS-AA/L rotamer optimization, and by 1.61 using many-body AMOEBA rotamer optimization. The latter placed all seven structures in the 100th MOLPROBITY percentile among structures of this resolution range (3.0 Å). Clash score was improved to the 100th percentile by all methods except PDB_REDO. The deposited structures averaged poor rotameric positions for 8.4% of side chains, which was not significantly improved by local minimization methods. DEE using both pairwise OPLS-AA/L and many-body AMOEBA algorithms reduced the percent of poor rotamers by 4.9 and 6.7%, respectively. Although both DEE methods yielded marked improvements in most structure quality metrics, the many-body AMOEBA improvements were greatest. Relative to OPLS-AA/L pairwise DEE, AMOEBA DEE shows mean additional improvements of a lower R_free by 0.5, lower MOLPROBITY score by 0.37, 1.8% fewer poor rotamers, better clash score, and more favorable Ramachandran values. These additional improvements are driven by the inclusion of many-body polarization and atomic multipole electrostatics, which are critically important to capture the bifurcated hydrogen bonding that stabilizes both α-helical and β-sheet secondary structure (Fig. 3 and Fig. S1 in the Supporting Material) (46). As shown in Table 3, truncation of the many-body expansion at pairwise interactions neglects ∼1 kcal/mol/residue of interaction energy under the AMOEBA polarizable force field. Fortunately, truncation at three-body interactions neglects <0.1 kcal/mol/residue, which is a reasonable compromise between efficiency and residual error due to higher-order neglected interactions (i.e., four-body and higher). Distributions of self, pair, and three-body energies for the wild-type structure, as well as distributions of slack (i.e., the amount of energy by which the elimination criterion was exceeded), are available in Fig. S4. Ninety-percent of three-body energies by absolute magnitude are greater than only 0.04% of self-elimination slacks and none of the pair slacks. The largest individual three-body energy, however, is >10 kcal/mol. We thus expect that there exist individual fourth- and higher-order energies (at short distances) with significant impact on elimination, but calculation of fourth-order energies represents an infeasible computational cost for structures of PCNA’s size. Comparison of run times for the methods tested herein is available in Table S4.

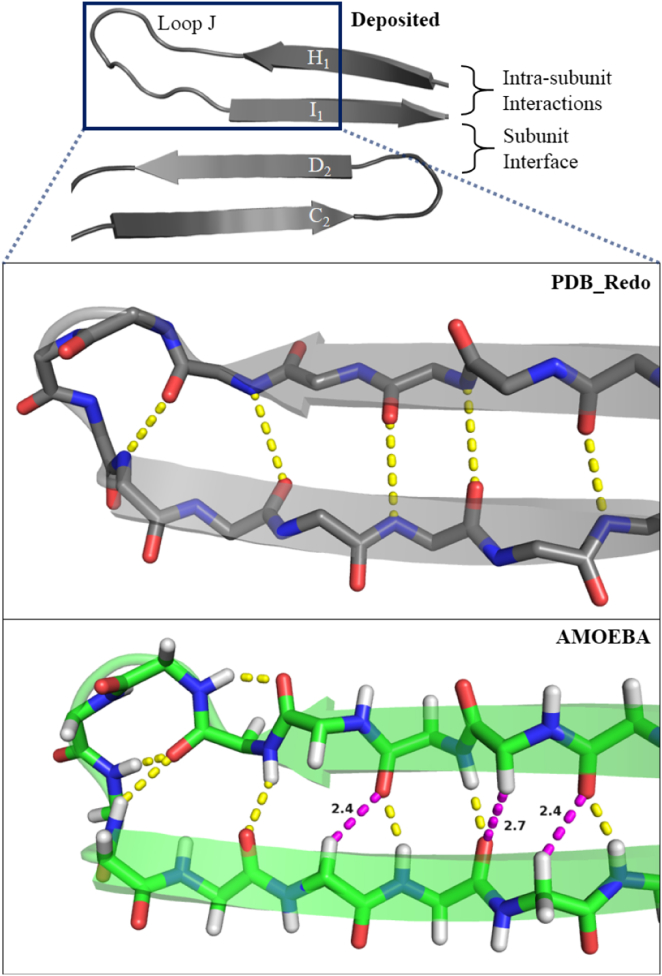
Figure 3.

The PCNA H₁ and I₁β-strands and loop J backbone electrostatic network for 3GPM from PDB_REDO and from the AMOEBA DEE refinement in FFX. The intrastrand interaction is stabilized by five backbone hydrogen bonds in the PDB_REDO structure (above), while the AMOEBA model (below) contains seven. The AMOEBA model has three additional low-energy C_αH···O bonds (purple). The bifurcated hydrogen bonding is driven largely by the quadrupole moment of the carbonyl oxygen. See Fig. S1 for similar improvements in α-helical structure.

Table 3.

Neglected higher-order energy when truncating at two- or three-body interactions when using the AMOEBA force field

Data Set	Etotal	Ebackbone	ΣEself	ΣEpair	ΣEtrimer	Eneglected		Eneglected/Residue
						Two-Body	Three-Body	Two-Body	Three-Body
3F1W	−7303.7	−2392.7	−2737.2	−2387.8	230.0	213.9	−16.0	0.8	−0.1
3GPM	−7777.1	−2459.3	−2886.1	−2687.5	283.0	255.7	−27.3	1.0	−0.1
3GPN	−7618.3	−2838.6	−2368.5	−2628.5	232.7	217.3	−15.4	0.9	−0.1
Wild-type	−7591.7	−2385.2	−2685.5	−2765.7	269.6	244.7	−24.9	1.0	−0.1
Mean						232.9	−20.9	0.9	−0.1

Total energy neglected when truncating the expansion after pairwise interactions is ∼1 kcal/mol/residue. By contrast, truncation after three-body interactions reduces the neglected energy by an order of magnitude to <0.1 kcal/mol/residue.

Structural insights into the relative stability of PCNA mutants

The newly refined AMOEBA models provide structural and mechanistic insights that are supported by the x-ray diffraction data, but were not achieved in the original models due to limitations in available refinement algorithms. To demonstrate this, we now focus on E113G and G178S TLS-deficient separation-of-function PCNA mutants (38,53). These substitutions, E113G in β-strand I₁ and G178S in β-strand D₂, are at the subunit interface of PCNA, where antiparallel strand interactions between I₁ and D₂ stabilize the PCNA trimer (36). The original structural models demonstrated partial separation of these β-strands in both mutant proteins relative to the wild-type protein (40). In addition, biochemical studies showed that both mutant proteins have significantly reduced trimer stability relative to the wild-type protein, which is responsible for their inability to support TLS (54).

The structural basis for the separation of β I₁ and β D₂ was indicated by the original model of the G178S mutant protein. The side-chain hydroxyl group on substituted Ser¹⁷⁸ (on β D₂) forms a new hydrogen bond with the backbone carbonyl of Glu¹¹³ (on β I₁), and this interaction alters the trajectory of β I₁ in the mutant protein (40). By contrast, the structural basis for the strand separation was not clear from the original model of the E113G mutant protein. The newly refined models, however, have provided what are, to our knowledge, novel insights into how the E113G substitution alters the structure of the subunit interface.

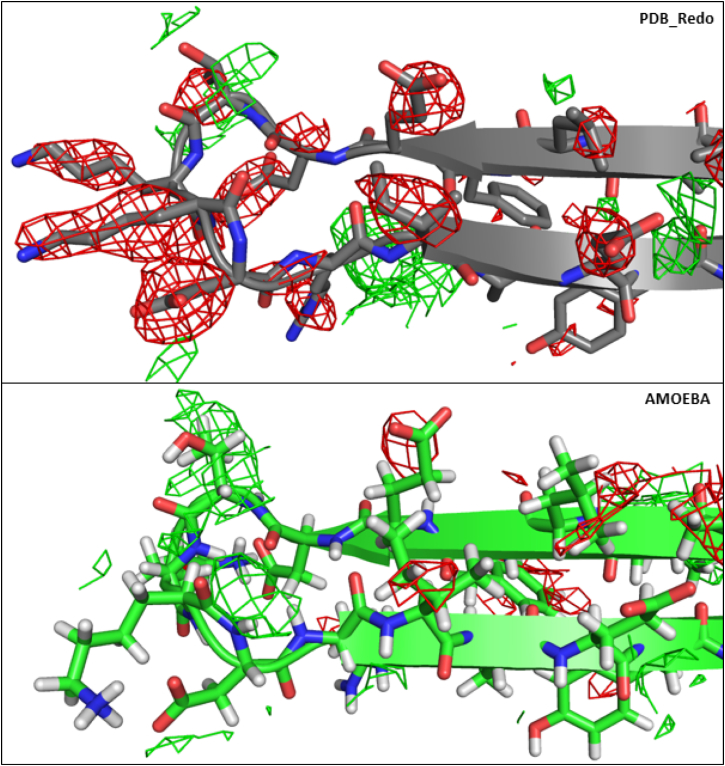
In the AMOEBA side-chain optimized model of the E113G mutant, the interaction between β I₁ and β H₁ is stabilized by increased hydrogen bonding. Comparing the structures of the wild-type and E113G mutant protein, we see that β H₁ is extended by one residue (position 105) and that β I₁ is extended by two residues (positions 109 and 110) in the mutant protein. In addition, the loop between β H₁ and β I₁ (loop J) appears to be in a more energetically favorable conformation in the mutant proteins. There are three intrastrand backbone hydrogen bonds in the mutant protein that are not present in AMOEBA side-chain optimized wild-type protein. A similar mechanism was proposed for a loss-of-flexibility S115P mutant (36) that caused trimer instability due to loss of interstrand hydrogen bonds. In wild-type PCNA, the trimeric form is more stable than the monomeric form by 1667 kcal/mol of AMOEBA energy; this stabilization drops to 1424 kcal/mol in the E113G mutant. Our results suggest a similar mechanism for the gain-of-flexibility E113G mutant based on an energetic tradeoff between the intermolecular interactions of β D₂ and β I₁ at the subunit interface and intramolecular interactions between β H₁ and β I₁ and within the backbone of loop J. The greater flexibility of β I₁ due to introduction of glycine at position 113 has shifted the balance in favor of stronger intramolecular β H₁-β I₁ interactions and loop-J hydrogen bonds (see Fig. 3 and Table S1). This is a possible explanation for the observed separation of the subunit interface and is consistent with reduced trimer stability. The AMOEBA PCNA electrostatic networks at the subunit interface are supported not only by lower MOLPROBITY score and lower R/R_free values, but also by dramatically cleaner σ_A-weighted F_o-F_c electron density maps (Fig. 4).

Figure 4.

The β-strands H₁ and I₁ of PCNA G178S mutant (3F1W) are shown with F_o-F_c maps contoured at 2σ (green) and −2σ (red) for PDB_REDO (above) and AMOEBA (below).

Conclusions

Biomolecular x-ray refinement strategies that place side chains, such as PDB_REDO (34) and RINGER (55), have achieved some success in improving the quality and interpretation of x-ray diffraction experiments. However, protein structure refinement methods have been limited by their assumption of side-chain independence and/or the absence of rigorous electrostatic interactions. For example, PDB_REDO is based on choosing a rotameric state for one residue at a time (56), which is reflected by a mean poor rotamer percentage of 6.6% for the PCNA structures examined here. On the other hand, many-body DEE using AMOEBA reduced the percentage of poor rotamers to 1.7% while simultaneously improving overall MOLPROBITY score and lowering both R_free and AMOEBA potential energy.

Model bias is an important consideration for any refinement procedure that optimizes atomic coordinates to a target function that depends on calculated phases. Neither systematic removal of backbone model bias nor optimization of backbone conformation beyond what is achieved by local minimization was considered in this work. However, several methods have been proposed for considering limited backbone flexibility during repacking, which could be coupled to many-body DEE in the future. For example, generation of a discrete set of backbone conformations to include during DEE has been described in Su and Mayo (57). Alternatively, deterministic DEE has been extended to find a flexible-backbone rigid-rotamer GMEC by calculating bounds on rotameric interaction energies given a limited range of backbone dihedral movements imposed by per-residue restraining boxes (58).

The side-chain repacking algorithm presented here, to our knowledge, is the first deterministic method compatible with many-body potential energy functions. This opens the door to using polarizable force fields, Poisson-Boltzmann electrostatics, and quantum mechanical potential energy functions alone or in combination with experimental data to improve protein structural models. In this work, a hybrid target function has shown success in improving MOLPROBITY score and lowering both R_free and AMOEBA potential energy based on a series of mid- to low-resolution PCNA x-ray diffraction data sets. In this case, electrostatic networks from coupled side-chain reorientations, which are difficult or impossible to refine by hand, revealed intramolecular stabilization of PNCA monomers at the expense of intermolecular hydrogen-bonding and destabilization of the active PNCA trimer.

In addition to x-ray structure determination, this work sets the foundation for application of many-body potential energy functions to computational protein design, homology modeling, and design of protein-ligand interactions. The advantage of many-body over pairwise DEE is of greatest importance for driving molecular forces that are inherently many-body in nature, including polarizable electrostatic interactions and the hydrophobic effect. For example, it has been suggested that the inherent many-body nature of the hydrophobic effect has made computational protein design a challenge for implicit solvents (59). Future applications of many-body DEE may help determine whether the use of polarizable force fields (26) and self-consistent reaction-field implicit solvents (28–30) can overcome the limitations of previous generation pairwise force fields (14) and pairwise implicit solvents (21–23) for computational protein design (15–17).

Author Contributions

S.D.L., S.G., W.T.A.T., and M.J.S. conceived the theory; S.D.L. performed the experiments; S.D.L., J.M.L., K.T.P., M.T.W., and M.J.S. analyzed the data; S.D.L., J.M.L., K.T.P., A.M.L., W.T.A.T., T.D.F., M.T.W., and M.J.S. contributed code/tools/structures; and S.D.L., J.M.L., K.T.P., M.T.W., and M.J.S. wrote the article.

Editor: Nathan Baker.