Switching of perpendicularly polarized nanomagnets with spin orbit torque without an external magnetic field by engineering a tilted anisotropy

Significance

When a spin orbit torque is applied to a magnet with perpendicular anisotropy, the induced spin accumulation is completely symmetric with respect to the magnetization. As a result, a deterministic switching cannot be achieved unless an external magnetic field is applied to break the symmetry. Here, we show that, by engineering a tilted anisotropy in a magnetic nanodot, the symmetry can effectively be broken and a deterministic switching of perpendicular magnetization can be achieved without needing the external magnetic field. These results are significant for the field of spintronics as the symmetry breaking provides new insight into the physics of spin orbit torque and the switching without a magnetic field could lead to significant impact in high-density storage applications.

Abstract

Spin orbit torque (SOT) provides an efficient way to significantly reduce the current required for switching nanomagnets. However, SOT generated by an in-plane current cannot deterministically switch a perpendicularly polarized magnet due to symmetry reasons. On the other hand, perpendicularly polarized magnets are preferred over in-plane magnets for high-density data storage applications due to their significantly larger thermal stability in ultrascaled dimensions. Here, we show that it is possible to switch a perpendicularly polarized magnet by SOT without needing an external magnetic field. This is accomplished by engineering an anisotropy in the magnets such that the magnetic easy axis slightly tilts away from the direction, normal to the film plane. Such a tilted anisotropy breaks the symmetry of the problem and makes it possible to switch the magnet deterministically. Using a simple Ta/CoFeB/MgO/Ta heterostructure, we demonstrate reversible switching of the magnetization by reversing the polarity of the applied current. This demonstration presents a previously unidentified approach for controlling nanomagnets with SOT.

Spin orbit coupling (SOC) and/or broken inversion symmetry in vertical heterostructures can generate accumulation of spins when a charge current is flowing through them. In doing so, it can exert a torque on an adjacent magnet (1–8). Indeed, high Z metals (Ta, Pt, W, etc.) with strong SOC have been used to inject spin currents into adjacent ferromagnetic layers and thereby to induce magnetic switching, oscillation, domain wall movement, etc. (1–5, 7–9). In a typical heterostructure such as Ta/CoFeB/MgO (from the bottom), an in-plane current flowing in the x direction (electrons flowing in the –x direction) generates $\widehat{\sigma }$ = $\widehat{y}$ polarized spins that accumulate at the Ta/CoFeB interface. Therefore, if the ferromagnet (CoFeB) is polarized in-plane, the spin accumulation can rotate it to the +y direction by a Slonczewski-like torque ${\overrightarrow{\tau }}_{sl}$ = ${\tau }_{sl}^0$ ($\widehat{m}\times \widehat{\sigma }\times \widehat{m}$) (10). The magnet can be switched to –y direction by reversing the polarity of the current. Thus, a deterministic switching is possible by an in-plane current when the magnet is also polarized in-plane. However, if the magnet has a perpendicular magnetic anisotropy (PMA), an in-plane current and resultant in-plane spin accumulation cannot break the reversal symmetry. Consequently, no deterministic switching of the PMA magnet can be obtained. For this reason, an external magnetic field has to be applied in-plane in the same (or opposite) direction of the current flow that breaks the symmetry and makes it possible to switch a PMA magnet with an in-plane current (11). It is, however, desirable to switch the magnetization without needing an external magnetic field. At the same time, PMA is more suitable for scaling magnets to ultrasmall dimensions while retaining reasonable thermal stability (12–14). This means that alternate ways need to be found that can lead to symmetry breaking and make it possible to switch perpendicularly polarized magnets with in-plane current without having to apply an external magnetic field. In this paper, we report on such a scheme where we have fabricated magnetic nanodots from a heterostructure stack of Ta/CoFeB/MgO such that their easy axes are slightly tilted from the film normal. This tilting breaks the symmetry with respect to an in-plane spin orbit torque (SOT). Indeed, pulsed currents flowing in-plane deterministically switch the magnetization up and down without any external magnetic fields. Notably, in a recent experimental work, Yu et al. (15) have shown that an in-plane current can switch perpendicularly polarized magnet by creating a thickness gradient in the film over the entire substrate. They showed that the structural symmetry breaking thus generated leads to a vertically oriented Rashba field that in turn switches the magnet. The physics of switching in our work, by contrast, is completely different. It is rather the nonconservative Slonczewski torque that is responsible for switching in our scheme and no distinguishable vertical Rashba field could be measured in our devices (as we discuss in details later).

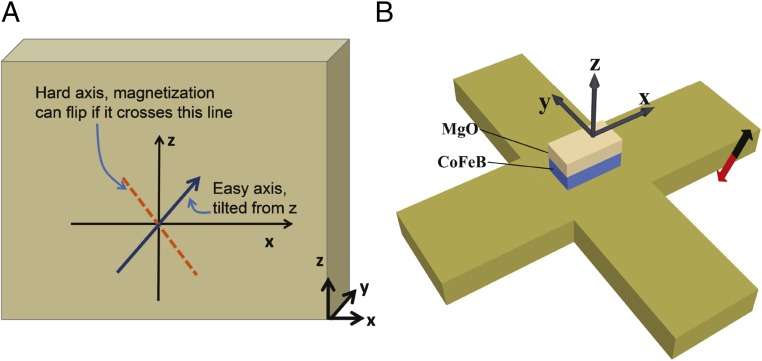
The essential idea is described in Fig. 1. Imagine a magnet that has an easy axis on the x–z plane but slightly tilted away from the z axis to x axis as shown in Fig. 1A. Here, x–y is the film plane. The actual device is made of a heterostructure consisting of Ta/CoFeB/MgO as shown in Fig. 1B. For brevity, when the magnet is in the (x, z) quadrature, we shall call it the “up” position. Similarly when it is in the (−x, −z) quadrature, we shall call it the “down” position. Now imagine a current is applied in the x direction such that a y polarized spin accumulation is generated at the Ta/CoFeB interface. Because y is orthogonal to the x–z plane, regardless of whether or not there is a tilt in the easy axis of the magnet in the x–z plane, no symmetry is broken and therefore the magnetization cannot be switched deterministically. However, this situation changes if a current is applied in the y or −y direction. This will generate a spin accumulation polarized in the –x or +x direction, respectively (for Ta). If the magnetization is in the x–z plane and tilted from the z axis, the direction of spin polarization (x or −x) is no longer symmetric with respect to the tilted easy axis of the magnet and this symmetry breaking can lead to deterministic reversal of the magnetization (16). For example, let us consider the situation when the magnet is polarized up and a current is flowing in the y direction leading to a spin polarization in the –x direction. If this accumulation is strong enough to rotate the magnetization to the –x direction, in the process, the magnet would cross over the hard axis, shown by the dotted line in Fig. 1A. This means that when the current is turned off, it is preferable for the magnet to now go to the down position in the (−x, −z) quadrature. On the other hand, if a current is applied in the –y direction, the spin accumulation is +x polarized. This means starting from up, the magnet, in the process of rotating to +x direction, does not cross over the hard axis. Thus, when the current is turned off, it is preferable for the magnet to go back to the up state. Thus, a current along +y switches the magnet from up to down. Similarly, a current along –y will switch the magnet from down to up. When the magnet is up, a current along –y does not change the state of the magnet. Similarly, when the magnet is down, a current along +y cannot change the state of the magnet. Thus, a fully deterministic switching of the perpendicular magnetization can be achieved without an external magnetic field.

Fig. 1.

Schematic description of switching mechanism and device structure. (A) Orientation of the easy axis and hard axis of an otherwise perpendicularly polarized magnet with slightly tilted anisotropy. (B) The fabricated device structure. The underneath Hall bar is composed of Ta and is used to generate spin accumulation through spin–orbit interaction and also to detect the direction of magnetization through anomalous Hall effect measurement. Current flowing along the short direction of the magnet (along the y axis) leads to a deterministic switching.

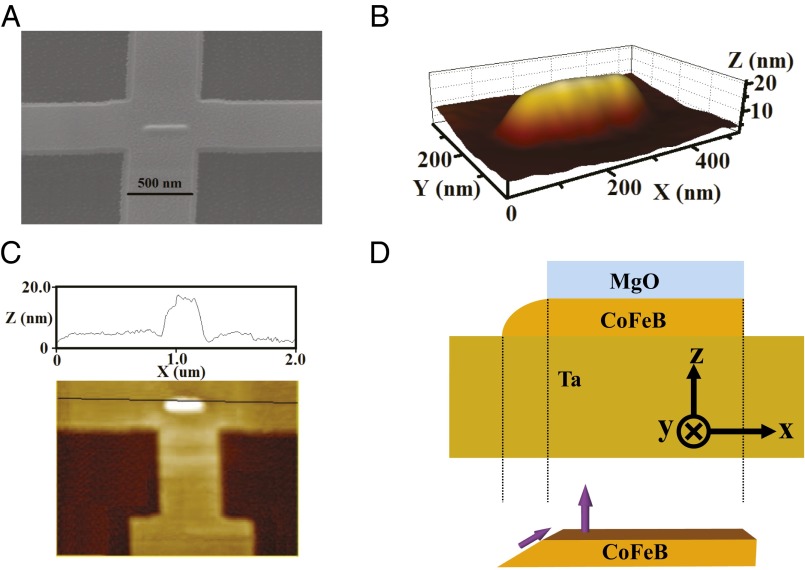
Our fabricated devices are based on a stack consisting of Ta (10 nm)/CoFeB (1 nm)/MgO (1 nm)/Ta (∼3 nm) (from the bottom). Vibrating sample magnetometer measurement shows excellent perpendicular anisotropy in the thin films (SI Appendix, section 1). First, small nanomagnets are patterned with a high aspect ratio (50 × 300 nm). Next, a wedge shape was created by carefully controlling the thickness of the hard mask and Ar⁺ ion milling such that the thickness of the magnet gradually goes to zero on one side (details are described in Methods and SI Appendix, Fig. S2). Fig. 2A shows an SEM micrograph of a typical nanodot and the underneath Hall structure for transport measurement. Fig. 2B shows an atomic force microscopy image of the nanodot. A wedge-like feature is clearly seen. The depth profile shown in Fig. 2C indicates that MgO with lateral size of around 50 nm in the left part of nanomagnet was completely etched, and CoFeB wedge was created. Because MgO was etched out, the magnetization in the wedge region no longer has a perpendicular anisotropy and will follow the edge of the wedge to minimize magnetostatic energy, thereby providing an overall tilt to the perpendicular magnet, directed away from the edge (17–20). Micromagnetic simulations (SI Appendix, section 2) confirm that this indeed is the case, as we will discuss later.

Fig. 2.

Engineering a tilted easy axis. (A) Scanning electron micrograph of the fabricated device. (B) Three-dimensional morphological characterization of nanomagnet by atomic force microscopy showing a wedge-like structure. (C) Quantitative measurement of the wedge using atomic force microscopy. (D) Schematic showing the structure and the tilt coming from the spins aligning to the wedge.

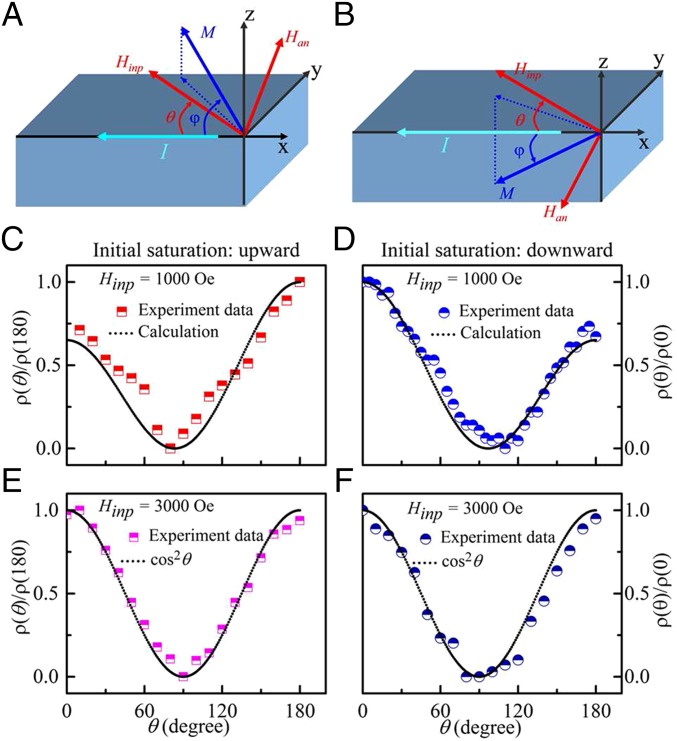
We have performed anisotropic magnetoresistance (AMR) measurements to investigate potential tilting of the easy axis. Note that all of the experiments in this work were done at the ambient temperature. In the coordinate axes as shown in Fig. 3 A and B, the dependence of resistivity on the rotation angle θ of the in-plane magnetic field (H_inp), as obtained from the AMR measurement, can be written as follows:

$$\rho \left(\theta \right)={\rho }_{\perp }+\left({\rho }_{//}-{\rho }_{\perp }\right){\cos }^2\varphi \left(\theta \right)={\rho }_{\perp }+\mathrm{\Delta }\rho {\cos }^2\varphi \left(\theta \right),$$ [1]

where φ is the angle between the magnetization M and the direction of current and (${\rho }_{//}$) is the resistivity when the magnetization is perpendicular (parallel) to the current direction. Let us consider the case when current is flowing in the −x direction and a H_inp of a specific amplitude is rotated in-plane, starting from the –x axis and ending on the +x axis. Because the current is applied along the x axis, from Eq. 1, the resistance is the maximum when the H_inp is also along the ±x direction. Resistance is lower when H_inp is rotated away from x axis. Notably, if the magnetic easy axis is purely out-of-plane to begin with, applying the same magnitude of H_inp in the +x or –x direction should give the same resistance value. By contrast, if the magnet is tilted on the +x axis, one would expect to see a larger resistance when the H_inp is in the +x direction in comparison with when the field is in the –x direction. This is exactly what we observe in our experiments. Starting from an initially up position, the resistance is larger when H_inp is in the +x direction compared with when it is in the direction and the resistance goes down away from the x axis (Fig. 3C). On the other hand, starting from an initial down position, the resistance is larger when H_inp is in the −x direction (Fig. 3D). This asymmetric resistance curve is also observed when magnetic fields of other magnitudes are applied such as 500, 800, 2,000 Oe, etc. (See SI Appendix, section 3, for details.) These data show that the easy axis of the magnetization is slightly tilted from the z axis and lies along (x, z) quadrature to (−x, −z) quadrature. The observed behavior can be modeled well from Eq. 1 including the fact that the lowest value of resistance arises slightly away from the y axis and the sign of the shift depends on the starting polarization of the magnet, i.e., up or down. Finally, we have done AMR measurements with large H_inp (∼3,000 Oe). Fig. 3 E and F show AMR data at this field starting from up and down positions, respectively. No asymmetry is observed between the AMR recorded for H_inp applied in the +x and –x direction. This is expected because now H_inp is strong enough to overcome the tilted anisotropy and the magnet follows the magnetic field. Thus, from the symmetric AMR along the x axis at high field and asymmetric AMR at low field, the existence of a tilted easy axis in the nanodots is confirmed. From the sign of the asymmetry, when the CoFeB wedge is in –x as shown in Fig. 2C, one can also conclude that the easy axis lies on the x–z plane, slightly tilted toward x from z, as shown in Fig. 1A. By AMR measurement, we can also estimate the angle of the tilt, which comes to be ∼2° with an error of 1° due to the uncertainty in the angle of the in-plane field. At the same time, from comparing the slant in the R-H loop of an anomalous Hall resistance measurement for the wedged dot to a circular dot, another estimate for the tilt amplitude can be made. This measurement gives the tilt angle to be ∼5° (SI Appendix, section 5). Based on these two measurements, we estimate the tilt angle to be between 2° and 5°.

Fig. 3.

Estimation of the tilt direction. The schematic configuration of the coordinate system used in the analysis of the AMR data. A and B show the configurations for the initial polarization of up and down, respectively. The sense current for AHE measurement flows along $-\widehat{x}$ direction pointing to the long axis of the nanomagnet. θ is the angle between the directions of the measurement current and the external in-plane field H_inp. θ = 0 corresponds to the orientation where the applied field is aligned to the direction of current flow. θ was taken as positive for an anticlockwise rotation of the field from current. φ is the angle between M and I. Calculated and measured values of AMR resistivity are shown when |H_inp| = 1,000 Oe and the magnet was initially polarized (C) upward and (D) downward. Calculated and measured values of AMR resistivity are shown when |H_inp| = 3,000 Oe, and the magnet was initially polarized (E) upward and (F) downward.

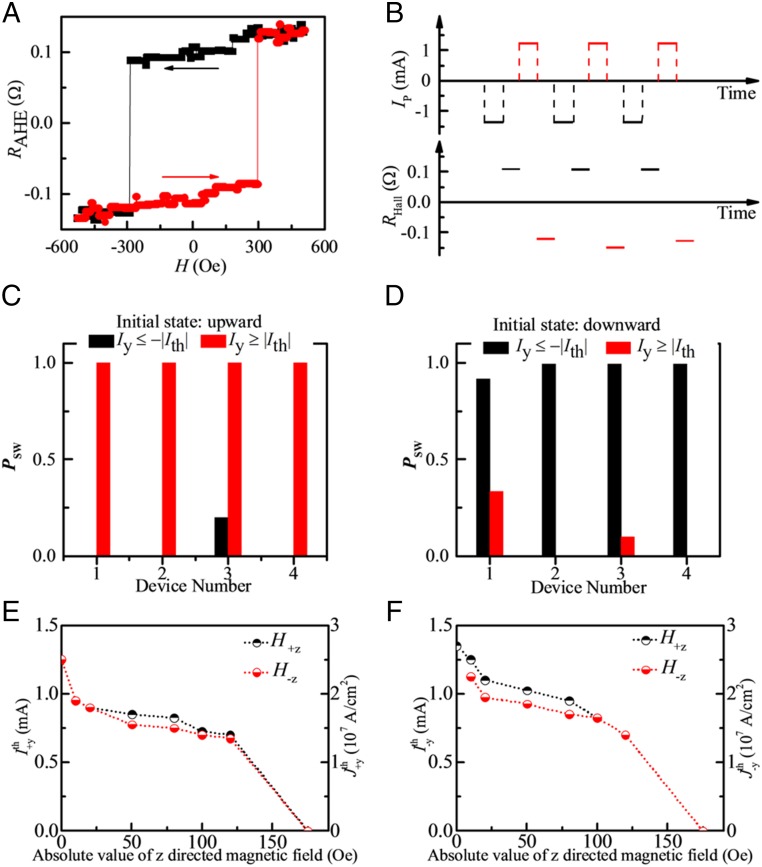
With such a tilted easy axis of the nanodots, the switching scenario described in the preceding paragraphs, namely a deterministic switching from up to down with a current in the y direction and from down to up with a current in the –y direction, should be possible. To demonstrate that we have performed anomalous Hall effect (AHE) measurements. The corresponding hysteresis loop is shown in Fig. 4A. Fig. 4B shows switching data at room temperature in the presence of zero external field. The magnet is saturated to down first by applying a strong vertical magnetic field in –z direction. Next, the field is turned off and a current pulse (∼1-s duration) of 1.25 mA (2.5 × 10⁷ A/cm²) is applied in the –y direction. After the pulse is off, an AHE measurement is done by applying a small sense current. The AHE resistance, as shown in the bottom panel of Fig. 4B, shows that the magnet is now up. Next, a current pulse of the same amplitude is applied in the +y direction. A subsequent AHE measurement finds the magnet in the down direction. In the process, value of R_AHE switches by ∼0.24 Ω. Comparing with Fig. 4A, this shows that a full switching of the magnet takes place. The full R-I loop measured in this way is provided in SI Appendix, section S.6.1.

Fig. 4.

In-plane current-induced switching without external magnetic field. (A) R-H hysteresis characteristic measured by AHE. Positive R_AHE corresponds to “upward” magnetization, whereas negative R_AHE corresponds to “downward” magnetization. (B) Evolution of R_AHE that corresponding to M_z as the direction of the current pulse reversed. (C and D) Histogram of the switching possibility on four different devices, all made from the same stack. The lateral sizes of devices 1, 2, 3, and 4 are 100 × 400 nm, 80 × 320 nm, 50 × 300 nm, and 40 × 280 nm, respectively. (E and F) Variation of the threshold amplitude of the switching current as a function of the absolute value of a magnetic field applied along the film normal for current flowing in the (E) +y direction and (F) −y direction.

We tested the reproducibility of the switching process by repeatedly reinitializing and subsequently switching the nanodot in one particular direction 10 times. Fig. 4C shows the observed behavior. First, the magnet is polarized in the up direction. Next, a +I_y (current flowing in the +y direction) is applied and a subsequent AHE measurement is done to find if the magnet has switched. Following that, the magnet is polarized up again with a magnetic field and again a +I_y is applied. This process is repeated 10 times. If the switching happens all 10 times, the switching probability (p_sw) is 1. Fig. 4C shows the switching probability for four different devices. We see that a 100% switching is observed for all devices. It is to be noted that starting from up –I_y is not supposed to change the state of the magnetization. To test that, the same experiment as described above is performed with the only exception that the current pulse is now applied in the –y direction. Among four different devices, each going through 10 repeated trials, only device 3 shows a small probability (0.2) of switching. We attribute this to thermal heating of the dots due to repeated pulsing. Next, a similar experiment is done on the same four devices but now starting from an initial down position and applying a −I_y. The data are shown in Fig. 4D. Again, an almost perfect switching probability is observed. Application of a +I_y is not expected to induce any switching in this case. We found that that is largely the case with some small errors in device 1 (0.3) and device 3 (0.1). This is again attributed to increased heating due to repeated pulsing. Fig. 4 B–D demonstrates deterministic switching of the magnetization without any external magnetic field by a current flowing along the y axis as described in the beginning of this paper. As it was mentioned, a current flowing in the x direction cannot break the reversal symmetry for our magnet, which lies on the x–z plane. Indeed, applying current pulses in the x direction did not lead to any deterministic switching of the magnet (SI Appendix, section S.6.2). A final test was done by using 200 × 200-nm magnets on a symmetric Hall bar without any wedge fabricated from exactly the same stack. Applying pulse current to such dots without any external magnetic field also did not lead to any deterministic switching (SI Appendix, section S.6.2).

Because there is a structural symmetry breaking due to the wedge shape in the fabricated nanodots in the x direction, it is possible to get a Rashba field in the out-of-plane direction when a current is flowing in the y direction (15). In principle, such a Rashba field can break symmetry and contribute to the switching of the nanodot. Second harmonic measurements in our devices show similar values for longitudinal and transverse field components to those that have been reported for similar structures in literature (6, 15, 21) (SI Appendix, section 8). To test the existence of an out-of-plane field in our devices, we have measured the threshold current needed to switch the magnetization in presence of an out-of-plane magnetic field. The basic idea is that if a current-induced Rashba field is present in the out-of-plane direction, the R_AHE vs. H_z hysteresis loop will be shifted left or right from its symmetric-around-zero position as shown in Fig. 4A. Fig. 4E shows the variation of threshold current flowing in the +y direction ($I_y^{th}$) as a function of the absolute value of an applied field in the z direction. First, note that at zero current the H_c and −H_c have the same absolute value, which is 175 Oe (note that this is a different device than that shown in Fig. 4A). If a Rashba field is present, a gap between H_z and –H_z should open up as the amplitude of applied current goes up. Therefore, the most important region to look at will be where the current amplitude is close to the threshold amplitude needed for zero magnetic field switching. However, in Fig. 4E, we observe that at these high current levels there is hardly any difference between H_z and –H_z. A similar trend is seen when a current is applied in the –y direction in Fig. 4F. This indicates that the contribution of an out-of-plane Rashba field, if any, is minimal in our devices.

In the intermediate range where neither the applied field nor the current alone is strong enough to switch the magnet, a gap between H_z and –H_z can be observed. Note that, in this intermediate range, there is significant difficulty in ascertaining the exact value of the threshold current. Essentially, after setting a specific absolute value of the magnetic field, say 75 Oe, multiple experiments had to be done by varying the amplitude of the applied current pulse to find the threshold value. These repeated trials led to some uncertainty as to the exact value of the threshold current and also heating of the samples, which can also influence threshold current nontrivially. We note that, for a given absolute value of the magnetic field, the difference between the switching currents never exceeded 10% of the applied pulse amplitude (Fig. 4 E and F). This is well within the experimental error in this intermediate region. As either the current or the field amplitude increases, the switching becomes easier and the uncertainty in the switching current goes down. In addition, if one tries to associate a Rashba field for this intermediate region, for +I_y it will be pointing in the –z direction from Fig. 4E. However, for –I_y, it is still in the –z direction (Fig. 4F), although reversing the current polarity should have reversed it. Because of the aforementioned two reasons, we believe that the gap observed between the magnetic field values in the intermediate region is an experimental artifact.

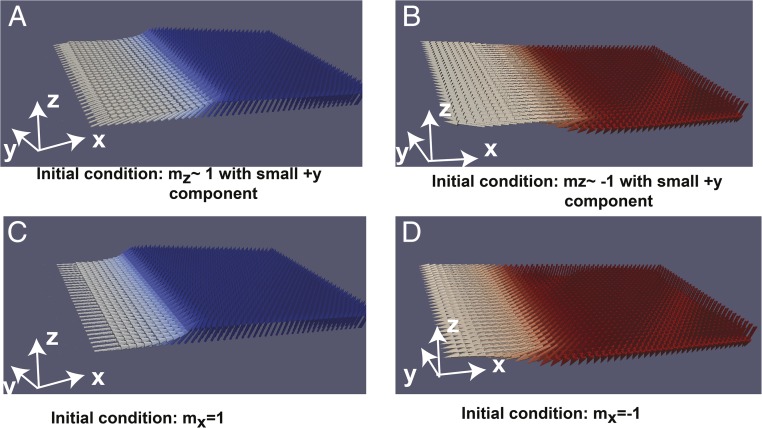
Detailed micromagnetic simulations were performed using the OOMMF package (22) to elucidate on the underlying physics (see SI Appendix, section 2, for details). A mesh was set up to capture the wedge in the magnet. With a magnet that closely follows the experimental dimensions (total 300 nm in length with 60-nm wedge, 90 nm wide, and 1.2 nm thick in the thickest area), the first set of tests were aimed at finding the equilibrium magnetization of the magnet. Starting from an initial condition of mostly up (with a slight component in the y direction to initiate the dynamics), when the magnet was allowed to relax, it went to an up position with a small component along the x direction, which is away from the wedge (Fig. 5A), exactly as it is observed in the experiments. The opposite happens when one starts from an initial condition of mostly down (Fig. 5B). This effect is understandable from magnetostatics. The magnetization in the wedge area has no perpendicular anisotropy because the MgO has been completely etched off. As a result, they follow the edge of the wedge such that the surface magnetic charge is minimized. Furthermore, they also try to align with the spins in the perpendicular region due to exchange coupling. As a result, they point in the +x direction when bulk of the magnet is +z and vice versa. What is reassuring is the fact that the overall tilt comes to be around 3° (SI Appendix, section S.2.2), which is very similar to what we have measured experimentally. Now starting from an initial magnetization along the x axis, as it will be when a current is applied along the y axis, depending on whether it started from +x or –x, the magnetization goes to +z or –z direction after the current is turned off, exactly as we have seen in our experiments (Fig. 5 C and D). Therefore, the simulations clearly show that the preferred direction of the tilt in our devices comes from minimizing the magnetostatic energy in the structure. Starting from that tilted position, the final state of the magnetization upon the application of current is also correctly predicted by the simulations. It also shows that the switching process is likely to be mediated by domains that form at the intersection of the wedged and nonwedged regions.

Fig. 5.

Micromagnetic simulation. (A) Starting from the magnet saturated in +z state with a small +y component, the system is allowed to relax. The final equilibrium state of the magnet is such that the moments in the wedge region point toward +x. Thus, average magnetization tilts toward +x. (B) Similarly starting from the magnet saturated in −z state, the magnetization tilts toward −x at equilibrium. (C) Starting from the magnet in +x, caused by spin accumulation in +x direction due to −y directed current pulse, the magnet evolves to +z state due to the tilt in the anisotropy axis. (D) Starting from the magnet in −x, caused by spin accumulation in −x direction due to +y directed current pulse, the magnet evolves to −z state. The blue arrow indicates that the magnetic moment is in +z, whereas the red arrow indicates it is in −z state.

To summarize, we have demonstrated that, by engineering a slightly tilted anisotropy axis in a perpendicular magnetic nanodot, it is possible to reversibly and deterministically switch it without applying any external magnetic field. The tilted easy axis breaks the symmetry that is otherwise present between an in-plane current-induced spin accumulation and a PMA magnet and makes it possible to switch it without needing to break the symmetry with an external magnetic field. Experimentally measured tilt in the magnetic easy axis direction is consistent with the polarity of the current needed to switch the magnet from up to down and vice versa, as it will be predicted by a Slonczewski-like torque. Although we have used a sophisticated fabrication method to engineer a tilted anisotropy in otherwise perpendicular magnetic stack, it is conceivable that a precise control of the tilt angle could be possible at the film level by combining a PMA hard layer (such as Pt/Co) with an in-plane soft layer (IMA, such as CoFeB, NiFe, Ni). Our demonstration of reversible switching without an external magnetic field could lead to combining the promise of ultralow current requirements in spin Hall systems to the scaling advantages of perpendicular media for next-generation storage and other spintronic applications.

Methods

A stack comprising a thermally oxidized Si substrate/Ta (10 nm)/CoFeB (1 nm)/MgO (1 nm)/Ta (∼3 nm) was fabricated into Hall bars by photolithography and argon ion milling. The Hall bars contained the entire thin-film stack with the region outside the Hall bars etched down to the insulating oxidized Si substrate. We used electron beam lithography with ZEP520A resist and ion milling to define the current channel and the detection channel, both being 500 nm long. The key challenge is to form the desired device pattern in the Ti layer, which acts as an etching mask and is used as a pattern transfer. First, 170-nm-thick poly(methyl methacrylate) was patterned by a second stage of aligned electron beam lithography onto a set of rectangle shapes (with aspect ratios varying from 4 to 7). Then, 4 nm of Ti was deposited normal to the substrate. Ti formed a wedge shape at the two sides along the long axis of the nanomagnet due to shadowing by the resist mask during evaporation of the Ti film, as shown in SI Appendix, Fig. S2A. This was followed by obliquely depositing 3 nm at the tilting angle of θ (15–45°) from the substrate normal, shown in SI Appendix, Fig. S2B. This prevents Ti deposition on one side ascribing to the shadowing effect of resist. After the lift-off process, rectangular Ti nanodots with nonuniform thickness were formed, as shown in SI Appendix, Fig. S2C. In particular, one side has wedge-shaped Ti with maximum thickness of 3 nm, whereas the thickness of other part is around 7 nm. Argon ion milling was used to etch the stack in the region outside the dot patterns down to the bottom tantalum layer. Meanwhile, a wedge shape was created at one side along the length (long axis) of the nanomagnet, as shown in Fig. 1B and SI Appendix, Fig. S2D.

For the anomalous Hall resistance measurement, current was applied using a current source and the Hall voltage was measured using a nanovoltmeter. The same current source was used to apply current pulses for switching and switching phase diagram measurements. A unipolar current pulse with a duration of ∼1 s was used for all measurements. Anisotropic magnetoresistance was measured using the standard four-probe technique. All measurements were performed at room temperature.