Nectar vs. pollen loading affects the tradeoff between flight stability and maneuverability in bumblebees

Significance

Many insects carry substantial loads during flight. Although this behavior is often critical for survival and reproduction, few studies have examined its consequences for flight performance. Bumblebees regularly carry two types of loads in different locations: pollen on their legs or nectar in their abdomen. We found that when bees carry a pollen load rather than a nectar load, they are more stable but less maneuverable in flight, supporting the concept of a tradeoff between stability and maneuverability—a notion that is frequently suggested but has rarely been tested, particularly in flying insects. Our findings also suggest that wind conditions may influence what resources pollinators choose to collect, which would have important consequences for pollination dynamics and colony fitness.

Abstract

Bumblebee foragers spend a significant portion of their lives transporting nectar and pollen, often carrying loads equivalent to more than half their body mass. Whereas nectar is stored in the abdomen near the bee’s center of mass, pollen is carried on the hind legs, farther from the center of mass. We examine how load position changes the rotational moment of inertia in bumblebees and whether this affects their flight maneuverability and/or stability. We applied simulated pollen or nectar loads of equal mass to Bombus impatiens bumblebees and examined flight performance in a wind tunnel under three conditions: flight in unsteady flow, tracking an oscillating flower in smooth flow, and flower tracking in unsteady flow. Using an inertial model, we estimated that carrying a load on the legs rather than in the abdomen increases a bee’s moment of inertia about the roll and yaw axes but not the pitch axis. Consistent with these predictions, we found that bees carrying a load on their legs displayed slower rotations about their roll and yaw axes, regardless of whether these rotations were driven by external perturbations or self-initiated steering maneuvers. This allowed pollen-loaded bees to maintain a more stable body orientation and higher median flight speed in unsteady flow but reduced their performance when tracking a moving flower, supporting the concept of a tradeoff between stability and maneuverability. These results demonstrate that the types of resources collected by bees affect their flight performance and energetics and suggest that wind conditions may influence resource selection.

The ability to carry external loads is an essential component of resource acquisition in many flying insects, including central place foragers that regularly transport provisions from the field back to their hive. Bumblebees, like all eusocial bees, rely exclusively on floral nectar and pollen to meet the energetic and nutritional demands of their colony, and much of a bumblebee forager’s life is spent gathering food resources. Bombus impatiens foragers spend an average of 7.5 h/d collecting and transporting food from flower patches to their hive over the course of 3–15 roundtrip flights (1), and the loads the bees carry can be quite substantial. Goulson et al. (2) measured an average load mass (pollen and/or nectar) equal to 23% of unladen body mass, and a maximum load of 77% body mass, in Bombus terrestris foragers. Free (3) measured Bombus sylvarum foragers ingesting nectar quantities ranging from 23% to 91% of their unladen body mass.

Because load carriage requires an increase in lift production to support the additional mass, and thus an increase in induced power output (4, 5), it is generally assumed that carrying extra weight should adversely affect flight performance in some way. However, the physiological and behavioral consequences of this common flight challenge have rarely been examined, and the few studies addressing the metabolic cost of load carriage have produced conflicting results. Some have found that load carriage has no effect on metabolic rates of honey bees (6, 7), nor does it alter their foraging behavior or efficiency (8), whereas others have found that metabolic rates do increase with load carriage (9, 10). The effect of load carriage on many other important aspects of insect flight performance, including stability and maneuverability, has rarely been explored.

Animal locomotion is often thought to involve a tradeoff between stability and maneuverability [although some animals appear to be both stable and highly maneuverable; thus, these traits are not always mutually exclusive (11–13)], but this tradeoff has rarely been tested empirically, particularly in flying insects. Stability is typically defined as the capacity to both resist and recover from disturbances to an intended trajectory (13). Maneuverability has been defined in various ways but, in the most general sense, is recognized as the ability to voluntarily change trajectory (13, 14). In the case of insect flight, both stability and maneuverability are thought to depend on the animal’s mass moment of inertia, because this property determines the torque required to create rotational body accelerations (15, 16), which result in reorientation of the aerodynamic force vector (17). The applied body torque may either be imposed upon the insect by external perturbations (relevant to stability) or generated by the insect as a steering behavior (relevant to maneuverability). Thus, a body with a lower moment of inertia requires less torque to initiate rotations, which may be beneficial for maneuverability but potentially disadvantageous for stability. This mechanical tradeoff is suggested by the flight dynamics of many insects, which are often the least stable to external perturbations about the roll axis—the axis with the lowest moment of inertia—and simultaneously display a propensity for maneuvering via rolling and lateral acceleration (14, 17–19).

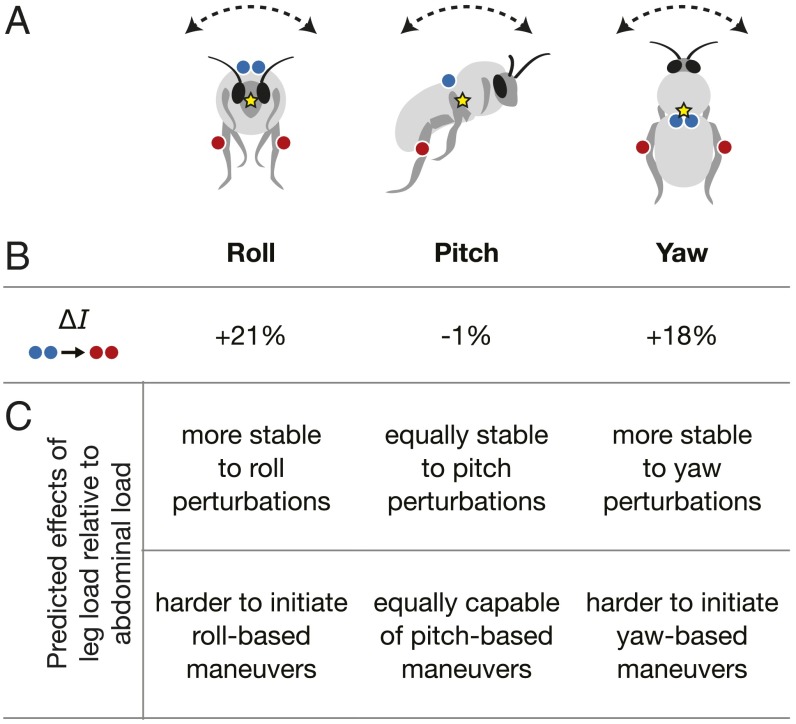
The presumed dependency of maneuverability and stability on a body’s moment of inertia raises the interesting possibility that nectar and pollen loads may differentially affect insect flight performance, because they are carried at different locations on the body. Whereas nectar is stored in a specialized stomach within the abdominal cavity, near the bee’s center of mass (COM), pollen is carried externally and more distally, packed into shallow cavities on the hind legs. To explore this hypothesis, we performed experiments on Bombus impatiens bumblebees in which we simulated pollen or nectar loads of equal mass, and examined flight performance in a wind tunnel under three different flight conditions: (i) unsteady flow in a von Kármán vortex street (VORT), designed to test flight stability; (ii) laminar airflow with a laterally oscillating flower (FLR), designed to test flight maneuverability; and (iii) unsteady vortex street flow combined with a laterally oscillating flower (VORT/FLR), designed to simultaneously test both stability and maneuverability (Movies S1–S3). We simulated pollen or nectar loads by attaching a small ball bearing to the corbicula (pollen basket) of each hind leg or a pair of ball bearings to the dorsal anterior region of the abdomen, respectively (Fig. 1A and Fig. S1). The combined mass of the ball bearings (∼25 mg) was ∼15% of the body mass of an average bee used in this study, which is well within the range of a typical pollen or nectar load for a bumblebee forager (2). We built a simple inertial model of a bee body (Fig. S2) to estimate the effects of our two load types on the body moment of inertia about the roll, pitch, and yaw axes and used these values to predict how each load treatment would affect flight stability and maneuverability (Fig. 1B).

Fig. 1.

Load treatments and their predicted effects on body moment of inertia, maneuverability, and stability. (A) Load treatments consisted of either attaching a pair of small steel ball bearings to the dorsal surface of the anterior-most plate of the abdomen, simulating a nectar load (blue) or attaching a single ball bearing to the corbicula (“pollen basket”) on the outer face of each hind tibia, simulating a pollen load (red). Yellow stars indicate the approximate location of the COM, around which the body rotates, based on results of the inertial model illustrated in Fig. S1. (B) Estimated change in moment of inertia (I) around the three rotational axes when a load is carried on the legs vs. on the abdomen. Values are derived from an inertial model of a bumblebee body subject to each load treatment (see Table S1 for MOI values). (C) Predicted consequences of the changes in MOI with leg loading (compared with abdominal loading) on flight stability (Upper) and maneuverability (Lower).

Fig. S1.

Still frames from high-speed videos of a bumblebee subjected to the abdominal load treatment (A) and the leg load treatment (B).

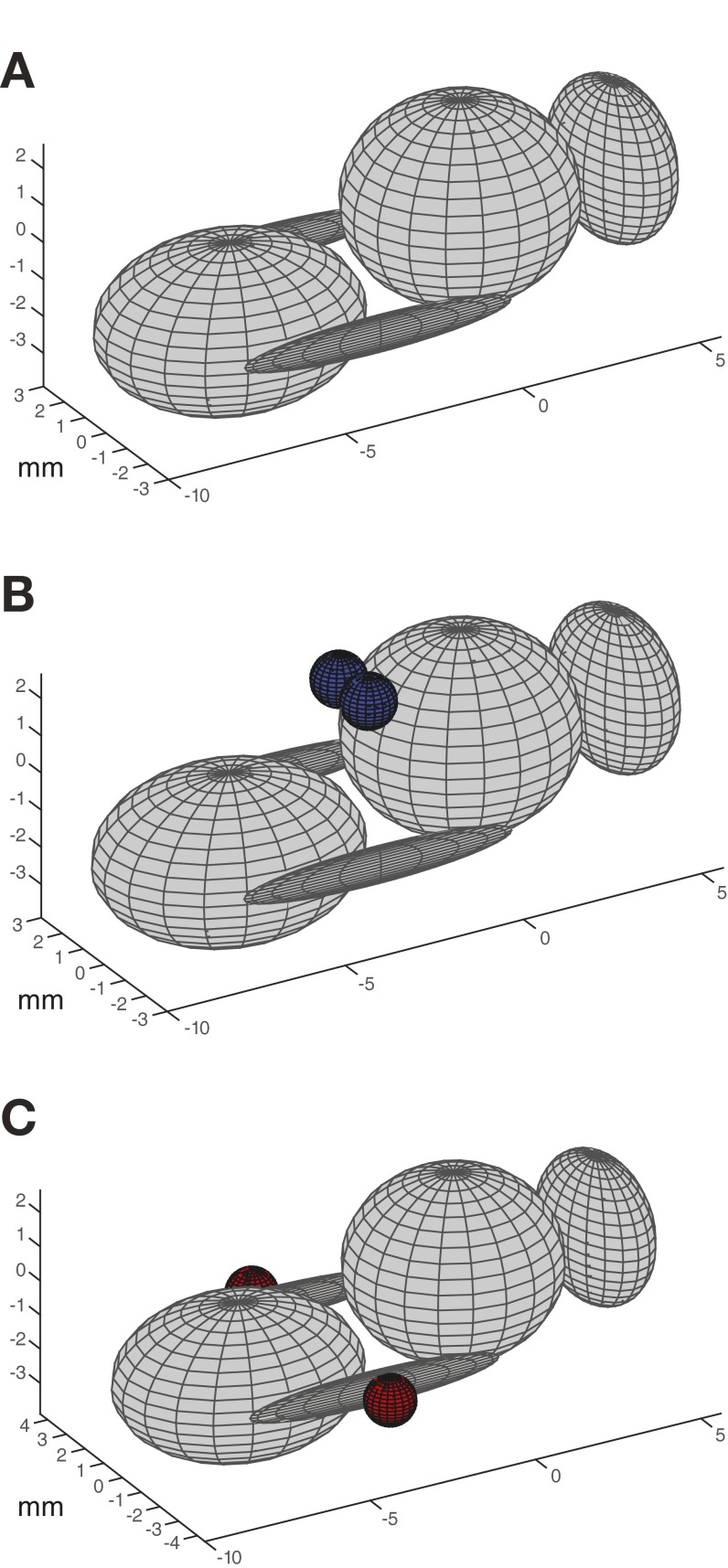
Fig. S2.

Model of a bumblebee body used to estimate moments of inertia, consisting of separate ellipsoids representing the head, thorax, abdomen, and two hind legs. Dimensions and masses for each body segment were taken from measurements of dissected bumblebees. (A) Unloaded body, with no additional weights attached. (B) Abdominal (simulated nectar) load treatment, with two blue spheres representing ball bearings as they were positioned on bees in our experiments (i.e., attached to the anterior plate of the abdomen). In the model, the ball bearings are not in direct contact with the abdominal segment because of limitations on the model’s abdominal angle imposed by the parallel axis theorem, as described in Materials and Methods. (C) Leg (simulated pollen) load treatment, with two red spheres representing ball bearings attached to the corbiculae on the hind legs. Estimated MOI values for each treatment are reported in Table S1.

We recorded flight trials with multiple high-speed cameras filming at 1,000 frames/second and reconstructed 3D flight trajectories and body attitudes using direct linear transformation software in MATLAB (20). We calculated body rotation rates around the roll, pitch, and yaw axes (Fig. 2), as well as median velocity along the bee’s flight path. To further explore how loading affects maneuverability, we examined how well bees were able to track the moving flower under each load treatment. For the two flight conditions with an oscillating flower, we calculated the phase lag and normalized correlation between the lateral position of the bee and the flower. We also calculated flight path sinuosity, which reflects how much a bee “overshoots” in its attempts to track the flower’s directional changes.

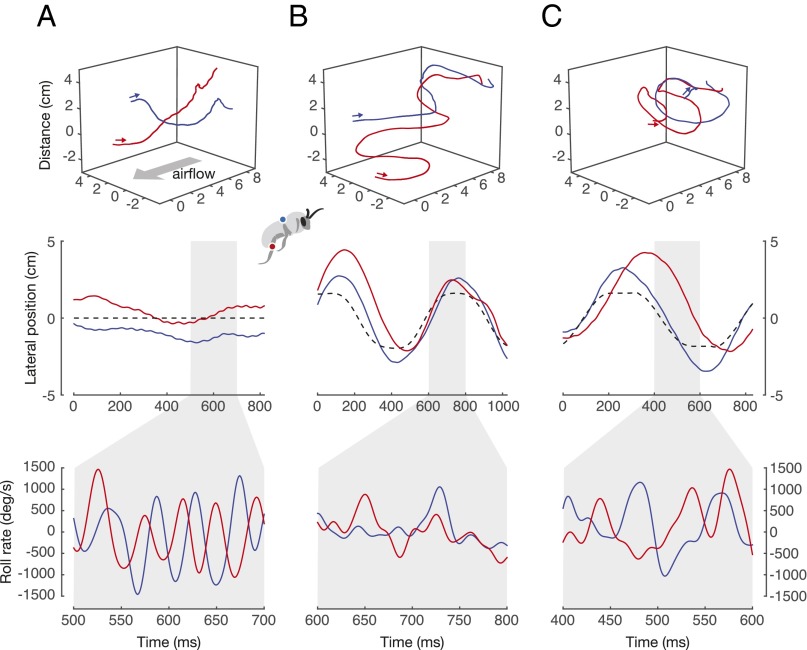
Fig. 2.

Representative paired flight trials under each load treatment (abdominal load in blue, leg load in red), for the three flight conditions. (A) Unsteady vortex street flow with a stationary flower (VORT). (B) Laminar airflow with a laterally oscillating flower (FLR). (C) Unsteady vortex street flow with a laterally oscillating flower (VORT/FLR). For each flight condition, we show the 3D trajectories (top row), lateral position of the bee relative to the flower (indicated by a black dashed line) through time (middle row), and a subsection of body roll rate through time (bottom row).

Results

Based on our inertial model, we estimated that placing a simulated pollen load on the legs as opposed to the abdomen would cause a 21% increase in moment of inertia (MOI) about the roll axis and an 18% increase about the yaw axis (Fig. 1B). Our model suggests that there would be a negligible difference (∼1%) in MOI about the pitch axis between the two load treatments. Relative to an unloaded bee, we estimated that the leg load would increase body MOI by 35% about the roll axis, 20% about the yaw axis, and 4% about the pitch axis, whereas the abdominal load would increase MOI by 11% about the roll axis, 2% about the yaw axis, and 6% about the pitch axis (see Table S1 for MOI values).

Table S1.

Estimated moments of inertia about the three axes of rotation for a model bumblebee body

Load treatment	Body moment of inertia, I (kg m2)
	Roll	Yaw	Pitch
No load	8.49 × e−10	3.57 × e−9	4.54 × e−9
Abdominal/nectar	9.44 × e−10	3.64 × e−9	4.79 × e−9
Leg/pollen	1.15 × e−9	4.29 × e−9	4.72 × e−9

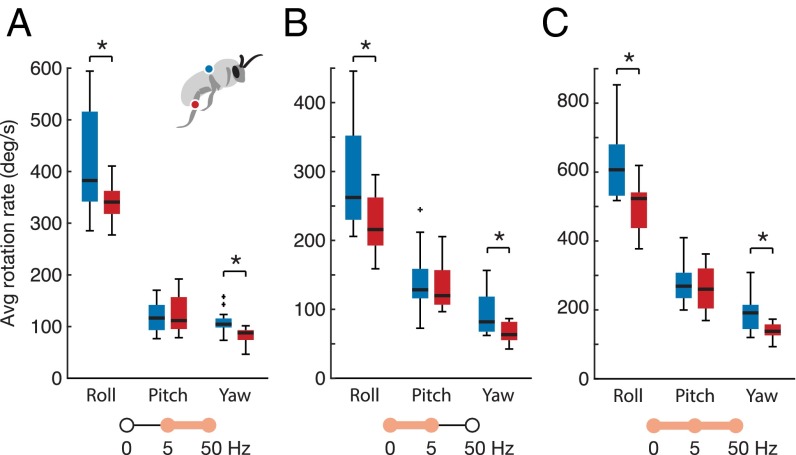
When flying bees carried loads on their legs, they displayed significantly lower average (absolute) roll and yaw rates compared with when they carried the same total load on their abdomen, and this was true across all three flight conditions (Fig. 3 and Table S2). For the VORT condition, mean roll rate decreased by 19%, from 420° to 340° per s on average (P = 0.016; n = 13), and yaw rate decreased by 24%, from 108° to 82.4° per s (P = 0.014). For the FLR condition, mean roll rate decreased by 23%, from 291° to 224° per s on average (P = 0.014; n = 12), and yaw rate decreased by 29%, from 93.2° to 66.3° per s (P = 0.013). For the VORT/FLR condition, mean roll rate decreased by 20%, from 625° to 499° per s on average (P = 0.027; n = 10), and yaw rate decreased by 26%, from 191° to 141° per s (P = 0.040). Mean pitch rates were never significantly different between load treatments in any of the flight conditions (Table S2).

Fig. 3.

Body rotation rates for each load treatment (abdominal load in blue, leg load in red) in the VORT condition (A), FLR condition (B), and VORT/FLR condition (C). Box and whisker plots show the median, quartiles, and range of data points, with outliers plotted as plus signs. Asterisks indicate a significant difference at P < 0.05. In all flight conditions, bees with leg loads displayed lower average (absolute) roll and yaw rates than they did with abdominal loads. (A) For the VORT condition, rotation rates were filtered to exclude frequencies below 5 Hz, to isolate the high-frequency body dynamics associated with unsteady flow perturbations. (B) For the FLR condition, rotation rates were filtered to exclude motions above 5 Hz, to isolate the low-frequency, voluntary casting motions associated with flower tracking. (C) For the VORT/FLR condition, the entire 0- to 50-Hz frequency range was analyzed.

Table S2.

P values from paired t tests to assess differences in body rotation rates between load treatments under the three flight conditions

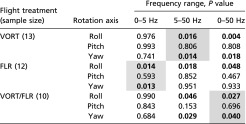We applied three different frequency filters to the rotation rates: 0–5 Hz to isolate low-frequency, voluntary casting motions associated with flower tracking; 5–50 Hz to isolate higher-frequency body dynamics associated with flow perturbations; and 0–50 Hz to assess combined effects on both low- and high-frequency body dynamics. In our analysis, we focused on the results highlighted in gray, because these were the most relevant frequency ranges for each flight treatment. Values in bold indicate significance at the 0.05 level; where a significant difference was found, bees always displayed higher rotation rates with the abdominal load.

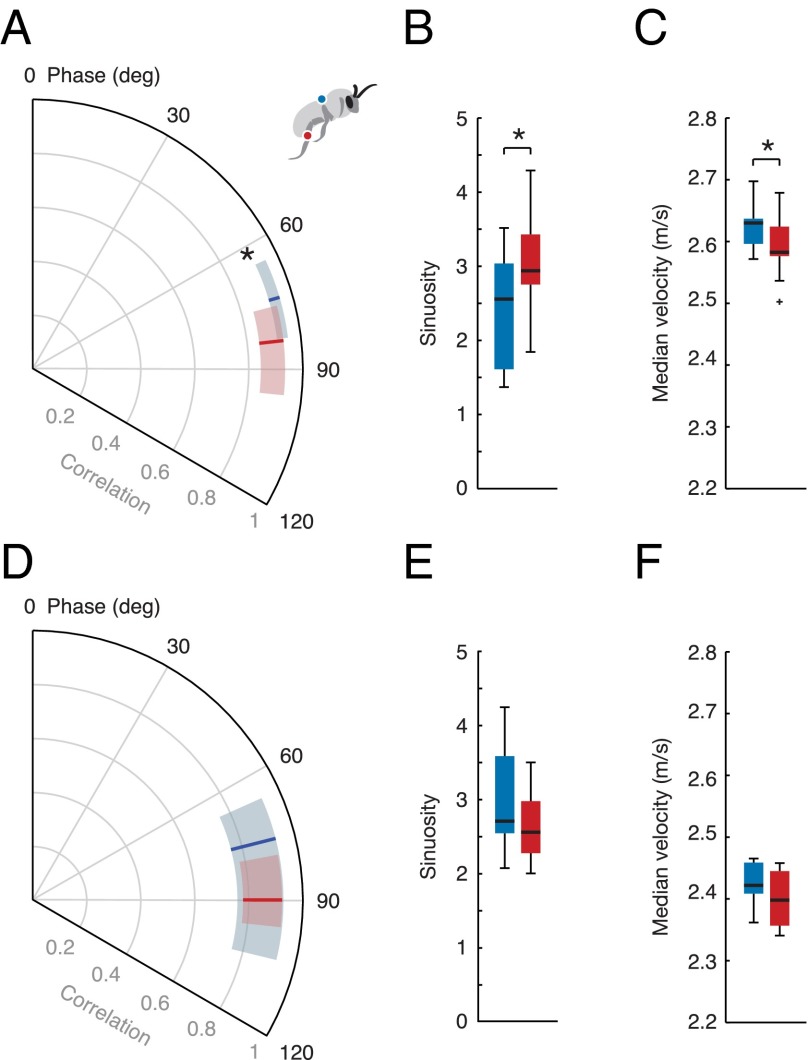
In the FLR condition, bees with loaded legs displayed significantly higher phase lags in tracking the flower’s motion and lower correlations with the flower’s instantaneous lateral position. Mean phase lag increased by 16% with leg loading, from 73.7° to 85.5° on average (P = 0.028; n = 12), and correlation decreased by 6%, from 0.935 to 0.881 (P = 0.037; Fig. 4A). Bees with loaded legs also exhibited flight paths with significantly higher sinuosity (P = 0.028; Fig. 4B) and lower median flight velocity (P = 0.041; Fig. 4C). In the VORT/FLR condition, bees with leg vs. abdominal loading displayed no significant difference in phase (P = 0.391; n = 10), correlation (P = 0.961), path sinuosity (P = 0.322), or median velocity (P = 0.168) (Fig. 4 D–F). In contrast to the FLR condition, bees flying toward the stationary post in the VORT condition displayed significantly higher median flight velocities with leg loading vs. abdominal loading (P = 0.044).

Fig. 4.

Flower tracking performance for each load treatment (abdominal load in blue, leg load in red) in the FLR condition (top row, A–C) and the VORT/FLR condition (bottom row, D–F). (A and D) Polar plots depicting the correlation between lateral position of the bee and the flower (displayed along the radial axis) and the bee’s phase lag in tracking flower oscillations (displayed along the angular axis). (B, C, E, and F) Box and whisker plots showing the median, quartiles, and range of data points, with outliers plotted as plus signs. Asterisks indicate a significant difference at P < 0.05. Bees with loaded legs in the FLR condition had a significantly lower correlation and a significantly higher phase lag than bees with loaded abdomens (A), exhibited significantly higher flight path sinuosity (B), and flew with a significantly lower median velocity (C). In the VORT/FLR condition, there was no significant difference in correlation, phase lag (D), path sinuosity (E), or median flight velocity (F) between bees with loaded legs vs. loaded abdomens.

Comparing tracking performance in the FLR vs. VORT/FLR conditions, bees with loaded legs showed no significant difference in phase (P = 0.207), correlation (P = 0.541), or sinuosity (P = 0.238) between these flight conditions. On the other hand, bees with abdominal loads displayed a significantly lower correlation (P = 0.020) in the VORT/FLR condition compared with the FLR condition, whereas phase (P = 0.196) and sinuosity (P = 0.129) were not significantly different.

Discussion

We found that load position and the changes in moment of inertia that result have a significant effect on body rotation rates during flight, which has repercussions for both maneuverability and stability in foraging bumblebees. Bees carrying a simulated pollen load on their legs displayed slower rotations about their roll and yaw axes, compared with when they were carrying an equivalent load on their abdomen—regardless of whether their body dynamics were driven by destabilizing airflows (VORT treatment) or self-initiated steering maneuvers (FLR treatment). In contrast, we measured no differences in pitch rotation rates for any flight treatment. These results support the predictions derived from our inertial model, in which we estimated that leg loading would increase MOI about the roll and yaw axes, but not the pitch axis, relative to abdominal loading (Fig. 1). For the roll and yaw axes, an increase in MOI leads to lower rotational accelerations in response to a given torque, and this in turn results in lower rotation rates.

The MOI changes predicted by our model may not be immediately obvious based solely on the relative load positions illustrated in Fig. 1A. For example, why does our model predict an increase in MOI about the roll axis but not the pitch axis, even though the distances between the added loads and the body COM appear similar in the two cases? The effect of load type on MOI depends not only on the distance of the added load from the COM (and thus the rotational axis) but also on the existing MOI of the unloaded body around the relevant rotational axis. Because a bee’s unloaded MOI is greatest about the pitch axis according to our model (Table S1), the moderate change in distance from the pitch axis to the leg vs. abdominal load has a negligible effect on the body’s overall MOI. In contrast, a bumblebee’s unloaded MOI is inherently lowest about the roll axis, so even a relatively small increase in load distance from the roll axis has a large effect on the bee’s MOI about that axis. An unloaded bee’s MOI about the yaw axis is larger than around the roll axis, but the change in distance from the yaw axis to the leg vs. abdominal load is more extreme than in either roll or pitch (Fig. 1A), resulting in an appreciable change in MOI.

One limitation inherent to examining free flight in unsteady airflow is that in the VORT conditions, we cannot separate the voluntary, “active” components of body motion from the “passive” dynamics caused by external flow perturbations. In the FLR treatment with laminar airflow, we are confident that the low-pass filtered body rotation rates consist primarily of active steering motions associated with flower tracking; even in the absence of an oscillating flower, bees typically display voluntary, low-frequency casting motions (17). However, in the VORT and VORT/FLR treatments, the body dynamics include a combination of passive flight perturbations, intertwined with both navigational (i.e., casting) and corrective steering responses. For this reason, we cannot definitively state whether the consequences of load position on body rotation rates in unsteady flow are driven by the effects of loading on passive body dynamics, active dynamics, or both. Nevertheless, it is reasonable to infer, based on a purely mechanical analysis, that the change in body MOI associated with load position has repercussions on both active and passive body dynamics, because the effect of MOI on angular acceleration (and thus on rotation rate) is indifferent to the source of the applied torque. Whether the torque is generated by the insect or imposed upon it, the bee’s MOI will determine how fast it rotates in response to a given torque. Thus, we assume that the increased MOI in leg-loaded bees caused reductions in both the passive and active components of body dynamics in unsteady flow.

Moving a bee’s load from its abdomen to its legs not only decreased roll and yaw rotation rates, but also diminished the bee’s flower tracking performance in laminar airflow. With loaded legs, bees were less adept at closely mirroring the flower’s position (lower correlation) and took longer to adjust their trajectory in response to a change in the flower’s motion (higher phase lag), which likely contributed to their more sinuous flight paths. Interestingly, however, the tracking benefits associated with abdominal loading and a lower MOI were largely lost when the bee was challenged to track the same moving flower in unsteady airflow; in the VORT/FLR condition, bees with abdominal loads showed a significantly lower positional correlation and higher average phase lag and path sinuosity (although not significantly so) compared with when these bees were tracking the flower in laminar flow (Fig. 4). In contrast, bees with leg loads—which already displayed relatively low maneuverability in the laminar FLR condition—showed no difference in performance when challenged by the addition of unsteady flow in the VORT/FLR condition. In fact, the tracking performance of bees with abdominal loads in the VORT/FLR condition dropped to match their performance with leg loads in the VORT/FLR condition. Thus, it seems that the benefits associated with a lower body MOI in terms of improved maneuverability were offset by a concomitant reduction in stability in this setting, where the ability to change trajectory and maintain stability were both similarly important.

Overall, our results strongly support the concept of a tradeoff between maneuverability and stability as a function of body moment of inertia—a notion that is frequently suggested (21–24) but has rarely been tested empirically, particularly in flying insects (but see ref. 18). The bumblebees in this study do not compensate (at least not fully) for the increased MOI effects of the pollen load, which they could theoretically do by either increasing power output to amplify their steering response or by anticipating and proactively responding to the flower motions. Whether this reduction in flight performance reflects a physiological constraint or a behavioral preference remains unknown. Although we suspect that the body rotation rates and tracking performance elicited here are near the limits of the bees’ maneuvering capacity, it is possible that the bees chose not to amplify their steering response when carrying a pollen load (despite the capacity to do so)—perhaps because the consequences of reduced tracking performance in this context are small relative to the energetic costs of correcting them.

How do the tradeoffs in flight performance associated with load position translate into real-world costs for a bee transporting pollen vs. nectar? Any quantitative answer to this question would be highly context-specific and would depend on a number of factors, including local wind conditions, patterns of resource distribution, and the energetics and foraging dynamics of a given bee. Nevertheless, based on our results, we can offer qualitative predictions of how energetic costs might vary under broadly different circumstances. We found that bees tracking a moving flower in smooth flow displayed a median flight velocity that was 1.4% lower on average when carrying a pollen load compared with a nectar load, which was presumably linked to their diminished capacity for enacting rapid directional changes. Conversely, we found that bees flying in unsteady airflow toward a stationary post displayed a median flight velocity that was 2.3% higher on average when carrying a pollen load, probably because of a reduction in course deviations caused by unexpected body rotations. Although small changes in flight speed do not entail a significant change in power output (25, 26), a bee flying more slowly will require more time to reach its target, and flight time is directly related to a bee’s overall energy consumption. Flight represents the primary energy cost of a hive (27). Thus, even a small increase in flight duration, when distributed across many foragers, could have important effects on the energy economy of a hive—the single-most important factor in its success, and the basis of nearly all foraging decisions in bumblebees (27). We also expect that if the bees were flying closer to their maximum forward velocity [∼6 m/s (28)], the difference in flight velocities we see between load types would be even more extreme.

Thus, when bees must fly in conditions where maneuverability is the overriding challenge, such as when tracking moving flowers or dodging obstacles in relatively smooth airflow (28), carrying a pollen load would likely increase a bee’s overall flight time and energy consumption. On the other hand, when the need for stability reigns, such as during transit flights between flower patches in windy conditions (29) or when making a rapid “bee line” back to the hive at the end of a foraging bout, carrying a pollen load would likely decrease a bee’s overall flight time and energy consumption. It is also worth noting two recent studies that found that hawkmoths (30) and bumblebees (31) display significantly higher wingbeat frequencies when flying in unsteady airflow compared with laminar airflow, a kinematic response that may enhance compensatory steering reactions in destabilizing conditions but one that presumably entails an increase in power output (32). The additional passive stability conferred by a pollen load might lessen the need for these types of energetically costly active control mechanisms, providing an additional means of energy savings during flight in unsteady airflow.

The present study highlights the complex interplay between maneuverability and stability in an integrative, ecologically relevant context, where flight performance depends on both of these traits in continually varying degrees. It seems evident that insects would benefit from the ability to vary their MOI to match the ever-changing demands of dynamic wind patterns, compliant environmental structures, and variable levels of environmental clutter. It is perhaps no surprise that some insects have been found to actively modulate their MOI to meet the task at hand, for example by extending their hind legs to improve roll stability when flying in unsteady airflow, at the expense of increased aerodynamic drag (16). Although we did not observe bumblebees in this study extending their hind legs while flying in either of the unsteady flow conditions, bees may display this behavior in more extreme destabilizing airflows or at higher flight speeds; if this is indeed the case, extending pollen-loaded legs would have an even greater effect on MOI than extending unloaded legs.

In a broader sense, our results shed light on several aspects of the evolution and ecology of hymenopterans. For example, unlike all other bees, female Megachillid bees collect and carry pollen on the ventral side of their abdomen (near their COM) rather than on their legs, but the reason for this behavior and its functional consequences have remained unclear. Based on our results, carrying pollen on their abdomen likely enhances the maneuverability of Megachillid bees relative to what it would be with the typical positioning of pollen on the legs. Whether or not the effect of MOI on Megachillid flight performance has played a role in the evolution of this unique pollen-carrying behavior is unknown, but it is interesting to note that Megachillids are recognized as excellent flyers, and female foragers perform darting, evasive flight maneuvers to escape large, harassing males attempting to mate with them (33)—a flight behavior that would likely benefit from a lower body MOI.

In addition, our results concerning load position and flight performance may have important ecological consequences for bees and the plants they pollinate. For example, the performance tradeoffs we demonstrated may lead bumblebees to preferentially forage for one food type over the other in response to current wind conditions. Peat and Goulson (34) found that B. terrestris bumblebees preferentially forage for pollen during warm, dry, and windy conditions. Although the authors hypothesized that warm, dry conditions may favor pollen collection and anther dehiscence, the authors did not elaborate on the measured association with wind. Our results demonstrate that carrying pollen on the legs would improve flight stability in windy conditions, which may motivate the type of foraging preference observed (34).

Bumblebees are important insect pollinators and all-weather foragers, and their ability to collect and transport both nectar and pollen is critical to colony growth and survival. We have shown that because these resources are carried at different locations on the body, they impose different functional tradeoffs on the flight performance of bumblebee foragers. Pollen loads carried on the legs enhance stability at the expense of maneuverability, whereas nectar loads carried in the abdomen are associated with greater maneuverability but reduced stability. These performance tradeoffs have significant effects on flight velocity under different conditions, indicating that the energetics of flight in bees depends not only on the mass carried, but also where it is carried—a discovery relevant to the development of predictive models of flight range and resource use (i.e., ref. 35). If environmental challenges to flight performance do indeed affect pollinator energetics or influence their choices concerning resource acquisition, then altered airflow conditions (e.g., resulting from changing weather patterns or habitat alteration) could have important consequences for pollination dynamics, as well as for the ecology, behavior, and evolution of bees.

Materials and Methods

Refer to SI Materials and Methods for details of the methods summarized below.

Load Treatments.

Bees were cold-anesthetized and outfitted with a tracking marker and an initial load treatment (simulated pollen or nectar loads). The tracking marker consisted of three black points representing the vertices of an isosceles triangle (Fig. S1), which served as landmarks for reconstructing time-resolved body positions and orientations during flight. We simulated nectar and pollen loads by attaching small steel ball bearings to the bee with UV-curing adhesive. Each steel ball measured 1.4 mm in diameter and weighed 11.5 mg. For the nectar load, we attached two steel balls adjacent to each other on the dorsal surface of the anterior-most plate of the abdomen, directly above the nectar crop. For the pollen load, we attached a steel ball to each corbicula (pollen basket), located on the outer face of the tibia of each hind leg (Fig. 1A and Fig. S1). The total mass of the two steel balls and adhesive combined was 25 ± 5 mg, which increased the mass of each bumblebee by ∼15%. Bees were allowed to recover, without access to food, for ∼2–3 h before experiments. We used a randomized, repeated measures experimental protocol to test flight performance under each load treatment. Thus, we randomized the order in which we applied the nectar and pollen loads, and after performing flight tests (in randomized order) under one load treatment, we reanesthetized the bee, removed the initial load, reattached steel balls in a different location for the new load treatment, and repeated the flight tests, again in randomized order. The two load treatments were compared within each flight condition (outlined below) by performing a paired t test, using the ttest function in MATLAB (R2014b; MathWorks) with a significance level of 0.05. This method was also used to compare the performance of bees across flight conditions, with a given type of load treatment.

Moment of Inertia Estimation.

We constructed a virtual model of a bumblebee body and calculated MOI about the three axes of rotation. The model consisted of a segmented body with separate ellipsoids representing the head, thorax, abdomen, and two hind legs (the mass of the remaining two leg pairs, which together account for only ∼7% of body mass, was added to the thorax), as well as two spheres representing the ball bearings applied in the load treatments. To imbue each ellipsoid with accurate dimensions and mass, we weighed and measured the major and minor axes of the associated body parts of three dissected bumblebees, and used the mean values of these measurements in the model. We determined an appropriate body posture for the model by selecting a video frame from a typical flight sequence representing each load treatment and digitizing the locations of key body landmarks. For each of the two load treatments, and for an unloaded body, we calculated MOI about the body center of gravity using the parallel axis theorem (Table S1).

Flight Tests.

Bees were trained to fly toward an artificial flower in the wind tunnel. Wind speed in all flight treatments was set to ∼2.55 m/s, which represents an intermediate cruising velocity for bumblebees (36).

Flight Condition 1: Unsteady Airflow, Stationary Flower (VORT).

A vertically oriented cylinder was placed at the upstream end of the wind tunnel, which created a von Kármán vortex street in its wake—a method that has been used to examine flying and swimming performance in several prior studies (17, 30, 37–39). The cylinder had a diameter of 25 mm, and with a flow velocity of 2.55 m/s, vortices were shed from the cylinder at a frequency of 23 Hz (17). The artificial flower was attached directly to the downwind side of the cylinder, forcing the bees to fly through the unsteady wake en route to the flower (Movie S1). A total of 13 bees were tested in this flight condition.

Flight Condition 2: Laminar Airflow, Oscillating Flower (FLR).

An artificial flower was attached to the tip of a thin vertical rod that passed through a narrow slot in the floor of the working section and connected to a linear actuator, which laterally oscillated the flower with a sinusoidal frequency of 1.5 Hz and amplitude of 3.5 cm (Movie S2). A total of 12 bees were tested in this flight condition.

Flight Condition 3: Unsteady Airflow, Oscillating Flower (VORT/FLR).

A combination of flight treatments 1 and 2, with the artificial flower positioned 8 cm downstream of the vertical cylinder (Movie S3). The flower oscillation amplitude was well within the lateral width of the cylinder wake, ensuring that bees were experiencing the combined effects of both treatments throughout their flight trajectory. A total of 10 bees were tested in this flight condition.

Kinematic Analysis.

We filmed bumblebees flying through a cubic interrogation volume (100 mm³) positioned downstream of the flower, using three spatially calibrated Photron SA3 high-speed cameras sampling at 1,000 Hz. The recorded flight sequences were digitized using DLTdv5, an open-source MATLAB-based program (20), using the automated tracking feature to localize the three black points on the triangular marker. The digitized data were initially processed with a fourth-order, Butterworth low-pass filter with a cutoff frequency of 100 Hz to remove high frequency noise associated with digitizing error. Median flight velocity was calculated by numerically differentiating the 3D position data, adding the wind speed (2.55 m/s) to the x component of all velocity vectors to account for the upwind component and then finding the median velocity magnitude. Body orientations were separated into roll, pitch, and yaw components, and instantaneous angular velocities were calculated by numeric differentiation. We focused on rotation velocities rather than accelerations in our analysis to reduce the additional noise introduced by numerically differentiating orientation data twice. To separate body motions into low-frequency, voluntary casting motions and higher frequency body dynamics, we applied fifth-order Butterworth filters to the body rotation rates, selecting cutoff frequencies according to the flight condition, to examine the most relevant body motions (analyses of all conditions in each frequency range are shown in Table S2). For the VORT condition, we used a band-pass filter to exclude frequencies below 5 Hz and above 50 Hz. For the FLR condition, we used a low-pass filter to exclude motions at frequencies above 5 Hz (17). For the combined VORT/FLR condition we considered the entire 0- to 50-Hz frequency range. The flower tracking performance of bees in flight conditions 2 and 3 was evaluated by measuring the cross-covariance between the lateral position of the bee and the oscillating flower using the xcov function in MATLAB. Phase lag was calculated by converting the time lag (τ, seconds) of maximum correlation between the position of the bee and flower to radians as follows: 2π × τ × 1.5, where 1.5 is the frequency of flower oscillation. We measured flight path sinuosity through a subinterrogation volume extending 6 cm downstream from the front of the main interrogation. Sinuosity was calculated as the total lateral distance traveled by the bee within this volume, divided by the length of the subinterrogation volume (6 cm).

SI Materials and Methods

Study Specimens and Load Treatments.

Bumblebees (B. impatiens) from a commercial breeder (BioBest) were maintained in the laboratory and given continuous access to a foraging chamber, where they could feed freely from an artificial flower. All bees selected for flight experiments were of similar body size (body length, 14 ± 0.5 mm; mass, 165 ± 10% mg). Before experiments, each bee was cold-anesthetized and outfitted with a tracking marker and an initial load treatment (simulated pollen or nectar loads). The triangular tracking marker was affixed to the dorsal side of the thorax with cyanoacrylate adhesive, and consisted of three black points representing the vertices of an isosceles triangle (measuring 2.7 × 2.3 mm; Fig. S1), which served as landmarks for reconstructing time-resolved body positions and orientations during flight.

We simulated nectar and pollen loads by attaching small steel ball bearings to the bee with UV-curing adhesive. Each steel ball measured 1.4 mm in diameter and weighed 11.5 mg. For the nectar load, we attached two steel balls adjacent to each other on the dorsal surface of the anterior-most plate of the abdomen, just posterior to the petiole (Fig. 1A and Fig. S1). This location was chosen because it was directly above the nectar crop. For the pollen load, we attached a steel ball to each corbicula (pollen basket), located on the outer face of the tibia of each hind leg (Fig. 1A and Fig. S1). The total mass of the two steel balls and adhesive combined was 25 ± 5 mg, which increased the mass of each bumblebee by ∼15%. Following application of the tracking marker and initial loading treatment, bees were placed in a transparent chamber (0.4 × 0.4 × 0.4 m) and allowed to recover and fly freely, without access to food, for ∼2–3 h before experiments.

We used a randomized, repeated measures experimental protocol to test flight performance under each load treatment. Thus, we randomized the order in which we applied the nectar and pollen loads, and after performing flight tests (in randomized order) under one load treatment, we reanesthetized the bee, removed the initial load, reattached steel balls in a different location for the new load treatment, and repeated the flight tests, again in randomized order.

The two load treatments were compared within each flight condition (outlined below) by performing a paired t test, using the ttest function in MATLAB (R2014b; MathWorks) with a significance level of 0.05. This method was also used to compare the performance of bees across flight conditions, with a given type of load treatment.

Moment of Inertia Estimation.

To estimate the effects of load treatment on body moment of inertia, we constructed a virtual model of a bumblebee body and calculated MOI about the three axes of rotation. The model consisted of a segmented body with separate ellipsoids representing the head, thorax, abdomen, and two hind legs (the mass of the remaining two leg pairs, which together account for only ∼7% of body mass, was added to the thorax), as well as two spheres representing the ball bearings applied in the load treatments. For each of the two load treatments, and for an unloaded body, we calculated MOI about the body center of gravity using the parallel axis theorem (Table S1).

To imbue each ellipsoid with accurate dimensions and mass, we weighed and measured the major and minor axes of the associated body parts of three dissected bumblebees and used the mean values of these measurements in the model. We determined an appropriate body posture for the model by selecting a video frame from a typical flight sequence representing each load treatment and digitizing the locations of the following landmarks: the three points on the tracking marker, the posterior tip of the abdomen, the anterior tip of the head, and the position of each steel ball. The digitized images revealed that bees typically hold their abdomens flexed ∼30° ventrally below the head-thorax axis. Because the parallel axis theorem requires that all objects contributing to the overall moment of inertia have major axes that are parallel to one another, we were unable to place the abdominal segment in this orientation for calculations of MOI. Instead, we represented the abdomen as an ellipse that was parallel to the head-thorax segments, but located a small distance below the thorax (i.e., not directly in contact with the thorax; Fig. S2). The location of the center of gravity with the model in this configuration was identical to that with the abdomen attached to the thorax and tilted by 30°, and the moments of inertia of the total body should similarly be representative of the bee in a realistic flight posture.

Flight Training and Experimental Setup.

All flight experiments were conducted in a 6-m-long, suction-type, open-return wind tunnel with a 0.9 × 0.5 × 0.5 m working section. Following the initial tagging procedure, load application, and 2–3 h of food deprivation, each bee was trained in the wind tunnel (with no airflow) to establish a repeatable behavior of flying toward an artificial flower. To be trained, a bee was initially brought to the flower and allowed to ingest nectar for ∼10 s. It was then separated from the flower and immediately released at the downstream end of the working section. If the bee did not subsequently fly toward the artificial flower to collect another nectar reward, it was captured and manually reintroduced to the nectar source for another 10 s. This procedure was repeated until the bee flew directly to the nectar source upon release.

Wind speed in all flight treatments was set to ∼2.55 m/s, which represents an intermediate cruising velocity for bumblebees (36). We analyzed flight sequences within a cubic interrogation volume (with dimensions of 100 mm) positioned downstream of the flower. The specific location of the interrogation volume relative to the artificial flower varied with the flight treatment, as detailed below.

Flight Condition 1: Unsteady Airflow, Stationary Flower (VORT).

To test flight stability, we challenged bumblebees to fly toward a stationary flower in unsteady, structured airflow and measured their sensitivity to aerial perturbations. To generate unsteady flow, we placed a vertically-oriented cylinder at the upstream end of the wind tunnel, which created a von Kármán vortex street in its wake—a method that has been used to examine flying and swimming performance in several prior studies (17, 30, 37–39). The cylinder had a diameter of 25 mm (corresponding to the average wing span of a bumblebee), and with a flow velocity of 2.55 m/s, vortices were shed from the cylinder at a frequency of 23 Hz. The artificial flower was attached directly to the downwind side of the cylinder, forcing the bees to fly through the unsteady wake en route to the flower (Movie S1). We positioned the front of our interrogation volume 10 cm downstream of the cylinder, ensuring that the von Kármán vortex street was fully developed and avoiding the recirculating region in the near wake of the cylinder. The flow characteristics resulting from this arrangement have been reported in a previous study (17). A total of 13 bees were tested in this flight condition, and paired trials of pollen and nectar load treatments were performed on each individual.

Flight Condition 2: Laminar Airflow, Oscillating Flower (FLR).

To test flight maneuverability, we challenged bumblebees to track a laterally oscillating flower in laminar airflow. An artificial flower was attached to the tip of a thin vertical rod that passed through a narrow slot in the floor of the working section and connected to a linear actuator, which laterally oscillated the flower with a sinusoidal frequency of 1.5 Hz and an amplitude of 3.5 cm. Both the artificial flower and the rod connecting it to the actuator had low aerodynamic profiles to minimize interference with the airflow. We positioned the front of our interrogation volume 2 cm downstream of the oscillating flower to capture flight kinematics associated with flower tracking but to avoid any behaviors associated with landing as the bee approached the flower (Movie S2). A total of 12 bees were tested in this flight condition, and paired trials of pollen and nectar load treatments were performed on each individual.

Flight Condition 3: Unsteady Airflow, Oscillating Flower (VORT/FLR).

To simultaneously test flight stability and maneuverability, we challenged bumblebees to track a laterally oscillating flower through unsteady airflow, combining flight treatments 1 and 2. The artificial flower was oscillated with the same kinematics as in treatment 1, but positioned 8 cm downstream of the vertical cylinder. The flower oscillation amplitude was well within the lateral width of the cylinder wake, ensuring that bees were experiencing the combined effects of both treatments throughout their flight trajectory. We positioned the front of our interrogation volume 2 cm downstream of the oscillating flower and 10 cm downstream of the cylinder (Movie S3). A total of 10 bees were tested in this flight condition, and paired trials of pollen and nectar load treatments were performed on each individual.

Kinematic Analysis.

We filmed bumblebees flying through the interrogation volume using three Photron SA3 high-speed cameras sampling at 1,000 Hz, two placed above and beside the wind tunnel at ∼30° from vertical and the third placed directly above the tunnel, viewing downstream at ∼40° from vertical. A static calibration cube that filled the interrogation volume was used for spatial calibration via direct linear transformation (20).

The recorded flight sequences were digitized using DLTdv5, an open-source MATLAB-based program (20), using the automated tracking feature to localize the three black points on the triangular marker. Subsequent analysis of the bee’s position and orientation was performed in MATLAB. Digitization error in localizing the centroids of marker points was on the order of 1–2 pixels, which is much smaller than the mean number of pixels separating the markers (∼30). The digitized data were initially processed with a fourth-order, Butterworth low-pass filter with a cutoff frequency of 100 Hz to remove high frequency noise associated with digitizing error. Median flight velocity was calculated by numerically differentiating the 3D position data, adding the wind speed (2.55 m/s) to the x component of all velocity vectors to account for the upwind component, and then finding the median velocity magnitude. Body orientations were separated into roll, pitch, and yaw components, and instantaneous angular velocities were calculated by numeric differentiation. The method detailed in Ravi et al. (17) was used to calculate the instantaneous orientation and rotation rates of the bees, as well as to evaluate of the errors associated with data capture and subsequent analysis. We focused on rotation velocities rather than accelerations in our analysis to reduce the additional noise introduced by numerically differentiating orientation data twice.

To separate body motions into low-frequency, voluntary casting motions and higher frequency body dynamics, we applied fifth-order Butterworth filters to the body rotation rates, selecting cutoff frequencies according to the flight condition, to examine the most relevant body motions (analyses of all conditions in each frequency range are shown in Table S2). For the VORT condition, we were most interested in the higher-frequency body dynamics associated with flow perturbations and recoveries (near the vortex shedding frequency of 23 Hz), so we used a band-pass filter to exclude frequencies below 5 Hz and above 50 Hz. For the FLR condition, we were most interested in examining the low-frequency, voluntary casting motions associated with tracking the flower (near the oscillation amplitude of 1.5 Hz), so we applied a low-pass filter to exclude motions at frequencies above 5 Hz (17). The cutoff frequency of 5 Hz was chosen somewhat arbitrarily; however, sensitivity to cutoff frequency was evaluated, and the filtered results were found to be relatively insensitive to cutoff frequency over a range of ∼3–10 Hz. For the combined VORT/FLR condition, we considered the entire 0- to 50-Hz frequency range.

The flower tracking performance of bees in flight conditions 2 and 3 was evaluated by measuring the cross-covariance between the lateral position of the bee and the oscillating flower using the xcov function in MATLAB. Phase lag was calculated by converting the time lag (τ, seconds) of maximum correlation between the position of the bee and flower to radians as follows: 2π × τ × 1.5, where 1.5 is the frequency of flower oscillation. We measured flight path sinuosity through a subinterrogation volume extending 6 cm downstream from the front of the main interrogation volume—chosen because this was the greatest longitudinal distance through which every bee in our experiments was continuously visible (as sometimes casting bees entered the main interrogation volume from the side). Although a longitudinal distance of 6 cm seems relatively small, bees spent an average of 0.77 s flying upwind through this volume, which translates to an equivalent ground distance of ∼2 m. Flight path sinuosity was calculated as the total lateral distance traveled by the bee within this volume, divided by the length of the subinterrogation volume (6 cm); thus, a bee that flew upstream along a straight line would have a path sinuosity of zero.