Iterative phasing for fluctuation X-ray scattering

Significance

Fluctuation X-ray scattering is an emerging imaging technique that seeks to overcome the low data-to-parameter ratio encountered in traditional small- and wide-angle X-ray scattering methods. By acquiring a large number of ultrashort X-ray exposures on an ensemble of molecules, this technique produces a dataset that contains structural information far beyond what is obtainable from traditional solution scattering methods without requiring crystallization. However, reconstructing the underlying molecular shape from this data is challenging, as the information in each image is averaged over several molecular orientations. In this article, we introduce a flexible iterative method that can rapidly determine molecular structure from fluctuation scattering data. This allows one to visualize structural details that may be inaccessible through traditional methods.

Abstract

Fluctuation X-ray scattering (FXS) is an extension of small- and wide-angle X-ray scattering in which the X-ray snapshots are taken below rotational diffusion times. This technique, performed using a free electron laser or ultrabright synchrotron source, provides significantly more experimental information compared with traditional solution scattering methods. We develop a multitiered iterative phasing algorithm to determine the underlying structure of the scattering object from FXS data.

X-ray solution scattering of macromolecular complexes is a versatile technique, providing low-resolution structural information that, when supplemented with high-resolution crystallographic data, can result in fundamental insights into the physiological behavior and function of macromolecular machines (1). Although solution scattering has been applied successfully to many problems in the biological sciences (2, 3), the technique suffers from a significant shortcoming. Due to the 3D averaging that occurs during the X-ray snapshots, the effective information content of the data is typically only around 9–15 independent parameters (4). This lack of sufficient information in the data ultimately results in nonunique or poorly determined structural hypotheses.

To overcome these issues, it was proposed to perform the solution scattering process at timescales below rotational diffusion times (5, 6). By avoiding physical rotational averaging, speckle patterns emerge from which angular correlation functions can be computed. These so-called fluctuation X-ray scattering experiments can be performed on modern synchrotrons (7) and free electron laser sources (8, 9). The angular correlation information provided from these experiments is directly related to the imaged structure (10) and contains significantly more information than standard small- and wide-angle X-ray scattering (SAXS/WAXS) data. Although the relation from real space structure to fluctuation scattering data is straightforward, the inverse problem of determining a molecular model from fluctuation scattering data is nontrivial (8).

For 2D systems, such as macromolecules randomly oriented around a single axis (11), an analytical route for image reconstruction is available (12). However, this approach requires triple correlation measurements across the full resolution range of interest, which may not be fully accessible due to experimental limitations.

Earlier work attempting to determine 3D shape from fluctuation scattering data was based on solving two phase problems consecutively. Although this route has shown success in cases where the scattering species has helical (13) or icosahedral symmetry (14), it fails to produce a structure for the general case. Another approach was developed in which the inverse problem was solved using a reverse Monte Carlo method (8), similar to what is used to determine macromolecular envelopes from SAXS data (15–17). Although this approach allows a real space object to be reconstructed without the need for symmetry constraints, the procedure is computationally expensive and, in general, convergence can be problematic (18). Furthermore, the existing reverse Monte Carlo method assumes a binary model, where voxels either have a scattering length or do not. The breakdown of this uniform density assumption ultimately limits the resolution of features that can be reconstructed through such an approach.

Here we develop a fundamentally different approach to structure solution from fluctuation scattering, based on a multitiered iterative phasing (MTIP) algorithm. In particular, we derive a series of projection operators, which are used to iteratively modify a model to satisfy specified real space constraints and match the derived model fluctuation scattering data to external observations. This approach does not require a uniform density assumption and solves the two inherent phase problems concurrently, which allows one to obtain a reconstruction with a reduced amount of fluctuation scattering data, or even SAXS/WAXS data alone, by compensating with the extra information provided through real space constraints.

The presented method allows one to study the structure of objects that cannot be easily crystallized, while achieving higher resolution than what is possible through standard SAXS/WAXS experiments. As a result, this approach can be used to gain deeper insight into biological structure and to expand the range of characterization methods for nanostructures (19). Furthermore, the framework developed here allows one to extend many of the density modification techniques developed for crystallography to solution scattering.

Background

Here we use $\mathbf{r}$ and $\mathbf{q}$ to denote real and Fourier space variables, respectively, and designate $r=\left|\mathbf{r}\right|$ and $q=\left|\mathbf{q}\right|$. The 3D scattered intensity I of an object is given by the squared magnitude of the Fourier transform of its electron density ρ:

$$I\left(\mathbf{q}\right)={\left|{\displaystyle \underset{{\mathrm{ℝ}}^3}{\int }\rho \left(\mathbf{r}\right)e^{-2\pi i\mathbf{q}\cdot \mathbf{r}}d\mathbf{r}}\right|}^2.$$

When the object is rotated by $R\in SO\left(3\right)$, the resulting intensities become $I_R\left(\mathbf{q}\right)=I\left(R\mathbf{q}\right)$. The diffraction pattern from the object with orientation R measured on a 2D detector with a beam of wavelength λ can be expressed in polar coordinates as ${\mathrm{ℐ}}_R\left(q,{\varphi }_I\right)=I_R\left(q,\theta \left(q\right),{\varphi }_I\right)$, where $\theta \left(q\right)=\pi /2$ for a flat Ewald sphere, $\theta \left(q\right)=\text{arccos}\left(q\lambda /2\right)$ for a curved Ewald sphere, and ${\varphi }_I$ is the angle about the incident beam axis.

In a fluctuation scattering experiment, one measures a series of $N_{dp}$ diffraction patterns ${\mathrm{ℐ}}_{R_n}$ from an ensemble of identical and randomly oriented particles. From these images, one computes the average angular cross-correlation function

$$C\left(q,q^{\prime },\varphi \right)=\frac{1}{2\pi N_{dp}}{\displaystyle \sum _{n=1}^{N_{dp}}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\mathrm{ℐ}}_{R_n}\left(q,{\varphi }_I+\varphi \right){\mathrm{ℐ}}_{R_n}\left(q^{\prime },{\varphi }_I\right)d{\varphi }_I}}.$$ [1]

If there are multiple particles per shot, then, for a sufficiently dilute system, this average converges to that of the single particle per shot case up to a zero frequency component (20).

The fluctuation scattering reconstruction problem is to determine the electron density ρ given the angular correlation data defined by Eq. 1, along with any a priori known constraints, e.g., compact support, symmetry, or upper and lower bounds. In particular, the angular correlation data yield information about the harmonic coefficients of the intensities, which can be exploited to determine information about ρ. In the following subsections, we describe how to extract this intensity harmonic coefficient information from the angular correlation data for both the 2D and 3D versions of the fluctuation scattering reconstruction problem. See SI Text and Figs. S1–S6 for an introduction to circular and spherical harmonics and an overview of fluctuation scattering data.

Two-Dimensional Case.

The 2D version of fluctuation scattering is obtained by assuming a flat Ewald sphere and that the particle orientations are randomly sampled from a uniform distribution of rotations about a single axis parallel to the incident beam. In this case, one can retrieve intensity information only along a flat 2D slice of the intensities, which, by the Fourier projection slice theorem, is equivalent to the squared Fourier magnitudes of the X-ray projection of ρ to a plane perpendicular to the rotation axis.* For the moment, assume that there is only one particle per shot.

A function $\rho \in L^2\left({\mathrm{ℝ}}^2\right)$ can be formally expressed in terms of its circular harmonic expansion as

$$\rho \left(r,\varphi \right)={\displaystyle \sum _{m=-\infty }^{\infty }{\rho }_m\left(r\right)e^{im\varphi }},$$ [2]

where the circular harmonic coefficients ${\rho }_m\left(r\right)$ are given by

$${\rho }_m\left(r\right)=\frac{1}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\rho \left(r,\varphi \right)e^{-im\varphi }d\varphi }.$$ [3]

The circular harmonic coefficients of ρ and its Fourier transform $\widehat{\rho }$ are related through the Hankel transform via

$${\widehat{\rho }}_m\left(q\right)=2\pi {\left(-i\right)}^m{\displaystyle \underset{0}{\overset{\infty }{\int }}{\rho }_m\left(r\right)J_m\left(2\pi qr\right)r\hspace{0.17em}dr},$$ [4]

$${\rho }_m\left(r\right)=2\pi \hspace{0.17em}{i}^m{\displaystyle \underset{0}{\overset{\infty }{\int }}{\widehat{\rho }}_m\left(q\right)J_m\left(2\pi qr\right)q\hspace{0.17em}dq},$$ [5]

where $J_m$ is a Bessel function of order m.

We denote the circular harmonic coefficients of the angular cross-correlations in Eq. 1 by $B_m\left(q,q^{\prime }\right)$, which can be expressed in terms of the intensity circular harmonic coefficients $I_m$ as

$$B_m\left(q,q^{\prime }\right)=I_m\left(q\right)I_m^{*}\left(q^{\prime }\right).$$ [6]

We denote the circular harmonic coefficients of the angular autocorrelations, i.e., $C\left(q,q\right)$, by $B_m\left(q\right)=B_m\left(q,q\right)$. In this case, one has

$$B_m\left(q\right)={\left|I_m\left(q\right)\right|}^2.$$ [7]

If there are K particles per shot, then, after rescaling, the $B_0$ data will be off by a factor of K; i.e., $B_0\left(q,q^{\prime }\right)=K^2{I}_0\left(q\right)I_0^{*}\left(q^{\prime }\right)$ and $B_m\left(q,q^{\prime }\right)=K{I}_m\left(q\right)I_m^{*}\left(q^{\prime }\right)$ for $m\ne 0$.

The cross-correlation circular harmonic coefficients form a rank one Gram matrix, which determines $I_m$ up to a single phase factor for each m. In particular, for a discretization $\left\{q_j\right\}$ of q and a fixed m, if we form the matrix with entries $B_m\left(q_j,q_k\right)$, then its top eigenvector $v_m$, with corresponding eigenvalue ${\lambda }_m$, is related to the intensity harmonic coefficients via

$$I_m\left(q_j\right)=v_m\left(q_j\right)\sqrt{{\lambda }_m}{e}^{i{\varphi }_m},$$ [8]

where ${\varphi }_m$ is a single unknown real-valued phase factor.

Three-Dimensional Case.

The 3D version of fluctuation scattering allows for a curved Ewald sphere and assumes that the particle orientations are randomly sampled from a uniform distribution over $SO\left(3\right)$. For the moment, assume that there is only one particle per shot.

A function $\rho \in L^2\left({\mathrm{ℝ}}^3\right)$ can be formally expressed in terms of its spherical harmonic expansion as

$$\rho \left(r,\theta ,\varphi \right)={\displaystyle \sum _{l=0}^{\infty }{\displaystyle \sum _{m=-l}^l{\rho }_{lm}\left(r\right)Y_l^m\left(\theta ,\varphi \right)}},$$ [9]

where the $Y_l^m$ are the spherical harmonics and the spherical harmonic coefficients ${\rho }_{lm}$ are given by

$${\rho }_{lm}\left(r\right)={\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{\pi }{\int }}\rho \left(r,\theta ,\varphi \right)Y_l^{m^{*}}\left(\theta ,\varphi \right)\sin \theta \hspace{0.17em}d\theta d\varphi }}.$$ [10]

The spherical harmonic coefficients of ρ and its Fourier transform $\widehat{\rho }$ are related through the spherical Hankel transform via

$${\widehat{\rho }}_{lm}\left(q\right)=4\pi {\left(-i\right)}^l{\displaystyle \underset{0}{\overset{\infty }{\int }}{\rho }_{lm}\left(r\right)j_l\left(2\pi qr\right)r^{2}dr},$$ [11]

$${\rho }_{lm}\left(r\right)=4\pi i^l{\displaystyle \underset{0}{\overset{\infty }{\int }}{\widehat{\rho }}_{lm}\left(q\right)j_l\left(2\pi qr\right)q^{2}dq},$$ [12]

where $j_l$ is the spherical Bessel function of order l.

In the limit of an infinite number of images, one has

$$C\left(q,q^{\prime },\varphi \right)={\displaystyle \sum _{l=0}^{\infty }{F}_l\left(q,q^{\prime },\varphi \right)B_l\left(q,q^{\prime }\right)},$$ [13]

where

$$F_l\left(q,q^{\prime },\varphi \right)=\frac{1}{4\pi }{P}_l\left(\cos \theta \left(q\right)\cos \theta \left(q^{\prime }\right)+\sin \theta \left(q\right)\sin \theta \left(q^{\prime }\right)\cos \varphi \right),$$

where $P_l$ is the Legendre polynomial of order l, and

$$B_l\left(q,q^{\prime }\right)={\displaystyle \sum _{m=-l}^l{I}_{lm}\left(q\right)I_{lm}^{*}\left(q^{\prime }\right)},$$ [14]

where the $I_{lm}$ are the spherical harmonic coefficients of the intensities (5). The corresponding autocorrelation data, $B_l\left(q\right)=B_l\left(q,q\right)$, yields

$$B_l\left(q\right)={\displaystyle \sum _{m=-l}^l{\left|I_{lm}\left(q\right)\right|}^2}.$$ [15]

For a fixed q and $q^{\prime }$, $B_l\left(q,q^{\prime }\right)$ can be retrieved by inverting the associated linear system in Eq. 13. If there are K particles per shot, then, after rescaling, the $B_0$ data will be off by a factor of K; i.e., $B_0\left(q,q^{\prime }\right)=K^2{I}_{00}\left(q\right)I_{00}^{*}\left(q^{\prime }\right)$ and $B_l\left(q,q^{\prime }\right)=K{\displaystyle {\sum }_{m=-l}^l{I}_{lm}\left(q\right)I_{lm}^{*}\left(q^{\prime }\right)}$ for $l\ne 0$.

Given a discretization $\left\{q_j\right\}$ of size N and a fixed l, the matrix $B_l$ with entries $B_l\left(q_j,q_k\right)$ is a rank $\text{min}\left(2l+1,N\right)$ Gram matrix with the eigendecomposition

$$B_l=V_l{\mathrm{\Lambda }}_l{V}_l^{*},$$ [16]

where $V_l$ is N by $\text{min}\left(2l+1,N\right)$ and ${\mathrm{\Lambda }}_l$ has nonnegative entries. This decomposition is related to the spherical harmonic coefficients of the intensities, expressed as an N by $2l+1$ matrix $I_l$ for each l, via multiplication by an unknown $2l+1$ dimensional unitary matrix $U_l$. In particular, if $2l+1\le N$, then

$$I_l=V_l\sqrt{{\mathrm{\Lambda }}_l}{U}_l,$$ [17]

and if $2l+1>N$, then one obtains a similar result by zero padding; i.e., $I_l=\left[\begin{array}{cc}{V}_l\sqrt{{\mathrm{\Lambda }}_l}& 0\end{array}\right]U_l.$

Polar Fourier Transform

To obtain a reconstruction algorithm, we have to enforce several constraints in real space while matching the circular or spherical harmonic information to the measured quantities that are defined in Fourier space. Therefore, it is desirable to compute the Fourier transform and its inverse on a polar grid, where circular and spherical harmonic transforms can be computed most efficiently. Here we describe approximations to the 2D and 3D Fourier transforms and their inverses on such a polar grid. This is accomplished by computing discrete circular/spherical harmonic transforms, approximating the Hankel/spherical Hankel transforms, and then computing the inverse discrete circular/spherical harmonic transforms. We assume, after rescaling, that the support of ρ is contained within $r<1$ and we resolve $\widehat{\rho }$ up to $q<Q$.

Two-Dimensional Polar Fourier Transform.

Here we use a polar grid with nodes equispaced in radii and equispaced in angle for each radius. Specifically, for $0\le n<N$, the real space radial node components are given by $r_n=n/N$, the Fourier space radial node components are given by $q_n=Qn/N$, and the number $M_n$ of angular nodes for each radius can be varied.

We use a fast Fourier transform (FFT) for each radius to compute the circular harmonic coefficients and invert them with an inverse fast Fourier transform (IFFT).^†

Note that for a smooth ρ, ${\rho }_m$ has a smooth even/odd extension to $\left[-\mathrm{1,1}\right]$ for m even/odd. Therefore, by expanding ${\rho }_m$ into a cosine/sine series, we obtain spectrally accurate quadrature rules for the transforms in Eqs. 4 and 5 via^‡

$${\widehat{\rho }}_m\left(q_n\right)\approx {\left(-i\right)}^m{\displaystyle \sum _{n^{\prime }=0}^{N-1}{\rho }_m\left(r_{n\prime }\right)w_{m,n,n^{\prime }}},{\rho }_m\left(r_n\right)\approx i^m{Q}^2{\displaystyle \sum _{n^{\prime }=0}^{N-1}{\widehat{\rho }}_m\left(q_{n\prime }\right)w_{m,n,n^{\prime }}},$$

where for m even

$$w_{m,n,n^{\prime }}=\frac{4\pi }{N}{\displaystyle \sum _{k=0}^{N-1}{c}_k{c}_{n^{\prime }}\cos \left(\pi k\frac{n^{\prime }}{N}\right)}{\displaystyle \underset{0}{\overset{1}{\int }}\cos \left(\pi kx\right)J_m\left(2\pi Q\frac{n}{N}x\right)x\hspace{0.17em}dx},$$

and for m odd

$$w_{m,n,n^{\prime }}=\frac{4\pi }{N}{\displaystyle \sum _{k=0}^{N-1}{c}_k{c}_{n^{\prime }}\sin \left(\pi k\frac{n^{\prime }}{N}\right)}{\displaystyle \underset{0}{\overset{1}{\int }}\sin \left(\pi kx\right)J_m\left(2\pi Q\frac{n}{N}x\right)x\hspace{0.17em}dx},$$

where $c_a$ is $1/2$ for $a=0$ and is 1 otherwise.

Three-Dimensional Polar Fourier Transform.

Here we use a polar grid with nodes whose radial components are equispaced, as described in the 2D case. For the nth radial component, the nodes lie on $L_n$ inclination angles, located at the arccosines of the Gauss–Legendre quadrature nodes, and for each inclination angle we have $2L_n-1$ equispaced azimuthal angles.

We compute the spherical harmonic transform and its inverse for each radius via the Gauss–Legendre approach, e.g., ref. 21.

Note that for a smooth ρ, ${\rho }_{lm}$ has a smooth even/odd extension to $\left[-\mathrm{1,1}\right]$ for l even/odd. Therefore, by expanding ${\rho }_{lm}$ into a cosine/sine series, we obtain spectrally accurate quadrature rules for the transforms in Eqs. 11 and 12 via

$$\begin{array}{c}{\widehat{\rho }}_{lm}\left(q_n\right)\approx {\left(-i\right)}^l{\displaystyle \sum _{n^{\prime }=0}^{N-1}{\rho }_{lm}\left(r_{n^{\prime }}\right)w_{l,n,n^{\prime }},}\\ {\rho }_{lm}\left(r_n\right)\approx i^l{Q}^3{\displaystyle \sum _{n^{\prime }=0}^{N-1}{\widehat{\rho }}_{lm}\left(q_{n^{\prime }}\right)w_{l,n,n^{\prime }}},\end{array}$$

where for l even

$$w_{l,n,n^{\prime }}=\frac{8\pi }{N}{\displaystyle \sum _{k=0}^{N-1}{c}_k{c}_{n^{\prime }}\cos \left(\pi k\frac{n^{\prime }}{N}\right)}{\displaystyle \underset{0}{\overset{1}{\int }}\text{cos}\left(\pi kx\right)j_l\left(2\pi Q\frac{n}{N}x\right)x^2\hspace{0.17em}dx},$$

and for l odd

$$w_{l,n,n^{\prime }}=\frac{8\pi }{N}{\displaystyle \sum _{k=0}^{N-1}{c}_k{c}_{n^{\prime }}\sin \left(\pi k\frac{n^{\prime }}{N}\right)}{\displaystyle \underset{0}{\overset{1}{\int }}\text{sin}\left(\pi kx\right)j_l\left(2\pi Q\frac{n}{N}x\right)x^2\hspace{0.17em}dx}.$$

Multitiered Iterative Phasing

Iterative phasing techniques were originally introduced to solve the phase retrieval problem, which is to reconstruct an object from its intensities while enforcing any applicable constraints. These techniques are based on iteratively applying a combination of projection operators to enforce constraints in both real and Fourier space until convergence is achieved. If a sufficient number of constraints are enforced, then, in general, ab initio reconstruction is possible via iterative phasing. For example, this can be accomplished when one samples the intensity data at twice the Nyquist rate and enforces the support constraint implied by this oversampling (22).

Here we extend these iterative phasing techniques to a multitiered algorithm that can reconstruct an object from its fluctuation scattering data, which requires one to determine both intensity and phase information. In particular, we seek a function ρ whose intensity harmonic coefficients match the constraints imposed by the correlation data in Eqs. 6 and 7 for the 2D case and in Eqs. 14 and 15 for the 3D case, while satisfying any applicable real space constraints, such as being supported within a given region, nonnegativity, upper bounds, and/or symmetry. However, in practice, noise and/or an insufficient number of images may limit the amount of information obtainable from the correlation data; i.e., one may be able to accurately determine $B_m$ and $B_l$ only for $\left|m\right|<m_{\text{max}}$ and $l<l_{\text{max}}$, or may be able to retrieve only autocorrelation data instead of the full cross-correlation data.

Now we define several projection operators used to enforce the previously mentioned constraints.^§

Real Space Projectors.

Given a support set S, the support projection operator $P_S$ projects a function to have support contained in S:

$$\left(P_S\rho \right)\left(\mathbf{r}\right)=\{\begin{array}{ll}\rho \left(\mathbf{r}\right),\hfill & \text{if}\hspace{0.17em}\mathbf{r}\in S,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$

Similarly, one can extend this definition to enforce nonnegativity, $P_{S+}\rho \left(\mathbf{r}\right)=\text{max}\left(P_S\rho \left(\mathbf{r}\right),0\right)$; an upper bound τ, $P_{S\tau }\rho \left(\mathbf{r}\right)=\text{min}\left(P_S\rho \left(\mathbf{r}\right),\tau \right)$; or both, $P_{S+\tau }\rho \left(\mathbf{r}\right)=\text{min}\left(P_{S+}\rho \left(\mathbf{r}\right),\tau \right)$.

To enforce symmetry given by a point group G, we define the associated orthogonal projection operator $P_G$, which projects a function to the closest function in the $L^2$ norm that is invariant under G. In 2D, this projection can be represented in terms of circular harmonic coefficients by

$${\left(P_G\rho \right)}_m\left(r\right)=\{\begin{array}{ll}{\rho }_m\left(r\right)+\frac{a}{2}\left({\rho }_{-m}\left(r\right)-{\rho }_m\left(r\right)\right),\hfill & \text{if}\hspace{0.17em}m\equiv 0\left(\text{mod}\hspace{0.17em}k\right),\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$

where G has a k-fold rotational element, and a is 1 if G has a reflection and is 0 otherwise. In 3D, this projection can be represented in terms of spherical harmonic coefficients by

$${\left(P_G\rho \right)}_{lm}\left(r\right)=\frac{1}{\left|G\right|}{\displaystyle \sum _{\mathcal{O}\in G}{\displaystyle \sum _{m^{\prime }=-l}^l{\left(\text{det}\left(\mathcal{O}\right)\right)}^l{D}_{lm{m}^{\prime }}\left(\text{det}\left(\mathcal{O}\right)\mathcal{O}\right){\rho }_{l{m}^{\prime }}\left(r\right)}},$$

where the $D_{lm{m}^{\prime }}$ are the Wigner D-matrix elements.

Two-Dimensional Correlation Projectors.

Given the circular harmonic coefficient magnitude data $B_m\left(q\right)$ in Eq. 7, we define the autocorrelation projection operator $P_A$, which projects a function I to the closest function in the discrete $L^2$ norm^¶ whose circular harmonic magnitudes match $B_m$. This projection can be expressed in terms of circular harmonic coefficients by

$${\left(P_{A}I\right)}_m\left(q\right)=\frac{I_m\left(q\right)}{\left|I_m\left(q\right)\right|}\sqrt{B_m\left(q\right)}.$$

If $I_m\left(q\right)=0$, then the quotient is replaced by 1. Additionally, we allow the coefficients to float for $\left|m\right|>m_{\text{max}}$; i.e., ${\left(P_{A}I\right)}_m=I_m$.

If cross-correlation data are available, then recall that $v_m\sqrt{{\lambda }_m}$ is equal to the intensity harmonic coefficients up to a single phase factor for each m. We define the cross-correlation projection operator $P_C$, which projects a function I to the closest function in the discrete $L^2$ norm whose circular harmonics coefficients satisfy Eq. 8. This projection can be expressed in terms of circular harmonic coefficients by

$${\left(P_{C}I\right)}_m\left(q\right)=v_m\left(q\right)\sqrt{{\lambda }_m}\frac{{\displaystyle {\sum }_j{I}_m\left(q_j\right)v_m^{*}\left(q_j\right)q_j}}{\left|{\displaystyle {\sum }_j{I}_m\left(q_j\right)v_m^{*}\left(q_j\right)q_j}\right|}.$$

If the denominator is 0, then the quotient is replaced by 1. Again, we set ${\left(P_{C}I\right)}_m=I_m$ for $\left|m\right|>m_{\text{max}}$.

Three-Dimensional Correlation Projectors.

Given the spherical harmonic coefficient data $B_l$, we define the spherical harmonic autocorrelation projection operator $P_A$, which projects a function I to the closest function in the discrete $L^2$ norm^# whose spherical harmonic coefficients satisfy Eq. 15. This projection can be expressed in terms of spherical harmonic coefficients by

$${\left(P_{A}I\right)}_{lm}\left(q\right)=\frac{I_{lm}\left(q\right)}{\sqrt{{\displaystyle {\sum }_{m=-l}^l{\left|I_{lm}\left(q\right)\right|}^2}}}\sqrt{B_l\left(q\right)}.$$

If the denominator is 0, then the quotient in the above definition is replaced by $1/\sqrt{2l+1}$. Additionally, we allow the coefficients to float for $l>l_{\text{max}}$; i.e., ${\left(P_{A}I\right)}_{lm}=I_{lm}$.

Recall that angular cross-correlation data determine the spherical harmonic coefficients up to multiplication by a unitary matrix via Eq. 17. Therefore, the l-th order spherical harmonic coefficients of the function closest to I that match the cross-correlation data are given in matrix form by $V_l\sqrt{{\mathrm{\Lambda }}_l}{U}_l$, where $U_l$ solves the unitary Procrustes problem,

$$\underset{U_l\in \text{U}\left(2l+1\right)}{\text{min}}{\Vert D\left(I_l-V_l\sqrt{{\mathrm{\Lambda }}_l}{U}_l\right)\Vert }_F,$$

where $U\left(2l+1\right)$ is the set of unitary $2l+1$ dimensional matrices; ${\Vert \cdot \Vert }_F$ is the Frobenius norm; $D=\text{diag}\left(q_0,\dots ,q_{N-1}\right)$ weights the norm to match the discrete $L^2$ norm; and we use zero padding if $2l+1>N$. In particular, given the singular value decomposition $\sqrt{{\mathrm{\Lambda }}_l}{V}_l^{*}{D}^2{I}_l={\mathcal{u}}_l{\displaystyle {\Sigma }_l{\mathcal{v}}_l^{\ast }}$, the minimizer is given by ${\mathcal{u}}_l{\mathcal{v}}_l^{*}$. This result allows us to define the spherical harmonic cross-correlation projection operator $P_C$, which projects a function I to the closest function in the discrete $L^2$ norm whose spherical harmonic coefficients satisfy Eq. 14. This projection can be expressed in terms of spherical harmonic coefficients by

$${\left(P_{C}I\right)}_l=V_l\sqrt{{\mathrm{\Lambda }}_l}{\mathcal{u}}_l{\mathcal{v}}_l^{*},$$

where ${\left(P_{C}I\right)}_l$ is the N by $2l+1$ matrix of spherical harmonic coefficients of $P_{C}I$. Again, we set ${\left(P_{C}I\right)}_l=I_l$ for $l>l_{\text{max}}$.

Fluctuation Scattering Operator.

We now define the fluctuation scattering operator F, which given a function ρ, projects its intensities to match the angular correlation data, projects the resulting quantities to the nearest nonnegative function, and then projects ρ to the closest function whose Fourier magnitudes match the square root of the projected intensities. This operator can be expressed in the Fourier domain as

$$\widehat{\left(F\rho \right)}\left(\mathbf{q}\right)=\frac{\widehat{\rho }\left(\mathbf{q}\right)}{\left|\widehat{\rho }\left(\mathbf{q}\right)\right|}\sqrt{\text{max}\left(\left(P_{\#}{\left|\widehat{\rho }\right|}^2\right)\left(\mathbf{q}\right),0\right)},$$

where, depending on what type of data is available, $P_{\#}$ is either $P_A$ or $P_C$. If $\widehat{\rho }\left(\mathbf{q}\right)=0$, then the quotient in the above definition is replaced by 1.

Iterative Phasing Algorithms.

Now we describe how to use these projection operators in an iterative procedure to reconstruct a function from its fluctuation scattering data while enforcing prescribed real space constraints. We start with some initial guess ${\rho }^{\left(0\right)}$ and iteratively apply a series of projection operators to produce the iterate ${\rho }^{\left(n\right)}$ after n steps.

One of the first developed iterative phasing techniques is the error-reducing (ER) method, which alternates between projecting constraints in Fourier space and in real space (23). Here we generalize ER for fluctuation scattering data, yielding^‖

$${\rho }^{\left(n+1\right)}\left(\mathbf{r}\right)=\left(P_{S\ast }F{\rho }^{\left(n\right)}\right)\left(\mathbf{r}\right),$$

where $P_{S\ast }$ is one of $P_S$, $P_{S+}$, $P_{S+\tau }$, or $P_{S\tau }$.

One of the main disadvantages of ER is that it often gets stuck in local minima. A popular method to circumvent this issue is the hybrid input–output (HIO) method, which uses negative feedback to inhibit stagnation (24). We formulate HIO for fluctuation scattering as

$${\rho }^{\left(n+1\right)}\left(\mathbf{r}\right)=\{\begin{array}{ll}\left(F{\rho }^{\left(n\right)}\right)\left(\mathbf{r}\right),\hfill & \text{if}\left(P_{S\ast }^{c}F{\rho }^{\left(n\right)}\right)\left(\mathbf{r}\right)=0,\hfill \\ {\rho }^{\left(n\right)}\left(\mathbf{r}\right)-\beta \left(P_{S\ast }^{c}F{\rho }^{\left(n\right)}\right)\left(\mathbf{r}\right),\hfill & \text{otherwise},\hfill \end{array}$$

where $\left(P_{S\ast }^c\rho \right)\left(\mathbf{r}\right)=\rho \left(\mathbf{r}\right)-\left(P_{S\ast }\rho \right)\left(\mathbf{r}\right)$ and $\beta \in \left(\mathrm{0,1}\right]$.

The iterative schemes listed above can be modified to enforce point group symmetry by replacing F with $P_{G}F$.

To obtain a good estimate of the true support region, we use the shrinkwrap method (25), which periodically convolves the iterate with a Gaussian of width σ and then applies a threshold ε to estimate the support; i.e., the updated support for the d-dimensional case is taken to be

$$S=\left\{\mathbf{r}:\frac{1}{{\left(2\pi {\sigma }^2\right)}^{d/2}}{\displaystyle \underset{{\mathrm{ℝ}}^d}{\int }{\rho }^{\left(n\right)}\left(\mathbf{s}\right)e^{-{\left|\mathbf{r}-\mathbf{s}\right|}^2/2{\sigma }^2}d\mathbf{s}\ge \mathit{ϵ}}\right\}.$$

In particular, we apply several iterations of HIO, followed by a few iterations of ER, perform shrinkwrap to update the support, and repeat this process until convergence is reached. See Fig. S7 for a summary of the described iterative procedure.

We note that the solution can be reconstructed only up to translation, rotation, reflection through a line, and inversion through a point. Furthermore, a general structure might not be uniquely determined by its fluctuation scattering data (26). However, whether this nonuniqueness corresponds to small perturbations around a single solution, several clusters of solutions, or a continuum of solutions and how it depends on $m_{\text{max}}$, $l_{\text{max}}$, and the imposed constraints are not fully understood and likely depend on the complexity of the structure.

Results

Here we test the presented iterative phasing schemes by reconstructing several structures from their theoretical $B_m/B_l$ data. In general, we enforce support and nonnegativity constraints; set $\beta =0.5$, $\sigma =1/N$, ε to be 2–10% of the maximum density value, $Q=N/2$; sample the fluctuation scattering data at least at twice the Nyquist rate; and initialize the procedure with the support S to be the ball of radius $1/2$ and the density ${\rho }^{\left(0\right)}$ to be 1 within the support and 0 outside of it. More details can be found in SI Text. Each reconstruction took less than 5 min on a single core of a 2.4-GHz Ivy Bridge processor.

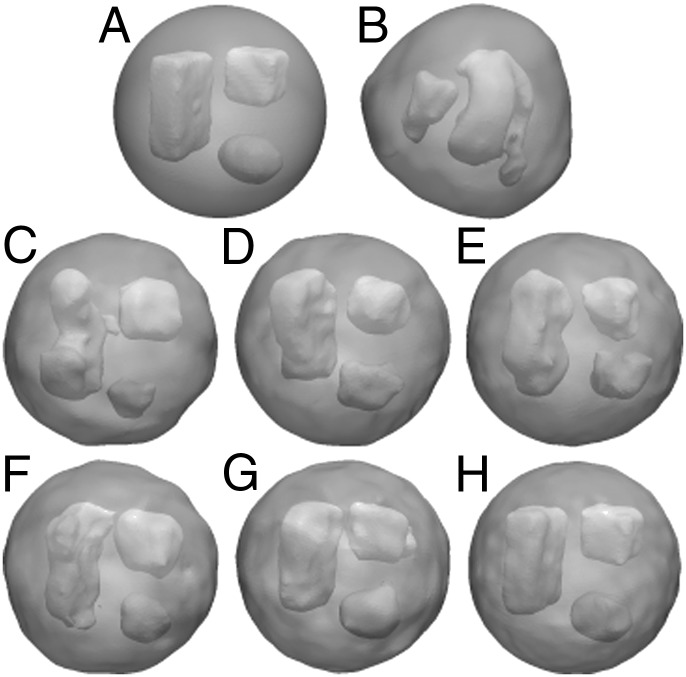
We present reconstructions from angular correlation data, using the 2D version of the iterative phasing approach in Figs. 1 and 2. In Fig. 1, the target shape was given a uniform density of 1 within a circle; had a rectangle, a triangle, and an ellipse cut out; and was then smeared onto the grid via convolution with a Gaussian of width 0.015. We show reconstructions of the target shape from SAXS data, autocorrelation data, and cross-correlation data for $m_{\text{max}}=\mathrm{4,10,20}$, both with and without upper-bound constraints, using $\tau =1$, and set $N=100$. In Fig. 2, we reconstruct the 2D X-ray projection of a pentameric ligand-gated ion channel (pLGIC), from Protein Data Bank entry 4NPP (27), through its symmetry axis. Here we use cross-correlation data up to a $1.4\text{-}\AA$ resolution with $m_{\text{max}}=20$, enforce a fivefold symmetry axis, and set $N=60$.

Fig. 1.

Two-dimensional shape reconstructions. (A) Original image. (B and C) Reconstructions from SAXS data without and with upper-bound constraint. (D–F) Reconstructions from autocorrelation data with $m_{\text{max}}=\mathrm{4,10,20}$. (G–I) Reconstructions from cross-correlation data with $m_{\text{max}}=\mathrm{4,10,20}$. (J–L) Reconstructions from autocorrelation data with upper-bound constraint with $m_{\text{max}}=\mathrm{4,10,20}$. (M–O) Reconstructions from cross-correlation data with upper-bound constraint with $m_{\text{max}}=\mathrm{4,10,20}$.

Fig. 2.

Reconstruction of the X-ray projection of the pLGIC. (Left) Original. (Right) Reconstruction from cross-correlation data with $m_{\text{max}}=20$.

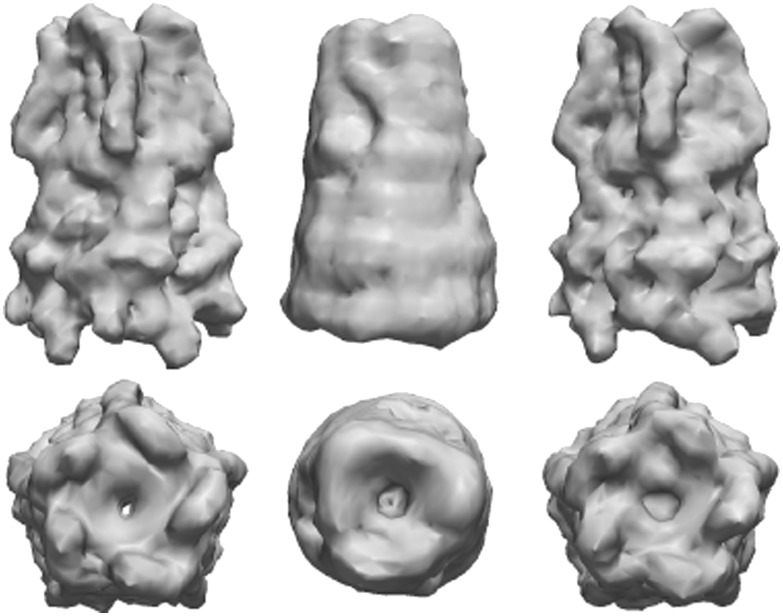
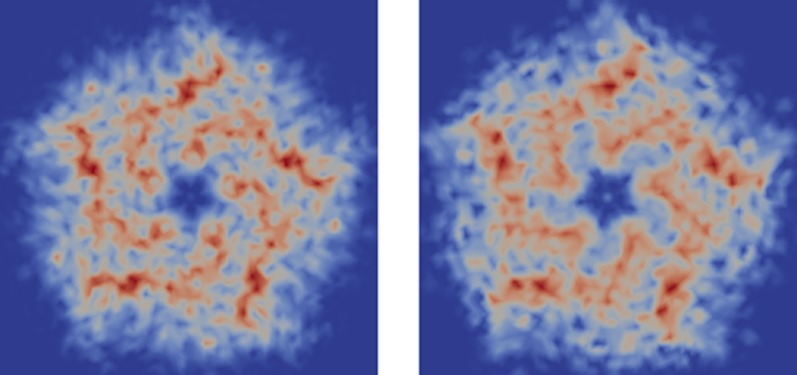
Results for the reconstruction of 3D objects from angular correlation data are shown in Figs. 3 and 4. In Fig. 3, the target shape was given a uniform density of 1 within a sphere; had a box, a cube, and an ellipsoid cut out; and was then smeared onto the grid via convolution with a Gaussian of width 0.015. We show reconstructions of the target shape from SAXS data, autocorrelation data, and cross-correlation data for $l_{\text{max}}=\mathrm{4,10,20}$, with an upper-bound constraint, using $\tau =1$, and set $N=42$. In Fig. 4, we reconstruct the 3D electron density of pLGIC from cross-correlation data up to a $4.8\text{-}\AA$ resolution with $l_{\text{max}}=20$, both with and without enforcing a fivefold symmetry axis, and set $N=42$.

Fig. 3.

Three-dimensional shape reconstructions, displayed as transparent density isosurfaces. (A) Original shape. (B) Reconstruction from SAXS data. (C–E) Reconstructions from autocorrelation data with $l_{\text{max}}=\mathrm{4,10,20}$. (F–H) Reconstructions from cross-correlation data with $l_{\text{max}}=\mathrm{4,10,20}$.

Fig. 4.

Reconstructions of the pLGIC, displayed as density isosurfaces for a side and top view. (Left) Original. (Center) Average reconstruction from cross-correlation data with $l_{\text{max}}=20$ and without a symmetry constraint. (Right) Reconstruction from cross-correlation data with $l_{\text{max}}=20$ and a symmetry constraint.

As shown in Figs. 1 and 3, the quality of the iterative phasing solution depends highly on the amount of experimental information and real space constraints used during the reconstruction process. In particular, the previously mentioned nonuniqueness manifests as small perturbations from the original structure, which decrease as more information is used. Nevertheless, even with a small amount of experimental information, low-resolution structure determination is still possible. However, the utilization of extra real space constraints, such as the upper density bound constraint used here, can compensate for a lack of reciprocal space information, such as the omission of cross-correlation data. In each example, the inclusion of higher-order terms allows for the recovery of finer details in the reconstructed models.

The reconstructions of pLGIC have a high degree of similarity to the target model, especially when symmetry is enforced. Without the symmetry constraint, the resulting reduction in information content leads to a lower-resolution 3D reconstruction, with spurious false details occurring below this resolution range. These false details were removed for this case by averaging over 24 aligned independent reconstructions with randomly perturbed starting densities. In contrast, utilization of the symmetry constraint yields a high-quality reconstruction without averaging. In particular, we achieved a 6-Å reconstruction with the symmetry constraint and a 12-Å reconstruction without it; see Table S1 for the reconstruction statistics.

Conclusions

We have demonstrated that it is possible to determine general structure from fluctuation X-ray scattering (FXS) data with an iterative phasing algorithm. The MTIP procedure outlined here is very flexible, as it allows for one to enforce a combination of autocorrelation, cross-correlation, or SAXS/WAXS data of various orders, depending on what information is experimentally available in each resolution shell. Furthermore, unlike other 3D solution methods for FXS, this approach does not require symmetry, is not limited to a binary model, and has a large region of convergence.

The quality of the structural models that can be obtained from this method depends on the experimental availability and accuracy of the FXS data and the amount of known prior information. At the very least, a low- to medium-resolution reconstruction is possible, but with sufficient information, high resolution can be achieved. In particular, the algorithm’s performance could be improved by using additional prior real space information, such as density histograms or local smoothness constraints, or by making use of any experimentally available higher-order intensity correlations.