Flourishing ocean drives the end-Permian marine mass extinction

Significance

This study provides geochemical evidence that links some of the most important finds associated with the end-Permian mass extinction, including climate warming, enhanced weathering, increased primary productivity, and widespread marine anoxia under a common denominator: the linked biogeochemical sulfur and carbon cycles. Lethal marine conditions are likely the result of climate feedback mechanisms acting to increase nutrient input to the ocean, thereby stimulating global organic carbon production. With future projected climate change in mind, such climate feedback mechanisms could induce widespread eutrophication and expansion of anoxic and sulfidic zones, thereby fundamentally altering marine ecosystems.

Abstract

The end-Permian mass extinction, the most severe biotic crisis in the Phanerozoic, was accompanied by climate change and expansion of oceanic anoxic zones. The partitioning of sulfur among different exogenic reservoirs by biological and physical processes was of importance for this biodiversity crisis, but the exact role of bioessential sulfur in the mass extinction is still unclear. Here we show that globally increased production of organic matter affected the seawater sulfate sulfur and oxygen isotope signature that has been recorded in carbonate rock spanning the Permian−Triassic boundary. A bifurcating temporal trend is observed for the strata spanning the marine mass extinction with carbonate-associated sulfate sulfur and oxygen isotope excursions toward decreased and increased values, respectively. By coupling these results to a box model, we show that increased marine productivity and successive enhanced microbial sulfate reduction is the most likely scenario to explain these temporal trends. The new data demonstrate that worldwide expansion of euxinic and anoxic zones are symptoms of increased biological carbon recycling in the marine realm initiated by global warming. The spatial distribution of sulfidic water column conditions in shallow seafloor environments is dictated by the severity and geographic patterns of nutrient fluxes and serves as an adequate model to explain the scale of the marine biodiversity crisis. Our results provide evidence that the major biodiversity crises in Earth’s history do not necessarily implicate an ocean stripped of (most) life but rather the demise of certain eukaryotic organisms, leading to a decline in species richness.

The end-Permian mass extinction (EPME) is marked by ∼80% marine biodiversity loss (1). This event is linked with turmoil in the biogeochemical carbon and sulfur cycles (2–4), alongside evidence for abrupt climate change and widespread euxinic (free H₂S) and anoxic water column conditions (5–7). Climate feedback mechanisms might have affected the biogeochemical cycles and may have spawned large-scale adverse conditions detrimental for many organisms (8). Regionally increased primary productivity (9–11) and successive enhanced organic matter degradation by microbial sulfate reduction (MSR), which produces H₂S as a by-product, has been held responsible for euxinic conditions during this time interval (12, 13). Even at a micromolar level, hydrogen sulfide is poisonous for most eukaryotic organisms, as it obstructs mitochondrial energy metabolism (14). The sulfate-reducing prokaryotes that drive this H₂S production are a key catalyst of the biogeochemical sulfur cycle (15) and are associated with a cell-internal reaction pathway connected with kinetic isotope fractionation for both sulfate oxygen and sulfur (16, 17). This biochemical transformation of sulfate linked with an additional oxidative sulfur subcycle, mainly as microbial sulfur disproportionation, and sedimentary sulfide burial can leave a distinct imprint on the isotope composition of the marine sulfate pool (15, 18). In addition, MSR is intimately tied to organic carbon (OC) availability and is the most important contributor to sedimentary OC remineralization on the continental shelf, after aerobic respiration, and thereby fuels the biogeochemical carbon cycle (15, 19, 20). Measuring sulfate sulfur and oxygen isotopes in marine sediments can provide important information about biologically induced sulfur transmissions among different reservoirs (21–23) and can record a global signal (15, 23).

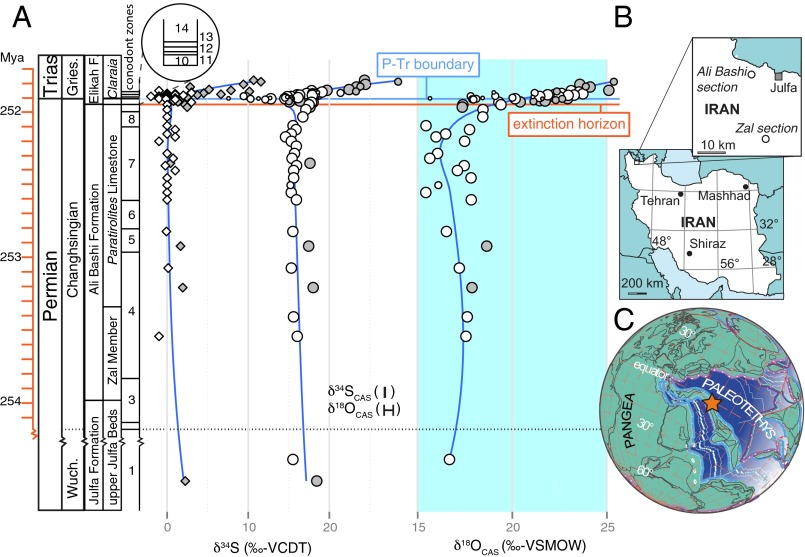
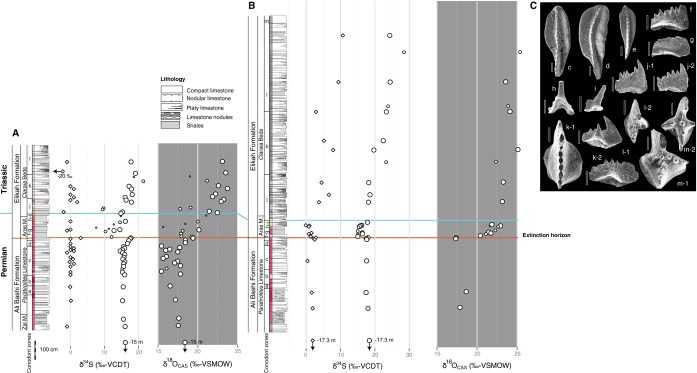
We produced a new high-resolution dataset of carbonate-associated sulfate (CAS) sulfur and CAS oxygen isotopes spanning the time interval of the EPME. Changes in the marine dissolved sulfate isotope composition are considered to be faithfully captured by CAS (4, 15, 23), and chromium-reducible sulfur (CRS) records the products of MSR (15, 24). Carbonate rock was collected at the Kuh-e-Ali Bashi 1 (38.940°N, 45.520°E) and Zal (38.733°N, 45.580°E) sections of the Julfa region (NW Iran, Fig. 1), which were situated on the north-northeastern margin of the NW Iranian Terrane, belonging to the Cimmerian Microcontinent during the latest Permian (ref. 25, Fig. 1). These sections represent an excellent stratigraphic correlation and age assignment (Timescale and Figs. S1 and S2). Carbonate rock successions spanning the Permian−Triassic (P−Tr) boundary interval in this area can be divided into two major lithological units: the Ali Bashi Formation made up of the Paratirolites Limestone Member marking the upper part and the Zal Member marking the lower part (Fig. S1). The Aras Member (26), or “Boundary Clay,” and the following limestone unit, belong to the Elikah Formation (Fig. S1). The Zal Member consists, predominantly, of shales with some intercalations of limestone and marls. The red nodular Paratirolites Limestone beds are classified as argillaceous limestone. Macrofossil assemblages consist of rare ammonoids, nautiloids, rugose corals, and brachiopods. This unit is conformably overlain by the Aras Member, which records a marked reduction of CaCO₃ (26). In addition, the Permian faunal elements disappear in this unit; therefore the boundary between these units is considered the extinction horizon (ref. 26, Fig. S1). On top of the clay-rich Aras Member, the remainder of the Elikah Formation consists of limestone beds. These lithologies were deposited as a deep-water carbonate platform and did not undergo large-scale sea level changes (Facies Description). Therefore, this carbonate platform with an isolated location in the Paleotethys (Fig. 1) bears a large potential for obtaining secular changes of ocean chemistry across the EPME (Fig. 1). Stratigraphic patterns in these CAS sulfur and oxygen isotope records allow for a better understanding of the sulfur cycle across the EPME, thus enabling the assessment of its potential impact on biodiversity.

Fig. 1.

Stratigraphy and geography. (A) Isotopic composition of CAS (circle) and CRS (diamond) of carbonates from Kuh-e-Ali Bashi (white) and Zal (gray). Significant changes in these geochemical records, discernable in the blue lines (loess fit), mark the extinction horizon and suggest a substantial perturbation of the sulfur cycle. Error bars denote reproducibility (2σ; Tables S1 and S2). The temporal framework is constructed by ages for conodont biozones (Figs. S1 and S2 and Timescale): 1, C. Orientalis; 2, transition; 3, C. subcarinata; 4, C. chanxingensis; 5, C. bachmanni; 6, C. nodosa; 7, C. yini; 8, C abadehensis; 9, C. hauschkei; 10, H. praeparvus-M. ultima; 11, H. parvus; 12, H. lobota; 13, I staeschei; and 14, I. isarcica. The size of individual CAS data points stands for the confidence of representing true seawater chemistry: large, high confidence; small, low confidence (high CRS and non-CAS); medium, intermediate confidence (high CRS or non-CAS; Fig. S3, Tables S3 and S4, and Reliability of the CAS Proxy). Geographic location of the sections (B) today and (C) during the P−Tr (modified from ref. 25).

Fig. S1.

Stratigraphic column of the (A) Kuh-e-Ali Bashi 1 and (B) Zal sections. Lithological column and stratigraphic position of δ³⁴S_CRS (diamond), δ³⁴S_CAS (circle), and δ¹⁸O_CAS (circle). Conodont zones: a, C. bachmanni; b, C. nodosa; other zones follow from C. (C) Characteristic Late Permian–Early Triassic conodonts from the Julfa region. (Scale bars, 100 μm.) All specimens are stored in the collection of the Ferdowsi University of Mashhad (overview in refs. 26 and 71); c, Clarkina yini, FUM# G258-6, Ali Bashi Formation, Main Valley section, upper view; d, Clarkina abadehensis abadehensis, FUM# 1J248-6, Ali Bashi Formation, Ali Bashi 1 section, upper view; e, Clarkina hauschkei, FUM# 1J249D-9, Ali Bashi Formation, Ali Bashi 1 section, upper view; f, Hindeodus praeparvus, FUM# G274-6, Elikah Formation, Main Valley section, lateral view; g, Hindeodus changxingensis, FUM# 1J252-11, Elikah Formation, Ali Bashi 1 section, lateral view; h, Stepanovites ?mostleri, M element, FUM# 1J253-16, Elikah Formation, Ali Bashi 1 section, lateral view; i, Merrillina ultima, Pa element, FUM# 4J203-7, Elikah Formation, Ali Bashi 4 section, lateral view’ j-1, Hindeodus parvus, FUM# G278-17, Elikah Formation, Main Valley section, lateral view; j-2, Hindeodus parvus, FUM# AJ206-2, Elikah Formation, Aras Valley section, lateral view; k-1, Hindeodus lobata, FUM# 4J217-5, Elikah Formation, Ali Bashi 4 section, upper view; k-2, Hindeodus lobata, FUM# 1J265-4, Elikah Formation, Ali Bashi 1 section, lateral view; i-1, Isarcicella staeschei, FUM# 1J270-4, Elikah Formation, Ali Bashi 1 section, lateral view; i-2, Isarcicella staeschei, FUM# 4J222-7, Elikah Formation, Ali Bashi 4 section, upper view; j-1, Isarcicella isarcica, FUM# 1J281-1, Elikah Formation, Ali Bashi 1 section, upper view; and j-2, Isarcicella isarcica, FUM# 4J225-4, Elikah Formation, Ali Bashi 4 section, upper view.

Fig. S2.

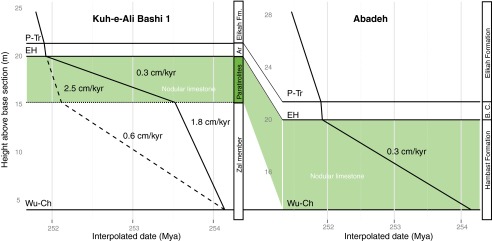
Age model for the P−Tr sections at Iran. Note the high sedimentation rates for the Paratirolites Limestone unit when relying on age-constrained conodont zones of the latest Permian (dotted line). An alternative age model for the latest Permian—used in this study to time-constrain the geochemical data—represents the sedimentation rate calculated for the Changhsingian nodular limestones of the Abadeh section (solid line). This latter sedimentation rate has been calculated by interpolated dates of the extinction horizon (EH) and the base of the Changhsingian system of the Abadeh section.

Facies Description

The successive lithological change from dominantly clastic to nodular Paratirolites Limestone has been related to drowning of the carbonate platform (52, 53). This notion is enforced by lithological features such as frequent hardgrounds as well as the distinctive red color of the latter unit—plausibly related to authigenic iron accumulation and suggesting a low rate of carbonate accumulation (53). The Zal Member in contrast to the Paratirolites Limestone Member probably had a higher siliciclastic input and resultantly higher sedimentation rates. Deposition of these units occurred at a depth below the storm wave base in a well-oxygenated environment by a productive skeletal carbonate factory (53, 54). The Aras Member has been assigned to increased terrigenous input, based on the thickness of the unit (52, 54), expressing high sediment accumulation rates (55). A concomitant reduction in carbonate production could have been equally important (52, 53). However, the water depth of deposition was still likely to have been below the storm wave base in an oxic environment, based on ostracod assemblages (55). Somewhat higher CRS values in this unit might relate to a higher local production of sulfide by MSR (Tables S3 and S4). Increased pyrite content, or other iron sulfides, in the sediment can be a function of lower oxygenation levels or higher OC availability, but the two parameters are likely linked (22). The sulfide oxygen front at these sites was most likely located within the sediments, as a high-resolution microfacies analysis (54) did not reveal framboidal pyrite, a sign of water column sulfide (31). A continuation of deep-water conditions, especially for the nodular lithology, which resembles the preextinction strata—deep water facies—has been implied for the first few meters above the Aras Member at the Kuh-e-Ali Bashi site (54). The platy limestone beds of the Elikah Formation might, however, indicate a somewhat shallower water depth (54) but no high-amplitude sea level changes (52, 54). Lithological indices for pervasive anoxia and euxinia, such as framboidal pyrite or high OC accumulation, are absent. However, assemblages of ostracods together with abundant bivalve specimens (Claraia) might indicate slight or episodic dysoxic bottom water conditions (52, 54, 55).

Table S3.

Dataset Kuh-e-Ali Bashi 1

Height,* m	Time, Mya	δ34SCRS, ‰ VCDT	δ34SCAS, ‰ VCDT	δ34Snon-CAS1,† ‰ VCDT	δ34Snon-CAS2,† ‰ VCDT	δ18OCAS, ‰ VSMOW	δ18Onon-CAS1,† ‰ VSMOW	CAS, μg/g	Non-CAS, μg/g	CRS, μg/g
4.12	251.86	−0.90	17.81	13.51	NA	23.11	16.29	1,319.55	87.82	3.81
3.5	251.87	−20.01	19.10	NA	NA	23.53	NA	567.26	72.33	13.10
3.3	251.87	2.98	18.59	11.15	NA	19.02	13.26	1.00	153.13	6.53
3.07	251.88	3.07	21.38	NA	NA	21.18	NA	438.62	304.94	3.39
2.8	251.88	0.38	17.20	8.22	NA	22.60	11.47	775.07	137.29	4.02
2.65	251.88	0.80	17.94	12.71	12.84	23.73	15.51	745.22	73.70	4.94
2.35	251.89	0.47	18.13	11.22	NA	22.24	13.08	1,128.17	25.49	7.02
2.2	251.89	0.61	16.05	9.13	NA	21.87	13.92	564.57	45.92	6.35
2.05	251.89	−0.09	16.34	13.00	NA	23.27	17.32	384.45	79.42	3.98
1.94	251.89	2.18	17.90	NA	NA	22.95	NA	326.58	11.41	5.90
1.61	251.90	0.07	9.73	5.68	NA	19.10	6.61	168.12	197.06	1.29
1.54	251.90	−0.64	9.43	5.66	NA	17.80	8.20	195.88	24.94	26.59
1.41	251.90	−1.67	15.27	7.08	NA	21.45	10.40	1,826.26	69.31	4.32
1.33	251.90	−5.43	14.82	5.85	NA	22.47	7.61	284.14	92.11	14.43
1.18	251.90	−0.66	14.81	NA	NA	21.08	NA	156.18	204.65	44.48
0.9	251.91	0.30	16.14	7.28	NA	NA	NA	291.53	24.56	24.58
0.85	251.91	0.09	14.54	5.91	NA	20.01	6.80	245.98	138.16	11.63
0.73	251.91	0.65	12.70	NA	NA	18.43	NA	225.61	205.75	31.72
0.56	251.91	−0.43	7.57	4.36	NA	15.65	4.94	110.97	152.35	38.57
0.5	251.92	0.03	11.26	4.81	NA	NA	NA	108.19	127.64	15.21
0.45	251.92	0.28	14.52	NA	NA	NA	NA	223.96	51.13	14.19
0.4	251.92	−0.63	12.79	NA	NA	20.15	NA	523.92	38.54	19.96
0.35	251.92	−0.49	10.28	NA	NA	18.10	NA	110.88	11.58	49.91
0.28	251.92	−0.14	NA	NA	NA	NA	NA	25.92	2.75	44.23
0.2	251.92	1.23	NA	NA	NA	17.88	NA	88.99	0.82	87.10
0.05	251.92	1.32	12.10	NA	NA	17.95	NA	95.98	0.78	50.00
0	251.94	3.22	17.80	NA	NA	19.29	NA	556.56	46.89	16.98
−0.05	251.96	−0.18	17.50	NA	NA	19.40	NA	554.94	145.37	5.16
−0.15	251.99	0.18	17.10	NA	NA	18.45	NA	369.85	82.95	NA
−0.3	252.04	−0.02	16.73	10.20	NA	18.44	13.07	648.12	54.04	8.99
−0.48	252.10	−0.02	15.52	NA	NA	15.44	NA	533.80	127.26	8.15
−0.56	252.13	0.96	15.90	11.53	NA	17.74	14.66	532.75	67.86	5.07
−0.65	252.16	0.07	15.30	NA	NA	16.48	NA	444.04	50.22	6.67
−0.71	252.18	0.70	14.60	NA	NA	15.97	NA	310.47	41.00	6.05
−0.8	252.21	−1.01	15.31	11.67	NA	17.48	13.29	537.49	28.66	5.39
−0.9	252.24	NA	15.93	10.86	NA	NA	NA	439.31	20.49	NA
−1.05	252.29	0.21	15.70	NA	NA	16.05	NA	390.96	64.36	1.73
−1.15	252.32	0.74	15.40	NA	NA	15.64	NA	570.94	89.15	2.47
−1.3	252.37	−0.23	15.96	10.30	NA	17.46	14.15	464.54	83.37	7.54
−1.4	252.41	0.62	15.60	NA	NA	17.10	NA	475.86	66.53	8.39
−1.55	252.46	−0.40	15.60	NA	NA	17.82	NA	418.12	25.30	5.41
−1.7	252.51	0.31	15.20	NA	NA	16.09	NA	265.94	121.50	4.85
−1.85	252.56	0.10	15.30	NA	NA	15.43	NA	342.31	82.78	1.42
−2	252.61	0.19	15.94	12.27	NA	17.83	15.21	430.40	70.48	5.32
−2.65	252.82	−0.09	15.50	NA	NA	16.52	NA	414.53	98.46	9.16
−3.4	253.07	0.13	15.31	9.62	NA	17.20	14.53	627.58	62.09	4.64
−4.4	253.41	NA	15.58	12.00	NA	17.62	16.18	499.99	153.13	NA
−4.8	253.54	−1.01	16.04	9.32	NA	17.55	13.31	826.41	71.04	19.13
−19.95	NA	NA	15.51	NA	NA	16.68	NA	NA	NA	NA

Identifier for all entries is AB. Sample labels are composed of identifier and height (meters). NA, not available.

^*Height is relative to the extinction horizon.

^†Numbering for non-CAS isotope values stands for the respective leaching procedures.

Table S4.

Dataset Zal

Height,* m	Time, Mya	δ34SCRS, ‰ VCDT	δ34SCAS, ‰ VCDT	δ34Snon-CAS1,† ‰ VCDT	δ18OCAS, ‰ VSMOW	δ18Onon-CAS1,† ‰ VSMOW	CAS, μg/g	Non-CAS, μg/g	CRS, μg/g
10.95	251.79	10.66	24.34	17.18	NA	NA	372.49	42.22	3.93
10.05	251.80	11.56	28.48	24.34	25.37	19.91	458.09	317.91	NA
8.45	251.82	9.41	24.45	10.99	23.57	11.75	358.42	104.00	17.53
6.85	251.84	2.84	23.35	NA	24.11	NA	514.81	62.86	34.15
5.30	251.85	5.17	22.43	8.81	NA	NA	425.00	49.27	16.96
4.80	251.86	7.87	19.71	12.10	25.10	15.45	880.07	78.00	26.25
4.15	251.87	10.15	23.28	19.84	22.35	15.11	492.91	295.38	21.93
3.05	251.88	4.50	18.23	NA	23.27	NA	761.12	87.81	54.50
2.40	251.89	6.64	18.58	NA	NA	NA	867.45	61.38	29.75
2.00	251.89	3.74	18.15	−9.35	23.15	10.60	754.67	222.46	69.04
0.92	251.91	2.45	17.83	7.43	NA	NA	NA	260.86	30.86
0.76	251.91	−0.08	16.17	11.03	21.84	14.50	467.20	49.61	10.82
0.74	251.91	0.99	15.86	11.60	NA	NA	482.99	45.23	9.68
0.69	251.92	0.79	15.53	NA	22.92	NA	466.59	36.17	11.68
0.67	251.92	0.64	15.34	9.36	21.59	13.23	74.98	64.97	10.68
0.65	251.92	0.69	15.27	NA	22.63	NA	416.49	292.77	13.71
0.45	251.93	0.49	14.98	4.82	22.29	12.92	434.60	208.71	17.44
0.35	251.93	1.56	16.31	NA	21.44	NA	452.90	123.91	44.57
0.30	251.93	0.79	16.38	NA	21.73	NA	410.07	51.03	27.97
0.25	251.93	1.36	15.02	NA	21.12	NA	194.85	61.45	72.93
0.16	251.94	1.33	15.06	4.92	20.42	4.04	775.09	97.07	38.62
0.10	251.94	2.89	18.00	11.82	NA	NA	666.02	73.15	61.26
0.05	251.96	2.18	17.52	NA	17.39	NA	712.32	97.65	56.74
0.00	251.97	2.48	17.62	12.26	17.36	15.76	551.42	75.02	17.98
−1.15	252.36	0.41	17.61	10.59	NA	NA	578.30	71.90	7.57
−2.85	252.92	1.65	17.45	12.27	18.65	NA	479.29	70.43	8.69
−3.70	253.21	1.93	18.01	NA	17.87	NA	391.17	99.70	17.43
−21.00	254.53	2.24	18.45	13.08	NA	NA	540.06	39.71	7.79

Identifier for all samples is Zl. Sample labels are composed of identifier and height (meters).

^*Height is relative to the extinction horizon.

^†Numbering for non-CAS isotope values stands for the respective leaching procedures.

Timescale

U−Pb geochronology has provided absolute dates for the chemostratigraphically and biostratigraphically well-resolved Meishan P−Tr section (56). Recent advances in U−Pb dating with isotopic dilution-thermal ionization mass spectrometery and especially the use of a more precisely calibrated tracer solution resulted in dates with analytical uncertainties of less than 100 ky (57). We used these radiometric dates to make linear interpolations for conodont zones of the Meishan P−Tr section (58). Notably, the top of Hindeodus parvus is 251.873 ± 0.004 Mya, and the first occurrence date (FAD) of Clarkina yini is 252.046 Mya. In addition to these interpolated dates, the FAD of H. parvus (251.902 ± 0.024 Mya), the extinction horizon [base bed 25 at the Meishan P−Tr section, 251.941 ± 0.037 Mya (57)], and the FAD of Clarkina wangi [254.150 Mya (56)] are also used in the age model. The linear interpolations have some inherent uncertainties, which potentially could be large, as the sediment accumulation rates, which are used, may not account for hiatuses in the Meishan P−Tr section. However, these dates, in our opinion, provide the best possibility for constructing a timeframe for the study sites in NW Iran.

Recently developed Late Permian high-resolution conodont zonation constructed by the sample population taxonomic approach for the Kuh-e-Ali Bashi as well as for Meishan P−Tr sections, together with some new data for the Early Triassic in Iran (Fig. S1), enables the correlation of these sections. However, the correlation is restricted to the extinction horizon and H. parvus zone only (55). The preextinction strata cannot be correlated based on conodont zonation, possibly due to the endemism of conodonts from the south Chinese basin (55). This is further supported by the resulting sedimentation rates for the Paratirolites Limestone Member and the Zal Member based on a conodont correlation scheme, which would contradict the facies interpretation of these units (Fig. S2 and Facies Description).

We, therefore, consider a sedimentation rate of 0.3 cm/ky for the Paratirolites Limestone Member (cf. ref. 52). Such a sedimentation rate can be calculated for a nodular limestone unit that spans the complete Changhsingian of the Abadeh section (central Iran; Fig. S2). In this way, the preextinction samples, belonging to the Paratirolites Limestone Member, together with the postextinction samples, can be placed into a temporal framework for the sites in NW Iran with a relatively high level of confidence.

Results and Discussion

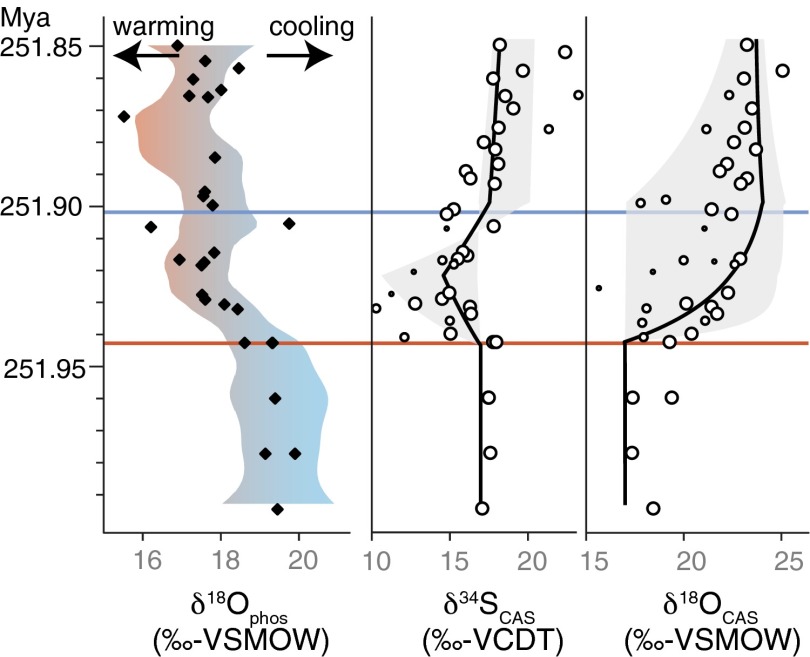
To obtain a primary seawater chemistry signal, samples likely to be contaminated during rock diagenesis by allochtonous sulfur sources, such as leachable sulfate (non-CAS) and sulfide minerals, are identified (Reliability of the CAS Proxy and Fig. S3). This enables the construction of the primary stratigraphic CAS oxygen and sulfur isotopic record (Fig. 1). In contrast to previous CAS studies of this time interval (3, 4), the preextinction CAS isotope record (∼2 My) is remarkably stable around 17‰ for both δ³⁴S_CAS and δ¹⁸O_CAS values with a spread of 1‰ and 2–3‰, respectively (Fig. 1). A ∼3‰ negative δ³⁴S_CAS excursion and a 5–7‰ positive shift in δ¹⁸O_CAS can be traced for both sites during a ∼40 ky period following the marine extinction horizon. A positive δ³⁴S_CAS excursion is found above the conodont-defined P−Tr boundary (∼3 m; Fig. S1) with values ∼5‰ heavier compared with preextinction strata.

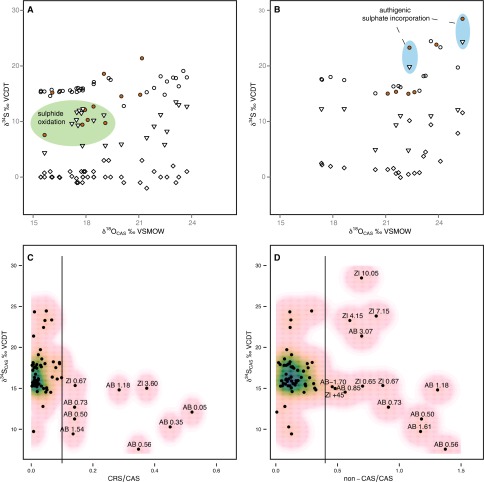
Fig. S3.

Relative concentrations and isotope composition of the extracted sulfur species. CRS (diamond) and leachable non-CAS (triangle) against CAS (circle) sulfur isotope values plotted against CAS oxygen isotope values of (A) Kuh-e-Ali Bashi 1 and (B) Zal sections. Most δ³⁴S from CRS, non-CAS, and CAS have distinctive values. However, some CAS are marked by δ³⁴S that plot in the region of non-CAS δ³⁴S values, and are often linked to comparatively high CRS/CAS or non-CAS/CAS ratios (red dots). These anomalous values accompanied by lower δ¹⁸O_CAS might represent oxidation of sulfide during diagenesis. On the other hand, some δ³⁴S_CAS, mainly the Zal section, are enriched as well as paired with high CRS/CAS or non-CAS/CAS ratios and high δ³⁴S_CRS, δ³⁴S_non-CAS, and δ¹⁸O_CAS and could therefore constitute postdepositional incorporation of CAS, from an evolved sulfate pool in a closed system. (C) CRS/CAS or (D) non-CAS/CAS ratios plotted against CAS sulfur isotopes. The lines represent static cutoff boundary values; samples to the right are presumed vulnerable to postdepositional alteration because relative high concentrations of CRS or non-CAS and could cause mixing of isotope signals.

Microbial sulfate reduction is an important aspect in the sulfur cycle, and the associated isotopic fractionation leads to ³⁴S and ¹⁸O enrichments of the residual sulfate pool (4, 27). Most of the MSR-produced H₂S will be reoxidized, and only a fraction is buried as sedimentary sulfide serving as a sink for ³²S (22); some H₂S can escape the sediment, especially under low O₂ concentrations (8). Hydrogen sulfide release from the sediment is, however, also a factor of sulfide formation and reactive iron availability (8, 22). Continental oxidative weathering and mantle-derived sulfur are fluxes that have a depleted sulfur and oxygen isotopic composition compared with seawater sulfate (4, 24, 27). Evaporite formation and successive burial (with a negligible fractionation) is a sink of sulfate, but its importance depends largely on the extent of suitable environments for deposition [with net evaporation rates (28)]. In contrast to the isotope value of sulfate sulfur, δ¹⁸O_SO4 is considerably affected by MSR and microbial sulfur disproportionation (29). Sulfur disproportionation produces sulfate with an oxygen isotope fractionation of ∼18‰ over the oxygen isotope composition of ambient sea water (29). In contrast to the sulfur isotope part of the sulfur cycle, this microbial-dominated sulfur subcycle is effectively a sink for ¹⁶O (4, 29). These different reaction pathways for the sulfur and oxygen ionic compounds of sulfate might lead to a dissimilar temporal evolution of marine sulfate sulfur and oxygen isotope composition, such as recorded by the deviating CAS δ³⁴S and δ¹⁸O at the extinction horizon in the dataset (Fig. 1).

A depleted sulfate reservoir, in comparison with modern values of 28 mM, has been implied for allowing rapid changes of seawater δ³⁴S_SO4 (21), such as observed here for the EPME (>0.1‰⋅ky⁻¹). The offset in δ³⁴S between CAS and CRS (Δ³⁴S) was often attributed to the kinetic isotope fractionation of MSR (15). A closed system of diagenetic sedimentary sulfide formation can lead to a small Δ³⁴S due to ongoing sulfate depletion by MSR (15, 30), whereas a sulfate unlimited system, such as water column pyrite formation (e.g., in the modern Black Sea), can lead to a Δ³⁴S of 45 ± 15‰ (15, 30, 31). The observed constant Δ³⁴S (15−16‰) is invariant to burial rate changes (Fig. S2), and might suggest low sulfate levels within sedimentary porewater and the water column (cf. refs. 24 and 30).

We applied a box model calculation (Methods) to delineate the fluxes that determine the isotopic composition of the marine sulfate across the P−Tr transition. Paleontological and sedimentological evidence from the Iranian sections show no indications of pervasive water column anoxia (Facies Description); this is in contrast to the inferred Late Permian marine anoxia at sites in South China and Australia (13, 32). This spatial heterogeneous pattern can be best explained by increased nutrient influx only into parts of the Tethys. This influx caused regional eutrophication associated with increasing extents of oxygen minimum zones (33) and euxinic conditions (12) rather than deep bottom water anoxia caused by a stagnant water column. Widespread ocean fertilization and drawdown of water column O₂ levels have been related to an increased influx of terrestrial material (12, 33) from soil erosion (34) and enhanced weathering (35) initiated by acid precipitation and destabilization of vegetation and soils (34), global warming, and an associated intensified hydrological cycle at that time (7). The climax of this biogeochemical cascade correlates with the greenhouse warming often associated with coeval Siberian Trap volcanism (2, 5). The importance of organic substrates for MSR justifies the incorporation of the OC pool and the link to continental weathering in our box model. This simplified approach is further justified because the continental supply of nutrients fertilizes the oceanic shelf connected with highest MSR activity and OC decomposition rates, which are almost equal in oxic and euxinic sediments (19, 20).

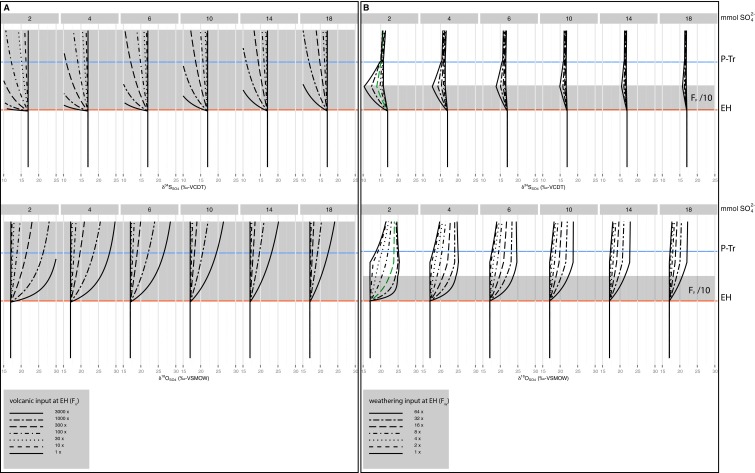
A best model fit, based on sensitivity experiments (Sensitivity Experiments and Fig. S4), suggests a 16-fold increase in the weathering flux that stimulates a >16-fold global marine OC inventory, starting at the extinction horizon and lasting for a period of 40 ky (Fig. 2). This stimulates large MSR activity (>17-fold) but also sulfur disproportionation (Methods), although it has been suggested that the latter could not explain an oxygen isotope fractionation of >18‰ between water and sulfate (29). An average δ¹⁸O_seawater of ∼−1‰ (6) and δ¹⁸O_CAS excursion to values of >20‰ make sulfur disproportionation an unlikely candidate. Increased OC degradation by MSR is a strong and robust argument for the reconstructed scenario and explains the observed δ¹⁸O_CAS excursion. Independent numerical exercises with higher complexity models suggest that >4 times enhanced continental weathering considerably increases the primary productivity in shelf settings (12, 36), followed by anoxic and sulfidic conditions as a consequence of increased (an)aerobic OC remineralization.

Fig. S4.

Sensitivity experiment for a volcanic- and weathering-induced sulfur cycle perturbation. (A) This scenario encompasses an influx of simultaneous isotopically depleted sulfur (δ³⁴S_SO4 = 3‰) and isotopically enriched oxygen flux (δ¹⁸O _SO4 = 34‰) from a volcanic source after the EH. Shaded time interval stands for the perturbation. (B) The fraction of sulfide buried as pyrite is lowered 10 times for an interval of 20 ky after the EH, after that, the fraction of pyrite burial is increased 2 times for an equivalent time period. Shaded time interval stands for the perturbation. Continental weathering is maintained to 7 times the preextinction value from the P−Tr boundary until the end of the model run. Red dotted line stands for the scenario closely correlating with CAS isotope data.

Fig. 2.

Isotopic composition of CAS (circle) and numerical solution when perturbing the system with a 16-fold increase in the global weathering flux after the extinction horizon (black line). Gray area represents range of sensitivity experiments (Fig. S4). Time-equivalent seawater temperature rise, seen in δ¹⁸O_phos (7), can enforce an enhanced hydrological cycle stimulating larger terrestrial weathering fluxes.

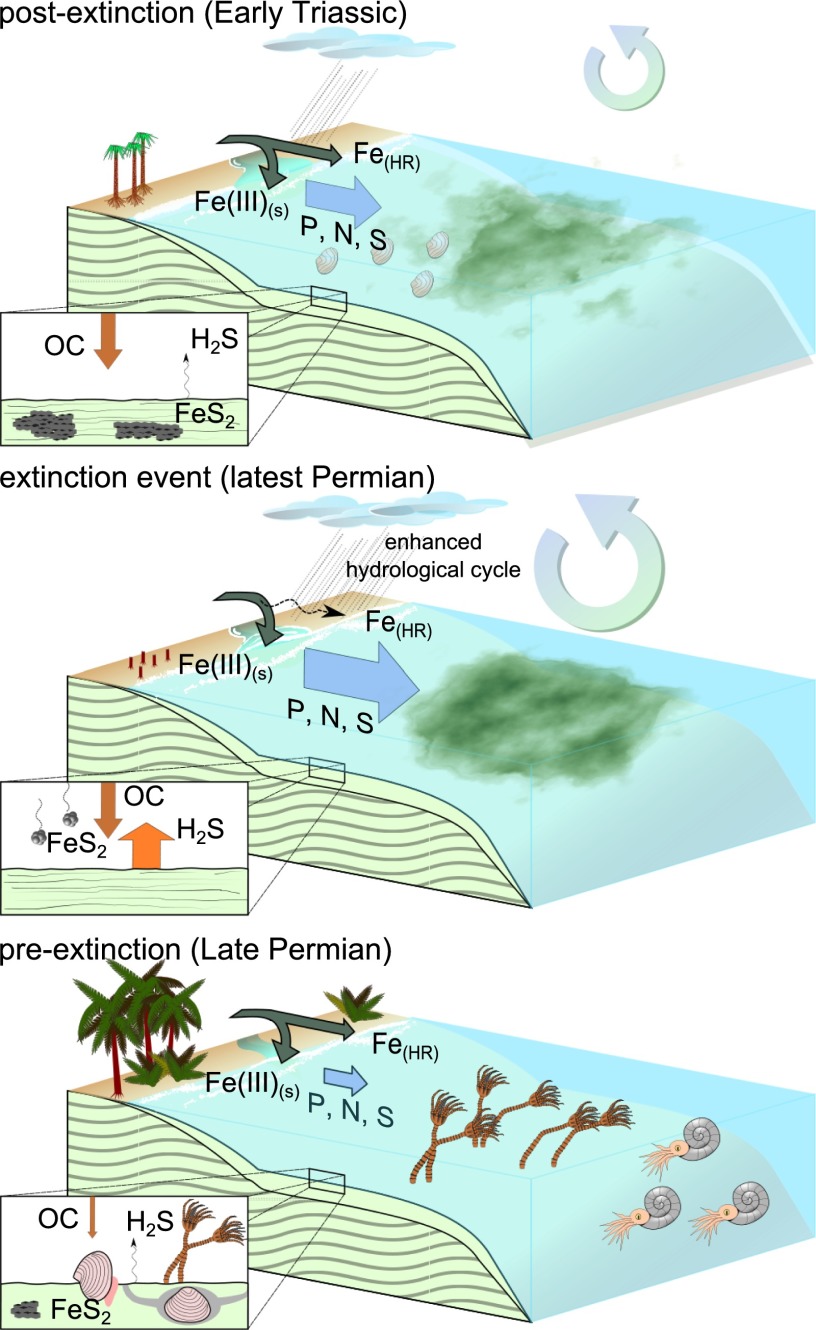
The initial negative δ³⁴S_CAS excursion also suggests that pyrite burial did not increase with enhanced MSR activity, as is often assumed (4, 27). The main controlling factors for pyrite formation are labile OC, sulfide formation, oxygenation conditions, and highly reactive iron [Fe_(HR)] availability in the sediment and water column (22). In sulfidic water column conditions, such as the modern Black Sea, which represents only a fraction of the total modern ocean volume (27), pyrite formation is a syngenetic process (Fig. 3) rather than a diagenetic process (31, 37). This pyrite sedimentation style depletes Fe_(HR) already in the water column and largely inhibits the pyrite formation within the sediment (31). In such euxinic settings, pyrite formation becomes iron-limited and pyrite burial becomes sensitive to the supply of Fe_(HR) to the ocean (38). Mechanisms for Fe_(HR) supply are hydrothermal input, windblown dust, riverine input, and diagenetic iron cycling on the shelf (39, 40). Although the iron flux from the continent is potentially large, 70–90% of the Fe_(HR) is already lost as particles in estuaries (40). The iron reaching the ocean is sensitive to water turbulence and grain concentrations delivered by rivers (40). Relating all this to the end-Permian scenario, a situation under a high sea level (5) and a sudden influx of soils (34) accompanied by high physical erosion rates (35) due to an intensified hydrological cycle in a warmer ocean (7) would create an environment that already depletes Fe_(HR) before entering the ocean (Fig. 3).

Fig. 3.

Conceptual model for environmental changes across the P−Tr boundary, depicting the shelf settings that are prone to be affected in a scenario of intensified continental influx. Preextinction Late Permian marine communities would consist of multiple trophic levels. Authigenic pyrite formation is supported by sulfide production during anaerobic OC remineralization via MSR and nonlimiting iron availability. The extinction event marks an increased terrigenous influx causing local eutrophication as well as the input of isotopically depleted sulfur, aided by an intensified hydrological cycle forced by global warming. Increased sediment load and turbulence of river discharge flocculates iron as Fe oxy(hydr)oxides in estuaries, reducing the ocean Fe_(HR) inventory. Consequential OC remineralization by MSR and Fe_(HR) limitation raises seawater H₂S. Sulfide toxicity alongside marine anoxia sustains a low-species richness but a high-biomass marine community. Pyrite sedimentation is limited to small amounts of syngenetic pyrite precipitation. Relaxation of physical continental weathering reduces ocean input of nutrients and raises Fe_(HR) delivery to the postextinction ocean, thereby reducing sulfidic water column conditions and relocating pyrite sedimentation toward the sediments, where decreased O₂ irrigation due to a less active benthic community stimulates authigenic pyrite formation. The enlarged OC pool is sustained due to carbon recycling by an active microbial community.

We do not provide an estimate for the pyrite flux change. However, under the Late Permian oceanic conditions, it was not necessary that pyrite burial increased concomitantly with increasing MSR. The diverging CAS sulfur and oxygen isotope pattern can be best explained by increased levels of MSR but decreased pyrite burial, compatible with an enlarged global extent of iron-limited euxinic seawater (Figs. 2 and 3). The presence of green sulfur bacteria—which thrive in H₂S-rich surface water—during the time interval of the sulfur cycle perturbation, evidenced by biomarker analyses (32), suggests widespread euxinia. Moreover, ocean fertilization is in concert with an independent model for the Late Permian ocean, suggesting 10 times higher nutrient levels to induce globally pervasive water column H₂S (12). The new CAS isotope data and the related environmental conditions suggest that the euxinic zones expanded suddenly at the extinction horizon (Fig. 3). Synchronicity of the two observations support the notion that sulfidic toxicity drove the marine biodiversity loss at the EPME, as first hypothesized by Kump et al. (8). However, the entire continental shelf area [∼5.8e⁶ km² for the latest Permian (28)] would be primarily affected in our conceptual model, in contrast to only upwelling regions with a comparatively smaller total dimension [∼0.4e⁶ km² for the modern ocean (8)]. Predominant sulfate reduction on the shelf, rather than in the deep sea, agrees with observations in the modern ocean of decreasing MSR with increasing distance to land (19, 22). In addition, a marine region would be targeted that is the locus of Paleozoic biological activity (the neritic realm), and thereby this conceptual model fulfills all criteria as suggested by Wignall and Twitchett (5) to explain a wholesale collapse of marine invertebrate diversity. However, the geography and nutrient load of weathering fluxes would also be an important determinant of the spatial distribution and severity of productivity-driven redox changes (oxic, nonsulfidic anoxic, and euxinic) (41). Regionally biased ecosystem destruction would leave refugia with less adverse conditions and would allow rapid recolonization of vacant ecospaces through migration of survivors. Postextinction species are frequently found to occur along a spectrum of environments, and within-habitat diversity is typically higher than diversity between habitats, a pattern explained by species that exploit the full range of the available niches under low competition pressure (42). Also, refilling of vacant ecospace by an ecologically diverse group of survivors can explain why, on a global scale, ecosystems remained operating even though species diversity collapsed (43).

This scenario to explain the EPME enhances the notion that life can influence seawater chemistry (22) and the relationship to OC remineralization (13). CAS isotopes provide a more direct view on biological productivity in past oceans, suggesting a flourishing of life. It is in stark contrast with the concept of decreased OC production, or “Strangelove” ocean, often implied in extinction scenarios (44). This study also emphasizes that, besides the property of organisms to construct a habitable planet (21), they can also act as a catalyst for destruction. However, marine life might have been very different with mainly prokaryotes dominating over eukaryotes (11, 45). A return to nearly preextinction δ³⁴S_CAS, within 40 ky, suggests recommencing pyrite burial; the disturbance was therefore a rather transient event, which agrees with the postulated short duration of soil erosion and local euxinic surface water conditions (32, 34). It argues for an enhanced supply of iron, possibly under reduced detrital loading of river discharge, a waning of the global extent of euxinic conditions and consequential increase of diagenetic pyrite accumulation, or a combination of both (Fig. 3).

The subsequent Early Triassic positive δ³⁴S_CAS is apparently not directly related to the biodiversity crisis (Fig. 1). Rather it records increased sequestration of sulfur by authigenic pyrite caused by the lack of organisms that normally irrigated sediments with O₂ by burrowing (22) (Fig. 3). Reduced sediment mixing has been documented by the decreased thickness of the sedimentary mixed layer and the absence of burrowing faunas at localities globally, a possible symptom of the widespread devastation (5, 46). The relatively stable and high δ¹⁸O_CAS in this period indicates that MSR remained important during the Early Triassic. Persisting high levels of MSR suggests a prevailing large OC pool, together with a long-lasting (∼800 ky) increase in continental weathering (35), a perturbed carbon cycle, and high global temperatures, the latter two returning in intervals throughout a period of almost 4 My (47, 48). These Earth surface processes are regarded as an important negative feedback loop of the carbon cycle, where enhanced production and sequestration of OC is stimulated by global warming and subsequent chemical weathering rates (36). The prolonged disturbance after the EPME contradicts a fast return (<100 ky) to predisturbance climate and carbon cycle, enforced by carbon sequestration, as suggested for other events marked by greenhouse warming, such as the Cenozoic hyperthermals (49). Degradation of organic substrates on the seafloor by sulfate-reducing microbes, possibly in conjunction with more-efficient water column carbon cycling of labile bacterial OC (45) and low fecal pellet production by reduced numbers of zooplankton (10), might all facilitate a sustained large marine OC pool. The postextinction prokaryote-dominated marine communities, in particular sulfate-reducing microbes, might therefore have had a crucial control on the Early Triassic carbon cycle and would affect marine redox conditions and climate with an adverse effect on the biotic recovery.

Reliability of the CAS Proxy

Sulfate is incorporated into the calcite lattice as an anion substitution with no apparent fractionation of the sulfur isotopes and therefore records the δ³⁴S composition of the ambient seawater sulfate (23). The reliability of CAS oxygen isotopes in recording certain aspects of the global sulfur cycle has been acknowledged in a recent study (59). These authors, however, point out that questions remain about the influence of possible vital fractionation effects and specific microhabitats upon δ¹⁸O_CAS. In contrast, other studies (4, 23) have shown that ancient CAS oxygen isotopes agree well with time-equivalent δ¹⁸O from sulfate locked in evaporites, suggesting that δ¹⁸O_CAS can be used as a proxy for seawater chemistry. Multiple high-amplitude variations in the isotopic composition of CAS—thought to represent original seawater chemistry—have been used to explain scenarios describing the EPME (3). This large δ³⁴S_CAS variability, however, may also reflect postdepositional alteration (3).

CRS, leachable non-CAS, and CAS are marked with distinct isotopic values (Fig. S3). Based on this observation, we infer that leachable non-CAS and CRS could be potential sources to alter the original isotopic composition of CAS. Hence, to identify possible alteration of the CAS isotope signature, the relative abundance of CRS, leachable non-CAS, and CAS for each sample is helpful in this respect, more so, considering the evidence that initially large CAS concentrations buffer against diagenetic overprinting of the primary isotope signal (60). To approximate the likelihood that our obtained isotope values reflect ambient seawater sulfate δ³⁴S and δ¹⁸O, concentrations of CRS and non-CAS sulfate relative to CAS are compared with δ³⁴S_CAS of each sample (Fig. S3).

Samples with comparatively high concentrations of CRS seem to be predisposed toward lower concentrations of δ³⁴S_CAS, whereas both depleted and enriched values dominate the sample population marked by a relatively high amount of leachable non-CAS (Fig. S3). It is noteworthy that depleted values of δ³⁴S_CAS, accompanied by high CRS/CAS or leachable non-CAS/CAS, are mainly found at an interval with a low carbonate content around the extinction horizon, especially for the Kuh-e Ali Bashi section (Figs. S1 and S3). It is therefore perceivable that these depleted δ³⁴S_CAS from low-carbonate samples, linked with low CAS concentrations, are in part an effect of oxidation of sulfide species, such as H₂S or sulfide minerals during rock diagenesis (23). These likely altered δ³⁴S_CAS values lie in the same range as the low δ³⁴S values of the CRS and leachable non-CAS fractions (Fig. S3). In addition, these low-carbonate rocks are also marked by the presence of some depleted δ¹⁸O_CAS relative to values bracketing those (Fig. S1). This observation suggests a common diagenetic mechanism for these samples with paired low δ³⁴S_CAS and low δ¹⁸O_CAS, for which oxidation of sulfide is the most likely one. This chemical reaction mainly uses H₂O as an oxygen source, with an oxygen isotope value close to that of the ambient seawater (23).

On the other hand, some of the samples, mainly from the Triassic part of the Zal section, with relatively high leachable non-CAS concentrations are marked by enriched δ³⁴S_CAS. These enriched values could be indicative of an isotopic evolution reflecting progressing MSR in an evolving sulfate pool approaching closed system conditions (23). This would also agree with the often relatively heavy concentrations of δ¹⁸O_CAS and δ³⁴S from leachable non-CAS and CRS, respectively (e.g., Zl 4.15 m and 10.05 m, Tables S3 and S4). Enriched sulfate δ³⁴S produced by isotope fractionation associated with MSR might be incorporated during authigenic carbonate formation.

As such, we argue that the ratios of CRS to leachable non-CAS with CAS provide a good impression of the likelihood that an actual seawater sulfate isotope signal is recorded in CAS. Based on the density distribution (Fig. S3), CRS/CAS of 0.1 and non-CAS/CAS of 0.4 are used as static cutoff boundaries for the herein-presented CAS isotope values. The resulting time series for δ³⁴S_CAS and δ¹⁸O_CAS, with the highest probability of capturing seawater sulfate, show nearly identical isotope patterns (Fig. 2).

Steady-State P−Tr Sulfur Cycle Model

Based on the measured preextinction δ³⁴S_CAS, the observed lower background value for Late Permian marine sulfate sulfur isotopic composition is 17‰ (Fig. 1). Low sulfur isotope marine sulfate reflects either a change in sulfur input (specifically the input of sulfur with a lower isotopic composition) or reduced global pyrite burial (61).We hypothesize that exposed Carboniferous and Permian strata on the continents were rich in isotopically depleted pyrite sulfur (62). Hence, to achieve steady state, we solved Eq. S1 for δ_w, assuming that Δ_MSR is −35‰ (24, 63), and taking Holocene values for the other parameters (Table S5).

$${\delta }_w=\frac{F_p({\mathrm{\delta }}_{\text{SO}4}+{\mathrm{\Delta }}_{\text{MSR}})+F_e{\mathrm{\delta }}_{\text{SO}4}-(Q_v{\delta }_v+Q_m{\delta }_m)}{Q_w}.$$ [S1]

This calculation yielded a value of 1.9‰ for δ_w, which is in the lower range of modern observed values (29). In addition, low oxygen isotope values for the weathering flux, which is normally assumed (29), cannot equate to the Permian background δ¹⁸O_SO4 values of 17‰ (Fig. 1). A different mechanism is required to explain this feature. The fluxes associated with anhydrite formation (F_s) and subsequent sulfide oxidation (Q_h) by the cycling of seawater through oceanic crust at hydrothermal systems, which only has a net effect on the sulfur isotope part of the sulfur cycle by Q_m (63), presents a good candidate. We postulate that F_s and Q_h could have been more important during the regarded time interval. The difference in F_s to Holocene values is estimated by solving the following:

$$F_s=\frac{(Q_w{\delta }_w+Q_v{\delta }_v+Q_h{\delta }_m+Q_{\text{ox}}{\delta }_{\text{ox}})-F_{\text{MSR}}({\mathrm{\delta }}_{\text{SO}4}+{\mathrm{\Delta }}_{\text{MSR}})+F_e{\mathrm{\delta }}_{\text{SO}4}}{{\mathrm{\delta }}_{\text{SO}4}}.$$ [S2]

Keeping Q_m constant, required for the sulfur isotope part of the sulfur cycle, necessitates a concomitant change in Q_h, seen in Eq. 5. To sustain steady state with P−Tr background values, the cycling of seawater to oceanic crust would be 5.2 times larger than proposed for the Holocene (63). The initial steady state between the OC (M_OC) and sulfate (M_SO4) reservoirs was reached by calculating a linear relationship between Q_po and Q_w.

Table S5.

Boundary conditions for reservoirs and fluxes used in the box model

Reservoir/flux	Description	Value	Reference
MSO4	initial size of SO4 reservoir	Var.	Sensitivity Experiments
MOC	initial size of OC pool	1.10e17 mol	(45)
Qw	flux of SO4 weathering	1.47e15 mol⋅ky−1	(63)
Qv	flux of SO4 volcanism	0.33e15 mol⋅ky−1	(63)
Qm	flux of SO4 hydrothermal/mantle	0.20e15 mol⋅ky−1	(63)
Qox	flux of microbial sulfide oxidation	Calc.	Methods
Qh	flux of hydrothermal sulfide oxidation	Calc.	Steady-State P−Tr Sulfur Cycle Model
Qpo	flux of OC primary production	$6\frac{\text{mol}}{{\text{m}}^2}{\text{yr}}^{-1}$	—
Fp	flux of pyrite burial	0.90e15 mol⋅ky−1	(63)
Fe	flux of SO4 evaporite burial	1.10e15 mol⋅ky−1	(63)
FMSR	flux of microbial SO4 reduction	40.00e15 mol⋅ky−1	(22)
Fs	flux of mantle SO4 anhydrite formation	17.00e15 mol⋅ky−1	Steady-State P−Tr Sulfur Cycle Model
FOC	flux of OC remineralization	$0.99Q_{\text{po}}-2F_{\text{MSR}}$	Methods
Fbo	flux of OC burial	$Q_{\text{po}}-F_{\text{OC}}$	Methods
δSO4	Initial isotopic value of SO4 reservoir	δ34S = 17‰; δ18O = 17‰	Steady-State P−Tr Sulfur Cycle Model
δw	Isotopic value of SO4 weathering flux	δ34S = calc.; δ18O = 4‰	Steady-State P−Tr Sulfur Cycle Model and ref. 29
δv	isotopic value of SO4 volcanic flux	δ34S = 3‰; δ18O = 11‰	(4, 63)
δm	isotopic value of SO4 mantle flux	δ34S = 3.5‰; δ18O = −1‰	(29, 63)
δox	isotopic value of sulfide oxidation	${\mathrm{\delta }}^{18}\text{O}={\mathrm{\Delta }}^{18}\text{O}\left(18\text{‰}\right)\hspace{0.17em}+{\mathrm{\delta }}^{18}{\text{O}}_{\text{seawater}}$	ref. 29 and assuming a Permian δ18Oseawater of −1‰ (6)
ΔMSR	fraction from seawater	Δ34S = −35‰; Δ18O = Δ34S /4	(63, 68)
k1	first-order removal constant OC remineralization	$\frac{1}{M_{\text{OC}}÷F_{\text{OC}}}$	—
k2	first-order removal constant OC burial	$\frac{1}{M_{\text{OC}}÷F_{\text{bo}}}$	—

Fluxes signified by Q are flowing into the reservoir, and those signified by F are flowing out of the reservoir. Calc., calculated value; Var., varying initial value.

Sensitivity Experiments

By conducting sensitivity experiments, we determined if the solutions with a best fit to the data are unique or can be explained in alternative scenarios. A critical aspect of the Permian and Triassic is the lowered marine sulfate levels with respect to modern oceanic levels. A low oceanic sulfate reservoir can explain sulfate isotope excursions constrained to short time intervals—shorter than the residence time of marine sulfate (submillion year)—without unrealistically large changes in fluxes (30). This would be appropriate for the excursions in the records of sulfate sulfur and oxygen isotope presented here, which occur within an interval shorter than 40 ky. This would require that P−Tr marine sulfate levels ranging from 18 mM [based on fluid inclusion in marine Late Permian halite (64)] to ≤4 mM [based on rate variation of 100‰ My⁻¹ in sulfur isotopes in the Early Triassic (30)] are valid and possibly a consequence of evaporite deposition during the Permian (30). We tested the influence of the initial seawater sulfate concentration by performing each experiment with a spectrum of sulfate concentrations between 2 mM and 18 mM (Fig. S4).

A plausible scenario to explain the observed sulfur cycle perturbation is volcanism (4), besides scenarios associated with the fluxes of MSR (3). The total volume of sulfur released by volcanic outgassing of Siberian Trap basalts is estimated at 6,300–7,800 Gt (65), with sulfur isotope values close to Holocene values for volcanism. Although crustal contamination of evaporite-derived sulfur has been suggested to enrich evolved sulfate with ³⁴S, this mechanism does not, in general, drive sulfur isotope values heavier than 5‰ (66). The main eruption phase of the Siberian Trap basalts has been constrained to a short magmatic event of <2 My, with the main phase correlated to bed 24 at the Meishan P−Tr section (67). Based on conodont correlation, this is close to the extinction horizon found at the studied sites in NW Iran. Volcanic pulses of less than 10 ky may have contributed to concentrated fluxes of volatiles into the atmosphere, in maybe as much as 25 pulses (65). This would constitute a sulfur flux ∼30 times bigger than background volcanism based on the accumulative volatile release during these pulses. The sulfate oxygen isotope composition of this flux could near 34‰ when considering that equilibrium between water and sulfate is faster in an acidic medium (68). Acidic meteoric water associated with Siberian trap volcanism could be realistic as concomitant land plant destruction has been related to acid rain (34). When constructing a model scenario with these boundary conditions, an excursion as observed in the geochemical data requires an unrealistically large sulfate contribution from volcanism over an extended period (Fig. S4).

Based on a set of analyses with our sulfur cycle coupled to an OC pool, we consider an increased weathering flux as most probable for producing a deviating pattern of sulfate δ³⁴S and δ¹⁸O. This scenario does not necessitate unrealistic changes in the isotopic composition or sizes of fluxes. The simultaneous reduction of sulfur burial as pyrite, and the increase of sulfur input via enhanced weathering, can explain the negative sulfate sulfur isotope excursion as observed in CAS, without temporary sequestration of microbial-produced H₂S (3); the latter is unlikely, as preextinction large-scale bottom water anoxia in a stagnant ocean has been largely dismissed (13, 33). A low marine sulfate level (2 mM) for the Late Permian to Early Triassic ocean (30) is, however, necessary to explain the observed fluctuations in δ³⁴S_CAS.

Supplementary Notes

The R programming environment and the ggplot2 package have been used for graphical plots, statistics, and the box model (69, 70).

Methods

The applied CAS extraction method minimizes the potential alteration of the CAS sulfur or oxygen isotope signal during the analytical procedure by the use of subsequent NaCl leaches (50). The NaCl leaches are precipitated with a BaCl₂ solution, and, subsequently, the concentration of the sulfate fraction not structurally substituted within the CaCO₃ lattice, leachable non-CAS, is determined gravimetrically. These steps are repeated until no leachable non-CAS is observed. In follow-up, acid digestion of the sample is performed with 25% HCl under restricted atmospheric exchange and in a time window generally not more than 3 h to prevent oxidation of sulfide species. The sulfate of the digested carbonate rock is also precipitated as barium sulfate, and CAS concentrations are gravimetrically determined.

The sulfur isotopic composition of the leachable non-CAS and CAS (Fig. S3) was obtained by an Elemental Analyzer (EA) connected to a ThermoFinnigan Delta Plus mass spectrometer and is reported in the standard (δ³⁴S) notation relative to Vienna Cañon Diablo Troilite (VCDT) in per mil. Precision was confirmed by repeated measurements on the international standards and internal laboratory standards. This yielded an accuracy of 0.09‰ and a reproducibility on average better than 0.40‰ (Table S1). The oxygen isotopic composition of the leachable non-CAS and CAS was measured with a high temperature conversion/EA interfaced to a ThermoFinnigan Delta Plus XL mass spectrometer and is reported in the standard (δ¹⁸O) notation relative to Vienna Standard Mean Ocean Water (VSMOW) in per mil. International standards and an in-house standard were used to determine the precision of the procedure. This resulted in an accuracy of 0.40‰ and a reproducibility of ±0.80‰ (Table S2).

Table S1.

Sulfur isotope composition of international and in-house standards

Standard	δ34S, ‰	SD, 2σ
IAEA -S-1
Measured	−0.35	0.20
Published	−0.30
IAEA -S-2
Measured	21.52	0.16
Published	21.55
IAEA -S-3
Measured	−31.31	0.44
Published	−31.40
NBS 127
Measured	20.38	0.17
Published	20.30
Ag2S (Lab.)
Measured	2.47	0.39
CdS (Lab.)
Measured	10.76	0.32

Isotope values obtained with replicate analyses of standard material and accepted values for certified reference material. Lab., in-house standard material.

Table S2.

Oxygen isotope composition of international and in-house standards

Standard	δ18O, ‰	SD, 2σ
NBS 127
Measured	8.94	0.85
Published	9.30
IAEA-SO-5
Measured	11.97	0.70
Published	12.00
IAEA-SO-6
Measured	−11.36	0.49
Published	−11.34
BaSO4 (Lab.)
Measured	12.59	1.05

Isotope values obtained with replicate analyses of standard material and accepted values for certified reference material. Lab., in-house standard material.

The CRS content was extracted from the remaining residue after the CAS extraction by the chromium reduction method (51). Under continuous N₂ flow, samples were reacted with HCl and chromium powder to produce acidic chromium chloride and were heated to a gentle boil for 1.5 h. Sulfur was trapped as zinc sulfide in a zinc acetate solution and converted to silver sulfide for filtrating and drying. The CRS concentrations of the residues were determined gravimetrically. For sulfur isotopic analyses (δ³⁴S), extracted silver sulfide was weighed into tin capsules withV₂O₅ added to aid in combustion. Isotope measurements were performed on a Costech Elemental Combustion System 4010 connected to a Thermo Delta V+ Isotope Ratio mass spectrometer with results reported relative to VCDT in per mil. Precision was confirmed by repeated measurements on the international standards [International Atomic Energy Agency (IAEA)-S-1, IAEA-S-2, IAEA-S-3, National Bureau of Standards (NBS)-127] and resulted in an accuracy of 0.24‰ and a reproducibility on average better than 0.40‰.

A box model was constructed, to delineate which fluxes could be responsible for isotopic changes in marine sulfate and thus could explain the stratigraphic CAS isotope record. Sulfate mass (M_SO4) and isotopic composition (δ_SO4) are estimated with the following equations, adapted from ref. 24:

$$\frac{d{\text{M}}_{\text{SO}4}}{dt}=Q_w+Q_v+Q_m-(F_p+F_e)$$ [1]

$$\frac{d{\mathrm{\delta }}_{\text{SO}4}}{dt}=\frac{Q_w{\delta }_w+Q_v{\delta }_v+Q_m{\delta }_m-{\delta }_{\text{SO}4}(Q_w+Q_v+Q_m)-F_p{\mathrm{\Delta }}_{\text{MSR}}}{{\text{M}}_{\text{SO}4}}$$ [2]

where Q_w represents the weathering input flux, δ_w is the isotopic composition of weathering input, Q_v is the volcanic input flux, δ_v is the isotopic composition of volcanic input, Q_m is the hydrothermal input flux, δ_m is the isotopic composition of the hydrothermal input flux, F_e is the evaporite burial flux, F_p is the pyrite burial flux, and Δ_MSR is the average isotopic fractionation associated with MSR. The oxygen and sulfur isotopic compositions of marine sulfate are affected by different processes. Two aspects are mainly responsible for this difference, microbial sulfur cycling and the exchange and cycling through the oceanic crust. Microbial sulfur cycling results in the loss of oxygen during MSR (F_MSR), whereas the product (sulfide) is oxidized and mainly via microbial sulfur disproportionation (29) transformed back to sulfate, Q_ox, both with an effect on the isotopic composition. The surplus of these bacterial processes will be buried as sedimentary sulfide, mainly pyrite, and can be envisioned as

$$F_p=F_{\text{MSR}}-Q_{\text{ox}},$$ [3]

whereas marine sulfate δ³⁴S is only affected by hydrothermal S input in one direction, sulfate δ¹⁸O is modified by oxidation of sulfides at these hydrothermal vents (Q_h) and acquires a δ¹⁸O similar to ocean water (29). On the other hand, anhydrite formation in the oceanic crust is an effective sink for sulfate oxygen (F_s), without fractionation (29) and can be described by

$$Q_m=Q_h-F_s.$$ [4]

To adjust for these differences imposed upon the marine sulfate δ¹⁸O, Eqs. 3 and 4, are substituted into Eq. 1, yielding

$$\frac{d{\mathrm{\delta }}_{{\text{SO}}_4}}{dt}=\frac{Q_w{\delta }_w+Q_v{\delta }_v+Q_h{\delta }_m+Q_{\text{ox}}{\delta }_{\text{ox}}-{\mathrm{\delta }}_{\text{SO}4}(Q_w+Q_v+Q_h+Q_{\text{ox}})-F_{\text{MSR}}{\mathrm{\Delta }}_{\text{MSR}}}{M_{\text{SO}4}}$$ [5]

where δ_ox stands for the isotopic composition of sulfate originating from sulfur disproportionation. Steady state was achieved by modifying Holocene reservoir and flux size and isotopic composition, to approximate the sulfur cycle of the P−Tr interval (Steady-State Sulfur Cycle Model and Table S5). To exploit the important impact of MSR on OC remineralization (19), an OC pool (M_OC) was introduced to the model, by linking Q_w linearly to ocean primary productivity (Q_po). OC burial (F_bo) and OC remineralization (F_OC) are determined by the size of the OC pool as first-order removal constants (k values); k values are determined by assuming that 99% of OC is remineralized of which part is remineralized by MSR (F_MSR; Table S5), and according to the stoichiometry of the two biochemical reactions

$${\text{CH}}_2\text{O}+{\text{O}}_2\iff {\text{CO}}_2+{\text{H}}_2\text{O}$$ [6]

$${2\text{CH}}_2\text{O}+{\text{SO}}_4\iff 2{\text{HCO}}_3+{\text{H}}_2\text{S}.$$ [7]

The size of the marine OC pool is described by

$$M_{\text{OC}\left(t\right)}=\left[\left(\frac{Q_{\text{po}\left(i\right)}}{k1+k2}\right)-\left[\left(\frac{Q_{\text{po}\left(i\right)}}{k1+k2}\right)-M_{\text{OC}\left(i\right)}\right]e^{(-(k1+k2)t)}\right]-2F_{\text{MSR}}$$ [8]

where (i) stands for the initial pool and (t) stands for the pool changing with time. The relation between the OC pool and MSR is described in the following equation, taken from ref. 22:

$$F_{\text{MSR}}=\alpha M_{\text{OC}}{\left[{\text{SO}}_4\right]}^y,$$ [9]

which considers that the size of the OC pool has a direct impact on the availability of OC for sulfate reduction. Factor α is calculated by solving the equation with the initial values, and y has been taken as 0.3, in accordance with ref. 22. The model was perturbed by varying the weathering flux concomitant with the extinction horizon for a duration of 40 ky. Various simulations were performed, with the weathering flux changing from 2 to 64 times larger than the background value. The Triassic weathering flux is taken to be 7 times higher than the Permian (35). To simulate the effect of a largely iron-limited euxinic ocean, the fraction of pyrite buried was set to 10 times reduced for 20 ky following the extinction horizon, followed by a twofold increase for another 20 ky compared with the preperturbed value.