Complex dynamics of synergistic coinfections on realistically clustered networks

Significance

Concurrent infection with multiple pathogens is an important factor for human disease. For example, rates of Streptococcus pneumoniae carriage (a leading cause of pneumonia) in children under five years can exceed 80%, and coinfection with other respiratory infections (e.g., influenza) can increase mortality drastically; despite this, examination of interacting coinfections on realistic human contact structures remains an understudied problem in epidemiology and network science. Here we show that clustering of contacts, which usually hinders disease spread, can speed up spread of both diseases by keeping synergistic infections together and that a microscopic change in transmission rates can cause a macroscopic change in expected epidemic size, such that clustered networks can sustain diseases that would otherwise die in random networks.

Abstract

We investigate the impact of contact structure clustering on the dynamics of multiple diseases interacting through coinfection of a single individual, two problems typically studied independently. We highlight how clustering, which is well known to hinder propagation of diseases, can actually speed up epidemic propagation in the context of synergistic coinfections if the strength of the coupling matches that of the clustering. We also show that such dynamics lead to a first-order transition in endemic states, where small changes in transmissibility of the diseases can lead to explosive outbreaks and regions where these explosive outbreaks can only happen on clustered networks. We develop a mean-field model of coinfection of two diseases following susceptible-infectious-susceptible dynamics, which is allowed to interact on a general class of modular networks. We also introduce a criterion based on tertiary infections that yields precise analytical estimates of when clustering will lead to faster propagation than nonclustered networks. Our results carry importance for epidemiology, mathematical modeling, and the propagation of interacting phenomena in general. We make a call for more detailed epidemiological data of interacting coinfections.

Individuals are at constant attack from infectious pathogens. Coinfection with two or more pathogens is common and can seriously alter the course of each infection from its own natural history. Infection with HIV increases susceptibility to many pathogens, especially tuberculosis, where coinfection worsens outcomes and increases transmission of both pathogens (1). Recent studies have examined epidemiological case counts to highlight the importance of upper respiratory infections (e.g., rhinovirus, influenza virus, respiratory syncytial virus [RSV]) and Streptococcus pneumoniae carriage leading to increased risk of pneumococcal pneumonia (2–5), although there are few dynamic transmission models of pneumococcus (PC) and other viral infections.

Models of disease transmission in structured populations have remained a main focus of network theory for over a decade as realistic descriptions of contact structures are necessary to understand how diseases are transmitted between individuals (6–11). Typically, specific structural properties (average degree, network size, clustering) are explored in isolation. It remains a strong (and potentially dangerous) assumption that results obtained with different models exploring distinct structural properties will give the same results when combined with other models exploring different properties. Disease transmission is a nonlinear problem with features of the propagation itself interacting in complex ways. In this paper, we focus on combining two much studied phenomena—realistic clustering of contact structure and the interaction of respiratory pathogens (influenza and PC pneumonia)—and show that a combination of these two phenomena leads to behavior that is unexpected given previous studies.

An impressive amount of research has focused on the impact of clustering on disease dynamics (12–19). Clustering is often simply described as the number of triangles (where the friend of my friend is also my friend) in a network, but usually also implies that links between nodes tend to be aggregated in well-connected groups. This aggregation tends to hinder the spread of the disease by keeping it within groups where links are more likely to connect to already infected (immune) nodes (18). Clustering plays an important role in Ebola virus transmission (20), respiratory infections (21, 22), and sexually transmitted infections (23, 24).

On the other hand, the interaction of two spreading agents has received a great amount of attention mostly due to the generality of such models (25, 26). These spreading agents can represent two different, but interacting, diseases (such as sexually transmitted infections) (26, 27); the propagation of awareness campaigns trying to stop the spread of an epidemic (25); or even the competition between a mutated strain of influenza and the original strain (10, 11, 28). These dynamics can by themselves exhibit complex behaviors; however, we will see here that they can be further influenced in equally complex ways by the structure imposed on the underlying network.

Here we describe a susceptible-infectious-susceptible (SIS) network model incorporating variable clustering strength and two interacting pathogens and provide a mean-field formalism to follow its dynamics. We find that synergistic coinfections can lead to faster disease spread on clustered networks than on an equivalent random network, contrary to previous studies considering single infections (18). We introduce a criterion based on tertiary infections (or two-step branching factor), which allows analytical prediction of whether a clustered or random network propagates infections most efficiently. Finally, we observe a first-order phase transition in epidemic final size, meaning that a microscopic change in transmissibility can lead to a macroscopic (and discontinuous) increase in disease prevalence. We also identify a dangerous parameter region where an infection would propagate in a clustered network but not in a random network, indicating that movement of coinfected individuals into new clustered networks of susceptible individuals could cause explosive outbreaks.

Network Structure and Epidemic Dynamics

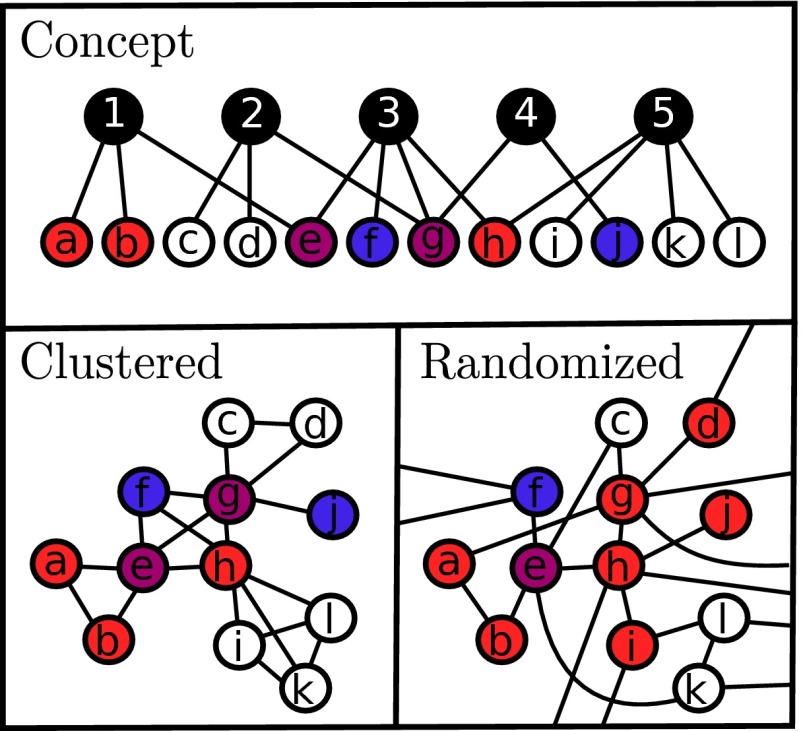
We extend a recent description of propagation dynamics on a highly clustered network using overlapping community structure (18). This particular arrangement of nodes leads to the aggregation (or clustering) of nodes into well-connected groups, representing for example a person’s family or workplace. Every connection in this structure can be decomposed in terms of groups, where even single links between two individuals can be considered as a group of size two. Assuming that we know the distribution of group sizes (number of nodes per group) and of node memberships (number of groups per node), we can define a maximally random ensemble of clustered networks with a fixed community structure by randomly assigning nodes to groups (Fig. 1). Hence, the entire network structure is solely defined by two probability distributions, $\left\{p_n\right\}$ and $\left\{g_m\right\}$, respectively, which are the probabilities that a randomly selected group will contain n members (size n) or that a randomly selected individual will participate in m groups (m memberships).

Fig. 1.

The effects of clustering on disease propagation (18). Schematization of the network topologies studied in this paper: we start with a random assignment of nodes to groups (Upper), from which we obtain a highly clustered network (Left) that can then be randomized for comparison (Right). The random network is obtained by randomly rewiring the clustered network, thereby preserving node degree. This rewiring allows the diseases to reach more nodes, but separates their paths of spread, lessening the effects of the synergism. In this cartoon, red and blue nodes correspond to individuals infected with a single disease, whereas purple nodes are coinfected.

The dynamics of a single disease on this community structure model was studied in ref. 18. Using a mean-field description, it was shown how the clustering of links in groups slowed down propagation as links are wasted on redundant (immune) connections instead of reaching new (susceptible) individuals. Expanding this study, we now study the effects of having two diseases interacting on these clustered networks.

To highlight the effects of community structured (CS) vs. random networks (RNs), both topologies will be studied analytically and numerically. The CS network will be compared with its equivalent random network (ERN): a network with exactly the same degree distribution but with randomly rewired links. This rewiring is done by setting $\left\{p_n\right\}={\delta }_{2,n}$ so that all groups are of size two (i.e., regular links) and then setting the membership distribution as equal to the initial degree distribution of the CS (18).

On these networks, we study the dynamics of two diseases exhibiting SIS dynamics. Without interaction with the other disease, an infectious individual would infect its susceptible neighbors with disease i at rate ${\beta }_i$ and recover at rate $r_i$. To keep track of both diseases simultaneously, we distinguish nodes by their state ${\left[XY\right]}_m$, where m is their membership number, $X\in \left\{S_1,I_1\right\}$ corresponds to the first disease, and $Y\in \left\{S_2,I_2\right\}$ corresponds to the second disease.

Similarly, we will distinguish groups by their size n and the states of the nodes they contain. Thus, ${\left[ijk\right]}_n$ is the fraction of cliques that are of size n with i individuals in state $\left[I_1{S}_2\right]$, j in state $\left[S_1{I}_2\right]$, and k in state $\left[I_1{I}_2\right]$, such that $n-i-j-k$ yields the number of $\left[S_1{S}_2\right]$ individuals. Both the infector and the infectee can modify transmission rates: a coinfected individual may have increased symptoms, such as coughing or sneezing or higher bacterial or viral loads of each pathogen, which may increase the transmission, and the infectee susceptible to one of the pathogens (disease i) may have a compromised immune response due to infection with the other pathogen (disease j). To quantify this, we say that in the presence of disease j, ${\beta }_i$ is increased by a factor α. For parsimony, we consider symmetric interactions where presence of disease j affects transmission of disease i in the same magnitude as i affects j. Assuming symmetry is reasonable due to the lack of detailed within host study of interacting infections and does not imply the diseases are identical. The parameters of the model are summarized in Table 1.

Table 1.

Description of parameters used in the model

Symbol	Definition
$\left\{g_m\right\}$	Distribution of groups per node (memberships)
$\left\{p_n\right\}$	Distribution of nodes per group (sizes)
${\beta }_{\left\{\mathrm{1,2}\right\}}$	Transmission rate of diseases 1 and 2, respectively
$r_{\left\{\mathrm{1,2}\right\}}$	Recovery rate of diseases 1 and 2, respectively
α	Factor of ${\beta }_i$ in the presence of the other disease

A mean-field description of the time evolution can be written in the spirit of existing formalisms (18, 29). Here we give a brief description of how the mean-field equations are obtained and provide the full system in SI Appendix. The mean-field description of the dynamics follows the rates that individuals move from one state to another. For instance, the fraction of individuals infected by disease 1 and susceptible to disease 2 will change as

$$\frac{d}{dt}{\left[I_1{S}_2\right]}_m=r_2{\left[I_1{I}_2\right]}_m-r_1{\left[I_1{S}_2\right]}_m+m\left({\beta }_1{B}_{SS}^{\left(1\right)}{\left[S_1{S}_2\right]}_m-{\beta }_2{B}_{IS}^{\left(2\right)}{\left[I_1{S}_2\right]}_m\right),$$ [1]

where the $B_{UV}^{\left(i\right)}$ are mean-field interactions (i.e., the average interaction on disease i per membership for a node in state $\left[UV\right]$). Notice that in the equation, the first row of terms is the recovery events, and the second row is the infection events. The challenge in correctly writing the equation is thus solely to correctly identify to which state each event transfers some population density.

The evolution of group states can be followed by a single, albeit more complicated, equation. This equation governs the rate of change in ${\left[ijk\right]}_n$. It involves recovery terms of the form

$$\left(k+1\right)r_1{\left[i\left(j-1\right)\left(k+1\right)\right]}_n,$$

for cliques with one more individual in state $\left[I_1{I}_2\right]$ which recovers from disease 1 (${\left[i\left(j-1\right)\left(k+1\right)\right]}_n\to {\left[ijk\right]}_n$). Notice that recoveries can increase the numbers i or j when one of the k coinfected individuals recovers from disease 2 or 1. Infection terms are similarly generalized, for example

$${\beta }_2\left(n-i-j+1-k\right)\left\{\left(j-1\right)+k\alpha +{\tilde{B}}_{SS}^{\left(2\right)}\right\}{\left[i\left(j-1\right)k\right]}_n,$$

for cliques with one less individual infected only with disease 2, such that the remaining $\left[S_1{S}_2\right]$ individuals (in parentheses) can be infected from within (first two terms in braces) or without (last term in braces).

Combining all possible recovery and infection terms yields the full equations as provided in SI Appendix. This new set of equations is coupled to the previous one through the mean-field of excess interactions ${\tilde{B}}_{UV}^{\left(x\right)}$ (interactions with outside groups)

$${\tilde{B}}_{UV}^{\left(x\right)}=\left\{\frac{{\displaystyle {\sum }_{m}m\left(m-1\right){\left[UV\right]}_m}}{{\displaystyle {\sum }_{m}m{\left[UV\right]}_m}}\right\}{B}_{UV}^{\left(x\right)}.$$ [2]

Finally, to close the model, we simply write the basic interaction mean-fields (average interaction within a given group) with the available information. For example, we find for disease 1

$$B_{SS}^{\left(1\right)}=\frac{{\displaystyle {\sum }_{{\left[ijk\right]}_n}\left(n-i-j-k\right)\left(i+k\alpha \right){\left[ijk\right]}_n}}{{\displaystyle {\sum }_{{\left[ijk\right]}_n}\left(n-i-j-k\right){\left[ijk\right]}_n}},$$ [3]

$$B_{SI}^{\left(1\right)}=\frac{{\displaystyle {\sum }_{{\left[ijk\right]}_n}j\left(i+k\right)\alpha {\left[ijk\right]}_n}}{{\displaystyle {\sum }_{{\left[ijk\right]}_n}j{\left[ijk\right]}_n}}.$$ [4]

Intuitively, for $B_{SS}^{\left(1\right)}$, the susceptible individual is two times more likely to be part of a clique with two times more susceptible nodes: this is the $\left(n-i-j-k\right)$ factor. We then just average the infection terms of each possible clique, i.e., $i{\alpha }_{SS}^{IS}+k{\alpha }_{SS}^{II}$, over this biased distribution of cliques. Note that one interesting type of correlation is not taken into account: the difference between individuals in the $\left[I_1{S}_2\right]$ state that were infected from the $\left[S_1{S}_2\right]$ state and those that relaxed from the $\left[I_1{I}_2\right]$ state. This difference could potentially inform us on the cliques to which an individual belongs, some transitions being more likely to be found in the vicinity of coinfections, but this would break the Markovian behavior of the mean-field model and only appear to be relevant at high coupling strength beyond what we consider here (SI Appendix).

Results

We validate our mean-field formalism with simulations of coinfections on highly clustered networks. We will focus on two diseases that can interact synergistically with their respective propagation, i.e., with $\alpha \ge 1$. Here, we focus on PC pneumonia with upper respiratory viral infections [e.g., influenza (3, 30) or RSV (5)]. As our baseline scenario, we use $\alpha =4$; which, although strong, represents an interaction well within the range of interaction observed for PC pneumonia and influenza, where estimates of increased acquisition of PC range from 2-fold to 100-fold (4, 30). Similarly, we use a very modular network where every node belongs to two cliques of size 10. These networks are chosen for two reasons: first, to avoid degree-degree correlations, where the effect of clustering will be the main structural effect (18); second, to feature a realistic local clustering coefficient (the ratio of triangles to pairs of links around a given node, here, $C\simeq 0.47$) (31).

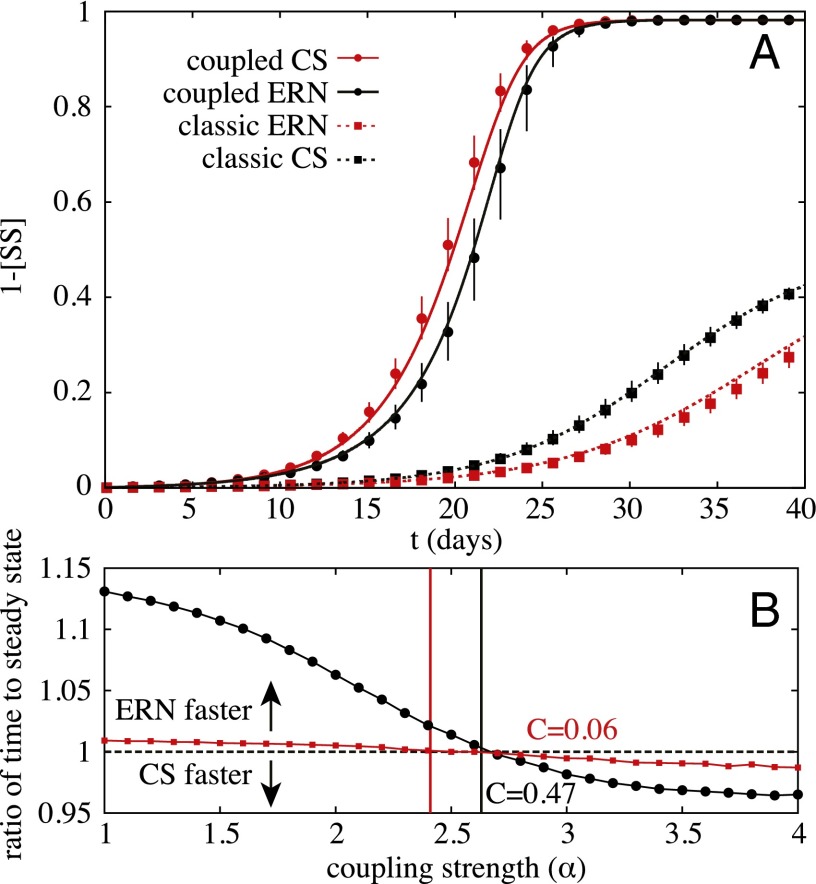
Fig. 2A presents the effects of clustering with noninteracting diseases and the same scenario in the presence of synergistically interacting diseases. We find that although clustering slows down the propagation of noninteracting diseases, it speeds up the propagation of synergistically interacting diseases. This result is important for network models of disease: random networks are considered worst case scenarios for the speed of disease propagation (18, 21), implying that models can justify working in a random network paradigm. However, this is clearly not always the case in the presence of interacting diseases with synergistic effect.

Fig. 2.

Example of infection dynamics on clustered and random networks. (A) Synergistic coinfections in a population where nodes all belong to two groups of 10. Markers represent median results of Monte Carlo simulations with error bars representing the 75% intervals over multiple runs on networks of 250,000 nodes. Solid curves are obtained by integrating the mean-field formalism. The dynamics follow $r_1=1/4$ d⁻¹, $r_2=1/10$ d⁻¹, and transmission rates fixed to set reproductive numbers $R_0=1.8$ for both diseases, with $\alpha =1$ for the noninteracting case and $\alpha =4$ for the interacting case. (B) Speed of randomized networks vs. two networks with different clustering: each node has 18 links divided in two groups of 10 (black, $C\simeq 0.47$) or 9 triangles (red, $C\simeq 0.06$). The results represent the ratio of time to get within ${10}^{-6}$ of the endemic steady state between the community structured (CS) network and the ERN for various coupling strengths and ${\beta }_i={\beta }_j=10r_i$, evaluated using the mean-field ODE system. The vertical lines indicate the prediction for the coupling strength when the CS begins spreading faster than the ERN, as given by Eq. 10.

Clustering Threshold.

We are now interested in identifying a simple analytical criterion, as a function of the clustering coefficient C, and the disease interaction parameters α, to determine when a clustered network structure is more efficient at synergistic disease transmission than a random structure. Because we are interested in the relative speed at which a pair of diseases move through a population, we can generalize the idea of the basic reproductive number, $R_0$ (32), to identify this clustering threshold. $R_0$ corresponds to the expected number of secondary infections caused by a single infected individual in an entirely susceptible population. The higher the $R_0$, in general, the faster a disease can spread. However, clustering is not taken into account for $R_0$, as it is a one-step branching factor: how many first neighbors will be infected during an individual’s infectious period. Clustering reflects how your neighbors might also be second neighbors, occurring on the second step of the branching process. We thus turn toward a generalized branching factor, $R_1$, equal to the number of tertiary infections caused by one coinfected individual (i.e., the number of second neighbors infected).

As the calculation of $R_1$ depends on the scenario of interest, we consider the case of equivalent diseases (${\beta }_1={\beta }_2=\beta$ and $r_1=r_2=r$). See SI Appendix for a treatment of the general case. The first step is to calculate $R_0$ taking into account which neighbors receive disease 1, disease 2, or both. A coinfected individual can transmit both diseases in two ways: by transmitting both while coinfected or by transmitting one, recovering, and transmitting the second. Summing the contribution of both possibilities gives the probability $T_2$ of transmitting both diseases

$$T_2=\frac{2\alpha \beta }{2\alpha \beta +2r}\left(\frac{\alpha \beta }{\alpha \beta +2r}+\frac{r}{\alpha \beta +2r}\frac{\alpha \beta }{\alpha \beta +r}\right).$$ [5]

From this expression, it is straightforward to also write the probability $T_1$ of transmitting only one disease

$$T_1=\frac{2\alpha \beta }{2\alpha \beta +2r}\left(1-\frac{\alpha \beta }{\alpha \beta +2r}-\frac{r}{\alpha \beta +2r}\frac{\alpha \beta }{\alpha \beta +r}\right)+\frac{2r}{2\alpha \beta +2r}\frac{\beta }{\beta +r},$$ [6]

whose terms represent blocking the second transmission in $T_2$ or recovering before transmitting. We now want to calculate how many infections will be caused by each of these $z_1\left(T_1+T_2\right)$ new infectious individuals ($z_1$ being the average excess degree).

The effect of this clustering coefficient is twofold: first, further infections are conditional on links not wasted with infected neighbors of the root node, and second, in the event of a single infection (probability $T_1$), the other disease can be received from these wasted links and boost the transmission rate for the nonwasted links. Considering that, on average, a node infected through the $T_1$ scenario, and now trying to infect a susceptible node, also has $n=\left(z_1-1\right)C\left(T2+T1/2\right)$ neighbors already infected with the other disease, the probability of a coinfection occurring is thus $1-{\left[2r/\left(2r+\alpha \beta \right)\right]}^n$. This discrete probability can be converted to an effective continuous rate of coinfection through triangles (SI Appendix)

$$x=r\left[{\left(\frac{2r}{2r+\alpha \beta }\right)}^{-n}-{\left(\frac{2r}{2r+\alpha \beta }\right)}^n\right].$$ [7]

With this in mind, we can write the probability of a tertiary infection caused by a secondary infection of only one disease

$$T_1\prime =\left[1-C\left(T1+T2\right)\right]\times \left[\frac{\beta }{\beta +r+x}+\frac{x}{\beta +r+x}\left(\frac{2\alpha \beta }{2\alpha \beta +2r}+\frac{2r}{2\alpha \beta +2r}\frac{\beta }{\beta +r}\right)\right],$$ [8]

which counts transmissions of a single or both diseases. The equivalent probability in the $T_2$ scenario is more straightforward if we neglect the probability of recovering and being reinfected (which is the standard way of calculating reproductive numbers). We thus write

$$T_2\prime =\left[1-C\left(T1+T2\right)\right]\left[\frac{2\alpha \beta }{2\alpha \beta +2r}+\frac{2r}{2\alpha \beta +2r}\frac{\beta }{\beta +r}\right].$$ [9]

Finally, $R_1$ is given by

$$R_1=z_1^2\left(T_1{T}_1\prime +T_2{T}_2\prime \right),$$ [10]

and comparing $R_1$ obtained with a given C or with $C=0$ (ERN) will determine which network (clustered or not) spreads the diseases faster.

This approach is validated on Fig. 2B. Once again, we use networks constructed from cliques of size 10, such that clustering not only comes through the root node but also from other newly infected nodes. We also examine another clustered network, with the same degree distribution, but composed only of triangles, leading to a clustering coefficient around 0.06. We can see that our approach is able to give precise estimates of the coupling strength for which both clustered networks start spreading faster than their equivalent random networks.

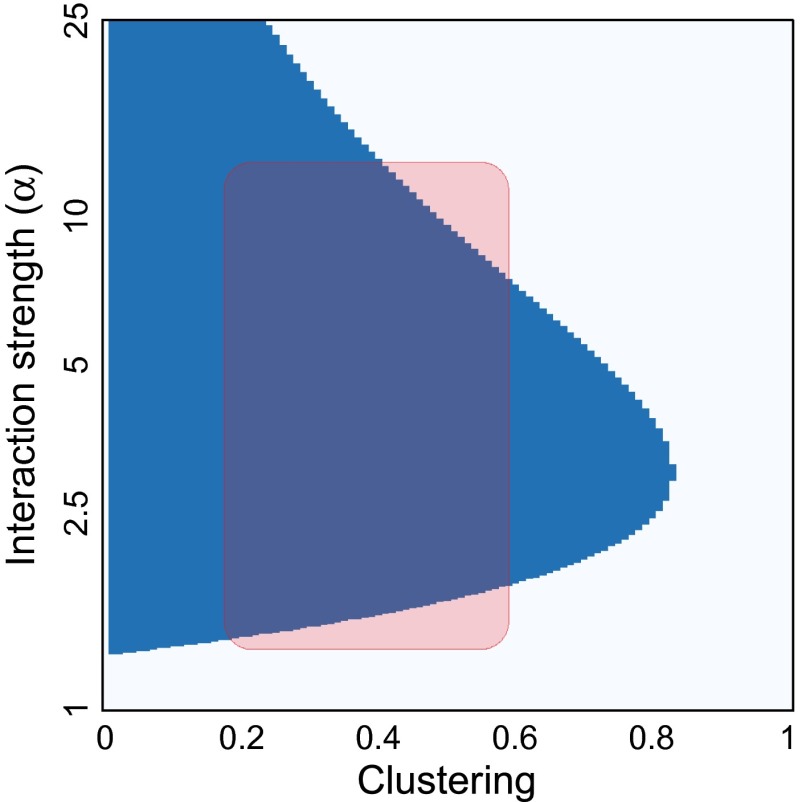
Fig. 3 demonstrates this over a broad range of parameters. For realistic ranges of clustering and disease interaction, we find faster propagation on clustered networks than random. Of course, for very clustered networks (i.e., when $C\to 1$), there is no interaction parameters that can compensate the clustering. For intermediate values of C, the range of α leading to faster propagation on clustered networks gets narrower. For very strong coupling, the diseases end up using the same pathways and thus follow each other whether the network is clustered or not. Hence, we see a second switch in optimal network structure as we increase α.

Fig. 3.

Effects of clustering hold over a broad range of parameters. The clustering criterion is used to investigate which network—a clustered structure (blue) or its equivalent random network (white)—propagates faster in varying interaction strength and clustering. The other parameters are set to those of Fig. 2. The shaded region is used to indicate a range of possible realistic scenarios for influenza and PC pneumonia.

First-Order Transitions and Outbreak Risk.

We have thus far investigated the impacts of varying the coupling α between the two diseases. However, impact of clustering is expected to be stronger for more transmissible diseases (larger ${\beta }_i/r_i$). In fact, clustering should barely matter around the epidemic threshold where the endemic steady state goes to zero. One can understand this phenomenon by thinking of the probability that a triangle is actually explored by the diseases, which falls as the probability of transmission to the third power.

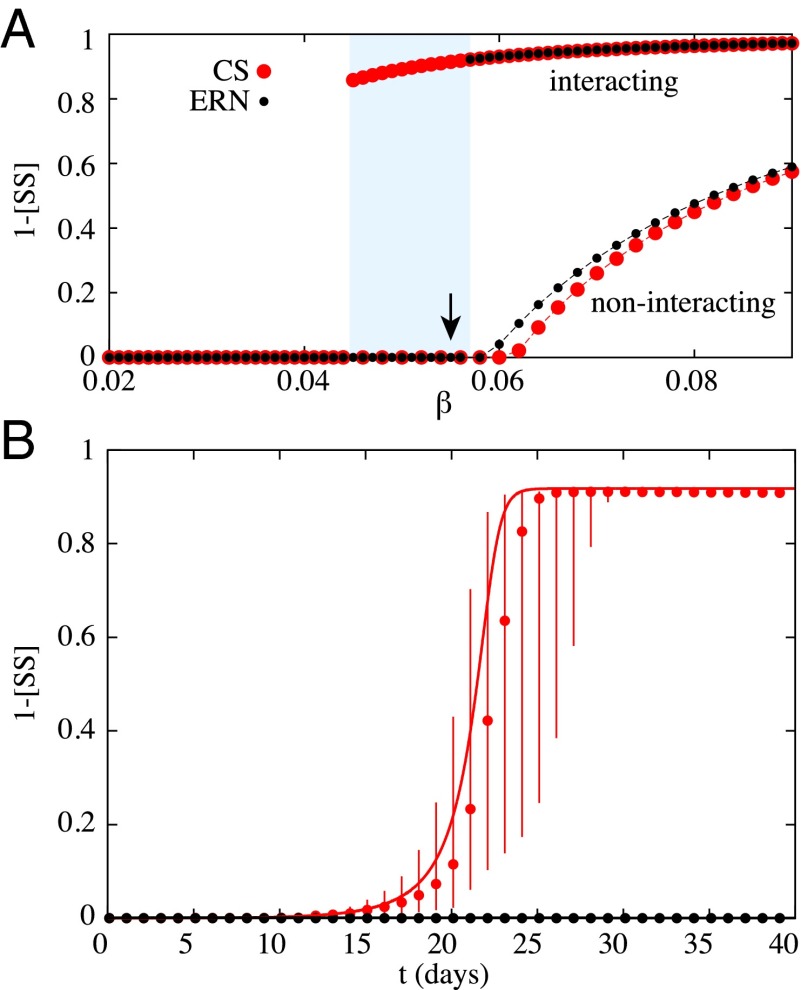
This standard assumption is not always justified, however. Fig. 4 presents endemic steady states for clustered and random networks over a range of transmission rates ${\beta }_i$, with and without coinfection synergism. We find two major results: One, clustering can lower the epidemic threshold; and two, strong synergy between diseases modifies the dynamics and leads to a first-order discontinuous transition. Typically, first-order phase transitions are the result of a build-up of latent heat, here corresponding to an epidemic potential. Just before the discontinuity both diseases are waiting for the other to prime the outbreak, which is similar to other recent observations of first-order transitions in disease spread requiring pathogen mutation (11) or multiple exposures (33).

Fig. 4.

First-order phase transition and epidemic latent heat. (A) Emergence of an endemic steady state for a scenario where equivalent diseases are either noninteracting ($\alpha =1$) or interacting ($\alpha =4)$ on the community structure (again, cliques of size 10) and its equivalent random network. Their transmission rates ${\beta }_1={\beta }_2$ are given as a fraction of the recovery rate $r_1=r_2$. The shaded region highlights a parameter region where interacting diseases on CS networks can spread explosively, whereas they cannot on the ERN. (B) Time evolution of the interacting diseases at the value ${\beta }_1={\beta }_2=0.056$ (indicated with an arrow in A). The markers give the median state of the Monte Carlo simulations with error bars corresponding to the 75% interval, whereas the curves give the prediction of our mean-field formalism. Note that the epidemics die out on the ERN and not on the CS, despite the heavy stochasticity caused by the nearby discontinuity (as seen in A).

Coupling these two surprising results, we see that for a critical range of parameters, a microscopic increase in transmissibility can cause a macroscopic difference in the expected epidemic size on a clustered network but not on an otherwise equivalent random network. This conclusion is confirmed in the shaded region of Fig. 4A: the diseases spread to around $90\text{\%}$ of nodes in the clustered network, whereas the outbreak is unnoticeable in the random network.

In the context of diseases that spread heavily in daycares and schools, this means that a small difference in the clustering of contacts could translate to a difference between no outbreak and a complete contagion for interacting pathogens such as influenza and PC pneumonia.

Discussion

Here we demonstrated that synergistic coinfections, such as pneumonia caused by S. pneumoniae and influenza, may actually spread faster and farther on clustered networks than on random networks. This result is similar to the recent observation that behaviors or opinions can propagate more rapidly in clustered social networks than in their random equivalent due to social reinforcement (34, 35). Our model thus suggests that we could also expect to see faster transmission on clustered networks in the context of diseases requiring multiple exposures before infection, which can also lead to discontinuous phase transitions (33).

We identified a threshold above which a clustered network structure will enhance the spread of synergistic coinfections. Finally, we demonstrated a first-order phase transition in final epidemic size and identified regions where coinfected individuals can start large outbreaks on clustered networks where they wouldn’t on random networks. Our results provided here have clear implications for understanding transmission dynamics of interacting diseases on realistic contact networks and for network based modeling of infectious disease transmission.

Understanding how diseases interact within host and between hosts in populations with realistic contact structure is of key importance to epidemiologists working to limit the transmission of diseases in these populations. Pneumococcal carriage rates in children under five years old interacting in highly clustered communities (daycares and households) can exceed 80% (36), and influenza infections are common. According to our results, transplanting a child coinfected with PC and influenza into a new clustered setting with susceptible hosts could result in an unexpectedly large outbreak. Similar outbreaks of sexually transmitted diseases could occur if individuals coinfected with syphilis and HIV (27), for example, entered into a clustered network of susceptible individuals, such as prostitution networks (24).

Our results are of importance to the field of epidemic modeling in general. Common practice is to run epidemic dynamics on random networks or mass action models, as these are considered worst case scenarios for transmission. We showed that network clustering facilitates synergistically interacting diseases because tight clustering keeps the diseases together. Our clustering threshold can be used by modelers to test whether they should be considering random or clustered network dynamics when trying to identify pessimistic transmission scenarios.

Our study has implications for epidemiology, mathematical modeling, and for the understanding the propagation of interacting phenomena in general. However, as illustrated by the problems encountered in trying to identify ranges of realistic parameters (Fig. 3), there is a dire need for data in the context of interacting epidemics. Not only is it hard to estimate realistic contact network properties, but one would also need to be able to estimate the transmissibility of a pathogen in both the absence and presence of other possible interacting diseases. Therefore, although this work is a step forward in terms of theory, it should also be taken as a call for better data.