Variable-Field Analytical Ultracentrifugation: I. Time-Optimized Sedimentation Equilibrium

Abstract

Sedimentation equilibrium (SE) analytical ultracentrifugation (AUC) is a gold standard for the rigorous determination of macromolecular buoyant molar masses and the thermodynamic study of reversible interactions in solution. A significant experimental drawback is the long time required to attain SE, which is usually on the order of days. We have developed a method for time-optimized SE (toSE) with defined time-varying centrifugal fields that allow SE to be attained in a significantly (up to 10-fold) shorter time than is usually required. To achieve this, numerical Lamm equation solutions for sedimentation in time-varying fields are computed based on initial estimates of macromolecular transport properties. A parameterized rotor-speed schedule is optimized with the goal of achieving a minimal time to equilibrium while limiting transient sample preconcentration at the base of the solution column. The resulting rotor-speed schedule may include multiple over- and underspeeding phases, balancing the formation of gradients from strong sedimentation fluxes with periods of high diffusional transport. The computation is carried out in a new software program called TOSE, which also facilitates convenient experimental implementation. Further, we extend AUC data analysis to sedimentation processes in such time-varying centrifugal fields. Due to the initially high centrifugal fields in toSE and the resulting strong migration, it is possible to extract sedimentation coefficient distributions from the early data. This can provide better estimates of the size of macromolecular complexes and report on sample homogeneity early on, which may be used to further refine the prediction of the rotor-speed schedule. In this manner, the toSE experiment can be adapted in real time to the system under study, maximizing both the information content and the time efficiency of SE experiments.

Introduction

Sedimentation equilibrium (SE) analytical ultracentrifugation (AUC) is a traditional first-principles-based method for measuring macromolecular molar masses in solution by analyzing their concentration distribution in thermodynamic equilibrium in a gravitational field (1,2). It is widely used to characterize attractive and repulsive intermolecular forces, and to determine the size and binding energy of specific complexes formed by reversible interactions between proteins and other macromolecules in dilute and crowded solutions (3–9). Many applications of SE have now been superseded by sedimentation velocity AUC (SV), as advanced computational data analysis methods (chiefly the emerging use of solutions of the master equation of centrifugal migration, the Lamm equation (10)) permit hydrodynamic studies of macromolecular size distributions and macromolecular interactions that offer higher resolution and shorter experiment times (11). However, SE is still invaluable as an orthogonal approach that directly measures buoyant molar masses and allows one to apply the framework of equilibrium thermodynamics to the analysis. This is true in particular for systems in which rapid chemical interconversion, on the timescale of sedimentation in SV, causes sedimentation boundary patterns that do not directly resolve the interacting species (12), or in which intermediate reaction kinetics, thermodynamic and hydrodynamic nonideality, or microheterogeneity complicate the computational analysis of sedimentation velocity boundary shapes. Unfortunately, although important progress has been made in many aspects of SE data analysis of noninteracting and interacting systems (9,13–17), SE remains limited by the sometimes prohibitively long experimental times required to reach equilibrium.

In the 1950s and 1960s, several strategies were explored to alleviate this problem. The earliest approach utilized synthetic boundary cells (18,19) in a layering technique to create single (18) or multiple (19) concentration steps in the solution column at the start of centrifugation. Unfortunately, this approach was experimentally complex and did not find many applications. The use of short (20) or ultrashort (21) columns can substantially reduce the equilibration times, but, unfortunately, these have the inherent drawback of reduced information content and significantly lower precision (21). A popular early strategy that eliminates the need to attain true equilibrium throughout the solution column is known as the Archibald method (22,23). This approach only considers gradients at the ends of the solution column, where the balance of sedimentation and diffusion fluxes report on the buoyant molar mass at any time. However, like short-column SE, this method can provide only limited information in the form of an average buoyant molar mass. A method to extrapolate the transient state to SE was found to be very sensitive to noise (24), and ultimately did not lead to any reported applications.

Due to the often ill-conditioned nature of modeling the Boltzmann distributions of interacting systems in SE, the method of choice in most laboratories is long-column SE experiments (6,8,13,16,25–27), which provide more precise data with higher information content. Usually, they are carried out such that equilibrium is achieved sequentially at different rotor speeds (25), combining the advantages of traditional low-speed (28) and high-speed (29) meniscus depletion configurations. Importantly, the redistribution of macromolecules at different centrifugal fields strongly enhances information about their interactions, tests for reversibility, and allows for soft mass conservation methods to be applied (13). Unfortunately, this exacerbates the time requirements.

The idea of transiently applying a higher rotor speed than the final equilibrium speed to initially accelerate sedimentation and thereby reduce the overall time required to reach equilibrium was first mentioned by Richards and Schachman (30). Shortly afterward, such overspeeding was described and analyzed in detail by Hexner et al. (31), and further improved by multiple groups in subsequent decades (25,28,32,33). At that time, theoretical analyses of overspeeding were based on analytical approximations assuming ideal monodisperse noninteracting systems. Although it was recognized to have significant potential, in theory, with >5-fold reduction in the times to reach equilibrium, the requirement for prior knowledge about the mass and frictional coefficient of the sedimenting species for its optimal use was found to present a significant practical drawback. If applied with incorrect macromolecular parameters, it can lead to highly concentrated or pelleted material at the base of the solution column, substantially extending the equilibration time rather than shortening it (24,25,34). Furthermore, even under optimal conditions, the high concentrations at the base of the cell can be of concern when studying proteins with limited solubility and a tendency to aggregate. This approach was found to be of more modest utility when applied more conservatively (25). For these reasons, overspeeding is rarely implemented in current experimental practice (26).

Here, we describe an approach that takes advantage of the recent surge in computational power that has spawned revolutionary developments in SV methodology (11). It extends the basic overspeeding idea to a more complex rotor-speed schedule that produces a time-varying gravitational field, and removes the two most critical obstacles of the classical overspeeding strategy. First, the method avoids high overconcentration at the base of the solution column, making it more robust. This is achieved by balancing the formation of gradients by sedimentation forces with diffusional relaxation throughout the solution column in a quasi-continuous variation of the centrifugal field, modeled with numerical Lamm equation solutions and optimized for short equilibrium times, with the constraint that a preset threshold concentration cannot be exceeded. Hence, we refer to this method as time-optimized SE (toSE). Although it is computationally complex, prediction of the rotor-speed profile takes only a few minutes in the dedicated software TOSE, which generates output files that enable straightforward implementation in current XLA/I analytical ultracentrifuges. Second, the dependence on prior knowledge about the sedimenting system is further reduced, as toSE generates initial experimental data that can be analyzed after a few hours into the run and used to adaptively adjust the field profile in real time. We expanded conventional SV data analysis to permit consideration of scans acquired in experiments with time-varying rotor speeds. In fact, the data from the size-dependent migration in the initial high field of toSE yields significantly more information than the corresponding migration during the approach to equilibrium at a fixed speed in conventional SE, and thereby produces higher-resolution size distributions. In conjunction with the reduced propensity for sample degradation during shorter experimental times, this can significantly enhance the experimental quality control in SE.

Materials and Methods

Sedimentation in time-varying fields

At the core of this work is the ability to solve the Lamm equation for sedimentation in a time-varying centrifugal field (10):

$$\frac{\partial c\left(r,t\right)}{\partial t}=-\frac{1}{r}\frac{\partial }{\partial r}\left(c\left(r,t\right)s\mathit{\omega }{\left(\mathit{t}\right)}^2{r}^2-D\frac{\partial c\left(r,t\right)}{\partial r}r\right),$$ (1)

where c(r,t) denotes the radial and temporal evolution of a macromolecular concentration in a solution column extending from the meniscus radius m to the bottom radius b and in a centrifugal field, given a macromolecular sedimentation coefficient s and diffusion coefficient D. The time dependence of the angular velocity ω(t) is approximated as segments of constant rotor speed connected by periods of constant acceleration or deceleration dω/dt. This closely mimics the current experimental possibilities for variation of rotor speed during a run. The numerical solution of Eq. 1 was based on an adaptive algorithm (35), with dynamic updating of the propagation matrices in time intervals depending on the magnitude of dω/dt. As a finite-element algorithm, it is not subject to the numerical diffusion errors that occurred in simpler differentiation schemes previously applied to the overspeeding problem (33).

As mentioned previously, within the designed numerical precision of the algorithm (35) (typically set to one-tenth of the precision of the experimental data acquisition), it converges after long times to the Boltzmann distribution in thermodynamic equilibrium:

$$c_{eq}\left(r,\mathit{\omega }\right)=c_0\frac{M_b{\mathit{\omega }}_{\mathit{eq}}^2\left(b^2-m^2\right)}{2RT}\times {\left(e^{\frac{M_b{\mathit{\omega }}_{\mathit{eq}}^2}{2\mathit{RT}}\left(b^2-m^2\right)}-1\right)}^{-1}\times {\mathit{e}}^{\frac{M_b{\mathit{\omega }}_{\mathit{eq}}^2}{2\mathit{RT}}\left(r^2-m^2\right)}$$ (2)

(with the loading concentration c₀ and the buoyant molar mass $M_b=sRT/D$, where R is the gas constant and T is the absolute temperature) in a sector-shaped solution column.

For the purpose of modeling and analyzing the approach to equilibrium from a preformed gradient of an ongoing experiment, the initial conditions c(r,t = 0) were allowed to include a calculated transient distribution resulting from sedimentation (Eq. 1) for a given period of time with a certain prior rotor-speed profile (c(r,t = 0) = c(r,t_ini) given ω_ini(t)), or, alternatively, following an SE distribution (Eq. 2) at a finite rotor speed (c(r,t = 0) = c_eq(r,ω_ini)).

Optimization of the rotor-speed profile for toSE

As a measure for closeness to equilibrium, we used the root-mean-square deviation (RMSD) Δ_eq between a concentration profile at time t, calculated from a superposition of Lamm equation solutions (Eq. 1) for one or several species, and the Boltzmann equilibrium profiles (Eq. 2) for the same species. It was calculated over a radial range of r_min to r_max (typically r_min = m + 0.01 cm and r_max = b – 0.05 cm) describing the relevant accessible region for experimental data acquisition. Distributions are considered sufficiently close to equilibrium when Δ_eq is below a threshold value ε × c₀ at time T_eq, where ε-values reflect the expected experimental signal/noise ratio. In this work, values of 0.001–0.007 were used. Δ_eq is evaluated on an equidistant grid of time intervals, and for a constant rotor speed the equilibration times T_eq were found to be satisfactorily consistent with the analytical predictions by van Holde and Baldwin (20) (who used a different criterion for closeness to equilibrium).

It is very important to carry out these simulations with correct values for solvent density, macromolecular partial-specific volume, and solvent viscosity. For example, experiments in aqueous solvents at 4°C will take 60% more time then experiments at 20°C due to the increased viscosity of water. Likewise, the intended solution column height is a critically important parameter; standard long-column SE experiments will have solution columns of 4–5 mm (8).

The time T_eq when Δ_eq first decreases below the threshold is used as a target function for minimization of the rotor-speed profile, but is modulated with dynamic penalty functions for subsequent increases at longer times (see below), as well as strong penalties for concentrations at the base of the solution columns exceeding a preset limit at any time. This limit was specified relative to the final equilibrium concentration at the base of the cell, as the ratio $\alpha =\underset{t}{\max }\left[c\left(b,t\right)/c_{eq}\left(b\right)\right]$. Typical values chosen for this parameter in this study were 1.2–1.5 for proteins and up to 2.0 for DNA. One may assign this more stringently to a smaller value when considering, among other factors, the solubility limit of the macromolecule under study.

The rotor-speed profiles ω(t) are discretized to a temporal grid of segments, at the beginning of which a rotor-speed change is initiated that will occur with preset acceleration or deceleration rates. Segments are constrained to have durations of no less than 10 min, and target rotor speeds are constrained to be multiples of 100 rpm increments, ensuring that a profile ω(t) can be experimentally implemented in the current XLA/I analytical ultracentrifuges. Further, ω(t) in toSE is forced to coincide with the target equilibrium rotor speed ω_eq after a preset time t₀, which is chosen to be at least a few hours (typically 2–3 h) less than the minimal predicted equilibration time (see Results).

To optimize ω(t), a parameterization of this function was used on the basis of an exponential decay toward ω_eq with certain time constant, modulated in its amplitude in N independent steps, where N is chosen by the user. As an alternative, we implemented a parameterization that simply reflects N constant steps of equal length. This appears more successful for longer solution columns with multimodal ω(t) profiles. Depending on the solution column length and macromolecular parameters, values for N between 5 and 10 are used. Higher values are useful for longer solution columns because they can describe more complex rotor-speed profiles, but they only marginally improve the equilibration time for conventional column lengths. Optimization of the rotor-speed profile was achieved by using several rounds of a simplex algorithm, optionally allowing simulated annealing (36). It should be noted that the resulting optimization problem is highly complex with many local minima, and usually several rounds of optimization need to be carried out. However, in contrast to optimization problems in data analysis, there is no need to find the parameters that lead to the absolute minimum in T_eq; instead, we just want to find an effective sequence of rotor speeds that will substantially reduce the experimental time required to reach SE, which may be satisfactory even when it does not provide the maximum savings theoretically possible.

Software

All computations related to the rotor-speed profiles of toSE are embedded in a new dedicated software called TOSE, which has a graphical user interface to display results and facilitate handling of simulation parameters and related files. Besides optimization, it can also display Δ_eq versus time for any given rotor-speed profile ω(t). Optimized rotor-speed profiles from TOSE are saved by default in speedsteps.txt files containing an ASCII table of times for the initiation of rotor-speed changes, the new speeds, and the acceleration/deceleration rate. The experimental execution of sequential rotor-speed and scan commands can be automated using equilibrium methods in the XLA/I graphical user interface, which are stored in .EQU files. Since the rules for equilibrium methods in the XLA/I graphical user interface are nonobvious and difficult to implement for precise timing, TOSE will convert the optimized rotor-speed profiles into an equilibrium methods .EQU file, which can be directly loaded in the XLA/I centrifuge user interface program as an SE method. A video tutorial for carrying out the XLA/I setup can be found at https://sedfitsedphat.nibib.nih.gov/tools/Protocols/TOSE_implementation.wmv. Briefly, to apply the generated equilibrium method, a dummy scan settings file with an equilibrium method must be created, closed, and reloaded after the XLA/I generated .EQU file is exchanged with the TOSE-generated version under the same filename. Additional utility functions to convert any speedsteps.txt ASCII file into an XLA/I method file .EQU and vice versa are implemented as a separate function in TOSE.

TOSE (version 1.0) can be downloaded from https://sedfitsedphat.nibib.nih.gov/software. A detailed description of how to optimize toSE and carry out such an SE experiment is provided in a video available from https://sedfitsedphat.nibib.nih.gov/tools/Protocols/TOSE_optimization.wmv.

The essential functions of TOSE are also accessible via the Sedimentation Equilibrium Options menu in the SEDFIT software. SEDFIT was further modified to accommodate the analysis of scan data acquired at different rotor speeds during the approach to equilibrium, which can be automatically recognized. In this case, a speedsteps.txt ASCII file is loaded, which must be located in the same folder as the experimental scans. It must contain a table with the times of the rotor-speed changes, the new target speed, and the rate of the rotor-speed change, which are tested for consistency with the experimental scans. The required speed-step file can be extracted from an XLA/I equilibrium method file and is generated as a default output in TOSE.

Rotor stretching, which depends on the rotor speed, translates the solution column to slightly different positions. This translation can cause errors in a detailed modeling of the experimental data, especially in the meniscus position and time-invariant noise structure (13). It is therefore advantageous to realign scans acquired at different rotor speeds using a previously determined rotor-stretching module (13). To maintain a record of the precise centrifugal field to which the solution column was exposed, a compensatory small change in the rotor-speed entry in the file header is introduced and propagated into the speedsteps.txt file. These operations were implemented as a new utility function in SEDFIT.

Experiments

Lyophilized bovine serum albumin (BSA, cat. No. 7030; Sigma-Aldrich, St. Louis, MO) was resuspended in phosphate-buffered saline and diluted to ∼0.5 mg/mL. Soybean trypsin inhibitor (SBTI) and α-chymotrypsin (CT) (cat. No. 3570 and 1475, respectively; Worthington, Lakewood, NJ) were resuspended in 0.2 M sodium chloride and 0.05 M sodium phosphate, pH 6.7, and purified by size-exclusion chromatography.

A synthetic 601 nucleosome positioning sequence (37) flanked by symmetric BamHI, EcoRV, and BpiI restriction endonuclease sites was prepared by annealing and sequential ligation of overlapping DNA oligomers. This fragment was cloned into pUC19 using the BamHI ends to generate p601-1 (this is the monomeric 601 plasmid in Schalch et al. (38)) and verified by DNA sequencing. PCR on p601-1 using primer pairs F162 (GGCCGCCCTGGAGAATCC) and R0 (CTTACATGCACAGGATGT) was carried out using a high-fidelity Phusion DNA polymerase (cat. No. M0530L; New England Biolabs, Ipswich, MA) according to the manufacturer’s protocol to generate a 162 bp double-stranded DNA (dsDNA) fragment. This fragment was purified by polyacrylamide gel electrophoresis according to standard protocols (39) and used in a second round of PCR to obtain DNA free of any contaminating parent plasmid. After treatment with phenol/chloroform and chloroform, and ethanol precipitation, the 162 bp dsDNA was purified to homogeneity by size-exclusion chromatography on a Superdex 200 HR 10/30 column (cat. No. 17-1088-01; GE Healthcare, Piscataway, NJ) in 50 mM sodium phosphate (pH 7.0). DNA was found to be monodisperse by sedimentation velocity with an s_20,w of 5.02 S, an estimated mass of 103 kDa (assuming a partial specific volume of 0.55 mL/g, the calculated mass is 107.730 kDa), and a frictional ratio of 2.89.

AUC experiments were carried out in XLA/I analytical ultracentrifuges (Beckman Coulter, Indianapolis, IN) subjected to regular calibration (40). Sample volumes as indicated for the different experiments were matched with reference buffer and placed in charcoal-filled Epon double-sector centerpieces according to standard procedures (8). The rotor with sample cell assemblies was installed into the rotor chamber and the temperature was equilibrated in high vacuum at the intended temperature for SE. Scan settings for monitoring the approach to equilibrium in continuous mode included radial increments of 0.003 cm and one acquisition per radius (overspeeding phase), and scan settings in the step mode included radial increments of 0.001 cm and 20 replicates per radius to record equilibrium profiles (approach equilibrium mode). Scans were acquired at a wavelength of 280 nm, 260 nm, 230 nm, or 250 nm depending on the sample. An overriding consideration for the setup of data collection is that the scans are not allowed to delay the progress in programmed rotor-speed changes. This can be achieved by keeping the total time for a cycle of scans less than the time delay between rotor-speed changes, i.e., ∼8 min or less with the discretization of ω(t) in the current implementation in TOSE. Therefore, when studying multiple samples in an An-50 Ti eight-hole rotor, the initial approach to equilibrium can only be monitored for a subset of samples.

We analyzed experimental toSE data for the approach to equilibrium in SEDFIT using standard procedures of SV analysis (8), based on Lamm equation solutions with variable fields (Eq. 1). Scans were translated in radius to compensate for differential rotor stretching with the use of a previously measured rotor-stretching modulus, allowing for the application of time-invariant noise models (41–43). Due to the prominent display of back-diffusion, we found it important to refine both the meniscus and bottom of the solution column. In conjunction with the c(s) analysis (44), the average frictional ratio was also refined.

We verified attainment of SE by comparing the last scans with each prior scan in SEDFIT. Additionally, the data were fitted in SEDFIT to a single-species model (based on Eq. 2) to determine an average buoyant molar mass across a radial window where signals did not exceed the linear range. For low-speed data where the baseline parameter was found to be correlated with the molar mass parameter, the baseline was fixed to a common value. In the case of interacting systems, scans acquired at multiple rotor speeds and loading concentrations were globally modeled in SEDPHAT, with mass conservation and mass action law coupled to Boltzmann exponentials (Eq. 2) in chemical equilibrium and SE as described previously (6,8).

Results

Computer simulations

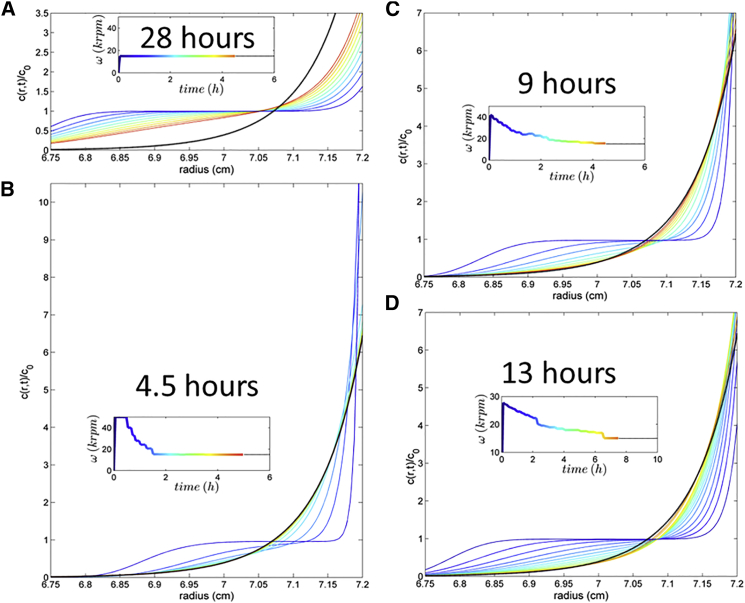
Initially, we carried out computer simulations to examine the potential use and properties of toSE in theory. Fig. 1 A shows the simulated concentration distributions for a 65 kDa protein containing 15% (by weight) dimer, in a 4.5 mm solution column (typically used in SE (8)) at 20°C, during the first 5 h in the standard approach to equilibrium at 15,000 rpm. The predicted equilibration time with ε = 0.007 (corresponding to the experimental signal/noise ratio in the instrument for the sample below) across the optically accessible radial range is ∼28 h. We also simulated the effect of traditional single-step overspeeding using parameters proposed by Chatelier (33), and calculated the sedimentation profiles after an initial exposure to 50,000 rpm for 43 min (as predicted to be optimal using Eqs. 10 and 11 in Chatelier (33)). The equilibration time was reduced substantially to 9.5 h. We note that during this process, the concentration at the base of the solution column transiently reached ∼5 times the final equilibrium concentration after 30 min, or ∼33 times the initial loading concentration.

Figure 1.

Calculated concentration profiles during the approach to equilibrium for different overspeeding conditions. The corresponding temporal rotor-speed profiles are shown in the insets, using the same color temperature map to indicate time. (A) Conventional SE experiment with a constant rotor speed. (B) Unconstrained toSE optimization leading to a transient fivefold overconcentration at the base of the cell. (C) toSE with overconcentration by a factor of <1.6. (D) toSE with overconcentration by a factor of <1.07. Equilibration times, assessed with ε = 0.007, were 28 h (A), 4.5 h (B), 9 h (C), and 13 h (D). All calculations are for a 65 kDa protein containing 15% dimer, each with frictional ratios of 1.4, in a 4.5 mm solution column corresponding to a 150 μL sample in a regular double-sector 12-mm-pathlength centerpiece, with final equilibrium at 15,000 rpm at 20°C. To see this figure in color, go online.

In toSE, we allowed the rotor speed to change during the first 5 h of sedimentation. First, iterative refinement with the sole objective of shortening the equilibration times led to the temporal rotor-speed profile shown in the inset of Fig. 1 B, which shows that the equilibrium distribution was attained with the same relative precision of 0.007 after a shorter period of 4.5 h. This was achieved by a brief burst of very high centrifugal force at the limit of the allowable rotor speed of an eight-hole rotor, which rapidly declined after 30 min (Fig. 1 B, inset). This allowed for strong migration of material from the meniscus, approaching the depletion required for SE. Simultaneously, it also created a very strong initial concentration gradient at the base of the solution column, which, after a reduction in the field strength, spawned strong diffusional fluxes that transported material back to smaller radii to reach the levels required for SE. It appears that in contrast to the single-step overspeeding, the slightly shorter duration of the highest field followed by a slower decay allows diffusional fluxes to set in while at the same time accelerated migration in the elevated field can still be taken advantage of, thereby saving additional time. In this process, the overconcentration at the base of the cell reaches high levels similar to those found in the single-step overspeeding described above.

The strong overconcentration at the base of the solution column can be of significant concern regarding the stability of the dissolved material, as it may promote aggregation, surface adsorption, and/or phase transitions. Also, for heterogeneous samples, this region will contain a disproportionately high fraction of the higher-molar-mass species, which may substantially disturb the chemical equilibria. Therefore, we introduced a constraint in the optimization of the temporal field strength such that overconcentration at the base of the cell at any time is strongly suppressed. With a value $\alpha =\underset{t}{\max }\left[c\left(b,t\right)/c_{eq}\left(b\right)\right]$ of 1.6, i.e., limiting overconcentration to 60%, the optimized rotor-speed schedule exhibits a lower initial rotor, followed by a more gradual decline during ∼3 h (Fig. 1 C, inset). This leads to an equilibration time of ∼9 h, which is similar to the single-step overspeeding approach but, as expected, exhibits much shallower concentration gradients (Fig. 1 C). It is possible to further suppress and avoid almost any overconcentration, and with the rotor-speed schedule shown in Fig. 1 D (inset), overconcentration is not more than ∼7% at any time (Fig. 1 D). The initial rotor speed is less than twice the final equilibrium speed, and it decays gently over ∼10.5 h, such that equilibration is achieved at ∼13 h (using the same criterion of ε = 0.007). This is still less than half the time required for standard SE. A rotor-speed profile that did not produce any overconcentration was found with an equilibration time of 18 h (data not shown). This shows that accelerated transport by sedimentation alone can achieve substantial savings, but suggests that even very modest overconcentration generating diffusional relaxation as an additional transport mechanism can lead to substantial further improvement.

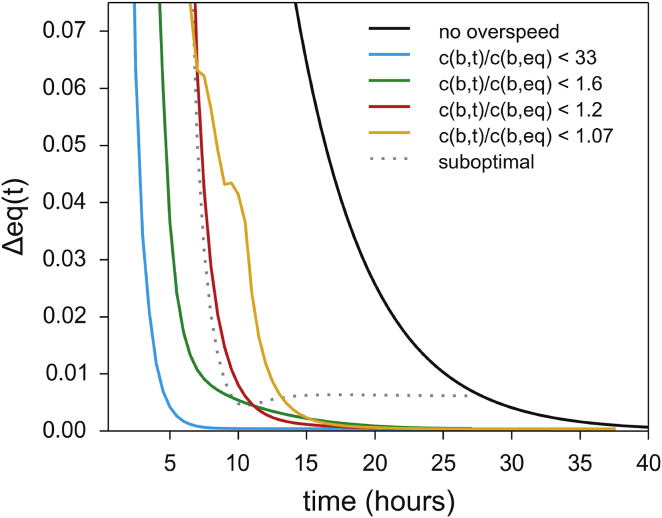
The time course of the approach to equilibrium, as characterized by the RMSD between the theoretical equilibrium and the concentration distribution across the detectable radial range, Δ_eq(t), is shown in Fig. 2. We found that the optimization of the rotor-speed schedule was often ill conditioned, with many different schedules that produced similar equilibration times, and therefore we had to carry out the optimization multiple times to avoid local minima. We enhanced the optimization process for ε-values that were more stringent than the experiment ultimately required in such a way as to penalize configurations that produced distributions that satisfied the ε criterion but lingered far from equilibrium for prolonged times (e.g., green trace in Fig. 2). In extreme cases, we obtained nonequilibrium distributions that were similar to the equilibrium distribution across the radial range of interest at early times, but they deviated again at later points in time. An example of such a Δ_eq(t) trace with an early minimum is shown as a dotted line in Fig. 2, which was obtained for a suboptimal rotor schedule.

Figure 2.

Time course of the approach to equilibrium Δ_eq as determined from the RMSD to the Boltzmann distributions over the experimentally accessible radial range of an AUC sample cell. The traces shown correspond to the simulations in Fig. 1 for conventional SE (black), the unconstrained toSE optimization (cyan), and the optimized toSE conditions with overconcentration constraints (green and orange, respectively). To illustrate an additional consideration of toSE optimization, the dotted line shows the time course for a suboptimal rotor-speed sequence that generates distributions with only transient similarity to the expected equilibrium, a condition that is automatically recognized from the minimum at intermediate times and penalized in the toSE optimization. To see this figure in color, go online.

An important question is, how much does the calculated equilibration time in toSE depend on precise knowledge of the molecular sedimentation parameters? To examine this, we first determined an optimal rotor-speed profile for a 65 kDa protein with a frictional ratio of 1.4 in a standard 4.5 mm solution column, not allowing overconcentration by more than a factor of α = 1.2. The time to reach equilibrium at 15,000 rpm within a relative precision of 0.005 was 10.5 h, compared with 30 h under constant-speed conditions. When we applied the same rotor-speed profile to predict the equilibration time of a molecule of half or twice the molar mass, we obtained equilibration times of 15 h and 11.5 h, respectively. Thus, a twofold deviation in the molar mass (and corresponding differences in the sedimentation parameters) will impair the equilibration time slightly, but can still allow for significant time savings with toSE.

Experimental tests with a model protein

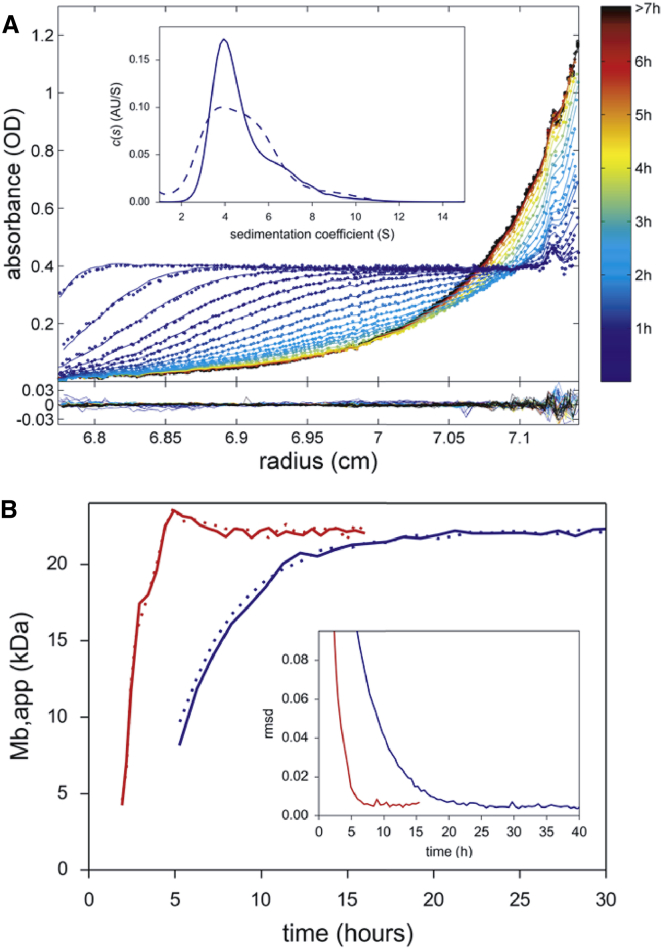
Next, we tested whether the predicted equilibration times could be experimentally achieved. Fig. 3 A shows absorbance scans for 165 μL BSA (creating an ∼4.5 mm solution column) subjected to the centrifugal field schedule of Fig. 1 C. Even though the transient overconcentration at the base of the cell is not visible in the experimental data, this was expected due to our inability to reliably scan steep absorbance profiles close to the base of the solution column. In principle, interference optical data acquisition would have been advantageous for our purposes here because of its ability to record steeper gradients at the end of the solution column; however, we did not attempt this during the approach to equilibrium in toSE due to potential complications in the rotor-speed dependence of the radial-dependent baseline profile (although it could certainly be acquired once SE has been attained, after suitable aging of the cell assemblies (13,45)). After making corrections for differential rotor stretching and accounting for the time-varying rotor speed, we were able to fit the absorbance data very well to a c(s) model describing a superposition of independently sedimenting particles with the sedimentation coefficient distribution shown in the inset of Fig. 3 A, and produce the residuals shown in the lower panel of Fig. 3 A. Based on the excellent quality of fit, we conclude that no significant convection arose from the stepwise small changes in rotor speed. After ∼7 h, the distribution attained equilibrium, as assessed both by fitting the absorbance profiles of each scan to a single-species model to extract an average buoyant molar mass and by monitoring the RMSD of scans relative to the last scan (Fig. 3 B). A control experiment carried out with the same sample under the same conditions but conventionally exposed to a constant rotor speed required ∼20 h, converging to the same average buoyant molar mass (when analyzed over the same radial range; Fig. 3 B). Thus, the toSE approach is experimentally effective and consistent with predictions (9.5 h).

Figure 3.

Experimental implementation of toSE for BSA under the conditions of Fig. 1C. Absorbance scans at 280 nm were acquired at each step in the rotor-speed profile, gradually decaying from an initial 41,600 rpm to the target equilibrium speed of 15,000 rpm during the first 5 h (following Fig. 1C, inset). Scans are radially translated to compensate for differential rotor stretching. (A) Experimental scans (dots) and best fit (lines) using the color scheme in the sidebar to indicate passage of time. The c(s) model produced the sedimentation coefficient distribution shown in the inset (solid line) and led to residuals shown in the lower plot with an RMSD of 0.0055 optical density (OD). The dotted line in the inset reflects the c(s) distribution obtained when only data from the first 3 h were considered. (B) The approach to equilibrium is visualized by the average buoyant molar mass obtained for data in the accessible radial range at different time points (red). For comparison, the results from a conventional SE experiment under equivalent conditions with constant rotor speed are shown in blue. The results of a replicate experiment are shown as dotted lines. The inset shows the time course of the RMSD difference between individual scans and the last scan for the toSE experiment (red) and the conventional approach to SE at constant speed (blue). To see this figure in color, go online.

Remarkably, the analysis of experimental data acquired after only a few hours allowed a c(s) distribution to be determined, and data from the first 3 h produced the distribution shown as a dotted line in the inset of Fig. 3 A. The resolution is lower than that typically obtained in a standard high-speed SV experiment, or in the complete approach to equilibrium of toSE, but is sufficient to assess the homogeneity and size of the macromolecules. In this case, the distribution reveals the presence of BSA monomer, dimer, and higher oligomers.

In a second experimental system, we tested whether toSE could correctly predict sedimentation behavior in a time-varying field of DNA, an elongated macromolecule that usually requires extremely long sedimentation times due to its very high frictional ratio under the conditions used. A 162 bp fragment of DNA was brought to low-speed SE in a 4.6 mm solution column at a final rotor speed of 7,000 rpm at 20°C. In a conventional constant-rotor-speed experiment, this would require ∼70 h. When the same sample was subjected to an optimized toSE rotor-speed schedule, starting with a speed of 21,700 rpm and slowly decreasing to 7,000 rpm during the first 5 h of the experiment (predicted to cause an overconcentration by ∼50%), substantially shorter equilibration times were necessary, with time-invariant RMSD and buoyant molar mass values observed after ∼20–30 h (depending on the criterion; Fig. S1 in the Supporting Material).

A time-honored strategy for diminishing excessive equilibration times in SE is to use shorter solution columns (20). Therefore, we asked whether toSE could be beneficially combined with this approach. Theoretical predictions for optimized toSE under conditions equivalent to those shown in Fig. 1, but reducing the standard 4.5 mm solution to 3.5 mm, suggest similar potential time savings by toSE. In an experiment with a 130 μL solution column of BSA, the time required to reach SE at 10,000 rpm in a standard experiment was reduced by >4-fold after application of an optimized time-varying centrifugal field during the first 2 h, with maximal overconcentration by a factor of 1.9 (Fig. S2).

We then sought to determine whether the potential to save time by toSE would make it feasible to carry out SE studies with longer than usual solution columns, which are more informative but—unless one is working with molecules smaller than 5 kDa—take a prohibitively long time to reach equilibrium. Specifically, a 5.5 mm solution column of the BSA sample, corresponding to 200 μL in a 12 mm centerpiece, reached equilibrium at 7,800 rpm after ∼60 h (Fig. S3 A). Interestingly, to minimize the equilibrium time while limiting the overconcentration to α = 1.7, toSE optimization converged to multimodal ω(t) profiles in which sequential high-field phases were separated by periods of diffusional relaxation (Fig. S3 A, inset). After this rotor-speed profile was implemented experimentally (Fig. S3 A), SE was attained at ∼15 h, as judged by the average buoyant molar mass, or after ∼30 h based on the time course of pairwise differences from the last scan (Fig. S3 B, inset).

Generally, a significant gain in precision of SE studies can be achieved by attaining equilibrium at multiple rotor speeds. Therefore, we calculated optimized toSE field profiles for the transition of SE under low-speed conditions to attain SE at medium speed, and then under high-speed meniscus depletion conditions. We subjected these profiles to an experimental test using BSA as in the standard conditions of Fig. 3, but now for sequential equilibrium rotor speeds of 6,000 rpm, 10,000 rpm, and 15,000 rpm. Fig. S4 shows the time course of the approach to equilibrium, as measured by the RMSD of scans at different time points from the last scans for a control experiment at constant speed (blue) and the toSE experiment (red) with the speed profiles optimized for the equilibrium transitions as indicated in the insets. Whereas a conventional experiment would require at least 4 days, toSE optimization can reduce this to ∼1.5 days.

Application to an interacting system

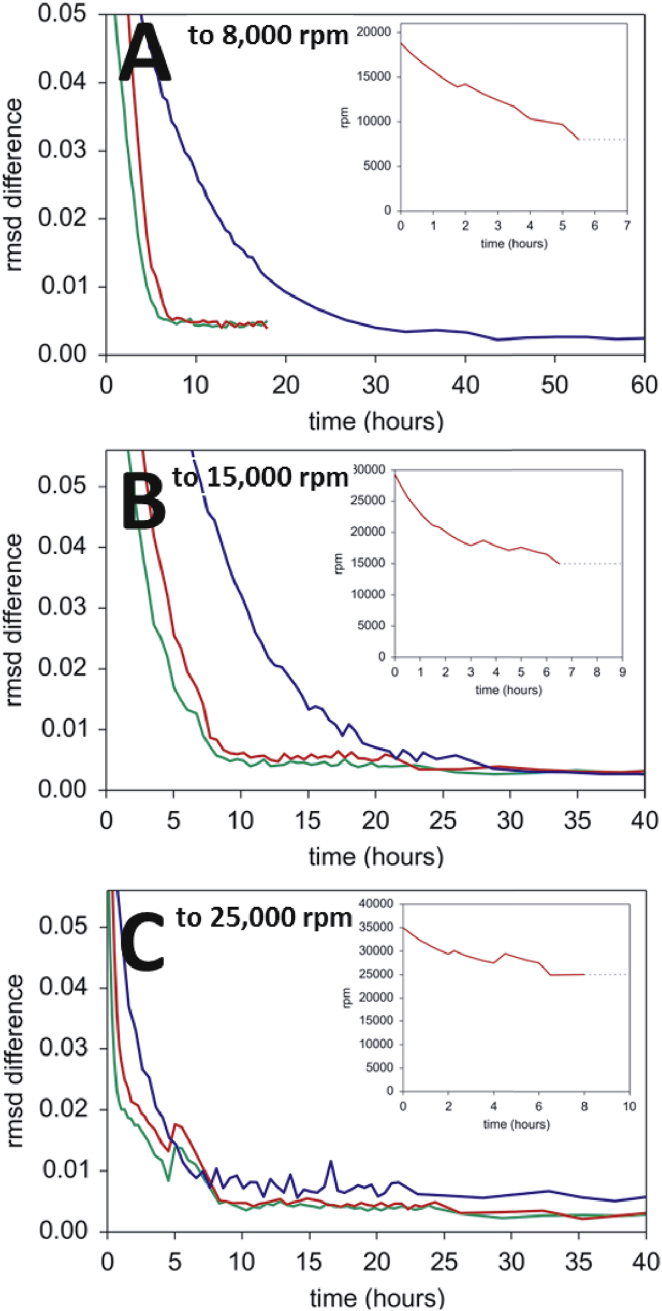
Finally, we applied the toSE method to the measurement of binding constants of an interacting system. We used the previously studied model system of SBTI with two binding sites for CT (6). A stock mixture with a CT/SBTI molar ratio of 1.5 was diluted to 160 μL samples (∼4.5 mm solution column) at final SBTI concentrations of ∼0.5–10 μM, placed in an eight-hole rotor alongside samples of 5 μM SBTI and 5 μM CT alone, and brought to equilibrium at 10°C sequentially at rotor speeds of 8,000 rpm, 15,000 rpm, and 25,000 rpm. SE experiments were carried out side by side in different instruments with either fixed target rotor speeds or toSE field profiles optimized for an equal mixture of the smallest molecule (SBTI) and the largest complex (2 CT/1 SBTI).

Monitoring the approach to equilibrium during toSE at the lowest speed was limited to a few cells at a single wavelength. Fig. 4 visualizes the attainment of SE distributions in both experimental series in the form of the RMSD difference between the previous scans and the last scan. (Due to different noise levels in the two ultracentrifuges used, the final absolute RMSD values are slightly different.) It can be clearly discerned that at the lower rotor speeds, the exposure to the toSE field profiles considerably hastened equilibration, even though the field optimization did not account for dynamic interactions that occur during macromolecular redistribution. The transition to the last rotor speed occurred most rapidly, and toSE did not seem to offer any advantage.

Figure 4.

(A–C) Sequential approach to multiple equilibria for CT/SBTI samples at rotor speeds of 8,000 rpm (A), 15,000 rpm (B), and 25,000 rpm (C), all at 10°C. Shown are the RMSDs of scans taken at 280 nm for the sample with 10 μM SBTI/15 μM CT in toSE (red) and constant speed (blue) at different points in time. For comparison, a higher-concentration sample of 14 μM SBTI/21 μM CT in toSE is shown (green). The toSE field profiles used for each step are shown in the insets (red). To see this figure in color, go online.

To ensure that overspeeding did not create artifacts in the final SE profiles, we carried out a conventional SE experiment for comparison. We globally fit absorbance profiles acquired at 280 nm, 250 nm, and 230 nm, including data for all mixtures and all rotor speeds, and applying implicit mass conservation constraints and constraints of the molar ratio of the loading mixtures (13). For the toSE experiment, the time point of the analysis was the start of the acquisition of high-precision scans at ∼22 h for all rotor speeds. To allow a higher scan rate for better monitoring of the approach to equilibrium, we acquired lower-precision scans before this point, which suggest that a state very close to equilibration was attained after ∼10 h at each speed. This low-precision scanning at high frequency is not necessarily required in future SE experiments. To optimally exploit the quick approach to equilibrium, it would be desirable to have a programmable switch that would automatically proceed from fast scanning during the overspeeding method to a sequence of slow high-precision scans. In the fixed-speed controls, the scans included in the SE analysis were acquired at 77 h, 37 h, and 23 h, respectively. We obtained highly consistent results in both experiments. The apparent molar mass of SBTI was 19.2 kDa (toSE) and 19.1 kDa (constant speed), that of CT was 23.3 kDa (toSE) and 23.0 (constant speed), and the apparent binding constant from the analysis of the mixtures with a two-equivalent-sites model was log(K₁) = 5.91 (5.86–5.96, 68.3% confidence interval) in toSE and log(K₁) = 5.84 (5.78–5.90, 68.3% confidence interval) in the constant-speed control. These results from the SE analysis are consistent with those previously reported for this interaction (6).

Discussion

SE offers a unique potential for rigorously measuring the thermodynamic equilibria of molecular interactions in free solution (2), but it has the practical drawback of very long experimental times. In the simple form originally conceived, the application of an initial higher rotor speed to transiently accelerate migration and improve attainment of equilibrium (28,30–32) has generally not proven to be very useful (25,26,34). In practice, the strong dependence on prior knowledge of the sedimentation parameters in conjunction with the high overconcentration at the base of the sample cell has the potential to cause extended, rather than shortened, equilibration times (25,34). To alleviate this concern, a two-step procedure in which an overspeeding phase is followed by a period of underspeeding was implemented by Richards et al. (28) based on intuition and the empirical observation that this produced profiles more closely resembling SE. In this work, we generalize the idea of centrifugal field changes and bring to bear modern computational tools that allow sedimentation to be analyzed in an arbitrarily time-varying centrifugal field and rationally optimized in toSE. This can avoid substantial overconcentration in a gentle migration that balances sedimentation and diffusion, thereby removing the principal hurdle of this approach and allowing SE to be obtained much more rapidly.

Two mechanisms contribute to the acceleration of the SE experiment. First, higher centrifugal fields cause faster migration, which aids in the depletion of macromolecules in the meniscus region and accumulation past the hinge point. Second, the generation of strong concentration gradients can act in some ways like a diffusional spring and generate back-flux opposite to sedimentation after the centrifugal field strength is lowered (which may include fields lower than the final target). Both can be balanced in different ways over time to achieve the objective of closeness to the Boltzmann distribution, while adhering to preset concentration limits during a given initial time period.

The required computations are encapsulated in a dedicated software program called TOSE (and implemented in SEDFIT). This still requires an estimate of macromolecular sedimentation parameters, but approximate prior knowledge of macromolecular size is needed similarly for the selection of a target equilibrium rotor speed. Within a factor of 2 in size, we observed that incorrect assumptions resulted in suboptimal equilibration times; however, these times were no longer than those required for conventional constant-speed SE. Furthermore, as it has become very straightforward to obtain high-resolution size and shape information from SV experiments (8,44), SE is often applied to obtain orthogonal information for studying macromolecular interactions, so estimating species sedimentation parameters and heterogeneity usually should not pose a real problem. Finally, the changes in SV data analysis that we have introduced in this work will now permit the analysis of data from time-varying fields, and will enable investigators to obtain some information about macromolecular size and homogeneity in real time during the first few hours of an experiment. Due to the initially higher centrifugal fields in toSE, this information is superior to that generated in standard SE at constant speed.

toSE optimization can be carried out assuming a mixture of species, and currently the TOSE user interface allows for two components. Although this is an important extension from the traditional single-species computations of overspeeding parameters, in practice more than two species may not be required. For interacting and multicomponent systems, we believe that carrying out the simulations with a mixture that reflects the smallest and largest expected species will be sufficient, because in practice several samples would be studied side by side (e.g., in a concentration series populating different states), and it would not be possible to ensure that the optimum toSE strategy is used for every sample. This is also guided by the recognition that, on one hand, we will always have only imperfect a priori knowledge about the behavior of an experimental sample, but on the other hand, the goal of toSE is merely operational, i.e., to shorten the experiment time rather than to determine the theoretically best possible conditions. Thus, it is not necessary to fully predict the contributions from species of intermediate size or the subtle influence of interactions on the transient concentration distributions during the gentle decrease of rotor speed in the overspeeding phase. We demonstrated this pragmatic approach in the experiments with BSA and the interaction of SBTI and CT, both of which exhibited savings in equilibration time that were reasonably close to the predictions even though we did not consider oligomers higher than the dimer for BSA, and did not model multiple species and dynamic interactions in the CT/SBTI system.

For a practical implementation of the rotor-speed schedule, which can exhibit changes at 10 min intervals, TOSE produces an equilibrium method file that can be conveniently loaded into the user interface of Beckman Coulter analytical ultracentrifuges and directly executed. A practical constraint in the current centrifugal control interface is the limited control over centrifugal acceleration and deceleration settings. However, the changes are small between steps, and consistent with earlier observations by Richards et al. (28) in the Spinco Model E and by Hexner et al. (31) in a magnetically suspended equilibrium ultracentrifuge, we observed no convection when the rotor speed was changed with maximum acceleration or deceleration. To extend the possible practical applications, we wrote TOSE with optional initial conditions so that future rotor-speed schedules can be optimized for an ongoing experiment. This should facilitate the study of samples for which very little prior knowledge is available. At this point, it is easily conceivable that the rotor-speed schedule could be changed automatically, i.e., that real-time analysis of the experimental toSE data could be used to dynamically adjust the rotor-speed schedule and optimize information content while minimizing the equilibration time. Unfortunately, though, such an automated feedback from data analysis to centrifuge control is not currently possible due to existing limitations of the centrifugal control interface.

For given macromolecular species and given target equilibrium rotor speeds (which may be determined as described in Zhao et al. (8)), the most critical parameter in the toSE optimization is the maximally allowed overconcentration. The shortest equilibration times were found without constraints, but this may lead to 10- to 100-fold greater loading concentrations that transiently accumulate close to the centerpiece surface, which introduces the potential for undesired processes. Considerations for acceptable overconcentration would depend on the particular sample and on factors such as solubility, aggregation propensity, surface adsorption properties, and/or the lifetimes of complexes that may be formed at high concentrations. Importantly, we found that under common SE conditions, even a moderate overconcentration by 20–50% over the final equilibrium concentration could allow time savings by a factor of 3–5, although the time savings were less when overconcentration was completely avoided.

It is common practice to carry out SE at low temperature to minimize sample degradation. In many cases, the more rapid equilibration in toSE may allow the experiment to be carried out at 20°C instead. After factoring in the typical need for lower temperatures in SE, but not in toSE, the time savings under moderate overconcentration conditions would be increased from a factor of 3–5 to a factor of 5–8, and in the scenario of Fig. 1 B, without the overconcentration constraint, the equilibration times would be 4.5 h in toSE at 20°C vs. 45 h in standard SE at 4°C, i.e., a difference of a factor of 10. Our initial attempts to introduce temperature as a variable during the toSE experiment, to further expedite the initial migration, failed because convection counteracted sedimentation. Therefore, if toSE experiments are to be carried out at low temperature, the rotor loaded with the sample cells will have to be precooled and the temperature equilibrated before the start of the experiment. In this regard, it should be noted that it is critical to use the correct solution viscosity at the targeted temperature in the toSE calculation of the rotor-speed schedule. Similarly, toSE predictions are only correct for double-sector-shaped centerpieces, and not for the rectangular solution columns in six-channel centerpieces. Further, to obtain the c(s) distribution from the data regarding the approach to equilibrium, the experiment has to be performed using such centerpieces.

In toSE, as in SE, it is of the utmost importance to verify that equilibrium has actually been attained. This can only be shown empirically by assessing the pairwise difference of subsequent scans. Therefore, the final approach to equilibrium at the target rotor speed needs to be observed for several hours, and this process cannot be abbreviated without risking errors in the data analysis. Close-to-equilibrium distributions may already follow Boltzmann exponentials, with exponents that are typically too low in conventional SE and may be too high in toSE. In this study, to allow time for true equilibration at the target rotor speed, we chose to use overspeeding times that were (for standard column lengths) at least 3 h shorter than the predicted equilibration time, to enable observation of the final equilibration process with at least two sets of high-precision equilibrium scans 3 h apart. Although longer overspeeding periods will generally have the potential to decrease the equilibration time, this requirement for the observation of true equilibration sets a practical upper limit for the useful overspeeding time.

In summary, we have described the use of optimized time-varying centrifugal fields to significantly expedite SE experiments by at least a factor of 2 and up to a factor of 10. We believe this method will not only streamline instrument usage but, more importantly, also enable SE studies that previously have not been feasible due to the limited stability of many macromolecules (46,47). We previously showed how trace degradation in SE can lead to highly inaccurate estimates of equilibrium constants for a high-affinity interaction, and similar can be expected in studies of low-affinity systems (47). Therefore, toSE has the potential to both widen the range of applications and improve the accuracy of SE.

Author Contributions

J.M., M.M., and R.G. performed research and analyzed data. H.Z. and P.S. analyzed data, contributed analytical tools, and wrote the manuscript.

Editor: Catherine Royer.