Spatial Intensity Distribution Analysis Reveals Abnormal Oligomerization of Proteins in Single Cells

Abstract

Knowledge of membrane receptor organization is essential for understanding the initial steps in cell signaling and trafficking mechanisms, but quantitative analysis of receptor interactions at the single-cell level and in different cellular compartments has remained highly challenging. To achieve this, we apply a quantitative image analysis technique—spatial intensity distribution analysis (SpIDA)—that can measure fluorescent particle concentrations and oligomerization states within different subcellular compartments in live cells. An important technical challenge faced by fluorescence microscopy-based measurement of oligomerization is the fidelity of receptor labeling. In practice, imperfect labeling biases the distribution of oligomeric states measured within an aggregated system. We extend SpIDA to enable analysis of high-order oligomers from fluorescence microscopy images, by including a probability weighted correction algorithm for nonemitting labels. We demonstrated that this fraction of nonemitting probes could be estimated in single cells using SpIDA measurements on model systems with known oligomerization state. Previously, this artifact was measured using single-step photobleaching. This approach was validated using computer-simulated data and the imperfect labeling was quantified in cells with ion channels of known oligomer subunit count. It was then applied to quantify the oligomerization states in different cell compartments of the proteolipid protein (PLP) expressed in COS-7 cells. Expression of a mutant PLP linked to impaired trafficking resulted in the detection of PLP tetramers that persist in the endoplasmic reticulum, while no difference was measured at the membrane between the distributions of wild-type and mutated PLPs. Our results demonstrate that SpIDA allows measurement of protein oligomerization in different compartments of intact cells, even when fractional mislabeling occurs as well as photobleaching during the imaging process, and reveals insights into the mechanism underlying impaired trafficking of PLP.

Introduction

A quantitative description of protein interactions and organization is key to understanding cell signaling mechanisms, but measuring such interactions directly within intact cellular environments has remained a daunting challenge due to the molecular scale of these events and the light diffraction resolution limit of conventional optical microscopy. Standard in vitro methods used to study protein interactions typically involve the separation of proteins obtained by cell lysis, via gel electrophoresis and Western blot analysis, but these approaches ignore many aspects of protein organization within cells. Important local changes (e.g., within subcellular compartments) inside cells, involving a small fraction of the total protein expressed by these cells, can be diluted and missed by such averaging assays. Additionally, conventional biochemical approaches ignore much of the dynamics of molecular events within cells. Yet, changes in the oligomerization state of many classes of receptors are directly linked to their function and activation in cellular signaling (1–3), so the ability to follow such changes in space and time is a prerequisite to building accurate models that reflect the molecular mechanisms that regulate signaling. Furthermore, receptor protein distribution and clustering state vary spatially and temporally throughout the cell during intracellular trafficking, membrane residency, and finally internalization (turnover) from the plasma membrane. It is essential to be able to concurrently measure these processes in different cellular compartments and, ultimately, to measure the effect of a stimulus on the distribution of receptors and their interactions in a given compartment within intact cells.

Spatial intensity distribution analysis (SpIDA) (4–11) can measure protein oligomeric size (in subunit counts) and density distributions from the intensity information recorded in individual conventional laser scanning fluorescence microscopy images. SpIDA was previously used to quantify the density of spatially mixed monomeric and dimeric populations of receptors localized on the plasma membrane of intact cells. The method is based on fitting fluorescence intensity histograms obtained from regions of interest (selected within single images) to obtain density maps of fluorescent molecules and molecular aggregates along with their quantal brightness, which indicates their oligomeric state. Because distributions are measured from single images, this analysis can be applied to both live and chemically fixed cells and tissues (4,5,9).

SpIDA was previously applied to detect and follow the temporal activation of the epidermal growth factor receptors (4,5,10) and the heterodimeric structure of the metabotropic transmembrane receptors for γ-aminobutyric acid GABA_B receptor in the rat spinal cord (4). SpIDA was also used to quantify the receptor tyrosine kinase activation and transactivation by G-protein-coupled receptors (5–8) and to map the density of dimers of the K⁺Cl⁻ cotransporter, isoform 2 (KCC2), along the dendrites of neurons in culture as well as to compare the oligomerization states of the electrogenic sodium bicarbonate cotransporter NBCe1-A both in cells lines and in rat kidney (9).

SpIDA also provided what we believe to be the first insights into the organizational structure of Robo1, a large single transmembrane domain polypeptide and the prototypic member of the Robo receptor family of guidance receptors (10). More recently, SpIDA was compared with alternative techniques to examine the intracellular accumulation of CellTrace calcein red-orange (Life Technologies, Carlsbad, CA) in a colorectal adenocarcinoma cell line and bovine aortic endothelial cells (12), demonstrating that SpIDA is a user-friendly tool compatible with conventional confocal microscopy that can be rapidly applied to obtain quantitative information on intracellular concentration and kinetics of fluorophore uptake. It was also proposed to use SpIDA as a rapid prognostic tool that can be used on biopsy tissue (13), given its full compatibility with immunofluorescence. SpIDA also revealed new insights, to our knowledge, into the receptor quaternary structure of the serotonin 5-HT2C receptor (11). The serotonin 5-HT2C receptor was shown to be present as a mixture of monomers, dimers, and higher-order oligomers and that these serotonin 5-HT2C receptors became predominantly monomeric upon antagonist treatment. SpIDA indicated that the 5-HT2C receptor exists as mixtures of forms that are regulated in an antagonist-dependent manner.

In this article, we present an extension of SpIDA to analyze higher-order oligomers from fluorescence microscopy images. An important technical challenge faced by all fluorescence microscopy-based oligomerization measurement techniques is the fidelity of receptor labeling, where, ideally, every subunit is being labeled with a single emitting and detectable fluorophore. In practice, imperfect labeling, photobleaching, or intermittent emission (blinking) of the fluorophore introduces systematic errors, which biases the measured distribution of oligomeric states. For example, in a cellular system with uniform expression of tetramers, fractional labeling of the receptor subunits will entail the presence of fluorescent monomers, dimers, and trimers (respectively clustered with three, two, or one unlabeled subunit(s)) along with fully labeled tetramers that will each be detected with different probabilities. This labeling artifact will generate a discrepancy between the true underlying biological and the observed fluorescent oligomeric distributions. This phenomenon is not only present with immunocytochemical labeling, but can also be observed when using genetically encoded fluorescent proteins to reveal receptors, as it has been reported that ∼20% of fluorescent proteins misfold and do not emit any fluorescence (14,15). We present a correction in SpIDA for stochastic mislabeling artifacts, allowing unbiased measurement of the oligomerization state of receptors that are organized in higher oligomeric states.

We begin by describing the theoretical approach and explain how the technique can resolve different oligomerization mixtures even in the presence of complex distributions of receptors (e.g., higher-order oligomers). We then discuss the impact of mislabeling and photobleaching on the study of oligomerization and suggest a correction to circumvent this artifact. Finally, we use SpIDA to quantify proteolipid protein (PLP) trafficking in COS-7 cells. A large number of mutations in the human PLP gene lead to abnormal myelination and oligodendrocyte death in Pelizaeus-Merzbacher disease. These established gene mutations lead to abnormal protein cross links and result in defective protein trafficking and retention in the endoplasmic reticulum (ER) due to the formation of abnormal protein cross linkages (16,17). In this article, we apply the newly developed SpIDA algorithm to study the spatial distributions of wild-type PLP in single cells and compare the oligomerization states of a mutant protein (PLP^D202N) that accumulates in the ER. We found that a large significant population of tetramers accumulated in the ER for the mutant protein, while the normal oligomerization state was measured for the smaller fraction of the receptor population that reached the membrane.

Materials and Methods

Theoretical background: spatial intensity distribution analysis

In this section, a brief overview of spatial intensity distribution analysis (SpIDA) is given while the theory and derivation of SpIDA is explained in full detail in previous publications (4–7). The first step in SpIDA is the calculation of an intensity histogram from pixels within a region of interest (ROI) from a single fluorescence microscopy image of a cell (4,5). The intensity histogram of an image ROI is calculated by counting the number of pixels present for each intensity value or intensity bin within the selected ROI. The intensity of each pixel in a confocal laser scanning microscope (CLSM) image is the integrated fluorescence intensity collected and detected from fluorescence originating within the region of the sample excited by the laser beam focal volume (i.e., as defined by the optical point-spread function, PSF). For a standard CLSM with analog detectors, the intensity is not a photon count.

The pixel intensity histograms for different ROIs are then fitted with super-Poissonian distributions defined as the intensity distribution of randomly (Poisson) distributed particles in space convolved with the optical PSF of the microscope. Fitting parameters in the analysis are the densities of the underlying fluorescent molecules and their quantal brightness values. In SpIDA, the quantal brightness is defined as the average intensity unit collected over the whole effective volume of the PSF for a distinct fluorescent entity (monomer or oligomer). SpIDA was inspired by the temporal photon counting histogram method (18), but the key difference is that it is applied in the spatial domain, enabling measurements on subregions within single images collected on conventional fluorescence microscopes equipped with analog photomultiplier tube (PMT) detectors (but it does require characterization and correction of the detector noise response, see below).

The one-population SpIDA model describes imaged regions that contain particles with the same (i.e., uniform) oligomeric state (Eq. 1). The histogram fitting functions of SpIDA are numerically calculated in an iterative manner. The first step is to calculate the intensity (k) distribution probability when exactly one single emitter of quantal brightness ε is randomly positioned in the PSF-defined focal volume. Then, the intensity distribution probability ρⁿ(ε;k), where exactly n emitters, each of brightness ε, are randomly positioned in the PSF focus is determined recursively from ρ¹(ε;k), in n−1 iterations. In other words, the fluorescence intensity distribution of all possible configurations of n particles of quantal brightness ε, in the beam focal volume is calculated from ρ¹(ε;k).

The intensity distribution for a single population in the ROI, with on average N particles per focal volume and quantal brightness ε, can be then calculated by adding all the n-particle distributions, ρⁿ(ε;k), weighted by their respective probabilities of having n particles in the focus, assuming a Poisson distribution of particles in space with mean N (Eq. 1). Combining the probability of observing an intensity of fluorescence k when exactly n particles are present in the focal volume, ρⁿ(ε;k), and the probability of having exactly n particles in the focal volume (Poisson distribution poi(n,N)), one can recover the fitting function for one population SpIDA,

$$H\left(\epsilon ,N;k\right)={\sum }_n{\rho }^n\left(\epsilon ;k\right)\cdot poi\left(n,N\right)\text{with}{\rho }^0\left(\epsilon ;k\right)={\delta }_{k,0},$$ (1)

where δ_k,0 is the Kronecker delta function, which equals 1 if k = 0 and 0 otherwise. Using this model, an intensity histogram of a single population in a ROI can be used to recover its density and quantal brightness, assuming that the intensity is proportional to the number of photons emitted by each of the distinct moieties in the population. In reality, labeling and emission artifacts will lead to a distribution of measured quantal brightness value that influences the accuracy of SpIDA measurements (4).

Oligomer-populations mixtures

When two different oligomer populations are mixed within the same region in space, the total histogram simply becomes the convolution of the two individual distributions,

$$H^{2\text{pop}}\left({\epsilon }_1,N_1,{\epsilon }_2,N_2,A;k\right)=A\cdot H\left({\epsilon }_1,N_1;k\right)\otimes H\left({\epsilon }_2,N_2;k\right),$$ (2)

where A is the number of pixels in the ROI. Once the monomeric quantal brightness has been defined, Eq. 2 is used to analyze the samples (assuming a mixture of two oligomerization states). If only one oligomerization state is present, the fitting routine simply yields a negligible density value for the other oligomerization state. A simplification of this model can be used if the oligomerization states present in the sample are known a priori. For example, if a sample is composed uniquely of monomers and dimers, then Eq. 2 can be simplified by assuming that ε₂ = 2 ^∗ ε₁, which yields Eq. 3:

$$H^{2\text{pop}}\left({\epsilon }_{1,}{N}_1,N_2,A;k\right)=A\cdot H\left({\epsilon }_1,N_1;k\right)\otimes H\left(2\cdot {\epsilon }_{1,}{N}_{2,};k\right).$$ (3)

Similarly, this model can further be simplified by using a known control sample to measure the monomeric quantal brightness (4,5,7,19). In this case, Eq. 3 only contains two nonlinear fitting parameters, the density variables N₁ and N₂.

Similar to the two-population case, if three oligomer populations are present, the final histogram will be the convolution of the three individual population distributions:

$$H^{3\text{pop}}\left({\epsilon }_1,N_1,{\epsilon }_2,N_2,{\epsilon }_3,N_3,A;k\right)=A\cdot H\left({\epsilon }_1,N_1;k\right)\otimes H\left({\epsilon }_2,N_2;k\right)\otimes H\left({\epsilon }_3,N_3;k\right).$$ (4)

In practice, Eq. 4, with its seven variables, does not converge readily. But here again, if the oligomeric states of the populations composing the mixture in the biological sample are known, then the model can be simplified and accurate densities can be recovered for the three populations.

Effect of mislabeling in SpIDA

The phenomenon of subunit mislabeling will introduce a systematic error when measuring densities and oligomerization states by SpIDA if not considered. We assume here that the sample consists of a uniform population of oligomers, n_mer, and that each of the subunits in an oligomer has a probability p of being fluorescent (and hence emitting). A binomial distribution is expected as we assume that each subunit has an equal probability of being fluorescent (p). Then, the intensity histogram distribution of the oligomer population will simply be the convolution of oligomer contributions for integer increments of emitting (labeled) subunits from monomer up to n_mer,

$$H_p\left(n_{\text{mer}}\cdot {\epsilon }_0,N;k\right)=H\left({\epsilon }_1^{n_{\text{mer}}},N_1^{n_{\text{mer}}};k\right)\otimes \dots \otimes H\left({\epsilon }_{n_{\text{mer}}-1}^{n_{\text{mer}}},N_{n_{\text{mer}}-1}^{n_{\text{mer}}};k\right)\otimes H\left({\epsilon }_{n_{\text{mer}}}^{n_{\text{mer}}},N_{n_{\text{mer}}}^{n_{\text{mer}}};k\right),$$ (5)

where ${\epsilon }_l^{n_{\text{mer}}}=l\cdot {\epsilon }_0$ and $N_l^{n_{\text{mer}}}=\left(n_{\text{mer}}!/(l!\cdot \left(n_{\text{mer}}-l\right)!)\right)\cdot p^l\cdot {\left(1-p\right)}^{n_{\text{mer}}-l}N$.

The theoretical distribution for two or three oligomer population mixtures can be obtained by convolution as for Eqs. 2 and 4, but with replacement of the one-population distribution (Eq. 1) by the one-population histogram with mislabeling (Eq. 5).

Confocal microscopy imaging

All images were obtained with a No. FV300-IX71 (Olympus America, Melville, NY) CLSM with a 60× plan-apochromatic oil immersion objective (NA 1.4), using laser excitation with the 488 nm line of an Argon ion laser, a dichroic filter FV-FCBGR 488/543/633, and a BA510IF long-pass emission filter (Chroma Technology, Rockingham, VT). For each experiment, optimal laser power and PMT voltage settings were chosen to maximize signal while avoiding pixel saturation and minimizing photobleaching. The CLSM settings were kept constant for all samples and controls (laser power, filters, dichroic mirrors, polarization voltage, scan speed) so that valid comparisons could be made between SpIDA measurements from different images taken over the course of a given experiment. Acquisition parameters were always set within the linear range of the detector (as determined by calibration (4,7)).

Determination of analog detector signal broadening

Ideally, SpIDA measures the fluorescence intensity fluctuations of the true signal in the image to return information on the number of particles and their quantal brightness values. Therefore, it is important to consider only the fluctuations that originate from true fluorescence signal variations of the labeled proteins in the sample and exclude noise fluctuations inherent to the detector. Analog PMT detector variance can be empirically determined using either back reflection of the laser from a mirror placed at focus or a bright fluorescent sample (e.g., a solution containing an extremely high concentration of fluorophores or a commercial fluorescent slide). This determination must be done with the same collection settings (PMT voltage, filter sets, scan speed), which will be used for imaging measurements of the actual samples. By performing this empirical characterization, a Gaussian noise distribution can be obtained for each mean pixel intensity. Further details on the calibration protocol can be obtained from Godin et al. (4), Barbeau et al. (6), and Zakrys et al. (10).

Computer simulations

All of the simulated images were generated and analyzed with custom-written routines in the software MATLAB (The MathWorks, Natick, MA) using two toolboxes (Image Processing Toolbox and Optimization Toolbox).

For single-population simulations, N particles were randomly distributed across a two-dimensional matrix. More than one particle can occupy the same matrix element and each particle contributes a value of 1. The quantal brightness is defined as the mean number of intensity counts detected from a particle within a focal volume, so each value in this integer matrix was multiplied by the product of the particle brightness, ε, and the area of a disk of radius, ω₀, where ω₀ is the e⁻² radius of the Gaussian convolution function used in the simulations. The final image matrix was obtained by convolution with a Gaussian function of user set e⁻² radius, which simulated integration with a TEM₀₀ laser beam of radius ω₀ (simulating a Gaussian intensity profile PSF in two dimensions). If not stated otherwise, for the simulations, the monomeric quantal brightness was set to 20 iu and the e⁻² convolution radius to 3 pixels.

For simulations of mixed populations, single-population images of the same dimensions were independently generated with their corresponding densities and quantal brightness values, and then all images were convolved with the same Gaussian function. The image matrices were then summed to generate a single image matrix containing the mixed populations. To model real systems, detector shot noise was simulated by adding white noise to all simulation images. For every pixel in the image, we simulated noise with a Gaussian probability distribution centered at the pixel intensity 〈i〉 and with variance equal to 10 iu ⋅ 〈i〉 (4,7–9). This value was measured from the calibration of our confocal microscope under the experimental conditions used to acquire our images.

We simulated mislabeling in samples by assuming that each emitting point particle had an emission probability p. This operation was applied to the image matrix of particles followed by the Gaussian (PSF) convolution and the addition of noise, as described previously.

Image analysis

The ROI sizes for SpIDA analysis were carefully set by establishing an optimal tradeoff between sampling different subcellular compartments in the real samples (smaller ROI) and increasing the fluctuation sampling statistics (larger ROI) needed to obtain reliable results. The fitting procedure times varied from <1 to 10 s, depending on the model used and the bin size.

For PLP analysis in COS-7 cells, an intensity mask using the Otsu threshold (20) was used to segment and identify the endoplasmic reticulum and the cytoplasmic membrane regions within the images. A contiguity process using dilatation and erosion was applied for spatial consistency of the masks. Then, a three-population analysis including mislabeling was applied to each of the regions independently (the probability of labeling each receptor is set to p = 80%, if not stated otherwise, as determined in calibration experiments).

Glutamate receptor transfection of human embryonic kidney cells

Human embryonic kidney (HEK) cells were grown in cultures in MEM α Medium 1X (Cat. No. 12571; Gibco, Life Technologies), supplemented with 4 mM L-glutamine, 10% fetal bovine serum, 100 units/mL penicillin, 0.1 mg/mL streptomycin, and 4500 mg/mL D-Glucose. The cells were passaged twice per week, and maintained in a humidified, 5% CO₂ atmosphere at 37°C. Cells were transfected with GluR1/R2 subunits (glutamate receptor (GluR)) using Lipofectamine LTX (Cat. No. 508857; Invitrogen, Life Technologies) together with the corresponding plus reagent (Cat. No. 501787; Invitrogen, Life Technologies) as described by the manufacturer. Cells were plated in petri dishes with a bottom coverslip insert (Cat. No. 1.5; MatTek, Ashland, MA). The coverslips were precoated with poly-D-lysine (0.2 mg/mL in phosphate-buffered saline (PBS) 7.4, Cat. No. F7886; Sigma-Aldrich, St. Louis, MO) by adding 1.5 mL of the substrate solution to completely coat the bottom of a MatTek dish. Cells were fixed in 4% paraformaldehyde for 1 h and then rinsed twice in PBS before imaging.

PLP transfection of COS-7 cells

COS-7 cells were transfected to express PLP as described in Dhaunchak et al. (17). Cells were maintained on untreated tissue-culture dishes (Falcon; VWR, Radnor, PA) in DMEM with 10% fetal bovine serum, at 37°C in a 5% CO₂ atmosphere, with the medium changed every third day. For passaging cells, confluent plates were washed once with PBS, followed by a short trypsination with 0.05% trypsin-EDTA (Sigma-Aldrich).

Molecular cloning

The plasmid pPLP–EGFP was generated to encode a fusion of the enhanced green fluorescent protein at the C-terminus of PLP (16,17). The product was cloned into vector pEGFP–N1 using EcoRI/NotI sites.

DNA transfection

One day before transfection, COS-7 cells were seeded on poly-L-lysine-coated cover glasses at 50% confluency and transfected using either Fugene 6 (Roche, Indianapolis, IN) or Lipofectamine 2000 (Invitrogen, Life Technologies) according to manufacturers’ protocols. Cells were then fixed in 4% paraformaldehyde for 1 h and then rinsed twice in PBS before imaging.

Results and Discussion

Limits of SpIDA for a single population and for mixtures of monomer and dimers

The accuracy and precision of SpIDA for a single population and for a two-population mixture of monomers and dimers have been discussed previously in Godin et al. (4). Here, we focus on mixtures containing multiple populations. In summary, assuming reasonable signal/noise (∼3:1) for a single oligomer population and a mixture of monomers and dimers, if the image ROI is large enough to provide sufficient sampling of fluorescence fluctuations (∼50 beam-focus areas (BAs) or ∼6 μm² for our confocal microscope with a 1.4 NA objective), SpIDA can give accurate results (<20% error on all fit parameters). Autofluorescence can be assessed by imaging the sample without the fluorescent probe; however, for many applications, autofluorescence can be neglected (<5% error in a single population SpIDA fit) if the signal/background > 3 (4). This condition was met in the samples measured in this study.

Measuring three populations of oligomers in single cells

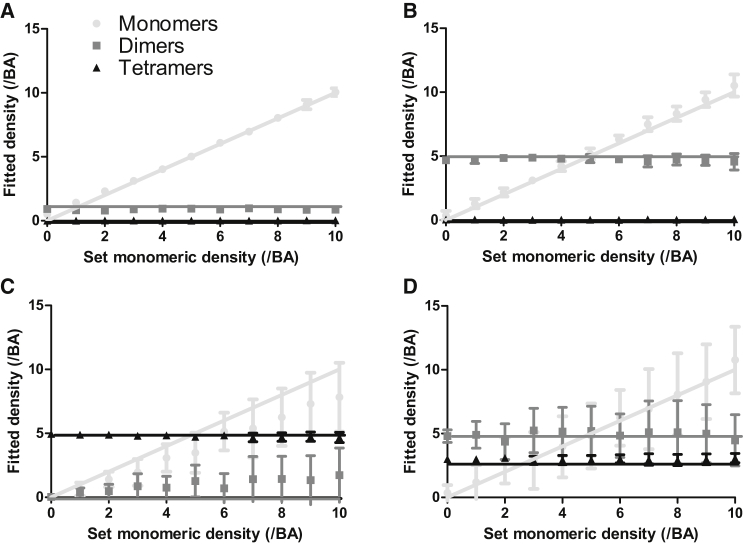
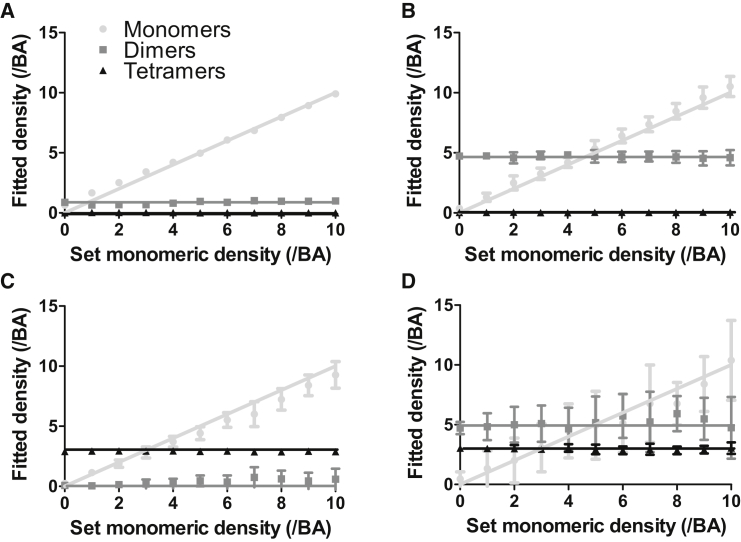
To test whether SpIDA can be applied to resolve three-population mixtures of oligomers, we generated large simulated images containing different numbers of dimers and tetramers and we varied the number of monomers. To generate realistic images, white noise was added to all simulated images (see Materials and Methods for details). To generate Fig. 1, we assumed that the oligomeric states of the populations present are known a priori (e.g., only monomers, dimers, and tetramers can be present) so only the population densities are fit in this case. We considered the assembly hierarchy scheme where monomers form dimers and then dimers group together to form tetramers because it is common in cell biology (e.g., Glutamate (21,22) and GABA_B (23) receptors). Fig. 1, A–C, shows that when we apply a three-population fitting model (Eq. 4) for cases where only two populations were actually present, SpIDA still converges to give reliable results (<20% error on all fit parameters), demonstrating that the analysis reveals whether an over-complete model is used (e.g., a three-population model when only two populations are present). However, as shown in Fig. 1, C and D, the results are not precise for the monomeric population, because the monomers in this case correspond to a small proportion of the total integrated intensity. Nevertheless, the accuracy is preserved; one only needs to acquire more data points in these cases to achieve good precision. The same explanation holds for the fit of the monomeric population in Fig. 1 D where the numbers of dimers and tetramers are higher than the number of monomers. For this reason, for each fitted distribution, it is important to consider the density-weighted contribution of each of the oligomer populations to the total intensity.

Figure 1.

Three-population SpIDA analysis. SpIDA analysis was applied to simulated images containing three distinct populations (monomers, dimers, and tetramers). Here, the results are for cases where we set the density of dimers (N2) and tetramers (N4) and varied the density of monomers (N1) in the image from 0 to 10 per BA. The results here were obtained using Eq. 4. (A) N2 = 1 dimer/BA, N4 = 0 tetramer/BA; (B) N2 = 5 dimers/BA, N4 = 0 tetramer/BA; (C) N2 = 0 dimer/BA, N4 = 5 tetramers/BA; and (D) N2 = 5 dimers/BA, N4 = 3 tetramer/BA. All the values in the graphs correspond to an average of 20 images. The lines correspond to the set values and the data points to the experimentally measured values. The ROI size was 500 × 500 pixels. The error bars correspond to SDs.

A single-population SpIDA fit model used on images in which both monomer-dimers are present will either fit a quantal brightness that is in between monomers and dimers or will inaccurately fit if the quantal brightness is fixed to that for either the monomer or dimer, indicating that another model should be used. However, applying the two-population SpIDA fit model with fixed quantal brightness (monomers and dimers) on images containing a single population of either monomers or dimers will produce an analysis that is still accurate and reveal the presence of just a single population. These three-population simulation results also demonstrate that SpIDA can still yields accurate results when mixtures of three oligomer populations are present in single images, if the signal/noise is sufficiently high (∼3:1 (4)) and there is sufficient spatial sampling in the ROI. Therefore, this more general model could be applied to all the two-population cases, providing a test for the presence of higher-order oligomers, while only increasing the computing time and data points requirements.

Nonfluorescent subunits in higher-order oligomers

An underlying assumption of SpIDA is that the oligomerization state is assumed to be proportional to the integrated fluorescence intensity per oligomer. In other words, if quenching between fluorophores on adjacent subunits is negligible and the detectors are in the linear regime, a dimer will be twice as bright as a monomer and, iteratively, an oligomer, made of n subunits (an n_mer), will be n-fold more intense than a monomer. Mislabeling of receptors or nonideal emission will always introduce a systematic perturbation because the integrated intensity will not represent the underlying subunit composition. This effect was previously demonstrated in studies of the oligomerization of ion channels using single-molecule-step photobleaching experiments (14,15). The effect of photobleaching of FPs labeling subunits contributes in an analogous manner to mislabeling, but in a time-dependent manner (24). Photobleaching can also have an impact on image correlation spectroscopy measurements and in certain cases can be corrected (25,26). It was elegantly shown that the effect on the degree of aggregation and cluster density of a sample evolves differently in an image time series undergoing photobleaching, depending on its oligomerization state, as the fraction of emitting fluorophores decreases (24). For a population of monomers, the recovered concentration will decrease while the degree of aggregation will remain constant as a function of time. Whereas, for a population of high-order oligomers, the recovered concentration will, to some extent, remain constant while the degree of aggregation will gradually decrease (24).

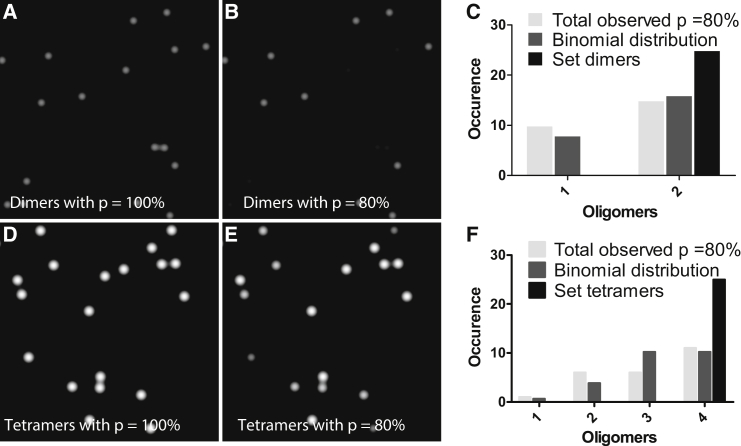
When studying higher-order oligomers with any biophysical fluorescence-based approach, nonfluorescent proteins (i.e., when a misfolded fluorescent protein does not emit) or proteins that are mislabeled (i.e., when the targeted protein is not labeled and revealed by a fluorescent probe) introduce a systematic error because only fluorescent/labeled species are observed and the true underlying distribution of subunits is not fully represented in the integrated signal. For a single population of dimers, some fluorescent monomers will be detected (Fig. 2, A–C) because some of the dimers have nonemitting subunits. Fig. 2 C shows the binomial distribution prediction for measuring monomers and dimers for the simulated image presented in Fig. 2 B. A binomial distribution is expected if the probability of any subunit being labeled is the same (p). We assume this to be the case in the remainder of the article. The correction to SpIDA functions to include mislabeling in the model is presented in Theoretical Background: Spatial Intensity Distribution Analysis, and can be summarized with Eq. 5.

Figure 2.

Effect of subunit mislabeling on the measured oligomeric distribution. Computer-simulated images showing the impact of mislabeling on sparse oligomers. Twenty-five dimers were randomly distributed in the image. Two cases are presented: (A) p = 100% particles labeling percentage; (B) p = 80% particle labeling percentage. The set oligomer distribution (A) and observed distribution when mislabeling occurs (B) are presented in (C). Computer-simulated images in which 25 tetramers are randomly distributed in the image are presented for p = 100% labeling (D) and p = 80% labeling (E). The set oligomer distribution (D) and the observed distribution when mislabeling occurs (E) are presented in (F). The monomeric quantal brightness was set to 20 iu, the e⁻² convolution radius was set to 50 pixels, and the ROI size was 1500 × 1500 pixels.

The phenomenon of subunit mislabeling will introduce a systematic error when measuring densities and oligomerization states by SpIDA if not properly accounted for and corrected. Assuming an incorrect mislabeling probability will introduce a systematic error on the measured density of each population that is, to first-order, proportional to the error on the assumed probability. Conversely, using the appropriate emission probability, p, enables correction for the nonemitting fluorophores and reveals the true underlying distribution of labeled molecules. As photobleaching is associated with a decrease in the probability p of being fluorescent, adjusting the p value along the time sequence, using the mean intensities of each image (i.e., $p\left(t=2\right)/p\left(t=1\right)={\langle i\rangle }_{t=2}/{\langle i\rangle }_{t=1}$), will compensate for photobleaching effects and, assuming sufficient signal, will provide accurate information on the real underlying distribution of labeled molecules.

Fig. 2 shows a computer-simulated example of randomly distributed dimers and tetramers with perfect labeling (Fig. 2, A and D) and with fractional labeling where p = 80% (Fig. 2, B and E). The corresponding distributions for the two cases are shown in Fig. 2, C and F.

Fig. 3 presents results from computer simulations to demonstrate the effect of fractional labeling on the detected distribution when only a single uniform oligomer population is present (e.g., only dimers, trimers, tetramers, or pentamers). However, it is possible to measure the labeling probability via SpIDA by using samples that are known to contain only a single uniform oligomer population. The recovered monomer and dimer distributions for a system with only true dimers present is shown in Fig. 3 A as a function of the subunit labeling probability p. This situation is conceptually analogous to photobleaching. As the fraction of fluorophores that are photobleached increases (i.e., p decreases), the amount of dimers that are seen as false monomers increases, which directly leads to an underestimation of the true oligomeric state of the system (Figs. 2, A–C, and 3 A). Similarly, if higher-order oligomers are mislabeled or photobleached (Fig. 2, D–F), the one-population SpIDA analysis (Eq. 4) will not provide the exact densities (Fig. 3 B) nor oligomeric states (Fig. 3 C), and the recovered values will be systematically underestimated.

Figure 3.

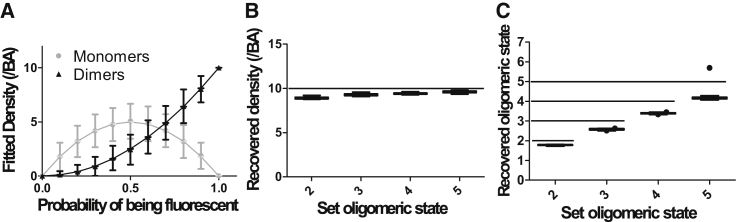
Effect of subunit mislabeling on SpIDA measurement of a uniform oligomeric state. (A) SpIDA results for simulated images containing only dimers as a function of labeling probability. Ten dimers where labeled with a subunit labeling probability p, and the distribution of observed fluorescent monomers and dimers was measured via SpIDA. This step was repeated 1000 times and the distribution of monomers and dimers as a function of the labeling probability is shown. The error bars correspond to SDs. The effect on the density (B) and quantal brightness (C) fits recovered with one-population SpIDA (Eq. 1) when only p = 80% of the oligomers are fluorescently labeled for different types of oligomers (n_mer = 2–5). Here, we deliberately applied the wrong one-population SpIDA model without accounting for mislabeling (i.e., p = 100% is forced in the fit). The images generated for those simulations were 250 × 250 pixels, the oligomer density was set to 10 oligomers/BA, and p = 80%. (Box and whiskers) Tukey method; (dot) outliers.

Measuring the labeling probability using SpIDA

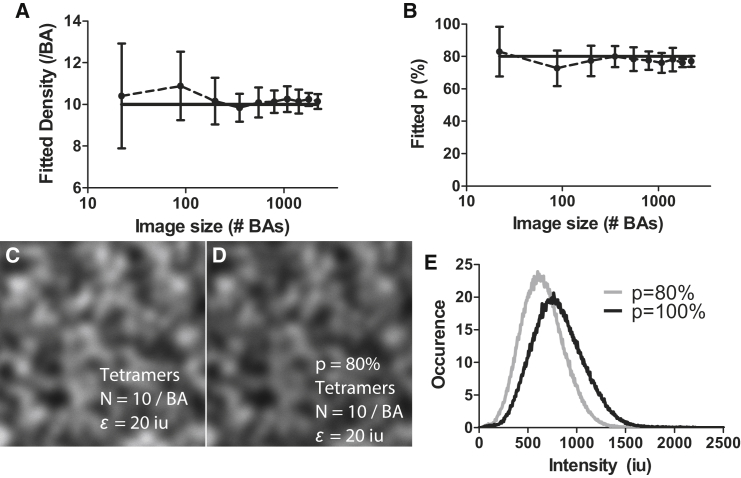
In the previous section, we showed the effect of mislabeling on the accuracy of SpIDA. Here, we now show that we can recover the density and the labeling probability from single images containing labeled species of known oligomeric state. For this, we generated computer-simulated images with 10 tetramers/BA with subunits randomly labeled with p = 80%. It can be seen in Fig. 4 that using one-population SpIDA, taking into account mislabeling (Eq. 2 with the mislabeling correction proposed in Eq. 5) on simulated images with varying size, it is possible to recover the set densities (Fig. 4 A) and the set labeling probability (Fig. 4 B), even if detector noise is present (see Materials and Methods). A precision of 20% can be obtained when analyzing images that have >100 BAs (∼12 μm²). Example images in which all subunits are labeled (Fig. 4 C) and with mislabeling (Fig. 4 D) are shown, along with their intensity histograms (Fig. 4 E). Our results suggest that, if one can prepare a sample with known fixed oligomers tagged with the label of interest (e.g., GFP), then the labeling constant p can be experimentally measured with SpIDA.

Figure 4.

Measuring densities and mislabeling probability by applying SpIDA to a single oligomer population. Twenty-five simulated images of varying size containing 10 tetramers/BA were generated to measure the accuracy of one-population SpIDA in the presence of mislabeling (Eq. 5). The set density (solid line), SpIDA recovered densities (A), set labeling percentage p = 80%, and measured p value (B) are presented as a function of the size of the image. The error bars correspond to SDs. Example images where all subunits are labeled (p = 100%) (C), and then mislabeled (p = 80%) (D), with the corresponding intensity histograms (E). The image size was 300 × 300 pixels.

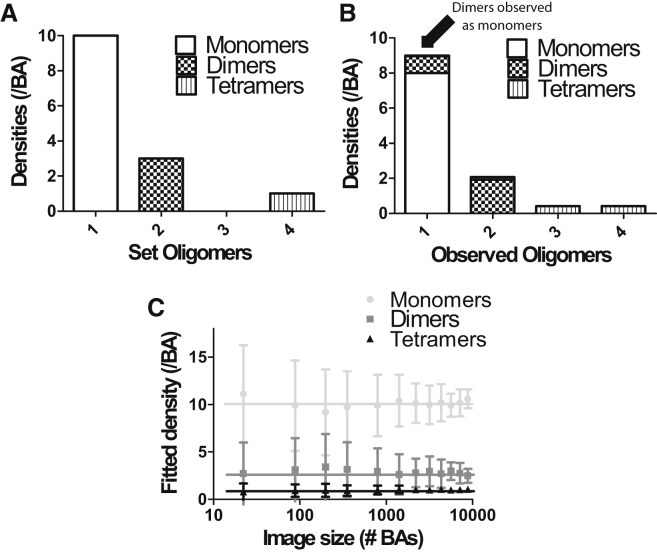
Measuring three-oligomer populations in single images including mislabeling

To verify that three-population SpIDA could accurately resolve a complex distribution of monomers, dimers, and tetramers in the presence of mislabeling, we simulated images of varying size containing 10 monomers/BA, 3 dimers/BA, and 1 tetramer/BA (Fig. 5, A–C). The effect of the mislabeling can be seen in Fig. 5, A and B. These simulations show that three-population SpIDA, using a measured labeling probability, accurately converges when there is mislabeling and that the precision improves as the ROI increases (Fig. 5 C).

Figure 5.

Effect of spatial sampling on measuring densities in images containing three population mixtures. Simulated images containing 10 monomers/BA, 3 dimers/BA, and 1 tetramer/BA were generated. The size of the images was varied to study the impact of spatial sampling on the recovered densities. The oligomer distributions when all (A) and when only p = 80% (B) of the subunits are labeled are shown. The recovered fit values for three-population SpIDA when there is mislabeling are presented in (C) as a function of the image size. In the fit function, the oligomer distribution (monomers, dimers, and tetramers) and the labeling percentage was set (p = 80%). The results presented here were obtained using Eq. 4. The error bars correspond to SDs.

Images formed of different densities of dimers and tetramers were generated to test the accuracy of three-population SpIDA in the presence of mislabeling (Fig. 6, A–D). The analysis was done for a range of monomer densities. Again, if only two populations are present, the three-population SpIDA model can still recover the set densities of the two populations present and indicates the absence of the third one (Fig. 6, A and B).

Figure 6.

Three-population SpIDA analysis with subunit mislabeling (p = 80%). SpIDA analysis was applied to simulated images containing three distinct populations (monomers, dimers, and tetramers) with 80% labeling of subunits. Here, the SpIDA results for many different cases where we set the density of dimers (N2) and tetramers (N4) and varied the number of monomers (N1) in the image from 0 to 10 per BA are shown. The results were obtained using Eq. 4 including mislabeling described in Eq. 5. (A) N2 = 1 dimer/BA, N4 = 0 tetramer/BA; (B) N2 = 5 dimers/BA, N4 = 0 tetramer/BA; (C) N2 = 0 dimer/BA, N4 = 3 tetramers/BA; and (D) N2 = 5 dimers/BA, N4 = 3 tetramers/BA. All the data points in the graphs correspond to averages of results from 20 images. The image size was 500 × 500 pixels. The error bars correspond to SDs.

This demonstrates that SpIDA can resolve the densities of mixtures of three-oligomer populations in the presence of mislabeling (Fig. 6 D) and that the fit parameter precision decreases for a population as a function of its decreasing density contribution.

As the number of distinct oligomer populations increases, the number of fitting variables necessarily increases and the fit model will not converge to unique solutions. For this reason, reducing the number of variables in a fit is essential for the accuracy of the analysis. For example, if only a fraction of the subunits forming a population of tetramers emits fluorescence, then fluorescent monomers, dimers, trimers, and tetramers will be detected and contribute to the resulting intensity histogram with different probability weights. Fitting for the densities of the monomers, dimers, trimers, and tetramers independently will not yield accurate results (five variables: four densities and one quantal brightness). However, by employing a simpler model that fits only for the number of tetramers and the probability that a single subunit will be fluorescent (three variables: one density, one quantal brightness and a subunit emission probability), the method can provide more accurate results. Therefore, we can also reduce the number of fitting variables when there is mislabeling for all of the cases previously discussed (Eqs. 1, 2, and 4).

Measuring higher-order oligomerization states with the single-population model

To experimentally assess the impact of subunit mislabeling on SpIDA measurements of higher oligomerization states in cells, we expressed the tetrameric (21) AMPA receptor (composed of 2 GluR1 and 2 GluR2 subunits) in HEK293 cells. Cells were transfected with different combinations of the receptor subunits with or without an mGFP label (the monomeric form of GFP (27)) to obtain samples with different distributions of fluorescent subunits: 2^∗(GluR1-GFP/GluR2), 2^∗(GluR1/GluR2-GFP), or 2^∗(GluR1-GFP/GluR2-GFP) (Fig. 7 A).

Figure 7.

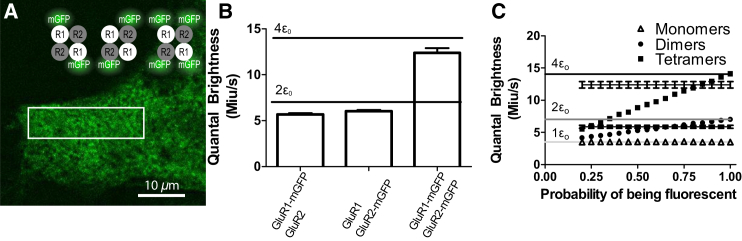
SpIDA analysis of tetrameric glutamate receptor (GluR). (A) A subregion of an image of a cell transfected with GFP-R1 and GFP-R2 plasmids. The image size is 1024 × 1024 pixels with pixel size of 0.092 μm. (Rectangle) A sample analyzed ROI. (B) Plot showing the mean fitted quantal brightness and the standard error for the three cases (GluR1-mGFP/GluR2 (N = 92), GluR1/GluR2-mGFP (N = 91), and GluR1-mGFP/GluR1-mGFP2 (N = 73)). For the case where R1-mGFP and R2-mGFP plasmids were transfected, the theoretical values for the quantal brightness of monomers, dimers, and tetramers are shown (green). Error bars = mean ± SE. (C) Graph showing the mean quantal brightness for an oligomer in which some of the GFPs are not fluorescent. The quantal brightness recovered for samples containing respectively only monomers (triangles), dimers (circles), and tetramers (squares) as a function of the probability that each GFP is nonfluorescent are present. Twenty-five simulations of 50 × 250 pi² with monomeric quantal brightness set to 20 iu and the e⁻² convolution radius was set to 3 pixels. The error bars correspond to SD. One-population SpIDA fit (Eq. 1) was used to fit those simulated images. The recovered fitted values for dimers and tetramers found in (B) are also shown. (Rectangle) Overlap of the simulated and experimental distributions. From this graph, we found a probability of 67 ± 7% (for dimers) and 84 ± 5% (for tetramers) of having a fluorescent GFP. The theoretical values for the quantal brightness of monomers, dimers, and tetramers for perfect labeling are also presented. To see this figure in color, go online.

We applied one-population SpIDA analysis (Eq. 1) to these samples. When only one of the two AMPA subunits was GFP-tagged, the measured quantal brightness obtained was close to two times that of the monomeric GFP control brightness, but 16% below the expected value for dimers (Fig. 7 B), corresponding to a labeling probability p of 67 ± 7%. The same value of quantal brightness was measured for both GluR1-GFP/GluR2 and GluR1/GluR2-GFP samples, indicating a preferred stoichiometry of 2:2, consistent with previous reports in Mansour et al. (28).

When both GFP-tagged subunits were expressed, labeling all four subunits in an oligomer, the quantal brightness measured was nearly four times that of the monomeric control GFP brightness (28), but 12% below the expected value for tetramers (Fig. 7 B), which corresponds to a labeling probability p of 84 ± 5%. The difference between the measured and expected theoretical brightness values for dimers and tetramers is unlikely due to quenching or energy transfer between GFPs, because previous experiments on a similar channel expression system showed that step-photobleaching of individual GFPs within tetrameric ionotropic receptors occurred with constant intensity drops independent of the number of remaining unbleached GFPs (14). The variability between the two experimental paradigms detailed here could be explained by experimental errors resulting from differences in maturation in the ER due to the additional GFP tags (two versus four tags) or differences in pre-photobleaching. Nevertheless, the differences obtained between the measured and theoretical values are in agreement with what is expected given a 15–25% proportion of nonfluorescent GFPs as previously reported in Ulbrich and Isacoff (14) and Durisic et al. (15).

Impaired trafficking of PLP is linked to its oligomerization state in the ER

We next applied SpIDA to a biological model involving protein oligomerization, namely the proteolipid protein (PLP). A large number of mutations in the human PLP gene, encoding the major integral membrane protein of central nervous system myelin, leads to abnormal myelination and oligodendrocyte death in Pelizaeus-Merzbacher disease (OMIM No. 312080). A major subgroup of Pelizaeus-Merzbacher disease mutations that map to the extracellular loop region of PLP leads to the failure of oligodendrocytes to form appropriate intramolecular disulfide bridges. This leads to abnormal protein cross links and retention of PLP protein in the ER (16,17). As most PLP mutations are lethal, they are commonly studied using cell lines where an exogenous PLP gene is expressed. Misfolded proteins in the ER can induce the unfolded protein response, which includes ER growth and transcriptional activation of genes encoding chaperones. In mammalian cells, unfolded protein response can also trigger apoptosis (29). Using Western blots of whole cells, Harding et al. (29) found that the PLP protein is mostly present in monomeric and dimeric forms but also noticed the abnormal presence of a band that would correspond to tetramers for some of the mutations (17). We studied the PLP^D202N mutation, which is located in the extracellular loop 2 of the protein, critical for folding. A large proportion of this mutant protein failed to reach the plasma membrane, and accumulated in the ER in a higher oligomer form (16,17).

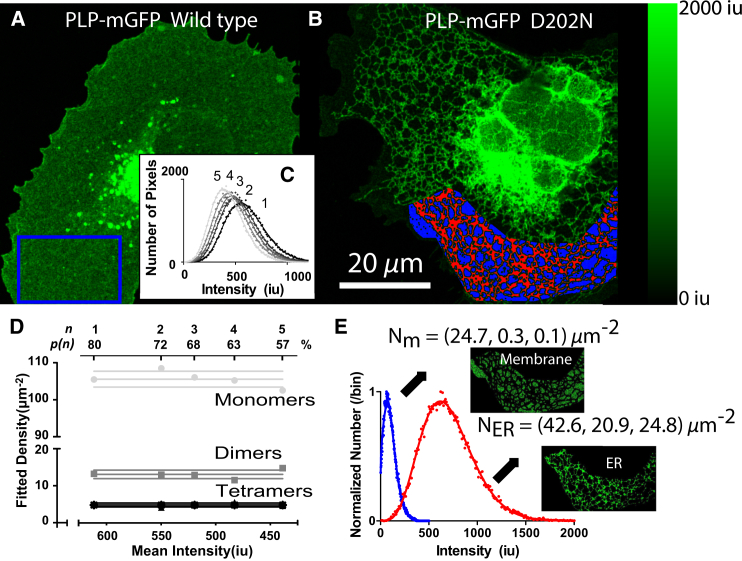
To compare the oligomerization state in intact cells, we measured the state (due to protein cross linking) of the PLP protein in COS-7 cells expressing either the wild-type protein PLP^WT or the D202N mutant protein, both fused to mGFP. We first measured the monomeric brightness of mGFP to use as a standard in our SpIDA analysis. For this, we transfected COS-7 cells with mGFP fused with a farnesyl group (mGFP-f) that targets it to the plasma membrane (27). We then used a one-population model (Eq. 1) to recover the quantal brightness. We obtained 3.9 ± 0.1 Miu/s (Miu/s: 10⁶ intensity units per s) and set that as the monomeric population quantal brightness for the rest of the analysis. For this last step, we corrected for the intensity broadening due to inherent noise of the analog photodetector as described in previous publications (4,5,7–9). As the analog detector noise calibration depends on many variables (dwell time, PMT voltage, scan speed, temperature, etc.), it was characterized for each set of imaging parameters.

Examples of images acquired for wild-type and mutant PLP are shown in Fig. 8, A and B, respectively. For this analysis, we assumed that initially the emission probability for each fluorescent protein was p = 80% as indicated in previous published reports for GFPs (14) and confirmed by our results of GluR1-mGFP/GluR1-mGFP2. As previously mentioned, an error in this estimate leads to a linear error in the measurements (e.g., a 10% error on p leads to 10% error in the fitted densities). For the wild-type, whole subregions were analyzed using three-population SpIDA with mislabeling correction (Eq. 4 with the mislabeling correction proposed in Eq. 5). To test the effect of photobleaching on the three-population SpIDA analysis, a confocal time series of five images was acquired. The fluorescence intensity decreased by roughly 30% during the whole imaging process. We analyzed each acquired image with SpIDA (Eq. 4 with the mislabeling correction proposed in Eq. 5) by iteratively adjusting the emission probability, p, using the mean intensity of each image $p\left(n\right)=80\%\cdot \left({\langle i\rangle }_n/{\langle i\rangle }_1\right)$. The intensity histograms of the selected region in Fig. 8 A for the five images are presented in Fig. 8 C with the corresponding fits. The SpIDA results of the cell region shown in Fig. 8 A as a function of time are presented in Fig. 8 D. As expected, when adjusting for the appropriate p value, the recovered densities for each oligomeric state, as a function of the image number n, remain constant within error. This suggests that SpIDA, together with the mislabeling correction presented, can potentially be used to measure the evolution of oligomeric states of complex mixtures in single cells, even in the presence of unavoidable photobleaching, if the bleaching rate can be accurately followed by calculating intensity ratios through the time series.

Figure 8.

Impaired trafficking of PLP. Example images of wild-type PLP (A) and PLP with the mutation D202N (B). Images are 1024 × 1024 pixels with pixel size of 0.058 μm with a pixel dwell time of 9.2 μs. Selected rectangle regions for the three-population SpIDA with mislabeling analysis are also shown. In (B), the mask of the endoplasmic reticulum is presented (red) and the membrane mask (blue). Five consecutive images of the cell presented in (A) were acquired. (C, Inset) The histograms and corresponding fits of the region that were presented in (A). The fit values for the first image membrane analysis of the cell expressing wild-type PLP was 106 monomers/μm², 13.3 dimers/μm², and 5.1 tetramers/μm². Along the time trace, the set value of p for the nth image SpIDA analysis was adjusted to compensate for photobleaching $\left(p\left(n\right)=p\left(1\right)\cdot \left({\langle i\rangle }_n/{\langle i\rangle }_1\right)\right)$. SpIDA results compensating for photobleaching are presented in (D). For each oligomer, the three lines correspond to the mean ± SD. The two histograms from masked subregions of cell in (B) are shown in (E). (Insets) Masks of the bright region (ER) and dim region (membrane). The fit values for the membrane analysis were 24.7 monomers/μm², 0.3 dimers/μm², and 0.1 tetramers/μm². The fit values for the ER analysis were 42.6 monomers/μm², 20.9 dimers/μm², and 24.8 tetramers/μm². To see this figure in color, go online.

For the mutant protein, there is a clear distinction between the ER and membrane compartments. We used a threshold-based algorithm to separate the two compartments in the images: we forced contiguity to ensure that isolated single pixels were not present in either of the masks. After segmentation, we removed the transitions between the two masks by eroding both masks, which allowed us to obtain two true super-Poissonian distributions that are not clipped around the set threshold value. Examples of the threshold procedures and the fit of each mask region are presented in Fig. 8, B and E.

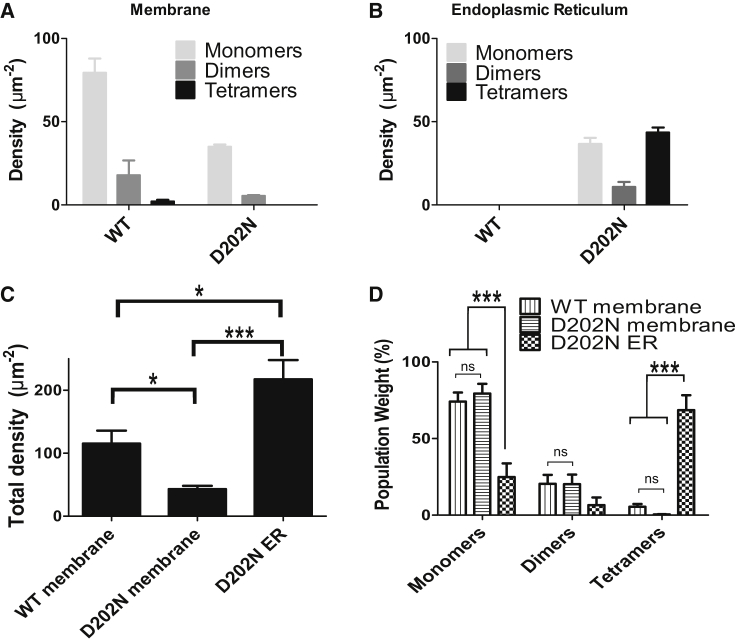
The results obtained using a three-population SpIDA for the membrane and the ER are shown in Fig. 9, A and B, respectively. The results reveal a different oligomerization state of PLP protein in the ER for the mutant compared to that in the membrane. Fig. 9 C shows a significant decrease in the total density of proteins that reach the membrane for the mutant (p_t-test = 0.035) with a significantly higher density retained in the ER compared to the wild-type (p_t-test = 0.047). A more detailed analysis of each population reveals that there is no significant difference between the distributions of the wild-type and the mutant protein in the membrane for monomers (Fig. 9 D). Within the ER, a significant population of tetramers for the mutant is observed (Fig. 9 D) (p_t-test < 0.001). Together with the dominant tetramer population, high densities of monomers and dimers were detected in the analysis of the ER region. Given the resolution limits of optical microscopy (30) in the axial direction, we cannot be certain that those monomers and dimers are really part of the ER as they could correspond to portions of the plasma membrane lying just below the ER region. Subtracting the distributions measured at the plasma membrane to the analysis obtained from the ER masked region reveals that the PLP proteins retained in the ER are virtually all present as tetramers. Our findings are in agreement with those in previous reports using traditional biochemical methods that involve extraction and isolation of cellular components (16,17), but here SpIDA allowed quantification of the impact of this mutation on protein oligomerization in different subcellular compartments in single intact cells using a nondestructive imaging method.

Figure 9.

Impaired trafficking of PLP from the ER is linked with its oligomerization state. The results for 11 cells for both the wild-type and the D202N mutation were analyzed by SpIDA and the results are shown in (A) for the wild-type (34 subregions) and in (B) for the D202N mutation (18 subregions). (C) A plot of the total protein density for all the cases studied. (D) The weight of each oligomeric population for the different cell compartments studied. For (C) and (D), dimers and tetramers have, respectively, two and four times the weight of the monomers (total protein density = 1 ^∗N1 + 2 ^∗N2 + 4 ^∗N4). The error bars correspond to mean ± SE. A two-tailed t-test was applied to every meaningful pair: ^∗p_t-test < 0.05; ^∗∗p_t-test < 0.01; ^∗∗∗p_t-test < 0.001; and ns, no significant difference.

Conclusions

In this article, we showed how SpIDA can be used to concurrently map the distribution and oligomerization state of receptors in different compartments of intact cells, even in the presence of mislabeling or nonfluorescent proteins. Using computer simulations, we set the basis for interpretation and determined the limits of this approach. We first validated the approach and showed that the new SpIDA algorithm permitted measurement of the mislabeling/emission fraction for GFPs in single cells when applied to the AMPA receptor system where we have a priori knowledge of the oligomerization distribution. We then applied the method to analyze human PLP, where mutations of this protein lead to a pathophysiology of abnormal myelination and oligodendrocyte death. Using SpIDA, we showed, quantitatively within intact cells, that the impaired trafficking was linked to retention of the protein in the ER and that the proteins were mainly present in a tetrameric state in the ER. Interestingly, there was no measured difference in oligomerization states in the distribution of receptors that reached the membrane. For the first time to our knowledge, we provide a quantitative measure of this abnormal protein retention in single cells. Such analysis could ultimately lead to a better understanding of protein oligomerization in disease phenotype and help in studying drug treatment efficacy.

Author Contributions

A.G.G., B.R., Y.D.K., and P.W.W. planned the research; A.G.G. and B.R. performed the experiments; A.G.G., B.R., and L.P.-T. contributed analytic tools; A.G.G. and B.R. analyzed data; and A.G.G., B.R., L.P.-T., T.E.K., Y.D.K., and P.W.W. wrote the article.

Editor: Christopher Yip.