Abstract
The nucleus has a smooth, regular appearance in normal cells, and its shape is greatly altered in human pathologies. Yet, how the cell establishes nuclear shape is not well understood. We imaged the dynamics of nuclear shaping in NIH3T3 fibroblasts. Nuclei translated toward the substratum and began flattening during the early stages of cell spreading. Initially, nuclear height and width correlated with the degree of cell spreading, but over time, reached steady-state values even as the cell continued to spread. Actomyosin activity, actomyosin bundles, microtubules, and intermediate filaments, as well as the LINC complex, were all dispensable for nuclear flattening as long as the cell could spread. Inhibition of actin polymerization as well as myosin light chain kinase with the drug ML7 limited both the initial spreading of cells and flattening of nuclei, and for well-spread cells, inhibition of myosin-II ATPase with the drug blebbistatin decreased cell spreading with associated nuclear rounding. Together, these results show that cell spreading is necessary and sufficient to drive nuclear flattening under a wide range of conditions, including in the presence or absence of myosin activity. To explain this observation, we propose a computational model for nuclear and cell mechanics that shows how frictional transmission of stress from the moving cell boundaries to the nuclear surface shapes the nucleus during early cell spreading. Our results point to a surprisingly simple mechanical system in cells for establishing nuclear shapes.
Introduction
The nucleus, the largest organelle in mammalian cells, has a smooth, regular appearance in normal cells. However, nuclear shape becomes altered in a number of pathologies such as cancer (1–5) and in laminopathies (6–9). The control of nuclear shapes for cells is particularly important because nuclear shape may directly control gene expression (10–12). Because the nuclear envelope binds to chromatin and organizes the genome spatially (13–16), tuning nuclear shape may be a mechanical mechanism for controlling access of transcription factors to chromatin, and thereby gene expression.
How the cell shapes the nucleus is not understood. Given the high rigidity of the nucleus, significant and dynamic changes in nuclear shape are expected to require forces that far exceed thermal forces in the cell. Such forces likely originate in the cytoskeleton, which is known to link to the nuclear surface through the LINC (linker of nucleoskeleton to cytoskeleton) complex (17–19). Candidates for shaping the nucleus include microtubule motors that can shear the nuclear surface (20,21) and intermediate filaments that can passively resist nuclear shape changes by packing around the nuclear envelope or transmitting forces from actomyosin contraction to the nuclear surface (22,23). The actomyosin cytoskeleton that can push (24), pull (25,26), or shear and drag the nuclear surface (27,28) is also assumed to be a significant component of the nuclear shaping machinery in the cell.
In this article, using a combination of experiments to disrupt the cytoskeleton and the LINC complex, and mathematical modeling and computation, we show that the motion of cell boundaries drives changes in nuclear shapes during cell spreading. Our results point to a surprisingly simple mechanical system in cells for establishing nuclear shapes.
Materials and Methods
Cell culture, plasmids, and drug treatment
NIH 3T3 fibroblasts were cultured in Dulbecco’s modified Eagle’s medium (DMEM) with 4.5g/L glucose (Mediatech, Manassas, VA) supplemented with 10% donor bovine serum (DBS, Gibco, Grand Island, NY) and 1% Penicillin Streptomycin (Mediatech). Mouse embryonic fibroblasts (MEFs) were cultured in DMEM, supplemented with 10% DBS. All cells were maintained at 37°C in a humidified 5% CO2 environment with passage at 80% confluence. For microscopy, cells were transferred onto 35 mm glass-bottom dishes (World Precision Instrument, Sarasota, FL) treated with 5 μg/ml fibronectin (BD Biosciences, San Jose, CA) at 10% confluence. Transient transfection of plasmids into cells was performed with Lipofectamine 2000 reagent (Life Technologies/Invitrogen, Carlsbad, CA) in OPTI-MEM media (Life Technologies/Invitrogen). For drug treatment studies, Y-27632 (EMD Millipore, Billerica, MA), Blebbistatin (EMD Millipore), or ML-7 (Sigma-Aldrich, St. Louis, MO) was added to the cells for inhibiting myosin activity at concentrations of 25, 50, and 25 μM, respectively. Nocodazole or Colcemid (Sigma-Aldrich) was used to disrupt microtubules at a concentration of 0.83 and 0.27 μM, respectively. To disrupt F-actin polymerization, cells were treated with 2 μM Cytochalasin D (Biomol, Plymouth Meeting, PA) and 5 μM Latrunculin A (Cayman Chemical, Ann Arbor, MI).
Cell spreading and trysinization assay
In the cell spreading assay, cells were trypsinized and then seeded onto fibronectin-coated glass-bottomed dishes. They were next incubated at 37°C in 5% CO2 for varying times and then fixed with 4% paraformaldehyde for 20 min. For myosin inhibition and disruption of F-actin and microtubule, the cells were pretreated with the appropriate dose of drug for 1 h, trypsinized, and resuspended in cell culture medium containing the same dose of drug. They were next seeded in the presence of the drug for varying time before fixation. In other drug treatment experiments, cells were allowed to grow on fibronectin-coated glass-bottom dishes for 24 h. They were then incubated with drug-containing medium for 1 or 2 h, after which the cells were fixed and stained. In the trysinization assay, cells were transfected with green fluorescent protein (GFP)-histone H1.1 and RFP-LifeAct (Ibidi, Verona, WI), and cultured on fibronectin-coated glass-bottom dishes for 24 h. After placing the dish onto the microscope stage, the culture medium was removed and the dish was washed once very gently with phosphate buffered saline (PBS). Then 0.25% (w/v) trypsin (high concentration) or 0.08% (w/v) trypsin in serum-free medium (low concentration) were added to detach the cells from the substratum.
Fixation and immunocytochemistry
Cells were first fixed with 4% (m/v) paraformaldehyde (Electron Microscopy Sciences, Hatfield, PA) for 20 min and then mounted with ProLong Gold Antifade Mountant (Life Technologies). To visualize F-actin and nuclei, the fixed cells were incubated with 1:40 Alexa Fluor 488 phalloidin (Life Technologies) and 1:100 Hoechst 33342 (Life Technologies) for 1 h at room temperature, respectively. To immunostain microtubules, cells were first treated with microtubule extraction buffer containing 0.5% (m/v) glutaraldehyde, 0.8% formaldehyde, and 0.5% Triton X-100 in PBS for 3 min before fixing with 1% (m/v) paraformaldehyde for another 10 min. Then a freshly prepared 1% (w/v) sodium borohydride in PBS solution was added to the cells for 10 min followed by blocking in 1% (m/v) bovine serum albumin in PBS. The cells were then incubated in 4°C overnight with rabbit polyclonal antibody to α-tubulin (1:1000, Abcam, Cambridge, MA) in 1% bovine serum albumin containing solution, washed with PBS and then incubated with Goat Anti-Rabbit IgG (H+L) antibody (1:500, Life Technologies) at room temperature for 1 h.
Protein silencing
Short-hairpin RNAs targeted to SUN2 (5′-tcggatcttcctcaggctatt-3′), Nesprin-2G 3′UTR (5′-gcacgtaaatgacctatat-3′), or Luciferase (5′-gtgcgttgttagtactaatcctattt-3′) were PCR and cloned into retroviral plasmid vector. 293T cells were transfected with the plasmid and pseudotyped envelope proteins to make virus by calcium phosphate transfection. Viruses were harvested 24 h after transfection. Then NIH 3T3 cells (0.5 × 105 cells/12 well) were infected by virus (0.6 ml virus) with 4 μg/ml polybrene and replated the second day. Cell culture media were changed to DBS DMEM overnight before cell spreading assay.
Western blotting
Transfected samples were harvested with 1X Laemmli sample buffer and boiled at 95°C for 10 min. Amersham Protran Premium 0.2 NC (10600004 GE Healthcare, Little Chalfont, UK) membrane was used for protein transference. Primary antibodies to probe proteins of interest in Western Blot were rabbit anti-SUN2, rabbit anti-Nesprin-2G (28), and mouse anti-GAPDH (clone 6C5, Life Technologies). LI-COR IRDye 680RD donkey antirabbit IgG (926-68073) and IRDye 800CW donkey antimouse IgG (926-32212) were used. Signals were detected by Odyssey LI-COR system (LI-COR Biosciences, Lincoln, NE). Images were processed by ImageJ (NIH).
Microscopy and image analyses
Fixed cells were imaged on a Nikon A1 laser scanning confocal microscope system (Nikon, Melville, NY) with 60×/1.40NA oil immersion objective. The live cell imaging was conducted on the same system within the environment of 37°C and 5% CO2. For measuring the nuclear height, z-stacks were taken at an interval of 0.3 μm and the x-z view projections were reconstructed using the NIS Elements application (Nikon). The maximum projection intensity analysis was applied to the x-z images of the stained nucleus, and the top and bottom edges of the nucleus were determined with the full width at half maximum (FWHM) technique (29) in MATLAB (The MathWorks, Natick, MA). The height was calculated as the distance between the top and bottom nuclear edge. Nuclear x-y dimensions (major and minor axis) were measured using ImageJ. The aspect ratio was calculated as the height divided by the length of the major axis in the x-y plan. The nuclear volume measurements were performed using Volocity Demo (Perkin Elmer, Akron, OH).
Computational model for nuclear deformation during cell spreading
Constitutive model for cytoskeletal network stress
The assumed constitutive equation for the stress tensor in the network phase of the cytoplasm is as follows:
| (1) |
where I is the unit dyadic, is the rate-of-strain tensor, and and are viscosity parameters. Equation 1 models the cytoskeletal network as a compressible contractile network. Network density changes, which may affect these properties, are assumed to equilibrate by local assembly/disassembly over the slow timescale of cell spreading; therefore, no continuity equation for the network density is required. Because network volume is not locally conserved, Eq. 1 reflects both shear and expansion/compression strains. If the strains caused by both modes of deformation have the equivalent resistances, then we can assume ∼0, reducing Eq. 1 to a single viscosity parameter . In linear elasticity, this is analogous to assuming Poisson’s ratio is zero such that the Young’s modulus (a measure of longitudinal stiffness) equates to twice the shear modulus (a measure of shear stiffness).
The longitudinal transmission of normal stress to a surface because of distant moving boundary is an important property of Eq. 1 that is relevant to our model for cell spreading. To illustrate this, consider first a one-dimensional case of a contracting network that is fixed at one end and moving with velocity V at a distance (i.e., ). The stress balance in the x-direction is as follows:
| (2) |
Applying the boundary conditions yields the following velocity field:
| (3) |
as well as the following stress field:
| (4) |
which is uniform in this case. Hence, noting the second term in Eq. 4, translating the one boundary at at speed transmits an additional stress to the surface at because of longitudinal friction, which is positive for expansion , and negative for compression .
Now consider a spherical cell of radius with a nucleus of radius , under the assumption of spherical symmetry, the stress balance in the cytoplasm is as follows:
| (5) |
where
| (6) |
Now assume that new network is assembled at the cell membrane and moves centripetally with speed , and allow the cell radius to expand at speed V (ignoring for now any volume constraints). Substituting Eqs. 6 into Eq. 5 and applying the boundary conditions, and yields the following r-velocity field:
| (7) |
Equation 6 then provides the following rr-component of the stress tensor:
| (8) |
such that stress of the nucleus surface is as follows:
| (9) |
(In the small gap limit, , Eqs. 7 and 8 become equivalent to Eqs. 3 and 4.) Therefore, similar to the one-dimensional case, the net tensile stress on the nucleus is increased by movement of the cell boundary to expand the network, but it is also reduced by assembly of network at the membrane and the resulting centripetal flow, which causes compression of the intervening network. In this way, the movement of the cell boundary and network assembly at the cell membrane can modulate the stresses on the nuclear surface. In general, the nucleus will tend to distort to follow the changes in cell shape and will follow the flow field generated by network assembly at the membrane. This is the basis for our model for nuclear shape changes during cell spreading.
Model for cell mechanics
We apply a simple mechanical model of the cell that takes the following into account: 1) the resistance of the nucleus to volume compression/expansion; 2) resistance of the nuclear surface to area expansion; 3) tension of the cell membrane; and 4) friction because of the centripetal flow of network tangent to the adhesive substratum. The network normal stress on the nuclear surface is balanced by the nuclear internal tension (or pressure when < 0) because of its resistance to volume changes, and the nuclear surface tension , because of its resistance to surface area expansion. The internal nuclear tension is modeled as follows:
| (10) |
where K is the bulk compressibility and is the unstressed volume. The surface tension of the nucleus is expected to depend on strained surface area of the nuclear lamina A above the unstressed area . We note that surface area undulations are evident in cross sectional images of nuclei, indicating roughly 20% to 40% excess area. Therefore, to account for the energy associated with smoothing the nuclear lamina, we estimated using the following equation, which is normally applied to calculate vesicle surface tension accounting for thermal undulations (30):
| (11) |
for , where is the area extensional modulus of the nuclear lamina, is its bending modulus of the lamina, and is a parameter that can be considered the magnitude of the energy driving the undulations (equal to —Boltzmann’s constant multiplied by temperature—for undulations driven by thermal energy). In this equation, the first logarithmic term dominates at low area expansion (low lamina tension), whereas the second term dominates at high area expansion. Assuming a value of ∼100 (Boltzmann’s constant multiplied by temperature) yields excess area in the observed range, which is reasonable noting intracellular energy fluctuations tend to be on the order of 100-fold larger that thermal fluctuations (31).
Except for the adhesive substratum, tangential traction stresses on cell and nuclear membrane surfaces are assumed negligible (i.e., slip boundary conditions). The normal stress exerted on the cell membrane is assumed to be balanced by the cell’s internal hydrostatic pressure (assumed uniform throughout the cell and nucleus) and the stress because of membrane tension . Because of the high cytoplasmic osmolality, cells are resistant to volume changes under typical cellular stresses, hence simulations were performed under the constraint of constant cell volume, maintained by varying .
For the boundary at the substratum, network flow at the substratum is assumed to exert a tangential stress vector equal to , where is the network velocity tangential to the substratum. The limit represents the case of perfect adhesion, such that (no-slip boundary condition). In either case, it is assumed there is no network flow in the direction normal to substratum.
To account for cortical actin assembly at the cell membrane, the net boundary velocity is increased by the actin assembly speed directed normal to the surface, except near the substratum contact boundary, where assembly occurs with speed directed tangential to the substratum. The net local velocity of the cell membrane is therefore equal to the difference between the network assembly velocity and the retrograde flow velocity.
Model parameters
Parameter estimates
A list of parameters used in the simulations is shown in Table 1. It should be emphasized that key qualitative conclusions from the model—network flow-driven translation of the nucleus to the surface, nuclear flattening resulting from cell spreading rather than network tension—do not strongly depend on several parameter values, as noted below. Values for the nucleus area modulus and nuclear bulk modulus were obtained from measurements by Dahl et al. (32), with the latter parameter value calculated from their measured osmotic resistance to volume expansion. Values for the membrane tension vary widely from 0.01 to 0.3 nN/μm (33,34), so a midrange value of 0.1 nN/μm was used (the quantitative predictions depend only weakly on the value of this parameter). The network assembly speed at the contact boundary was estimated from the observed initial speed of cell spreading (0.5 μm/min). The assembly speed of network at the cell cortex is not known, but we show results for two cases: and , to demonstrate that cytoskeleton assembly and resulting flow is necessary for initial translation and flattening of the nucleus against the surface. The value of network viscosity was estimated from the literature (35). The contractile stress could be estimated from Eqs. 9 and 10, noting that volume was ∼50% reduced on myosin inhibition. If is assumed to be zero in this case, then for the control case can be estimated from the volume difference. Under typical values of other parameters, the second term in Eq. 9 is relatively small, such that for a 50% volume reduction. However, as in the main text, a key prediction is that shape changes during spreading do not significantly on this background network tension.
Table 1.
Model parameters
| Parameter | Symbol | Value | Source |
|---|---|---|---|
| Contractile stress | 0.19 nN/μm2 | estimated from myosin-induced nuclear volume change | |
| Nucleus bulk modulus | 0.25 nN/μm2 | Ref (32), isolated Xenopus oocyte nuclei | |
| Nucleus area modulus | 25 nN/μm | Ref (32), isolated Xenopus oocyte nuclei | |
| Membrane tension | 0.1 nN/μm | Ref (33), moving fish keratocytes; Ref (34) | |
| Network viscosity parameter | 0.21 nN-s/μm2 | Ref (35), adherent J774 macrophages | |
| Nuclear lamina bending stiffness | 3.5 × 10−4 nN-μm | Ref (36), MEFs | |
| Surface friction coefficient | varied | ||
| Network assembly speed at contact boundary with substratum | 0.5 μm/min | estimated from spreading speed | |
| Network assembly speed at cell cortex | varied | ||
| Energy parameter in area expansion equation | 3.2 × 10−4 nN-μm | estimated from excess surface area | |
| Nuclear radius | 6.3 μm | measured | |
| Cell radius (rounded) | 8.3 μm | measured |
Parametric sensitivity
The key model predictions (translation of the nucleus to the substratum and flattening of the nucleus during cell spreading) were found to depend only on the following quantities. The speed of network assembly at the cortex relative to the contact boundary assembly speed, determines how fast the nucleus translates to the surface while the cell spreads. The nuclear envelope stiffness relative to viscous stresses (dimensionless ratio ) as well as amount of excess nuclear surface area (reflected in Eq. 11) determines the extent of nucleus flattening in a fully spread cell. The substratum adhesivity relative to the viscous stresses (dimensionless ratio ) determines the steady-state cell spreading area (hence the amount of flattening). Model simulations were found to not depend strongly on the bulk modulus of the nucleus, because nuclear shape changes during flattening can proceed without requiring volume compression (i.e., at constant volume). The contractility parameter was unimportant because the tension this parameter quantifies was assumed to be uniform throughout the cytoplasm, hence it acts uniformly on all surfaces, and motion is driven by the divergence of the stress tensor, (see Eq. 1), in which case the constant disappears. The assumed value of cell membrane tension relative to viscous stresses (dimensionless ratio, ) had a modest effect on the curvature of the cell membrane of a spread cell but had little effect the predicted cell spreading dynamics and nuclear shape changes.
Methods for simulating cell spreading
The resulting quasistatic stress balance based on Eq. 1 is mathematically equivalent to the classic problem of elastostatic deformation of an isotropic elastic medium. Therefore, axisymmetric velocity field at position can be obtained from the following boundary integrals over the nucleus, substratum, and cell membrane boundaries (represented by ) as follows:
| (12) |
where and are velocities and tractions, respectively, arising from a concentrated point force located at position , given by Kelvin’s fundamental solutions for the axisymmetric case for linear elasticity (see (37)), but with the shear modulus replaced with and the Poisson ratio set to zero. The tensor is equal to the Kronecker delta (identity tensor) , on the cytosplasmic domain and is a known tensor on the surface . The boundary element method was used to estimate the instantaneous velocities and stresses at the boundaries (38), such that the evolution of cell and nuclear shapes could be simulated by numerically integrating the boundary positions over time. The cell surface was discretized into 100 axisymmetric quadratic boundary elements and the nuclear surface into 50 elements. Integrals on the elements were approximated with 10th-order Gauss quadrature except strongly singular integrals, which were obtained from analytical rigid body translation (z-direction) and plan strain (r-direction) conditions (37). At each time step, the surface velocities and stresses were calculated under the constraint of constant volume, and time-stepping was performed using the 4th-order Runge-Kutta method. The constraint of constant volume was imposed by simultaneously solving for the hydrostatic pressure at each time step that keeps the net volume change equal to zero. The node spacing was reset at each time step by interpolation using cubic Hermite interpolating polynomials (MATLAB function pchip). To prevent close approach of the nuclear surface to the cell membrane (which is mathematically allowed by way of Eq. 1, but creates numerical issues because of surface singularities in the boundary element method), a close-range repulsive pressure was imposed for close separation distances z of the form . The initial condition was set to a nearly spherical cell with a small contact area of ∼0.5% of the total cell membrane surface area.
Results
Collapse of apical nuclear surface contributes to nuclear flattening during early cell spreading
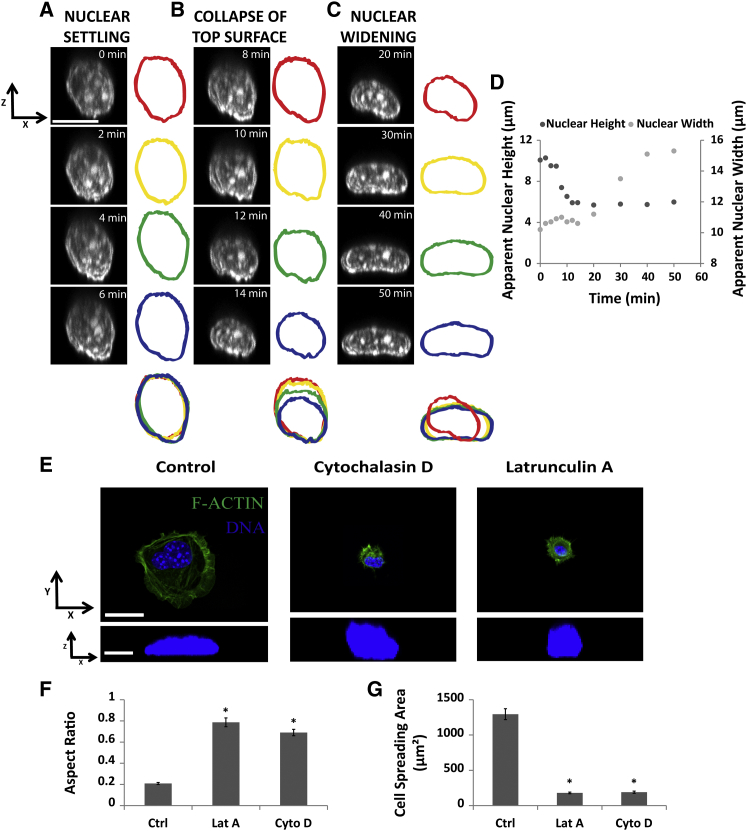
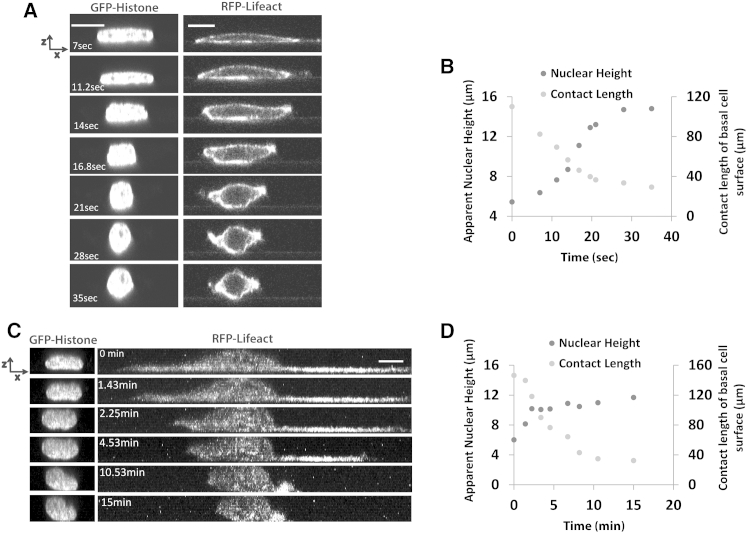
We used x-z laser scanning confocal fluorescence microscopy of NIH 3T3 fibroblasts expressing GFP-histone to prepare time-lapse images of the nucleus as they settled from suspension onto a fibronectin-coated glass dish. Three distinct nuclear behaviors could in general be discerned during the spreading. First, the nucleus translated toward the base of the cell and the lower surface of the nucleus began to flatten against the substratum in the first few minutes of attachment (Fig. 1 A). The speed of initial translation of the nucleus toward the substratum was surprisingly fast—about 20-fold faster than would be expected from gravitational settling (based on the assumed cytoskeleton viscosity in Table 1). Next, the top surface of the nucleus collapsed while the length of the flattened bottom surface stayed roughly constant. This change in the nuclear shape happened over a duration of 5 to 6 min (Fig. 1 B). In the third phase, the collapsed nucleus increased in width at nearly constant height (Fig. 1 C; see Fig. 1 D for quantification of the shape in Fig. 1, A and C; these findings were consistent among five other live cell imaging experiments; see Movies S1 and S2 for examples). By constructing x-z nuclear shapes from different view angles, we confirmed that the flat nuclear shapes were because of deformation of the nucleus instead of already-flat nuclei toppling onto their sides (Movies S1 and S2 and Fig. S1 A in the Supporting Material. In addition, by inverting the substrate on which the cells spread, we confirmed that gravity did not affect the initial nuclear translation to the substratum nor the rate of the subsequent flattening (Fig. S1, B–D). In addition, nuclear flattening only occurred during cell spreading; inhibition of actin assembly and cell spreading by cytochalasin D or latrunculin A prevented nuclear flattening, as quantified by the aspect ratio (height/major axis length) (Fig. 1, E–G).
Figure 1.
The dynamics of nuclear flattening during early cell spreading. (A–C) Vertical cross sections of a nucleus in a cell that settles and spreads on the substratum. The images were captured using x-z laser scanning confocal fluorescence microscopy; the nucleus is expressing GFP-histone H1. Three phases were discernible in the nuclear flattening process: (A) a settling phase where the basal surface of the nucleus contacted the basal cell surface and started to spread, the height was roughly constant during this time; (B) a collapse of the top surface where the basal surface of the nucleus did not spread much; and (C) a widening phase where the basal surface of the nucleus continued to spread and contributed to nuclear widening; the height was roughly constant in this phase. Scale bar is 10 μm. (D) Plot shows nuclear height and contact length in (A–C) with time. (E–G) Nuclei did not flatten when cell spreading was prevented by inhibitors of actin assembly, cytochalasin-D or latrunculin-A, based on nuclear aspect ratio (height divided by the length of the major-axis in the x-y plane) after 1 h spreading in the presence of the drugs (n ≥ 31, ∗p < 0.05; all comparisons are with untreated control). Scale bar in (E) is 20 μm in the x-y view and 5 μm in x-z view. All data are shown as mean ± SEM. To see this figure in color, go online.
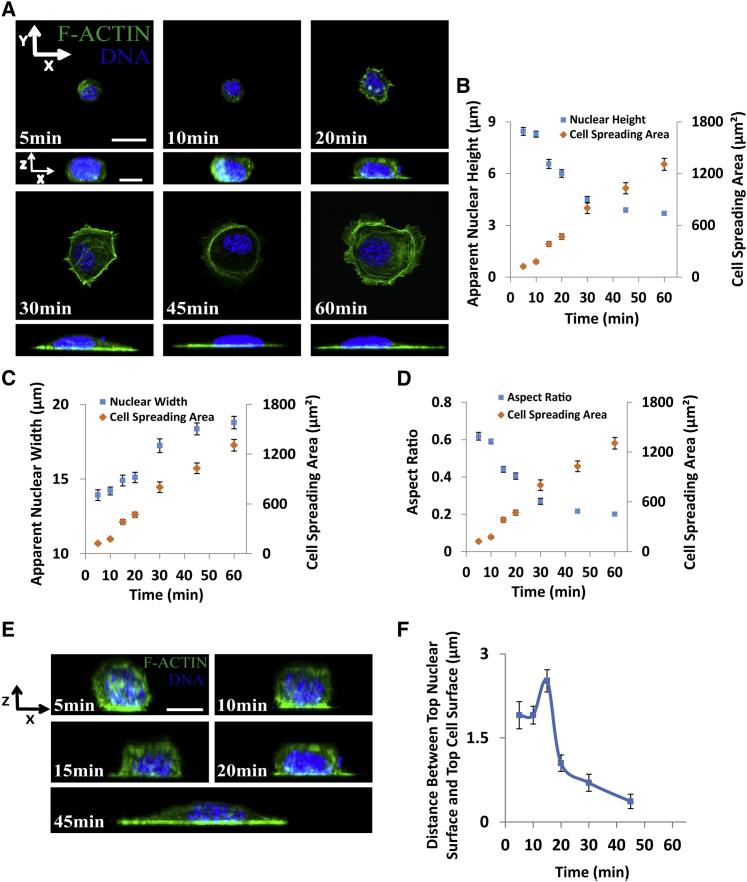
Although cells spread continuously in the first 60 min, increasing their spread area from less than 200 μm2 to nearly 1400 μm2 (Fig. 2, A and B), the nuclei flattened and reached a steady-state height early during cell spreading in the first 20 to 30 min, when the cell itself had only spread to less than 50% of its final area (Fig. 2, A and B). Nuclear width stayed roughly constant during the first 20 min (Fig. 2 C) and then increased steadily as the cell spread. As seen in Fig. 2 D, the aspect ratio decreased to around 0.25 by 30 min, indicative of a flat nucleus with a width that is four times its height. We also observed that there was a separation between the nuclear surface and the cell membrane (Fig. 2 E), which increased slightly and then decreased over time as the cell spread and the nucleus flattened (reaching a peak separation of around 2 μm). The increase in the separation coincided with the collapse of the top nuclear surface (compare Fig. 2, B and F).
Figure 2.
The nucleus flattens completely in a partially spread cell. (A) Images show cells at different stages in the spreading process. Nuclei (blue) were completely flattened at roughly 20 to 30 min when the cells (green F-actin) had not spread completely. Scale bar is 20 μm for the x-y views and 10 μm for the x-z views. Also shown are (B) average nuclear heights, (C) average nuclear widths, and (D) nuclear aspect ratio (height/width) at different times during the cell spreading process, and the corresponding areas of cell spreading. The nuclear heights reached an approximate steady state at around 30 min, when the cells were spread to ∼50% of the final area (n 32 cells). (E) The apical surface of the cell was separated by some distance from the apical surface of the nucleus as can be seen in the vertical cross sections of the cell and nucleus. Scale bar is 10 μm. (F) The gap between the top cell surface and the top nuclear surface plotted with time (n 25 cells). The gap increased at the beginning reflecting the collapse of the nuclear surface and then decreased over time to near zero levels. All data are shown as mean SEM. To see this figure in color, go online.
Nuclear flattening does not require actomyosin contraction in spreading cells
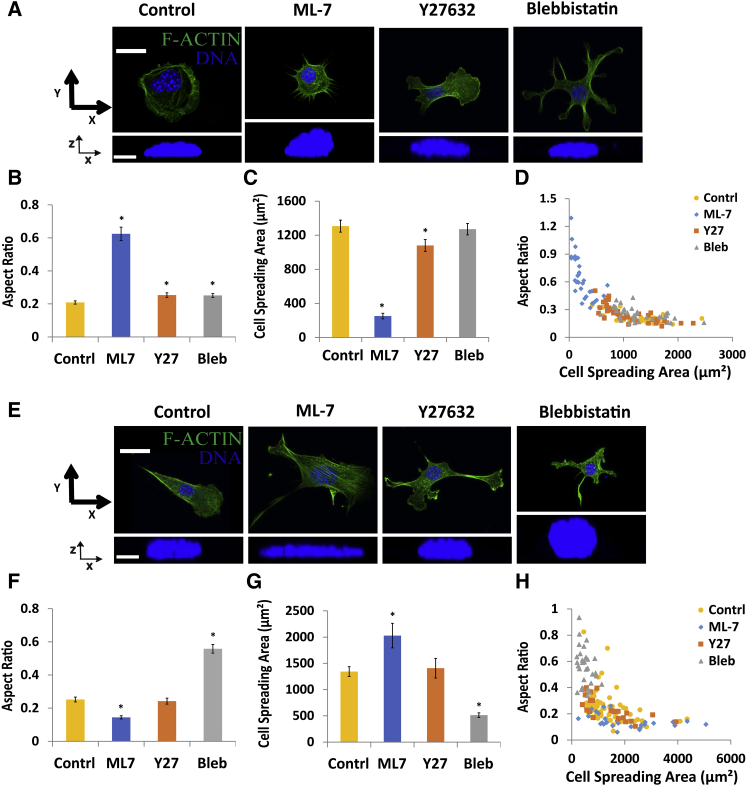
We pretreated well-spread cells with three different inhibitors: Y-27632, a ROCK inhibitor; ML-7, a myosin light chain kinase (MLCK) inhibitor; or blebbistatin, a direct inhibitor of myosin II activity. Our approach was to pretreat cells for 1 h at the appropriate dose, trypsinize cells, and to allow them to attach for 1 h in medium containing the inhibitor (Fig. 3 A). Neither blebbistatin (50 μM) nor Y-27632 (25 μM) interfered with the nuclear flattening process observed in normal cells (Figs. 3, A and B, and S2, A–D), suggesting that myosin II activity is not required for nuclear flattening. However ML-7 (25 μM) treatment interfered with both nuclear flattening and cell spreading (Fig. 3, A and B). To understand the differential effects of the drugs on nuclear flattening, we measured the area of cell spreading (Fig. 3 C) and correlated nuclear aspect ratio with the cell spreading area (Fig. 3 D; correlations between nuclear height and width with cell spreading area are in Fig. S2, C and D).
Figure 3.
Nuclear flattening does not require actomyosin contraction. (A) Images show cells pretreated with drug for 1 h, trypsinized, and then seeded onto substrates for 1 h in the presence of the drug. Cells in the presence of Y-27632 and blebbistatin showed clear effects on the cell morphology compared with the control, but the nucleus was still flattened as evident from the x-z cross section. ML-7 treatment on the other hand prevented the spreading of the cell as well as the flattening of the nucleus. Scale bar for x-y views is 20 μm and for x-z views is 5 μm. (B) Nuclear aspect ratio was larger in ML-7 treated cells reflecting unflattened nuclei, consistent with the fact that the cells were unable to spread in presence of ML-7 (C) Minor differences in aspect ratio on Y-27632 or blebbistatin treatment reflect minor effects on degree of cell spreading. (D) Aspect ratio correlates with the degree of cell spreading. In ML-7 treated cells, the cells were unable to spread (blue diamonds) corresponding to the large aspect ratio; none of the other treatments prevented nuclear flattening but concomitantly, they did not prevent cell spreading (n 31 for all conditions, ∗p < 0.05; all comparisons are with untreated controls). The experiments in (E)–(H) show the corresponding results on treating well-spread cells (cultured overnight on fibronectin-coated glass-bottom dishes) with myosin inhibitors. Blebbistatin treatment rounded up spread cells, and caused rounded nuclear shapes. Images are shown in (E), whereas the scatter plots of aspect ratio versus cell spreading area are shown in (H). (F) and (G) show the average aspect ratio and areas for the different myosin inhibitors (n 24, ∗p < 0.05; all comparisons are with untreated control). Scale bar in (H) is 20 μm for the x-y view and 5 μm for the x-z view. All data are shown as mean SEM. To see this figure in color, go online.
The degree of cell spreading decreased dramatically in ML-7 cells (Fig. 3, C and D). This revealed a potential reason for the differential effects: ML-7 treatment prevented cell spreading whereas Y-27632 or blebbistatin treatment altered cell shapes but did not prevent cell spreading. Nuclear aspect ratios and cell spreading areas were comparable in untreated control cells at 15 min (Fig. 2 D) and ML-7 treated cells (Fig. 3, B and C). Taken together, these data suggest that the degree of cell spreading appears to be a predictor of nuclear flattening in myosin-inhibited cells. We and others have shown in the past that inhibiting myosin activity in well-spread cells rounds the nucleus (25,26). In consideration of the above results, we examined the effect of the three myosin inhibitors on nuclear height in well-spread cells. Myosin inhibition again resulted in a rounded nucleus only when the cell was rounded by the action of the drug (Fig. 3 E). In these experiments, blebbistatin (but not Y-27632 and ML-7) treatment resulted in rounded cell morphologies; only blebbistatin-treated cells showed rounded nuclear x-z cross sections (Figs. 3, F–H, and S2, E and F, correlations between nuclear height and width with cell spreading area are in Fig. S2, G and H).
We next examined whether myosin inhibition altered aspects of nuclear flattening, such as the initial collapse of the top surface. Inhibiting myosin with Y-27632 did not change the qualitative nature of the drop in nuclear height (except for an initial lag time where the Y-27632 treated cell is unable to spread and the nucleus does not flatten in that time, Fig. S3 A) The distance between the apical cell surface and apical surface of the nucleus during collapse of the top surface increased significantly more than control cells to a maximum of around 4 μm (Fig. S3 B). Hence, myosin inhibition did not produce qualitative changes in the nuclear spreading dynamics. We did find that inhibiting myosin with Y-27632 decreased the width of the flattened nucleus and its volume (Fig. S3, C and D) by a measureable amount. Thus, although the myosin inhibition does not alter nuclear flattening, it appears that actomyosin forces may contribute to some increase in nuclear volume by widening the nucleus after the initial flattening (Fig. S3 D).
We note that the differential effects of ML-7 on initial cell spreading (which it prevents) and on already spread cells can be explained by its differential effects on retrograde flow in slow versus fast moving cells as shown by Jurado et al. (39). In spreading cells where adhesions are relatively smaller, ML-7 treatment causes complete disassembly of adhesions and is predicted to increase retrograde flow and prevent spreading, whereas in well-spread cells, the retrograde flow would be reduced because of a decrease in the raking of adhesions. Blebbistatin treatment prevented cell spreading and nuclear flattening if cells were allowed to spread for longer time (6 h, Fig. S3, E–G); thus blebbistatin uniformly appears to decrease retrograde flow but presumably it inhibits adhesions at a slower rate, which would explain why it does not completely inhibit initial cell spreading at 1 h.
Intermediate filaments and microtubules are dispensable for nuclear flattening in spreading cells
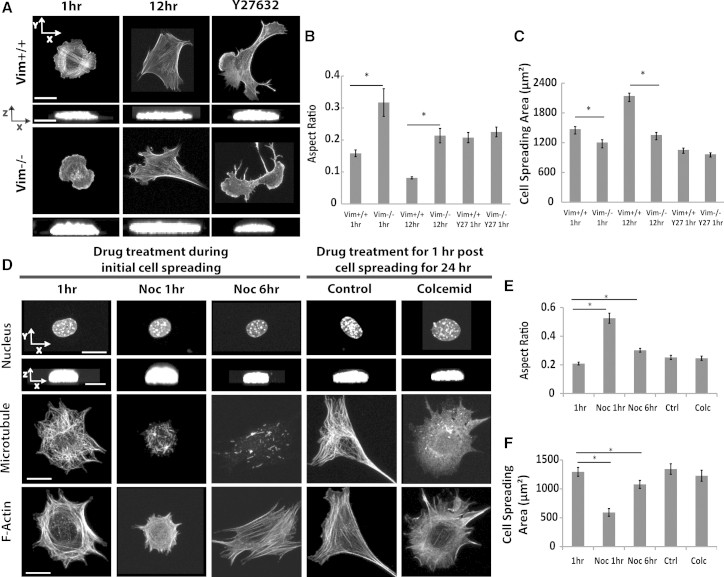
Given that actomyosin contraction was not required for flattening, but instead nuclear flattening correlated strongly with the degree of cell spreading, we examined the role of the other two cytoskeletal structures in the cell: intermediate filaments and microtubules. The nuclear aspect ratio was measured and compared between wild-type mouse embryonic fibroblasts (vim+/+) and vimentin null MEFs (vim−/−). Compared with control cells, the nucleus was more rounded (although it was still significantly flattened to an aspect ratio of 0.3) in vim−/− MEF cells after 1 h of cell spreading (Fig. 4, A and B), but consistent with our observations above, the cell was comparatively less spread (Fig. 4 C). Importantly, over longer time (12 h), the nucleus was flattened in vim−/− cells (Fig. 4 B). Thus, although the absence of vimentin intermediate filaments reduced the rate of nuclear flattening, it did not have an effect on the extent of nuclear flattening. To test if myosin activity was causing nuclear flattening in vim−/− MEFs, we inhibited myosin activity in these cells with Y-27632. The nucleus was flattened in myosin inhibited vim−/− MEFs (Fig. 4 B). Together, these results suggest that the nucleus can flatten in the absence of myosin activity and intermediate filaments. The experiments with these cells again point to a strong correlation between the spreading area of the cell and nuclear flattening.
Figure 4.
The absence of intermediate filaments or the disruption of microtubules does not prevent nuclear flattening during cell spreading. (A) Intermediate filaments are not required for nuclear flattening during cell spreading. The nucleus is flattened in vim−/− cells similar to vim+/+ cells at 12 h after cell seeding although vim−/− nuclei are slightly rounded at 1 h into the spreading process. Y-27632 treatment in vim−/− cells did not prevent nuclear flattening. Scale bar in x-y view is 20 μm and in the x-z view is 5 μm. (B) and (C) show the average aspect ratio and spreading areas; all the differences in aspect ratio can be attributed to the corresponding (inversely related) differences in the degree of cell spreading (∗p < 0.05, n 30). (D) The effect of nocodazole (0.83 μM) on nuclear flattening and cell spreading, and the effect of colcemid (0.27 μM) on well spread cells. At 6 h, the nocodazole-treated cells were spread and had flattened nuclei, while no microtubules were visible. Likewise, colcemid treatment for 1 h disrupted microtubules in originally well-spread cells but did not alter nuclear height. Collectively the data suggests that microtubules are not required to establish or maintain a flattened nucleus. Measurements of the (E) aspect ratio and (F) spreading area of the cells under various conditions (n 30, ∗p < 0.05; all comparisons are with untreated control). Scale bar in (E) is 10 μm for x-y view and 5 μm for x-z view. All data are shown as mean SEM.
To determine the role of microtubules in nuclear flattening, we disrupted microtubules with nocodazole and colcemid. At a dose of 1.65 μM nocodazole, microtubules were completely eliminated from the cell, but the cell was unable to spread 1 h after seeding, and concomitantly, the nucleus did not flatten (Fig. S4). Upon decreasing the dose to 0.83 μM, microtubules were greatly fragmented, but the cell was not spread as well as the control cells at 1 h. At 6 h into the spreading process, cells had no discernible microtubules (Fig. 4 D) but were able to spread (Fig. 4 F) and the nuclei were flat (Fig. 4 E). We next allowed cells to spread overnight and treated cells with 0.27 μM colcemid. The treatment did not cause cell rounding (Fig. 4 F) even though microtubules were completely disrupted (Fig. 4 D) and the nucleus remained flat (Fig. 4 E). Together, both these results suggest that microtubules are not required for nuclear flattening when cells are able to spread.
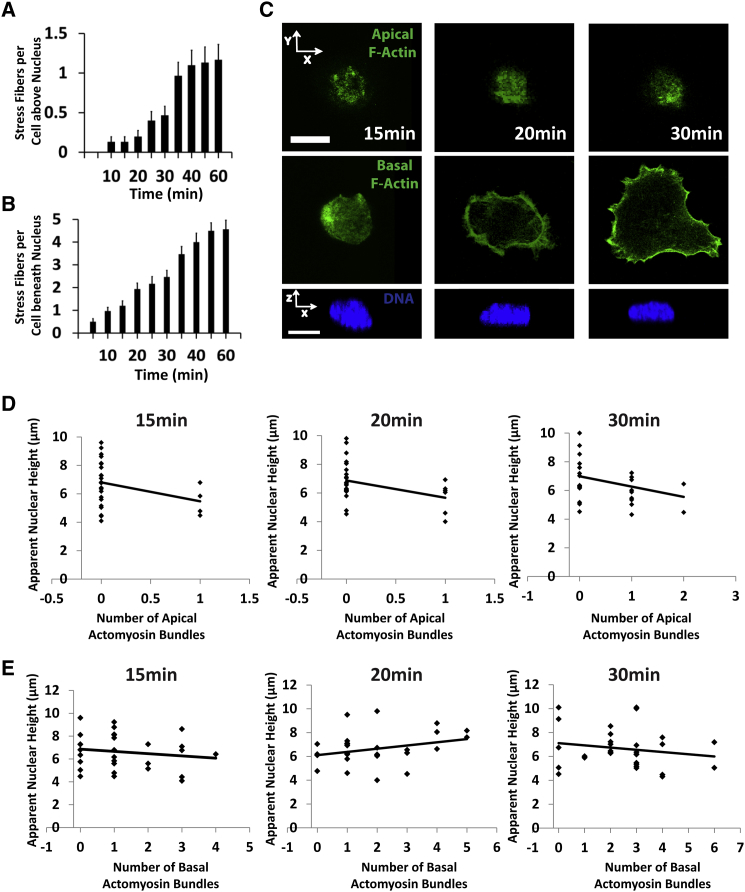
Apical and basal actomyosin bundles are not required for nuclear flattening during initial cell spreading
Actomyosin stress fibers have been implicated in shaping the nucleus (24). In light of our results above that suggest that myosin activity is not required for nuclear flattening, we examined the presence of actomyosin bundles in spreading cells. In the first 20 min when the nucleus flattened significantly, the average number of actomyosin bundles above the nucleus was found to be ∼0.2, i.e., one out of five cells have one apical bundle (Fig. 5 A). The number of basal fibers under the nucleus coinciding with the time of nuclear flattening was ∼1–2 per cell (Fig. 5 B). We next examined the correlation between the nuclear height and the number of apical and basal bundles at different times in the cell spreading process. Fig. 5 C shows three examples where neither basal nor apical fibers could be discerned during initial cell spreading, although the nucleus had been flattened to a considerable extent. As seen in the plots, there were several cells where no fibers are discernible (apical or basal), but the nucleus is clearly flat (Fig. 5, D and E). These results, combined with the myosin inhibition experiments above argue against a mechanical explanation in which apical or basal actomyosin bundles play a significant role in flattening the nucleus during initial cell spreading.
Figure 5.
Apical and basal actomyosin bundles are not required for nuclear flattening during initial cell spreading. (A) Apical actomyosin bundles were counted above the nucleus in spreading cells (actin cables were visualized by phalloidin staining). Apical bundles appear only after 30 to 40 min by which time the nucleus has flattened completely (n 30). (B) In spreading cells, one basal actomyosin bundle on average appeared under the nucleus by around 15 min. Basal cables were only counted if they ran beneath the nucleus. Times represent time after initial seeding, n 30. (C) Images show examples at different times after seeding of apical and basal F-actin stained cells (green) that lack actomyosin bundles, but have significantly flattened nuclei (blue). Scale bar is 10 μm for both panels. (D) and (E) show plots of the nuclear height with the number of apical and basal actomyosin bundles at 15, 20, and 30 min. A number of examples can be seen where there are zero apical or basal actomyosin bundles but the nucleus is still significantly flattened (n 30 cells). All data are shown as mean SEM. To see this figure in color, go online.
Nuclear flattening can be reversed by detachment of the cell from the substratum
The different experiments described above seem to consistently indicate that nuclear flattening is strongly correlated with the extent of cell spreading. A rounded cell is predicted to have a rounded nuclear x-z cross section, whereas a well-spread cell is expected to have flat nucleus. To further test the relationship between the degree of cell spreading and nuclear height, we treated well-spread cells with trypsin and measured the nuclear x-z cross section. At concentrations of trypsin (0.25% w/v) normally used for cell passage, the nucleus rounded up remarkably fast (in a few seconds) coupled with fast cell rounding (Fig. 6 A). There was a strong relationship between the degree of cell rounding as measured by the contact length between the cell and the surface of the substratum, and the nuclear height, at different times during the trypsinization process (Fig. 6 B). We next treated cells with trypsin at reduced concentrations (0.08% w/v). This slowed the cell rounding process significantly (several minutes). Consistent with the expectation that nuclear height is determined primarily by the degree to which the cell is spread, the nucleus did not round until the cell had significantly changed its shape through release of cell-substratum adhesions (Fig. 6 C). This occurred over several minutes (Fig. 6 D). These results strongly support the concept that nuclear height correlates with the degree of cell spreading.
Figure 6.
Nuclear flattening can be reversed by detachment of the cell from the substratum. Trypsinization of cells rounded the nucleus (A) in a remarkably short time of a few seconds. Importantly, the nuclear rounding closely followed the cell rounding—the dynamics of height changes (gray circles) and changes in contact length of the basal cell surface (black circles) are similar (B). Scale bar is 10 μm for both panels in (A). This concept was tested further in (C) by trypsinizing cells at one-third the dose of the trypsin concentration used in (A). The nucleus rounded much more slowly (several minutes) and closely reflected the rounding up of the cell body (the nuclear height and cell contact length are shown in (D). Thus, the degree of cell spreading determines the degree of nuclear rounding during cell detachment. Scale bar is 20 μm for both panels. All data are shown as mean SEM.
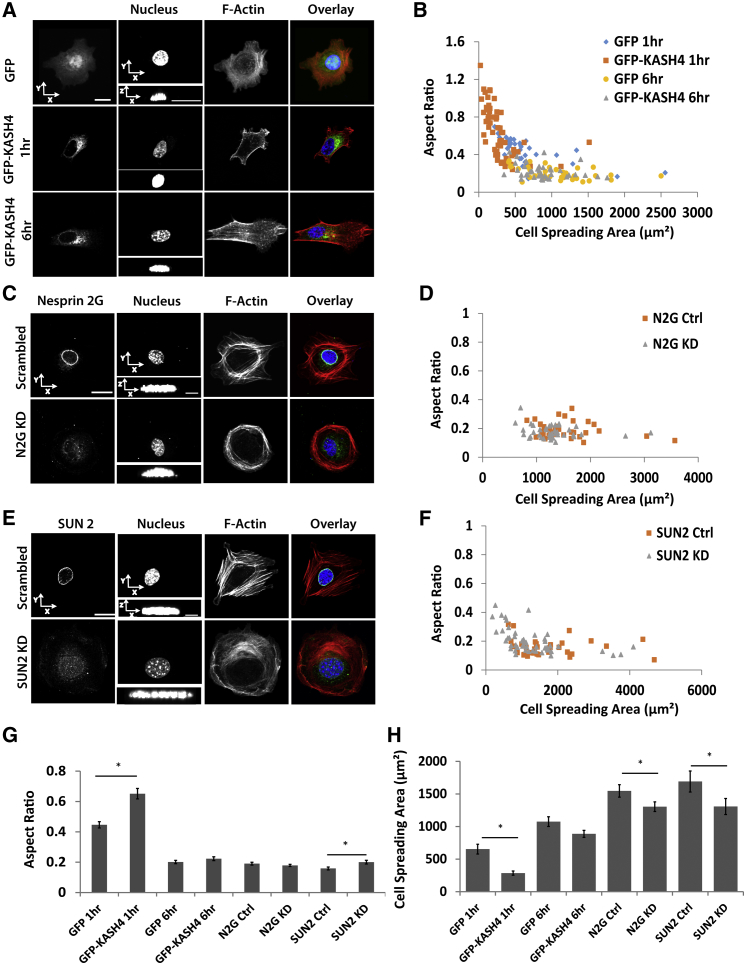
The LINC complex is not required for nuclear flattening
The LINC complex has been shown to transmit mechanical forces from the cytoskeleton to the nucleus (19). We therefore asked if an intact LINC complex is required for nuclear flattening. The disruption of the LINC complex by overexpression of GFP-KASH4 (KASH4 is the KASH domain from nesprin 4 that competitively binds to the SUN proteins, but lacks the cytoskeletal linker domain) (40) slowed the flattening of the nucleus (Fig. 7, A and B) but it also slowed normal spreading of the cells (see also Fig. 7, G and H). Importantly, at 6 and 24 h (Fig. S5, A–C), GFP-KASH4 expressing cells were well spread and displayed flat nuclei. Similarly, the knockdown (Fig. S5 D) of nesprin 2G (Fig. 7, C and D) and SUN2 (Fig. 7, E and F) with shRNA interference did not have any effect on nuclear flattening during initial cell spreading (see Fig. 7, G and H for a statistical comparison of all the data). The data indicates that an intact LINC complex is not required for nuclear flattening and cell spreading.
Figure 7.
The LINC complex is not required for nuclear flattening during cell spreading. (A) GFP-KASH4 expression in cells prevented flattening of nuclei at 1 h, but also prevented cell spreading. At 6 h into the spreading, the nucleus did flatten in GFP-KASH4 expressing cells. Scale bar in x-y and x-z views are both 20 μm. (B) Scatter plots of nuclear aspect ratio versus cell spreading area in GFP expressing (control) versus GFP-KASH4 expressing cells; GFP-KASH4 expressing cells did not spread well at 1 h after seeding, which correlated with the expected response of a lack of nuclear flattening. (C and D) Nesprin 2 knockdown did not produce any effects on aspect ratio nor the degree of cell spreading. (E and F) SUN2 knockdown produced no effects on aspect ratio and degree of cell spreading. Scale bar in x-y view is 20 μm and x-z view is 5 μm in (C) and (E). (G) and (H) show comparisons of average aspect ratio, and cell spreading area at the different conditions. Only when the cell is not able to spread does the nucleus remain unflattened (∗p < 0.05, n 35). All data are shown as mean SEM. To see this figure in color, go online.
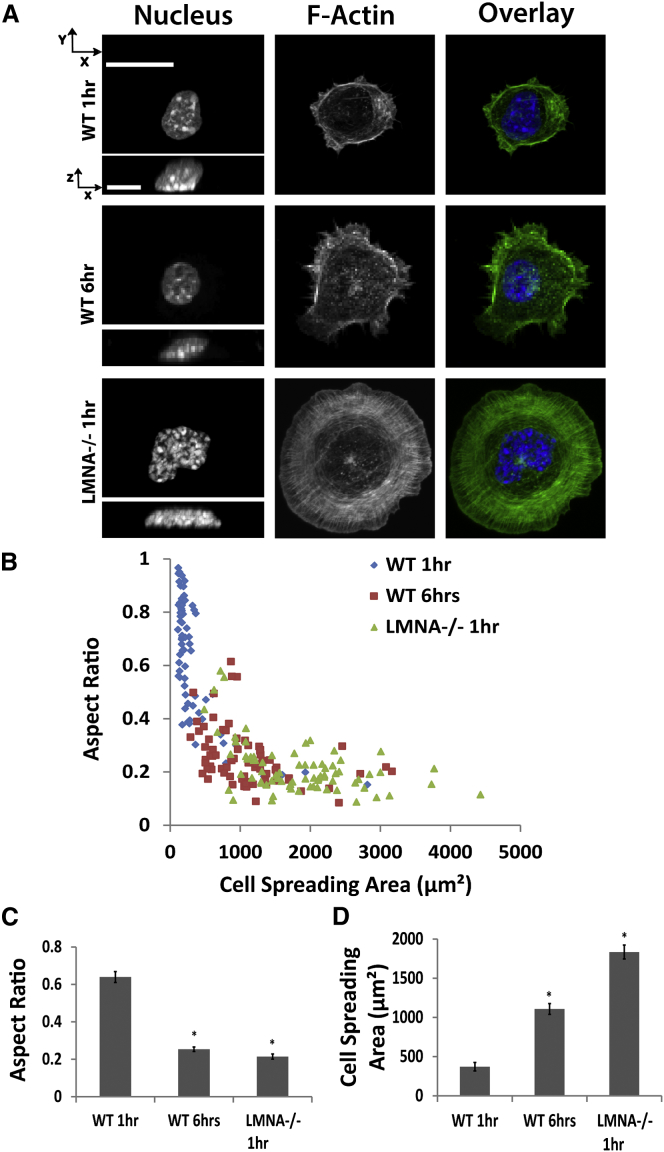
We next examined the effect of lamin A/C on the degree of nuclear flattening (Fig. 8). At 60 min, MEFs lacking lamin A/C (LMNA−/−) had more flattened nuclei compared with WT MEFs. However, WT MEFs did not spread significantly at 60 min (Fig. 8 A). When allowed 6 h to spread, however, WT MEFs were able to spread and flatten their nuclei. These results suggest that the absence of lamin A/C correlates with an increased rate of nuclear flattening, leading to a flattened nucleus in LMNA−/− MEFs compared with WT MEFs during cell spreading.
Figure 8.
Nuclei in LMNA−/− MEFs flatten faster than WT cells. Nuclei in WT MEFs are less flattened at 1 h after cell seeding (A) compared with LMNA−/− cells that have extremely flat nuclei. The degree of cell seeding is small in WT at 1 h and increases by 6 h; LMNA−/− cells, however, are well spread at 1 h. Scale bar in the x-y view is 20 μm and in the x-z view it is 10 μm. The lack of cell spreading, higher nuclear heights and lower nuclear widths at 1 h in WT cells compared with LMNA−/− cells is evident in the scatter plots of nuclear aspect ratio versus cell spreading area (B), as well in the average values of nuclear aspect ratio and spreading area (C) and (D) (∗p < 0.05; n 43; all comparisons are with WT cells at 1 h spreading). All data are shown as mean SEM. To see this figure in color, go online.
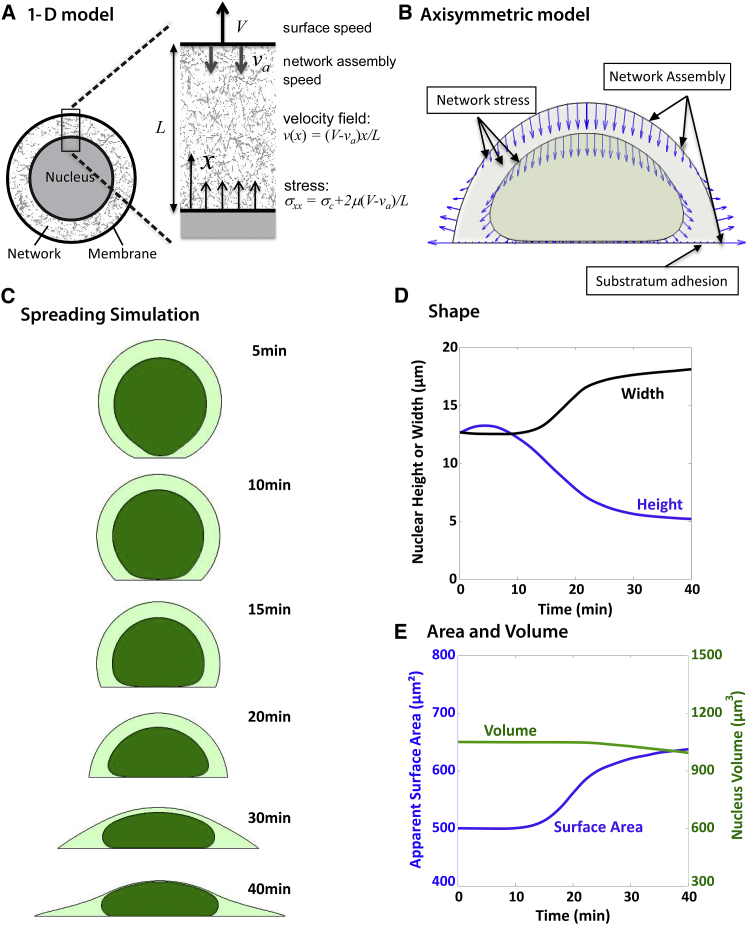
A mathematical model for nuclear flattening and cell spreading
The presence of individual cytoskeletal elements (microtubules, intermediate filaments), myosin activity, or an intact LINC complex, which transmits forces from the cytoskeleton to the nucleus, is not required for flattening the nucleus as long as the cell is able to spread. We found that inhibiting F-actin polymerization that prevents cell spreading prevented nuclear flattening (Fig. 1, E–G). Thus, nuclear flattening correlates with the degree of cell spreading. Based on these results, we propose a simple mechanical model that shows that stresses arising from cellular shape changes and cytoskeletal network assembly from the apical cell cortex are sufficient to explain nuclear translation to the surface and flattening against the substratum. We modeled the cell’s cytomatrix, i.e., the cytoskeletal network phase connecting the nucleus to the cell membrane, as a contractile compressible material that resists compression/expansion and shear strains (similar to the approach by Dembo and coworkers (41–43)). On the slow timescale of spreading (several minutes), only the viscous resistance to deformation is considered relevant (i.e., elastic forces are considered negligible given the remodeling that occurs in the cell over long timescales), such that the stress tensor is proportional to the rate-of-strain tensor, i.e.,
| (13) |
where is the contractile stress because of myosin motor activity, is the unit dyadic, is the rate-of-strain tensor, and is viscosity that measures the modulation of stress due to both expansion/compression and shear deformations of the compressible network phase. Note that both shear and expansion/compression modes in are relevant because the network is assumed compressible. Equation 13 can be considered a slow-flow limit of the more general two-phase reactive interpenetrating flow models for cells developed by Dembo and coworkers (41–43) where network contractile/viscous properties can be assumed to be uniform and hydrostatic pressure gradients are assumed negligible.
Solving the momentum balance with the appropriate boundary conditions yields the stress and velocity fields of the network. Before we discuss the full general model for cell and nuclear mechanics during nuclear flattening, we show a simple model that illustrates the key predictions of the general model. The simple model (Fig. 9 A) is an approximate representation of the gap between the cell apex and the nuclear apical surface when the gap is small compared with the inverse curvature of the nucleus. The main purpose of this model is to show how movements of the top cell membrane and flow from the membrane of network can exert a stress on the nuclear surface. To illustrate the relevant properties of a cell containing contractile/viscous medium obeying Eq. 1, consider a simplified one-dimensional case illustrated in Fig. 9 A, which represents the planar approximation of the local gap of length between the cell membrane and the nuclear envelope (the exact derivation for a spherical cell is presented in Materials and Methods). Let the gap expand at speed by moving the cell membrane and keeping the nuclear surface fixed, and assume new network assembles at the cell membrane (where f-actin is primarily generated) at speed . In the special case where , there is no network flow because the network assembles at exactly the rate required to fill the volume behind the moving membrane. Otherwise, there will be network expansion or compression , either of which will modulate the stress on the nuclear surface at the base. As derived in Materials and Methods, the resulting velocity and stress fields for the 1-D approximation are as follows:
| (14) |
| (15) |
Because stress is uniform in this case, the tensile stress on the nuclear surface is equal to . From Eqs. 14 and 15, the following important properties regarding transmission of stress to the nuclear surface are evident: 1) expansion of the gap between the cell membrane and the nuclear envelope will increase the net tensile stress on the nuclear surface; and 2) compression of the gap or assembly of network at the cell membrane will decrease the net tension on the nuclear surface. An important corollary to these predictions is that when the nuclear surface stress is fixed (instead of fixing the nuclear surface position), the nuclear surface will move at a speed such that the gap expansion speed satisfies the stress balance in Eq. 3. For example, if the nuclear surface stress is in balance with the network contractile tension, such that , then . Consequently, the nuclear surface will move together with the membrane keeping when , or it will move away from the cell membrane at speed when . In this way, the nuclear surface movements will tend to follow the movements of the nearby cell membrane boundary, but will also tend to move away from cell membrane surfaces where network is being assembled. These are the important properties of the network that govern the more general model that now follows for nuclear shape changes during cell spreading.
Figure 9.
Mathematical model for nuclear deformation during cell spreading. (A) Predictions of a simplified one-dimensional model for the cytoskeletal network spanning the gap between the nuclear surface and the cell membrane. Movement of the membrane relative to the nuclear surface (speed ) or assembly of network at the surface and resulting retrograde flow (speed ) results in expansion or compression of the intervening network, thereby generating a stress on the nucleus surface. (B) Key components of the model for a spreading cell. The model cell accounts for 1) resistance of the nucleus to volume expansion/compression; 2) resistance of the nuclear surface (lamina) to area expansion; 3) cell membrane tension; and 4) the cytoskeletal network phase of the cytoplasm, which is assembled at the cell cortex and at the contact boundary with the substratum. Centripetal flow of network and the frictional resistance to shear and to volume expansion/compression causes movement of the cell membrane and nuclear surfaces (surface velocities of cell and nuclear surfaces are shown by blue vectors). (C) Snapshots from a simulation of cell spreading and nuclear shape changes showing the three phases of nuclear deformation observed experimentally: 1) vertical distension and translation of the nucleus toward the substratum, driven by flow of network from the apical membrane where it is generated; 2) initial flattening against the substratum with a decrease in nuclear height and little change in nuclear width as the cell begins to spread and the nuclear is compressed vertically by the lowering upper cell surface; and 3) widening of the nucleus with lesser change in height, as the widening cell boundary pulls the nucleus laterally. Widths and height are plotted in (D). As in the experimental observation, the nucleus quickly flattens vertically early in the process of cell spreading, then widens more slowly as the cell continues to spread. (E) Plot of nuclear area and volume versus time. While the nuclear volume remains nearly constant, the area expands until the assumed excess area is smoothed and the stiffer true surface area is reached, at which point the surface area starts to level off toward a constant value. To see this figure in color, go online.
To model the case of a spreading cell (Fig. 9 B), new network is assumed to assemble where F-actin is generated at the cortex and at the cell edge on the substratum, but not at any other substratum-cell membrane interface (see Materials and Methods for model and simulation details). Throughout the network phase, F-actin and the other constituents of the cytoskeletal network (intermediate filaments, microtubules) are assumed to assemble/dissemble to reequilibrate the density and mechanical properties of the network relatively quickly on the slow timescale of cell spreading. As shown in Fig. 9 C (Movie S3), these assumptions and the constitutive stress equation (Eq. 1) are sufficient to predict cell spreading very similar to the experimental observations, including the observed initial distension and net translation of the nucleus toward the substratum and initial flattening against the substratum. Cell spreading is the result of assembly of network at the contact boundary, which generates a centripetal flow of network. Substratum adhesion hinders this centripetal flow, resulting in a net outward expansion of the cell boundary near the substratum. Expansion near the substratum corresponds to retraction of the upper cell surface away from the substratum to preserve cell volume (assumed constant because of the cell’s osmotic resistance to volume changes). Because of viscous resistance to network expansion (Eq. 1), the movement of the cell boundaries generates stress on the nucleus as the intervening network expands or compresses, and movements of the nucleus boundary tend to follow those of the cell boundaries. Assembly of new network at the cortex has the effect of increasing the downward compressive flow of network. Because the network is assumed not to assemble at the cell-substratum interface (except at the contact boundary), this flow causes an initial vertical distension of the nucleus followed by a net translation of the nucleus toward the substratum (Fig. 1 C). Although network assembly at the cortex is required to predict the initial rapid downward translation of the nucleus given the assumed network viscosity, cell spreading and the resulting nuclear flattening only requires an assumption of network assembly at the contact boundary, as discussed below. As shown in Fig. 9 D, the time-dependent nucleus height and width predicted by this model agree well with the experimentally observed trends.
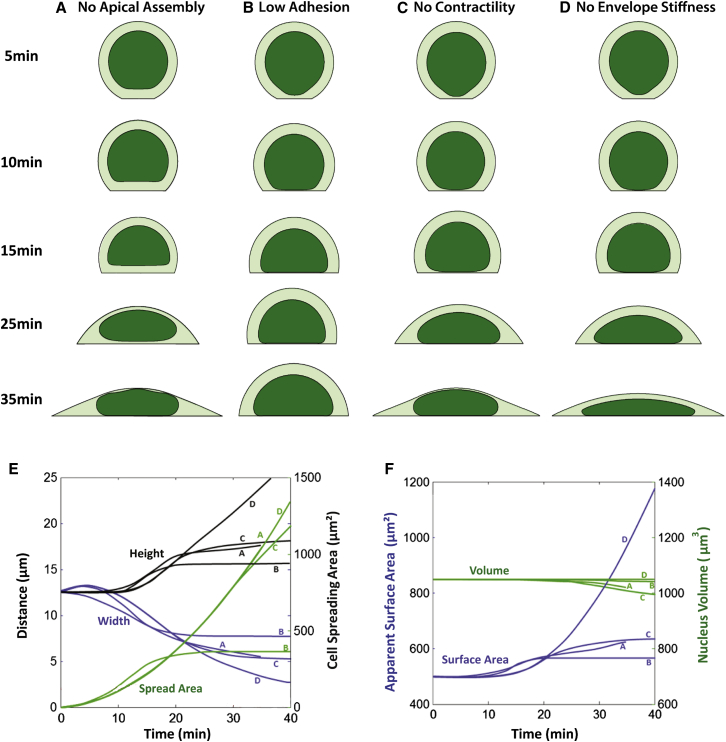
As detailed in Materials and Methods, our mechanical model of the nucleus accounts for resistance to compression, and a resistance to nuclear envelope expansion that accounts for an excess of surface area of the nuclear lamin network above that of a smooth sphere with the same volume. This excess surface area is evident from the observed undulations in the lamin network (44). As shown in Fig. 9 E, the nuclear volume remained nearly constant during cell spreading, but the apparent surface area of the nuclear envelope increased; once the surface area expansion approached the true surface area, further shape changes were minimal because of the large mechanical resistance to further surface area changes. Hence, a steady-state nuclear shape is reached before spreading stops, consistent with our observations, and the steady-state shape of the flattened nucleus depends primarily on the stiffness of the nuclear lamina and the excess surface area of the initially rounded nucleus. Without the assumption of network flow from the cortex, the nucleus is still predicted to flatten as the cell spreads because of the vertical compression and horizontal expansion arising from the moving cell boundaries (Fig. 10 A; Movie S4). However, reproducing the relatively rapid approach and flattening of the nucleus against the substratum early in cell-spreading processes requires an assumption of network assembly and flow from the apical cell cortex. Although the initial nuclear dynamics are similar, the fully spread model cell with or without apical cortical network assembly appear very similar at longer times. Hence, our results suggest that apical cortical network assembly and flow is necessary to translate the nucleus to the substratum early in spreading, but it is not required to explain the ultimate flat nuclear shapes such as those observed in experiments. Reproducing the observed flattening dynamics therefore does not require the assumption of continued network assembly at the apical cortex at longer time (< ∼25 min).
Figure 10.
Snapshots for simulation results for different parameters. (A) Simulation for case of no cytomatrix assembly at the cortex (assembly occurs only at the contact boundary). Network assembly at the cortex is required for translation toward the substratum. (B) Simulation showing the effect of reduced adhesion. Reducing adhesion allows retrograde flow at the substratum; ultimately the flow speed matches the speed of network assembly, yielding steady-state cell and nucleus shapes. The nucleus shape changes cease when spreading stops. (C) Simulation with no contractile stress within the network . Nuclear flattening is predicted to arise from flow alone without requiring actomyosin contractile stresses in the network, consistent with the observation of flattening under myosin inhibition. (D) Simulation of a cell with no resistance to nuclear lamina area expansion. Without area stiffness, the nucleus continues to flatten at a nearly constant volume. (E) Plot of nuclear height (blue line), width (black line), and cell spreading area (green line) versus time for the cases show in (A)–(D). (F) Plot of apparent nuclear surface area (blue line) and volume (green line) for cases (A)–(E). To see this figure in color, go online.
When the substratum adhesion frictional parameter η is reduced, the speed of retrograde flow near the substratum increases (consistent with the molecular clutch model (45)). At a sufficiently low adhesion, cell spreading slows and stops at a steady state before the cell can fully spread, and the nucleus also stops flattening when the cell stops spreading (Fig. 10 B; Movie S5). This result reinforces the prediction that nucleus shape changes tend to follow cell shape changes.
Interestingly, the predicted dynamics of nucleus spreading do not depend significantly on the background tension of network, as shown in the simulation results in Fig. 10 C (Movie S6), where the network tension parameter was set to zero. The differential stresses that cause nuclear shape changes arise primarily from the resistance to expansion or compression of the network, not from the background contractile tension of the network, which is treated in this study as a uniform tension that acts equally on all surfaces. The predicted lack of dependence on contractile tension is consistent with our experimental observation that inhibition of myosin does not prevent nucleus flattening in spreading cells. (It should be noted, however, that if were to vary spatially, the contractility gradient would drive local network flow in the gradient direction.)
As mentioned above, the shape of the flattened nucleus depends on the area stiffness of the nuclear surface. When the area modulus was set to zero, the nucleus continued to flatten as long as the cell continued spreading (Fig. 10 D; Movie S7). This predicted behavior is consistent with the increased nuclear flattening in LMNA−/− MEFs (Fig. 8). Because the nucleus can flatten without changing volume, the dynamics of nucleus flattening did not significantly depend on the value of volume (bulk) modulus of the nucleus (see Materials and Methods for a fuller discussion of sensitivity of the predictions to model parameters).
In summary, the key predictions of the model and simulations are 1) distension/translation of the nucleus toward the surface is driven by assembly of actin at the apical cortex, 2) nuclear flattening is driven by stresses caused by cytoskeletal network expansion/compression upon movement of the cell boundaries, and 3) nuclear shape changes arising without network contractile tension or stress fibers. The model predictions therefore provide an explanation for the experimental observations of nuclear flattening against the substratum without significant actomyosin contractile tension.
Discussion
The flattened nucleus is a common feature of cultured cells, but the mechanisms by which it is flattened have remained obscure. There is mounting evidence that the cytoskeleton exerts forces on the nucleus to position it (20,46–48). In this study, however, we show that as long as the cell was able to spread, inhibiting actomyosin forces, microtubule-based forces and intermediate filaments, as well as the LINC complex, did not prevent nuclear flattening. Remarkably, nuclear height correlated tightly with the degree of cell spreading. Independent of the type of cytoskeletal force perturbed, the nucleus is flat unless the perturbation prevents initial cell spreading, or rounds a spread cell.
This robust feature of nuclear shaping suggests that it is the dynamic deformation of the cell shape itself that causes nuclear flattening consistent with our previous results reporting reversible nuclear deformation caused by proximal cell protrusions in migrating cells (49). The fact that the nuclear apex collapses during the nuclear flattening, opening up a significant distance between the cell apex and the nuclear apex (on the order of a few microns), argues against the cell cortex directly compressing the nucleus downward. The near complete absence of apical actomyosin bundles argues against any explanation for flattening that requires a downward compressive force on the nuclear apex by large actomyosin bundles (see, for example, (50)). That apical fibers do not participate in the flattening process does not argue against later distortion of the nucleus by fully developed actomyosin bundles as reported by others (51).
Neither intermediate filaments nor microtubules are required for flattening. Finally, disruption of the LINC complex via KASH4 overexpression failed to prevent nuclear flattening. It slowed the rate of cell spreading, suggesting perhaps that a coupled nuclear-cytoskeleton is required for rapid F-actin polymerization, but it did not prevent flattening over longer times. Given that myosin activity, microtubules and vimentin intermediate filaments are not required, that the LINC complex is dispensable is perhaps not surprising. We have shown before that KASH4 overexpression results in rounded nuclear shapes in cells on polyacrylamide gels (52). This difference may be because of possibly different cell spreading dynamics on gels versus glass. We note that the cell spreading area in KASH4 cells was lower on gels, suggesting that the relationship between nuclear flattening and cell spreading is conserved on other types of surfaces.
Our computational model demonstrates that expansive/compressive stresses arising from movement of the cell boundaries and centripetal flow of cytoskeletal network from the cell membrane is sufficient to explain translation of the nucleus toward the substratum and subsequent flattening against the substratum. The fact that the experimentally observed flattening dynamics could be closely reproduced using one constitutive equation (Eq. 1), a simple model for cell mechanics, and one fitted parameter provides strong support for the validity of the model assumptions. Moreover, the model successfully predicts a number of experimental findings: the approach to a steady-state flattened nuclear shape despite continued cell spreading, nuclear flattening in the absence of actomyosin tension, increased nuclear flattening in the absence of lamin A/C, and the cessation of nuclear flattening upon the cessation of cell spreading.
Consistent with the assumption that the nucleus is under tension, we found that the volume of the nucleus decreased in myosin-inhibited cells. However, our experiments show that flattening is not a consequence of tension. As explained by the computational model, flattening can instead arise from the motion of the cell boundary transmitting stresses to the nuclear surface because the intervening cytoskeletal network resists expansion or compression. As a result, the nuclear shape changes tend to mimic changes in cell shape during cell spreading.
Interestingly, the presence of actomyosin contraction in normal cells does not alter the dynamics of nuclear shape changes during cell spreading. In the presence of contraction, the net stress on the nuclear surface in the absence of any F-actin assembly from the membrane (such as in serum-starved cells) is likely tensile. However, even if this stress in the network is net compressive (such as when myosin is inhibited), the differential stresses between apex and sides of the nucleus that drive nuclear shape dynamics during cell spreading are predicted to be similar (Fig. 10 C).
In summary, our results point to a surprisingly simple mechanical system in cells for establishing nuclear shapes. Our computational model suggests that nuclear shape changes result from transmission of stress from the moving cell boundary to the nuclear surface because of frictional resistance to expansion/compression of the intervening cytoskeletal network. Nuclear shaping are thus driven by cell shape changes.
Author Contributions
T.P.L., R.B.D., and G.G.G. designed the experiments. R.B.D. did the simulations. Y.L., D.L., Q.Z., R.A.K., S.N., and R.J.Z. conducted the experiments. Y.L., D.L., Q.Z., and R.A.K. analyzed the data. T.P.L., R.B.D., and G.G.G. wrote the manuscript.
Acknowledgments
This work was supported by research grants NIH ROI GM099481 (G.G.G.), NIH R01 EB014869 (T.P.L.), and NIH RO1 GM102486 (T.P.L. and R.B.D.).
Editor: David Odde.
Footnotes
Five figures and seven movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00710-9.
Contributor Information
Tanmay P. Lele, Email: tlele@che.ufl.edu.
Richard B. Dickinson, Email: dickinso@che.ufl.edu.
Supporting Material
The nucleus distends and translates to the substratum then widens as the cell spreads.
All other parameters are shown in Table S1. The nucleus shape mimics changes in boundary shapes.
The cell stops spreading and the nucleus stops flattening at a steady state.
References
- 1.Chow K.H., Factor R.E., Ullman K.S. The nuclear envelope environment and its cancer connections. Nat. Rev. Cancer. 2012;12:196–209. doi: 10.1038/nrc3219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dey P. Cancer nucleus: morphology and beyond. Diagn. Cytopathol. 2010;38:382–390. doi: 10.1002/dc.21234. [DOI] [PubMed] [Google Scholar]
- 3.Jevtić P., Levy D.L. Mechanisms of nuclear size regulation in model systems and cancer. Adv. Exp. Med. Biol. 2014;773:537–569. doi: 10.1007/978-1-4899-8032-8_25. [DOI] [PubMed] [Google Scholar]
- 4.de Las Heras J.I., Batrakou D.G., Schirmer E.C. Cancer biology and the nuclear envelope: a convoluted relationship. Semin. Cancer Biol. 2013;23:125–137. doi: 10.1016/j.semcancer.2012.01.008. [DOI] [PubMed] [Google Scholar]
- 5.True L.D., Jordan C.D. The cancer nuclear microenvironment: interface between light microscopic cytology and molecular phenotype. J. Cell. Biochem. 2008;104:1994–2003. doi: 10.1002/jcb.21478. [DOI] [PubMed] [Google Scholar]
- 6.Burke B., Stewart C.L. Life at the edge: the nuclear envelope and human disease. Nat. Rev. Mol. Cell Biol. 2002;3:575–585. doi: 10.1038/nrm879. [DOI] [PubMed] [Google Scholar]
- 7.Isermann P., Lammerding J. Nuclear mechanics and mechanotransduction in health and disease. Curr. Biol. 2013;23:R1113–R1121. doi: 10.1016/j.cub.2013.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Larrieu D., Britton S., Jackson S.P. Chemical inhibition of NAT10 corrects defects of laminopathic cells. Science. 2014;344:527–532. doi: 10.1126/science.1252651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Worman H.J., Bonne G. “Laminopathies”: a wide spectrum of human diseases. Exp. Cell Res. 2007;313:2121–2133. doi: 10.1016/j.yexcr.2007.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thomas C.H., Collier J.H., Healy K.E. Engineering gene expression and protein synthesis by modulation of nuclear shape. Proc. Natl. Acad. Sci. USA. 2002;99:1972–1977. doi: 10.1073/pnas.032668799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Vergani L., Grattarola M., Nicolini C. Modifications of chromatin structure and gene expression following induced alterations of cellular shape. Int. J. Biochem. Cell Biol. 2004;36:1447–1461. doi: 10.1016/j.biocel.2003.11.015. [DOI] [PubMed] [Google Scholar]
- 12.Misteli T. Beyond the sequence: cellular organization of genome function. Cell. 2007;128:787–800. doi: 10.1016/j.cell.2007.01.028. [DOI] [PubMed] [Google Scholar]
- 13.Solovei I., Wang A.S., Joffe B. LBR and lamin A/C sequentially tether peripheral heterochromatin and inversely regulate differentiation. Cell. 2013;152:584–598. doi: 10.1016/j.cell.2013.01.009. [DOI] [PubMed] [Google Scholar]
- 14.Mekhail K., Moazed D. The nuclear envelope in genome organization, expression and stability. Nat. Rev. Mol. Cell Biol. 2010;11:317–328. doi: 10.1038/nrm2894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wilson K.L., Berk J.M. The nuclear envelope at a glance. J. Cell Sci. 2010;123:1973–1978. doi: 10.1242/jcs.019042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ye Q., Callebaut I., Worman H.J. Domain-specific interactions of human HP1-type chromodomain proteins and inner nuclear membrane protein LBR. J. Biol. Chem. 1997;272:14983–14989. doi: 10.1074/jbc.272.23.14983. [DOI] [PubMed] [Google Scholar]
- 17.Crisp M., Liu Q., Hodzic D. Coupling of the nucleus and cytoplasm: role of the LINC complex. J. Cell Biol. 2006;172:41–53. doi: 10.1083/jcb.200509124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sosa B.A., Rothballer A., Schwartz T.U. LINC complexes form by binding of three KASH peptides to domain interfaces of trimeric SUN proteins. Cell. 2012;149:1035–1047. doi: 10.1016/j.cell.2012.03.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tapley E.C., Starr D.A. Connecting the nucleus to the cytoskeleton by SUN-KASH bridges across the nuclear envelope. Curr. Opin. Cell Biol. 2013;25:57–62. doi: 10.1016/j.ceb.2012.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wu J., Lee K.C., Lele T.P. How dynein and microtubules rotate the nucleus. J. Cell. Physiol. 2011;226:2666–2674. doi: 10.1002/jcp.22616. [DOI] [PubMed] [Google Scholar]
- 21.Levy J.R., Holzbaur E.L.F. Dynein drives nuclear rotation during forward progression of motile fibroblasts. J. Cell Sci. 2008;121:3187–3195. doi: 10.1242/jcs.033878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dupin I., Sakamoto Y., Etienne-Manneville S. Cytoplasmic intermediate filaments mediate actin-driven positioning of the nucleus. J. Cell Sci. 2011;124:865–872. doi: 10.1242/jcs.076356. [DOI] [PubMed] [Google Scholar]
- 23.Gerashchenko M.V., Chernoivanenko I.S., Minin A.A. Dynein is a motor for nuclear rotation while vimentin IFs is a “brake.”. Cell Biol. Int. 2009;33:1057–1064. doi: 10.1016/j.cellbi.2009.06.020. [DOI] [PubMed] [Google Scholar]
- 24.Versaevel M., Grevesse T., Gabriele S. Spatial coordination between cell and nuclear shape within micropatterned endothelial cells. Nat. Commun. 2012;3:671. doi: 10.1038/ncomms1668. [DOI] [PubMed] [Google Scholar]
- 25.Sims J.R., Karp S., Ingber D.E. Altering the cellular mechanical force balance results in integrated changes in cell, cytoskeletal and nuclear shape. J. Cell Sci. 1992;103:1215–1222. doi: 10.1242/jcs.103.4.1215. [DOI] [PubMed] [Google Scholar]
- 26.Chancellor T.J., Lee J., Lele T.P. Actomyosin tension exerted on the nucleus through nesprin-1 connections influences endothelial cell adhesion, migration, and cyclic strain induced reorientation (vol 99, pg 115, 2010) Biophys. J. 2012;102:2411. doi: 10.1016/j.bpj.2010.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Folker E.S., Ostlund C., Gundersen G.G. Lamin A variants that cause striated muscle disease are defective in anchoring transmembrane actin-associated nuclear lines for nuclear movement. Proc. Natl. Acad. Sci. USA. 2011;108:131–136. doi: 10.1073/pnas.1000824108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Luxton G.W.G., Gomes E.R., Gundersen G.G. Linear arrays of nuclear envelope proteins harness retrograde actin flow for nuclear movement. Science. 2010;329:956–959. doi: 10.1126/science.1189072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kuypers L.C., Decraemer W.F., Timmermans J.-P. A procedure to determine the correct thickness of an object with confocal microscopy in case of refractive index mismatch. J. Microsc. 2005;218:68–78. doi: 10.1111/j.1365-2818.2005.01457.x. [DOI] [PubMed] [Google Scholar]
- 30.Evans E., Rawicz W. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 1990;64:2094–2097. doi: 10.1103/PhysRevLett.64.2094. [DOI] [PubMed] [Google Scholar]
- 31.Brangwynne C.P., MacKintosh F.C., Weitz D.A. Force fluctuations and polymerization dynamics of intracellular microtubules. Proc. Natl. Acad. Sci. USA. 2007;104:16128–16133. doi: 10.1073/pnas.0703094104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dahl K.N., Kahn S.M., Discher D.E. The nuclear envelope lamina network has elasticity and a compressibility limit suggestive of a molecular shock absorber. J. Cell Sci. 2004;117:4779–4786. doi: 10.1242/jcs.01357. [DOI] [PubMed] [Google Scholar]
- 33.Lieber A.D., Yehudai-Resheff S., Keren K. Membrane tension in rapidly moving cells is determined by cytoskeletal forces. Curr. Biol. 2013;23:1409–1417. doi: 10.1016/j.cub.2013.05.063. [DOI] [PubMed] [Google Scholar]
- 34.Gauthier N.C., Masters T.A., Sheetz M.P. Mechanical feedback between membrane tension and dynamics. Trends Cell Biol. 2012;22:527–535. doi: 10.1016/j.tcb.2012.07.005. [DOI] [PubMed] [Google Scholar]
- 35.Bausch A.R., Möller W., Sackmann E. Measurement of local viscoelasticity and forces in living cells by magnetic tweezers. Biophys. J. 1999;76:573–579. doi: 10.1016/S0006-3495(99)77225-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Vaziri A., Lee H., Kaazempur Mofrad M.R. Deformation of the cell nucleus under indentation: mechanics and mechanisms. J. Mater. Res. 2006;21:2126–2135. [Google Scholar]
- 37.Bakr A.A. Springer-Verlag; Heidelberg, Germany: 1985. The boundary integral equation method in axisymmetric stress analysis problems. [Google Scholar]
- 38.Brebbia C.A., Telles J.C.F., Wrobel L.C. Theory and Applications in Engineering. Springer-Verlag; Heidelberg, Germany: 1984. Boundary element techniques. [Google Scholar]
- 39.Jurado C., Haserick J.R., Lee J. Slipping or gripping? Fluorescent speckle microscopy in fish keratocytes reveals two different mechanisms for generating a retrograde flow of actin. Mol. Biol. Cell. 2005;16:507–518. doi: 10.1091/mbc.E04-10-0860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Roux K.J., Crisp M.L., Burke B. Nesprin 4 is an outer nuclear membrane protein that can induce kinesin-mediated cell polarization. Proc. Natl. Acad. Sci. USA. 2009;106:2194–2199. doi: 10.1073/pnas.0808602106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Alt W., Dembo M. Cytoplasm dynamics and cell motion: two-phase flow models. Math. Biosci. 1999;156:207–228. doi: 10.1016/s0025-5564(98)10067-6. [DOI] [PubMed] [Google Scholar]
- 42.Dembo M., Harlow F. Cell motion, contractile networks, and the physics of interpenetrating reactive flow. Biophys. J. 1986;50:109–121. doi: 10.1016/S0006-3495(86)83444-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dembo M. Mechanics and control of the cytoskeleton in Amoeba proteus. Biophys. J. 1989;55:1053–1080. doi: 10.1016/S0006-3495(89)82904-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Swift J., Ivanovska I.L., Discher D.E. Nuclear lamin-A scales with tissue stiffness and enhances matrix-directed differentiation. Science. 2013;341:1240104. doi: 10.1126/science.1240104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mitchison T., Kirschner M. Cytoskeletal dynamics and nerve growth. Neuron. 1988;1:761–772. doi: 10.1016/0896-6273(88)90124-9. [DOI] [PubMed] [Google Scholar]
- 46.Wu J., Kent I.A., Lele T.P. Actomyosin pulls to advance the nucleus in a migrating tissue cell. Biophys. J. 2014;106:7–15. doi: 10.1016/j.bpj.2013.11.4489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Petrie R.J., Koo H., Yamada K.M. Generation of compartmentalized pressure by a nuclear piston governs cell motility in a 3D matrix. Science. 2014;345:1062–1065. doi: 10.1126/science.1256965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gundersen G.G., Worman H.J. Nuclear positioning. Cell. 2013;152:1376–1389. doi: 10.1016/j.cell.2013.02.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Alam S.G., Lovett D., Lele T.P. The nucleus is an intracellular propagator of tensile forces in NIH 3T3 fibroblasts. J. Cell Sci. 2015;128:1901–1911. doi: 10.1242/jcs.161703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Vishavkarma R., Raghavan S., Pullarkat P.A. Role of actin filaments in correlating nuclear shape and cell spreading. PLoS One. 2014;9:e107895. doi: 10.1371/journal.pone.0107895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Versaevel M., Braquenier J.-B., Gabriele S. Super-resolution microscopy reveals LINC complex recruitment at nuclear indentation sites. Sci. Rep. 2014;4:7362. doi: 10.1038/srep07362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lovett D.B., Shekhar N., Lele T.P. Modulation of nuclear shape by substrate rigidity. Cell. Mol. Bioeng. 2013;6:230–238. doi: 10.1007/s12195-013-0270-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The nucleus distends and translates to the substratum then widens as the cell spreads.
All other parameters are shown in Table S1. The nucleus shape mimics changes in boundary shapes.
The cell stops spreading and the nucleus stops flattening at a steady state.