Partners or rivals? Strategies for the iterated prisoner's dilemma

Abstract

Within the class of memory-one strategies for the iterated Prisoner's Dilemma, we characterize partner strategies, competitive strategies and zero-determinant strategies. If a player uses a partner strategy, both players can fairly share the social optimum; but a co-player preferring an unfair solution will be penalized by obtaining a reduced payoff. A player using a competitive strategy never obtains less than the co-player. A player using a zero-determinant strategy unilaterally enforces a linear relation between the two players' payoffs. These properties hold for every strategy used by the co-player, whether memory-one or not.

Highlights

• •We consider 3 different strategy classes for the Iterated Prisoner's Dilemma.
• •With partner strategies, players ensure that mutual cooperation is a stable equilibrium.
• •A player using a competitive strategy never obtains less than the co-player
• •With a ZD strategy, a player can unilaterally enforce a linear relation between payoffs.
• •We characterize these 3 classes within the space of memory-one strategies.

1. Introduction

In a one-shot Prisoner's Dilemma (PD) game, the two players have to choose between C and D (to cooperate resp. to defect). Following the notation in Rapoport and Chammah (1965), the payoff matrix is given by

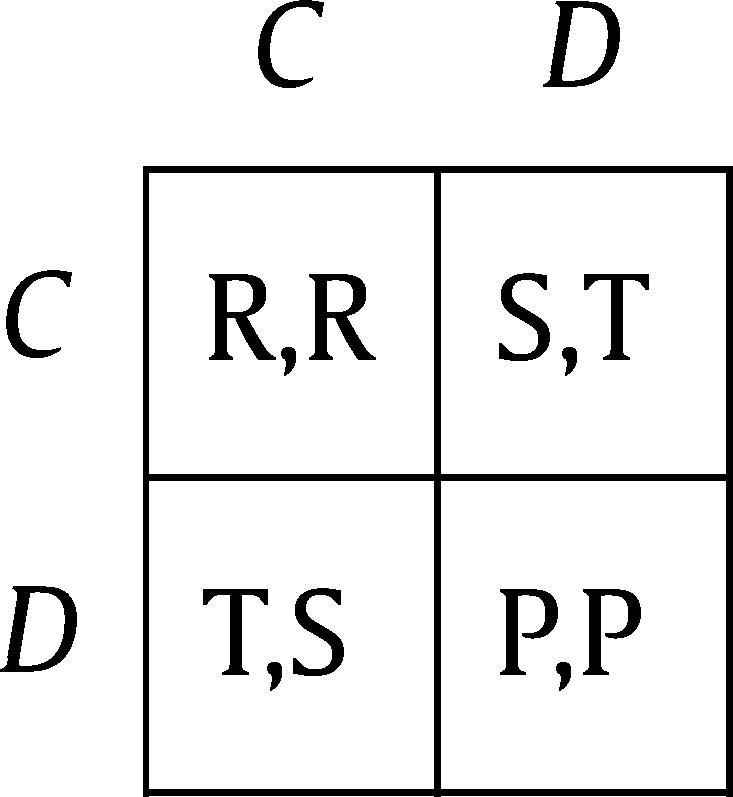(1)

in which the four payoff variables represent the reward for mutual cooperation R, the sucker's payoff S, the temptation to defect T, and the punishment for mutual defection P. Payoffs satisfy the inequalities $T>R>P>S$, such that defection is a dominant strategy, but mutual cooperation is preferred over mutual defection. In addition to these inequalities, we shall also assume that

$$2R>T+S,$$ (2)

such that mutual cooperation is unanimously preferred from a group perspective.¹ In such cases, experimental evidence suggests that many players want to achieve conditional cooperation. They are willing to play C, provided the co-player also plays C (see, e.g., Fehr and Fischbacher, 2003; Yamagishi et al., 2005). However, short of a commitment device, this cannot be ensured. Thus, players either have to trust their co-player, or else use their dominant strategy.

The situation is different for an iterated PD game (IPD). Diverse ‘folk theorems’ state that any feasible and individually rational outcome can be sustained as an equilibrium if the probability δ of a further round is sufficiently large. Such outcomes can be enforced in various ways, and under a wide range of circumstances (see, e.g., Friedman, 1971; Aumann, 1981; Aumann and Shapley, 1994; Fudenberg and Maskin, 1986; Kalai, 1990; Myerson, 1991; Mailath and Olszewski, 2011). If subjects can make binding commitments ahead of the game, then analogous results can be obtained even for one-shot games (Kalai et al., 2010).

Experimental research has uncovered considerable heterogeneity in human social preferences (Colman, 1995; Kagel and Roth, 1997; Camerer, 2003), and a similar variety can be found among the strategies that are played in the IPD (Milinski and Wedekind, 1998; Dal Bó and Fréchette, 2011; Fudenberg et al., 2012). Players who in the one-shot game would opt for conditional cooperation should be willing to engage in ‘partner’ strategies. Such strategies aim for an average payoff R per round, which necessarily provides the same payoff R for the co-player; should the co-player not go along, however, then the co-player's payoff will be less than R. Thus, a partner strategy appeals to the co-player's self-interest in order to further the own self-interest. It is fair, and provides an incentive for the co-player to also be fair. In contrast, some players tend to view their co-player as a rival, rather than a partner. The main purpose, for such competitive players, is to do better, or at least as well as the other player. A preference for dominating the co-player is particularly likely in the context of a game, which often has antagonistic connotations.

The aim of the present manuscript is two-fold: first, we are going to characterize all memory-one strategies which are either competitive, or partner strategies in the sense above. We emphasize that players using such strategies can enforce their preferences against all comers, since we impose no restrictions on the strategies used by the co-players. For partner strategies, the corresponding results in the limiting case of an IPD without discounting have been obtained within the last two years (Akin, 2013; Stewart and Plotkin, 2013, 2014). Here, we are going to extend the theory by allowing for discount factors $\delta \le 1$ (which may either be interpreted as the constant continuation probability of having another round, or as the players' common discount rate on future payoff streams). The recent progress was stimulated by the unexpected discovery of so-called zero-determinant (ZD) strategies, a class of memory-one strategies enforcing a linear relationship between the payoffs of the two players, irrespective of the co-player's strategy (Press and Dyson, 2012). In particular, ZD strategies can fix the co-player's payoff to an arbitrary value between P and R; or ensure that the own ‘surplus’ (over the maximin value P) is twice as large as the co-player's surplus; etc. Also for ZD strategies, we are going to extend the theory to the case when future payoffs are discounted, and $\delta \le 1$.

The nature of our results is somewhat different from usual treatments of repeated games. Our article does not focus on equilibrium behavior (in particular, we do not aim to explore which payoffs rational players can achieve). Instead, we define some interesting properties that a player's strategy may have (e.g., being competitive); and then we are going to characterize all memory-one strategies that have the respective property (independent of whether such a strategy can be sustained as an equilibrium). Thereby, we do not make any assumptions on the behaviors of the co-players (e.g., we do not require them to play best responses, or to follow a predefined equilibrium path). Nevertheless, there are natural connections between several of the described strategy classes and equilibrium behavior, and in that case we will discuss these connections in detail.

In the discussion, we will briefly review the previous development, and in particular the relevant findings in evolutionary game theory (Stewart and Plotkin, 2012, 2013, 2014; Adami and Hintze, 2013; Hilbe et al., 2013a, 2013b; Akin, 2013; Szolnoki and Perc, 2014a, 2014b; Wu and Rong, 2014). In a nutshell, these findings say that in the context of populations of adapting players, partner strategies do well, whereas competitive strategies fare poorly.

2. A fundamental lemma on mean distributions

We consider the standard setup of an IPD with perfect monitoring. In each round, the two players choose whether to cooperate or to defect. That is, they choose an action from their respective action set $A_i=\{C,D\}$, with $i\in \{I,\mathit{II}\}$. The outcome of a given round t can then be described by an action profile $a^t\in A=A_I\times A_{\mathit{II}}$. After each round, both players observe the chosen action profile, and they receive the respective payoffs as specified in the payoff matrix (1). The round t history is a vector $h^t=(a^0,a^1,\dots ,a^{t-1})\in A^t$, and the set of possible histories is the union $\mathcal{H}={\cup }_{t=0}^{\infty }{A}^t$, with the initial history $A^0$ being defined as the null set $A^0=\{\varnothing \}$. A strategy for player i is a rule that tells the player how to act after any possible history; that is, a strategy is a map ${\sigma }_i:\mathcal{H}\to \mathrm{\Delta }(A_i)$, where $\mathrm{\Delta }(A_i)$ denotes the set of probability distributions over the action set $A_i$.²

For given strategies of the two players, let $v_a(t)$ denote the probability that the resulting action profile played in round t is $a\in \{\mathit{CC},\mathit{CD},\mathit{DC},\mathit{DD}\}$. For convenience, we use the following vector notation:

$\mathbf{v}(t)=(v_{\mathit{CC}}(t),v_{\mathit{CD}}(t),v_{\mathit{DC}}(t),v_{\mathit{DD}}(t))$${\mathbf{g}}_{\mathbf{I}}=(R,S,T,P)$${\mathbf{g}}_{\mathbf{II}}=(R,T,S,P)$ (3)

Using this notation, we can write the players' expected payoffs in round t as ${\pi }_I(t)={\mathbf{g}}_{\mathbf{I}}\cdot \mathbf{v}(t)$ and ${\pi }_{\mathit{II}}(t)={\mathbf{g}}_{\mathbf{II}}\cdot \mathbf{v}(t)$. For a discount factor $\delta <1$, the expected payoffs of the repeated game can then be defined by the Abelian means

$${\pi }_I=(1-\delta )\sum _{t=0}^{\infty }{\delta }^t{\pi }_I(t)={\mathbf{g}}_{\mathbf{I}}\cdot \mathbf{v},$$ (4)

and similarly ${\pi }_{\mathit{II}}={\mathbf{g}}_{\mathbf{II}}\cdot \mathbf{v}$, where $\mathbf{v}=(v_{\mathit{CC}},v_{\mathit{CD}},v_{\mathit{DC}},v_{\mathit{DD}})$ refers to the (Abelian) mean distribution

$$\mathbf{v}=(1-\delta )\sum _{t=0}^{\infty }{\delta }^t\mathbf{v}(t).$$ (5)

In the limiting case $\delta =1$, the payoff per round is given by the Cesaro mean

$${\pi }_I=\underset{\tau \to \infty }{\lim }\frac{1}{\tau +1}\sum _{t=0}^{\tau }{\pi }_I(t)$$ (6)

(if this limit exists), and a similar expression for ${\pi }_{\mathit{II}}$.³ A theorem by Frobenius states that if the Cesaro mean exists, it is the limit of the Abelian mean, for $\delta \nearrow 1$.

In the following, we will sometimes focus on players who only take the decisions in the previous round into account.

Definition 1

A strategy σ is a memory-one strategy if $\sigma (h^t)=\sigma ({\tilde{h}}^{t^{\prime }})$ for all histories $h^t=(a^0,\dots ,a^{t-1})$ and ${\tilde{h}}^{t^{\prime }}=({\tilde{a}}^0,\dots ,{\tilde{a}}^{t^{\prime }-1})$ with $t,t^{\prime }\ge 1$ and $a^{t-1}={\tilde{a}}^{t^{\prime }-1}$.

For rounds $t\ge 1$, the move of a memory-one player is therefore solely determined by the action profile played in the previous round (in particular, we note that such players do not condition their behavior on the round number, as sometimes considered in models of bounded recall, e.g. Mailath and Olszewski, 2011). Such memory-one strategies can be written as a 5-tuple $\mathbf{p}=(p_{\mathit{CC}},p_{\mathit{CD}},p_{\mathit{DC}},p_{\mathit{DD}};p_0)$. The element $p_0$ denotes the probability to cooperate in the initial round. The continuation vector $\tilde{\mathbf{p}}:=(p_{\mathit{CC}},p_{\mathit{CD}},p_{\mathit{DC}},p_{\mathit{DD}})$ denotes the conditional probabilities to cooperate in rounds $t\ge 1$, depending on the outcome of the previous round (slightly abusing notation, we let the first letter in the subscript refer to the player's own action in the previous round, and the second letter to the co-player's action. Using this convention, we ensure that the interpretation of a memory-one strategy does not depend on whether the player acts as player I or as player II, see Nowak and Sigmund, 1995). Examples of memory-one strategies include $\mathit{AllD}=(0,0,0,0;0)$, Tit For Tat $(1,0,1,0;1)$, or Win-Stay, Lose-Shift $(1,0,0,1;1)$, see Sigmund (2010) for a comprehensive discussion.

When both players apply a memory-one strategy, the resulting mean distribution v can be calculated explicitly (Nowak and Sigmund, 1995): if player I uses the memory-one strategy $\mathbf{p}=(p_{\mathit{CC}},p_{\mathit{CD}},p_{\mathit{DC}},p_{\mathit{DD}};p_0)$ against a player II with memory-one strategy $\mathbf{q}=(q_{\mathit{CC}},q_{\mathit{CD}},q_{\mathit{DC}},q_{\mathit{DD}};q_0)$, then

$$\mathbf{v}=(1-\delta )\mathbf{v}(0)\cdot {(I_4-\delta M)}^{-1},$$ (7)

where $\mathbf{v}(0)=(p_0{q}_0,p_0(1-q_0),(1-p_0)q_0,(1-p_0)(1-q_0))$ is the initial distribution, $I_4$ is the $4\times 4$ identity matrix, and M is the transition matrix of the Markov chain,

$$M=\left(\begin{array}{cccc}\hfill p_{\mathit{CC}}{q}_{\mathit{CC}}\hfill & \hfill p_{\mathit{CC}}(1-q_{\mathit{CC}})\hfill & \hfill (1-p_{\mathit{CC}})q_{\mathit{CC}}\hfill & \hfill (1-p_{\mathit{CC}})(1-q_{\mathit{CC}})\hfill \\ \hfill p_{\mathit{CD}}{q}_{\mathit{DC}}\hfill & \hfill p_{\mathit{CD}}(1-q_{\mathit{DC}})\hfill & \hfill (1-p_{\mathit{CD}})q_{\mathit{DC}}\hfill & \hfill (1-p_{\mathit{CD}})(1-q_{\mathit{DC}})\hfill \\ \hfill p_{\mathit{DC}}{q}_{\mathit{CD}}\hfill & \hfill p_{\mathit{DC}}(1-q_{\mathit{CD}})\hfill & \hfill (1-p_{\mathit{DC}})q_{\mathit{CD}}\hfill & \hfill (1-p_{\mathit{DC}})(1-q_{\mathit{CD}})\hfill \\ \hfill p_{\mathit{DD}}{q}_{\mathit{DD}}\hfill & \hfill p_{\mathit{DD}}(1-q_{\mathit{DD}})\hfill & \hfill (1-p_{\mathit{DD}})q_{\mathit{DD}}\hfill & \hfill (1-p_{\mathit{DD}})(1-q_{\mathit{DD}})\hfill \end{array}\right).$$ (8)

But even if only one of the players is using a memory-one strategy p, there is still a powerful relationship between p and the resulting mean distribution v.

Lemma 1

Suppose player I applies a memory-one strategy p, and let the strategy of player II be arbitrary, but fixed.

• (i)
  In the case with discounting $(\delta <1)$, let v denote the mean distribution of the repeated game. Then

  $$(\delta p_{\mathit{CC}}-1)v_{\mathit{CC}}+(\delta p_{\mathit{CD}}-1)v_{\mathit{CD}}+\delta p_{\mathit{DC}}{v}_{\mathit{DC}}+\delta p_{\mathit{DD}}{v}_{\mathit{DD}}=-(1-\delta )p_0,$$ (9)

  or in vector notation, $(\delta \tilde{\mathbf{p}}-{\mathbf{g}}_{\mathbf{0}})\cdot \mathbf{v}=-(1-\delta )p_0$, where $g_0=(1,1,0,0)$.
• (ii)
  In the case without discounting, we have

  $$\underset{\tau \to \infty }{\lim }\frac{1}{\tau +1}\sum _{t=0}^{\tau }(\tilde{\mathbf{p}}-{\mathbf{g}}_{\mathbf{0}})\cdot \mathbf{v}(t)=0.$$ (10)

  In particular, if the Cesaro mean distribution v exists, $(\tilde{\mathbf{p}}-{\mathbf{g}}_{\mathbf{0}})\cdot \mathbf{v}=0$.

Proof

Suppose $\delta <1$, and let $q_I(t)$ denote the probability that player I cooperates in round t. Then $q_I(t)={\mathbf{g}}_{\mathbf{0}}\cdot \mathbf{v}(t)$ and $q_I(t+1)=\tilde{\mathbf{p}}\cdot \mathbf{v}(t)$. It follows that $w(t):=\delta q_I(t+1)-q_I(t)$ is given by

$$w(t)=(\delta \tilde{\mathbf{p}}-{\mathbf{g}}_{\mathbf{0}})\cdot \mathbf{v}(t).$$ (11)

Multiplying each $w(t)$ by $(1-\delta ){\delta }^t$ and summing up over $t=0,\dots ,\tau$ yields

$$(1-\delta ){\sum }_{t=0}^{\tau }{\delta }^{t}w(t)=(1-\delta )(\delta q_I(1)-q_I(0)+{\delta }^2{q}_I(2)-\delta q_I(1)\dots )=(1-\delta ){\delta }^{\tau +1}{q}_I(\tau +1)-(1-\delta )q_I(0)\to -(1-\delta )p_0.$$ (12)

On the other hand, due to Eq. (11),

$$(1-\delta )\sum _{t=0}^{\tau }{\delta }^{t}w(t)=(1-\delta )\sum _{t=0}^{\tau }{\delta }^t(\delta \tilde{\mathbf{p}}-{\mathbf{g}}_{\mathbf{0}})\cdot \mathbf{v}(t)\to (\delta \tilde{\mathbf{p}}-{\mathbf{g}}_{\mathbf{0}})\cdot \mathbf{v}$$ (13)

As both limits need to coincide, we have confirmed Eq. (9). For the case without discounting, an analogous calculation as in Eq. (12) yields

$$\frac{1}{\tau +1}\sum _{t=0}^{\tau }w(t)\to 0,$$ (14)

whereas Eq. (13) becomes

$$\frac{1}{\tau +1}\sum _{t=0}^{\tau }w(t)=\frac{1}{\tau +1}\sum _{t=0}^{\tau }(\tilde{\mathbf{p}}-{\mathbf{g}}_{\mathbf{0}})\cdot \mathbf{v}(t).$$ (15)

It follows that the limit of $\frac{1}{\tau +1}{\sum }_{t=0}^{\tau }(\tilde{\mathbf{p}}-{\mathbf{g}}_{\mathbf{0}}).\cdot \mathbf{v}(t)$ for $\tau \to \infty$ exists and equals zero.  □

It is worthwhile to stress the generality of Lemma 1: it neither makes any assumption on the strategy used by the co-player, nor does it depend on the specific payoff constraints of a prisoner's dilemma. In the limiting case $\delta =1$, Lemma 1 allows a geometric interpretation: the mean distribution v (if it exists) is orthogonal to $\tilde{\mathbf{p}}-{\mathbf{g}}_{\mathbf{0}}$ (see Akin, 2013).

3. Partner strategies and competitive strategies

Definition 2

A player's strategy is nice, if the player is never the first to defect. A player's strategy is cautious if the player is never the first to cooperate.

For memory-one strategies, nice strategies fulfill $p_0=p_{\mathit{CC}}=1$, and cautious strategies $p_0=p_{\mathit{DD}}=0$. As an example, the strategy TFT $(1,0,1,0;1)$ is nice, whereas the defector's strategy AllD $(0,0,0,0;0)$ is cautious.

Lemma 2

If $2R>T+S$, then payoffs satisfy ${\pi }_I+{\pi }_{\mathit{II}}\ge 2R$ if and only if ${\pi }_I={\pi }_{\mathit{II}}=R$ (which for $\delta <1$ holds if and only if both players are nice). Similarly, if $2P<T+S$, then ${\pi }_I+{\pi }_{\mathit{II}}\le 2P$ if and only if ${\pi }_I={\pi }_{\mathit{II}}=P$ (which for $\delta <1$ is equivalent to both players being cautious).

Proof

Due to Eq. (4), ${\pi }_I+{\pi }_{\mathit{II}}=({\mathbf{g}}_{\mathbf{I}}+{\mathbf{g}}_{\mathbf{II}})\cdot \mathbf{v}=(2R,T+S,T+S,2P)\cdot \mathbf{v}$. As $2R>T+S$, the inequality ${\pi }_I+{\pi }_{\mathit{II}}\ge 2R$ implies $v_{\mathit{CC}}=1$. For $\delta <1$, this requires both players to cooperate in every round (if $\delta =1$, it only requires the players to cooperate in almost every round). Similarly, for a prisoner's dilemma with $2P<T+S$, the inequality ${\pi }_I+{\pi }_{\mathit{II}}\le 2P$ implies $v_{\mathit{DD}}=1$.  □

Definition 3

• (i)
  A partner strategy for player I is a nice strategy such that, irrespective of the co-player's strategy,

  $${\pi }_I<R\Rightarrow {\pi }_{\mathit{II}}<R.$$ (16)
• (ii)
  A competitive strategy for player I is a strategy such that, irrespective of the co-player's strategy,

  $${\pi }_I\ge {\pi }_{\mathit{II}}.$$ (17)

Fig. 1 gives a schematic illustration of these two strategy classes. The definition of partner strategies implies that these strategies are best replies to themselves, and thus they are Nash equilibria. Even more, because condition (16) is equivalent to $({\pi }_{\mathit{II}}\ge R)\Rightarrow ({\pi }_I\ge R)$, we can conclude due to Lemma 2 that $({\pi }_{\mathit{II}}\ge R)\Rightarrow ({\pi }_I={\pi }_{\mathit{II}}=R)$. Thus, no matter which best reply the co-player applies, a player with a partner strategy will always obtain the mutual cooperation payoff R.

Fig. 1.

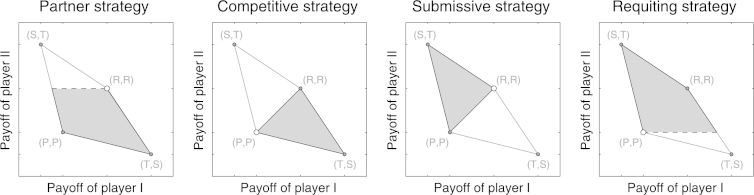
Schematic representation of partner strategies, competitive strategies, submissive strategies and requiting strategies. The grey-shaded area depicts the set of possible payoff pairs when player I adopts a strategy of the respective strategy class. The white dot represents the payoff that player I gets against a co-player using the same strategy.

On the other hand, players with a competitive strategy always obtain at least the co-player's payoff. It is easy to see that for $\delta <1$ a competitive strategy needs to be cautious (otherwise the focal player would be outcompeted by an AllD-player). In the limiting case $\delta =1$, competitiveness is closely related to the concept of being unbeatable, as introduced by Duersch et al. (2012). A strategy for player I is unbeatable, if against any co-player and for any number of rounds, the payoff differential ${\sum }_{t=0}^{\tau }({\pi }_{\mathit{II}}(t)-{\pi }_I(t))$ is bounded from above (in particular, if the average payoffs per round converge to ${\pi }_I$ and ${\pi }_{\mathit{II}}$, then ${\pi }_I\ge {\pi }_{\mathit{II}}$).

Proposition 1

For a player I with a nice memory-one strategy p, the following are equivalent:

• (i)p is a partner strategy;
• (ii)If the co-player uses either AllD or the strategy $(0,1,1,1;0)$, then ${\pi }_{\mathit{II}}<R$;
• (iii)
  The two inequalities $B_1<0$ and $B_2<0$ hold, with

  $B_1=\delta (T-R)p_{\mathit{DD}}-\delta (R-P)(1-p_{\mathit{CD}})+(1-\delta )(T-R)$$B_2=\delta (T-R)p_{\mathit{DC}}-\delta (R-S)(1-p_{\mathit{CD}})+(1-\delta )(T-R).$ (18)

Proof

(i) ⇒ (ii)

Assume to the contrary that ${\pi }_{\mathit{II}}\ge R$. Then the definition of partner strategies implies that ${\pi }_I={\pi }_{\mathit{II}}=R$. Since all players use memory-one strategies, this would require that everyone cooperates after mutual cooperation, which is neither true for $\mathit{AllD}=(0,0,0,0;0)$ nor for the strategy $(0,1,1,1;0)$.

(ii) ⇒ (iii)

Against a player using a nice memory-one strategy p (with $p_0=p_{\mathit{CC}}=1$), the payoff of an AllD co-player is given by

$${\hat{\pi }}_{\mathit{II}}=\frac{(1-\delta )T+\delta P-\delta P{p}_{\mathit{CD}}+\delta T{p}_{\mathit{DD}}}{1+\delta (p_{\mathit{DD}}-p_{\mathit{CD}})}.$$ (19)

We note that this payoff is also defined when $\delta =1$, because $p_{\mathit{CD}}<1$ (otherwise p would satisfy $p_0=p_{\mathit{CC}}=p_{\mathit{CD}}=1$, and player I would always cooperate. In that case, an AllD co-player would receive $T>R$, which is ruled out by (ii)). Elementary algebra yields

$$\begin{array}{ccc}\hfill B_1\hfill & \hfill =\hfill & (1+\delta (p_{\mathit{DD}}-p_{\mathit{CD}}))({\hat{\pi }}_{\mathit{II}}-R),\hfill \end{array}$$ (20)

In particular, $B_1$ has the same sign as ${\hat{\pi }}_{\mathit{II}}-R$. On the other hand, if the co-player uses the strategy (0,1,1,1;0), the co-player's payoff is

$${\tilde{\pi }}_{\mathit{II}}=\frac{(1-\delta )T+\delta S+\delta ((1-\delta )R-S)p_{\mathit{CD}}+\delta (T+\delta R)p_{\mathit{DC}}}{1+{\delta }^2(p_{\mathit{DC}}-p_{\mathit{CD}})+\delta p_{\mathit{DC}}},$$ (21)

and

$$\begin{array}{ccc}\hfill B_2\hfill & \hfill =\hfill & (1+{\delta }^2(p_{\mathit{DC}}-p_{\mathit{CD}})+\delta p_{\mathit{DC}})({\tilde{\pi }}_{\mathit{II}}-R).\hfill \end{array}$$ (22)

Therefore, $B_2$ has the same sign as ${\tilde{\pi }}_{\mathit{II}}-R$.

(iii) ⇒ (i)

Suppose that $B_1<0$ and $B_2<0$, and that ${\pi }_{\mathit{II}}\ge R$. We need to show that ${\pi }_{\mathit{II}}={\pi }_I=R$. As ${\pi }_{\mathit{II}}-R=({\mathbf{g}}_{\mathbf{II}}-R\mathbf{1})\cdot \mathbf{v}$, with $\mathbf{1}=(1,1,1,1)$, we note that ${\pi }_{\mathit{II}}\ge R$ is equivalent to

$$(T-R)v_{\mathit{CD}}-(R-S)v_{\mathit{DC}}-(R-P)v_{\mathit{DD}}\ge 0.$$ (23)

Using the linear equations $\mathbf{1}\cdot \mathbf{v}=1$ and $(\delta \tilde{\mathbf{p}}-{\mathbf{g}}_{\mathbf{0}})\cdot \mathbf{v}=-(1-\delta )$ (Lemma 1 with $p_0=p_{\mathit{CC}}=1$, since the memory-one strategy is nice), we calculate $v_{\mathit{CD}}$ as a function of $v_{\mathit{DC}}$ and $v_{\mathit{DD}}$:

$$v_{\mathit{CD}}=\frac{(1-(1-p_{\mathit{DC}})\delta ))v_{\mathit{DC}}+(1-(1-p_{\mathit{DD}})\delta )v_{\mathit{DD}}}{(1-p_{\mathit{CD}})\delta }.$$ (24)

The denominator of $v_{\mathit{CD}}$ is positive, as $B_1<0$ implies $p_{\mathit{CD}}<1$. Plugging (24) into (23) and multiplying both sides with $(1-p_{\mathit{CD}})\delta$ shows that ${\pi }_{\mathit{II}}\ge R$ if and only if

$$B_2{v}_{\mathit{DC}}+B_1{v}_{\mathit{DD}}\ge 0,$$ (25)

with $B_1$ and $B_2$ as defined in (18). Thus, the assumptions $B_1<0$ and $B_2<0$ indicate that $v_{\mathit{DC}}=v_{\mathit{DD}}=0$, and by (24) that $v_{\mathit{CD}}=0$. We conclude that $v_{\mathit{CC}}=1$, and therefore ${\pi }_I={\pi }_{\mathit{II}}=R$, i.e., p is a partner strategy.

 □

For example, TFT is a partner strategy if and only if $\delta >\frac{T-R}{T-P}$ and $\delta >\frac{T-R}{R-S}$, whereas WSLS is a partner strategy if and only if $\delta >\frac{T-R}{R-P}$ and $\delta >\frac{T-R}{T-S}$, which is a sharper condition. In analogy to the definition of partner strategies, one may define a mild partner strategy for player I as a nice strategy such that ${\pi }_I\le R$ implies ${\pi }_{\mathit{II}}\le R$, irrespective of the co-player's strategy.⁴ For memory-one strategies, the characterization of mild partner strategies is analogous to the characterization of partner strategies (only the strict inequalities in Proposition 1 need to be replaced by weak inequalities).

Proposition 1 also provides an interesting connection to the folk theorems. The existence of an equilibrium with individually rational payoffs (${\pi }_I,{\pi }_{\mathit{II}}$) in the IPD is typically shown by applying trigger strategies – any deviation from the equilibrium path is punished with relentless defection (as for example in Friedman, 1971).⁵ The following Corollary states that trigger strategies are, in some sense, the most effective means to enforce a cooperative equilibrium in the IPD.

Corollary 1

For a given prisoner's dilemma and a given continuation probability δ, there exists a memory-one partner strategy if and only if the trigger strategy Grim $=(1,0,0,0;1)$ is a partner strategy.

Proof

The two quantities $B_1$ and $B_2$ in Proposition 1 are minimal for $p_{\mathit{CD}}=p_{\mathit{DC}}=p_{\mathit{DD}}=0$. Thus, if there is a memory-one strategy that meets the inequalities $B_1<0$ and $B_2<0$, then the corresponding inequalities are also met by Grim.  □

From Corollary 1, we may also conclude that partner strategies exist if and only if $\delta >\frac{T-R}{T-P}$ (this condition for the existence of fully cooperative equilibria has been previously derived by Roth and Murnighan, 1978; Stahl, 1991).

Let us next give a characterization of competitive memory-one strategies:

Proposition 2

Suppose player I applies the memory-one strategy p. Then the following are equivalent:

• (i)p is competitive.
• (ii)If the co-player uses either AllD or the strategy $(0,0,0,1;0)$, then ${\pi }_I\ge {\pi }_{\mathit{II}}$.
• (iii)The entries of p satisfy $p_0=p_P=0$ and $\delta (p_{\mathit{CD}}+p_{\mathit{DC}})\le 1$.

Proof

(i) ⇒ (ii)

Follows immediately from the definition, a competitive strategy yields ${\pi }_I\ge {\pi }_{\mathit{II}}$ against any co-player.

(ii) ⇒ (iii)

If player II applies AllD, then an explicit calculation of payoffs yields

$${\pi }_I-{\pi }_{\mathit{II}}=-\frac{(T-S)((1-\delta )p_0+\delta p_{\mathit{DD}})}{1+\delta (p_{\mathit{DD}}-p_{\mathit{CD}})},$$ (26)

and thus ${\pi }_I\ge {\pi }_{\mathit{II}}$ implies $p_0=p_{\mathit{DD}}=0$. Similarly, if player II applies the strategy $(0,0,0,1;0)$, we obtain (using $p_0=p_{\mathit{DD}}=0$):

$${\pi }_I-{\pi }_{\mathit{II}}=\frac{\delta (T-S)(1-\delta (p_{\mathit{CD}}+p_{\mathit{DC}}))}{1+\delta (1-(1+\delta )p_{\mathit{CD}}+\delta p_{\mathit{DC}})}.$$ (27)

This is non-negative if and only if $\delta (p_{\mathit{CD}}+p_{\mathit{DC}})\le 1$.

(iii) ⇒ (i)

By Lemma 1 and as $p_{\mathit{DD}}=p_0=0$,

$$\delta p_{\mathit{DC}}{v}_{\mathit{DC}}=(1-\delta p_{\mathit{CC}})v_{\mathit{CC}}+(1-\delta p_{\mathit{CD}})v_{\mathit{CD}}.$$ (28)

Using the inequality $\delta p_{\mathit{DC}}\le 1-\delta p_{\mathit{CD}}$, this leads to

$$(1-\delta p_{\mathit{CD}})v_{\mathit{DC}}\ge (1-\delta p_{\mathit{CC}})v_{\mathit{CC}}+(1-\delta p_{\mathit{CD}})v_{\mathit{CD}},$$ (29)

or equivalently $(1-\delta p_{\mathit{CD}})(v_{\mathit{DC}}-v_{\mathit{CD}})\ge (1-\delta p_{\mathit{CC}})v_{\mathit{CC}}$. This implies $v_{\mathit{DC}}\ge v_{\mathit{CD}}$. As a consequence, ${\pi }_I-{\pi }_{\mathit{II}}=({\mathbf{g}}_{\mathbf{I}}-{\mathbf{g}}_{\mathbf{II}})\cdot \mathbf{v}=(T-S)(v_{\mathit{DC}}-v_{\mathit{CD}})\ge 0$.

 □

Fig. 2 shows the space of partner strategies (and the space of competitive strategies) as subsets of the nice memory-one strategies (cautious memory-one strategies), respectively. One can also define the dual properties, and derive the corresponding characterizations: a strategy for player I is said to be submissive if payoffs always satisfy ${\pi }_I\le {\pi }_{\mathit{II}}$, irrespective of the strategy of player II; and a cautious strategy for player I is said to be requiting if ${\pi }_I>P$ implies ${\pi }_{\mathit{II}}>P$ (see Fig. 1 for a schematic representation of these strategy classes). The corresponding characterizations are:

Fig. 2.

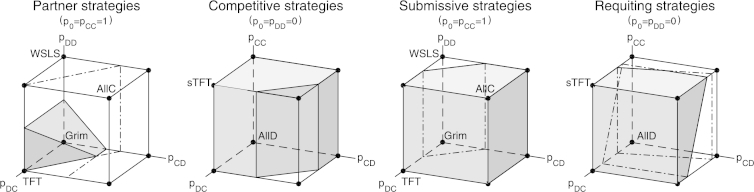
The space of partner strategies, competitive strategies, submissive strategies and requiting strategies. Each grey block represents the set of strategies that fulfill the respective constraints in Propositions 1–4. For this representation, the continuation probability was set to δ = 2/3, using the payoff values in Axelrod (1984), i.e. T = 5, R = 3, P = 1, S = 0. The depicted pure strategies are: TFT = (1,0,1,0;1), Grim = (1,0,0,0;1), Win-stay lose-shift: WSLS = (1,0,0,1;1), AllC = (1,1,1,1;1), AllD = (0,0,0,0;0) and suspicious Tit For Tat: sTFT = (1,0,1,0;0).

Proposition 3

Suppose player I applies the memory-one strategy p. Then the following are equivalent:

• (i)p is submissive;
• (ii)If the co-player uses either AllC or the strategy $(0,1,1,1;1)$, then ${\pi }_I\le {\pi }_{\mathit{II}}$;
• (iii)The entries of p satisfy $p_0=p_{\mathit{CC}}=1$ and $\delta (1-p_{\mathit{CD}})+\delta (1-p_{\mathit{DC}})\le 1$.

Proposition 4

Suppose the game payoffs satisfy $2P<T+S$. Then, for a player I with a cautious memory-one strategy p, the following are equivalent:

• (i)p is requiting;
• (ii)If the co-player uses either AllC or the strategy $(0,0,0,1;1)$, then ${\pi }_{\mathit{II}}>P$;
• (iii)
  The two inequalities $B_1>0$ and $B_2>0$ hold, with

  $B_1=\delta (R-P)p_{\mathit{DC}}+\delta (P-S)p_{\mathit{CC}}-(P-S),$$B_2=\delta (T-P)p_{\mathit{DC}}+\delta (P-S)p_{\mathit{CD}}-(P-S).$ (30)

4. ZD-strategies

The previous results have highlighted how Lemma 1 can be used to characterize several interesting strategy classes within the space of memory-one strategies (for example, the strategies that allow a player to outcompete the opponent, or the strategies that provide incentives to reach the social optimum). In the following, we present another application of Lemma 1: there are strategies with which a player can unilaterally enforce a linear relationship between the players' payoffs.

Definition 4

A memory-one strategy p is said to be a ZD strategy if there exist constants $\alpha ,\beta ,\gamma$ such that

$$\delta \tilde{\mathbf{p}}=\alpha {\mathbf{g}}_{\mathbf{I}}+\beta {\mathbf{g}}_{\mathbf{II}}+(\gamma -(1-\delta )p_0)\mathbf{1}+{\mathbf{g}}_{\mathbf{0}}.$$ (31)

Proposition 5

Let $\delta <1$, and suppose player I applies a memory-one strategy p satisfying Eq. (31). Then, irrespective of the strategy of the co-player,

$$\alpha {\pi }_I+\beta {\pi }_{\mathit{II}}+\gamma =0.$$ (32)

The same relation holds for $\delta =1$, provided that the payoffs ${\pi }_I$ and ${\pi }_{\mathit{II}}$ exist.⁶

Proof

This follows directly from Lemma 1, using the identities ${\pi }_I={\mathbf{g}}_{\mathbf{I}}\cdot \mathbf{v}$, ${\pi }_{\mathit{II}}={\mathbf{g}}_{\mathbf{II}}\cdot \mathbf{v}$, and $1=\mathbf{1}\cdot \mathbf{v}$.  □

In the following, let $\delta <1$. We proceed with a slightly different representation of ZD strategies, using the parameter transformation $\alpha =\varphi \chi$, $\beta =-\varphi$, and $\gamma =\varphi \kappa (1-\chi )$.⁷ Under this transformation, ZD strategies take the form

$$\begin{array}{ccc}\delta \tilde{\mathbf{p}}\hfill & \hfill =\hfill & \varphi [(1-\chi )(\kappa \mathbf{1}-{\mathbf{g}}_{\mathbf{I}})+({\mathbf{g}}_{\mathbf{I}}-{\mathbf{g}}_{\mathbf{II}})]-(1-\delta )p_0\mathbf{1}+{\mathbf{g}}_{\mathbf{0}},\hfill \end{array}$$ (33)

and the enforced payoff relationship according to (32) becomes

$${\pi }_{\mathit{II}}-\kappa =\chi ({\pi }_I-\kappa ).$$ (34)

Eq. (34) implies that the payoffs lie on a line segment intersecting the diagonal at some value κ (the payoff for the ZD-strategy against itself) and having a slope χ (see Fig. 3).

Fig. 3.

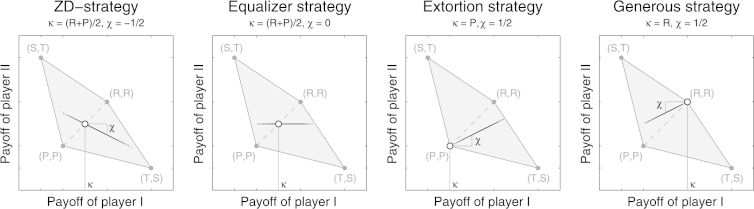
Characteristic payoff relations for ZD strategies, equalizer strategies, extortion strategies and generous strategies. The grey-shaded area represents the set of feasible payoffs. In each graph, the strategy of player I was fixed, whereas for the strategy of player II we sampled 1000 random memory-one strategies. The resulting payoffs were drawn as black dots. For general ZD-strategies, these dots are on a line (intersecting the diagonal at κ, and having slope χ). Equalizer strategies have the additional property that the slope χ is zero, i.e. the payoff of co-player II is fixed to κ, independent of the co-player's strategy. Extortion strategies are ZD-strategies with κ = P and 0 < χ < 1, and generous strategies fulfill κ = R and 0 < χ < 1. For this figure, we have used the payoff values in Axelrod (1984), T = 5, R = 3, P = 1, S = 0, and continuation probability δ = 4/5. For the strategy of player I we have used: (i) ZD-strategy p = (0.85,0.725,0.1,0.35;0.1); (ii) Equalizer strategy p = (0.875,0.375,0.375,0.125;0.5); (iii) Extortion strategy p = (1,0.125,0.75,0;0); (iv) Generous strategy p = (1,0.125,0.75,0;1).

Players cannot use ZD strategies to enforce arbitrary payoff relationships of the form (34): since the entries of the continuation vector $\tilde{\mathbf{p}}$ correspond to conditional probabilities (and hence need to be in the unit interval), the parameters κ, χ and ϕ need to obey certain restrictions. This gives rise to the following definition.

Definition 5

For a given δ, we call a payoff relationship $(\kappa ,\chi )\in {\mathbb{R}}^2$ enforceable if there are $\varphi \in \mathbb{R}$ and $p_0\in [0,1]$ such that each entry of the continuation vector $\tilde{\mathbf{p}}$ according to Eq. (33) is in [0,1]. We refer to the set of all enforceable payoff relationships as ${\mathcal{E}}_{\delta }$.

Proposition 6

• (i)The set of enforceable payoff relationships is monotonically increasing in the discount factor: if ${\delta }^{\prime }\le {\delta }^{″}$, then ${\mathcal{E}}_{{\delta }^{\prime }}\subseteq {\mathcal{E}}_{{\delta }^{″}}$.
• (ii)
  There is a $\delta <1$ such that $(\kappa ,\chi )\in {\mathcal{E}}_{\delta }$ if and only if $-1<\chi <1$ and

  $$\max \{P,\frac{S-T\chi }{1-\chi }\}\le \kappa \le \min \{R,\frac{T-S\chi }{1-\chi }\},$$ (35)

  with at least one inequality in (35) being strict.

Proof

• (i)
  According to the definition, $(\kappa ,\chi )\in {\mathcal{E}}_{\delta }$ if and only if one can find $\varphi \in \mathbb{R}$ and $p_0\in [0,1]$, such that the corresponding continuation vector $\tilde{\mathbf{p}}$ according to Eq. (33) satisfies $\mathbf{0}\le \delta \tilde{\mathbf{p}}\le \delta \mathbf{1}$, or equivalently,

  $$(1-\delta )(1-p_0)\le \varphi (1-\chi )(R-\kappa )\le 1-(1-\delta )p_0$$ (36a)

  $$(1-\delta )(1-p_0)\le \varphi [(1-\chi )(S-\kappa )+T-S]\le 1-(1-\delta )p_0$$ (36b)

  $$(1-\delta )p_0\le \varphi [(1-\chi )(\kappa -T)+T-S]\le \delta +(1-\delta )p_0$$ (36c)

  $$(1-\delta )p_0\le \varphi (1-\chi )(\kappa -P)\le \delta +(1-\delta )p_0$$ (36d)

  We note that in (36a)–(36d), the left hand side is monotonically decreasing in δ, whereas the right hand side is monotonically increasing in δ. In particular, if the conditions (36) are satisfied for some ${\delta }^{\prime }\le 1$ they are also satisfied for any ${\delta }^{″}\ge {\delta }^{\prime }$.
• (ii)
  • (⇒)
    Suppose $(\kappa ,\chi )\in {\mathcal{E}}_{\delta }$, and therefore the conditions (36) hold for appropriate parameters ϕ and $p_0$. Summing up the first inequality in (36a) and the first inequality in (36d) shows

    $$1-\delta \le \varphi (1-\chi )(R-P).$$ (37)

    Similarly, by taking the inequalities in (36b) and (36c), we get

    $$1-\delta \le \varphi (1+\chi )(T-S).$$ (38)

    In particular, $0<\varphi (1-\chi )$ and $0<\varphi (1+\chi )$, and therefore $\varphi >0$ and $-1<\chi <1$. Moreover, the conditions (36) imply

    $0\le \varphi (1-\chi )(R-\kappa )$$0\le \varphi [(1-\chi )(S-\kappa )+T-S]$$0\le \varphi [(1-\chi )(\kappa -T)+T-S]$$0\le \varphi (1-\chi )(\kappa -P).$ (39)

    Since $\varphi >0$ and $\chi <1$, these conditions are equivalent to condition (35). If none of the inequalities in (35) was strict, then (36a) or (36b) would require $p_0=1$, whereas (36c) or (36d) would require $p_0=0$.
  • (⇐)
    Conversely, let $-1<\chi <1$, and suppose $\max \{P,\frac{S-T\chi }{1-\chi }\}\le \kappa <\min \{R,\frac{T-S\chi }{1-\chi }\}$. Then the inequalities (39) hold for any choice of $\varphi >0$, with the first two inequalities being strict. In particular, we can choose a ϕ sufficiently small such that each term on the right hand's side of (39) is bounded from above by 1/2. By setting $p_0=0$ and choosing a δ sufficiently close to one, it thus follows that all inequalities in (36) can be satisfied. An analogous argument holds when $\kappa =\min \{R,\frac{T-S\chi }{1-\chi }\}$, in which case one needs to set $p_0=1$.

 □

The first part of Proposition 6 shows that a given linear payoff relationship of the form (34) is easier to enforce when players are sufficiently patient. As $\delta \to 1$, the limiting set of enforceable payoff relationships ($\kappa ,\chi$) is characterized by Proposition 6(ii); Fig. 4 provides an illustration.

Fig. 4.

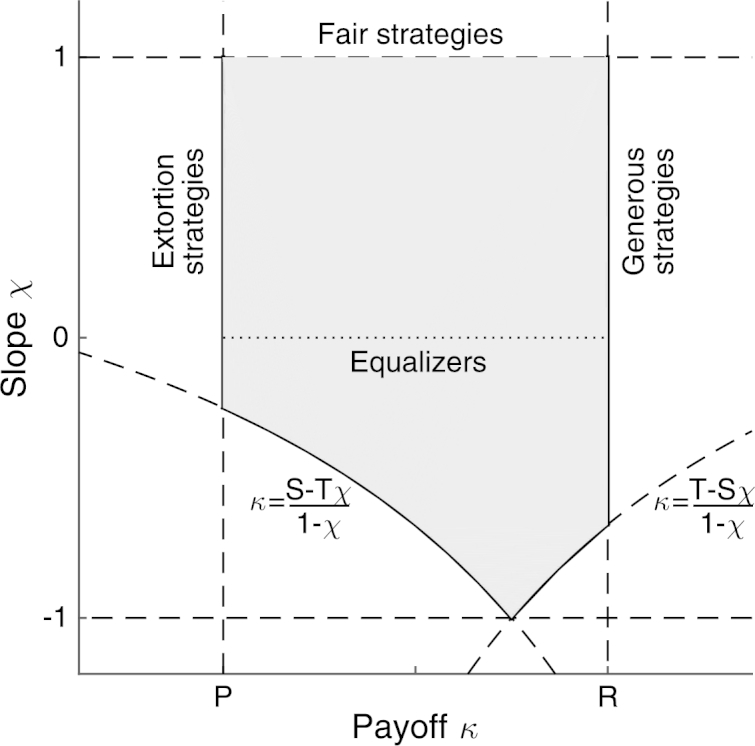
Enforceable payoff relationships for players with a ZD strategy. The grey area depicts all pairs (κ,χ) that are enforceable when the discount factor δ is sufficiently close to one, as characterized in Proposition 6. The graph also depicts some particular subclasses of ZD strategies: equalizer strategies (χ = 0), extortion strategies (κ = P, χ > 0), and generous strategies (κ = R, χ > 0). The so-called fair strategies (with χ = 1) do only exist in the limit of no discounting, δ = 1. For the illustration, we have taken the payoff values in Axelrod (1984), i.e. T = 5, R = 3, P = 1, S = 0.

There are various remarkable subclasses of ZD strategies (as depicted in Fig. 3 and Fig. 4). For $\chi =0$, we encounter so-called equalizer strategies (see Boerlijst et al., 1997; Press and Dyson, 2012). By Eq. (34), player I can make use of such strategies to prescribe κ as payoff for player II. A player can thus determine the opponent's payoff (however, player I cannot fix the own payoff, since this would require χ to be unbounded, which is ruled out by Proposition 6). Press and Dyson (2012) also highlighted the class of extortion strategies (with $\kappa =P$ and $0<\chi <1$). Extortion strategies guarantee that the own ‘surplus’ over the minimax payoff P exceeds the opponent's surplus by a factor of ${\chi }^{-1}$. Moreover, since $\chi >0$, the payoffs of the two players are positively related. Hence, to maximize the own payoff, player II needs to maximize player I's payoff: the best response against an extortioner is to cooperate unconditionally. As a counterpart to extortioners, Stewart and Plotkin (2012) defined the class of generous strategies, which satisfy Eq. (34) with $\kappa =R$ and $0<\chi <1$. Players using a generous strategy shoulder a larger burden of the loss (with respect to the social optimum R) than their co-player. Since $\chi >0$, they also ensure that the payoffs of the two players are aligned, thereby motivating the co-player to cooperate. Finally, for games without discounting it was noted that strategies with $\chi =1$ enforce ${\pi }_I={\pi }_{\mathit{II}}$ (for $\delta =1$, TFT is an example of such a fair strategy, see Press and Dyson, 2012; Hilbe et al., 2014b). However, as Proposition 6 shows, fair strategies cease to exist when future payoffs are discounted, and only approximately fair strategies (with χ close to one) may be feasible.

ZD strategies can also be connected to the strategy classes discussed in the previous section. Generous strategies, for example, are exactly the ZD strategies which are submissive partner strategies (in particular it follows that every generous strategy is a Nash equilibrium of the IPD). On the other hand, for stage games with $2P<T+S$ (which ensures ${\pi }_I+{\pi }_{\mathit{II}}\ge 2P$), extortion strategies are precisely those ZD strategies which are requiting and competitive.

We note that herein, we have entirely focused on the repeated prisoner's dilemma, due to the central role that this simple game situation takes in the literature on the evolution of cooperation (Rapoport and Chammah, 1965; Trivers, 1971; Sugden, 1986; Axelrod, 1984; Sigmund, 2010). However, the proofs of Lemma 1 and Proposition 5 did not require any assumptions on the payoff values (and in the proof of Proposition 6, we have only made use of the assumptions $R>P$ and $T>S$). Moreover, for $\delta =1$, it was recently shown that similar results can also be obtained for stage games with 2 actions but $n\ge 2$ players (Hilbe et al., 2014b). Thus, while we believe that our results are most intuitive in the context of a prisoner's dilemma, the mathematics can be extended to more general strategic situations.

5. Discussion

The recent development began with the paper of Press and Dyson (2012) introducing ZD strategies for repeated games without discounting. In this context, Press and Dyson derived the linear relation (32). Their proof was based on a neat formula for the payoffs achieved if both players use memory-one strategies. This formula only involves vanishing determinants, which explains the name ZD. Press and Dyson highlighted those ZD strategies that fix the co-player's payoff to a given value between P and R, as well as the sinister properties of extortion strategies. They also stressed the fact that more complex strategies (based on larger memories, for instance) are not able to profit from their sophistication to gain the upper hand. The intriguing aspects of ZD strategies raised considerable attention (see, e.g., Ball, 2012). In the News section of the American Mathematical Society, it was stated that 'the world of game theory is currently on fire.' A more skeptical view could be found among economists. The well-known folk theorem for repeated games states that trigger strategies can induce a rational co-player to agree to any feasible payoff pair above the minimax level P, by threatening to switch to relentless defection otherwise (see Aumann, 1981; Kalai, 1990; Fudenberg and Maskin, 1986, 1990). Seen from this angle, the progress consisted merely in displaying memory-one strategies with a similar power to enforce specific payoff pairs. However, there is a subtle difference: whereas the Folk theorems are based on the assumption that players wish to maximize their payoffs, the results presented herein are independent of such an assumption. Interpreted in this way, we have explored how much control player I can exert on the resulting payoffs without being sure about the motives of player II.

Memory-one strategies able to fix the co-player's payoff had already been derived in Boerlijst et al. (1997) and Sigmund (2010), based on an approach different from that of Press and Dyson (2012). This method was used in Hilbe et al. (2013a) to provide another derivation of (32), not involving any determinants. It was substantially extended by Akin (2013) to yield a general equation for the mean distribution of memory-one strategies when $\delta =1$. In this case, the mean distribution is understood in the sense of Cesaro, and need not always exist. In Lemma 1, we have extended this approach to cover the case $\delta <1$, from which Akin's result for $\delta =1$ immediately follows. Lemma 1 offers a geometric tool for the investigation of memory-one strategies. The vector $\delta \tilde{\mathbf{p}}$ consists of the conditional probabilities to play C in the next round (δ is the probability that there is a next round), whereas ${\mathbf{g}}_{\mathbf{0}}$ can be viewed as 'conditional probability' to play C in the current round. In the limit of no discounting, Lemma 1 states that no matter which strategy player II is using, the limiting distribution v (if it exists) is on a hyperplane orthogonal to the difference of these two conditional probabilities. It was also Akin (2013) who extended the investigations beyond the case of ZD-strategies, to characterize partner strategies for $\delta =1$ (calling them 'good' strategies, a term we feel is too general).

In a comments article, Stewart and Plotkin (2012) introduced an example of a generous strategy, and showed that in a round robin tournament conducted after the fashion of Axelrod (1984), this generous strategy emerged as winner. Stewart and Plotkin also asked whether ZD strategies were relevant for evolutionary game theory. In this context, one considers a population of players, each equipped with a strategy. The players are then allowed to imitate other strategies, preferentially those with a higher payoff (see, e.g., Weibull, 1995; Samuelson, 1997; Hofbauer and Sigmund, 1998; Nowak, 2006; Sandholm, 2010).

It is obvious that extortion strategies cannot spread too much in such an evolutionary context; if they become too common, they are likely to encounter their own, which bides ill. If player I obtains twice the surplus of II, and II twice the surplus of I, each surplus is zero. However, Hilbe et al. (2013a) showed that extortion strategies can pave the way for the emergence of cooperative strategies, similar to TFT (which, for $\delta =1$, can be regarded as a limiting case of an extortion strategy, Press and Dyson, 2012). This catalytic role of extortion strategies has also been confirmed for games on networks, in which players only interact within a small neighborhood (Szolnoki and Perc, 2014a, 2014b; Wu and Rong, 2014). Overall, these studies confirm that extortionate strategies have problems to succeed within a population. However, if the games are played between members of two distinct populations – for instance, between hosts organisms and their symbionts – then extortion strategies can emerge in whichever population is slower to adapt (Hilbe et al., 2013a). The slower rate of evolution acts as a commitment device. In effect, the slowly evolving organism becomes the Stackelberg leader in a sequential game, in which the slow player learns to adopt extortion strategies, whereas the faster evolving player learns to play the best response, and to cooperate unconditionally (Bergstrom and Lachmann, 2003; Damore and Gore, 2011; Gokhale and Traulsen, 2012).

But even in a one-population setup, certain ZD strategies prove successful: Stewart and Plotkin showed that evolutionary trajectories often visit the vicinity of generous strategies. The dynamics leads ‘from extortion to generosity’ (the title of Stewart and Plotkin, 2013). This is also confirmed, by analytical means based on adaptive dynamics, by Hilbe et al. (2013b). Remarkably, Stewart and Plotkin (2013, 2014) derived a characterization of all memory-one strategies which are robust in an evolutionary sense, for given population size N. This means that the replacement probability, as a resident strategy, is at most $1/N$ (which is the probability to be replaced if the mutant is neutral). In the limit of weak selection, which roughly means that the choice between two strategies is only marginally influenced by payoff (see Nowak et al., 2004), all robust ZD strategies need to be generous (Stewart and Plotkin, 2013). These predictions have also been tested in a recent behavior experiment, in which human subjects played against various computer opponents (Hilbe et al., 2014a). Although extortionate programs outcompeted their human co-players in every game, generous programs received, on average, higher payoffs against the human subjects than extortionate programs. Humans were hesitant to give in to extortion; although unconditional cooperation would have been their best response in all treatments, they only became more cooperative over time if their co-player was generous.

Intriguingly, if a player uses a generous strategy and the co-player does not go along, then the focal player will always shoulder a larger part of the loss (with respect to the mutual cooperation payoff R). Despite their forbearance, generous strategies do very well – which is not the least of the surprises offered by the Iterated Prisoner's Dilemma game.